Analysis of Multi-Objective Optimization of Machining Allowance Distribution and Parameters for Energy Saving Strategy

Abstract

Machining allowance distribution and related parameter optimization of machining processes have been well-discussed. However, for energy saving purposes, the optimization priorities of different machining phases should be different. There are often significant incoherencies between the existing research and real applications. This paper presents an improved method to optimize machining allowance distribution and parameters comprehensively, considering energy-saving strategy and other multi-objectives of different phases. The empirical parametric models of different machining phases were established, with the allowance distribution problem properly addressed. Based on previous analysis work of algorithm performance, non-dominated sorting genetic algorithm II and multi-objective evolutionary algorithm based on decomposition were chosen to obtain Pareto solutions. Algorithm performances were compared based on the efficiency of finding the Pareto fronts. Two case studies of a cylindrical turning and a face milling were carried out. Results demonstrate that the proposed method is effective in trading-off and finding precise application scopes of machining allowances and parameters used in real production. Cutting tool life and surface roughness can be greatly improved for turning. Energy consumption of rough milling can be greatly reduced to around 20% of traditional methods. The optimum algorithm of each case is also recognized. The proposed method can be easily extended to other machining scenarios and can be used as guidance of process planning for meeting various engineering demands.

1. Introduction

Despite the increasing use of low carbon energy sources, fossil fuels remain as the dominant energy sources worldwide [1,2], with their share accounting for 81% in 2008 to 74% in 2035 [3,4]. The rising demand for fossil fuels led to CO₂ emissions rising from 29.3 gigatons (Gt) in 2008 to 35.4 Gt in 2035 [5,6]. Researchers suggested that the widely-used machining processes are responsible for about 84 percent of energy-related CO₂ emissions and 90 percent of the energy consumption in the industrial sector [7,8,9]. Therefore, reasonable planning of the machining process can be effective in improving the energy consumption and carbon emission situation [10]. Energy savings up to 6%–40% can be obtained based on the optimum choice of cutting parameters and machining allowance distribution [11].

While in real production, the optimization focus varies with different phases of the process. During rough machining, the equilibrium between production rate and energy consumption will be the main consideration. However, the quality of the products is the priority during finish machining.

In this research, for the comprehensive optimization of production quality, efficiency and energy-saving, a method to optimize the machining planning strategy of the whole process is presented. Modeling of optimization objectives on each phase was carried out, including steps of theoretical analysis, experiment, and statistical regression. The optimum machining allowance and parameters of different phases were obtained, which is based on the principle of finding Pareto fronts for multi-objective optimization.

Outer cylinder turning and face milling were carried out as case studies. It is revealed that the proposed method is effective in finding the equilibrium between low-carbon manufacturing and production demand fulfillment. The overall flow of this research is shown in Figure 1.

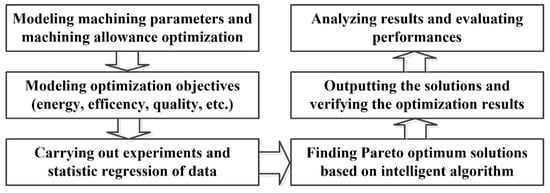
Figure 1. The overall flow of this research.

The remainder of this paper is organized as follows. The literature review is presented in the next section. Detailed discussions of the modeling method for machining allowance distribution and multi-objective optimizations are given in section “Modeling of machining process considering machining allowance distribution”, followed by case studies to verify the proposed method in section “Case studies”. Finally, the conclusion and future research directions are summarized in section “Conclusion and future work”.

2. Literature Review

Reasonable planning of the machining process, which includes optimization of machining parameters and machining allowance distribution, etc., can be effective in improving the energy consumption and carbon emission situation.

Therefore, many researchers have highlighted the optimization of machining parameters. For example, Lv et al. [12] carried out an investigation into methods for predicting material removal energy consumption in turning. Jia et al. [13] established prediction models for feeding power and material drilling power to support sustainable machining. Franco et al. [14] analyzed a parametric model of energy consumption in micro-drilling processes. Sealy [15] proposed a new parametric energy consumption model with high accuracy in precision hard milling for sustainability.

While research of merely modeling or single-objective optimizations has limits in trading-off., machining parameters implicated by sustainability requirements should not give way to deteriorations affecting quality and productivity [16,17].

Therefore, many of the existing works are multi-objective optimization problems (MOP), considering the equilibrium between energy saving and economic objectives. For example, Li et al. [18] carried out selection of optimum parameters in multi-pass face milling for maximum energy efficiency and minimum production cost. Albertelli et al. [19] presented an energy-oriented multi cutting parameter optimization in face milling. Wang et al. [20] carried out multi-objective optimization considering energy consumption, cost, and surface roughness for a turning process. Yan and Li [21] proposed a multi-objective optimization method called RSM in the milling process, which is to evaluate trade-offs between sustainability, production rate, and cutting quality.

However, these studies ignored the fact that, in real production, optimization focus varies in accordance with different phases of processes. The machining allowance distribution of each phase should also be taken into consideration.

Machining allowance is the workpiece provided beyond the finished contours on a prepared component, which is subsequently removed in machining. There are two machining allowances for each of the process phases, which typically include the rough machining and the finish machining. The machining allowance distribution of each phase can be crucial in meeting the demands in real production, and related machining parameter optimization of each phase should also be taken into consideration comprehensively.

However, during the rough machining phase, the machining process mainly focuses on process efficiency in real production. For example, Camposeco-Negrete [22] presented an experimental study to optimize machining time under roughing conditions. On the other hand, however, the finish machining phase mainly focuses on quality demands. For example, Wei et al. [23] carried out a prediction of cutting force of ball-end milling for high efficiency, precision, and equipment utilization. Hanafi et al. [24] determined the optimal setting of machining parameters in terms of minimum surface roughness and cutting power.

These studies barely consider the comprehensive distribution of machining allowance to find the equilibrium of different phases, and the energy consumption issues were ignored or incompletely involved in reducing carbon emission.

For the machining allowance analysis, Zhang et al. [25] proposed a force-measuring-based approach for feed rate optimization considering the machining allowance. Jiang et al. [26] proposed a non-uniform allowance allocation method for NC programming of structural parts.

However, these studies either barely focus on energy consumption, or dwell on the system-level, which implies that the optimization results will have little value in improving the process in detail. Actually, according to our investigation, the existing studies about machining allowance distribution rarely concern process improvement for energy saving so far.

In summary, machining allowance distribution and parameter optimization for energy-saving strategies deserve further study.

3. Modeling of Machining Process Considering Machining Allowance Distribution

In this research, the most commonly used machining processes of cylindrical turning and step milling are used as case studies for deliberating the problem. The analysis of the two kinds can be used as guidance for future applications in other complex scenarios.

3.1. Optimization Focuses During Different Machining Phases

When the total volume to be tooled is fixed, the allowance distribution of different machining phases can be crucial to meet the production demands. Figure 2 shows the machining allowance distribution of a typical cylindrical turning process with rough turning and finish turning. $l_t$ is the total axial length of the workpiece to be tooled. $d_1$ and $d_2$ are the radial distance of the workpiece for rough turning and finish turning, and they are taken as the machining allowances of the two turning phases.

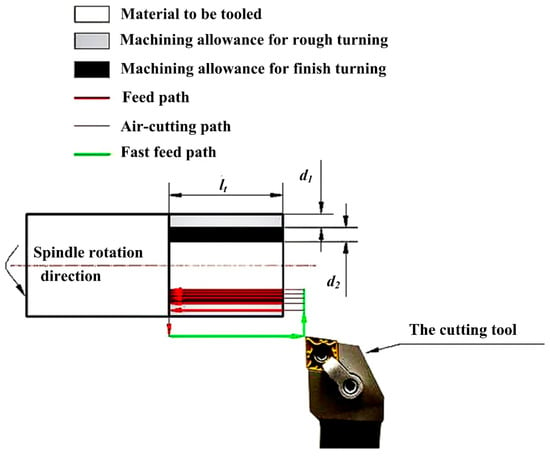
Figure 2. Machining allowance distribution of a cylindrical turning.

Therefore, the total material volume to be tooled in a turning process $V_t$ can be expressed as Equation (1). $R$ is the radius of the original cylindrical workpiece.

$$V_t=l_t·\pi ·\left[R^2-{\left(R-d_1-d_2\right)}^2\right]$$

(1)

During different phases of the turning process, machining parameter groups can be different. During rough turning, the cutting parameters include cutting speed ${\mathrm{v}}_{\mathrm{rt}}\left[\mathrm{m}/\min \right]$, spindle rotation speed ${\mathrm{n}}_{\mathrm{rt}}\left[\mathrm{rpm}\right]$, feed rate ${\mathrm{f}}_{\mathrm{rt}}\left[\mathrm{mm}/\mathrm{rec}\right]$, feed speed ${\mathrm{f}}_{\mathrm{vrt}}\left[\mathrm{mm}/\min \right]$, cutting depth ${\mathrm{a}}_{\mathrm{prt}}\left[\mathrm{mm}\right]$, and during finish turning, those include cutting speed ${\mathrm{v}}_{\mathrm{ft}}\left[\mathrm{m}/\min \right]$, spindle rotation speed ${\mathrm{n}}_{\mathrm{ft}}\left[\mathrm{rpm}\right]$, feed rate ${\mathrm{f}}_{\mathrm{ft}}\left[\mathrm{mm}/\mathrm{r}\right]$, feed speed ${\mathrm{f}}_{\mathrm{vft}}\left[\mathrm{mm}/\min \right]$, cutting depth ${\mathrm{a}}_{\mathrm{pft}}\left[\mathrm{mm}\right]$, respectively.

The optimization focus of these parameters depends on different optimization objectives of each phase. During rough turning, the optimization objectives include reducing energy consumption ${\mathrm{E}}_{\mathrm{rt}}\left[\mathrm{J}\right]$ for low-carbon emission, minimizing feeding time ${\mathrm{t}}_{\mathrm{frt}}\left[\min \right]$ for production efficiency. Besides, because of the relatively big cutting parameters causing damage to cutting tools, the cutting tool life ${\mathrm{TL}}_{\mathrm{rt}}\left[\min \right]$ should also be taken into consideration. On the other hand, the optimization objectives of finish turning phase include reducing energy consumption ${\mathrm{E}}_{\mathrm{ft}}\left[\mathrm{J}\right]$, minimizing feeding time ${\mathrm{t}}_{\mathrm{fft}}\left[\min \right]$ for production efficiency, minimizing surface roughness ${\mathrm{R}}_{\mathrm{at}}\left[\mathsf{\mu }\mathrm{m}\right]$ for quality assurance, and because of the frequently used high-speed cutting during finish turning, the cutting tool life during finish turning ${\mathrm{TL}}_{\mathrm{ft}}\left[\min \right]$ should also be considered.

Similarly, Figure 3 shows the machining allowance distribution of a typical step milling process. ${\mathrm{l}}_{\mathrm{m}}\left[\mathrm{mm}\right]$ is the length of the workpiece to be tooled, $\mathrm{w}\left[\mathrm{mm}\right]$ is the width, ${\mathrm{h}}_1\left[\mathrm{mm}\right]$ and ${\mathrm{h}}_2\left[\mathrm{mm}\right]$ are heights of the workpiece for rough milling and finish milling. Therefore, the total workpiece volume to be tooled in a milling process ${\mathrm{V}}_{\mathrm{m}}$ can be expressed as Equation (2):

$$V_m=l_m·w·\left(h_1+h_2\right)$$

(2)

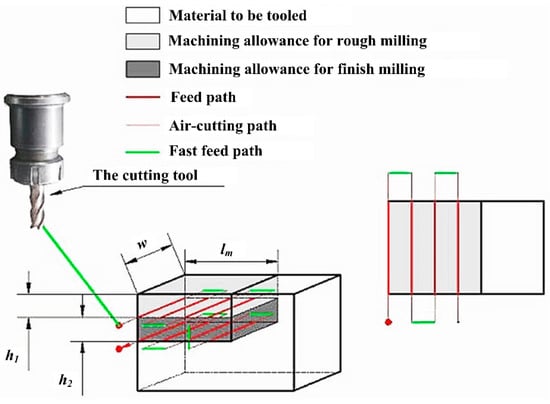
Figure 3. Machining allowance distribution of a step milling.

During rough milling, machining parameters include cutting speed ${\mathrm{v}}_{\mathrm{rm}}\left[\mathrm{m}/\min \right]$, spindle rotation speed ${\mathrm{n}}_{\mathrm{rm}}\left[\mathrm{rpm}\right]$, feed rate ${\mathrm{f}}_{\mathrm{rm}}\left[\mathrm{mm}/\mathrm{rec}\right]$, feed speed ${\mathrm{f}}_{\mathrm{vrm}}\left[\mathrm{mm}/\min \right]$, cutting depth ${\mathrm{a}}_{\mathrm{prm}}\left[\mathrm{mm}\right]$, cutting width ${\mathrm{a}}_{\mathrm{erm}}\left[\mathrm{mm}\right]$, and for finish milling, those include cutting speed ${\mathrm{v}}_{\mathrm{fm}}\left[\mathrm{m}/\min \right]$, spindle rotation speed ${\mathrm{n}}_{\mathrm{rm}}\left[\mathrm{rpm}\right]$, feed rate ${\mathrm{f}}_{\mathrm{fm}}\left[\mathrm{mm}/\mathrm{rec}\right]$, feed speed ${\mathrm{f}}_{\mathrm{vrm}}\left[\mathrm{mm}/\min \right]$, cutting depth ${\mathrm{a}}_{\mathrm{pfm}}\left[\mathrm{mm}\right]$, and cutting width ${\mathrm{a}}_{\mathrm{efm}}\left[\mathrm{mm}\right]$.

Similarly, the optimization objectives of rough milling include reducing energy consumption ${\mathrm{E}}_{\mathrm{rm}}\left[\mathrm{J}\right]$ for low-carbon emission, minimizing cutting time ${\mathrm{t}}_{\mathrm{frm}}\left[\min \right]$ for production efficiency, and extending cutting tool life ${\mathrm{TL}}_{\mathrm{rm}}\left[\min \right]$, and for finish turning, those include reducing energy consumption ${\mathrm{E}}_{\mathrm{fm}}\left[\mathrm{J}\right]$, minimizing cutting time ${\mathrm{t}}_{\mathrm{ffm}}\left[\min \right]$, minimizing surface roughness ${\mathrm{R}}_{\mathrm{am}}\left[\mathsf{\mu }\mathrm{m}\right]$ for quality assurance, and extending cutting tool life during finish turning ${\mathrm{TL}}_{\mathrm{fm}}\left[\min \right]$.

The information about cutting parameters, optimization objectives and machining allowance distribution for both turning and milling processes are listed in Table 1 as follows.

Table 1. Cutting parameters, optimization objectives and machining allowances.

Machining Type	Turning Process		Milling Process
Machining phases	Rough turning	Finish turning	Rough milling	Finish milling
Machining parameters	Cutting speed vrt Spindle speed nrt Feed speed fvrt Feed rate frt Cutting depth aprt	Cutting speed vft Spindle speed nft Feed speed fvft Feed rate fft Cutting depth apft	Cutting speed vrm Spindle speed nrt Feed speed fvrm Feed rate frm Cutting depth aprm Cutting width aerm	Cutting speed vfm Spindle speed nft Feed speed fvfm Feed rate ffm Cutting depth apfm Cutting width aefm
Optimization objectives	Energy consumption Ert Cutting time trt Cutting tool life TLrt	Energy consumption Eft Cutting time tft Surface roughness RatCutting tool life TLft	Energy consumption Erm Cutting time trm Cutting tool life TLrm	Energy Efm Cutting time tfm Surface roughness RamCutting tool life TLfm
Machining allowance	Radial distance for rough turning d1	Radial distance for finish turning d2	Height of the workpiece for rough milling h1	Height of the workpiece for finish milling h2

3.2. Modeling of Relation between Cutting Parameters and Optimization Objectives

3.2.1. Modeling of Energy Consumption During Machining Process

According to our previous work [27,28], the energy consumption objective $E_o$ during a machining process with a fixed group of machining parameters can be approximately expressed as Equation (3). $t_f$ is the lasting time of feed movement, $t_c$ is the lasting time of cutting materials. Figure 4 shows the power profile of a typical milling process:

$$E_o=\left(P_b+P_s+P_r+P_f\right)t_f+P_c{t}_c.$$

(3)

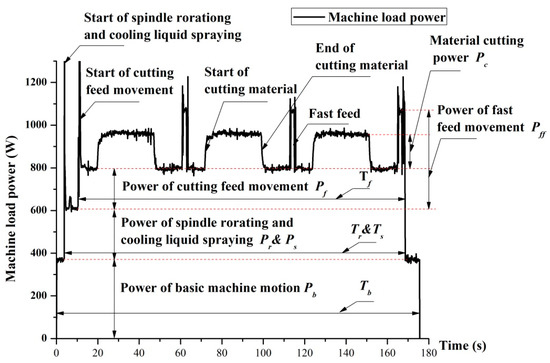
Figure 4. Power profile of a typical milling process [28].

By carrying out experiments, the values of basic machine motion power $P_b$ and fluid spraying power $P_s$ can be directly measured [27]. The selection of parameters, set-up, data acquisition, and analysis methods of the experiments can be found in our previous work [29,30], and Figure 5 shows the diagram of the experimental set-up.

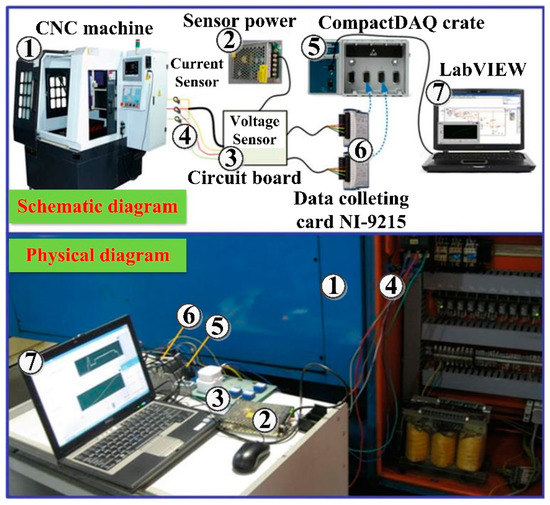
Figure 5. Diagram of experimental set-up [32].

There is a piecewise relation between the spindle rotation power ${\mathrm{P}}_{\mathrm{r}}$ and spindle speed $\mathrm{n}\left[\mathrm{r}/\min \right]$. This can be expressed as a piecewise function as Equation (4), where ${\mathrm{C}}_{\mathrm{rA}1}$,${\mathrm{C}}_{\mathrm{rA}2}$,$C_{rB1}$,$C_{rB2}$,$C_{rC1}$,$C_{rC2}$ are the coefficients of the three linear functions. $n_M^{BA}$ and $n_M^l$ are the turning points of this function, which has three sections according to [31]. The values of these coefficients can be obtained by power measurement and linear regression of the obtained data.

$$P_r=\{\begin{array}{c}{C}_{rA1}n+C_{rA2}\hspace{1em}(n<n_M^{BA})\\ C_{rB1}n+C_{rB2}\hspace{1em}(n_M^{BA}<n<n_M^l)\\ C_{rC1}n+C_{rC2}\hspace{1em}(n>n_M^{BA})\end{array}$$

(4)

The feed power ${\mathrm{P}}_{\mathrm{f}}$ can be expressed as Equation (5) [29], where feed speed ${\mathrm{f}}_{\mathrm{vt}}$ is with the unit of$\left[\mathrm{mm}/\min \right]$. The values of the two constants can be obtained by experimental power measurements and quadratic regression like our previous work [27].

$$P_f=C_{f1}\times f_v+C_{f2}\times f_v^2.$$

(5)

Material removal power${\mathrm{P}}_{\mathrm{c}}$ for a turning process ${\mathrm{P}}_{\mathrm{ct}}$ can be expressed as a function of cutting speed $v_t$, feed rate $f_t$ and cutting depth$a_{pt}$ as Equation (6) shows. $C_{ct},C_{vct},C_{fct},C_{apct}$ represent the coefficients of the function.

$$P_{ct}=C_{ct}·v_t^{C_{vct}}·{f_t}^{C_{fct}}·{a_{pt}}^{C_{apct}}$$

(6)

Similarly, material removal power for a milling process$P_{cm}$ can be expressed as a function of rotation speed $n_m$ or cutting speed$v_m$, feed speed $f_{vm}$, cutting depth $a_{pm}$ and cutting width$a_{em}$, which is shown as Equation (7). $C_{cm},C_{ncm},C_{fcm},C_{apcm},C_{aecm}$ represent the coefficients, respectively.

$$P_{cm}=C_{cm}·n_m^{C_{ncm}}·{f_{vm}}^{C_{fcm}}·{a_{pm}}^{C_{apcm}}·{a_{em}}^{C_{aecm}}$$

(7)

To get all these constants in the two equations, the Taguchi experimental design method was introduced to obtain the values of $P_c$ like [30].

3.2.2. Modeling of Machining Time

The feed time $t_f$is often used as the machining efficiency objective $t_o$ [27].

For a turning process with a fixed group of the three machining parameters, feed time $t_{ft}\left[\min \right]$ can be expressed as Equation (8). $f_{vti}$ is feed speed of the ith cutting [mm/min], ${\mathrm{L}}_{\mathrm{st}}$ is the length of feed path for one single cutting $\left[\mathrm{mm}\right]$, $N_t$ is the feed times needed to cut the whole volume to be tooled.

$$t_{ft}={\displaystyle \sum }_{i=1}^{N_t}\frac{L_{st}}{f_{vti}}$$

(8)

Feed speed of the ith cutting $f_{vti}$ can be calculated by using Equation (9), where $n_i$ is the spindle rotation speed of the ith cutting [r/min].

$$f_{vti}=f_t·n_i=\frac{1000v_t·f_t·\left[r\right]}{\pi \left[2R-a_{pt}\left(i-1\right)\right]}$$

(9)

The feed times needed to cut the whole volume to be tooled $N_t$ can be obtained by using Equation (10), where $d$ is the total radial distance of the workpiece to be tooled in $\left[\mathrm{mm}\right]$.

$$N_t=\frac{d}{a_{pt}}$$

(10)

By introducing Equations (9) and (10) into Equation (8), feed time $t_{ft}\left[\min \right]$ for a turning process with a fixed group of the three machining parameters can be expressed as Equation (11).

$$t_{ft}=\frac{\pi L_{st}\left[4Rd-d^2+a_{pt}·d\right]}{2000v_t·f_t·a_{pt}·\left[r\right]}$$

(11)

For the milling process, feed time $t_{fm}\left[\min \right]$ can be expressed as Equation (12), where $L_{sm}$ is the length of a single cutting path$\left[\mathrm{mm}\right],D_T$ is the diameter of the cutting tool$\left[\mathrm{mm}\right],h$ is the total height of the workpiece to be tooled [27].

$$t_{fm}=\frac{\pi ·L_{sm}·D_T·l_m·h}{1000v_m·f_m·a_{pm}·a_{em}\left[r\right]}$$

(12)

The material cutting time $t_c\left[min\right]$ is determined by the cutting volume $V\left[{\mathrm{mm}}^3\right]$ and material removal rate$MRR\left[{\mathrm{mm}}^3/\min \right]$, which is expressed as Equation (13):

$$t_c=\frac{V}{MRR}$$

(13)

The value of MRR depends on the machining type and for the turning process, $MR{R}_t$ can be expressed as Equation (14) [33].

$$MR{R}_t=1000v_t·f_t·a_{pt}·\left[r\right]$$

(14)

By introducing Equation (14) into Equation (13), the material cutting time of a turning process $t_{ct}\left[\min \right]$ can be expressed as Equation (15).

$$t_{ct}=\frac{V_t}{1000v_t·f_t·a_{pt}·\left[r\right]}$$

(15)

For the milling process, $MR{R}_m$ can be expressed as Equation (16) [33].

$$MR{R}_m=\frac{1000v_m·f_m·a_{pm}·a_{em}·\left[r\right]}{\pi ·D_T}$$

(16)

From Equations (15) and (16), the material cutting time of a milling process $t_{cm}\left[\min \right]$ can be expressed as Equation (18):

$$t_{cm}=\frac{\pi ·D_T·V_m}{1000v_m·f_m·a_{pm}·a_{em}·\left[r\right]}$$

(17)

3.2.3. Modeling of Surface Roughness from Machining Process

According to Manupati [34] and Grote and Antonsson [35], with fixed machine and cutting tool, the surface roughness of workpieces after the turning process can be estimated, and the corner radius of the cutting tool must be considered.

If the corner radius $r_{\epsilon }$ is very small, surface roughness $R_{at}\left[\mathsf{\mu }\mathrm{m}\right]$ can be calculated by using Equation (18), where ${\kappa }_r$ is main cutting edge angle, ${\kappa }_r^{\prime }$ is a secondary cutting edge angle.

$$R_{at}=\frac{f_t}{cot{\kappa }_r+cot{\kappa }_r^{\prime }}$$

(18)

If the corner radius $r_{\epsilon }$ is relatively large and feed rate is relatively small, $R_{at}$ can be calculated by using Equation (19):

$$R_{at}=\frac{f_t^2}{8r_{\epsilon }}(0<f_t\le 1.25mm/r)$$

(19)

If the corner radius is small and the feed rate is relatively large, $R_{at}$ is calculated by Equation (20):

$$R_{at}=\frac{f_t-r_{\epsilon }\left(tan\frac{{\kappa }_r}{2}+tan\frac{{\kappa }_r^{\prime }}{2}\right)}{cot{\kappa }_r+cot{\kappa }_r^{\prime }}(f_t>1.25mm/r)$$

(20)

For the milling process respectively, with fixed machine, cutting tool and workpiece, it is assumed that surface roughness of workpieces after the milling process $R_{am}\left[\mathsf{\mu }\mathrm{m}\right]$ can be estimated by using Equation (21), where $C_{Ram},C_{Ravm},C_{Rafm},$ $C_{Raapm}$, $C_{Raaem}$ are the coefficients of the equation. The values of them can be obtained by orthogonal experiments and statistical regression according to Sun et al. [36].

$$R_{am}=C_{Ram}·v_m^{C_{Ravm}}·f_m^{C_{Rafm}}·a_{pm}^{C_{Raapm}}·a_{em}^{C_{Raaem}}$$

(21)

3.2.4. Modeling of Cutting Tool Life

For the turning process, the cutting tool life can be expressed as Equation (22), with the form of Taylor’s equations according to Armarego and Brown [37], where $C_{TLt},C_{TLtv},C_{TLtf},C_{TLtap}$ are the coefficients of these equations. Those values can be obtained based on the type of cutting tool and material.

$$T{L}_t=\frac{C_{TLt}}{v_t^{C_{TLtv}}{f}_t^{C_{TLtf}}{a}_{pt}^{C_{TLtap}}}$$

(22)

Similarly, for the milling process, the tool life during rough milling and finish milling can be expressed as Equation (23) according to Armarego and Brown [37] or Wu and Zhou [38].

$$T{L}_m=\frac{C_{TLm}}{v_m^{C_{TLmv}}{f}_m^{C_{TLmf}}{a}_{pm}^{C_{TLmap}}{a}_{em}^{C_{TLmae}}}$$

(23)

4. Machining Parameter Optimization and Machining Allowance Distribution Based on Modeling Results and PARETO Fronts Method

The machining allowance distribution heavily depends on cutting parameter optimization of different machining phases. Therefore, the above modeling results can be used to find the optimum machining allowance distribution and machining parameters.

According to our previous work [27], finding the Pareto fronts, namely none-determined solution sets of MOPs, is an effective approach to describe the characteristics of the multi-objective solution space. By carrying out the solving process, either the none-determined solutions prior to one single objective or those prior to the overall trade-off can be effectively found simultaneously. And the performance of a certain intelligent algorithm is mainly determined by its efficiency to find the Pareto fronts.

Based on the conclusions of related research [20,39] and our work [27], non-dominated sorting genetic algorithm II (NSGA-II) and multi-objective evolutionary algorithm based on decomposition (MOEA/D) are widely used intelligent algorithms based on GA. The two algorithms have shown great abilities in solving similar engineering problems. Therefore, the optimization algorithm applied in this study is NSGA-II and MOEA/D. To determine the most optimum algorithm for each specific scenario, the average solving time, and the number of effectively found Pareto solutions of the two are compared.

4.1. Determining Rules and Parameters of Basic Genetic Algorithm, NSGA-II and MOEA/D

The coding and decoding rules of chromosome are used for preparation. The basic genetic algorithm parameters include initial population $M$, gap between two generations$G$, crossover rate$R_c$, mutation rate$R_m$ and maximum evolution generations$N$. For more details about the parameters of the basic genetic algorithm, please check our previous work [27]. The preset values of the operating parameters of GA are listed in Table 2.

Table 2. Operating parameters of GA.

Operating Parameters	Remarks	Values
$M$	Size of the initial population	500
$G$	Gap between parents and children	0.9
$R_c$	Crossover rate	0.7
$R_m$	Mutation rate	0.7/Lind
$N$	The maximum evolution generations	300

The basic principles of NSGA-II and MOEA/D are applied accordingly [40,41]. Specifically, for NSGA-II, tournament selection is chosen as the selection policy, and the tournament size $S_{tour}$ is set as 5. For MOEA/D, the neighbor size $S_{nei}$ is set as 30. The decomposition method is the Tchebycheff approach.

4.2. Normalized Expression of Multi-Objective Problems Using Modeling Results

The normalization is realized using Equation (24), where $f_i\left(X\right)$ represents one of the sub-objective functions, $f_i^{\prime }\left(X\right)$ is the one after normalization, $X$ represents the variables, $D$ is the value range of $X$. The maximum and minimum values of $f_i\left(X\right)$ can be acquired by using the basic GA process.

$$f_i^{\prime }\left(X\right)=\frac{f_i\left(X\right)-max\left(f_i\left(X\right)\right)}{max\left(f_i\left(X\right)\right)-min\left(f_i\left(X\right)\right)}\hspace{1em}X\in D$$

(24)

Therefore, by introducing the modeling results above, namely Equation (3), Equation (11), Equations (19)–(22), into Equation (24), the machining allowance distribution with MOP of the machining parameters for a cylindrical turning process are expressed from Equation (25) to Equation (30), where $E_{rt}^{\prime }$, $t_t^{\prime }$, $T{L}_{rt}^{\prime }$, $E_{ft}^{\prime }$, $R_{at}^{\prime }$, $T{L}_{ft}^{\prime }$ are the normalized objective values to be optimized during the rough turning or the finishing turning phases.

For rough turning phase:

$$OBJ1=Min\left[E_{rt}^{\prime }\left(v_{rt},f_{rt},a_{prt},d_1\right)\right]$$

(25)

$$OBJ2=Min\left[\frac{1}{T{L}_{rt}^{\prime }\left(v_{rt},f_{rt},a_{prt},d_1\right)}\right]$$

(26)

For finish turning phase:

$$OBJ3=Min\left[E_{ft}^{\prime }\left(v_{ft},f_{ft},a_{pft},d_2\right)\right]$$

(27)

$$OBJ4=Min\left[R_{at}^{\prime }\left(f_{ft}\right)\right]$$

(28)

$$OBJ5=Min\left[\frac{1}{T{L}_{ft}^{\prime }\left(v_{ft},f_{ft},a_{pft},d_2\right)}\right]$$

(29)

For the overall efficiency:

$$\{\begin{array}{c}OBJ6=Min\left(t_t^{\prime }\right)\\ t_t^{\prime }={\left[t_{frt}\left(v_{rt},f_{rt},a_{prt},d_1\right)+t_{fft}\left(v_{ft},f_{ft},a_{pft},d_2\right)\right]}^{\prime }\end{array}$$

(30)

Equations (25)–(30) are all subject to constrains expressed by Equation (31), where $n_{tMax}$, $v_{tMax}$, $f_{tMax}$ and $a_{ptMax}$ are the maximum values of the parameters the turning machine can bear. $d$ is the total distance machining allowance of the part to be tooled, and it is determined by the design scheme.

$$st:constrains=\{\begin{array}{c}{n}_{rt},n_{ft}\in \left[0,n_{tMax}\right]\\ v_{rt},v_{ft}\in \left[0,v_{tMax}\right]\\ f_{rt},f_{ft}\in \left[0,f_{tMax}\right]\\ a_{prt},a_{pft}\in \left[0,a_{ptMax}\right]\\ d_1+d_2=d\end{array}$$

(31)

Similarly, the MOP of a face milling process are expressed from Equation (32) to Equation (37).

For rough milling phase:

$$OBJ1=Min\left[E_{rm}^{\prime }\left(v_{rm},f_{rm},a_{prm},a_{erm},h_1\right)\right]$$

(32)

$$OBJ2=Min\left[\frac{1}{T{L}_{rm}^{\prime }\left(v_{rm},f_{rm},a_{prm},a_{erm},h_1\right)}\right]$$

(33)

For finish milling phase:

$$OBJ3=Min\left[E_{fm}^{\prime }\left(v_{fm},f_{fm},a_{pfm},a_{efm},h_2\right)\right]$$

(34)

$$OBJ4=Min\left[R_{am}^{\prime }\left(v_{fm},f_{fm},a_{pfm},a_{efm},h_2\right)\right]$$

(35)

$$OBJ5=Min\left[\frac{1}{T{L}_{fm}^{\prime }\left(v_{fm},f_{fm},a_{pfm},a_{efm},h_2\right)}\right]$$

(36)

For the overall efficiency:

$$\{\begin{array}{c}OBJ6=Min\left(t_{rm}^{\prime }\right)\\ t_{rm}^{\prime }={\left[t_{frm}\left(v_{rm},f_{rm},a_{prm},a_{erm},h_1\right)+t_{ffm}\left(v_{fm},f_{fm},a_{pfm},a_{efm},h_2\right)\right]}^{\prime }\end{array}$$

(37)

The constrains are expressed by Equation (38), where $v_{mMax}$, $f_{mMax}$, $a_{pmMax}$ and $a_{emMax}$ are the maximum values of the parameters, $h$ is the total distance machining allowance.

$$st:constrains=\{\begin{array}{c}{v}_{rm},v_{fm}\in \left[0,v_{mMax}\right]\\ f_{rm},f_{fm}\in \left[0,f_{mMax}\right]\\ a_{prm},a_{pfm}\in \left[0,a_{pmMax}\right]\\ a_{erm},a_{efm}\in \left[0,a_{emMax}\right]\\ h_1+h_2=h\end{array}$$

(38)

4.3. Performance Evaluation Indicators of Intelligent Algorithms

The algorithms to be compared and selected are NSGA-II and MOEA/D, and the main consideration is the solving efficiency, which is determined by two aspects. One is the average operating time for a certain number of repeats of solving. This indicator is calculated by using Equation (39), where $I_t$ in $\left[\mathrm{s}\right]$ is the average operation time, $n_I$ is the number of repeats, and $t_i$ in $\left[\mathrm{s}\right]$ is the lasting time of a single operation. Therefore, $I_t$ can be regarded as an indicator to evaluate the solving speed.

$$I_t=\frac{{{\displaystyle \sum }}_{i=1}^{n_I}{t}_i}{n_I}$$

(39)

Another key aspect is the number of effective Pareto solutions found eventually. That is represented by the symbol of $I_n$. By carrying out the $n_I$ repeats, all of the Pareto solutions are gathered, and those suitable for application are picked out to get the final value of $I_n$. $I_n$ can be regarded as the indicator to evaluate the efficiency of finding Pareto solutions.

In addition, the value of $n_I$ can be set depending on circumstances, and all of the solving experiments are carried out by using MATLAB.

5. Case Studies

5.1. Case 1: A Cylindrical Turning Process

The first case is a cylindrical turning process carried out on a CK6153i lathe cutting C45E4 carbon steel, using VNMG160408-YBC351. Figure 6 shows the real scene of the cylindrical turning process. Table 3 shows the geometrical parameters of the cutting tool.

Figure 6. A case of cylindrical turning process.

Table 3. Geometrical parameters of VNMG160408-YBC351 cutting tool.

$\mathrm{Clearance}\mathrm{angle}{\alpha }_o$	$7^{°}$
Main cutting edge angle ${\kappa }_r$	${93}^{°}$
Secondary cutting edge angle ${\kappa }_r^{\prime }$	${52}^{°}$
Corner radius $r_{\epsilon }$	0.8 mm

5.1.1. Modeling Results of Energy Consumption of the Cylindrical Turning

The power modeling results of basic machine movement $P_{bt}$ and spraying cooling fluid $P_{st}$ can be obtained by direct experiment measurement. The results are $P_{bt}=3320W$ and $P_{st}=3740W$ according to the experiment data.

The spindle rotation power $P_{rt}\left[\mathrm{W}\right]$ has a piecewise function with the spindle rotation speed $n_t\left[\mathrm{r}/\min \right]$, a machining parameter. This can be expressed as a piecewise function according to Equation (4). To obtain the coefficients in the piecewise function, $P_{rt}$ was measured when $n_t$ ranges from 0 to 1500 rpm with the increment of 100 rpm, and all these coefficients could be obtained by statistical regression. The results are shown as Equation (40).

$${\mathrm{P}}_{\mathrm{rt}}=\{\begin{array}{c}1.120{\mathrm{n}}_{\mathrm{t}}+44.320\hspace{1em}(0\mathrm{rpm}<{\mathrm{n}}_{\mathrm{t}}\le 1000\mathrm{rpm})\\ 0.560{\mathrm{n}}_{\mathrm{t}}+608.500\hspace{1em}(1000\mathrm{rpm}<{\mathrm{n}}_{\mathrm{t}}\le 1300\mathrm{rpm})\\ 1.289{\mathrm{n}}_{\mathrm{t}}-360.540\hspace{1em}(1300\mathrm{rpm}<{\mathrm{n}}_{\mathrm{t}}\le 1500\mathrm{rpm})\end{array}$$

(40)

The feed power $P_{ft}\left[W\right]$ can be expressed as a quadratic function of feed speed $f_{vt}$ according to Equation (5). The values of the two constants can be obtained by experimental power measurements and quadratic regression. Therefore, $P_{ft}$ was measured when $f_{vt}$ ranges from 0 to 2000 mm/min with an increment of 200 rpm, and the two constants in Equation (5) can be obtained by quadratic regression. The result is shown as Equation (41).

$$P_{ft}=0.0135f_{vt}+5\times {10}^{-6}{f}_{vt}^2.$$

(41)

The material cutting power $P_{ct}\left[W\right]$ can be expressed as an index function according to Equation (6), and all these coefficients can be obtained using Taguchi experiments and statistical regression like our previous work by Lv et al. [29].

As presented in Table 4, four levels of cutting speed $v_t$, feed rate $f_t$ and cutting depth $a_{pt}$ were selected from the tool manufacturers’ recommendation. The design matrix for turning experiments is shown in Table 5. The regression result is expressed as Equation (42).

$$P_{ct}=44.60v_t^{0.910}{f}_t^{0.658}{a}_{pt}^{0.918}$$

(42)

Table 4. Taguchi experiment levels of turning parameters.

Turning Parameters	Level 1	Level 2	Level 3	Level 4
Cutting speed $v_t\left[\mathrm{m}/\min \right]$	50	100	150	200
Feed rate $f_t\left[\mathrm{mm}/\mathrm{r}\right]$	0.05	0.1	0.15	0.2
Cutting depth $a_{pt}\left[\mathrm{mm}\right]$	0.5	1	1.5	2

Table 5. Parameter design matrix of turning experiments.

Experiment Order	Turning Parameters
	Cutting Speed ${\mathit{v}}_{\mathit{t}}\left[\mathit{m}/\mathit{m}\mathit{i}\mathit{n}\right]$	Feed Rate ${\mathit{f}}_{\mathit{t}}\left[\mathit{m}\mathit{m}/\mathit{r}\right]$	Cutting Depth ${\mathit{a}}_{\mathit{p}\mathit{t}}\left[\mathit{m}\mathit{m}\right]$
1	50	0.05	0.5
2	50	0.1	1
3	50	0.15	1.5
4	50	0.2	2
5	100	0.05	1
6	100	0.1	0.5
7	100	0.15	2
8	100	0.2	1.5
9	150	0.05	1.5
10	150	0.1	2
11	150	0.15	0.5
12	150	0.2	1
13	200	0.05	2
14	200	0.1	1.5
15	200	0.15	1
16	200	0.2	0.5

For this specific cylindrical turning process, we selected a cylindrical workpiece with the radius$R=50\mathrm{mm}$, the axial length of the workpiece to be tooled $l_t$ was 100 mm, the radial distance to be tooled $d=25\mathrm{mm}$ and the length of a single feed path $L_{st}$ was set to be 110 mm to avoid collisions. Therefore, by introducing all this size information into Equation (11), the feed time of rough turning $t_{frt}\left[\min \right]$ and finish turning $t_{fft}\left[\min \right]$ can be expressed as Equations (43) and (44).

$$t_{frt}=\frac{11\pi \left[200d_1-d_1^2+a_{prt}·d_1\right]}{200v_{rt}·f_{rt}·a_{prt}}$$

(43)

$$t_{fft}=\frac{11\pi \left[4\times \left(50-d_1\right)d_2-d_2^2+a_{pft}·d_2\right]}{200v_{ft}·f_{ft}·a_{pft}}$$

(44)

By introducing these size information into Equation (15), the cutting time of rough turning $t_{crt}\left[\min \right]$ and finish turning $t_{cft}\left[\min \right]$ can be expressed as Equations (45) and (46).

$$t_{crt}=\frac{\pi \left(100d_1-d_1^2\right)}{10v_{rt}·f_{rt}·a_{prt}}$$

(45)

$$t_{cft}=\frac{\pi \left(100-2d_1-d_2\right)d_2}{10v_{ft}·f_{ft}·a_{pft}}$$

(46)

where machining allowance of the two phases should confine to Equation (47):

$$d_1+d_2=d=25mm$$

(47)

Table 2 shows the geometrical parameters of the cutting tool. Therefore, by introducing all these parameters into Equations (19) and (20), the surface roughness after this turning process $R_{at}\left[\mathsf{\mu }\mathrm{m}\right]$ can be expressed as Equation (48) or Equation (49):

$$R_{at}=\frac{f_t^2}{6.400}(0<f_t\le 1.250mm/r)$$

(48)

$$R_{at}=\frac{f_t-1.233}{0.746}(f_t>1.250mm/r)$$

(49)

According to Equation (23), the cutting tool life during rough turning $T{L}_{rt}\left[\min \right]$ and finish turning $T{L}_{ft}\left[\min \right]$ can be approximately estimated using Equation (50) by looking through Armarego and Brown [37] based on the information about the cutting tool and the material.

$$T{L}_t\approx \frac{{6.100}^{11}}{v_t^5{f}_t^{1.750}{a}_{pt}^{0.750}}$$

(50)

Therefore, for rough turning process, the energy objective $E_{rt}\left[\mathrm{J}\right]$ can be expressed as Equation (51) according to Equation (3):

$$E_{rt}=\left(P_{bt}+P_{st}+P_{ft}+P_{rt}\right)t_{frt}+P_{ct}·t_{crt}$$

(51)

Furthermore, by introducing all these modeling results and case information into Equation (51), $E_{rt}$ can be expressed as Equation (52):

$$\begin{gathered} E_{rt}=\left[7060+0.0135f_{vrt}+5\times {10}^{-6}{f}_{vrt}^2+P_{rt}\left(n_{rt}\right)\right]\times \frac{11\pi \left[200d_1-d_1^2+a_{prt}·d_1\right]}{200v_{rt}·f_{rt}·a_{prt}} \\ +44.60v_{rt}^{0.910}{f}_{rt}^{0.658}{a}_{prt}^{0.918}·\frac{\pi \left(100d_1-d_1^2\right)}{10v_{rt}·f_{rt}·a_{prt}} \end{gathered}$$

(52)

Because of the near-to-linear relation as Equation (9) shows, the feed speed of the rough turning process $f_{vrt}$ and spindle rotation speed $n_{rt}$ in Equation (52) were assumed to be their average, and they can be calculated by using Equations (53) and (54).

$$f_{vrt}=\frac{1000f_{rt}{v}_{rt}}{\pi \left(2R-d_1\right)}=\frac{1000f_{rt}{v}_{rt}}{\pi \left(100-d_1\right)}$$

(53)

$$n_{rt}=\frac{1000v_{rt}}{\pi \left(2R-d_1\right)}=\frac{1000v_{rt}}{\pi \left(100-d_1\right)}$$

(54)

The tool life during rough turning $T{L}_{rt}$ can be expressed as Equation (55):

$$T{L}_{rt}\approx \frac{{6.100}^{11}}{v_{rt}^5{f}_{rt}^{1.750}{a}_{prt}^{0.750}}$$

(55)

Similarly, for finish turning process, by introducing all these modeling results and case information into Equation (3), the energy objective $E_{ft}\left[\mathrm{J}\right]$ can be expressed as Equation (56):

$$\begin{array}{ll}& E_{ft}=\left[7060+0.0135f_{vft}+5\times {10}^{-6}{f}_{vft}^2+P_{rt}\left(n_{ft}\right)\right]\\ \times & \frac{11\pi \left[4\times \left(50-d_1\right)d_2-d_2^2+a_{pft}·d_2\right]}{200v_{ft}·f_{ft}·a_{pft}}+44.600v_{ft}^{0.910}{f}_{ft}^{0.658}{a}_{pft}^{0.918}\\ ·& \frac{\pi \left(100-2d_1-d_2\right)d_2}{10v_{ft}·f_{ft}·a_{pft}}\end{array}$$

(56)

In Equation (56), the feed speed of finish turning process $f_{vft}$ and spindle rotation speed $n_{ft}$ were assumed to be their average, and they can be calculated by using Equations (57) and (58).

$$f_{vft}=\frac{1000f_{ft}{v}_{ft}}{\pi \left(100-2d_1-d_2\right)}=\frac{1000f_{ft}{v}_{ft}}{\pi \left(50+d_2\right)}$$

(57)

$$n_{ft}=\frac{1000v_{ft}}{\pi \left(100-2d_1-d_2\right)}=\frac{1000v_{ft}}{\pi \left(50+d_2\right)}$$

(58)

According to Equation (48) or Equation (49), the surface roughness objective for this turning process $R_{aot}$ can be expressed as Equation (59) or Equation (60):

$$R_{at}=\frac{f_{ft}^2}{6.400}(0<f_{ft}\le 1.250mm/r)$$

(59)

$$R_{at}=\frac{f_{ft}-1.233}{0.746}(f_{ft}>1.250mm/r)$$

(60)

The tool life during finish turning $T{L}_{ft}\left[\min \right]$ can be expressed as Equation (61):

$$T{L}_{ft}\approx \frac{{6.100}^{11}}{v_{ft}^5{f}_{ft}^{1.750}{a}_{pft}^{0.750}}$$

(61)

The cutting time objective $t_{ot}\left[\min \right]$ can be expressed as Equation (62):

$$t_t=\frac{11\pi \left[200d_1-d_1^2+a_{prt}·d_1\right]}{200v_{rt}·f_{rt}·a_{prt}}+\frac{11\pi \left[4\times \left(50-d_1\right)d_2-d_2^2+a_{pft}·d_2\right]}{200v_{ft}·f_{ft}·a_{pft}}$$

(62)

Based on machine conditions and engineering experiences, all of the above machining parameters were subject to constrain, as Table 6 shows. The accuracy of the machining parameters and allowance to meet the demands were listed as follows: 10 rpm for$n_t$, 0.1 mm/r for$f_t$, 0.1 mm for$a_{pt}$, 0.1 mm for $d_1$ and $d_2$.

Table 6. Constrains of machining parameters for this turning process.

Machining Parameters	Constrains
Cutting speed $v_t$	$0\mathrm{m}/\min \le {\mathrm{v}}_{\mathrm{t}}\le 200\mathrm{m}/\min$
Rotation speed $n_t$	$100\mathrm{r}/\min \le {\mathrm{n}}_{\mathrm{t}}\le 1500\mathrm{r}/\min$
Feed rate $f_t$	$0.1\mathrm{mm}/\mathrm{r}\le {\mathrm{f}}_{\mathrm{t}}\le 2\mathrm{mm}/\mathrm{r}$
Cutting depth $a_{pt}$	$0.1\mathrm{mm}\le {\mathrm{a}}_{\mathrm{pt}}\le 5\mathrm{mm}$

5.1.2. Normalized MOP Expression of the Objective Cylindrical Turning

By introducing all the modeling results and constrains into equations from Equation (25) to Equation (30), the machining allowance distribution with MOP of the machining parameters for this cylindrical turning process are expressed as equations from Equation (63) to Equation (68):

For rough turning phase:

$$OBJ1=Min\left(E_{rt}^{\prime }\right)$$

(63)

$$OBJ2=Min\left(\frac{1}{T{L}_{rt}^{\prime }}\right)$$

(64)

For finish turning phase:

$$OBJ3=Min\left(E_{ft}^{\prime }\right)$$

(65)

$$OBJ4=Min\left(R_{at}^{\prime }\right)$$

(66)

$$OBJ5=Min\left(\frac{1}{T{L}_{ft}^{\prime }}\right)$$

(67)

For the processing efficiency:

$$OBJ6=Min\left(t_t^{\prime }\right)$$

(68)

Following Equation (31), the constraints of this case scenario are $n_{tMax}=800\mathrm{r}/\min$, $v_{tMax}=200\mathrm{m}/\min$, $f_{tMax}=2\mathrm{mm}/\mathrm{r}$, $a_{ptMax}=5\mathrm{mm}$, so the objective functions from Equation (63) to Equation (68) are subject to the constrain as Equation (69) shows:

$$st:constrains=\{\begin{array}{c}{n}_{rt},n_{ft}\in \left[100,1500\right]\\ v_{rt},v_{ft}\in \left[0,200\right]\\ f_{rt},f_{ft}\in \left[0.1,2\right]\\ a_{prt},a_{pft}\in \left[0.1,5\right]\\ d_1+d_2=25\end{array}$$

(69)

The basic GA algorithm was used to get the value ranges of each sub-objective function subject to all the constraints, and the results are listed in Table 7. The minimum and the maximum values can be used to calculate the normalized values of individuals, as Equation (24) shows, and backwards as equal.

Table 7. Calculation results of value ranges of sub-object functions.

Objectives (st: Constrains)	${\mathit{E}}_{\mathit{r}\mathit{t}}$	$1/\mathit{T}{\mathit{L}}_{\mathit{r}\mathit{t}}$	${\mathit{E}}_{\mathit{f}\mathit{t}}$	${\mathit{R}}_{\mathit{a}\mathit{t}}$	$1/\mathit{T}{\mathit{L}}_{\mathit{f}\mathit{t}}$	${\mathit{t}}_{\mathit{t}}$
Minimum values	0	$3.765\times {10}^{-8}$	0	$1.563\times {10}^{-3}$	$3.765\times {10}^{-8}$	0.205
Maximum values	$2.322\times {10}^7$	428.456	$2.322\times {10}^7$	1.028	101.675	3210.167

5.1.3. MOP Solving Using NSGA-II and MOEA/D, Optimization Results, and Validations

Following the algorithm evaluation method proposed in 4.3 and Equation (39), the number of the operation repeating time was set to be 100, namely $n_I=100$. After the repeating, the lasting time of each operation $t_i$ and all the Pareto solutions were gathered, then Equation (39) was used to calculate the evaluation indexes. The results are listed in Table 8:

Table 8. Performance evaluation indexes for the objective turning process.

Performance Evaluation Indexes	${\mathit{I}}_{\mathit{t}}\left[\mathit{s}\right]$	${\mathit{I}}_{\mathit{n}}$
NSGA-II	34.5	306
MOEA/D	17.5	355

To analyze the performance of the Pareto solutions gathered by the process, we compared machining parameter groups acquired from handbook [34,35,42] and 10 solutions obtained from Pareto fronts (each five from each algorithm). The values of each sub-objective were all calculated five times to get the average. The data of the calculations are listed in Table 9. The relevant decoded parameters are listed in Table 10.

Table 9. Simulation experiment data of objective turning process.

Solution Type:		Data of Validation Experiments (Average of Five Repeats):
		Ert [J]	TLrt [min]	Eft [J]	Rat [μm]	TLft [min]	tt [min]
Solutions from handbooks	No. 1	$3.653\times {10}^4$	15.324	$2.243\times {10}^4$	$2.954\times {10}^{-2}$	20.235	6.864
	No. 2	$4.456\times {10}^4$	63.678	$2.223\times {10}^4$	$2.926\times {10}^{-2}$	21.234	4.987
	No. 3	$3.764\times {10}^4$	45.865	$1.445\times {10}^4$	$2.558\times {10}^{-1}$	21.238	4.765
Pareto solutions from NSGA-II	No. 1	$3.431\times {10}^5$	$3.456\times {10}^3$	$1.746\times {10}^4$	$4.827\times {10}^{-2}$	$7.856\times {10}^3$	44.908
	No. 2	$5.623\times {10}^5$	215.353	$1.669\times {10}^5$	$5.927\times {10}^{-2}$	$1.368\times {10}^4$	25.098
	No. 3	$2.612\times {10}^5$	$2.345\times {10}^3$	$9.325\times {10}^3$	$9.398\times {10}^{-2}$	$2.454\times {10}^3$	29.564
	No. 4	$3.432\times {10}^5$	$3.569\times {10}^3$	$2.076\times {10}^4$	$6.725\times {10}^{-2}$	$6.621\times {10}^3$	38.908
	No. 5	$2.532\times {10}^5$	$2.324\times {10}^3$	$2.278\times {10}^4$	$5.098\times {10}^{-2}$	$1.382\times {10}^4$	30.235
Pareto solutions from MOEA/D	No. 1	$7.876\times {10}^4$	164.098	$4.259\times {10}^4$	$5.987\times {10}^{-2}$	$2.766\times {10}^4$	10.874
	No. 2	$5.432\times {10}^4$	179.098	$1.587\times {10}^5$	$4.092\times {10}^{-2}$	$1.047\times {10}^4$	20.375
	No. 3	$4.234\times {10}^4$	109.543	$1.434\times {10}^5$	$4.987\times {10}^{-2}$	$9.647\times {10}^3$	18.098
	No. 4	$7.875\times {10}^4$	147.987	$4.778\times {10}^4$	$4.876\times {10}^{-2}$	$2.663\times {10}^4$	10.75
	No. 5	$3.543\times {10}^5$	$3.523\times {10}^3$	$2.648\times {10}^4$	$4.098\times {10}^{-2}$	$1.787\times {10}^4$	36.985

Table 10. Decoded solutions of objective turning process.

Solution Type		Relevant Decoded Parameters
		nrt [rpm]	frt [mm/r]	aprt [mm]	d1 [mm]	nft [rpm]	fft [mm/r]	apft [mm]	d2 [mm]
Solutions from handbooks	No. 1	500	1.0	1.5	20.0	1000	0.5	0.5	5.0
	No. 2	350	1.0	2.0	20.0	1000	0.5	0.5	5.0
	No. 3	350	1.5	1.5	20.0	800	1.0	0.5	5.0
Pareto solutions from NSGA-II	No. 1	260	0.5	0.5	21.5	250	0.7	1.1	3.5
	No. 2	250	1.9	0.5	14.0	250	0.5	0.5	11.0
	No. 3	270	0.5	0.6	22.0	300	0.8	1.5	3.0
	No. 4	250	0.5	0.5	21.6	280	0.6	1.0	3.4
	No. 5	270	0.5	0.6	22.0	250	0.6	0.8	3.0
Pareto solutions from MOEA/D	No. 1	290	1.7	0.6	22.0	250	0.5	0.5	3.0
	No. 2	260	2.0	0.6	14.0	260	0.5	0.5	11.0
	No. 3	280	1.9	0.6	14.0	260	0.5	0.5	11.0
	No. 4	300	1.7	0.6	21.6	250	0.5	0.5	3.4
	No. 5	250	0.5	0.5	21.9	250	0.5	0.8	3.1

For validations of the objective models above, validation experiments were carried out accordingly. The deviation percentages between the average calculations and the real experiment measurements were also calculated. The deviations of the models are listed in Table 11. It can be seen in Table 11 that all of the models have a deviation of less than 6%, so the accuracies of the objective models are validated.

Table 11. Deviations of the objective turning models.

Solution Type		Deviation Percentages of the Models:
		Ert	Eft	Rat	tt
Solutions from handbooks	No. 1	3.533%	5.421%	2.544%	5.422%
	No. 2	4.652%	5.644%	1.235%	5.642%
	No. 3	2.451%	4.324%	2.654%	4.765%
Pareto solutions from NSGA-II	No. 1	4.311%	4.655%	2.654%	5.235%
	No. 2	1.235%	5.654%	1.654%	5.423%
	No. 3	4.321%	3.434%	3.543%	3.644%
	No. 4	3.543%	5.655%	2.533%	4.643%
	No. 5	3.342%	3.654%	1.644%	4.542%
Pareto solutions from MOEA/D	No. 1	4.325%	5.422%	1.952%	5.321%
	No. 2	1.652%	4.345%	1.744%	5.322%
	No. 3	4.311%	3.654%	2.652%	4.564%
	No. 4	5.323%	5.312%	2.654%	4.653%
	No. 5	4.345%	2.534%	3.443%	3.564%

5.2. Case 2: A Step Milling Process

A case of step milling conducted on an XHK-714F CNC machine center. The material used was C45E4 carbon steels, and the cutting tool was YongTuo HSEM-4EML1435100. Figure 7 shows the real scene of the step milling.

Figure 7. A case of step milling process.

5.2.1. Modeling Results of Energy Consumption of the Step Milling

Like the cylindrical turning, the power modeling results of basic machine movement and spraying cooling fluid are $P_{bm}=3640\mathrm{W}$ and ${\mathrm{P}}_{\mathrm{sm}}=2510\mathrm{W}$, which were obtained by experiment measurements.

According to Equation (4), the coefficients in the piecewise function of spindle rotation power $P_{rm}\left[\mathrm{W}\right]$ were obtained by piecewise linear regressions, and the rotation speed $n_m$ ranges from 0 to 6000$\mathrm{rpm}$ with the increment of 100$\mathrm{rpm}$. The results are shown as Equation (70):

$$P_{rm}=\{\begin{array}{c}8.580\times {10}^{-2}{n}_m+14.812\hspace{1em}(0rpm<n_m\le 2200rpm)\\ 2.453\times {10}^{-2}{n}_m+157.432\hspace{1em}(2200rpm<n_m\le 3300rpm)\\ 6.028\times {10}^{-2}{n}_m+31.543\hspace{1em}(3300rpm<n_m\le 6000rpm)\end{array}$$

(70)

According to Equation (5), the coefficients in the quadratic function of feed power $P_{fm}\left[W\right]$ were obtained by quadratic regression when feed speed $f_{vm}$ ranges from 0 to 8000$\mathrm{mm}/\min$ with the increment of 100$\mathrm{mm}/\min$. The result is shown as Equation (71):

$$P_{fm}=4.683\times {10}^{-2}{f}_{vm}+8.421\times {10}^{-7}{f}_{vm}^2.$$

(71)

According to Equation (7), all these coefficients of the function for material cutting power $P_{cm}\left[\mathrm{W}\right]$ can be obtained by using Taguchi experiments and statistical regression like Lv et al. [29] and Jia et al. [33].

As presented in Table 12, four levels of rotation speed $n_m$, feed speed $f_{vm}$, cutting depth $a_{pm}$ and cutting width $a_{em}$ were selected from the tool manufacturers’ recommendation. The design matrix for milling experiments is shown in Table 13. The length of the cut for each test was 30 mm in axial direction.

Table 12. Taguchi experiment levels of milling parameters.

Milling Parameters	Level 1	Level 2	Level 3	Level 4
Rotation speed $n_m\left[\mathrm{rpm}\right]$	100	500	1500	3000
Feed speed $f_{vm}\left[\mathrm{mm}/\mathrm{r}\right]$	100	500	1500	3000
Cutting depth $a_{p\mathrm{m}}\left[\mathrm{mm}\right]$	0.1	1	3	5
Cutting width $a_{e\mathrm{m}}\left[\mathrm{mm}\right]$	0.1	1	3	5

Table 13. Parameter design matrix of milling experiments.

Experiment Order	Milling Parameters
	$\mathbf{Rotation}\mathbf{Speed}{\mathbf{n}}_{\mathbf{m}}\left[\mathbf{r}\mathbf{p}\mathbf{m}\right]$	$\mathbf{Feed}\mathbf{Speed}{\mathbf{f}}_{\mathbf{v}\mathbf{m}}\left[\mathbf{m}\mathbf{m}/\mathbf{r}\right]$	$\mathbf{Cutting}\mathbf{Depth}{\mathbf{a}}_{\mathbf{p}\mathbf{m}}\left[\mathbf{m}\mathbf{m}\right]$	$\mathbf{Cutting}\mathbf{Width}{\mathbf{a}}_{\mathbf{e}\mathbf{m}}\left[\mathbf{m}\mathbf{m}\right]$
1	100	100	0.1	0.1
2	100	500	1	1
3	100	1500	3	3
4	100	3000	5	5
5	500	100	3	5
6	500	500	5	3
7	500	1500	0.1	1
8	500	3000	1	0.1
9	1500	100	5	1
10	1500	500	3	0.1
11	1500	1500	1	5
12	1500	3000	0.1	3
13	3000	100	1	3
14	3000	500	0.1	5
15	3000	1500	5	0.1
16	3000	3000	3	1

The regression result is expressed as Equation (72):

$$P_{cm}=6.709\times {10}^{-2}{n}_m^{0.163}{f}_{vm}^{0.803}{a}_{pm}^{0.938}{a}_{em}^{1.115}$$

(72)

For this specific step milling process, we selected a square workpiece with the cutting length $l_m=50\mathrm{mm}$, the width $w=50\mathrm{mm}$, the total height to be tooled $h=25\mathrm{mm}$, the diameter of the cutting tool $D_T=14\mathrm{mm}$, and the length of a single feed path $L_{sm}$ was set to be 65 mm to avoid collisions ($L_{sm}>l_m+0.5D_T$). Therefore, by introducing all these size information into Equation (12), the feed time of rough milling $t_{frm}\left[\min \right]$ and finish milling $t_{ffm}\left[\min \right]$ can be expressed as Equations (73) and (74):

$$t_{frm}=\frac{45.500\pi \times h_1}{v_{rm}·f_{rm}·a_{prm}·a_{erm}\left[r\right]}$$

(73)

$$t_{ffm}=\frac{45.500\pi \times h_2}{v_{fm}·f_{fm}·a_{pfm}·a_{efm}\left[r\right]}$$

(74)

By introducing these size information into Equation (17), the cutting time of rough milling $t_{crm}\left[\min \right]$ and finish milling $t_{cfm}\left[\min \right]$ can be expressed as Equations (75) and (76):

$$t_{crm}=\frac{35\pi \times h_1}{v_{rm}·f_{rm}·a_{prm}·a_{erm}\left[r\right]}$$

(75)

$$t_{cfm}=\frac{35\pi \times h_2}{v_{fm}·f_{fm}·a_{pfm}·a_{efm}\left[r\right]}$$

(76)

Where machining allowance of the two phases should confine to Equation (77):

$$h_1+h_2=h=25mm$$

(77)

By referring to related machining handbooks according to the scenario information, and then introducing all these parameters into Equation (21), the surface roughness after this milling process $R_{am}\left[\mathsf{\mu }\mathrm{m}\right]$ can be expressed as Equation (78):

$$R_{am}=37.05·f_{vm}^{0.471}·n^{-0.918}·a_{pm}^{0.512}·a_{em}^{0.771}$$

(78)

According to Equation (23), based on the information about the cutting tool and the material, the cutting tool life during the milling process $T{L}_m\left[\min \right]$ can be approximately estimated using Equation (79) by looking through Armarego and Brown [37].

$$T{L}_m\approx \frac{39611829.711}{v_m^{2.263}{f}_m^{0.121}{a}_{pm}^{0.557}{a}_{em}^{0.340}}$$

(79)

Therefore, for rough turning process, the energy objective $E_{orm}$ can be expressed as Equation (80) from Equation (3):

$$E_{rm}=\left(P_{bm}+P_{sm}+P_{fm}+P_{rm}\right)t_{frm}+P_{cm}·t_{crm}$$

(80)

Furthermore, by introducing all these modeling results and case information into Equation (82), $E_{orm}\left[\mathrm{J}\right]$ can be expressed as Equation (81):

$$\begin{array}{ll}{E}_{rm}& =\left[6150+4.683\times {10}^{-2}{f}_{vrm}+8.421\times {10}^{-7}{f}_{vrm}^2+P_{rm}\left(n_{rm}\right)\right]\\ & \times \frac{45.500\pi \times h_1}{v_{rm}·f_{rm}·a_{prm}·a_{erm}}+6.709\times {10}^{-2}{n}_{rm}^{0.163}{f}_{vrm}^{0.803}{a}_{prm}^{0.938}{a}_{erm}^{1.115}\\ & \times \frac{35\pi \times h_1}{v_{rm}·f_{rm}·a_{prm}·a_{erm}}\end{array}$$

(81)

In addition, the relation between $n_m$, $v_m$ and tool diameter $D_T$ can be calculated by using Equation (82), and that between feed rate $f_m$ and feed speed $f_{vm}$ by Equation (83):

$$v_m=\pi D_T{n}_m/1000$$

(82)

$$f_m=f_{vm}/n_{rm}$$

(83)

The objective of tool life during rough milling $T{L}_{orm}\left[\min \right]$ can be expressed as Equation (84):

$$T{L}_{rm}\approx \frac{39611829.711}{v_{rm}^{2.263}{f}_{rm}^{0.121}{a}_{prm}^{0.557}{a}_{erm}^{0.340}}$$

(84)

Similarly, for finish milling process, the energy objective $E_{fm}\left[J\right]$ can be expressed by introducing all these modeling results and case information into Equation (3) as Equation (85):

$$\begin{gathered} E_{fm}=\left[6150+4.683\times {10}^{-2}{f}_{fm}+8.421\times {10}^{-7}{f}_{fm}^2+P_{fm}\left(n_{fm}\right)\right]\times \frac{45.500\pi \times h_2}{v_{fm}·f_{fm}·a_{pfm}·a_{efm}} \\ +6.709\times {10}^{-2}{n}_{fm}^{0.163}{f}_{fm}^{0.803}{a}_{pfm}^{0.938}{a}_{efm}^{1.115}\times \frac{35\pi \times h_2}{v_{fm}·f_{fm}·a_{pfm}·a_{efm}} \end{gathered}$$

(85)

The surface roughness objective for this milling process $R_{aom}$ can be expressed as Equation (86) according to Equation (78):

$$R_{am}=37.05·f_{vfm}^{0.471}·{n_{fm}}^{-0.918}·a_{pfm}^{0.512}·a_{efm}^{0.771}$$

(86)

The tool life during finish milling $T{L}_{ft}$ can be expressed as Equation (87):

$$T{L}_{fm}\approx \frac{39611829.711}{v_{fm}^{2.263}{f}_{fm}^{0.121}{a}_{pfm}^{0.557}{a}_{efm}^{0.340}}$$

(87)

The cutting time objective $t_m\left[min\right]$ can be expressed as Equation (88):

$$t_m=\frac{45.500\pi \times h_1}{v_{rm}·f_{rm}·a_{prm}·a_{erm}}+\frac{45.500\pi \times h_2}{v_{fm}·f_{fm}·a_{pfm}·a_{efm}}$$

(88)

The objective of tool life during finish milling $T{L}_{oft}\left[\min \right]$ can be expressed as Equation (89):

$$T{L}_{fm}\approx \frac{39611829.711}{v_{fm}^{2.263}{f}_{fm}^{0.121}{a}_{pfm}^{0.557}{a}_{efm}^{0.340}}$$

(89)

The cutting time objective $t_m\left[\min \right]$ can be expressed as Equation (90):

$$t_m=\frac{45.500\pi \times h_1}{v_{rm}·f_{rm}·a_{prm}·a_{erm}}+\frac{45.500\pi \times h_2}{v_{fm}·f_{fm}·a_{pfm}·a_{efm}}$$

(90)

Based on machine conditions and engineering experiences, all of the above machining parameters were subject to constrain, as Table 14 shows. The accuracy of the machining parameters and allowance to meet the demands are listed as follows: $0.01\mathrm{m}/\min$ for $v_m$, $10\mathrm{r}/\min$ for $n_m$, $0.01\mathrm{mm}/\min$ for$f_m$, $0.1\mathrm{mm}$ for $a_{pm}$, $a_{em}$, $h_1$ and $h_2$.

Table 14. Constrains of machining parameters for this milling process.

Machining Parameters	Constrains
Rotation speed $n_m$	$100\mathrm{r}/\min \le n_m\le 6000\mathrm{rpm}$
Cutting speed $v_m$	$0\mathrm{m}/\min \le v_m\le 200\mathrm{m}/\min$
Feed speed $f_m$	$100\mathrm{mm}/\mathrm{r}\le f_m\le 8000\mathrm{mm}/\min$
Cutting depth $a_{pm}$	$0.1\mathrm{mm}\le a_{pm}\le 5\mathrm{mm}$
Cutting width $a_{em}$	$0.1\mathrm{mm}\le a_{em}\le 5\mathrm{mm}$

5.2.2. Normalized MOP Expression of the Objective Step Milling

By introducing all the modeling results and constrains into equations from Equation (32) to Equation (37), the machining allowance distribution with MOP of the machining parameters for this step milling process can be expressed as equations from Equation (91) to Equation (95).

For rough milling phase:

$$OBJ1=Min\left(E_{rm}^{\prime }\right)$$

(91)

$$OBJ2=Min\left(\frac{1}{T{L}_{rm}^{\prime }}\right)$$

(92)

For finish milling phase:

$$OBJ3=Min\left(E_{fm}^{\prime }\right)$$

(93)

$$OBJ4=Min\left(R_{am}^{\prime }\right)$$

(94)

$$OBJ5=Min\left(\frac{1}{T{L}_{fm}^{\prime }}\right)$$

(95)

Figure 6 following Equation (38), the constraints of this case scenario are $n_{mMax}=6000\mathrm{rpm}$, $v_{mMax}=200\mathrm{m}/\min$, $f_{mMax}=8000\mathrm{mm}/\min$, $a_{pmMax}=5\mathrm{mm}$, $a_{emMax}=5\mathrm{mm}$, so the objective functions from Equation (91) to Equation (95) are subject to the constrain of Equation (96):

$$st:constrains=\{\begin{array}{c}{n}_{rm},n_{fm}\in \left[100,6000\right]\\ v_{rm},v_{fm}\in \left[0,200\right]\\ f_{vrm},f_{vfm}\in \left[100,8000\right]\\ a_{prm},a_{pfm}\in \left[0.1,5\right]\\ a_{erm},a_{efm}\in \left[0.1,5\right]\\ h_1+h_2=25\end{array}$$

(96)

The value ranges of each sub-objective functions are listed in Table 15, and those can be used to calculate the normalized values by using Equation (26), and backwards as equal.

Table 15. Calculation results of value ranges of sub-object functions.

Objectives (St: Constrains)	${\mathit{E}}_{\mathit{r}\mathit{m}}$	$1/\mathit{T}{\mathit{L}}_{\mathit{r}\mathit{m}}$	${\mathit{E}}_{\mathit{f}\mathit{m}}$	${\mathit{R}}_{\mathit{a}\mathit{m}}$	$1/\mathit{T}{\mathit{L}}_{\mathit{f}\mathit{m}}$	${\mathit{t}}_{\mathit{m}}$
Minimum values	0	$6.466\times {10}^{-15}$	0	$5.750\times {10}^{-3}$	$6.466\times {10}^{-15}$	0.406
Maximum values	$5.306\times {10}^8$	$6.360\times {10}^{-9}$	$5.306\times {10}^8$	293.712	$6.360\times {10}^{-9}$	$8.125\times {10}^4$

5.2.3. MOP Solving Using NSGA-II and MOEA/D, Optimization Results, and Validation

Like the cylindrical turning, the number of the operation repeating time was set to be 100, namely $n_I=100$. Equation (41) was used to calculate the evaluation indexes, as Table 16 shows. The data of experiments are listed in Table 17. The decoded solutions are listed in Table 18.

Table 16. Performance evaluation indexes for the objective step milling process.

Performance Evaluation Indexes	${\mathit{I}}_{\mathit{t}}$	${\mathit{I}}_{\mathit{n}}$
NSGA-II	46.43	354
MOEA/D	23.54	287

Table 17. Validation experiment data of objective step milling process.

Solution Type		Data of Validation Experiments (Average of Five Repeats):
		Erm [J]	TLrm [min]	Efm [J]	Ram [μm]	TLfm [min]	tm [min]
Solutions from handbooks	No. 1	$5.364\times {10}^4$	$9.783\times {10}^4$	$2.835\times {10}^4$	4.375	$5.732\times {10}^3$	12.734
	No. 2	$4.803\times {10}^4$	$1.032\times {10}^5$	$3.016\times {10}^4$	5.395	$1.094\times {10}^4$	10.285
	No. 3	$3.545\times {10}^4$	$1.721\times {10}^5$	$2.733\times {10}^4$	3.294	$8.041\times {10}^3$	9.273
Pareto solutions from NSGA-Ⅱ	No. 1	$4.476\times {10}^4$	$3.227\times {10}^5$	$1.756\times {10}^4$	0.864	$4.762\times {10}^2$	25.293
	No. 2	$7.024\times {10}^3$	$5.174\times {10}^5$	$3.388\times {10}^4$	10.284	$1.437\times {10}^5$	6.092
	No. 3	$8.167\times {10}^3$	$5.466\times {10}^5$	$3.305\times {10}^4$	11.245	$6.928\times {10}^4$	6.235
	No. 4	$7.554\times {10}^3$	$5.223\times {10}^5$	$6.593\times {10}^4$	9.457	$1.915\times {10}^4$	10.283
	No. 5	$8.125\times {10}^3$	$6.327\times {10}^5$	$9.318\times {10}^4$	1.092	$7.585\times {10}^2$	12.083
Pareto solutions from MOEA/D	No. 1	$8.676\times {10}^3$	$4.826\times {10}^5$	$1.148\times {10}^5$	1.863	$5.083\times {10}^2$	18.092
	No. 2	$7.625\times {10}^4$	$2.138\times {10}^5$	$2.713\times {10}^4$	6.098	$1.082\times {10}^5$	15.098
	No. 3	$6.956\times {10}^3$	$5.913\times {10}^5$	$7.033\times {10}^4$	5.987	$1.867\times {10}^5$	10.875
	No. 4	$9.825\times {10}^3$	$3.772\times {10}^5$	$2.494\times {10}^5$	0.345	$1.612\times {10}^3$	32.098
	No. 5	$1.056\times {10}^4$	$3.543\times {10}^5$	$1.259\times {10}^5$	1.972	$2.072\times {10}^3$	19.092

Table 18. Decoded solutions of objective step milling process.

Solution Type		Relevant Decoded Parameters
		nrm [rpm]	fvrm [mm/min]	aprm [mm]	aerm [mm]	h1 [mm]	nfm [rpm]	fvfm [mm/min]	apfm [mm]	aefm [mm]	h2 [mm]
Solutions from handbooks	No. 1	500	800	2.0	5.0	20.0	1500	500	1.5	5.0	5.0
	No. 2	500	750	2.0	6.0	20.0	1200	350	2	5.0	5.0
	No. 3	450	700	4.5	3.5	18.0	1500	450	3.5	3.5	7.0
Pareto solutions from NSGA-II	No. 1	1920	2430	1.7	3.2	22.3	3000	300	1.0	1.0	2.7
	No. 2	320	2450	4.8	4.7	15.0	450	560	4.0	2.7	10.0
	No. 3	300	2030	4.3	4.4	13.0	620	680	3.9	3.0	12.0
	No. 4	320	2470	4.7	4.8	16.0	370	380	3.5	2.1	9.0
	No. 5	300	2500	5.0	5.0	19.1	2910	510	1.0	2.6	5.9
Pareto solutions from MOEA/D	No. 1	330	2450	4.8	4.6	17.9	1470	300	2.1	2.0	7.1
	No. 2	340	910	2.0	3.4	22.0	400	620	1.6	2.2	3.0
	No. 3	310	2380	5.0	5.0	15.6	370	360	3.6	2.1	9.4
	No. 4	350	2420	4.7	3.7	17.0	2140	310	2.0	1.1	8.0
	No. 5	360	2390	4.5	3.8	17.4	2070	410	2.1	1.5	7.6

Like the turning case, for validations of the objective models above, validation experiments were carried out accordingly. The deviations of the models are listed in Table 19. It can be seen in Table 19 that all of the models have a deviation of less than 5%, so the accuracies of the objective models are validated.

Table 19. Deviations of the objective milling models.

Solution Type		Deviation Percentages of the Models:
		Erm	Efm	Ram	tm
Solutions from handbooks	No. 1	2.633%	4.765%	1.353%	4.986%
	No. 2	3.563%	4.654%	1.653%	4.844%
	No. 3	4.321%	4.654%	1.653%	4.876%
Pareto solutions from NSGA-II	No. 1	3.533%	4.953%	3.234%	4.876%
	No. 2	2.542%	4.568%	2.422%	4.327%
	No. 3	3.653%	4.567%	3.675%	3.874%
	No. 4	4.312%	4.965%	1.563%	3.876%
	No. 5	2.564%	4.345%	1.784%	4.875%
Pareto solutions from MOEA/D	No. 1	4.642%	4.653%	1.895%	4.873%
	No. 2	4.565%	4.865%	1.752%	3.543%
	No. 3	4.654%	4.953%	2.236%	3.765%
	No. 4	4.654%	4.843%	2.963%	4.886%
	No. 5	4.964%	4.754%	3.326%	3.986%

5.3. Analysis and Discussions

The analysis part generally includes experiment reviews and results analysis for both of the two cases separately. The performance evaluations of algorithms are also carried out. The comparison discussions with previous researches are presented in the end.

The preparations for this section are carried out as follow:

Based on contents listed in Table 9 and Table 10, the optimization results of the turning are presented in a scatter plot in Figure 8 (the lower the spot, the better for each objective), and the relative decoded solutions are presented in Figure 9.

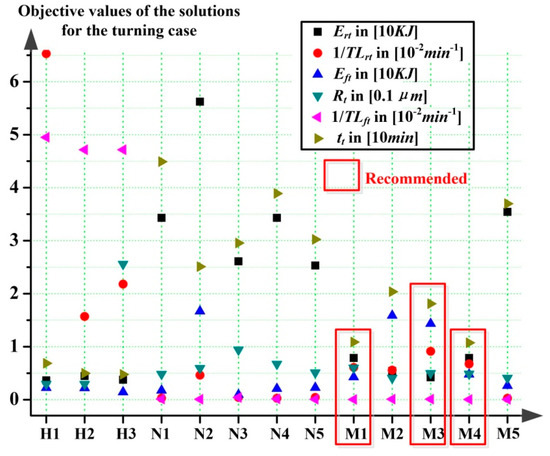
Figure 8. Objective values of the solutions for the case of turning.

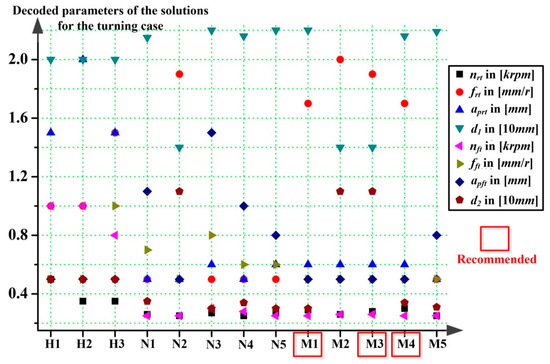
Figure 9. Decoded parameters of the solutions for the case of turning.

For the milling, similarly, based on Table 17 and Table 18, the optimization results are presented in Figure 10 and the decoded solutions are presented in Figure 11.

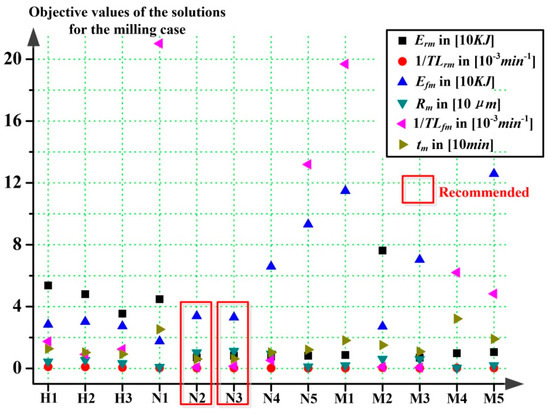
Figure 10. Objective values of the solutions for the case of milling.

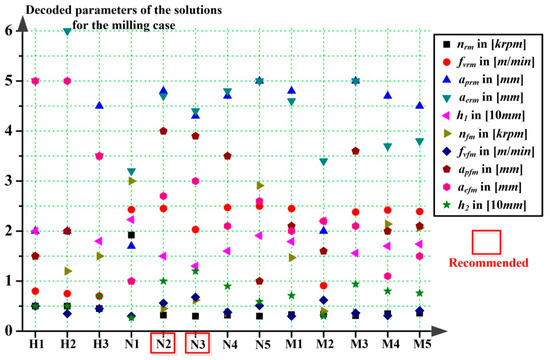
Figure 11. Decoded parameters of the solutions for the case of milling.

From Figure 8 to Figure 11, solutions obtained from handbooks, NSGA-Ⅱ and MOEA/D are represented by using symbols of H, N, and M, respectively. The following number denotes the order of the solution. For instance, H1 stands for the No. 1 solution obtained from the handbooks, and likewise afterwards.

5.3.1. Analysis of the Turning Case

For the case of turning specifically, based on Figure 8 and Figure 9, the analysis results can be summarized in the following aspects:

First, the solutions of M1, M3, and M4 apparently outperformed other solutions in each aspect of optimization objective. They are the most recommended solutions used in future real production scenarios. By using this kind of solutions, with a little sacrifice of energy costs and efficiency, the other objectives can all be greatly improved compared to traditional methods from handbooks, especially for cutting tool life and surface roughness.

Second, based on the first analysis result and Figure 9, the decoded parameters and allowances of the most recommended solutions can be used as guidance for future process planning. Generally, the allowance of rough turning phase should be set around 21 to 22 mm, and the machining parameters should be set with a combination of low spindle rotation speed around 280 to 300 rpm, high feed rate around 1.7 to 1.9 mm/r and large cutting depth around 0.5 to 0.6 mm for rough turning. For finishing turning, it should be with allowance around 3 to 4 mm, spindle rotation speed around 250 to 260 rpm, low feed rate around 0.5 mm/r, and small cutting depth around 0.5 mm. The recommended ranges of machining allowances and related parameters of the turning case are listed in Table 20.

Table 20. Recommended scope of machining parameters for case No. 1 and No. 2.

Case Information			Cylindrical Turning (Case No. 1)	Face Milling (Case No. 2)
Mechanical scenario		Machine	CK6153i-AH	XHK-714F
		Cutter	VNMG160408-YBC351	W400-FS
		Blank workpiece	CACE45	CACE45
		Cutting type	Wet cutting	Wet cutting
		Total allowance	d = 25	H = 25
Machining allowances and parameters	Rough machining phase	Spindle speed [rpm]	280 < nrt < 300	300 < nrm < 320
		Feed speed [mm/min] or feed rate [mm/r]	1.7 < frt < 1.9	2000 < fvrm < 2500
		Cutting depth [mm]	0.5 < aprt < 0.6	4.3 < aprm < 4.8
		Cutting width [mm]	/	4.4 < aerm < 4.7
		Allowance [mm]	21.0 < d1 < 22.0	16.0 < h1 < 22.0
	Finishing machining phase	Spindle speed [rpm]	250 < nft < 260	450 < nfm < 620
		Feed speed [mm/min] or feed rate [mm/r]	fft ≈ 0.5	560 < fvfm < 680
		Cutting depth [mm]	apft ≈ 0.5	apfm ≈ 4.0
		Cutting width [mm]	/	2.7 < aefm < 3.0
		Allowance [mm]	3.0 < d2 < 4.0	10.0 < h2 < 12.0

Third, there are not many improvements in the energy states when comparing the Pareto solutions with those obtained from handbooks. However, it is also obvious that they can significantly prolong the cutting tool life 200% to 500% longer estimably, and that is applicable both for the rough and finishing turning. This improvement will result in cutting down of resource use and production costs without harming the energy costs too much.

5.3.2. Analysis of the Milling Case

For the case of milling specifically, based on Figure 10 and Figure 11, the analysis results can be summarized in the following aspects:

First, the solutions of N2 and N3 apparently outperformed other solutions in each aspect, and they are the most recommended solutions. Specifically, the energy consumption of rough milling can be greatly reduced to around 20% of traditional methods from handbooks.

Second, based on Figure 11, the decoded parameters and allowances of N1 and N2 can be used as guidance for future process planning. Generally, the allowance of rough milling phase should be set around 13 to 15 mm, and the machining parameters should be set with a combination of low spindle rotation speed around 300 to 320 rpm, high feed speed around 2000 to 2500 mm/min, large cutting depth around 4.3 to 4.8 mm and small cutting width around 4.4 to 4.7 mm for rough milling. For finishing milling, it should be with allowance around 10 to 12 mm, spindle rotation speed around 450 to 620 rpm, feed speed around 560 to 680 mm/min, cutting depth around 4 mm and cutting width around 2.7 to 3 mm.

The recommended ranges of machining allowances and related parameters for the two cases are both listed in Table 20. From Table 20, workers can choose among those to meet various kinds of engineering demands accordingly.

5.3.3. Performance Evaluations of Algorithms and Related Discussion

The performance evaluation indicators $I_t$ and $I_n$ can be used to compare the intelligent algorithms. They can offer a reference for future algorithm determining strategies.

As Table 8 and Table 16 show, the solving speeds of NSGA-Ⅱ are faster than those of MOEA/D. However, MOEA/D generally outperformed NSGA-Ⅱ in finding effective Pareto solutions for the turning case, because of the diversity and fast solving speed as well. Namely, MOEA/D is more effective in providing solutions located in the area of multi-objective equilibrium for the turning case. Those solutions are more likely to be used in real engineering scenarios. And NSGA-Ⅱ is more suitable for the milling case, respectively, for the same reasons.

5.3.4. Discussions

Compared with previous research, the analysis results revealed facts of the following aspects:

(1)

Rather than parameter optimizations of a single machining phase like the works of [20,21], comprehensive optimization considering machining allowance distributions of different machining phases is more likely to be used in real production. The generated solutions provide not only energy-oriented machining parameters, but also various groups of parameters and allowances for better implementation. The priorities of each phase can all be met by doing so.

(2)

This research further enhances the recommendation of relative larger setting of machining allowance of rough machining, and small setting of finishing machining, like [4,26].

(3)

It is revealed that the high-speed cutting technique recommended by many previous studies, like [13,30], are not always suitable for application. Specifically, for multi-objective considerations like energy costs and tool protection, relative low cutting speeds of the finishing phases are recommended in this research.

(4)

Contrary to our previous finding of [27], NSGA-Ⅱ outperformed MOEA/D in the milling case once machining allowance distribution is involved. Namely, the selection of optimization strategies should be well-adjusted, considering the characteristics and uniqueness of the specific problem.

6. Conclusions and Future Work

The major contributions of the research are listed as follows:

(1)

Improved modeling of machining allowance distribution is proposed, integrated with parameter optimization. Energy-saving demands of different machining phases can be comprehensively met. With the machining allowance distribution well-addressed, the proposed method is relatively practical compared to traditional methods, consistent with the actual situation.

(2)

The most recommended optimization solutions are picked out, and they can be used in real production directly. Workers can choose among those non-determined solutions for their optimization priority, without harming any of the economic objectives too much. With a little sacrifice of energy costs and efficiency, cutting tool life and surface roughness can all be greatly improved for turning, and energy consumption of rough milling can be greatly reduced to around 20% of traditional methods.

(3)

The most suitable scope of machining allowances and parameters is precisely recommended. It can be concluded that during rough machining, the machining should be set with the combination of large allowance, high cutting speed, high feed rate and large cutting depth. During finish machining, it should be the combination of small allowance, low cutting speed, low feed speed, and small cutting depth.

(4)

The performance of different strategies, including and MOEA/D was studied. The selection of algorithms can be adjusted as needed considering the performance analysis. Generally, MOEA/D is more likely to be used for turning and NSGA-Ⅱ is more likely to be used for milling for real applications.

The limits of this research are listed as follows:

(1)

So far, only cylindrical turning and step milling have been studied. Other machining scenarios and demands, like drilling, grinding, and complex surface machining, are necessary to further validate the proposed method should be considered.

(2)

How do the limitations and constraints used affect the results has not been not discussed. Factors like high-speed cutting technique, machine tolerance changes, cutting tool conditions, and change of cooling paths will affect the results.

(3)

The possibility of uncertainty will affect the results, like the changes of machine types, layouts, cutting tools, materials, and optimization priorities.

As the next step, we will investigate other machining processes and situations, like drilling and grinding. And the definition of limitations and constraints should be well-adjusted according to the scenario. For example, the high-speed cutting technique may have a great influence on the results, which deserve further investigation. Rather than intelligent algorithms we used, the performance of other optimization techniques will be studied. We will study how to incorporate the proposed method to uncertainties of changes, such as choice of machines, materials and cutting tools, etc.