Abstract
The current use of natural resources in the textile industry leads us to introduce a new economic concept called inverse Malthusianism describing a context in which population grows linearly and resource consumption grows exponentially. Inverse Malthusianism implies an exponential increase in environmental impact that recycling may contribute to reduce. Our main goal is to extend the analysis of materials selection under the principle of equimarginality proposed by Jevons. As a first result, we show the particular circumstances under which policies excluding recycled supplies are never optimal. We also aim to overcome the difficulties of reducing environmental aspects to monetary units. To this end, we propose a multicriteria approach to solve the conventional-recycled materials dilemma considering not only economic but also environmental criteria. Then, we allow producers to enrich their decision-making process with relevant information about the environmental impact of materials selection. Although we use examples of the textile industry to illustrate our results, most of the insights in this paper can be extended to other industries.
1. Introduction
Demography, economics and environmental impact are three key elements that are necessarily related. People become economic agents when they exchange some goods in return for other goods that are produced using natural and other resources. The larger the population, the more complex the economic relations and, ultimately, the larger the impact on the environment. Thomas Robert Malthus [1,2] has a place in economics history due to his vision on the evolution of the population. Malthus argued that the physical limitations of the planet would make food production to grow arithmetically (linearly) while the population would grow geometrically (exponentially). However, the opposite has happened in the textile industry in the last 70 years from 1950 to 2020 [3,4]. The world population has increased linearly while the consumption of textile fibers has increased exponentially. We call this situation inverse Malthusianism and it is formally defined in this paper. The undesired result of this exponential resource consumption is its environmental impact [5,6,7].
In this paper, we address the problem of the environmental impact caused by economic activity. Among all aspects of environmental economics, we here focus on two particular areas: economics of recycling and multicriteria environmental economics. Materials selection is crucial in determining the impact that manufacturing activities have on the environment. In this sense, recycling of materials is usually viewed as highly beneficial to sustainability [8]. McInerney [9] provided a basic framework for the graphical analysis of natural resource economics including non-renewable stock resources with recyclable services. Our main goal in this paper is to extend the analysis of materials selection when considering two basic options: conventional and recycled materials. Relying on the concept of equimarginality or Jevonsian equilibrium [10,11,12], we explore the economic conditions to select the best materials mix including conventional and recycled alternatives. An additional goal of this paper is to overcome the difficulties of reducing environmental aspects to monetary units. To this end, we propose a multicriteria approach to solve the conventional-recycled materials dilemma considering not only economic but also environmental criteria.
Our main findings can be summarized as follows. First, we describe a method to analytically set the optimal policy mix considering two types of materials, namely, conventional and recycled materials, and a market size restriction imposed by inverse Malthusianism. More precisely, we show the particular circumstances under what policies excluding recycled supplies are never optimal. Our analytic results provide novel perspectives for policy making since they are derived in the particular context of inverse Malthusianism. Second, we propose an extension of the concept of Jevonsian equilibrium from a multiple criteria decision-making perspective. Since the concept of sustainability is inherently multidimensional, there is a need for a language that integrate economic and environmental aspects. By linking the concept of Jevonsian equilibrium to multiple criteria decision-making (MCDM) we provide a suitable way to demonetizing user costs in environmental economics. Instead of using a framework in which all aspects must be monetized, we propose a bi-criteria model that includes both economic benefits and environmental impact.
Since we introduce the concept of inverse Malthusianism showing data coming from the textile industry, we use related examples to illustrate our results throughout the paper. The reason to rely in this case study is the environmental impact that the textile industry may provoke due to its increasing resource consumption [13,14]. This case study serves not only to illustrate the results but to show the implications that can be derived from this paper. Producers can now enrich their decision-making process with relevant information about the environmental impact of materials selection. Textile companies can derive insights to implement recycling policies to alleviate the impact that their operations have on the environment. However, many other industries in which recycling may be a potentially suitable option can also apply our results. Summarizing, we highlight the following contributions of this paper:
- We introduce the concept of inverse Malthusianism, describe a paradigmatic case and explore the possible reasons behind this phenomenon.
- We show the conditions under what policies excluding recycled supplies are never optimal.
- We propose a method to demonetize user costs by means of MCDM.
In addition to this introduction, Section 2 reviews the literature related to the topics addressed in this paper. Section 3 provides a formal definition of the concept of inverse Malthusianism. Section 4 relies on the equilibrium of Jevons to derive novel theoretical results on recycling policies. Section 5 links the concept of Jevonsian equilibrium with the concept of Pareto efficiency to propose an MCDM method in the context of environmental economics. Section 6 concludes proposing natural extensions of this work.
2. Literature Review
Environmental economics has produced hundreds of publications [15,16,17,18,19]. Among all aspects of environmental economics, we here focus on two particular areas: economics of recycling and multicriteria environmental economics. McInerney [9] provided a basic framework for the graphical analysis of natural resource economics including non-renewable stock resources with recyclable services. This framework has become a standard tool for the analysis of intergenerational use of natural resources [19,20,21].
Recycling and reuse are the key elements of circular economy [22,23]. Turning goods disposed by one economic agent into resources for other agents is a clear alternative to the linear economy based on the make, use and dispose paradigm. The implications of recycling in terms of savings and environmental impact of materials such as metals and textiles have been considered by different authors [7,13,24]. In addition, the manufacturing and the use of recycled materials imply making decisions about materials selection for sustainability [25]. However, none of these works addresses the conditions under what a non-recycling policy is suboptimal.
Environmental economics presents many dimensions that deserve to be carefully considered [8,26]. Indeed, one of the limitations of the traditional resource depletion analysis is the need to rely on user costs [27,28] to account for the opportunity cost associated with forgone future benefits due to current consumption. To overcome the estimations issues related to user costs, MCDM [12,29,30,31] allows us to incorporate not only economic attributes but also environmental ones, and possibly many others, to determine the optimal policy.
In addition to be one of the most pollutant industries, the textile sector consumes an increasing amount of natural resources [5,6,7,13,14]. In order to evaluate the environmental impact of textile manufacturing, the Sustainable Apparel Coalition proposed in 2012 the use of the Higg Materials Sustainability Index [32,33,34]. The Higg index is a material scoring tool based on life cycle assessment data for different fiber types such as cotton, polyester and wool in terms of different aspects such as global warming, eutrophication, water scarcity, abiotic resource depletion of fossil fuels or chemicals used in the production activity. Since the Higg index integrates many different aspects the result is a score without measure units following the logic that the higher the score the larger the environmental impact of the material under consideration. By developing a common scoring tool, the textile industry has now the possibility to evaluate the environmental impact of production activities.
3. A Formal Definition of Inverse Malthusianism
In this section, we first provide a quantitative definition of Malthusianism in the way it is usually understood in the economic literature. Next, we formally define the opposite phenomenon, namely, inverse Malthusianism. We later describe the paradigmatic case of inverse Malthusianism observed in the textile industry.
3.1. Malthusianism and Inverse Malthusianism
Formally, we can express the exponential growth of world population over time t by means of the following differential equation:
where g is a positive growth rate. In addition, we can express the linear growth of a generic variable representing the resource consumption as follows:
where k and are positive constants. Solving Equations (1) and (2) by means of direct integration, we obtain the consumption per capita:
where is the initial population. Since consumption per each individual person in Equation (3) is a decreasing function, Malthusianism predicted social problems when this consumption represents a critical element such as food. If we now invert the exponential and linear features of population and resource consumption, we can describe the evolution of both variables by means of the following expressions:
where k and are again positive constants and r is a positive the rate of growth, in this case, of consumption. Now, the combination of Equations (4) and (5) leads to a different function of consumption per capita:
where represents now the initial resource consumption. This consumption clearly increases over time and characterizes what we call inverse Malthusianism, namely, a linear increase in population and an exponential increase in consumption of resources. For generality, consumption may include resources of different types: renewable or non-renewable resources, water, energy, materials, food or human resources. However, we keep world population as reference function to respect the demographic origin of the concept of Malthusianism. Next we consider a paradigmatic case of inverse Malthusianism observed in the textile industry.
3.2. The Case of the Textile Industry
At least during the last 70 years, both the world population and the consumption of textile materials have experimented a considerable increase as summarized in Table 1. However, the world population evolved linearly whereas the consumption of textiles has increased exponentially as shown in Figure 1. Blue and orange points represent population and consumption data. Dotted lines are, respectively, a linear and an exponential interpolation for population and consumption. The mathematical expressions for these interpolations are shown in the chart, together with the coefficient of determination of the adjustment. In both cases, represents year 1950, represents year 1960, and finally, represents year 2020 where both population and consumption points are estimations based on current data. The coefficient of determination measures the accuracy of the adjustment of the interpolation to the real data in the range . In both cases, this coefficient is above 0.99, hence showing a very good description of the underlying population and consumption time processes.

Table 1.
Consumption of textiles in the last 70 years [3,4] (*) Estimation.
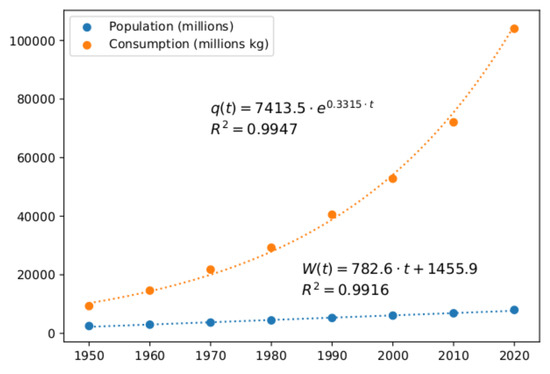
Figure 1.
An example of inverse Malthusianism in the textile industry. Source: own elaboration from data in [3,4].
By analyzing the evolution over time of population and consumption in Figure 1, we conclude that we are facing a case of inverse Malthusianism in which world yearly consumption of textile materials reaches an amount of 13 kg per individual person at present time. However, the environmental impact of inverse Malthusianism in the textile industry may provoke serious problems for future generations. An exponential growth of consumption of resources such as water and oil required to produce the most widely used fibres in the textile industry such as cotton and polyester is clearly non-sustainable in the long term [5,6]. In what follows, we discuss the suitability of recycling policies to face the problem of inverse Malthusianism from an analytical perspective within the field of multicriteria economics.
3.3. Reasons for Inverse Malthusianism
It is usually assumed that environmental impact is proportional to population (W), affluence (A), and technology (T) as summarized in the equation. In the case of inverse Malthusianism as defined in Section 3.1, population grows linearly and we should expect a linear increase in the environmental impact of human activity, other factors being equal. On the other hand, improvements in technology are assumed to reduce environmental impact as efficiency gains should lead to lower consumption of resources. However, evidences of technological improvement followed by increased consumption led to the Jevons’ paradox [35,36]. Jevons observed an increased consumption of coal and other resources derived from efficiency gains. Possible motives for this situation to happen are profitability reasons, price elasticity of demand, new uses and applications for materials and products. A typical example is that a more efficient vehicle enables us to drive longer because of the lower use of fuel per unit of distance [36]. Additional empirical evidence of the Jevons’ paradox can be found in [37,38].
A distinctive feature of inverse Malthusianism is the combined observation of an exponential growth of resources consumption and a linear increase in population. Along the lines of the Jevons’ paradox, we here argue that technological improvement is a possible reason for inverse Malthusianism. In other words, the effect that efficiency gains have on profits, prices and demand may produce more consumption than expected. In this case, we are facing a paradoxical effect of a change in the T of the equation. An example of technological improvement in the textile industry is the open-end spinning system developed in 1960 decade [39]. Open-end spinning machines do not require the use of a spindle and are faster than conventional ring spinning systems. In addition, innovations in the supply chain management introduced the fast-fashion model in textile retailing [40,41]. Fast-fashion is usually linked to low prices and an increase in the use of resources.
On the other hand, consumer behavior can change without efficiency gains. In this case, we are considering the effect of a change in the A of the equation. New uses and applications for products may provoke an increase in resource consumption. Within a sociological theory of consumption [42], individuals not only follow utility reasons but also the desire to consume at least as the rest of their social group do and to consume as past generations did. As a result, sociological factors are likely to fuel consumption and provoke an exponential use of resources.
Summarizing, if the increase of demand produced by either efficiency gains (T) or changes in the consumer behavior (A) is large enough to be added to a linear population increase (W), the result is that more people consume more, causing an exponential consumption of resources and a sustainability problem.
4. The Equilibrium of Jevons and Recycling Economics
In this section, we rely on the principle of Jevons to face inverse Malthusianism. We pay special attention to recycling and we find the conditions under which non-recycling policies do not satisfy the principle of Jevons. Illustrative examples are given as an extension of the case of inverse Malthusianism in the textile industry.
From Section 3.1, we face an inverse Malthusianism situation when consumption increases exponentially over time as described in Equation (5) while population grows linearly. A particular case of this situation is mathematically and graphically illustrated in Figure 1 for the case of the textile industry. If the environmental impact of this unstable situation is neglected, companies in the textile industry may feel very satisfied since the size of the market follows a monotonically increasing function:
where and r are positive constants. Indeed, the Net Present Value (NPV) over time t of profits associated with the whole textile industry with continuous discounting is given by:
where is a profit function per unit of product sold over time t, is a price function, is a cost function, and is a discounting factor at interest rate i. By combining Equations (7) and (8), we obtain the NPV function for the case of inverse Malthusianism:
An optimal economic policy is given by maximizing Equation (9). By calculating its first derivative of with respect to time, we obtain the first order condition to maximize the NPV function:
that is equivalent to:
where the prime symbols denote derivative functions. In words, the first-order condition to maximize the NPV in the inverse Malthusianism case is that the marginal benefit per unit (or the rate of growth of the benefit) equals the difference between the rate of interest and the rate of growth of the market size. This condition is an unstable variant of the well-known Hotelling’s rule [15]. In order to make products by extracting exhaustible resources, the marginal benefit per unit should be lower than the difference between the rate of interest and the rate of growth. Since a realistic economic assumption is that is positive, this first order condition only holds when . From the case of the textile industry in Section 3.2, we know that and we can reasonably assume that holds in most countries. Then, the first-order condition advises to wait for the future to exploit resources because the market will be larger. Indeed, Equation (9) is a monotonically increasing function when , as it seems to be the case of the textile industry. This fact gives raise to the following questions. Why do not textile producers wait for the future to exploit their resources? Are they not making optimal decisions? Here, economic theory seems to fail. A possible explanation is that they are making decisions in the short-term and not in the long-term. They do not probably believe that market size will ever grow at the current rate because this belief would imply the unrealistic assumption of unlimited natural resources.
Intuitively, the concept of Jevonsian equilibrium (or equimarginality condition) refers to the alternative uses that an economic agent can give to either a monetary, material or natural resource [10,11,12]. The agent faces the problem of allocating resources to alternative uses to maximize utility. The solution to this problem is the one that results in the same increase of utility when an additional unit of every resource is considered. In other words, optimal allocation occurs when the marginal utility of alternative uses is the same. More formally, if an economic agent considers how to split a given resource q into two alternative uses and such that , we can represent the utility derived from the use of the resource as follows:
In order to maximize the utility of the agent, we can build the following Lagrangian where is the multiplier:
Deriving Equation (13) first with respect to , and second with respect , we derive the first order conditions that lead to the Jevonsian equilibrium that states that the maximum global utility is achieved when the marginal utility for the two alternative uses is the same:
We next rely on the concept of Jevonsian equilibrium to answer a critical question: what is the optimal mix of products? To this end, let us first assume that the ultimate goal of all manufacturers is to maximize their utility expressed as the sum of profits for n alternative products combined in the final product mix. This assumption should be considered as a first step in our study according to the traditional microeconomic analysis [43]. We later extend this utility function definition to incorporate further environmental aspects in Section 5.
subject to:
where is the quantity of the i-th alternative product characterized by price function and cost function . By considering this quantity dependent functions, we aim to incorporate the effects of supply and demand in prices and costs as it is customary in environmental economics. In addition, the sum of all quantities must be equal to the total market size estimated by in the case of inverse Malthusianism. We can now build the Lagrangian with Equations (15) and (16):
The first-order conditions to maximize are the following:
By dividing equations in group (18) in pairs, we find that the optimal allocations are achieved when the following Jevonsian equilibrium holds at time t:
In other words, to maximize their utility, the marginal benefit achieved per each unit of alternative product must be equal. If this equilibrium condition does not hold, then producers should reallocate production resources to items with higher marginal benefit and get more profits until a perfect balance of partial utilities is achieved. For instance, consider a textile producer that is able to make and sale both cotton and polyester products with marginal benefits of €/kg and €/kg, respectively. By dedicating more production and sales resources to the item with higher marginal benefit (cotton), this producer can rise its utility to the optimal point in which additional efforts result in equal marginal benefits due to the assumption of diminishing marginal returns.
The Jevonsian equilibrium described in Equation (19) is a key element in our approach to recycling as a potentially suitable way to face the sustainability problems caused by inverse Malthusianism. We here propose a special mix of products with only two alternatives: conventional and recycled products. Then, producers have two products to build their product mix: those made with conventional materials such as virgin cotton, and those others made with recycled materials such as mechanically recycled cotton. Then, in the case of inverse Malthusianism, we have:
where represents the production of conventional products and represents the production of recycled products at time t. Let us further assume that quality attributes of products are incorporated in price functions and to formulate the following Jevonsian equilibrium for conventional and recycled products within an industry:
Let us focus now on present time to continue our analysis without time indexing to simplify notation. In our context, the Jevonsian equilibrium is achieved when the difference of profits and cost functions for conventional and recycled materials are equal:
Along the lines of the proposal by McInerney [9], we next consider a conventional material linear marginal price function , where and are positive constants. There is also a marginal cost function, which is also linear in :
where is a positive extraction cost and is a positive user cost. Note that marginal prices and costs ultimate depend on quantity produced and sold to account for the effects that supply and demand have on prices and costs. For instance, marginal price function implements the typical negative correlation between prices and demand quantities. In addition, marginal cost function implies a higher user cost when quantities produced are larger.
The use of conventional materials imposes a cost to future uses of these materials by the next generations. Then, this use comes at the expense of potentially future users and it represents an opportunity cost that must be considered. Intuitively, the user cost is an externality, a loss of benefits imposed on future generations. However, estimation difficulties makes that this user cost is neglected in many decision-making processes in economics when environmental impacts are not considered.
Similarly, for recycled materials, we consider a marginal price function , where and are positive constants. There is also a marginal cost function built as the sum of the initial extraction cost of the materials to be later recycled at a unitary cost , net of the extractive cost of the additional material that would otherwise have been necessary [9]:
The difference is also called the net marginal recycling cost. In case that both extraction costs are equal , the only cost to be charged to the recycled materials alternative is the recycling cost. In what follows, we assume that since it seems reasonable that extraction costs are not likely to vary on the short-term.
Relying on the previous price and cost functions, McInerney [9] graphically showed that the optimal conventional-recycled policy occur when the combined marginal cost of producing conventional and recycled materials equals the marginal revenues. Notice that this result is an additional demonstration of the principle of Jevons since the optimal conventional-recycled policy satisfies the equilibrium condition. By analyzing the optimal conventional-recycled policy given by the Jevonsian equilibrium in Equation (22), we next consider under what conditions a given conventional-recycled mix is not an optimal policy in the following suitable cases:
- Equal prices. If marginal prices and are equal for conventional and recycled materials, Equation (22) becomes a comparison of marginal costs and . Even though this price-equality situation may seem infrequent at first glance, it may arise in the textile industry for some polyester products whose differences in prices are sometimes negligible. In addition, it allows us to focus on costs as a first exploratory analysis. Producers should then allocate resources to conventional or recycled products by only focusing on differences in cost. The following alternative situations may turn out.
- (a)
- , and and positive constants. When user costs are neglected or when there is no user cost due to the non-exhaustible nature of resources (e.g., solar energy), producers have an incentive to recycle only when . Since this relation in constant, the equilibrium condition provides the optimal recycled quantity:as shown in Figure 2. Since we have the market restriction in Equation (20), the optimal quantity of conventional materials can also be determined.
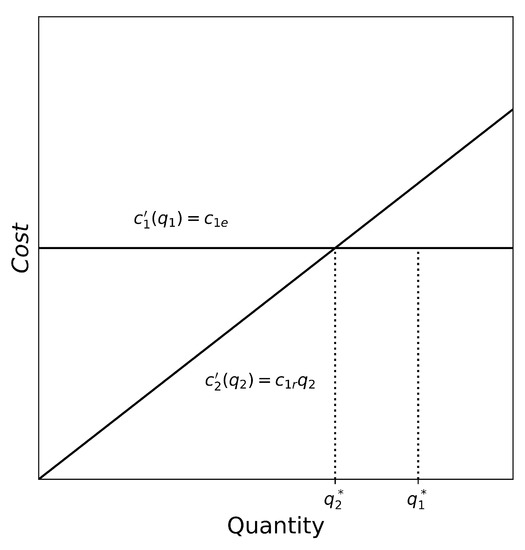 Figure 2. Illustration of case (a) equal prices.
Figure 2. Illustration of case (a) equal prices. - (b)
- constant, and . Then, the marginal cost of recycling increases more rapidly than the marginal cost of producing conventional material. Then, there is an intersection point of marginal costs given by:However, this point does not provide the optimal policy . The optimal policy is given by the Jevons equilibrium condition:together with the market restriction at each time t. If , then and the optimal policy recommends to produce more recycled than conventional materials. On the contrary, if , then and the optimal policy recommends to produce more conventional than recycled materials. This situation is caused by the different slope of the marginal cost functions as shown in Figure 3. In this case, the horizontal dashed line represents the cost level of the equimarginality condition of Jevons.
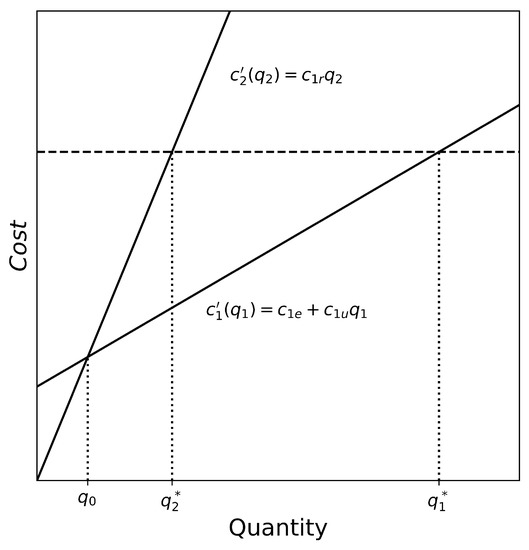 Figure 3. Illustration of case (b) equal prices.
Figure 3. Illustration of case (b) equal prices. - (c)
- constant, and . Then, the marginal cost of producing conventional materials increases more rapidly than the marginal cost of recycling. As a result, marginal costs never intersect. However, the equilibrium condition described in Equation (27) and the market restriction (20) provide the optimal policy . In this case, recycled quantity is always larger than conventional quantity .
Summarizing, the previous cases analyze different situations in which user, extraction and recycling costs determine the optimal material selection policy. Even in the unrealistic case in which user costs are neglected, recycled materials seem to should be playing a more important role than they currently do in the context of inverse Malthusiansim. In the USA, the recycling rate for all textiles was 15% in 2017 [44]. In Europe, about 15 to 20% of disposed textiles are collected and about 50% is downcycled and 50% is reused [13]. If we assume, for example, an average recycling rate of 20%, the implication is that marginal costs of recycling must be, at least, four times larger than user cost to guarantee an optimal policy in the sense of Jevons according to Equation (27). This assumption seems to be unrealistic for the most consumed fibers (polyester and cotton) so that we argue that the textile industry is far from following an optimal conventional-recycled path. This conclusion can be extended to each sector situation in which recycling rates and total consumption are known to analyze the degree of suboptimality of current materials selection policies. - Different prices. Quality differences, taxes and many other factors may provoke that marginal prices , for conventional materials, and marginal prices , for recycled materials, are not equal. As a result, profit functions obtained as the difference between marginal price and cost functions in Equation (22) play a key role to derive the optimal conventional-recycled materials policy. Next, we consider two alternative situations.
- (a)
- Prices for recycled materials above prices for conventional materials. This situation arises when , and . Benefits for conventional and recycled materials are, respectively, decreasing functions of and . This fact implies the existence of two limiting quantities equal to the intersection of the marginal profit functions with the horizontal axis:Beyond these quantities, profits are negative. Then, an additional constraint that must be satisfied is . Otherwise, the market restriction is impossible to fulfill. The Jevonsian equilibrium in the case of different prices for conventional and recycled materials with linear dependence on quantities for marginal price and cost functions is as follows:In this case, if and , the marginal benefit of conventional materials decreases more rapidly with quantities than the marginal benefit of recycling. Both marginal functions never intersect. Then, will always be larger than . The optimal policy implies producing more recycled than conventional materials. On the contrary, if , but , there is another intersection point:Together with the market restriction , if , then and the optimal policy recommends to produce more recycled materials than conventional. On the contrary, if , then and the optimal policy recommends to produce more conventional materials than recycled.
- (b)
- Prices for recycled materials below prices for conventional materials. This situation arises when , and . Again, benefits are decreasing functions of quantities and there are two limiting points that must satisfy the restriction . Otherwise, the market restriction is impossible to fulfill. The optimal policy can be computed by means of the Jevonsian equilibrium described in Equation (30). Similarly to point 2.(a) above, if and , the optimal policy implies producing more conventional than recycled materials. On the contrary, if , but , there is another intersection point that can be again computed by means of Equation (31). Together with the market restriction , if , then and the optimal policy recommends to produce more conventional materials than recycled. On the contrary, if , then and the optimal policy recommends to produce more recycled materials than conventional.
- (c)
- Mixed marginal price functions when , but , or , but . As a result, marginal benefits may produce different optimal policies that, however, can be computed by means of the Jevonsian equilibrium described in Equation (30).
The concept of Jevonsian equilibrium in the context of inverse Malthusianism and marginal profit functions allows us to provide further insight on the conditions that must be met to follow an optimal conventional-recycling policy. More precisely, we next describe two theoretical results: one for the case of equal prices and another one for the case of different prices.
Proposition 1.
Given utility function , a linear marginal cost function for conventional materials , a linear marginal cost function for recycled materials , with , and a market restriction , with , a policy without recycling is never optimal if .
Proof.
If , then is the optimal amount of conventional materials with , and since the Jevonsian equilibrium condition for optimality is . If , then the optimal amount of recycled materials must be positive, since is a linear function of quantity . As a result, policy without recycling is never optimal. □
As illustrated in Figure 4, Proposition 1 shows that non-recycling policies are suboptimal in the common context of positive marginal costs for producing conventional materials from exhaustible resources when the ultimate goal is to satisfy demand with minimum cost. In the textile industry, the small differences observed in prices for polyester fibers must encourage producers to introduce in their product mix some quantities of recycled materials. The results provided above will guide them to determine their optimal conventional-recycled policy according to their particular cost functions.
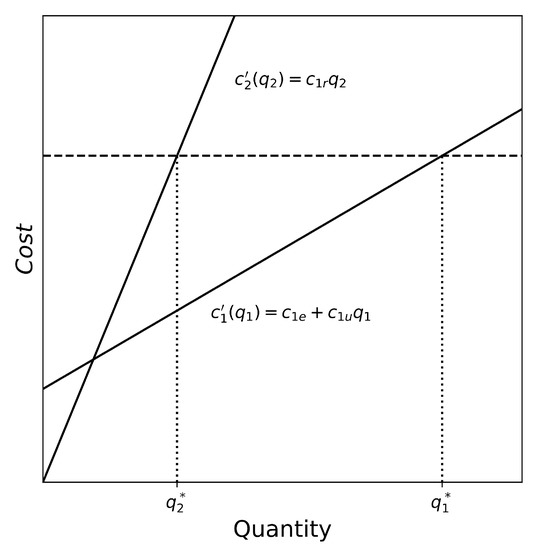
Figure 4.
Illustration of Proposition 1.
In case that price differences for conventional and recycled materials are relevant, we next provide an additional theoretical result that describes the condition under a non-recycling policy is optimal.
Proposition 2.
Given utility function , two linear marginal price functions , for conventional materials, and , for recycled materials, two linear marginal cost functions , for conventional materials, and , for recycled materials, and a market restriction , with , a policy without recycling is only optimal when the following condition holds:
Proof.
According to the Jevonsian equilibrium condition, policy is optimal if and . Since function , then . As a result, . Reorganizing terms, we obtain the conventional materials quantity , which must be as least as large as to be optimal and satisfy the market size restriction. □
As illustrated in Figure 5, Proposition 2 implies not only the condition for optimality for a policy without recycling but also a motivation for a mixed conventional-recycled policy when this condition is not satisfied. Summarizing, economic agents have now the possibility to set optimal policies by means of the well-known concept of equimarginality proposed by Jevons. In the particular case of inverse Malthusianism such as the one observed in the textile industry, this concept may result of great help to face the impact of resource consumption in both economical and environmental sustainability. However, economic agents may also find difficulties to incorporate externality costs in a user costs parameter (). To solve this problem, we next propose an extension of the concept of Jevonsian equilibrium from a multiple criteria decision-making perspective.
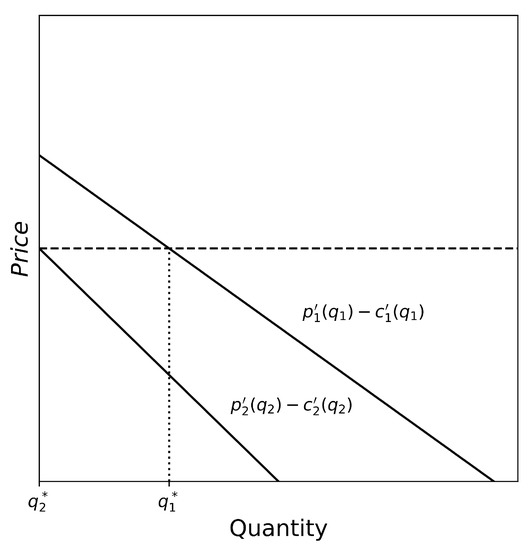
Figure 5.
Illustration of Proposition 2.
5. Demonetizing User Costs by Means of MCDM
There is a need for a common language about sustainability of materials selection including not only economic but also environmental aspects. One suitable way to address the problem of demonetizing user costs in order to enrich the analysis is multiple criteria decision-making. In this section, we focus on the conventional-recycled materials selection dilemma to propose a bicriteria model in which the economic dimension is assessed by means of the traditional benefit analysis and the environmental dimension is measured by a recently proposed impact index.
Pareto efficiency is defined as an optimum state of a group of people in which no person can improve his/her situation without worsening the situation of any other person [31]. Let us now consider that each person has chosen a quantitative criterion to measure the achievement of a desired attribute. These attributes may be economical, social, environmental and possibly of many other types. For instance, companies may want to maximize long-term profits, employees representatives may want to maximize equality in salaries paid to men and women, and the government may be interested in reducing environmental impact of economic activities. As a result, optimal policies within this group require Pareto efficiency as a core concept in multiple criteria decision-making.
On the other hand, we know from Section 4 that the Jevonsian equilibrium provides optimal policies for alternative uses of resources, namely, conventional-recycled policies. If we consider that the benefits derived from conventional materials is one of the criteria under analysis and that the benefits derived from recycled materials is an additional criterion of interest, we are indeed facing a multiple criteria decision-making problem. However, in Section 4, we use economic concepts such as prices, costs and benefits to measure the utility derived from alternative uses of resources. Here, we move one step further by considering a wider set of desired attributes. Our approach will help us to answer a critical question: how can (textile) manufacturers incorporate sustainability as an additional goal to reduce the environmental impact of exponential resource consumption observed in inverse Malthusianism?
To answer this question, we reformulate the utility maximization problem encoded in Equations (15) and (16) as a multiobjective problem. The purpose of the following analysis is to allow manufacturers to make better materials selection decisions in terms of both economic and environmental criteria. To this end, we assume that the ultimate goal is to maximize the utility expressed as a set of m alternative criteria measuring the distinct achievement of n alternative products combined in the final mix:
subject to:
where is one of the m different achievement functions that evaluate the utility derived from the product mix . In our recycling economics context, we restrict the analysis to two products, namely, conventional materials, denoted by , and recycled materials, denoted by . Furthermore, we propose to consider not only economic criteria such as benefits but also the environmental impact of both conventional and recycled materials. The rationale behind this approach is to overcome the difficulties of monetizing user costs in a strict economic evaluation. Furthermore, this approach allows us to consider user costs associated not only to conventional materials but also to recycled materials since the production of these materials also implies an environmental impact. As a result, we make decisions in terms of two or more criteria. For instance, we keep the economic perspective by setting to:
In addition, we introduce the environmental perspective by considering the impact that each type of material has according to the Higg materials sustainability index [32,33,34]. The Higg index is a normalized score based on life cycle impact assessment methodology that considers five different categories of impact for one kilogram of material [34]:
- Global warming potential (kg CO eq) is a measure of how much heat a greenhouse gas traps in the atmosphere and indicates the potential change in climate patterns.
- Eutrophication (kg PO eq) occurs when excessive nutrients enter a body of water and causes a dense growth of plant life and death of animal life from lack of oxygen.
- Abiotic resource depletion of fossil fuels (MJ) is the consumption of a resource such as carbon or oil faster than it can be replenished.
- Water scarcity (m) measures the environmental impacts of freshwater consumption in three areas: human health, ecosystem quality and resources.
- Chemicals used (points) are qualitatively assessed by considering finishes applied to a given material and chemical standards such as Oeko-tex.
Once midpoints are calculated for each category of impact, the results are normalized to create a common unit that can be added together to allow comparisons between materials and categories. The Higg index is available for the most commonly used materials in the textile industry, including conventional and recycled materials. The result is a score without measure units for each material and textile process under the logic that the higher the score the larger the environmental impact of the material under consideration. As a result, we next propose the use of the Higg index as a measure of the impact of both conventional and recycled materials:
where and are, respectively, impact functions based on the Higg index for conventional and recycled materials. Since this impact function aims to replace the marginal user cost function described in Section 4, it seems reasonable to assume again linear marginal impact functions and , for conventional and recycled materials, respectively. In these impact functions, and are, respectively, the Higg index of the conventional and recycled materials.
A critical topic in multiple criteria decision-making is normalization of achievement functions to avoid a meaningless comparison of criteria with different units and scales. Furthermore, policy-makers may want to attach different weights to the criteria under consideration as an expression of their preferences. For instance, a textile company may want to incorporate the environmental impact of their operations in decision-making, but they think that the economic goal is currently twice more important than the environmental goal for them. Both aspects, normalization and particular preferences for the achievement of alternative goals can be implemented in objective function (33) as follows:
where and are normalization factors, and and are the weights attached to the achievement of economic and environmental goals expressing the particular preferences of a given manufacturer. Percentage normalization is possibly the easiest way to elicit factors and . If and are set to the maximum values attainable by functions and , then utility measures the weighted achievement in per unit terms with respect to the maximum benefit and the maximum impact of alternative policies. Note also the negative sign before the second term of the right-hand side of Equation (37). Indeed, if measures the environmental impact of both conventional and recycled materials, then the larger the impact the lower the utility derived from this impact.
There are many other ways to implement a multiple criteria objective function [29,31,45]. However, the simplicity of Equation (37) allows us to better explain the extension of the principle of Jevons as a multiple criteria equilibrium condition. Indeed, the equimarginality condition in Equation (19) is fully applicable when considering multiple criteria. In our context, a multiple criteria Jevonsian equilibrium condition for optimal policies in conventional-recycled materials policies is expressed as follows:
This multiple criteria Jevonsian equilibrium condition should be read as follows. The optimal policy will be given by feasible quantities and such that the weighted normalized marginal contributions of and to the achievement of the alternative criteria under consideration are equal. In our context, this new equilibrium condition for conventional and recycled materials with linear marginal price, cost, and environmental impact functions can be rewritten as follows:
Note that in Equation (39) we replace cost user with the environmental impact measured by the Higg index. In practice, this expression can be simplified to:
where , , and are:
Therefore, utility becomes a weighted function in which economic benefit is reduced by environmental impact. As a result, the lower the impact of conventional and recycled materials the larger the quantity of the optimal policy. In case that recycled materials show a lower environmental impact than conventional materials, a Pareto optimal policy recommends larger quantities of recycled materials. This recommendation represents a suitable way to incorporate environmental aspects in economics.
As an illustrative example, consider the Higg sustainability index for the most widely used textile fibres as summarized in Table 2. This table compares the Higg index for both conventional and recycled materials obtained from [34]. In order to obtain a global impact index, we compute a weighted average of impact indexes and using the production mix observed in 2017 [4]. In our analysis of the extended Jevonsian equilibrium described in Equation (40), we could set to represent a neutral situation in which the economic and the environmental goal are equally important. We could set normalizing factor to the maximum marginal profit attainable given by , since both marginal profit functions are linear and decreasing in quantities. Furthermore, we could set normalizing factor to the largest sustainability impact given by conventional materials according to Table 2, which we assumed to be an increasing function of quantities. Then, where q may represent either or .

Table 2.
Materials sustainability index for the most widely used textile fibers. Source: Higg index from [34] and Production 2017 from [4].
As a result, we can derive the optimal conventional-recycled policy by solving the extended Jevonsian equilibrium in Equation (40) subject to the inverse Malthusianism market size restriction . Graphically, prices and quantities that characterize the optimal policy can be obtained by considering the price level, depicted by a horizontal dashed line in Figure 6, that allows the condition of equimarginality provided that the market restriction is satisfied.
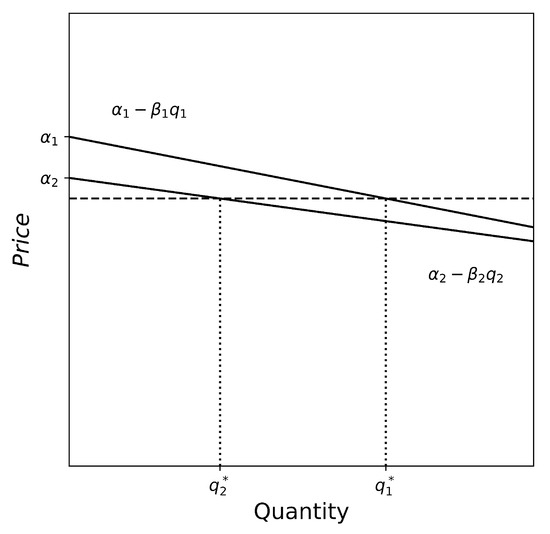
Figure 6.
Jevonsian equilibrium considering economic and environmental aspects.
Numerically, if we set as the maximum marginal profit attainable within a neutral context in which both the economic and the environmental perspective are equally important (), then . Let us further assume that to represent the case where marginal prices for conventional materials are above prices for recycled materials for small quantities. Then, as shown in Figure 6. From Table 2, we infer that the relationship between the global impact for conventional materials is . If we set , then we can rewrite and as follows:
As a result, the consideration of both economic and environmental aspects within a Jevonsian equilibrium results in the increase of units in the slope of the normalized marginal profit function of conventional materials and the increase of less than one unit (35/58) in the slope of the normalized marginal profit function of recycled materials. As long as quantity is either above or below 35/58, recycled materials will receive a better or worse treatment than in the case of estimating user costs as described in Section 4. However, the main advantage of the procedure introduced in this section to derive optimal conventional-recycled policies is that there is no need to monetize user costs.
6. Conclusions
Producers, consumers and policy-makers require a common language to evaluate the economic and environmental potential of recycling as a way to face the challenges imposed by unprecedented consumption figures. On the one hand, by observing current trends in consumption and world population growth we introduce the concept of inverse Malthusianism to characterize a challenging situation from an environmental perspective. On the other hand, one may ask what are the conditions of the best conventional-recycled materials selection policies. Finally, to overcome the difficulties of monetizing environmental aspects, multiple criteria decision-making may help to enhance the analysis. We next further elaborate on these three key elements and their implications.
On the impacts of inverse Malthusianism. The increasing resource consumption due to population growth and economic development imposes a cost on future generations due to associated environmental impact. The novel concept of inverse Malthusianism serves to illustrate the situation in which production increases exponentially and population grows linearly. This situation implies a tremendous environmental challenge. One suitable option to face this challenge is the combination of conventional and recycled materials that we here discuss.
On the conventional-recycled materials dilemma. The set of conditions characterizing optimal materials selection policies considering both conventional and recycled materials is one the main concerns of producers along the whole supply chain. What mix of materials should they use to maximize utility within a context of inverse Malthusianism? Relying on the concept of Jevonsian equilibrium, we show that materials selection policies excluding recycled supplies are never optimal under some well-defined conditions. Current recycling rates in the textile industry seem to indicate that there is room for improvement in long-term sustainability through recycling.
On the difficulties to monetize user costs. The conditions for optimal conventional-recycled policies are based on user costs as an attempt to monetize the impact of current consumption in future generations. To overcome the difficulties of reducing environmental aspects to monetary units, we propose a multicriteria approach linking the concept of equimarginality and Pareto efficiency. We argue that further insights can be derived by approaching the challenges of environmental economics from a multiobjective perspective.
A reductionist understanding of the economic activity and its environmental impact may lead to undesired consequences. In order to face our present and future challenges, we require a more general approach to economics that incorporate sustainability elements. One of this elements is materials selection considering recycled materials as a suitable alternative from both an economic and an environmental perspective. From the analysis described in this paper, manufacturers and policy makers are able to study the degree of suboptimality of their current materials selection policies. One of the limitations of our multiple criteria decision-making approach to demonetize user costs is the assumption of a particular weight to both the economic and the environmental criteria because different weights may lead to different recommended policies. However, these weights allow economic agents to express their preferences that can be very different among economic agents and that may vary in time. The examples in the textile industry help us illustrate the results presented in this paper. However, most of the insights can be extended to other industries. Thus, additional empirical studies to explore the presence of inverse Malthusianism in other industries represent natural extensions of this work. Finally, the study of the ultimate reasons for inverse Malthusianism is also an interesting future line of work.
Author Contributions
Conceptualization, F.S.-M., D.P.-S., M.L.V.-F. and J.R.-M.; methodology, F.S.-M., D.P.-S. M.L.V.-F. and J.R.-M.; validation, F.S.-M., D.P.-S., M.L.V.-F. and J.R.-M.; formal analysis, F.S.-M., D.P.-S., M.L.V.-F. and J.R.-M.; investigation, F.S.-M., D.P.-S., M.L.V.-F. and J.R.-M.; resources, F.S.-M., D.P.-S., M.L.V.-F. and J.R.-M.; data curation, F.S.-M.; writing—original draft preparation, F.S.-M., D.P.-S., M.L.V.-F. and J.R.-M.; writing—review and editing, F.S.-M., D.P.-S., M.L.V.-F. and J.R.-M.; visualization, F.S.-M., D.P.-S., M.L.V.-F. and J.R.-M.; supervision, F.S.-M.; project administration, D.P.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Malthus, T.R. An Essay on the Principle of Population; J. Johnson: London, UK, 1798. [Google Scholar]
- Malthus, T.R. An Essay on the Principle of Population; Electronic Scholarly Publishing Project: Electronic Edition; Electronic Scholarly Publishing: Bellingham, WA, USA, 1998. [Google Scholar]
- Textile Exchange. Preferred Fiber & Materials Market Report 2018; Textile Exchange: Lamesa, TX, USA, 2018. [Google Scholar]
- Textile Exchange. Preferred Fiber & Materials Market Report 2019; Textile Exchange: Lamesa, TX, USA, 2019. [Google Scholar]
- Chapagain, A.K.; Hoekstra, A.Y.; Savenije, H.H.; Gautam, R. The water footprint of cotton consumption: An assessment of the impact of worldwide consumption of cotton products on the water resources in the cotton producing countries. Ecol. Econ. 2006, 60, 186–203. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Chapagain, A.K.; Mekonnen, M.M.; Aldaya, M.M. The Water Footprint Assessment Manual: Setting the Global Standard; Earthscan: London, UK, 2011. [Google Scholar]
- Esteve-Turrillas, F.A.; De la Guardia, M. Environmental impact of Recover cotton in textile industry. Resour. Conserv. Recycl. 2017, 116, 107–115. [Google Scholar] [CrossRef]
- Costanza, R.; Cumberland, J.H.; Daly, H.; Goodland, R.; Norgaard, R. An Introduction to Ecological Economics; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- McInerney, J. The simple analytics of natural resource economics. J. Agric. Econ. 1976, 27, 31–52. [Google Scholar] [CrossRef]
- Jevons, W.S. The Theory of Political Economy; Macmillan: London, UK, 1879. [Google Scholar]
- Peart, S. The Economics of WS Jevons; Routledge: London, UK, 1996. [Google Scholar]
- Romero, C. Economics of natural resources: In search of a unified theoretical framework. Span. J. Agric. Res. 2012, 10, 29–33. [Google Scholar] [CrossRef]
- Sandin, G.; Peters, G.M. Environmental impact of textile reuse and recycling—A review. J. Clean. Prod. 2018, 184, 353–365. [Google Scholar] [CrossRef]
- Leal Filho, W.; Ellams, D.; Han, S.; Tyler, D.; Boiten, V.; Paco, A.; Moora, H.; Balogun, A.L. A review of the socio-economic advantages of textile recycling. J. Clean. Prod. 2019, 218, 10–20. [Google Scholar] [CrossRef]
- Hotelling, H. The economics of exhaustible resources. J. Political Econ. 1931, 39, 137–175. [Google Scholar] [CrossRef]
- Fisher, A.C. Resource and Environmental Economics; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Solow, R.M. Intergenerational equity and exhaustible resources. Rev. Econ. Stud. 1974, 41, 29–45. [Google Scholar] [CrossRef]
- Pearce, D.W.; Turner, R.K. Economics of Natural Resources and the Environment; Harvester Wheatsheaf: New York, NY, USA, 1990. [Google Scholar]
- Thampapillai, D.J.; Ruth, M. Environmental Economics: Concepts, Methods and Policies; Routledge: London, UK, 2019. [Google Scholar]
- Thampapillai, D.J. Trade-offs for conflicting social objectives in the extraction of finite energy resources. Int. J. Energy Res. 1985, 9, 179–192. [Google Scholar] [CrossRef]
- Just, R.E.; Hueth, D.L.; Schmitz, A. The Welfare Economics of Public Policy: A Practical Approach to Project and Policy Evaluation; Edward Elgar Publishing: Cheltenham, UK, 2005. [Google Scholar]
- Stahel, W.R. The circular economy. Nature 2016, 531, 435–438. [Google Scholar] [CrossRef]
- Geissdoerfer, M.; Savaget, P.; Bocken, N.M.; Hultink, E.J. The Circular Economy—A new sustainability paradigm? J. Clean. Prod. 2017, 143, 757–768. [Google Scholar] [CrossRef]
- Ayres, R.U. Metals recycling: Economic and environmental implications. Resour. Conserv. Recycl. 1997, 21, 145–173. [Google Scholar] [CrossRef]
- Ljungberg, L.Y. Materials selection and design for development of sustainable products. Mater. Des. 2007, 28, 466–479. [Google Scholar] [CrossRef]
- Garcia-Bernabeu, A.; Hilario-Caballero, A.; Pla-Santamaria, D.; Salas-Molina, F. A Process Oriented MCDM Approach to Construct a Circular Economy Composite Index. Sustainability 2020, 12, 618. [Google Scholar] [CrossRef]
- Scott, A.D. Notes on user cost. Econ. J. 1953, 63, 368–384. [Google Scholar] [CrossRef]
- Scott, A. Natural Resources: The Economics of Conservation; University of Toronto Press: Toronto, ON, Canada, 1983. [Google Scholar]
- Steuer, R.E. Multiple Criteria Optimization: Theory, Computation, and Application; Wiley: New York, NY, USA, 1986; Volume 233. [Google Scholar]
- Romero, C. Multicriteria decision analysis and environmental economics: An approximation. Eur. J. Oper. Res. 1997, 96, 81–89. [Google Scholar] [CrossRef]
- Ballestero, E.; Romero, C. Multiple Criteria Decision Making and Its Applications to Economic Problems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Radhakrishnan, S. The sustainable apparel coalition and the Higg index. In Roadmap to Sustainable Textiles and Clothing; Springer: New York, NY, USA, 2015; pp. 23–57. [Google Scholar]
- Laitala, K.; Klepp, I.; Henry, B. Does use matter? Comparison of environmental impacts of clothing based on fiber Type. Sustainability 2018, 10, 2524. [Google Scholar] [CrossRef]
- Sustainable Apparel Coalition. Materials Sustainability Index. 2019. Available online: https://msi.higg.org (accessed on 19 July 2020).
- Jevons, W.S. The Coal Question; An Inquiry Concerning the Progress of the Nation, and the Probable Exhaustion of Our Coal-Mines; Macmillan: London, UK, 1865. [Google Scholar]
- Alcott, B. Jevons’ paradox. Ecol. Econ. 2005, 54, 9–21. [Google Scholar] [CrossRef]
- Roy, J. The rebound effect: Some empirical evidence from India. Energy Policy 2000, 28, 433–438. [Google Scholar] [CrossRef]
- Polimeni, J.M.; Mayumi, K.; Giampietro, M.; Alcott, B. The Myth of Resource Efficiency: The Jevons Paradox; Earthscan: London, UK, 2008. [Google Scholar]
- Lawrence, C.A. Advances in Yarn Spinning Technology; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Crofton, S.; Dopico, L. Zara-Inditex and the growth of fast fashion. Essays Econ. Bus. Hist. 2007, 25, 41–54. [Google Scholar]
- Cambra-Fierro, J.; Ruiz-Benitez, R. Advantages of intermodal logistics platforms: Insights from a Spanish platform. Supply Chain Manag. Int. J. 2009, 14, 418–421. [Google Scholar] [CrossRef]
- Ballestero, E.; Blanco, V. A Socio-Cultural Model of Consumption. In 1984 Academy of Marketing Science (AMS) Annual Conference; Springer: New York, NY, USA, 2015; pp. 134–139. [Google Scholar]
- Mas-Colell, A.; Whinston, M.D.; Green, J.R. Microeconomic Theory; Oxford University Press: New York, NY, USA, 1995; Volume 1. [Google Scholar]
- United States Environmental Protection Agency. Advancing Sustainable Materials Management: 2017 Fact Sheet; United States Environmental Protection Agency: Washington, DC, USA, 2019. [Google Scholar]
- Jones, D.; Tamiz, M. Practical Goal Programming; Springer: Berlin, Germany, 2010; Volume 141. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).