Flexural Performance Evaluation of Novel Wide Long-Span Composite Beams Used to Construct Lower Parking Structures

Abstract

Efficient parking structures are urgently required in Korea. The design of parking structures more than 8 m in height is difficult because both fire and seismic resistance must be considered. Existing designs are uneconomical and conservative. However, the design of parking structures less than 8 m in height is relatively simple and there are few restrictions to the construction. It is essential to optimize the design of parking structures less than 8 m in height. Here, we describe novel wide long-span composite beams that reduce the story height of low parking structures. The flexural capacity of seven of the beams was evaluated; all beams were loaded at two points prior to monotonic bending tests. We also performed finite element analysis (FEA) based on the material properties of the test specimens, and compared the results to those of the structural tests. The flexural strength of the wide composite steel beams increased by approximately 20% as the steel thickness rose by 3 mm, from 6 to 9 mm. The rebar shape (triangular or rectangular) did not affect flexural strength. The flexural strength of beams without rebar was 10% less than that of beams with rebar. The FEA and test results were in good agreement. The section plastic moments were free from global and local instability.

1. Introduction

The higher load, as well as the longer span on buildings such as high-rise buildings and parking structures, the floor system consisting of beams and slabs of the total structures accounts for more than 70% of the structural construction cost. In addition, the need for technologies to reduce the floor height and cope with long-span is increasing, as they have a significant impact on the economy of available area, material saving, and energy reduction. Due to climate change caused by global warming, on the other hand, the number of days that cannot be carried out on-site construction work is continuously increasing, thus the need for minimized on-site construction technology is emerging to reduce greenhouse gas emissions in the building sector. Recently, a competition for developing the technologies minimizing on-site construction work based on composite structures for realizing long-span, floor height reduction, and construction period reduction has intensified in connection with a heightened interest in research areas of low-carbon green growth due to climate change and a development of high-density and high-rise building technologies in urban areas around the world.

In Korea, there is also a growing interest in technology to minimize on-site construction, which is capable of reducing the burden of construction costs due to rising labor costs and transforming the profit structure of the construction industry. In addition, since the goal of reducing greenhouse gas emissions in Korea is set at 26.9% in the building sector in 2020, it is absolutely necessary to develop technology to minimize on-site construction using composite structural system.

Against this research background, in this study, we proposed a new composite beam system used to construct parking structures, which has a long-span and can save floor height, in order to solve the parking problems in urban Korea. The parking problems in urban area in Korea are getting more serious with rapid increasing of cars. The urban parking problem can cause various social problems, such as traffic disorder and traffic safety, and it is a significant obstacle to increase the efficiency of the urban transportation. The Korean government has suggested various solutions for parking problems, including providing additional parking space and several campaign to improve the parking culture in Korea. However, there is a certain limit to cover the rapid increase of parking space needs, thus innovative technologies to maximize parking space on limited land are highly needed.

In Korea, parking lots over 8 m in height (thus over two stories) must meet rigorous fire and seismic specifications; such lots are expensive to construct and conservative in design. For the parking structures with below 8 m height, however, the registration process is very simple in Korea and there are few restrictions for the construction of the parking structure. Thus, the design and construction technology to maximize parking space for the parking structure with below 8 m height are necessary. Therefore, it is of great importance to reduce the floor height and increase the beam spans of such parking structures.

However, current techniques for reducing the floor height and increasing the beam spans for parking structures with below 8 m height, including those described in the Hoesch Additive Floor system (HBS (2019) [1]; Darko, Boris, and Ivan (2015) [2]), the Cellular Beam system (Pachpor, Gupta, and Deshpande (2014) [3]), the Ultra Shallow Floor Beam system (Tsavdaridis, D’Mello, and Hawes (2009) [4]), and the Delta Beam system (DCB (2014) [5]; Nadasky (2012) [6]), are not suitable for the long-spanned and floor height-reduced composite structures, including shortening of construction period.

According to the Hoesch Additive Floor system (HBS (2019) [1]; Darko, Boris, and Ivan (2015) [2]), it is a traditional composite system modified to reduce the height of the flooring, as shown in Figure 1. It doesn’t need secondary beams, and can be usefully compared to the slim floor systems. This floor system (also called the H-system) comprises of rolled symmetric I-beams and square steel bars welded to the top flanges and supporting deep decking. Nelson studs are used to ensure composite action. The system, which is patented from the German society Hoesch, has the advantage of limited structural steel weight, but the apparent disadvantage of leading to significantly higher floor heights.

Figure 1. The Hoesch Additive Floor system (HBS (2019) [1]; Darko, Boris, and Ivan (2015) [2]).

The Cellular Beam system (Pachpor, Gupta, and Deshpande (2014) [3]), developed and applied by Westok Company in the U.K., are made from I or H sections, whose web is cut longitudinally in the desired format. Then, the two halves are displaced and welded by the axis, in order to generate openings in sequence along the web and increase in height of the cross section, as shown in Figure 2. Although it has advantages of easy construction of the facility duct and good looks, it does not significantly reduce the flooring height and required of structural members for transverse buckling prevention due to a long-span.

Figure 2. The Cellular Beam System (Pachpor, Gupta, and Deshpande (2014) [3]).

The Ultra Shallow Floor Beam (USFB) system (Tsavdaridis, D’Mello, and Hawes (2009) [4]) is a type of composite floor beam, and was developed by Westok Company, as depict in Figure 3. The steel section is fabricated by welding two highly asymmetric cellular tees together along the webs, resulting in a large bottom flange. Either precast concrete floor units or profiled steel decking rest on the bottom flange of the USFB, creating a very shallow floor beam construction system, thus minimizing the overall structural depth.

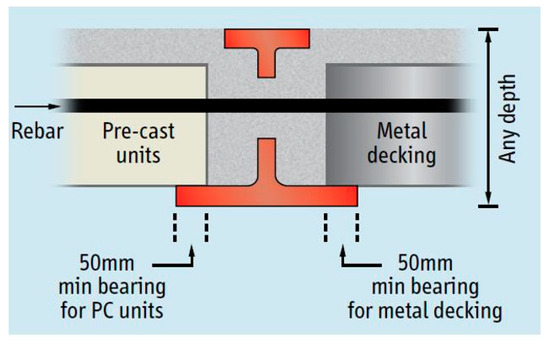
Figure 3. The Ultra Shallow Floor Beam (USFB) (Tsavdaridis, D’Mello, and Hawes (2009) [4]).

A special end diaphragm is used for deep decking floor applications so that the concrete fully surrounds the steel section, apart from the bottom plate. The web openings provide a passage for reinforcing tie bars and service ducts within the depth of the beam. However, the USFB system has limitations in implementing long-span, and it does not have much effect in reducing the floor height as well as shortening the construction period.

According to the Delta Beam system (DCB (2014) [5]); Nadasky, P. (2012) [6]), the standard shape of the system, which was developed by Peico Group Corporation in Finland for the first time in the world and is actively applied to northern Europe, is made of boxed sections, thus various dimensions can be manufactured according to application, as depict in Figure 4. The Delta Beam is a slim-floor composite beam which is integrated into the floor. The beam is completely filled with concrete on-site. The infill concrete and the Delta Beam form a composite structure after the concrete has hardened. The Delta Beam system acts as a steel beam before the infill concrete has reached the required strength. The system is made of cut steel plates and welded together at the factory. It can be used with all common floor types. This system can reduce the floor height and also minimize on-site construction work. Due to a simple connection of joints, however, the lateral-load resistance performance is remarkably reduced. Thus, the system is not suitable for the long-spanned composite structures.

Figure 4. The Delta Beam system (DCB (2014) [5]; Nadasky, P. (2012) [6]).

The main objective of this study was to develop a novel wide composite beam system for the parking structures with below 8 m height, which can reduce beam height, but have greater beam span.

The proposed wide composite beam technique can reduce construction costs and resources by reducing the floor height and realizing the long-span. Also, it is possible to improve constructability and shorten the construction period since major components are manufactured in the factory and assembled in the field. As a result, the proposed methodology minimizing on-site construction work could reduce the material usages and the carbon dioxide emissions. By reducing its carbon dioxide emissions, it is the vital approach of sustainability in the construction industry, since the cement and concrete industry is the second largest industrial emitter of the carbon dioxide in the world.

On the basis of experimental investigations, in this study, the flexural performances of the proposed beams while varying the thickness of the steel plate, the shape of the slab supports, and the type of truss bar were evaluated. Seven test specimens were designed and fabricated, all of which were loaded at two points prior to monotonic bending tests. We also performed finite element analysis (FEA) based on the material properties of the specimens and compare the results to those of the structural tests.

2. Novel Wide Composite Beams for Construction of Parking Structures

Figure 5 shows a schematic of the parking structure considered herein, which has a height of 7.95 m (2.65 m × 3 stories) and width of 16 m (2 × 5 m × 2 parking areas with a 6-m “pass area” in-between). The beam heights in the parking and pass areas are 550 and 350 mm, respectively. Among previous works, the beam cross-section (Figure 5) often varied. However, it is difficult to appropriately link regions differing in cross-section. We partially embedded the upper concrete slab into the steel web; this reduces the height but may be associated with undesirable non-composite effects.

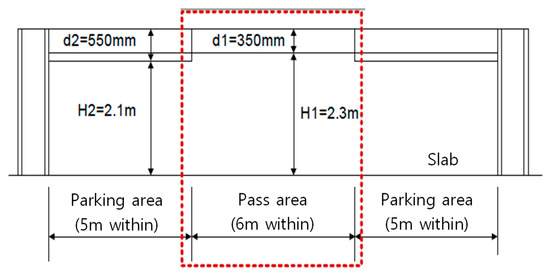
Figure 5. The prototype parking lot.

Figure 6 and Figure 7 show the novel wide composite beam with a height of 350 mm. The slab supports (the angle and C-channel) are mechanically attached to the wide U-shaped steel component. The supports and the lateral reinforcing bars are embedded into the concrete slab; the slab and steel thus work together. Longitudinal reinforcing and truss bars featuring pre-stressed cambers provide additional stiffness and strength (Gschwindner (1994) [7]; Mohan (2005) [8]).

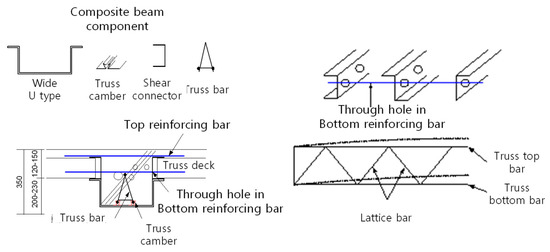
Figure 6. Components of the steel-concrete composite beam.

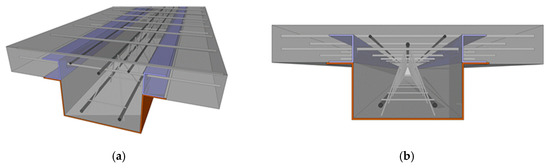
Figure 7. The steel-concrete composite beam: (a) Isometric view; (b) front view.

3. Theoretical Flexural Strength of the Novel Wide Composite Beam

We used a simple method to evaluate the flexural strength of the wide composite beam. The beam used in the car-passing region is shown in Figure 5; a more general reinforced concrete/steel-composite beam is used in the parking region. A pin connects the car-passing and parking regions. Thus, the wide composite beam is supported in terms of flexure (Figure 8); the maximum design bending moment, $M_u$, is $w{L}^2{/}_8$.

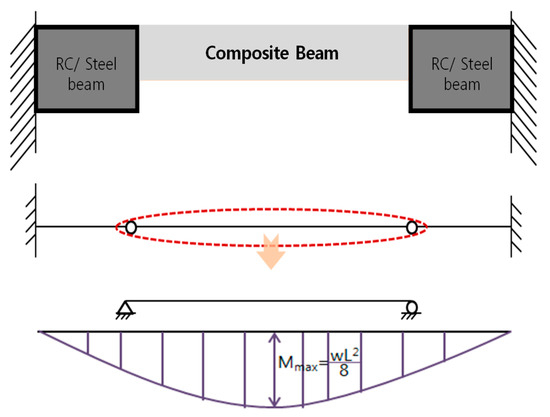
Figure 8. The moment of the composite beam.

To evaluate the moment of the beam, we used the plastic stress distributions shown in Figure 9; the relative slip between the steel and concrete was neglected. The upper and lower longitudinal reinforcing bars (in the concrete slab and truss, respectively) were assumed to be fully stressed, as was the U-shaped steel region. When the plastic stress distribution is in equilibrium, the plastic neutral axis (PNA) is located between the upper reinforcing bar of the concrete slab and the upper flange of the U-shaped steel component (Figure 9). The distance from the top of the concrete slab to the PNA ($y_p$) is:

$$y_p=\frac{A_s{F}_y+A_{sr1}{f}_y-A_{sr2}{f}_y-A_{sr3}{f}_y}{0.85f_{ck}{b}_e}$$

(1)

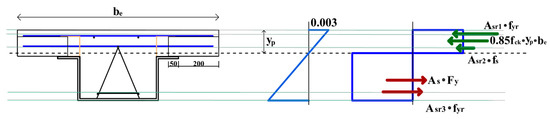
Figure 9. Plasticity stress distribution in a composite beam.

Note that $y_p$ of Equation (1) does not include the top reinforcing bar of the truss. The stresses in the upper bar of the truss may thus remain unknown. The strain and stress of the top truss reinforcing bar should be calculated using the strain distribution. The stress is (Namdeo (2012) [9]; ECS (2004) [10]):

$$0.85f_{ck}{b}_e{y}_p+A_{sr1}{f}_y+A_{sr2}{f}_s-A_{sr3}{f}_y-A_s{F}_y=0$$

(2)

The stress of the top truss reinforcing bar ($f_s)$ can also be expressed in terms of $y_p$, as follows:

$$f_s=\frac{600\left(y_p-y_{sr2}\right)}{y_p}$$

(3)

Substitution of Equation (3) into Equation (2) yields a $y_p$ value that includes the effect of $f_s$. The moment arm length can then be calculated for each stress. The moment capacity of the composite beam is (ACI 318 (2014) [11]; AIJ (2018) [12]; BS 5950 (1994) [13]; Chen (2003) [14]; Calixto (1998) [15]):

$$M_n=\left(0.85f_{ck}{b}_e{d}_1\right)+\left(A_{sr1}{f}_{yr}{d}_2\right)+(A_{sr2}{f}_s{d}_3)+\left(A_{sr3}{f}_{yr}{d}_4\right)+\left(A_s{F}_y{d}_5\right)$$

(4)

where, f_ck is the specified compressive strength of concrete (MPa), y_p is the distance from the top of concrete slab to the plastic neutral axis (mm), b_e is the slab effective width (mm) of the composite beam (mm), A_sr1 is the cross sectional area of the top reinforcing bar of slab included within b_e (mm²), A_sr2 and A_sr3 are the cross sectional area of the top and the bottom reinforcing bars of beam (mm²), respectively, f_yr is the yield strength of the rebar (MPa), f_s is the stress of the top reinforcing bar of beam (MPa), A_s and F_y show the cross-sectional area (mm²) and the yield strength of the steel plate (MPa), d₁ shows the distance from stress center of compressive concrete to the top of steel beam (mm), d₂ shows the distance from center of the top reinforcing bar of slab to the top of steel beam (mm), d₃ shows the distance from center of the top reinforcing bar of beam to the top of steel beam (mm), d₄ shows the distance from center of the bottom reinforcing bar of beam to the top of steel beam (mm), and d₅ shows the distance from center of the steel beam to the top of steel beam (mm). The moment arm lengths, $d_1~d_5$, of Equation (4) are shown in Figure 10:

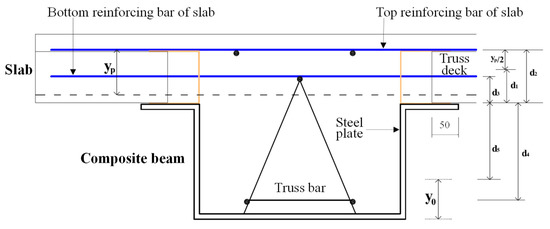
Figure 10. The distance from the center of the stress to the top of the steel beam.

4. Flexural Performance of the Wide Composite Beam

4.1. The Specimens and Test Setup

The flexural performance of the wide composite beam was evaluated. We varied the thickness of the U-shaped steel component (6 and 9 mm), the shape of the slab supports (the angle and C-channel), and the shape of the truss bar (triangular or rectangular). Seven specimens were fabricated and tested (Table 1). SPC6-C-P is a reference specimen lacking a truss bar. The beam height was 350 mm and the span was 6 m (clear span, 5.8 m) for all specimens. The effective width of the concrete slab was 1000 mm. SM490-grade steel and SD400 steel reinforcing bars were used for all specimens. The concrete compressive strength was 25.1 and 24.6 MPa for specimens with 6- and 9 mm-thick steel plates, respectively (Table 1). The details are shown in Figure 11 and Figure 12. Figure 13 shows the two-point bending test setup. Displacement was induced using a 2800 kN actuator working at 0.04 mm/s. Vertical displacement was measured at the 25, 50, and 75% span points.

Table 1. The test specimens.

No.	Specimen	Specimen Parameters			Material Properties
		Steel Thickness of U Shape [mm]	Slab Support Shape	Truss Type	Concrete Compressive Strength [MPa]	Reinforcing Bar Yield Strength [MPa]			Steel Yield Strength [MPa]
						D10	D13	D16	4.5T	6T	9T
1	SPC6-C-P	6.0		Non	25.1	469	445	424	440	422	402
2	SPC6-C-T
3	SPC6-A-T
4	SPC6-C-R
5	SPC9-C-T	9.0
6	SPC9-A-T				24.6
7	SPC9-C-R

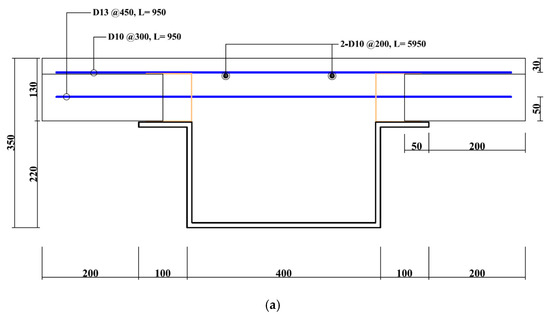
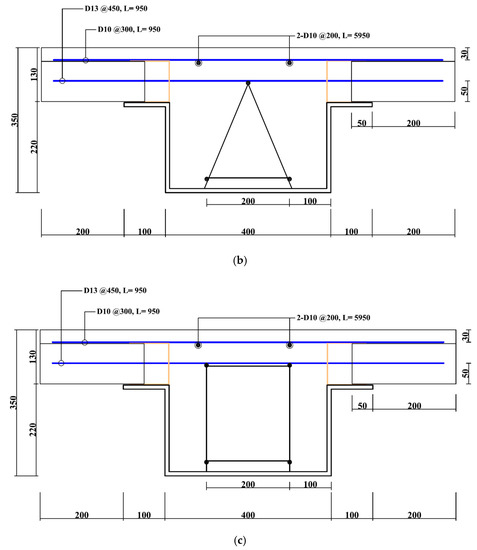
Figure 11. Details of the test specimens (unit: mm): (a) Sectional shape of SPC6-C-P; (b) sectional shape of SPC6-C-T; (c) sectional shape of SPC6-C-R.

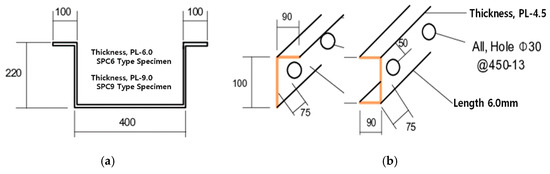
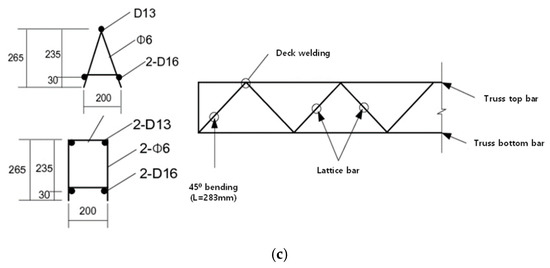
Figure 12. Specimen parameters: (a) Thicknesses of the U-shaped steel; (b) the slab supports; (c) the truss types.

Figure 13. Test setup.

4.2. Test Results

4.2.1. Failure Mode and Load-Displacement Relationship

The test results are summarized in Table 2. The theoretical strengths were calculated without consideration of the attachment angle. The theoretical flexural strengths were in good agreement with the test results. The yield strengths and displacements listed in Table 2 were obtained at an axial bottom reinforcing bar strain of 0.002. The load-central displacement relationships and failure modes of the specimens are shown in Figure 14 and Figure 15, respectively.

Table 2. Test results.

Specimen		Theoretical Strength (kN)	Strength (kN)		Displacement (mm)		Ductility Ratio
			${\mathit{P}}_{\mathit{y}}$	${\mathit{P}}_{\mathit{u}}$	${\mathit{\delta }}_{\mathit{y}}$	${\mathit{\delta }}_{\mathit{u}}$	${\mathit{P}}_{\mathit{y}}/{\mathit{P}}_{\mathit{u}}$	${\mathit{\delta }}_{\mathit{y}}/{\mathit{\delta }}_{\mathit{u}}$
1	SPC6-C-P	675.71	538.82	741.42	37.46	146.96	0.73	0.25
2	SPC6-C-T	769.03	692.87	826.80	43.62	126.18	0.84	0.35
3	SPC6-A-T	769.03	666.20	832.18	40.68	134.58	0.80	0.30
4	SPC6-C-R	770.72	695.42	848.09	40.42	142.92	0.82	0.28
5	SPC9-C-T	932.22	831.84	989.56	48.16	145.56	0.84	0.33
6	SPC9-A-T	836.38	842.17	970.06	52.30	108.78	0.87	0.48
7	SPC9-C-R	937.85	873.86	1019.72	47.74	132.64	0.86	0.36

$P_y$: yield strength, $P_u$: maximum strength, ${\delta }_y$: yield displacement, ${\delta }_u$: maximum displacement, $P_y/P_u$: strength ratio, ${\delta }_y/{\delta }_u$: displacement ratio.

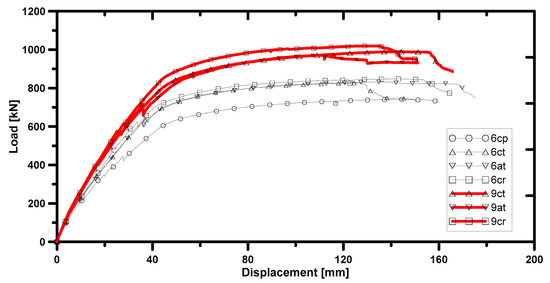
Figure 14. Relationship between load and displacement.

Figure 15. Failure patterns for specimens (a) SPC6-C-P, (b) SPC6-C-T, (c) SPC6-A-T, (d) SPC6-C-R, (e) SPC9-C-T, (f) SPC9-A-T and (g) SPC9-C-R.

(1) Effect of the thickness of the U-shaped steel region

The variations in flexural strength are shown in Table 3. The strength increased by about 20% as the steel thickness rose from 6 to 9 mm. Both the yield and ultimate strength of the C-T specimens increased by 20%; the respective values for the A-T and C-R specimens were 26% and 17%, and 26% and 20%, respectively.

Table 3. Strength increases with variation of the parameters.

Specimen		Strength Increase Ratio		Main Parameter
		Yield Strength ${\mathit{P}}_{\mathit{y}}$	Maximum Strength ${\mathit{P}}_{\mathit{u}}$
2	SPC6-C-T	1.20	1.20	Thickness of the U-shaped steel region (6.0 mm)
5	SPC9-C-T
3	SPC6-A-T	1.26	1.17
6	SPC9-A-T			Thickness of the U-shaped steel region (9.0 mm)
4	SPC6-C-R	1.26	1.2
7	SPC9-C-R
2	SPC6-C-T	0.96	1.01	Shape of slab support
3	SPC6-A-T
5	SPC9-C-T	1.01	0.98
6	SPC9-A-T
1	SPC6-C-P	0.78	0.90	Truss type
2	SPC6-C-T	1	1
4	SPC6-C-R	1.00	1.03
5	SPC9-C-T	1	1
7	SPC9-C-R	1.05	1.03

(2) Effect of the slab supports

For specimens with 6-mm-thick plates, the yield strength of the specimen with a channel (C) was 4% greater than that of the specimen with an angle (A); the ultimate strengths were near-identical. For specimens with 9-mm-thick plates, the yield strengths were similar, regardless of the shape of the slab supports; the ultimate strength of the specimen with an angle (A) was only 2% lower than that of the specimen with a channel (C). Thus, any effect of slab support shape was negligible because the slab supports lay near the PNA; any effect on flexural strength was also small.

(3) The effects of truss bars

C-T specimens featured triangular truss bars [one top reinforcing (D13) and two bottom reinforcing bars (D16)]; C-R specimens featured rectangular truss bars, and C-P specimens no bars. The yield and ultimate strength of the C-P specimen were 78% and 90%, respectively, those of the C-T specimen. The yield and ultimate strength ratio (C-R:C-T) were 1.04 and 1.03, respectively. For specimens with 9-mm-thick plates, the yield and ultimate strength of the C-R specimen were 5% and 3% greater than those of the C-T specimen. Truss bars affected both yield and ultimate strength; the bottom reinforcing bars yielded fully. Strain analysis revealed that the axial tensile strain of the bottom reinforcing bars was almost 0.002 (0.2%), associated with yield. However, the effect of bar shape was small because the top reinforcing bar lay near the PNA. The strain of the top reinforcing bar was about −0.0005 (0.05% compression), thus contributing only slightly to the observed strength.

4.2.2. Normal Bending Strain Distributions

We placed 12 strain gages to analyze strain distribution: Three on the top surface (350 mm from the bottom), Three on the bottom surface, and one each 30, 110, 190, 220, 250, and 320 mm from the bottom. During early loading, the neutral axis moved upward, but then loading increased because tensile forces were generated in certain compression components. Finally, the neutral axis rose slightly at final loading because the compressive strain in the last fiber of the concrete slab reached 0.003 and the tensile strain thus increased. Therefore, the length of the neutral axis also increased. Table 4 shows the distance of the neutral axes from the bottom of the specimens. For the SPC6-C-P specimen, the distance increased up to 500 kN of load and then decreased after 600 kN. At the ultimate load (741 kN) the distance increased again, to 266.1 mm. For the SPC6-C-T specimen, the neutral axis distance increased during early loading, to approximately 224 mm between 300 and 800 kN. The distance increased further, to 234 mm, at the ultimate load of 827 kN. For the SPC6-A-T specimen, the neutral axis distance increased by about 5 mm over the loading range 100 to 300 kN, and then remained almost unchanged up to a load of 700 kN. The distance increased by 20 mm at a load of 800 kN, and was 253 mm at the ultimate load of 832 kN.

Table 4. Distance to the neutral axes from the bottom of the specimens.

	100 (kN)	200 (kN)	300 (kN)	400 (kN)	500 (kN)	600 (kN)	700 (kN)	800 (kN)	900 (kN)	Max (kN)
SPC6-C-P	210	230	232	230	230	214	212	-	-	267
SPC6-C-T	204	218	224	225	225	224	222	225	-	234
SPC6-A-T	197	212	220	221	221	220	222	242	-	253
SPC6-C-R	198	215	224	225	225	225	225	231	-	246
SPC9-C-T	202	212	220	221	221	220	218	208	203	214
SPC9-A-T	195	201	207	210	213	212	209	193	191	199
SPC9-C-R	199	208	219	220	220	221	220	218	217	219

The neutral axis distance of the SPC6-C-R specimen increased by more than 7 mm over the load range of 100 to 400 kN, and then remained unchanged up to a load of 800 kN, increasing thereafter to 245 mm at the ultimate load (848 kN). For the SPC9-C-T specimen, the neutral axis distance increased up to a load of 300 kN, and then barely changed up to 700 kN, decreasing thereafter (to 214 mm) at the ultimate load of 990 kN. The neutral axis distance of the SPC9-A-T specimen increased continuously up to 700 kN and then decreased. The neutral axis distance at the final load increased slightly to 199 mm. For the SPC9-C-R specimen, the neutral axis distance increased up to 300 kN of load and remained at about 220 mm up to the ultimate load of 1020 kN.

The neutral axis did not change between loads of 400 and 500 kN for specimens with uniformly neutral axes, except during early and final loading. The C-P specimen exhibited the maximal value, of 230 mm. The neutral axis distance for C-T and C-R specimens with 6-mm-thick plates was 225 mm, but was 221 mm for the A-T specimen with a 6-mm-thick plate. Specimens with 9-mm-thick plates behaved similarly. For C-T and C-R specimens with 9-mm-thick plates, the neutral axis distance was 220 mm, but was 210 mm for the A-T specimen. In the C-T and C-R specimens, the lower flanges of the channels lay at 220–224.5 mm. Thus, compressive forces were generated, reducing such forces within the concrete slab and the neutral axis, which was shorter in the A-T versus C-T and C-R specimens because the angle (A) lacked a lower flange.

The tensile stresses of specimens with 9-mm-thick plates were less than those of specimens with 6-mm-thick plates because the area of steel increased. Thus, both the tensile strains and the neutral axis distances decreased. At ultimate loading, the extreme fiber strain was near-constant at 0.003. However, the tensile strain increased rapidly, in turn increasing the neutral axis distance.

4.2.3. Deflection Analysis

To be useful, beams must be serviceable and meet the deflection limit of AISC 303-10 (2010) [16]; the deflection must be less than L/240 during service loading. The novel beam in this study was 5800 mm in length, and the deflection limit was thus 24.16 mm. The dead weight of the beam was calculated using the KBC (2016) [17] method, and a live load of 4.0 kN/m² was applied. Elastic beam theory yielded an SPC6-C-P deflection of 2.05 mm, which was much less than the limit. We also determined deflection limits experimentally. For SPC6-C-P, the live load was calculated as 10.6 kN/m² using the effective width (1000 mm) and length (5800 mm) of the beam; the live load was equivalent to an applied load of P = 61.48 kN. The central deflections of test specimens at this applied load are shown in Table 5. The test deflections were somewhat smaller than the theoretical values; stiffness was reduced by 75%. The beams met the serviceability limits.

Table 5. Relationship between service load and deflection for the test specimens.

	Dead Load	Live Load	Load Conversion	Theoretical Values	Theoretical Values (Stiffness 75%)	Test Values
SPC6-C-P	6.60	4.0	61.48	2.05	2.73	2.32
SPC6-C-T	6.62		61.60	1.93	2.57	2.12
SPC6-A-T	6.62		61.60	1.93	2.57	2.12
SPC6-C-R	6.63		61.54	1.92	2.57	2.23
SPC9-C-T	6.80		62.64	1.76	2.35	1.99
SPC9-A-T	6.80		62.64	1.82	2.43	2.01
SPC9-C-R	6.80		62.64	1.76	2.35	1.93

5. Finite Element Analysis of Wide Composite Beams

5.1. Model Description

We used FEA to investigate composite beam behaviors and to calculate stress distributions predisposing the beams to failure. We used a general-purpose, structural analysis program (ABAQUS (2010) [18]) and employed an eight-node solid element and a four-node shell element to model the concrete and steel of each U-shaped beam (Figure 16).

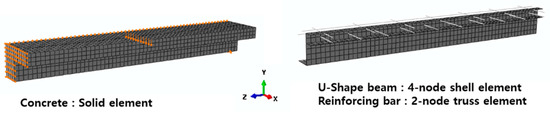
Figure 16. Finite element analysis (FEA) of a composite beam.

We used a truss-node reinforcing bar embedded into the solid element; the interface between the concrete and the bar was perfectly bonded. We also assumed that the concrete and steel U-shaped beam were perfectly bonded. The relative slip between the concrete and the steel beam was thus negligible. Figure 17 shows the concrete materials used. The compressive stress–stain relationship of Sanez (1964) [19] was employed; a linear elastic response was assumed at up to 50% of the compressive strength $f_c^{\prime }$. The elastic modulus $E_c$ was assumed to be 4700 $\sqrt{f_c^{\prime }}$ [ACI 318 (2014)]. We assumed that the tensile stress decreased after $f_{cr}$ (Figure 17); $f_{cr}$ was obtained as described by Hue & Mo (2010) [20]. We used a perfectly elastoplastic model of the steel stress–strain relationship. The tests showed that the average concrete $f_c^{\prime }$ was 25 MPa. For steel U-shaped beams, $f_y$ was 422 and 402 MPa for 6- and 9-mm-thick plates, respectively. For the reinforcing bar, $f_y$ was 446 MPa. We used the damaged concrete plasticity model of ABAQUS (2010) to simulate the three-dimensional response of concrete. The model employs a non-associated flow rule; an additional rule is required. The flow rule is a function of the dilation angle, which was assumed to be 31º (Lee & Fevans (1998) [21]). We applied the isotropic hardening rule to the steel. Figure 18 shows the boundary and loading conditions used. To reduce the computational time, a 1/4-scale model was developed by invoking symmetries (Figure 18). Z-direction displacement at the left end was restrained. The bottom right end was restrained in both the x- and y-directions to simulate roller support. Displacement loading was then applied at the middle (Figure 18).

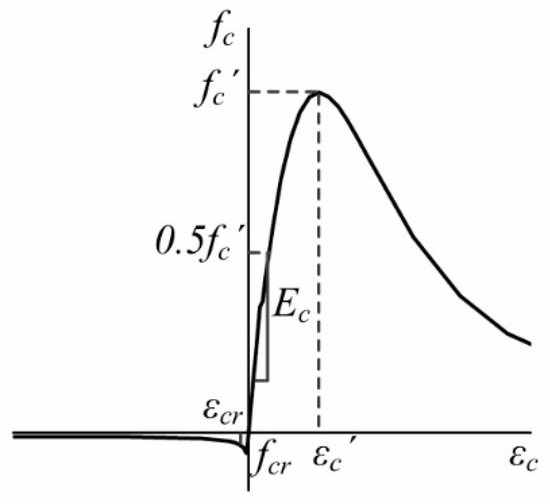
Figure 17. The material concrete model.

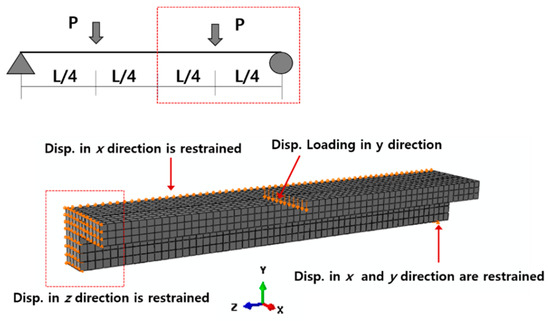
Figure 18. Boundary and loading conditions for FEA.

5.2. Results

We analyzed seven models using the methods described in the previous section. The load-displacement curves obtained via FEA were compared to the test results (Figure 19a–g). The data were in good agreement; the initial stiffness value and ultimate load were well-matched, with a maximum discrepancy of 5%. Thus, the FEA model well-simulated the behavior of the composite beam. The stress distributions in the concrete and steel regions at 120 mm of central displacement are shown in Figure 20a–c for the SPC6-C-N, SPC6-C-T, and SCP9-C-T specimens, respectively. SPC6-C-N is the reference specimen, as it has no internal lattice structure. The SPC6-C-T beam is the same as SPC6-C-N, but has an internal triangular lattice. The SPC9-C-T and SPC6-C-T beams feature 6- and 9-mm-thick steel plates, respectively. FEA showed that both the upper flange and the lower region of the steel yielded. Simultaneously, the concrete stress in the upper flange attained the compressive strength $f_c^{\prime }$. Most of the U-shaped steel web yielded. Thus, the required plastic moment was attained in the absence of both global and local instability. The stress distributions of the SPC6-C-N and SPC-C-T beams were near-identical; no effect of the internal lattice was evident. The failure modes of all three beams were similar (Figure 20a–c). Thus, FEA showed that the section plastic moments required were attained by all beams, as revealed by the stress distributions.

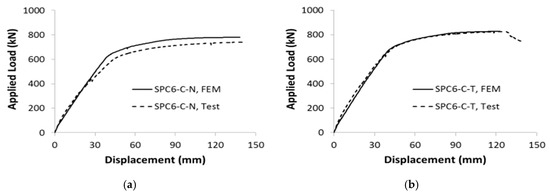
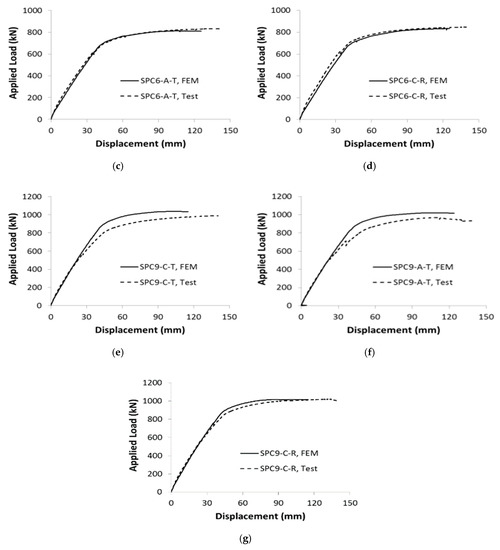
Figure 19. Load-displacement relationships for specimens (a) SPC6-C-N, (b) SPC6-C-T, (c) SPC6-A-T, (d) SPC6-C-R, (e) SPC9-C-T, (f) SPC9-A-T, and (g) SPC9-C-R.

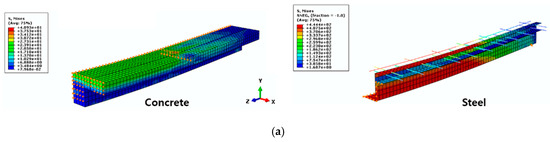
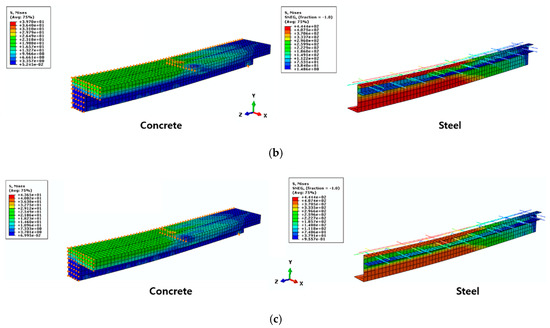
Figure 20. Stress distributions for specimens (a) SPC6-C-N, (b) SPC6-C-T, and (c) SPC9-C-T.

6. Conclusions

We developed wide composite beams for parking structures less than 8 m in height, to maximize the parking space. Each beam reduces the story height by over 200 mm and spans 16 m. We experimentally tested, and performed FEA of beam flexural performance. The key findings were as follows:

(1)

Flexural strength rose by 20% when steel thickness increased from 6- to 9-mm;

(2)

The shape of the slab-supporting components (the angle (A) or channel (C)) had a negligible effect on the flexural strength; these components lay near the PNA;

(3)

The truss bar affected flexural strength because the bottom reinforcing bars enhanced beam tensioning. However, the truss bar shape minimally affected flexural strength, because the top bar lay near the PNA and experienced only a low compressive strain;

(4)

During early loading, the neutral axis initially moved upward but then fell as loading increased, because tensile stresses developed during compression;

(5)

The results of FEA were in good agreement with the test results. The section plastic moments did not trigger global or local instability.

(6)

The novel wide composite beam system proposed in this research can reduce construction costs and resources by reducing the floor height and realizing the long span. Also, it is possible to improve constructability and shorten the construction period since major components are manufactured in the factory and assembled in the field. It should be noted that the proposed system appears to be a suitable candidate for technology minimizing on-site construction work that can reduce greenhouse gas emissions.