A Hierarchical SVM Based Behavior Inference of Human Operators Using a Hybrid Sequence Kernel

Abstract

To train skilled unmanned combat aerial vehicle (UCAV) operators, it is important to establish a real-time training environment where an enemy appropriately responds to the action performed by a trainee. This can be addressed by constructing the inference method for the behavior of a UCAV operator from given simulation log data. Through this method, the virtual enemy is capable of performing actions that are highly likely to be made by an actual operator. To achieve this, we propose a hybrid sequence (HS) kernel-based hierarchical support vector machine (HSVM) for the behavior inference of a UCAV operator. Specifically, the HS kernel is designed to resolve the heterogeneity in simulation log data, and HSVM performs the behavior inference in a sequential manner considering the hierarchical structure of the behaviors of a UCAV operator. The effectiveness of the proposed method is demonstrated with the log data collected from the air-to-air combat simulator.

1. Introduction

An unmanned combat aerial vehicle (UCAV) performs a combat task by being controlled by a human operator who is located in a cockpit separate from the vehicle [1,2]. The probability that UCAVs survive and win a combat task is directly related to the skill of the operator. For this reason, the bulk of research [3,4,5] has been conducted toward improving the quality of the training strategy for operators.

Simulation-based training techniques are widely used to train UCAV operators [5]. Rigby et al. classified the simulation-based studies into four categories including historic simulation, role-play, behavior fidelity, and scenario-based training [6]. They concluded that the last of the approaches mentioned is a well-established practice to improve the skill of UCAV operators. In detail, the scenario-based training is a time-tested methodology to provide a realistic and instructionally-sound scenario that replicates what operators would expect to encounter in a real-world combat situation [7,8].

Although the existing training method was successful at serving as a means of gaining experiences regarding UCAV operational missions [8], it has the limitation that the behaviors of enemies are implemented in a predetermined manner in a given scenario. For this reason, both unexpected behaviors of operators and the differences in behavioral skills among trainees are difficult to consider. However, it is important to construct a real-time training environment where an enemy appropriately responds to the action performed by an operator.

Motivated by the remarks above, to reproduce the enemy’s behavior effectively in the training situation, we propose a novel method for the behavior inference of a UCAV operator using a hybrid sequence (HS) kernel-based hierarchical support vector machine (HSVM). As our problem is to reproduce a human behavior using a dataset, we adopted data-driven machine learning methods rather than optimization or meta-heuristic approaches such as genetic algorithms and particle swarm approaches. Moreover, SVM was selected for the following reasons. First, SVM is known for its high performance and less over-fitting as it minimizes an upper bound of the generalization error [9,10]. Second, it does not require a large amount of training data unlike an artificial neural network (ANN)-based method and neuro-fuzzy inference system, which also suffer from the difficulty in designing the architecture of the networks and selecting fuzzy rules, respectively [11,12].

For the simulation log of a UCAV operator given in the form of a vector, the proposed method uses SVMs in a hierarchical manner: the first SVM determines the behavior group of the corresponding vector and the second SVM provides the actual behavior in each group. Here, the behavior group consists of fire, velocity, and rotate. Then, the behavior of the vector is determined using the corresponding classifier in each behavior group. Specifically, the proposed HS kernel is designed to measure similarities between heterogeneous data, defined as the combination of data collected by different types of sensors or devices. The effectiveness of the proposed method is investigated through numerical experiments on simulation log data collected from a simulator.

The rest of the paper is organized as follows. The next section will review the related work. Section 3 presents the proposed method for inferring the behaviors of a UCAV operator using hierarchical SVMs with an HS kernel. Experiment results are reported in Section 4. Finally, the paper is concluded in Section 5.

2. Related Work

2.1. Inferring the Behavior of an Unmanned Combat Aerial Vehicle

There have been only a few studies conducted for the behavior inference of UCAV operators. For a more extensive literature review, the publications related to unmanned aerial vehicles (UAVs) are additionally summarized. In previous research, the maneuvering of a vehicle was a subject to be formulated by using mathematical models at the beginning of the development of algorithms for UAVs [13]. These studies utilized deterministic models, which led to the fact that they were not able to respond to unpredictable situations.

Later, many research efforts were made to model operator’s decisions and behaviors through rule-based methods [14,15,16]. The main drawbacks of the rule-based methods are that they require predefined rules and that some situations cannot be resolved into rules. Moreover, it is hard to avoid the scalability issue whereby conflicts between rules may occur, and a large amount of computation time is required for the behavior inference when various rules are defined to describe diverse situations fully.

Attempts were also made to predict the behavior of a UCAV operator using statistical learning-based methods [17]. Statistical learning is a machine learning framework for extracting patterns or regularity contained in given data [18]. SVM [19], ANN [20], decision tree (DT) [21], and hidden Markov models (HMM) [22] are representative examples of the statistical learning-based methods. These methods estimate the parameters of a model using a large number of training data. Then, the labels of the new data are predicted by the trained model [19].

As data composed of the behaviors performed by UCAV operators become available, an approach based on statistical learning methods for the behavior inference has gained interest in both academia and industry. Some of the studies investigated HMM to predict the trajectory of UAVs [23,24]. In particular, Lowe et al. proposed a probabilistic trajectory method representing aircraft motion as HMM, where the state space consisted of mode change points [24]. The linear regression model combined with HMM was developed to model UAV operator’s approach control [25]. However, most of them focused on a specific behavior group such as landing approach control and navigation [26].

To the best our knowledge, there has been no paper investigating SVMs to infer the behavior of a UCAV operator. Although SVM is applicable to non-linear data by utilizing the kernel, which is capable of measuring the similarity between two instances by mapping the data into higher dimensions [27], it is known to be vulnerable to handling sequential dependent data [28]. Meanwhile, this paper attempts to resolve the limitation mentioned above by using a novel kernel, which enables SVM to work well with sequential dependent data.

2.2. Statistical Learning from Heterogeneous Data

Attributed to the advance in sensor data and data storage technologies, data related to operators, vehicles, and environments of UCAVs are generated and collected during maneuvering. The inherent properties, high dimensionality, and sequentiality of the generated data make them heterogeneous, meaning that the data are composed of values of diverse types. Das et al. highlighted that the attributes of log data collected from vehicles in military domains are time-series data that are continuously generated over time, which include both discrete and continuous values [29].

The application of statistical learning methods to the heterogeneous data is challenging. This is because most statistical learning methods for classification assume that all attributes of the data can be represented as vectors of real numbers [30]. In other words, using statistical learning methods for heterogeneous data without preprocessing is highly likely to result in the degradation of classification performance due to a decrease in the accuracy of calculating the similarity between vectors [31].

Previous studies are grouped into two types with respect to the method of addressing different value types of attributes. First, most studies utilized the attributes of only one type while ignoring others, resulting in information loss [17,32]. The second line of research examined approaches to discretize continuous attributes [33,34]. However, there exists information loss during the process, and enormous training data for discretization are required in some cases.

Attribute selection methods are widely used for the removal of attributes that are not related to labels [35,36]. A condition feature utilization method was developed by Kim et al. to select the appropriate attributes for each instance [37]. These methods have the limitation of selecting attributes without considering the correlations between them. This disadvantage can be resolved by weighted similarity algorithms, which emphasize the effect of highly-correlated attributes by providing weights for them [38,39]. However, existing weighted similarity algorithms do not present a weight assignment method for sequence dependence attributes.

To address this problem, a multiple kernel learning method was proposed [40]. In this method, different kernels are applied to different attributes, and combinations of the similarity results are utilized as the final similarity. Although the multiple kernel learning method is successful at measuring the similarity between vectors composed of heterogeneous attributes compared to the conventional method, it suffers from high computational complexity as the number of attributes increases.

3. Behavior Inference of UCAVs

3.1. Overview

This work aims to infer the behavior of a UCAV operator by using a simulation log. We are given a simulation log, $L=\left\{({\overrightarrow{x}}_t,y_t)\right|t=1,\cdots ,T\}$, where ${\overrightarrow{x}}_t$ and $y_t$ mean the state vector and the behavior of an operator at the $t^{\mathrm{th}}$ moment, respectively, and T is the total number of instances in the simulation log. Specifically, ${\overrightarrow{x}}_t$ is defined as an N-dimensional vector, and the value of the $n^{\mathrm{th}}$ state attribute for the $t^{\mathrm{th}}$ moment is denoted as $x_{n,t}$. For the inference of $y_t$, the vectors collected in the past than $t^{\mathrm{th}}$ moment are also utilized, and the number of preceding vectors from the $t^{\mathrm{th}}$ moment is denoted as w. Therefore, the purpose of this study is to infer the behavior, $y_{t^{\prime }}$, of a UCAV operator for the moment $t^{\prime }$ using ${\overrightarrow{x}}_{t^{\prime }-w+1},\cdots ,{\overrightarrow{x}}_{t^{\prime }}$.

We present three considerations for the inference of a UCAV operator as follows. First, a set of attributes consisting of a state vector is represented as A, and an attribute in A is denoted by $\alpha$. A is composed of N state attributes such as the velocity and altitude of a UCAV. Table 1 indicates four categories of attributes according to the value type and sequence dependency. In detail, sequence-independent continuous, sequence-dependent continuous, sequence-independent discrete, and sequence-dependent discrete attributes are represented as $IC$, $DC$, $ID$, and $DD$, respectively.

Table 1. Four categories of attributes according to the sequence dependency and the value type.

	Value Type	Continuous (C)	Discrete (D)
Sequence Dependency
Sequence-independent (I)		$IC$	$ID$
Sequence-dependent (D)		$DC$	$DD$

Second, as shown in Figure 1, the behavior of a UCAV operator has a hierarchical structure with three behavior groups including fire, velocity, and rotate. Each behavior group is related to whether firing is required or not, the control of velocity, and the control of rotating, respectively. The descriptions of each behavior are as follows. FM (fire more) and FL (fire less) represent the behaviors of raising and reducing the intention of firing weapons, respectively; VM (velocity more) and VL (velocity less) for those of raising the intention of increasing and decreasing velocity, respectively; and RM (rotation more) and RL (rotation less) for those of raising and reducing the intention of rotating the vehicle, respectively. Here, the behavior group of $y_t$ at the $t^{\mathrm{th}}$ moment is denoted at $z_t$. In this paper, we classify a given state vector (${\overrightarrow{x}}_t$) into one of the behavior groups ($z_t$) and then determine the behavior ($y_t$).

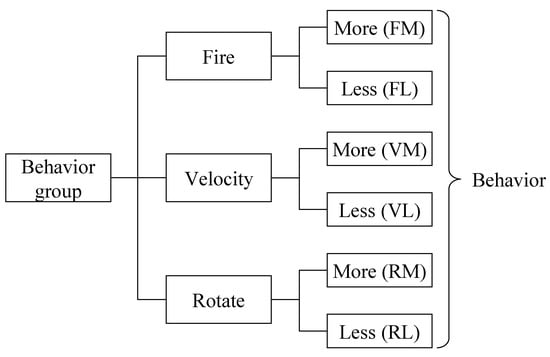
Figure 1. Hierarchical structure of the behavior of an unmanned combat aerial vehicle (UCAV) operator.

Finally, each behavior group has a different set of attributes that are highly correlated with the group. For instance, the target distance of a UCAV, which means the distance between the vehicle and an enemy, is related to the fire group. Furthermore, it is known that the proper attribute subset selection can improve the performance of inference models [41]. Therefore, three attribute sets corresponding to each behavior group are selected, and the details of the attribute selection are described in the following section.

3.2. Inferring Behaviors Using Hierarchical SVMs with a Hybrid Sequence Kernel

3.2.1. Attribute Selection

To improve the inference performance in terms of accuracy and computation time, the attribute selection was performed using the correlation-based feature selection (CFS) method proposed by [42]. This method is based on the hypothesis that good attribute subsets contain attributes highly correlated with the target behavior and uncorrelated with each other. In this study, the CFS method was used as follows.

First, we divided L into three groups, $L_f$, $L_v$, and $L_r$, depending on $z_t$ corresponding to each instance. Here, $L_f$, $L_v$, and $L_r$ indicate simulation logs where their $z_t$ are fire, velocity, and rotate groups, respectively. Then, attribute groups for each simulation log are selected by using the merit of attribute subsets, which measures the usefulness of the individual attributes for predicting the behavior. In detail, the merit of a subset S of A for behavior $b\in \{f,v,r\}$, $M_S^z$, is calculated using Equation (1) with $L_z$, where f, v, and r mean fire, velocity, and turn, respectively.

$$M_S^z=\frac{\left|S\right|{\overline{\rho }}_{\alpha z}}{\sqrt[]{\left|S\right|+\left|S\right|\left(\right|S|-1){\overline{\rho }}_{\alpha \alpha }}},$$

(1)

where $\left|S\right|$ is the number of elements in S; ${\overline{\rho }}_{\alpha z}$ indicates the average attribute correlation with the behavior, and ${\overline{\rho }}_{\alpha \alpha }$ indicates the average attribute inter-correlation. According to the value of $M_S^z$, $A_f$, $A_v$, and $A_r$ are selected from A. To be more specific, $A_f$, $A_v$, and $A_r$ represent sets of attributes used to infer specific behavior corresponding to fire, velocity, and rotate, respectively.

3.2.2. Similarity Calculation

Figure 2 shows how the proposed HS kernel measures the similarity between two state vectors by using different kernels depending on the attribute type. In this figure, $K_I$, $K_{CD}$, and $K_{DD}$ represent kernels for I, $DC$, and $DD$, respectively, and $K_{HS}$ is the HS kernel calculated as Equation (2):

$$K_{HS}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)={\lambda }_I{K}_I({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)+{\lambda }_{DC}{K}_{DC}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)+{\lambda }_{DD}{K}_{DD}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j),$$

(2)

where $\overrightarrow{x_i}$ and ${\overrightarrow{x}}_j$ are the state vectors for moments i and j, respectively, ${\lambda }_I$, ${\lambda }_{DC}$, and ${\lambda }_{DD}$ are the weights or importance of I, $DC$, and $DD$. Specifically, each weight is obtained by dividing the number of attributes corresponding to the weight by the total number of attributes, leading to ${\lambda }_I+{\lambda }_{CD}+{\lambda }_{DD}=1$.

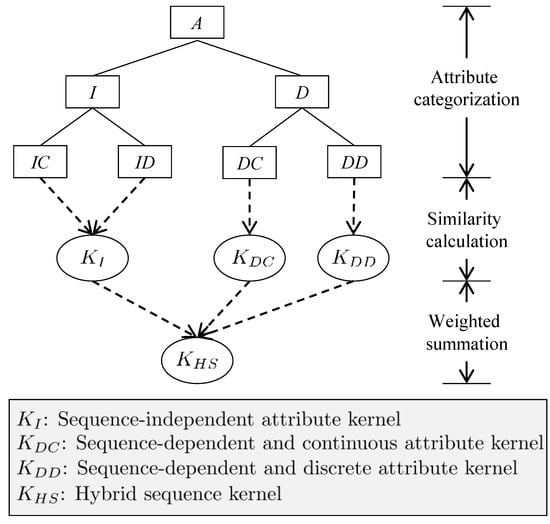
Figure 2. Overview of the hybrid sequence (HS) kernel.

Equation (3) shows how $K_I$ computes the similarity between two state vectors.

$$K_I({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)=k_{linear}({\overrightarrow{x}}_i^I,{\overrightarrow{x}}_j^I),$$

(3)

where ${\overrightarrow{x}}_i^I$ and ${\overrightarrow{x}}_j^I$ are defined as sub-vectors of ${\overrightarrow{x}}_i$ and ${\overrightarrow{x}}_j$, respectively, and they only consist of the attributes corresponding to I. $k_{linear}$ is a linear kernel that separates data linearly and is defined as the inner product of two given vectors, as shown in Equation (4).

$$k_{linear}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)={\overrightarrow{x}}_i·{\overrightarrow{x}}_j.$$

(4)

Meanwhile, the Gaussian kernel, which is known to work well for time-series data [43], utilizes the Euclidean distance of two input vectors as its similarity; it is defined in Equation (5).

$$k_{Gaussian}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)=exp(-\gamma ||{\overrightarrow{x}}_i-{\overrightarrow{x}}_j{\left|\right|}^2),$$

(5)

where $\left|\right|{\overrightarrow{x}}_i-{\overrightarrow{x}}_j\left|\right|$ is the Euclidean distance between ${\overrightarrow{x}}_i$ and ${\overrightarrow{x}}_j$. A kernel for $DC$ using the Gaussian kernel is given by Equation (6).

$$K_{DC}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)=\sum _{n=1}^N{k}_{DC}(x_{n,i},x_{n,j}),$$

(6)

where $k_{DC}(x_{n,i},x_{n,j})$ is a kernel that calculates the similarity between values of the $n^{\mathrm{th}}$ attribute for moments i and j, defined in Equation (7).

$$k_{DC}(x_{n,i},x_{n,j})=k_{Gaussian}({\overrightarrow{s}}_{n,i},{\overrightarrow{s}}_{n,j}),$$

(7)

where ${\overrightarrow{s}}_{n,i}$ and ${\overrightarrow{s}}_{n,j}$ indicate sequence vectors denoted as ${\overrightarrow{s}}_{n,i}=<x_{n,i-w+1},\cdots ,x_{n,i}>$ and ${\overrightarrow{s}}_{n,j}=<x_{n,j-w+1},\cdots ,x_{n,j}>$, respectively.

To develop a kernel for $DD$, we employed a spectrum kernel [44] introduced for the similarity calculation among genomes in the bioinformatics field. The spectrum kernel calculates the similarity between two vectors based on the product between the number of occurrences of given patterns in the vectors, and it is defined as Equation (8).

$$k_{spectrum}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)=\sum _{q\in Q}C(q,{\overrightarrow{x}}_i)·C(q,{\overrightarrow{x}}_j),$$

(8)

where Q is a set of predefined meaningful patterns and $C(q,{\overrightarrow{x}}_i)$ counts the number of occurrences of pattern q in ${\overrightarrow{x}}_i$.

The spectrum kernel is required to be modified to fit the $DD$ of the considered dataset. Since the attributes are composed of a small number of unique values and each value lasts for a relatively long duration, meaningful patterns are hard to capture by the spectrum kernel. To resolve the problem, we summarized a sequence before the similarity calculation. The modified spectrum kernel is defined in Equation (9).

$$k_{MSP}({\overrightarrow{s}}_{n,i},{\overrightarrow{s}}_{n,j})=\sum _{p\in P_n}C(p,S\left({\overrightarrow{s}}_{n,i}\right))·C(p,S\left({\overrightarrow{s}}_{n,j}\right)),$$

(9)

where $S\left({\overrightarrow{s}}_{n,i}\right)$ summarizes ${\overrightarrow{s}}_{n,i}$ by replacing a sequence of repeated values with one value, $P_n$ is defined as a set of sequence patterns extracted from the $n^{\mathrm{th}}$ attribute, and p represents a sequence pattern that remains distinct after summarization. Thus, a kernel for $DD$ is defined in Equation (10).

$$K_{DD}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)=\sum _{n=1}^N{k}_{DD}(x_{n,i},x_{n,j}).$$

(10)

where $k_{DD}(x_{n,i},x_{n,j})$ is presented in Equation (11).

$$k_{DD}(x_{n,i},x_{n,j})=k_{MSP}({\overrightarrow{s}}_{n,i},{\overrightarrow{s}}_{n,j})$$

(11)

3.2.3. Inferring Behavior

HSVM predicts the UCAV operator’s behavior using sets of attributes (A, $A_f$, $A_v$, and $A_r$), training datasets (L, $L_f$, $L_v$, and $L_r$), and the HS kernel introduced in Section 3.2.2. The overall framework of the proposed HSVM is presented in Figure 3. We note that SVMs employ the proposed HS kernel to calculate the similarity between state vectors in both the training and inference phases.

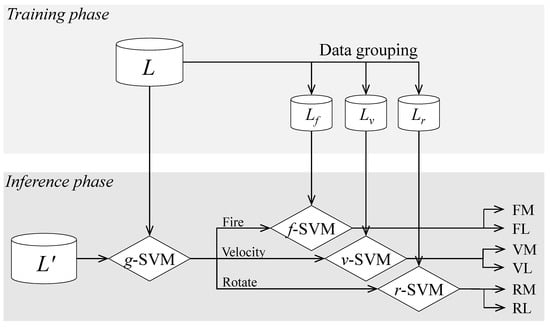
Figure 3. Overview structure of the proposed hierarchical support vector machine (HSVM).

In the training phase, L is divided into three groups including $L_f$, $L_v$, and $L_r$ with respect to $y_t$ for all ts. Then, L is utilized to train g-SVM, and $L_f$, $L_v$, and $L_r$ are utilized for training f-SVM, v-SVM, and r-SVM, respectively. All attributes of log data are required to train g-SVM, which is designed to determine the behavior group, while only the sets of selected attributes, $A_f$, $A_v$, and $A_r$, are used to train f-SVM, v-SVM, and r-SVM, respectively. Algorithm 1 presents the training process of the four SVMs constituting HSVM.

In the inference phase, behavior ${\widehat{y}}_{t^{\prime }}$ of new instance ${\overrightarrow{x}}_{t^{\prime }}$ is predicted using the trained SVMs. The inference phase is composed of two steps and summarized in Algorithm 2. First, ${\widehat{z}}_{t^{\prime }}$ of ${\overrightarrow{x}}_{t^{\prime }}$ is determined by using g-SVM (Line 2). Then, ${\widehat{y}}_{t^{\prime }}$ is predicted by the corresponding trained SVM of ${\widehat{z}}_{t^{\prime }}$ (Lines 3–9). In Lines 3–9, a set of selected attributes is utilized for the corresponding SVM.

Algorithm 1 Training process of HSVM.

Input: A, $A_f$, $A_v$, $A_r$, L, $L_f$, $L_v$, $L_r$

Output: g-SVM, f-SVM, v-SVM, r-SVM 1.4

1: procedure Training

2:     g-SVM ← behavior group classifier trained from L using A

3:     f-SVM ← fire behavior classifier trained from $L_f$ using $A_f$

4:     v-SVM ← velocity behavior classifier trained from $L_v$ using $A_v$

5:     r-SVM ← rotate behavior classifier trained from $L_r$ using $A_r$

6: end procedure

Algorithm 2 Inference phase of HSVM.

Input: ${\overrightarrow{x}}_{t^{\prime }}$, A, $A_f$, $A_v$, $A_r$, g-SVM, f-SVM, v-SVM, r-SVM

Output: ${\widehat{y}}_{t^{\prime }}$

1:  procedure INFERENCE

2:    ${\widehat{z}}_{t^{\prime }}$← predicted behavior group of ${\overrightarrow{x}}_{t^{\prime }}$ classified by g-SVM using A

3:    switch ${\widehat{z}}_{t^{\prime }}$ do

4:        case fire

5:           ${\widehat{y}}_{t^{\prime }}$← predicted behavior of ${\overrightarrow{x}}_{t^{\prime }}$ classified by f-SVM using $A_f$

6:         case velocity

7:           ${\widehat{y}}_{t^{\prime }}$← predicted behavior of ${\overrightarrow{x}}_{t^{\prime }}$ classified by v-SVM using $A_v$

8:        case rotate

9:           ${\widehat{y}}_{t^{\prime }}$← predicted behavior of ${\overrightarrow{x}}_{t^{\prime }}$ classified by r-SVM using $A_r$

10: end procedure

4. Experiment

4.1. Data Description

We prepared the datasets generated by the simulator because it is impossible to use actual combat logs for security reasons. However, we believe that the performance of the proposed method on the log collected from a simulator is highly likely to be similar to that tested on an actual log. Figure 4 presents the snapshot of a simulation conducted on the considered simulator, which represents one-on-one combat.

Figure 4. Snapshots of the simulation from the air-to-air combat simulator.

The simulator performs a simulation according to a scenario containing information on the initial conditions of combat. A scenario includes details such as the types of UCAVs involved in combat and the kinds of offensive and defensive weapons that the vehicles carry. Table 2 presents an example of a scenario used for the generation of a simulation log. The combat type and the field of view (FOV) were set to one-on-one and 60 degrees, respectively. When the scenario was simulated, two UCAVs, a KF-16 and a MIG29, with the same weapons performed the battle according to the engagement sequence.

Table 2. Example of a scenario used for the generation of a simulation log.

Basic setting	Combat	One-on-one
	FOV	60
	Radar range	8000
Scenario		Friendly UCAV	Enemy UCAV
	Type	KF-16	MIG29
	Offensive weapon	AIM120A, AA11, machine gun
	Defensive weapon	Chaff, flare
	Engagement sequence	Friendly UCAV identifies an enemy and fires AIM120A The enemy dodges Two UCAVs fire AA11 Friendly UCAV dodges, and enemy is shot down

Our goal in the data collection was to build a dataset as large as possible, and the 113 scenarios were generated and simulated, which was the maximum number of scenarios that we were able to utilize within a given time limit. Each scenario was simulated for 100 s and composed of 37 behaviors on average. The simulation log consisted of 54 state attributes, and several examples of the state attributes are presented in Table 3. Attributes in the table are grouped into four categories including $IC$, $DC$, $ID$, and $DD$. In detail, aim intensity, altitude, mid-range missile measure, and move aim belong to $IC$, $DC$, $ID$, and $DD$, respectively. Table 4 shows six behaviors, their behavior groups, and the number of occurrences of each behavior in the dataset. We note that the number of occurrences of behaviors belonging to the rotate group is small compared to those of behaviors belonging to the fire and velocity groups.

Table 3. Description of the examples of the state attributes.

Attribute	Category	Description
Aim intensity	$IC$${}^{\mathrm{a}}$	Aim intensity against a target
Altitude	$DC$${}^{\mathrm{b}}$	Altitude of the vehicle
Mid-range missile measure	$ID$${}^{\mathrm{c}}$	Quantity of mid-range missiles
Move aim	$DD$${}^{\mathrm{d}}$	Aiming of a target
Target altitude difference	$DC$	Altitude difference from a target
Target distance	$DC$	Distance from a target
Target speed difference	$DC$	Speed difference from a target
Velocity	$DC$	Velocity of the vehicle

${}^{\mathrm{a}}$ Sequence-independent continuous; ${}^{\mathrm{b}}$ sequence-dependent continuous; ${}^{\mathrm{c}}$ sequence-independent discrete; ${}^{\mathrm{d}}$ sequence-dependent discrete.

Table 4. Number of occurrences of behavior groups and behaviors considered in the experiments.

Behavior Group	Behavior	Number of Occurrences
Fire	FM	300
	FL	1243
Velocity	VM	2039
	VL	793
Rotate	RM	124
	RL	59

4.2. Experimental Settings

In order to select three sets of attributes of the corresponding three behavior groups, $A_f$, $A_v$, and $A_r$, the CFS method was performed on A. Table 5 indicates the results of attribute selection. $A_f$ and $A_v$ consisted of nine and seven attributes, respectively, whereas $A_r$ had only three attributes. Most attributes in $A_f$ were related to a target UCAV or an engagement situation, except for velocity and altitude. On the other hand, $A_v$ had attributes that were mainly related to the maneuvering situation except for short-range missile fire.

Table 5. Results of attribute selection for the three behavior groups.

Attribute Set	Selected Attributes
$A_f$	Target gun distance difference
	Target short-range missile distance
	Velocity
	Short-range missile fire
	Target horizontal LOS
	Target vertical LOS
	Overshoot
	Lock on target
	Altitude
$A_v$	Velocity
	Target speed difference
	Target altitude difference
	Behavior No.
	Short-range missile fire
	Target horizontal LOS
	Gamma
$A_r$	Target speed difference
	Control velocity
	Gamma

As a performance measure for the inference of a behavior, we employed the accuracy defined as the ratio of the number of correctly-classified instances to the total number of instances, which is presented in Equation (12).

$$Accuracy=\frac{1}{T}\sum _{t=1}^T\delta ({\widehat{y}}_t=y_t),$$

(12)

where $\delta ({\widehat{y}}_t=y_t)$ returns a value of one if ${\widehat{y}}_t$ is equal to $y_t$ and returns a value of zero otherwise. For example, when behaviors inferred at three moments in combat were given as {VM, VL, FM} and the actual behaviors were {VL, VM, FM}, the accuracy was 0.33.

Finally, the performance of the proposed method was evaluated by five-fold cross-validation. Specifically, for all performance comparison experiments, the log data extracted from the randomly-selected 90 scenarios among the total of 113 scenarios were used as the training data, while those extracted form the remaining were used to test the performance of the classifiers.

The over-fitting problem may occur as our problem deals with a relatively small dataset. We tried to avoid the problem by adopting SVM, which is known for its generalization power [9], and by evaluating the performances of the proposed method using the five-fold cross-validation method described above. Moreover, all parameters were carefully controlled, and the fine-tuning of the parameters was not encouraged, as it is known that improper selection of the parameters of the kernels is likely to cause over-fitting problems [45].

4.3. Experimental Results

4.3.1. HS Kernel Evaluation Results

In this section, to evaluate the effectiveness and efficiency of the HS kernel for inferring behaviors, we used only log data where $y_t$ was FM or FL. Two experiments were performed as follows. We first measured the accuracies of the HS kernel for different values of w and then selected the w value that yielded the best performance. In subsequent experiment, the performance of the HS kernel was compared to those of the existing kernel functions. The parameters of the sub-kernels (Gaussian, linear, etc.) in the proposed method were determined by performing an exhaustive search according to the test accuracies. The parameters of the sub-kernels were intactly utilized for the kernels in the compared method.

Figure 5 indicates the behavior inference accuracies of the HS kernel according to w. The best performance (of 0.95) was achieved when w was 10. After the maximum value of accuracy was obtained, the accuracy gradually decreased with increasing the value of w. This is because as the value of w increased, values far from the given vector were included in the similarity calculation, which increased the likelihood of concluding that the two vectors representing the different situation were similar.

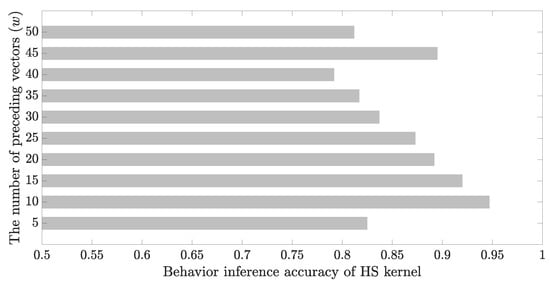
Figure 5. Accuracy of the HS kernel according to the number of preceding vectors (w).

However, exceptionally high accuracy (of 0.895) was observed when the value of w was 45. As mentioned above, although the sequence-dependent discrete kernel overestimated the similarity when w was large, it was effective for utilizing sufficiently large w values for inference in the case of attributes having small changes. Therefore, it can be assumed that the similarity of an attribute was measured effectively when w was 45. It was expected that the utilization of different w values for different attributes would result in performance improvement.

Figure 6 presents the performance comparison results for the HS, multiple, Gaussian, and linear kernels in terms of the accuracy and training time. In this figure, the left Y-axis corresponds to the bar graphs representing accuracies, and the right Y-axis corresponds to the line graphs displaying the training time. The w value of HS and multiple kernels was set to 10. In the case of the multiple kernels, to consider sequence-dependent attributes, the Gaussian and spectrum kernels were used to address continuous and discrete values, respectively.

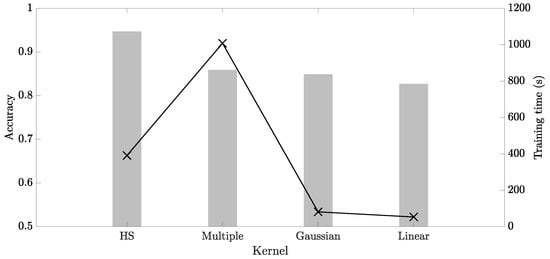
Figure 6. Performance comparison results of HS, multiple, Gaussian, and linear kernels in terms of accuracy and training time.

The HS and multiple kernels required a longer training time than the Gaussian and linear kernels since w additional preceding vectors were involved in the similarity calculation. In terms of the accuracy, the HS kernel outperformed the existing kernels, and the multiple kernels also showed better performance than the others except the proposed kernel. Based on the above observation, we can conclude that the use of the preceding vectors was effective for the inference.

In terms of both accuracy and training time, the HS kernel outperformed the multiple kernels. Since the HS kernel reduced the number of similarity calculations by using the linear kernel for sequence independent attributes, the training time of the HS kernel was much shorter than that of the multiple kernels. Moreover, the results implied that considering only one state vector at one moment for some attributes yielded higher accuracy than considering the preceding vectors for all attributes.

Figure 7 indicates an example scenario where a UCAV operator conducted the behaviors related to the fire group. Figure 7a represents changes in the values of state attributes including aim intensity, target distance, and target speed difference. While the value of the target distance decreased, that of the aim intensity rose dramatically, meaning that two UCAVs were in the engagement situation. Therefore, it can be observed from Figure 7b that the intention of firing weapons was maintained at a high level.

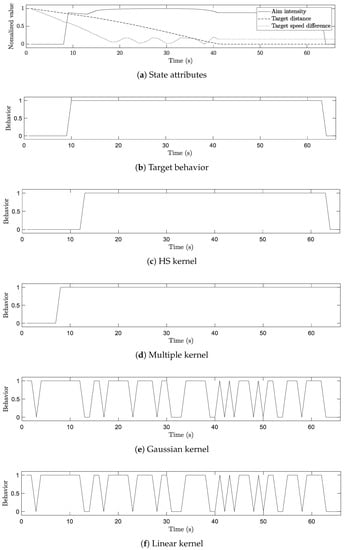
Figure 7. An example scenario involving state attributes, target behavior, and the results of the kernels.

Figure 7c–f indicate that the results of the HS and multiple kernels yielded stable patterns that were similar to those of the target behavior presented in Figure 7b, whereas those of the Gaussian and linear kernels showed severe fluctuations. This difference can be attributed to the fact that the HS and multiple kernels utilized sequential information, while others did not.

Meanwhile, although the results of the HS and multiple kernels were similar to each other, the pattern generated by the HS kernel was more similar to that of the target behavior. Since the HS kernel utilized only meaningful sequential information while the multiple kernels regarded sequence-independent attributes as sequential information, the HS kernel was capable of inferring behaviors more accurately than multiple kernels.

4.3.2. HSVM Evaluation Results

Table 6 presents the performance comparison results for HSVM and the conventional SVM. Here, the Gaussian kernel, which yielded the best performance among the existing kernels in the previous experiments, was used as the kernel function of the one-level SVM. As shown in Table 6, the HSVM with the HS kernel outperformed the one-level SVM that used the existing kernel. The value of the accuracy of the proposed method was 0.645, which may not be satisfactory for practical use. However, this is a promising result since the accuracy of the classifier that randomly predicts one of six behaviors was 0.17.

Table 6. Performance results of HSVM and conventional SVM.

Model	Accuracy
HSVM	0.645
SVM	0.470

5. Conclusions

This paper presented a novel method for inferring the behavior of a UCAV operator from a simulation log that was composed of heterogeneous data of multi-type attributes in terms of the value type and sequence dependency. To resolve the data heterogeneity, we developed the HS kernel, which was designed to measure the similarity of two vectors using the kernel assigned to each attribute type. Furthermore, the hierarchical structure of the behaviors of a UCAV operator was utilized for HSVM, where classification was performed in a sequential manner.

Through the experimental validation on the log data collected from an air-to-air combat simulator, we successfully demonstrated the effectiveness of the proposed method. While the proposed HS kernel required a longer training time than the Gaussian and linear kernels, it showed better performance in terms of accuracy. Especially, the HS kernel outperformed the existing multiple kernels in terms of both accuracy and training time. Finally, HSVM with the HS kernel inferred the behaviors of a UCAV operator more precisely than one-level SVM using the existing kernel.

The proposed method had a limitation that it assumed the six types of behaviors for UCAV operators took place in an exclusive manner, whereas a UCAV operator may perform several behaviors simultaneously in actual combat. For future work, diverse methods allowing multiple behavior inference can be employed to relax the behavior independence assumption of the proposed method. In detail, we plan to investigate the techniques for selecting parameters that are responsible for determining the number of behaviors to be performed. Moreover, future work will focus on developing a method to prevent conflicting behaviors from being selected at the same time.