Abstract
The selection of fresh product suppliers is a multi-criteria decision making (MCDM) problem with great significant and application value. This requires trade-offs between multiple criteria to prove its ambiguity and uncertainty. Therefore, a novel two-stage fuzzy integrated MCDM method to select suitable suppliers is employed. In the first stage, two collective relationship matrixes are constructed by quality function development (QFD), and relationships among customer requirements (CRs), company strategies (CSs) as well as selection criteria are considered separately in the two matrixes. Subjective criteria weights are obtained by fuzzy best-worst method (BWM) appropriately. In the second stage, the objective criteria weights are obtained using Shannon’s entropy method, and the fuzzy multi-objective optimization by ratio analysis plus the full multiplicative form (MULTIMOORA) is applied to rank suppliers. Finally, an application case is applied to prove the feasibility of the proposed method. These conclusions can help companies improve their CSs and increase their market competitiveness.
1. Introduction
Under the highly competitive environment, as the research focus of the supply chain (SC), the supplier’s selection relates to the cost control, response speed, product quality and efficiency of the entire SC, which in turn affects customer satisfaction and the overall competitiveness of SC. Choosing the suitable supplier can achieve a stable cooperation relationship with the supplier and significantly improve customer satisfaction. However, in the traditional meaning, the important purpose of supply chain management (SCM) is to reduce the cost of SC. Nowadays, as non-profit organizations, governments, and people increase their awareness of environmental protection, companies cannot ignore environment-related factors if they want to gain a foothold in the global competition. Based on this background, the concept of green supply chain management (GSCM) has emerged and been widely discussed by many scholars [1,2,3]. GSCM is a SCM method based on the concept of sustainable development and ecological protection [4,5,6,7], which focuses on providing high-quality and environmentally-friendly products and services. Selecting the appropriate green supplier is the basis and prerequisite for establishing a green SC, which is an inevitable choice for achieving sustainable development. In view of the uncertainties and information limitations of the GSCM, fuzzy methods are used to select suppliers [8]. At the same time, due to the existence of qualitative and quantitative evaluation criteria [9,10,11], it is very necessary to establish a suitable and highly flexible supplier selection method [12,13,14,15].
The government has successively introduced various laws and regulations, and put forward more stringent requirements for the production process of fresh product companies in order to guarantee the quality of fresh products. This requires that fresh product companies must actively improve the product quality management level and integrate GSCM into the entire fresh product supply process in order to truly realize the GSCM. Recently, in the research field of fresh product supply chains, only few researchers have focused on the supplier selection [16,17,18,19,20,21]. Therefore, a novel two-stage integrated fuzzy multi-criteria decision making (MCDM) method is proposed for the selection of green suppliers of fresh products. This method can consider the interrelationships between the supplier selection criteria. In practice, it can also help companies identify customer requirements (CRs) and recognize the pros and cons of companies at the current stage. In this paper, the proposed method is elaborated based on comprehensive perspective. Concretely, in the first stage, the integrated attribute values (the real numbers and linguistic fuzzy variables coexist) are transformed into trapezoidal fuzzy numbers (TrFNs). Then the CRs are transformed into company strategies (CSs) by quality function development (QFD). The weight of quantitative assessment is obtained by fuzzy best-worst method (BWM). In the second stage, the Shannon entropy method is presented to obtain qualitative assessment. The multi-objective optimization by ratio analysis plus the full multiplicative form (MULTIMOORA) method is used to rank. Finally, an application case is illustrated to highlight the implementation, availability, and feasibility of the method. Furthermore, comparative analysis and sensitive analysis are also applied to validate the feasibility and efficiency of the method.
The rest of this paper is structured as follows. A literature review is presented in Section 2. The two-stage integrated MCDM method using TrFNs is proposed in Section 3. Subsequently, Section 4 is a case study on green fresh product supplier selection. Section 5 conducts the comparative and sensitivity analysis. The managerial implications are discussed in Section 6. Finally, Section 7 summarizes several conclusions and contributions, as well as suggestions for future work.
2. Literature Review
The literature is briefly reviewed in three different but relevant streams: fresh product SC, supplier selection criteria, and selection methods.
2.1. Fresh Product Supply Chain (SC)
In the traditional SC model, the loss caused by product quality is generally not considered. However, in the fresh product SC, fresh products such as vegetables, meat, etc., during the trading time, due to their perishable nature, fresh products become non-fresh as time passes, resulting in a decrease in saleable quantity. Therefore, some scholars have summarized and reviewed the research on the SC of perishable products such as fresh products [22,23].
In the research of fresh product SC, Ghoreishi et al. [24] assumed that the loss rate of fresh agricultural products was small, and established a metamorphic inventory model in which the metamorphic rate was time-varying and the repurchase rate was dependent on the time. Chang et al. [25] studied the model of external loss-sharing based on the revenue sharing and risk sharing of perishable products between suppliers and manufacturers. Calvo et al. [26] studied the SC ordering strategy of short life cycle products based on the incentive model in game theory. Kumar et al. [27] studied the ordering strategy of partial shortages under stochastic demand and the product’s metamorphic rate as a fuzzy number. Samir et al. [28] assumed that the consumer’s demand would change with the degree of deterioration of fresh product, and studied the management of fresh product inventory in this case. In summary, although quite a lot of literature has studied fresh agricultural products, perishable products and short life cycle products, their research focused on inventory management and ordering strategies. There is less research on the SC of fresh product based on the combination of CRs and CSs with an integrated MCDM method.
2.2. Supplier Selection Criteria
Nowadays, research on supplier selection criteria and decision models has received extensive attention from scholars and rich results have been obtained. These research works addressed various aspects of supplier decision-making that focused on green themes and sustainability in SC management [16,29,30,31,32]. A considerable amount of research has already addressed the trade-off between the weights of these criteria aim to select the optimal solution for specific problem variables and constraints [33].
In research into the traditional supplier selection, by comparing the selection of criteria by Dickson and Weber [34], certain criteria (such as price, delivery time, production equipment, production capacity, and technical capability) are most widely used for selection. Among the green supplier selection literature, scholars have introduced some new concerns. Govindan et al. [16] reviewed the GSCM and proposed that the environmental management system (EMS) is the most considerable criteria compared to other related criteria. Akman [35] presented a two-stage supply assessment concept method (economic criteria and green criteria) for evaluating green suppliers. Sarkis and Dhavale [36] believed that the supplier’s choice was crucial to the achievement of sustainable SC partnerships, and proposed a supplier assessment and selection framework using the the triple bottom line approach (TBL). Grimm et al. [37] described the SCM and constructed an evaluation framework from a green perspective. A concept method was proposed to measure how well sub-supplier management complies with sustainability standards. Trapp and Sarkis [38] proposed a mathematic model considering supplier selection, supplier development and sustainability issues. From these studies, we can conclude that green and sustainability criteria are used increasingly.
In our research, we construct the green supplier selection criteria from seven aspects, namely QA (quality adaptation), P (price), ENRC (energy and natural resource consumption), DS (delivery speed), GD (green design), RRR (reuse and recycling rate), and PP (production and planning). The established criteria were used and suppliers were evaluated in conjunction with green supplier criteria. The weights of each criterion is evaluated and weighted according to the proposed method.
2.3. Supplier Selection Methods
Numerous researchers have developed a variety of supplier selection methods from single methods to integrated methods. Integrated methods using two or more techniques have attracted more interest due to their practicality and flexibility [39]. The most popular objective and subjective MCDM methods of green supplier selection are analyzed as follows.
Using the analytic hierarchy process (AHP) and analytic network process (ANP) to obtain the subjective importance coefficient of supplier evaluation criteria is widely applied for research [40,41]. For the above methods, some necessary pairwise comparisons should be performed at the appropriate level of accuracy, which requires consistent user participation and consistency of judgment [42]. In addition, the number of suppliers criteria included in the comparative assessment is preferably limited to nine to avoid jeopardizing the consistency of human judgment [43]. In order to enable companies to effectively plan their products and services and adapt to a market-oriented environment, the goals set by the company need to consider CRs. QFD has a wide range of applications that can transform CRs into CSs and help companies provide competitive products and services [21,44,45,46]. However, one of the major limitations of conventional QFD methods is the application of absolute priority to determine the relative weights of CRs. To overcome this defect, the AHP and ANP have been integrated with QFD to select suppliers [40,44]. However, it still requires a tedious cumbersome pair comparison between elements. Therefore, we will consider combining QFD with fuzzy BWM to reduce the cumbersome nature of pairwise comparisons. BWM is a subjective method that was first developed by Rezaei to determine the priority of the standard [47]. BWM has several significant advantages. One is to provide a structured pairwise comparison matrix, which only requires the comparison of two vectors rather than acomplete pairwise comparison. Compared with AHP, the time of comparison is significantly reduced. Second, the method can be combined easily with other MCDM methods [48,49]. In addition, Guo and Zhao proposed fuzzy BWM using triangular fuzzy numbers [50]. This proposed method facilitates decision makers (DMs) to determine the priorities of criteria through qualitative judgment.
Although subjective approaches can be applied to identify the criteria weights, the assessment procedure may be affected by inconsistencies, human errors and other factors owing to the different knowledge and experience of the DMs. Objective methods, such as information entropy, can be used to be the weighting method to eliminate artificial uncertainty and get more realistic results. In particular, Shannon entropy can be used to determine the degree of confusion in system information and effectiveness. Taking into account the attributes of this research indicator, Shannon’s concept has the ability to be used as a weight calculation method [51].
In terms of alternative supplier ranking, widely used methods include TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution), VIKOR (VIsekriterijumska Optimizacija I Kompromisno Resenje) and COPRAS (Complex Proportional Assessment) [52,53,54,55,56,57]. Different from the common MCDM methods, Baležentis et al. [58] presented a MULTIMOORA method for supplier evaluation and ranking. It includes the ratio system (RS), the maximal objective reference point (MORP) and multiplicative form (MF) [59]. In practice, MULTIMOORA is proved to be the insensitivity method of multi-objective optimization (MOO) and high frequency used to solve MCDM problems under an uncertainty environment, because there is no other method that can meet all the robustness conditions of MOO [58,60]. Therefore, MULTIMOORA was used for company operation evaluation in many cases [61,62]. Although MULTIMOORA offers many effective and practical solutions to deal with complex and actual MCDM issues under uncertain environments, so far, no research has been done to combine fuzzy MULTIMOORA with other fuzzy evaluation methods for comprehensive assessment of green fresh product suppliers.
In conclusion, by synthesizing multiple MCDM methods, a selection model with specific functions and characteristics can be constructed, and this method has been increasingly used by scholars due to its high degree of flexibility. In order to realize the suitable supplier selection under a fuzzy environment, a comprehensive two-stage selection method composed of QFD, fuzzy BWM, the Shannon entropy weight method and the MULTIMOORA method was proposed. This research is helpful for fresh product supplier selection considering qualitative and quantitative criteria. In the first stage, two collective relationship matrixes were constructed by QFD, and the relationship between CRs and CSs was considered separately, taking into account their outstanding characteristics. Fuzzy BWM can appropriately derive the subjective criteria weights. In the second stage, Shannon entropy measurement was proposed to get objective criteria weights. Meanwhile, fuzzy MULTIMOORA was applied to rank suppliers according to each criterion. Taking into account the advantages of these methods, the developed two-stage integrated MCDM method can derive more robust and comprehensive results [63]. An application example is created to test the provided method. Comparing the proposed method with TOPSIS, VIKOR and COPRAS, and sensitivity analysis can also confirm the feasibility and effectiveness of the proposed method.
3. The Novel Integrated Two-Stage Multi-Criteria Decision Making (MCDM) Method
This paper focuses on selection of green fresh products suppliers. Supplier selection includes two stages: the establishment of criteria and the presentation of the selection method. In the first stage, two matrices were constructed based on QFD. The relationship among CRs, CSs, and selection criteria was considered separately in the two matrices. Meanwhile, the fuzzy BWM was obtained to calculate the priority of CRs, CSs and the subjective criteria weights. In the second stage, Shannon’s entropy method was used to obtain the objective criteria weights, and the supplier was ranked using the fuzzy MULTIMOORA. The exhaustive steps of the proposed two-stage integrated method are shown in Figure 1.
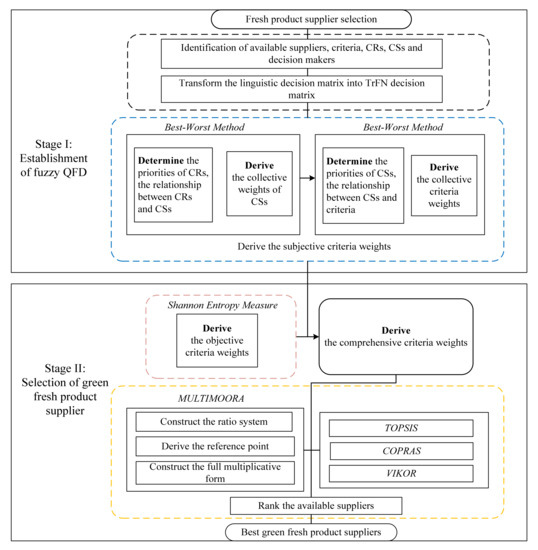
Figure 1.
Assessment framework of proposed approach.
3.1. Fuzzy Set Theory
In the selection process, the data information that people get when dealing with practical problems often has uncertainty, language variables can be used in situations where it is difficult to describe these conditions using traditional quantitative expressions [64], such as interval numbers (INs), triangular fuzzy numbers (TFNs), trapezoidal fuzzy numbers (TrFNs), etc. It is proved that TrFNs are the most commonly applied types of fuzzy numbers. It is characterized by . The corresponding membership function is demonstrated as follows [65].
where, , , and are the vectors of the fuzzy number.
Definition 1.
For two positive TrFNs parameterized byandfor,. After that, the algebraic operations for the TrFNs are demonstrated as follows:
Addition operation:
Subtraction operation:
Multiplication operation:
Division operation:
Scalar Multiplication:
Distance between two TrFNs:
Definition 1.
Converting fuzzy numbers to crisp numbers is a significant step in the application of fuzzy numbers. The centroid-based defuzzified value is as follows [66].
DMs can use linguistic term sets with different granularities and membership functions to transform their opinions. In this paper, we use seven-point TrFNs to characterize the weights of indicators and the ratings for green fresh product suppliers as shown in Figure 2. In addition, the experience and knowledge of DMs in the field varies from person to person. Therefore, considering this factor, we weight them based on the years of experiences they have. These linguistic terms can be mapped by TrFNs, as shown in Figure 3.
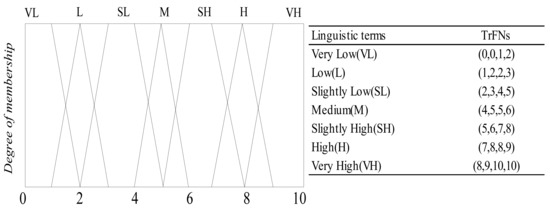
Figure 2.
Membership functions and linguistic terms for pair-wise comparisons of criteria.
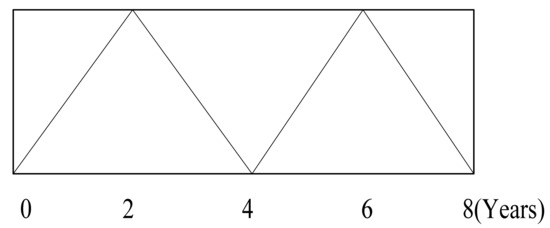
Figure 3.
Representation of decision makers’ (DMs) experience using linguistic term.
3.2. Fuzzy Best-Worst Method and Subjective Weights
BWM was proposed by Rezaei [47]. This method is a very effective subjective method for obtaining weights (see Figure 4).Compared with n(n − 1)/2 times of AHP, the BWM is only 2n − 3 times [50]. In addition, the final weights are highly robust. Moreover, the CI (consistency index) is needed for checking the consistency. The maximum possible value of CI corresponding to the linguistic terms is shown in Table 1. The detailed steps are as follows:
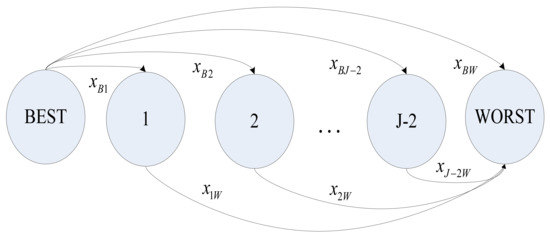
Figure 4.
Reference comparisons.

Table 1.
Linguistic terms and corresponding consistency index (CI) values.
Step 1. Define the decision criteria .
Step 2. Select the best criterion and the worst criterion .
Step 3. Obtain the priority of the best criterion over all the other criteria and the priority of the other criteria over the worst criterion (particularly, , ). The priorities are converted to TrFNs by the language terms in Table 1. The best to others (BO) and the others to worst (OW) vectors are expressed as follows:
Step 4. Obtain the optimal weight vector .
The optimal fuzzy criterion weight is the one where, for every fuzzy pair and , the following formulas should be satisfied:
Using Equation (11), the weight vector and CI are calculated. cannot exceed the maximum possible CI value. Table 1 lists the largest possible CI for different linguistic variables. In addition, the Consistency Ratio (CR) equals to . When , the calculation result is acceptable, the closer the CR is to 0, the stronger the consistency [59].
3.3. Shannon Entropy and Objective Weights
Objective weights can be obtained using the entropy method. The Shannon entropy is proposed by Shannon that is suitable for calculating the relative importance of criteria [51,67], the corresponding steps are as follows:
Step 1. Standardize the criterion:
Step 2. Obtain the divergence of each criterion:
Step 3. Derive the normalized objective weights of criteria:
3.4. Multi-Objective Optimization by Ratio Analysis Plus the Full Multiplicative Form (MULTIMOORA) and Supplier Ranking
The MULTIMOORA method is used to solve supplier selection of green fresh product by ranking the alternatives, i.e., suppliers [58]:
Step 1. Transform the initial matrix into a normalized matrix:
where, matrix are the original criteria values of alternatives ; is a dimensionless value of .
Step 2. The RS.
The priority of the supplier, according to the relative significance of supplier with regard to criteria can be obtained as follows:
where the parameters, which’s footnote is , , are the maximized criteria and the minimized criteria respectively; is the weights of criteria.
Step 3. The MORP.
In order to express MORP, the ideal supplier needs to be determined, it includes the benefit and cost criteria. Then, the Min-Max metric is used to rank the suppliers:
Step 4. The MF.
The utility of the suppliers can be calculated as follows:
where and are calculated for benefit criteria and cost criteria, respectively. and are calculated as follows:
3.5. The Proposed Integrated Two-Stage MCDM Method
A two-stage method is presented in this subsection. This method integrates QFD, fuzzy BWM, Shannon entropy and fuzzy MULTIMOORA. Supposed I alternatives, namely, (); criteria, namely, (); DMs denoted as ; some other notations, such as, and , namely, and , respectively. Finally, the corresponding fuzzy weight of DMs denotes as .
Stage 1. Derive the subjective criteria weights
In this stage, the two QFD matrixes and are constructed. indicates the relationships between CRs and CSs, represents the relationship between CSs and the selection criteria. The output of is the input for the matrix as shown in Figure 5. Then the subjective criteria weights are calculated. The detailed procedure is described in the following.
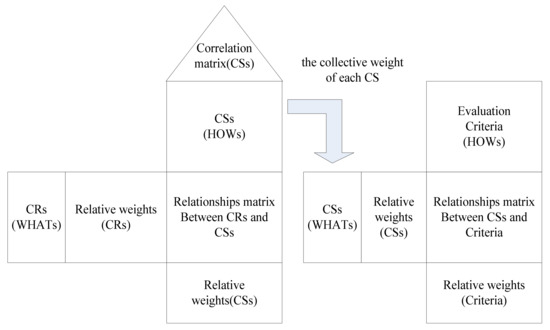
Figure 5.
Representation of the quality function development (QFD) process.
Step 1. Determine the best criteria and worst criterion, separately.
After recognizing CRs, those criteria separately expressed by and are determined by DMs.
Step 2. Execute the comparisons.
The BO vector and OW vector of are derived as follows:
where, and are represented by TrFNs. Particularly, .
Step 3. Gain the optimal solutions.
The optimal solution is derived, and the fuzzy priorities of customer requirements can be obtained below [50]:
where , denote the defuzzified collective priorities of CRs, which is calculated by using Equation (8); and denote the priority of , , which is determined by DMs.
By using Equation (22), the optimal solutions and the corresponding optimal CI (namely, ) are derived.
Step 4. Calculate the collective priorities of CRs.
where denote the collective priorities of CRs; present the collective priorities in crisp values of CRs.
Step 5. Calculate the collective criteria weights of CSs.
DMs rate the relationship degree between CRs and CSs using linguistic terms. The relationship matrix of is denoted by , in which .
The collective relationship matrix can be calculated as follows:
where, .
Then, the collective weights of CSs can be calculated as follows:
where, denote the fuzzy collective weights of CSs, denote the deffuzified collective weights of CSs.
The second matrix represents the relationship of the CSs and the criteria. The output of the collective priorities in Step 5 is used as input of the next step. Steps 6–10 output the collective criteria weights, which comprise the subjective criteria weights. The relationship matrix of DMs is established after identifying the criteria. The relationship matrix of is defined by , where .
Steps 6–9. Similar to Steps 1–4, the collective priorities of CSs can be calculated as follows:
where, represent the fuzzy collective priorities of CSs; denote the defuzzified collective priorities of CSs.
Step 10. Calculate the subjective weights of criteria.
DMs measure the relationship rate between CSs and the corresponding criteria using linguistic terms. The second QFD matrix of is denoted by , where .
The collective QFD matrix can be obtained as shown below:
where .
The collective criteria weights of criteria can be calculated as shown below:
where, denote the fuzzy collective criteria weights, represent the collective criteria weights in crisp values.
The collective criteria weights and the subjective weights are different in magnitude. Therefore, the collective criteria weights should be normalized and the subjective criteria weights can be obtained as follows:
Stage 2. Selection of green fresh product supplier
In the second stage, the objective weights are determined by the Shannon entropy method. Furthermore, the fuzzy MULTIMOORA method is used for ranking all of the green fresh product suppliers.
Step 1. Obtain the standardized decision matrix.
Qualitative and quantitative methods are both involved in the criteria. The qualitative method is expressed as linguistic variable alternatives to the criteria converted to TrFNs by referring to Table 2. Quantitative evaluations were expressed in terms of crisp values converted to TrFNs by the idea of Yao and Wu [68]. For a crisp value , the corresponding TrFN is . Then the fuzzy decision matrix of on alternative to each criterion is derived , where .

Table 2.
Customer requirements (CRs), company strategies (CSs) and criteria.
Step 2. To keep the ranges of standardized TrFNs belong to the interval , the standardized fuzzy decision matrix of is represented as , in which .
Step 3. Calculate the collective matrix.
The collective matrix by using the simple arithmetic is shown below:
where .
Step 4. Obtain the objective criteria weights by using Shannon entropy method.
Step 4.1. Normalization of criteria which yields the projection value of criteria, and is transformed to , which is calculated by Equation (38).
where denote the collective criteria weights in crisp values.
Step 4.2. Calculate the divergence of criteria.
Step 4.3. Derive the normalized objective criteria weights.
Step 5. Derive the combination of the subjective and objective criteria weights.
By Equations (35) and (42), the subjective weights as well as the objective weights are obtained respectively. The combined criteria weights are calculated as follows [68].
where expresses the subjective weights for the relative effectiveness of the objective weights, its value range is set to . Generally, the value is set as , which shows that the subjective weights and objective weights are the same in the importance synthesis.
Step 6. Rank all suppliers.
The fuzzy MULTIMOORA is used as shown below:
Step 6.1. Derive the RS.
where is the number of beneficial criteria; are the number of cost criteria; denote the combined criteria weights, which are yielded by Equation (43); represent the utility of supplier.
Step 6.2. Obtain the MORP.
The MORP is based on the weighted fuzzy decision matrix . The normalized is within . Therefore, the MORP is defined as for the benefit criterion and for the cost criterion. Moreover, Equation (7) can be used to obtain the maximal deviation from the MORP for each supplier.
Then, the suppliers are sorted in ascending order by .
Step 6.3. Construct the MF.
The overall utility can be obtained as shown below:
where represent the benefit criteria outcome of with g being the maximized criteria number; represent the cost criteria outcome of with . The suppliers are then sorted in descending order through .
Step 6.4. Rank the alternatives.
The dominance analysis approach is used to summarize the three values provided by MULTIMOORA [58].
4. Case Study
The supplier selection analysis involves a company that supplies a range of fresh product. Pitaya, pineapple, red delicious, cherry and other fruits are the company’s main business products. The data is used in this section to compare supplier selection analysis. The purpose is to complete supplier selection analysis for every product purchase.
For a specific fresh product, the company orders the product from a large planting base, that is, each supplier. After the order is generated, the company will contact its alternative suppliers, who are responsible for picking, packaging, and then transporting it to destinations such as Japan and the United States. The company is a direct customer and the producer will be a supplier. Through the initial screening process, five fresh product suppliers were identified. For the supplier’s choice, the decision maker must very carefully assess the needs of all customers and consider how each supplier can fully achieve these goals.
Five different supplier samples are provided to the company. In order to get accurate assessments, four are invited to form an expert group to make the evaluation.
The decision group includes a senior manager of a fresh agricultural production organization, a manager of a fresh product company, a decision-making professor and a public sector official, who all have extensive experience and knowledge in the field of fresh product. In addition, according to their different working years, this study adds their respective weights to their evaluations as shown in Figure 3. An inexperienced DM is given , while a general experience DM is given , and an experienced DM is given . In addition, the weights of DMs are , here, , , and . Six CRs, eight CSs and seven evaluation criteria are selected through market research, as shown in Table 2.
Customer requirements refer to a broad and in-depth understanding of the actual needs of customers to help companies make the right decisions. In actual life, customers prefer to buy fresh and healthy ingredients, and get a product experience that has just been freshly picked from the orchard, so their first concern is the quality factor of fresh products such as size, shape, color, elasticity and odor. Secondly, whether the implementation standards for production of fresh products are strict, whether there are pesticide residues, and whether the detection of heavy metal content, microorganisms, mycotoxins, etc. meets the requirements are also of great concern to customers. Any customer is very concerned about price; they all prefer to buy fresh and healthy fresh products at the lowest price, so there is more demand for products with good quality and low prices . Moreover, the company’s credit, prestige, and overall recognition level in the industry , as well as the ability to provide fresh product in terms of quality and quantity , and the ability to effectively perceive, respond quickly, and effectively meet CRs are also the important customer demand for a satisfied fresh company.
In response to CRs, eight CSs and seven evaluation criteria are also selected according to the literature survey. Seven evaluation criteria, namely QA, P, ENRC, DS, GD, RRR and PP are explained as follows. The essence of the argument about QA is to understand quality from the perspective of customer use. P refers to the quotation per unit of agricultural products provided by the supplier. ENRC are the total amount of resources consumed by suppliers to provide products. DS refers to the supplier’s cold chain transport speed to ensure the fresh products’ arrival at the target company. It is numerically equal to the distance traveled in unit time. GD refers to the ecological guarantee and the ability to reduce packaging materials. RRR refers to the ratio of the sum of the quality of discarded products that can be recycled (including re-use, recycling, and energy recovery) to the quality of recovered waste products. PP refers to suppliers who can reasonably formulate production plans so that products can be supplied with quality and quantity. P and ENRC are criteria to be minimized and the remaining are criteria to be maximized.
Based on collective background information of five suppliers and the rate is given by the DMs, the , , and were determined based on the company background information of five suppliers and the evaluation results provided by the decision group, as shown in Table 3. ,, and are shown in Table 4 and Table 5. After the corresponding CRs determines the CSs, the linguistic terms shown in Table 2 are used to represent the correlation assessment between CRs and the corresponding CSs to establish the first QFD matrix, as shown in Table 6. The range of language terms determines the degree of relationship. In particular, the blank element indicates that there is no relationship between CRs and CSs. In the same way, the second QFD matrix is established, as shown in Table 7, which demonstrates the degree of relationship between CSs and the corresponding criteria. Finally, according to the background information of the five suppliers, the suppliers are evaluated by five DMs. The calculation results are listed in Table 8. Since the form of DMs is a linguistic term, we need to convert linguistic terms to corresponding TrFNs according to the rules shown in Table 1 and Figure 2. The two-stage decision method proposed is applied to this case. The detailed solution steps are as shown below:

Table 3.
The CRs and CSs identified by DMs.

Table 4.
The best to others (BO) vectors of CRs and CSs identified by DMs.

Table 5.
The others to worst (OW) vectors of CRs and CSs identified by DMs.

Table 6.
Correlation assessments of DMs on CRs and CSs.

Table 7.
Correlation assessments of DMs on CSs and criteria.

Table 8.
Assessments of DMs on suppliers with respect to criteria.
Stage 1. Derive the subjective criteria weights
, , and can be collected into , , and using Equations (20) and (21). DM’s optimal solution and the optimal CI can be obtained. The results are acceptable because the values of the consistency ratio are all below 0.1. The fuzzy collective priorities of the CRs can be calculated and expressed as = (0.3754, 1.8741, 5.6328, 10.2744), = (0.5449, 2.9109, 10.6813, 21.7885), = (0.4048, 1.8645, 7.0667, 12.4848), = (0.3036, 1.4240, 4.4778, 8.4931), = (0.1560, 0.6938, 2.1468, 4.3733), = (0.1650, 0.7750, 2.3543, 4.2982). Then, = (0.1712, 0.3426, 0.2053, 0.1391, 0.0702, 0.0716).
After the collective relationship between the CRs and CSs is obtained by Equation (25), the collective CSs weights are obtained by Equation (26).
Then, = (3.2724, 2.2107, 1.5170, 4.6807, 4.1323, 4.1071, 2.4394, 1.8209). Using Equation (28), the collective priorities of CSs can be obtained as = (0.2727, 1.5626, 5.1966, 10.3455), = (0.2821, 1.3288, 4.3797,8.3510), = (0.2356, 1.1271, 3.7303, 7.4155), = (0.4077, 2.4179, 7.7427, 17.0088), = (0.1964, 0.9180, 2.8988, 5.5564), = (0.2416, 1.1051, 3.4990, 6.6200), = (0.1204, 0.5357, 1.7249, 3.1286), = (0.1682, 0.6805, 2.0790, 3.9177). Then, = (0.1726, 0.1359, 0.1168, 0.2643, 0.0826, 0.1110, 0.0508, 0.0660).
The collective relationship between CSs and the corresponding criteria and the collective relative weights of CSs are obtained by Equations (32)–(34). Then, the subjective criteria weights are obtained using Equation (33). The results are demonstrated in Table 9.

Table 9.
Criteria weights (when ).
Stage 2. Selection of green fresh product supplier
Firstly, the normalized fuzzy matrix of DMs can be obtained using Equation (36). Then, the corresponding fuzzy collective matrix can be calculated through Equation (34). Finally, the objective and the combination criteria weights can be obtained using Equations (38)–(42). The calculation results are shown in Table 9.
Equations (40)–(44) are applied to obtain the result of the suppliers ranking. The suppliers ranking is obtained based on the dominance analysis approach. The calculation results are listed in Table 10. The suppliers ranking is and the supplier with the best performance is .

Table 10.
Ranking result of suppliers.
5. Results and Discussion
The MULTIMOORA method is compared with the COPRAS, the VIKOR and the TOPSIS. The results of comparative suppliers ranking are shown in Figure 6. Obviously, although the rankings of the suppliers are slightly different, the best supplier obtained by the four methods is still and the worst supplier is . As a result, this comparative analysis validates the robustness and effectiveness of the MULTIMOORA method.
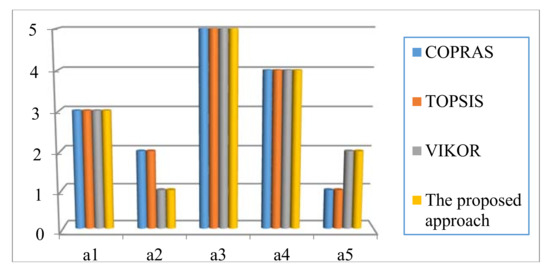
Figure 6.
Comparative ranking of suppliers.
Sensitivity analysis includes the impact of the variable values of on the ranking of suppliers. In order to study the change of the rank of, varying were set.
The ranking results with varying of supplier ranking are demonstrated in Figure 7. The ranking of suppliers is , when . Although the value of is changed, the best and worst choices are still and , respectively. Therefore, this result proves the applicability of this method.
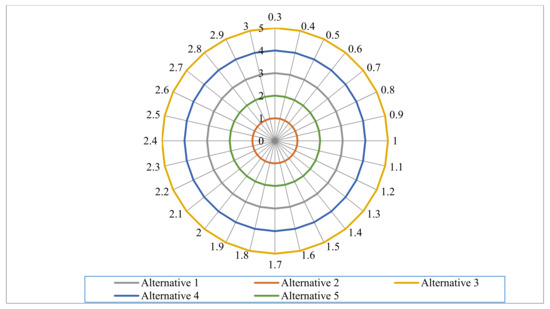
Figure 7.
The radar plot showing the ranking results with varying .
6. Managerial Implications
The proposed two-stage method has provided solutions and recommendations for studying the advantages and disadvantages of the fresh product GSCM. Furthermore, the model makes contributions to fresh product companies for improving competitive performance.
(1) For CRs, the test standard of security (TSS) is assigned the highest priority of 0.3426, it proves that customers attach much significance to the test standard of product security. Therefore, a fresh product company should provide high-standard products to customers. Moreover, people not only prefer product security but also pay attention to the price of fresh product. Thus, managers are recommended to reduce product prices on the premise of guaranteeing security standards.
(2) The MC (management commitment) is the most critical CSs and has a priority of 0.2643 in performance evaluation. As shown in Table 6, since the MC has the highest internal correlation with Q (quality), the MC in the CSs can make a reasonable and effective response to the Q in the CRs. Therefore, company managers must not only focus on the quality of products and services, but also put more emphasis on management commitments. For example, companies can try to help employees implement their career planning as much as possible to achieve their desired life.
In sum, this proposed method is a customer-oriented work that can improve the performance of fresh product companies. Other related industry companies can refer to the proposed method to enhance their business competition. In addition, due to the applicability of the proposed method, they can also modify the CRs and CSs according to the company’s specific situation.
7. Conclusions
GSCM has become a significant concern for green fresh product companies to gain competitive advantage. Thus, a novel two-stage integrated MCDM method is established to comprehensively select the optimal fresh product supplier and provide advice for companies to improve their production, service and management. The improvements of this MCDM method are as follows.
(1) Qualitative and quantitative criteria are all considered in selection criteria. Meanwhile, fuzzy set theory is used to evaluate the criteria.
(2) The proposed method integrates QFD, fuzzy BWM, Shannon entropy and fuzzy MULTIMOORA. Among this proposed method, fuzzy BWM is applied to derive the subjective criteria weights. Shannon entropy is used to obtain objective weights. Thus, a composite selection process is established to take into account the priorities of CRs and CSs. In addition, the subjective and objective weights are all considered, which makes the selection procedure more accurate.
(3) In order to select the suppliers, the fuzzy MULTIMOORA method and other three ranking approaches are implemented. The results, showed in Section 4, illustrate that the proposed method is applicable when selecting the fresh product supplier. Meanwhile, by changing the value of parameters , the proposed method is further proved to be reasonable and robust.
(4) The method illustrated with a numerical example, might be a practical solution for enhancing the management level of fresh product supply companies. Thus, the results of this study may be the most convincing choice.
This research also has some limitations, which provide an opportunity for further research. In order to accommodate the management needs in the selection of fresh product supplier in the future, evaluation criteria need to be further improved, it should be more feasible than the existing research. In addition, game theory and Taguchi loss function can be used in the integrated method to solve MCDM problems from a different perspective.
Author Contributions
A.L., Y.X. and S.-B.T. proposed the research. Y.X., H.L. and X.J. did the research and finished the paper. H.L., S.-B.T. and J.C. checked the English language and style. K.W., H.L., X.J. and J.W. put forward revised suggestions. All authors checked the final manuscript.
Funding
The study was supported by “State Key Laboratory for Manufacturing Systems Engineering (Xi’an Jiaotong University)” (sklms2017005), “Central University Science Research Foundation of China” (JB170609), “Shaanxi Natural Science Foundation Project” (2017JM7004), “Natural Sciences Foundation of China” (Nos. 71771002), “Natural Science Foundation of Anhui Province of China” (Nos. 1808085MG214), Provincial Nature Science Foundation of Guangdong (No. 2015A030310271 and 2015A030313679).
Acknowledgments
The authors especially thank the editors and anonymous referees for their kindly review and helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chatterjee, K.; Pamucar, D.; Zavadskas, E.K. Evaluating the performance of suppliers based on using the R’AMATEL-MAIRCA method for green supply chain implementation in electronics industry. J. Clean. Prod. 2018, 184, 101–129. [Google Scholar] [CrossRef]
- Hsu, C.W.; Hu, A.H. Applying hazardous substance management to supplier selection using analytic network process. J. Clean. Prod. 2009, 17, 255–264. [Google Scholar] [CrossRef]
- Mathiyazhagan, K.; Govindan, K.; Noorulhaq, A.; Geng, Y. An ISM approach for the barrier analysis in implementing green supply chain management. J. Clean. Prod. 2013, 47, 283–297. [Google Scholar] [CrossRef]
- Fallahpour, A.; Olugu, E.U.; Musa, S.N.; Wong, K.Y.; Noori, S. A decision support model for sustainable supplier selection in sustainable supply chain management. Comput. Ind. Eng. 2017, 105, 391–410. [Google Scholar] [CrossRef]
- Wilhelm, M.; Blome, C.; Wieck, E.; Xiao, C.Y. Implementing sustainability in multi-tier supply chains: Strategies and contingencies in managing sub-suppliers. Int. J. Prod. Econ. 2016, 182, 196–212. [Google Scholar] [CrossRef]
- Wilhelm, M.M.; Blome, C.; Bhakoo, V.; Paulraj, A. Sustainability in multi-tier supply chains: Understanding the double agency role of the first-tier supplier. J. Oper. Manag. 2016, 41, 42–60. [Google Scholar] [CrossRef]
- Mishra, D.; Gunasekaran, A.; Papadopoulos, T.; Hazen, B. Green supply chain performance measures: A review and bibliometric analysis. Sustain. Prod. Consum. 2017, 10, 85–99. [Google Scholar] [CrossRef]
- Kazemi, N.; Olugu, E.U.; Abdul-Rashid, S.H.; Ghazilla, R.A.R. A fuzzy EOQ model with backorders and forgetting effect on fuzzy parameters: An empirical study. Comput. Ind. Eng. 2016, 96, 140–148. [Google Scholar] [CrossRef]
- Amin, S.H.; Razmi, J. An integrated fuzzy model for supplier management: A case study of ISP selection and evaluation. Expert Syst. Appl. 2009, 36, 8639–8648. [Google Scholar] [CrossRef]
- Liu, F.H.F.; Hai, H.L. The voting analytic hierarchy process method for selecting supplier. Int. J. Prod. Econ. 2005, 97, 308–317. [Google Scholar] [CrossRef]
- Chai, J.; Ngai, E.W.T. Multi-perspective strategic supplier selection in uncertain environments. Int. J. Prod. Econ. 2014, 166, 215–225. [Google Scholar] [CrossRef]
- Liao, Z.; Rittscher, J. A multi-objective supplier selection model under stochastic demand conditions. Int. J. Prod. Econ. 2007, 105, 150–159. [Google Scholar] [CrossRef]
- Turki, S.; Didukh, S.; Sauvey, C.; Rezg, N. Optimization and Analysis of a Manufacturing-Remanufacturing-Transport-Warehousing System within a Closed-Loop Supply Chain. Sustainability 2017, 9, 561. [Google Scholar] [CrossRef]
- Son, D.; Kim, S.; Park, H.; Jeong, B. Closed-Loop Supply Chain Planning Model of Rare Metals. Sustainability 2018, 10, 1061. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Z. Dual-Recycling Channel Decision in a Closed-Loop Supply Chain with Cost Disruptions. Sustainability 2017, 9, 2004. [Google Scholar] [CrossRef]
- Govindan, K.; Rajendran, S.; Sarkis, J.; Murugesan, P. Multi criteria decision making approaches for green supplier evaluation and selection: A literature review. J. Clean. Prod. 2015, 98, 66–83. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, Y.; Zhen, L. A two-stage decomposition method on fresh product distribution problem. Int. J. Prod. Res. 2017, 55, 4729–4752. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X. Joint order and pricing decisions for fresh produce with put option contracts. J. Oper. Res. Soc. 2018, 69, 474–484. [Google Scholar] [CrossRef]
- Banaeian, N.; Mobli, H.; Fahimnia, B.; Nielsen, I.E.; Omid, M. Green supplier selection using fuzzy group decision making methods: A case study from the agri-food industry. Comput. Oper. Res. 2018, 89, 337–347. [Google Scholar] [CrossRef]
- Blome, C.; Hollos, D.; Paulraj, A. Green procurement and green supplier development: Antecedents and effects on supplier performance. Int. J. Prod. Res. 2014, 52, 32–49. [Google Scholar] [CrossRef]
- Sivasamy, K.; Arumugam, C.; Devadasan, S.R.; Murugesh, R.; Thilak, V.M.M. Advanced models of quality function deployment: A literature review. Qual. Quant. 2016, 50, 1399–1414. [Google Scholar] [CrossRef]
- Goyal, S.K.; Giri, B.C. Recent trends in modeling of deteriorating inventory. Eur. J. Oper. Res. 2001, 134, 1–16. [Google Scholar] [CrossRef]
- Bakker, M.; Riezebos, J. Review of inventory systems with deterioration since 2001. Eur. J. Oper. Res. 2012, 221, 275–284. [Google Scholar] [CrossRef]
- Ghoreishi, M.; Mirzazadeh, A.; Weber, G.W. Optimal pricing and ordering policy for non-instantaneous deteriorating items under inflation and customer returns. Optimization 2014, 63, 1785–1804. [Google Scholar] [CrossRef]
- Chang, H.L.; Rhee, B.D.; Cheng, T.C.E. Quality uncertainty and quality-compensation contract for supply chain coordination. Eur. J. Oper. Res. 2013, 228, 582–591. [Google Scholar]
- Calvo, E.; Albéniz, V.M.D. Sourcing strategies and supplier incentives for short-life-cycle goods. Manag. Sci. 2016, 62, 436–455. [Google Scholar] [CrossRef]
- Kumar, S.; Rajput, U.S. Fuzzy Inventory Model for Deteriorating Items with Time Dependent Demand and Partial Backlogging. Appl. Math. 2015, 6, 496–509. [Google Scholar] [CrossRef]
- Samir, O.; Jean-Pierre, K.; Ali, G. Production and Replacement Policies for a Deteriorating Manufacturing System under Random Demand and Quality. Eur. J. Oper. Res. 2018, 264, 623–636. [Google Scholar]
- Chai, J.; Liu, J.N.K.; Ngai, E.W.T. Application of decision-making techniques in supplier selection: A systematic review of literature. Expert Syst. Appl. 2013, 40, 3872–3885. [Google Scholar] [CrossRef]
- Grimm, J.H.; Hofstetter, J.S.; Sarkis, J. Critical factors for sub-supplier management: A sustainable food supply chains perspective. Int. J. Prod. Econ. 2014, 152, 159–173. [Google Scholar] [CrossRef]
- Kumar, S.; Luthra, S.; Govindan, K.; Kumar, N.; Haleem, A. Barriers in green lean six sigma product development process: An ISM approach. Prod. Plan. Control 2016, 27, 604–620. [Google Scholar] [CrossRef]
- Rostamzadeh, R.; Govindan, K.; Esmaeili, A.; Sabaghi, M. Application of fuzzy VIKOR for evaluation of green supply chain management practices. Ecol. Indic. 2015, 49, 188–203. [Google Scholar] [CrossRef]
- Kumar, A.; Jain, V.; Kumar, S. A comprehensive environment friendly approach for supplier selection. Omega 2014, 42, 109–123. [Google Scholar] [CrossRef]
- Weber, C.A.; Current, J.R.; Benton, W.C. Vendor selection criteria and methods. Eur. J. Oper. Res. 1991, 50, 2–18. [Google Scholar] [CrossRef]
- Akman, G. Evaluating suppliers to include green supplier development programs via fuzzy c-means and VIKOR methods. Comput. Ind. Eng. 2015, 86, 69–82. [Google Scholar] [CrossRef]
- Sarkis, J.; Dhavale, D.G. Supplier selection for sustainable operations: A triple-bottom-line approach using a Bayesian framework. Int. J. Prod. Econ. 2015, 166, 177–191. [Google Scholar] [CrossRef]
- Grimm, J.H.; Hofstetter, J.S.; Sarkis, J. Exploring sub-suppliers’ compliance with corporate sustainability standards. J. Clean. Prod. 2016, 112, 1971–1984. [Google Scholar] [CrossRef]
- Trapp, A.C.; Sarkis, J. Identifying Robust portfolios of suppliers: A sustainability selection and development perspective. J. Clean. Prod. 2016, 112, 2088–2100. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Dawal, S.Z.M.; Nukman, Y.; Aoyama, H. A hybrid approach for fuzzy multi-attribute decision making in machine tool selection with consideration of the interactions of attributes. Expert Syst. Appl. 2014, 41, 3078–3090. [Google Scholar] [CrossRef]
- Dey, P.K.; Bhattacharya, A.; Ho, W. Strategic supplier performance evaluation: A case-based action research of a UK manufacturing organization. Int. J. Prod. Econ. 2015, 166, 192–214. [Google Scholar] [CrossRef]
- Lam, J.S.L. Designing a sustainable maritime supply chain: A hybrid QFD–ANP approach. Transp. Res. Part E-log. 2015, 78, 70–81. [Google Scholar] [CrossRef]
- Kannan, D.; Khodaverdi, R.; Olfat, L.; Jafarian, A.; Diabat, A. Integrated fuzzy multi criteria decision making method and multi-objective programming approach for supplier selection and order allocation in a green supply chain. J. Clean. Prod. 2013, 47, 355–367. [Google Scholar] [CrossRef]
- Kim, J.; Hwang, Y.; Park, K. An assessment of the recycling potential of materials based on environmental and economic factors; Case study in South Korea. J. Clean. Prod. 2009, 17, 1264–1271. [Google Scholar] [CrossRef]
- Lam, J.S.L.; Lai, K. Developing environmental sustainability by ANP-QFD approach: The case of shipping operations. J. Clean. Prod. 2015, 105, 275–284. [Google Scholar] [CrossRef]
- Chowdhury, M.M.H.; Quaddus, M.A. A multi-phased QFD based optimization approach to sustainable service design. Int. J. Prod. Econ. 2016, 171, 165–178. [Google Scholar] [CrossRef]
- Bhatia, S.M.; Sharma, A.K. Fuzzy quality function deployment and software engineering—A literature review. Softw. Eng. Technol. 2014, 6, 159–168. [Google Scholar]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Ahmad, W.N.K.W.; Rezaei, J.; Sadaghiani, S.; Tavasszy, L.A. Evaluation of the external forces affecting the sustainability of oil and gas supply chain using Best Worst Method. J. Clean. Prod. 2017, 153, 242–252. [Google Scholar] [CrossRef]
- Pamučar, D.; Petrović, I.; Ćirović, G. Modification of the Best–Worst and MABAC methods: A novel approach based on interval-valued fuzzy-rough numbers. Expert Syst. Appl. 2018, 91, 89–106. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, H. Fuzzy best-worst multi-criteria decision-making method and its applications. Knowl. Based Syst. 2017, 121, 23–31. [Google Scholar] [CrossRef]
- Wang, T.C.; Lee, H.D. Developing a fuzzy TOPSIS approach based on subjective weights and objective weights. Expert Syst. Appl. 2009, 36, 8980–8985. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, S. A GRA-based intuitionistic fuzzy multi-criteria group decision making method for personnel selection. Expert Syst. Appl. 2011, 38, 11401–11405. [Google Scholar] [CrossRef]
- Zouggari, A.; Benyoucef, L. Simulation based fuzzy TOPSIS approach for group multi-criteria supplier selection problem. Eng. Appl. Artif. Intell. 2012, 25, 507–519. [Google Scholar] [CrossRef]
- Chang, T.H. Fuzzy VIKOR method: A case study of the hospital service evaluation in Taiwan. Inf. Sci. 2014, 271, 196–212. [Google Scholar] [CrossRef]
- Tsai, S.B.; Chien, M.F.; Xue, Y.; Li, L.; Jiang, X.; Chen, Q.; Zhou, J.; Wang, L. Using the fuzzy DEMATEL to determine environmental performance: A case of printed circuit board industry in Taiwan. PLoS ONE 2015, 10, e0129153. [Google Scholar] [CrossRef] [PubMed]
- You, X.Y.; You, J.X.; Liu, H.C.; Zhen, L. Group multi-criteria supplier selection using an extended VIKOR method with interval 2-tuple linguistic information. Expert Syst. Appl. 2015, 42, 1906–1916. [Google Scholar] [CrossRef]
- Zhao, R.; Su, H.; Chen, X.; Yu, Y. Commercially Available Materials Selection in Sustainable Design: An Integrated Multi-Attribute Decision Making Approach. Sustainability 2016, 8, 79. [Google Scholar] [CrossRef]
- Baležentis, A.; Baležentis, T.; Brauers, W.K.M. MULTIMOORA-FG: A Multi-Objective Decision Making Method for Linguistic Reasoning with an Application to Personnel Selection. Informatica 2011, 2, 173–190. [Google Scholar]
- Li, Z.H. An Extension of the MULTIMOORA Method for Multiple Criteria Group Decision Making Based upon Hesitant Fuzzy Sets. J. Appl. Math. 2014, 2014, 1–16. [Google Scholar] [CrossRef]
- Ceballos, B.; Lamata, M.T.; Pelta, D.A. Fuzzy Multi criteria Decision-Making Methods: A Comparative Analysis. Int. J. Intell. Syst. 2017, 32, 722–738. [Google Scholar] [CrossRef]
- Liu, H.C.; Fan, X.J.; Li, P.; Chen, Y.Z. Evaluating the risk of failure modes with extended MULTIMOORA method under fuzzy environment. Eng. Appl. Artif. Intell. 2014, 34, 168–177. [Google Scholar] [CrossRef]
- Zhao, H.; You, J.X.; Liu, H.C. Failure mode and effect analysis using MULTIMOORA method with continuous weighted entropy under interval-valued intuitionistic fuzzy environment. Soft Comput. 2017, 21, 5355–5367. [Google Scholar] [CrossRef]
- Senthil, S.; Srirangacharyulu, B.; Ramesh, A. A robust hybrid multi-criteria decision making methodology for contractor evaluation and selection in third-party reverse logistics. Expert Syst. Appl. 2014, 41, 50–58. [Google Scholar] [CrossRef]
- Zadeh, L.A. A New Frontier in Computation-Computation with Information Described in Natural Language. Int. J. Comput. Commun. 2007, 3, 5–6. [Google Scholar]
- Liu, H.C.; Liu, L.; Liu, N.; Mao, L.X. Risk evaluation in failure mode and effects analysis with extended VIKOR method under fuzzy environment. Expert Syst. Appl. 2012, 39, 12926–12934. [Google Scholar] [CrossRef]
- Shemshadi, A.; Shirazi, H.; Toreihi, M.; Tarokh, M.J. A fuzzy VIKOR method for supplier selection based on entropy measure for objective weighting. Expert Syst. Appl. 2011, 38, 12160–12167. [Google Scholar] [CrossRef]
- Kanapeckiene, L.; Kaklauskas, A.; Zavadskas, E.K.; Seniut, M. Integrated knowledge management model and system for construction projects. Eng. Appl. Artif. Intell. 2010, 23, 1200–1215. [Google Scholar] [CrossRef]
- Yao, J.S.; Wu, K. Ranking fuzzy numbers based on decomposition principle and signed distance. Fuzzy Set Syst. 2000, 116, 275–288. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).