Research on Path Planning Based on Multi-Dimensional Optimized RRT Algorithm

Abstract

The Rapidly Exploring Random Tree (RRT) is widely employed in the field of intelligent vehicles, but traditional RRT has issues like inefficient blind expansion, tortuous/discontinuous paths, and slow convergence. Thus, a multi-dimensional optimized RRT is proposed. First, a heuristic search method is adopted to reduce blind sampling, guiding sampling toward the target and cutting irrelevant searches. Second, to fix RRT’s inability to adjust step size dynamically (limiting complex road adaptability), step size is optimized based on environmental information. Third, since treating vehicles as mass points leads to unreasonable paths, sampling points are expanded for practicality. Finally, redundant points are removed via a greedy strategy, and paths are smoothed with quasi-uniform cubic B-splines to meet ride comfort needs. MATLAB R2022b simulations validate the algorithm: in simple scenarios, optimized RRT reduces sampling points to 232 (24.4% of traditional RRT), runtime to 3.25 s (79.4% cut), path length to 673.84 m (15.6% reduction); in complex scenarios, 636 points (37.0%), 11.07 s runtime (58.8% cut), 699.61 m path (21.6% reduction), outperforming traditional RRT and Q-RRT*.

1. Introduction

With the rise of the artificial intelligence field, intelligent driving vehicles have become a development trend in the future automotive, computer, and other industries, and intelligent driving technology has accordingly emerged as one of the most popular research directions [1,2,3,4,5]. Driven by the continuous advancement of technologicalization, intelligent driving vehicles have become an inevitable outcome of the intelligentization process. As a core technology in the field of intelligent driving, in the realm of technical research, path planning technology has developed into a critical research focus across multiple industries. The core of path trajectory planning lies in generating a collision-free path for the vehicle from the initial point to the end point in its operating environmental space, while satisfying constraints such as vehicle curvature limits and kinematic characteristics. Within path planning research, relevant techniques can generally be classified into various types: random sampling-driven approaches Probabilistic Roadmap (PRM) [6] and Rapidly Exploring Random Tree (RRT) [7,8], graph search-based methods A* [9], curve fitting-based methods quintic polynomial curves [10], and numerical optimization-based methods (e.g., artificial potential field technique and model predictive control method).

In the category of sampling-based planning algorithms, the Rapidly Exploring Random Tree (RRT) has been extensively studied and applied due to its extended properties such as probabilistic completeness and strong adaptability [11,12,13,14,15]. However, the basic RRT algorithm has obvious shortcomings, including blindness and randomness in the path search process, as well as low search efficiency in narrow regions. Currently, some researchers domestically and internationally have proposed derivative algorithms developed from the basic version of RRT to address the above issues [16,17,18,19,20]. Jordan M et al. [21] introduced the B-RRT* algorithm, which adopts a bidirectional expansion strategy from the start point and target point to further improve the algorithm’s convergence speed. Jeong et al. [22] introduced the Q-RRT* algorithm, adopting multi-level parent vertices to conduct comparisons during the local reconstruction of new nodes within the random tree and adopts the node with the minimum cost as the new parent node, thereby reducing the path length of the produced path. These methods exhibit asymptotic optimality but involve a large amount of computation.

As a heuristic algorithm for selecting local optima, the greedy strategy is commonly used in path planning for scenarios such as redundant node elimination and path simplification. Its core logic is to prioritize the current optimal solution in each decision step and gradually approach the global optimal goal through iterative updates, featuring advantages of low computational complexity and high execution efficiency. In intelligent vehicle path planning, paths created by the traditional RRT algorithm often contain a great many redundant nodes, resulting in tortuous paths and increased difficulty in vehicle tracking. The greedy strategy can quickly eliminate invalid redundant nodes through the method of “direct line collision detection between start and target points”—for example, during path backtracking, starting from the initial node, it sequentially detects whether the line connecting to subsequent nodes collides with obstacles. If there exists no obstacle, it directly retains end vertex and updates the start location, thereby achieving path stretching and simplification. Currently, there have been some explorations on the application of the greedy strategy in RRT algorithm improvement: Huang et al. [23] adopted the greedy idea to optimize the node expansion direction in their improved RRT algorithm, but it was limited to single-dimensional node screening; although the Q-RRT* algorithm introduced by Jeong et al. introduced local cost optimization, it failed to combine the greedy strategy for path post-processing, resulting in remaining path redundancy. In contrast, the greedy strategy in this paper is not only used for redundant point removal but also forms a “preprocessing-postprocessing” collaborative mechanism with node expansion and B-spline smoothing; on the basis of ensuring obstacle avoidance safety through node expansion, the path structure is simplified via the greedy strategy, and then the curvature continuity is optimized by B-spline curves. Ultimately, it achieves the path planning goal of “safety-simplicity-smoothness” and fills the gap in the systematic application of the greedy strategy in multi-dimensional optimization of RRT.

Improvements to the traditional RRT algorithm mostly focus on a single dimension (such as sampling direction or step size adjustment), while the multi-dimensional RRT algorithm emphasizes collaborative optimization throughout the entire process of “sampling strategy—step size control—vehicle modeling—path smoothing” and acts as a key direction for solving trajectory planning problems of intelligent vehicles in complex scenarios. Existing research on multi-dimensional improvements has limitations in two aspects: one is the lack of synergy between dimensions; for instance, Göktas et al. combined PRM and RRT algorithms to optimize sampling efficiency but ignored the impact of vehicle geometric dimensions on path feasibility; the other is insufficient adaptability, as most algorithms are only designed for simple static environments and struggle to meet the requirements of both search efficiency and path safety in scenarios like narrow areas or dynamic obstacles. The multi-dimensional optimized RRT algorithm introduced in this paper achieves breakthroughs through in-depth coupling of four core dimensions: it adopts heuristic sampling biased towards the target in the sampling dimension to reduce searches in irrelevant areas; dynamically modifies the step size according to obstacle density in the step size dimension to balance search rate and accuracy; introduces a node expansion mechanism in the modeling dimension to upgrade the vehicle from a particle model to a “safe circle envelope” model; and combines the greedy strategy with quasi-uniform cubic B-splines in the smoothing dimension to achieve path simplification and curvature optimization. This multi-dimensional collaborative framework can cover the core needs of intelligent vehicle path planning, and compared with existing single-dimension improved algorithms, it shows significant improvements in adaptability to complex environments, path quality, and execution efficiency.

To make the planned path conform to actual driving conditions and meet the requirements of real vehicle operation, this study proposes a multi-level improvement method based on the traditional RRT algorithm. Firstly, heuristic sampling biased toward the target node is adopted to replace random sampling. This guides the path expansion toward the target point and reduces the blindness of sampling. Secondly, the standard RRT algorithm cannot dynamically adjust the step size, resulting in insufficient search capability in complex road environments. This study optimizes the dynamic adjustment of the sampling step size based on environmental information. Thirdly, the RRT algorithm usually treats the vehicle as a mass point, which leads to unreasonable path planning in complex path scenarios. In this study, the sampling points are subjected to an expansion process, rendering the planned path more in line with real-world conditions. Fourthly, a greedy strategy is utilized to stretch the pathway. Finally, a B-spline profile is applied to smoothen the trajectory curvature. These improvements achieve path length optimization and solve the problem of path smoothness.

2. Vehicle Dynamics Model

2.1. Establishment of Vehicle Dynamics Model

In the research on trajectory following control for smart driving, constructing an appropriate dynamic model serves as the foundation. Since a vehicle is a complex time-varying system, starting from the target of trajectory tracking control, this study focuses on the relationships between the vehicle’s forces in lateral control and parameters including fore-and-aft speed, side-to-side speed, fore-and-aft acceleration, side-to-side acceleration, and yaw rate. Furthermore, a two-degree-of-freedom vehicle dynamics model is constructed based on the vehicular lateral displacement y and yaw angle φ.

As a classic model, the two-degree-of-freedom model has significant advantages: it is simple yet capable of capturing the main contradictions, with high accuracy between calculation results and experimental results. It achieves relatively accurate calculations with the minimum number of degrees of freedom, simplifies complexity, meets control requirements, and allows the separation of lateral and longitudinal control. Due to the great complexity of the vehicle dynamics model, the following assumptions are formulated for the model:

(1)

It is assumed that the vehicle and the suspension are rigidly connected, and the suspension characteristics are not considered.

(2)

This paper holds that the vehicle cabin moves only within a plane parallel with the ground. The vehicle’s movement in the direction of the z-axis, as well as the pitch angle about the y-axis and the roll angle around the x-axis, are all equal to zero.

(3)

The roll acceleration is confined to within 0.4 g to secure that the tire cornering characteristics are situated in the linear region; (During simulation, the lateral acceleration is monitored in real time. If it exceeds 0.4 g (≈3.92 m/s²), the controller adjusts the front wheel steering angle to reduce lateral load transfer, ensuring roll acceleration stays within the linear range.)

(4)

Under the condition of small driving force, we ignore the ground tangential force on the tires and air resistance, as well as the modifications to tire behaviors induced by load fluctuations on the left and right wheels and the influence of tire aligning torque.

(5)

The vehicle is assumed to be simplified into a bicycle model, and the lateral load transfer is not considered.

(6)

When the vehicle speed is assumed to be constant, the vehicular system is equipped with just two degrees of freedom: lateral displacement and yaw.

In Figure 1, $F_{yf}$ represents the front wheel cornering force, $F_{yr}$ represents the rear wheel cornering force, ${\alpha }_f$ represents the slip angle of the front wheels, ${\alpha }_r$ represents the slip angle of the front wheels, $\beta$ represents the vehicle’s center-of-mass sideslip angle, δ represents the front wheel steering angle, a represents the longitudinal distance from the front axle to the center of mass, b represents the longitudinal distance from the rear axle to the center of mass, v represents the velocity at the vehicle’s center of mass, $V_f$ represents the front wheel velocity of the vehicle, $V_r$ represents the rear wheel velocity of the vehicle, and φ represents the vehicle yaw angle.

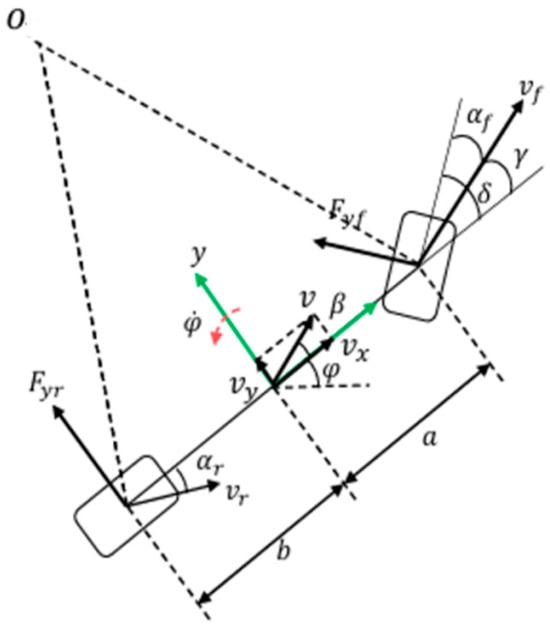
Figure 1. Two degree of freedom vehicle model.

By applying Newton’s second law the following equations are obtained:

$$\sum F_y={ma}_y\to {ma}_y=F_{y}cos\delta +F_{yr}$$

(1)

$$\sum M=I\ddot{\phi }\to I\ddot{\phi }=F_{yr}cos\delta ·a-F_{yr}·b$$

(2)

Cornering Force and Slip Angle of Tires:

$$F_y=C_{\alpha }\alpha$$

(3)

In the equation, $C_{\alpha }$ denotes the cornering stiffness.

For an intelligent vehicle in stable driving, its front wheel steering angle is very small. Assuming δ is relatively small, $cos\delta =1$ holds. According to Equation (3), the following can be obtained:

$${ma}_y=F_y+F_{yr}=C_{{\alpha }_f}{\alpha }_f+C_{{\alpha }_r}{\alpha }_r$$

(4)

$$I\ddot{\phi }=F_{yr}·a-F_{yr}·b=a{C}_{{\alpha }_f}{\alpha }_f-b{C}_{{\alpha }_r}{\alpha }_r$$

(5)

By transforming the rear wheel velocity and the front wheels’ velocity relative to the vehicle’s center of mass respectively, the following can be obtained:

$${\alpha }_r={\displaystyle \frac{v_y-\dot{\phi }b}{v_x}} {\alpha }_f={\displaystyle \frac{\dot{\phi }a+v_y}{v_x}}-\delta$$

(6)

Substituting Equation (6) into Equations (4) and (5) yields:

$$m(\dot{v_y}+v_x\dot{\phi })=C_{{\alpha }_f}({\displaystyle \frac{\dot{\phi }a+v_y}{v_x}}-\delta )+C_{{\alpha }_r}{\displaystyle \frac{v_y-\dot{\phi }b}{v_x}}$$

(7)

$$I\ddot{\phi }=a{C}_{{\alpha }_f}({\displaystyle \frac{\dot{\phi }a+v_y}{v_x}}-\delta )-b{C}_{{\alpha }_r}{\displaystyle \frac{v_y-\dot{\phi }b}{v_x}}$$

(8)

From $v_y\leftrightarrow \dot{y}$, the following can be obtained:

$$\left({\displaystyle \genfrac{}{}{0pt}{}{\ddot{y}}{\ddot{\phi }}}\right)=\left(\begin{array}{c}{\displaystyle \frac{C_{{\alpha }_f}+C_{{\alpha }_r}}{m{v}_x}} {\displaystyle \frac{a{C}_{{\alpha }_f}-b{C}_{{\alpha }_r}}{m{v}_x}}-v_x \\ {\displaystyle \frac{a{C}_{{\alpha }_f}-b{C}_{{\alpha }_r}}{I{v}_x}} {\displaystyle \frac{{a^{2}C}_{{\alpha }_f}+b^2{C}_{{\alpha }_r}}{I{v}_x}} \end{array}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\dot{y}}{\dot{\phi }}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{C_{{\alpha }_f}}{m}}{-\frac{a{C}_{{\alpha }_f}}{I}}}\right)\delta$$

(9)

Let $x=\left({\displaystyle \genfrac{}{}{0pt}{}{\dot{y}}{\dot{\phi }}}\right)$ and $u=\mathsf{\delta }$, then Equation (9) can be simplified as $\dot{x}=Ax+Bu$.

2.2. Vehicle Dynamic Model Validation

To ensure the stability and rationality of the path presented in subsequent sections, the accuracy of the established 2-degree-of-freedom (2-DOF) vehicle dynamics model was verified and analyzed. Under the operating condition of a front-wheel angle input in the form of a step signal with a wheel angle of 0.09 rad at a speed of 80 km/h, the comparison curves of parameter responses between the 2-DOF model and the CarSim vehicle are shown in Figure 2.

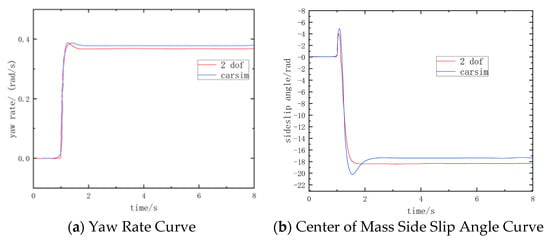
Figure 2. Response curve of two degree of freedom vehicle model.

Figure 2 shows the vehicle’s yaw rate and the side slip angle corresponding to its center of mass curves of the established 2-degree-of-freedom (2-DOF) vehicle model and the CarSim vehicle model, respectively. The dynamic response properties of the established 2-DOF vehicle model are in good agreement with those of the CarSim vehicle model. This is specifically reflected in the high consistency of the trend of the response curves for the side slip angle at the vehicle’s center of mass and yaw rate, and the dynamic error between the two is maintained within a small range. This result verifies that the established simplified 2-DOF model can effectively characterize the actual dynamic characteristics of the vehicle, thereby providing a reliable model foundation.

3. Principle of Basic RRT Algorithm

The Rapidly Exploring Random Tree (RRT) algorithm was initially put forward by American scholar Professor LaValle [24] in 1998. As a type of path planning algorithm rooted in random sampling, it explores high-dimensional spaces by constructing and expanding random trees, and acts as an efficient spatial search method. Compared with traditional path planning algorithms, the RRT algorithm has significant advantages: it not only possesses probabilistic completeness—meaning that regardless of whether there are obstacles in the spatial environment, as long as there exists a workable path starting from the initial position to the target position, the algorithm can find the target point given sufficient time—but also has strong adaptability to high-dimensional spaces, enabling it to effectively solve path planning problems in complex environments [25]. After its proposal, the algorithm first gained extensive attention and application in the field of robotics, particularly performing well in scenarios such as manipulator motion planning and mobile robot navigation. With the rapid development of intelligent driving technology, the RRT algorithm, due to its efficient random search capability and adaptability to dynamic environments, has gradually been introduced into the path planning field of intelligent vehicles. For instance, it is applied in aspects like local path planning of intelligent driving vehicles, parking trajectory optimization, and obstacle avoidance in complex traffic environments. In addition, the algorithm has been extended to applications in multiple fields including UAV path planning and character motion control in virtual reality, demonstrating strong versatility and scalability. Owing to its high computational efficiency and simple implementation, RRT series algorithms remain one of the important research directions in the field of motion planning to this day.

The basic flow of the RRT algorithm is as follows:

(1)

In the initial setup phase, a random tree (Tree) is constructed, and the start point Xstart is set to be the root node of the tree. At this time, the tree structure contains only this single root node.

(2)

Perform random sampling in the map environment. A point Xrand is randomly generated in the environment through the Random Node function. Then, search for the node Xnear with the lowest cost among all the nodes within the random tree to this random point.

(3)

Produce a new node. First, define the step size as stepsize. By connecting nodes Xnear and Xrand, determine whether the line between them intersects with obstacles. In the event that no collision exists, a new node Xnew is generated from Xnear according to the step size Stepsize. Subsequently, check whether the line between Xnear and Xnew collides with obstacles. If no collision occurs, Xnew is inserted into the random tree to complete a tree expansion; if a collision occurs, this expansion is abandoned. Repeat steps 2 and 3.

(4)

Complete the planning. Once the target node Xgoal is included in the tree, the search process terminates. At this time, a shortest path is formed by connecting the line segment connecting the target point Xgoal and the starting point Xstart. Figure 3 shows the flow framework of the algorithm.

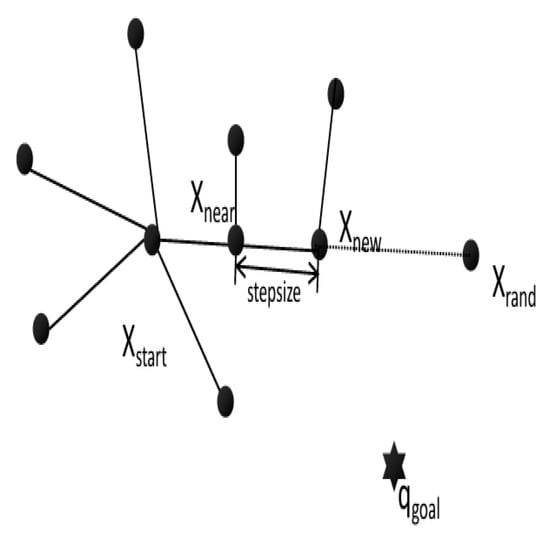Figure 3. Algorithm Structure Diagram.

The Rapidly Exploring Random Tree (RRT) algorithm consists of three core processes in its main implementation steps: First is the random sampling process, which randomly generates target points in the configuration space; second is the random tree expansion process, which expands from the current tree node toward the direction of the sampled point; third is the traversal and point-finding process, which searches the tree structure for the node closest to the sampled point and uses it as the starting point for expansion. These three steps are executed cyclically until a target path is found or a termination condition is met. Figure 4 shows the path-finding graph of the basic RRT algorithm, The red path represents the generated path.

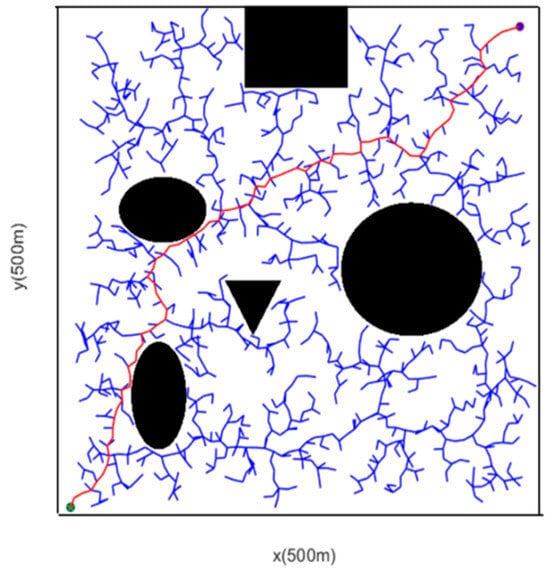
Figure 4. Path-Finding Diagram of the Basic RRT Algorithm.

Although the basic RRT algorithm can improve the search efficiency in high-dimensional spaces through random spatial sampling and realize path planning from the start point to the end point, it has many defects: its search is highly random and lacks target orientation, which generates a great quantity of redundant points and increases the calculation time; improper setting of the fixed step size will slow down the convergence speed, lengthen the path, and also impair the search ability in narrow areas or regions with many obstacles; the generated path contains numerous redundant points, shows obvious curvature, and has poor quality, and it even has corners and excessive angle changes, failing to meet the needs for the vehicle’s continuous curvature trajectory; in addition, it treats sampling points as mass points and ignores the vehicle’s geometric parameters, leading to a significant discrepancy between theoretical planning and actual driving, which may easily cause collision accidents. Therefore, this paper will improve the basic RRT to address these issues.

4. Multi-Dimensional Optimized RRT Algorithm

4.1. Target-Biased Random Sampling Strategy

The heuristic information search adopted in the “target-node-biased random point generation strategy” of this study focuses on dynamically adjusting the sampling method by combining the environmental obstacle density and the direction corresponding to target point: first, the ratio of obstacles within the safe distance of the sampling point is detected through a grid map. If the proportion of obstacles is less than 30%, sampling points are generated in the direction of the target sampling point at a 70% probability and random sampling is performed with a 30% probability to accelerate convergence toward the target; if the proportion of obstacles is high, the probability is adjusted in the opposite direction to reduce sampling in the target direction and avoid collision risks. The core differences between this heuristic information search and traditional as well as relevant improved technologies lie in information utilization and environmental adaptability: the traditional RRT uses random sampling without any heuristic information, generating sampling points only through uniform randomness, which results in strong blindness and slow convergence; although Informed RRT* performs sampling based on the “start-goal” ellipse constraint, it only relies on distance information and is prone to sampling failure due to ellipse truncation in narrow obstacle areas; RRT-Connect narrows the search range through bidirectional sampling but does not consider obstacle density, leading to frequent failures in bidirectional tree connection in high-obstacle areas. In contrast, the method in this study integrates dual information of obstacle density and target direction, and can dynamically adjust the sampling strategy according to environmental complexity. It not only solves the blindness of traditional methods but also makes up for the insufficient adaptability of other improved technologies in complex environments, achieving a balance between search efficiency and obstacle avoidance safety.

The traditional RRT algorithm lacks a clear direction during random expansion and exhibits a certain degree of randomness, which leads to a comparatively slow convergence rate. The RRT path diagram before optimization is shown in Figure 5. To accelerate the growth of the tree and enable it to expand toward the target point as much as possible, it is necessary to improve the algorithm’s strategy. This research advances a heuristic sampling strategy that biases the search toward the target direction. The optimized RRT path diagram is shown in Figure 6. First, it detects whether there are obstacles within the safe distance. If there are no obstacles or there are few obstacles, the rand function is used to randomly generate a decimal number between 0 and 1. In this way, the random point has a 50% probability of moving toward the target point, which accelerates the contraction speed and avoids blind search. The remaining 50% probability is used to determine the generation of the final random point based on the weighted sum of the target point and the random point. When there are many obstacles, the situation is exactly the opposite.

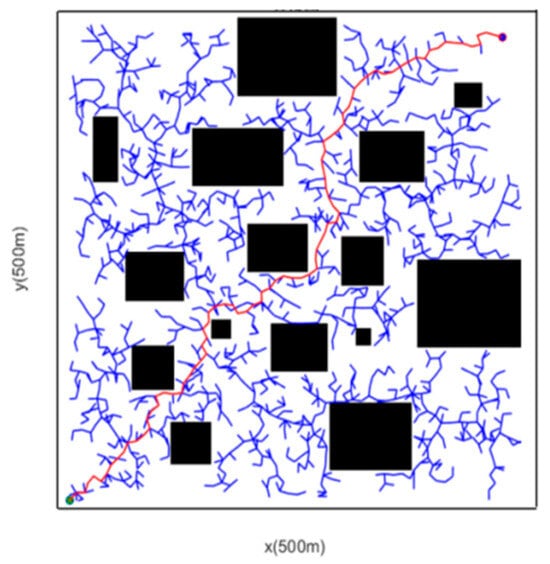
Figure 5. RRT Path Diagram Before Optimization.

Figure 6. RRT Path Diagram After Optimization.

It can be seen from the various parameters in Table 1 that the adoption of the heuristic information search method biased toward the target has achieved significant improvements in terms of the count of sampling points and running time. It also reduces the search in the irrelevant areas marked by the red frame, which ensures the operation safety of intelligent vehicles.

Table 1. Comparison of parameters before and after heuristic information search optimization.

	Number of Sampling Points	Running Time (s)	Path Length (m)
Before Optimization	1404	28.4	873.3
After Optimization	371	3.6	796.9

4.2. New Node Expansion Method with Adaptive Step Size

The standard RRT algorithm does not adjust the step size dynamically. From the data illustrated in Figure 7 and Table 2, the sampling method with a fixed step size results in slow algorithm convergence, a relatively long path, and insufficient search capability when facing complex road environments. Therefore, this paper designs a new node sampling method with dynamic step size, as shown in Figure 8, and the formula is as follows:

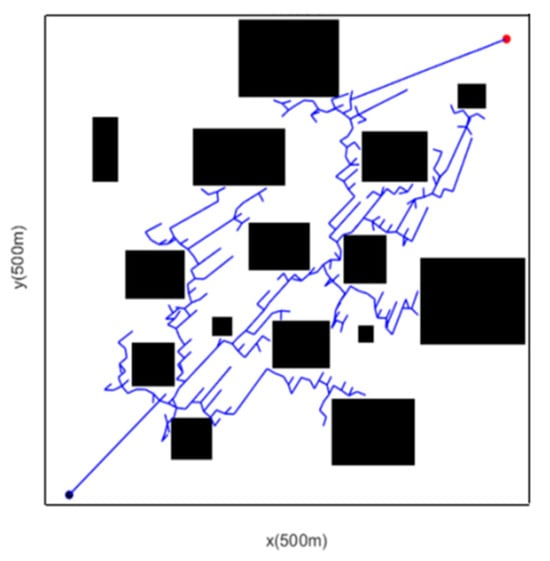
Figure 7. Fixed Step length.

Table 2. Comparison of parameters before and after adaptive step size optimization.

	Number of Sampling Points	Running Time (s)	Path Length (m)
Fixed Step Size	904	12.0	831.8
Dynamic Step Size	797	9.6	783.4

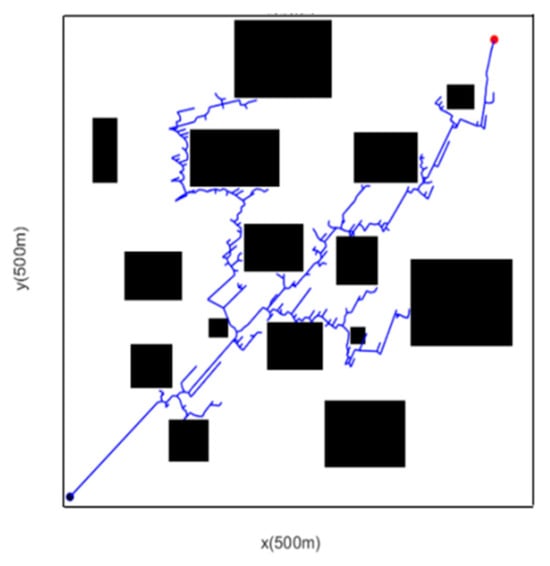
Figure 8. Dynamic Step length.

$$Step=\left\{\begin{array}{c}step1 \mathrm{W}\mathrm{h}\mathrm{e}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \mathrm{a}\mathrm{r}\mathrm{e} \mathrm{m}\mathrm{a}\mathrm{n}\mathrm{y} \mathrm{o}\mathrm{b}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{s} \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{f}\mathrm{i}\mathrm{r}\mathrm{s}\mathrm{t}\text{-}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e} \mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e}\mathrm{t}\mathrm{y} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\\ \left\{\begin{array}{c}step2 \mathrm{W}\mathrm{h}\mathrm{e}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \mathrm{a}\mathrm{r}\mathrm{e} \mathrm{m}\mathrm{a}\mathrm{n}\mathrm{y} \mathrm{o}\mathrm{b}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{s} \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\text{-}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e} \mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e}\mathrm{t}\mathrm{y} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\\ step3 \mathrm{W}\mathrm{h}\mathrm{e}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \mathrm{a}\mathrm{r}\mathrm{e} \mathrm{f}\mathrm{e}\mathrm{w} \mathrm{o}\mathrm{b}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{s} \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\text{-}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e} \mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e}\mathrm{t}\mathrm{y} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\end{array}\right.\end{array}\right.$$

$step1,step2,step3$ refer to the three types of step sizes defined initially, which are the minimum, sub-minimum, and maximum step sizes in sequence. These step sizes are set differently for different working scenarios. The algorithm dynamically adjusts the step magnitude based on obstacle collision detection between the two types of safety distances, thereby determining the next new node.

It can be seen from the various parameters in Table 2 that the adoption of the dynamic step size adjustment method reduces the count of sampling points, shortens the running time by 20%, and decreases the trajectory length by 48.4 m. This indicates that the expansion method with adaptive step size has achieved improvements in all aspects.

4.3. Node Inflation

In view of various specific scenarios in real driving environments, such as narrow spaces and dense obstacles, random sampling points may guide the vehicle to move toward obstacles, posing significant safety risks. The basic RRT algorithm alone cannot meet the vehicle’s obstacle avoidance requirements. Therefore, it is urgent to establish a more rigorous obstacle detection strategy to improve the feasibility of the path.

In the node sampling process of traditional path planning algorithms, vehicles are usually simplified as particle models, without considering the vehicle’s own size. However, in actual driving, both obstacles and vehicles are entities with geometric parameters. If this factor is not taken into account, there is a risk of the vehicle colliding with obstacles when tracking the path. Therefore, to meet the obstacle avoidance requirements (as shown in Figure 9), this paper proposes an improved scheme: by introducing a node inflation mechanism, an obstacle detection circle is constructed to effectively avoid collision risks [26,27,28,29].

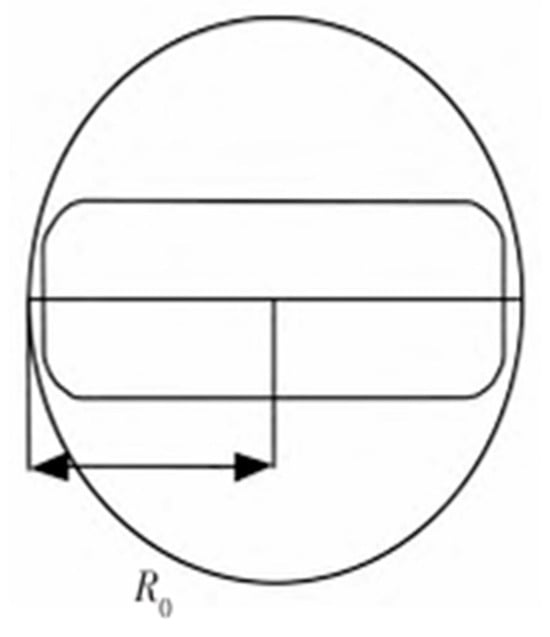
Figure 9. Node Inflation Processing.

A safety circle is used to enclose the vehicle, with an appropriate enlargement. Taking the vehicle’s center point ($x_0,y_0$) as the center and $R_0$ taken as the radius, the equation for a circle is thus obtained as follows:

$${\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2={\displaystyle \frac{{R_0}^2}{4}}$$

(10)

In the formula, $R_0$ represents half of the vehicle’s length in the actual environment.

The definition of the obstacle detection circle is as follows: The inflated circle is used to enlarge the detection area by a certain proportional coefficient λ:

$${\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2={\displaystyle \frac{{\left(R_0\lambda \right)}^2}{4}}$$

(11)

The improved algorithm constructs two types of obstacle detection circles with $\lambda$ = 1.5. The introduction of this strategy enables large-range obstacle detection and ensures that the vehicle can avoid obstacles effectively within a sufficiently spacious area. One of the constraint conditions for path planning algorithms is the steering angle constraint; most vehicles have a steering angle constraint within 30°. In this paper, the vehicle is normalized into a circle, so that the vehicle avoids collision with obstacles regardless of its heading direction.

Figure 10 shows the path planned without inflation processing. As can be seen from the yellow box, the environment here is very narrow and the distance to obstacles is extremely close. In practice, the vehicle would have collided long ago, so the planned path does fall short of the demands. From Figure 11, it can be observed that after the node inflation processing is applied, the algorithm bypasses the narrow area, and the planned path more closely matches the actual operation of the vehicle during actual travel By introducing the proportional coefficient λ, this strategy enables large-range obstacle detection and ensures that the vehicle can avoid obstacles effectively within a sufficiently spacious area.

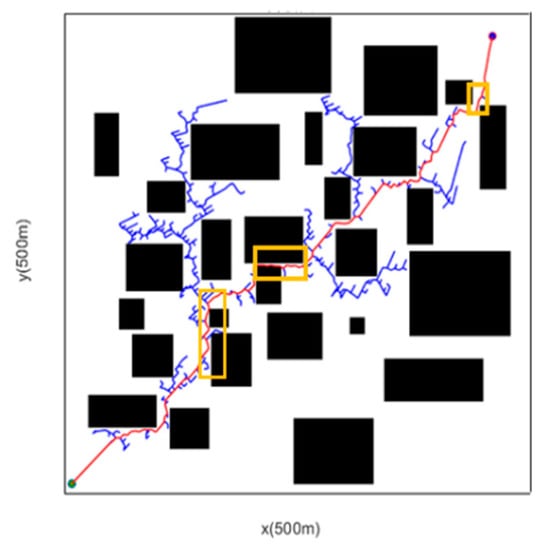
Figure 10. Before Inflation Processing.

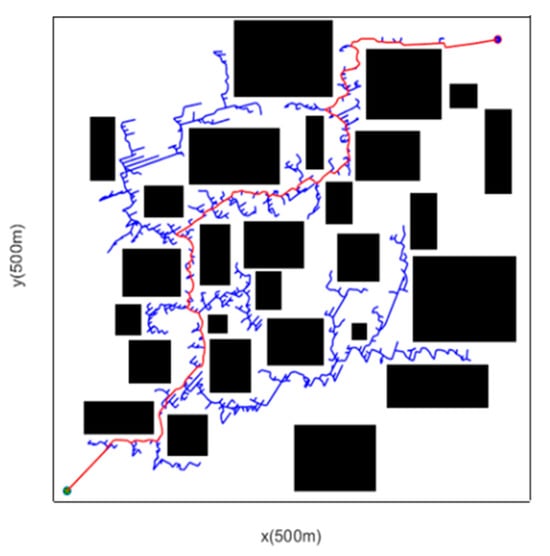
Figure 11. After Inflation Processing.

4.4. Removal of Redundant Nodes

The path generated by the standard RRT algorithm usually contains a large number of redundant nodes, resulting in a curved path with high path cost and poor overall quality. From the content presented in Figure 12, the final path formed by backtracking has excessively high cost and numerous twists and turns. Therefore, a greedy strategy is designed to remove redundant nodes from the path and straighten it.

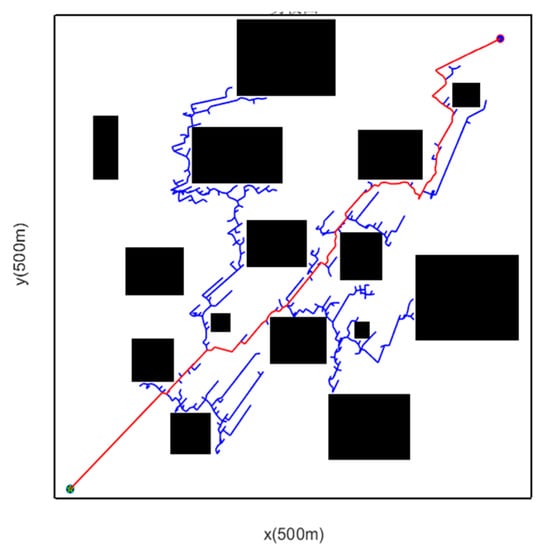
Figure 12. Path Backtracking Diagram.

Its principle is shown in Figure 13. Starting from point n(0), obstacle detection is performed sequentially between each node and the starting point n(0). If there is no obstacle between n(0) and n(i), a line is connected from n(0) to n(i), and n(i) is regarded as the new starting point, The red cross in the picture indicates a path that cannot be taken. This process is repeated until the target point is finally connected.

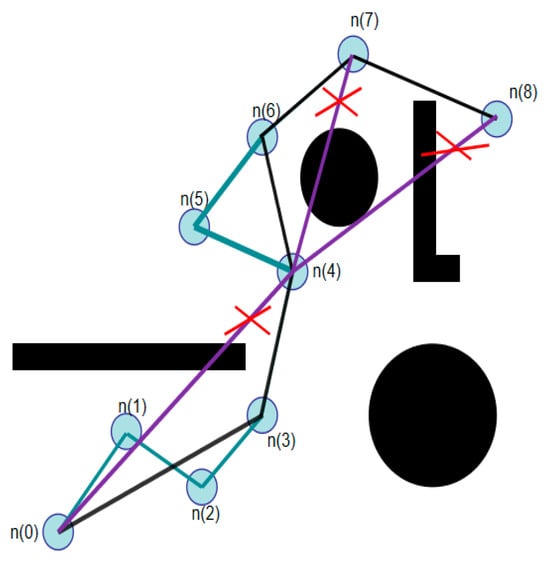
Figure 13. Schematic Diagram of Path Straightening Principle.

4.5. Path Smoothing Processing

The path optimized by node processing achieves the goal of optimal path length. However, the resulting path is still a continuous polyline—it is not smooth enough and has discontinuous curvature. When the vehicle tracks this path, the heading angle will change abruptly, which seriously affects the vehicle’s ride comfort and safety. Therefore, the path must be smoothed to obtain the optimal path that truly meets the vehicle’s tracking requirements. A B-spline curve serves to perform smooth fitting on the path, and this type of curve is widely applied in the path planning of intelligent vehicles [30,31,32].

Suppose there are n + 1 control points, whose function is to specify the direction as well as the boundary range of the spline curve applied in path optimization. Subsequently, the definition of the k-th order B-spline curve, as applied to path smoothing, is as follows:

$$P(u)=[P_0{P}_1\cdots P_n]\left[\begin{array}{c}{B}_{0,K}\left(u\right)\\ B_{1,K}\left(u\right)\\ ·\\ ·\\ B_{n,K}\left(u\right)\end{array}\right]={\sum }_{i-0}^n{P}_i{B}_{i,K}(u)$$

(12)

In the formula, $B_{i,K}\left(u\right)$ denotes the i-th K-order B-spline basis function, which corresponds to the control point $P_i$, where K ≥ 1 and u ∈ [0, 1] functions as the independent variable. The basis function adheres to the De Boor-Cox recurrence relation as below:

$${ B}_{i,K}\left(u\right)=\left\{\begin{array}{c}\left\{\begin{array}{c}1, u_i\le u<u_{i+1} \\ 0, else \end{array}\right. k=1 \\ {\displaystyle \frac{u-u_i}{u_{i+k-1}}}{B}_{i,K-1}\left(u\right)+{\displaystyle \frac{u_{i+k}-u}{u_{i+k}-u_{i+1}}}{B}_{i+1,K-1}\left(u\right) k\ge 2 \end{array}\right.$$

(13)

Within this formula, $u_i$ is a continuously changing value of a non-decreasing sequence referred to as the knot vector. The first and last values are typically set as 0 and 1, with the sequence in the form of [$u_0,u_1\cdots u_k,u_{k+1},\cdots u_n,u_{n+1},\cdots u_{n+k}$]. Generally speaking, the degree has a significant impact. Considering that cubic B-spline curves can ensure the continuity of the second derivative, it is finally decided to adopt quasi-uniform cubic B-spline curves to perform smoothing processing on the simplified path. The cubic B-spline curve function is as follows:

$$\left\{\begin{array}{l}{b}_{\mathrm{0,3}}\left(u\right)={\displaystyle \frac{1}{6}}{\left(1-u\right)}^2 \\ b_{\mathrm{1,3}}\left(u\right)={\displaystyle \frac{1}{6}}\left(3u^3-6u^2+4\right) \\ b_{\mathrm{2,3}}\left(u\right)={\displaystyle \frac{1}{6}}\left(-3u^3-3u^2+3u+1\right) \\ b_{\mathrm{3,3}}\left(u\right)={\displaystyle \frac{1}{6}}{u}^3 \\ P_{\mathrm{0,3}}\left(u\right)=P_0\times b_{\mathrm{0,3}}\left(u\right)+P_1\times b_{\mathrm{1,3}}\left(u\right)+P_2\times b_{\mathrm{2,3}}\left(u\right)+P_3\times b_{\mathrm{3,3}}\left(u\right)\end{array}\right.$$

(14)

In the formula, $b_i$ represents the cubic B-spline curve’s basis function, and $P_i$ denotes the control point in the curve, where i = 1, 2, 3.

5. Simulation Analysis

From the perspective of a simplified map, this study selects a rectangular grid map as the experimental map environment, with a resolution of 1 m × 1 m. To verify the proposed multi-modified RRT algorithm, 20 simulation experiments were conducted respectively in simple and complex scenarios using MATLAB as the simulation tool, within a 500 m × 500 m grid scenario map. Additionally, due to the random sampling characteristic of the RRT algorithm during path searching, the path results are not unique; thus, one of the path planning results is selected as the simulation result for comparison in this study.

5.1. Simple Obstacle Scenario

We placed obstacles between the initial point (10, 10) and the end target point (480, 480) to test the obstacle avoidance capability of the algorithm. The path planning result from the simulation is shown in Figure 14.

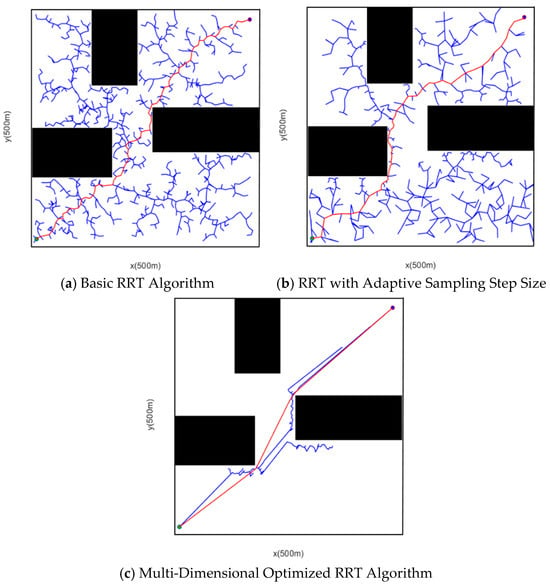
Figure 14. Comparison of Simulation Results in Simple Obstacle Scenario.

A comparison of the simulation results within Figure 14 reveals the improvements of the proposed algorithm: although the adaptive step size sampling method decreases the number of sampling points, the RRT algorithm with multiple optimizations significantly reduces redundant nodes. The red line represents the generated path, and the black geometry represents obstacles. This realizes the maximum utilization of environmental information, greatly enhances the planning efficiency of the algorithm, then obtains a path with optimal length and smoothness, which meets the vehicle tracking requirements and has universal applicability. Owing to the randomness of the algorithm, 20 path planning simulation instances were conducted in this scenario. The simulation results of the three algorithms were statistically analyzed, where all indicator results are average values. The data of the simulation instances are shown in Table 3.

Table 3. Simulation Data in Simple Obstacle Scenario.

Algorithm	Number of Sampling Points	Running Time (s)	Path Length (m)
RRT	949	15.7948	798.2348
RRT with adaptive sampling step size	622	6.4107	774.8383
Multi-Dimensional Optimized RRT	232	3.25258	673.8413

According to 20 simulation experiments in Table 3, when the basic RRT algorithm is utilized to calculate the initial path, the mean number of samplings is 949, the mean time consumed is 15.7948 s, and mean path length is 798.2348 m. When searching for the shortest path, the algorithm put forward in this paper—after multi-dimensional optimization—has an average of 232 samplings, an average time consumption of 3.25258 s, and an average path length of 673.8413 m. There is a qualitative improvement in running time, the path length is lessened by 14.5%, and the curvature of the planned path is more consistent with the requirements of vehicle driving.

Based on the simulation comparison data of the simple obstacle scenario in Table 4, the multi-dimensionally optimized RRT algorithm advanced in this study demonstrates prominent core performance advantages in comparison with the Basic RRT algorithm and the classic improved algorithm Q-RRT* (Ref. [22]): The Basic RRT algorithm requires 949 sampling points, a running time of 15.79 s, and a path length of 798.23 m. Restricted by the blindness of random sampling and fixed step size, it suffers from low search efficiency and path redundancy; although Q-RRT* outperforms the Basic RRT in respect of the number of sampling points (723), running time (11.56 s), and path length (738.45 m), it still has shortcomings such as relatively large computational load and limited environmental adaptability due to the failure to fully integrate multi-dimensional optimization strategies; in contrast, the multi-dimensionally optimized RRT algorithm only requires 232 sampling points, shortens the running time to 3.25 s, and further reduces the path length to 673.84 m, achieving comprehensive improvements in sampling efficiency, running speed, as well as path quality in simple environments.

Table 4. Simulation Comparison of Simple Obstacle Scenarios.

Algorithm	Number of Sampling Points	Running Time (s)	Path Length (m)
RRT	949	15.79	798.23
Q-RRT* (Ref. [22])	723	11.56	738.45
Multi-Dimensional Optimized RRT	232	3.25	673.84

5.2. Complex Obstacle Scenario

To verify the path planning effect of the algorithm in complex and narrow scenarios, the start point is set at coordinates (10, 10) and the target point at coordinates (480, 480). Multiple obstacles are placed between them to test the obstacle avoidance capability of algorithm. The path planning result obtained from the simulation is illustrated in Figure 15.

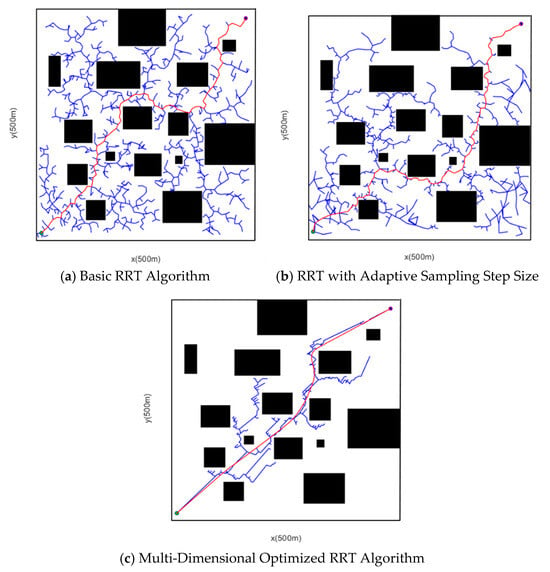
Figure 15. Comparison of Simulation Results in Complex Obstacle Scenario.

It can be observed from the simulation results in Figure 15 that all three algorithms can search for feasible paths. Among them, the RRT algorithm takes up a long time to search for the path, the resulting path is tortuous, and the path contains a large quantity of nodes, which is not suitable for the actual execution of vehicle trajectory tracking. Compared with the RRT algorithm, the RRT algorithm featuring adaptive sampling step size cuts down the time spent on path search and the number of sampling points to a certain extent, but the finally formed path still does not cater to the requirements of vehicle driving and is not optimal. The improved RRT algorithm proposed in this paper adds multiple layers of improvements and optimizations rooted in the RRT algorithm, which diminishes the random sampling nature of the algorithm. The algorithm converges with very few iterations, and the path processed via the B-spline curve is smoother, which favors vehicle tracking and driving. Due to the randomness of the algorithm, 20 path planning simulation instances were conducted for the scenario, and the simulation results of the three algorithms were statistically analyzed. All indicator results are average values, and the data of the simulation instances are displayed in Table 5.

Table 5. Simulation Data in Complex Obstacle Scenario.

Algorithm	Number of Sampling Points	Running Time (s)	Path Length (m)
RRT	1010	26.8499	892.3703
RRT with adaptive sampling step size	933	23.1196	870.7378
Multi-Dimensional Optimized RRT	636	11.0702	699.6111

Table 5 presents the average values of data obtained from 20 simulation experiments. When utilizing the basic RRT algorithm to calculate the initial path, the mean number of samplings is 1010, the average time consumed is 26.8499 s, and the mean path length amounts to 892.3703 m. However, when the multi-dimensionally optimized algorithm searches for the shortest path, the mean number of samplings is 636, the average time consumed is 11.0702 s, and the mean path length is 699.6111 m. The running time is shortened by 57.6%, the path length is decreased by 32.8%, and the curvature of the planned path is more in line with the requirements of vehicle driving.

Based on the simulation comparison data of the complex obstacle scenario in Table 6, under complex obstacle scenarios, the multi-dimensionally optimized RRT algorithm presented in this research exhibits significant core performance advantages in comparison with the Basic RRT algorithm and the classic improved algorithm Q-RRT* (Ref. [22]): The Basic RRT algorithm requires 1010 sampling points, a running time of 26.85 s, and a path length of 892.37 m. Due to issues such as the blindness of random sampling and fixed step size, it has low efficiency and path redundancy; although Q-RRT* outperforms the Basic RRT in the aspect of the number of sampling points (892), running time (20.14 s), and path length (812.36 m), it still has limitations including relatively large computational load and insufficient adaptation to complex environments; in contrast, the multi-dimensionally optimized RRT algorithm only requires 636 sampling points, shortens the running time to 11.07 s, and further reduces the path length to 699.61 m. It achieves comprehensive improvements in sampling efficiency, running speed, and path quality in complex environments, and is more consistent with the actual driving requirements for intelligent vehicles for path safety, smoothness, and real-time performance.

Table 6. Simulation Comparison of Complex Obstacle Scenarios.

Algorithm	Number of Sampling Points	Running Time (s)	Path Length (m)
RRT	1010	26.85	892.37
Q-RRT* (Ref. [22])	892	20.14	812.36
Multi-Dimensional Optimized RRT	636	11.07	699.61

6. Conclusions

To address the core issues of the traditional RRT algorithm in intelligent vehicle path planning—like blind search, fixed step size, simplified vehicle modeling, and unsmooth paths—this study proposes a multi-dimensionally optimized RRT algorithm covering the “sampling-step size-modeling-smoothing” process. The research is conducted in conjunction with a 2-degree-of-freedom (2-DOF) automotive dynamics model (verified via CarSim to exhibit good consistency with the dynamic characteristics of actual vehicles). First, to resolve the problem of blind sampling, a heuristic sampling strategy integrating obstacle density and target direction is proposed: the probabilities of “target-biased sampling” and “random sampling” are dynamically adjusted using a grid map. This strategy reduces the number of sampling points from 1404 to 371 and shortens the running time from 28.4 s to 3.67 s, significantly improving convergence efficiency. To overcome the limitation of fixed step size, an adaptive step size mechanism based on two types of safety distances is designed. Second, to mitigate the obstacle avoidance risks associated with particle-based vehicle modeling, a node expansion mechanism is introduced to construct a vehicle model. To address path redundancy and tortuosity, a process combining “greedy strategy for redundancy removal + quasi-uniform cubic B-spline smoothing” is adopted. This process not only eliminates invalid nodes but also optimizes curvature through the continuity of the second derivative, satisfying the vehicle’s kinematic constraints. Simulation verification based on MATLAB in a 500 m × 500 m grid map shows the following results: In the simple obstacle scenario (start point (10,10), target point (480,480)): The number of sampling points of the proposed algorithm (232) accounts for only 24.4% of that of Basic RRT (949) and 32.1% of that of Q-RRT* (723); the running time (3.25 s) is reduced by 79.4% and 71.9% compared with the two algorithms, respectively; and the path length (673.84 m) is decreased by 15.6% and 8.8%, respectively. In the complex obstacle scenario: The number of sampling points of the algorithm proposed in this study (636) is decreased by 37.0% in comparison with Basic RRT (1010) and by 28.7% compared with Q-RRT* (892); the running time (11.07 s) is shortened by 58.8% and 45.0%, respectively; the path length (699.61 m) is reduced by 21.6% and 13.9%, respectively; and the continuous path curvature is suitable for vehicle tracking.

In conclusion, the multi-dimensionally optimized RRT algorithm proposed in this study achieves collaboration across four core dimensions, breaking through the limitations of single-dimensional improvements in traditional algorithms. It realizes multi-objective optimization of “search efficiency-obstacle avoidance safety-path smoothness-vehicle adaptability,” providing an efficient technical solution for intelligent vehicle path planning in complex scenarios and offering a “multi-dimensional collaboration” methodological reference for random sampling-based algorithms. Future research may explore adaptive optimization for scenarios involving dynamic obstacles and multi-vehicle interaction.