Abstract
The multi-objective optimization of an electric prototype racing vehicle is addressed in this study. The goal was to identify the optimal combination of battery type, pilot weight, and power mode to maximize operational time and distance while minimizing energy consumption. A structured factorial design was implemented, and the resulting data were analyzed through Response Surface Methodology (RSM) in combination with the Desirability Function Approach (DFA). The experimental design included two battery configurations, three weight levels, and three power settings, while data acquisition was performed through a custom Arduino-based system validated against commercial instruments. The results revealed that the configuration with the smallest battery, the lowest weight (66 kg), and the lowest power mode (N5) achieved the most efficient performance, yielding an operating time of 1.12 h, a travel distance of 24.63 km, and an energy performance index of 2.90 km/Ah. The integration of RSM with DFA provided a robust framework for identifying optimal multiparameter conditions under competition constraints. Unlike previous studies that examined these variables in isolation, this work advances the state of the art by demonstrating the feasibility of multiparameter optimization in real-world racing contexts, offering methodological and practical insights for sustainable electric mobility.
1. Introduction
Efforts to reduce the environmental impact of road transportation have been widely undertaken by the automotive industry. Among the most prominent strategies, the development of eco-friendly vehicles and the introduction of advanced technologies that improve the energy performance index (km/Ah) have been prioritized. Within this global framework, international initiatives such as the Shell Eco-Marathon have been recognized for their pivotal role in promoting the design and construction of high-efficiency prototypes. Through these events, the limits of sustainable mobility have been continuously extended by combining innovation in research, engineering, and performance optimization [1].
In Colombia, comparable efforts have been pursued within academic institutions. At Pascual Bravo University, extensive expertise in the design and construction of prototype race cars has been consolidated within the Faculty of Engineering. The development pathway has been structured around three stages: concept formulation, engineering design, and physical construction with testing, through which compliance with safety, performance, and the energy performance index (km/Ah) is verified prior to participation in competitive events. In recent years, several electric race cars have been engineered and assembled by the university team, with notable results being achieved in local competitions.
The National Electric Vehicle Competition has been established as a key arena for testing and showcasing technological advances in electric mobility. The event is held annually, and university teams across the country are brought together to design, build, and test electric vehicles, with the primary objective of maximizing the energy performance index (km/Ah). Vehicles are required to resemble passenger cars while employing sophisticated energy-management strategies. As illustrated in Figure 1, a battery-powered electric city car, designed by the Pascual Bravo University team, was entered in the third edition of this event, held in Medellín, Colombia. Top honors were earned, with outstanding results demonstrated in technical innovation, the energy performance index (km/Ah), and sustainable engineering practices [2].

Figure 1.
Electric race car competing in a national competition.
Electric vehicles (EVs) such as these prototypes are typically powered through the integration of lithium-ion (Li-ion) batteries, brushless direct current (BLDC) motor controllers, and battery management systems (BMS). Li-ion batteries have become the standard due to their high energy density, long lifespan, absence of memory effect, and flexibility in charging and discharging operations [3,4]. Despite these advantages, EV prototypes face persistent challenges, particularly under competition conditions. Among these are the fluctuating power demands, the weight and type of battery employed, and the thermal behavior of the energy system [5].
The comparison of battery types, power settings, and total weight in electric prototype race cars has been regarded as essential for optimizing both overall performance and the energy performance index (km/Ah). In prior studies, these determinants have typically been examined individually to inform vehicle design and operation. For instance, the influence of battery selection on energy output, stability, and temperature control has been demonstrated through analyses of lithium-ion cells under racing conditions [5]. In parallel, improvements in the energy performance index (km/Ah) and in overall performance have been reported when weight reduction was pursued via lightweight materials and efficient cooling strategies [6]. Moreover, regenerative braking has been examined as a means of extending the available energy and increasing travel distance, with encouraging results being achieved [7]. Taken together, these findings have underscored how battery selection, weight reduction, and energy recovery are recognized as central levers for advancing the performance of electric race cars.
Beyond these contributions, complementary insights into regenerative braking and its broader implications for electric-vehicle performance have been reported. A state-of-the-art review of regenerative braking systems (RBS) was presented by Szumska (2025) [8], in which advances in system design, control strategies such as Model Predictive Control (MPC), machine learning, and hybrid storage solutions combining batteries with supercapacitors were highlighted. The efficiency of energy recovery was emphasized as being strongly influenced by external and kinematic factors. In parallel, Chidambaram et al. (2023) [9] examined the effect of regenerative braking on battery lifetime, showing that high and repeated charging currents during braking may accelerate degradation, particularly under non-optimal temperature and state-of-charge conditions. When viewed together, these perspectives extend the discussion beyond the energy performance index (km/Ah), bringing system reliability and battery durability to the forefront.
Despite these advances, most studies have investigated such variables in isolation, without considering their combined effects. A comprehensive comparative analysis that simultaneously integrates battery configurations, weight levels, and power settings has yet to be established in the current literature [10,11,12,13,14,15]. To address this limitation, the present work applies a multiparameter experimental design that evaluates the joint influence of these critical factors. Furthermore, the integration of advanced statistical tools, namely, Response Surface Methodology (RSM) and the Desirability Function Approach (DFA), provides a robust optimization framework, enabling the identification of operational conditions that balance competing objectives, such as distance traveled, time, and energy consumption [16,17,18,19,20,21,22,23].
The principal gaps and the specific contribution of this study are summarized in Table 1.

Table 1.
Summary of literature gaps and contributions of this study.
In summary, the state of the art is advanced by bridging a critical gap: the simultaneous evaluation of batteries, weight levels, and power settings in electric prototype race cars. By combining factorial experimentation with RSM and DFA, a rigorous yet practical framework is provided to identify operating conditions that maximize distance and time while minimizing energy consumption.
While previous studies have advanced knowledge on battery selection, weight reduction, and regenerative braking independently [5,6,7], they have generally examined these factors in isolation without exploring their combined effects. Recent reviews confirm the lack of experimental validation under factorial multiparameter designs [10,11,12,15]. The novelty of the present work lies in bridging this gap through a comprehensive evaluation that simultaneously integrates battery configuration, vehicle weight, and power settings using a structured factorial design. To the best of our knowledge, this is the first study to validate such an approach in a real competition environment, thereby advancing the literature with practical insights into multiparameter optimization for electric racing vehicles.
2. Materials and Methods
The performance of the electric racing vehicle was optimized in this study by seeking to maximize time and distance while minimizing energy consumption through a multiparameter approach. A sequential optimization strategy based on Response Surface Methodology (RSM), guided by the steepest descent/ascent algorithm, was implemented. The procedure was carried out in five stages: experimental design, instrumentation and data acquisition, data collection, data cleaning, and RSM–DFA analysis, as illustrated in Figure 2.
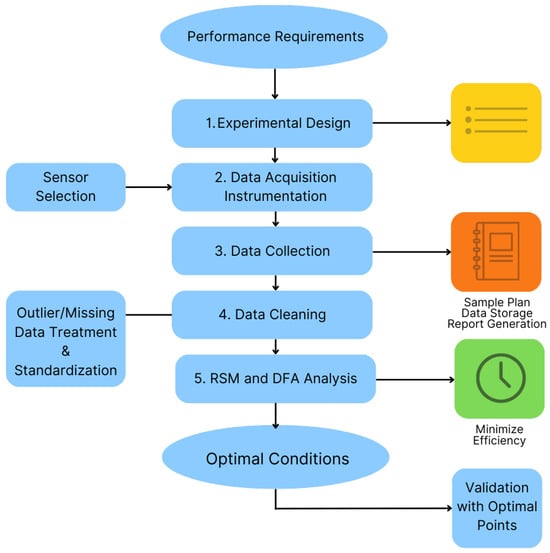
Figure 2.
Methodological workflow of the study. The process begins with defining performance requirements, followed by sensor selection and system integration. Experimental validation is then conducted through data acquisition and cleaning. The final stages involve optimization using Response Surface Methodology (RSM) and validation of optimal points with the Desirability Function Approach (DFA).
2.1. Experimental Design
The experiments were conducted in six steps, adhering to the methodology outlined by [24], as follows.
- Identification of problemsElectric vehicles (EVs) are being adopted at an increasing rate as the global transition from fossil fuels is accelerated by declining technology costs and supportive government incentives. In this context, the establishment of a performance baseline is regarded as essential to evaluate improvements that improve the energy performance index (km/Ah) and contribute to the broader shift towards sustainable energy. In competitions for electric vehicles, optimal operating conditions are sought by examining variations in battery type, power settings, and vehicle weight to minimize energy consumption while maximizing the Energy Performance Index (km/Ah). Ultimately, the distance achieved on a single full battery charge under competitive conditions is considered the defining measure of success.
- Selection of response variables and input factorsIn this experiment, three input variables were considered, each selected to capture a critical aspect of vehicle performance. The first variable, battery type (), corresponded to a pack delivering a nominal voltage of 48 V and a capacity of 480 Wh. Each pack was composed of Samsung 18650 Li-ion cells rated at 3.7 V and 2500 mAh, arranged in a mixed configuration of four cells in parallel and thirteen such groups connected in series (4p × 13s). This configuration was chosen to optimize energy storage and discharge performance while meeting the physical constraints of the vehicle; Although the triangular arrangement minimized the occupied volume, it simultaneously limited heat dissipation from the innermost cells.The second variable, weight (), was adjusted by maintaining a constant pilot mass of 66 kg and introducing additional ballast weights of 10 kg and 20 kg. This procedure allowed the effect of vehicle mass on both the energy performance index (km/Ah) and travel speed to be examined systematically.The third variable, power mode (), was defined through the commercial BLDC motor controller, which incorporates adjustable output-current limits via an LCD interface. The three predefined modes, N5 (400 W), N7 (500 W), and N9 (600 W), approximately correspond to specific maximum current values as detailed in [25]. These settings are commonly employed in electric prototype competitions to balance performance and efficiency and were therefore selected to simulate realistic driving conditions and assess their influence on battery behavior.In addition to the input factors (battery type, pilot weight, and power mode), three response variables were recorded. Time (Y1) represented the total duration of each trial, expressed in hours total_time_hours. Distance (Y2) denoted the cumulative distance traveled, expressed in kilometers total_distance_km. Finally, the Energy Performance Index (Y3) was calculated as the ratio between distance traveled and the total ampere-hours consumed, expressed in km/Ah Energy_Performance.
- Selection of the Experimental DesignResponse Surface Methodology (RSM) was employed to evaluate and optimize vehicle performance. This methodology comprises a set of mathematical and statistical techniques designed to model and improve a response variable influenced by multiple input factors. A principal advantage is that complex interactions among variables can be efficiently explored and represented through second-order polynomial models. By concentrating on regions near local optima, RSM enables identification of favorable operating conditions without exhaustive experimentation, thereby reducing time and resource requirements. The resulting models not only provide predictive capability but also facilitate interpretation, offering insights into the relative influence of each factor and supporting data-driven design refinements.
- Conducting the experiment.The experiment was carried out through 12 randomized runs, spanning the set of factor combinations defined for the study and as further described in the results section. In each run, the electric vehicle was driven on the test track shown in Figure 3 until the battery was fully discharged. The circuit measured 0.241 km in length and exhibited a surface friction coefficient ranging from 0.5 to 0.7, thereby introducing moderate variability in traction conditions.
 Figure 3. Track used for vehicle performance testing. Source: Authors’ own elaboration.
Figure 3. Track used for vehicle performance testing. Source: Authors’ own elaboration. - Data preparation and modelingA statistical analysis based on a factorial design was performed to evaluate the effects of battery type (), weight (), and power mode () on time, distance, and the Energy Performance Index (km/Ah) (–). Raw telemetry and timing records were curated to remove incomplete laps and obvious sensor artifacts, after which the response variables were computed for each run. Response Surface Methodology (RSM) models were then fitted to relate – to –, including main effects, two-way interactions, and quadratic terms where appropriate. Model adequacy was assessed through residual diagnostics, goodness-of-fit statistics, and lack-of-fit checks, and influential points were examined to ensure that conclusions were not driven by outliers or data-logging transients. This approach enabled the identification of operating conditions that maximized time, distance, and the Energy Performance Index. Where multi-objective trade-offs arose, the Desirability Function Approach (DFA) was applied to balance criteria. For all statistical procedures, a confidence level of 90% () was adopted.
- Conclusions and recommendationsMulti-objective optimization was performed using the Desirability Function Approach (DFA) to balance the goals of maximizing (time), (distance), and (Energy Performance Index, km/Ah). When total energy consumption (Ah) was considered, it was treated as an auxiliary constraint with decreasing desirability. Composite desirability surfaces were examined to identify operating regions offering favorable trade-offs among endurance, range, and energy performance. The recommended settings were then subjected to confirmation trials on the same test track to verify predictive accuracy under competition-representative conditions, thereby supporting the external validity of the optimized configuration.All mathematical and statistical calculations were performed using RStudio Desktop 4.3.3.
2.2. Data Acquisition and Instrumentation
Several sensors and electronic components were integrated into the project, including the Arduino MEGA 2560 microcontroller, the ACS712 current sensor, the A3144 magnetic Hall effect sensor, LEDs, resistors, and a soldered breadboard. The car battery was connected to the Arduino via a current sensor and a voltage divider, while a Hall effect magnetic sensor was also attached to measure speed. An SD card module was also employed for data logging. The overall configuration of these elements is shown in Figure 4.
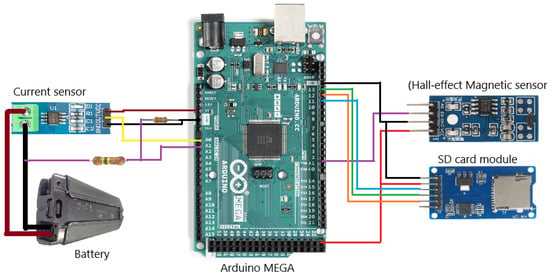
Figure 4.
Physical implementation of the Arduino-based DAQ installed on the vehicle during experiments.
The Arduino MEGA provides 54 digital I/O pins (15 capable of PWM), 16 analog inputs with 10-bit resolution, a 16 MHz quartz crystal, 4 UARTs, a power jack, USB connection, ICSP header, and a reset button. It can be connected to a computer via USB or powered through an adapter or battery. Programming is performed through the Arduino IDE, which allows code uploads to the ATmega2560 microcontroller via its integrated bootloader, eliminating the need for an external hardware programmer.
The Arduino-based low-cost DAQ prototype was designed and implemented according to several key requirements. In particular, it was intended for academic use within engineering programs, where cost-effective and accessible instrumentation is essential. The use of low-cost components ensured affordability, while the adoption of open-source software enhanced flexibility and usability. The Arduino IDE was selected as the development environment, providing the necessary tools for programming and customizing specific measurement setups, thereby expanding the prototype’s functionality and educational value [26].
The ACS712 current sensor was employed to calculate DC current as:
where S depends on the ACS712 range (5 A, 20 A, 30 A, respectively).
The ADC input voltage is computed from raw counts (10-bit ADC) as:
For the Hall sensors, distance and speed are derived from pulses:
where C is the wheel circumference (m), P is pulses per wheel revolution, is the pulse increment in interval .
Data were recorded by the Arduino-based DAQ at a sampling frequency of 9.615 kHz with 10-bit resolution. This was considered sufficient given the relatively smooth acceleration profiles observed during testing. Each experiment was designed so that, at each predefined power level, the vehicle was accelerated once at the beginning until reaching a stable mean speed. Thereafter, velocity was maintained as constant as possible. Deceleration was permitted only when the first signs of battery depletion appeared, specifically, when the vehicle exhibited a noticeable loss of power despite throttle engagement and when the battery indicator reached its minimum flashing level. At that point, the trial was concluded and the telemetry system was switched off, even though a residual charge remained in the battery that would normally allow the vehicle to return to the starting point. Thus, each trial contained only one acceleration phase and one deceleration phase, both of which were excluded from the statistical analysis to avoid bias. To improve signal stability, samples were averaged over five records, and processed data were stored at 200 ms intervals. Calibration was performed to ensure accuracy of the measurements. Each Hall effect sensor was referenced against wheel rotations and validated with a commercial tachometer across the operational range. The ACS712 current sensor was calibrated using a precision 0.1 shunt resistor, and its accuracy was verified with a calibrated digital multimeter under different load conditions. For the voltage divider, known reference voltages spanning the expected battery range were applied and compared with multimeter readings, allowing gain and offset corrections to be derived. Although the system was not designed to capture high-frequency transients, the calibrated configuration was sufficient to characterize the dynamics of acceleration and deceleration in the context of electric vehicle competitions.
To further ensure reliability, the Arduino-based DAQ system was validated against commercial instruments. Voltage and current measurements were compared with a calibrated Fluke digital multimeter, while speed readings were cross-checked with a handheld tachometer. The precision shunt resistor also confirmed current sensing accuracy. A detailed description of calibration procedures, including acceptance criteria and uncertainty estimates, is presented in the following subsection.
2.3. Data Collection
The objective of the methodology was to apply Montgomery’s Design of Experiments (DoE) framework to evaluate vehicle performance systematically under varying conditions. Through this structured approach, the optimization of key parameters was pursued with the intention of ensuring both repeatability and reliability of the results.
The trials were conducted on a synthetic grass field measuring 52 m by 30 m. The circuit was delineated within a 3 m wide lane positioned between the perimeter fence and the inner side of the field, and orange safety cones were used to provide guidance and ensure safety. To minimize environmental variability, all tests were carried out within a fixed time window between 12:00 and 12:30 p.m. Thus, all trials were performed on a synthetic-turf track under controlled conditions. This surface was selected to reduce the influence of wind disturbance and surface irregularities, thereby improving consistency in data collection. It is nevertheless acknowledged that alternative track surfaces, such as asphalt, may alter vehicle dynamics and the energy performance index (km/Ah). For this reason, further validation on different terrains is recommended to broaden the external validity of the findings.
For the experiment, the vehicle was equipped with a data-acquisition system powered by two 48 V, 10 Ah Li-ion batteries—one designated for the primary test and the other retained as a backup in case of operational issues. The batteries were charged using a charger capable of delivering up to 2 A and featuring an automatic disconnect to prevent overheating due to overcharge. Prior to each trial, the microSD card in the data-acquisition system was formatted to ensure accurate data recording and to avoid data loss or overwriting. Data were recorded by the Arduino-based DAQ at a sampling frequency of 9.615 kHz with 10-bit resolution, which was considered sufficient to capture the relatively smooth acceleration profiles observed during testing.
To simulate different weight conditions, sandbags were added to the vehicle in addition to the driver’s weight, according to the experimental plan. The primary factors varied in this study were battery type (pack configuration), vehicle weight (driver plus ballast), and power setting. The power levels referred to as N5, N7, and N9 corresponded to predefined modes in the commercial BLDC motor controller with an LCD interface and approximately represented operating power limits of 400 W (N5), 500 W (N7), and 600 W (N9). Such settings are routinely employed in electric-prototype competitions to regulate performance and the energy performance index (km/Ah).
A factorial design was employed to study the main effects and interactions among the factors. Specifically, a factorial structure was adopted to reflect two battery configurations, three weight levels, and three power settings. The order of trials was randomized to mitigate the influence of uncontrolled factors, and each condition was replicated at least three times to enhance the statistical reliability of the results. Daily runs were planned the day before in accordance with the DOE schedule; batteries and ballast availability were verified, the vehicle underwent mechanical and visual inspection at the test site, and the same driver was used throughout to maintain uniform operating conditions.
With the data-acquisition system activated, the vehicle was operated according to the predetermined experimental conditions. After each run, the recorded data were secured for subsequent analysis. Raw telemetry and timing records were curated to remove incomplete laps and obvious sensor artifacts, after which the response variables—time, energy consumption, and distance—were computed for each run. Statistical analyses were performed to evaluate the impact of each factor and their interactions; an Analysis of Variance (ANOVA) was used to determine statistical significance at a 90% confidence level (). Where appropriate, Response Surface Methodology (RSM) models were fitted to capture curvature and interaction effects, and these models were used to identify operating regions associated with improved performance.
By following this comprehensive methodology grounded in Montgomery’s DOE framework, reliable and actionable insights were generated into the key factors affecting vehicle performance. The systematic approach strengthened internal validity, supported repeatability, and provided clear guidance for future improvements in electric prototype racing vehicles.
2.4. Data Cleaning
Data cleaning was undertaken as a critical step to ensure the accuracy and reliability of the experimental data used in the Response Surface Methodology (RSM) analysis. The raw data obtained from each test run of the electric vehicle Furtivo II were first inspected to verify the completeness and consistency of key parameters, including voltage, current, speed, distance, and time. Inconsistent or missing values were identified, and when necessary, the corresponding tests were repeated under identical experimental conditions to preserve data integrity.
Outliers resulting from measurement errors or unexpected disturbances during testing were treated using statistical techniques such as Z-scores and the interquartile range (IQR). Data points that deviated substantially from expected trends were flagged for evaluation, and in cases where significant anomalies were detected, the affected trials were rerun to strengthen the robustness of the dataset.
Following this validation process, several performance metrics were derived. Total energy consumption was computed in ampere-hours (Ah) by integrating current over time, and in kilowatt-hours (kWh) by integrating the product of voltage and current. The distance traveled was converted to kilometers, while average power and average speed were calculated to support performance assessment. From these results, the three key response variables were obtained: total time (, in hours), total distance (, in kilometers), and the Energy Performance Index (, in km/Ah). These variables were then used as the basis for the optimization models.
To facilitate comparative analysis across all test conditions, the cleaned data were standardized and synchronized. Codification was then applied to the input factors (battery type, pilot weight, and power mode) in accordance with the factorial design framework. A final validation step confirmed consistency between the cleaned dataset and the experimental logbooks, after which first- and second-order RSM models were fitted and employed to identify the optimal operating conditions.
2.5. RSM and DFA Analysis
The determination of the optimal operating conditions for the vehicle began with the experimental design outlined in Section 2.1. Response Surface Methodology (RSM) models were subsequently fitted and validated using Analysis of Variance (ANOVA). Surface and contour plots were then generated to visualize the response surfaces for each variable. Each response was individually optimized by applying the steepest descent method for minimization or steepest ascent for maximization, thus identifying the optimal performance regions. To locate global optima, contour plots from individual response surfaces were overlaid, producing an integrated visualization of compromise solutions.
The modeling process was based on the estimation of first- and second-order polynomials using the ordinary least squares method. A second-order response surface model was developed, as represented in Equation (5), with the experimental design described in Table 2.
where:
: are the response variables Time, Consumption, and Distance,
: are the factors battery, weight, and power,
: is the intercept,
: is the effect of each factor on every response variable ,
is the effect of the interaction between and and,
is the error therm.

Table 2.
Variables and levels for the experimental design. Weight is expressed in kilograms (kg). Battery and Mode are categorical experimental factors without physical units.
Table 2.
Variables and levels for the experimental design. Weight is expressed in kilograms (kg). Battery and Mode are categorical experimental factors without physical units.
| Variable | Level Values | ||
|---|---|---|---|
| Low (−1) | High (+1) | Central Point (0) | |
| Battery (categorical) | 1 | 2 | – |
| Weight (kg) | 66 | 86 | 76 |
| Mode (categorical) | 5 | 9 | 7 |
To ensure robustness under competition constraints, a factorial design with 12 runs was used as the most feasible option. Although the number of trials was relatively small to support fully robust second-order models, reduced models, specifically, FO + TWI (first order with two-way interactions) and FO + PQ (first-order with pure quadratic terms), were applied. These specifications provided a balance between explanatory power, numerical stability, and interpretability while avoiding aliasing and singularities associated with full second-order designs. Although this decision limited the ability to capture more complex non-linearities, the practical constraints of data collection, such as the impossibility of additional replications and intermediate points, required a design capable of systematically exploring interactions without imposing restrictive assumptions.
Randomization of trial order was applied during the planning stage using R-based design generation to minimize bias. Human variability was controlled by fixing a single pilot throughout all runs, while additional ballast was employed to simulate higher weight levels and maintain consistency in driving style and posture. Although formal blocking was not implemented, tests were concentrated within the same daily interval (12:00–12:30 p.m.) under controlled track conditions, and systematic verification of both the vehicle and battery state was performed before each run. Outlier trials resulting from disturbances were repeated, and statistical techniques such as Z-scores and the interquartile range (IQR) were applied to clean the data, thereby reducing uncertainty in the final dataset.
Separate models were developed for each response variable, operational time, distance, and efficiency, in order to preserve statistical coherence. However, a multi-response optimization was implemented through the desirability function, which combined the three models into a unified framework and enabled the simultaneous identification of compromise solutions. The convergence of results obtained through desirability optimization, individual model optimization, and contour plot superposition reinforced the robustness of the methodology. Future studies may extend this framework by employing Central Composite or Box–Behnken designs with additional runs to enhance the modeling of non-linearities and to further validate the external reliability of the findings.
3. Results and Discussion
3.1. Data Acquisition and Instrumentation
The acquisition and recording of data were carried out using a system specifically designed to withstand multiple tests and variable weather conditions. Two Hall effect sensors were mounted on a horseshoe-type support attached to one of the front tires. An on/off system was implemented to control the acquisition device, while a protective enclosure was used to isolate the Arduino and the current sensor from external elements. To prevent additional energy consumption that could affect the system’s efficiency, the device and sensors were powered independently by a 9 V battery.
A voltage divider, composed of a resistor array, was installed at the analog input A0 to reduce the input voltage from 100 V to a maximum of 5 V, corresponding to the board’s operating limit. In this way, voltages above 5 V were proportionally reduced to levels appropriate for acquisition. The analog input A2 was connected to the ACS712 current sensor, which measured the current flow through a serial array. Digital pin 2 was configured to count the number of interrupts occurring in the HIGH state, enabling the measurement of wheel revolutions per minute. Similarly, digital pin 3 was used to measure wheel displacement associated with the vehicle’s traction. Pin 8 served as a visual indicator of the microSD memory status, with the blue LED lighting up (HIGH) during recording and turning off (LOW) once recording stopped. Additionally, pin 9 functioned as an indicator that the data acquisition board was connected, as illustrated in Figure 5.

Figure 5.
System architecture of the low-cost Arduino-based DAQ (schematic of sensors, wiring, and logging).
All data were stored in a microSD module, with variables such as voltage, current, power, revolutions per minute, vehicle speed (km/h), distance traveled (m and km), and time stamps being recorded for efficiency analysis. Distance and speed were calculated from the sampling time and the Hall effect sensor, while consumption was derived from current and voltage measurements.
The tests were conducted by students under the supervision of a teacher, in accordance with the pre-established experimental design. The Arduino-based DAQ system demonstrated reliability when validated against a commercial controller, acquiring the same variables with consistent accuracy across repeated runs.
3.2. Data Collection
For the development of the tests, a synthetic grass field measuring 52 m by 30 m was employed as the track. The field was marked with orange safety cones, and the circuit was defined as a 3 m lane formed between the perimeter fence and the inner side of the field. All tests were conducted within a fixed time window between 12:00 and 12:30 p.m., and each experimental run was scheduled in advance according to the framework established in the experimental design.
Preparations were carried out the day before each run. These included the inspection of two 48 V, 10 Ah Li-ion batteries: one designated for the following day’s test and the other retained as a backup in case of operational issues. The condition of the 9 V battery used to power the data acquisition system was also verified. Any battery showing a voltage below the nominal value was recharged using a charger capable of delivering a peak current of 2 A per hour. The charger was equipped with an automatic disconnection feature to prevent overheating caused by overcharging. The microSD card for data acquisition was preferably formatted before each run to ensure proper data storage and to avoid overwriting errors, and it was left installed in the device.
On the day of the experimental run, the vehicle was transported from its storage location—where it was maintained under conditions that minimized humidity and dust exposure—to the test field. Once positioned at the center of the circuit, the vehicle underwent a general mechanical and visual inspection. This inspection included verification of the steering system, brakes, Hall effect sensors, and tire pressure. To maintain uniformity across tests, a single driver was used throughout all runs, ensuring that driving style and potential variability remained consistent. Weight conditions were varied as required by the experimental design: the driver’s body weight represented the first level, while the second and third levels were simulated by placing one or two sandbags inside the vehicle. For this reason, sandbags of the appropriate weight were prepared prior to each trial.
Following inspection, the driver entered the vehicle, and the batteries were placed into their respective compartments and switched to the ON position. The microSD card was checked, and the two mushroom-type emergency switches installed in series with the power were verified to be in the NC (normally closed) position. The SW900 information screen was then turned on, and the setup menu was accessed to program the power level to be tested. After exiting the setup, the system was validated by engaging the brakes and attempting to accelerate. Proper brake function was confirmed if the vehicle did not attempt to move from its starting position, and this procedure was repeated individually for each brake.
Once all verifications had been completed, the vehicle was deemed ready to operate. The data acquisition module was activated through a switch positioned within the driver’s reach, equipped with two LED indicators. The driver ensured that both the power LED and the microSD status LED were illuminated, confirming that the system was fully operational and ready for data collection.
3.3. Data Cleaning
The initial step of the data cleaning process was the consolidation of the raw experimental outputs of each trial into a unified dataset. Each record was labeled with an identifier corresponding to its respective test (EXPERIMENT), thereby preserving traceability across conditions. A filtering procedure was then applied to remove any rows with missing values in critical variables such as battery type, pilot weight, power mode, elapsed time, distance traveled, and energy consumption. This step ensured that each experimental run retained a complete and analyzable structure. Furthermore, appropriate data types were assigned to all variables according to their nature (categorical or numerical), and consistency checks were implemented to detect out-of-range values or acquisition errors originating from the vehicle’s telemetry system.
Once the dataset was structured and validated, specific calculations were performed to derive the key response variables. These included the total duration of each test expressed in hours (, total_time_hours), the cumulative distance covered in kilometers (, total_distance_km), and the Energy Performance Index expressed in km/Ah (, energy_performance_km_per_ah).
To calculate , the total energy consumed in ampere-hours (energy_consumed_ah) was obtained as the sum of the instantaneous current multiplied by the corresponding time interval and divided by 3600, to convert seconds into hours:
The Energy Performance Index was then computed as
In addition, total energy consumption in kilowatt-hours (energy_consumed_kwh) was computed from instantaneous power readings, which allowed the derivation of a secondary performance metric expressed in km/kWh (energy_performance_km_per_kwh). While km/kWh provided complementary insight into the energy use, the primary response variable for optimization was the Energy Performance Index (km/Ah). These derived metrics enabled a more detailed evaluation of vehicle energy behavior under different test conditions and supported accurate comparison and optimization within the factorial experimental design.
3.4. RSM and DFA Analysis
The experimental methodology was implemented within a Response Surface Methodology (RSM) framework following a structured sequence. First, the factors influencing the responses were specified and the corresponding experiments were executed. Using the steepest ascent technique, the models identified operating regions that favored improvements in , , and . The consolidated results in Table 3 summarize the outcomes for each factor combination and include auxiliary metrics, such as mean power and total ampere-hours consumed, that enable a more comprehensive interpretation of vehicle behavior across conditions.

Table 3.
Data collected.
The previously described experimental methodology was implemented using Response Surface Methodology (RSM), following a structured approach. Initially, the factors influencing the response variables were identified, and the corresponding experiments were conducted. In the subsequent stage, the optimal values for each response variable were determined. A tailored RSM design was developed to maximize operational time (), distance traveled (), and the energy performance index (), using the steepest ascent technique. The consolidated data presented in Table 3 summarize the outcomes obtained for each factor combination and include additional performance indicators, such as mean power and energy consumed in ampere-hours (Ah), supporting a more detailed understanding of the system’s behavior under varying experimental conditions.
Notably, the experiment recorded a maximum operational time of 1.12 h, a maximum distance of 24.63 km, and a peak Energy Performance Index of 2.82 km/Ah, all achieved under the conditions of Trial E5. Likewise, the minimum total energy consumption was recorded at 6.98 Ah in Trial E1. To validate the optimal points identified through RSM, the Desirability Function Approach (DFA) was applied as a complementary technique. This allowed for the simultaneous evaluation of multiple objectives, reinforcing the robustness of the proposed solution and ensuring a balanced optimization between performance, autonomy, and the Energy Performance Index (km/Ah) of the electric racing vehicle.
To perform the response surface analysis, the input variables were codified using the standard transformation , which centers and scales each factor around its midpoint. Specifically, battery type () was coded as , pilot weight () as , and power mode () as . This transformation ensures that all input factors are scaled to a comparable range and centered around zero, facilitating the fitting of second-order polynomial models. The codified dataset, used as input for the response surface modeling process, is summarized in Table 4.

Table 4.
Data codified.
This study presents a methodology for identifying the optimal configuration in a multi-parameter optimization framework, with the objective of maximizing operational time (), travel distance (), and the Energy Performance Index (, km/Ah). The experimental approach was based on a factorial design incorporating three control factors: battery type (), pilot weight (), and power mode (). Response Surface Methodology (RSM) was employed to model system behavior and quantify the effects of these factors on the defined responses.
For the response variable (total_time_hours), the factor power mode () was found to be statistically significant, with a p-value below 0.01. While pilot weight () did not exhibit a significant main effect, its interaction with power mode () was statistically relevant (). This highlights the importance of considering interaction effects in accurately describing the system’s performance.
Among the four candidate models evaluated—first-order (FO), first-order with two-way interactions (FO + TWI), full second-order (SO), and a hybrid model including selected quadratic terms (FO + PQ (, ))—the FO + TWI model was selected as the most appropriate for . This specification provided a balance between explanatory capacity, numerical stability, and interpretability, avoiding the coefficient aliasing issues encountered in the full second-order model.
The selection was further validated by the statistical performance of the FO + TWI model, which achieved an adjusted of 0.842 and a global p-value of 0.0098, as summarized in Table 5. In particular, the power mode () was highly significant (), and the interaction between weight and power mode () was also significant (). These results confirm the adequacy of including interaction effects in the modeling framework and support the use of this model for optimization and canonical path analysis.

Table 5.
Estimated coefficients and model fit statistics for the selected model (FO + TWI) for total_time_hours.
For the response variable (total_distance_km), a comparative evaluation of four candidate models was conducted. The model that combined first-order effects with quadratic terms for pilot weight and power mode (FO + PQ (, )) was identified as the most suitable specification. Although the full second-order model yielded a marginally higher adjusted (0.8951), it exhibited aliasing problems that hindered the reliability of canonical analysis and the tracing of optimal paths. In contrast, the FO + PQ model provided a more appropriate balance between statistical accuracy, numerical stability, and interpretability, achieving an adjusted of 0.8346 and a global p-value of 0.0043, as summarized in Table 6.

Table 6.
Estimated coefficients and model fit statistics for the selected model (FO + PQ (, )) for total_distance_km.
Importantly, the quadratic effect of pilot weight () was statistically significant (), confirming the existence of non-linear patterns in the response surface. Incorporating this curvature improved the model’s capacity to describe relevant behavioral dynamics of the system without leading to overfitting or loss of interpretability. These results validate the choice of the FO + PQ (, ) model as the most adequate for analyzing the influence of design factors on the vehicle’s travel distance and for guiding optimization within the response surface methodology (RSM) framework.
For the response variable , corresponding to the vehicle’s Energy Performance Index (EPI) expressed in kilometers per ampere-hour (km/Ah), four candidate models were considered: the first-order (FO), the first-order with two-way interactions (FO + TWI), the full second-order (SO), and a reduced specification including principal effects and quadratic terms for selected factors (FO + PQ (, )). Although the full SO model exhibited a high unadjusted (0.9349), it presented multicollinearity and aliasing problems that limited its reliability for canonical analysis and numerical optimization.
After assessing both statistical performance and interpretability, the FO + PQ (, ) model was selected as the most appropriate specification for , as summarized in Table 7. This model achieved the highest adjusted (0.8553) among the valid alternatives, with a statistically significant overall fit (). Notably, both pilot weight () and power mode () exerted significant effects ( and , respectively), confirming their relevance for the response. The incorporation of quadratic terms improved model adequacy without introducing singularities, enabling a valid canonical analysis and the identification of a stationary point. Consequently, the FO + PQ (, ) model was established as the most suitable for optimizing the Energy Performance Index (km/Ah) of the electric vehicle within the response surface methodology (RSM) framework.

Table 7.
Estimated coefficients and model fit statistics for the selected FO + PQ (, ) model for energy_performance_km_per_ah.
The ANOVA results, presented in Table 8, were employed to validate the statistical significance and predictive capacity of the selected models for each response variable. For operational time (: total_time_hours), the first-order model with two-way interactions (FO + TWI) was identified as the most appropriate specification. This model offered a favorable balance between complexity and interpretability, with statistically significant main effects, an adjusted of 0.842, and a global model p-value of 0.0098.

Table 8.
ANOVA for the selected models for each response variable.
For distance traveled (: total_distance_km) and the Energy Performance Index (: energy_performance_km_per_ah), the models combining first-order terms with quadratic effects in pilot weight and power mode (FO + PQ ()) were selected. These specifications successfully captured the non-linear behavior of the responses without introducing coefficient aliasing, thereby enabling valid canonical analysis. Both models exhibited strong explanatory power, with adjusted values of 0.8346 and 0.8553, respectively, and global p-values below 0.005. In particular, the significance of the quadratic term in the distance model () confirmed the presence of curvature in the response surface, further supporting the adequacy of the chosen models for optimization purposes.
Figure 6 presents the two-dimensional (2D) contour plots and three-dimensional (3D) surface graphs derived from the selected FO + TWI model for the response variable (total_time_hours). These visualizations illustrate how combinations of battery type (), pilot weight (), and power mode () influence vehicle endurance. The 2D contour plots reveal consistent trends: at a fixed power mode (N7), operational time increases modestly as pilot weight decreases, particularly for intermediate battery levels; at a constant weight of 75 kg, operational time declines with increasing power mode, clearly favoring low-power settings (e.g., N5). Furthermore, when holding the battery constant at a midrange value (), longer operational times are concentrated in the low-weight, low-power region, suggesting an interaction effect between and .
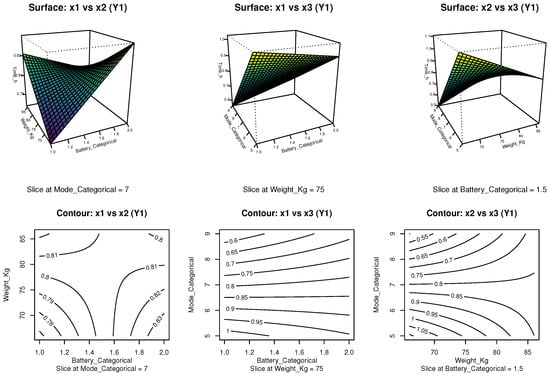
Figure 6.
Response surface and contour plots for the response variable (operational time), based on the FO + TWI model. Source: Author’s own elaboration.
The 3D response surfaces confirm these observations by highlighting a well-defined optimal region: maximum operational time is achieved when the pilot weight is minimized (66 kg) and the power mode is set to N5. Among the three factors, the power mode () exerts the strongest influence on the response, as indicated by the steep gradients along that axis. The effect of pilot weight, while less pronounced, aligns with the direction of maximum ascent identified in the RSM optimization. Moreover, the smooth and gently curved surfaces indicate the absence of significant second-order effects, reinforcing the adequacy of the FO + TWI model in describing the system behavior without requiring quadratic terms. These graphical insights validate the statistical model and provide practical guidance for configuring the vehicle to extend operational autonomy under energy-conserving conditions.
The graphical analysis presented in Figure 7 corresponds to the response surface and contour plots derived from the selected FO + PQ () model for the response variable (total_distance_km). The contour plots reveal that maximum distances are achieved at low pilot weights and low power modes (N5), combined with intermediate to high battery levels. Specifically, in the vs. projection, with power mode fixed at N7, greater distances are obtained with lighter pilots and higher-capacity batteries. Similarly, the vs. projection, with weight fixed at 75 kg, confirms that increasing the power mode reduces travel range. The vs. plot displays a clear curvature, supporting the inclusion of quadratic terms in the model specification.
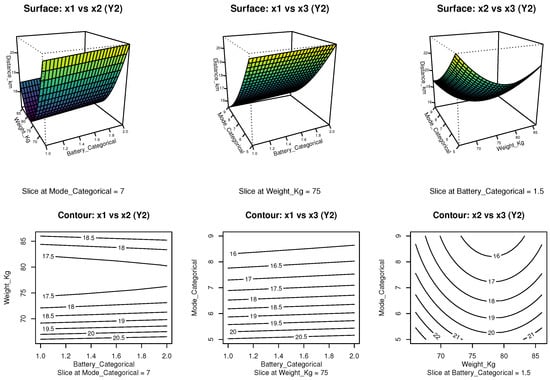
Figure 7.
Response surface and contour plots for the response variable (distance traveled), based on the FO + PQ () model. Source: Author’s own elaboration.
The 3D surface plots corroborate the trends observed in the contours and emphasize the non-linear nature of the response. In particular, the curved surface along the and axes illustrates the quadratic interaction affecting travel distance. The optimal region is identified in the configuration combining a low pilot weight (66 kg), a conservative power mode (N5), and a battery level close to 2.0. These graphical insights confirm the adequacy of the FO + PQ model and provide practical guidance for optimizing distance performance in electric vehicle operation.
The graphical analysis presented in Figure 8 corresponds to the response surface and contour plots derived from the FO + PQ () model for the response variable (energy_performance_km_per_ah). These visualizations show that maximum values of the energy performance index are achieved under low pilot weights (66 kg) and conservative power modes (N5). The 2D contour plots highlight the interaction between weight and power mode, while the 3D surfaces confirm the existence of curvature in the response surface, indicating partial non-linear effects. This validates the inclusion of quadratic terms in the model specification and demonstrates that lightweight configurations combined with reduced power demand constitute the most favorable operating strategy for maximizing energy performance.
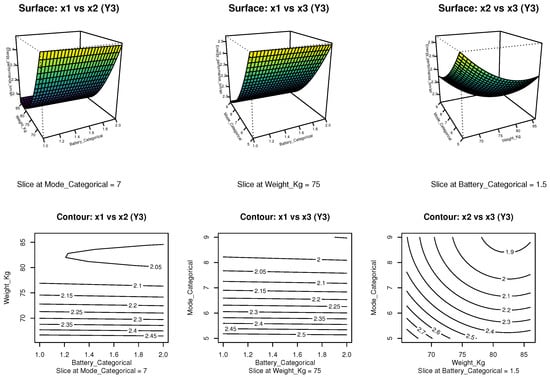
Figure 8.
Response surface and contour plots for the variable (energy performance), based on the FO + PQ () model. Source: Author’s own elaboration.
The 3D surface plots reinforce these findings by illustrating steeper efficiency gradients in the low-weight and low-power regions. Among the three factors, pilot weight () and power mode () exert the strongest influence on energy performance, while the battery factor () plays a secondary role. These graphical insights confirm the adequacy of the FO + PQ model for capturing the system’s behavior and provide practical guidance for defining operational strategies aimed at enhancing energy-saving performance in electric vehicles.
Figure 9 presents the simultaneous contour plots for the three response variables: operational time (), total distance traveled (), and the energy performance index (, km/Ah), as functions of battery type () and pilot weight (). The plots are stratified across three fixed levels of the power mode factor (), corresponding to coded values of , 0, and 1, which translate into the real operating settings of N5, N7, and N9, respectively. This graphical multi-response optimization enables the identification of operating regions within the experimental domain where all three responses simultaneously exhibit favorable performance.
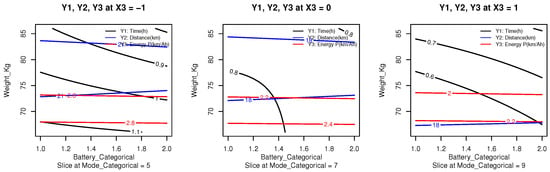
Figure 9.
Superimposed contour plots for the response variables (operational time), (travel distance), and (energy performance), at three fixed levels of power mode . Source: Author’s own elaboration.
To generate these plots, predictions were obtained from the fitted RSM models for each response, and the corresponding contour lines were overlaid within a common coordinate system using distinct colors: black for , blue for , and red for . The graphical superposition highlights a common optimal region located at the lower bounds of pilot weight and battery size, particularly under the conservative power mode N5. These results are consistent with the outcomes of the canonical path analysis and the desirability function approach, reinforcing N5 as the most energy-efficient and robust operating configuration under lightweight conditions.
In addition to the contour superposition method applied for graphical multi-response optimization, individual optimizations were performed for each response variable by evaluating the fitted RSM models over a fine grid of experimental conditions. This procedure enabled the identification of the optimal levels of the control factors—battery type (), pilot weight (), and power mode ()—that maximize each response independently within the experimental region.
For operational time (), the optimal configuration corresponded to the lowest tested battery size (1.0), the minimum pilot weight (66 kg), and the lowest power mode (N5), yielding a maximum predicted duration of 1.129 h. For travel distance (), the best performance was obtained under the same lightweight and low-power conditions, but with the highest battery capacity tested (2.0), producing an estimated maximum of 24.446 km. In the case of the energy performance index (, km/Ah), the optimal configuration coincided with that of —battery size 1.0, pilot weight 66 kg, and power mode N5—achieving a predicted value of 2.942 km/Ah. These results highlight the relevance of lightweight configurations and conservative power settings as consistent strategies for maximizing both operational autonomy and energy efficiency in electric vehicles.
Finally, a multi-response optimization was conducted using the desirability function approach (DFA), which enables the simultaneous maximization of multiple responses by transforming them into a common desirability scale ranging from 0 (undesirable) to 1 (fully desirable). Individual desirability functions were defined for each response variable, targeting 1.2 h for operational time (), 24 km for distance traveled (), and 2.8 km/Ah for the energy performance index (). The global desirability index was then calculated as the geometric mean of the three individual desirabilities across all experimental runs.
The optimal configuration identified through DFA corresponded to the codified factor levels , , and , which in real units, translate to a battery size of 1.0, a pilot weight of approximately 66 kg, and power mode N5. Under these conditions, the predicted responses were h, km, and km/Ah, yielding a high overall desirability score of 0.945. These results confirm the consistency of the optimization strategies and reinforce the effectiveness of lightweight configurations combined with conservative power settings as the most suitable operating conditions for maximizing electric vehicle performance across multiple objectives.
The integrated analysis of optimization strategies—including contour-based visual exploration, individual RSM model predictions, and composite desirability evaluation—provided a comprehensive and convergent understanding of the optimal operating conditions for maximizing electric vehicle performance.
In the individual optimization of each response variable, all three models consistently identified the lowest pilot weight (66 kg) and the lowest power mode (N5) as the most favorable conditions to maximize operational time (), total distance traveled (), and the energy performance index (, km/Ah). Nevertheless, a divergence was observed in the battery factor: while the smallest battery size (1.0) yielded the highest performance for and , the longest distance () was obtained with the larger battery (2.0). This outcome highlights a trade-off between maximizing the energy performance index (km/Ah) and extending range, where larger batteries support longer travel distances but may compromise efficiency and the advantages of lightweight configurations.
The contour superposition method, illustrated in the comparative plots, revealed a common favorable region in the design space characterized by low battery values (1.0–1.2), pilot weight between 66 and 70 kg, and the lowest power mode (N5). This region visually aligned with the numerically derived optima, confirming the validity of the response surface methodology (RSM) in identifying multi-objective trade-offs. The overlay of response surfaces further demonstrated that, despite slight differences in the optimal battery choice across objectives, a feasible convergence zone exists where all three responses achieve satisfactory performance.
The composite desirability optimization reinforced this convergence, identifying the best compromise solution at (Battery = 1.0), (Weight = 66 kg), and (Mode = N5). Under these conditions, the predicted responses were 1.121 h for , 23.71 km for , and 2.90 km/Ah for , with an overall desirability score of 0.945. This result confirmed the suitability of lightweight and low-power configurations as the most effective balance between endurance, range, and energy performance.
All three methods—individual optimization, contour-based graphical analysis, and the desirability function—converged in identifying low pilot weight and low power mode as universally favorable operating conditions. While the optimal battery type varied slightly (1.0 for and ; 2.0 for ), the desirability function favored the lighter configuration, consistent with the objective of energy-efficient operation. This convergence across methodologies underscores the robustness and reliability of the proposed modeling framework, providing a solid foundation for guiding sustainable electric vehicle design decisions.
3.5. Discussion
The optimization and modeling approach presented in this study integrates both graphical and numerical strategies to determine optimal operating conditions for a pilot-controlled electric vehicle. By combining experimental data with statistical modeling, a robust framework for multi-criteria decision making was achieved for endurance, distance, and energy performance index (km/Ah). Specifically, the integration of individual response surface models (RSM), graphical contour superposition, and the global desirability function (DFA) ensured consistency between complementary methods of analysis.
A systematic application of the Response Surface Methodology (RSM) and the Desirability Function Approach (DFA) was employed to optimize performance, with the goal of maximizing output while minimizing energy consumption. This approach facilitated a thorough evaluation of the combined effects of battery type, vehicle mass, and power mode on efficiency. Solutions prioritizing low vehicle weight and conservative energy use were consistently identified across different analytical perspectives, including individual optimization, contour plot superposition, and desirability function maximization [27]. The convergence of results across these methods reinforced the robustness of the proposed modeling framework for sustainable electric vehicle (EV) design decisions [28].
The experimental results demonstrated that the combination of the smallest battery tested (1.0), the minimum pilot weight (66 kg), and the lowest power mode (N5) yielded the highest overall performance in terms of operational time, distance, and efficiency. This optimal configuration was validated by both individual optimization and the global desirability function, which yielded a score of 0.945. Under controlled experimental conditions, lightweight configurations combined with conservative power settings were therefore confirmed as key strategies to enhance endurance and energy performance index (km/Ah) in electric race vehicles. These findings provide clear guidelines for the configuration of competitive prototypes aimed at maximizing autonomy without compromising range or energy consumption.
The broader optimization of EVs for endurance and efficiency involves not only energy storage but also powertrain control, thermal management, and structural design. In powertrain systems, Continuously Variable Transmissions (CVTs) have been shown to improve lap times relative to Fixed-gear Transmissions (FGTs), despite the added mass, by maintaining motors in optimal efficiency zones [29,30]. Motor sizing and configuration are also decisive: in-wheel double-axle (IWM-DA) systems enhance acceleration, while single-axle (IWM-SA) layouts balance performance and control [30,31]. Among emerging motor technologies, Switched Reluctance Motors (SRMs) are increasingly attractive for their torque density and robustness, with control strategies that minimize torque ripple [28,32], while induction motors benefit from loss-minimization algorithms that optimize d-axis current during operation [33].
Battery and energy management remain central challenges. Vehicles equipped with CVTs often rely on larger-capacity packs [30], yet electrode structure optimization has demonstrated the potential to increase lithium-ion energy density by more than 50% [34]. Effective cooling systems—including air, liquid, phase-change materials, and Peltier devices—extend battery lifetime and improve safety [35,36]. Charging optimization strategies that leverage telemetry data and RSM have also been shown to shorten recharge cycles while controlling thermal rise [37]. Furthermore, vehicle mass reduction continues to be one of the most effective methods for improving efficiency, as supported by mass–energy correlation studies in electric race cars [38,39].
From the optimization of individual response variables, it was observed that the configuration delivering maximum operational time (), distance traveled (), and the energy performance index (km/Ah) () consistently included the smallest battery (1.0), the lowest pilot weight (66 kg), and the lowest power mode (N5). An exception occurred in the optimization of distance, where the highest value was achieved using the larger-capacity battery (2.0). This discrepancy highlights a trade-off between the energy performance index (km/Ah) and energy capacity, confirming that lighter batteries enhance efficiency and endurance, while larger batteries can extend range through increased stored energy.
The graphical method of contour plot superposition (Figure 9) supported these results by visually identifying a convergence region in which all three objectives performed optimally under similar low-level factor settings. The graphical consistency with numerical optimization strengthened the validity of the RSM models as practical tools for refining performance predictions during early-stage design and calibration.
Furthermore, the application of the global desirability function yielded results identical to those predicted by individual analyses: Battery type 1.0, Weight 66 kg, and Mode 5. The predicted performance at this configuration was 1.121 h of operation, 23.71 km of distance traveled, and 2.90 km/Ah in the energy performance index (km/Ah), with a global desirability score of 0.945. This outcome reinforced the consistency and reliability of the methodology, confirming the suitability of low-weight, low-power settings for optimizing performance.
These findings align with recent studies on EV performance optimization. For example, ref. [40] emphasized the importance of mechanical and structural optimization to improve behavior under static and dynamic loading conditions. Similarly, ref. [37] highlighted the role of real-time telemetry integration in refining battery performance prediction, underscoring the influence of control strategy in racing applications. The growing use of predictive modeling, as demonstrated by machine learning applications in telemetry-based optimization [39], further reinforces the importance of data-driven methods to guide sustainable and competitive EV design.
The proposed methodology thus provides a replicable and data-driven framework for optimizing electric vehicle performance through experimental design and statistical modeling. By bridging design, operation, and data-based decision-making, it contributes to emerging efforts in sustainable, intelligent, and competitive electric mobility development.
3.6. Key Findings and Model Performance
The experimental data, analyzed through a factorial design, were found to reveal significant relationships between the input factors and the vehicle’s performance metrics. Among these, the power mode () emerged as the most statistically significant factor influencing operational time (), with a p-value below 0.01. This result highlights the decisive role of power management in extending vehicle endurance. Furthermore, the interaction between weight and power mode () was identified as significant (), suggesting that the influence of vehicle mass on endurance is strongly dependent on the selected power setting.
For total distance traveled () and the energy performance index (km/Ah) (), the best-fitting models incorporated quadratic terms for pilot weight () and power mode (). This finding indicates that the relationship between these factors and the corresponding response variables is inherently non-linear, requiring more sophisticated models to adequately capture curvature effects. Such results are consistent with other engineering applications of RSM in which non-linear influences are frequently observed [16]. The adjusted values of 0.8346 for distance and 0.8553 for efficiency further confirmed the explanatory power of the selected models, which were also supported by global p-values below 0.005. Notably, the significance of the quadratic term for pilot weight () in the distance model () pointed to the existence of diminishing returns or an optimal weight threshold in relation to distance covered. Similarly, both weight () and power mode () were shown to exert statistically significant effects on the energy performance index (km/Ah) () ( and , respectively), reinforcing their critical roles in optimizing energy use. These results align with prior studies that emphasized the contribution of weight reduction to improved the energy performance index (km/Ah) in electric race vehicles [6].
The selection of the first-order model with two-way interaction (FO + TWI) for operational time and the first-order model with principal and quadratic effects (FO + PQ) for distance and efficiency was made to balance statistical accuracy with interpretability and numerical stability. Although full second-order models offered slightly higher unadjusted values, issues such as coefficient aliasing were encountered, which limited their reliability for canonical analysis and optimization. The chosen specifications therefore provided a more robust analytical framework, allowing the visualization of response surfaces and delivering clear insights into the optimal operating conditions of the electric vehicle.
3.7. Implications of Optimization Results
The individual optimization of each response variable consistently indicated that low pilot weight (66 kg) and low power mode (N5) were the most influential conditions for maximizing vehicle performance. This finding suggests that, in competitive events focused on endurance and efficiency, minimizing total mass and operating under conservative power settings are paramount. Such a conclusion aligns with established engineering principles, whereby reduced mass lowers the energy required for acceleration and speed maintenance, while lower power settings inherently decrease energy consumption [6].
A divergence, however, was observed regarding the optimal battery type. Whereas the smallest tested battery (1.0) proved optimal for maximizing operational time and the energy performance index (km/Ah), the longest travel distance was obtained with a higher-capacity battery (2.0). This outcome highlights a fundamental trade-off between the energy performance index (km/Ah) and total energy storage capacity. A lighter, smaller battery enhances efficiency by reducing the mass that must be propelled; conversely, a larger battery, despite its additional weight, offers greater stored energy that can extend range if vehicle efficiency is preserved. The optimal choice therefore depends on the intended design goal of the electric vehicle—whether to prioritize efficiency, maximize range, or achieve a balance between the two. These results complement earlier studies on battery selection and its role in determining energy output and control [5].
The superimposed contour plots further validated these insights by revealing a convergence region in the design space defined by low battery (1.0–1.2), low weight (66–70 kg), and low power mode (N5). This graphical agreement with the numerical results reinforces the robustness of the optimization process and highlights the utility of RSM in visually identifying multi-objective operating regions that balance endurance, distance, and efficiency.
In addition, the composite desirability optimization [22,23] yielded results consistent with both individual optimization and contour superposition. The most desirable compromise solution, with a global desirability score of 0.945, corresponded to battery type 1.0, pilot weight of approximately 66 kg, and power mode N5. This convergence across methodologies confirms that prioritizing lightweight configurations and conservative power usage are the most impactful strategies for improving the overall performance of electric race vehicles.
The observed superiority of the smaller-capacity battery in terms of efficiency can be explained by its higher C-rate characteristics. Although smaller packs tend to discharge more rapidly, the reduction in system weight compensates by lowering overall energy demand. This trade-off emphasizes the importance of effective thermal management and precise state-of-charge (SOC) monitoring in competition environments, where short distances and variable power demands dominate performance outcomes. From a strategic standpoint, optimizing the balance between C-rate and weight may ultimately prove more decisive than maximizing absolute capacity, providing practical guidance for teams competing in energy-efficiency challenges.
3.8. Methodological Contributions and Limitations
This study successfully implemented a comprehensive methodology that integrated Montgomery’s Design of Experiments [24] with Response Surface Methodology (RSM) and the Desirability Function Approach (DFA), providing a structured framework for optimizing multi-parameter vehicle performance. A notable methodological contribution was the development and validation of a low-cost Arduino-based data acquisition (DAQ) prototype, which demonstrated reliability comparable to commercial controllers [26]. This system expands access to advanced data collection, particularly in academic and resource-constrained environments, thereby strengthening its value for both educational and research applications.
Nonetheless, the study has certain limitations. The experiments were conducted on a synthetic grass track characterized by moderate surface friction, and performance outcomes may differ on alternative surfaces such as asphalt or dirt, or under varying environmental conditions, including temperature, humidity, and wind. Although the use of a constant pilot and fixed test schedule was intended to minimize variability, external factors may still have exerted subtle influences on performance. Furthermore, only two battery configurations were evaluated, limiting the scope of inference. Future studies should expand the range of battery chemistries and capacities to provide deeper insights into the trade-off between energy storage and efficiency, particularly in light of challenges such as thermal behavior and battery weight that are critical in EV competitions [5].
It must also be acknowledged that the factorial design involved only 12 experimental runs, inherently restricting the ability to capture higher-order interactions and increasing the risk of aliasing or overfitting. To mitigate these limitations, model selection was constrained to FO + TWI and FO + PQ structures, and run randomization was implemented to reduce bias. Despite these measures, future work should consider larger experimental designs with replication or the application of cross-validation techniques to enhance the statistical robustness and external validity of multi-parameter optimization.
3.9. Future Work
Building on these findings, future research should explore dynamic optimization strategies capable of adapting power modes and even implementing “virtual” weight adjustments (e.g., through load redistribution) in real time, depending on competition conditions. Another critical avenue is the investigation of the thermal behavior of the battery system under optimal operating conditions [4,5], as highlighted in the introduction. This aspect is particularly relevant for ensuring long-term reliability and safety, especially considering the triangular arrangement of the battery pack used in this study.
In parallel, the integration of machine learning techniques to predict performance from sensor data and environmental variables could enable the design of more adaptive and efficient control systems for high-efficiency prototypes. Furthermore, the role of regenerative braking in enhancing energy recovery and overall efficiency, as emphasized in prior research [7], warrants deeper investigation in future studies to complement the current optimization framework.
Overall, these directions underscore the practical implications of the present work for the design and operation of high-efficiency electric vehicles, particularly within competitive contexts such as the National Electric Drive Vehicle Competition [2]. The robust optimization methodology developed here provides a structured pathway for improving vehicle performance while also advancing the broader goal of sustainable transportation, as promoted by international initiatives such as the Shell Eco-Marathon [1].
4. Conclusions
The application of Response Surface Methodology (RSM) within a factorial experimental design enabled the systematic identification of optimal operating configurations for the electric vehicle, supporting the simultaneous maximization of operational time and travel distance while minimizing overall energy consumption. The results indicated that the most favorable configuration was obtained with a pilot weight of 75 kg and a conservative power mode (N5, 500 W).
The study demonstrated that the combined selection of battery type, power mode, and vehicle mass exerts a significant influence on performance outcomes. Notably, an intermediate weight configuration (76 kg) combined with a moderate power setting (N9) was found to be more efficient in reducing energy consumption, underscoring the importance of evaluating trade-offs between endurance, range, and efficiency when defining optimal strategies.
By integrating factorial design with RSM, a robust analytical framework was established for assessing the effects of multiple interacting factors. The combination of statistical modeling with visualization techniques such as contour and surface plots enabled the clear identification of interactions among variables and their influence on the response metrics. This methodological approach proved effective, offering results that can be directly applied to the optimization of electric vehicles in both competitive racing contexts and prototype development.
Future work should extend this methodology to encompass alternative battery chemistries and traction configurations in order to validate and generalize the findings across diverse electric vehicle architectures. Furthermore, incorporating environmental variables such as ambient temperature, track surface, and weather conditions would allow for a more comprehensive characterization of performance and strengthen external validity.
This study advances the current body of knowledge by moving beyond single-factor analyses of electric vehicle efficiency. Through the integration of battery type, vehicle mass, and power mode within a factorial multi-parameter design, combined with RSM and DFA optimization, a robust framework was developed for identifying operating conditions that balance distance, time, and energy consumption. Unlike previous studies, this work validates multi-parameter optimization under real competition conditions, thereby providing actionable insights for both researchers and practitioners committed to advancing sustainable electric mobility.
Author Contributions
Conceptualization A.F.V.-S., E.M.G., S.E. and I.N.G.-M.; methodology, A.F.V.-S., I.N.G.-M., A.F.R.-M., A.P.-G. and J.D.V.-G.; formal analysis, A.F.V.-S., I.N.G.-M., A.F.R.-M., J.D.V.-G. and A.P.-G.; Validation E.M.G. and S.E.; investigation, A.F.V.-S., E.M.G., S.E., I.N.G.-M., A.F.R.-M., J.D.V.-G. and A.P.-G.; data curation, A.F.V.-S., S.E., E.M.G. and I.N.G.-M.; original draft preparation, A.F.V.-S., I.N.G.-M. and A.P.-G.; writing—review and editing, A.F.V.-S.; supervision, A.F.V.-S., I.N.G.-M., A.F.R.-M., S.E., J.D.V.-G., E.M.G. and A.P.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The dataset generated and analyzed during the current study is available from the corresponding author on reasonable request.
Acknowledgments
The authors would like to thank the IUPB University for allowing us to carry out the experiments within the framework of the institutional project ‘Escudera Bravo’.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shell. Shell Eco-Marathon Partners, Energy Efficiency Competitions, Shell Eco-Marathon. 2025. Available online: https://www.shellecomarathon.com/ (accessed on 10 July 2025).
- REDTTU. ETITC y la IU Pascual Bravo dominaron la III Competencia Nacional de Vehículos Eléctricos. 2025. Available online: https://www.redttu.edu.co/es/etitc-y-iu-pascual-bravo-dominaron-la-iii-competencia-nacional-de-vehiculos-electricos/ (accessed on 10 July 2025).
- Khan, F.N.U.; Rasul, M.G.; Sayem, A.; Mandal, N. Maximizing energy density of lithium-ion batteries for electric vehicles: A critical review. Energy Rep. 2023, 9, 11–21. [Google Scholar] [CrossRef]
- Lan, C.; Xu, J.; Qiao, Y.; Ma, Y. Thermal management for high power lithium-ion battery by minichannel aluminum tubes. Appl. Therm. Eng. 2016, 101, 284–292. [Google Scholar] [CrossRef]
- Sehil, K.; Alamri, B.; Alqarni, M.; Sallama, A.; Darwish, M. Empirical Analysis of High Voltage Battery Pack Cells for Electric Racing Vehicles. Energies 2021, 14, 1556. [Google Scholar] [CrossRef]
- Stabile, P.; Ballo, F.; Mastinu, G.; Gobbi, M. An Ultra-Efficient Lightweight Electric Vehicle—Power Demand Analysis to Enable Lightweight Construction. Energies 2021, 14, 766. [Google Scholar] [CrossRef]
- Rego, N.; Castro, R. Regenerative Braking Applied to a Student Team’s Electric Racing Motorcycle Prototype: A Theoretical Study. Appl. Sci. 2023, 13, 3784. [Google Scholar] [CrossRef]
- Szumska, E.M. Regenerative Braking Systems in Electric Vehicles: A Comprehensive Review of Design, Control Strategies, and Efficiency Challenges. Energies 2025, 18, 2422. [Google Scholar] [CrossRef]
- Chidambaram, R.K.; Chatterjee, D.; Barman, B.; Das, P.P.; Taler, D.; Taler, J.; Sobota, T. Effect of Regenerative Braking on Battery Life. Energies 2023, 16, 5303. [Google Scholar] [CrossRef]
- Garud, K.S.; Tai, L.D.; Hwang, S.G.; Nguyen, N.H.; Lee, M.Y. A Review of Advanced Cooling Strategies for Battery Thermal Management Systems in Electric Vehicles. Symmetry 2023, 15, 1322. [Google Scholar] [CrossRef]
- Chan, C.K.; Chung, C.H.; Raman, J. Optimizing Thermal Management System in Electric Vehicle Battery Packs for Sustainable Transportation. Sustainability 2023, 15, 11822. [Google Scholar] [CrossRef]
- Fu, P.; Zhao, L.; Wang, X.; Sun, J.; Xin, Z. A Review of Cooling Technologies in Lithium-Ion Power Battery Thermal Management Systems for New Energy Vehicles. Processes 2023, 11, 3450. [Google Scholar] [CrossRef]
- Perez, A.F.; Taborda-Jaramillo, J.; Ramírez-Jiménez, O.; Carrillo-Perilla, O.; Leal-Perez, P.; Agudelo, J.R. Adquisición de variables físicas de un automóvil Renault Logan y transmisión inalámbrica vía GPRS a un servidor. Preprint 2012. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Der, O.; Patel, G.M.; Giasin, K.; Ercetin, A. State-of-the-art review of energy consumption in machining operations: Challenges and trends. Renew. Sustain. Energy Rev. 2025, 188, 116073. [Google Scholar] [CrossRef]
- Togun, H.; Basem, A.; dhabab, J.M.; Mohammed, H.I.; Sadeq, A.M.; Biswas, N.; Abdulrazzaq, T.; Hasan, H.A.; Homod, R.Z.; Talebizadehsardari, P. A comprehensive review of battery thermal management systems for electric vehicles: Enhancing performance, sustainability, and future trends. Int. J. Hydrogen Energy 2025, 97, 1077–1107. [Google Scholar] [CrossRef]
- Uslu, S. Optimization of diesel engine operating parameters fueled with palm oil-diesel blend: Comparative evaluation between response surface methodology (RSM) and artificial neural network (ANN). Fuel 2020, 276, 117990. [Google Scholar] [CrossRef]
- Silva, A.F.; Neves, P.; Rocha, S.M.; Silva, C.M.; Valente, A.A. Optimization of continuous-flow heterogeneous catalytic oligomerization of 1-butene by design of experiments and response surface methodology. Fuel 2020, 259, 116256. [Google Scholar] [CrossRef]
- Vega-Garzon, L.P.; Gomez-Miranda, I.N.; Peñuela, G.A. Benzophenone-3 ultrasound degradation in a multifrequency reactor: Response surface methodology approach. Ultrason. Sonochemistry 2018, 43, 201–207. [Google Scholar] [CrossRef]
- Anfar, Z.; Ahsaine, H.A.; Zbair, M.; Amedlous, A.; Fakir, A.A.E.; Jada, A.; Alem, N.E. Recent trends on numerical investigations of response surface methodology for pollutants adsorption onto activated carbon materials: A review. Crit. Rev. Environ. Sci. Technol. 2020, 50, 1043–1084. [Google Scholar] [CrossRef]
- Panwar, V.; Kumar Sharma, D.; Pradeep Kumar, K.; Jain, A.; Thakar, C. Experimental investigations and optimization of surface roughness in turning of en 36 alloy steel using response surface methodology and genetic algorithm. Mater. Today Proc. 2021, 46, 6474–6481. [Google Scholar] [CrossRef]
- Savaş, A.; Şener, R.; Uslu, S.; Der, O. Experimental study on performance and emission optimization of MgO nanoparticle-enriched 2nd generation biodiesel: A method for employing nanoparticles to improve cleaner diesel combustion. J. Energy Inst. 2025, 118, 102024. [Google Scholar] [CrossRef]
- Gamero-Salinas, J.; López-Fidalgo, J. Response Surface Methodology using desirability functions for multiobjective optimization to minimize indoor overheating hours and maximize useful daylight illuminance. Sci. Rep. 2025, 15, 12173. [Google Scholar] [CrossRef]
- Bartz-Beielstein, T. Multi-Objective Optimization and Hyperparameter Tuning with Desirability Functions. arXiv 2025, arXiv:2503.23595. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley and Sons: Hoboken, NJ, USA, 2007; Volume 2. [Google Scholar]
- Taller Bicicletas Madrid. Manual del Panel LCD5 Plus Para Bicicleta Eléctrica. Available online: https://www.tallerbicicletasmadrid.com/blog/manual-display-lcd5-plus-para-bici-electrica/ (accessed on 8 September 2025).
- Uppal, M.; Gupta, D.; Goyal, N.; Imoize, A.L.; Kumar, A.; Ojo, S.; Pani, S.K.; Kim, Y.; Choi, J. A Real-Time Data Monitoring Framework for Predictive Maintenance Based on the Internet of Things. Complexity 2023, 2023, 9991029. [Google Scholar] [CrossRef]
- Jeong, I.J.; Kim, K.J. An interactive desirability function method to multiresponse optimization. Eur. J. Oper. Res. 2009, 195, 412–426. [Google Scholar] [CrossRef]
- Siddique, F.; Singh, B.; Shastri, S. RSM Assisted MOGA for SRM EV Drive Control Factors Optimization. IEEE Trans. Ind. Appl. 2024, 60, 3200–3209. [Google Scholar] [CrossRef]
- Borsboom, O.; Fahdzyana, C.A.; Salazar, M. Time-optimal Control Strategies for Electric Race Cars with Different Transmission Technologies. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference, Virtual, 18 November–16 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Borsboom, O.; Fahdzyana, C.A.; Hofman, T.; Salazar, M. A Convex Optimization Framework for Minimum Lap Time Design and Control of Electric Race Cars. IEEE Trans. Veh. Technol. 2021, 70, 8478–8489. [Google Scholar] [CrossRef]
- Othaganont, P.; Assadian, F.; Auger, D.J. Multi-objective optimisation for battery electric vehicle powertrain topologies. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 1046–1065. [Google Scholar] [CrossRef]
- Cheri, J.; Sundaramoorthy, P. Pioneering Sustainable Transportation: SRM Motor Optimization for Enhanced Electric Vehicle Dynamics. In Proceedings of the 2024 10th International Conference on Electrical Energy Systems, Chennai, India, 22–24 August 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Akhtar, M.J.; Behera, R.K.; Al Hosani, K.; Muduli, U.R. Enhanced Electric Vehicle Powertrain Efficiency with Optimized Loss-Minimizing Control. In Proceedings of the 2024 IEEE 4th International Conference on Sustainable Energy and Future Electric Transportation, Hyderabad, India, 31 July–3 August 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, D.C.; Lee, J.J.; Kim, C.W. Optimization for maximum specific energy density of a lithium-ion battery using progressive quadratic response surface method and design of experiments. Sci. Rep. 2020, 10, 15586. [Google Scholar] [CrossRef]
- Xia, Q.; Wang, Z.; Ren, Y.; Yang, D.; Sun, B.; Feng, Q.; Qian, C. Performance reliability analysis and optimization of lithium-ion battery packs based on multiphysics simulation and response surface methodology. J. Power Sources 2021, 490, 229567. [Google Scholar] [CrossRef]
- Sabarimuthu, M.; Radha, J.; Gomathy, S.; Eswaran, R.; Kaushik, A.U.; Koushika, S. Integrated Battery Management and Thermal Control System for Lithium-Ion Battery Pack in Electric Vehicle. In Proceedings of the 2024 2nd International Conference on Self Sustainable Artificial Intelligence Systems, Erode, India, 23–25 October 2024; pp. 1685–1690. [Google Scholar] [CrossRef]
- Villa-Salazar, A.F.; Gomez-Miranda, I.N.; Romero-Maya, A.F.; Velásquez-Gómez, J.D.; Lemmel-Vélez, K. Optimizing Electric Racing Car Performance through Telemetry-Integrated Battery Charging: A Response Surface Analysis Approach. World Electr. Veh. J. 2024, 15, 317. [Google Scholar] [CrossRef]
- Pusztai, Z.; Kőrös, P.; Szauter, F.; Friedler, F. Vehicle Model-Based Driving Strategy Optimization for Lightweight Vehicle. Energies 2022, 15, 3631. [Google Scholar] [CrossRef]
- Rao, A.; Gupta, H.; Singh, P.; Mittal, S.; Singh, U.; Vishwakarma, D.K. Optimizing Electric Vehicle Efficiency with Real-Time Telemetry using Machine Learning. In Proceedings of the 2024 10th International Conference on Mechatronics and Robotics Engineering, Milan, Italy, 27–29 February 2024; pp. 213–219. [Google Scholar] [CrossRef]
- Villa Salazar, A.F.; Gonzalez Montoya, E.; Romero Maya, A. Diseño del chasis de un vehículo eléctrico para la II Competencia Nacional de Vehículos de Tracción Eléctrica. Rev. CINTEX 2022, 27, 16–31. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).