Abstract
Accurately determining load model parameters is of the utmost importance for conducting power system simulation analysis and designing effective control strategies. Measurement-based approaches are commonly employed to identify load model parameters that closely reflect the actual operating conditions. However, these methods typically rely on iterative parameter search processes, which can be time-consuming, particularly when dealing with complex models. To address this challenge, this paper introduces a parameter identification method for the generalized synthetic load model (SLM) using the Extreme Learning Machine (ELM) technique, with the aim of enhancing computational efficiency. Furthermore, to achieve better alignment with load response curves, a Quantum Particle Swarm Optimization (QPSO) algorithm is adopted to train the ELM model. The proposed QPSO-ELM-based SLM parameter identification method is subsequently evaluated using a standard test system. To assess its effectiveness, parameter sensitivity analysis is performed, and simulation results are analyzed. The findings demonstrate that the proposed method yields favorable outcomes, offering improved computation efficiency in load model parameter identification tasks.
1. Introduction
Power system simulation software currently in use exhibit high accuracy in simulating components such as prime movers, generators, speed control systems, excitation systems, transformers, transmission lines, new energy sources, DC systems, and power electronic equipment, taking into account their physical characteristics and operational mechanisms. However, the load model, considered an important user, presents challenges due to its time-varying nature, complexity, and other factors. The current approach involves employing an idealized overall model for the load, with generic parameter values, and only a subset of parameters being differentiated at the provincial network level. Consequently, this approach fails to accurately reflect the actual load characteristics, resulting in substantial deviations in the model’s response and adversely impacting the accuracy of system simulations [,,]. Therefore, there is an urgent need to address the parameter identification problem associated with the load model, as it holds significant practical importance for enhancing the safe and stable operation of the power grid.
Once the model structure is determined, the identification of model parameters becomes a nonlinear numerical optimization problem, where the unknown parameters are adjusted to minimize the objective function, which measures the best fit between the model’s output and the measured data []. Commonly used identification algorithms can be categorized into traditional algorithms and intelligent optimization algorithms. Traditional algorithms include least squares, maximum likelihood, Kalman filter, and gradient-based optimization methods. For load model parameter identification, the least squares method was utilized in [], the step acceleration method in [], an improved version of least squares known as the steady-state constrained weighted least squares method in [], and the use of a third-order cumulative quantity as the objective function along with a variable forgetting factor to enhance the recursive least squares (RLS) algorithm in []. The latter approach, employing a variable forgetting factor, exhibits improved noise suppression and tracking performance compared to the traditional RLS algorithm. However, traditional algorithms primarily rely on local optimization methods and are highly sensitive to initial values. Moreover, they assume the system to be Gaussian and only consider the second-order moments of the error, rendering them less effective for nonlinear or non-Gaussian systems.
In recent years, the rapid development of intelligent algorithms has led to the widespread adoption of optimization algorithms with both global and local search capabilities, such as particle swarm algorithms, genetic algorithms, and clonal selection algorithms, in the field of load model parameter identification. These intelligent algorithms have significantly enhanced the accuracy of load models [,,,,,]. For instance, chaos and quantum mechanics theories were applied in [] to improve the particle swarm algorithm, resulting in superior performance compared to the traditional particle swarm algorithm. Genetic algorithms were employed for parameter identification in [], while [] proposed a genetic ant colony algorithm that leverages the advantages of fast convergence in the early stage and accelerated convergence in the late stage due to pheromone accumulation. The wolf algorithm was introduced in [] for load model parameter identification, combined with the conventional particle swarm algorithm. Additionally, the Coyote algorithm was introduced in [], and its measured data analysis demonstrated faster convergence compared to the conventional particle swarm algorithm. However, due to the complex and dynamic nature of the load model’s structural parameters, there is still a need for further research to strike the right balance between local and global optimization in evolutionary algorithms. Consequently, the exploration of new evolutionary algorithms that offer faster convergence and higher accuracy remains an area worthy of further investigation.
In this paper, we proposed a QPSO-ELM method that integrates Quantum Particle Swarm Optimization (QPSO) with Extreme Learning Machine (ELM), enabling efficient parameter identification for renewable energy resources. Compared to conventional Artificial Neural Networks (ANNs), the QPSO-ELM method demonstrates efficiency and accuracy owing to its quantum-inspired optimization strategy, particularly in intricate parameter identification tasks. The contributions primarily consist of two key elements. First, we present an enhanced structure for the load model that accommodates renewable energy resources, particularly photovoltaic systems. This modification is intended to reflect the evolving landscape of power systems with increased renewable energy integration. Second, we propose a pioneering approach that leverages artificial intelligence techniques, specifically the Quantum Particle Swarm Optimization (QPSO) algorithm coupled with the Extreme Learning Machine (ELM), for the identification of load model parameters.
The subsequent sections of this paper are organized as follows: Section 2 presents the structure of the SLM (load model) with photovoltaic power, and sensitivity analysis is applied to identify the significant parameters of the generalized SLM. Section 3 introduces the load model parameter identification method based on QPSO-ELM (Quantum-behaved Particle Swarm Optimization–Extreme Learning Machine), along with the algorithm for constructing QPSO-ELM. In Section 4, a typical test system is employed to validate the performance of the proposed method. Finally, Section 5 concludes the paper.
2. Load Model Structure and Parameter Sensitivity Analysis
2.1. Synthesis Load Model with Distributed Photovoltaic Sources
The inclusion of a synthesis load model has gained widespread recognition as an essential component encompassing static, motor, and reactive compensation models to accurately represent dynamic loads. However, the conventional SLM fails to capture the dynamic behavior of distribution networks experiencing significant integration of distributed photovoltaic and electric vehicle sources. Hence, an expansion of the SLM structure by incorporating a supplementary component to account for distributed PV is warranted, resulting in the development of a generalized SLM. The structure of this enhanced model, referred to as the generalized SLM, is illustrated in Figure 1.
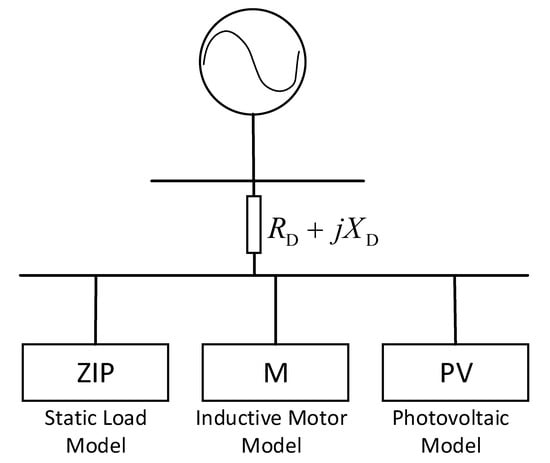
Figure 1.
Structure of the generalized SLM.
It has been widely recognized that the traditional SLM is unable to describe the dynamic response of the distribution network with high penetration of distributed photovoltaic and electric vehicle sources. Consequently, in this study, the generalized SLM is chosen as the fundamental load model for conducting further research on parameter identification. In Figure 1, the static load model is depicted as a polynomial model, while the inductive motor model is represented by a third-order induction motor model. As for the photovoltaic model, it is assumed to be a single-stage photovoltaic system model, which is illustrated in Figure 2.
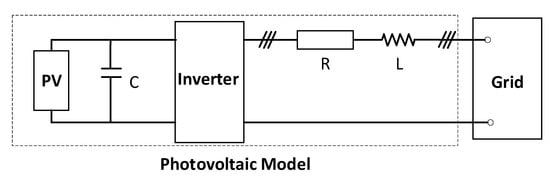
Figure 2.
Structure of the photovoltaic model.
2.2. Identification of Key Parameters
The identification of load model parameters in the generalized synthesis load model poses a significant challenge due to the large parameter dimensionality involved. Typically, parameter sensitivity analysis is employed to identify the crucial parameters in the model, thereby reducing the complexity of parameter identification. However, when dealing with distributed photovoltaic systems, this approach may prove ineffective as these systems encompass both electrical and control parameters, with the effects of control parameters often exhibiting minimal changes. Consequently, this paper adopts a combined method for recognizing critical parameters, which consists of two steps.
Firstly, parameter sensitivity analysis is utilized to determine the critical parameters in the generalized SLM for the static model and motor model. Secondly, the critical parameters of the photovoltaic model are identified through experience analysis. The parameter sensitivity analysis procedure involves making slight adjustments to the parameters and observing the resulting changes in responses. The selected responses are based on the dynamic characteristics of the load, encompassing variables such as load voltage and load parameters. This process is illustrated in the following formula:
where Zresponse is recognized as the comprehensive observation. P(k) and U(k) are load power and load voltage at the k-th time step, respectively. P0 and U0 are load power and load voltage at the initial step, respectively.
Due to the inherent strong nonlinearity of load models, traditional analytical sensitivity analysis methods are often inadequate for analyzing them. Therefore, in order to address this limitation, the sensitivity analysis of parameter θj can be computed using a mathematical calculation approach, as demonstrated by the following formula.
Following the mathematical sensitivity analysis, a subset of critical parameters has been identified for both the static model and motor model, resulting in a selection of 4 parameters out of the original 14. These critical parameters encompass distributed network reactance (XD), inductive motor active power proportion (PMP), load ratio (KL), stator reactance (Xs), and constant reactance load proportion (KZ).
Regarding the photovoltaic model, certain parameters can be acquired from device records, including the photovoltaic array’s short-circuit current, open-circuit voltage, and current and voltage at the maximum power point. Additionally, specific control parameters, such as the time constant of the active power measurement module and the magnification factor of the active power proportion module, can be obtained from standard device parameter settings. Consequently, the critical parameters of the photovoltaic model are determined to be the direct-current side capacitor (C) and the photovoltaic output equivalent reactance (XPV).
By implementing the parameter reduction procedure, the dimensionality of the generalized synthesis load model parameters to be identified has been reduced from 24 to 7, significantly improving the efficiency of load model parameter identification. The parameters of the generalized SLM that are to be identified are determined and listed in the Table 1 below.

Table 1.
Parameters of the generalized SLM.
3. Identification of QPSO-ELM-Based Load Model Parameters
3.1. Machine-Learning-Based Parameter Identification Method for Load Model
Currently, machine learning methods have demonstrated promising performance in effectively capturing the relationship between input and output data. Once the training process is completed and verified, machine-learning-based models can efficiently and accurately provide output results. Consequently, employing machine learning techniques can be advantageous for load model parameter identification, considering the complexity of load models and the demand for computational efficiency. In this paper, a structure for load model parameter identification based on machine learning is proposed, as depicted in Figure 3.
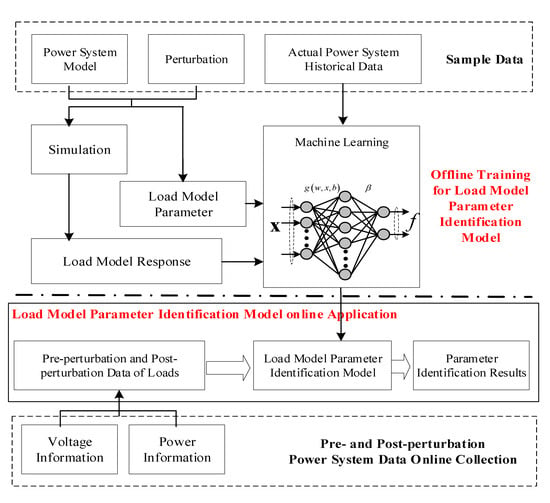
Figure 3.
Structure of the construction and application of the machine-learning-based load model parameter identification method.
Figure 3 illustrates that the machine-learning-based parameter identification method consists of two main components: offline construction and online application. In the offline training phase, the initial step involves collecting sample data from power system simulations or historical data from actual power systems, serving as the foundation for constructing the parameter identification model. Constructing the parameter identification model requires both the load model responses before and after perturbations, as well as the real load model parameters. The former data are employed as input features, while the latter parameters are considered sample labels. In this study, the input features are defined as the pre-perturbation and post-perturbation load responses in terms of voltage and power. The observation window spans 1 s before and 1 s after the perturbation, with a sampling rate of 10 Hz.
Upon completion of the machine learning training process, the offline construction phase concludes, and the load model parameter identification model is ready for online application. The first step in the online application is to collect pre-perturbation and post-perturbation voltage and power data from the loads. These collected data are then used as inputs for the load model parameter identification model. Subsequently, the parameter identification model produces the expected load model parameter results.
3.2. Theorem of QPSO-ELM Algorithm
The QPSO-ELM algorithm is a hybrid approach that combines the strengths of two powerful algorithms, namely Quantum Particle Swarm Optimization (QPSO) and Extreme Learning Machine (ELM). QPSO is a global optimization algorithm inspired by principles from quantum mechanics, while ELM is a neural network algorithm primarily used for regression and classification tasks.
In the QPSO-ELM algorithm, QPSO is employed to optimize the input weights and biases of the ELM neural network. Specifically, QPSO performs a search in the search space to determine the optimal values for the input weights and biases. This search process aims to minimize the mean square error (MSE) between the desired output and the actual output. The QPSO algorithm adopts a wave function to represent the positions of individual particles in the search space. These positions are then updated using a quantum operator based on the Schrödinger equation, enabling the algorithm to evolve and refine the particle positions iteratively.
On the other hand, ELM is a feedforward neural network that consists of a single hidden layer. In ELM, the input weights and biases are initialized randomly, while the output weights are calculated analytically. Compared to other neural network algorithms, ELM has demonstrated notable advantages, including rapid learning speed, strong generalization performance, and low computational cost.
The integration of QPSO and ELM in the QPSO-ELM algorithm capitalizes on the robust optimization capabilities of QPSO and the efficient learning characteristics of ELM, offering a powerful and effective approach to various tasks requiring optimization and learning within a neural network framework.
The QPSO-ELM algorithm commences by initializing the input weights and biases of the ELM network with random values. Subsequently, QPSO is employed to optimize these input weights and biases, aiming to minimize the mean square error (MSE). The optimized input weights and biases obtained from QPSO are then utilized to train the ELM network using the provided training data. Once the ELM network is trained, it can be employed to predict the output for new input data. The application of QPSO-ELM spans various domains, such as power system load forecasting, image classification and financial time series prediction. Extensive evaluations have indicated that the hybrid QPSO-ELM algorithm outperforms individual implementations of ELM or QPSO. By combining the global search capability of QPSO with the rapid learning and low computational cost of ELM, the QPSO-ELM algorithm proves to be a potent optimization approach for addressing a range of optimization and prediction problems. The general procedure for integrating QPSO and ELM is as follows:
Step 1: Initialization: Randomly initialize the input weights and biases of the ELM network and define the particle swarm for QPSO.
Step 2: Particle Swarm Optimization: Employ QPSO to optimize the input weights and biases of the ELM network. Each particle in the swarm represents a specific set of input weights and biases. The fitness function used to assess the performance of each particle is typically the mean square error (MSE) between the predicted outputs and the actual outputs.
Step 3: Update Input Weights and Biases: Update the input weights and biases of the ELM network using the optimized values obtained from QPSO.
Step 4: Training: Train the ELM network using the updated input weights and biases to learn the nonlinear relationship between the input features and the target outputs.
Step 5: Testing: Evaluate the performance of the QPSO-ELM model on a validation or test set.
Step 6: Repeat Steps 2 to 5: Repeat Steps 2 to 5 for a predefined number of iterations or until a stopping criterion is met.
3.2.1. Theorem of ELM
ELM has garnered significant attention in the research community due to its simplicity and effectiveness in addressing a wide range of classification and regression problems, including applications in the field of power systems [,]. While ELM is built upon the principles of feedforward neural networks, it distinguishes itself from other neural network models by employing a distinct training technique that differs from the popular backpropagation algorithm. In conventional neural network models, the weights connecting the hidden and output layers, as well as those between the hidden and input layers, are iteratively trained using the backpropagation algorithm. This iterative optimization process gradually adjusts the weights to minimize the discrepancy between the predicted output and the actual output.
However, this iterative optimization procedure can be computationally expensive and time-consuming, particularly when dealing with large datasets. ELM overcomes this constraint by employing a random initialization of the hidden layer weights, which can be executed much more quickly compared to the iterative optimization process. In ELM, the output layer weights are analytically determined using the pseudo-inverse of the hidden layer output matrix, while the input and hidden layer weights are arbitrarily set and fixed. This approach enables a rapid and effective learning process, particularly for large datasets. ELM offers several notable advantages over conventional neural network models. Firstly, the training process is streamlined, and the computational complexity is reduced as ELM does not require an iterative optimization approach. Secondly, ELM exhibits remarkable speed and can train large datasets in a fraction of the time required by traditional neural network models. Furthermore, ELM can accommodate diverse types of input data, including continuous, discrete, and categorical data. Figure 4 illustrates the structure of ELM.
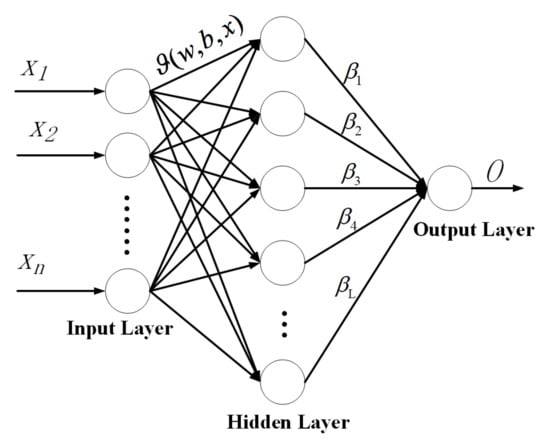
Figure 4.
Structure of ELM.
Consider a set of N sample instances denoted as SN = {(Xi,ti)|Xi ∈ Rn, ti ∈ Rm}, where Xi= [xi1, xi2, …, xin]T ∈ Rn represents the input data consisting of voltage and power measurements of the load before and after perturbations, and ti = [ti1, ti2, …, tim]T ∈ Rm represents the load model parameters to be identified. In this study, the structure depicted in Figure 4 is employed, and the mathematical formulation of the ELM model with L hidden neurons and the activation function g(x) can be expressed as follows.
where is the output matrix and is the output of the j-th hidden node on input feature xi. is the weight matrix between the input nodes and j-th hidden node. is the bias of the j-th hidden node. α is the output weight matrix. T is the vector consisting of training labels, which are load model parameters in this paper.
Hα = T is then solved using a least squares calculation, because and are fixed and α is the only parameter to be determined, which becomes a linear calculation problem. It can be solved with the following formula.
where H+ is the Moore–Penrose generalized reverse matrix of output weight matrix H.
3.2.2. Algorithm of QPSO
PSO is an optimization algorithm rooted in swarm intelligence. It leverages the principles of collaboration and competition among individuals to solve optimization problems. Inspired by the collective behavior of birds or fish moving in flocks or schools, PSO is a population-based technique. Each particle in the swarm represents a potential solution to the optimization problem, and the swarm collectively explores the search space by adjusting the position and velocity of each particle based on its own experience and that of its neighbors. The algorithm updates the position and velocity of each particle based on its best position thus far and the best position of its neighbors.
Building upon this foundation, the QPSO method introduces concepts from quantum mechanics. In quantum space, a particle’s state is represented by a wave function, and its probability density function can be derived by solving Schrödinger’s equation. Unlike the traditional PSO algorithm that updates particle positions and velocities using basic arithmetic equations, QPSO represents each particle as a wave function, which characterizes its position in terms of probability amplitude and phase. The evolution of the wave function is governed by a quantum operator, defined by a set of parameters controlling the algorithm’s behavior. This operator is derived from the Schrödinger equation, which describes the dynamics of a quantum system over time. Specifically, the quantum operator acts on the wave function of each particle to update its position and velocity. QPSO has demonstrated effectiveness in addressing a wide range of optimization problems, including continuous, discrete, mixed-integer, multi-objective, dynamic, and constrained optimization problems.
To address limitations and enhance performance, various variants of QPSO have been proposed. Hybrid versions combine QPSO with other metaheuristic algorithms such as genetic algorithms or simulated annealing to improve search capabilities. Adaptive QPSO algorithms dynamically adjust parameters based on problem characteristics and search progress. Parallel QPSO algorithms leverage multiple processors or computing nodes to expedite optimization.
QPSO boasts several advantages over other metaheuristic algorithms. It efficiently explores the search space, focusing on promising regions while avoiding less-favorable areas through adjustments of probability amplitude and phase. It can also overcome local optima, which are points in the search space where an algorithm gets stuck without finding a better solution. QPSO achieves this through quantum tunneling effects, enabling particles to navigate barriers that would pose difficulties for classical optimization methods.
In this study, QPSO is utilized to enhance the performance of the load parameter identification model trained with ELM, replacing the least-square-based training process. The application of QPSO in the training process of ELM involves the following steps:
Step 1: Set the number of particles in the population to M and the upper limit of computation steps to T. The ideal particle s in the group consists of input weight values and biases of hidden neurons. It is assumed that the ELM has L hidden neurons.
Step 2: The initial population is created by assigning values randomly to the parameters within set S, while ensuring that all elements of a particle fall within the range [0, 1]. This random assignment process is repeated M times to generate the initial population . For the i-th particle in population S0, its position vector can be expressed as follows:
Step 3: At the k-th iteration of the computation, the fitness of each particle within this population is evaluated. The fitness calculation formula is depicted below
where Ntrain denotes the number of training samples, ti represents the output load parameter of the ELM model, and oi represents the actual load model parameter.
Step 4: For particle i within the population St, the historical best position is updated along with the population’s overall best position . Additionally, the local attractor of each particle as well as the average best position, , are computed utilizing the following formula:
where and . is the j-th element of particle i of the historical best position at the time step k. is the j-th element of the population historical best position at the time step k. is a random value in the range [0, 1]. Then, update the position of each particle using the following formula:
where is the j-th element of particle i at time step k + 1. u is a random value in the range [0, 1]. is the scaling factor decided via the linear reduction strategy.
Step 5: Iterate through steps 3 and 4 until the maximum computation step T is reached. At this point, the optimization result is obtained, which ultimately determines the input weights and biases of the hidden neurons in the ELM model.
4. Case Study
In this section, the proposed load model parameter identification method based on QPSO-ELM is validated using a standard system implemented in PSASP software. The standard system employed is the infinite system equipped with the generalized SLM, as illustrated in Figure 1. To address the substantial differences in load model parameter values, the outputs of the QPSO-ELM algorithm are normalized using the maximum and minimum normalization method.
4.1. Sample Generation
To train the ELM model, a total of 1500 samples are generated based on the standard system. These samples encompass various configurations of load model parameters and three-phase short-circuit faults characterized by different short-circuit reactance. Among the generated samples, 1350 are designated for training purposes, while the remaining 150 samples are used for testing. The ranges of critical load model parameters are specified in Table 2.

Table 2.
Range region of critical load model parameters.
4.2. Performance Comparison between PSO and Common ELM Method
To compare the performance of the Particle Swarm Optimization (PSO) and conventional Extreme Learning Machine (ELM) methods, the PSO algorithm is preconfigured with a maximum iteration step of 100, and the fitness function is defined as the root mean square error of load responses in power and voltage. The critical load model parameters identified from both the PSO and ELM methods are listed in Table 3.

Table 3.
Comparison of PSO and common ELM method.
Table 3 shows that the PSO method exhibits superior accuracy compared to the conventional ELM method, as indicated by the mean average percentage errors of 4.77% and 5.12% for PSO and conventional ELM, respectively. However, it should be noted that the conventional ELM method exhibits significantly higher computational efficiency, with a computational time of only 0.03 s, whereas the PSO method requires 5.2 min. Consequently, the conventional ELM method demonstrates better suitability for online applications due to its acceptable accuracy rate and computational efficiency.
4.3. Performance Comparison between Common ELM Method and QPSO-ELM Method
After completing the training process for ELM and QPSO-ELM, the load model parameter identification models based on ELM and QPSO-ELM are constructed. These models are then validated using samples from the testing set. The performance of these two models in accurately estimating the load model parameters XD, PMP, and KL is depicted in Figure 5. The figure clearly illustrates that QPSO-ELM outperforms the conventional ELM method in terms of accuracy.
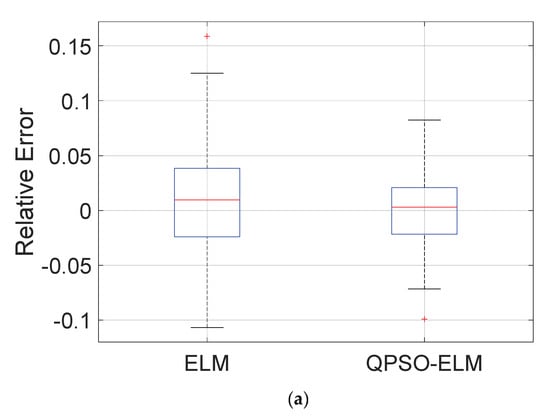
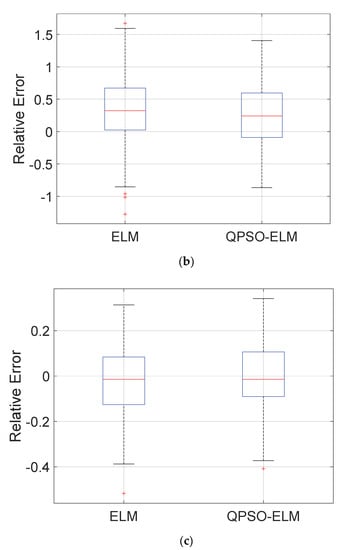
Figure 5.
Performance comparison between ELM and QPSO-ELM: (a) Relative error comparison for parameter XD between ELM and QPSO−ELM. (b) Relative error comparison for parameter PMP between ELM and QPSO−ELM. (c) Relative error comparison for parameter KL between ELM and QPSO−ELM.
Furthermore, in addition to comparing the accuracy of these three load model parameters, the remaining results for the test samples in the testing set are listed and compared in the Table 4 below. From the findings, it can be inferred that the QPSO-ELM method demonstrates enhanced performance through incorporating the PSO algorithm to determine the input weights and biases of the hidden nodes in the ELM model, as opposed to random determination.

Table 4.
MAPE index comparison of common ELM and QPSO-ELM method.
5. Discussion
The motivation of this research encompasses two main aspects. Firstly, the primary motivation is to explore the potential of artificial intelligence (AI) methods in load model parameter identification, leveraging their advantages such as fast computation speed and adaptability to complex load models. Secondly, considering the numerous AI methods available, the selection of the Extreme Learning Machine (ELM) method in this study is driven by its high training efficiency and strong generalization ability. However, the conventional ELM method is limited by its random determination of input weights. Consequently, an additional motivation of this research is to enhance the training process of conventional ELM by incorporating the Quantum Particle Swarm Optimization (QPSO) algorithm. The proposed improvements are then validated through comparative simulations between conventional ELM and QPSO-ELM.
In this paper, we propose a load model parameter identification method using the QPSO-ELM approach for synthetic load models. The QPSO-ELM method is employed for load model parameter identification and its performance is compared with the conventional ELM method, thereby validating the effectiveness of the proposed load model parameter identification scheme. To illustrate the efficacy of the proposed method, typical test results are selected and presented in this paper. However, we are currently expanding the scale of the test system and considering more complex load models, such as those involving electric vehicles, distributed wind power, and distributed storage. It is important to note that the sample generation process for large power systems with diverse loads is time-consuming and complex. Therefore, adequate space for discussion and further explanations is required, particularly when addressing this challenge using transfer learning methods. Including these additional explanations and results in the current paper would exceed the page limitations.
6. Conclusions
This paper introduces a novel method based on Quantum Particle Swarm Optimization and Extreme Learning Machine for load model parameter identification in the context of a generalized synthetic load model (SLM) considering the impact of distributed photovoltaic sources. The structure of the SLM, incorporating distributed photovoltaic sources, is analyzed using sensitivity analysis to determine critical parameters. The proposed QPSO-ELM method utilizes load voltage and power responses as input features and provides the identified critical parameters for the generalized SLM. The effectiveness of the proposed method is demonstrated through validation in a typical test system. In future work, further improvements to the QPSO-ELM-based parameter identification method will be summarized in subsequent papers, with a focus on enhancing its adaptability to complex scenarios.
Author Contributions
Methodology, B.X. and Y.Y.; software, J.Y. and G.L.; writing—original draft preparation, Z.L.; writing—review and editing, D.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Project of China Southern Power Grid Co., Ltd. (Item No.: 032000KK52220006(GDKJXM20220163)).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
Yanhe Yin, Baojun Xu, Junjie Yu, and Guohao Li are employees of Zhongshan Power Supply Bureau of Guangdong Power Grid Co., Ltd.; Zhuohuan Li and Duotong Yang are employees of Digital Grid Research Institute, China Southern Power Grid. The paper reflects the views of the scientists, and not the company. The authors declare no conflict of interest.
References
- Dandeno, P.L.; Brown, H.H.; Dube, C.; Johnston, D.W.; Kovlakas, C.; Lewis, W.A.; Olive, D.W.; Shipley, R.B.; Skooglund, R.B.; Stagg, G.W.; et al. System Load Dynamics-Simulation Effects and Determination of Load Constants. IEEE Trans. Power Appar. Syst. 1973, 2, 600–609. [Google Scholar] [CrossRef]
- Renmu, H.; Jin, M.; Hill, D.J. Composite load modeling via measurement approach. IEEE Trans. Power Syst. 2006, 21, 663–672. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Z.; Wang, Y.; Diao, R.; Shi, D. Mathematical Representation of WECC Composite Load Model. J. Mod. Power Syst. Clean Energy 2020, 8, 1015–1023. [Google Scholar] [CrossRef]
- Pal, M. Assessment of corrective measures for voltage stability considering load dynamics. Int. J. Electr. Power Energy Syst. 1995, 17, 325–334. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, Y.; Kundu, S.; Tang, Y.; James, D.; Liu, Y.; Etingov, P. Aggregate Protection Response of Motor Loads in Commercial Buildings. In Proceedings of the 2018 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Denver, CO, USA, 16–19 April 2018; pp. 1–5. [Google Scholar]
- Ma, J.; Han, D.; He, R.-M.; Dong, Z.-Y.; Hill, D.J. Reducing identified parameters of measurement-based composite load model. IEEE Trans. Power Syst. 2008, 23, 76–83. [Google Scholar] [CrossRef]
- Reger, J.; Ramirez, H.; Fliess, M. On non-asymptotic observation of nonlinear systems. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 4219–4224. [Google Scholar]
- Fadil, H.; Giri, F.; Ouadi, H. Adaptive sliding mode control of PWM boost DC–DC converters. In Proceedings of the 2006 IEEE International Conference on Control Applications, San Jose, CA, USA, 4–6 October 2006; pp. 3151–3156. [Google Scholar]
- Gensior, A.; Weber, J.; Guldner, H.; Rudolph, J. An algebraic parameter identification algorithm and asymptotic observers for estimation of the load of a boost converter. In Proceedings of the 2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 7–11. [Google Scholar]
- Fliess, M.; Sira-Ramírez, H. An algebraic framework for linear identification. ESAIM Control Optim. Calc. Var. 2003, 9, 151–168. [Google Scholar] [CrossRef]
- Jahromi, M.E.; Ameli, M.T. Measurement-based modelling of composite load using genetic algorithm. Electr. Power Syst. Res. 2018, 158, 82–91. [Google Scholar] [CrossRef]
- Hiskens, I. Nonlinear dynamic model evaluation from disturbance measurements. IEEE Trans. Power Syst. 2001, 16, 702–710. [Google Scholar] [CrossRef]
- Gensior, A.; Weber, J.; Rudolph, J.; Guldner, H. Algebraic Parameter Identification and Asymptotic Estimation of the Load of a Boost Converter. IEEE Trans. Ind. Electron. 2008, 55, 3352–3360. [Google Scholar] [CrossRef]
- Mirjalili, S.; Dong, J.S. Multi-Objective Optimization Using Artificial Intelligence Techniques; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Wang, Q.; Li, F.; Tang, Y.; Xu, Y. Integrating Model-Driven and Data-Driven Methods for Power System Frequency Stability Assessment and Control. IEEE Trans. Power Syst. 2019, 34, 4557–4568. [Google Scholar] [CrossRef]
- Li, Y.; Gu, X. Power system transient stability assessment based on online sequential extreme learning machine. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 8–11 December 2013; pp. 1–4. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).