Neural Network-Informed Lotka–Volterra Dynamics for Cryptocurrency Market Analysis
Abstract
1. Introduction
2. Dynamics of Interacting Populations Under Competition
- Predator–prey: One population’s growth decreases while the other’s increases.
- Competition: Growth rates of both populations decrease.
- Mutualism (symbiosis): Growth rates of both populations increase.
3. Deep Neural Network Model for Crypto Dynamics
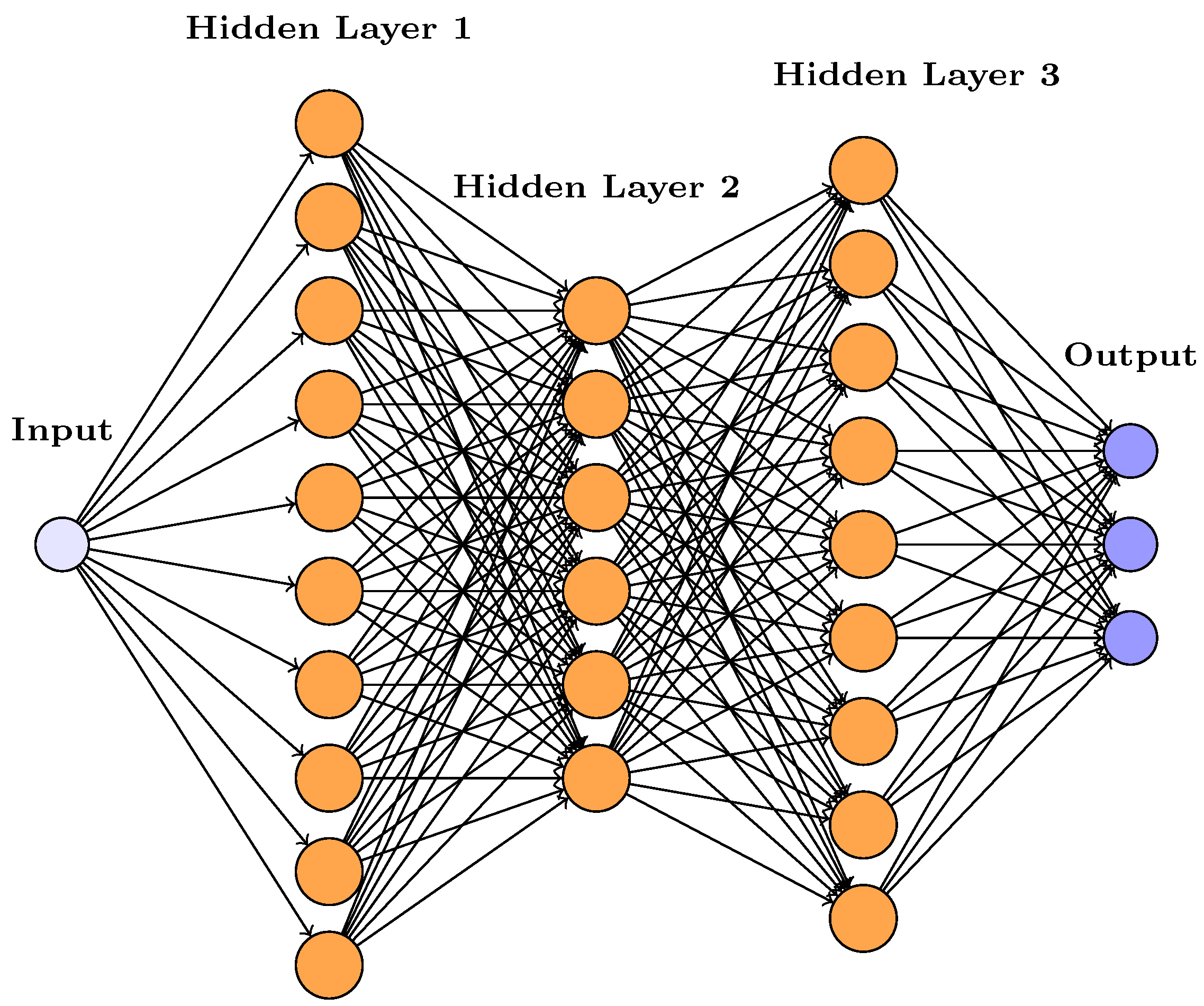
3.1. Feed-Forward Neural Network Architecture
- Input layer: accepts a single input feature corresponding to time, denoted as t.
- Hidden layers: Three fully connected hidden layers, with 10.6 and 9 neurons each and using the hyperbolic tangent (tanh) activation function. To promote stable learning, weights were initialized to small values and biases were set to zero.
- Output layer: A fully connected layer with three outputs, representing the estimated values of the variables , , and . Each output is connected to a regression layer, which calculates the loss based on the deviation between predicted and actual values.
- Time-series prediction: The neural network is trained on datasets to learn and predict their evolution over time. Once trained, it produces predictions for the three variables based solely on time input.
- Modeling underlying relationships: by learning from data, the NN approximates the hidden relationships between the variables and time, capturing complex and nonlinear behaviors that traditional models might overlook.
- Preparing for optimization: After prediction, the outputs obtain continuous estimates of the state variables. These are then used to compute numerical derivatives , , and . These derivatives are essential for the next phase of analysis, where model parameters are estimated via optimization using lsqnonlin.
3.2. Feed-Forward Propagation
4. Hybrid Neural Network—ODE Framework for Parameter Estimation and Forecasting
4.1. Mathematical Formulation
| Algorithm 1 Proposed method |
|
4.2. Numerical Integration via Runge–Kutta
- h represents the time step, s denotes the number of stages in the method, are the intermediate stage values, and are coefficients specifying the particular Runge–Kutta scheme.
4.3. Model Evaluation
| Algorithm 2 Selection of best neural network architecture |
|
5. Numerical Experiment
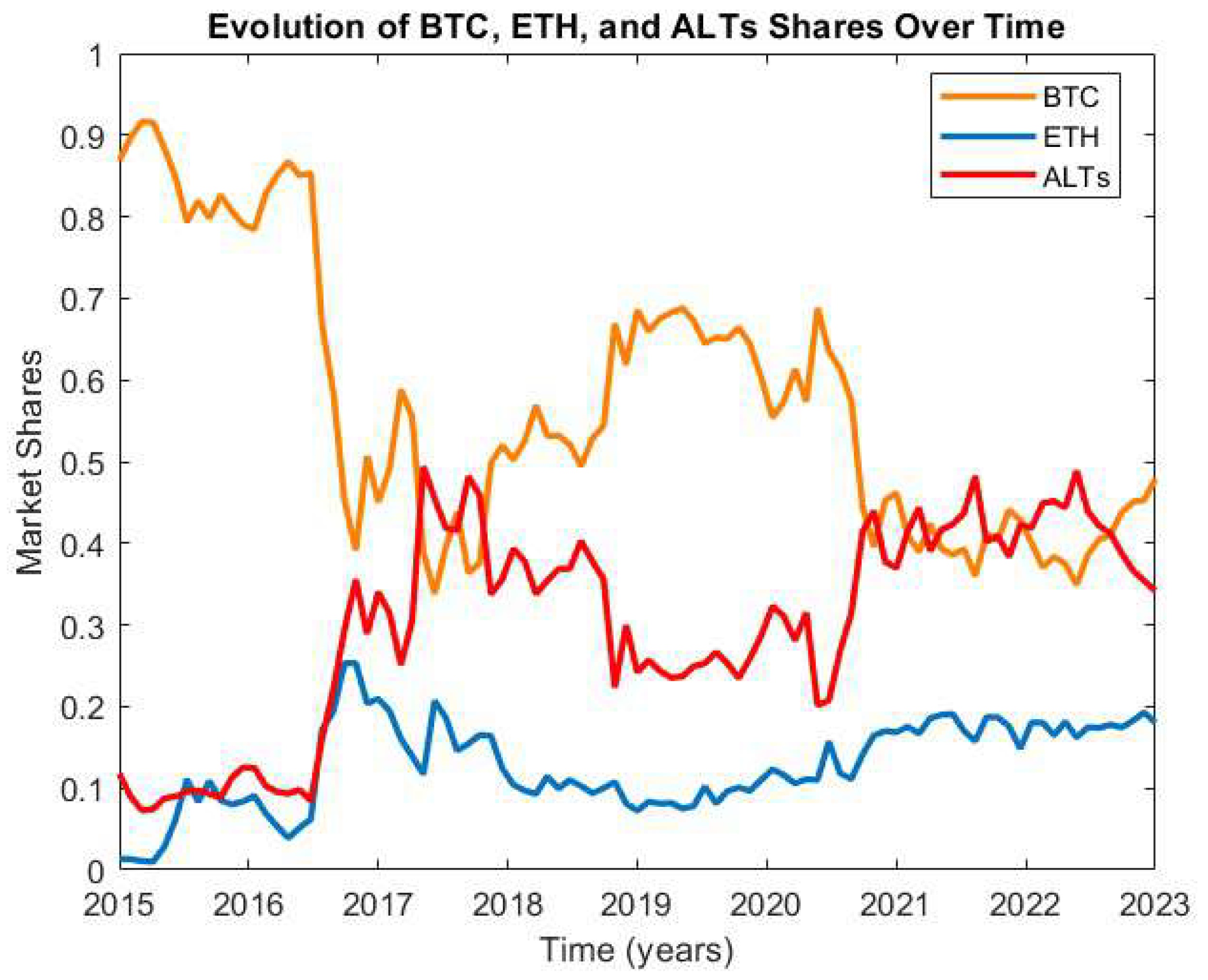
5.1. Case Study Description
- The intrinsic growth rates— for BTC, for ETH, and for ALTs—suggest that BTC and ETH may experience positive baseline growth in isolation, while ALTs are closer to neutral. The confidence interval for BTC is relatively narrow (low uncertainty), while those for ETH and ALTs are much wider, reflecting high or medium uncertainty and indicating that considerable variability is possible.
- The self-interaction parameters (BTC, low uncertainty), (ETH, high uncertainty), and (ALTs, high uncertainty) are negative, consistent with self-limitation effects. However, only the BTC self-limitation is statistically well identified; ETH and ALT self-regulation remain uncertain due to wide confidence intervals and large standard errors.
- Parameters reflecting competition or inhibition between asset classes—such as , , , , , and —vary in both sign and certainty. BTC-related cross-interactions ( and ) are estimated with medium uncertainty, while most others, particularly those involving ETH and ALTs, have high uncertainty, meaning the direction and strength of these effects cannot be robustly established from the current data.
5.2. System Stability Testing
5.3. Case Study Results
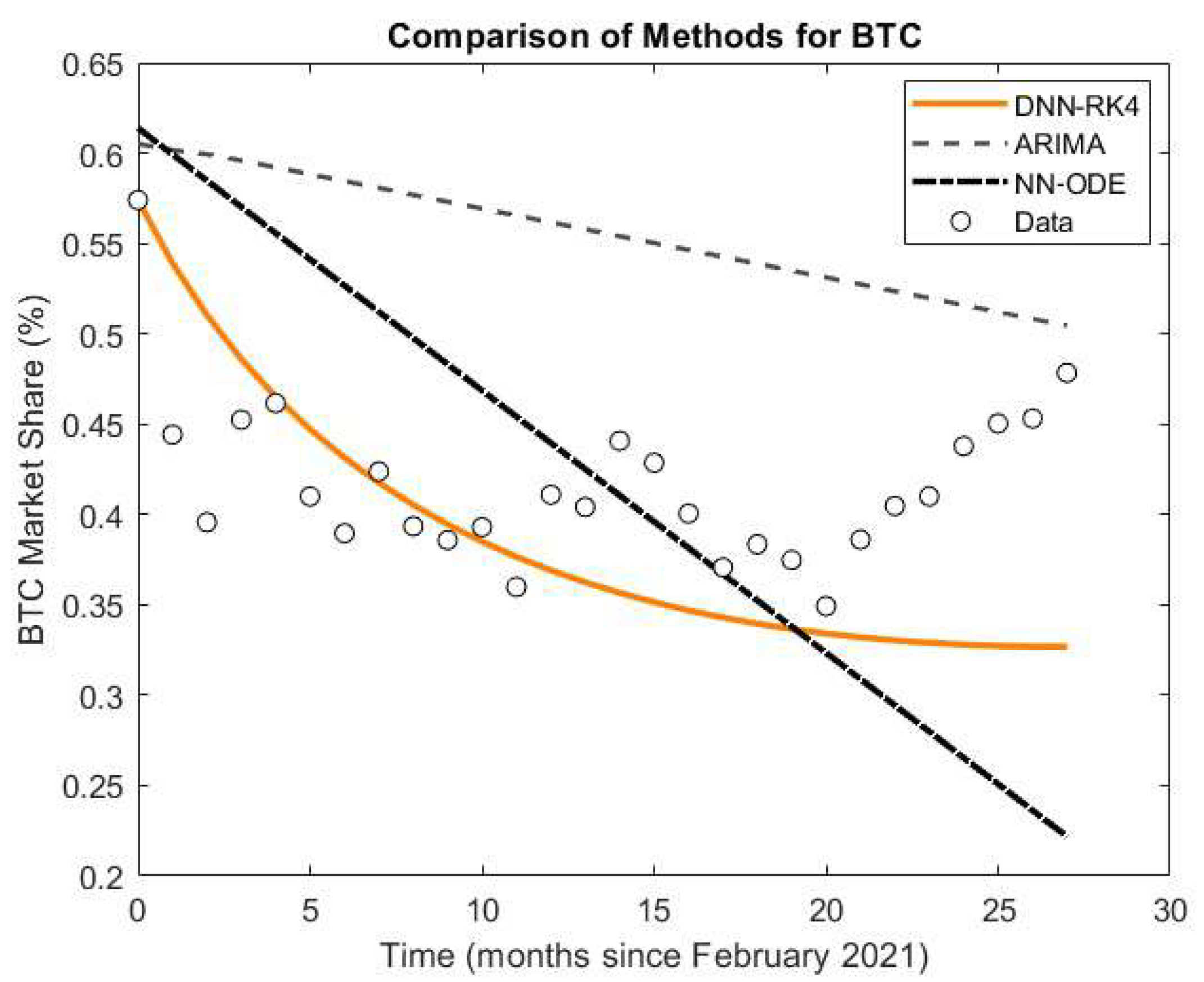
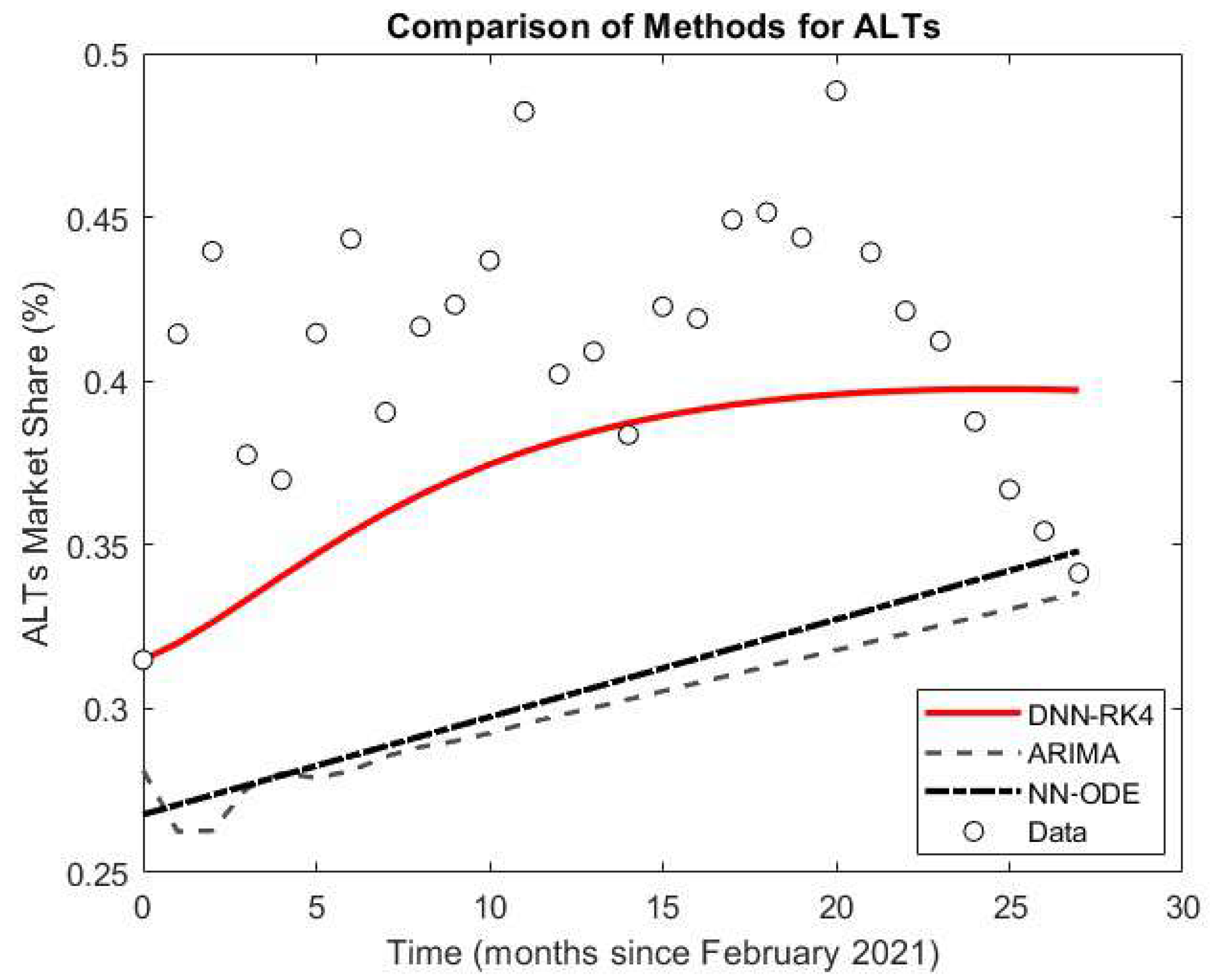
- BTC: DNN–RK4 halves the error of ARIMA (0.0687 vs. 0.1474 RMSE).
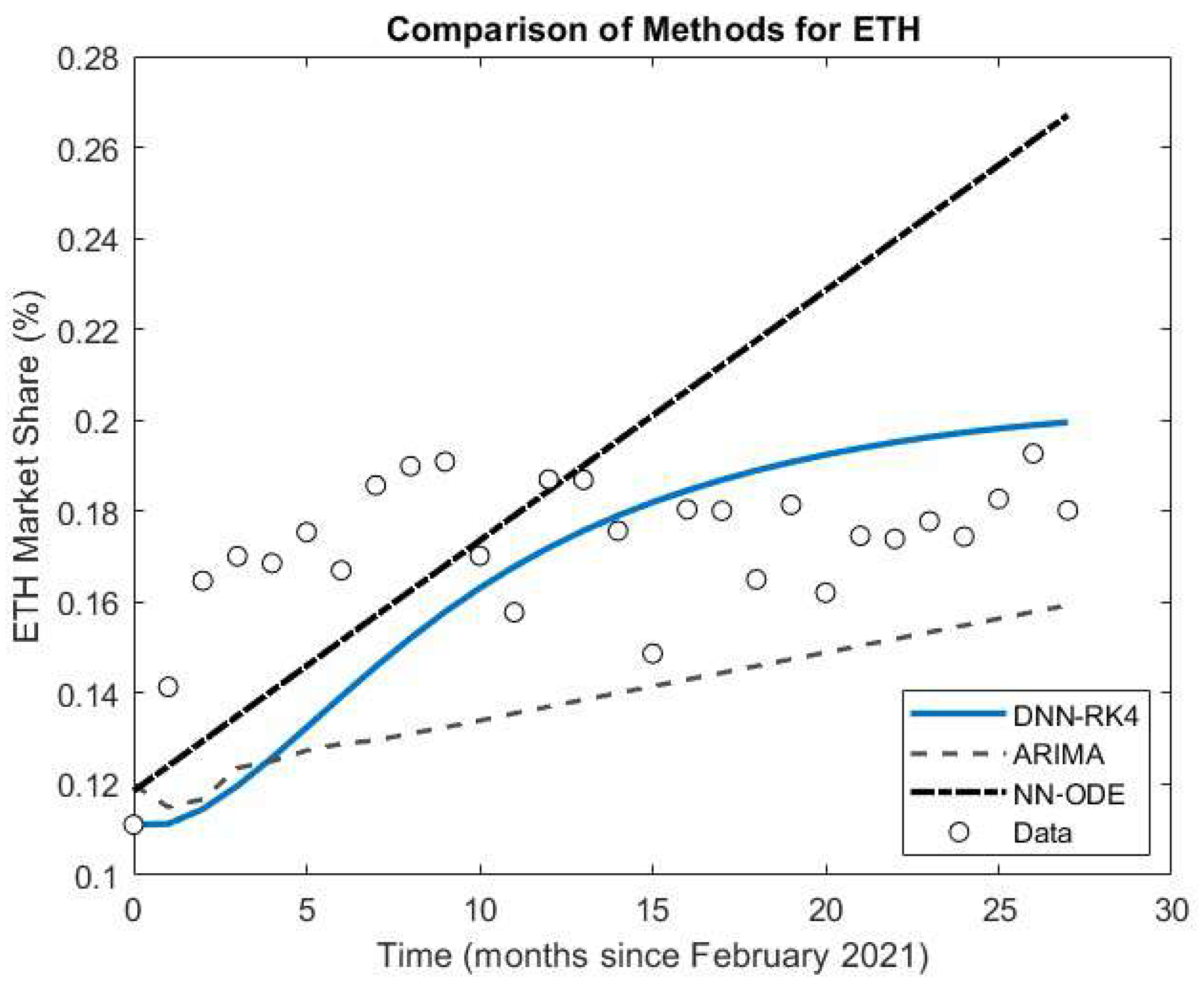
- ETH: DNN–RK4 outperforms by approx. 27% (0.0268 vs. 0.0367 RMSE).
- ALTs: DNN–RK4 reduces error by approx. 53% (0.0558 vs. 0.1189 RMSE).
- Aggregate: Mean RMSE drops from 0.101 (ARIMA) and 0.092 (NN–ODE) to 0.050 (DNN–RK4).
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- White, G.R. Future applications of blockchain in business and management: A Delphi study. Strateg. Change 2017, 26, 439–451. [Google Scholar] [CrossRef]
- Bitcoin.org. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 2 April 2025).
- Tradingview.com. Available online: https://www.tradingview.com/symbols/BTC/ (accessed on 5 April 2025).
- Taleb, N. Prospective applications of blockchain and bitcoin cryptocurrency technology. TEM J. 2019, 8, 48–55. [Google Scholar] [CrossRef]
- Navamani, T.M. A Review on Cryptocurrencies Security. J. Appl. Secur. Res. 2021, 18, 49–69. [Google Scholar] [CrossRef]
- Nandy, T.; Verma, U.; Srivastava, P.; Rongara, D.; Gupta, A.; Sharma, B. The Evaluation of Cryptocurrency: Overview, Opportunities, and Future Directions. In Proceedings of the 2023 7th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 17–19 May 2023; pp. 1421–1426. [Google Scholar]
- Tradingview.com. Available online: https://www.tradingview.com/symbols/ETH/ (accessed on 8 April 2025).
- Forbes.com. Available online: https://www.forbes.com/sites/lawrencewintermeyer/2021/08/12/institutional-money-is-pouring-into-the-crypto-market-and-its-only-going-to-grow/?sh=1a5424261459 (accessed on 8 April 2025).
- Taleb, N.N. Bitcoin, currencies, and fragility. Quant. Financ. 2021, 21, 1249–1255. [Google Scholar] [CrossRef]
- Visual Capitalist. Available online: https://www.visualcapitalist.com/crypto-ownership-growth-by-region/ (accessed on 12 April 2025).
- Javarone, M.A.; Wright, C.S. From bitcoin to bitcoin cash: A network analysis. In Proceedings of the 1st Workshop on Cryptocurrencies and Blockchains for Distributed Systems, Munich, Germany, 15 June 2018; pp. 77–81. [Google Scholar]
- Donet, J.A.D.; Pérez-Sola, C.; Herrera-Joancomartí, J. The bitcoin p2p network. In Proceedings of the International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 3–7 March 2014; pp. 87–102. [Google Scholar]
- Kjærl, F.; Khazal, A.; Krogstad, E.A.; Nordstrøm, F.B.; Oust, A. An analysis of bitcoin’s price dynamics. J. Risk Financ. Manag. 2018, 11, 63. [Google Scholar] [CrossRef]
- Velankar, S.; Valecha, S.; Maji, S. Bitcoin price prediction using machine learning. In Proceedings of the 2018 20th International Conference on Advanced Communication Technology (ICACT), Chuncheon, Republic of Korea, 11–14 February 2018; pp. 144–147. [Google Scholar]
- ElBahrawy, A.; Alessandretti, L.; Kandler, A.; Pastor-Satorras, R.; Baronchelli, A. Evolutionary dynamics of the cryptocurrency market. R. Soc. Open Sci. 2017, 4, 170623. [Google Scholar] [CrossRef]
- Wu, K.; Wheatley, S.; Sornette, D. Classification of cryptocurrency coins and tokens by the dynamics of their market capitalizations. Soc. Open Sci. 2018, 5, 180381. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology; Springer: New York, NY, USA, 1993. [Google Scholar]
- Wijeratnea, A.W.; Yi, F.; Wei, J. Biffurcation analysis in the diffu- sive Lotka-Voltera system: An application to market economy. Chaos Solitons Fractals 2009, 40, 902–911. [Google Scholar] [CrossRef]
- Neal, D. Introduction to Population Biology; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems, 8th ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Fisher, J.C.; Pry, R.H. A simple substitution model of technological change. Technol. Forecast. Soc. Change 1971, 3, 75–88. [Google Scholar] [CrossRef]
- Rai, L.P. Appropriate models for technology substitution. J. Sci. Ind. Res. 1999, 58, 14–18. [Google Scholar]
- Begon, M.; Townsend, C.; Harper, J. Ecology: From Individuals to Ecosystems, 4th ed.; Blackwell: Oxford, UK, 2006. [Google Scholar]
- Fay, T.H.; Greeff, J.C. A three species competition model as a decision support tool. Ecol. Modell 2008, 211, 142–152. [Google Scholar] [CrossRef]
- Leach, P.G.L.; Miritzis, J. Analytic behaviour of competition among three species. J. Nonlinear Math. Phys. 2006, 13, 535–548. [Google Scholar] [CrossRef]
- Olivença, D.V.; Davis, J.D.; Voit, E.O. Inference of dynamic interaction networks: A comparison between Lotka-Volterra and multivariate autoregressive models. Front. Bioinform. 2022, 2, 1021838. [Google Scholar] [CrossRef] [PubMed]
- Kastoris, D.; Giotopoulos, K.; Papadopoulos, D. Neural Network-Based Parameter Estimation in Dynamical Systems. Information 2024, 15, 809. [Google Scholar] [CrossRef]
- Michalakelis, C.; Sphicopoulos, T.S.; Varoutas, D. Modelling competition in the telecommunications market based on the concepts of population biology. Trans. Syst. Man Cybern. Part C Appl. Rev. 2011, 41, 200–210. [Google Scholar] [CrossRef]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Huang, L.; Qin, J.; Zhou, Y.; Zhu, F.; Liu, L.; Shao, L. Normalization Techniques in Training DNNs: Methodology, Analysis and Application. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10173–10196. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 2016; Volume 3, pp. 143–331. [Google Scholar]
- Delin, T.; Zheng, C. On A General Formula of Fourth Order Runge-Kutta Method. J. Math. Sci. Math. Educ. 2012, 7, 1–10. [Google Scholar]
- Dormand, J.R.; El-Mikkawy, M.E.A.; Prince, P.J. Families of Runge-Kutta-Nyström formulae. IMA J. Numer. 1987, 7, 235–250. [Google Scholar] [CrossRef]
- Papadopoulos, D.F.; Simos, T.E. The use of phase lag and amplification error derivatives for the construction of a modified Runge-Kutta-Nyström method. Abstr. Appl. Anal. 2013, 2013, 910624. [Google Scholar] [CrossRef]
- Papadopoulos, D.F.; Anastassi, Z.A.; Simos, D.F. The use of phase-lag and amplification error derivatives in the numerical integration of ODEs with oscillating solutions. AIP Conf. Proc. 2009, 1168, 547–549. [Google Scholar]
- Papadopoulos, D.F. A Parametric Six-Step Method for Second-Order IVPs with Oscillating Solutions. Mathematics 2024, 12, 3824. [Google Scholar] [CrossRef]
- Steyerberg, E.W.; Harrell, F.E., Jr.; Borsboom, G.J.; Eijkemans, M.J.C.; Vergouwe, Y.; Habbema, J.D.F. Internal validation of predictive models: Efficiency of some procedures for logistic regression analysis. J. Clin. Epidemiol. 2001, 54, 774–781. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap, 1st ed.; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Coinmarketcap.com. Available online: https://coinmarketcap.com/historical/ (accessed on 16 April 2025).
- Schulz, A.W. Equilibrium modeling in economics: A design-based defense. J. Econ. Methodol. 2024, 31, 36–53. [Google Scholar] [CrossRef]
- Kontopoulou, V.I.; Panagopoulos, A.D.; Kakkos, I.; Matsopoulos, G.K. A Review of ARIMA vs. Machine Learning Approaches for Time Series Forecasting in Data Driven Networks. Future Internet 2023, 15, 255. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Kim, S.; Shin, D. Transformer-based cryptocurrency price prediction using social media sentiment. IEEE Access 2021, 9, 140697–140709. [Google Scholar]
- Choi, I.; Kim, W.C. A temporal information transfer network approach considering federal funds rate for an interpretable asset fluctuation prediction framework. Int. Rev. Econ. Financ. 2024, 96, 103562. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Xiong, L.; Chang, R.; Wang, W.; Chen, L. Stock price prediction with attentive temporal convolution-based generative adversarial network. Array 2025, 25, 100374. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Wei, J. Graph-Neural-Network-Based Transaction Link Prediction Method for Public Blockchain in Heterogeneous Information Networks. Blockchain Res. Appl. 2025, 6, 100265. [Google Scholar] [CrossRef]
- Chen, R.T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural Ordinary Differential Equations. Adv. Neural Inf. Process. Syst. 2018, 31, 3–4. [Google Scholar]
- Coelho, C.; da Costa, M.F.P.; Ferrás, L.L. XNODE: A XAI Suite to Understand Neural Ordinary Differential Equations. AI 2025, 6, 105. [Google Scholar] [CrossRef]
- Gurgul, V.; Lessmann, S.; Härdle, W.K. Deep learning and NLP in cryptocurrency forecasting: Integrating financial, blockchain, and social media data. Int. J. Forecast. 2024, 2, 4. [Google Scholar] [CrossRef]

| BTC | ETH | ALTs | MRMSE | LR | Epochs | |||
|---|---|---|---|---|---|---|---|---|
| 10 | 6 | 9 | 0.056355 | 0.097497 | 0.096556 | 0.083469 | 0.0001 | 200 |
| 10 | 6 | 9 | 0.063268 | 0.092336 | 0.097758 | 0.084454 | 0.0001 | 100 |
| 8 | 10 | 10 | 0.068767 | 0.097675 | 0.101360 | 0.089267 | 0.0001 | 200 |
| 7 | 7 | 6 | 0.062612 | 0.100960 | 0.102480 | 0.088684 | 0.0001 | 200 |
| 7 | 10 | 10 | 0.071430 | 0.096462 | 0.102860 | 0.090251 | 0.0001 | 200 |
| 6 | 5 | 10 | 0.063437 | 0.101870 | 0.102940 | 0.089416 | 0.0001 | 200 |
| 9 | 10 | 5 | 0.071015 | 0.099051 | 0.103100 | 0.091055 | 0.00005 | 200 |
| 9 | 9 | 10 | 0.068600 | 0.099730 | 0.104540 | 0.090957 | 0.0001 | 200 |
| 10 | 8 | 10 | 0.058409 | 0.114040 | 0.105150 | 0.092533 | 0.0001 | 200 |
| 9 | 10 | 5 | 0.072399 | 0.100790 | 0.105270 | 0.092820 | 0.0001 | 100 |
| Parameter | Estimate | Std (Uncertainty) | 95% CI Range | Uncertainty Level |
|---|---|---|---|---|
| 0.5358 | 0.0995 | [0.3409, 0.7308] | Low | |
| −0.4521 | 0.0826 | [−0.6139, −0.2903] | Low | |
| 0.7681 | 0.1440 | [0.4859, 1.0502] | Medium | |
| −1.3624 | 0.2519 | [−1.8562, −0.8687] | Medium | |
| 1.4664 | 2.1373 | [−2.7227, 5.6554] | High | |
| −1.2830 | 1.7878 | [−4.7871, 2.2210] | High | |
| −1.6997 | 2.7787 | [−7.1458, 3.7465] | High | |
| −1.7748 | 5.2371 | [−12.0395, 8.4899] | High | |
| 0.1941 | 0.4939 | [−0.7739, 1.1622] | Medium | |
| −0.1602 | 0.4119 | [−0.9675, 0.6471] | Medium | |
| −0.5119 | 0.6752 | [−1.8352, 0.8115] | High | |
| −0.1015 | 1.2280 | [−2.5085, 2.3054] | High |
| Method | BTC (RMSE) | ETH (RMSE) | ALTs (RMSE) | BTC (MAE) | ETH (MAE) | ALTs (MAE) |
|---|---|---|---|---|---|---|
| DNN-RK4 | 0.06865 | 0.02682 | 0.05581 | 0.05432 | 0.02259 | 0.04735 |
| ARIMA (2,1,2) | 0.14742 | 0.03665 | 0.11890 | 0.13906 | 0.03370 | 0.10986 |
| NN-ODE | 0.11757 | 0.04507 | 0.11305 | 0.09701 | 0.03806 | 0.10388 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kastoris, D.; Papadopoulos, D.; Giotopoulos, K. Neural Network-Informed Lotka–Volterra Dynamics for Cryptocurrency Market Analysis. Future Internet 2025, 17, 327. https://doi.org/10.3390/fi17080327
Kastoris D, Papadopoulos D, Giotopoulos K. Neural Network-Informed Lotka–Volterra Dynamics for Cryptocurrency Market Analysis. Future Internet. 2025; 17(8):327. https://doi.org/10.3390/fi17080327
Chicago/Turabian StyleKastoris, Dimitris, Dimitris Papadopoulos, and Konstantinos Giotopoulos. 2025. "Neural Network-Informed Lotka–Volterra Dynamics for Cryptocurrency Market Analysis" Future Internet 17, no. 8: 327. https://doi.org/10.3390/fi17080327
APA StyleKastoris, D., Papadopoulos, D., & Giotopoulos, K. (2025). Neural Network-Informed Lotka–Volterra Dynamics for Cryptocurrency Market Analysis. Future Internet, 17(8), 327. https://doi.org/10.3390/fi17080327







