Abstract
In this work, we exploit a multi-antenna cooperative jammer to enable secure short packet communications in Internet of Things (IoT) networks. Specifically, we propose three jamming schemes to combat eavesdropping, i.e., the zero forcing beamforming (ZFB) scheme, null-space artificial noise (NAN) scheme, and transmit antenna selection (TAS) scheme. Assuming Rayleigh fading, we derive new closed-form approximations for the secrecy throughput with finite blocklength coding. To gain further insights, we also analyze the asymptotic performance of the secrecy throughput in the case of infinite blocklength. Furthermore, we investigate the optimization problem in terms of maximizing the secrecy throughput with the latency and reliability constraints to determine the optimal blocklength. Simulation results validate the accuracy of the approximations and evaluate the impact of key parameters such as the jamming power and the number of antennas at the jammer on the secrecy throughput.
1. Introduction
The Internet of Things (IoT), which is expected to connect various surrounding physical nodes such as different kinds of controllers and sensors, serves as a crucial architecture for e-health, home automation, smart cities, environmental monitoring, intelligent transportation, etc. [1,2,3]. Note that enormous amounts of confidential and sensitive information, e.g., financial files, trade secrets, and personal privacy, are exchanged via wireless channels in the IoT networks. For example, e-health contains personal confidential information such as physiological information and real-time location. If this private information is obtained by illegal eavesdroppers, it will result in very serious consequences. Therefore, privacy and security protection are a fundamental requirement in the design of IoT networks [4,5]. Conventionally, security for IoT is addressed by cryptographic techniques. The encryption-based security techniques have inherent high complexity in secret key generation, distribution, and management, which makes it difficult to apply for IoT networks with many resource-constrained sensors and actuators [6,7,8].
Compared with cryptographic techniques, physical layer security utilizes the inherent randomness of the wireless medium, such as fading, noise, and interference, to guarantee secure information transmission. Since physical layer security does not need the complicated key exchange procedure and provides a low-complexity and effective security solution, it is more favorable for IoT networks [9,10,11,12]. The physical layer security performance can be further enhanced by a jamming strategy. By designing an artificial noise signal, the difference between the quality of the legitimate link and the eavesdropping link can be enlarged, which will lead to a high secrecy rate. In particular, a secure downlink IoT network was considered in [13], where the power allocation between the legitimate signal and the artificial noise signal and the number of transmit antennas were jointly optimized to maximize the network secrecy throughput. A cooperative jammer in [14] sends jamming signals to confuse the eavesdroppers for downlink transmission in IoT networks. The artificial noise sent by the IoT devices was proposed in [15] for secrecy performance enhancement and the sum secrecy rate was maximized, subject to the transmit power constraint. The authors in [16] derived the secrecy outage probability of multihop IoT networks with a cooperative jamming scheme.
The above studies on IoT networks in the context of physical layer security assumed that the coding blocklength is large enough to achieve the secrecy capacity. However, the primary feature of IoT networks is the use of short packet transmissions to reduce communication latency. From [2,5,17,18], we know that the packet length in IoT applications is only a few hundreds bits, e.g., 10–300 bytes of factory automation. In this case, perfect decoding cannot be achieved even when the data rate is below the Shannon capacity. Therefore, the physical layer security based on classic infinite blocklength design cannot be directly adopted to the IoT networks with short packet transmissions. The authors in [19] evaluated the maximal achievable secrecy rate for general wiretap channels under a given information leakage, error probability, and blocklength. Based on this achievable secrecy rate, Reference [20] derived the secrecy throughput of an IoT network in the presence of a multi-antenna eavesdropper. Later, the work in [20] was extended to a wiretap channel with multiple eavesdroppers [21], multiuser multiple-input-multiple-output (MIMO) networks [22], and cognitive IoT networks with a multi-antenna relay [23]. Additionally, Reference [24] considered the relationship between secrecy throughput and secrecy coding under finite blocklength, and provided the optimal code rates and blocklength in terms of maximizing the secrecy throughput. Furthermore, the work [25] proposed some approaches to minimize the total transmit power or maximize the weighted throughput. In addition, the non-orthogonal multiple access (NOMA) technique has been incorporated to design the secure short packet communications schemes [26,27,28]. However, all these works only considered the secure communications of legitimate parties without an external helper, and most of them neglected the impact of cooperative jamming on the system performance, which may lead to an underestimation of the secrecy performance.
Motivated by the above background, in this paper, we investigate secure short packet communications in an IoT network, where an access point (AP) sends confidential information to a connected actuator in the presence of a cooperative jammer equipped with multiple antennas and an eavesdropper. Specifically, we propose three jamming schemes, i.e., the zero-forcing beamforming (ZFB) scheme, null-space artificial noise (NAN) scheme, and transmit antenna selection (TAS) scheme, for security improvement. The main contributions of our work are summarized as follows.
- 1.
- We first derive new closed-form approximations for the secrecy throughput of an IoT network with three different jamming transmission schemes, i.e., the ZFB scheme, NAN scheme, and TAS scheme. To achieve further insights, we also investigate the asymptotic secrecy throughput in the case of infinite blocklength.
- 2.
- We present the optimal design for the three different jamming transmission schemes. The blocklength is optimally determined in terms of maximizing the secrecy throughput subject to the constraints on the latency and reliability.
- 3.
- The results demonstrate that both the ZFB scheme and the NAN scheme strictly outperform the TAS scheme in terms of secrecy throughput. Moreover, increasing the number of antennas at the jammer provides significant performance gains for the three proposed schemes, which can be used to compensate for the performance loss from short packet transmissions.
The rest of the paper is organized as follows. We describe the system model of an IoT network with a multi-antenna cooperative jammer in Section 2. In Section 3, we present the analytical expressions of the secrecy throughput and asymptotic secrecy throughput and characterize the maximization of the secrecy throughput. Finally, we give simulation results in Section 4 and conclude this work in Section 5.
2. System Model
We consider an IoT downlink short packet communications system, as shown in Figure 1, which consists of an AP (Alice), a legitimate actuator (Bob), a cooperative jammer, and an eavesdropper (Eve). Similar to [29,30], we assume that all nodes are equipped with a single antenna, except that the jammer has antennas. We also assume that all the involved channels follow quasi-static Rayleigh block fading, such that the channel coefficients keep constant within each transmission block and change independently between different blocks.
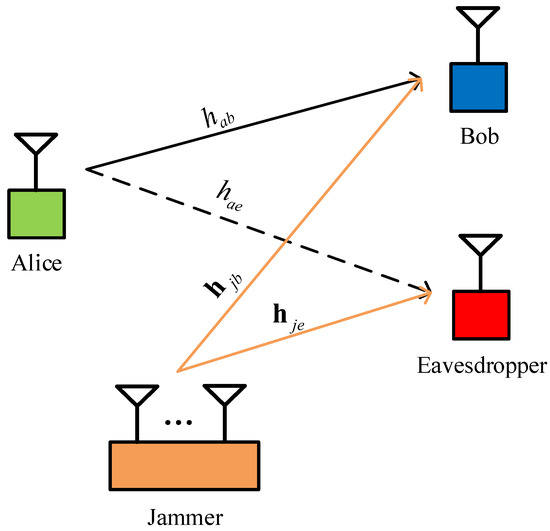
Figure 1.
A multi-antenna jammer-assisted secure short packet communications in the presence of an eavesdropper.
To exploit the advantages of both multiple antenna and cooperative jamming techniques, we consider three different secure transmission schemes, i.e., the ZFB scheme, NAN scheme, and TAS scheme. For the ZFB scheme, the jammer aims to maximize the interference at Eve, while avoiding interference to Bob. Thus, the beamforming vector is the solution of the following optimization problem:
where † is the conjugate transpose operator, is the Frobenius norm, is the channel vector for the jammer to Eve link with entries following identical and independently distributed (i.i.d.) Rayleigh fading with parameter , and is the channel vector for the jammer to Bob link with entries following i.i.d. Rayleigh fading with parameter . By using projection matrix theory [31], the beamforming vector can be expressed as:
where is the projection idempotent matrix with rank . Accordingly, the received signal-to-noise ratios (SNRs) at Bob and Eve of the ZFB scheme, respectively, can be expressed as:
and
where is the transmit power of Alice, is the transmit power of the jammer, is the Rayleigh channel coefficient for Alice to Bob link with parameter , is the Rayleigh channel coefficient for Alice to Eve link with parameter , and is the noise variance at each receiver.
For the NAN scheme, the jammer sends artificial noise in the null space of the legitimate channel to guarantee secure communication. Thus, the beamforming matrix at the jammer is designed as , where is a weighted vector used for the jammer to Bob link, and is a weighted matrix for the null space of , i.e., . As in [29,32], we assume that the transmit power of the jammer is uniformly allocated in the directions. Accordingly, the received SNRs at Bob and Eve of the NAN scheme, respectively, can be expressed as:
and
In addition to transmit beamforming, TAS is regarded as another effective method to improve the physical layer security performance. Moreover, TAS is particularly well adapted to systems with computational constraints, since it has two main advantages: low cost and easy implementation. For the TAS scheme, the jammer selects an antenna, which minimizes the interference imposed on Bob, to transmit the jamming signal. Accordingly, the received SNRs at Bob and Eve of the TAS scheme, respectively, can be expressed as:
and
where is the Rayleigh channel coefficient for the i-th antenna of the jammer to Bob link, and is the Rayleigh channel coefficient for the selected antenna of the jammer to Eve link.
According to [19], the maximal instantaneous secrecy rate of the IoT downlink short packet communications system with a cooperative jammer for a given information leakage probability , decoding error probability , and blocklength N can be approximated as:
where is the secrecy capacity for the infinite number of channel uses, , is the channel dispersion, is the inverse Q-function , and . For the reader’s convenience, we define and .
3. Secrecy Performance Analysis
In this section, we give a comprehensive analysis on the secrecy performance of the three proposed schemes. We first derive closed-form approximations for the secrecy throughput. Then, we analyze the asymptotic secrecy throughput in the case of infinite blocklength to gain further insights. Furthermore, the optimization problem in terms of maximizing the secrecy throughput is investigated under the latency and reliability constraints.
3.1. Secrecy Throughput
The secrecy throughput is the average secrecy rate where confidential messages from Alice are reliably transmitted to Bob under a certain secrecy constraint. Mathematically, it can be expressed as:
where B is the information bits delivered over N channel uses and is the average decoding error probability.
3.1.1. ZFB Scheme
The closed-form expression for the secrecy throughput of the IoT downlink short packet communications system with the ZFB scheme can be approximated as (here, we assume that ; when , the result can be directly derived by similar procedures):
where is the exponential integral function and , , , , and are defined in Appendix A.
Proof.
See Appendix A. ☐
3.1.2. NAN Scheme
The closed-form expression for the secrecy throughput of the IoT downlink short packet communications system with the NAN scheme can be approximated as (here, we assume that ; when , the result can be directly derived by similar procedures):
Proof.
Since is a chi-squared random variable with degrees of freedom [33], by following similar steps as the ZFB scheme, we can obtain the desired expression in (12) after some mathematical manipulations. □
3.1.3. TAS Scheme
The closed-form expression for the secrecy throughput of the IoT downlink short packet communications system with the TAS scheme can be approximated as (here, we assume that ; when , the result can be obtained by similar analysis):
where .
Proof.
Since is an exponentially distributed random variable and the probability density function (PDF) of is given by [29], by following a similar procedure as the ZFB scheme, we can derive the desired result in (13) after some mathematical manipulations.
The derived analytical results in (11)–(13) provide an efficient means to evaluate the secrecy throughput of the IoT downlink short packet communications system with the three proposed transmission schemes. Moreover, the approximations for the secrecy throughput of finite blocklength will be verified via simulations. □
3.2. Asymptotic Analysis
In an effort to understand the relationship between infinite blocklength and finite blocklength and gain more physical insights, in this subsection, we look into the asymptotic secrecy throughput under the infinite blocklength regime, i.e., . When , we have as long as from (9). Therefore, the asymptotic secrecy throughput in the case of infinite blocklength can be mathematically expressed as:
Corollary 1.
The asymptotic secrecy throughput of the ZFB scheme in the infinite blocklength regime is given by:
where and are given by:
and
Corollary 2.
The asymptotic secrecy throughput of the NAN scheme in the infinite blocklength regime is given by:
where and are given by:
and
Corollary 3.
The asymptotic secrecy throughput of the TAS scheme in the infinite blocklength regime is given by:
where and and are given by:
and
According to (15), (18), and (21), the secrecy throughput of the three proposed transmission schemes approaches zero as . However, the secrecy capacity of the three proposed transmission schemes is not zero for this particular case. Moreover, the asymptotic secrecy throughput of the three proposed transmission schemes is independent of the parameter . This is because the secrecy rate can always be achieved without leaking any information to the eavesdropper in the infinite blocklength regime, when .
3.3. Secrecy Throughput Maximization
We note that there exists a transmission latency–reliability tradeoff introduced by the blocklength. As such, in this subsection, we determine the optimal blocklength in terms of maximizing the secrecy throughput subject to the given latency and reliability constraints. Mathematically, the problem is formulated as:
where (24b) is the reliability constraint of the considered system, (24c) is the transmission latency constraint of the considered system, and is the non-negative integer set.
Next, we will clarify that is quasi-concave with respect to N. In the first step, by taking the first-order and second-order derivative of on N, we have:
and
where . Note that is generally much smaller than to ensure high reliability [34]; thus, we have , , and . Then, we analyze the sign of and . By taking the first-order and second-order derivative of on N, we have:
and
From (27) and (28), it is straightforward to obtain that and . Thus, we know that is a convex decreasing function with respect to N. Based on the Leibniz integral rule, is also a convex decreasing function with respect to N. Accordingly, is a quasi-concave function with respect to N.
Based on the above discussions, problem (24) can be simplified as:
where is the solution of . We clarify that the optimal blocklength in terms of maximizing the secrecy throughput exists only when , where is the ceiling operation. Now, we present the optimal blocklength in terms of maximizing the secrecy throughput in the following corollary.
Corollary 4.
When , the optimal blocklength in terms of maximizing the secrecy throughput is:
where is the solution of and is the floor operation.
Proof.
Firstly, the integer constraint in problem (29) is relaxed. Then, based on the fact that is a convex decreasing function with respect to N and is a quasi-concave function with respect to N, the optimal blocklength can be derived directly. ☐
4. Simulation Results
In this section, computer simulations by Matlab are provided to verify the analytical results of the three proposed transmission schemes and evaluate the secrecy throughput performance of the three proposed transmission schemes. In simulations, unless specified otherwise, we assume that , , , , , and dBm. From the figures, we can see that the analytical results coincide well with the computer simulation points, which demonstrates the correctness of our analysis.
Figure 2, Figure 3 and Figure 4 plot the secrecy throughput of the ZFB, NAN, and TAS schemes with different values of B, respectively. It is clear that the secrecy throughput first increases and then decreases as N increases, i.e., an optimal value for N exists to maximize the secrecy throughput. This phenomenon is explained as follows: when N is relatively small, increasing N is beneficial to improve the transmission reliability, which, of course, will lead to a higher secrecy throughput. However, when N is very large, the communication latency is large, which, consequently, will result in the degradation of the secrecy throughput. The second observation is that the optimal blocklength increases as B increases. This is because compared with communication latency, the decoding error at Bob becomes more obvious when the number of information bits gets larger.
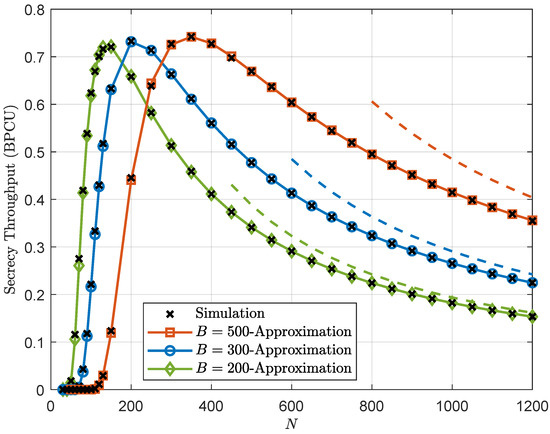
Figure 2.
Secrecy throughput of the ZFB scheme versus the blocklength N with different values of B for dBm and dBm, where the dashed lines are (15) to represent the asymptotic secrecy throughput.
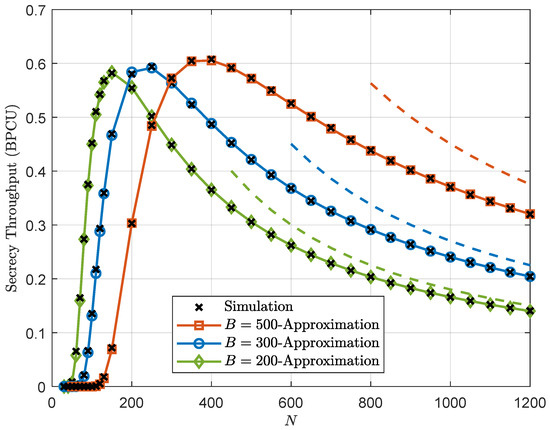
Figure 3.
Secrecy throughput of the NAN scheme versus the blocklength N with different values of B for dBm and dBm, where the dashed lines are (18) to represent the asymptotic secrecy throughput.
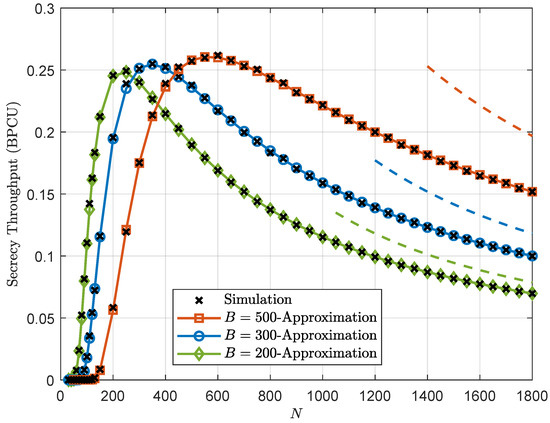
Figure 4.
Secrecy throughput of the TAS scheme versus the blocklength N with different values of B for dBm and dBm, where the dashed lines are (21) to represent the asymptotic secrecy throughput.
Figure 5 investigates the impact of the transmit power on the secrecy throughput with the three proposed schemes. Moreover, we present a benchmark scheme for comparison, i.e., without the jammer scheme, which consists of a source, a destination, and an eavesdropper, as in [20]. It is clear that the secrecy throughput of all the proposed schemes increases first and then stays constant as increases. This is because the ratio of average channel gain on the legitimate link to the eavesdropping link becomes the bottleneck of the secrecy throughput in the high-SNR regime. In addition, we observe that the ZFB and NAN schemes always attain better performance than the TAS and benchmark schemes. This is because the jamming signals of the ZFB scheme and the NAN scheme only selectively interfere with the eavesdropper and have no impact on the signal reception of the legitimate user. Thus, the multi-antenna jammer can be employed to improve the system performance.
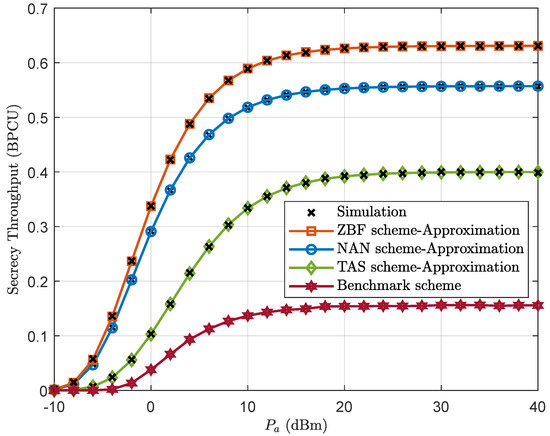
Figure 5.
Secrecy throughput of the ZFB, NAN, TAS, and benchmark schemes versus for , , and dBm.
Figure 6 shows the impact of the jamming power on the secrecy throughput with the three proposed schemes. We first observe that when is sufficiently large, the secrecy throughput converges to a constant for the ZFB and NAN schemes, whereas it goes to zero for the TAS scheme. This can be explained by the fact that the use of the TAS scheme not only degrades the channel condition of the eavesdropper, which is beneficial to secure transmission, but also deteriorates the channel condition of the legitimate user, which is adverse to secure transmission. It is also worth noting that the TAS scheme outperforms the benchmark scheme in certain regimes, i.e., when the jamming power is small. Therefore, the designer has to carefully choose the jamming power of the TAS scheme.
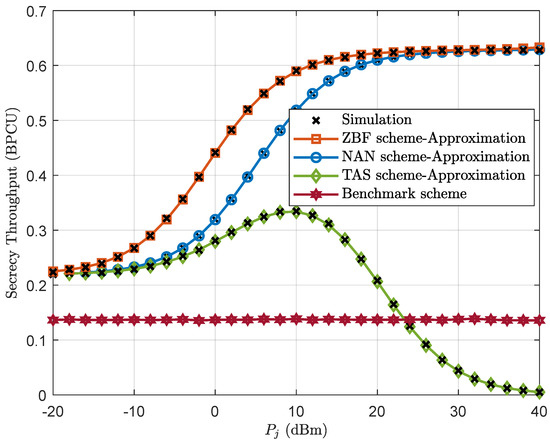
Figure 6.
Secrecy throughput of the ZFB, NAN, TAS, and benchmark schemes versus for , , and dBm.
Figure 7 examines the secrecy throughput of the three proposed schemes versus the number of antennas at the jammer. It is clear that the secrecy throughput of the three proposed schemes increases as the number of antennas at the jammer increases. Therefore, we conclude that increasing the number of antennas at the jammer can compensate for the performance loss from short packet transmissions. In particular, the TAS scheme can achieve more significant performance gains by adding more antennas at the jammer. This is attributed to the fact that increasing the number of antennas at the jammer will make it easier to select a better antenna, which reduces the jamming interference at the legitimate user.
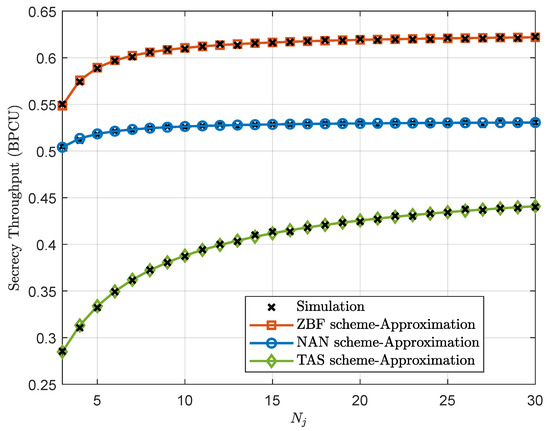
Figure 7.
Secrecy throughput of the ZFB, NAN, and TAS schemes versus for , , dBm, and dBm.
Figure 8 depicts the optimal blocklength and the corresponding maximum secrecy throughput versus the transmit power subject to the latency and reliability constraints. When the optimization problem in terms of maximizing the secrecy throughput is infeasible, we set the optimal blocklength to zero and the maximum secrecy throughput is set to zero. We first observe that one critical point exists and when does not exceed this point, the maximum secrecy throughput is zero. This is not surprising, since when is small, it is unable to meet the reliability constraint. We further observe that both the optimal blocklength and the maximum secrecy throughput converge to nonzero constants as . This is because the secrecy throughput of the considered system is independent of in the high SNR regime.
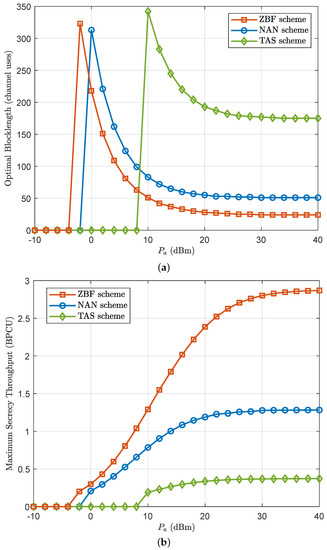
Figure 8.
(a) The optimal blocklength and (b) the corresponding maximum secrecy throughput versus for , , dBm, , and .
Figure 9 illustrates the optimal blocklength and the corresponding maximum secrecy throughput versus the jamming power subject to the latency and reliability constraints. We first observe that when is either extremely small or large, the maximum secrecy throughput of the TAS scheme approaches zero. This is because the decoding error probability of the TAS scheme is large in the two extreme cases. Therefore, the TAS scheme can only achieve its best performance for in-between values of . We further observe that the optimal blocklength of the TAS scheme first decreases and then increases as increases. This is because there exists a tradeoff between decoding error and transmission latency.
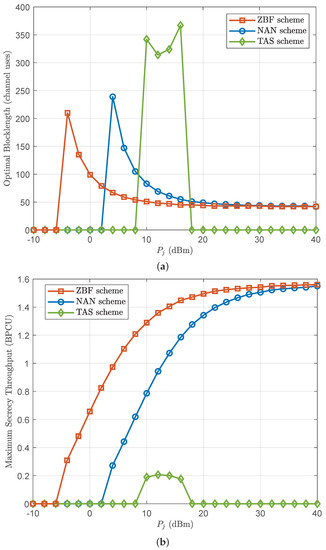
Figure 9.
(a) The optimal blocklength and (b) the corresponding maximum secrecy throughput versus for , , dBm, , and .
5. Conclusions
In this paper, we investigated the secrecy performance of IoT networks with finite blocklength coding. To exploit the available multi-antenna jammer for secrecy enhancement, we proposed three different secure transmission schemes. Specifically, we derived approximate closed-form expressions for the secrecy throughput of all the proposed schemes. Moreover, we presented the asymptotic secrecy throughput in the case of infinite blocklength to gain further insights. In addition, we determined the optimal blocklength that maximizes the secrecy throughput subject to the latency and reliability constraints. Numerical results demonstrated that both the ZFB scheme and the NAN scheme strictly outperform the TAS scheme in terms of the secrecy throughput, and the performance loss from short packet transmissions can be compensated for by increasing the number of antennas at the jammer.
Author Contributions
Methodology, D.C., J.L., J.H., and X.Z.; formal analysis, D.C., J.L., J.H., X.Z., and S.Z.; writing—original draft preparation, D.C. and J.L.; writing—review and editing, J.H., X.Z., and S.Z.; supervision, X.Z. and S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Doctoral Research Start-up Funding of Nanyang Normal University under Grant 2022ZX017; in part by the Cultivating Fund Project for the National Natural Science Foundation of China of Nanyang Normal University under Grant 2022PY024; in part by the open research fund of Key Lab of Broadband Wireless Communication and Sensor Network Technology (Nanjing University of Posts and Telecommunications), Ministry of Education, under Grant JZNY202107; in part by the Key Scientific Research Projects of Colleges and Universities in Henan Province of China under Grant 21A520033, 23A520038, and 23A510001; and in part by the Key Scientific and Technological Research Projects in Henan Province under Grant 222102320369, 232102210121, and 232102220101.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
For the delivery of B information bits through N channel uses, the decoding error probability of the ZFB scheme can be characterized by:
conditioned on . Note that, if . In order to obtain a closed-form expression of the secrecy throughput, we use a linear approximation of Q-function [35] and approximate the decoding error probability as:
where , , , and .
Let and ; the secrecy throughput of the ZFB scheme can be approximated as:
where is based on the fact that when and , while as , is obtained by using (A2), is obtained by leveraging the Riemann integral approximation [36], is the PDF of , is the PDF of , and is the cumulative distribution function (CDF) of .
Noticing that is an exponentially distributed random variable, its CDF is given by:
On the other hand, in order to derive the PDF of , we first give the PDF of the random variable as [37]:
Then, the CDF of is given by:
To simplify the integral in (A8), we introduce a sufficiently large parameter to ensure , when , and then (A8) can be approximated as:
where . By using Gaussian–Chebyshev quadrature [38], the integral can be approximated as:
where is a parameter for the complexity accuracy tradeoff, , and . According to [3.353.1] [39], the integral can be derived as:
References
- Brincat, A.A.; Pacifici, F.; Mazzola, F. IoT as a service for smart cities and nations. IEEE Internet Things Mag. 2019, 2, 28–31. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, W.; Cai, Y.; Ding, Z.; Song, Y.; Zou, Y. NOMA-assisted secure short-packet communications in IoT. IEEE Wirel. Commun. 2020, 27, 8–15. [Google Scholar] [CrossRef]
- Lianghai, J.; Han, B.; Liu, M.; Schotten, H.D. Applying device-to-device communication to enhance IoT services. IEEE Commun. Stand. Mag. 2017, 1, 85–91. [Google Scholar] [CrossRef]
- Ji, B.; Liu, Y.; Xing, L.; Li, C.; Zhang, G.; Han, C.; Wen, H.; Mumtaz, S. Survey of Secure Communications of Internet of Things with Artificial Intelligence. IEEE Internet Things Mag. 2022, 5, 92–99. [Google Scholar] [CrossRef]
- Feng, C.; Wang, H.M. Secure short-packet communications at the physical layer for 5G and beyond. IEEE Commun. Stand. Mag. 2021, 5, 96–102. [Google Scholar] [CrossRef]
- Hu, J.; Cai, Y.; Yang, N. Secure transmission design with feedback compression for the Internet of Things. IEEE Trans. Signal Process. 2018, 66, 1580–1593. [Google Scholar] [CrossRef]
- Farhat, J.; Brante, G.; Souza, R.D.; Vilela, J.P. On the secure spectral efficiency of URLLC with randomly located colluding eavesdroppers. IEEE Internet Things J. 2021, 8, 14672–14682. [Google Scholar] [CrossRef]
- Feng, C.; Wang, H.M.; Poor, H.V. Reliable and secure short-packet communications. IEEE Trans. Wirel. Commun. 2022, 21, 1913–1926. [Google Scholar] [CrossRef]
- Mukherjee, A. Physical-layer security in the Internet of Things: Sensing and communication confidentiality under resource constraints. Proc. IEEE 2015, 103, 1747–1761. [Google Scholar] [CrossRef]
- Li, C.; She, C.; Yang, N.; Quek, T.Q.S. Secure transmission rate of short packets with queueing delay requirement. IEEE Trans. Wirel. Commun. 2022, 21, 203–218. [Google Scholar] [CrossRef]
- Xie, Y.; Ren, P. Optimizing training and transmission overheads for secure URLLC against randomly distributed eavesdroppers. IEEE Trans. Veh. Technol. 2022, 71, 11921–11935. [Google Scholar] [CrossRef]
- Xu, D.; Zhao, H.; Zhu, H. Resource allocation for secure short packet communications in wireless powered IoT networks. IEEE Trans. Veh. Technol. 2023. early access. [Google Scholar] [CrossRef]
- Hu, J.; Yang, N.; Cai, Y. Secure downlink transmission in the Internet of Things: How many antennas are needed? IEEE J. Sel. Areas Commun. 2018, 36, 1622–1634. [Google Scholar] [CrossRef]
- Hu, L.; Wen, H.; Wu, B.; Pan, F.; Liao, R.; Song, H.; Tang, J.; Wang, X. Cooperative Jamming for Physical Layer Security Enhancement in Internet of Things. IEEE Internet Things J. 2018, 5, 219–228. [Google Scholar] [CrossRef]
- Xu, D.; Zhu, H. Secure transmission for SWIPT IoT systems with full-duplex IoT devices. IEEE Internet Things J. 2019, 6, 10915–10933. [Google Scholar] [CrossRef]
- Abdullah, Z.; Chen, G.; Abdullah, M.A.M.; Chambers, J.A. Enhanced secrecy performance of multihop IoT networks with cooperative hybrid-duplex jamming. IEEE Trans. Inf. Forensics Secur. 2021, 16, 161–172. [Google Scholar] [CrossRef]
- Schulz, P.; Matthe, M.; Klessig, H.; Simsek, M.; Fettweis, G.; Ansari, J.; Ashraf, S.A.; Almeroth, B.; Voigt, J.; Riedel, I.; et al. Latency Critical IoT Applications in 5G: Perspective on the Design of Radio Interface and Network Architecture. IEEE Commun. Mag. 2017, 55, 70–78. [Google Scholar] [CrossRef]
- Ma, R.; Yang, W.; Shi, H.; Lu, X.; Liu, J. Covert communication with a spectrum sharing relay in the finite blocklength regime. China Commun. 2023, 20, 195–211. [Google Scholar] [CrossRef]
- Yang, W.; Schaefer, R.F.; Poor, H.V. Wiretap channels: Nonasymptotic fundamental limits. IEEE Trans. Inf. Theory 2019, 65, 4069–4093. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Q.; Ding, Z.; Poor, H.V. Secure short-packet communications for mission-critical IoT applications. IEEE Trans. Wirel. Commun. 2019, 18, 2565–2578. [Google Scholar] [CrossRef]
- Ar, N.; Thomos, N.; Musavian, L. Performance analysis of short packet communications with multiple eavesdroppers. IEEE Trans. Commun. 2022, 70, 6778–6789. [Google Scholar] [CrossRef]
- Wei, L.; Yang, Y.; Jiao, B. Secrecy throughput in full-duplex multiuser MIMO short-packet communications. IEEE Wirel. Commun. Lett. 2021, 10, 1339–1343. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Yu, B.; Zhang, T.; Cai, Y. Relay-assisted secure short-packet transmission in cognitive IoT with spectrum sensing. China Commun. 2021, 18, 37–50. [Google Scholar] [CrossRef]
- Zheng, T.-X.; Wang, H.-M.; Ng, D.W.K.; Yuan, J. Physical layer security in the finite blocklength regime over fading channels. IEEE Trans. Wirel. Commun. 2020, 19, 3405–3420. [Google Scholar] [CrossRef]
- Ren, H.; Pan, C.; Deng, Y.; Elkashlan, M.; Nallanathan, A. Resource allocation for secure URLLC in mission-critical IoT scenarios. IEEE Trans. Commun. 2020, 68, 5793–5807. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, W.; Cai, Y.; Xiong, J.; Ding, Z.; Song, Y. Secure transmission in a NOMA-assisted IoT network with diversified communication requirements. IEEE Internet Things J. 2020, 7, 11157–11169. [Google Scholar] [CrossRef]
- Lai, X.; Wu, T.; Zhang, Q.; Qin, J. Average secure BLER analysis of NOMA downlink short-packet communication systems in flat Rayleigh fading channels. IEEE Trans. Wirel. Commun. 2021, 20, 2948–2960. [Google Scholar] [CrossRef]
- Lv, S.; Xu, X.; Han, S.; Tao, X.; Zhang, P. Energy-efficient secure short-packet transmission in NOMA-assisted mMTC networks with relaying. IEEE Trans. Veh. Technol. 2022, 71, 1699–1712. [Google Scholar] [CrossRef]
- Tao, L.; Yang, W.; Lu, X.; Ma, R.; Yang, L.; Song, Y. Multi-antenna Jammer assisted covert communications in data collected IoT with NOMA. China Commun. 2023, 20, 217–231. [Google Scholar] [CrossRef]
- Tao, L.; Yang, W.; Lu, X.; Wang, M.; Song, Y. Achieving covert communication in uplink NOMA systems via energy harvesting jammer. IEEE Commun. Lett. 2021, 25, 3785–3789. [Google Scholar] [CrossRef]
- Basilevsky, A. Applied Matrix Algebra in the Statistical Sciences; North-Holland: New York, NY, USA, 1983. [Google Scholar]
- Yang, M.; Zhang, B.; Huang, Y.; Yang, N.; da Costa, D.B.; Guo, D. Secrecy enhancement of multiuser MISO networks using OSTBC and artificial noise. IEEE Trans. Veh. Technol. 2017, 66, 11394–11398. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, L.; Chen, H.-H. Covert communications in D2D underlaying cellular networks with antenna array assisted artificial noise transmission. IEEE Trans. Veh. Technol. 2020, 69, 2980–2992. [Google Scholar] [CrossRef]
- Wang, K.; Pan, C.; Ren, H.; Xu, W.; Zhang, L.; Nallanathan, A. Packet Error Probability and Effective Throughput for Ultra-Reliable and Low-Latency UAV Communications. IEEE Trans. Commun. 2021, 69, 73–84. [Google Scholar] [CrossRef]
- Makki, B.; Svensson, T.; Zorzi, M. Wireless energy and information transmission using feedback: Infinite and finite block-length analysis. IEEE Trans. Commun. 2016, 64, 5304–5318. [Google Scholar] [CrossRef]
- Lai, X.; Zhang, Q.; Qin, J. Cooperative NOMA short-packet communications in flat Rayleigh fading channels. IEEE Trans. Veh. Technol. 2019, 68, 6182–6186. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, Y.; Cai, Y.; Zhong, C.; Yang, W.; Karagiannidis, G.K. Secure multiantenna cognitive wiretap networks. IEEE Trans. Veh. Technol. 2017, 66, 4059–4072. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th ed.; US Govt. Print: Washington, DC, USA, 1972.
- Gradshteyn, I.S.; Ryzhik, I.M.; Jeffrey, A.; Zwillinger, D.; Technica, S. Table of Integrals, Series, and Products, 7th ed.; Academic: New York, NY, USA, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).