Abstract
Solid-state drives represent the preferred backbone storage solution thanks to their low latency and high throughput capabilities compared to mechanical hard disk drives. The performance of a drive is intertwined with the reliability of the memories; hence, modeling their reliability is an important task to be performed as a support for storage system designers. In the literature, storage developers devise dedicated parametric statistical approaches to model the evolution of the memory’s error distribution through well-known statistical frameworks. Some of these well-founded reliability models have a deep connection with the 3D NAND flash technology. In fact, the more precise and accurate the model, the less the probability of incurring storage performance slowdowns. In this work, to avoid some limitations of the parametric methods, a non-parametric approach to test the model goodness-of-fit based on combined permutation tests is carried out. The results show that the electrical characterization of different memory blocks and pages tested provides an FBC feature that can be well-modeled using a multiple regression analysis.
1. Introduction
The amount of data generated in 2022 by an average of 3.7 billion Internet users has been estimated at 2.5 exabytes per day [1], with a growing trend anticipated in the next few years. By 2025, data storage analysts forecast a global data sphere of 160 zettabytes to be stored per year [2]. The same challenge exists in collecting and storing data by large scientific facilities connected across the world [3]. The ever-increasing data generation speed requires dense yet performant storage platforms to collect and filter the data, save the data through high-speed networks, and prevent the loss of valuable data.
Nowadays, solid-state drives (SSD) represent the preferred backbone storage solution for either on-premise data centers or in-cloud computing facilities thanks to their low latency and high throughput capabilities compared to mechanical hard disk rrives (HDD) [4]. The positive performance is achieved through complex monitoring and dynamic management provided by a synergy between the SSD controller (i.e., the computing brain of a drive) and the integrated storage medium, namely the 3D NAND flash [5]. In particular, the performance of a drive is intertwined with the reliability of the memories [6]; therefore, modeling this feature remains an important task to be performed as a support for storage system designers. All the firmware solutions implemented in an SSD controller have the ultimate goal of mitigating the inherent bit error rate (BER) exposed by the 3D NAND flash memories in different storage working conditions (e.g., endurance stress, data retention at high temperatures, etc.) and improving the drive’s performance. Significant efforts in SSD design are dedicated to tailoring the error correction code (ECC) [7] strengths and the secondary correction schemes, like soft decoding [8], moving read references [6], and even RAID [9].
To this extent, storage designers have devised dedicated parametric statistical models [10,11,12,13,14,15,16] to capture the evolution of the memory’s error distribution through well-known statistical frameworks (probability distributions), like Gaussian, binomial, Poisson, gamma, and so on. Concerning the model abstraction level, we identify two families: (i) statistical models of the flash channel (i.e., the cells’ threshold voltage distributions) used to extrapolate the memory reliability characteristics; and (ii) statistical models or machine-learning-based approaches directly applied to the reliability features extracted from measurements.
In the first set of models, many parametric continuous probability distributions (e.g., Weibull, lognormal, gamma) are proposed to represent the threshold voltage () distributions of flash cells and then extrapolate the memory reliability in different scenarios through the calculation of the number of corrupted bits per distribution. Reports in the literature suggest the use of the Gaussian function for its simplicity although it has been found that other mathematical functions exhibit a better fit and even that the tail regions of the distributions in the flash memory are mainly exponential due to the random telegraph noise [17,18,19]. To further improve the fitting quality, previous works have proposed modeling distributions with a mixture of Gaussian with data-dependent variances [10,11,12,14], by using a normal-Laplace mixture model [19], developing tailored Monte Carlo models in the crossover regions between different distributions [20], or by relying on the physics-based model associated with the NAND flash architecture [21]. In some cases [11,12], it is stated that the reliability features extracted from the models tend to be underestimated. Parameterized versions [19] for particular operating conditions, like endurance degradation, describe well the evolution of the model parameters as a function of the memory lifetime, though they rely on complex fitting procedures. For the first time, the authors in [18] discussed the possibility of considering non-parametric models for distribution fitting, although few details were shared with the reader, limiting the model evaluation possibilities.
The second set of models used in flash memory targets well-defined metrics for reliability evaluation either at the device or at the system level (i.e., in solid-state storage platforms), namely the bit error rate (BER) or the fail bits count (FBC). Both metrics indicate the number of corrupted bits in a precise location of the NAND flash memory due to specific physical mechanisms, like endurance wear, retention loss, and so on. A seminal work is that of [22], where the BER was modeled in different operating corners. A similar approach, although oriented to 3D NAND flash architectures was proposed in [23], where, for the first time, the authors introduced the use of the gamma-Poisson distribution for error modeling, and in [24], where a generalized Pareto distribution was used to model real disturb errors. Other interesting solutions have relied on machine learning algorithms for memory lifetime classification and prediction [13,15,16] and on deep neural networks [25,26,27]. However, some of the developed models require a huge characterization dataset and significant computing power to run the model training process or the creation of a dedicated computational framework based on neural networks to optimize the device characteristics, such as the case discussed in [28] though for a different technology.
Some of these well-founded reliability models have a deep link with the failure mechanisms in the NAND Flash technology [29]. In general, the more precise and accurate the model, the lower the probability of incurring storage performance slowdowns due to improperly calibrated error correction techniques.
In this work, we target the second category of models using for the first time, to the best of our knowledge, an approach based on non-parametric inference on the regression coefficients to characterize the FBC in 3D NAND flash memories tested with endurance stress. We focus here on the statistical testing of the model validity (goodness-of-fit test), where the full model, which includes all the considered explanatory variables, is compared to the null model, which lacks explanatory power. To this extent, a non-parametric approach is carried out. The proposed test, unlike the parametric approaches, does not require the assumption that the distribution of the responses follows a specific family of probability laws. Such a test is very powerful, especially (but not only) when the typical assumptions of the parametric approaches (such as the normality of data in the classic regression analysis) are not satisfied and the parametric tests are not reliable [30]. Furthermore, this method is more flexible and robust with respect to the parametric tests [31]. In this work, a permutation test on the goodness-of-fit of a multiple regression model is applied. In particular, we consider such a problem as a multiple test on the significance of the single regression coefficients (partial tests), and the proposed solution is based on the combination of the p-values of the partial tests. In other words, we study the performance of the 3D NAND flash memories in terms of the sum of the number of errors without assuming a specific probability distribution. In fact, we adopt a regression approach to analyze the relationship between the 3D NAND flash errors and some explanatory factors in order to determine whether such factors affect the number of errors and which factors produce a significant effect. This method is valid regardless of the assumed distribution of the errors.
Hence, the main objective of the paper consists in proposing a robust and flexible method to test the validity of the model to predict the performance of the 3D NAND flash memories. Such a method is based on the permutation approach and it is preferable to the classic parametric approach because it is distribution-free and powerful regardless of the underlying data distribution.
2. The 3D NAND Flash Endurance Reliability Case Study
2.1. Experimental Setup and Measurement Protocol
The modeling activities in this work are based on the endurance reliability electrical characterization results performed on commercial 3D NAND flash devices integrated with the triple level cell (TLC) storage paradigm. The considered technology is a sub-100 layers (≥72) generation considering the block device structure and the distribution coding using all the TLC pages [32] (i.e., the lower page is the lower significant bit—LSB, the middle page is the central significant bit—CSB, and the upper page is the most significant bit—MSB), as described in Figure 1. The electrical measurements required to characterize the memory devices were performed using custom-developed automated test equipment (ATE), allowing the topological extraction of the FBC after a read operation for every single location of a memory block (see Figure 2). The system is constituted by a laptop that controls the test flow running on a field programmable gate array (FPGA) device using a custom software interface that sets the proper voltages to drive the 3D NAND flash under test (i.e., chip power supply and to supply the bus interface for memory data I/O and commands), and the chip temperature with a heater/cooler element. Both and are taken as the typical values provided by the memory vendor in the datasheet. The connection between the tester unit, supplied with 12–48 V, and the laptop is achieved via an Ethernet 1Gbps link.
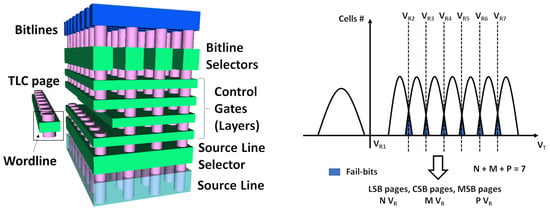
Figure 1.
TLC 3D-NAND Flash architecture considered in this work (left) and definition of fail bits according to their distribution coding (right). Reprinted from [32] under Creative Commons License (CC BY 4.0).

Figure 2.
A Schematic of the ATE used in this work for the electrical characterization of the 3D NAND flash endurance (top). Cycling protocol used for extracting the FBC at defined readout steps until reaching EoL (bottom).
The characterization of the 3D NAND flash lifetime concerning the achievable endurance must follow the JEDEC standards provided in [33,34]. In particular, the memory device needs to be exercised with consecutive program/erase (P/E) operations in 500 h at a 70 C temperature until the rated endurance by the vendor, also called the end-of-life (EoL), is reached. Samples were programmed with a random pattern. All the endurance characterizations were performed on two different and independent memory blocks and multiple dies of the same 3D NAND flash test chip ensuring inclusion of manufacturing variability (although not considering the lot-to-lot one) in the results. The experiment protocol is summarized in Figure 2.
Figure 3 shows the results of an endurance characterization performed on a 3D NAND flash block up to EoL. In the plot, we report the FBC per TLC memory page as a function of the achieved operations. As expected from previous studies [35,36,37], the number of errors is page-dependent and grows as a function of the memory wear status. The average trend in the errors is fitted with the following exponential law:
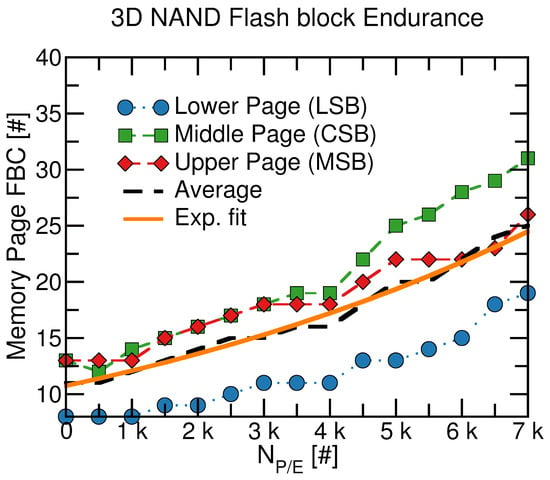
Figure 3.
FBC extracted during an endurance stress-test in different 3D NAND flash memory TLC pages as a function of the lifetime (). The average behavior between pages has been reported as a guideline for general reliability considerations.
Our modeling attempts target a fresh device ( = 0) and the EoL point as the most critical situation for memory reliability, although the methodology described in the following sections of the work can be applied without lack of generality to every .
2.2. Data and Model
The dataset employed was reduced from the original endurance characterization dataset retrieved from 3D NAND flash measurements. The new dataset used for modeling purposes consisted of 144 rows and 16 columns (variables). The variable denominated sum-Errors is the model output and represents the FBC retrieved for each measured TLC-page in a memory block. A TLC-page consists of a 16 kB data readout plus the parity size used for ECC purposes. Since our experimental setup allows measuring 4 kB chunks (i.e., Layer), we measured the FBC per layer and summed them to calculate the FBC per page. The variable Block is an identifier of the tested 3D NAND flash block. Further, the variable Page was split into 12 clusters (one for each 32), and then 11 dummy variables were created based on the clusters. These clusters represent homogeneous topological areas of a memory block and were identified according to the device structure. The variable TLC-Page indicates whether the read page in a block is associated with the LSB, CSB, or MSB. Finally, the variable PE-cycles represents the endurance lifetime points where the FBC of the 3D NAND flash block was characterized (i.e., fresh device or at EoL).
In this list, we report the variables of the model that consider both physical, topological, and logical features of the 3D NAND flash devices tested in this work:
- sum-Errors, the dependent variable which represents the sum of the number of errors in Layer 0, 1, 2, 3 and for each TLC-Page;
- d-block, dummy explanatory variable which is 1 for block A and 0 for block B;
- d-page-c2, dummy explanatory variable which is 1 for cluster 2 of Page and 0 for all the other clusters in the measured block;
- d-page-c3, dummy explanatory variable which is 1 for cluster 3 of Page and 0 for all the other clusters in the measured block;
- d-page-c4, dummy explanatory variable which is 1 for cluster 4 of Page and 0 for all the other clusters in the measured block;
- d-page-c5, dummy explanatory variable which is 1 for cluster 5 of Page and 0 for all the other clusters in the measured block;
- d-page-c6, dummy explanatory variable which is 1 for cluster 6 of Page and 0 for all the other clusters in the measured block;
- d-page-c7, dummy explanatory variable which is 1 for cluster 7 of Page and 0 for all the other clusters in the measured block;
- d-page-c8, dummy explanatory variable which is 1 for cluster 8 of Page and 0 for all the other clusters in the measured block;
- d-page-c9, dummy explanatory variable which is 1 for cluster 9 of Page and 0 for all the other clusters in the measured block;
- d-page-c10, dummy explanatory variable which is 1 for cluster 10 of Page and 0 for all the other clusters in the measured block;
- d-page-c11, dummy explanatory variable which is 1 for cluster 11 of Page and 0 for all the other clusters in the measured block;
- d-page-c12, dummy explanatory variable which is 1 for cluster 12 of Page and 0 for all the other clusters in the measured block;
- d-tlcpage-1, dummy explanatory variable which is 1 if the read Page is associated with Middle Page (CSB) and 0 otherwise;
- d-tlcpage-2, dummy explanatory variable which is 1 if the read Page is associated with Upper Page (MSB) and 0 otherwise;
- PE-cycles, dummy explanatory variable representing the memory lifetime which is 1 for PE-cycles = EoL and 0 for PE-cycles = 0 (fresh device).
From a descriptive point of view, the main effect plots of the explanatory variables are represented in Figure 4. The typical block-to-block, page-to-page, and TLC page error variability are expected as already confirmed in previous literature reports [35].

Figure 4.
Main effect plots of the explanatory variables.
The univariate linear model, with k explanatory variables, can be represented as follows:
where is the random variable from which the i-th observed value of the response was generated, are the regression coefficients, is the i-th observed value of the u-th explanatory variable, and the random variable is the i-th error term, with . In classical regression analysis, the error terms should be uncorrelated normal random variables with zero mean and constant variance. The milder assumption of exchangeability of the error terms under is the only condition required for inferential intents, instead of normality and uncorrelation of errors [38,39]. A permutation test on the significance of all regression coefficients, that have been taken into account together, can be carried out if the exchangeability assumption is met. Since, in the null hypothesis, all the regression coefficients are equal to zero, and the model includes only the intercept , exchangeability holds. As a consequence, the null permutation distribution of the test statistics can be obtained by permuting the rows of the matrix of the explanatory variables and keeping fixed the vector of the observed values of the response.
It should be emphasized that the presence of a large number of predictors, especially dummy variables, implies a high risk of multicollinearity. Hence, a preliminary analysis based on the variance inflation factor (VIF), to detect and eliminate explanatory variables involved in collinearity problems (VIF > 5), is necessary [40].
2.3. Hypotheses
As mentioned above, we want to test the significance of all regression coefficients, jointly taken into account. Therefore, the null hypothesis that the dependent variable is not affected by any explanatory variable is tested against the alternative hypothesis that at least one explanatory variable has an effect on the response. In terms of regression coefficients, the hypothesis to be tested is given below:
Therefore, the test problem can be considered to be a multiple test, where the partial tests are the single tests on the significance of the estimates of the coefficients. is the null hypothesis of the partial test on the coefficient linked to the j-th independent variable and is the alternative hypothesis of the partial test. Therefore, the null and alternative hypotheses of the overall problem can be represented as follows:
where the intersection means that all the partial null hypotheses are true under , and the union indicates that, under , at least one partial alternative hypothesis is true.
3. Nonparametric Inference on the Regression Model
A suitable methodological solution to this problem is represented by the combined permutation test (CPT). To deal with the overall problem, we combine the p-values of the k partial permutation tests, according to the CPT methodology. The absolute value of the least squares estimator of the regression coefficient is an appropriate test statistic for the partial test concerning the single regression coefficient. In other words, formally speaking, the j-th partial permutation test statistic, suitable for testing versus , is . We assume that the null (partial and overall) hypotheses are rejected for large values of the test statistics, without losing generality. Furthermore, an appropriate combination of the p-values can be obtained by applying the Fisher combining function as follows:
where is the p-value of the j-th partial test.
The control of the family-wise error (FWE) is required when the null hypothesis is rejected [41], especially with the goal of attributing the overall significance to specific partial tests (i.e., to specific explanatory variables). To put it another way, we have to adjust the partial p-values so that there is no inflation of the type I error in the global test. For this purpose, the Bonferroni–Holm rule is a suitable method that controls the FWE, but is less conservative than the classic Bonferroni approach or other methods. Original R scripts created by the authors were used for the implementation of the methodology.
4. Results and Discussion
The VIFs of all the independent variables are shown in Table 1; all the values are less than 5, indicating no multicollinearity problem.

Table 1.
Variance inflation factors of the explanatory variables.
The significance level was set equal to 0.10 and we applied the CPT illustrated above to the data in order to test the hypotheses defined in Equation (4). The global p-value of the test is equal to , which indicates significance at the level . The adjusted partial p-values on the significance of the coefficient estimates with the Bonferroni–Holm correction are shown in Table 2.

Table 2.
Estimation of the coefficients, partial p-values on the significance of the coefficients estimates, non-adjusted and adjusted with the Bonferroni–Holm method (significance in bold).
Looking at the adjusted p-values, the significance of the overall test can be limited to a few of the regression coefficients. In particular, it appears that the sum of the number of errors in Layers 0, 1, 2, and 3 is strongly affected by the variables d-page-c6, d-page-c12, d-tlcpage-2, and PE-cycles. A moderate effect on the dependent variable is seen with d-page-c9, d-page-c10, and d-page-c11. Finally, we found a weak significance of d-page-c5 on the sum of the number of errors. From an experimental standpoint, we were expecting to identify the PE-cycles variable as one of the most significant in affecting the response variable of the model, given the experimental results of the endurance characterization provided in Figure 3. In addition, this finding is consistent with the expectation from the 3D NAND flash endurance test standards [33,34]. Concerning the variable d-tlcpage-2, we were also expecting that most of the endurance failures would come from TLC pages associated with the CSB or MSB, as demonstrated in the experimental results section of this work. Regarding the dependency of the response variable on the topological position, we would like to refer to the work reported in [37], where it is shown that some 3D NAND flash memory blocks have some specific locations (due to manufacturing variability) that are more sensitive in the generation of corrupted bits (i.e., errors).
Furthermore, the condition of normality of the model errors, typical of the classical parametric approach to regression analysis, is not satisfied. The normal probability plots that confirm this statement are shown in Figure 5, graphs (a) and (b). In accordance with the analysis of the residuals, marginal error distributions may be asymmetric (see graphs (c) and (d)).
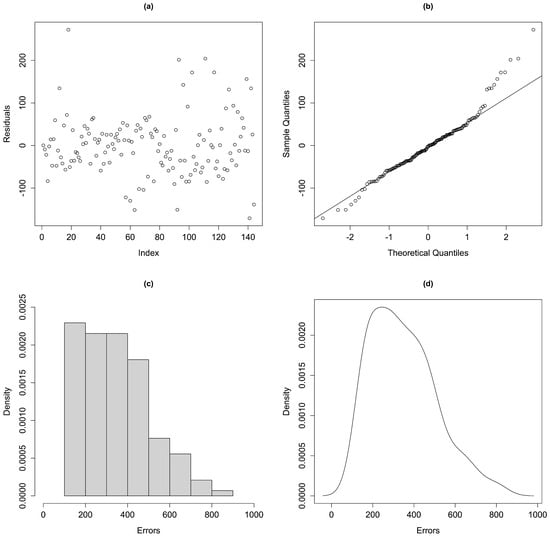
Figure 5.
Diagnostic analysis of residuals. (a) Plot of the residuals. (b) Normal Q-Q plot of the residuals. (c) Histogram of the residuals’ distribution. (d) Estimated probability density distribution of the residuals.
These results support the belief in the benefit of embracing a nonparametric approach, which does not require the assumption that the underlying distribution follows a certain family of probability laws, such as Weibull or others typically used in parametric approaches. Hence, this test, unlike its parametric competitors, is powerful regardless of the underlying probability distribution. Furthermore, the use of CPT allows us to test the validity of the model and to determine which explanatory variables affect the number of errors.
5. Conclusions
In this work, we have presented a non-parametric modeling approach related to the errors retrieved after endurance stress in 3D NAND flash memories for solid-state storage. The electrical characterization of different memory blocks and pages tested according to the JEDEC guidelines has provided an FBC feature that can be well-modeled using an OLS regression on the model coefficient. This is proved by the significance of the CPT test applied to the data described in Section 2. The proposed approach is suitable every time there is not sufficient room for an a priori assumption of the statistical distribution to be considered in the discussion of errors feature and, therefore, can be a valuable asset in understanding the factors affecting the reliability of a particular technology, such as the 3D NAND flash. We have demonstrated that we can capture the effect of the topology (memory location in a block), the logical coding of the TLC pages, and the wear (P/E cycles) on the errors produced during the endurance stress.
This work creates the potential for usage of non-parametric modeling tools for 3D NAND flash, even extending toward different working corners of the technology (e.g., during read disturb and temperature issues), or radically addressing storage technologies based on 3D NAND flash, such as solid-state drives or embedded multimedia cards. Future work will also be dedicated to a comparison of state-of-the-art modeling approaches with respect to the one proposed here.
Author Contributions
Conceptualization, M.B., C.Z., R.M. and S.B.; methodology, S.B. and M.B.; software, S.B. and M.B.; validation, M.B., C.Z., R.M. and S.B.; formal analysis, S.B. and M.B.; investigation, C.Z. and R.M.; resources, C.Z. and R.M.; data curation, C.Z. and R.M.; writing—original draft preparation, M.B., C.Z., R.M. and S.B.; writing—review and editing, M.B., C.Z., R.M. and S.B.; visualization, M.B., C.Z., R.M. and S.B.; supervision, M.B., C.Z., R.M. and S.B.; project administration, M.B., C.Z., R.M. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to industrial restriction policies from Avaneidi srl.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SSD | Solid-State Drive |
| BER | Bit Error Rate |
| FBC | Fail Bits Count |
| OLS | Ordinary Least Squares |
| ANOVA | Univariate Analysis of Variance |
| VIF | Variance Inflation Factor |
References
- Dawson, D. The Future of Data Storage. 2022. Available online: https://circleid.com/posts/20220107-the-future-of-data-storage (accessed on 8 August 2023).
- Rydning, J.; Reinsel, D. Worldwide Global StorageSphere Forecast, 2021–2025: To Save or Not to Save Data, That Is the Question. Technical Report IDC Doc #US47509621, IDC Corp. 2021. Available online: https://www.marketresearch.com/IDC-v2477/Worldwide-Global-StorageSphere-Forecast-Save-14315473/ (accessed on 20 August 2023).
- Dang, S.; Han, R. An In-Network Cooperative Storage Schema Based on Neighbor Offloading in a Programmable Data Plane. Future Internet 2022, 14, 18. [Google Scholar] [CrossRef]
- Bayati, M.; Bhimani, J.; Lee, R.; Mi, N. Exploring Benefits of NVMe SSDs for BigData Processing in Enterprise Data Centers. In Proceedings of the 2019 5th International Conference on Big Data Computing and Communications (BIGCOM), Qingdao, China, 9–11 August 2019; pp. 98–106. [Google Scholar] [CrossRef]
- Goda, A. Recent Progress on 3D NAND Flash Technologies. Electronics 2021, 10, 3156. [Google Scholar] [CrossRef]
- Mielke, N.R.; Frickey, R.E.; Kalastirsky, I.; Quan, M.; Ustinov, D.; Vasudevan, V.J. Reliability of Solid-State Drives Based on NAND Flash Memory. Proc. IEEE 2017, 105, 1725–1750. [Google Scholar] [CrossRef]
- Zuolo, L.; Zambelli, C.; Micheloni, R.; Olivo, P. Solid-State Drives: Memory Driven Design Methodologies for Optimal Performance. Proc. IEEE 2017, 105, 1589–1608. [Google Scholar] [CrossRef]
- Zhang, T. Using LDPC Codes in SSD — Challenges and Solutions. In Proceedings of the Flash Memory Summit, Santa Clara, CA, USA, 21–23 August 2012. [Google Scholar]
- Li, Y.; Lee, P.P.; Lui, J.C. Analysis of Reliability Dynamics of SSD RAID. IEEE Trans. Comput. 2016, 65, 1131–1144. [Google Scholar] [CrossRef]
- Peleato, B.; Agarwal, R. Maximizing MLC NAND lifetime and reliability in the presence of write noise. In Proceedings of the 2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 3752–3756. [Google Scholar] [CrossRef]
- Moon, J.; No, J.; Lee, S.; Kim, S.; Choi, S.; Song, Y. Statistical Characterization of Noise and Interference in NAND Flash Memory. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 2153–2164. [Google Scholar] [CrossRef]
- Lee, D.h.; Sung, W. Decision Directed Estimation of Threshold Voltage Distribution in NAND Flash Memory. IEEE Trans. Signal Process. 2014, 62, 919–927. [Google Scholar] [CrossRef]
- Fitzgerald, B.; Hogan, D.; Ryan, C.; Sullivan, J. Endurance prediction and error Reduction in NAND flash using machine learning. In Proceedings of the 2017 17th Non-Volatile Memory Technology Symposium (NVMTS), Aachen, Germany, 30 August–1 September 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, W.; Wu, F.; Zhou, J.; Zhang, M.; Yang, C.; Lu, Z.; Wang, Y.; Xie, C. Modeling of Threshold Voltage Distribution in 3D NAND Flash Memory. In Proceedings of the 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 1–5 February 2021; pp. 1729–1732. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Chen, Z.; Pan, Y.; Lu, Z.; Liu, Z. An SVM-Based NAND Flash Endurance Prediction Method. Micromachines 2021, 12, 746. [Google Scholar] [CrossRef] [PubMed]
- Santikellur, P.; Buddhanoy, M.; Sakib, S.; Ray, B.; Chakraborty, R.S. A shared page-aware machine learning assisted method for predicting and improving multi-level cell NAND flash memory life expectancy. Microelectron. Reliab. 2023, 140, 114867. [Google Scholar] [CrossRef]
- Monzio Compagnoni, C.; Ghidotti, M.; Lacaita, A.L.; Spinelli, A.S.; Visconti, A. Random Telegraph Noise Effect on the Programmed Threshold-Voltage Distribution of Flash Memories. IEEE Electron Device Lett. 2009, 30, 984–986. [Google Scholar] [CrossRef]
- Cai, Y.; Haratsch, E.F.; Mutlu, O.; Mai, K. Threshold voltage distribution in MLC NAND flash memory: Characterization, analysis, and modeling. In Proceedings of the 2013 Design, Automation and Test in Europe Conference and Exhibition (DATE), Grenoble, France, 18–22 March 2013; pp. 1285–1290. [Google Scholar] [CrossRef]
- Parnell, T.; Papandreou, N.; Mittelholzer, T.; Pozidis, H. Modelling of the threshold voltage distributions of sub-20nm NAND flash memory. In Proceedings of the IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2351–2356. [Google Scholar] [CrossRef]
- Li, H. Modeling of Threshold Voltage Distribution in NAND Flash Memory: A Monte Carlo Method. IEEE Trans. Electron Devices 2016, 63, 3527–3532. [Google Scholar] [CrossRef]
- Wang, K.; Du, G.; Lun, Z.; Chen, W.; Liu, X. Modeling of program Vth distribution for 3-D TLC NAND flash memory. Sci. China Inf. Sci. 2019, 62, 42401. [Google Scholar] [CrossRef]
- Mielke, N.; Marquart, T.; Wu, N.; Kessenich, J.; Belgal, H.; Schares, E.; Trivedi, F.; Goodness, E.; Nevill, L.R. Bit error rate in NAND Flash memories. In Proceedings of the 2008 IEEE International Reliability Physics Symposium, Phoenix, AZ, USA, 27 April–1 May 2008; pp. 9–19. [Google Scholar] [CrossRef]
- Wang, N.J.; Lee, K.Y.; Lin, H.Y.; Hsiao, W.H.; Lee, M.Y.; Kuo, L.K.; Lin, D.J.; Chao, Y.H.; Lu, C.Y. Statistical Analysis of Bit-Errors Distribution for Reliability of 3-D NAND Flash Memories. In Proceedings of the 2020 IEEE International Reliability Physics Symposium (IRPS), Dallas, TX, USA, 28 April–30 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Zambelli, C.; Crippa, L.; Micheloni, R.; Olivo, P. Investigating 3D NAND Flash Read Disturb Reliability With Extreme Value Analysis. IEEE Trans. Device Mater. Reliab. 2021, 21, 486–493. [Google Scholar] [CrossRef]
- Nakamura, T.; Deguchi, Y.; Takeuchi, K. Adaptive Artificial Neural Network-Coupled LDPC ECC as Universal Solution for 3-D and 2-D, Charge-Trap and Floating-Gate NAND Flash Memories. IEEE J. Solid-State Circuits 2019, 54, 745–754. [Google Scholar] [CrossRef]
- Abe, M.; Matsui, C.; Mizushina, K.; Suzuki, S.; Takeuchi, K. Computational Approximate Storage with Neural Network-based Error Patrol of 3D-TLC NAND Flash Memory for Machine Learning Applications. In Proceedings of the 2020 IEEE International Memory Workshop (IMW), Dresden, Germany, 17–20 May 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Mei, Z.; Cai, K.; He, X. Deep Learning-Aided Dynamic Read Thresholds Design for Multi-Level-Cell Flash Memories. IEEE Trans. Commun. 2020, 68, 2850–2862. [Google Scholar] [CrossRef]
- Khodadadian, A.; Parvizi, M.; Teshnehlab, M.; Heitzinger, C. Rational Design of Field-Effect Sensors Using Partial Differential Equations, Bayesian Inversion, and Artificial Neural Networks. Sensors 2022, 22, 4785. [Google Scholar] [CrossRef] [PubMed]
- Marquart, T.A. Solid-State-Drive qualification and reliability strategy. In Proceedings of the 2015 IEEE International Integrated Reliability Workshop (IIRW), South Lake Tahoe, CA, USA, 11–15 October 2015; pp. 3–6. [Google Scholar] [CrossRef]
- Pesarin, F. Nonparametric Combination Methodology. In Multivariate Permutation Tests with Applications in Biostatistics, 2nd ed.; Wiley: Chichester, UK, 2001. [Google Scholar]
- Harrar, S.W.; Bathke, A.C. A non-parametric version of the Bartlett-Nanda-Pillai multivariate test. Asymptotics, approximations, and applications. Am. J. Math. Manag. Sci. 2008, 28, 309–335. [Google Scholar]
- Zambelli, C.; Micheloni, R.; Scommegna, S.; Olivo, P. First Evidence of Temporary Read Errors in TLC 3D-NAND Flash Memories Exiting From an Idle State. IEEE J. Electron Devices Soc. 2020, 8, 99–104. [Google Scholar] [CrossRef]
- JESD22-A117E; Electrically Erasable Programmable ROM (EEPROM) Program/Erase Endurance and Data Retention Stress Test. JEDEC: Arlington, VA, USA, 2018.
- JESD47L; Stress-Test-Driven Qualification of Integrated Circuits. JEDEC: Arlington, VA, USA, 2022.
- Papandreou, N.; Pozidis, H.; Parnell, T.; Ioannou, N.; Pletka, R.; Tomic, S.; Breen, P.; Tressler, G.; Fry, A.; Fisher, T. Characterization and Analysis of Bit Errors in 3D TLC NAND Flash Memory. In Proceedings of the 2019 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 31 March–4 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, M.; Guo, Y.; Chen, F.; Chen, B.; Zhan, X.; Wu, J.; Wu, F.; Chen, J. Work-in-Progress: High-Precision Short-Term Lifetime Prediction in TLC 3D NAND Flash Memory as Hot-data Storage. In Proceedings of the 2022 International Conference on Compilers, Architecture, and Synthesis for Embedded Systems (CASES), Shanghai, China, 7–14 October 2022; pp. 11–12. [Google Scholar] [CrossRef]
- Raquibuzzaman, M.; Hasan, M.M.; Milenkovic, A.; Ray, B. Layer-to-Layer Endurance Variation of 3D NAND Flash Memory. In Proceedings of the 2022 IEEE International Reliability Physics Symposium (IRPS), Dallas, TX, USA, 27–31 March 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Bonnini, S.; Corain, L.; Marozzi, M.; Salmaso, L. Nonparametric Hypothesis Testing, Rank and Permutation Methods with Applications in R; Wiley: Hoboken, NY, USA, 2014. [Google Scholar]
- Pesarin, F.; Salmaso, L. Permutation Tests for Complex Data: Theory, Applications and Software; Wiley: Hoboken, NY, USA, 2010. [Google Scholar]
- Shrestha, N. Detecting multicollinearity in regression analysis. Am. J. Appl. Math. Stat. 2020, 8, 39–42. [Google Scholar] [CrossRef]
- Westfall, P.H.; Young, S. Resampling-Based Multiple Testing: Examples and Methods for p-Value Adjustment; Wiley-Interscience: New York, NY, USA, 1992. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).