Ant Colony Optimization Task Scheduling Algorithm for SWIM Based on Load Balancing

Abstract

This paper focuses on the load imbalance problem in System Wide Information Management (SWIM) task scheduling. In order to meet the quality requirements of users for task completion, we studied large-scale network information system task scheduling methods. Combined with the traditional ant colony optimization (ACO) algorithm, using the hardware performance quality index and load standard deviation function of SWIM resource nodes to update the pheromone, a SWIM ant colony task scheduling algorithm based on load balancing (ACTS-LB) is presented in this paper. The experimental simulation results show that the ACTS-LB algorithm performance is better than the traditional min-min algorithm, ACO algorithm and particle swarm optimization (PSO) algorithm. It not only reduces the task execution time and improves the utilization of system resources, but also can maintain SWIM in a more load balanced state.

1. Introduction

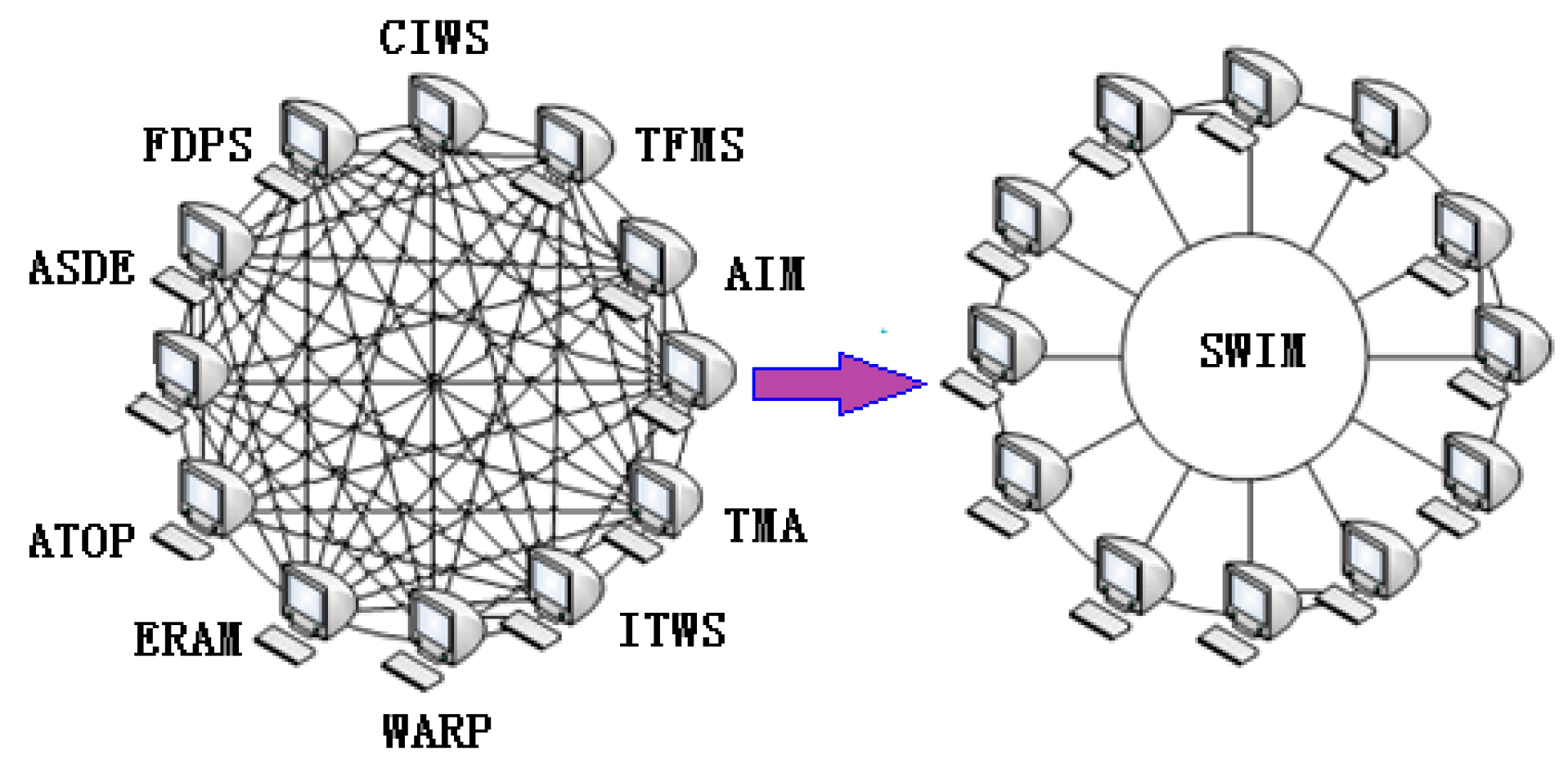
In 1997, EUROCONTROL proposed the System Wide Information Management (SWIM) concept to the Federal Aviation Administration [1]. The International Civil Aviation Organization accepted this concept in 2002 [2]. The System Wide Information Management is a large-scale network system with high integration, which integrates and manages internal resources. SWIM, as an information sharing platform, provides a unified data transmission and exchange mechanism for different subsystems of civil aviation businesses. In order to achieve interoperability and consistency among the relevant units of civil aviation, as well as reduce the difficulty of integrated dispatching, this system enables data to be processed and integrated among independent systems. The basic idea of SWIM is to allow all air traffic participants, such as airports, air traffic control, airlines and other related civil aviation units, to share and exchange the latest information. Moreover, it ensures that information can be shared safely, effectively and in a timely manner. Thus, for accurate and timely cooperative decision-making, SWIM can greatly improve the predictability and effectiveness of decisions and meet the needs of civil aviation in terms of efficient and coordinated operation. The comparison of the traditional civil aviation mesh communication network and the SWIM bus communication structure is shown in Figure 1 [3].

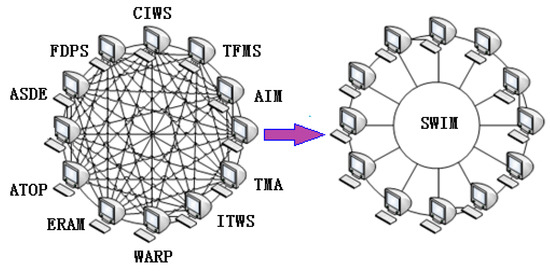
Figure 1. Traditional mesh communication structure (left) and System Wide Information Management (SWIM) bus communication structure (right) comparison chart.

In order to improve SWIM resource utilization and sharing rate, it is necessary to solve the problem of system task scheduling. Because of the distribution, heterogeneity and autonomy of resources in a SWIM environment, SWIM task scheduling is more complex and difficult. As an algorithm for solving combinatorial optimization problems, the ant colony algorithm has the characteristics of parallelism and strong robustness. It can quickly obtain high-quality solutions and is very suitable for solving SWIM task scheduling problems.

Although the existing improved ant colony algorithm can improve the efficiency of task scheduling, it does not significantly improve the system load imbalance. This paper summarizes the existing network task scheduling technology in combination with SWIM’s own characteristics, on the basis of the classical ant colony algorithm, focusing on solving the problem of unbalanced resource load of service nodes in task scheduling. According to the hardware performance and load situation of service node update pheromones, the SWIM ant colony task scheduling algorithm based on load balancing (ACTS-LB) is proposed. This ACTS-LB algorithm can reduce task execution time and improve system load balancing, thus ensuring that the user’s task scheduling needs can be met as much as possible.

The remainder of the paper is structured as follows. We give some related works in Section 2. We introduce SWIM load balancing requirements and related definitions in Section 3. Section 4 presents the details of the ACTS-LB algorithm. We give the simulation results and analysis in Section 5 and conclude this paper in Section 6.

2. Related Work

At present, experts and scholars both at home and abroad have conducted much research on task scheduling in large-scale network systems, such as cloud computing, grid and other network systems. Among them, the min-min algorithm, max-min algorithm and other task scheduling algorithms are the early classic methods. There are also exact algorithms to solve the task scheduling problems, such as branch-and-bound algorithms, linear programming and cross-entropy methods. The heuristic algorithms were used to solve optimization problems, such as genetic algorithm (GA), simulated annealing (SA), ant colony (AC) algorithm, particle swarm optimization (PSO) and greedy algorithm. These algorithms have different characteristics, which are based on the idea of optimizing minimizing scheduling objectives. They have been applied in the task scheduling of these network systems and have become the reference object for subsequent research on scheduling algorithms.

In [4], the authors proposed a new approach for solving the shift minimization personnel task scheduling problem. These properties are used to develop a new branch and bound scheme, which is used in conjunction with two column generation based approaches and a heuristic algorithm to create an efficient solution procedure. In [5], the authors presented a novel distributed implementation of multiple hypothesis tracking (MHT). Based on hash-tree distributed content storing approach to enable fast operations on local trees and also allow sharing of hypotheses between local and remote nodes. In [6], the authors proposed a general algorithm for fast estimation of probability of error of linear block codes on BSC channels based on the importance sampling and the cross-entropy method for rare-events that can be employed for any hard-decision decoder. When optimal decoding is used the algorithm reduces to a single simulation run that can estimate, with a given accuracy, performances for a whole range of sufficiently high signal-to-noise ratios. In [7], a multi-objective task scheduling algorithm was proposed based on the fusion of a genetic algorithm and a particle swarm algorithm to improve the global search ability and convergence speed. In [8], this paper introduced an optimized algorithm for task scheduling based on genetic simulated annealing algorithm in cloud computing and its implementation. Algorithm considers the QoS requirements of different type tasks, the QoS parameters are dealt with dimensionless. In addition, a hybrid algorithm based on ant colony optimization (ACO) and Cuckoo was used to reduce task execution time, as proposed by RG Babukarthik [9]. In [10], the authors proposed a new heuristic algorithm combined with the particle swarm optimization (PSO) algorithm. It has the characteristics of strong optimization search ability, fast convergence speed and high solving quality, providing a new direction for solving task scheduling problems in a cloud computing environment. In [11], the authors comprehensively considered the characteristics of tasks and virtual machine resources in the cloud environment and proposed a task scheduling strategy that improves the greedy algorithm to improve the overall scheduling efficiency of the system in the cloud computing environment. These algorithms have good performance in processing task scheduling, but they seldom confer benefits from the perspective of system load balancing.

In the research of task scheduling algorithms aimed at load balancing, Arul Xavier and others proposed a cloud computing load balancing task aware scheduling algorithm for the task scheduling problems in various heterogeneous virtual machines [12]. In [13], by analyzing and comparing some cluster load balancing algorithms, a task load balancing scheduling algorithm based on ant colony optimization (WLB-ACO) was proposed. The algorithm task completion efficiency is good, but the task scheduling quality is difficult to guarantee. In [14], the authors presented a particle swarm optimization with the random forest classifier algorithm, which is used to solve the load balancing problem of virtual machines. In order to balance the utilization of virtual machine resources, the total task working time on a virtual machine is taken as the optimization objective. However, this method relies too much on intermediate nodes. In [15], a cloud computing resource scheduling method based on a parallel genetic algorithm was proposed. This method can reduce the overall execution time of scheduling tasks to a certain extent, but it easily falls into local solutions. In [16], the authors introduced the concept of virtual machine relative fitness according to the performance of virtual machine resources in a cloud environment, which makes it possible for virtual machine resources with a high virtual machine relative fitness to obtain greater variation and can thus speed up the convergence of the algorithm. The comparison of the related work references are shown in Table 1.

Table 1. The comparison of the relevant work references.

Serial Number	Reference Number	Author	Algorithm Name	Advantages	Disadvantages
1	[4]	Baatar, D	Proposed a new approach for solving the shift minimization personnel task scheduling problem.	Create an efficient solution procedure.	Do not confer benefits from the perspective of system load balancing.
2	[5]	Domenico C	Presented a novel distributed implementation of Multiple Hypothesis Tracking (MHT).	Can enable fast operations on local trees and also allow sharing of hypotheses between local and remote nodes.	Do not confer benefits from the perspective of system load balancing.
3	[6]	Romano, G	Proposed a general algorithm for fast estimation of probability.	Can reduce to a single simulation run that can estimate.	Do not confer benefits from the perspective of system load balancing.
4	[7]	Liu, C.	Presented a multi-objective task scheduling algorithm based on the fusion of a genetic algorithm and a particle swarm algorithm.	It can improve the global search ability and convergence speed.	Do not confer benefits from the perspective of system load balancing.
5	[8]	Guoning, G	Presented an optimized algorithm for task scheduling based on genetic simulated annealing algorithm in cloud computing and its implementation.	Algorithm considers the QoS requirements of different type tasks.	Do not confer benefits from the perspective of system load balancing.
6	[9]	Babukarthik, R.G.	Proposed a hybrid algorithm based on ant colony optimization (ACO) and Cuckoo.	It was used to reduce task execution time.	Do not confer benefits from the perspective of system load balancing.
7	[10]	Tong, Z.	Proposed a new heuristic algorithm combined with the particle swarm optimization (PSO) algorithm	It has the characteristics of strong optimization search ability, fast convergence speed.	Do not confer benefits from the perspective of system load balancing.
8	[11]	Wang, X.	Proposed a task scheduling strategy that improves the greedy algorithm.	It can improve the overall scheduling efficiency.	Do not confer benefits from the perspective of system load balancing.
9	[12]	V. M, Arul Xavier.	Proposed an algorithm for the task scheduling problems in various heterogeneous virtual machines.	In the research of task scheduling algorithms aimed at load balancing.	The task scheduling is not efficient.
10	[13]	Zhao, M.	Proposed a task load balancing scheduling algorithm based on ant colony optimization (WLB-ACO).	The algorithm task completion efficiency is good.	The task scheduling quality is difficult to guarantee.
11	[14]	Jiang, W.	Presented a particle swarm optimization with the random forest classifier algorithm.	In order to balance the utilization of virtual machine resources.	This method relies too much on intermediate nodes.
12	[15]	Chen, J.	Presented a resource scheduling method based on a parallel genetic algorithm.	It can reduce the overall execution time of scheduling tasks to a certain extent.	It easily falls into local solutions.
13	[16]	Ren, J.	Introduced the concept of virtual machine relative fitness.	It can obtain greater variation.	It speeds up the convergence of the algorithm.

On the basis of the existing research results, this paper analyzes and refers to a large number of network task scheduling algorithms in distributed and heterogeneous environments. Combined with the characteristics of SWIM, the adopted ant colony algorithm is improved. We propose a SWIM ant colony task scheduling algorithm based on load balancing (ACTS-LB). The simulation experiment results show that the performance of the ACTS-LB algorithm is better than that of the traditional min-min algorithm, ACO algorithm and PSO algorithm. The specific contributions of this study are as follows:

(1) The ACTS-LB algorithm reduces the task scheduling completion time and improves SWIM resource utilization;

(2) It can ensure that SWIM has better load balancing performance;

(3) It is of great significance to promote the SWIM application for civil aviation industry development.

3. SWIM Load Balancing Requirements and Related Definitions

3.1. SWIM Load Balancing Requirements

SWIM is a large-scale network system with high integration, which integrates and manages internal resources. In order to improve the utilization rate of system information and the sharing rate of resources, it is necessary to solve the problem of system task scheduling load balancing and find suitable nodes to deal with user needs. This makes SWIM load balancing and task scheduling more complicated and difficult. The selection of a resource node with a smaller load to complete user requirements is a very challenging task.

The SWIM infrastructure has a huge amount of computing and storage resources. Existing and future civil aviation applications require these resources to have the ability to perform large-scale, real-time interactions. This can result in a huge load on the data center, and it is easy to produce load imbalance. Different from load balancing in small database systems, SWIM—as a large-scale data center network—needs to respond to a high throughput of concurrent requests. Resource task scheduling and allocation become key, which puts forward higher requirements for load balancing methods [17].

(1) Large-scale information network systems have a huge amount of data resources, so a traditional load balancer cannot meet the application requirements. It is necessary to design a new load balancing method.

(2) Although the complex load balancing algorithm can achieve a good balancing effect, it occupies too much of the system’s own resources. Especially in the case of a large number of system resource nodes, there will be risks of algorithm dead-cycle or paralysis. Therefore, it is also necessary to design a lightweight load balancing algorithm that can achieve a good load balancing effect and has low algorithm complexity.

(3) The load balancing method must work under conditions of a large amount of data, in the form of concurrent requests, as well as satisfy the requirement of reasonable load allocation in the case of resource competition.

3.2. Relevant Definitions

(1) System total resource set $S=\{s_1,s_2\cdots s_j\cdots s_m\}$, where the system consists of m resource nodes and $s_j$ is the system resource nodes;

(2) System total scheduling task $T=\{t_1,t_2\cdots t_i\cdots t_n\}$, including n scheduled tasks, where $t_i$ is the system scheduling tasks;

(3) Expected time to compute (ETC), $ETC=\left\{\begin{array}{l}e{t}_{11}\cdots e{t}_{1m}\\ ⋮\cdots e{t}_{ij}\cdots ⋮\\ e{t}_{n1}\cdots e{t}_{nm}\end{array}\right\}$, where $e{t}_{ij}$ is the expected completion time of scheduling task $t_i$ on resource node $s_j$;

(4) $Tabu$ is the search table.

The mathematical symbols in the formula of this paper are shown in Table 2.

Table 2. The mathematical symbols notations.

Serial Number	Symbol	Notation
1	$P_{ij}^k(t)$	The transition probability value
2	${\tau }_{ij}(t)$	The pheromone value
3	${\eta }_{ij}(t)$	The heuristic function
4	$\alpha$	The information heuristic factor
5	$\beta$	The expect heuristic factor
6	$Mip(s_j)$	The computing power
7	$Bandwidth(s_j)$	The communication bandwidth
8	$Performance(s_j)$	The hardware performance
9	$L{B}_j$	The load balancing value
10	$C(s_j)$	The CPU utilization rate
11	$M(s_j)$	The memory usage
12	$B(s_j)$	The bandwidth occupancy
13	$LA$	The average value of the load
14	$LS$	The load standard deviation
15	$\mu$	The information residual factor
16	$\Delta {\tau }_{ij}$	The pheromone increment value

4. Ant Colony Optimization Algorithm Based on Load Balancing

4.1. Ant Colony Optimization Algorithm Analysis

Marco Dorigo first proposed an ant colony optimization algorithm in 1991 to achieve global optimization by simulating ant foraging behavior [18]. Suppose that $P_{ij}^k(t)$ is the transition probability value of ant $k$ from resource node $i$ to resource node $j$ at time $t$, using this value to select the next task to schedule. It is expressed by Equation (1).

$$P_{ij}^k(t)=\{\begin{array}{l}\raisebox{1ex}{${[{\tau }_{ij}(t)]}^{\alpha }\ast {[{\eta }_{ij}(t)]}^{\beta }$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{i=1}^n{[{\tau }_{ij}(t)]}^{\alpha }\ast {[{\eta }_{ij}(t)]}^{\beta }}$}\right., j\in A\\ 0, \mathrm{Others}\end{array}$$

(1)

In Equation (1), ${\tau }_{ij}(t)$ is the pheromone value for transferring resource node $i$ to resource node $j$ at time $t$; ${\eta }_{ij}(t)$ is the heuristic function for transferring resource node $i$ to resource node $j$ at time $t$; $\alpha$ is the information heuristic factor, which represents the relative importance of scheduling order; $\beta$ is the expect heuristic factor, which represents the importance of heuristic information in ant selection scheduling sequence. The larger the value of $\beta$, the more likely the ants are to choose the scheduling sequence autonomously. Set $A$ as the task that ant $k$ can choose to perform in the next step.

According to Equation (1), the two key factors affecting the selection of resource nodes are ${\tau }_{ij}(t)$ and ${\eta }_{ij}(t)$. The improvement of these two factors is the difficulty and emphasis of the algorithm research. The ACTS-LB algorithm proposed in this paper is based on the standard ant colony algorithm to make corresponding improvements to ${\tau }_{ij}(t)$, and to update pheromone rules according to the node resource hardware performance and load balancing value.

4.2. Ant Colony Optimization Task Scheduling Algorithm Rule

In the actual SWIM, in order to achieve effective load balancing, the hardware performance of the node resources must be considered. First, reasonably assign tasks to each node according to the node processing capacity. The hardware performance is represented by two key indicators—computing power and system communication bandwidth of resource nodes. The hardware performance can be expressed by Equation (2).

$$Performance(s_j)={\omega }_1\ast Mip(s_j)+{\omega }_2\ast Bandwith(s_j).$$

(2)

In Equation (2), $Mip(s_j)$ represents the computing power of resource node $s_j$, $Bandwidth(s_j)$ represents the communication bandwidth of resource node $s_j$, and ${\omega }_1$ and ${\omega }_2$ are constants.

In SWIM, the indicators of impact on resource nodes load are mainly composed of CPU utilization, memory utilization and system bandwidth occupancy. The load balancing value of SWIM resource nodes can be expressed by Equation (3).

$$L{B}_j={\delta }_1\ast C(s_j)+{\delta }_2\ast M(s_j)+{\delta }_3\ast B(s_j).$$

(3)

In Equation (3), $L{B}_j$ represents the load balancing value of resource node $s_j$; $C(s_j)$ represents the CPU utilization rate of resource node $s_j$; $M(s_j)$ represents the memory usage of resource node $s_j$; $B(s_j)$ represents the bandwidth occupancy of resource node $s_j$; the coefficients ${\delta }_1$, ${\delta }_2$ and ${\delta }_3$ are constants, representing the weights of the three items, and ${\delta }_1+{\delta }_2+{\delta }_3=1$.

The average value of the load of all resource nodes in SWIM is expressed by Equation (4).

$$L{A}_j=\raisebox{1ex}{${\displaystyle \sum _{j=1}^{m}L{B}_j}$}\!\left/ \!\raisebox{-1ex}{$m$}\right..$$

(4)

Then the resource node load standard deviation is expressed by Equation (5).

$$L{S}_j=\sqrt{\frac{1}{m}{\displaystyle \sum _{j=1}^m{\left(L{B}_j-L{A}_j\right)}^2}}.$$

(5)

By calculating the resource node load standard deviation $LS$ in SWIM, it can reflect the system load balance degree. The larger the value of $LS$, the more unbalanced the system load. The smaller the value of $LS$, the more balanced the system load.

The ant colony algorithm pheromone update is expressed by Equation (6).

$${\tau }_{ij}(t+n)=(1-\mu ){\tau }_{ij}(t)+\Delta {\tau }_{ij}.$$

(6)

In Equation (6), $\mu$ is the information residual factor, $1-\mu$ is the pheromone volatilization coefficient, which is employed to avoid the pheromone infinite accumulation. The $\mu$ value range is limited to $0<\mu <1$. ${\tau }_{ij}(t+n)$ is the pheromone concentration value on the path ($i,j$) at time $t+n$; $\Delta {\tau }_{ij}$ is the pheromone increment value on the selected path ($i,j$), the initial time is $\Delta {\tau }_0$ = 0.

This paper uses the resource node hardware performance parameters and the system average load difference to update the pheromone ${\tau }_{ij}$, as expressed by Equation (7).

$$\Delta {\tau }_{ij}={\displaystyle \sum _{k=1}^m\Delta {\tau }_{ij}^k}$$

(7)

$$\Delta {\tau }_{ij}^k=Performance(s_j)\ast (1-L{S}_j)=[{\omega }_1\ast Mip(s_j)+{\omega }_2\ast Bandwith(s_j)]\ast (1-L{S}_j)$$

(8)

The heuristic function ${\eta }_{ij}$ in ant colony algorithm can be expressed by Equation (9).

$${\eta }_{ij}=1/e{t}_{ij}$$

(9)

In order to maximize the utility, we must also consider the completion time factor of all tasks and try to minimize the task completion time. So, the expected completion time $e{t}_{ij}$ is used to calculate the heuristic function of the ant colony algorithm. The smaller the expected completion time, the larger the value of ${\eta }_{ij}$ and the higher the value of $P_{ij}^k(t)$. Thus, the degree of expectation that an ant will transfer from task $t_i$ to node $s_j$ is improved.

The pheromone update calculation in Equation (6) and heuristic function calculation in Equation (9) are substituted into Equation (1) to obtain the probability value that task $t_i$ is scheduled to resource node $s_j$ after the optimization of the ant colony algorithm. The computational complexity of the improved ACO algorithm presented in this paper is expressed as $O(N{C}_{\max }\ast n^3)$, where $N{C}_{\max }$ is the number of cycles and $n$ is the total number of tasks.

4.3. Ant Colony Task Scheduling Algorithm Optimization Process

The main idea is to select the best order of task scheduling through the ant colony algorithm, in which the scheduler can be regarded as an ant and the task scheduling process is compared with the ant foraging process. The pheromone is updated according to the hardware performance parameters of the system resource node and the system average load difference, and the expected time to complete all tasks is at a minimum. So, the expected completion time is used to calculate the heuristic function of the ant colony algorithm. Finally, a resource node with high pheromone concentration (high performance and low load) and minimum completion time is selected to handle the assigned task.

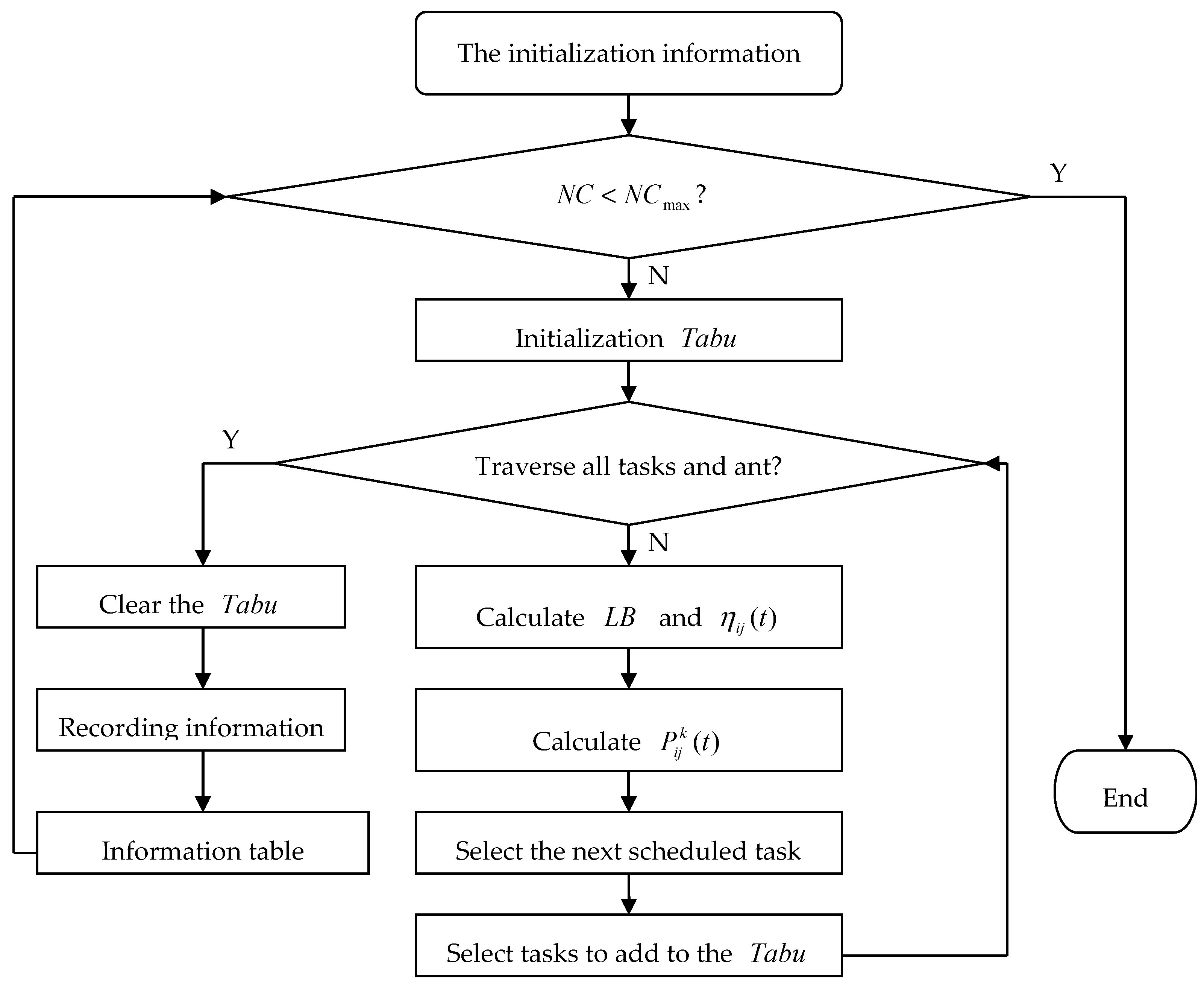
The research content of SWIM task scheduling is to map each task to resource set $S$ in task set $T$, and to improve the task scheduling performance of the system on the premise of ensuring load balancing. The specific steps of the ant colony optimization task scheduling algorithm for SWIM based on load balancing are as follows. The flow chart of the algorithm is shown in Figure 2.

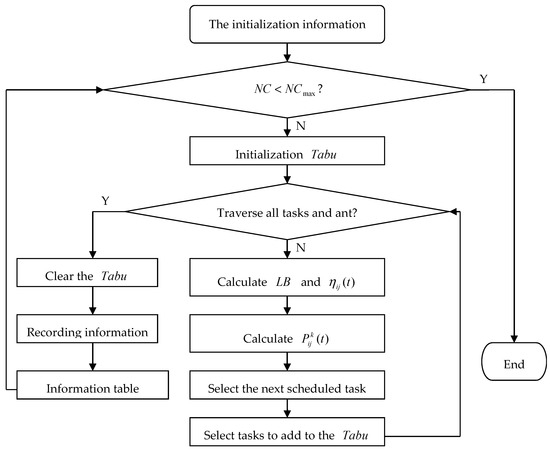
Figure 2. The flow chart of the ant colony optimization task scheduling algorithm based on load balancing.

Step 1: First, initialize the parameters in the algorithm. There are $n$ tasks, $m$ resources, the number of ants is $q$, the maximum number of cycles is $t_{\max }$, the initial time $t$ is set to 0 (it can be assumed that there are $n$ air flight planning missions and $m$ navigation information resources in SWIM in this scenario).

Step 2: Make $t=t+1$. If $t\le t_{\max }$, after initializing the search table, all ants search the path from the initial position and stop searching when all tasks enter the search table.

Step 3: The hardware performance and load balance difference of the resource nodes are obtained by calculations, and the transferred probability $P_{ij}^k(t)$ of each resource node is calculated by Equation (1), using $P_{ij}^k(t)$ to select the perform task resource node.

Step 4: Update the search table and add the scheduling task to the search table. Use $Tabu$ to record the set of tasks that ant $k$ is currently passing through. Do not repeatedly select the path that has already passed as the next path.

Step 5: Update the pheromone of the ant colony algorithm according to Equation (6) and save the selected ant information with the best scheduling result.

Step 6: Repeat the above steps until $t>t_{\max }$, when the algorithm ends [19].

5. Experiment and Results Analysis

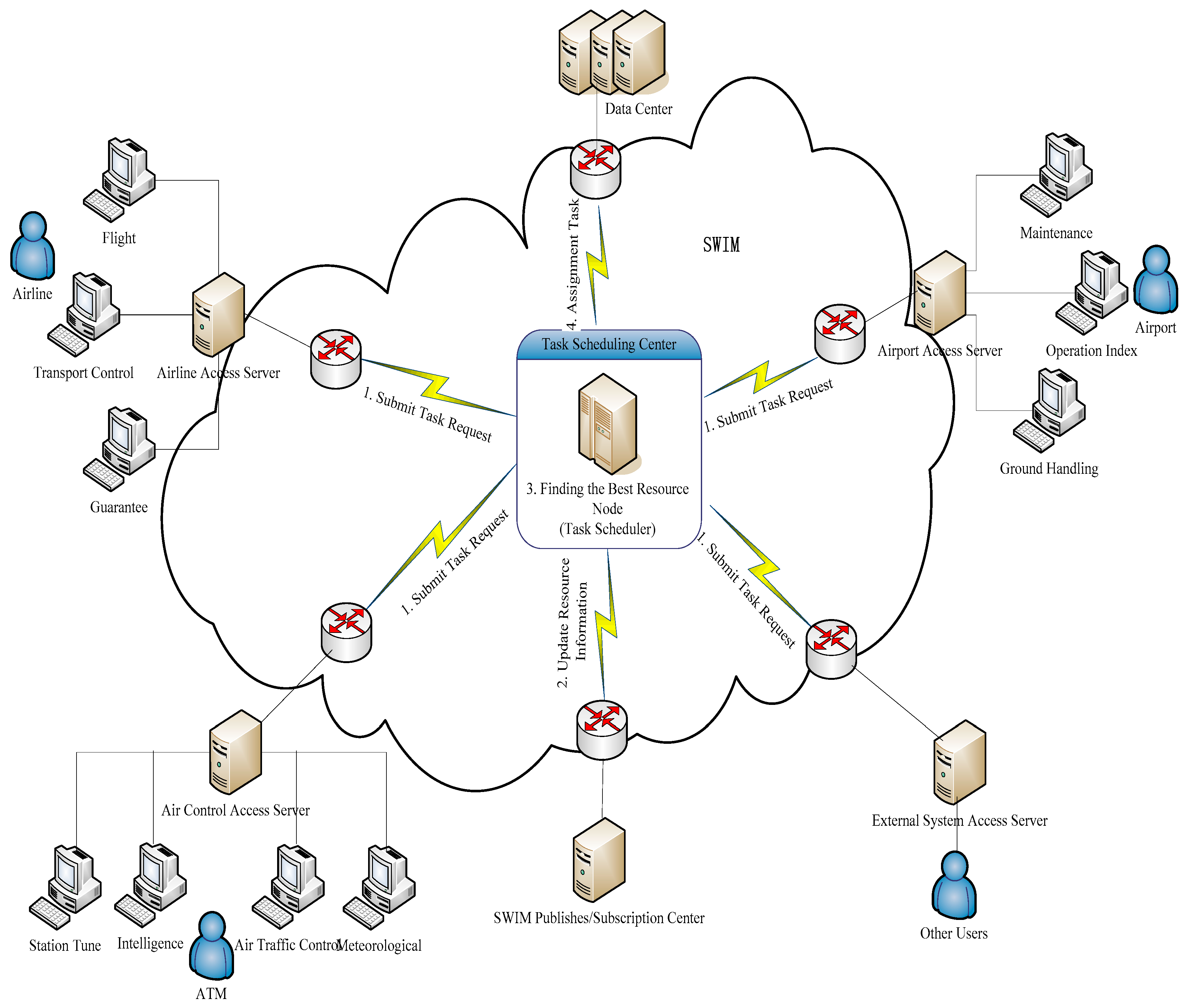
In the experiment, we referred to the SWIM structure that is already deployed by an air traffic administration of civil aviation, and we used the network simulation tool—NS-3 to verify the algorithm performance. The SWIM local task scheduling structure is shown in Figure 3.

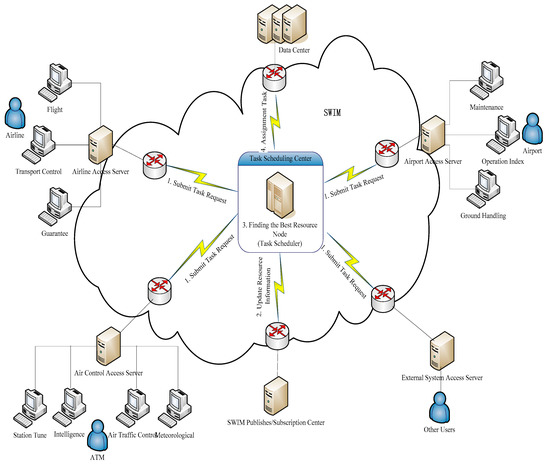
Figure 3. SWIM task scheduling structure diagram.

5.1. Experimental Environment

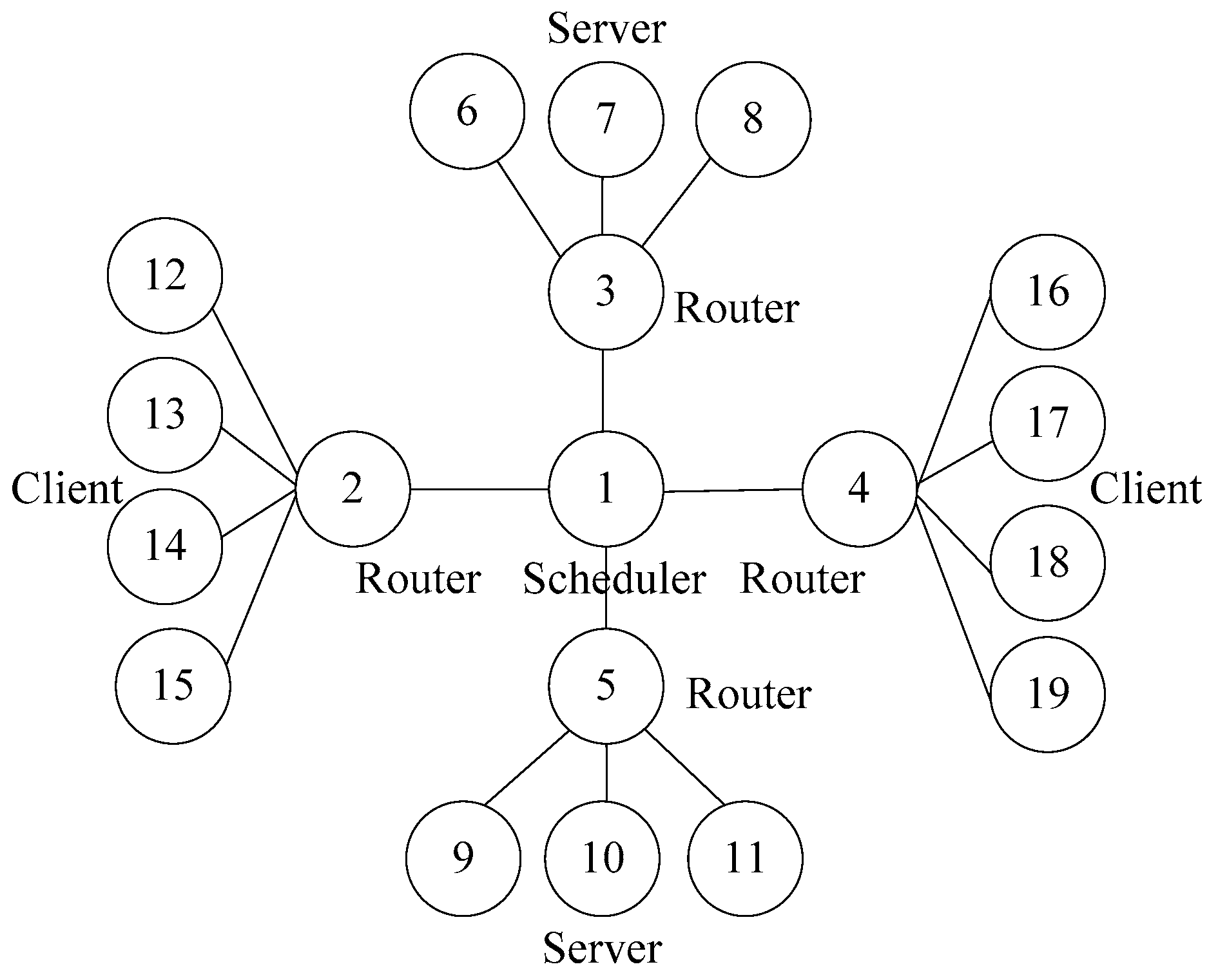
The simulation experiment designed a topology model with one scheduler, four routers, six servers and eight clients. The node 1 is the scheduler, nodes 2–5 are the routers, nodes 6–11 are the servers, and nodes 12–19 are the clients. The link bandwidth between the client and the router, between the router and the scheduler, and between the router and the server is 150 Mbps, and the one-way delay of 10 ms. The simulation experiment test topology is shown in Figure 4.

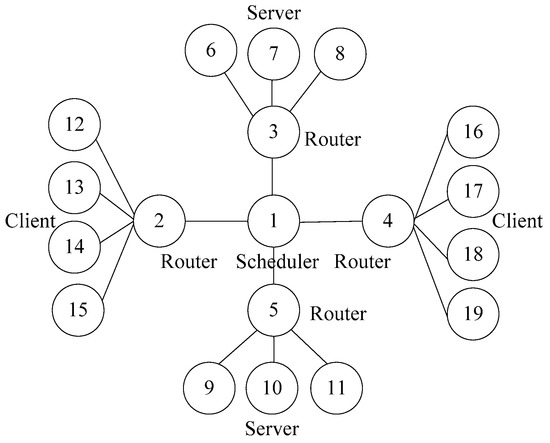
Figure 4. Topology diagram of the SWIM task scheduling simulation experiment.

5.2. Experimental Parameter Settings

For the selection of parameters $\alpha$, $\beta$ and $\mu$ in the ant colony algorithm, there is no general method to determine their optimal combination. It should be noted that these parameters have a great impact on the performance of the ant colony algorithm. The smaller the value of $\mu$, the smaller the influence of the previously searched path on the current search, making the algorithm difficult to converge. The larger the value of $\mu$, the greater the influence of the previous search path on the current search, but this also increases the risk of falling into a local optimum. So, the $\mu$ value is generally set at 0.5. In the parameter selection experiment, the $\alpha$ and $\beta$ values were set as $\mu$ = 0.5 and $\mu$ = 0.6. The simulation program was cycled 1000 times, the best result was selected as one experiment, taking the average value of 100 experiments. The parameters are substituted into the algorithm for the simulation test. The simulation experiment data are shown in Table 3.

Table 3. Parameter combination test results.

Serial Number	$\mathit{\mu }$	$\mathit{\alpha }$	$\mathit{\beta }$	Optimal Path	Running Time (S)
1	0.5	1.0112	2.7375	568.10969	39.98
2	0.5	1.0351	2.6856	568.19446	40.37
3	0.5	1.0323	2.7685	568.19446	40.56
4	0.5	1.0289	2.7386	568.10969	40.33
5	0.5	1.0156	2.7235	568.10969	40.25
6	0.5	4.3589	1.5195	568.19446	41.79
7	0.5	5.2368	2.4978	568.10969	41.65
8	0.5	5.3646	2.5568	568.10969	41.15
9	0.5	6.3567	4.2556	568.19446	42.48
10	0.5	6.3551	4.2550	568.19446	42.68
11	0.6	1.0253	2.7526	568.10969	39.86
12	0.6	1.0362	2.6898	568.19446	40.29
13	0.6	1.0387	2.7365	568.19446	40.53
14	0.6	1.0236	2.7472	568.10969	40.25
15	0.6	1.0187	2.7356	568.10969	40.27
16	0.6	4.3789	1.5387	568.19446	41.58
17	0.6	5.2468	2.4998	568.10969	41.31
18	0.6	5.3846	2.5368	568.10969	41.02
19	0.6	6.3985	4.2673	568.19446	42.29
20	0.6	6.3653	4.2672	568.19446	42.37

From Table 3, we can see that the optimal path is 568.10969, the running time is 39.86 s, $\mu$ = 0.6, $\alpha$ = 1.0253 and $\beta$ = 2.7526. After the comparative study and multiple experiments, the parameters in this paper simulation experiment were set to $\alpha$ = 1.0, $\beta$ = 2.7 and $\mu$ = 0.6. In the experiment, we found that when the same parameters were used for experiments of different scales, the results obtained were different. The weight parameters of the resource node load impact indicator in SWIM were set to ${\delta }_1$ = 0.4, ${\delta }_2$ = 0.3 and ${\delta }_3$ = 0.3. The population size was 50, and the maximum number of iterations was 150. The simulation experiment test parameters are shown in Table 4.

Table 4. Simulation experiment test parameters.

Parameter Name	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\mu }$	Bandwidth	Delay	${\mathit{\delta }}_1$	${\mathit{\delta }}_2$	${\mathit{\delta }}_3$	Population Size	$\mathit{N}{\mathit{C}}_{\mathbf{max}}$
Parameter value	1.0	2.7	0.6	150 Mbps	10 ms	0.4	0.3	0.3	50	150

5.3. Experimental Results and Analysis

In order to verify the effectiveness of the ACTS-LB algorithm designed in this paper, we tested the method using the same parameter configuration conditions but in two different situations: (1) The service nodes number is fixed, but scheduling tasks number is changed; (2) The scheduling tasks number is fixed, but the resource nodes number is changed. This was compared with the classic min-min algorithm [20], the ACO algorithm [21] and the PSO algorithm [10] in terms of transmission delay, task execution time and system load deviation value.

Experiment 1: The transmission delay comparison.

(1) Set the number of service nodes at m = 20 and the number of scheduling tasks at 10 < n < 200.

(2) Set the number of scheduling tasks at n = 100 and the number of service nodes at 5 < m < 50.

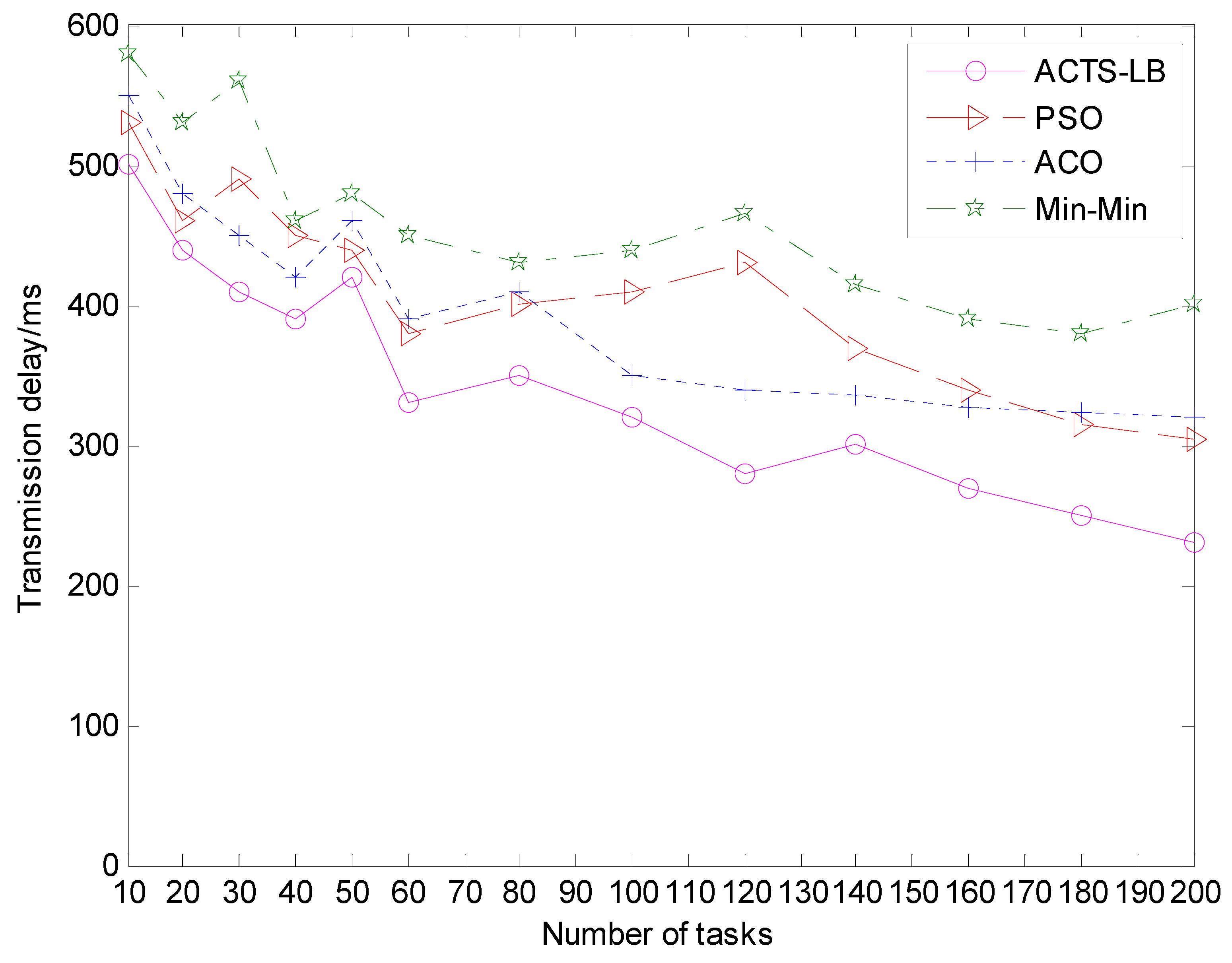
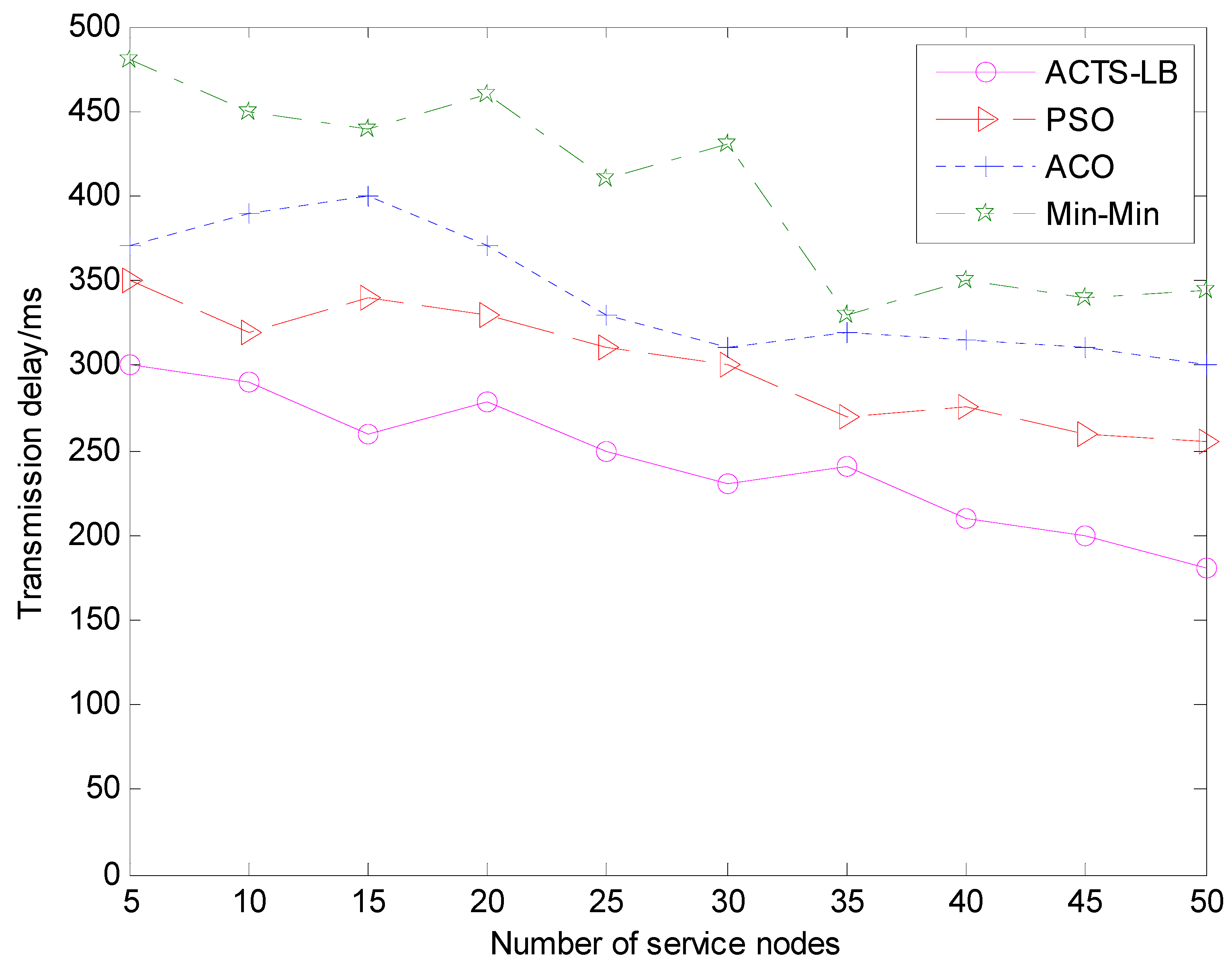
In the above two cases, by running the simulation software NS-3, the time delay data of the path was obtained by measuring different iterations of the ACTS-LB algorithm, min-min algorithm, ACO algorithm and PSO algorithm in the path finding process. The trace file obtained was counted and analyzed by the statistical analysis tool Wireshark. We obtained the total time delay value of the path after each iteration for each of the four algorithms, and the average value of each algorithm was obtained after each iteration was run 1000 times. The result was processed by MATLAB. The results are shown in Figure 5 and Figure 6.

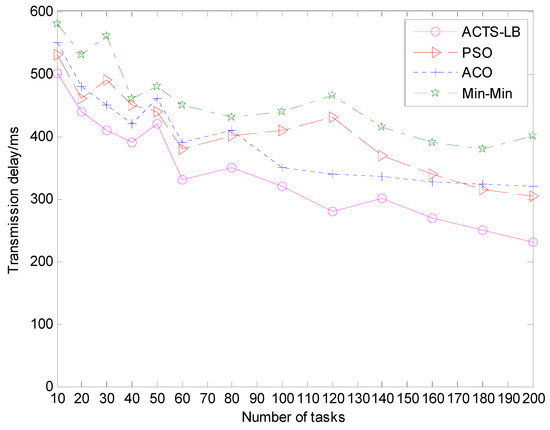
Figure 5. The comparison of transmission delay under different scheduling tasks.

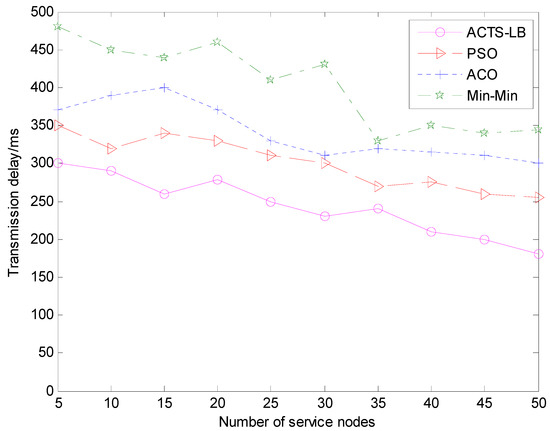
Figure 6. The comparison of transmission delay under different service nodes.

It can be seen from the experimental results in Figure 5 and Figure 6 that, at the beginning of ant colony routing, the four algorithms have large fluctuations in the total transmission delay of the path and have the same performance. After 100 iterations, the ACO algorithm basically leveled off and no longer changed, indicating that the ACO algorithm falls into premature convergence after the 100th iteration and could no longer search for a better path. When the number of tasks increased in the later period, the transmission delay variation of the min-min algorithm and PSO algorithm were not obvious. The ACTS-LB algorithm expanded the path space due to the optimized updating of pheromones, and the ants disturbed other paths so that the obtained paths were evenly distributed in the path space, ensuring that the ants had a stronger search ability and could find better quality transmission paths. Thus, it can be seen that the ACTS-LB algorithm can effectively solve the premature convergence problem of the ACO algorithm, providing ants with a stronger search ability and obtaining a better-quality path set.

Experiment 2: The task execution time span comparison.

(1) Set the number of service nodes at m = 20 and the number of scheduling tasks at 10 < n < 200.

(2) Set the number of scheduling tasks at n = 100 and the number of service nodes at 5 < m < 50.

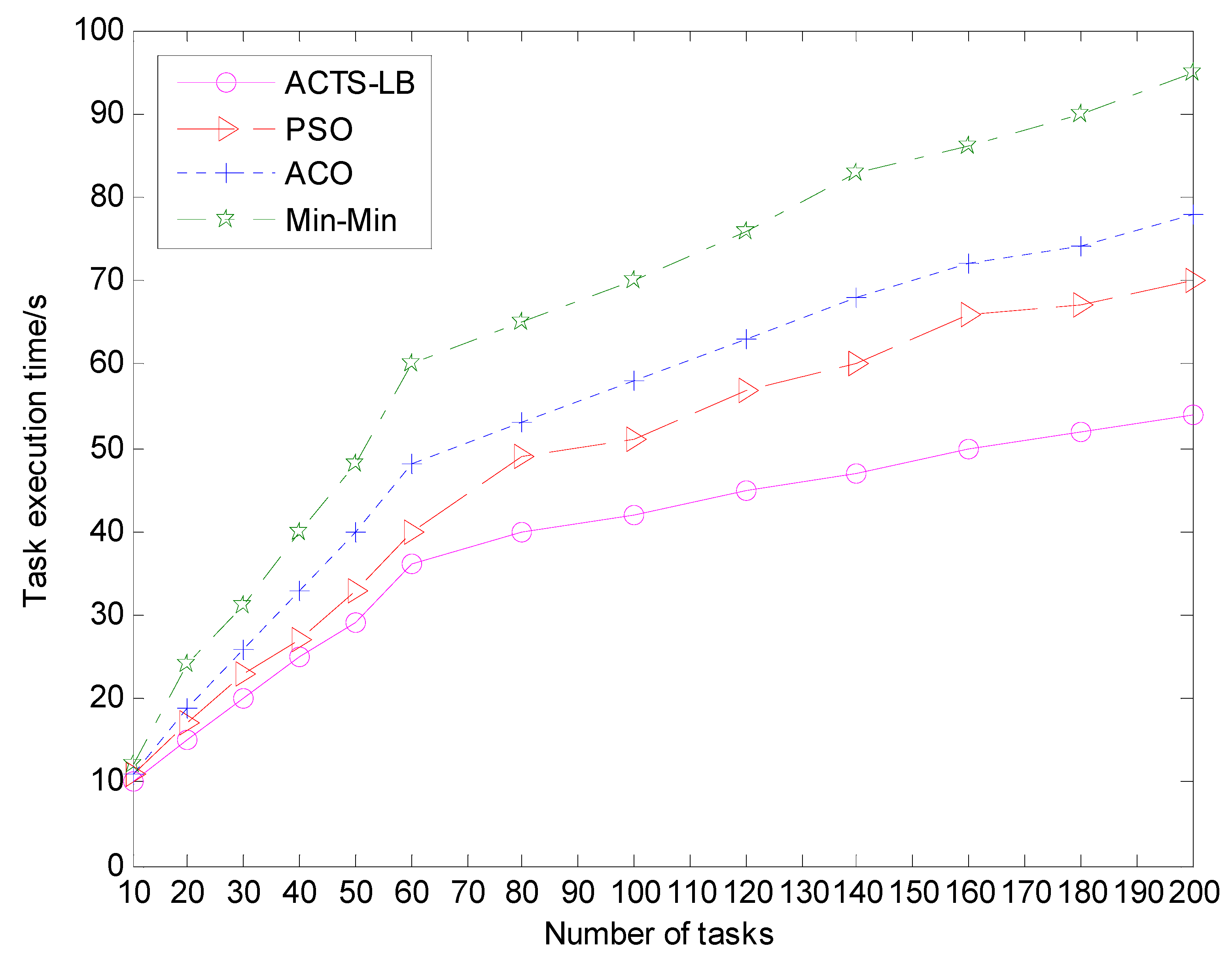
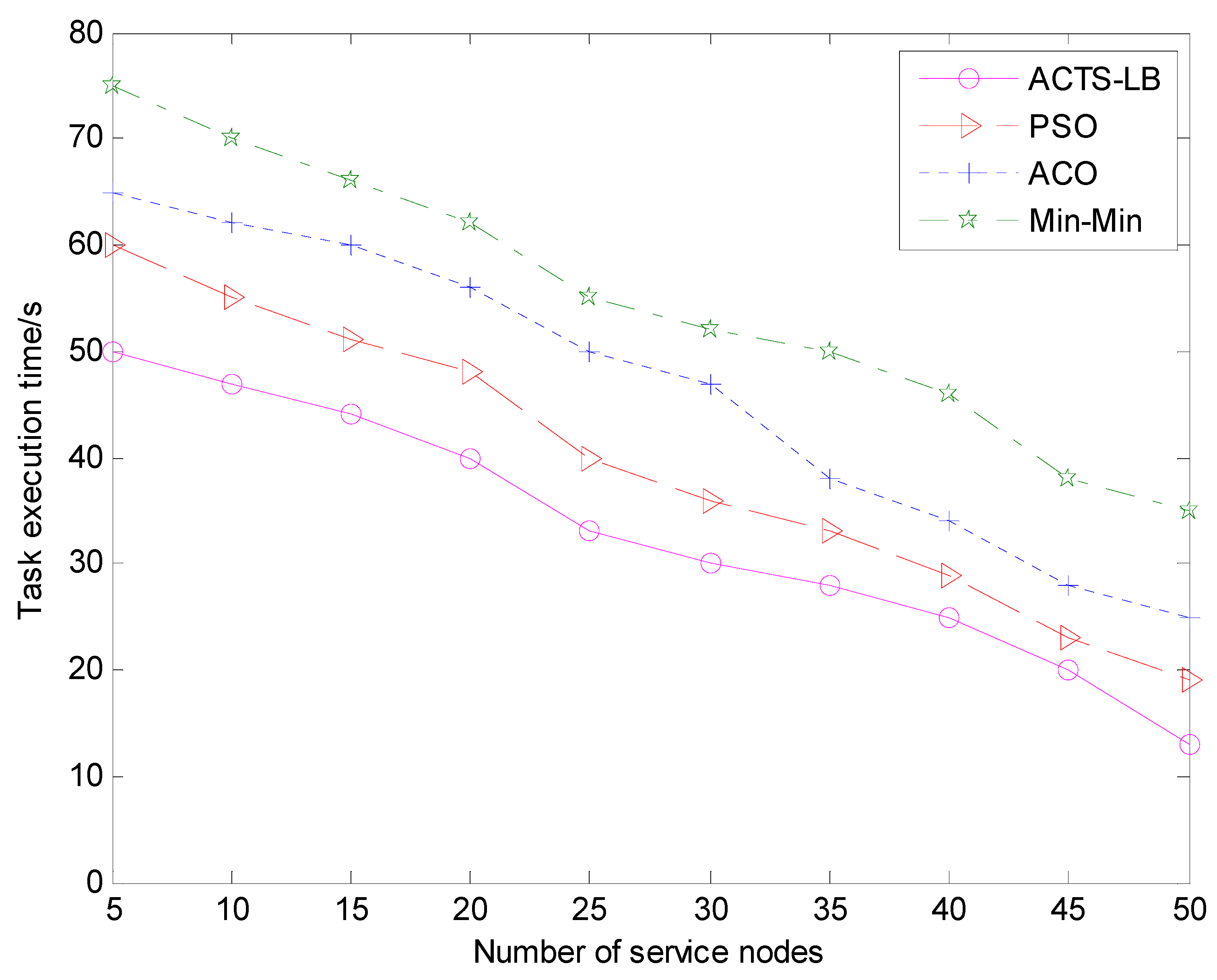
In the above two cases, the task execution time of the ACTS-LB algorithm, min-min algorithm, ACO algorithm and PSO algorithm were tested in the context of task scheduling. The experimental results were sorted according to the data in NS-3. The four algorithms were executed 1000 times and averaged. The results of the task execution time span are shown in Figure 7 and Figure 8.

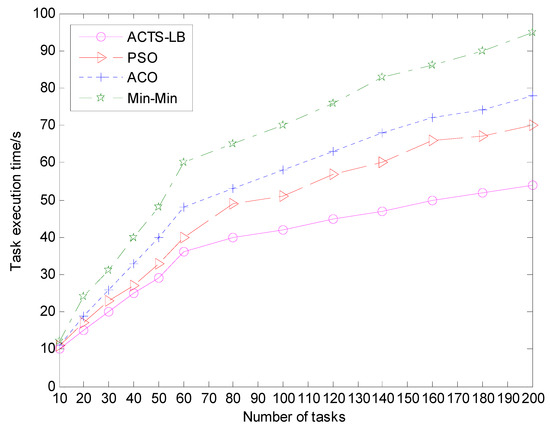
Figure 7. The comparison of task execution time span under different scheduling tasks.

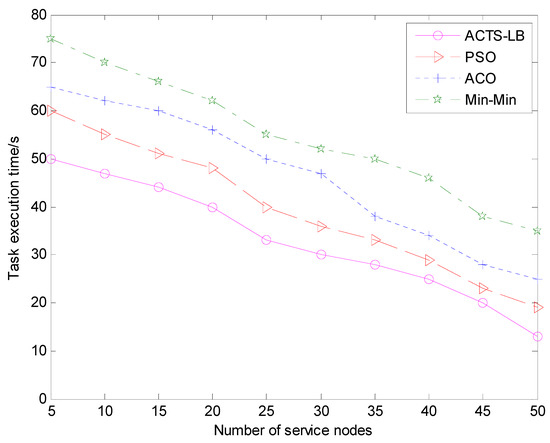
Figure 8. The comparison of task execution time span under different service nodes.

It can be seen from the experimental results in Figure 7 that, in the initial stage of task scheduling, the task execution time of the ACTS-LB algorithm, min-min algorithm, ACO algorithm and PSO algorithm are basically the same. However, the task execution time of the ACTS-LB algorithm becomes smaller than that of the other three algorithms as the number of tasks increases. From the experimental results in Figure 8, it can also be seen that when the number service nodes increased, the ACTS-LB algorithm execution task scheduling time was less than that of the min-min algorithm, ACO algorithm and PSO algorithm. This shows that the method of calculating heuristic function by using expected execution time in the ACTS-LB algorithm plays an effective role in shortening the task execution time, and ants tend to choose the path with high pheromone concentration and minimum completion time. It can be concluded that the ACTS-LB algorithm can improve task execution efficiency and enable ants to have a stronger task scheduling ability.

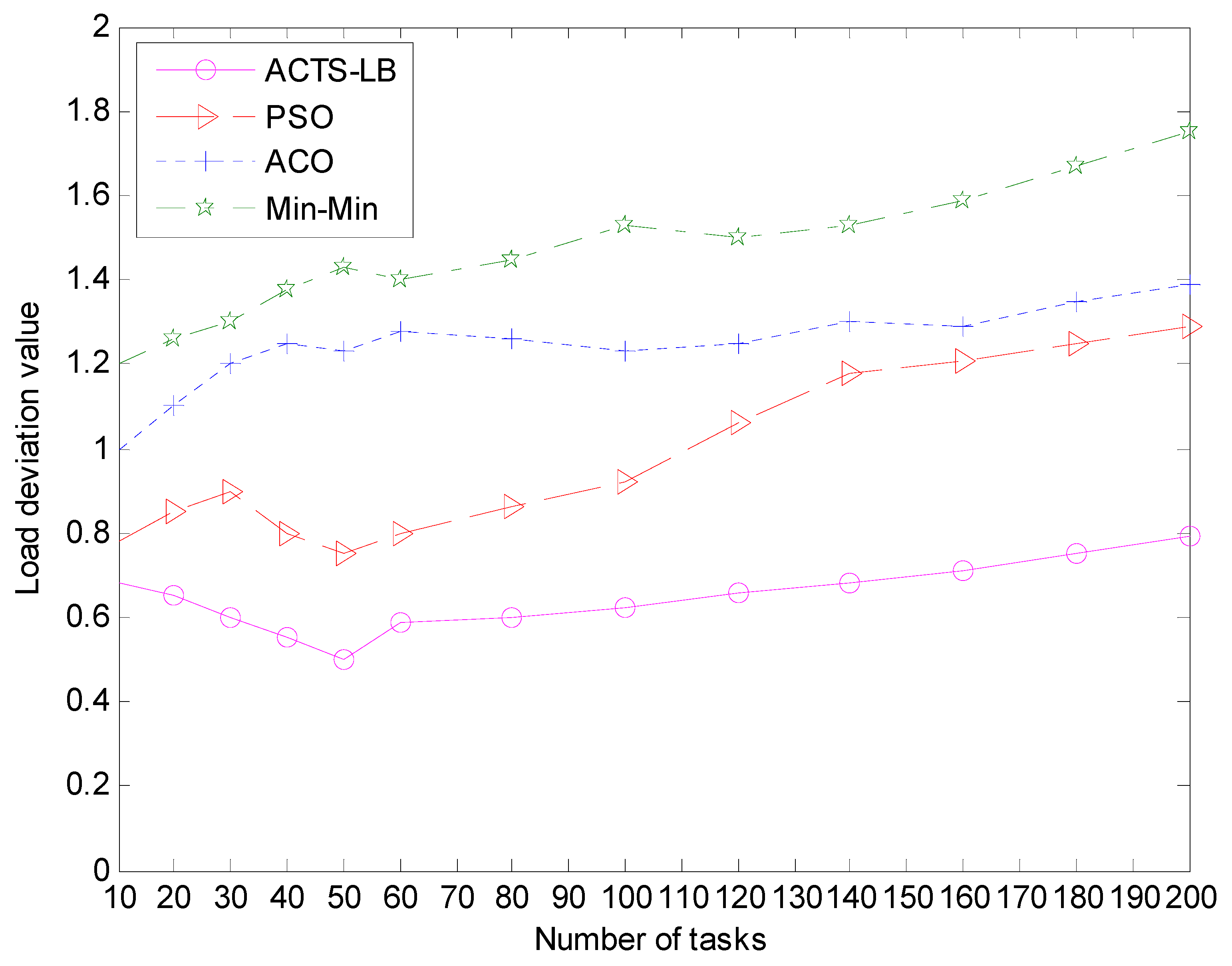
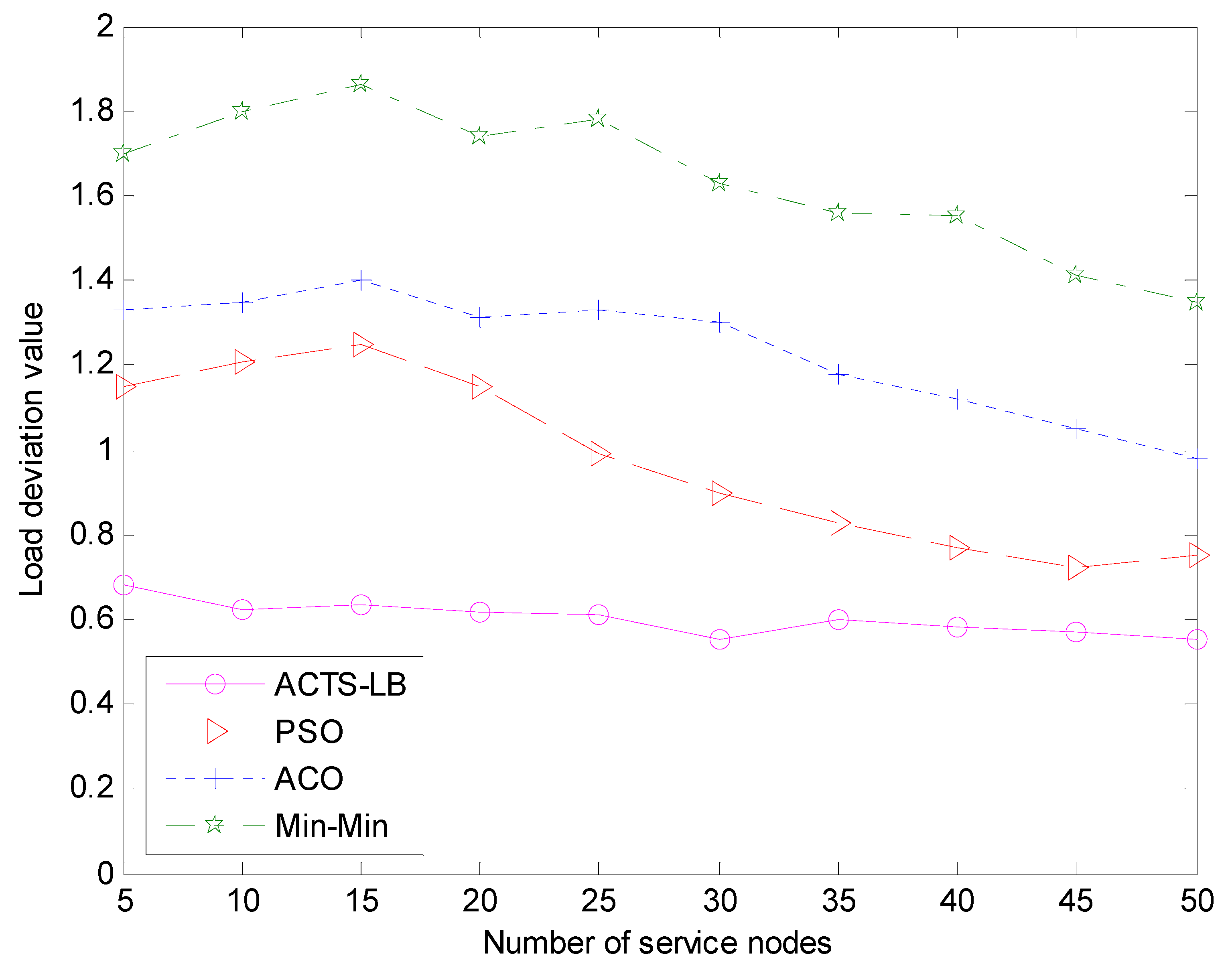
Experiment 3: The system load deviation comparison.

(1) Set the number of service nodes at m = 20 and the number of scheduling tasks at 10 < n < 200.

(2) Set the number of scheduling tasks at n = 100 and the number of service nodes at 5 < m < 50.

In this paper, the load deviation value ($LDV$) of SWIM resource nodes is proposed as a reference standard for evaluating load balancing in task scheduling. The $LDV$ definition can be expressed by Equation (10).

$$LDV=\raisebox{1ex}{$L{B}_{\max }-L{B}_{\min }$}\!\left/ \!\raisebox{-1ex}{$LA$}\right.$$

(10)

The definition of the SWIM resource nodes load value $LB$ is the same as in Equation (3); $L{B}_{\max }$ and $L{B}_{\min }$ are the maximum and minimum values of $LB$, respectively; $LA$ is the average of all resource node loads. According to the experimental results, the load deviation values of the resource nodes during the task scheduling of the four algorithms were obtained. The results are shown in Figure 9 and Figure 10.

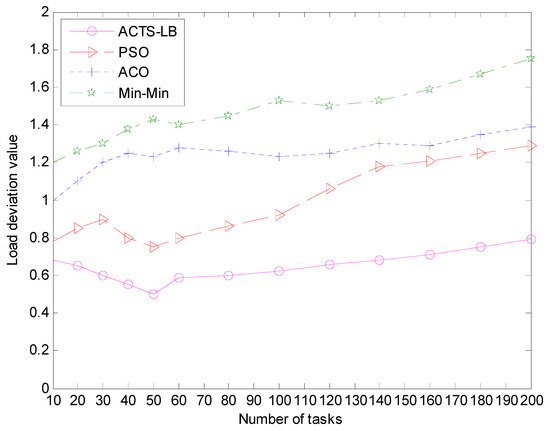
Figure 9. The comparison of system load deviation values under different scheduling tasks.

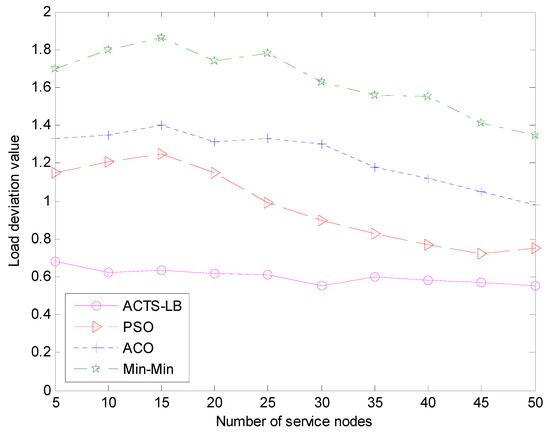
Figure 10. The comparison of system load deviation values under different service nodes.

It can be seen from Figure 9 and Figure 10, the $LDV$ value of the ACTS-LB algorithm is smaller than that of the min-min algorithm, ACO algorithm and PSO algorithm, and the transformation becomes slower as the number of tasks increases. This is because in the ACTS-LB algorithm, pheromones are updated according to the hardware quality and the load balancing of node resources, so ants tend to aim for resource nodes with high pheromone concentrations (high performance and low load of resource nodes) when selecting the next task processing target node. It can be concluded that the ACTS-LB algorithm with $LDV$ as the reference standard can achieve the goal of load balancing and improve the overall performance of task scheduling.

5.4. ACTS-LB Algorithm Shortcomings

The ACTS-LB algorithm, however, can still be further improved, which requires further optimization and in-depth study in the following aspects:

(1) Because the ant colony algorithm has a slow convergence rate in the initial stage, it can easily fall into the local optimum. Therefore, the ACTS-LB algorithm also has some shortcomings. In the subsequent algorithm improvement, we will draw on other heuristic algorithm advantages, such as the simulated annealing (SA) algorithm and genetic algorithm, etc. The comprehensive application of these algorithms’ different characteristics, and the fact that their advantages and disadvantages complement each other, will aid us in improving the algorithm’s overall task scheduling performance.

(2) The ant colony algorithm parameter setting is very important. If it is not set properly, it will slow down the solving speed and affect the quality of the results. In the next SWIM task scheduling study, we will consider the task dynamics and the service quality of the system. We plan to dynamically adjust the corresponding parameters in the algorithm and study the impact of ant colony parameters and local search methods on the overall performance of the system, so as to continuously improve and perfect the task scheduling strategy.

6. Conclusions

In this paper, we proposed the SWIM ant colony optimization task scheduling algorithm based on load balancing (ACTS-LB). By improved the traditional ant colony optimization algorithm, the hardware performance quality index and load standard deviation function of resource nodes in SWIM were comprehensively adopted to improve the pheromone updating strategy of the algorithm. The ACTS-LB algorithm improved the defect that pheromone updating can easily fall into the local optimum and ensures that the system’s load balancing requirements were maximized while the scheduling task was effectively completed. The experimental simulation using NS-3 showed that the ACTS-LB algorithm performs better than the classic min-min algorithm, ACO algorithm and PSO algorithm, as it can maintain SWIM in a balanced load state and improved the efficiency of system task scheduling and execution. However, in this paper, we presented the ACTS-LB algorithm, which was tested only in a simulated SWIM environment. The algorithm had not yet been tested in an actual SWIM application environment and the experimental results were not convincing. Next, in order to further verify the validity of the proposed ACTS-LB algorithm, we will try to simulate the algorithm in a real SWIM environment.