Nonlinear Analysis of Built-in Sensor in Smart Device under the Condition of Voice Actuating

Abstract

A built-in sensor in a smart device, such as the accelerometer and the gyroscope, will produce an obvious nonlinear output when it receives voice signal. In this paper, based on the chaotic theory, the nonlinearity of smartphone built-in accelerometer is revealed by phase space reconstructing after we calculate several nonlinearity characteristics, such as best delay time, embedding dimension, and the attractor of accelerometer system, under the condition of voice commands inputting. The results of theoretical calculation and experiments show that this specific nonlinearity could lay a foundation for further signal extraction and analysis.

1. Introduction

Nowadays, the high-performance chips largely enhance the real-time computation of the modern smart device. Moreover, a smart device also enables rich interactive experiences while extending the functions by using various built-in sensors, such as the accelerometer and the gyroscope.

Built-in sensors in the smart device are kinds of microelectromechanical systems that capture the subtle changes of light, heat, and temperature. For instance, a tiny embedded accelerometer in a smartphone has the capability to detect instantaneous acceleration magnitude on three coordinate axes. Researchers also attempt to acquire accurate velocity and direction of the smart device from these instantaneous acceleration magnitudes in order to identify the motion state of a human target including walking up, running and tumbling [1].

Recently, researchers found that built-in sensors in a smart device could output response when they receive voice as actuating signals [2,3]. Based on this feature, built-in sensors gradually replace microphone to realize voice control in various application scenarios. At present, the voice-activated communication between user and smart device increasingly becomes a brand-new interactive pattern. For instance, Siri in iOS system and Google Now in Android system [4,5] are two successful voice interactive platforms in mobile devices. Generally, these two systems would receive the specific voice commands and transform them into instructions to control a smart device to complete multiple real-time tasks by using a built-in microphone. Meanwhile, the microphone has to be kept in working condition to give immediate feedback to users. This significant energy consumption mode undoubtedly becomes a challenge in the battery-powered smart device. Therefore, a low-power built-in sensor is considered to become a viable alternative to resolve the conflict between high-energy consumption and real-time monitoring of speech signal [6,7].

Due to its hardware structure constraint, the output signal of a built-in sensor usually appears strong non-linear [8]. Therefore, on the basis of non-linear dynamics chaotic theory, we attempt to reveal the chaotic features of output signal of the built-in accelerometer when the smart device receives voice commands. We also try to develop a suitable mathematical model to express the nonlinear properties of built-in accelerometer for realizing accurate output signal prediction, characteristics extraction, and pattern recognition.

The main contributions of this paper are as follow:

(1)

We attempt to apply nonlinear dynamics and chaotic theory to built-in sensor signal analysis.

(2)

We calculate the optimal delay time and proper correlation dimension, and then we reveal the nonlinear properties of built-in accelerometer in the smart device by reconstructing the attractors.

The remaining parts of the paper are arranged as follows:

In Section 2, we illustrate the feasibility of built-in accelerometer in smart-device. In Section 3, the optimal delay time and proper correlation dimension are calculated. In addition, the attractors are also reconstructed. We present the results of experiments in Section 4. We also try to show the results of nonlinear mapping between microphone and accelerometer in Section 5. The conclusions and subsequent research directions are finally presented in Section 6.

2. Feasibility of Built-in Accelerometer

Current MEMS (Micro-Electro-Mechanical System) built-in accelerometers in smart devices are usually composed of three main components–an inertial mass, spring legs, and stationary fingers. As shown in Figure 1, a change in the capacitance between the stationary fingers would be caused by inertial mass moving when an accelerometer is working. This change is recorded as an accurate acceleration. Moreover, three separate sets of components could be employed to measure the accelerations separately in three directions.

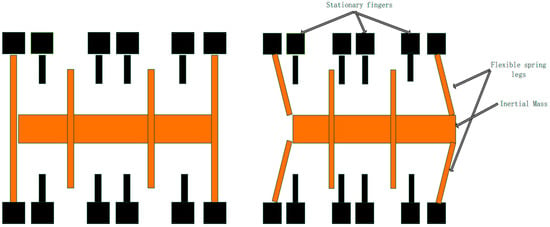
Figure 1. The sketch of a MEMS built-in accelerometer.

Owing to the limitations of hardware, capturing the voice signal is not the target of the built-in sensors in the smart device. Therefore, the accurate frequency response range under the condition of voice actuating should be determined.

As shown in the Figure 2, we placed two smartphones on a table, and 0–22,000 Hz chirp sound signals were generated by a small louder-speaker which was fixed 10 cm vertical above the two smartphones. One of these smartphones was used to record the responding signal to the chirp sound signals. Meanwhile, the responding signal of the built-in accelerometer to the same chirp signals was recorded by another smartphone for comparison.

Figure 2. Two smartphones record chirp sound signals.

It is clearly found from Figure 3 that the built-in microphone of the mobile phone can successfully capture the chirp signal. In addition, the response signal was also an approximately straight line from 0 to 4000 Hz without aliasing. Conversely, the response signal frequency of the built-in accelerometer was mainly concentrated below 200 Hz, although the frequency of the input chirp sound signals was gradually increasing. This means that the built-in accelerometer usually filters out the sound signal above 250 Hz while arising nonlinearly distorted.

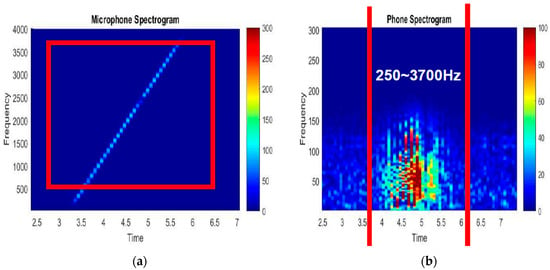
Figure 3. Time-frequency diagram of response signals to chirp signal. (a) Microphone (b) Built-in accelerometer.

Next, we use two chirp signals with different starting frequencies as input sound signals which are shown in the Figure 4. The response time-frequency diagrams of respond signals could be found in Figure 5. It was found that both microphone and accelerometer can capture the two chirp signals. Similarly, we also found that for multiple frequency signals, the response signal frequency range of the built-in accelerometer was still mainly concentrated below 200 Hz and nonlinear distortion also still existed.

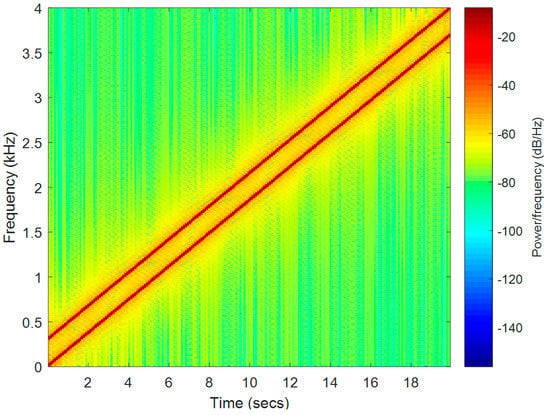
Figure 4. Two chirp signals with different starting frequencies.

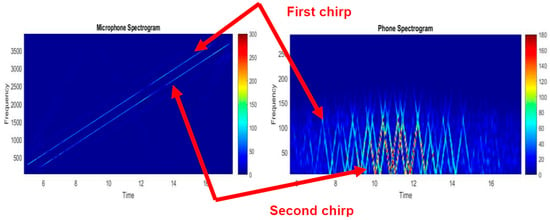
Figure 5. Time-frequency diagram of response signals to two chirp signals.

3. Nonlinear Characteristics Analysis

Chaotic time series analysis is one of the most important methods in nonlinear dynamics theory, and phase space reconstruction is also the main goal which would be achieved. Usually, the basic target of phase space reconstruction is to demonstrate the inherent nonlinearity of a system by studying the chaotic attractor and characteristic parameters of a specific variable in the phase space. So, how to find the most accurate attractor to effectively reconstruct the phase space for this particular built-in acceleration system? Assuming that we obtain a univariate time series output signal of accelerometer through the observation or experiment as $\left\{Xn\right\}=X_1,X_2,\dots ,X_N$ a state variable of the reconstructed phase space can be expressed as:

$$X_k=\{X(k),X(k+\tau ),\dots ,X(k+(m+1)\tau )\},k=1,2,3,\dots ,N$$

(1)

Thus, an $m$ dimensional state space $Rm$ could be formed. Moreover, the mathematical model is to be established in the state space $Rm$:

$$Xn+1=G(Xn)$$

(2)

In [9,10], Takens and Mane proved that the reconstructed state space $Rm$ has the same topological structure and geometric features with the original chaotic dynamic system, provided that the parameters $m$ and $\tau$ are properly selected. It also means that all these differential and topological invariants in the original chaotic dynamic system could be calculated in the reconstructed state space. Furthermore, the dynamic system can be analyzed and predicted by establishing a specific mathematical model in the state space $Rm$. It is clear that the correct determination of delay time $\tau$ and embedding dimension $m$ is the key for phase space reconstruction. In the modern chaos theory, it is generally believed that these two parameters are dependent on each other [11,12]. Therefore, we could obtain the attractor of a built-in accelerometer system and complete phase space reconstruction just after the two parameters have been simultaneously determined.

It can be known from the delay embedding theorem [13,14] that the delay time $\tau$ can be randomly selected if the time series is infinitely long, noiseless, and infinitely accurate. However, in a general practical application, the accelerometer output signal would be a time-limited sequence with noise pollution and measurement error. Thus, the delay time $\tau$ can only be chosen depending on experience. Basically, the principle of it is to give $Xn$ and $Xn+\tau$ a certain degree of independence to process them as independent coordinates during the reconstruction of phase space. If $\tau$ is small $Xn$ and $Xn+\tau$ would get too close to effectively differentiate in the phase space. Moreover, they are also very close to the “diagonal” in the reconstructed phase space, which means a large amount of redundant information would be carried by the attractor. Thus, the phase space would be disordered and mixed without rules. On the contrary, the attractor track would be projected in two completely opposite directions because of the minor relevancy between $Xn$ and $Xn+\tau$, which means that the actual evolution rule of the trajectory in the phase space cannot be reflected.

Referencing to the C-C algorithm [15,16], we define ${\tau }_w=(m-1){\tau }_d$ as the delay time window while $\tau (\tau =t)$ is the delay time. So, the correlation integral can be represented as follows:

$$C_s^m(m,N,r,t)=\frac{2}{M(M-1)}{\displaystyle \sum _{1\le i<j\le M}\theta \{r-\Vert X_i-X_j\Vert \}}$$

(3)

In Equation (3), $\theta (a)$ is a step function, $N$ and $M=N-(m-1)t$ represent the length of the data set and $m$ dimensions embedding points, respectively. The correlation integral in Equation (3) is a cumulative distribution function, which shows that the probability of the distance between any two points in the phase space is less than the radius $r$. Further, we define a statistic:

$$S_1(m,N,r,t)=C(m,N,r,t)-C^m(1,N,r,t)$$

(4)

When the excitation input of built-in accelerometer in the smart device is a voice signal, in order to calculate the detection statistic in Equation (4), we split the output variable time series $\left\{Xn\right\}=X_1,X_2,\dots ,X_N$ into $t$ disjoint sub-sequences which are shown in Equation (5):

$$\begin{array}{l}\{X_1,X_{1+t},\dots ,X_{N-t+1}\}\\ \{X_2,X_{2+t},\dots ,X_{N-t+2}\}\\ \dots \\ \{X_i,X_{i+t},\dots ,X_{N-t+i}\}\\ \dots \\ \{X_t,X_{2t},\dots ,X_N\}\end{array}$$

(5)

The lengths of all these sub-sequences are $Ns=N/t$, $t$ is reconstruction delay time. The detection statistic in Equation (4) of each sub-sequence can be calculated as follows:

$$S_2(m,N,r,t)=\frac{1}{t}{\displaystyle \sum _{s=1}^t\{C(m,\frac{N}{t}},r,t)-C_{\mathrm{s}}^m(1,\frac{N}{t},r,t)\}$$

(6)

Generally, output signal sequences of the built-in accelerometer are time-limited and correlated between each other. Therefore, $S_2(m,N,r,t)$ is not zero. Moreover, the autocorrelation characteristics between these output signals also can be reflected by $S_2(m,N,r,t)\sim t$.

According to the autocorrelation properties of statistics signal, in order to make all points in the reconstructing phase space close to a uniform distribution, there are two optional values for the optimal delay time ${\tau }_d$. One is the first zero coordinated point of $S_2(m,N,r,t)\sim t$, another is time point of the minimum mutual differentiation between $S_2(m,N,r,t)\sim t$ to all radius $r$. In addition, an equation can be defined as follows to measure this differentiation.

$$\Delta S_2(m,t)=\max \{S_2(m,r_i,t)\}-\min \{S_2(m,r_i,t)\}$$

(7)

Therefore, local maximum time would be the zero coordinate points of $S_2(m,N,r,t)\sim t$ or minimum value of $\Delta S_2$. Besides, the optimal delay time ${\tau }_d$ would be the first one among these local maximum time points [17,18,19,20].

Then, the relevant statistics can be calculated by selecting proper parameters. According to the mathematical statistics results of asymptotic distribution, we chose $N=3000$, $m=2,3,4,5$, $i=1,2,3,4$ and put them into Equations (6) and (7) separately:

$$\overline{S_2}(t)=\frac{1}{16}{\displaystyle \sum _{m=2}^5{\displaystyle \sum _{i=1}^4{S}_2}}(m,r_i,t)$$

(8)

$$\Delta \overline{S_2}(t)=\frac{1}{4}{\displaystyle \sum _{m=2}^5\Delta S_2}(m,t)$$

(9)

By this stage, the first zero of $\overline{S_2}(t)$ or the first minimum point of $\overline{S_2}(t)$ is the optimal time delay ${\tau }_d$ in the reconstructed phase space of built-in accelerometer. Further, Equations (8) and (9) also can be synthesized as to follow:

$$S_c(t)=\Delta \overline{S_2}(t)+\left|\overline{S_2}(t)\right|$$

(10)

The globe minimum value of $S_c(t)$ is time-window length of the built-in accelerometer output signal sequence. An instance of $\overline{S_2}(t)$, $\Delta \overline{S_2}(t)$ and $S_c(t)$ base on a measured acceleration signal is shown in Figure 6.

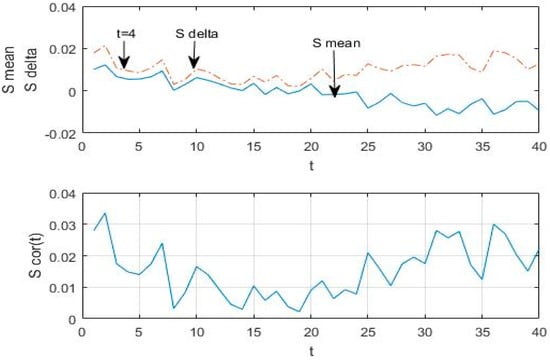
Figure 6. An instance of $\overline{S_2}(t)$, $\Delta \overline{S_2}(t)$ and $S_c(t)$ from the measured signal.

4. Experiments and Results Analysis

We verified the nonlinearity of built-in accelerometer in the smart device by experiments. As shown in Figure 7, we placed two smartphones (one is the Motorola Nexus 6, another is the HUAWEI Honor 8) closely on the surface of a still wooden table. In order to obtain the voice excitation signal with stable intensity and frequency, the smart-phones received the voice signal from two loudspeakers which were fixed above at close distance. Then, the output signals of an accelerometer in the Motorola Nexus 6 were extracted. Simultaneously, the original voice from loudspeakers was recorded by HUAWEI Honor 8 as a comparison. As excitation signals, the three specific words “on”, “zero” and “two” were spoken and played by loudspeakers. Each word was repeated 10 times with 3 seconds intervals between each repetition. Moreover, we repeated the experiment under a different distance between the speaker and mobile phone with 5 cm, 10 cm, 15 cm, 25 cm, and 30 cm, respectively.

Figure 7. Experiment setup. (a) Experiment equipment; (b) Experiment setup.

The output signals of the built-in accelerometer on X, Y and Z-axis at different distances from loudspeakers are shown in Figure 8. As a comparison, the output signals of the built-in microphone at different distances are shown in Figure 9. Besides, it is important to note that the gravity which is loaded on the Z-axis signal needs to be eliminated. It can be clearly found that the built-in accelerometer had obvious response output when we made voice as an excitation although with noise effect.

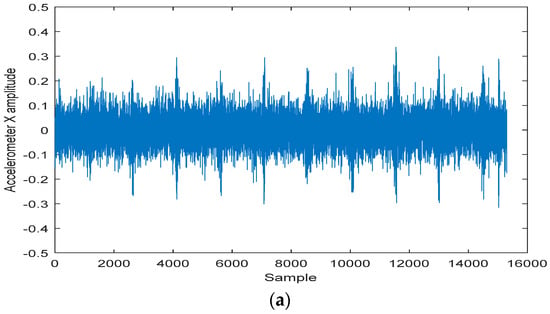
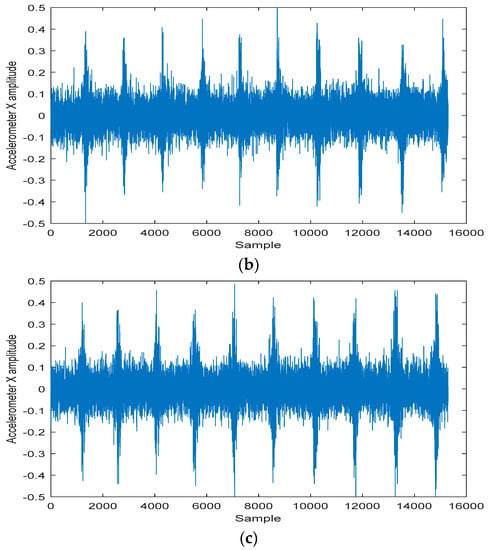
Figure 8. The output signal of the accelerometer at different distances. (a) The output signal of the accelerometer at distance of 5 cm; (b) The output signal of the accelerometer at distance of 10 cm; (c) The output signal of the accelerometer at distance of 15 cm.

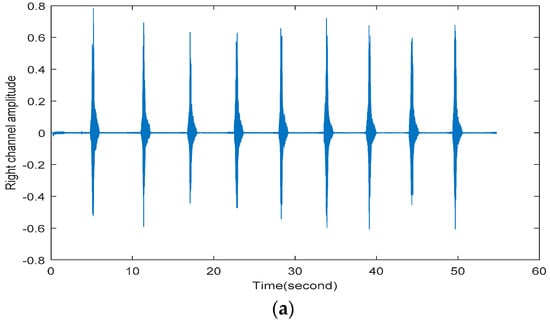
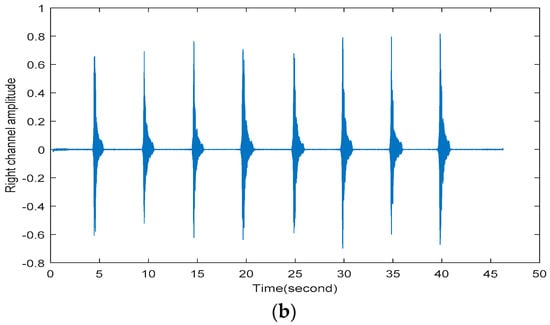
Figure 9. The recorded voice at 5 cm and 30 cm, respectively for comparison. (a) The recorded voice at 5 cm; (b) The recorded voice at 30 cm.

Using the optimal delay time $\tau$ and embedding dimension $m$ which was determined by previous calculation, the reconstruction attractors with the condition of $\tau =3,4,5,6$ for X, Y and Z-axis of the built-in accelerometer shown in Figure 10, Figure 11 and Figure 12 are attractors.

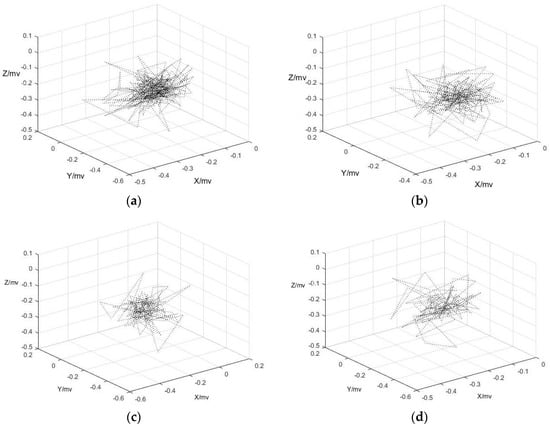
Figure 10. The attractors of $\tau$ = 3,4,5,6 at X-axis when saying “oh”. (a) The attractor of $\tau$ = 3; (b) The attractor of $\tau$ = 4; (c) The attractor of $\tau$ = 5; (d) The attractor of $\tau$ = 6.

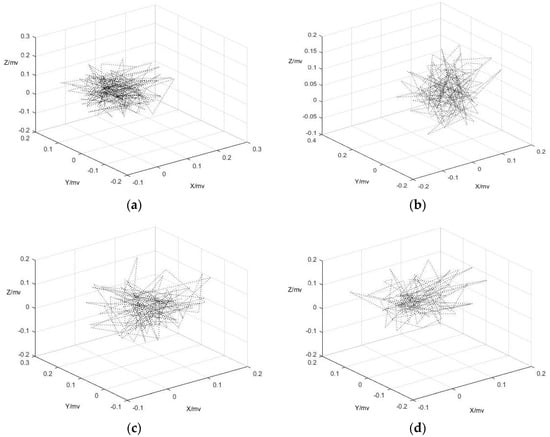
Figure 11. The attractors of $\tau$ = 3,4,5,6 at Y-axis when saying “two”. (a) The attractor of $\tau$ = 3; (b) The attractor of $\tau$ = 4; (c) The attractor of $\tau$ = 5; (d) The attractor of $\tau$ = 6.

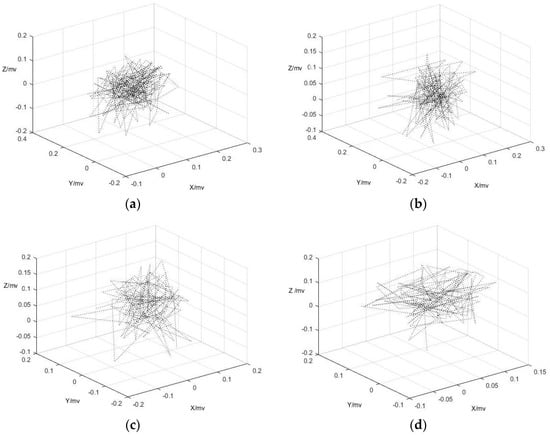
Figure 12. The attractors of $\tau$ = 3,4,5,6 at Z-axis when saying “zero”. (a) The attractor of $\tau$ = 3; (b) The attractor of $\tau$ = 4; (c) The attractor of $\tau$ = 5; (d) The attractor of $\tau$ = 6.

It was clearly found from these figures that the convergence of attractors when $\tau$ = 3, 4 and $m$ = 4 are better than others, which is consistent with the calculation results in Section 3. However, the edges of these attractors were not smoothing due to the effect of white noise in original output signals which were generated by metal plate capacitance vibration inside the acceleration when it received voice signal.

5. Nonlinear Mapping between Microphone and Accelerometer

Since the sampling rates of a microphone of VCS (44 kHz) and built-in accelerometer (200 Hz) have a large gap, it is hard to match their record voice directly. The nonlinear mapping phenomenon motivated us to find a matching relation between the microphone readings and the low sampling rate sensor data. By using nonlinear mapping, we could convert the microphone data to low-frequency data and compare that with the same frequency range motion sensor for similarity check.

We used a voice application to generate a sound of pure frequency tones in the frequency range of 100 Hz–1600 Hz (with 100 Hz interval) and checked whether the signal could be observed in the frequency domain of microphone and built-in accelerometer. Figure 13 shows that some high-frequency voices could be observed in accelerometer (230 Hz). Significant frequency response on accelerometer readings was on 400 Hz and 1600 Hz.

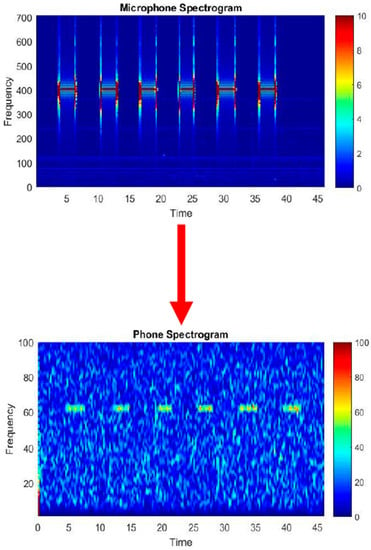
Figure 13. Nonlinear mapping between microphone and accelerometer.

6. Conclusions

Besides collecting user’s information, such as the speed and direction, the output signal of the built-in sensor in the smart device shows obvious nonlinear characteristics when the voice commands as excitation. In this paper, using chaotic system theory, we calculated the optimal delay time and the best embedding dimension, and further attractors for a nonlinear system. In addition, we also made phase space reconstruction of the built-in acceleration system under the condition of inputting voice commands. Therefore, this is the foundation of further feature extraction and nonlinear analysis of built-in sensor output signals.