A Game-Theoretic Analysis for Distributed Honeypots

Abstract

A honeypot is a decoy tool for luring an attacker and interacting with it, further consuming its resources. Due to its fake property, a honeypot can be recognized by the adversary and loses its value. Honeypots equipped with dynamic characteristics are capable of deceiving intruders. However, most of their dynamic properties are reflected in the system configuration, rather than the location. Dynamic honeypots are faced with the risk of being identified and avoided. In this paper, we focus on the dynamic locations of honeypots and propose a distributed honeypot scheme. By periodically changing the services, the attacker cannot distinguish the real services from honeypots, and the illegal attack flow can be recognized. We adopt game theory to illustrate the effectiveness of our system. Gambit simulations are conducted to validate our proposed scheme. The game-theoretic reasoning shows that our system comprises an innovative system defense. Further simulation results prove that the proposed scheme improves the server’s payoff and that the attacker tends to abandon launching attacks. Therefore, the proposed distributed honeypot scheme is effective for network security.

1. Introduction

There have been many security issues regarding networks over the past few decades. Since traditional defense technology is passive with respect to defending against intruders, an active honeypot becomes a crucial component for defenders to safeguard their system. A honeypot [1,2] is a decoy tool in network security that lures attacker to interact with it, further exhausting the attacker’s resources. It can be a partial or full duplication of a specific system replying to the attacker in disguise. The attacker gains access to fake resources and has no idea about the real ones. The resources of attackers being occupied by the honeypot are isolated, meaning they cannot be used to launch an effective attack.

As a decoy tool, the honeypot uses meaningless resources to interact with the attacker. Due to its fake nature, it is likely to be recognized by the intruder [3]. Then, the honeypot becomes an unmeaningful technology, and the attacker can avoid it and acquire the real resources. Among some related technologies, the static honeypot is the easiest one to identify. The static honeypot remains unchanged, which indicates that some of its properties can be easily identified by some attack tools. This helps the attacker abandon a honeypot and search for the real system.

The dynamic honeypot improves the disadvantages of the static honeypot, whose configurations are dynamically transformed. The dynamic characteristic is mainly reflected in the configuration. By adjusting the configuration information, the honeypot can demonstrate a high attraction feature. Therefore, the attacker cannot distinguish the honeypot from the system. However, most locations of such honeypots are stationary. Once the attackers find these flaws, they tend to bypass these exposed honeypots, which makes them insufficient in dealing with the attacks.

Game theory [4,5] can be used for system analysis regarding security issues under different strategies for modeling the behavior of a variety of participants. In network security, the interactions between the defender and its adversary can be modeled as game analysis. The payoff of one player usually depends on the action of the other player.

In this paper, we propose a dynamic honeypot scheme whereby the locations are distributed [6]. Besides, these honeypots and real services are always changing. Uncertainty exists in this system; thus, it presents uncertaintyto the attackers. A honeypot-related Bayesian system game model is introduced to illustrate our scheme’s effectiveness. We prove that the optimal equilibrium condition can be achieved by adjusting the proportion of honeypots.

The main contributions of this paper are summarized as follows:

• We propose a distributed honeypot scheme with changeable services, which forms our traps for the attacker.
• We introduce game theory into the proposed system model to analyze the players’ strategies and payoffs. The effectiveness of our system is proven by Bayesian equilibriums.
• We conduct simulations to validate the effectiveness of our scheme.

The rest of this paper is organized as follows. In Section 2, we review the related literature on honeypots and game theory. The system model is described in Section 3. In Section 4, we illustrate the effectiveness of our proposed system in the context of game theory. Simulations are conducted in Section 5. Finally, Section 6 concludes this paper.

2. Related Work

In this section, we propose a summary of the state-of-the-art literature on honeypots and game theory. Honeypots serve as decoy systems to interact with attackers. They have been applied to safeguard systems in quite a few fields. The defender and its opponent can be modeled in a game. Game theory [7,8,9,10,11,12] is used for analyzing an attack-defense process and for obtaining dominant strategies.

2.1. Honeypot in Network Security

The honeypot has been widely used in network for system protection. It can be applied to some fields, such as unmanned aerial vehicles and cloud computing. It functions for detecting malware, identifying illegal traffic, learning behavior of an intruder, tracking an attack, etc..

With a fuzzy approach, a spoofing attack detection mechanism is proposed in [13]. The low-interaction honeypot called KFSensor gathers the experimental data for analysis. A micro-honeypot is presented to track a web attack using browser fingerprinting technology [14]. Any attackers’ identification information will be recorded by the honeypot. Even if these attackers hide themselves, the honeypot can still track them and collect their local IPs (internet protocol addresses). In [15], a low-interaction honeypot and a darknet are correlated by the observed attack time. The scheme can be used to detect scanning attack activities and to estimate the corresponding scale, in which the honeypot records payload data in TCP (transmission control protocol) stream. Besides, the honeypot only responds to TCP SYN (synchronize sequence numbers) and ICMP (internet control messages protocol) echo packets. A medium-interaction honeypot called HoneyDrone is proposed for protecting UAVs (Unmanned Aerial Vehicles) [16]. It emulates some UAV-related protocols to lure an attacker into launching an attack. A new threat intelligence model is proposed in [17]. a honeypot is deployed in a cloud to obtain attack logging. The obtained data are examined to explore the attack pattern in an internet event.

A deep Q-Learning algorithm is involved in an SSH self-adaptive honeypot system [18], further guiding the honeypot named Cowrie to interact with adversaries. Cowrie is modified to be capable to learn the behavior of an intruder. In [19], a dynamic extensible two-way honeypot is introduced into, which allows incoming and outgoing traffic. The outgoing traffic is held when it contains malicious shellcode and the shellcode is copied and replaced. The mechanism monitors how an intruder interacts with a victim host. Based on machine learning technology, a dynamic honeypot is presented for threat intelligence in a context-aware way [20]. The honeypot is featured with intelligence in deployment with no preset configuration. At the beginning of defense, the honeypot in [21] detects and tags attack flows. The autonomous dynamic honeypot routing is proposed for the identified illegal traffic. Mixture of server nodes and honeypots in DMZ (demilitarized zone) safeguard the network. An adaptive honeypot is integrated with dynamic taint analysis technology [22]. By capturing the commands issued by an intruder, it can detect rootkits. Monitoring sensors and Dionaea-based honeypots constitute a dynamic honeynet system [23]. According to an intruder’s behavior, the honeynet reacts flexibly. Detection efficiency is improved via dynamic configuration and the system is efficient in identifying attackers. The framework mentioned in [24] uses honeypots to generate several interesting points for attackers, further detecting zero-day vulnerabilities and some other attack technologies.

2.2. Game Theory for System Analysis

Game theory can be used to analyze the performance of a system with multiple players whenever rational conditions are assumed. Non-cooperative game theory and evolutionary game theory are applied to some fields (e.g., wireless sensor network, opportunistic network and software defined network).

Non-cooperative game theory with a decentralized clustering algorithm is present in [25] to solve the problem of prolonging a network’s maximum lifetime. The game theory is adopted for limiting activities of a sensor and its neighbors to save battery energy. Based on evolutionary game theory, the work [26] presents an active defense model in wireless sensor network. The reliability and stability in a network equipped with malicious nodes are analyzed. A preventive mechanism is established to force these nodes to abandon attack activities. A PT-based game-theoretic security protocol is presented in [27], which counters black hole attacks in opportunistic network (OppNets). An evolutionary game theory model is applied to this defense mechanism for analyzing the decision-making ability.

A multi-layered game is proposed in [28]. The IDS (intrusion detection system) and the malicious vehicle are modeled as a non-cooperative game and the Nash equilibrium strategy of probabilistic IDS monitoring is adopted. The work [29] proposes a dynamic SDN (software defined network) framework with a game-theoretic model to analyze its security performance in attack protection. In the game, a defender and its adversary compete for the right of control in some controllers. Three levels (i.e., sensor level, cluster level and base station level) are applied to the proposed framework in [30], which uses a combination of specific rules and a lightweight neural network to identify illegal sensors. Based on the multi-layered intrusion detection framework, two players form out a non-cooperative Bayesian game. Game theory is used in wide scan [31] for analyzing mass scanning problem. A scanner and its target act as players in an antagonistic game. Based on game theory and reinforcement learning mechanism, a two-stage distributed algorithm is proposed [32] to improve quality of experience at runtime. A multi-cell device is modeled [33]. The allocation issue in resource block is formulated as a bilateral symmetric interaction game. Decision-making scenarios are modeled as games in information warfare [34]. The participants include an offensive player and a defensive one.

2.3. Game-Theoretic Approaches to Model Honeypots

There have been some works that combine a honeypot with game theory in term of security issues. The system equipped with honeypots serves as a player (i.e., the defender) and the other (i.e., the attacker) acts as its adversary. Payoffs are analyzed and the results of some specific purposes are derived.

In [35], a game-theoretic model that involves an attacker and a defender is applied to IoT (Internet of Things). Two players interact with the other in disguise. The former employs several attack techniques and the latter uses a honeypot as a deception tool. Such a problem is modeled as Bayesian game of incomplete information. A honeypot is applied to social network [36]. In the proposed pseudo honeypot game model, the attacker is rational and will choose the optimal strategy according to the defender’s strategy. Bayesian Nash equilibriums are proved under different circumstances, capable of reducing energy consumption and of improving efficiency.

A honeypot is introduced into the advanced metering infrastructure network [37]. Via analysis of interactions between the defenders and their adversaries, optimal strategies are derived, and several Bayesian Nash equilibriums are proved. A game-theoretic model for defending against attacks is studied in honeypot-enabled IoT [38]. A Stackelberg-style game, which consists of a leader and its follower, is employed in an enterprise network [39]. In this model, the defender serves as a leader to identify the optimal placement of firewalls, IDS, and honeypots simultaneously. A signaling game with perfect Bayesian equilibrium is used in [40] for performance analysis of denial of service (DoS) defense. As a deceptive tool, a honeypot can deceive attackers. Then, a deception-based protection mechanism is proposed, involving game theory to model the interactive activities among players. In the studied scenario, the defender takes first step to decide whether to camouflage or not. After that the attacker responds with three different actions (i.e., attack, observe, and retreat). Since the adversary is uncertain of the system type, this is a game of incomplete information. A honeypot is incorporated with the proposed model, serving as a probing device [41]. A game-theoretic approach is adopted in cloud infrastructure for mitigating the economic denial of sustainability attack. In a static game scenario, an interactive game is modeled to find the optimal strategic threshold value for limiting incoming flow via Nash equilibriums.

A game-theoretic approach is used to explore the best solution in detection of low-rate denial of service attacks (e.g., Shrew) [42]. The presented solution relies on the bandwidth threshold, below which the flow will be transmitted to a honeypot server. In a static simultaneous game, determination of firewalls’ best detection option is the defender’s strategy. Meanwhile, the attacker’s strategy is to exploit some related mechanisms and elude the low-rate detector. Both parties’ payoffs are calculated. Flexibility features Content delivery network, in which distributed nodes suffer from some security problems. An optimal hybrid algorithm is proposed to cope with intrusion issues, which contains game theory, signature and honeypots [43]. Combination thwarts illegal intruders and solves resource allocation problems. This proposal combines both cooperative and non-cooperative game theories due to its hybrid nature. A methodology provided by game theory is used in [44] for decision support. Two players and multistage game are modeled for network defense where a honeypot distracts an attacker as a decoy host. As a player, the administrator chooses the optimal decision in allocation of honeypots, which can minimize the cost and loss brought by an attacker. Meanwhile, the attacker adopts the strategy that maximizes the value of destabilizing a network and that minimizes the corresponding cost.

3. System Model

In this section, we introduce the distributed honeypots model. The notations used in this section are shown in

Table 1. Notations used in system model.

Symbol	Description
$t_i$	A point of time
$T_i$	A period
$Serve{r}_i$	A server
$Servic{e}_{fake}$	honeypot
$Servic{e}_{real}$	Real service
$Servic{e}_{null}$	Closed service
$Su{m}_{server}$	Sum of servers
$Su{m}_{service}$	Sum of services

.

Figure 1 demonstrates the system structure. There are several hosts in our system, which serve as servers for providing some necessary services. These services are installed in every server, such as a web service, a database service and a file service. There are two categories in each service: fake service (i.e., honeypot) and real service.

Resources regarding a real service are in a specific folder. Besides, a different folder contains fake resources for a honeypot, which aims at luring, interacting, and identifying an attacker. A real service may be on one of the servers $\{serve{r}_1,serve{r}_2,\dots ,serve{r}_{Su{m}_{server}}\}$. At the meantime, there exist some fake services among them, which serve as decoys for unexpected intruders.

Next, we present formalization description regarding the distribution of services. A two-dimensional array is formed:

$$serviceArr[Su{m}_{server},Su{m}_{service}]=\{\{0,1,\dots ,1,0\},\{1,0,\dots ,0,1\},\dots ,\{0,1,\dots ,0,1\},\{0,1,\dots ,0,0\}\}.$$

The row illustrates all services in a server. As illustrated in

Table 2. The illustration of 01 codes.

Codes	Symbol	Description
00	$Servic{e}_{null}$	Service is closed
10	$Servic{e}_{real}$	Real service is opened
01	$Servic{e}_{fake}$	Honeypot is opened

, every two 01 codes indicate the state of one service.

Figure 2 presents distribution of all services at $t_0$. There are five servers and eight kinds of services. As illustrated in

Table 3. The overall information of services at $t_0$.

Server	Services	01 codes
$Serve{r}_1$	$MySQ{L}_{real},Ngin{x}_{fake},Apach{e}_{null},Vsftp{d}_{fake}$	$1,0,0,1,0,0,0,1$
$Serve{r}_2$	$MySQ{L}_{fake},Ngin{x}_{real},Apach{e}_{null},Vsftp{d}_{fake}$	$0,1,1,0,0,0,0,1$
$Serve{r}_3$	$MySQ{L}_{null},Ngin{x}_{null},Apach{e}_{real},Vsftp{d}_{fake}$	$0,0,0,0,1,0,0,1$
$Serve{r}_4$	$MySQ{L}_{null},Ngin{x}_{fake},Apach{e}_{null},Vsftp{d}_{null}$	$0,0,0,1,0,0,0,0$
$Serve{r}_5$	$MySQ{L}_{fake},Ngin{x}_{null},Apach{e}_{fake},Vsftp{d}_{real}$	$0,1,0,0,0,1,1,0$

, the two-dimensional array at $t_0$ is $serviceAr{r}_{t_0}[5,8]=\{\{1,0,0,1,0,0,0,1\},\{0,1,1,0,0,0,0,1\},\{0,0,0,0,1,0,0,1\},\{0,0,0,1,0,0,0,0\},\{0,1,0,0,0,1,1,0\}\}$.

As shown in Figure 3, all services are periodically changing. Traffic identification is done once an invasion of a honeypot occurs. Any intrusion records detected in honeypots are labeled as illegal traffic. There are three possible cases for an attacker:

• Honeypot. The attacker intrudes into a honeypot. For example, Nginx is a honeypot at $t_0$. Any access to Nginx will be labeled as illegal traffic.
• Real service ⟹ honeypot. The attacker gains access to a real service. However, it becomes a honeypot at $t_1$ in the next period $T_1$. For example, MySQL is a real service at $t_0$ and becomes a honeypot at $t_1$. Any access to MySQL will be identified as illegal traffic at $t_1$.
• Real service ⟹ Real service $⟹\dots ⟹$ honeypot. The attacker intrudes into a real service for s times. Since the real services are always unpredictable for an attacker, the probability to meet a real service is $\frac{1}{Su{m}_{server}\times Su{m}_{service}}$. In such case, the general probability is approximately equal to the minimum number ${\{\frac{1}{Su{m}_{server}\times Su{m}_{service}}\}}^s$.

In general, illegal traffic can be recognized. Besides, a legal user has access to real services via encrypted communication with distributed servers. Therefore, the user can always avoid honeypot traps and gain real resources. Based on our proposed system model, strategies and payoffs of all players are analyzed in Section 4.

4. Game Theory Analysis

In this section, we present a game model based on the distributed honeypots to define payoff functions and to derive Bayesian Nash equilibriums. Then, we illustrate the effectiveness of our scheme. The notations used in the game are shown in

Table 4. Notations used in the game.

Symbol	Description
$\mathsf{\Theta }$	The set of players
${\mathsf{\Theta }}_1$	The set of services
${\mathsf{\Theta }}_2$	The set of visitors
${\theta }_{1i0}$	A real service
${\theta }_{1i1}$	A honeypot
${\theta }_{20}$	A legal user
${\theta }_{21}$	An illegal attacker
${\pi }_{10}$	Service is closed
${\pi }_{11}$	Service is opened
${\pi }_{2i0}$	Visitor accesses a real service
${\pi }_{2i1}$	Visitor accesses a fake service
${\pi }_{20}$	Visitor does not access the server
${\pi }_{21}$	Visitor accesses the server
${\mu }_{{\theta }_{1ij}\left({\pi }_{1k}\right)}$	Payoff of a server
${\mu }_{{\theta }_{2i}\left({\pi }_{2k}\right)}$	Payoff of a visitor
q	Probability of a honeypot
p	Probability of an attacker
$P\left({\theta }_{20}\right)$	A priori probability of a user
$P\left({\theta }_{21}\right)$	A priori probability of an attacker
$P\left({\theta }_{1n0}\right)$	A priori probability of a real service
$P\left({\theta }_{1n1}\right)$	A priori probability of a honeypot
$P^{{}^{\prime }}\left({\theta }_{20}\right|{\pi }_{21})$	a posteriori probability of a user
$P^{{}^{\prime }}\left({\theta }_{21}\right|{\pi }_{21})$	a posteriori probability of an attacker
$P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{11})$	a posteriori probability of a real service
$P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})$	a posteriori probability of a honeypot

.

4.1. Game Model of the Distributed Honeypots

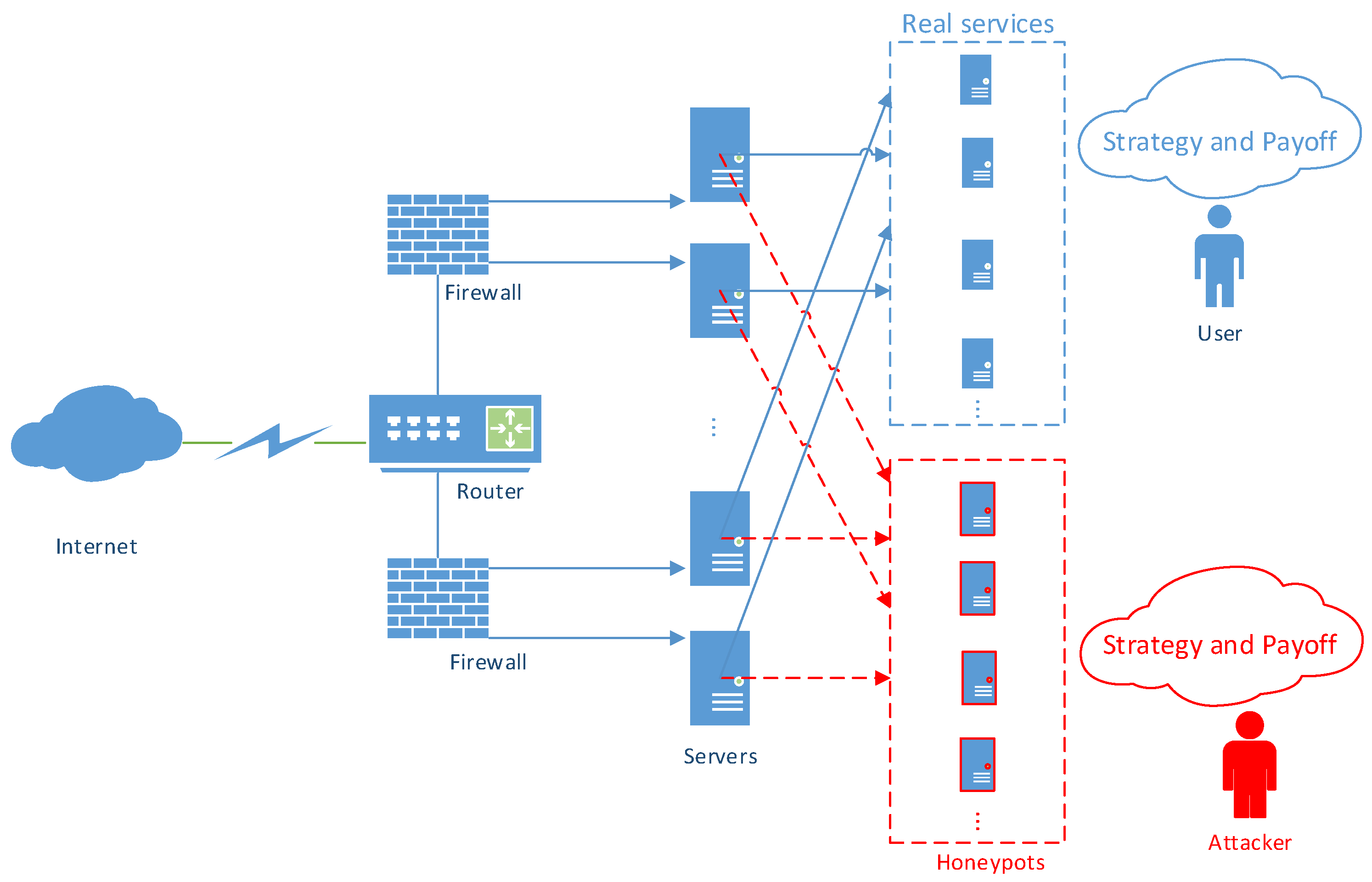
Taking attack-defense countermeasure into consideration, there are two kinds of players (i.e., attacker and defender) participating in a game. Since both the real service and honeypot exist in the same server and the real one aims at providing real resources for legal users to access, there are three kinds of players $\mathsf{\Theta }$ = {$server,attacker,user$}. We model our proposed scheme as follows.

There are n kinds of services ${\mathsf{\Theta }}_1$ = {${\theta }_{11}$, ${\theta }_{12}$, …, ${\theta }_{1n}$}. Because of the existence of honeypots, these services are changed to ${\mathsf{\Theta }}_1$ = {${\theta }_{110}$, ${\theta }_{111}$, ${\theta }_{120}$, ${\theta }_{121}$, …, ${\theta }_{1n0}$, ${\theta }_{1n1}$}, and these parameters can be generalized into ${\mathsf{\Theta }}_1$ = {${\theta }_{1i0}$, ${\theta }_{1i1}$}, i∈ [1,n]. Visitors ${\mathsf{\Theta }}_2$ = {${\theta }_{21}$, ${\theta }_{20}$} = {$Attacker$, $User$} is a common name for the last two players mentioned in $\mathsf{\Theta }$. Therefore, players participating in the game are included in $\mathsf{\Theta }$ = {$Server$, $Visitors$}. They may take different activities in a game. However, they will only choose a relatively good strategy when they interact with each other under different circumstances.

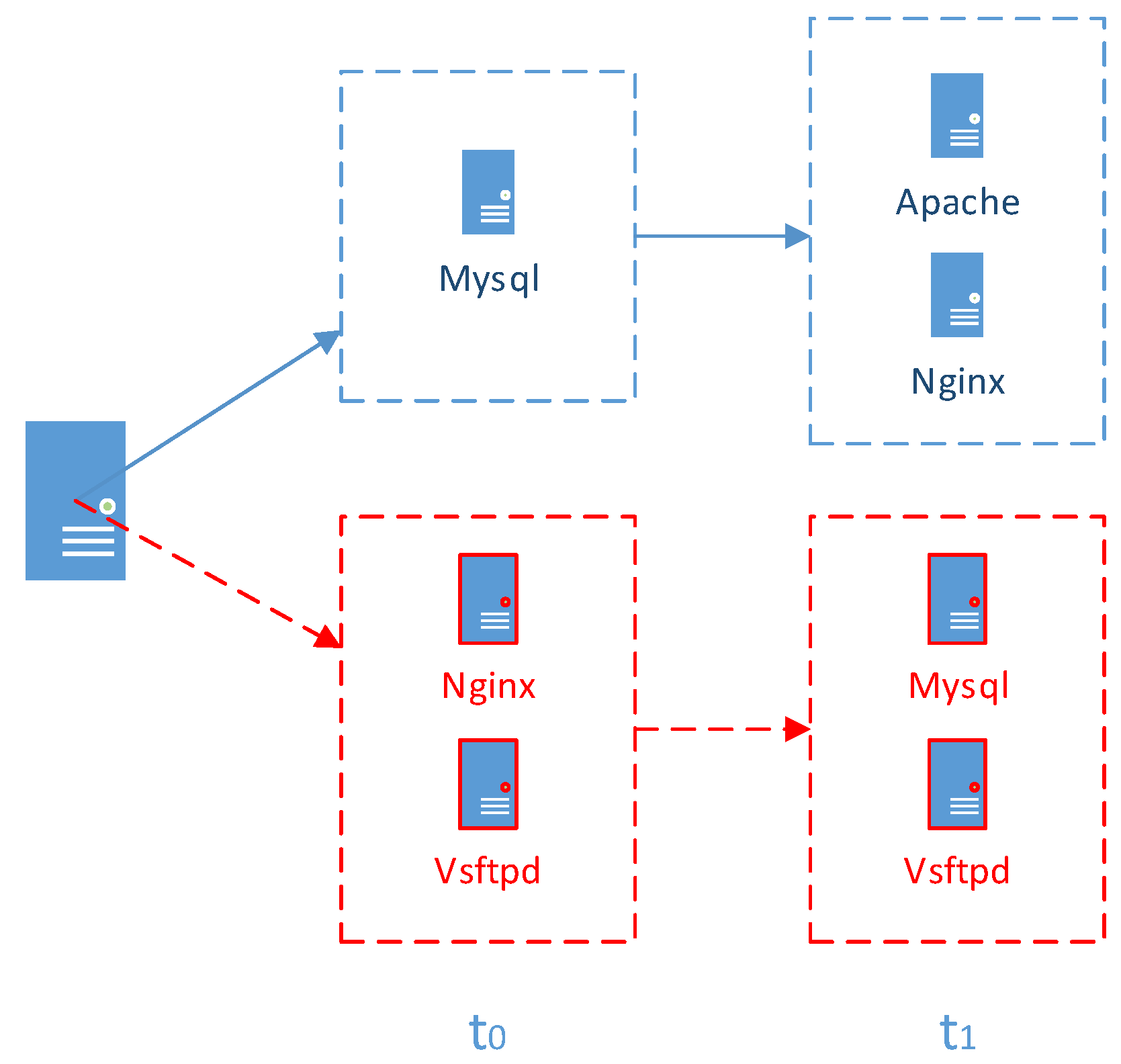
As mentioned above, there are several services provided in our system. Due to a variation characteristic, every server provides different kinds of services during different periods. Therefore, a server can turn on a service or turn off it. As for visitors, they can decide whether to access it or not. The strategy sets are composed of $A_1$ = {${\pi }_{11}$,${\pi }_{10}$} and $A_2$ = {${\pi }_{210}$, ${\pi }_{211}$, …, ${\pi }_{2n0}$, ${\pi }_{2n1}$, ${\pi }_{20}$} for a server and a visitor respectively.

It is necessary to specify the basic parameters that reflect all players’ payoffs, as shown in

Table 5. List of parameters of the players.

Parameters	Conditions	Descriptions
a	$a>0$	the fundamental payoff of server
b	$a\ge b>0$	the attack cost of attacker
c	$c>0$	the basic payoff for honeypot
$\gamma$	$\gamma \ge 1$	the damage factor in a hack
$\eta$	$\eta \ge 1$	the decoy factor of honeypot

.

Based on our system model, the payoffs are described for two cases as follows.

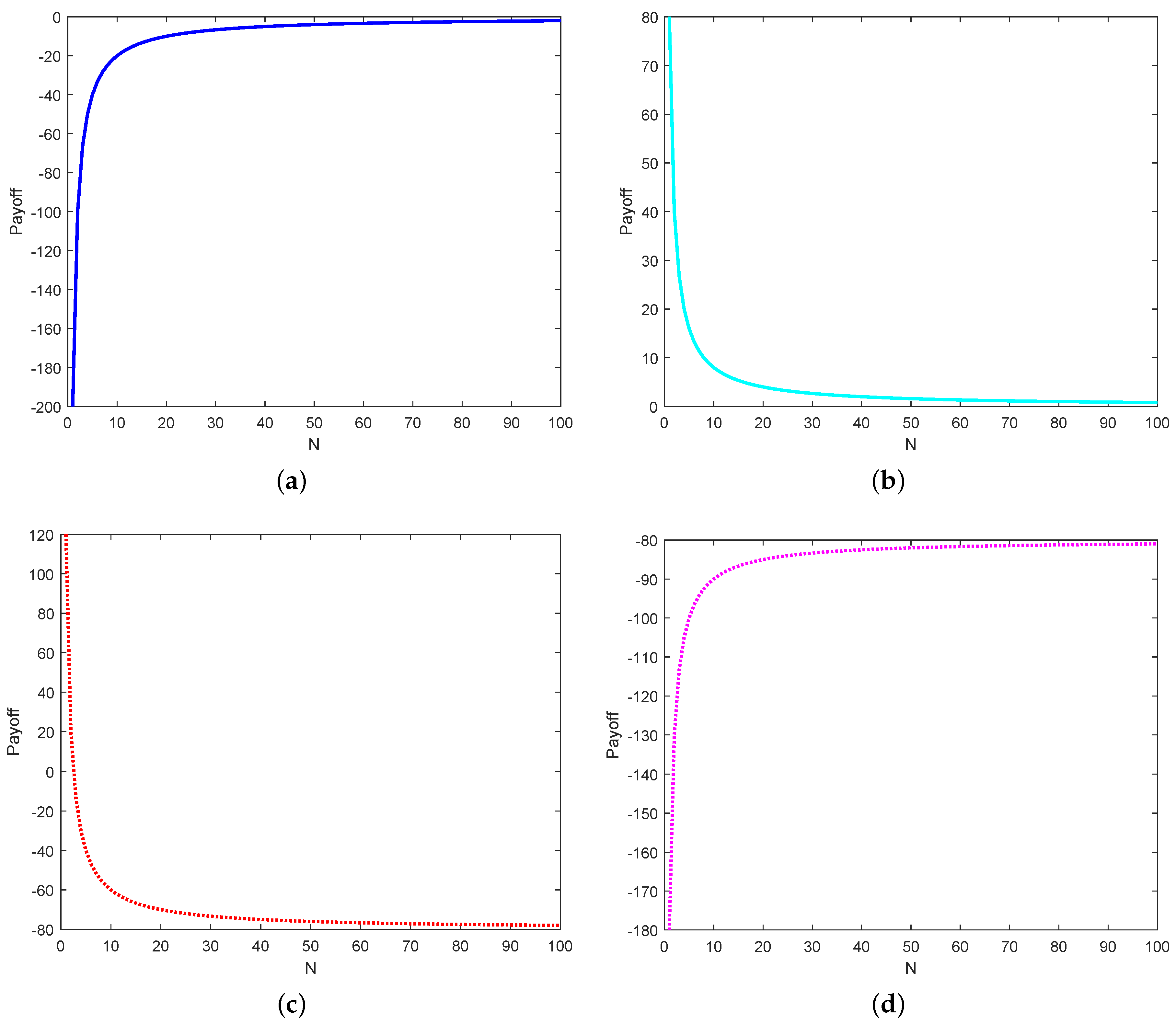
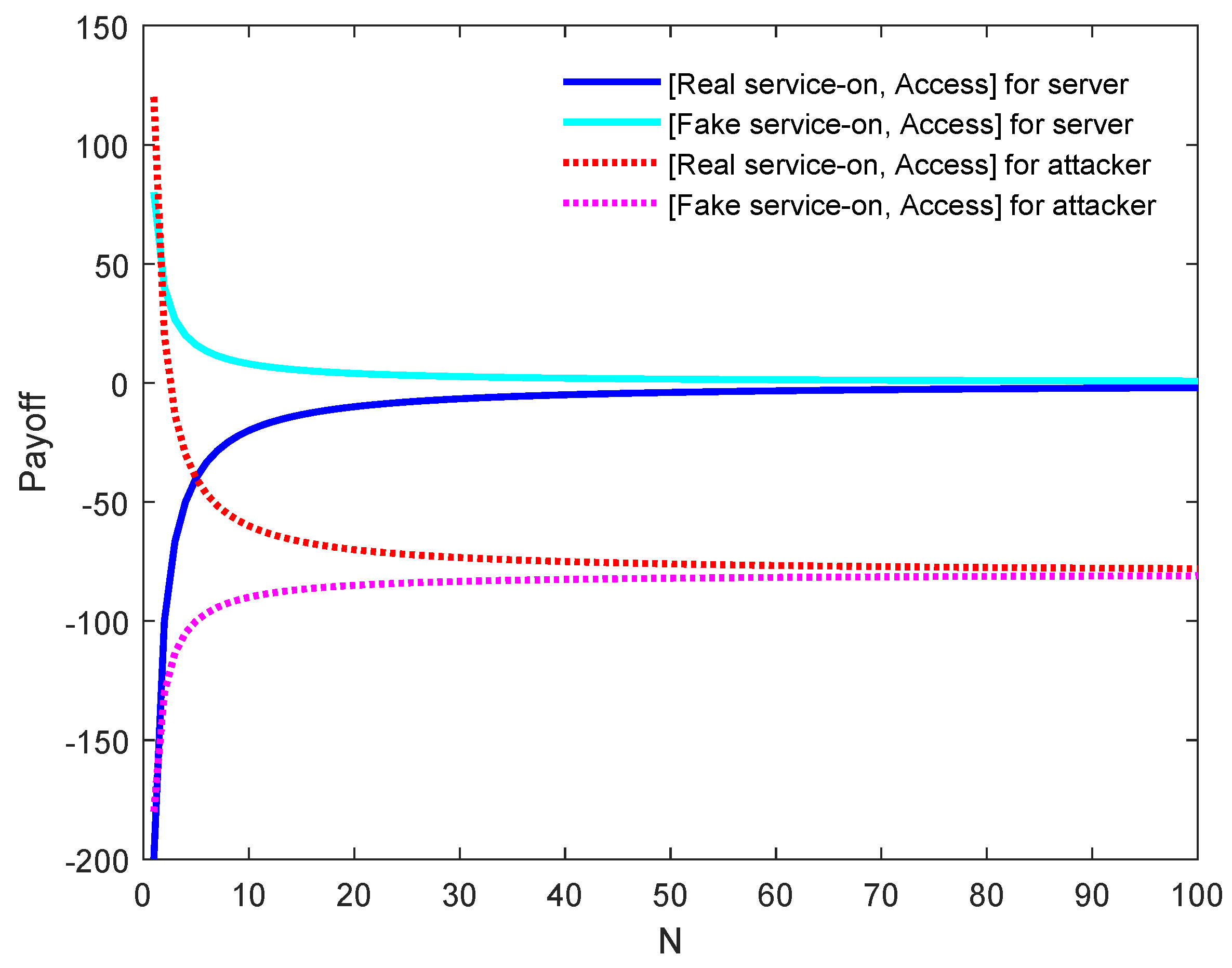
• A real service ${\theta }_{1n0}$ is provided by a server. If an attacker gains access to a real service (i.e., ${\pi }_{2n0}$), the payoffs are $(-\gamma a,\gamma a-b)$ for $\{Server,Attacker\}$. The server suffers from providing a real service to the attacker. If a user accesses a real service (i.e., ${\pi }_{2n0}$), the payoffs are $(a,a)$ for $\{Server,User\}$. Both have normal payoffs, which indicates that the server provides the legal user with a normal service. If visitors access other services, the payoffs are $(0,-b)$ for $\{Server,Attacker\}$ and $(-a,-a)$ for $\{Server,User\}$, which means that they are suffering a loss when they do not have access to real resources.
• A fake service ${\theta }_{1n1}$ is provided by a server. If an attacker visits a fake service (i.e., ${\pi }_{2n1}$), the payoffs are $(\eta c,-\eta c-b)$ for $\{Server,Attacker\}$. The attacker suffers a loss in attacking the honeypot and the server’s payoff is an optimistic value. If a user accesses a fake service (i.e., ${\pi }_{2n1}$), the payoffs are $(0,-a)$ for $\{Server,User\}$. In this case, the fake resources are provided to the user who ought to access a real service, making it suffer losses. Besides, if visitors do not access any service (i.e., ${\pi }_{20}$), the payoff is 0 for all players.

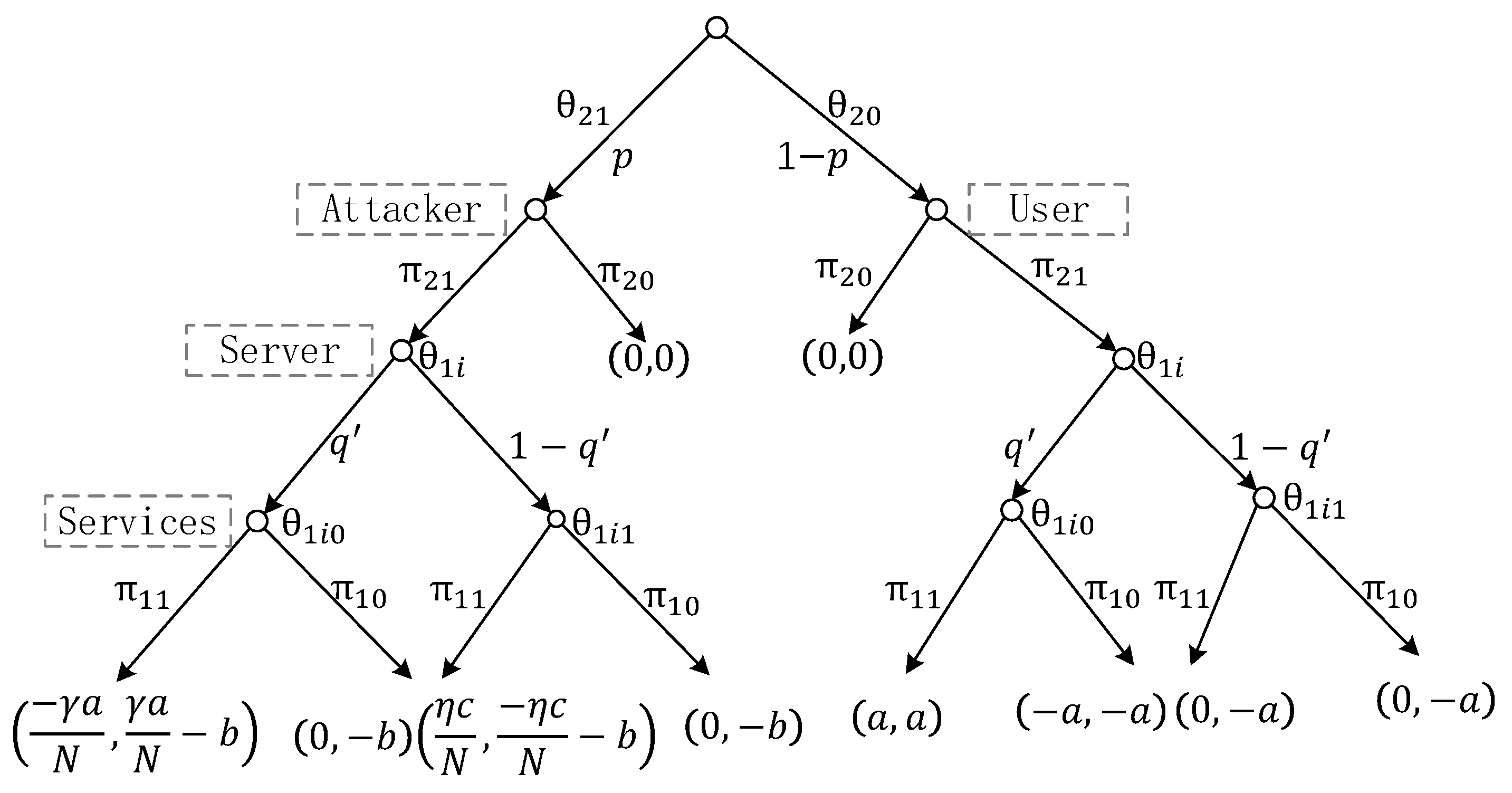
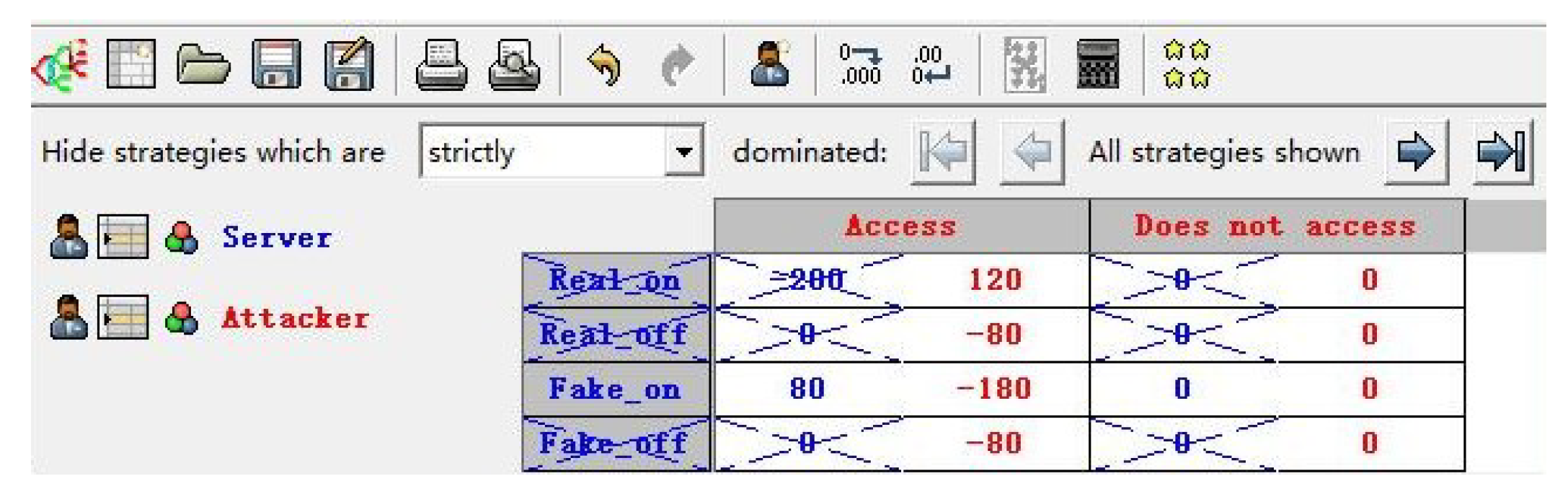
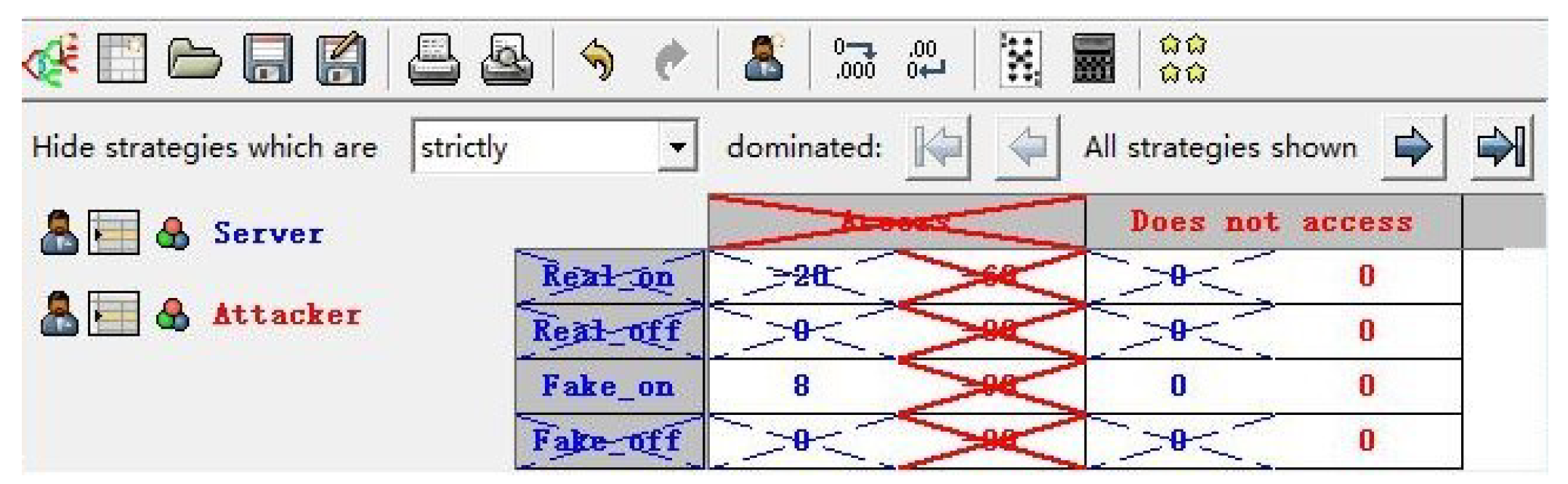
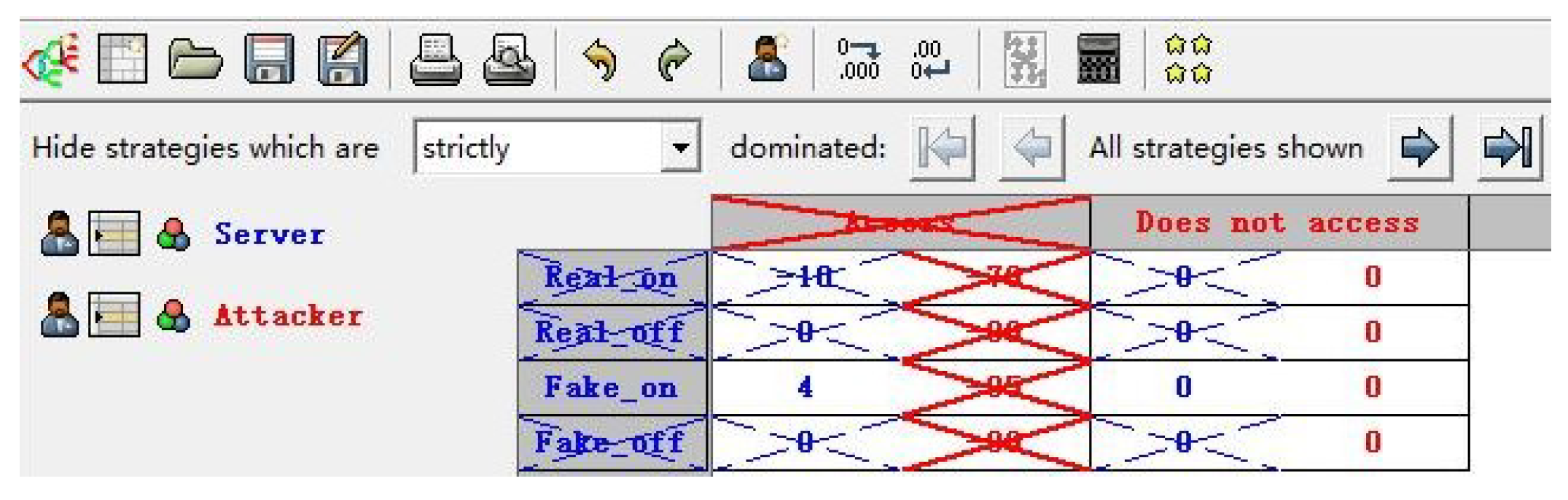
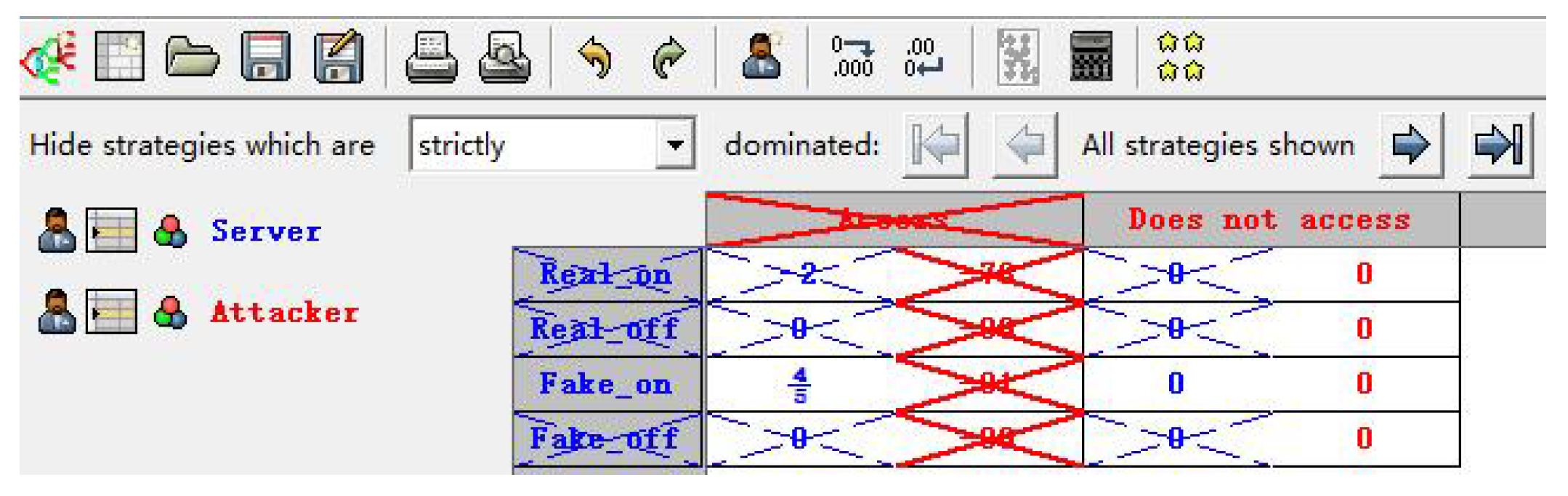
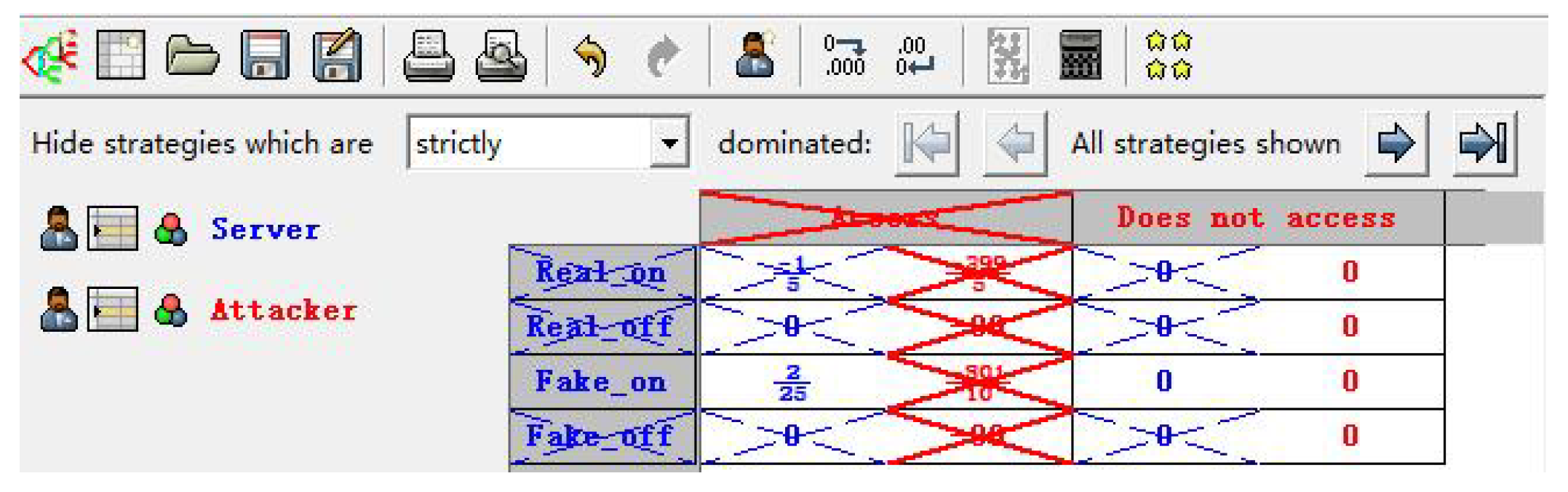
The corresponding payoff matrix is shown in

Table 6. Payoffs matrix table.

				$\mathbf{Attacker}$						$\mathbf{User}$
				${\mathit{\pi }}_{\mathbf{210}}$	${\mathit{\pi }}_{\mathbf{211}}$	⋯	${\mathit{\pi }}_{\mathbf{2}\mathit{N}\mathbf{0}}$	${\mathit{\pi }}_{\mathbf{2}\mathit{N}\mathbf{1}}$	${\mathit{\pi }}_{\mathbf{20}}$	${\mathit{\pi }}_{\mathbf{210}}$	${\mathit{\pi }}_{\mathbf{211}}$	⋯	${\mathit{\pi }}_{\mathbf{2}\mathit{N}\mathbf{0}}$	${\mathit{\pi }}_{\mathbf{2}\mathit{N}\mathbf{1}}$	${\mathit{\pi }}_{\mathbf{20}}$
$Server$	${\theta }_{11}$	${\theta }_{110}$	${\pi }_{11}$	($-\gamma a,\gamma a-b$)	$(0,-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(a,a)$	$(-a,-a)$	⋯	$(-a,-a)$	$(-a,-a)$	$(0,0)$
			${\pi }_{10}$	$(0,-b)$	$(0,-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(-a,-a)$	$(-a,-a)$	⋯	$(-a,-a)$	$(-a,-a)$	$(0,0)$
		${\theta }_{111}$	${\pi }_{11}$	$(0,-b)$	$(\eta c,-\eta c-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(0,-a)$	$(0,-a)$	⋯	$(0,-a)$	$(0,-a)$	$(0,0)$
			${\pi }_{10}$	$(0,-b)$	$(0,-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(0,-a)$	$(0,-a)$	⋯	$(0,-a)$	$(0,-a)$	$(0,0)$
	${\theta }_{12}$	${\theta }_{120}$	${\pi }_{11}$	$(0,-b)$	$(0,-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(-a,-a)$	$(-a,-a)$	⋯	$(-a,-a)$	$(-a,-a)$	$(0,0)$
			${\pi }_{10}$	$(0,-b)$	$(0,-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(-a,-a)$	$(-a,-a)$	⋯	$(-a,-a)$	$(-a,-a)$	$(0,0)$
		${\theta }_{121}$	${\pi }_{11}$	$(0,-b)$	$(0,-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(0,-a)$	$(0,-a)$	⋯	$(0,-a)$	$(0,-a)$	$(0,0)$
			${\pi }_{10}$	$(0,-b)$	$(0,-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(0,-a)$	$(0,-a)$	⋯	$(0,-a)$	$(0,-a)$	$(0,0)$
						⋮						⋮
	${\theta }_{1N}$	${\theta }_{1N0}$	${\pi }_{11}$	$(0,-b)$	$(0,-b)$	⋯	($-\gamma a,\gamma a-b$)	$(0,-b)$	$(0,0)$	$(-a,-a)$	$(-a,-a)$	⋯	$(a,a)$	$(-a,-a)$	$(0,0)$
			${\pi }_{10}$	$(0,-b)$	$(0,-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(-a,-a)$	$(-a,-a)$	⋯	$(-a,-a)$	$(-a,-a)$	$(0,0)$
		${\theta }_{1N1}$	${\pi }_{11}$	$(0,-b)$	$(0,-b)$	⋯	$(0,-b)$	$(\eta c,-\eta c-b)$	$(0,0)$	$(0,-a)$	$(0,-a)$	⋯	$(0,-a)$	$(0,-a)$	$(0,0)$
			${\pi }_{10}$	$(0,-b)$	$(0,-b)$	⋯	$(0,-b)$	$(0,-b)$	$(0,0)$	$(0,-a)$	$(0,-a)$	⋯	$(0,-a)$	$(0,-a)$	$(0,0)$

. The simplified payoff matrix is shown in

Table 7. The simplified payoff matrix.

		$\mathbf{Attacker}$		$\mathbf{User}$
		${\mathit{\pi }}_{\mathbf{21}}$	${\mathit{\pi }}_{\mathbf{20}}$	${\mathit{\pi }}_{\mathbf{21}}$	${\mathit{\pi }}_{\mathbf{20}}$
${\theta }_{110}$	${\pi }_{11}$	$(-\gamma a/N$,$\gamma a/N-b)$	$(0,0)$	$(a,a)$	$(0,0)$
	${\pi }_{10}$	$(0,-b)$	$(0,0)$	$(-a,-a)$	$(0,0)$
${\theta }_{111}$	${\pi }_{11}$	$(\eta c/N$,$-\eta a/N-b)$	$(0,0)$	$(0,-a)$	$(0,0)$
	${\pi }_{10}$	$(0,-b)$	$(0,0)$	$(0,-a)$	$(0,0)$

and its game tree is illustrated in Figure 4.

An essential assumption of our game model is that players are insensible of each other’s strategies. For judgment of a server and visitors, the priori probabilities are assumed to be: $\{P\left({\theta }_{21}\right)=p,P\left({\theta }_{20}\right)=1-p\},$ $\{P\left({\theta }_{1n1}\right)=q,P\left({\theta }_{1n0}\right)=1-q\}.$

As aforementioned in Table 7, ${\pi }_{21}$ and ${\pi }_{20}$ are two basic strategies for visitors. They can decide whether to access a server or not. ${\pi }_{11}$ and ${\pi }_{10}$ are two basic strategies for servers. They can choose to open or close a service. There are two strategy sets, each one consists of four strategy subsets: $\{({\pi }_{21},{\pi }_{21}),({\pi }_{21},{\pi }_{20}),({\pi }_{20},{\pi }_{21}),({\pi }_{20},{\pi }_{20})\},$ $\{({\pi }_{11},{\pi }_{11}),({\pi }_{11},{\pi }_{10}),({\pi }_{10},{\pi }_{11}),({\pi }_{10},{\pi }_{10})\}.$

The former denotes visitors’ tactics to access a service or not. Meanwhile, the latter is a set of strategies of servers, in which real services and honeypots will be turned on or turned off.

4.2. Bayesian Equilibriums of the Server

From the perspective of a server, there are four kinds of access strategies of visitors. Among these strategies, $({\pi }_{21},{\pi }_{21})$ is in line with reality. Therefore, taking $({\pi }_{21},{\pi }_{21})$ as an example, we analyze whether a game equilibrium exists or not. Based on the strategy $({\pi }_{21},{\pi }_{21})$, the server knows that opposite players will visit the system. Posteriori probabilities are assumed to be: $\{P^{{}^{\prime }}\left({\theta }_{21}\right|{\pi }_{21})=p,P^{{}^{\prime }}\left({\theta }_{20}\right|{\pi }_{21})=1-p\}.$

Based on the posteriori probabilities, payoffs of a honeypot for the strategies ${\pi }_{11}$ and ${\pi }_{10}$ are denoted as ${\mu }_{{\theta }_{111}\left({\pi }_{11}\right)}$ and ${\mu }_{{\theta }_{111}\left({\pi }_{10}\right)}$ where

$$\begin{array}{cc}\hfill {\mu }_{{\theta }_{111}\left({\pi }_{11}\right)}& =P^{{}^{\prime }}\left({\theta }_{21}\right|{\pi }_{21})(\eta c/N)+P^{{}^{\prime }}\left({\theta }_{20}\right|{\pi }_{21})\times \left(0\right)=p(\eta c/N),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\mu }_{{\theta }_{111}\left({\pi }_{10}\right)}& =P^{{}^{\prime }}\left({\theta }_{21}\right|{\pi }_{21})\times 0+P^{{}^{\prime }}\left({\theta }_{20}\right|{\pi }_{21})\times \left(0\right)=0.\hfill \end{array}$$

(2)

From Equations (1) and (2), it can be inferred that ${\mu }_{{\theta }_{111}\left({\pi }_{11}\right)}>{\mu }_{{\theta }_{111}\left({\pi }_{10}\right)}$, which indicates ${\pi }_{11}$ is an absolutely dominant strategy for ${\theta }_{111}$. No matter which kind of visitors enters, the honeypot tends to be on.

As for real services, we get the following payoff equations.

$$\begin{array}{cc}\hfill {\mu }_{{\theta }_{110}\left({\pi }_{11}\right)}& =P^{{}^{\prime }}\left({\theta }_{21}\right|{\pi }_{21})(-\gamma a/N)+P^{{}^{\prime }}\left({\theta }_{20}\right|{\pi }_{21})a=p(-\gamma a/N)+(1-p)a\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mu }_{{\theta }_{110}\left({\pi }_{10}\right)}& =P^{{}^{\prime }}\left({\theta }_{21}\right|{\pi }_{21})\times 0+P^{{}^{\prime }}\left({\theta }_{20}\right|{\pi }_{21})(-a)=(1-p)(-a)\hfill \end{array}$$

(4)

Solving Equations (3) and (4) simultaneously, we obtain $2N/(r+2N)=p$. Consider the case when $p<2N/(r+2N)$. In this case, the dominant strategy is ${\pi }_{11}$ for a real server. When $p>2N/(r+2N)$, ${\pi }_{10}$ is the optimal choice. Considering the absolutely dominant strategy ${\pi }_{11}$ of a honeypot, we can infer that $({\pi }_{11},{\pi }_{11})$ and $({\pi }_{10},{\pi }_{11})$ respectively acts as the optimal selection for a server under circumstances of $p<2N/(r+2N)$ and $p>2N/(r+2N)$, as illustrated in

Table 8. List of equilibriums for server.

Player	Condition	Dominant Strategy	Equilibrium
$Realservice$	$p<2N/(r+2N)$	${\pi }_{11}$	$({\pi }_{11},{\pi }_{11})$
$Honeypot$	$p<2N/(r+2N)$	${\pi }_{11}$
$Realservice$	$p>2N/(r+2N)$	${\pi }_{10}$	$({\pi }_{10},{\pi }_{11})$
$Honeypot$	$p>2N/(r+2N)$	${\pi }_{11}$

.

4.3. Bayesian Equilibriums When $p<2N/(r+2N)$

Then, we illustrate if there exist a dominant strategy for visitors in the case of $({\pi }_{11},{\pi }_{11})$ and $p<2N/(r+2N)$. The posteriori probabilities are set to $\{P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})=q,P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{11})=1-q\}.$

The payoff equations for an attacker can be calculated as:

$$\begin{array}{cc}\hfill {\mu }_{{\theta }_{21}\left({\pi }_{21}\right)}& =P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})(-\eta c/N-b)+P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{11})(\gamma a/N-b)=q(-\eta c/N-b)+(1-q)(\gamma a/N-b)\hfill \end{array}$$

(5)

$${\mu }_{{\theta }_{21}\left({\pi }_{20}\right)}=P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})\times 0+P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{11})\times 0=0$$

(6)

Similarly to Equations (3) and (4), we assume ${\mu }_{{\theta }_{21}\left({\pi }_{21}\right)}={\mu }_{{\theta }_{21}\left({\pi }_{20}\right)}$. Then, we have $\gamma a-bN/\gamma a+\eta c=q$. When $\gamma a-bN/\gamma a+\eta c>q$, it is obviously that the strategy ${\mu }_{{\theta }_{21}\left({\pi }_{21}\right)}$ gains more profits than ${\mu }_{{\theta }_{21}\left({\pi }_{20}\right)}$. We can infer that if $q<(\gamma a-bN)/(\gamma a+\eta c)$, the strategy ${\pi }_{21}$ will dominate in the view of an attacker. When $\gamma a-bN/\gamma a+\eta c<q$, we obtain ${\mu }_{{\theta }_{21}\left({\pi }_{21}\right)}<{\mu }_{{\theta }_{21}\left({\pi }_{20}\right)}$ where the attacker would like to choose the strategy ${\pi }_{20}$ to abandon visiting the server.

The payoff equations for a user can be calculated as:

$$\begin{array}{cc}\hfill {\mu }_{{\theta }_{20}\left({\pi }_{21}\right)}& =P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})(-a)+P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{11})\left(a\right)=q(-a)+(1-q)\left(a\right)\hfill \end{array}$$

(7)

$${\mu }_{{\theta }_{20}\left({\pi }_{20}\right)}=P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})\times 0+P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{11})\times 0=0$$

(8)

Assuming that ${\mu }_{{\theta }_{20}\left({\pi }_{21}\right)}={\mu }_{{\theta }_{20}\left({\pi }_{20}\right)}$, we have $1/2=q$. When $q<1/2$, the strategy ${\pi }_{21}$ will be better for the user. Otherwise, the strategy ${\pi }_{20}$ is a better choice. Since our system should provide the user with normal services, the strategy ${\pi }_{20}$ (i.e., the user does not visit the server) is inconsistent with the reality, which should be aborted.

Equilibriums of visitors are illustrated in

Table 9. List of equilibriums for visitors.

Player	Condition	Dominant Strategy	Equilibrium
$Attacker$	$q<\gamma a-bN/\gamma a+\eta c$	${\pi }_{21}$	$({\pi }_{21},{\pi }_{21})$
$User$	$q<1/2$	${\pi }_{21}$
$Attacker$	$q>\gamma a-bN/\gamma a+\eta c$	${\pi }_{20}$	$({\pi }_{20},{\pi }_{21})$
$User$	$q<1/2$	${\pi }_{21}$

. Based on the dominant strategy $({\pi }_{11},{\pi }_{11})$ and $p<2N/(r+2N)$, the best access condition for an attacker and a user are individually $q<\gamma a-bN/\gamma a+\eta c$ and $q<1/2$, where

$$\eta c\ge \gamma a-2bN$$

(9)

In general, there are two Bayesian equilibriums for all players, shown in

Table 10. List of Bayesian equilibriums for all players when $p<2N/(r+2N)$.

Player	Condition	Dominant strategy	Bayesian Equilibrium
$Visitor$	$q<1/2,q<\gamma a-bN/\gamma a+\eta c$	$({\pi }_{21},{\pi }_{21})$	$\left(({\pi }_{11},{\pi }_{11})({\pi }_{21},{\pi }_{21})\right)$
$Server$	$p<2N/(r+2N)$	$({\pi }_{11},{\pi }_{11})$
$Visitor$	$\gamma a-bN/\gamma a+\eta c<q<1/2$	$({\pi }_{20},{\pi }_{21})$	$\left(({\pi }_{11},{\pi }_{11})({\pi }_{20},{\pi }_{21})\right)$
$Server$	$p<2N/(r+2N)$	$({\pi }_{11},{\pi }_{11})$

. In the condition of $p<2N/(r+2N)$, $q<1/2$ and $\eta c\ge \gamma a-2bN$, a Bayesian equilibrium is formed under the strategy set $(({\pi }_{11},{\pi }_{11}),({\pi }_{21},{\pi }_{21}))$. The other is obtained when $\gamma a-bN/\gamma a+\eta c<q<1/2$ in the strategy set $(({\pi }_{11},{\pi }_{11}),({\pi }_{20},{\pi }_{21}))$. Such a strategy set illustrates an ideal circumstance in our life, indicating that the attacker will not launch an attack and the legal user will access the server.

4.4. Bayesian Equilibriums When $p>2N/(r+2N)$

Next, we take $({\pi }_{10},{\pi }_{11})$ with $p>2N/(r+2N)$ into account. Payoff equations for two visitors can be calculated as:

$$\begin{array}{cc}\hfill {\mu }_{{\theta }_{21}\left({\pi }_{21}\right)}& =P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})(-\eta a/N-b)+P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{10})(-b)=q(-\eta a/N-b)+(1-q)(-b)\hfill \end{array}$$

(10)

$${\mu }_{{\theta }_{21}\left({\pi }_{20}\right)}=P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})\times 0+P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{10})\times 0=0$$

(11)

$$\begin{array}{cc}\hfill {\mu }_{{\theta }_{20}\left({\pi }_{21}\right)}& =P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})(-a)+P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{10})(-a)=q(-a)+(1-q)(-a)\hfill \end{array}$$

(12)

$${\mu }_{{\theta }_{20}\left({\pi }_{20}\right)}=P^{{}^{\prime }}\left({\theta }_{111}\right|{\pi }_{11})\times 0+P^{{}^{\prime }}\left({\theta }_{110}\right|{\pi }_{10})\times 0=0$$

(13)

Via comparing Equation (10) with Equation (11), we conclude that the attacker tends to access a server when $q<-bN/\eta a$ and it will eventually abandon the server when $q>-bN/\eta a$. The Equation (12) is always less than Equation (13) (i.e., $-a<0$), which illustrates that the user will not visit a server. Thus, we draw a conclusion that $(({\pi }_{10},{\pi }_{11}),({\pi }_{21},{\pi }_{21}))$ is inconsistent with Bayesian equilibrium when $p>2N/(r+2N)$. The corresponding Bayesian equilibriums are shown in

Table 11. List of Bayesian equilibriums for all players when $p>2N/(r+2N)$.

Player	Condition	Dominant Strategy	Bayesian Equilibrium
$Visitor$	$q<-bN/\eta a$	$({\pi }_{21},{\pi }_{20})$	$\left(({\pi }_{10},{\pi }_{11})({\pi }_{21},{\pi }_{20})\right)$
$Server$	$p>2N/(r+2N)$	$({\pi }_{10},{\pi }_{11})$
$Visitor$	$q>-bN/\eta a$	$({\pi }_{20},{\pi }_{20})$	$\left(({\pi }_{10},{\pi }_{11})({\pi }_{20},{\pi }_{20})\right)$
$Server$	$p>2N/(r+2N)$	$({\pi }_{10},{\pi }_{11})$

. When $p>2N/(r+2N)$ and $q>-bN/\eta a$, $(({\pi }_{10},{\pi }_{11}),({\pi }_{20},{\pi }_{20}))$ forms out the Bayesian equilibrium. Obviously, the equilibrium $(({\pi }_{10},{\pi }_{11}),({\pi }_{20},{\pi }_{20}))$ (i.e., only a fake service is started, and visitors do not access it) is meaningless.

4.5. Effectiveness Analysis of Our System

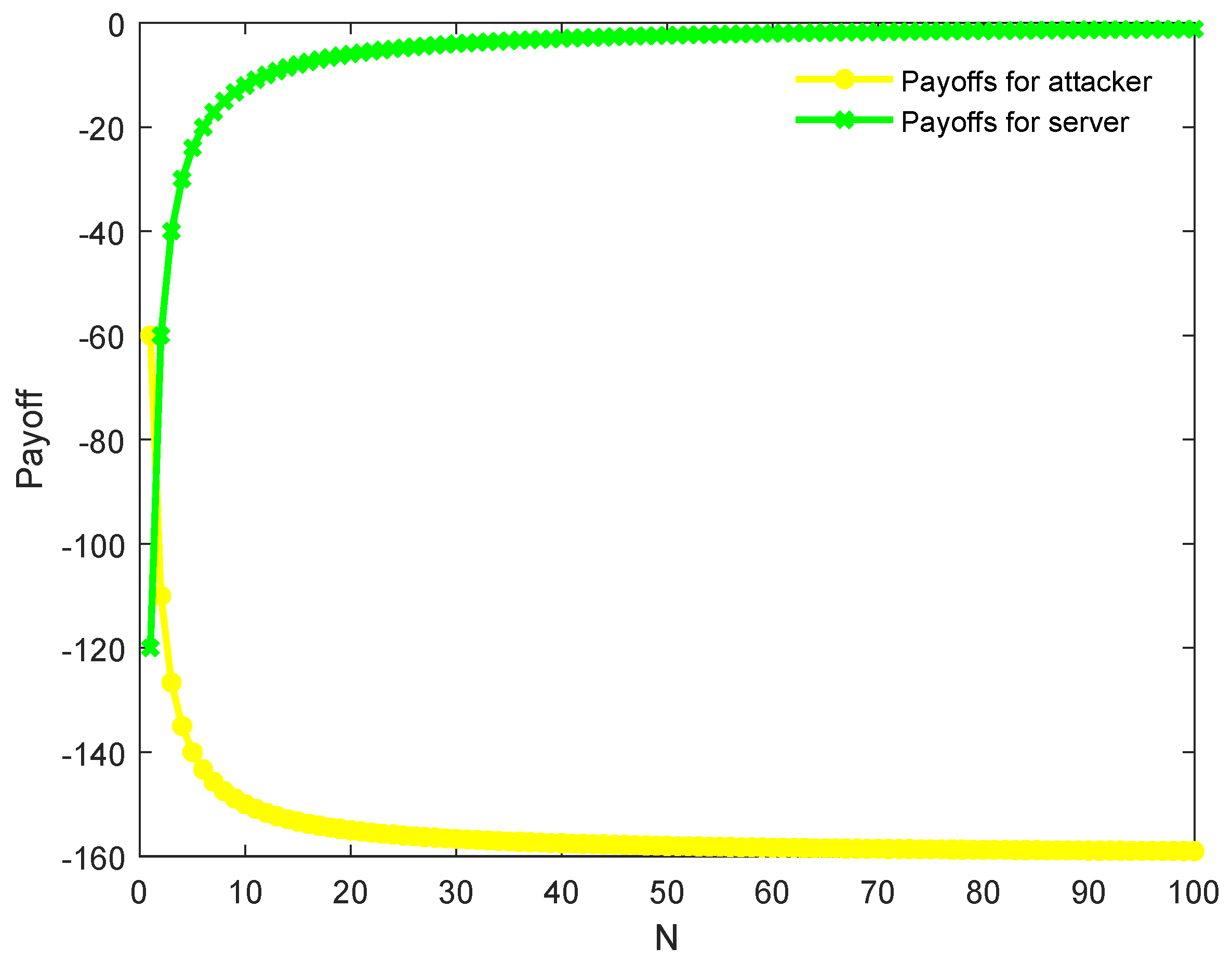
From the above, we arrive at a conclusion that the relationship between q and $(\gamma a-bN)/(\gamma a+\eta c)$ determines different Bayesian equilibriums when $p<2N/\gamma +2N$. This indicates that the aforementioned relationship plays an important role in payoffs of diverse strategies. It is conspicuous that $(({\pi }_{11},{\pi }_{11}),({\pi }_{20},{\pi }_{21}))$ (i.e., an attacker does not access to a server and a user visits it) is the optimal choice for the system defender. Its precondition contains $1/2>q>(\gamma a-bN)/(\gamma a+\eta c)$, a decisive factor related to q rather than p, which means our system comprises an innovative system defense by adjusting the probability value q in network defense.

As indicated above, $q<(\gamma a-bN)/(\gamma a+\eta c)$ is a requirement for $(({\pi }_{11},{\pi }_{11}),({\pi }_{21},{\pi }_{21}))$. Namely, if honeypots are deployed with a lower probability, an attacker tends to intrude into a system. At the meantime, $\gamma a-2bN$ in Equation (9) means that attack cost grows with the increase of N. N is determined by the number of services and hosts, which can be adjusted dynamically, further indicating proactive protection of our system.

$q>(\gamma a-bN)/(\gamma a+\eta c)$ indicates the deployment of honeypots is a high-probability event. Since the honeypot trap will bring an attacker more losses than profits it makes by attacking a server, the attacker will not access the system in such a circumstance. The service allocation algorithm of our system keeps occurrence of honeypots in a high probability by periodically changing all services. The attacker may suffer a lot when it attacks our decoy system. Due to periodical transformation, services are unpredictable for an attacker and its traffic can be recognized quickly. Besides, a user can keep pace with real services via synchronization mechanism (i.e., the user can always access to real resources). Therefore, our scheme is effective.

5. Simulation Evaluations

In this section, we focus on the game between a server and an attacker. Gambit v15.1.1 and MATLAB R2017b v9.3.0 are used for evaluating the effectiveness of our scheme. Gambit is a software tool for game theory graphical interface. Some related parameters for simulation are shown in

Table 12. Simulation parameters.

Parameter	Values
a	100
b	80
c	80
$\gamma$	2
$\eta$	1
N	1, 10, 20, 100, 1000

. As mentioned above, the attacker’s cost becomes higher with N increasing. We use several different values N to analyze our scheme in following simulations.

5.1. Dominance Results in Gambit

First, we should take $N=1$ into consideration, which is a symbol of a common system with only one server. As is shown in Figure 5, when a real service is turned on and the attacker gains access to it, the latter’s payoff is more than that of the former. Obviously, when there are no distributed honeypots, the server suffers great losses, indicating an absolute predominance of its adversary.

Next, in Figure 6, Figure 7 and Figure 8, $N=10,N=20$ and $N=100$ are simulated. It is apparent that the strategy $Access$ of the attacker is eliminated. Because it suffers a lot with the value of N increasing, it will not access our system. However, reduction of the server’s payoff is clear from $N=10$ to $N=100$, due to the increased deployment cost of honeypots.

Finally, we assume $N=1000$ as a maximum value to simulate a final condition in Figure 9. Apparently, the payoff of the attacker is nearly minus 80. Nevertheless, the payoff of the server is a positive number. Compared with the simulation result in Figure 5, the situation completely reverses. This illustrates the effectiveness of our proposed scheme.

5.2. Payoff Results in MATLAB

In this subsection, payoff curves in the strategy set $(({\pi }_{11},{\pi }_{11}),{\pi }_{21})$ for two players are taken into consideration. Payoff curves for the server are shown in Figure 10.

Figure 10a presents payoffs of a server in the strategy set (Real-on, Access) (i.e., real services are turned on and attacked). When $N=1$, the payoff is $-200$, a huge loss for the server. Along the N axis, the payoffs improve a lot and their curve is escalating faster, indicating a great improvement for the server. The payoffs in the strategy set (Fake-on, Access) are presented in Figure 10b. Because of the deployment cost of honeypots, they decrease with N increasing.

Figure 10c,d illustrate payoffs of an attacker. They show the payoffs in the strategy sets (Real-on, Access) and (Fake-on, Access). The attacker’s initial payoff value is 120 in Figure 10c. That means it makes profits when $N=1$. After the distributed honeypots are deployed, the payoff is decreasing rapidly. Therefore, the honeypots bring the attacker great losses. Since real services are deployed, the probability of attacking a real service exists. The curve ascends in Figure 10d. Nevertheless, services are always changing and unpredictable. Attack traffic will be recognized by honeypots. Therefore, the attacker cannot inflict losses on the system. The final numerical value is approximately to $-80$. Such a negative number means that the attacker still suffers a loss.

All the payoff curves are aggregated in Figure 11. $N=1$ is the closest point to $payoff$ axis (i.e., distributed honeypots have not been deployed). At that point, an attacker possesses an apparent advantage over a server. However, with the increase of N, there is a dramatic decline in the red curve of the attacker. One of payoff curves of the server shows an upward trend along N axis. Due to the deployment cost of honeypots, the other is slightly declining. Finally, the attacker’s payoffs tend to be negative numbers and the server’s payoffs are always higher than them. To better illustrate tendency of overall payoffs, we combine the strategy sets of two players respectively in Figure 12. The server’s curve comes up and its adversary runs towards the opposite direction. The overall trends illustrate that our scheme is effective in defending against an attacker.

6. Conclusions

In this paper, we have proposed a framework based on distributed honeypots to safeguard real services. The proposed scheme can identify illegal traffic and can scare off an attacker by periodically changing services. Game-theoretic analysis verified the effectiveness of our proposed scheme theoretically. Equilibriums show that our scheme is proactive in system defense through adjustment of the probability of honeypots. Simulation results show that payoffs for both a server and an attacker are influenced with the increase of N. The attacker may give up intruding into the server with N increasing. In summary, our proposed scheme is effective in defending against attackers in network security.