You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Pharmaceutics
Download PDF
  • Article
  • Open Access

1 November 2025

A Systematic Intelligent Optimization Framework for a Sustained-Release Formulation Design

,
,
,
,
,
,
,
,
and
1
Department of Health Statistics, School of Public Health, Shanxi Medical University, Taiyuan 030001, China
2
Shanxi Provincial Key Laboratory of Major Diseases Risk Assessment, Shanxi Medical University, Jinzhong 030600, China
*
Author to whom correspondence should be addressed.
Pharmaceutics2025, 17(11), 1419;https://doi.org/10.3390/pharmaceutics17111419
This article belongs to the Section Physical Pharmacy and Formulation
Version Notes
Order Reprints

Abstract

Objectives: This study proposes a systematic strategy for optimizing sustained-release formulations using mixture experiments. Methods: Model variables were identified and screened via LASSO regression, Smoothly Clipped Absolute Deviation (SCAD), and Minimax Concave Penalty (MCP), leading to the construction of a quadratic inference function-based objective model. Using this model, three multi-objective optimization algorithms—NSGA-III, MOGWO, and NSWOA—were employed to generate a Pareto-optimal solution set. Solutions were further evaluated through the entropy weight method combined with TOPSIS to reduce subjective bias. Results: The MCP-screened model demonstrated strong fit (AIC = 19.8028, BIC = 45.2951) and suitability for optimization. Among the Pareto-optimal formulations, formulation 45, comprising HPMC K4M (38.42%), HPMC K100LV (13.51%), MgO (6.28%), lactose (17.07%), and anhydrous CaHPO4 (7.52%), exhibited superior performance, achieving cumulative release rates of 22.75%, 64.98%, and 100.23% at 2, 8, and 24 h, respectively. Compared with the original formulation, drug release was significantly improved across all time points. Conclusions: This integrated workflow effectively accounted for component interactions and repeated measurements, providing a robust and scientifically grounded approach for optimizing multi-component sustained-release formulations.

1. Introduction

Sustained-release formulations are drug delivery systems designed to release active compounds at a predetermined rate, thereby maintaining stable plasma concentrations over an extended period to enhance therapeutic efficacy and reduce dosing frequency [1,2,3]. Such formulations are of great clinical importance in the long-term treatment of chronic diseases characterized by short drug half-lives, including cardiovascular disorders, diabetes, and central nervous system diseases [4,5,6]. However, existing studies still face limitations in modeling and optimization. Conventional full polynomial models fail to adequately capture complex component interactions, and the exponential growth of model variables with the increase in formulation components often leads to data non-saturation and variable redundancy. Moreover, most studies have not sufficiently accounted for the time dependence of cumulative release profiles, resulting in incomplete characterization of drug release kinetics. Single-objective transformation methods used in formulation optimization also rely heavily on subjective weighting, making it difficult to achieve balanced trade-offs among multiple objectives. Therefore, integrating mathematical modeling with intelligent optimization algorithms for multi-objective coordination has emerged as a promising research direction. Previous studies on lidocaine microemulsions and polycaprolactone microspheres experimentally demonstrated that combining mathematical modeling with multi-objective optimization can improve formulation development efficiency and predictive performance [7,8]. Thus, employing complex mathematical models in sustained-release formulation development is essential for systematically capturing component interactions, accounting for temporal release patterns, and enabling rational multi-objective optimization, ultimately facilitating the design of robust and high-performance formulations.
In this study, the monitored response variables were the cumulative drug release rates at 2 h, 8 h, and 24 h (Y2, Y8, and Y24), representing the initial, intermediate, and sustained-release stages, respectively. These responses provide a direct assessment of the formulation’s release performance over time and serve as the primary objectives for subsequent multi-objective optimization. To achieve efficient modeling, it is essential to address the problem of data non-saturation arising from high-dimensional variables in mixture design. Traditional full polynomial models are inherently limited as, the number of generated variables increases exponentially with the number of formulation components, leading to insufficient sample size and increased experimental burden. The q-Component Centered Polynomial (q-CCP) method refines polynomial terms within a (q − 1)-dimensional simplex while maintaining model symmetry, thereby reducing experimental cost and improving predictive accuracy [9,10,11]. When the number of variables far exceeds the sample size, feature selection becomes crucial. Least Absolute Shrinkage and Selection Operator (LASSO) achieves variable selection through coefficient shrinkage but may introduce bias in highly correlated settings [12,13]. Smoothly Clipped Absolute Deviation (SCAD) reduces small-coefficient estimation bias via non-convex penalties while satisfying the oracle property [14,15], and the Minimax Concave Penalty (MCP) mitigates local optimum risks by tuning penalty concavity, making it suitable for non-saturated data [14]. These approaches enable the identification of key interaction effects and improve the robustness and predictive accuracy of sustained-release models.
After variable selection, capturing time dependence becomes critical for building robust statistical models. The cumulative release rate of sustained-release systems typically exhibits repeated measurements and temporal correlation. The Quadratic Inference Function (QIF) provides improved estimation efficiency and robustness over Generalized Estimating Equations (GEE) as, it does not rely on strict assumptions regarding the correlation matrix and achieves greater computational stability and variance consistency, particularly under limited sample conditions or with unknown correlation structures [16,17]. The QIF has been widely applied in pharmacokinetic and longitudinal biomedical analyses, maintaining high estimation efficiency and predictive accuracy even in datasets with strong temporal dependence or small sample sizes [18,19]. Incorporating the QIF into sustained-release modeling allows for more precise characterization of component interactions and time-dependent effects, offering a statistically robust foundation for subsequent multi-objective optimization.
Formulation optimization represents a critical step in enhancing the performance of sustained-release systems. Traditional methods such as goal programming and contour plotting typically convert multi-objective problems into single-objective ones through weight assignment or target transformation; however, these approaches are highly dependent on subjective weighting and fail to capture trade-offs among objectives comprehensively [20]. In contrast, intelligent multi-objective optimization algorithms possess strong global search capabilities, enabling simultaneous balancing of multiple objectives while generating diverse Pareto-optimal solutions and reducing the likelihood of local optima [21]. Recently developed algorithms—including the Non-Dominated Sorting Genetic Algorithm III (NSGA-III), the Multi-Objective Grey Wolf Optimizer (MOGWO), and the Non-Dominated Sorting Whale Optimization Algorithm (NSWOA)—have demonstrated high efficiency, robustness, and rapid convergence in complex optimization tasks such as path planning, scheduling, and resource allocation [22,23]. Compared with traditional genetic algorithms and single-objective optimization strategies, these methods are particularly suitable for high-dimensional multi-objective problems as, they preserve solution diversity and uniformity while providing more stable and comprehensive optimization outcomes. Therefore, applying intelligent multi-objective optimization algorithms to sustained-release formulation design holds significant potential, especially for complex multi-objective decision scenarios.
In summary, this study establishes a systematic methodological framework for modeling and optimizing sustained-release formulations. The proposed framework employs the q-CCP method for variable generation; integrates LASSO, SCAD, and the MCP for key variable selection and interaction identification; utilizes the QIF for time-dependent modeling; and finally implements multi-objective global optimization through NSGA-III, MOGWO, and NSWOA. This framework provides a generalized mathematical and decision-support platform for sustained-release formulation design and process optimization, enhancing model robustness, predictive precision, and overall development efficiency.

2. Materials and Methods

2.1. Materials

This study was based on experimental data of glipizide–hydroxypropyl-β-cyclodextrin sustained-release tablets reported in the literature [24] for modeling and optimization. The original formulation, designed using a D-optimal mixture design, included five key excipients—HPMC K4M (X1), HPMC K100LV (X2), MgO (X3), lactose (X4), and anhydrous CaHPO4 (X5)—which were treated as study factors in the modeling analysis. According to the original study, all components were passed through an 80-mesh sieve, weighed according to the designed proportions and mixed using the equal-volume incremental method. The cumulative drug release rate was used as the formulation evaluation metric to assess drug release behavior under different pH conditions: the 2 h cumulative release in pH 1.2 medium (Y2) reflected the initial release, while the 8 h (Y8) and 24 h (Y24) cumulative release in pH 6.8 medium represented sustained-release performance and release completeness. Using this dataset, formulation variable screening, interaction analysis, and multi-objective optimization were performed without actual tablet preparation. The composition and dosage ranges of the formulations are listed in Supplementary Table S1.
According to the quality requirements for glipizide-related preparations specified in the Chinese Pharmacopoeia, the acceptable ranges for Y2, Y8, and Y24 are 15–25%, 55–65%, and 80–110%, respectively, with 110% set as the upper limit for complete dissolution. Based on preliminary formulation research results, the formulation components and their dosage ranges were further determined (shown in Supplementary Material Table S1), serving as the foundation for formulation optimization studies. The experimental protocol and results for the glipizide sustained-release tablets are presented in Table 1.
Table 1. Experimental protocol and results for glipizide pH-non-dependent sustained-release tablets.

2.2. Methods

2.2.1. Feature Selection Methods

Regularization-based variable selection techniques are widely used for high-dimensional modeling in pharmaceutical formulation studies. Among them, LASSO, proposed by Tibshirani in 1996, introduces an L1 penalty into least squares regression to simultaneously perform coefficient estimation and variable selection, achieving sparsity and interpretability while avoiding the high computational burden of traditional subset selection methods [13]. However, LASSO applies uniform shrinkage to all coefficients, which may cause “group selection bias” when variables are highly correlated, and its performance is sensitive to the penalty parameter determined via cross-validation [14]. Fan and Li developed SCAD in 2001 to address these limitations. SCAD employs a non-convex penalty that strongly shrinks small coefficients while limiting shrinkage on large coefficients, mitigating estimation bias and improving stability [15]. It possesses Oracle-like properties and handles correlated variables more effectively than LASSO, though the non-convex optimization can result in local optima and higher computational cost. The MCP, proposed by Zhang in 2010, further reduces estimation bias while preserving sparsity by gradually decreasing the penalty on large coefficients through a concavity parameter γ [25]. Compared with SCAD, the MCP has a simpler functional form, faster convergence, and greater robustness in the case of non-saturated or high-dimensional data, though it still requires careful tuning of γ.
Overall, LASSO, SCAD, and the MCP represent a progressive evolution of regularization-based variable selection methods, balancing sparsity, stability, and computational efficiency. In this study, these three methods were independently applied to the q-CCP-based high-dimensional feature set to screen formulation and interaction variables significantly associated with the cumulative drug release behavior of glipizide sustained-release tablets. We aimed to evaluate the respective effectiveness and suitability of each method for formulation modeling by comparing the selected variables and predictive performance. Table 2 summarizes the main characteristics of the models and differences between them, providing a concise reference for selecting an appropriate method in complex formulation optimization.
Table 2. Comparative Overview of LASSO, SCAD, and MCP.

2.2.2. Quadratic Inference Function

GEE is a classical method for modeling repeated measurements or longitudinally correlated data introduced by Liang & Zeger (1986) that estimates parameters based on a specified working correlation matrix [26]. However, the accuracy and efficiency of GEE depend strongly on correct correlation specification; misspecification can lead to biased estimates and reduced efficiency, particularly with complex correlation structures or limited sample sizes. The QIF, proposed by Qu et al. in 2000, extends GEE by representing the inverse of the correlation matrix as a linear combination of basis matrices [18], which addresses these shortcomings. This reformulation eliminates the need for explicit estimation of complex correlation parameters and enhances robustness in case of model misspecification. The quadratic construction of the QIF further enables the direct evaluation of model goodness-of-fit, facilitating model selection and comparison.
Compared with GEE, the QIF provides several distinct advantages: (i) it yields consistent estimates even when the working correlation matrix is misspecified, thereby reducing model bias; (ii) it naturally integrates model fit assessment within its estimation framework; and (iii) it demonstrates higher efficiency in small-sample or complex correlation scenarios. Nevertheless, its performance can be sensitive to the selection of basis matrices, and computational demands may increase under high-dimensional or large-scale data conditions.
In the context of this study, the cumulative drug release data of glipizide sustained-release tablets represent longitudinal observations measured at multiple time points (2 h, 8 h, and 24 h), where successive measurements are correlated within each formulation. Here, the QIF was employed to model these intra-formulation correlations by estimating regression parameters that link formulation variables (excipient proportions and interaction terms) with the observed cumulative release rates. The correlation structure among repeated measurements was incorporated through basis matrices within the QIF framework, allowing more accurate estimation of time-dependent release characteristics and improving the interpretability and stability of the predictive model. Thus, the QIF provided a statistically robust approach for analyzing correlated release profiles and optimizing formulation performance. Table 3 summarizes the principal differences between GEE and the QIF.
Table 3. Comparison of QIF and GEE.

2.2.3. Exterior Penalty Function Method

In multi-objective optimization, it is often necessary to balance multiple conflicting objectives under a set of constraints. In the optimization of sustained-release formulations based on mixture design, an equality constraint arises from the requirement that the sum of all component proportions equals 1 (or 100%) [27,28] This constant-sum constraint ensures that the total content of excipients remains fixed, reflecting the physical and practical boundaries of the formulation system.
The exterior penalty function method is widely applied to address such constrained problems for its simplicity and flexibility. It introduces penalty terms into the objective function to account due to constraint violations, converting the constrained problem into an unconstrained one which is solvable via standard optimization algorithms. When a constraint is violated, a penalty proportional to the deviation is imposed, guiding the solution toward feasibility. The method’s performance depends on the penalty coefficient, a value that is too small may yield infeasible results, while an excessively large value can cause instability and slow convergence. Proper tuning of the penalty factor is therefore essential for both feasibility and computational efficiency [14,25,29].
In this study, the exterior penalty function was integrated into the multi-objective optimization framework to manage the equality constraint inherent in the mixture design ( ∑ X i = 82.8 % ). This ensured that the total proportion of the five excipients—HPMC K4M, HPMC K100LV, MgO, lactose, and anhydrous CaHPO4—remained constant during optimization. The objectives were defined according to the cumulative release rates at 2 h, 8 h, and 24 h (Y2, Y8, and Y24), representing the initial, intermediate, and terminal phases of drug release. The penalty term maintained compositional feasibility while allowing intelligent optimization algorithms to identify Pareto-optimal solutions with balanced release performance across time points, ensuring both mathematical validity and physical interpretability in sustained-release formulation design.

2.2.4. Multi-Objective Optimization Algorithm

Three representative intelligent optimization algorithms were employed in this study to address the multi-objective conflicts and complex constraints inherent in sustained-release formulation optimization—NSGA-III, MOGWO, and NSWOA. These algorithms improve convergence efficiency while maintaining the diversity and uniformity of Pareto-optimal solutions, enabling comprehensive exploration of the solution space.
NSGA-III, proposed by Deb et al. (2014), is an advanced extension of NSGA-II specifically developed for high-dimensional multi-objective problems [30,31]. It introduces a reference-point mechanism and adaptive normalization strategy to achieve uniform solution distribution along the Pareto front, effectively balancing convergence and diversity during population evolution. MOGWO, developed by Mirjalili et al. (2015), extends the Grey Wolf Optimizer to handle multi-objective problems by mimicking the social hierarchy and cooperative hunting strategies of grey wolves [32,33]. It employs a leader-based search structure (α, β, and δ wolves) and an external archive to preserve non-dominated solutions, enhancing convergence speed, robustness, and Pareto front uniformity in nonlinear optimization scenarios. NSWOA, an improved version of the Whale Optimization Algorithm by Mirjalili and Lewis (2016), integrates non-dominated sorting and crowding distance mechanisms to extend WOA’s capability to multi-objective optimization [34]. NSWOA is inspired by the foraging behavior of humpback whales—encircling prey, bubble-net feeding, and random search—and achieves uniform Pareto front coverage and balanced global exploration [35].
In this study, these three algorithms were applied to the same multi-objective optimization framework, where the decision variables were the proportions of five excipients (HPMC K4M, HPMC K100LV, MgO, lactose, and anhydrous CaHPO4) under the equality constraint ∑ X i = 82.8 % . The objective functions were defined using the cumulative release rates at 2 h (Y2), 8 h (Y8), and 24 h (Y24), representing the initial, intermediate, and sustained-release stages, respectively. By comparing their convergence behavior, distribution characteristics, and optimization performance, we evaluated the effectiveness of each algorithm in identifying Pareto-optimal formulation designs that balance early burst control, release stability, and overall dissolution completeness.

2.2.5. Multi-Objective Optimization Evaluation

In multi-objective optimization, a large number of Pareto-optimal solutions are typically generated, often exhibiting considerable variability across objectives. When multiple and potentially conflicting criteria are involved, selecting a single, most desirable solution becomes a key challenge as improvement in one objective often results in deterioration of others [36]. The Entropy Weight Method (EWM) and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) were combined in this study for post-optimization evaluation to achieve a rational and quantitative selection of the optimal sustained-release formulation. The optimization objectives were the cumulative release rates at 2 h, 8 h, and 24 h (Y2, Y8, and Y24), which collectively describe the release performance of the sustained-release system.
The EWM was first applied to determine the objective weights of these release indicators based on their information entropy, ensuring that the weighting process reflected the intrinsic variability of each parameter without subjective bias [37]. The normalized decision matrix X was constructed from the Pareto solutions, and the probability distribution Pij and entropy values ej were calculated to derive the weight vector. These weights were then incorporated into the TOPSIS method, which evaluates and ranks Pareto-optimal formulations according to their Euclidean distance from the positive and negative ideal solutions [38].

2.2.6. Function Transformation

The experimental data in this study must satisfy the constant-sum constraint of the mixture design which means the sum of all mixture components is a fixed value (X1 + X2 + X3 + X4 + X5 = 82.8%). The exterior penalty function method was accordingly used to transform the objective function optimization problem with equality constraints into an unconstrained extremum problem. The initial penalty factor σ was set to 1000 by constructing an unconstrained extremum-seeking function:
Q = Y ^ + σ P x
where P x = ∑ j = 1 l φ h j x denotes the penalty term, hj(x) is the constraint function, and φ (⋅) is the penalty function. The corresponding transformations were implemented for the subobjective functions at different time points:
When t = 2 h, the transformed objective function was
Q 1 = − Y ^ 2 + σ P x
When t = 2 h, the transformed objective function was
Q 2 = − Y ^ 8 + σ P x
When t = 2 h, the transformed objective function was
Q 3 = − Y ^ 24 + σ P x
Through the conversion, the original constrained optimization problem was transformed into an unconstrained optimization problem, enabling the efficient determination of optimal solutions at each time point while ensuring that the fixed and constraint conditions of the mixture design were satisfied. This method provided a mathematical guarantee for the subsequent optimization of the model.

2.2.7. Software and Parameter Settings

The LASSO, SCAD, and MCP methods from the ncvreg package in R version 4.3.3 were employed to screen variables generated with Scheffe center polynomial modeling. Optimization for all three methods was performed using the Optimization Toolbox in MATLAB R2022a. The NSGA-III parameter settings were as follows: single-point crossover probability Pc = 0.8, mutation probability Pm = 0.05. The MOGWO parameter settings were as follows: initial population size N = 100, grid expansion factor alpha = 0.1, leader selection pressure factor beta = 5, additional archived individual selection pressure gamma = 2. In the NSWOA parameter settings, the result output frequency during iteration was set to ishow = 10. The initial population size N was uniformly set to 100, and the number of evolutionary generations is set to 200. Each algorithm was independently run 15 times to ensure the reliability and reproducibility of results. Using the SPSS 26.0 software, the objective weights for each evaluation metric were calculated via the entropy method.

3. Results

3.1. Results of the Feature Selection

Using 10-fold cross-validation, three variable selection methods—LASSO, SCAD, and the MCP—were applied to screen characteristic variables from the mixture design sustained-release formulation trial data of glipizide pH-independent sustained-release tablets. LASSO, SCAD, and the MCP identified 16, 12, and 10 variables, respectively. The selected features and their regression coefficients for each method are presented in Supplementary Information Tables S2–S4. As evidenced by the above results, the MCP obtained fewer variables during variable selection than LASSO and SCAD, while its post-selection model demonstrated superior interpretability. Furthermore, the MCP method better accounted for interactions among variables during the selection process, enhancing the model’s predictive capability and stability. The MCP method consequently exhibited superior performance in this study, providing a more streamlined and effective feature variable set for subsequent model construction.

3.2. Results of the QIF Modeling

A correlation analysis was conducted on the drug release levels of the sustained-release formulation at three time points, with results shown in Figure 1. The analysis revealed correlation coefficients of 0.23 between Y2 and Y8, 0.62 between Y2 and Y24, and 0.69 between Y8 and Y24. This indicated that measurements at one time point exhibited a certain degree of correlation with those at adjacent time points, demonstrating characteristics of autocorrelation. Therefore, an autocorrelation matrix structure was set to account for the data’s autocorrelation when establishing models using secondary inference functions, thereby better reflecting the dependencies among data points. This configuration contributed to enhancing the model’s fitting accuracy and stability.
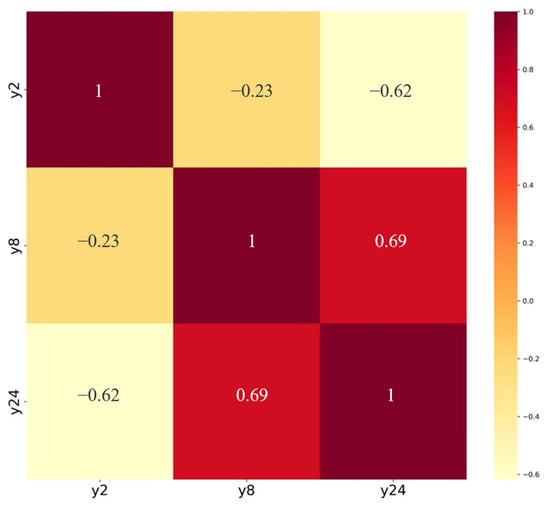
Figure 1. Heatmap of correlation coefficients for cumulative release levels at three time points.
To evaluate the impact of different variable selection methods on model fit, we modeled the data using three approaches: no variable selection, LASSO, SCAD, and the MCP. Model fit was assessed using AIC and BIC metrics. The results are presented in Supplementary Material Table S5. It is evident that models without variable selection exhibit relatively poor fit, as indicated by higher AIC and BIC values. In contrast, model fitting improved after variable selection using the LASSO, SCAD, and MCP methods. The model with variables selected via the MCP method performed best, yielding an AIC value of 19.8028 and a BIC value of 45.2951. Therefore, the Scheffe-centered polynomial model based on the MCP method demonstrated the best model fit. This model was ultimately selected as the final modeling result for this study. The specific model establishment results are shown in Table 4.
Table 4. Results of the second-order regression function modeling for glipizide pH-independent sustained-release tablets.
Based on the results in Table S5 of Supplementary Information, the QIF model was established after variable selection using the MCP method for Scheffe’s central polynomials. The model was expressed as follows:
Y ^ = − 4.27112 − 0.01113 X 2 X 4 − 0.00974 X 2 X 5 − 0.61399 X 3 X 5 − 0.00165 X 1 X 3 X 4 + 0.01076 X 1 X 3 X 5 + 0.00005 X 1 X 2 X 3 X 4 X 5 + 0.02473 X 3 t − 0.00049 X 5 t − 0.21985 t 2 + 9.08641 t
By substituting different time points (t = 2, 8, and 24 h) into the above model, sub-objective function models corresponding to each release stage were established. The detailed mathematical formulations of these sub-objective functions are provided in the Supplementary Information. Based on this model, the cumulative drug release at different time points can be quantitatively predicted, allowing for comprehensive analysis of the effects of formulation variables on release behavior. This modeling framework effectively captures both the interaction among components and the temporal dynamics of drug release, thereby offering a reliable quantitative basis for subsequent multi-objective formulation optimization.

3.3. Results of the Multi-Objective Algorithm Optimization

Q1, Q2, and Q3 were identified as target functions requiring optimization to achieve optimal drug release at different time points in this study. Three intelligent optimization algorithms were employed to conduct optimization searches within the search space. Each multi-objective optimization method underwent 15 random searches, ultimately yielding a set of superior and relatively reasonable optimization solutions. During the optimization process, the maximum fitness evolution curve is used to evaluate the algorithm’s convergence performance. It reflects the trend of changes in the best solution the algorithm can find during iterations and serves as a key indicator for determining whether the algorithm can approach the global optimum. The average fitness evolution curve, on the other hand, reflects the overall evolutionary level and dynamic performance of the population. It can be used to observe population diversity and the stability of the algorithm during the optimization process.
As illustrated in Figure 2 and Figure 3, the MOGWO algorithm exhibited a rapid convergence trend, with both the mean and maximum fitness values stabilizing after approximately 6–12 generations. This indicates that the algorithm efficiently balanced exploration and exploitation during the optimization process, achieving satisfactory convergence stability. The convergence behaviors of NSGA-III and NSWOA, presented in Supplementary Information Figures S1–S4, followed similar patterns. Specifically, NSGA-III reached a stable convergence state between generations 7 and 10, while NSWOA demonstrated slightly faster stabilization between generations 5 and 9. These results collectively confirm that all three algorithms successfully achieved convergence within a limited number of iterations, ensuring the reliability and robustness of the optimization process.
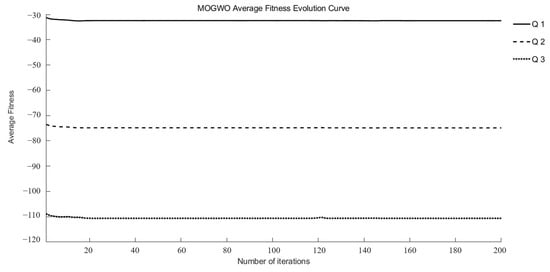
Figure 2. Evolutionary curves of average fitness for MOGWO.
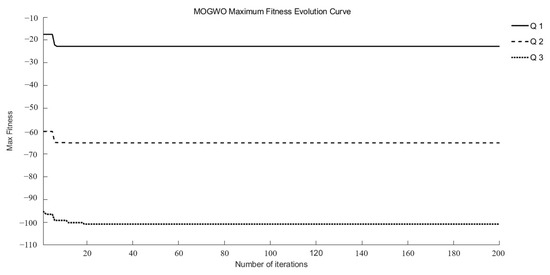
Figure 3. Evolutionary curves of maximum fitness for MOGWO.
As summarized in Table 5, the optimal solutions obtained by the three multi-objective optimization algorithms all satisfied the relevant drug release criteria under fixed component ratio constraints. Notably, NSGA-III and NSWOA exhibited superior convergence efficiency and solution stability, whereas MOGWO, despite converging at a slightly slower rate, was still capable of producing feasible and effective optimization outcomes.
Table 5. Satisfactory solution sets for glipizide pH-independent sustained-release tablets optimized using three multi-objective optimization algorithms.
As shown in Table 5, all three multi-objective optimization algorithms yielded optimal solutions meeting drug release standards while satisfying mixing ratios and constraints. To eliminate subjectivity from manual selection, the entropy weight method and TOPSIS method were employed in this study for comprehensive evaluation of the 45 optimized candidate solutions. The evaluation results effectively distinguished the relative merits of different solutions, ultimately identifying satisfactory Pareto-optimal solutions that provide scientifically viable references for optimizing drug preparation processes.

3.4. Results of the Entropy Weight-TOPIS Method Optimization Evaluation

The cumulative release degree was employed as an evaluation metric in this study given the potential for significant subjective bias in the traditional manual selection of optimal solutions. A comprehensive evaluation was conducted on the 45 optimized solutions by integrating a multi-objective assessment framework combining the entropy weight method and TOPSIS method. Through this evaluation approach, a set of satisfactory Pareto-optimal solutions was successfully identified, providing decision-makers with an objective, scientific, and practical drug preparation plan. The specific analysis results indicated that in a pH 6.8 medium, the weight assigned to the 8 h cumulative drug release rate (Y8) was the highest. Relevant data are shown in Supplementary Material Table S6. Based on the weight values of each evaluation indicator, the data were weighted and subjected to TOPSIS analysis. Since the cumulative release degree was a positive indicator, the value of the negative ideal solution was 0. A set of satisfactory Pareto-optimal solutions was ultimately selected by calculating the similarity (C value) between each evaluation object and the satisfactory solution scheme and then sorting them by C value. Partial results are shown in Table 6 (complete results are shown in Supplementary Information Table S8).
Table 6. Results of the TOPSIS.

3.5. Comparison of Optimization Results

In this study, the q-CCP method was employed to generate modeling variables during the optimization process. An optimal modeling framework combining three variable selection methods based on coefficient compression was constructed to form the objective function. Prescription optimization was conducted using three multi-objective optimization algorithms, yielding multiple Pareto solution sets. Finally, an integrated assessment combining the entropy weight method and TOPSIS were performed to screen a set of objectively feasible and satisfactory Pareto non-dominated solutions. Compared to the original formulation, Solution 45 in the optimal solution set achieved significant improvements in cumulative drug release rates: a 1.85% increase in the 2 h cumulative release rate at pH 1.2, a 5.48% increase in the 8 h cumulative release rate at pH 6.8, and an 8.73% increase in the 24 h cumulative release rate. Correspondingly, the formulation composition of the drug preparation also underwent notable changes. The proportions of HPMC K100LV, MgO, and lactose increased by 35.13%, 25.50%, and 13.79%, while the proportions of HPMC K4M and anhydrous CaHPO4 decreased by 3.95% and 41.23%, respectively. This formulation possessed good rationality and optimization effects while satisfying the mixing ratio and constraint conditions. Specific optimization results are shown in Table 7. Additionally, Table 8 lists other schemes superior to the original scheme (e.g., Schemes 29, 15, and 44). Researchers can select the most suitable scheme from these preferred options based on specific experimental requirements and conditions.
Table 7. Comparison of optimization results.
Table 8. Comparison of Satisfactory Schemes with Original Scheme.

4. Discussion

A novel integrated optimization framework for sustained-release formulation design was proposed and applied in this study. This method combines the q-CCP approach, regularization-based variable selection methods (LASSO, SCAD, and MCP), QIF modeling, multi-objective intelligent optimization algorithms (NSGA-III, MOGWO, and NSWOA), and the entropy weight–TOPSIS comprehensive evaluation approach. This framework enables the simultaneous characterization of high-order interactions and nonlinear effects in mixture designs, identifies key variables, and balances drug release performance with formulation feasibility during multi-objective optimization. Finally, a quantitative ranking of the Pareto-optimal solution set was achieved through the entropy weight–TOPSIS evaluation, allowing objective screening and decision support for optimized formulations, and providing a systematic pathway toward intelligent sustained-release formulation design [39,40].
In terms of optimization performance, the proposed framework achieved a notable improvement compared with the reference formulation reported in the literature. The reference formulation was derived using Design-Expert, which was used to perform statistical analysis and polynomial fitting of experimental data to generate ten candidate formulations within the specified composition range. The final formulation was selected based on the evaluation index and the maximum similarity factor (f2) [24]. In contrast, the optimized formulation predicted in this study showed increases in cumulative drug release of 1.85%, 5.48%, and 8.73% at 2 h, 8 h, and 24 h, respectively, indicating a potential enhancement in sustained-release performance. Furthermore, the multi-objective optimization process generated not only a single optimal solution but also a series of Pareto-optimal formulations satisfying the mixture constraints [41]. This provides researchers with greater flexibility to select appropriate formulations according to specific experimental requirements, process conditions, or development priorities. Based on model predictions, these candidate formulations notably demonstrated potential advantages in release behavior and formulation rationality, suggesting that the proposed optimization framework may exhibit good robustness and practical applicability [42].
From a pharmaceutical mechanistic perspective, the adjustment of excipient proportions in the optimized formulation was highly consistent with the known mechanisms of sustained-release matrix tablets. An increased amount of HPMC K100LV enhanced gel layer formation and system viscosity, prolonging the diffusion path and leading to smoother drug release [43]. A higher MgO content regulated the microenvironmental pH within the tablet, improving the stability and dissolution of weakly acidic drugs in acidic media [44]. An increased proportion of lactose contributed to the formation of a porous matrix structure, enhancing liquid penetration and diffusivity [43]. Meanwhile, a moderate reduction in HPMC K4M and anhydrous dibasic calcium phosphate content prevented excessive gel compaction, maintaining tablet integrity and an appropriate release rate [45]. These compositional adjustments align well with the release kinetics of sustained-release formulations, indicating that the optimization results are not only numerically reasonable but also pharmaceutically mechanistic and theoretically sound.
A high-order q-CCP model was employed in this study at the methodological and statistical modeling levels to capture the complex nonlinear and high-order interaction effects among excipients [42,46]. Compared with traditional response surface and full factorial designs, the q-CCP model provides a more comprehensive characterization of nonlinear relationships in mixture designs, offering richer information for multivariate formulation systems [47]. By integrating the MCP variable selection method, model sparsity was achieved, allowing the effective retention of key variables and their interactions while suppressing redundant factors, thereby improving model interpretability. It is noteworthy that although the non-convex penalty structure of the MCP enhances the identification of significant variables [48], its performance may be influenced by factors such as sample size, variable correlation, and data distribution characteristics; therefore, the variable selection results should be interpreted in the context of specific data conditions. An autocorrelation matrix structure was incorporated in this study for the repeated-measures cumulative release data, and the QIF for model fitting. Compared with the traditional Generalized Estimating Equations approach, QIF provides more robust modeling of within-subject correlation structures, improving estimation efficiency for repeated-measures data and enhancing the reliability and interpretability of multi-time point release predictions [39,49]. This methodological foundation ensured strong statistical support for subsequent optimization procedures.
In the multi-objective optimization phase, the combined application of NSGA-III, MOGWO, and NSWOA effectively balanced global search capability and the diversity of Pareto-optimal solutions. NSGA-III maintained a uniform distribution of solutions in high-dimensional objective spaces and rapidly approached the Pareto front [50]; MOGWO exhibited strong local search and adaptive capabilities [51]; and NSWOA demonstrated the ability to explore potential solution sets under complex constraint conditions [52]. The integration of these three algorithms not only enhanced optimization space coverage but also reduced the local optimum bias inherent to single algorithms, thereby improving the diversity and representativeness of the Pareto solution set. Subsequently, the EWM combined with TOPSIS was used to comprehensively rank the Pareto-optimal solutions, enabling quantitative comparison of multi-indicator schemes that balance drug release performance and formulation feasibility while minimizing subjective bias in decision-making [53]. This approach provides an operable and quantitative basis for sustained-release formulation design under multi-constraint and multi-objective conditions.
Overall, a systematic optimization framework for sustained-release formulation design was established in this study by integrating high-order polynomial modeling, sparse variable selection, autocorrelation fitting, multi-objective intelligent optimization, and entropy-weighted TOPSIS evaluation. The proposed framework not only improved the model’s interpretability for complex nonlinear and interactive effects but also generated diverse and practical candidate solutions in the multi-objective optimization process, providing researchers with a rational basis for selecting optimal formulations under varying constraints. Moreover, the proposed methodology simultaneously considers drug release performance, formulation rationality, and process feasibility, offering quantitative guidance and a referential operational framework for the development and industrialization of sustained-release formulations.

5. Conclusions

Our study proposed an optimization workflow integrating the q-CCP approach with variable selection methods. The formulation parameters of sustained-release tablets were systematically optimized via the combination of the QIF and multi-objective optimization algorithms. Through comprehensive evaluation using the EWM and TOPSIS, a satisfactory Pareto non-dominated solution set was identified. Based on the modeling results derived from the experimental data reported by Fang et al., the optimized formulation exhibited improved predicted cumulative release performance compared with traditional methods, with simulated release rates at 2 h, 8 h, and 24 h increasing by 1.847%, 5.483%, and 8.727%, respectively. Although this study provides a systematic and scientific framework for formulation optimization in sustained-release drug delivery, future experimental validation will be necessary to confirm its practical applicability.

6. Limitations

Although our study introduced methodological innovations and proposed a comprehensive optimization process, certain limitations remain. First, while we obtained optimization results and demonstrated significant improvements, we did not conduct actual experimental validation. Consequently, the effectiveness and feasibility of the optimization scheme in practical applications cannot be confirmed. Subsequent studies should incorporate experimental validation to confirm the performance of the proposed optimization scheme in actual production. Meanwhile, our research primarily focused on enhancing drug release rates, while other drug properties such as stability and dissolution rates require further consideration. Future work may incorporate these factors into the optimization objectives to construct a more comprehensive optimization model.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/pharmaceutics17111419/s1, Table S1: Scope setting table for each component, Table S2: Lasso screening variables and regression coefficients, Table S3: SCAD screening variables and regression coefficients, Table S4: MCP screening variables and regression coefficients, Table S5: Model fitting results for different variable selection methods, Table S6: Weighting results calculated using the entropy method, Table S7: Positive and negative ideal solutions, Table S8: Results of TOPSIS, Figure S1: Evolutionary curves of average fitness for NSGA-III, Figure S2: Evolutionary curves of maximum fitness for NSGA-III, Figure S3: Evolutionary curves of average fitness for NSWOA, Figure S4: Evolutionary curves of maximum fitness for NSWOA. A detailed introduction to the methods section is provided in the supplementary materials [54,55,56].

Author Contributions

Y.Q.: Conceptualization, Methodology, Formal Analysis, Writing—Original Draft. Y.W.: Conceptualization, Methodology, Formal Analysis. M.H.: Conceptualization, Methodology, Investigation, Validation. H.R.: Conceptualization, Methodology, Investigation, Validation. Y.C.: Investigation, Validation. Y.L.: Investigation, Validation. X.W.: Conceptualization, Investigation, Validation. C.H.: Investigation, Validation. Q.F.: Formal Analysis, Writing—Review and Editing. L.Q.: Resources, Supervision, Writing—Review and Editing, Funding Acquisition. All authors have read and agreed to the published version of the manuscript.

Funding

This study was financially supported by the National Natural Science Foundation of China (Grant No. 81973155, Principal Investigator: Lixia Qiu).

Data Availability Statement

All data generated or analyzed during this study are included in the article and its Supplementary Materials.

Acknowledgments

The authors are grateful to the faculty members of the Statistical Research Office of Shanxi Medical University for their valuable guidance and support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gunawardana, M.; Remedios-Chan, M.; Miller, C.S.; Fanter, R.; Yang, F.; Marzinke, M.A.; Hendrix, C.W.; Beliveau, M.; Moss, J.A.; Smith, T.J.; et al. Pharmacokinetics of long-acting tenofovir alafenamide (GS-7340) subdermal implant for HIV prophylaxis. Antimicrob. Agents Chemother. 2015, 59, 3913–3919. [Google Scholar] [CrossRef] [PubMed]
  2. Khandave, S.S.; Sawant, S.V.; Joshi, S.S.; Bansal, Y.K.; Kadam, S.S. Comparative bioequivalence studies of tramadol hydrochloride sustained-release 200 mg tablets. Drug Des. Dev. Ther. 2010, 4, 367–374. [Google Scholar] [CrossRef] [PubMed]
  3. Elwerfalli, A.M.; Al-Kinani, A.; Alany, R.G.; ElShaer, A. Nano-engineering chitosan particles to sustain the release of promethazine from orodispersables. Carbohydr. Polym. 2015, 131, 447–461. [Google Scholar] [CrossRef]
  4. Verberkt, C.A.; van den Beuken-van Everdingen, M.H.J.; Schols, J.; Hameleers, N.; Wouters, E.F.M.; Janssen, D.J.A. Effect of Sustained-Release Morphine for Refractory Breathlessness in Chronic Obstructive Pulmonary Disease on Health Status: A Randomized Clinical Trial. JAMA Intern. Med. 2020, 180, 1306–1314. [Google Scholar] [CrossRef]
  5. Mitsuboshi, S.; Imai, S.; Kizaki, H.; Hori, S. Comparison of different sustained-release opioids and acute respiratory conditions in patients with cancer and chronic kidney disease. Pharmacotherapy 2024, 44, 122–130. [Google Scholar] [CrossRef]
  6. Ferreira, D.H.; Boland, J.W.; Kochovska, S.; Honson, A.; Phillips, J.L.; Currow, D.C. Patients’ and caregivers’ experiences of driving with chronic breathlessness before and after regular low-dose sustained-release morphine: A qualitative study. Palliat. Med. 2020, 34, 1078–1087. [Google Scholar] [CrossRef]
  7. Qiao, Y.; Wang, X.; Ren, H.; Cui, Y.; Ren, J.; Hao, C.; Zhao, Z.; Liu, J.; Zhao, R.; Li, Y.; et al. A study on the preparation conditions of lidocaine microemulsion based on multi-objective genetic algorithm. Front. Pharmacol. 2023, 14, 1272454. [Google Scholar] [CrossRef]
  8. Qiao, Y.; Kang, S.; Wu, Y.; Cui, Y.; Wang, X.; Ren, H.; Han, M.; Lou, Y.; Tian, Q.; Qiu, L. Application of multi-objective optimization algorithm to the preparation of polycaprolactone microsphere formulations. Int. J. Pharm. 2025, 681, 125859. [Google Scholar] [CrossRef]
  9. Huang, Y.B.; Tsai, Y.H.; Yang, W.C.; Chang, J.S.; Wu, P.C. Optimization of sustained-release propranolol dosage form using factorial design and response surface methodology. Biol. Pharm. Bull. 2004, 27, 1626–1629. [Google Scholar] [CrossRef] [PubMed]
  10. Ferreira, S.L.; Bruns, R.E.; Ferreira, H.S.; Matos, G.D.; David, J.M.; Brandão, G.C.; da Silva, E.G.; Portugal, L.A.; dos Reis, P.S.; Souza, A.S.; et al. Box-Behnken design: An alternative for the optimization of analytical methods. Anal. Chim. Acta 2007, 597, 179–186. [Google Scholar] [CrossRef]
  11. Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef] [PubMed]
  12. Simon, N.; Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent. J. Stat. Softw. 2011, 39, 1–13. [Google Scholar] [CrossRef] [PubMed]
  13. Tibshirani, R.; Bien, J.; Friedman, J.; Hastie, T.; Simon, N.; Taylor, J.; Tibshirani, R.J. Strong rules for discarding predictors in lasso-type problems. J. R. Stat. Society. Ser. B Stat. Methodol. 2012, 74, 245–266. [Google Scholar] [CrossRef] [PubMed]
  14. Fan, J.; Lv, J. Non-Concave Penalized Likelihood with NP-Dimensionality. IEEE Trans. Inf. Theory 2011, 57, 5467–5484. [Google Scholar] [CrossRef]
  15. Breheny, P.; Huang, J. Coordinate Descent Algorithms for Nonconvex Penalized Regression, with Applications To Biological Feature Selection. Ann. Appl. Stat. 2011, 5, 232–253. [Google Scholar] [CrossRef]
  16. Offorha, B.C.; Walters, S.J.; Jacques, R.M. Analysing cluster randomised controlled trials using GLMM, GEE1, GEE2, and QIF: Results from four case studies. BMC Med. Res. Methodol. 2023, 23, 293. [Google Scholar] [CrossRef]
  17. Luo, L.; Zhou, L.; Song, P.X. Real-Time Regression Analysis of Streaming Clustered Data With Possible Abnormal Data Batches. J. Am. Stat. Assoc. 2023, 118, 2029–2044. [Google Scholar] [CrossRef]
  18. Odueyungbo, A.; Browne, D.; Akhtar-Danesh, N.; Thabane, L. Comparison of generalized estimating equations and quadratic inference functions using data from the National Longitudinal Survey of Children and Youth (NLSCY) database. BMC Med. Res. Methodol. 2008, 8, 28. [Google Scholar] [CrossRef]
  19. Cao, H.; Li, Z.; Yang, H.; Cui, Y.; Zhang, Y. Longitudinal data analysis for rare variants detection with penalized quadratic inference function. Sci. Rep. 2017, 7, 650. [Google Scholar] [CrossRef]
  20. Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
  21. Stokes, Z.; Mandal, A.; Wong, W.K. Using Differential Evolution to Design Optimal Experiments. Chemom. Intell. Lab. Syst. 2020, 199, 103955. [Google Scholar] [CrossRef]
  22. Dagal, I.; Ibrahim, A.W.; Harrison, A.; Mbasso, W.F.; Hourani, A.O.; Zaitsev, I. Hierarchical multi step Gray Wolf optimization algorithm for energy systems optimization. Sci. Rep. 2025, 15, 8973. [Google Scholar] [CrossRef] [PubMed]
  23. Zhang, H.; Yan, J.; Wang, L. Hybrid Tabu-Grey wolf optimizer algorithm for enhancing fresh cold-chain logistics distribution. PLoS ONE 2024, 19, e0306166. [Google Scholar] [CrossRef] [PubMed]
  24. Fu, F.; Huang, J.; Lin, H.; Xie, Y. Optimization the formulation of pH-independent sustained release tablets of glipizide using D-optimal mixture design. J. Guangdong Pharm. Univ. 2018, 34, 547–553. [Google Scholar]
  25. Huang, J.; Breheny, P.; Ma, S. A Selective Review of Group Selection in High-Dimensional Models. Stat. Sci. 2012, 27, 481–499. [Google Scholar] [CrossRef]
  26. Westgate, P.M. Criterion for the simultaneous selection of a working correlation structure and either generalized estimating equations or the quadratic inference function approach. Biom. J. 2014, 56, 461–476. [Google Scholar] [CrossRef]
  27. Hare, L.B.; Altan, S.; Coppenolle, H. Correction to “Mixture Experimentation in Pharmaceutical Formulations: A Tutorial”. Pharm. Stat. 2025, 24, e70017. [Google Scholar] [CrossRef]
  28. Bilil, H.; Aniba, G.; Gharavi, H. Dynamic Appliances Scheduling in Collaborative MicroGrids System. IEEE Trans. Power Syst. 2017, 32, 2276–2287. [Google Scholar] [CrossRef]
  29. Wang, L.; Kim, Y.; Li, R. Calibrating Non-Convex Penalized Regression in Ultra-High Dimension. Ann. Stat. 2013, 41, 2505–2536. [Google Scholar] [CrossRef]
  30. Lyu, J.; Jiang, Y.; Xu, C.; Liu, Y.; Su, Z.; Liu, J.; He, J. Multi-objective winter wheat irrigation strategies optimization based on coupling AquaCrop-OSPy and NSGA-III: A case study in Yangling, China. Sci. Total Environ. 2022, 843, 157104. [Google Scholar] [CrossRef]
  31. Wang, S.; Wang, Y.; Wang, Y.; Wang, Z. Comparison of multi-objective evolutionary algorithms applied to watershed management problem. J. Environ. Manag. 2022, 324, 116255. [Google Scholar] [CrossRef]
  32. Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.d.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
  33. Al-Qaness, M.A.A.; Helmi, A.M.; Dahou, A.; Elaziz, M.A. The Applications of Metaheuristics for Human Activity Recognition and Fall Detection Using Wearable Sensors: A Comprehensive Analysis. Biosensors 2022, 12, 821. [Google Scholar] [CrossRef]
  34. Nadimi-Shahraki, M.H.; Zamani, H.; Asghari Varzaneh, Z.; Mirjalili, S. A Systematic Review of the Whale Optimization Algorithm: Theoretical Foundation, Improvements, and Hybridizations. Arch. Comput. Methods Eng. 2023, 30, 4113–4159. [Google Scholar] [CrossRef] [PubMed]
  35. Jangir, P.; Jangir, N. Non-Dominated Sorting Whale Optimization Algorithm (NSWOA): A Multi-Objective Optimization Algorithm for Solving Engineering Design Problems. Glob. J. Res. Eng. 2017, 17, 15–42. [Google Scholar]
  36. Hadka, D.; Reed, P. Borg: An auto-adaptive many-objective evolutionary computing framework. Evol. Comput. 2013, 21, 231–259. [Google Scholar] [CrossRef]
  37. Pan, X.; Kang, Y.; Lu, J.F.; Yu, X.Z. Using the TOPSIS method to select the best low-toxicity organic cosolvent for rice-based toxicity tests. Ecotoxicol. Environ. Saf. 2025, 290, 117733. [Google Scholar] [CrossRef]
  38. de Oliveira, B.R.; Zuffo, A.M.; Aguilera, J.G.; Steiner, F.; Ancca, S.M.; Flores, L.A.P.; Gonzales, H.H.S. Selection of Soybean Genotypes under Drought and Saline Stress Conditions Using Manhattan Distance and TOPSIS. Plants 2022, 11, 2827. [Google Scholar] [CrossRef]
  39. Liang, H.; Wang, X.; Peng, Y.; Niu, Y. Improving marginal hazard ratio estimation using quadratic inference functions. Lifetime Data Anal. 2023, 29, 823–853. [Google Scholar] [CrossRef]
  40. Ketabat, F.; Pundir, M.; Mohabatpour, F.; Lobanova, L.; Koutsopoulos, S.; Hadjiiski, L.; Chen, X.; Papagerakis, P.; Papagerakis, S. Controlled Drug Delivery Systems for Oral Cancer Treatment-Current Status and Future Perspectives. Pharmaceutics 2019, 11, 302. [Google Scholar] [CrossRef]
  41. Lambrinidis, G.; Tsantili-Kakoulidou, A. Multi-objective optimization methods in novel drug design. Expert Opin. Drug Discov. 2021, 16, 647–658. [Google Scholar] [CrossRef]
  42. Costa, P.; Sousa Lobo, J.M. Modeling and comparison of dissolution profiles. Eur. J. Pharm. Sci. 2001, 13, 123–133. [Google Scholar] [CrossRef]
  43. Siepmann, J.; Peppas, N.A. Modeling of drug release from delivery systems based on hydroxypropyl methylcellulose (HPMC). Adv. Drug Deliv. Rev. 2001, 48, 139–157. [Google Scholar] [CrossRef]
  44. Siepmann, J.; Peppas, N.A. Higuchi equation: Derivation, applications, use and misuse. Int. J. Pharm. 2011, 418, 6–12. [Google Scholar] [CrossRef] [PubMed]
  45. Kanjickal, D.G.; Lopina, S.T. Modeling of drug release from polymeric delivery systems—A review. Crit. Rev. Ther. Drug Carr. Syst. 2004, 21, 345–386. [Google Scholar] [CrossRef]
  46. Verma, R.; Kaushik, D. Design and optimization of candesartan loaded self-nanoemulsifying drug delivery system for improving its dissolution rate and pharmacodynamic potential. Drug Deliv. 2020, 27, 756–771. [Google Scholar] [CrossRef]
  47. Petrovic, A.; Cvetkovic, N.; Ibric, S.; Trajkovic, S.; Djuric, Z.; Popadic, D.; Popovic, R. Application of mixture experimental design in the formulation and optimization of matrix tablets containing carbomer and hydroxy-propylmethylcellulose. Arch. Pharmacal Res. 2009, 32, 1767–1774. [Google Scholar] [CrossRef] [PubMed]
  48. Arimura, E.; Matsumoto, C.; Okuyama, S.; Takada, S.; Hashimoto, S.; Shimomura, Y. Quantification of metamorphopsia in a macular hole patient using M-CHARTS. Acta Ophthalmol. Scand. 2007, 85, 55–59. [Google Scholar] [CrossRef]
  49. Adams, E.; Coomans, D.; Smeyers-Verbeke, J.; Massart, D.L. Non-linear mixed effects models for the evaluation of dissolution profiles. Int. J. Pharm. 2002, 240, 37–53. [Google Scholar] [CrossRef]
  50. Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
  51. Jing, T.; Sun, H.; Cheng, J.; Zhou, L. Optimization of a Screw Centrifugal Blood Pump Based on Random Forest and Multi-Objective Gray Wolf Optimization Algorithm. Micromachines 2023, 14, 406. [Google Scholar] [CrossRef]
  52. Chen, H.; Xu, Y.; Wang, M.; Zhao, X. A Balanced Whale Optimization Algorithm for Constrained Engineering Design Problems. Appl. Math. Model. 2019, 71, 45–59. [Google Scholar] [CrossRef]
  53. Zhu, T.; Yu, Y.; Tao, T. A comprehensive evaluation of liposome/water partition coefficient prediction models based on the Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) method: Challenges from different descriptor dimension reduction methods and machine learning algorithms. J. Hazard. Mater. 2023, 443 Pt A, 130181. [Google Scholar] [CrossRef] [PubMed]
  54. Witten, D.M.; Tibshirani, R.J. Extensions of sparse canonical correlation analysis with applications to genomic data. Stat. Appl. Genet. Mol. Biol. 2009, 8, 28. [Google Scholar] [CrossRef] [PubMed]
  55. Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
  56. Habib, B.A.; Abdeltawab, N.F.; Salah Ad-Din, I. D-optimal mixture design for optimization of topical dapsone niosomes: In vitro characterization and in vivo activity against Cutibacterium acnes. Drug Deliv. 2022, 29, 821–836. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Amodiaquine Modulates Aggregation and Disassembly of Amyloid-β and Tau and Attenuates Neuroinflammatory Responses and Aβ Production
Previous
Innovative Strategies for the Targeted Degradation of Viral Proteins: Paving the Way for Next-Generation Therapeutics
Next