Abstract
Markov chain models have been applied for a long time to simulate forest dynamics based on transitions in matrices of tree diameter classes or areas of forest size and structure types. To date, area-based matrix models have been applied assuming either even-aged or uneven-aged forest management. However, both management systems may be applied simultaneously due to land-use constraints or the rationality of combining the systems, which is called any-aged management. We integrated two different Markov chain models, one for even-aged and another for uneven-aged forest management, in an area-based approach to analyze wood supply from any-aged forest management. We evaluate the impacts of parameterizing the model based on available data sets, namely permanent and temporary Finnish National Forest Inventory (NFI) sample plots and a plot-level simulator to determine transitions due to different types of thinning treatments, and present recommendations for the related methodological choices. Our overall observation is that the combined modelling chain simulated the development of both the even- and uneven-aged forest structures realistically. Due to the flexibility of the implementation, the approach is very well suited for situations where scenario assumptions need to be varied according to expected changes in silvicultural practices or land-use constraints, for example.
1. Introduction
The demand for wood-based biomass is predicted to increase globally [1,2,3,4]. However, many other uses of forests should be considered. The conflicting goals and uses may reduce the amount of forests available for wood supply (FAWS) through land segregation. According to recent studies, the amount of forest not available for wood supply (FNAWS) varies a lot between countries [5,6]. In addition to or instead of segregation, so called multiple-use [7] or integrated [8] forest management has become more commonly applied [9]. From the wood supply point of view, these forests can be referred to as forests with restrictions on availability for wood supply (FRAWS).
In recent years, the supply of wood-based biomass has been estimated at national [10] and European levels [11,12,13]. The national level estimates are usually based on detailed forest inventory data, while the European level studies have often relied on aggregated statistical data [11]. This difference is problematic with respect to up- or downscaling the results: On one hand, it is not possible to sum up (upscale) the more detailed national level results to European level because of the variation in definitions and assumptions applied. On the other hand, the harmonized assumptions on, for example, availability of forests for wood supply at the European level may lead to serious under- or overestimates when downscaling the results to the national levels [5].
In Europe, the wood supply analyses have been based on different approaches from increment-based estimates [14] to modelling of future biomass supply [10]. In countries where wood-based industry is important, analyses of harvesting potential are based on data from National Forest Inventories (NFIs) and plot- or stand-level simulations [15,16,17,18] and similar approaches can be applied to simulate the provisioning of non-wood forest products or other ecosystem services. Also less data-intensive models, such as the European Forest Information Scenario Model (EFISCEN, [19]) have been applied [20,21]. The EFISCEN model originates from the so called International Institute for Applied System Analysis (IIASA) model developed by Nilsson et al. [22] and is based on the concept of Markov chain matrix models adopted by Sallnäs [23] from the ideas of Usher [24,25,26]. EFISCEN has been used to model forest dynamics from regional to European levels [11,19,20,21,27], but only in the context of even-aged forestry, although the Markov chain approach is fundamentally applicable for simulations of uneven-aged forest management [28,29,30]. A more recent Markov chain model, the European Forest Dynamics Model (EFDM, [31]) was tested also for modelling the development of uneven-aged forests [32]. However, rational forestry practices combine both even- and uneven-aged management [33] and, in many countries in Europe, both management systems and shifts between systems appear with implications on future wood supply. Yet, none of the area-based matrix models used in Europe is applicable for simulating combined even- and uneven-aged management, also known as any-aged forest management [34,35,36].
The aim of this study is to analyze wood supply from any-aged forest management based on NFI data. The main objective is to integrate two different Markov chain models, one for even-aged and another for uneven-aged forest management, in a single simulation run based on the EFDM approach. The second objective is to evaluate the impact of different choices when selecting the parameterization of the model based on available data sets.
2. Materials and Methods
2.1. The Markov Chain Model
2.1.1. General Description
Methodologically, EFDM is a simple Markov chain model, which simulates the development of unit areas of forest land according to probabilities indicating transitions due to natural processes or management actions. The distribution of the forest land, i.e., the state space S, is presented as a matrix defined by a collection of classifying factors, which determine the dimensions of the matrix and thus combinations of possible states. The cell values of the matrix represent areas in each state. As explained in detail in the original documents of the EFDM [31,37], a simulation step is obtained as transition of S affected by activities A and transition probabilities P. Consequently, the basic output from an EFDM simulation is a sequence of areas in each state after each of requested number of time steps. By defining a new state space or sets of the classifying factors and transition probabilities, the EFDM can be flexibly tailored for different ecological and socio-economic conditions and different scenario assumptions. This property could be utilized, for example, by simulating variations in the transitions according to expectations on future land-use—climate policies.
We downloaded v. 2.0. of the EFDM implemented in the R statistical (R Foundation for Statistical Computing, Vienna, Austria) modelling environment [38] from the EFDM project repository [39], where it is available as open source under the European Union Public License (EUPL) license [40]. In the implementation, separate transition matrices with axes corresponding to so called dynamic factors are used [31]. The number of matrices is determined by static factors, which define the forest dynamics or are otherwise included e.g., for reporting purposes (geographic region, owner, site, etc.). In the context of even-aged forests, the dynamic factors are usually defined by classes for age and standing volume [31]. To simulate uneven-aged forestry, Sallnäs et al. [32] replaced age and volume by stem number and volume. We used age and volume (denoted in the further text by “Age-Vol”) and stem number and volume (“N-Vol”) matrices to model the development of even- and uneven-aged forests, respectively. We intentionally leave further details of the EFDM simulations to the original publications [31,32,37], but focus on describing how the input data should be arranged to simulate any-aged forest management using the current implementation of the EFDM.
2.1.2. Application of the EFDM for the Simulations of Any-Aged Forest Management
A given forest area was always simulated according to either even- or uneven-aged management based on Age-Vol or N-Vol matrices, respectively. This decision was made in the beginning of the simulation and no transitions between the silvicultural systems were applied during the simulations. We assumed that the land-use restriction determined the silvicultural system applied. In Finland, conventional instructions of forest management have been based on even-aged silviculture [41], which has consequently dominated the management of the FAWS. The FNAWS may have been left outside of forestry for many reasons such as ecological conservation, but also due to restrictions set in community planning. A high proportion of these forests can also be characterized as even-aged forests: for instance, the dominant age is measured in the NFI from all FNAWS. However, different forms of unven-aged silviculture are expected to be most common choices for integrated forest management [8]. Based on this background, areas marked as FAWS were assumed to be managed according to an even-aged silviculture using Age-Vol matrices and FRAWS according uneven-aged silviculture and N-Vol matrices. FNAWS were not managed, but their natural process was simulated according to the Age-Vol matrices. According to the comparison of the simulated development presented in the results, no difference would have been observed if N-Vol matrices were applied for the latter purpose (see Section 3.1).
To consider any-aged forest management, the development of both the Age-Vol and N-Vol matrices had to be simulated in parallel. We chose not to modify the EFDM software for this purpose, but defined artificial “0-classes” to distinguish the plots to be simulated according to either the Age-Vol or N-Vol matrices, which is explained in detail in Section 2.4.1. Only one function of the EFDM code had to be modified to enable modeling transitions of both the Age-Vol and N-Vol matrices, as explained in Section 2.4.2.
2.2. Steps of the Analysis
The workflow required to prepare the data and run the analyses described above consisted of the following steps:
- Preparing the initial forest inventory data and pairwise observations for modeling the transitions (Section 2.3);
- Parameterizing the EFDM model with respect to the initial state space, transition and activity probabilities, and output coefficients (Section 2.4);
- Running the EFDM with scenario assumptions specified in Section 2.5.
The results are presented from two viewpoints: first, we evaluate the choices related to the parameterization of the EFDM-specific state space, activities, and their transition probabilities. Recommendations on these choices are given based on the results. Second, we present results of the scenario analyses using the EFDM.
2.3. Forest Inventory Data
2.3.1. An Overview of Parameterizing the EFDM with the Input Data
Sample plots of the 10th and 11th Finnish National Forest Inventory, denoted by NFI10 and NFI11, respectively, were used to derive the input data for the EFDM. The NFI11 plots were the primary data for the analyses, while the NFI10 plots were included for validation and deriving pairwise observations for modelling the transitions.
All components of the EFDM software (initial state space, transition and activity probabilities, and output coefficients) need to be parameterized to run the analyses. However, the components are generic and running the simulations only requires that those are somehow initialized. The parameter values may come from many sources: for instance, the probability values can be computed directly based on observations, growth functions, or expert opinion, or any of the aforementioned can be converted to pairwise observations to be used with subsequent estimation routines to derive the probabilities. No clear recommendations or remarks on capabilities of different data sources can be found from the previous literature. Based on this background, we either fixed the data sources according to our knowledge or examined the effects of different data sources in sensitivity analyses. The data sources are outlined below and described in a very high technical detail in the following sections:
- The initial state was determined based on the full NFI11 (or NFI10 in one validation analysis). The data processing involved the initial estimation (Section 2.3.2) and formatting the data for the EFDM (Section 2.4.1).
- Two alternative data sets were used to derive the pairwise observations to model the transitions due to natural processes. The data sets were permanent NFI10-11 and temporary NFI11 plots, which slightly differ in terms of estimating the pairwise observations, as detailed in Section 2.3.3 and Section 2.4.2 with respect to estimation and EFDM-specific formatting, respectively. The two plot types were used to derive two distinct sets of transition probabilities, which were switched as the input data when running the analyses, but the permanent and temporary plots were never merged when modeling the transitions. Notably, the transitions estimated based on both the permanent and temporary plot data included only growth and not potential reductions due to calamities or natural disturbances [32], for example. Including these effects is discussed in Section 4 and Section 5.
- A simulator was implemented to derive the pairwise observations from situations before and after thinning treatments. The thinnings took place in the beginning of each simulation period and the growth of the thinned forests in that period was simulated applying the transition probabilities of forests not managed. The forests affected by final fellings were forced to transit to the beginning of the even-aged rotation. The data processing involved the initial estimation (Section 2.3.3) and formatting the data for the EFDM (Section 2.4.2).
- The activity probabilities, which give the proportion of different types of forests to be managed, were defined in two steps with two assumptions. First, the initial allocation of the harvests to the different types of forests was assumed to follow either the proportion of harvests realized during the most recent five-year period (“business-as-usual allocation”, ABAU) or the proportion of forests that should be harvested strictly according to the instructions of forest management [41] (“schoolbook allocation”, ASB). Second, the final values for the activity probabilities of both the allocations were obtained by iteratively adjusting the initial probabilities to produce the harvesting levels aimed at in the future large-area scenarios. The data processing related to both the steps is explained in detail in Section 2.4.3 and Section 2.5.
- Output coefficients were prepared to translate the areas in different volume, age, and stem number classes to timber assortment and total volumes. The related steps are explained in Section 2.4.4.
2.3.2. Measurements and Estimation Principles of the NFI Data
Our analyses used NFI data from productive and poorly productive forest land in the entire Finland [42], excluding the Åland islands and the three northernmost municipalities of Lapland. These areas were excluded due to a partial lack of data (no plot measurements in both NFIs), but also due to considerable differences in forest structure and minor importance for forestry compared to other parts of the country. The NFI11 data covered altogether 51,827 plots and an area of 21.28 mill·ha. Altogether, 11,987 of the plots were permanent and the rest temporary. Altogether, 7.3% or 10.1% and 9.3% or 10.6% of the total number of plots or the total area were classified as FNAWS and FRAWS, respectively, the rest being FAWS.
The NFI10 and NFI11 were carried out in 2004–2008 and 2009–2013, respectively, using the measurement and estimation protocol explained by Korhonen [42] and detailed by Tomppo et al. [43]. Sample trees were selected using angle count sampling with a relascope factor and the maximum inclusion zone for the tally trees varying in different sampling regions within the country. The stem and assortment volumes of the sampled trees were estimated and converted to unit-area mean values represented by each tree using methods explained by Tomppo et al. [43]. The area represented by a sample plot was computed by dividing the known land area of one sampling region by the number of plot centres located in land and in that sampling region. Total values were estimated as the product of the estimates of unit-area mean values and the corresponding areas.
2.3.3. Pairwise Observations
The plot data readily included relevant administrative and soil/site information, both stand-level and detailed plot-level information on the tree stock, and records on past and planned future treatments needed for the parameterization of the EFDM. The transition probabilities due to management actions were computed from pairwise observations, which were derived from the NFI plots as described in the following text. Separate pairwise observations were required to model (1) transitions due to growth and (2) transitions due to management. These were obtained as follows:
- Deriving the growth observations is explained separately for the two alternative data sets, namely (a) permanent and (b) temporary NFI plots:
- (a)
- Permanent NFI sample plots, which were matched between data sets with certainty and had no treatments between the two subsequent inventories, were identified from the data. The positive differences in the total volumes between NFI10 and NFI11 were recorded as the pairwise data.
- (b)
- Pairwise observations were derived from temporary NFI11 plots using the increment estimates. In the NFI, every seventh tree (continuously over plot clusters) is measured for diameter and height increment, from which a volume growth percent was estimated following Tomppo et al. [43]. Due to the low number of observations, the percent was estimated at the level of sampling regions and the percent computed for a sampling region was applied for all plots in the region. This percent was used to estimate the difference of volumes between the two subsequent inventories for the plots without treatments, i.e., the pairwise observations were obtained as the difference between the observed volume and that deducted by the estimated growth.
- To determine transitions due to management by thinning treatments, a plot-level simulator was implemented to assess the proportion of the total and assortment volume to be removed in future thinning treatments. The NFI11 plots were used as the input data. The simulator determined the thinning removal following two types of instructions:
- (a)
- A thinning from below corresponding to traditionally applied instructions for forest management [41] was simulated according to thinning curves downloaded from the repository of the SIMO software (Simosol Py, Riihimäki, Finland, [44]). The curves predict the thinning limit and remaining basal area as the function of tree species, site type and dominant height (estimated as mean stand height +1.75 m [45]). The lower curves of two available thinning intensity levels were used and the harvesting removal was determined as the difference between the thinning need and remaining basal area.
- (b)
- A thinning from above was simulated by predicting the remaining basal area using the plot-level forest attributes as predictors of Equation (2) of Pukkala et al. [46]. The thinning intensity is determined in terms of interest rate used as a predictor of the aforementioned equation. We used the curves corresponding to an interest rate of 3% and determined the harvesting removal as the difference between the initial and remaining basal area.
Mimicking an operational implementation, 50% of the harvesting removal was obtained from the smallest trees and 50% systematically among larger trees in the thinnings from below. In thinnings from above, 50% of the harvesting removal was obtained from the largest trees and 50% systematically among smaller ones. The thinnings were simulated for plots with initial basal area >10 m2/ha and mean height >10 m and also the remaining basal area was forced to be at least 10 m2/ha to simulate treatments that are profitable and legal according to the instructions of forest management [41].
2.4. Parameterization of the Markov Model
2.4.1. State Space
In our analyses, the forest land was classified according to four static and two dynamic factors. The definitions and classification levels of the static factors were determined based on the field data as follows:
- Known land-use restrictions: FAWS, FRAWS, FNAWS
- Forest ownership: private, public + other (cf. [42]).
- Site fertility: altogether, five categories corresponding to four taxation classes traditionally used in Finland + fifth class including all poorly productive forest land.
- Dominant species: pine, spruce, deciduous trees.
According to the reasoning above, we used the Age-Vol and N-Vol matrices for the projections of even-aged and uneven-aged stand structures, respectively. These attributes were observed from the plots in a continuous scale and had to be classified for the EFDM. The class limits for both the volume and stem number were derived as the values of the 10th, 20th, …, 90th and 95th quantiles of the pairwise observations made from the permanent plots. This choice ensured the availability of an equal amount of observations per class. An exception is made with the last two classes, in which the number of observations was halved due to including the 95th quantile. However, if treated as a single class, the value range of the last class would have been manifold to other classes, for which reason the reduction in the number of observations was considered as justified. The age classes were defined as 0, 5, 10, …, 120, 120+ years, the interval corresponding to the measurements, which also determined the simulation step used in the analyses. The class limits derived from the data are presented as Appendix A.
The dynamics of any-aged forest management were simulated by using the forest area classified in the Age-Vol and N-Vol matrices as an input for the EFDM. Although the EFDM would principally allow an unlimited number of the dynamic factors, we always used two dynamic factors at the time for ease of maintaining control of the inputs and outputs. To implement this, an extra 0-class of age and stem number was introduced in addition to the classes derived from the data. The transition probabilities were always modelled using all plots with pairwise observations, but such that either the age (for the simulations based on N-Vol) or stem number (for the simulations based on Age-Vol) was assigned as an extra static factor with only one level (0). When preparing for the simulations, the stem number or age of the plots to be managed according to the even- or uneven-aged silviculture, respectively, was assigned to the 0-class. To summarize the data structure:
- In the input data for the simulations, every plot representing even-aged forest had a value of 0 as the stem number class and the values of age and volume ranged according Appendix A. Every plot representing uneven-aged forest had a value of 0 as the age class and the values of stem number and volume ranged according to Appendix A.
- In the input data for modeling the transition probabilities, the set of plots with pairwise observations was duplicated. Thus, every plot was included twice with either the age or stem number class set as 0, i.e., the data to model the transitions of both Age-Vol or N-Vol were always the same except for the variable combination.
2.4.2. Transition Probabilities
The transition probabilities were estimated using the pairwise observations classified according to the static and dynamic factors as described above. The estimation was based on an iterative Bayesian algorithm, which is included in the EFDM package [37] (pp. 2–3). The main idea of the algorithm is to derive a loose prior for the transition probability based on all available observations and adjust it for each factor combination using the specific observations, the amount of which may be small or even completely missing.
The transition probabilities of the natural process were computed separately from the pairwise observations of both the permanent and temporary plots without treatments between the inventories (Section 2.3.3, numbered point 1). The transition probabilities due to thinnings were computed from the selection of plots, for which the thinning had been simulated, i.e., which had a basal area higher than the thinning limit (Section 2.3.3, numbered point 2). Forest areas affected by final fellings were forced to transit from the class prior to the treatment to the first Age-Vol class. To allow estimating the transitions probabilities also for the N-Vol matrices, all statements referring to “age” in the pre.estimate function (file hackfunctions.R of the EFDM package) were converted to “n” to correspond our naming conventions.
2.4.3. Activity Probabilities
The activities applied in our simulations were “no management”, “final felling”, “thinning from below”, and “thinning from above”. The activities sum up to one and describe the proportions of areas classified according to the factors affected by each activity in each simulation step. The activity proportions were computed assuming the future harvests to follow either business-as-usual (ABAU) or schoolbook (ASB) allocation based on realized or proposed harvests, respectively, in the data classified according to the factor combinations. More specifically, ABAU was obtained as the proportion of areas with no management, thinning or final felling observed in the pairwise data from the permanent plots between NFI10 and NFI11. ASB was the proportion of areas, in which a need for thinning or final felling within the next five years according to the forestry guidelines [43] was recorded in the field inventory. In both cases, there was none or a very limited number of observations on the activities for a number of static and dynamic factor combinations, which would have resulted in unrealistic activity probabilities if computed as factor-specific based on the data. For this reason, both the ABAU and ASB were computed by pooling the activities for the Age-Vol or N-Vol classes over the static factors, i.e., the probability of a certain activity was the same for the given dynamic factors in all static factor combinations.
A simple iteration procedure was added to the EFDM to adjust the activity probabilities to fulfill the harvesting objectives determined in Section 2.5. The standing volume or drain, depending on the objective, was first determined applying the output coefficients (Section 2.4.4) and the initial level of the activity probabilities. The difference to the goal was calculated and the probabilities were repeatedly multiplied by 1.01 or 0.99, depending on the sign of the difference, until the harvesting goal was met or the activity probabilities could not be changed. Notably, the multiplication only affected the probabilities ≠0, which were forced to remain ≤1 using additional rules.
2.4.4. Output Coefficients
To produce meaningful information in addition to the simulated class distribution, coefficients for translating the classes to other variables of interest were specified and applied using the “output request” functions of the EFDM. The standing volume was obtained as the mean value (m3/ha) of each volume class. The timber assortment drain was determined by computing the average proportion of log- and pulpwood relative to the total volume in each factor combination and multiplying it with the total volume. The coefficient values for thinnings were based on the simulations (Section 2.3.3) and determined according to the number of volume class to be applicable in simulations based on the both Age-Vol and N-Vol matrices. The coefficients for final fellings were based on all NFI11 plots and determined according to numbers of both age and volume classes.
2.5. Harvesting Scenarios Used in the Simulations of Any-Aged Forest Management
We projected the development of the forest stock and timber assortment drain using the two Markov models for any-aged management and harvesting targets determined according to three different scenarios: Business-As-Usual (BAU), National Forest Programme (NFP) and Non-Declining Volume (NDV). The harvesting targets of BAU and NFP were obtained from the National Forest Strategy of Finland [47] as the initial level of 65 mill m3/a (BAU) and target level of 80 mill m3/a in 2025 (NFP). However, as the total growing stock analyzed here represented approximately 95% of the total growing stock in Finland [48], we applied this percent also to the harvesting targets to obtain the final levels used in the analyses (61.75 mill m3/a and 76 mill m3/a in BAU and NFP, respectively). In NDV, the harvesting target was adjusted to a level, which did not decrease the volume of the growing stock. The amount was obtained by iterating the activity probabilities (Section 2.4.3) either in the beginning of the simulations or between the individual simulation steps.
To assure that the simulations were in compliance with the land-use constraints stated above, restrictions were applied in the analyses as follows. Areas marked as FAWS were assumed to be available for wood production without restrictions on the management actions, but the activities were based either on observed (ABAU) or proposed (ASB) treatments (Section 2.4.3), i.e., thinnings from below were applied due to the seldom historical use of other types of thinnings in FAWS. In areas marked as FRAWS, thinnings of young stands were carried out as thinnings from below similar to FAWS, but final fellings were replaced by thinning from above. This combination allowed managing FRAWS for wood production, but always retained a minimum forest cover as specified in the legislation. In areas marked as FNAWS, no management actions were allowed, i.e., the probabilities of all other activities were set to 0.
3. Results
3.1. Effects of the Parameterization of the EFDM on the Projections
Figure 1 illustrates the magnitudes of transitions in the dynamic factors, when the pairwise observations were derived from either permanent or temporary plots. Note that the age classes were forced to develop according to the simulation interval (5 years) and this information is not shown in Figure 1. Using the temporary plots, no information on the development of the stem number was obtained, for which reason the stem number always remained in the same class in the simulations based on the permanent plots, which was the most typical transition of stem number also according to the results based on the permanent plots (Figure 1, right). Using permanent plots, an average transition of volume was one class upwards with exceptions found only in the highest volume classes. Stem number remained in the same class, on average, except for class #2, where it increased to the next class. However, compared to volume, the degree of variation in transitions was considerably higher based on the stem number classes. When the pairwise observations were derived from the temporary plots, fewer transitions of more than one class were observed. An important difference in the transitions based on the permanent plots compared to the temporary plots is also that the volume class was most frequently the same in small stands until volume class #5, excluding class #1.
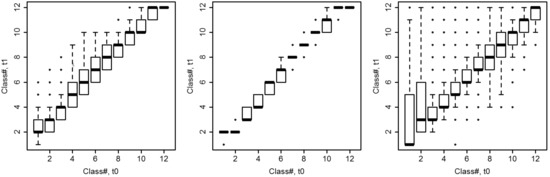
Figure 1.
Transitions from the initial (Class#, t0) to the subsequent class (Class#, t1) in volume classes derived from permanent (left) and temporary plots (middle) and stem number classes derived from permanent plots (right). The thick horizontal lines depict the median, the bottom and top of the boxes the interquartile range between the 25th and 75th percentiles, the whiskers the lowest data within 1.5 times the interquartile range, and dots the data not included in categories above.
The Age-Vol or N-Vol matrices with average transitions as in Figure 1 were further tested for simulating the complete natural process. Considerably different development patterns regarding the future proportions of the different classes were obtained based on data derived from the permanent and temporary plots, as shown in Figure 2 and Figure 3, respectively. However, using permanent plots (Figure 2), the trend of the development was highly similar independent of whether the Age-Vol or N-Vol matrix was used. Differences started to occur after four simulation steps (20 years), when a higher proportion of area was observed in volume classes #3–7 and lower in classes ≥#10 in matrices based on Age-Vol and vice versa in the matrices based on N-Vol. The data based on the temporary plots (Figure 3) indicated more differences between the Age-Vol and N-Vol matrices. Corresponding to the average development based on transitions computed from the temporary plots (Figure 1, middle panel), the area of the classes <#4 moved slower to the higher volume classes than in the case of transitions based on the permanent plots. This naturally shows further as the increased proportion of the classes #5–7 in the last simulations steps (Figure 3).
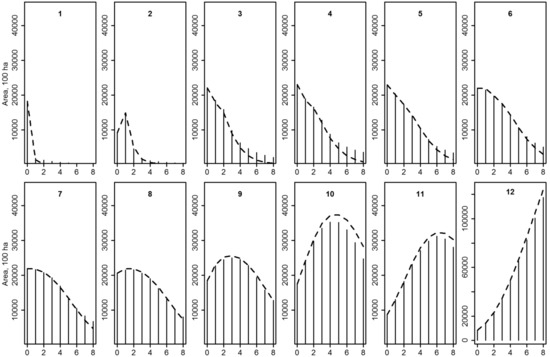
Figure 2.
A comparison of Age-Vol (vertical bars) and N-Vol (dashed lines) matrices derived from the permanent plots in the simulations of the natural process. The subplots illustrate the development of the volume class indicated in the plot along the number of simulation steps of 5 years given in the x-axis (step 0 indicates the initial state). Note that the scale of y-axis of the volume class 12 differs from the others.
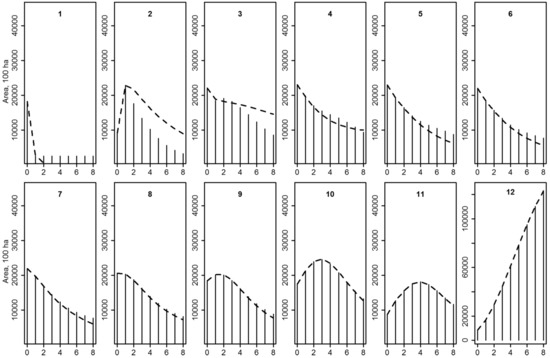
Figure 3.
A comparison of Age-Vol (vertical bars) and N-Vol (dashed lines) matrices derived from the temporary plots in the simulations of the natural process. The subplots illustrate the development of the volume class indicated in the plot along the number of simulation steps of five years given in the x-axis (step 0 indicates the initial state). Note that the scale of y-axis of the volume class 12 differs from the others.
Figure 4 is included to evaluate the realism of the simulated thinning alternatives. Given that field plot observations represent treatments carried out up to five years before the inventory, the simulated transitions are mainly in line with the observed (Figure 4, two upper rows) and provide more pairwise data especially with respect to high values (Figure 4, top row). Transitions according to the stem number classes correspond better to the observed transitions than those based on the volume classes (Figure 4, middle row). Finally, the bottom row of Figure 4 shows the proportion of trees remaining as the re-generation stock after a thinning from above. Notably, only thinnings from below were observed in the NFI field data, for which reason a comparison between the simulated and observed values of thinning from above cannot be shown.
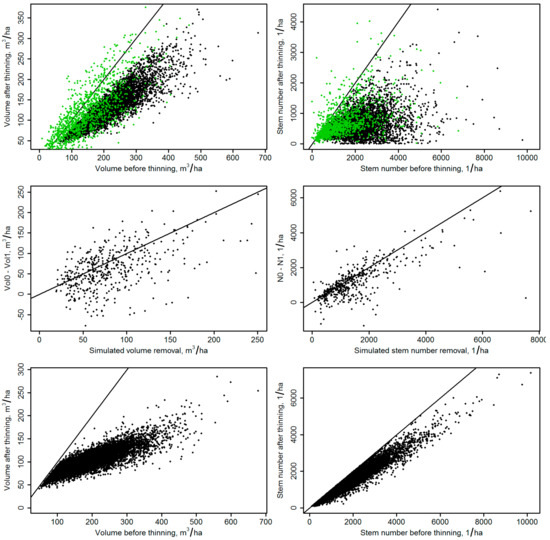
Figure 4.
A comparison of the volume (left) and stem number (right) of the simulated harvests. Top row: Values before and after thinning from below, black and green dots corresponding to simulated values and pairwise observations of the permanent plots, respectively. Middle row: The correspondence of the simulated removal with the difference computed from the pairwise observations. Bottom row: Values before and after simulated thinning from above.
To test the entire set of inputs for scenario modelling, the EFDM was used to predict the situation of NFI10 or NFI11 using the other inventory as an input. The resulting distribution of volume classes is shown in Figure 5. Especially, when forecasting with the transition and activity probabilities derived from the permanent plots, the predicted distribution corresponded to the observed one for most of the classes. According to the full data of both NFI10 and NFI11, the same proportion of area remained treeless between the inventories, which was the main deviation between the simulations and observations. However, no particular reason for this proportion could be identified based on the data, it was not present in the pairwise data for the transition probabilities, and overall assuming the presence of such an area did not seem reasonable regarding the future projections of the forest.
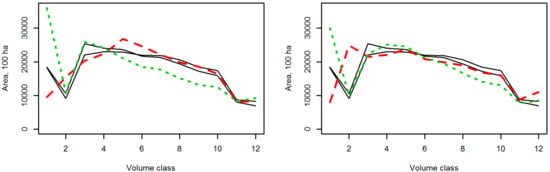
Figure 5.
The development of the volume class distribution in one simulation step. The black solid lines indicate the class distribution observed in the NFI10 and NFI11 data. The red and green broken lines represent predictions based on forecasting from NFI10 data or backcasting from the NFI11 data, respectively, with the transition probabilities derived from the permanent (left) and temporary (right) plots for pairwise observations.
Based on the results above, we felt safe to use both Age-Vol and N-Vol matrices with transition probabilities derived from the permanent plot data to model both even-aged and uneven-aged forestry in the same run for the scenario analyses below.
3.2. Results of the Scenario Analyses
The harvesting target of the BAU scenario could be achieved with an even level of harvests, regardless of whether the activity probabilities were adjusted to this level by iterating between the simulation steps (Figure 6, left column) or using activity probabilities set in the beginning of the simulation (Figure 7, left column). The BAU scenario resulted in a fairly even timber assortment drain between the simulation steps, being on average altogether 62.7 mill m3/a, and an end volume of 2451 mill m3 (+9.6% from the start of the simulation), on average, based on the current land-use restrictions and all simulations.
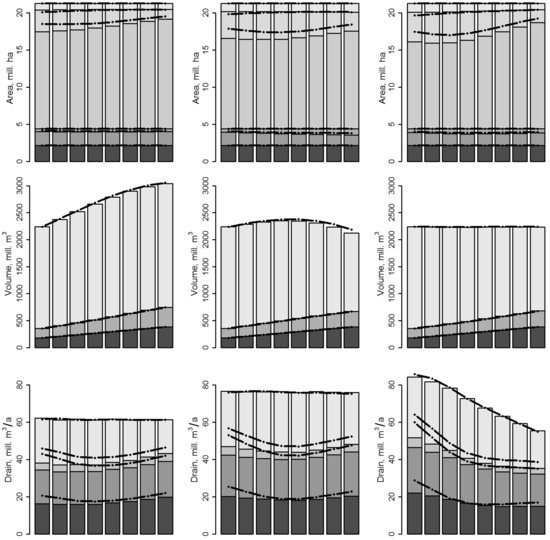
Figure 6.
Land use, growing stock, and timber assortment drain given by bars corresponding to the eight simulation steps, when the activity probabilities ABAU (bars) or ASB (broken lines) were iterated between the individual simulation steps to obtain the harvesting goals BAU (left column), NFP (middle column), and NDV (right column). From top to bottom, the colors within the bars represent the proportion of (top row) FAWS managed for final felling, FAWS thinned, FAWS not treated, FRAWS thinned, FRAWS not treated, and FNAWS; (middle row) standing volume in FAWS, FRAWS, and FNAWS; (bottom row) pulpwood from thinnings, sawnwood from thinnings, pulpwood from final fellings, and sawnwood from final fellings, respectively.
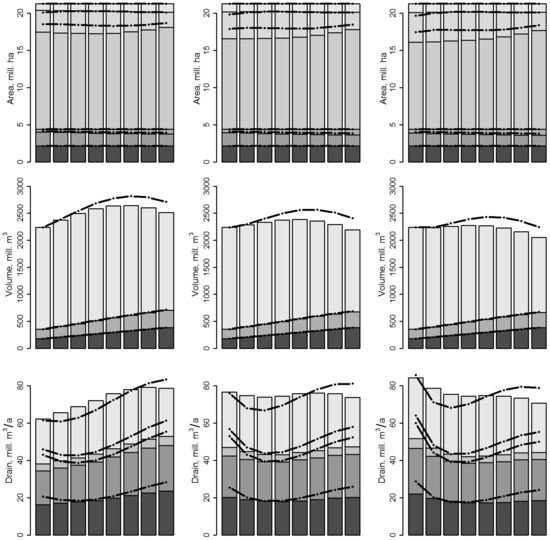
Figure 7.
Land use, growing stock and timber assortment drain, when the activity probabilities were set in the beginning of the simulation. Refer to the caption of Figure 6 for the interpretation of the image.
The harvest target of NFP could also be filled, although with a reduction to the growing stock until the end of the simulation period. Iterations between the steps to reach the harvesting target intensified the land use pressure, for example resulting in a higher proportion of the uneven-aged forests being managed for thinnings. When the activity probabilities were iterated to reach the harvesting goals, only in the beginning of the simulation, the standing volume did not decrease and the harvests slightly increased towards the end of the simulation period (Figure 7, middle column).
The NDV scenario resulted in a drain that was between the fixed targets with a range from 51.8 to 84.2 mill m3/a and the variation shown in Figure 6 and Figure 7 (right column). According to the goal, the growing stock did not decline. Land use did not markedly differ from that of the BAU scenario (compare the upper row of Figure 6 and Figure 7). Figure 6 and Figure 7 also illustrate the differences of applying ABAU vs. ASB as activity probabilities when implementing the harvests. The main difference was that in the allocation based on ASB, more harvests were focused on older and heavily stocked stands. As a result, final fellings yielded more drain and the harvesting targets could be achieved by managing less area.
4. Discussion
To the best of our knowledge, this is the first study to simulate the future development of the forest according to any-aged management using an area-based matrix model. Although a number of matrix models have been applied for a long time, such models are usually understood as diameter class models for stand-level simulations [49]. We used an area-based model parameterized by areas of forest size and structure types according to NFI data. Although such models have also been presented (see Section 1), the EFDM differs from many earlier implementations due to the flexibility of parameterization. Finally, our implementation of two separate Markov models to allow even-aged and uneven-aged management within a single simulation run differs considerably from the earlier applications of the EFDM. The sections above detail how the EFDM should be parameterized to enable simulations of any-aged forest management and evaluate effects resulting from such methodological choices. Finally, these results are discussed with respect to the strengths and weaknesses of the EFDM.
4.1. Parameterization of the Markov Model for the Simulations of Any-Aged Forest Management
Except for different sources of data, the division to factor levels constitutes a potential source of variation that was not evaluated. While the classification to static factors is determined according to the properties related to the operational environment and reporting needs, dynamic factors should be selected to mimic a realistic forest growth pattern. Here Age-Vol and N-Vol matrices were used to capture the dynamics of even-aged and uneven-aged forests, respectively, but the class division was based on obtaining an adequate number of observations for each class covered in the pairwise data. Even though growth dynamics was thus not explicitly considered, this division also seemed to reproduce the growth pattern of forests realistically: For instance, the class width increased (cf. [23]). While Sallnäs [23] reasoned the selection of the class limits based on applying a growth function, no such reasoning is presented in later publications [32,50]. Our choice to select the class limits in terms of the number of observations is well reasoned based on the background that the transition probabilities need to be estimated from the data.
When modelling the transitions due to harvesting, we relied on a simulator instead of observations. Figure 3 shows that the simulated removals match with observations from permanent plots, with the removal of stem number showing a better match, and that an extended number of pairwise observations is obtained using the simulator compared to plot data alone. On the other hand, it can be seen that the number of the plots thinned during the last five year period had grown, while our simulators represent the situation immediately after thinning. Therefore, we decided to simulate the growth of the thinned forests applying the transition probabilities of forests not managed. However, the positive effects of thinning are partly realized after the five-year simulation period [51], which should be depicted by the transition probabilities applied in the following simulation steps. Except for the potential differences in the growth after thinning, the differences in the post-thinning volumes between the simulated and observed values may also originate from low intensities of the actual thinning treatments: the proportion of trees removed in the simulated thinnings was always in accordance with the management guidelines, which may not always be the case in practice. Finally, the small size of the plots may affect the simulator result. The NFI measurements are based on truncated angle count plots with a maximum radius for tree measurements varying within the country, but being approximately 12.5 m. The competition measures such as stand density vary depending on the size of the inventory unit, which was found to affect the predictions of growth and mortality in unthinned stands, but negligible effects in the thinned ones [52]. It is unclear how the result above translates to thinning simulations, but due to the difference between the thinned and unthinned stands [52], it could have an effect that should be studied in the future. However, the need to use simulated observations was fundamental to implement the full analysis because no information on the transitions due to thinnings from above and no information of the thinning drain of any type of thinning could have been obtained otherwise.
Even though uncertainties in the applied parameterization should be taken account, our overall observation is that the combined simulation chain produced realistic results on both the even- and uneven-aged forestry, when the transition probabilities were derived from the permanent plot data. Principally, the temporary plots could also be used for the same purpose. However, in our case, the number of sample trees with growth measurements was very limited and the growth percent determined at the level of the sampling regions did not account for varying growth rates in different development stages, which is clearly seen in Figure 1. Thus, if the temporary plots were used, the growth would have needed adjustments according to the growth pattern observed from the permanent plots, for example. Furthermore, the temporary plots did not produce information on the development of the stem number.
The projections of forest structure could be validated for one simulation step based on the existence of the two subsequent inventories (Figure 5). Although the conclusions on the reliability for longer simulation periods may be limited, the simulations reproduced the pattern of volume class distribution between the NFIs rather well. However, based on the increased proportion of volume class #2 in the simulations based on the temporary plots, the incorrectly reproduced growth pattern (Figure 1) discussed above is also visible in these results. In both cases, the main inaccuracy was related to the proportion of treeless areas after final felling (class #1). However, this could be more likely related to a fixed proportion of area in this class due to a delayed re-generation, for example, rather than an incorrect proportion of areas assigned for final felling by the EFDM. Finally, we ran the experiments by both forecasting from NFI10 to NFI11 and backcasting from NFI11 to NFI10. For the latter purpose, the transition probabilities were applied in an opposite order (transition from NFI11 to NFI10) than when forecasting and it is not clear whether the harvested areas “recover back” to the correct Age-Vol or N-Vol class, for example. However, such a setup appears as an interesting possibility to validate forest simulators based on historical data and should be studied further in the future.
Earlier, Nabuurs et al. [19] validated the EFISCEN model based on a longer time series of historical inventory data and concluded that the model could be used to project forest resources of large areas for periods of up to 50–60 years. However, the underestimated growth after thinning (see above) started to show in the results with the longest simulation periods. Overall, although a direct comparison is difficult due to differences in the modelling approaches (e.g., assessments of age class distributions only in [19]), the results obtained here based on validating the single simulation step are mainly in agreement with those presented by Nabuurs et al. [19] and their discussion is recommended to an interested reader as further reading regarding the nuances related to different parameter choices of area-based matrix models.
4.2. On the Use of the EFDM Approach for Projecting Future Wood Supply
Although a few other researchers have used the corresponding Finnish NFI11 or NFI10 data to project future harvests with other analysis methods [53,54], it is difficult to directly compare our results with those. It can be noted that both the growing stock and drain levels are lower in our analyses, but a detailed comparison of the numerical results is omitted because the differences can be credibly attributed with the considerably different logic in allocating the harvests based on the EFDM approach, as elaborated below.
Overall, the harvested amounts based on the EFDM should be lower than those based on even-flow harvesting goals determined by optimization due to a few clear differences in the modelling principles. First, the representation of the growing stock in classes may be assumed to average the harvesting potential and also growth to some degree. More importantly, the harvests of the EFDM are not focused according to profitability criteria such as the net present value, but an even proportion of areas in classes affected by the activity probabilities is always harvested. Finally, the output coefficients, which are required for converting the class distribution to assortment-related measures, are determined somewhat separately from the simulation process. In our analyses, the coefficients were based on the average volume or drain of all plots in the simulation data. If an analyst had a reason to assume that the real-world harvests were focused only on the most profitable forests within the classes, he/she could use another fraction such as the highest quartile of thinned plots for computing the coefficients and thus increasing the drain proportion based on the aforementioned expert opinion.
The activity probabilities considerably affect the harvest allocation of the future projections (cf. outcomes based on ABAU or ASB in Figure 6 and Figure 7). The probabilities used in our analyses were factor- combination-specific ratios of areas of each activity to the total area in the initial state and determined in the beginning of the simulations. Although these probabilities were adjusted to yield the desired harvesting level during the simulations (Section 2.4.3), the applied iteration procedure did not change the relative proportions of the activities. Especially with demanding harvest goals, the forest areas in classes with high initial harvesting probabilities reduced considerably faster than the in- growth to these classes. Although the harvesting goals were fulfilled by increasing other classes to be harvested, a considerably different harvest allocation might have been obtained by considering where the harvests are most feasible with respect to the forest structure distribution in each future simulation step. As can be seen by comparing the proportions of timber assortments harvested using ABAU or ASB (Figure 6 and Figure 7), the harvesting objectives were more efficiently achieved using ASB with more final fellings. Even higher proportion of final fellings (or thinnings from above) could have been proposed to reach demanding harvest targets, but the present iteration did not increase their proportion very much due to the lower proportion in the beginning. It is overall intuitive that future management practices and their proportions should be determined according to the predicted state of the forest. Although no such functionality currently exists in the EFDM, considerable future opportunities are seen related to such implementations (see Section 4.3).
The above discussion on the stationarity of the activity probabilities should be extended to cover the Markovian property, according to which the future state of forest depends only on the present state and not on the management history. This implies, for example, that the data used for computing the transition probabilities should include an adequate number of plots thinned in the earlier management periods to correctly reproduce the recovery and development of the growing stock after thinning, which might not be true in our data, considering limited observations of thinnings from above. More importantly, when the memoryless Markov property is combined with demanding harvesting goals, nothing principally prevents the same areas from being thinned in subsequent simulation steps more often than would be practical or feasible with respect to a proper recovery period. However, these difficulties are common to any simulation approach based on empirical harvest models without other restrictions and may be even more severe with the EFISCEN model, where the thinning goals are fulfilled by harvesting the growth of matrix cells marked for thinning without any further adjustments on the allocation of the harvests [55].
Problems related to the stationarity of the transition probabilities during the simulation have already been mentioned in earlier EFDM studies [31], but those related to the Markov property are rarely considered. The stationarity of the transition probabilities is more related to expected changes of the future environment, while the stationarity of the activity probabilities may affect all analyses in which the class distribution is altered, unless accounted for. Based on this discussion, the area-based matrix modelling approach as applied here should not be used for determining a sustainable even-flow harvesting level. Instead, due to the flexibility of determining and varying scenario assumptions, it is very well suited for assessing the effects to the composition of the wood supply and land use, when the harvest level is given but silvicultural practices or land-use restrictions are expected to change due to political decisions, for example. In this sense, the EFDM model seems more flexible with respect to parameterization (see previous sections) compared to existing area-based matrix models such as EFISCEN (cf. [55]).
4.3. Recommendations for Further Research
The state space of the EFDM is fundamentally determined as a combination of the factor levels. The division to static and dynamic factors can depend on the activity. For example, in case a sequential activity is defined to cover final felling followed immediately by planting, it is possible to change species, age, and volume simultaneously. Thus, static factor levels can be realistically changed during the re-generation of even-aged forestry. In addition, if, for instance, an uneven-aged forest was assumed to be re-generated as an even-aged forest, a new tree generation could be established using some factor values. However, this does not work in the opposite direction: if it is decided that an even-aged forest will be managed for uneven-aged forestry, it should be able to decide in which stem number class the development should start with. Similar problems occur in other situations regarding transitions between static factor levels and this logic should be considered in future.
Although the state space, transition probabilities, and output coefficients can be feasibly determined based on the current inventory data, considerations should be placed on whether these probabilities are realistic with respect to the future. For example, the transition probabilities may change due to improved silvicultural practices or additional growth or calamities occurring in the warming climate. Although expected increment or decrement rates could simply be accounted for by adjusting the transition probabilities, as done in the EFISCEN approach [55], it is unrealistic to assume that these changes would develop in a systematic, trend-like manner [56], and their realistic modeling in an area-based matrix approach requires more care.
Currently, the simulation results are assumed to be deterministic, i.e., uncertainties jointly related to the state space, activities, transition probabilities, and output coefficients are not considered. In this sense, the analyses could be improved: for instance, management activities could be simulated as if all possible drain was not obtained due to quality or corresponding issues. Such sensitivity analyses would require observations or expert information on both the magnitudes of transitions and probabilities of the uncertain events to occur. If such information existed, the risks or uncertainties could potentially be accounted for by simulating multiple transition probability matrices, changing their activity probabilities and coefficients for the desired outputs.
5. Conclusions
The results suggest the EFDM as a feasible tool for projecting the development of forest stock and analyzing impacts of different harvesting scenarios. According to our results, both the Age-Vol and N-Vol matrices can be equally applied for simulating the future development of the forest and simulations based on the different matrices can be combined in a single simulation run, which is essential with respect realistic modeling of different management practices that are often applied in parallel. The main development needs are related to iterating the activity probabilities such that the resulting harvests are feasible with respect to the predicted future forest, which could potentially be formulated as a goal function accounting for changes in the forest structure during the simulation.
In a wider perspective, our work can be seen to contribute as a harmonized methodology to incorporate land-use constraints into model-based biomass supply analyses. It could be developed to analyze trade-offs between biomass supply and other ecosystem products and services in forest-based value chains across Europe. For instance, the model could be added with coefficients to convert the output to units of carbon or non-wood forest products. It could be parameterized by activities based on generic management systems or silvicultural alternatives and harmonized sustainability criteria to determine the level of harvests for international and national policy support. Except for the work carried out by Jonsson et al. [50], we are not aware that economic models for harvest demand would have been connected with area-based matrix models for forest resources.
Acknowledgments
The research work has received funding from the European Union’s Horizon 2020 research and innovation programme under Grant No. 633464 to project “Distributed, Integrated and Harmonised Forest Information for Bioeconomy Outlooks (DIABOLO)”. We thank Kari T. Korhonen for providing useful comments in various stages of the study.
Author Contributions
T.P. developed the research idea; J.V. and T.P. designed the experiments; J.V. carried out all computations and analyses; J.V. and T.P. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Class limits used in all analyses.
Table A1.
Class limits used in all analyses.
| Volume Classes 1 | Age Classes 1 |
|---|---|
| 1. (∞, 0.0000) | 1. (∞, 0) |
| 2. (0.0000, 10.5884) | 2. (0, 5) |
| 3. (10.5884, 29.8618) | 3. (5, 10) |
| 4. (29.8618, 51.3846) | 4. (10, 15) |
| 5. (51.3846, 73.6844) | 5. (15, 20) |
| 6. (73.6844, 96.5440) | 6. (20, 25) |
| 7. (96.5440, 122.8744) | 7. (25, 30) |
| 8. (122.8744, 153.2864) | 8. (30, 35) |
| 9. (153.2864, 191.3348) | 9. (35, 40) |
| 10. (191.3348, 248.0352) | 10. (40, 45) |
| 11. (248.0352, 303.3532) | 11. (45, 50) |
| 12. (303.3532, ∞) | 12. (50, 55) |
| 13. (55, 60) | |
| Stem number classes 1 | 14. (60, 65) |
| 1. (∞, 0.0000) | 15. (65, 70) |
| 2. (0.0000, 69.8725) | 16. (70, 75) |
| 3. (69.8725, 330.6332) | 17. (75, 80) |
| 4. (330.6332, 509.0106) | 18. (80, 85) |
| 5. (509.0106, 676.9061) | 19. (85, 90) |
| 6. (676.9061, 875.1651) | 20. (90, 95) |
| 7. (875.1651, 1108.6395) | 21. (95, 100) |
| 8. (1108.6395, 1384.8279) | 22. (100, 105) |
| 9. (1384.8279, 1754.0609) | 23. (105, 110) |
| 10. (1754.0609, 2398.5651) | 24. (110, 115) |
| 11. (2398.5651, 2975.8412) | 25. (115, 120) |
| 12. (2975.8412, ∞) | 26. (120, ∞) |
1 Units in m3/ha for volume, 1/ha for stem number, and years for age.
References
- Hanssen, S.V.; Duden, A.S.; Junginger, M.; Dale, V.H.; Hilst, F. Wood pellets, what else? Greenhouse gas parity times of European electricity from wood pellets produced in the south-eastern United States using different softwood feedstocks. Glob. Chang. Biol. Bioenergy 2017. [Google Scholar] [CrossRef]
- Johnston, C.M.; van Kooten, G.C. Global trade impacts of increasing Europe’s bioenergy demand. J. For. Econ. 2016, 23, 27–44. [Google Scholar] [CrossRef]
- Raunikar, R.; Buongiorno, J.; Turner, J.A.; Zhu, S. Global outlook for wood and forests with the bioenergy demand implied by scenarios of the Intergovernmental Panel on Climate Change. For. Pol. Econ. 2010, 12, 48–56. [Google Scholar] [CrossRef]
- Börjesson, P.; Hansson, J.; Berndes, G. Future demand for forest-based biomass for energy purposes in Sweden. For. Ecol. Manag. 2017, 383, 17–26. [Google Scholar] [CrossRef]
- Alberdi, I.; Michalak, R.; Fischer, C.; Gasparini, P.; Brändli, U.B.; Tomter, S.M.; Kuliesis, A.; Snorrason, A.; Redmond, J.; Hernández, L.; et al. Towards harmonized assessment of European forest availability for wood supply in Europe. For. Pol. Econ. 2016, 70, 20–29. [Google Scholar] [CrossRef]
- Fischer, C.; Gasparini, P.; Nylander, M.; Redmond, J.; Hernandez, L.; Brändli, U.B.; Pastor, A.; Rizzo, M.; Alberdi, I. Joining criteria for harmonizing European Forest Available for Wood Supply estimates. Case studies from National Forest Inventories. Forests 2016, 7, 104. [Google Scholar] [CrossRef]
- Fürstenau, C.; Badek, F.W.; Lasch, P.; Lexer, M.J.; Linder, M.; Mohr, P.; Suckow, F. Multiple-use forest management in consideration of climate change and the interests of stakeholder groups. Eur. J. For. Res. 2007, 126, 225–239. [Google Scholar] [CrossRef]
- Diaci, J.; Kerr, G.; O’Hara, K. Twenty-first century forestry: Integrating ecologically based, uneven-aged silviculture with increased demands on forests. Forestry 2011, 84, 463–465. [Google Scholar] [CrossRef]
- Pukkala, T. Which type of forest management provides most ecosystem services? For. Ecosyst. 2016, 3, 9. [Google Scholar] [CrossRef]
- Barreiro, S.; Schelhaas, M. J.; Kändler, G.; Antón-Fernández, C.; Colin, A.; Bontemps, J. D.; Alberdi, I.; Condés, S.; Dumitru, M.; Ferezliev, A.; et al. Overview of methods and tools for evaluating future woody biomass availability in European countries. Ann. For. Sci. 2016, 73, 823–837. [Google Scholar] [CrossRef]
- Verkerk, P.J.; Anttila, P.; Eggers, J.; Lindner, M.; Asikainen, A. The realisable potential supply of woody biomass from forests in the European Union. For. Ecol. Manag. 2011, 261, 2007–2015. [Google Scholar] [CrossRef]
- Bentsen, N.S.; Felby, C. Biomass for energy in the European Union—A review of bioenergy resource assessments. Biotechnol. Biofuels 2012, 5, 25. [Google Scholar] [CrossRef] [PubMed]
- Rettenmaier, N.; Köppen, S.; Gärtner, S.O.; Reinhardt, G.A. Life cycle assessment of selected future energy crops for Europe. Biofuels Bioprod. Biorefin. 2010, 4, 620–636. [Google Scholar] [CrossRef]
- Mantau, U.; Gschwantner, T.; Paletto, A.; Mayr, M.L.; Blanke, C.; Strukova, E.; Avdagic, A.; Camin, P.; Thivolle-Cazat, A.; Döring, P.; et al. From inventory to consumer biomass availability—The ITOC model. Ann. For. Sci. 2016, 73, 885–894. [Google Scholar] [CrossRef]
- Monserud, R.A.; Sterba, H. A basal area increment model for individual trees growing in even-and uneven-aged forest stands in Austria. For. Ecol. Manag. 1996, 80, 57–80. [Google Scholar] [CrossRef]
- Siitonen, M.; Anola-Pukkila, A.; Haara, A.; Härkönen, K.; Redsven, V.; Salminen, O.; Suokas, A. (Eds.) MELA Handbook, 2000 ed.; The Finnish Forest Research Institute: Helsinki, Finland, 2001; p. 498. Available online: http://mela2.metla.fi/mela/julkaisut/oppaat/mela2000.pdf (accessed on 5 July 2017).
- Wikström, P.; Edenius, L.; Elfving, B.; Eriksson, L.O.; Lämås, T.; Sonesson, J.; Öhman, K.; Wallerman, J.; Waller, C.; Klintebäck, F. The Heureka forestry decision support system: An overview. Math. Comp. For. Nat. Res. Sci. 2011, 3, 87–94. [Google Scholar]
- Bösch, M.; Elsasser, P.; Rock, J.; Rüter, S.; Weimar, H.; Dieter, M. Costs and carbon sequestration potential of alternative forest management measures in Germany. For. Pol. Econ. 2017, 78, 88–97. [Google Scholar] [CrossRef]
- Nabuurs, G.J.; Schelhaas, M.J.; Pussinen, A. Validation of the European Forest Information Scenario Model (EFISCEN) and a projection of Finnish forests. Silva Fenn. 2000, 34, 167–179. [Google Scholar] [CrossRef]
- Thürig, E.; Schelhaas, M.J. Evaluation of a large-scale forest scenario model in heterogeneous forests: A case study for Switzerland. Can. J. For. Res. 2006, 36, 671–683. [Google Scholar] [CrossRef]
- Eriksson, L.O.; Sallnäs, O.; Ståhl, G. Forest certification and Swedish wood supply. For. Pol. Econ. 2007, 9, 452–463. [Google Scholar] [CrossRef]
- Nilsson, S.; Sallnäs, O.; Duinker, P. Future Forest Resources of Western and Eastern Europe; A Report on the IIASA Forest Study; The Parthenon Publishing Group: Casterton Hall, Camforth, UK, 1992; p. 496. Available online: http://pure.iiasa.ac.at/3589/1/XB-92-001.pdf (accessed on 5 July 2017).
- Sallnäs, O. A Matrix Growth Model of the Swedish Forest; Studia Forestalia Suecica; Swedish University of Agricultural Sciences, Faculty of Forestry: Uppsala, Sweden, 1990; p. 23. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:slu:epsilon-9-13 (accessed on 5 July 2017).
- Usher, M.B. A matrix approach to the management of renewable resources, with special reference to selection forests. J. Appl. Ecol. 1966, 3, 355–367. [Google Scholar] [CrossRef]
- Usher, M.B. A matrix model for forest management. Biometrics 1969, 25, 309–315. [Google Scholar] [CrossRef]
- Usher, M.B. Markovian approaches to ecological succession. J. Anim. Ecol. 1979, 48, 413–426. [Google Scholar] [CrossRef]
- Nabuurs, G.J.; Päivinen, R.; Schantz, H. Sustainable management regimes for Europe’s forests—A projection with EFISCEN until 2050. For. Pol. Econ. 2001, 3, 155–173. [Google Scholar] [CrossRef]
- Buongiorno, J.; Peyron, J.L.; Houllier, F.; Bruciamacchie, M. Growth and management of mixed-species, uneven-aged forests in the French Jura: Implications for economic returns and tree diversity. For. Sci. 1995, 41, 397–429. [Google Scholar]
- Virgilietti, P.; Buongiorno, J. Modeling forest growth with management data: A matrix approach for the Italian Alps. Silva Fenn. 1997, 31, 27–42. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Buongiorno, J.; Gobakken, T. Predicting the growth of stands of trees of mixed species and size: A matrix model for Norway. Scand. J. For. Res. 2008, 23, 167–178. [Google Scholar] [CrossRef]
- Packalen, T.; Sallnäs, O.; Sirkiä, S.; Korhonen, K.; Salminen, O.; Vidal, C.; Robert, N.; Colin, A.; Belouard, T.; Schadauer, K.; et al. The European Forestry Dynamics Model: Concept, Design and Results of First Case Studies; JRC Science and Policy Reports; EUR 27004; Publications Office of the European Union: Luxembourg, 2014; Volume 93450, p. 20. [Google Scholar] [CrossRef]
- Sallnäs, O.; Berger, A.; Räty, M.; Trubins, R. An area-based matrix model for uneven-aged forests. Forests 2015, 6, 1500–1515. [Google Scholar] [CrossRef]
- Haight, R.G. Evaluating the efficiency of even-aged and uneven-aged stand management. For. Sci. 1987, 33, 116–134. [Google Scholar]
- Haight, R.G.; Monserud, R.A. Optimizing any-aged management of mixed-species stands. I. Performance of a coordinate-search process. Can. J. For. Res. 1990, 20, 15–25. [Google Scholar] [CrossRef]
- Haight, R.G.; Monserud, R.A. Optimizing any-aged management of mixed-species stands: II. Effects of decision criteria. For. Sci. 1990, 36, 125–144. [Google Scholar]
- Pukkala, T.; Lähde, E.; Laiho, O. Optimizing any-aged management of mixed boreal forest under residual basal area constraints. J. For. Res. 2014, 25, 627–636. [Google Scholar] [CrossRef]
- Sirkiä, S. Methodology and System Design—Some Mathematics behind EFDM. Appendix 1 in Developing and Testing a Prototype for European Forestry Dynamics Model (EFDM); Anon.; Specific Contract 10 Report, Framework Contract for the Provision of Forest Data and Services in Support to the European Forest Data Centre; Reference: 2007/ S 194–235358 of 09/10/2007; Available online: https://webgate.ec.europa.eu/CITnet/stash/projects/FISE/repos/efdm/browse/documents/EFDMinstructions/Seija_Mathematics_behind_EFDM.pdf (accessed on 5 July 2017).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016; Available online: https://www.R-project.org/ (accessed on 5 July 2017).
- Forest Information System for Europe. EFDM. Software Repository. Available online: https://webgate.ec.europa.eu/CITnet/stash/projects/FISE/repos/efdm/browse (accessed on 5 July 2017).
- Anon. European Forestry Dynamics Model; MediaWiki. Available online: https://forestwiki.jrc.ec.europa.eu/efdm/index.php/Main_Page (accessed on 5 July 2017).
- Yrjölä, T. Forest Management Guidelines and Practices in Finland, Sweden and Norway; Internal Report; European Forest Institute: Joensuu, Finland, 2002; Volume 11, Available online: http://www.efi.int/files/attachments/publications/ir_11.pdf (accessed on 5 July 2017).
- Korhonen, K.T. Finland. In National Forest Inventories—Assessment of Wood Availability and Use; Vidal, C., Alberdi, I.A., Hernández Mateo, L., Redmond, J.J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 369–384. [Google Scholar]
- Tomppo, E.; Heikkinen, J.; Henttonen, H.M.; Ihalainen, A.; Katila, M.; Mäkelä, H.; Tuomainen, T.; Vainikainen, N. Designing and Conducting A Forest Inventory—Case: 9th National Forest Inventory of Finland; Managing Forest Ecosystems, Springer: Dordrecht, The Netherlands, 2011; Volume 21, p. 270. [Google Scholar]
- Simosol Oy. Thinning Limit Model Library—Source File; SIMO—Adaptable Simulation and Optimization, Simosol Oy: Riihimäki, Finland, 2007; Available online: http://svn.simo-project.org/simo/trunk/src/models/Finland/c/Thinningmodel Library.c (accessed on 5 July 2017).
- Ojansuu, R.; Halinen, M.; Härkönen, K. Metsätalouden suunnittelujärjestelmän virhelähteet männyn ensiharvennuskypsyyden määrityksessä. Metsätieteen Aikakauskirja 2002, 3, 441–457. [Google Scholar] [CrossRef]
- Pukkala, T.; Lähde, E.; Laiho, O. Which trees should be removed in thinning treatments? For. Ecosyst. 2015, 2, 32. [Google Scholar] [CrossRef]
- Ministry of Agriculture and Forestry. National Forest Strategy 2025—Government Resolution of 12 February 2015; Ministry of Agriculture and Forestry: Helsinki, Finland, 2015; Volume 6, p. 56. Available online: http://mmm.fi/documents/1410837/1504826/National+Forest+Strategy+2025/197e0aa4-2b6c-426c-b0d0-f8b0f277f332 (accessed on 5 July 2017).
- Peltola, A. (Ed.) Finnish Statistical Yearbook of Forestry 2014; Finnish Forest Research Institute, Tammerprint Oy: Tampere, Finland, 2014; p. 450. [Google Scholar]
- Liang, J.; Picard, N. Matrix model of forest dynamics: An overview and outlook. For. Sci. 2013, 59, 359–378. [Google Scholar] [CrossRef]
- Jonsson, R.; Rinaldi, F.; Räty, M.; Sallnäs, O. Integrating forest-based industry and forest resource modeling. iFor. Biogeosci. For. 2016, 9, 743–750. [Google Scholar] [CrossRef]
- Mehtätalo, L.; Peltola, H.; Kilpeläinen, A.; Ikonen, V.P. The response of basal area growth of Scots pine to thinning: A longitudinal analysis of tree-specific series using a nonlinear mixed-effects model. For. Sci. 2014, 60, 636–644. [Google Scholar] [CrossRef]
- Hynynen, J.; Ojansuu, R. Impact of plot size on individual-tree competition measures for growth and yield simulators. Can. J. For. Res. 2003, 33, 455–465. [Google Scholar] [CrossRef]
- Heinonen, T.; Pukkala, T.; Mehtätalo, L.; Asikainen, A.; Kangas, J.; Peltola, H. Scenario analyses for the effects of harvesting intensity on development of forest resources, timber supply, carbon balance and biodiversity of Finnish forestry. For. Pol. Econ. 2017, 80, 80–98. [Google Scholar] [CrossRef]
- Hynynen, J.; Salminen, H.; Ahtikoski, A.; Huuskonen, S.; Ojansuu, R.; Siipilehto, J.; Lehtonen, M.; Eerikäinen, K. Long-term impacts of forest management on biomass supply and forest resource development: A scenario analysis for Finland. Eur. J. For. Res. 2015, 134, 415–431. [Google Scholar] [CrossRef]
- Pussinen, A.; Schelhaas, M.J.; Verkaik, E.; Heikkinen, E.; Liski, J.; Karjalainen, T.; Päivinen, R.; Nabuurs, G.J. Manual for the European Forest Information Scenario Model (EFISCEN 2.0); Internal Report; European Forest Institute: Joensuu, Finland, 2001; Volume 5, Available online: http://www.efi.int/files/attachments/publications/ir_05.pdf (accessed on 5 July 2017).
- Henttonen, H.M.; Nöjd, P.; Mäkinen, H. Environment-induced growth chances in the Finnish forests during 1971–2010—An analysis based on National Forest Inventory. For. Ecol. Manag. 2017, 386, 22–36. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).