Abstract
Tree stability under wind loading is a critical concern for risk management in urban and natural environments. Despite advances in assessment methods, discrepancies persist between theoretical predictions and real-world tree behaviour. This study presents results from an extensive field investigation conducted at the University of Dundee Botanic Gardens to evaluate tree uprooting stability through non-destructive static, dynamic, and uprooting tests. This paper focusses on the programme of non-destructive and uprooting tests conducted across twenty-one trees of a variety of coniferous and deciduous species. Regarding the non-destructive tests, multiple tests were carried out on the same trees, varying both the pulling direction and the pulling height. Geotechnical properties, including shear strength, water content, soil water retention behaviour, and granulometry, were characterized to assess their role in root anchorage. These characteristics were seen to be at least as important as species. The results revealed that the maximum overturning moment (ML) occurred between a 1.6 and 2.9° inclination during uprooting for the partially saturated ground conditions at the time of testing, irrespective of species or biometric parameters. The findings contribute to refining tree stability assessments, offering practical insights for arboriculture and urban planning.
1. Introduction
Trees are fundamental components of the urban landscape, valued not only for their aesthetic and cultural significance but also for the vital ecosystem services they provide. These services include temperature regulation, stormwater management, air purification, carbon sequestration, and noise attenuation []. Despite these benefits, trees can become sources of hazards in urban environments, particularly under high-wind conditions. Storms and strong wind gusts—now more frequent and intense due to climate change—can lead to tree failure, resulting in structural damage, injuries, or even fatalities. Traditional qualitative assessments, such as the Visual Tree Assessment (VTA) method developed by [], are still widely employed in arboriculture due to their simplicity and non-invasive nature. Despite the development of more quantitative techniques [], VTA remains a practical first-line tool for identifying external signs of structural weakness and potential failure in trees.
Over the last two decades, various quantitative methodologies have been developed to evaluate tree stability under lateral loading, especially due to wind. A milestone in this field is the static pulling test, a non-destructive procedure introduced by [,,,]. This test estimates the tree’s overturning moment by applying a controlled lateral force using a winch-and-rope system, while monitoring the resulting trunk rotation up to a defined elastic limit (typically 0.25°). The moment–rotation data is then interpreted through an empirical model, obtained from 400 tests, to extrapolate the tree’s maximum load capacity. Several other authors in the literature have conducted winch tests, reporting soil type, tested tree species, tree height range, and the resulting range of failure moment and critical inclination angle [,,,,,]. Fraser and Gardiner conducted 368 pulling tests on Picea sitchensis, reporting a failure moment (ML) range of 16–53 kNm at a critical inclination angle range between 10° and 25°. Crook and Ennos performed 22 tests on Larix europea × japonica, obtaining ML values between 6–24 kNm at angles between 16° and 28°. Dèfossez et al. [] carried out 12 tests on Picea sitchensis, with ML values ranging from 8–16 kNm at inclination angles between 6° and 20°. Similarly, Urata performed 12 tests on Picea glehnii, recording ML values of 3–29 kNm and critical angles between 14° and 22°. Galli et al. performed full-scale uprooting tests, capturing real failure moments and identifying significant deviations from theoretical predictions, especially under non-standard pulling configurations and complex root architectures []. Zhang et al. demonstrated through centrifuge modelling that root morphology, soil moisture, and fine root content significantly affect tree overturning resistance and the rotation angle at which this occurs, revealing that traditional winching tests may overestimate stability for horizontal applications due to vertical confinement effects []. It is evident that there is a fairly wide range of critical moments and critical inclination angles measured in the tests described.
Other authors have focused on the relationship between root systems and soil. Nicoll et al., 2008, studied how root system architecture and soil conditions influence resistance to lateral forces []. Achim and Nicoll proposed a resistance model that assumes a rigid root–soil plate and incorporates soil–root mechanical interaction []. More recently, the macroelement approach, treating the root system as an equivalent embedded shallow foundation, has also been proposed to model root–soil interactions of tree pull-over as a function of soil properties and the combination of loads/stress path applied [,,,].
In this context, the present study investigates tree uprooting stability through a comprehensive experimental campaign conducted at the University of Dundee Botanic Gardens (Scotland, UK). This testing principally aimed to consider the effects of pulling directions and pulling heights on overturning stability and to link overturing behaviour with detailed geotechnical characterization of subsoil. A total of twenty-one mature trees, from both coniferous and deciduous species (Pinus nigra, Picea abies, Tsuga, Betula, Quercus, Acer platanoides, Nothofagus, Eucalyptus), were tested under varying loading configurations, an aspect that has not been explored before to the authors’ knowledge. Each tree was subjected to multiple static pulling tests, changing both the direction and angle of load application to simulate diverse wind scenarios, as shown in Figure 1. Additionally, for a subset of the specimens, destructive uprooting tests were carried out to obtain full failure curves. The measured responses were then compared with those predicted using Wessolly’s (and other) extrapolation methods, with the aim of evaluating its reliability under variable loading directions and inclinations.
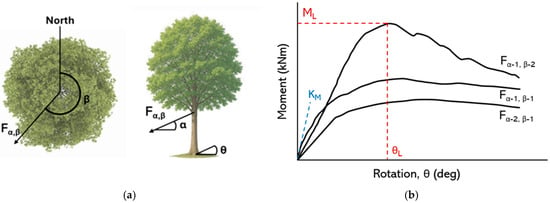
Figure 1.
(a) Plan and elevation views of a tree showing pulling direction (β), inclination angle (α), rotation at the root-plate (θ), and pulling force (Fα,β); (b) schematic uprooting curves from different pulling directions and heights, showing definitions of limit moment and limit rotation angle (ML, θL) and stiffness KM.
2. Materials and Methods
2.1. Site Details and Testing Summary
2.1.1. Overview
The University of Dundee Botanic Garden, established in October 1971, serves as an exemplary site where nature-based and community-focused solutions address climate adaptation and mitigation challenges []. Spanning 9.5 hectares and overlooking the River Tay, the garden hosts a diverse collection of plants, including both indigenous British species and significant specimens from around the world. Figure 2 highlights the site boundaries (indicated by the white line). Specific areas within the garden have been designated as outdoor laboratories for research purposes, including tree testing. Trees selected for testing were identified as healthy specimens that were well established from the initial planting of the gardens that nevertheless required removal as part of a broader renovation project designed to enhance biodiversity. Test trees and the specific testing conducted at each (as reported in this paper) are shown in Figure 3.

Figure 2.
University of Dundee Botanic Gardens—study area, western Dundee (UK, Scotland), and 365 m from the River Tay; 9.5 ha with about 5000 trees.
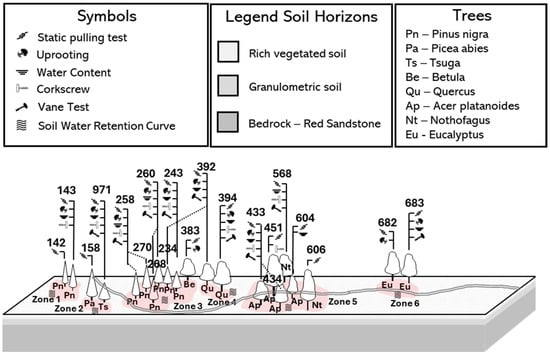
Figure 3.
Testing summary. The legend shows the symbols of the different tests performed on the trees, the stratigraphy, and the tree species; the zones are shown in red.
2.1.2. Geological Settings
The Dundee Formation, defined by [], is composed mainly of cross-bedded sandstones with interbedded siltstone and mudstone, representing lacustro-deltaic to delta-front deposits. In the area of Dundee Botanic Garden, there are (i) raised marine deposits from the late glacial period, including littoral sand, deltaic sand, silt, and subtidal clay; and (ii) glacial meltwater deposits consisting of sand and gravel. The gardens are situated on a sloping terrace at the summit of an ice-age cliff. The bedrock of the garden consists of sandstone at the lower levels and volcanic felsite at the higher levels (however, the boundary is not indicated). The superficial deposits in the area include sands, gravels, and clays from marine and glacial deposits during the ice age. This information suggests that the gardens have likely undergone significant landscaping, potentially involving the movement or importation of soil. Figure 4 shows images following some of the uprooting tests that will be described later. It is evident that there is potential for variations in the water content of the soil at different depths. Other visual evidence includes the presence of cobbles and plates of sandstone with varying thickness (2–5 cm in size).

Figure 4.
Visual evidence of ground conditions following uprooting tests.
2.1.3. Topsoil Characterization
A range of in situ and laboratory tests were undertaken to characterize the topsoil where tree roots were located. This included the following:
- Corkscrew (CS) device testing, as described in [,]. The tool was rotated into the soil and extracted vertically at 100 mm/min using a lever system connected to a load cell, which recorded the force required for pull-out []. Shear stress was calculated from the measured force and the surface area of the sides of the soil cylinder encapsulated by the corkscrew. Tests were performed at four points around each tree, typically at one-meter distances in cardinal directions, and conducted sequentially with depth where possible (i.e., until refusal was reached).
- Vane shear testing (VST), as usually used for in situ shear strength measurements in cohesive soils []. Tests were conducted at four cardinal points (N-E-S-W) around each tree, as well as additional positions, when necessary, as performed with the corkscrew.
- Water content measurements, using a ML2 Theta Probe (Delta-T, Cambridge, UK) employing capacitive technology to measure the soil’s dielectric constant. Measurements were taken at four cardinal points (N-E-S-W) around each tree, as performed with the corkscrew and vane test.
- Obtaining disturbed soil samples from the areas of Pinus nigra (258, 260, 268, 270), Acer platanoides (433, 434, 604), and Nothofagus (568, 606), which were used to determine the particle size distribution (PSD) curve using a combination of vibrational sieving and sedimentation techniques. For visualization, different zones were identified within the Botanic Garden, within which the trees were grouped (see Figure 3). Due to the high organic matter content, samples were wetted before sieving for the finest portion (silt–clay), and an automated Pario sedimentation analyzer (Meter Group, Washington, DC, USA) was used. Sediment was shaken in distilled water for 60 s, allowed to settle for 2.5 h, and analyzed to determine the grain size percentages. Combining these methods produced continuous PSD curves, which were consistent across two samples at each sampling location (Figure 5a). All samples were classified as sandy loam (Figure 5b).
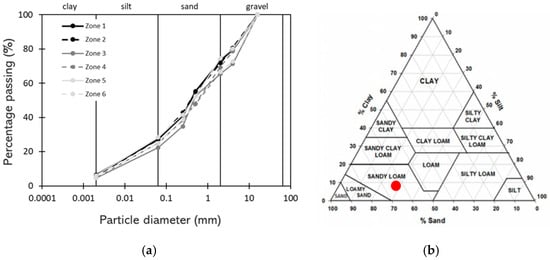 Figure 5. (a) Particle size distribution curves and (b) soil texture (the red dot) of the Botanic Garden topsoil.
Figure 5. (a) Particle size distribution curves and (b) soil texture (the red dot) of the Botanic Garden topsoil.
- Taking soil samples (50 mm diameter, 40 mm high) for soil water retention curve (SWRC) determination. After 24 h saturation in degassed water, the soil cores were placed on a ceramic plate with an air entry value (AEV) = 100 kPa (Soil moisture Equipment Corp, Goleta, CA, USA) to achieve hydraulic contact and suction equilibration at 1, 5, 20, and 50 kPa. A pressure plate apparatus (Soil moisture Equipment Corp, Goleta, CA, USA) was subsequently used to test in the range of 50–1500 kPa. The resulting data was fitted using the van Genuchten curve []. Figure 6 shows the soil water retention curve for rich vegetated soil of zone 3 as an example. Data for the other zones can be found in Appendix A.
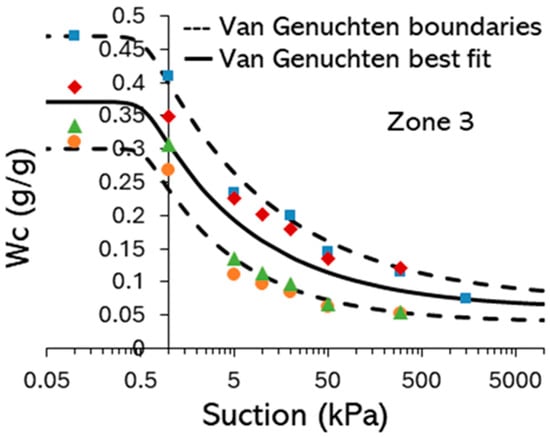 Figure 6. Example soil water retention curve for Botanic Garden topsoil (rich vegetated soil, zone 3, Figure 3). Dashed lines indicate upper and lower limits. Each colour series, along with its distinct symbol, represents a different soil-sample dataset.
Figure 6. Example soil water retention curve for Botanic Garden topsoil (rich vegetated soil, zone 3, Figure 3). Dashed lines indicate upper and lower limits. Each colour series, along with its distinct symbol, represents a different soil-sample dataset.
- Collection of three cylindrical soil samples (150 mm diameter, 300 mm high) from zones 2, 3, and 5 (see Figure 3). A custom metal tube of these internal dimensions was used for sampling and hammered into the soil until it was flush with the ground surface with a protective rubber separator. After extraction with a lever system (the same used for the corkscrew), the samples were transferred to pre-prepared plastic cylinders using a press to minimize disturbance and were otherwise sealed to avoid moisture content changes. The plastic cylinders were divided into two parts (100 mm and 200 mm high) with separators to define the cutting surface, and a draining mesh was placed at the base. Direct shear tests were conducted using a specialized apparatus [] at a shearing speed of 100 mm/min. Tests were performed on samples which were saturated for 24 h and drained manually prior to sharing. Shear curves (Figure 7) lacked distinct peaks, likely due to visible roots enhancing soil shear strength [].
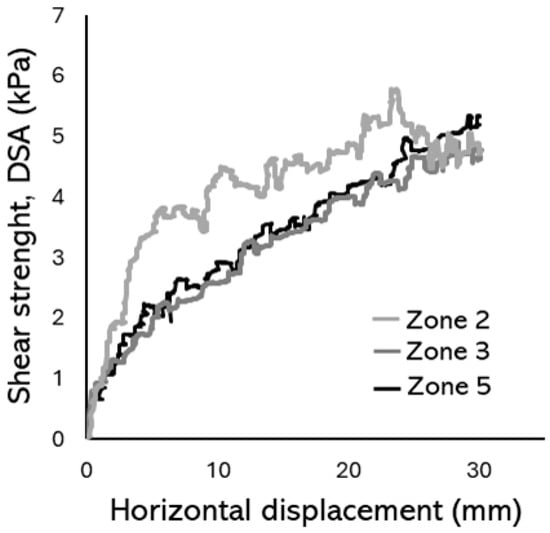 Figure 7. Large-sample direct shear apparatus (DSA) test curves.
Figure 7. Large-sample direct shear apparatus (DSA) test curves.
Figure 8 synthesizes the shear strength and water content measurements at a single location (268 Pinus nigra, zone 3). Figure 8c indicates root locations in the subsoil; no roots were observed to penetrate bedrock in any of the destructive tests. Similar synthesized data for the other zones can be found in Appendix A. This shows that as depth increases, the shear strength of the soil decreases. This is not due to an increased level of saturation in the soil, as the water content also decreases in depth (the soil is under-drained by the sandstone). The most plausible explanation is that the soil layer containing the root system (mainly the upper 0.4 m) exhibits higher shear strength due to the presence of the tree roots. This is supported by the variability in shear strength as a function of position around the tree within this upper layer, indicating different amounts of root material being encountered. The DSA test data on the un-rooted soil provides a lower bound to the shear strength data measured by the other techniques within the root bulb. In Figure 8, CS and VST data are correlated against each other and plotted by depth range. The VST measurements are consistently higher than those measured by the CS test, and this is consistent with the upper-bound of the range found by [] based on testing around Picea stichensis grown in a sandy silt (see Figure 9).
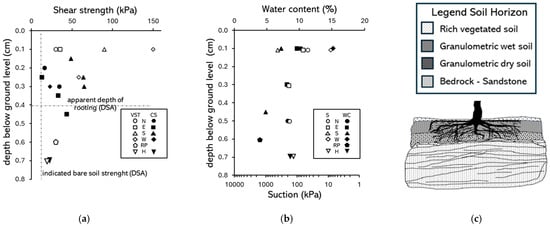
Figure 8.
Comparative summary of soil state and strength data (Zone 3): (a) shear strength from corkscrew (CS), vane shear tests (VST), and DSA; (b) depth distribution of soil water content and suction inferred from zone 3 SWRC; (c) soil profile indicating soil horizons. Test data from different locations related to the trunk, where N, E, S, and W are cardinal directions, RP = root-plate, and H = soil under root-plate.
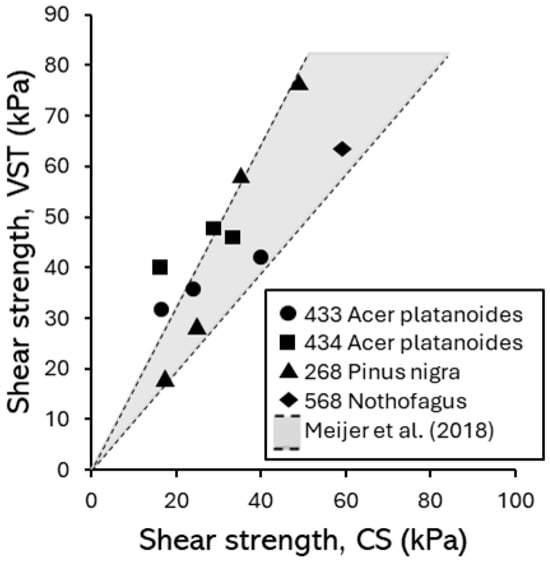
Figure 9.
Correlation between corkscrew (CS) and vane shear test (VST) data and comparison to measurements in a similar soil type at an alternative site [].
2.2. Winching Test Setup
Winching tests were conducted either to a serviceability limit state (0.25° rotation in the direction of pulling at the base of the trunk), hereafter referred to as ‘non-destructive’, or for uprooting (ultimate limit state). As shown in Figure 10, a rope was attached at a specified height on the test tree and tied through a winch to a nearby anchor tree (at its base). The winch was equipped with an in-line load cell (Kaliber 5 t force meter—Budapest (Hungary): working load limit 50 kN, resolution 10 N, sampling rate 1 Hz) to measure the tensile (pulling) force, while two perpendicular inclinometers (range +/−30°, resolution 0.001°, sampling rate 10 Hz; aligned parallel and perpendicular to the pulling direction; dual-axis inclinometer of the DynaTree Root and Trunk Testing System—BtFakopp Enterprise Bt—Ágfalva (H 9423), Fenyo u. 26, Sopron, Hungary) were attached horizontally at the tree base. Before testing, trees were pruned to avoid the rope snagging on branches, and the distance between trees, rope anchor height on both trees, and initial tree dimensions were recorded. Tests were conducted for each tree in two perpendicular directions (predominantly N-S and E-W), where the dominant regional wind direction at the site was N-S. Tests were also conducted at varying rope connection heights to vary the ratio of vertical, horizontal, and moment actions on the root system. During the larger deformation uprooting tests, inclinometers required periodic re-levelling due to excessive rotation. After reaching peak resistance, the residual resistance phase was recorded. Complete resistance loss was not observed as the inclinometers were removed once significant rotation was visually apparent.
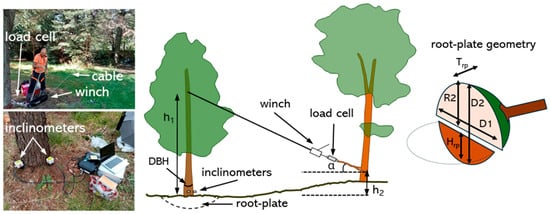
Figure 10.
Setup of non-destructive and uprooting tests.
Figure 11 shows the test location and directions of pulling for the winching tests reported in this study. A total of 21 trees were tested, divided into conifers and deciduous species. The conifers included Pinus nigra, Picea abies, and Tsuga, while the deciduous species consisted of Acer platanoides, Nothofagus, Betula, Eucalyptus, and Quercus. Each tree was assigned a unique identification code (ID), codes used by curator of the Botanic Garden. Table 1 summarizes the individual tree characteristics (height, H, and diameter at breast height, DBH) and test types conducted at each location.
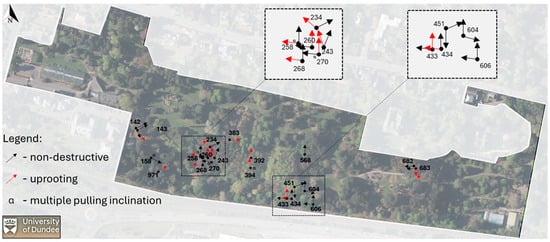
Figure 11.
Summary of different pulling tests, indicating pulling directions.

Table 1.
Summary of the individual tree characteristics and test types conducted at each location.
Trees were tested first under non-destructive conditions such that multiple tests (2–4 per tree, in all but two cases) could be conducted on the same tree under the same groundwater conditions. For some trees, the direction of pull (in-plan) was varied with the pulling angle to the horizontal (α) kept as constant as possible within the constraints of finding suitable nearby trees for anchorage of the rope. These tests were subsequently used to evaluate whether stiffness and capacity were different in the predominant wind direction compared to the direction perpendicular to this. For other trees, the plan direction was held constant, and α was varied either by changing the attachment point on the tree (i.e., h1 in Figure 10) or by anchoring to a different nearby tree, changing the horizontal distance between the pulling and anchorage points. Non-destructive pulling test are conventionally used to estimate the maximum uprooting resistance of a tree by extrapolating the moment–rotation data up to 0.25° using the Wessolly and M. Erb moment (M) rotation at the base of the trunk (θ) curve []:
ML is the estimated moment (overturning) capacity that was obtained by fitting Equation (1) using a least-squares fitting procedure. Finally, fifteen of the twenty-one trees were subjected to uprooting tests after the programme of non-destructive tests was complete. The system configuration used for these tests was similar to that employed for the standard pulling test, but winching was continued until failure by uprooting. For safety reasons, the canopy was completely removed prior to the uprooting tests.
3. Results
3.1. Non-Destructive Tests
Figure 12 shows pull test results for tree 260. The extrapolated ML and rotational stiffness KM are summarized in Table 2. In the table, the loading direction (using cardinal direction symbols) and the angle of pull to the horizontal (α) are also reported. Pull test curves of the other trees are reported in Appendix B.
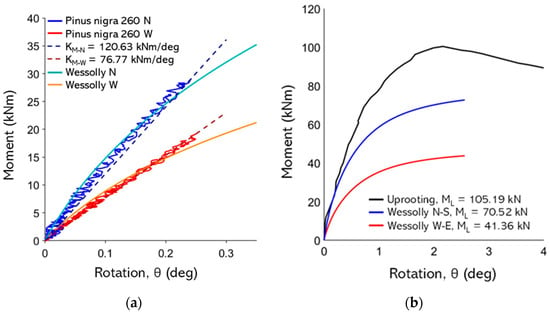
Figure 12.
(a) non-destructive test curves with Wessolly interpolation and stiffness (N pulling angle α = 16.6°, W pulling angle α = 17.8°); (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction N pulling angle α = 16.6°).

Table 2.
Non-destructive pulling tests results. h1 and h2 are the heights, as indicated in Figure 10. KM is the stiffness, and ML is the maximum moment predicted by Equation (1). N, E, S, and W represent the cardinal directions north, east, south, and west.
3.2. Uprooting Tests
The moment–rotation curves obtained from all the uprooting tests are shown in Figure 13, while Figure 12b shows how the extrapolated Wessolly curve for two pulling directions compares to the experimental data for tree 260. Table 3 summarizes key data from all uprooting tests: h1, h2, α, and pull direction are as defined previously (see Figure 10), while ML and θL (limit inclination) are measured from the test. Root-plate measurements are also given as measured post-test. The results highlight that peak rotations range between 1.59 and 2.93 degrees.
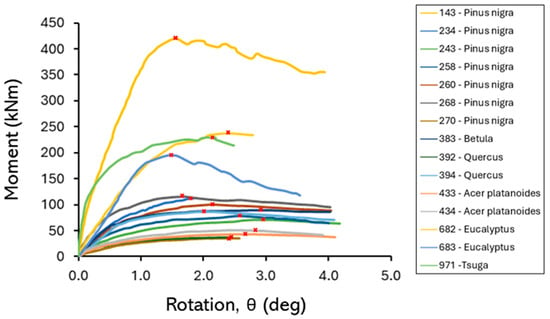
Figure 13.
Summary of moment–rotation curves from uprooting tests. The red crosses indicate the peak values of the moment for each curve.

Table 3.
Key data from the uprooting tests.
4. Discussion
4.1. Effect of Direction of Pull (In Plan)
Regarding bias in overturning resistance in the predominant wind direction, Table 4 summarizes the data for the ten analysed trees along the west and north pulling directions.

Table 4.
Comparison between extrapolated limit moment in west (MLW) and north (MLN) directions.
Figure 14 shows the parity line (dashed), where the ratio between the extrapolated moments in the two directions is 1, and the solid line represents the threshold where the ratio between the moments extrapolated in the north and west directions is 2. Only three exhibited greater mechanical strength in the west (W) direction. In contrast, the remaining individuals were stronger in the north (N) direction, with differences reaching up to 66%. When considering the entire dataset, the root systems demonstrated an average increase in mechanical strength of 23% in the N direction, as inferred from the extrapolated maximum loading (ML) according to the Wessolly method. This directional asymmetry in anchorage capacity suggests a potential adaptive response to prevailing wind patterns, favouring enhanced stability along the dominant wind axis.
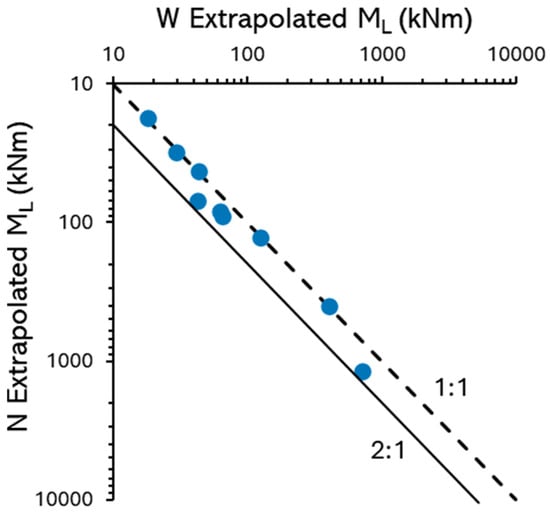
Figure 14.
Effect of loading direction on extrapolated limit moment. The blue symbols represent different individual trees.
4.2. Effect of Height of Pull (Angle of Pull in Elevation)
Table 5 summarizes the results from the non-destructive tests, first conducted at different pulling heights and then after uprooting ( is the average of dimensions D1 and D2 of the root-plate geometry; Figure 10). Moment capacity based on extrapolated values appears to be insensitive to even very large changes in the pulling angle, as shown in Figure 15. Using a VHM yield surface approach gives the following []:
where the normalized vertical load (ξ) is given by:
and η = 3, β = 0.95, μ = 150, and Vt/Vc = −0.12. Substituting the VHM stress path for a winching test [], which is defined by:
it can be shown that the moment capacity (ML) is insensitive to alpha. For trees 258 and 270, the maximum difference between the extrapolated ML values and the mean value are 10% and 5%, respectively, despite the maximum tested angle being approximately three times the minimum. For tree 392, the maximum difference between the extrapolated M values and the mean value is 17%, with the maximum tested angle being approximately five times the minimum. For tree 394, the maximum difference between the extrapolated M values and the mean value is 5%, with the maximum tested angle being approximately five times the minimum. The small differences in the extrapolated moment are consistent with the analytical insensitivity to alpha. Additional data from a large database of uprooting tests from [], which is also shown in Figure 15, also shows no clear trend between α and measured ML.

Table 5.
Comparison of extrapolated limit moments for different pull angles with measured limit moments from uprooting tests.
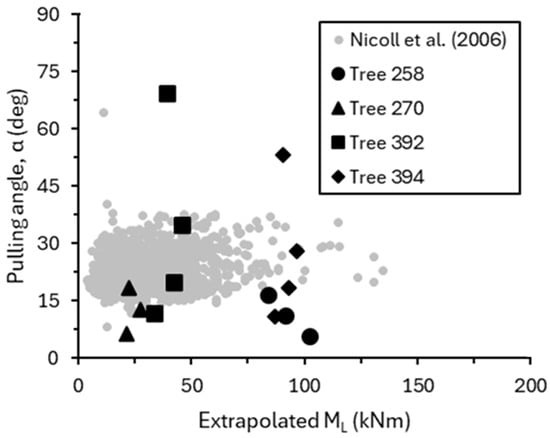
Figure 15.
Insensitivity of extrapolated limit moment to pulling angle (α). Data from a large UK uprooting test database [] shown for context.
4.3. Suitability of Extrapolation Method for Non-Destructive Tests
In the destructive tests, peak bending moments were observed between 1.6 and 2.9° of rotation, which aligns reasonably well with the predictions of the Wessolly and Erb model (Equation (1)). For 9 out of 15 trees, the percentage difference between the observed and estimated moment is within 20% (6 below 10% and 3 between 10%–20%). For the remaining six trees, the percentage difference ranges from 35% up to a maximum of 107% (in the case of Pinus nigra 270). Only for 4 out of 15 trees was the predicted overturning moment capacity overestimated compared to the measured value with a maximum percentage difference of 4%. An alternative stiffness-based approach to determining capacity from non-destructive test data is based on the fact that for rotations from 0 to 0.25 degrees, the response falls within the elastic range, and therefore the moment–rotation curve can be approximated by a straight line. According to the Wessolly and Erb model, a rotation of 0.25° corresponds to 40% of the maximum moment, and thus the law is as follows:
It is noteworthy that for 11 out of 15 trees, the maximum overturning moment underestimated by either Equation (1) or Equation (6) represents an inherent safety factor. This finding supports the general applicability of both the moment-based and stiffness-based approaches for estimating tree anchorage capacity (Figure 16a), at least for the soil and groundwater conditions considered herein. The variability in the value of rotation when peak moment is reached can, in part, be explained by local soil conditions; for instance, Zhang et al. (2023) demonstrated that soil saturation levels significantly influence rotational behaviour during winching tests, a parameter that is typically not recorded during field assessments []. Water content and suction data for the different zones considered at the Botanic Gardens that is shown in the Appendix A demonstrates local variation in groundwater conditions between zones. Alternative prediction approaches which do not utilize non-destructive test data, such as the root-plate model proposed by [], capture the general trend observed in the [] dataset, albeit with considerable scatter (Figure 16b). However, when applied to the Botanical Garden dataset, the fit appears less satisfactory, especially when using the formulation where resistance is proportional to the square of the equivalent root-plate diameter (). This discrepancy suggests that factors beyond root-plate weight may influence anchorage capacity. In particular, it is plausible that structural roots extending beyond the conventional root-plate contribute additional resistance, which is not adequately accounted for in simplified geometric models. It also demonstrates that there is additional value in conducting non-destructive tests to obtain improved predictions of capacity and therefore better estimates of risk.
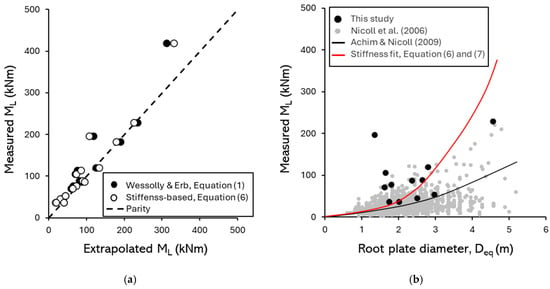
Figure 16.
(a) Comparison between measured limit moment and extrapolated values using the Wessolly and Erb method and a stiffness-based approach; (b) effect of measured root-plate diameter on measured limit moment. Data (grey dots) from a large UK uprooting test database [] shown for context and model fitting by [].
Applying the circular footing model to the Botanic Garden dataset (Figure 17), the interpolation appears less satisfactory. This suggests that the stiffness of the model may be proportional to the cube of the root-plate diameter and possibly less than the square, as assumed in the model by [].
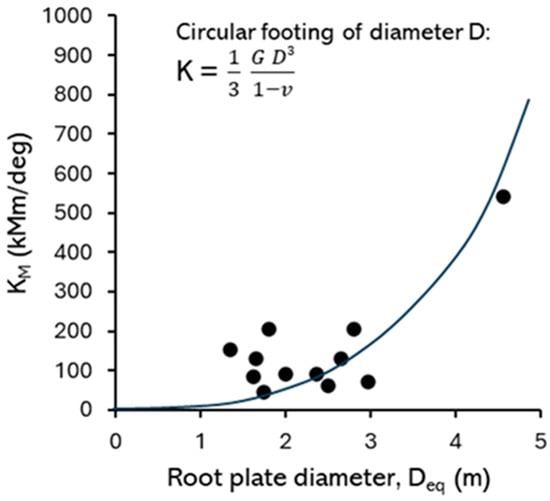
Figure 17.
Effect of measured root-plate diameter on measured stiffness from uprooting tests and comparison to an equivalent circular footing of diameter Deq.
5. Conclusions
In this work, static pulling tests were conducted to study the stability of mature trees. Specifically, non-destructive tests were performed, varying both the pulling directions and angles, as well as uprooting tests. Soil characteristics, such as shear strength, moisture content, suction, and particle size distribution, were analyzed to evaluate their influence on root anchorage. The tests were conducted on twenty-one trees from the Botanic Garden of Dundee University, belonging to eight different species (Pinus nigra, Picea abies, Tsuga, Betula, Quercus, Acer platanoides, Nothofagus, Eucalyptus). Fifteen out of the twenty-one trees were uprooted to determine the maximum overturning moment and compare it with the values estimated using the cited methods. The data collected and analysed indicate that the following:
- As depth increases, the shear strength of the soil decreases. This is not due to an increased level of saturation, as the water content also decreases in depth (the soil is under-drained by the sandstone). The most plausible explanation is that the soil layer contains the root system.
- Peak moments in destructive tests were observed between 1.59° to 2.93°. This confirms the need for destructive testing so that the ultimate limit state is verified.
- Regarding bias in overturning resistance in the predominant wind direction, among the 10 trees tested along the north (main wind direction) and west directions, for 7 of them, the predicted overturning moment was higher in the north direction compared to the west.
- Regarding the insensitivity of moment capacity to pull angle, the moment capacity appears unaffected by substantial changes in the pulling angle.
- Regarding the evaluation of existing methods for predicting overturning moment, only 4 out of 15 trees had their predicted overturning moment overestimated compared to the experimental values. For the remaining 11 trees, the maximum overturning moment underestimated by both models provides a safety margin. These results appear to support the general applicability of both the moment-based and stiffness-based approaches for estimating tree anchorage capacity.
- Attempting to fit the data using the root-plate model, which assumes that the ultimate overturning resistance is proportional to the square of the root-plate diameter, did not yield satisfactory results. In contrast, a reasonable fit was obtained using the circular foundation root-plate model, where the stiffness is assumed to be proportional to the cube of the root-plate diameter.
- In conclusion, there is no correlation between the maximum overturning moment for uprooting and trees of the same species with similar biometric parameters. This suggests that overturning stability depends much more on the site-specific conditions of each individual tree.
Author Contributions
Conceptualization, M.O.C.; methodology, M.A., G.M., A.M., D.B., M.O.C. and J.K.; software, M.O.C., A.M. and M.A.; validation, M.A. and G.M.; formal analysis, M.A., M.O.C. and J.K.; investigation, M.A., G.M. and A.M.; resources, M.O.C., R.P.C. and D.B.; data curation, M.A. and M.O.C.; writing—original draft preparation, M.A., M.O.C. and J.K.; writing—review and editing, M.A., G.M., D.B., M.O.C. and J.K.; visualization, M.A., M.O.C. and J.K.; supervision, M.O.C. and R.P.C. All authors have read and agreed to the published version of the manuscript.
Funding
Scottish Research Partnership in Engineering (SRPe), SRPe-IDP/011 research grant Rural & Environment Science & Analytical Services Division of the Scottish Government (RESAS 22-27: “Achieving Multi-Purpose Nature-Based Solutions (JHI-D2-2)”, “Healthy Soils for a Green Recovery (JHI-D3-1)”; Project funded under the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.4—Call for tender No. 3138 of 16 December 2021, rectified by Decree n. 3175 of 18 December 2021 of Italian Ministry of University and Research funded by the European Union—NextGenerationEU, Project code CN_00000033, Concession Decree No. 1034 of 17 June 2022 adopted by the Italian Ministry of University and Research, CUP H43C22000530001, Project title “National Biodiversity Future Center—NBFC”. PB acknowledges support from Italian Ministry of Universities and Research.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed at the corresponding author.
Acknowledgments
The authors gratefully acknowledge Kevin Frediani, former University of Dundee Botanic Garden Curator, for all the support provided during the field-testing campaign. Brett of Brett Bain Tree Services and Ian Barnes of Tree Diagnostics are also acknowledged for their service in the field testing.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| KM | Stiffness |
| ML | Limit moment |
| MLW | Limit moment along west direction |
| MLN | Limit moment along north direction |
| VTA | Visual tree assessment |
| θL | Limit rotation angle |
| Pn | Pinus nigra |
| Pa | Picea abies |
| Ts | Tsuga |
| Be | Betula |
| Qu | Quercus |
| Ap | Acer platanoides |
| Nt | Nothofagus |
| Eu | Eucalyptus |
| Cs | Corkscrew |
| VST | Vane shear test |
| PSD | Particle size distribution |
| SWRC | Soil water retention curve |
| DBH | Diameter breast height |
| h1 | Winch height |
| h2 | Height between base of pulled tree and cable on constraining tree |
| R2 | Radius of root-plate visible after uprooting |
| D2 | Diameter of root-plate along uprooting direction |
| D1 | Diameter of root-plate along transverse of uprooting direction |
| Trp | Thickness of root-plate along uprooting direction |
| Hrp | Thickness of root-plate part inside soil after uprooting |
| α | Pulling angle inclination |
| ML-EXP | Experimental limit moment during uprooting |
| θL-EXP | Experimental limit rotation during uprooting |
| Deq | Equivalent root-plate diameter |
| D | Diameter |
| G | Shear modulus |
| ν | Poisson’s number |
Appendix A
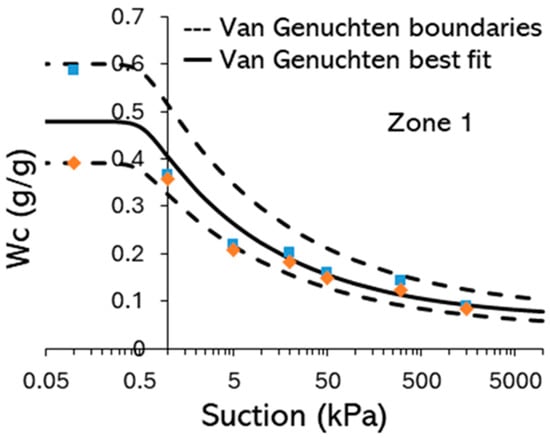
Figure A1.
Example soil water retention curve for Botanic Garden topsoil (rich vegetated soil, zone 1, Figure 3). Dashed lines indicate upper and lower limits. Each colour series, along with its distinct symbol, represents a different soil-sample dataset.
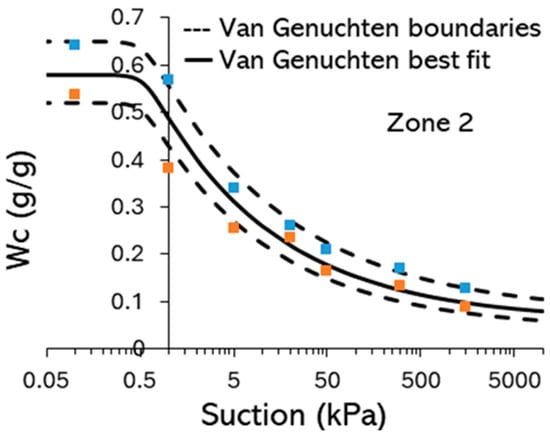
Figure A2.
Example soil water retention curve for Botanic Garden topsoil (rich vegetated soil, zone 2, Figure 3). Dashed lines indicate upper and lower limits. Each colour series, along with its distinct symbol, represents a different soil-sample dataset.
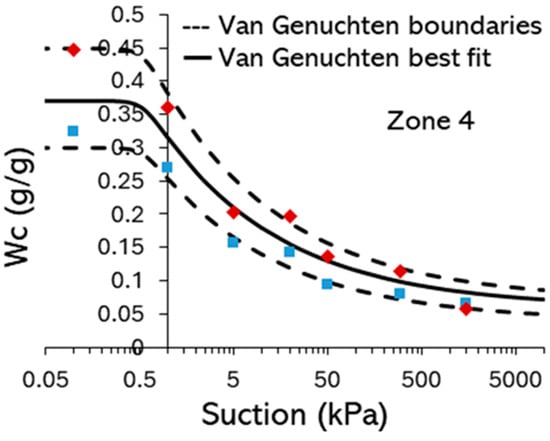
Figure A3.
Example soil water retention curve for Botanic Garden topsoil (rich vegetated soil, zone 4, Figure 3). Dashed lines indicate upper and lower limits. Each colour series, along with its distinct symbol, represents a different soil-sample dataset.
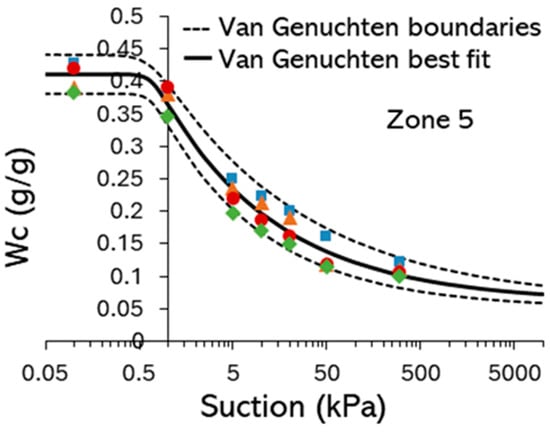
Figure A4.
Example soil water retention curve for Botanic Garden topsoil (rich vegetated soil, zone 5, Figure 3). Dashed lines indicate upper and lower limits. Each colour series, along with its distinct symbol, represents a different soil-sample dataset.
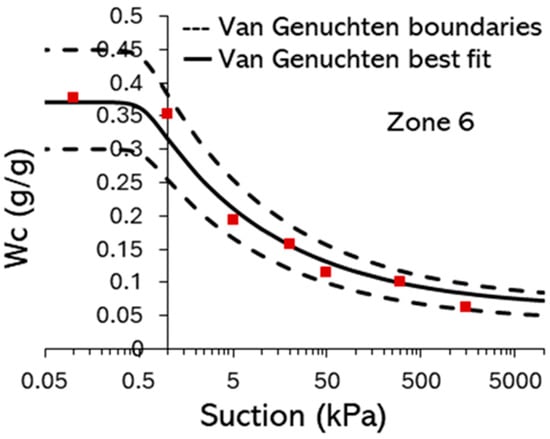
Figure A5.
Example soil water retention curve for Botanic Garden topsoil (rich vegetated soil, zone 6, Figure 3). Dashed lines indicate upper and lower limits. The red square markers indicate the soil-sample dataset.
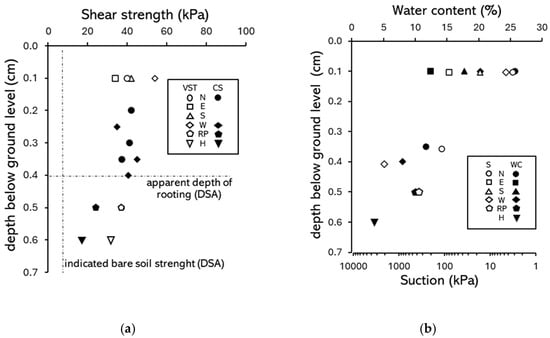
Figure A6.
Comparative summary of soil state and strength data (433—Acer platanoides): (a) shear strength from corkscrew (CS), vane shear tests (VST), and DSA; (b) depth distribution of soil water content and suction inferred from zone 3 SWRC. Test data from different locations relative to the trunk, where N, E, S, and W are cardinal directions, RP = root-plate, and H = soil under root-plate.
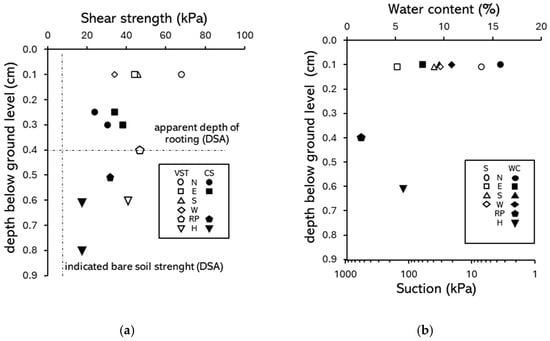
Figure A7.
Comparative summary of soil state and strength data (434—Acer platanoides): (a) shear strength from corkscrew (CS), vane shear tests (VST), and DSA; (b) depth distribution of soil water content and suction inferred from zone 3 SWRC. Test data from different locations related to the trunk, where N, E, S, and W are cardinal directions, RP = root-plate, and H = soil under root-plate.
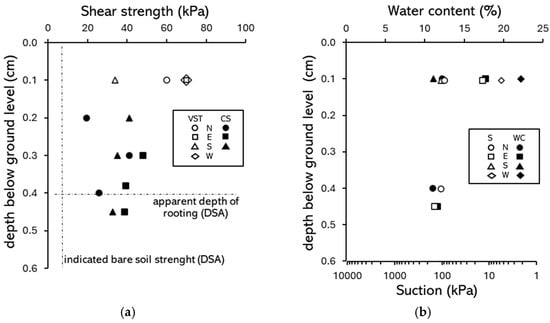
Figure A8.
Comparative summary of soil state and strength data (568—Nothofagus): (a) shear strength from corkscrew (CS), vane shear tests (VST), and DSA; (b) depth distribution of soil water content and suction inferred from Zone 3 SWRC. Test data from different locations related to the trunk, where N, E, S, and W are cardinal directions, RP =root-plate, and H = soil under root-plate.
Appendix B
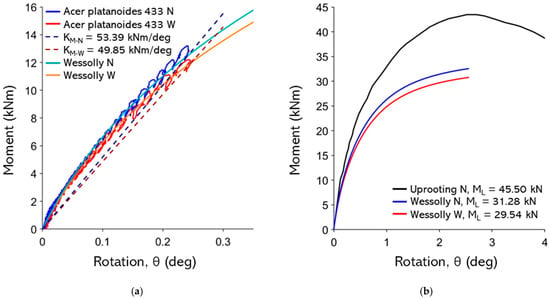
Figure A9.
(a) non-destructive test curves with Wessolly interpolation and stiffness (N pulling angle α = 17.6°, W pulling angle α = 21.9°); (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction N pulling angle α = 17.6°).
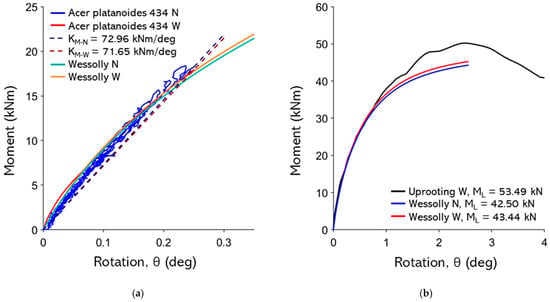
Figure A10.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (N pulling angle α = 23.4°, W pulling angle α = 21.3°); (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction W pulling angle α = 21.3°).
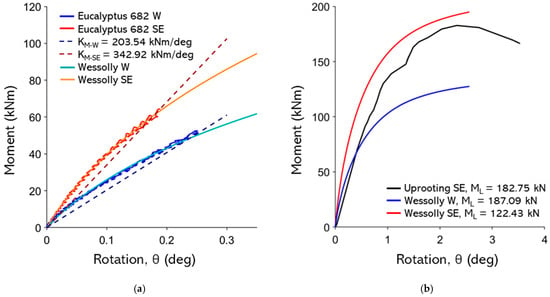
Figure A11.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (SE pulling angle α = 14.0°, W pulling angle α = 9.9°); (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction SE pulling angle α = 14.0°).
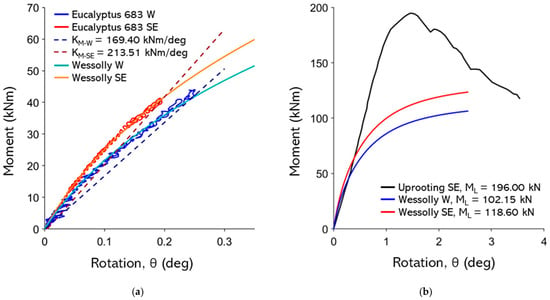
Figure A12.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (SE pulling angle α = 14.0°, W pulling angle α = 11.8°); (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction SE pulling angle α = 14.0°).
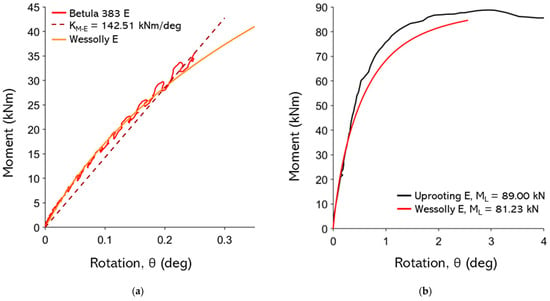
Figure A13.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (E pulling angle α = 20.8°; (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction E pulling angle α = 20.8°).
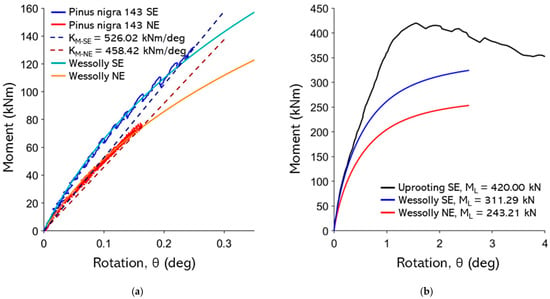
Figure A14.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (SE pulling angle α = 35.7°, NE pulling angle α = 24.1°); (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction SE pulling angle α = 35.7°).
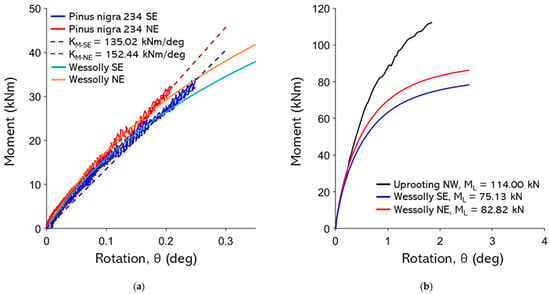
Figure A15.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (NW pulling angle α = 19.5°, SE pulling angle α = 33.2°); (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction NW pulling angle α = 33.2°).
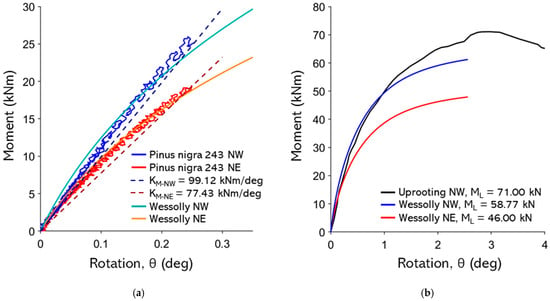
Figure A16.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (NW pulling angle α = 33.2°, NE pulling angle α = 25.5°); (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction NW pulling angle α = 33.2°).
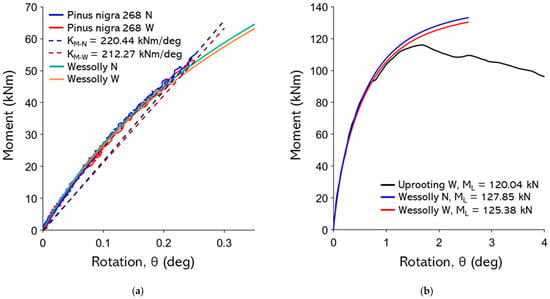
Figure A17.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (N pulling angle α = 11.8°, W pulling angle α = 16.3°); (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction W pulling angle α = 16.3°).
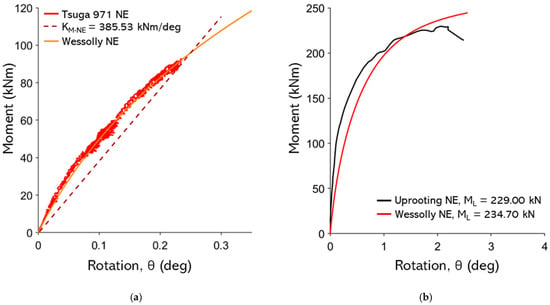
Figure A18.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (NE pulling angle α = 11.6°; (b) comparison of extrapolated Wessolly curves with uprooting test (uprooting direction NE pulling angle α = 11.6°).
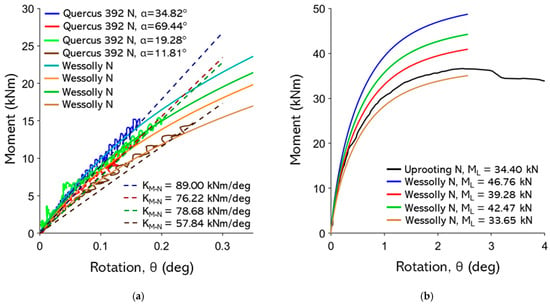
Figure A19.
(a) Non-destructive test curves with Wessolly interpolation and stiffness; (b) comparison of extrapolated Wessolly curves with uprooting test, uprooting direction N pulling angle 69.4°.
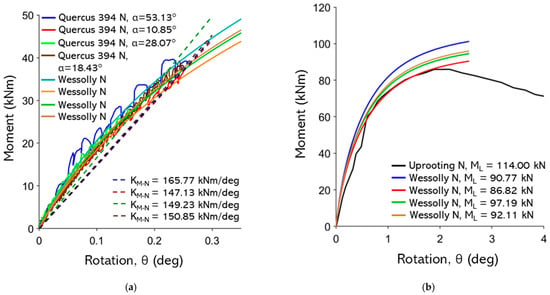
Figure A20.
(a) Non-destructive test curves with Wessolly interpolation and stiffness; (b) comparison of extrapolated Wessolly curves with uprooting test, uprooting direction N pulling angle 10.9°.
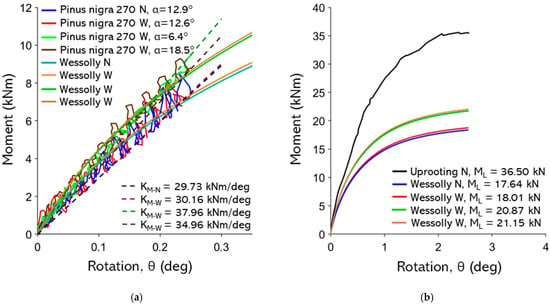
Figure A21.
(a) Non-destructive test curves with Wessolly interpolation and stiffness; (b) comparison of extrapolated Wessolly curves with uprooting test, uprooting direction N pulling angle 12.9°.
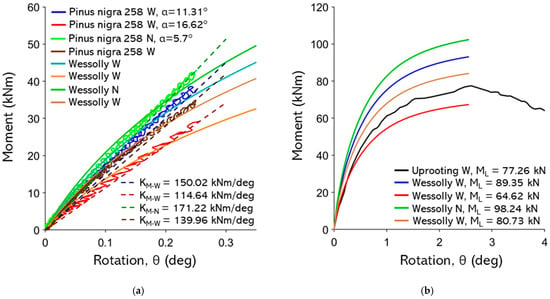
Figure A22.
(a) Non-destructive test curves with Wessolly interpolation and stiffness; (b) comparison of extrapolated Wessolly curves with uprooting test, uprooting direction N pulling angle 16.6°.
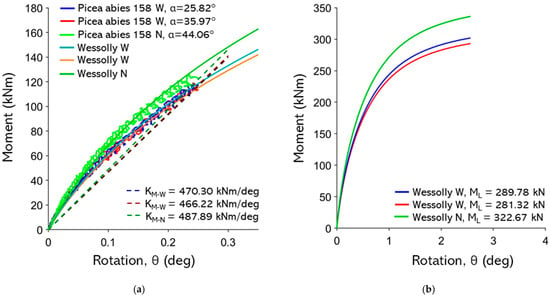
Figure A23.
(a) Non-destructive test curves with Wessolly interpolation and stiffness; (b) comparison of extrapolated Wessolly curves with uprooting test.
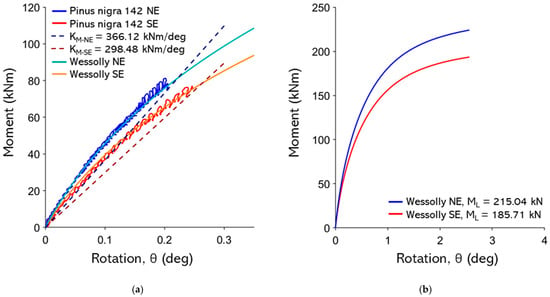
Figure A24.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (NE pulling angle α = 20.2°, SE pulling angle α = 25.7°); (b) comparison of extrapolated Wessolly curves with uprooting test.
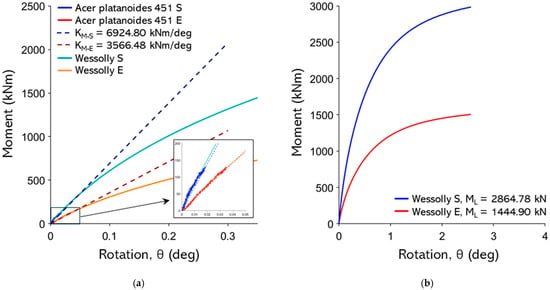
Figure A25.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (E pulling angle α = 16.0°, S pulling angle α = 26.3°); (b) comparison of extrapolated Wessolly curves with uprooting test.
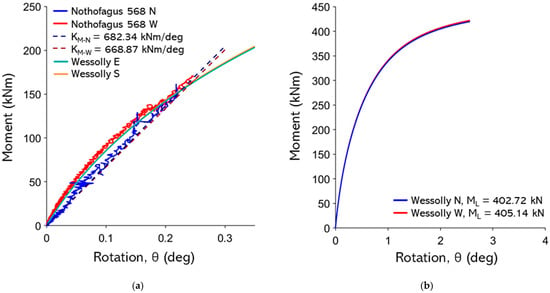
Figure A26.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (N pulling angle α = 20.9°, W pulling angle α = 20.2°); (b) comparison of extrapolated Wessolly curves with uprooting test.
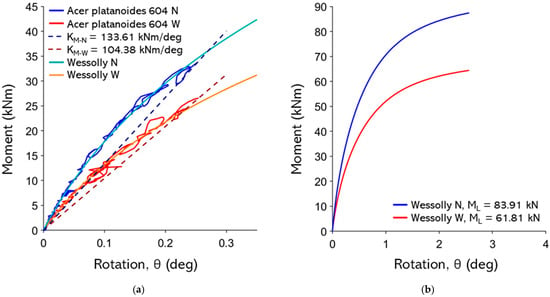
Figure A27.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (N pulling angle α = 17.7°, W pulling angle α = 15.2°); (b) comparison of extrapolated Wessolly curves with uprooting test.
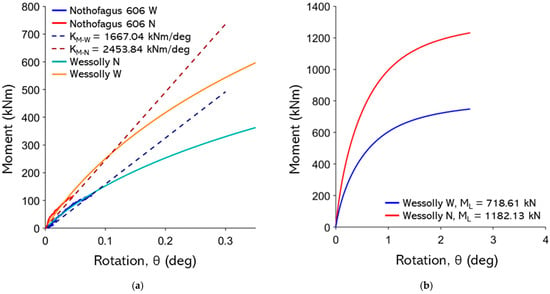
Figure A28.
(a) Non-destructive test curves with Wessolly interpolation and stiffness (N pulling angle α = 24.8°, W pulling angle α = 25.2°); (b) comparison of extrapolated Wessolly curves with uprooting test.
References
- Cavender-Bares, J.M.; Nelson, E.; Meireles, J.E.; Lasky, J.R.; Miteva, D.A.; Nowak, D.J.; Pearse, W.D.; Helmus, M.R.; Zanne, A.E.; Fagan, W.F.; et al. The hidden value of trees: Quantifying the ecosystem services of tree lineages and their major threats across the contiguous US. PLOS Sustain. Transform. 2022, 1, e0000010. [Google Scholar] [CrossRef]
- Mattheck, C.; Breloer, H. FIELD GUIDE FOR VISUAL TREE ASSESSMENT (VTA). Arboric. J. 1994, 18, 1–23. [Google Scholar] [CrossRef]
- Marsiglia, A.; Galli, A.; Marrazzo, G.; Castellanza, R.; Ciantia, M.O. Uprooting Safety Factor of Trees from Static Pulling Tests and Dynamic Monitoring. In Geotechnical Engineering in the Digital and Technological Innovation Era; Springer Series in Geomechanics and Geoengineering; Springer: Cham, Switzerland, 2023; pp. 218–225. [Google Scholar] [CrossRef]
- Wessolly, L. Fracture Diagnosis of Trees Part 1: Statics-Integrated Methods-Measurement with Tension Test the Expert’s Method. In Stadt und Grün; gGmbH German Institute of Urban Affairs (Difu): Berlin, Germany, 1995. [Google Scholar]
- Wessolly, L. Fracture Diagnosis of Trees Part 2: Statics-Integrated Methods-Statically-Integrated Assessment (SIA) The Practitioner’s Method of Diagnosis. In Stadt und Grün; gGmbH German Institute of Urban Affairs (Difu): Berlin, Germany, 1995. [Google Scholar]
- Wessolly, L. Standsicherheit von Bäumen. Der Kippvorgang ist geklärt. Stadt Grün 1996, 45, 268–272. [Google Scholar]
- Wessolly, L.; Erb, M. Handbuch der Baumstatik und Baumkontrolle; Patzer Verlag: Berlin, Germany, 1998. [Google Scholar]
- Fraser, A.I.; Gardiner, J.B.H. Rooting and Stability in Sitka Spruce. 1967. Available online: https://cdn.forestresearch.gov.uk/1967/03/fcbu040.pdf (accessed on 1 October 2025).
- Crook, M.J.; Ennos, A.R. The anchorage mechanics of deep rooted larch, Larix europea × L. japonica. J. Exp. Bot. 1996, 47, 1509–1517. [Google Scholar] [CrossRef]
- Défossez, P.; Veylon, G.; Yang, M.; Bonnefond, J.M.; Garrigou, D.; Trichet, P.; Danjon, F. Impact of soil water content on the overturning resistance of young Pinus Pinaster in sandy soil. For. Ecol. Manag. 2021, 480, 118614. [Google Scholar] [CrossRef]
- Urata, T.; Shibuya, M.; Koizumi, A.; Torita, H.; Cha, J.Y. Both stem and crown mass affect tree resistance to uprooting. J. For. Res. 2012, 17, 65–71. [Google Scholar] [CrossRef]
- Marchi, L.; Costa, M.; Gardiner, B.; Locatelli, T.; Lingua, E. Effect of repeated pulling loads on Norway spruce (Picea abies (L.) Karst.) trees. For. Ecol. Manag. 2024, 567, 122071. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, C.; Leung, A.K.; Mohammad, S.; Choi, C.E. Uprooting dynamics of a model tree under rockfall impact: Combined experimental and numerical insights. Earth Surf. Process Landf. 2025, 50, e70114. [Google Scholar] [CrossRef]
- Galli, A.; Sala, C.; Castellanza, R.; Marsiglia, A.; Ciantia, M.O. Lesson learnt from static pulling tests on trees: An experimental study on toppling behaviour of complex foundations. Acta Geotech. 2024, 19, 1477–1494. [Google Scholar] [CrossRef]
- Zhang, X.; Knappett, J.A.; Leung, A.K.; Ciantia, M.O.; Liang, T.; Nicoll, B.C. Centrifuge modelling of root-soil interaction of laterally loaded trees under different loading conditions. Geotechnique 2023, 73, 766–780. [Google Scholar] [CrossRef]
- Nicoll, B.C.; Gardiner, B.A.; Peace, A.J. Improvements in anchorage provided by the acclimation of forest trees to wind stress. Forestry 2008, 81, 389–398. [Google Scholar] [CrossRef]
- Achim, A.; Nicoll, B.C. Modelling the anchorage of shallow-rooted trees. For. Int. J. For. Res. 2009, 82, 273–284. [Google Scholar] [CrossRef]
- Dattola, G.; Ciantia, M.O.; Galli, A.; Blyth, L.; Zhang, X.; Knappet, J.A.; Castellanza, R.; Sala, C. A Macroelement Approach for the Stability Assessment of Trees. Lect. Notes Civ. Eng. 2020, 40, 417–426. [Google Scholar] [CrossRef]
- Mansour, M.A.; Rhee, D.M.; Newson, T.; Peterson, C.; Lombardo, F.T. Estimating wind damage in forested areas due to tornadoes. Forests 2021, 12, 17. [Google Scholar] [CrossRef]
- Marrazzo, G.; Ciantia, M.O.; Riccio, T.; Knappett, J.A.; Galli, A. Multi-axis loading tests on a small-scale tree roots model. In Proceedings of the 5th European Conference on Physical Modelling in Geotechnics, Delft, The Netherlands, 2–4 October 2024. [Google Scholar] [CrossRef]
- Zhang, X.; Knappett, J.; Zhang, T.; Zheng, Z.; Liang, T.; Ke, S.; Ciantia, M.; Leung, A. Mechanical Behaviour of Leeward Lateral Roots During Tree Overturning. Forests 2025, 16, 1692. [Google Scholar] [CrossRef]
- Frediani, K. Botanic Garden and Grounds Strategy; University of Dundee: Dundee, UK, 2021. [Google Scholar]
- Armstrong, M.; Paterson, I.B. The Lower Old Red Sandstone of the Strathmore Region; HM Stationery Office: Norwich, UK, 1970. [Google Scholar]
- Meijer, G.J.; Bengough, A.G.; Knappett, J.A.; Loades, K.W.; Nicoll, B.C. In situ measurement of root reinforcement using corkscrew extraction method. Can. Geotech. J. 2018, 55, 1372–1390. [Google Scholar] [CrossRef]
- Meijer, G.; Bengough, G.; Knappett, J.; Loades, K.; Nicoll, B. Measuring the strength of root-reinforced soil on steep natural slopes using the corkscrew extraction method. Forests 2019, 10, 1135. [Google Scholar] [CrossRef]
- Chandler, R.J. The in-situ measurement of the undrained shear strength of clays using the field vane. In Vane Shear Strength Testing in Soils: Field and Laboratory Studies; Astm Intl: West Conshohocken, PA, USA, 1988. [Google Scholar]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Liang, T.; Knappett, J.A.; Duckett, N. Modelling the seismic performance of rooted slopes from individual root-soil interaction to global slope behaviour. Geotechnique 2015, 65, 995–1009. [Google Scholar] [CrossRef]
- Nicoll, B.C.; Gardiner, B.A.; Rayner, B.; Peace, A.J. Anchorage of coniferous trees in relation to species, soil type, and rooting depth. Can. J. For. Res. 2006, 36, 1871–1883. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).