Abstract
This paper reports on the location of sources contributing to a point flux measurement in the southern taiga, Russia. The measurement tower is surrounded by a coniferous forest with a mean aerodynamically active height of 27 m (h). Aerodynamical parameters of the forest, such as displacement height d and aerodynamic roughness , derived from wind speed profile measurements for 2017–2019, were used to estimate the seasonal and daily behavior of the flux footprint. Two analytical footprint models driven by d and z0 were used to estimate the footprint for canopy sources. The Lagrangian simulation (LS) approach driven by flow statistics from measurements and modeling was used to estimate the footprint for ground-located sources. The Flux Footprint Prediction (FFP) tool for assessing canopy flux footprint applied as the option in the EddyPro v.7 software was inspected against analytical and LS methods. For model comparisons, two parameters from estimated footprint functions were used: the upwind distance (fetch) of the peak contribution in the measured flux (Xmax) and the fetch that contributed to 80% of the total flux (CF80). The study shows that Xmax varies slightly with season but relies on wind direction and time of day. All methods yield different Xmax values but fall in the same range (60–130 m, around 2–5 h); thus, they can estimate the maximum influence distance with similar confidence. The CF80 values provided by the FFP tool are significantly lower than the CF80 values from other methods. For instance, the FFP tool estimates a CF80 of about 200 m (7 h), whereas other methods estimate a range of 600–1100 m (25–40 h). The study emphasizes that estimating the ground source footprint requires either the LS method or more complex approaches based on Computational Fluid Dynamics (CFD) techniques. These findings have essential implications in interpreting eddy-flux measurements over the quasi-homogeneous forest.
1. Introduction
Forests play a crucial role in the ecosystem by interacting with the atmosphere and impacting both local and global climates (e.g., [1]). Understanding this interaction is critical to finding ways to address climate change in the future. This understanding relies on long-term data about the matter exchange between the atmosphere and the forest. The eddy covariance (EC) measurement system is a standard tool that provides the necessary information [2].
The flux measurements of different compounds over forests are going instantly around the world (e.g., [3,4,5,6,7]). Almost all results of such measurements are associated with the average forest properties surrounding the tower. During the early days of eddy-covariance, experiments in boundary-layer meteorology were conducted in near-ideal conditions with uniform ground cover to ensure accurate data interpretation (c.f. [8]). However, as ideal conditions are uncommon, researchers have expanded their measurements to more complex areas. To enhance measurement accuracy, researchers have employed various techniques, including assessing turbulent characteristics using different criteria and implementing multiple corrections. One key aspect of interest, particularly in non-ideal conditions, is the upwind area associated with the measured signal. To address this issue, it is highly recommended to use an add-on tool like a footprint to separate the contributions from different types of vegetation and underlying soils in the signal.
Quantitatively, the relation between a source strength Q and the value of a signal F registered at the location is described by ‘‘source weight function’’ or ‘‘footprint’’ f [9]:
where r′ is the separation between measurement and forcing, and is the integration domain. During the last decades, considerable progress has been made in developing mathematical tools that allow for estimating the actual “source area” affecting the sensor response. These include analytical methods [10,11,12], the use of Lagrangian stochastic (LS) models [13,14,15,16,17], and the employment of models based on numerical solutions of the Navier–Stokes equations [18,19]. Each class includes models with different levels of complexity and numerical demands. The advantages and disadvantages of existing models are given in detail in the following reviews on this subject [20,21,22,23].
Although the footprint concept has shown practical applications and has helped to explain some unexpected properties of measured fluxes behind the island since its inception [23], it has been misused for a significant period. It was primarily applied to show the spatial aspect of measurement rather than interpreting the measured signals. The research of Amiro [24] was a significant breakthrough in understanding the applicability of footprints. It was established that footprint climatology provides vital information about the area sampled while measuring long-term evapotranspiration (ET). Leclerc and Foken [23] provide a comprehensive review of the development of the footprint tool and offer recommendations on how this tool can help interpret observations. A recent study by Chu et al. [25] emphasizes the importance of considering the spatial-temporal dynamics of flux footprints, particularly within heterogeneous landscapes, when using flux data in model-data benchmarking. They advised “the modelling and synthesis communities to be ‘footprint-aware’ when using large-scale flux datasets (e.g., FLUXNET2015, AmeriFlux BASE data products), especially in research such as point-scale simulations and spatially-explicit land surface models, remote-sensing-based models, and machine-learning upscaling studies”. To optimize the global carbon cycle quantification, it is also crucial to consider spatial matching between tower footprints and remote-sensing data when analyzing satellite-derived observations of terrestrial vegetation [26,27].
The Ru-Fyo tower in Southern Taiga, Tver region, Russia is part of the worldwide Fluxnet system. The tower was established in 1998 [28] in a homogeneous forest on flat ground, following basic recommendations for an ideal site. Homogeneity in this context means that the measured signal can be easily assigned to the surrounding forest types. However, some important factors have not been considered until now, such as the actual area detected by the sensor and how it changes seasonally and due to prevailing wind direction. It is also worth considering whether non-dominant tree species could contribute to the measured signal. Careful consideration of these issues can provide new insights into the interaction between the atmosphere and the forest at this site. This may require a revision of flux observation regarding primary sources of measured fluxes. Thus, the main goal of this study is to use modeling and experimental data analysis to determine the seasonal and directional changes in the flux footprint for the Ru-Fyo tower. Additionally, we aim to evaluate the limitations that footprint models may face in cost-effectively computing these changes.
The paper is structured as follows: In Section 2, we provide a brief introduction to the experimental site and discuss the methods for estimating footprints that are suitable for completing our tasks. We also cover the information needed to drive each method and the issue of how this data can be obtained from existing measurements. In Section 3, we analyze the aerodynamic parameters derived from measurements and discuss the results of the footprint modeling based on these parameters. We also consider the limitations of the footprint models used in our study. Finally, in Section 4, we summarize the findings of our study and outline future research perspectives.
2. Materials and Methods
2.1. Research Area, Site Measurement Design, and Data Selection
The research was conducted in the Central Forest State Natural Biosphere Reserve (CLGZ: http://www.clgz.ru (accessed on 1 July 2023)) at Fyodorovskoye, Tver region, Central European Russia, about 300 km WNW of Moscow (see Figure 1A). The experimental site is situated in a paludified shallow-peat spruce forest, which is a widespread forest type in the northern, central, and southern taiga, which represents the Sphagnum–Vaccinium myrtillus community on peaty podzolic gley soil with a peat depth of 30–50 cm. This forest type is located in the middle and lower parts of soft slopes and shallow depressions with very weak surface runoff and high ground-water levels [28]. According to forest inventory, the stand is 190 years old and comprises 85.5% Picea abies (L.) Karst and 14.5% Betula pubescens L. The ground flora is dominated by Vaccinium myrtillus L. (covering 34.5%), Vaccinium vitris-idea L. (2.9%), and a moss layer of Sphagnum girgensohnii Russ. (56.8%), Sphagnum angustifolium Russ. (13.0%), and Peurozium schreberrii (8.6%).
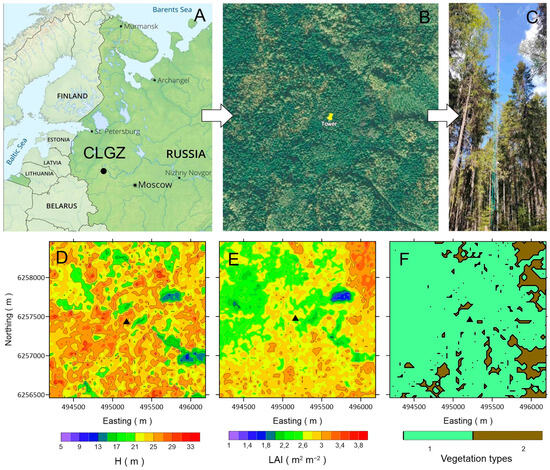
Figure 1.
(A) Geographical location, (B) satellite image, and (C) photo of the study area in forest stand in southern taiga, Tver region, Russia. Spatial distribution of (D) heights of trees, H, (E) LAI, and (F) main forest types—coniferous (1) and broadleaves (2)—around the tower indicated by black triangle symbol.
The measurement tower (56°27’43.70” N, 32°55’18.50” E, 265 m a.s.l.) (see Figure 1C) is situated in a shallow depression. The territory around the tower is rather heterogeneous. The surrounding area is diverse, with a dominant spruce stand that appears relatively uniform (as seen in Figure 1B) but is limited in size and has varying tree heights. In 2020, tree heights measured within the 60 m × 60 m space around the tower ranged from 3.4 m to 25.30 m, with an average height of 16.9 m and a standard deviation of 6.4 m. Birch and aspen forests, as well as windfalls of different ages, can be found within 200–1000 m from the tower. To better understand the forest, Figure 1D–F show the height distribution of forest trees, leaf area index (LAI), and species type around the stand interpolated from Landsat images, respectively. The uneven distribution of obstacles affects the airflow and transportation of compounds, ultimately impacting the footprint.
Continuous eddy covariance measurements of carbon dioxide, water vapor, heat, and momentum fluxes were measured at a height of 42 m since June 2014. The measurement system consisted of 3D ultrasonic anemometer WindMaster Pro (Gill Instruments, Lymington, UK) and CO2/H2O gas analyzer LI-7200A (LI-COR Inc., Lincoln, NE, USA). Since April 2015, carbon dioxide, water vapor concentrations, and air temperature were measured along a vertical profile at eight heights (0.5, 1, 2, 7, 14.5, 19.5, 29.5, and 42.0 m) using the AP200 integrated CO2 and H2O atmospheric profile system (Campbell Scientific, Logan, UT, USA). Also, at the same heights, wind velocity and wind direction were measured along a vertical profile using DS-2 sonic anemometers (Decagon Devices, Inc., Pullman, WA, USA).
Ecosystem fluxes were calculated for 30 min intervals using the Eddy Pro software v.7 (LI-COR Inc., USA) [29]. All corrections and statistical tests were implemented under this processing. Quality flags were assigned to the calculated CO2 fluxes using the 0–2 flag policy according to [30].
This study used observations from 2017 to 2019 for analysis. From this data set, only data that met the criteria of being in quality class 0 for CO2 flux were chosen.
2.2. Flux Footprint Estimation
Calculating the footprint in complex terrain can be challenging and often requires advanced tools such as Large Eddy Simulation (LES) or Reynolds-Averaged Navier–Stokes (RANS) equations-based models. These models can provide a three-dimensional distribution of airflow parameters over time [23]. To estimate the footprint for horizontally inhomogeneous conditions, backward LS models (with a pre-defined sensor location) [17] or models that are able to consecutively activate sources within the model domain [31] can also be used. However, the primary concern is the computing expense, particularly for LES-based simulations.
For the sake of simplicity, this study assumes that the upwind area has uniform properties, as measured by a single point that reflects the overall impact of all flow variations. Additionally, the study focuses on the crosswind-integrated flux footprint, which assumes that the sources are infinite in a crosswind direction. This particular case of footprint function introduced in Equation (1) has two dimensions (i.e., distance along the wind direction (x) and measuring height (zm)). Throughout this text, the term “footprint” will be used for brevity to refer to the entire above definition. As a result, calculating the footprint for sources located within the forest canopy can be done analytically, requiring only basic knowledge of aerodynamic parameters of canopy flow, such as displacement height d and aerodynamic roughness z0. Two analytical models developed by Schuepp et al. (SP) [10] and Kormann and Meixner (KM) [12] are used for this purpose. These models have varying assumptions for the wind speed profile and eddy diffusivity within the surface boundary layer.
A little more complicated but still user-friendly way to estimate the area of influence on the tower sensor is the Flux Footprint Prediction (FFP) tool [32] included in the basic package of the EddyPro software v.7 [29]. This model is semi-empirical and relies on solving stochastic backward trajectories of particles. It can calculate the footprint for a specific measurement point, rather than just an average over a sensor volume. No coordinate transformation is required, which means horizontal flow homogeneity is not necessary [33]. Data used in the simulation are wind velocity, wind direction, measurement height, surface roughness, friction velocity, Obukhov length (see Equation (3) below for definition), and zero-plane displacement. Initializing with measurement data such as friction velocity, stability parameters, and location, the tool provides the researcher with the following parameters: the fetch of maximal influence, fetches for cumulative fluxes of 70%, 80%, and 90%. The model is available as an online tool [34] and, in this case, can provide a three-dimensional footprint. If the displacement height and roughness length are not specified, EddyPro calculates them as 0.67 times the canopy height and 0.15 times the canopy height, respectively. The FFP footprint parameters used in this study were automatically estimated during data processing for a canopy height of 25 m (see Section 2.1).
An alternative method for calculating the footprint involves using the LS footprint model in forward mode. Though this approach is still complex, it is relatively inexpensive regarding computing time. The model operates under the assumption of a uniform underlying surface and uniform turbulence characteristics, similar to analytical models. The Lagrangian stochastic trajectory model uses drift terms in Langevin equations described by Kurbanmuradov and Sabelfeld [15] and requires vertical distribution of the turbulence parameters in the boundary layer. Past studies have highlighted the dependence of the footprint function on the vertical source location, including [16,35,36]. In this study, we assumed that the canopy sources are concentrated in one point, at the level of d + z0, to simplify and make comparisons among different footprint models. We also used LS techniques in forward mode to estimate the ground footprint, with sources near the soil surface at z = 0.1 m.
When using Lagrangian dispersion models, it is essential to pre-describe the turbulence. Vertical profiles of turbulence statistics measured on site provide more accurate footprint estimation, but this information was unavailable in our case. As such, we attempted to derive statistics, such as vertical profiles of mean wind , standard deviations of wind fluctuations , momentum flux , and the dissipation rate of turbulent kinetic energy ε inside and above the vegetation canopy, using the CFD approach. Previous studies have found that the RANS SCADIS model [37,38,39] effectively generates similar statistics, which help estimate the footprint by the LS model for forest sites. Our site experiences highly variable background airflow conditions, which limits our ability to fit simulated (using a one-dimensional model) and measured air flow properties for multiple scenarios. We were only able to successfully achieve results for one scenario—at noon during the summer season. To achieve accurate results for other scenarios, we require a complete three-dimensional modeling approach that includes a detailed description of vegetation distribution. Therefore, we opted not to employ the CFD approach and instead depended on empirical formulas for turbulence within a canopy (see Section 2.3 below). However, we utilize the scenario with the CFD approach to compare various footprint models (see Section 3.2.1 below).
2.3. Estimation of Aerodynamic Properties
The wind profile in the surface layer is approximated by (cf. [40])
where is the average wind speed at the measurement height , above the soil surface, is the displacement height, is the aerodynamic roughness, and are the Obukhov length and the friction velocity, is the von Karman constant (0.4), and is the integrated universal momentum function, in which a slight dependence on is neglected. The Obukhov length is defined as
where is the volumetric heat capacity at constant pressure (with = 1005 J kg−1 K−1), Tv is the virtual temperature, g is the acceleration due to gravity (9.81 m s−2), and is the buoyancy (virtual heat) flux.
When stability is considered, it is not easy to figure out how to estimate d and z0 from Equation (2). The literature offers recursive methods that enable the calculation of both parameters using a single measuring point (e.g., [41]). Graf et al. [42] examined those methods and concluded that it is essential to compare the results of several methods rather than rely on a single one. They recommended using an ensemble average or median of the results to achieve more reliable estimates, potentially after eliminating methods that produce outliers. In addition, a shear or roughness layer may form at the canopy top, which can disrupt the logarithmic wind speed solution [43]. Recently, Cintolesi et al. [44] discovered that in a forest with equivalent geometric features and measurement methods as the Ru-Fyo site, the roughness layer extended to the highest point of measurement. As a result, a complex analytical solution was necessary to estimate d and z0.
Analyzing three-year period data, we discovered that half-hour measurements with < 20 were less than 10% at noon, less than 5% at night, and less than 7% overall from all measurements. Additionally, cases with < 10 accounted for less than 3% of all analyzed data. As the percentage of changes in wind profile due to stability was minimal, we decided to exclude the impact of atmospheric stability on the forest’s aerodynamic parameters in this study for simplicity. This simplification is acceptable since the footprint estimation relies on monthly or seasonal averaged aerodynamic parameters. The averaging procedure also helped us to avoid considering the effect of the roughness sublayer on those parameters.
To estimate aerodynamic parameters of vegetation d and z0, we apply wind speed measurement and from levels = 29.5 m and = 42.0 m, respectively, and dynamical velocity from 42 m. Assuming the log-law profiles above the forest and the fact that these two levels are above the forest top (see Section 2.1), d is estimated as
and as
With these two parameters and the known value of , it is possible to estimate the footprint using analytical methods.
The LS method requests additional information about turbulence distribution. For description flow characteristics above trees, we apply the logarithmic profile for wind speed and assume a uniform distribution of momentum flux, as well as standard deviations of wind speed in the horizontal and vertical direction. Inside the canopy, we apply the parameterization used by Rannik et al. [16]. Initially, we start by defining the mean upwind height of vegetation, h, as
which is based on the assumption that for dense forest (LAI > 2), the relation is valid, with a constant estimated by different authors from 0.36 to 0.4 [45,46,47]. We took an average value of 0.38. As we see below (Section 3.1), the forest height defined by Equation (6) is not constant and varies across different months and seasons. Furthermore, it is also affected by wind directions. It is important to note that in the context of Equation (6), h does not represent the actual height of the forest but rather the inflection point of the vertical distribution of wind speed at the forest–atmosphere interface, where the logarithmic wind profile above the canopy and the exponential wind profile within the canopy connect. A concept first suggested by Raupach et al. [43], and later Thomas and Foken [48], referred to this height as aerodynamic canopy height and confirmed it to be in good agreement with a visual estimate for the canopy height. Further validation of this concept has been performed in [49].
After that, the expression for the estimation of wind speed above h follows from Equation (2) while neglecting the stability effect and the roughness sublayer effect:
The exponential profile for wind speed was assumed inside the canopy as
where is the wind speed at the tree-top height, z = h, and α is the attenuation factor varied for different types of vegetation from 2 to 4 [50,51]. The authors of [16] used α = 2 in their simulation. Here, α in each case is estimated in such a way as to provide agreement with the wind speed calculated by Equation (8), with the wind speed observed at the height of 7 m, . Thus, it is
Following [16], and are defined from the friction velocity through correspondent coefficients = 2.5 and = 1.3 above the forest canopy as
The momentum flux is defined as
Inside the canopy, those parameters are described by the following expressions:
and
with = 0.25. Following the results of the model comparison described below (see Section 3.2), we modified the expression for inside a canopy from linear attenuation, as in [16], to power one as
The analytical and empirical expressions (7)–(14) were used in the LS model based on Kurbanmuradov and Sabelfeld’s [15] description of drift terms in Langavian equations (see Appendix A). In the following text, this model will be referred to as the LS analytical model. The LS model, which is driven by flow statistics obtained from the RANS SCADIS model, will be referred to as LS SCADIS. The reader is invited to refer to [37] for details on how the SCADIS model outputs drive the LS simulation.
3. Results and Discussion
3.1. Measurements
Figure 2 shows monthly average values of dynamical velocity over the forest and monthly average values of aerodynamic parameters d and z0. The behavior of (Figure 2A) through three considered years is quite similar, with relatively small differences in absolute values associated with different weather conditions in different seasons. The behavior of dynamical velocity values has a clear day course, with the highest values in the afternoon and the lowest ones at night. In general, the dynamical, or friction, velocity depends on the atmospheric stability and background wind speed, and, as such, describes general airflow properties above the forest surrounding the tower. Concerning footprint, increasing usually results in gaining more information by a sensor from a shorter upwind distance. A decrease in results in the opposite.
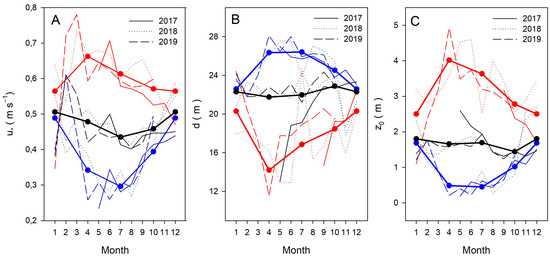
Figure 2.
Seasonal plot of monthly average (thin lines) values of (A) dynamical velocity , (B) displacement height d, and (C) roughness length for nighttime 0.00–4.00 a.m. (blue lines), noontime 0.00–4.00 pm (red lines), and a whole day (black lines) at the measuring tower for different years. Solid thick lines with circles are seasonal average values.
The forest around the tower is not homogeneous (see Figure 1). Apart from the dynamical effect expressed by , the footprint will be affected by canopy aerodynamic properties described by displacement height and roughness. In Figure 2B, it is clear that displacement values are generally highest in the afternoon and lowest at night, which is expected. However, d values significantly deviate from this trend in some years and months. Figure 2C shows that roughness values follow the opposite trend to d values, as expected, with corresponding deviations.
To estimate the seasonal variation in footprint, we calculate the average values of dynamic velocity and aerodynamic parameters over three years. Averaged , d, and z0 data plotted in Figure 2A–C, respectively, show that parameters, calculated using whole-day observations, have small variability throughout the year, with mean values of = 0.45 ms−1, d = 22 m, and z0 = 1.7 m. Such a result was expected, because the forest is mainly populated by mature coniferous trees. The data suggest that the mean aerodynamically active height of the forest is approximately 27 m (calculated using Equation (6)), which is slightly taller than the maximum height of trees near the tower (see Section 2.1). There was a noticeable difference in parameter values between daytime and nighttime observations, indicating daily changes in stability. The amplitude of parameter values was highest in spring and summer, whereas in winter, it tended to be lowest.
3.2. Footprints
3.2.1. Intermodel Comparison Test
By comparing the outcomes of different models initialized by the same turbulence conditions, we can gain valuable insights into the assumptions made by these models and their influence on the estimation of footprints. This type of comparison can also be used to validate the models [38,52]. Conducting an intermodel comparison is particularly beneficial when field data on source contributions are scarce, making it challenging to justify the methods used directly. The issue of verifying footprint models has been extensively discussed in [23,53]
It is widely reported in the scientific literature that for the same atmospheric and surface conditions, there are noticeable differences in the behavior of analytical footprint models [32,52,54,55]. These differences are caused by underlying assumptions regarding the description of surface-layer turbulence. Unfortunately, the only way to evaluate analytical models is by directly comparing their footprint predictions with observations. Recently, Kumari et al. [56] conducted artificial tracer (CO2) experiments in unstable conditions over an open field to evaluate three analytical footprint models (SP, KM, and Hsieh et al. (HS) [57]) and also the FFP model under variable source-receptor settings. The results indicate that the KM model is in good agreement with the EC measurements under ideal conditions compared to other analytical models and the FFP model. The KM model captured both the footprintmaximum and its location. Though results were derived for open field conditions, we can assume that the KM model will demonstrate a better performance than other models also for the forest surface, and it can be considered as a benchmark for comparison of the models used here.
To make intermodal comparison possible, we must ensure that the flow statistics within the forest canopy agree with those measured above the forest. As mentioned above, CFD models can provide such data when information about forest structure is known. This information is necessary to set up drag forces inside the forest canopy using the CFD approach. However, we could not access detailed information about the leaf area density (LAD) distribution. As a result, we could only obtain reasonable simulation results for the summer afternoon condition using a fitted LAD distribution, as shown in Figure 3. Figure 3 demonstrates that the wind profiles obtained via observation, CFD simulation, and log-law relationship are consistent with each other. Additionally, it displays the averaged wind profiles during summer nights, which were impossible to generate using the SCADIS model with the LAD profile applied in the noon simulation or with any other assumptions. This is due to the wind profile above the forest at the measurement point being influenced by the upwind tree composition. This complex function varies based on wind direction and atmospheric stability. Furthermore, the one-dimensional model does not consider the vertical air movements resulting from this tree composition.
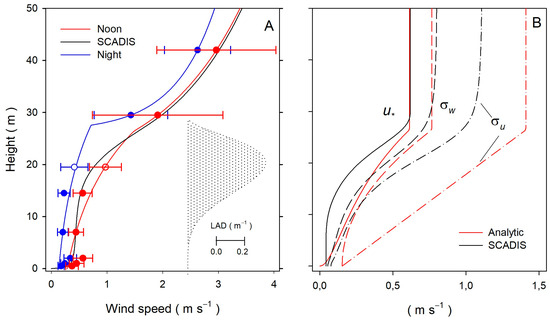
Figure 3.
(A) Summer wind speed profiles derived using analytical expressions (lines) and based on three-years observations (filled symbols) for noon (red) and nighttime (blue). The black line is the wind speed profile simulated by SCADIS applying the LAD profiles given in dots. Unfilled symbols are for the 2017 year, for which only wind speed measurements at the height of 19.5 were available. Whiskers are for standard deviation. (B) Flow statistics used in the LS method for footprint estimation based on SCADIS simulations (black lines) and analytical expression (red lines) for noon time.
Figure 3 shows that the wind profile used in the LS analytical model derived by Equations (8) and (9) provides a good fit with observation. Thus, an intermodel comparison has been made for summer noon.
Studies [38,58] have demonstrated that using observed turbulence statistics to accurately predict footprints using LS methods is essential. Without such statistics, the accuracy of LS models can be affected by the choice of empirical relations used for high-order moment data within the forest canopy. A comparison of the footprint predictions made by the LS analytical model, which is based on original turbulence parameterizations of [19], and the LS SCADIS model, which is based on SCADIS model outputs, shows that the canopy footprints are almost identical in both cases. However, the ground footprints are different. The ground footprint derived by the LS analytical model has the region of maximum signal contribution much closer to the tower than the LS SCADIS model estimated (not shown). This result is due to the turbulence description in both models being similar above the level d + z0 but different below this level.
In a previous study conducted by Sogachev et al. [38], the Lagrangian stochastic trajectory model by Kurbanmuradov and Sabelfeld [18] was utilized to predict footprints for both canopy and ground sources. The results were similar to those obtained using the direct method of footprint estimation based on RANS output models, as described in [33]. This gives us confidence that the ground footprint estimated by LS SCADIS is more realistic. Therefore, some modifications to the input information for the LS Analytical model are necessary. As previously mentioned, we have modified the original expression for inside the canopy (see Equation (14)). The turbulence parameters used in both models are shown in Figure 3B. Although there is a difference between the two models, several sensitivity studies (c.f. [58,59]) have shown that in conditions of low turbulence within the canopy, the wind speed profile for horizontal transport and the profile for vertical transportation are the essential parameters for footprint prediction.
The modification (Equation (14)) improves the situation. It enables us to obtain similar footprint shapes and cumulative fluxes between the two LS models used (as shown in Figure 4). The figure shows that the performance of the KM model in canopy footprint prediction is comparable to that of the LS analytical model. It is also clear that the SP model provides a significantly different footprint function for canopy-located sources.
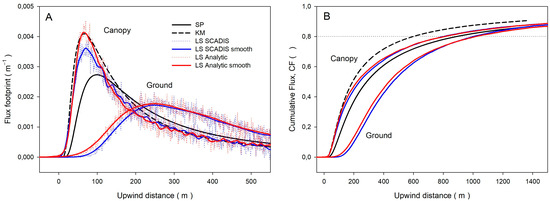
Figure 4.
(A) Flux footprints and (B) cumulative fluxes (CF) for canopy- and ground-located sources for average flow conditions during afternoon of summer season. Footprints estimated by analytical methods and by LS model driven by flow statistics based on SCADIS model simulation (LS SCADIS) and provided from analytical expressions (LS analytic) (see Figure 3 and text for details). Smoothed lines for LS simulations are derived from simulated data using the Epanechnikov kernel function (see Appendix B). The dotted line in (B) is for the threshold of CF80 (see text for details).
The LS method does not provide a clear upwind position for the maximum footprint value due to estimation procedures. Different simulations will result in fluctuated functions with varying local maximums and minimums but with similar shapes. Increasing the number of particles released can result in a smoother function, but it also increases computational costs. To compare the results of the LS model with analytical models and simplify further analysis, we use Epanechnikov kernel functions to smooth the LS footprints. Appendix B provides more details. Figure 3A displays the smoothed footprint functions, and Figure 3B shows smoothed cumulative flux functions that are almost indistinguishable from unsmoothed ones.
3.2.2. Seasonal Dynamics of Footprints
The simulated footprints have a different shape depending on the flow conditions used for their estimation. Mathematically, the surface area of influence on the entire flux goes to infinity, and thus, one must always define the % level for the source [60]. Often, 50, 75, or 90% source regions contributing to a point flux measurement are considered. For further analysis, we extracted two fetches from footprints estimated by different methods: (1) the fetch with the maximal influence of sources on the measuring signal (Xmax) and (2) the fetch whose contribution to the measured signal or cumulative flux is 80% (CF80). The threshold of 80% is chosen for practical reasons to reduce the distance when particles are considered leaving the domain in LS and, as such, to speed up the calculation. Figure 5 shows the seasonal distribution of these two parameters, Xmax and CF80, for different upwind sectors.
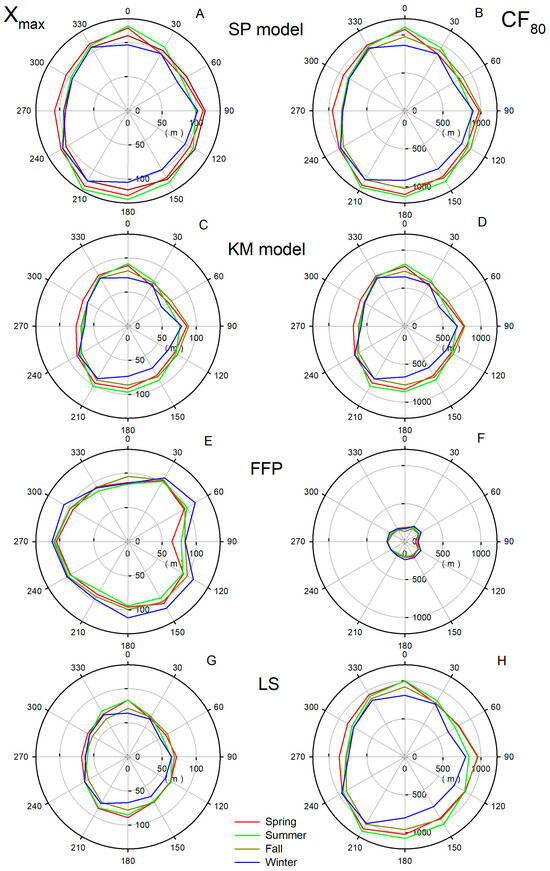
Figure 5.
Directional plot of seasonal average fetch of maximal influence (Xmax) (A,C,E,G) and fetch of 80% flux contribution (CF80) (B,D,F,H) of canopy-located sources on measuring tower derived by different methods. The scale of Xmax to CF80 is 1:9.
Based on the data in Figure 5, it can be seen that there is a clear correlation between Xmax and CF80 for both the analytical models and the FFP. The distribution of Xmax and CF80 is similar, and one parameter can be estimated from the other using a specific multiplicator. When using analytical models to estimate CF80 from Xmax, a factor of approximately 9 should be used, whereas FFP requires a factor of about 2.5. This is expected, as all flow characteristics, when scaled on , are the same. However, when it comes to LS simulations, the factors are direction-dependent and range from 10 to 15. This is because above the canopy height, the flow characteristics scaled on are equivalent to those in analytical models and follow the log-law relationship. In contrast, inside the canopy, they are unique in each direction.
Figure 6 shows the footprint estimated by the LS method for canopy and ground sources. A simple empirical expression can be used to calculate the total day footprint, combining the ground and canopy footprints with the prescribed source strengths of different signs. However, negative values for the footprint can occur in certain situations, making the evaluation of Xmax and CF80 confusing or even impossible. For more information, the reader can refer to [31,35]. To simplify things, we assume that the canopy photosynthesis is the primary signal contribution in the afternoon, which makes the canopy footprint a noon footprint of the tower. Similarly, we can assume that the ground footprint describes the night footprint of the tower sensor, considering steam and needle respiration to be minor.
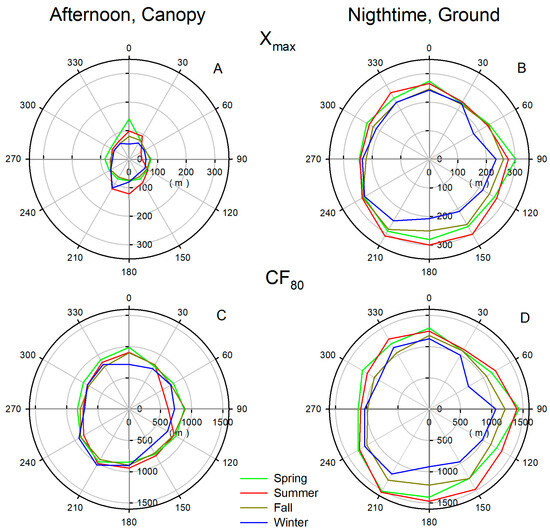
Figure 6.
Directional plot of seasonal average fetch of maximal influence (Xmax) (upper plot, (A,B)) and fetch of 80% flux contribution (CF80) (lower plot, (C,D)) of canopy-located sources (left, (A,C)) and ground-located sources (right, (B,D)) derived by LS method.
Based on Figure 6A,B, it appears that the location area with the highest signal contribution during the day is approximately three to four times closer to the tower than the peak area of ground sources. This ratio can vary depending on the direction of the prevailing wind. It is important to keep this in mind when interpreting the signal. Some outliers in the measured signal may be explained by applying footprint analysis. The differences in CF80 for different sources are insignificant and vary by approximately one-and-a-half to two times depending on the direction. This is because the air parcel with information coming from the canopy source is transported not only in well-mixed and windy conditions in the upper part of the forest but also through the entire canopy, as is the case with the air parcel released on the ground surface.
Figure 7 summarizes the footprint behavior at the tower in different seasons. The daily canopy footprint peaks estimated by the SP and FFP methods are similar and occur approximately 100 m upwind from the tower. However, the KM and LS methods estimate the peak location to be closer to the tower, with an average distance of 70–80 m. The SP and KM models estimate Xmax to be further from the tower at night and closer to the tower during the day, although no straightforward stability effect was taken into account. The observed wind speed profiles and dynamical velocity scale exhibit the turbulence behavior of the day. The FFP method estimates Xmax differently, which may be due to the method’s sensitivity to stability parameters involved in the footprint estimation. This sensitivity is more direct, because the FFP method uses a prescribed d and z0.
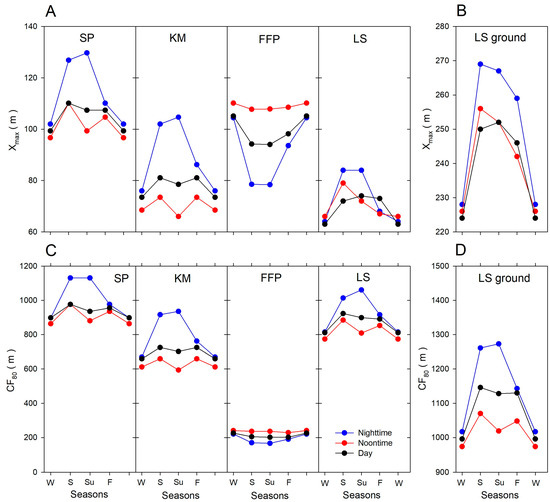
Figure 7.
Seasonal plot of the distance of maximal influence (Xmax) (A,B) and the distance of cumulative flux of 80% (CF80) (C,D) at measuring tower derived by different models for canopy (A,C)- and ground (B,D)-located sources for different time moments. Note that plots for ground-located sources (B,D) have different scales for Xmax and CF80. Abbreviations W, S, Su, and F stand for winter, spring, summer, and fall, respectively.
The LS method does not show a clear correlation between Xmax and time of day. In spring, Xmax is higher at noon and night than during average daytime conditions, whereas the opposite is true in autumn. Xmax behaves similarly to that derived by the SP and KM models during the summer months. This is because, as previously mentioned, the LS method relies on flow statistics within the canopy, cf. wind speed at a height of 7 m, and even for canopy sources, flow parameters are not the same as in the analytical models. The behavior of these parameters can be different in different seasons and during other times of the day.
All models show minimal differences in Xmax during winter for noon, night, and whole-day conditions. For ground sources, the daily and noon average Xmax estimated by the LS method have similar values, with slightly higher Xmax at night. The difference in Xmax for ground sources during winter is minimal for canopy sources. Xmax for ground sources reaches its minimum values during the winter season.
As observed with Xmax, the CF80 seasonal patterns are similar for both the analytical and the FFP models. The SP and KM models do not show significant seasonal variation in their estimated CF80 values. CF80 is located further from the tower at night and closer during the day. The FFP method estimates CF80 to be four times shorter than other methods, with minimal daily and no explicit seasonal dependency. Surprisingly, the LS method shows CF80 patterns similar to analytical methods with direct time-of-day dependence. CF80 estimated by the LS method for ground sources also displays seasonal and daily dependency, with maximum values in summer and at night.
In general, the LS method produces Xmax estimates for the canopy source that are similar to those generated by the KM method and CF80 values that are close to those produced by the SP method. Therefore, for the tower under investigation, the LS method can be replaced by the KM and SP methods, which are less time-consuming. However, the LS method is no substitute for estimating ground footprint. The results of analytical methods can be used to preliminarily determine Xmax values for ground sources. As a result, the Xmax for a ground source is approximately two-and-a-half to three times further upwind than the canopy source estimated by analytical methods. Similarly, the same can be applied for CF80 using a factor of 1.1 for SP- and 1.3 for KM-estimated values.
In our previous discussion, we utilized LS simulation sources within the canopy at a single level for comparison purposes. However, the distribution of these sources depends not only on the vertical density of leaves but also on factors such as solar radiation within the canopy and the aerodynamic resistance of the leaves. Accounting for these factors could result in a different daily and seasonal pattern of Xmax and CF80 derived by the LS method [35]. Additionally, we have simplified the analysis by not considering the turning of wind within the canopy, which causes the transport of air parcels to have a different direction at different levels. Therefore, carefully considering these factors may lead to a directional distribution of Xmax and CF80 that differs significantly from what is presented in Figure 6B,D and Figure 7B,D. When analyzing the data, it is essential to consider these factors by utilizing simple analytical or LS models for homogeneous conditions.
4. Conclusions
In this study, our focus was not to connect estimated footprints with measured environmental fluxes. Instead, we aimed to identify the most significant factors that affect footprints. We began by evaluating a footprint estimation method that, though not new, is not commonly used in environmental flux research. This method is based on d and z0 and can be utilized for any measuring tower with multilevel observations. Using this technique, one can eliminate any subjective guesswork regarding the mean aerodynamic height of the forest surrounding a particular tower.
As was expected, the footprint function for the measuring tower located in the southern taiga has weak seasonal dynamics due to the predominance of coniferous trees in the area. Nevertheless, during the summer, all methods of footprint estimation, except for FFP, revealed that the maximal contribution into the signal shifted upwind of the tower by approximately 10%–15% compared to winter. It is essential to note that small areas of broad-leaved forest at remote fetches can alter the footprints in specific directions, but this requires further investigation. Small patches of low or less dense vegetation can also affect the shape of the footprint function for sectors where airflow passes over them. Therefore, directional differences for Xmax and CF80 exist even when looking at seasonal average data.
The footprint is significantly impacted by atmospheric stability, which is the critical factor. Although we did not explicitly include this factor in our analysis, it is apparent that the aerodynamic properties, which follow the general course of the turbulent regime and the thermal state of the surface boundary layer, can lead to diverse footprints throughout the day.
Overall, our research sheds light on the typical behavior of the source area for the measuring tower in question. This knowledge can aid in accurately interpreting the recorded vertical fluxes.
We plan to apply the method outlined in this study to analyze a challenging site. A new measuring mast was recently installed in a forest clearcut in the same area of the southern taiga region. We believe that additional observations will further validate our method and enable us to accurately interpret the source of environmental fluxes in these intricate surroundings.
Author Contributions
Conceptualization and methodology, A.S. and A.V.; experimental data, A.V.; software, A.S.; writing—review and editing, A.S. and A.V. All authors have read and agreed to the published version of the manuscript.
Funding
The experimental activity at Fyodorovskoye site, in CLGZ, Tver region, Russia conducted by A. Varlagin was supported by the Russian Science Foundation (grant no. 21-14-00209). The modeling study conducted by A. Sogachev was supported by a state assignment of the Ministry of Science and High Education of the Russian Federation FFER-2022-0002 (theme no. 1022031600002-1-1.6.19).
Data Availability Statement
The experimental and modeled data used in the study can be requested from the authors at andreysogachev@sev-in.ru and varlagin@sevin.ru.
Acknowledgments
We appreciate the assistance of Robert Sandlerskiy from HSE University and Ivan Shironya from CLGZ in collecting data on forest structure.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Forward LS Footprint Model
The Lagrangian stochastic (LS) models describe the diffusion of a scalar by means of a stochastic differential equation, a generalized Langevin equation,
where and denote trajectory coordinates and velocity as a function of time , is the Kolmogorov constant, ε is the mean dissipation rate of turbulent kinetic energy (TKE), and describes the three-dimensional Wiener process [22].
This equation determines the evolution of a Lagrangian trajectory in space and time by combining the evolution of the trajectory as a sum of deterministic drift a and random terms. The drift terms are to be specified for each LS model constructed for a specific flow regime [61]. In this study, the Lagrangian stochastic trajectory model of Kurbanmuradov and Sabelfeld [15], which satisfies the well-mixed condition, was used.
The conventional approach to using a Lagrangian model for footprint calculation is to release particles at the surface point source and track their trajectories downwind of this source toward the measurement location forward in time (e.g., [13,16]). Particle trajectories and particle vertical velocities are sampled at the measurement height. In the case of horizontally homogeneous and stationary turbulence, the mean flux at the measurement location due to a sustained source located at height can be described as
where is the number of released particles, and is the number of intersections of particle trajectory with the measurement height ; , , and denote the vertical velocity and the coordinates of particle at the intersection moment, respectively. The above equation applies identically also to elevated sources located at an arbitrary height. The flux footprint can be determined as follows:
Similarly, the mean concentration at the measurement location and the concentration footprint can be determined (for detail, see [22,23]). For the estimation of the footprint function, trajectories were simulated.
Appendix B. Kernel Function
The information about kernel function is given here for the reader’s quick inquiry and is based on Wikipedia sources.
In statistics, kernel density estimation is the application of kernel smoothing for probability density estimation, i.e., a non-parametric method to estimate the probability density function f of a random variable distributed on fixed locations , based on kernels as weights. We are interested in estimating the shape of this unknown ƒ at any given point x. Its kernel density estimator is
where K is the kernel—a non-negative function—and > 0 is a smoothing parameter called the bandwidth. Epanechnikov kernel functions were used:
with a bandwidth of 10 m for footprints of canopy-located sources and of 50 m for footprints of ground-located sources.
References
- Malhi, Y.; Baldocchi, D.D.; Jarvis, P.G. The Carbon Balance of Tropical, Temperate and Boreal Forests. Plant Cell Environ. 1999, 22, 715–740. [Google Scholar] [CrossRef]
- Aubinet, M.; Grelle, A.; Ibrom, A.; Rannik, Ü.; Moncrieff, J.; Foken, T.; Kowalski, A.S.; Martin, P.H.; Berbigier, P.; Bernhofer, C.; et al. Estimates of the Annual Net Carbon and Water Exchange of Forests: The EUROFLUX Methodology. Adv. Ecol. Res. 1999, 30, 113–175. [Google Scholar] [CrossRef]
- Wofsy, S.C.; Goulden, M.L.; Munger, J.W.; Fan, S.-M.; Bakwin, P.S.; Daube, B.C.; Bassow, S.L.; Bazzaz, F.A. Net Exchange of CO 2 in a Mid-Latitude Forest. Science 1993, 260, 1314–1317. [Google Scholar] [CrossRef] [PubMed]
- Baldocchi, D.; Valentini, R.; Running, S.; Oechel, W.; Dahlman, R. Strategies for Measuring and Modelling Carbon Dioxide and Water Vapour Fluxes over Terrestrial Ecosystems. Glob. Chang. Biol. 1996, 2, 159–168. [Google Scholar] [CrossRef]
- Running, S.W.; Baldocchi, D.D.; Turner, D.P.; Gower, S.T.; Bakwin, P.S.; Hibbard, K.A. A Global Terrestrial Monitoring Network Integrating Tower Fluxes, Flask Sampling, Ecosystem Modeling and EOS Satellite Data. Remote Sens. Environ. 1999, 70, 108–127. [Google Scholar] [CrossRef]
- Lindroth, A.; Grelle, A.; Morén, A.S. Long-Term Measurements of Boreal Forest Carbon Balance Reveal Large Temperature Sensitivity. Glob. Chang. Biol. 1998, 4, 443–450. [Google Scholar] [CrossRef]
- Valentini, R.; Matteucci, G.; Dolman, A.J.; Schulze, E.-D.; Rebmann, C.; Moors, E.J.; Granier, A.; Gross, P.; Jensen, N.O.; Pilegaard, K.; et al. Respiration as the Main Determinant of Carbon Balance in European Forests. Nature 2000, 404, 861–865. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Hincks, B.B.; Meyers, T.P. Measuring Biosphere-Atmosphere Exchanges of Biologically Related Gases with Micrometeorological Methods. Ecology 1988, 69, 1331–1340. Available online: http://www.jstor.org/stable/1941631refer (accessed on 22 September 2023). [CrossRef]
- Wilson, J.D.; Swaters, G.E. The Source Area Influencing a Measurement in the Planetary Boundary-Layer—The Footprint and the Distribution of Contact Distance. Bound.-Layer Meteorol. 1991, 55, 25–46. [Google Scholar] [CrossRef]
- Schuepp, P.H.; Leclerc, M.Y.; MacPherson, J.I.; Desjardins, R.L. Footprint Prediction of Scalar Fluxes from Analytical Solutions of the Diffusion Equation. Bound.-Layer Meteorol. 1990, 50, 355–373. [Google Scholar] [CrossRef]
- Horst, T.W.; Weil, J.C. Footprint Estimation for Scalar Flux Measurements in the Atmospheric Surface Layer. Bound.-Layer Meteorol. 1992, 59, 279–296. [Google Scholar] [CrossRef]
- Kormann, R.; Meixner, F.X. An Analytical Footprint Model for Non-Neutral Stratification. Bound.-Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]
- Leclerc, M.Y.; Thurtell, G.W. Footprint Prediction of Scalar Fluxes Using a Markovian Analysis. Bound.-Layer Meteorol. 1990, 52, 247–258. [Google Scholar] [CrossRef]
- Baldocchi, D. Flux Footprints Within and Over Forest Canopies. Bound.-Layer Meteorol. 1997, 85, 273–292. [Google Scholar] [CrossRef]
- Kurbanmuradov, O.; Sabelfeld, K. Lagrangian Stochastic Models For Turbulent Dispersion In The Atmospheric Boundary Layer. Bound.-Layer Meteorol. 2000, 97, 191–218. [Google Scholar] [CrossRef]
- Rannik, Ü.; Aubinet, M.; Kurbanmuradov, O.; Sabelfeld, K.K.; Markkanen, T.; Vesala, T. Footprint Analysis For Measurements Over A Heterogeneous Forest. Bound.-Layer Meteorol. 2000, 97, 137–166. [Google Scholar] [CrossRef]
- Flesch, T.K. The Footprint for Flux Measurements, from Backward Lagrangian Stochastic Models. Bound.-Layer Meteorol. 1996, 78, 399–404. [Google Scholar] [CrossRef]
- Leclerc, M.Y.; Shen, S.; Lamb, B. Observations and Large-Eddy Simulation Modeling of Footprints in the Lower Convective Boundary Layer. J. Geophys. Res. Atmos. 1997, 102, 9323–9334. [Google Scholar] [CrossRef]
- Sogachev, A.; Menzhulin, G.V.G.V.; Heimann, M.; Lloyd, J. A Simple Three-Dimensional Canopy—Planetary Boundary Layer Simulation Model for Scalar Concentrations and Fluxes. Tellus Ser. B Chem. Phys. Meteorol. 2002, 54, 784–819. [Google Scholar] [CrossRef]
- Schmid, H.P. Footprint Modeling for Vegetation Atmosphere Exchange Studies: A Review and Perspective. Agric. For. Meteorol. 2002, 113, 159–183. [Google Scholar] [CrossRef]
- Vesala, T.; Kljun, N.; Rannik, U.; Rinne, J.; Sogachev, A.; Markkanen, T.; Sabelfeld, K.; Foken, T.; Leclerc, M.Y.Y.; Rannik, Ü.; et al. Flux and Concentration Footprint Modelling: State of the Art. Environ. Pollut. 2008, 152, 653–666. [Google Scholar] [CrossRef] [PubMed]
- Rannik, U.; Sogachev, A.; Foken, T.; Göckede, M.; Kljun, N.; Leclerc, M.Y.; Vesala, T. Footprint Analysis. In Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Aubinet, M., Ed.; Springer: Dordrecht, The Netherlands, 2012; pp. 211–261. ISBN 9789400723511. [Google Scholar]
- Leclerc, M.Y.; Foken, T. Footprints in Micrometeorology and Ecology; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-54544-3. [Google Scholar]
- Amiro, B.D. Footprint Climatologies for Evapotranspiration in a Boreal Catchment. Agric. For. Meteorol. 1998, 90, 195–201. [Google Scholar] [CrossRef]
- Chu, H.; Luo, X.; Ouyang, Z.; Chan, W.S.; Dengel, S.; Biraud, S.C.; Torn, M.S.; Metzger, S.; Kumar, J.; Arain, M.A.; et al. Representativeness of Eddy-Covariance Flux Footprints for Areas Surrounding AmeriFlux Sites. Agric. For. Meteorol. 2021, 301–302, 108350. [Google Scholar] [CrossRef]
- Kong, J.; Ryu, Y.; Liu, J.; Dechant, B.; Rey-Sanchez, C.; Shortt, R.; Szutu, D.; Verfaillie, J.; Houborg, R.; Baldocchi, D.D. Matching High Resolution Satellite Data and Flux Tower Footprints Improves Their Agreement in Photosynthesis Estimates. Agric. For. Meteorol. 2022, 316, 108878. [Google Scholar] [CrossRef]
- Huang, X.; Lin, S.; Li, X.; Ma, M.; Wu, C.; Yuan, W. How Well Can Matching High Spatial Resolution Landsat Data with Flux Tower Footprints Improve Estimates of Vegetation Gross Primary Production. Remote Sens. 2022, 14, 6062. [Google Scholar] [CrossRef]
- Milyukova, I.M.; Kolle, O.; Varlagin, A.V.; Vygodskaya, N.N.; Schulze, E.-D.; Lloyd, J. Carbon Balance of a Southern Taiga Spruce Stand in European Russia. Tellus B Chem. Phys. Meteorol. 2002, 54, 429. [Google Scholar] [CrossRef][Green Version]
- Eddy Covariance Processing Software, Version 7.0.8. [Software]; 4. LI-COR Biosciences. 2021. Available online: www.licor.com/EddyPro (accessed on 1 July 2023).
- Mauder, M.; Foken, T. Impact of Post-Field Data Processing on Eddy Covariance Flux Estimates and Energy Balance Closure. Meteorol. Z. 2006, 15, 597–609. [Google Scholar] [CrossRef]
- Sogachev, A.; Lloyd, J. Using a One-and-a-Half Order Closure Model of the Atmospheric Boundary Layer for Surface Flux Footprint Estimation. Bound.-Layer Meteorol. 2004, 112, 467–502. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A Simple Two-Dimensional Parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Kljun, N.; Rotach, M.W.; Schmid, H.P. A Three-Dimensional Backward Lagrangian Footprint Model for a Wide Range of Boundary-Layer Stratifications. Bound.-Layer Meteorol. 2002, 103, 205–226. [Google Scholar] [CrossRef]
- Kljun, N. Online Tool. A Simple Two-Dimensional Parameterisation for Flux Footprint Prediction (FFP). Available online: https://footprint.kljun.net/ (accessed on 1 July 2023).
- Markkanen, T.; Rannik, Ü.; Marcolla, B.; Cescatti, A.; Vesala, T. Footprints and Fetches for Fluxes over Forest Canopies with Varying Structure and Density. Bound.-Layer Meteorol. 2003, 106, 437–459. [Google Scholar] [CrossRef]
- Prabha, T.V.; Leclerc, M.Y.; Karipot, A.; Hollinger, D.Y.; Mursch-Radlgruber, E. Influence of Nocturnal Low-Level Jets on Eddy-Covariance Fluxes over a Tall Forest Canopy. Bound.-Layer Meteorol. 2008, 126, 219–236. [Google Scholar] [CrossRef]
- Sogachev, A.; Leclerc, M.Y.Y.; Karipot, A.; Zhang, G.; Vesala, T. Effect of Clearcuts on Footprints and Flux Measurements above a Forest Canopy. Agric. For. Meteorol. 2005, 133, 182–196. [Google Scholar] [CrossRef]
- Sogachev, A.; Leclerc, M.Y. On Concentration Footprints for a Tall Tower in the Presence of a Nocturnal Low-Level Jet. Agric. For. Meteorol. 2011, 151, 755–764. [Google Scholar] [CrossRef]
- Sogachev, A.; Dellwik, E. Flux Footprints for a Tall Tower in a Land–Water Mosaic Area: A Case Study of the Area around the Risø Tower. Agric. For. Meteorol. 2017, 237–238, 326–339. [Google Scholar] [CrossRef]
- Foken, T. Micrometeorology; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-642-25439-0. [Google Scholar]
- Martano, P. Estimation of Surface Roughness Length and Displacement Height from Single-Level Sonic Anemometer Data. J. Appl. Meteorol. 2000, 39, 708–715. [Google Scholar] [CrossRef]
- Graf, A.; van de Boer, A.; Moene, A.; Vereecken, H. Intercomparison of Methods for the Simultaneous Estimation of Zero-Plane Displacement and Aerodynamic Roughness Length from Single-Level Eddy-Covariance Data. Bound.-Layer Meteorol. 2014, 151, 373–387. [Google Scholar] [CrossRef]
- Raupach, M.R.; Finnigan, J.J.; Brunei, Y. Coherent Eddies and Turbulence in Vegetation Canopies: The Mixing-Layer Analogy. Bound.-Layer Meteorol. 1996, 78, 351–382. [Google Scholar] [CrossRef]
- Cintolesi, C.; Barbano, F.; Trudu, P.L.; Finco, A.; Gerosa, G.; Di Sabatino, S. Characterisation of Flow Dynamics within and around an Isolated Forest, through Measurements and Numerical Simulations. Agric. For. Meteorol. 2023, 339, 109557. [Google Scholar] [CrossRef]
- Thom, A.S. Momentum, Mass and Heat Exchange of Vegetation. Q. J. R. Meteorol. Soc. 1972, 98, 124–134. [Google Scholar] [CrossRef]
- Kondo, J. Relationship Between the Roughness Coefficient and Other Aerodynamic Parameters. J. Meteorol. Soc. Jpn. Ser. II 1971, 49, 121–124. [Google Scholar] [CrossRef]
- Maki, T. Interrelationships between Zero-Plane Displacement, Aerodynamic Roughness Length and Plant Canopy Height. J. Agric. Meteorol. 1975, 31, 7–15. [Google Scholar] [CrossRef]
- Thomas, C.; Foken, T. Flux Contribution of Coherent Structures and Its Implications for the Exchange of Energy and Matter in a Tall Spruce Canopy. Bound.-Layer Meteorol. 2007, 123, 317–337. [Google Scholar] [CrossRef]
- Nakai, T.; Sumida, A.; Kodama, Y.; Hara, T.; Ohta, T. A Comparison between Various Definitions of Forest Stand Height and Aerodynamic Canopy Height. Agric. For. Meteorol. 2010, 150, 1225–1233. [Google Scholar] [CrossRef]
- Inoue, E. On the Turbulent Structure of Airflow Within. J. Meteorol. Soc. Jpn. Ser. II 1963, 41, 317–326. [Google Scholar] [CrossRef]
- Cionco, R.M. A Mathematical Model for Air Flow in a Vegetative Canopy. J. Appl. Meteorol. 1965, 4, 517–522. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, X. Flux Footprint Climatology Estimated by Three Analytical Models over a Subtropical Coniferous Plantation in Southeast China. J. Meteorol. Res. 2015, 29, 654–666. [Google Scholar] [CrossRef]
- Foken, T.; Leclerc, M.Y. Methods and Limitations in Validation of Footprint Models. Agric. For. Meteorol. 2004, 127, 223–234. [Google Scholar] [CrossRef]
- Heidbach, K.; Schmid, H.P.; Mauder, M. Experimental Evaluation of Flux Footprint Models. Agric. For. Meteorol. 2017, 246, 142–153. [Google Scholar] [CrossRef]
- Prajapati, P.; Santos, E.A. Estimating Methane Emissions from Beef Cattle in a Feedlot Using the Eddy Covariance Technique and Footprint Analysis. Agric. For. Meteorol. 2018, 258, 18–28. [Google Scholar] [CrossRef]
- Kumari, S.; Kambhammettu, B.V.N.P.; Niyogi, D. Sensitivity of Analytical Flux Footprint Models in Diverse Source-Receptor Configurations: A Field Experimental Study. J. Geophys. Res. Biogeosci. 2020, 125, 1–17. [Google Scholar] [CrossRef]
- Hsieh, C.-I.; Katul, G.; Chi, T. An Approximate Analytical Model for Footprint Estimation of Scalar Fluxes in Thermally Stratified Atmospheric Flows. Adv. Water Resour. 2000, 23, 765–772. [Google Scholar] [CrossRef]
- Panferov, O.; Sogachev, A. Influence of Gap Size on Wind Damage Variables in a Forest. Agric. For. Meteorol. 2008, 148, 1869–1881. [Google Scholar] [CrossRef]
- Rannik, Ü.; Markkanen, T.; Raittila, J.; Hari, P.; Vesala, T. Turbulence Statistics Inside and Over Forest: Influence on Footprint Prediction. Bound.-Layer Meteorol. 2003, 109, 163–189. [Google Scholar] [CrossRef]
- Schmid, H.P. Source Areas for Scalars and Scalar Fluxes. Bound.-Layer Meteorol. 1994, 67, 293–318. [Google Scholar] [CrossRef]
- Thomson, D. Criteria for the Selection of Stochastic Models of Particle Trajectories in Turbulent Flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).