Abstract
Recently, wireless sensor networks (WSNs) have drawn great interest due to their outstanding monitoring and management potential in medical, environmental and industrial applications. Most of the applications that employ WSNs demand all of the sensor nodes to run on a common time scale, a requirement that highlights the importance of clock synchronization. The clock synchronization problem in WSNs is inherently related to parameter estimation. The accuracy of clock synchronization algorithms depends essentially on the statistical properties of the parameter estimation algorithms. Recently, studies dedicated to the estimation of synchronization parameters, such as clock offset and skew, have begun to emerge in the literature. The aim of this article is to provide an overview of the state-of-the-art clock synchronization algorithms for WSNs from a statistical signal processing point of view. This article focuses on describing the key features of the class of clock synchronization algorithms that exploit the traditional two-way message (signal) exchange mechanism. Upon introducing the two-way message exchange mechanism, the main clock offset estimation algorithms for pairwise synchronization of sensor nodes are first reviewed, and their performance is compared. The class of fully-distributed clock offset estimation algorithms for network-wide synchronization is then surveyed. The paper concludes with a list of open research problems pertaining to clock synchronization of WSNs.
Keywords:
wireless sensor networks; synchronization; clock offset; clock skew; time; estimation; algorithm; statistics 1. Introduction
A wireless sensor network (WSN) is a group of spatially-distributed autonomous sensors, which monitor physical or environmental conditions, such as temperature, humidity, speed, pressure, etc., and then transmit the recorded data to a central computing unit for analysis. WSNs originate from military-oriented applications, such as battlefield surveillance and movement monitoring. Nowadays, WSNs have witnessed a rapid growth and have been implemented in a variety of promising applications, which can be classified as follows:
- Military [1]: battlefield surveillance; forces monitoring; battle damage assessment.
- Health [2,3]: tracking and monitoring patients; telemonitoring of human physiological data.
- Environment [4,5]: air pollution monitoring; water quality monitoring; forest fire detection.
- Home [6,7]: home automation; home appliances management and monitoring.
- Industry [8]: machine health monitoring; waste monitoring; data logging.
Most of these applications require the clocks of network nodes to be synchronized, because performing a joint task requires all of the nodes to operate on a common time scale. For instance, data logging is a basic operation that collects, processes and transmits data and is used for temporal and spatial monitoring of a habitat. The advantage of data logging in WSNs over the conventional data logging lies in the property of real-time data being collected, which requires some or all nodes in the network to share a common time frame.
Each sensor in a WSN operates independently and has its own clock. Even if the clocks of sensors are initially tuned perfectly, due to the imperfections of the clock oscillator, they may drift away from the ideal time as time evolves [9]. Hence, developing efficient clock synchronization protocols is critical in WSNs. In the literature, many clock synchronization algorithms rely on the clock information from the Global Positioning System (GPS). However, GPS is not ubiquitously available and requires a high-power receiver [10]. This fact makes it impractical to implement GPS technology in the clock synchronization of WSNs, since WSNs generally consist of small sensors that have limited energy. Furthermore, sensors sometimes are positioned in an environment where the GPS signal is not available, as is the case with underwater or underground sensors for water quality monitoring. For clock synchronization applications in computer networks, the network time protocol (NTP) represents one of the oldest and standard Internet timing protocols in current use [11]. However, NTP is still not suitable for WSNs, due to the lack of energy availability and unstable working environment in WSNs. Therefore, a variety of synchronization protocols have been particularly designed for WSNs. In general, these protocols perform clock synchronization via timing message exchanges among sensors. However, due to the power requirement for each individual sensor, sensors have a limited communication range, and they are not able to communicate with every other sensor. An example of a WSN with nine sensors is shown in Figure 1a, where each circle denotes a sensor and each edge represents the communication link (if present) between the corresponding pair of sensors.
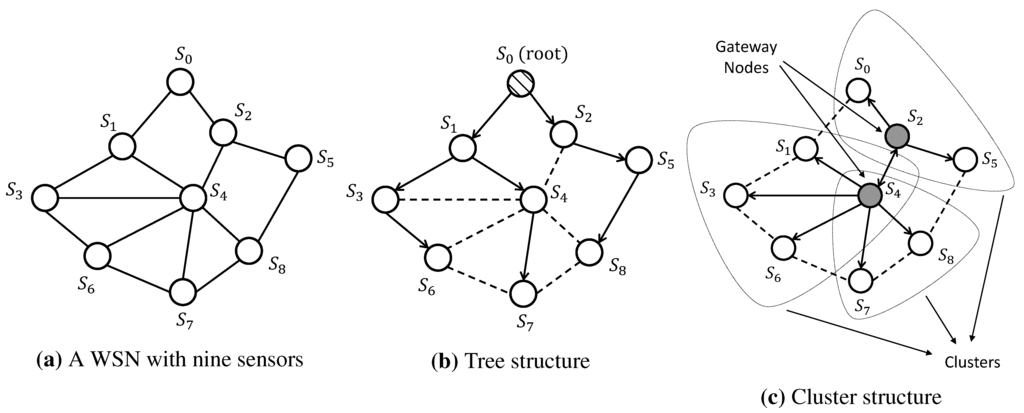
Figure 1.
Network topology for different synchronization approaches.
Traditional synchronization protocols for WSNs generally include two steps: first, the synchronization is conducted within a pair of neighboring nodes; second, a multi-hop structure is built, such that the synchronization can be extended into all of the nodes through a layer-by-layer synchronization. One natural approach to deal with the multi-hop structure of WSNs is to construct a tree-based network. Specifically, as illustrated in Figure 1b, a sensor is selected as the reference node, then a spanning tree rooted at this node is built, and each sensor synchronizes with its parent pairwisely along the unique path from that sensor to the root. On the other hand, the cluster-based structure divides the network into several interconnected single-hop clusters, as graphically shown in Figure 1c. In each cluster, a reference node is selected, and all of the other nodes are pairwisely synchronized by the reference node. The reference nodes of different clusters act as gateways to adjust the local clock of different clusters into one common time frame. In general, the core of these protocols is based on timing message exchanges between a pair of nodes, in which accurate and efficient pairwise clock synchronization algorithms play a key role. In the literature, some widely-used clock synchronization protocols, such as the timing-sync protocol for sensor networks (TPSN) [12], the tiny/mini synchronization [13], the light-weight time synchronization (LTS) [14] and the flooding time synchronization protocol (FTSP) [15], employ a two-way message exchange mechanism to adjust the clock between any two nodes.
However, the traditional synchronization protocols suffer from large overhead in building and maintaining the spanning-tree or cluster structure. In addition, some nodes act as a root (in the spanning-tree structure) or as a gateway (in the cluster structure), and the failure of such nodes may lead to the failure of a large number of nodes connecting to it. To tackle this problem, several algorithms based on a fully-distributed communication topology have been proposed. In such algorithms, there are no special nodes, such as roots and gateways, and thus, no structure needs to be built. With all of the nodes performing exactly the same algorithm and communicating with their neighboring nodes, these protocols are robust to the topology changes and failures of nodes.
In this paper, the latest algorithms in the realm of clock synchronization for WSNs are surveyed following a statistical signal processing viewpoint. Specifically, the rest of the paper is organized as follows. Section 2 introduces the clock model and the two-way message exchange mechanism for pairwise clock synchronization. Based on the two-way message exchange mechanism, the state-of-the-art pairwise clock synchronization algorithms under Gaussian random delays are investigated in Section 3. Section 4 overviews the pairwise clock synchronization algorithms in the presence of exponential random delays. Section 5 surveys the signal processing techniques employed in WSNs when the random delays are unknown. In Section 6, synchronization algorithms that assume a fully-distributed operation are discussed. Finally, Section 7 concludes the paper and provides some open research topics.
In the literature, surveys for clock synchronization in WSNs have been presented by [9,10,16,17]. The focus of [10,16] lies in the clock synchronization protocols that are applied in WSNs. The survey paper [17] provides a technical overview of the history, recent advances and challenges in distributed clock synchronization for distributed wireless networks, while this article presents synchronization algorithms with emphasis on the mathematical and statistical techniques employed for clock synchronization parameters estimation. The work in [9] surveys the latest advances in the clock synchronization of WSNs following a signal processing viewpoint. However, only pairwise synchronization methods are investigated in [9], while our paper discusses both pairwise and fully-distributed synchronization algorithms.
2. System Model for Pairwise Clock Synchronization
In this section, the clock model for each senor node is first introduced and the notions of clock offset and skew are described. Then, the classic mechanism for message exchange between two adjacent nodes, namely the two-way message exchange mechanism, is presented.
2.1. Clock Offset and Skew
As discussed earlier, each sensor node in a WSN works independently and has its own clock. Ideally, the clock of a sensor node is modeled as
, where t represents the reference time [9]. However, due to the imperfections of the clock oscillator, as well as the environmental factors, such as pressure, temperature and hardware aging, the clock is subject to change as time evolves. Generally, the clock function of node i can be expressed as:
where
and
denote the clock offset (phase difference) and the clock skew (frequency difference) for sensor node i, respectively [9]. In this way, if the clock of Node A is selected to be the reference time, it follows that:
where θ and f stand for the clock offset and skew between Nodes A and B, respectively. A graphical interpretation of the relationship between the clocks of Nodes A and B is shown in Figure 2. It can be seen that if
and
, then Nodes A and B are perfectly synchronized. Otherwise, the synchronization process aims to estimate the clock offset θ and skew f, such that Node B can adjust its local clock to the reference time (Node A). As time evolves, the clock offset and skew are subject to change due to various reasons, such as the changes induced by the environment and sensor hardware aging. Therefore, the clock parameters are synchronized periodically, such that they are tuned up-to-date.
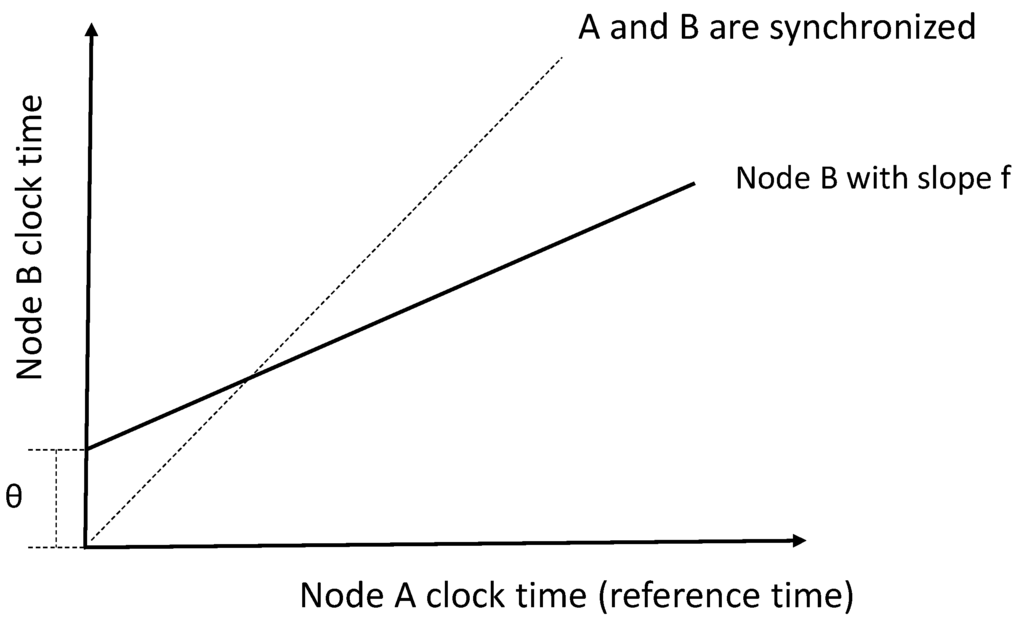
Figure 2.
Clocks of sensor nodes.
2.2. Two-Way Message Exchange Mechanism
The two-way message exchange is a classic mechanism for communicating the timing messages between two adjacent nodes and has been widely used in the literature [12,13,14,15]. For pairwise synchronization, one of the sensor nodes is selected as the reference node. For example, a two-way message exchange model between Node A and Node B is shown in Figure 3 in the situation when Node A is serving as the reference node. During message exchange round i, the synchronization begins at Node A, and a synchronization message containing the sending time
is sent to Node B. Next, Node B records the reception of the message at its clock time
and sends an acknowledgment message to Node A at
. The acknowledgment message contains the timestamps
and
. At last, Node A receives the acknowledgment message at
, and the message exchange round i ends. This process is repeated N times, where N stands for the required number of observations.
Based on the procedure depicted above, the clock synchronization problem can be mathematically modeled as
where θ and f represent the clock offset and clock skew, respectively. Moreover,
and
denote the random delays from Node A to Node B and from Node B to Node A, respectively, and d stands for the fixed portion of delays. In addition,
and
are time stamps recorded at Nodes A and B, respectively.
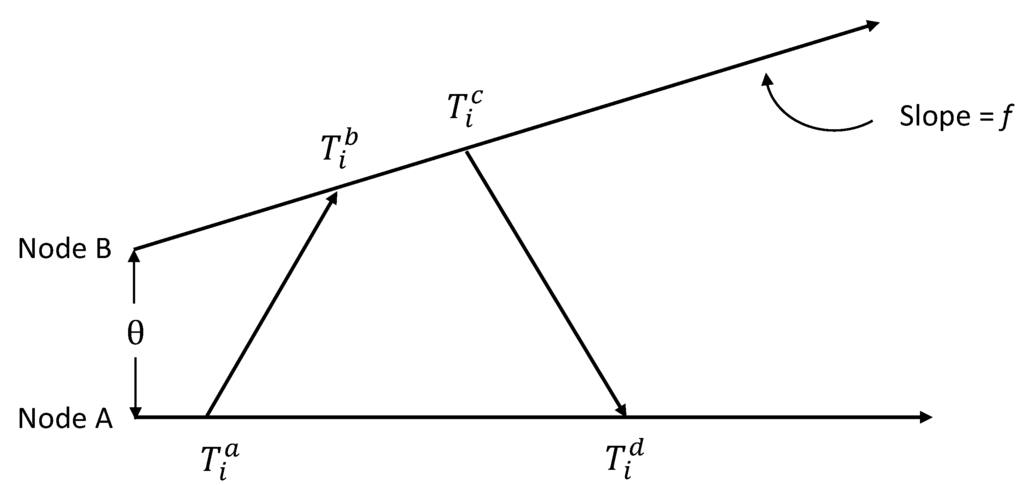
Figure 3.
Two-way message exchange mechanism (with skew).
If we consider only the clock (phase) offset between two adjacent nodes, i.e.,
, the system model in Equation (2) can be expressed as:
The equations in Equation (3) can be further simplified as:
where
and
contain the clock information and are defined as
and
, respectively.
3. Pairwise Clock Synchronization under Gaussian Delays
In general, probability density function (PDF) models have been employed for modeling the random portion of delays in WSNs. Examples of PDFs that have been adopted in the literature include exponential, Gaussian, Weibull and Gamma [18,19,20,21]. In this section, we use the Gaussian distribution to characterize the random delay in WSNs, i.e.,
and
are Gaussian random variables with parameters
and
, respectively. The reasons for selecting the Gaussian distribution for modeling the random delays are as follows:
- The central limit theorem (CLT) states that the PDF of the sum of a large number of independent and identically-distributed (i.i.d.) random variables is approximately normally distributed. Therefore, the Gaussian model is appropriate if the random delays are assumed to be the summation of multiple independent random variables.
- Experimental results based on two Texas Instruments ez430-RF2500 evaluation boards were recorded in [22] to demonstrate the fitness of the Gaussian distribution in modeling the random portion of delays in WSNs.
The most representative pairwise clock synchronization algorithms in the literature focused on developing maximum likelihood estimators (MLEs) for the clock offset and skew. The MLE is one of the most widely-used estimators in the area of parameter estimation, since it achieves asymptotically the Cramér–Rao lower bound (CRLB).
Based on the two-way message exchange model in Equation (4), where only the clock offset is considered, [18] derived the MLE for clock offset by assuming a known fixed delay d and symmetric random delays, i.e.,
and
. In this framework, the likelihood function is expressed as:
The MLE of clock offset is derived by differentiating the log-likelihood function with respect to θ and setting the corresponding derivative to zero, and it assumes the expression:
where
and
stand for the sample means of observations
and
, respectively. It can be verified that the estimator Equation (5) is unbiased and achieves the CRLB. The MLE estimator Equation (5) represents also the minimum variance unbiased estimator (MVUE).
Following the same assumptions, i.e., a known fixed delay and symmetric random delays, the joint maximum likelihood estimates of the clock offset and skew were also proposed in [18] based on the two-way message exchange model in Equation (2). Specifically, the likelihood function is first formulated as:
where
. Differentiating the log-likelihood function with respect to θ leads to an equation of θ in terms of
. In addition, differentiating the log-likelihood function with respect to
results in an equation of
in terms of θ. The joint estimates of θ and
, denoted as
and
, can be obtained by combining those two equations, and the MLE of f is obtained as
, due to the invariance principle [23].
However, in some practical cases, the value of the fixed delay d is unknown and sometimes even represents a parameter that needs to be estimated, as is the case with the node localization application [24]. Therefore, efficient algorithms for joint estimation of the clock offset, clock skew and fixed delay are of great interest. Based on the two-way message exchange mechanism in Equation (2), Leng et al. [24] extended the result in [18] by assuming an unknown fixed delay d. First, the signaling model Equation (2) is re-formulated in matrix form as:
where
,
and
with dimension
.
Since
and
are independent Gaussian random variables, i.e.,
,
the log-likelihood function for Φ and d is expressed as:
For a fixed d, the MLE of Φ is given by:
Plugging Equation (6) into the log-likelihood function results in a compressed likelihood function with only one variable d. The MLE of d is derived by taking the derivative over the resulting log-likelihood function with respect to d, and the MLE of Φ is obtained by plugging the corresponding estimate of d back into Equation (6). Finally, the MLEs of θ and f are obtained from the MLE of Φ using the invariance principle [23].
4. Pairwise Clock Synchronization under Exponential Delays
In the literature, the exponential distribution is also commonly exploited to represent the random portion of delays in WSNs. The reasons behind choosing the exponential distribution include:
- For the point-to-point hypothetical reference connection (HRX) between two nodes, a single-server M/M/1queue can appropriately represent the aggregate link delay, where the random delays are modeled as independent exponential random variables [25].
- Experiment results were carried out in [26,27] to verify the appropriateness of choosing the exponential distribution to characterize the random delays in WSNs.
- Among all distributions with a fixed mean in the support , the exponential distribution achieves the maximum differential entropy, and thus, it is the least informative.
The most representative clock offset estimation methods for pairwise synchronization in the presence of exponential delays are the maximum likelihood estimator (MLE), the best linear unbiased estimator (BLUE) and the minimum variance unbiased estimator (MVUE), and they will be first reviewed in this section. The MLE for joint estimation of the clock offset and skew will be investigated later. Finally, an important statistical concept, referred to as the confidence interval for the clock offset, will be investigated.
4.1. Clock Offset Estimation under Exponential Delays
4.1.1. Maximum Likelihood Estimator
In the two-way message exchange mechanism Equation (4) where only clock offset exists, we assume that
and
are exponentially-distributed random variables with means
and
, respectively. Assuming a known fixed delay, Abdel-Ghaffar [25] reported that the MLE of the clock offset does not exist when the exponential random delays are assumed to be known and symmetric, i.e.,
, since the likelihood function does not admit a unique maximum. However, Jeske [28] derived a closed-form solution for the MLE of clock offset by assuming an unknown fixed delay and an unknown mean for the exponential delay. In this way, a joint estimation of
and λ can ensure a unique maximum of the likelihood function. Specifically, assuming symmetric exponential delays with a common mean λ, the likelihood function for
is expressed as:
where
denotes the indicator function. Let the first order statistics
and
denote the minimum values of observations
and
, respectively. It can be shown that for fixed values of d and θ, the optimal value of λ that maximizes the likelihood function is given by
. Therefore, the likelihood function Equation (7) can be simplified to:
It can be observed that the indicator function poses a high impact on the value of the likelihood function, and moreover, the indicator function depends on
and
. Hence, in order to maximize the likelihood function, different assumptions on
and
are discussed in [28], e.g.,
,
and the region where
is illustrated separately for each assumption. The value of θ that maximizes the likelihood function is found graphically from the corresponding support region. It is shown that all of the different assumptions on
and
lead to the same MLEs for the vector
:
Our primary interest is the MLE of the clock offset , but in the meantime, the MLEs for d and λ are also derived. It can be verified that is unbiased and has a variance . Interestingly, if d is unknown and the variable portions of delays are not symmetric, i.e., , the MLE of θ also admits the form . However, in this case, the MLE is biased.
Different from the graphical analysis used in [28], [29] analytically derived the MLE of clock offset under exponential delays using convex optimization tools. In particular, the system model in Equation (4) is re-written as:
where and . The goal is to determine the MLEs of ξ and ψ, i.e.,
and , such that the MLE of θ can be obtained from:
based on the invariance principle [23]. Towards this end, the density functions of and are expressed as:
The resulting MLE of ξ can be formulated as a convex optimization problem:
and it follows that The analysis of ψ is analogous to the case of ξ, and it yields that
Thus, the MLE of θ follows from Equation (10) and admits the form:
which coincides with the result in Equation (8). The advantage of this analytical approach is that it provides a more general derivation of MLEs, which can by applied to obtain the MLEs for the delays under other types of distributions, which include Gaussian and log-normal as special cases [29].
4.1.2. Best Linear Unbiased Estimator
In the statistical signal processing field, the minimum mean square error (MSE) is commonly selected as the criterion to measure the performance of estimators. The MSE of an estimator is defined as:
where var stands for the variance of and bias.
In general, the MVUE is referred to as the “optimal” estimator, since it minimizes the variance in the class of unbiased estimators. However, it frequently occurs that the MVUE is difficult or impossible to be derived or might not even exist [23]. For such scenarios, a suboptimal estimator is required. A common approach is to constrain the estimator to be linear in terms of the observations and to find the linear estimator that is unbiased and achieves the minimum variance. Such an estimator is referred to as the BLUE. The BLUE of the clock offset under asymmetric exponential delays was first derived by Jeske and Sampath in [30] using the order statistics of the observations where and . Specifically, the BLUE is formulated as a linear combination of the order statistics:
The variance of estimator T and the unbiasedness condition are further expressed in terms of and . Using Lagrange multipliers, it can be shown that the minimum of the variance subject to the unbiasedness condition is achieved when with and for . Thus, the BLUE of the clock offset admits the form:
On the other hand, the BLUE of the clock offset under symmetric exponential delays can also be derived following the aforementioned steps, and it is expressed as:
Using statistical signal processing techniques, [31] later re-derived the joint BLUEs for the fixed delay, the clock offset and the mean of exponential delays under symmetric and asymmetric exponential delays, as shown in Equations (16) and (17), respectively.
These results were further used as a prerequisite to find the MVUE of the clock offset, a result that will be presented in the next sub-section.
4.1.3. Minimum Variance Unbiased Estimator
As discussed earlier, the MVUE is an unbiased estimator that exhibits lower variance than any other unbiased estimator. Finding the MVUE usually requires usage of the concept of sufficient statistics, the Neyman–Fisher factorization theorem and the Rao–Blackwell–Lehmann–Scheffe theorem [23] (p. 101).
Let Φ denote the parameters to be estimated and z represent the set of the observations; then, the Neyman–Fisher factorization theorem states that if the likelihood function can be factorized as:
where g is a function depending on z only through and h is a function depending on z only, then is a sufficient statistic for Φ. In a two-way message exchange mechanism under symmetric exponential delays, and . The MVUE of Φ was derived in [31] by implementing the following procedure. Express first the likelihood function in terms of the unit step function as follows:
and factorize Equation (18) as:
where:
In the above equations, is independent of the unknown parameters Φ and are functions depending on the data only through . Using the Neyman–Fisher factorization theorem, it turns out that T is a sufficient statistic. Moreover, the Rao–Blackwell–Lehmann–Scheffe theorem (p. 109 in [23]) claims that a sufficient statistic T is complete if there is only one function of T that is unbiased, and this function leads to the MVUE, i.e., . Therefore, the remaining task is to prove that T is complete or, equivalently, that only one function of T is unbiased, and to find that function.
The authors in [31] employed a one-to-one transformation of T, denoted as
. Then, it was shown that is complete by assuming that there are two functions of leading to unbiasedness, i.e., , and then, proving that, actually,
. It turns out that T is also complete, since the sufficient statistics are unique within one-to-one transformations [23]. To this end, what remains to prove is to find an unbiased estimator for Φ as a function of T, which represents the MVUE according to the Rao–Blackwell–Lehmann–Scheffe theorem. It seems difficult to find three unbiased functions of T for each of and λ just by inspection. However, it can be observed that the BLUE in Equation (16) is a function of T and is also unbiased. Therefore, it is concluded that the BLUE is also the MVUE:
Following an analogous approach, it was reported in [31] that the MVUE of the clock offset is also equivalent to the BLUE in the presence of asymmetric exponential delays:
4.1.4. Comparison of Estimators
A comparison of MLE, BLUE and MVUE under both symmetric and asymmetric exponential delays is shown in Table 1. The criteria adopted in Table 1 include the estimator formula in terms of observations, bias, variance and MSE. It is observed that the BLUE and MVUE coincide in the presence of both symmetric and asymmetric distributions. Furthermore, all three estimators admit the same expression when the random delays are symmetrically exponential distributed. Under asymmetric exponential delays, albeit unbiased, the MLE can still outperform the MVUE when:
or equivalently:
It can be seen that the MLE achieves a better performance when the means of the exponential delays are close to each other. In this way, the right-hand side of Equation (20) resumes being a large number, and the inequality Equation (20) generally holds with a reasonable selection of N.

Table 1.
Comparison of estimators.
| Clock Offset | Symmetric Delays | Asymmetric Delays | ||||||
|---|---|---|---|---|---|---|---|---|
| Formula | Bias | Variance | MSE | Formula | Bias | Variance | MSE | |
| MLE [28,29] | 0 | |||||||
| BLUE [30,31] | 0 | 0 | ||||||
| MVUE [31] | 0 | 0 | ||||||
4.2. Joint Estimation of Clock Offset and Skew under Exponential Delays
In general, the clock synchronization in WSNs involves two steps. The first step assumes synchronizing the nodes by adjusting the clock phase offset (close offset), while the second step resumes correcting the clock frequency offset (clock skew). The clock skew correction plays a critical role in clock synchronization, especially for long-term synchronization, since it reduces the number of exchanged messages and, thus, brings down the energy consumption. Therefore, we discuss the joint estimation of clock offset and skew in this section.
In the literature, based on a two-way message exchange mechanism, the studies for joint estimation of clock offset and skew mainly concentrated on the development of MLEs, and there is no closed-form solution for the joint estimation of clock offset and skew under exponential delays. Roughly speaking, the algorithms for developing MLEs can be categorized into two types: in the first category, a suboptimal model is built by removing some nuisance parameters, and the corresponding MLEs are derived, while in the second category, the joint estimation is conducted directly.
4.2.1. Removing Nuisance Parameters
Based on the two-way message exchange mechanism in Equation (2) and assuming symmetric exponential delays, the likelihood function based on observations and is given by:
It is observed that the likelihood function Equation (21) assumes a complicated expression, and the MLEs might be difficult to derive. According to this observation, an algorithm for joint estimation of clock offset and skew, referred to as the ML-like estimator (MLL), was proposed in [18] by using the first and last observations of timing message exchanges. Specifically, from the first equation in Equation (2), subtracting from yields:
Similarly, from the second equation in Equation (2), subtracting from leads to:
Such an approach helps to remove the explicit dependency on the nuisance parameters λ, d and θ. In addition, an ML-like estimate of the clock skew is derived using Equation (22) and (23). Finding an estimate of the clock offset is achieved by rewriting Equation (2) as:
where
and . It can be seen that the above model shares the same form as the no-skew model in Equation (4). Therefore, an ML-like estimate of the clock offset is obtained . The above algorithm for joint estimation of clock offset and skew is computationally simple, but it exhibits a suboptimal performance compared to the maximum likelihood estimator, since it exploits a reduced set of statistics. That is the reason why the above estimator is referred to as the ML-like estimator.
Another approach to remove the nuisance parameter was reported in [32] by adding two equations in Equation (2). It follows that:
where the nuisance parameter d is removed. Dividing the above expression by f and defining and leads to a new model represented in matrix form as follows:
Assuming symmetric exponential delays, it is easy to verify that follows a Laplace distribution with location parameter zero and scale parameter . Thus, the log-likelihood function for model Equation (25) is expressed as:
Therefore, the MLEs of and can be found by maximizing Equation (26), and the corresponding estimators for θ and f are obtained using the relationships and .
4.2.2. Direct Joint Estimation of Clock Offset and Skew
Assuming symmetric exponential delays with a known mean λ, [33] addressed the problem of MLEs for clock offset and skew by optimizing over nonlinear constraints iteratively. In terms of the estimates , four different cases were considered: (1) d and θ known, f unknown; (2) θ known, d and f unknown; (3) d known, θ and f unknown; (4) unknown. The ultimate goal is to jointly estimate in the fourth case. However, similar to the derivation of the MLE in [28] when no skew is considered, the MLEs are also determined by exploiting the boundary conditions of the support regions. For Cases 1 and 2, the support regions are 2D, and the discussion of these two cases gives an insight to further analyze Cases 3 and 4, where the support regions admit a 3D visualization.
Li and Jeske [34] proposed a computationally-simpler algorithm to find the MLEs of clock offset and skew. Asymmetric exponential delays with unknown means were assumed in [34], such that the estimation algorithm can be applied to a more general framework. In this case, the likelihood function resumes as:
Re-parameterizing in terms of and leads to:
To find the MLEs for likelihood function Equation (27), or equivalently Equation (28), the concept of profile likelihood function is employed in [34], such that the MLEs can be alternatively found by maximizing the profile likelihoods. In particular, fixing and , the conditional MLEs of and are shown to be:
Plugging the above equations into Equation (28) yields the profile likelihood as a function of and , which is denoted as . Following the same procedure with respect to
, the conditional MLEs for and are expressed as:
To this end, the original five-dimensional optimization problem Equation (27) is simplified to the maximization of a one-dimensional function , whose solution represents the MLE for clock skew, and it is denoted as . Additionally, the MLE for clock offset is obtained via:
since the corresponding estimates of and are and
, respectively.
4.3. Confidence Interval for Clock Offset
From a statistical point of view, a confidence interval (CI) is used to describe the amount of uncertainty associated with a sample estimate of a parameter. More specifically, if a CI is constructed among a series of experiments, the proportion of such an interval that contains the true value of the parameter is given by the confidence level. Mathematically, suppose X to be a random sample from a probability distribution with parameter θ, a CI is an interval with endpoints , such that the following property holds:
where γ stands for the confidence level.
In terms of the confidence interval for clock offset under exponential delays, Li et al. [35] derived satisfactory CIs using an approximate pivotal quantity (APQ). By assuming asymmetric exponential delays, the authors in [35] derived the relative likelihood function for θ, say , based on the likelihood function from model Equation (4). It was then shown that is an asymptotic pivot in the sense that its limiting distribution does not depend on any unknown parameter. Thus, the asymptotic pivot property of , as well as its easily invertible form lead to a way to obtain an asymptotic CI for θ as follows:
A generalized pivotal quantity (GPQ) was also employed in [35] to propose a generalized confidence interval for θ. Even though generalized confidence intervals generally do not have frequentist coverage probabilities that are exactly equal to the nominal value, the proposed GPQ actually leads to frequentist coverage probabilities that are very close to the nominal value. Furthermore, APQ and GPQ CIs under exponential delays were also extended in [35] to any distribution within the one-parameter scale family.
Further discussions about CIs of clock offset were carried out in [36,37]. Specifically, under exponential network delays, [36] explored sequential intervals with a preset width and proved that these CIs provide a satisfactory solution to minimize the number of samples. In this way, sequential CIs can be used to obtain the smallest sample size required to achieve a specified precision for the clock offset estimation. On the other hand, by considering the correlation between the uplink and downlink random delays, [37] extended the CI procedure to bivariate models where the random delays are formulated as Freund and Marshall–Olkin bivariate exponential delays. In addition, the MLEs for clock offset under Freund and Marshall–Olkin models were also derived.
5. Pairwise Clock Synchronization under Unknown Random Delays
Although the assumptions of Gaussian and exponential distributions for the random delay component of WSNs are plausible, it might happen that the underlying PDF of the network random delays is unknown in advance. In fact, it is well known that the distribution of the network random delays is difficult to characterize succinctly [30]. Therefore, the performance of estimators particularly designed for a certain distribution may degenerate greatly under another type of distribution, and there is a need for developing efficient estimation methods that are robust to the unknown random delays of WSNs. Based on the classic two-way message exchange mechanism, we describe several robust estimation methods in this section, namely the bootstrap bias correction [30], the composite particle filtering [38] and the least squares estimator [39].
5.1. Bootstrap Bias Correction
Bootstrap bias correction is a statistical approach that aims to reduce the bias of an estimator at the expense of increased variance, but with a total effect of reduced MSE [40]. For example, the MLE of clock offset derived under exponential delays is given by . However, the random delays may not follow an exponential distribution exactly, and the MLE derived under the exponential assumption may perform poorly under other distributions. For such scenarios, the bootstrap bias correction approach can be applied to reduce the bias and eventually the MSE of the estimator.
Suppose the observations x follow an unknown distribution F and the estimator is a statistic
; the bias of is defined as . The bootstrap estimate of the bias can be expressed as:
and the bias corrected estimator admits the form:
where denotes the empirical distribution of observations.
In the context of clock offset estimation under exponential delays, the observations between two nodes are denoted as and , and the MLE is given by . The bias of resumes as:
where and stand for the unknown distributions of observations
and , respectively. The bootstrap estimate of
can be further expressed as:
Defining and leads to the empirical distribution [30]:
Plugging Equation (34) back into Equation (33) yields
and eventually the bias-corrected estimator of
:
Following the same procedure described above, the bias-corrected estimator of the BLUE under asymmetric exponential delays, i.e., Equation (15), was also derived in [30]. Experimental results in [30] showed that under common distribution assumptions other than exponential, e.g., Gamma, Weibull and log-normal, the bias-corrected estimator of BLUE has the smallest MSE, while also outperforms the MLE and the BLUE derived for exponential delays.
The work in [41] investigated the BLUE and its corresponding bias-corrected estimator under a Pareto distribution: a heavy-tailed distribution that was adopted to model network delays for recent applications [42,43,44]. The authors in [41] examined the effectiveness of bootstrap bias correction of different estimators under varying assumptions for network delays. Some interesting examples were reported where bootstrap bias correction fails in the sense that the MSE increases or even the absolute bias increases. For instance, a somewhat surprising result is that the bootstrap bias correction of the exponential BLUE leads to a large absolute bias under Pareto network delays. Among these estimators and their corresponding bootstrap bias corrections, the bias-corrected estimator in Equation (35) was considered to be a significantly more robust estimator in [41].
Moreover, another bias correction method, referred to as the Jackknifebias-correction, was reported in [45]. The Jackknife bias-corrected estimator of the exponential MLE, , was proposed and compared to the corresponding bootstrap bias-corrected estimator Equation (35). Simulation results in [45] illustrated that the Jackknife bias correction does a better job at reducing bias, but is generally eroded by a variance increase, which yields a larger MSE.
5.2. Composite Particle Filtering
The idea of composite particle filtering is to model the estimation problem in the form of a state-space representation and to exploit an optimal Bayesian approach for state estimation [9]. In terms of clock offset estimation, the system model in Equation (4) is rewritten in compact form matrix representation:
where can assume any distribution. Since the value of clock offset is time varying, it is assumed to obey a Gauss-Markov dynamic model:
where the noise term is modeled as a Gaussian random variable with zero mean and covariance matrix . The aim is to obtain the minimum mean square error (MSEE) estimator of state , which is expressed as the conditional mean state estimator:
where stands for the observations up to time i.
The optimal state estimator consists of two steps. In the first step, the posterior distribution is updated and supposed known, then the predictive distribution is updated as follows:
where the transition PDF is obtained from Equation (37). In the second step, the posterior distribution at time i is evaluated:
where represents the likelihood function obtained from Equation (36), and:
is a normalization constant.
In the composite particle filtering algorithm adopted in [38], the posterior and predictive distributions are recursively modeled by finite Gaussian mixtures, and the components of the Gaussian mixtures are updated using the Kalman filter in conjunction with particle filters. Computer simulation results illustrate that the performance of the composite particle filter algorithm is superior in the presence of delays with unknown distribution (such as Gamma, Weibull, log-normal or arbitrary mixtures) relative to the performance exhibited by the MLEs derived specifically under the assumption of Gaussian or exponential delays.
5.3. Least Squares Estimators
The least squares approach in [39] provides a general framework for joint estimation of clock offset and skew, irrespective of the network delay distribution type. The model adopted by the least squares approach is obtained by adding two equations in Equation (2) together and reduces to:
Thus, we can regard Equation (41) as a linear regression model in terms of ,
, where θ represents the intercept, f stands for the slope and denotes the error term. Based on the model Equation (41), θ and f can be naively estimated via a standard least squares approach as follows:
and:
where for represent sample means.
However, in general, neither the mean nor the covariance of the error term is zero, which may result in poor estimation performance. Therefore, several alternative least squares estimators were proposed in [39] to further improve the estimation accuracy of clock offset and skew. An example of an enhanced least squares estimator is referred to as the constrained least squares (CLS) estimator, and it is found by minimizing the sum of squared residuals subject to a set of constraints on θ and f formed by considering the time stamp model in Equation (2):
The disadvantage of the CLS lies in the challenging computations to solve the minimization problem. Therefore, two additional least squares estimators, referred to as the feasibility checked least squares (FLS) estimator and the Paxson-based estimator, respectively, were proposed in [39] to reduce the computational complexity. Experimental results showed that the FLS estimator and the Paxson-based estimator perform comparably and sometimes better than the CLS estimator, while exhibiting the advantage of much less computational complexity.
6. Fully-Distributed Clock Synchronization Algorithms
The centralized signal processing techniques can only help address the problem of pairwise synchronization. As discussed in Section 1, the network-wide synchronization requires a specified network structure to extend the pairwise synchronization approach to all of the sensor nodes. This increases the overhead of the communication and makes the network vulnerable to node failures. More recent works on clock synchronization mainly concentrated on applying decentralized signal processing methods (e.g., distributed estimation techniques) to develop clock synchronization algorithms in a fully-distributed manner.
6.1. System Model
In a fully-distributed clock synchronization algorithm, the synchronization is not performed pairwisely, but simultaneously among all of the sensor nodes. Therefore, instead of estimating the clock offset difference and the relative clock skew between two nodes, we aim to find the clock offset and skew for each individual sensor node. A two-way message exchange between nodes i and j in the n-th round of their message exchange is modeled in Figure 4. Following the same message exchange procedure described in Section 2.2, we can write:
where and denote the fixed delays from node i to node j and from node j to node i, respectively, and stand for the random delays. If only the effect of clock offset is considered, i.e.,
, and the network topology is assumed stationary, i.e., , the system model in Equations (45) and (46) reduces to the more simplified model:
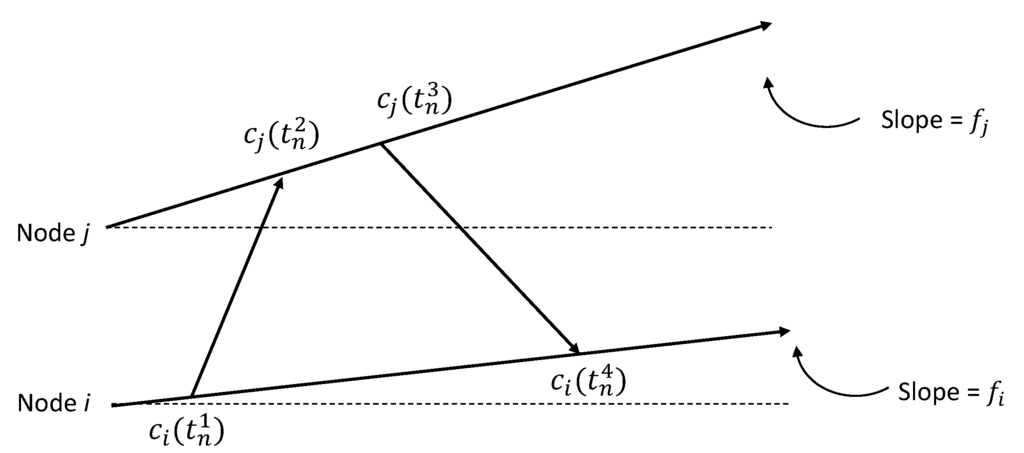
Figure 4.
Two-way message exchange between nodes i and j.
6.2. Fully-Distributed Clock Synchronization Algorithms under Gaussian Delays
The Gaussian assumption for the random delay component of WSNs is justifiable due to the CLT and many experimental results (see, e.g., [22]). The state-of-the-art of fully-distributed clock synchronization algorithms under Gaussian random delays are discussed in the following sub-section.
6.2.1. Belief-Based Synchronization Algorithms
Existing fully-distributed algorithms in [22,46,47] are based on the belief propagation method in the Bayesian framework. Under the assumption of Gaussian random delays, [46] proposed a belief-based algorithm to estimate the clock offset in a distributed manner. Specifically, the system model is modified by adding Equation (47)–(48), and it leads to:
where . Stacking all of the observations in a vector as
leads to the likelihood function denoted as
. In the Bayesian scenario, the clock offset of each sensor node, denoted as , is regarded as a random variable with prior distribution . The estimate is obtained by maximizing the posterior distribution of the clock offset.
The posterior distribution of for a network with only two nodes i and j is expressed as:
Extending the above idea to a WSN with M sensor nodes, the posterior distribution of clock offset is expressed as:
where stands for the indices of neighboring sensors of node i. It can be seen that the joint distribution depends on interactions among all of the variables, and the integration is almost impossible to calculate. Therefore, belief propagation (BP) is employed to compute the posterior distribution without fully integrating Equation (50).
BP takes advantage of the graphical model structure. Factor graphs represent one of the most widely used graphical models and have been adopted in [46]. An example of a factor graph for two nodes i and j is depicted in Figure 5. The two sensor nodes i and j are represented in terms of the variable nodes (circles), and they are connected to a square factor node , which stands for the likelihood function
. On the other hand, nodes i and j are also connected to factor nodes and , which represent the prior distributions of
and , respectively. During each iteration, i.e., for the iteration l, the BP algorithm in [46] is carried out via the following three steps:
- (1)
- Each variable node transmits its current belief to all of its neighboring factornodes .
- (2)
- Acting like an intermediate node, the message from a factor node to a variable node is calculated based on the belief received from :
- (3)
- After variable node receives all of the messages from its neighboring factor nodes, i.e., , it updates its belief as follows:
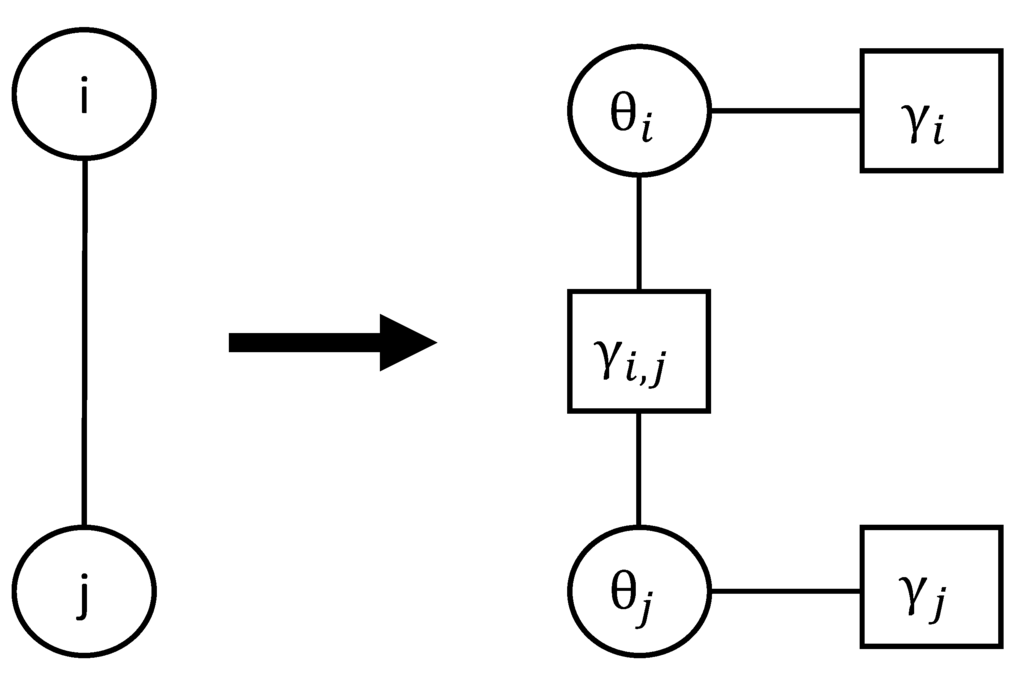
Figure 5.
The factor graph of nodes i and j.
If no prior information is given about , we set to a Gaussian PDF with zero mean and very large variance. Furthermore, the belief of each node is initially set as its prior distribution, i.e., . Beliefs and messages are then iteratively updated at variable nodes and factor nodes, respectively. After convergence, the belief at each node reaches the posterior distribution exactly when the network topology is loop free and approximately when the network topology presents loops [48]. Thus, the maximum a posteriori probability (MAP) estimate is obtained by maximizing the converged belief at each node. Since each node runs the same algorithm only with its neighbors, the estimates are achieved in a fully-distributed manner.
However, only the problem of clock offset estimation is investigated in [46]. Moreover, the algorithm is performed in a synchronous way, i.e., every node updates its belief only after receiving messages from all of its neighboring factor nodes. Due to the random packet dropouts, the synchronous algorithm may converge slowly. To account for these aspects, Du et al. [47] generalized the belief-based algorithm to jointly estimate the clock offset and skew under Gaussian random delays using both synchronous and asynchronous algorithms. In the asynchronous algorithm, some nodes are allowed to update their beliefs more frequently as long as they receive messages from their neighbors within a preset time period.
Following the two-way message exchange model in Equations (45) and (46), the authors in [47] eliminated the fixed delay d by adding these two equations together. It turns out that:
where and are N-by-two matrices with the n-th row representing and , respectively, , and
. Thus, the likelihood function can be obtained from Equation (53), and it is denoted by .
The message passing procedure adopted in [47] is slightly different from the one in [46]. In Step 1, instead of broadcasting the belief to all of its neighboring factor nodes, the message transmitted from variable node
to factor node is evaluated via:
which is simply the product of the incoming messages on the other links. Thus, in Step 2, the message from a factor node to a variable node is updated via:
and the belief is further updated as:
It is illustrated analytically in [47] that the asynchronous algorithm converges regardless of the network topology, and the MSE of the estimation parameters achieves the centralized CRLB asymptotically. Simulation results further show that the asynchronous algorithm converges faster than the synchronous one.
In parallel to the work in [47], Etzlinger et al. [22] proposed a BP algorithm and a mean field (MF) algorithm and adopted a Bayesian model with Gaussian random delays. The MAP estimates of clock offset and skew are derived using some simplifications of the measurement likelihoods and prior distributions. The message update rule in the BP algorithm is analogous to the one in [47] (see, e.g., Equations (54) and (55)). As concerns the implementation of the MF algorithm, each variable node broadcasts its current belief to all of its neighboring factor nodes, and the same step as in [46] is followed. However, in the second step, the message transmitted from a variable node to a factor node is alternatively evaluated as:
Numerical results corroborate the attractive performances exhibited by both BP and MF algorithms.
6.2.2. Consensus-Based Synchronization Algorithms
The fully-distributed algorithms reported in [49,50,51] rely on the average consensus principle. However, the message delays are not considered in these algorithms, and their performance degenerates significantly when message delays exist [46]. Other consensus-based distributed synchronization algorithms, such as [52,53], typically suffer from slow convergence speed and require a high number of data packages [22]. To overcome this issue, Berger et al. [54] recently presented a fully-distributed low-complexity consensus-based synchronization algorithm for embedded WSNs. Another fully-distributed clock synchronization method based on a cascade of two consensus algorithms was proposed by Schenato et al. [55], which exhibits the advantage of being asynchronous and being robust to packet losses, node failures and communication topology changes. The details of these consensus-based algorithms are omitted herein, since they are not based on the statistical framework described in Section 6.1. Xiong et al. [56] generalized the consensus-based algorithm to estimate the clock offset by taking into account both fixed delays, as well as random Gaussian delays. In each iteration of the generalized consensus-based algorithm, each node processes and decodes the timestamps from its neighbors and then updates its local clock time using a weighted average of the time differences with its neighbor nodes. Such a strategy naturally leads to the introduction of a special network topology referred to as the time delay balanced network in which average timing consensus is achieved in the presence of Gaussian random delays.
6.3. Fully-Distributed Clock Synchronization Algorithms under Exponential Delays
Compared to the fully-distributed clock synchronization algorithms that assume Gaussian network delays, fewer works have been proposed to account for exponential network delays in a fully-distributed manner. Considering only the estimation of clock offset, Zennaro et al. [57] pioneered a fully-distributed algorithm under exponential delays based on a factor-graph representation of the network and a max-product message update algorithm. From the two-way message exchange model in Equations (47) and (48), since the MLE for the clock offset difference is given by , where and denote the first order statistics of and , respectively, the modified system model is expressed as:
where is a Laplace random variable, since and are both assumed to be exponentially distributed. Thus, the likelihood function is formulated based on the model in Equation (58). The factor graph representation of the network is identical to the one employed in [46]. In terms of the message update rule, the message transmitted from variable node to factor node is given by:
Moreover, the message from a factor node to a variable node is updated by the “max” operator:
and the belief update is expressed as:
Under exponential random delays, [58] proposed a fully-distributed synchronization algorithm for joint estimation of clock offset and skew. The joint maximum likelihood estimation of the clock offset and skew is first formulated as a linear programming (LP) problem and solved in a centralized way. With the help of auxiliary replica variables, the original LP problem is re-formulated as an equivalent optimization problem with the structure more amenable for decomposition, which is further decoupled into a series of subtasks. By applying the classic alternating direction method of multipliers (ADMM), these subtasks are solved in a distributed way while still guaranteeing the convergence to the centralized solution.
7. Conclusions and Open Problems
Wireless sensor networks can be applied to a variety of applications, and most of these applications require synchronization among the sensor nodes. Based on the two-way message exchange system model described in Section 2.2, this paper surveyed the most representative pairwise and fully-distributed clock synchronization algorithms from a statistical signal processing viewpoint. The interested reader is referred to [59,60,61,62,63] for references based on other system models. Specifically, similar to Equation (2), [59] adopted a two-way message exchange mechanism where no random delay is considered and the fixed portion of delays is different for the uplink and downlink (i.e., replace d in Equation (2) by and ). The main result is that while estimating the clock skew between two nodes is possible, it is impossible to determine the clock offset for pairwise synchronization, unless the delays in two-way message communication are symmetric, i.e.,
. The same result was later extended in [60] for the network case. Recently, timestamp-free synchronization algorithms were reported in [61,62] to avoid the overhead brought by timestamp exchanges. The approach employed in [61] is based on conveying implicit timing information in the physical layer via the timing responses from the receiver to the transmitter. The work in [62] avoids timestamp exchanges using the round-trip-time data, which can be measured by a time-to-digital converter in the master node. The clock parameters, such as the offset and skew, as well as the unknown range between the master and slave nodes were experimentally estimated and verified with an accuracy in the order of a nano-second. Without considering the random delays, a fully-distributed network-wide synchronization algorithm was presented in [63] by assuming the constraint that the relative clock offsets in any network loop sum to zero. Recently, Jeske [64] developed a statistical process control (SPC) algorithm that can be used in the context of the two-way message exchange mechanism to detect translations in the delay distribution.
In reflecting on the research problems which have been addressed, we have observed several open research topics that need further investigation. On the one hand, the algorithms presented in this article all assume a line-of-sight transmission. The fixed portion of delays d herein is actually related to the propagation delay between the transmitter and the receiver nodes. It may occur that some obstacles exist in the signal path, and they might reflect or simply absorb the signal. In this case, the received signal strength and the propagation delay may be significantly affected, and thus, the mathematical system model proposed in this article might not be plausible. To our best knowledge, the clock synchronization problem under non-line-of-sight transmissions is still open. In addition, even though many references that exploit the statistical system model from Section 2.2 have been reported in the literature, more convincing experimental results based on large-scale WSN testbeds are necessary for a more accurate clock synchronization system model. Other possible future research topics lie in the investigation of the convergence rate and computational complexity of the proposed distributed synchronization algorithms. Due to the limited energy of sensors in WSNs, designing new distributed synchronization schemes with reduced energy consumption, low implementation complexity and a fast convergence rate represents another fruitful research direction.
Acknowledgments
This work was supported by NSF Award CCF-1318338.
Author Contributions
Xu Wang contributed to draft writing. Daniel Jeske and Erchin Serpedin proposed the framework of the paper and helped to improve the manuscript. All authors read and approved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Durisic, M.P.; Tafa, Z.; Dimic, G.; Milutinovic, V. A survey of military applications of wireless sensor networks. In Proceedings of the IEEE 2012 Mediterranean Conference on Embedded Computing (MECO), Bar, Montenegro, 19–21 June 2012; pp. 196–199.
- Alemdar, H.; Ersoy, C. Wireless sensor networks for healthcare: A survey. Comput. Netw. 2010, 54, 2688–2710. [Google Scholar] [CrossRef]
- Mainwaring, A.; Culler, D.; Polastre, J.; Szewczyk, R.; Anderson, J. Wireless sensor networks for habitat monitoring. In Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks and Applications, Atlanta, GA, USA, 28 September 2002; pp. 88–97.
- Corke, P.; Wark, T.; Jurdak, R.; Hu, W.; Valencia, P.; Moore, D. Environmental wireless sensor networks. IEEE Proc. 2010, 98, 1903–1917. [Google Scholar] [CrossRef]
- Ye, D.; Gong, D.; Wang, W. Application of wireless sensor networks in environmental monitoring. In Proceedings of the IEEE 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, China, 19–20 December 2009; Volume 1, pp. 205–208.
- Herring, C.; Kaplan, S. Component-based software systems for smart environments. IEEE Pers. Commun. 2000, 7, 60–61. [Google Scholar] [CrossRef]
- Gokbayrak, A.B.; Divarci, S.; Urhan, O. Wireless sensor network gateway design for home automation applications. In Proceedings of the IEEE 22nd Signal Processing and Communications Applications Conference (SIU), Trabzon, Turkey, 23–25 April 2014; pp. 1770–1773.
- Flammini, A.; Ferrari, P.; Marioli, D.; Sisinni, E.; Taroni, A. Wired and wireless sensor networks for industrial applications. Microelectron. J. 2009, 40, 1322–1336. [Google Scholar] [CrossRef]
- Wu, Y.C.; Chaudhari, Q.; Serpedin, E. Clock synchronization of wireless sensor networks. IEEE Signal Process. Mag. 2011, 28, 124–138. [Google Scholar] [CrossRef]
- Rhee, I.K.; Lee, J.; Kim, J.; Serpedin, E.; Wu, Y.C. Clock synchronization in wireless sensor networks: An overview. Sensors 2009, 9, 56–85. [Google Scholar] [CrossRef] [PubMed]
- Mills, D.L. Internet time synchronization: The network time protocol. IEEE Trans. Commun. 1991, 39, 1482–1493. [Google Scholar] [CrossRef]
- Ganeriwal, S.; Kumar, R.; Srivastava, M.B. Timing-sync protocol for sensor networks. In Proceedings of the 1st International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 5–7 November 2003; pp. 138–149.
- Sichitiu, M.L.; Veerarittiphan, C. Simple, accurate time synchronization for wireless sensor networks. In Proceedings of the IEEE Wireless Communications and Networking (WCNC), New Orleans, LA, USA, 16–20 March 2003; Volume 2, pp. 1266–1273.
- Van Greunen, J.; Rabaey, J. Lightweight time synchronization for sensor networks. In Proceedings of the 2nd ACM International Conference on Wireless Sensor Networks and Applications, San Diego, CA, USA, 19 September 2003; pp. 11–19.
- Maróti, M.; Kusy, B.; Simon, G.; Maróti, M.; Kusy, B.; Simon, G.; Lédeczi, Á. The flooding time synchronization protocol. In Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems, Baltimore, MD, USA, 3–5 November 2004; pp. 39–49.
- Youn, S. A comparison of clock synchronization in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2013, 2013. [Google Scholar] [CrossRef]
- Simeone, O.; Spagnolini, U.; Bar-Ness, Y.; Strogatz, S.H. Distributed synchronization in wireless networks. IEEE Signal Process. Mag. 2008, 25, 81–97. [Google Scholar] [CrossRef]
- Noh, K.L.; Chaudhari, Q.M.; Serpedin, E.; Suter, B.W. Novel clock phase offset and skew estimation using two-way timing message exchanges for wireless sensor networks. IEEE Trans. Commun. 2007, 55, 766–777. [Google Scholar] [CrossRef]
- Ahmad, A.; Noor, A.; Serpedin, E.; Nounou, H.; Nounou, M. On clock offset estimation in wireless sensor networks with Weibull distributed network delays. In Proceedings of the IEEE 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; pp. 2322–2325.
- Papoulis, A. Random Variable and Stochastic Processes; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Bovy, C.; Mertodimedjo, H.; Hooghiemstra, G.; Uijterwaal, H.; Van Mieghem, P. Analysis of end-to-end delay measurements in Internet. In Proceedings of the ACM Conference on Passive and Active Leasurements (PAM), Fort Collins, CO, USA, 25–26 March 2002.
- Etzlinger, B.; Wymeersch, H.; Springer, A. Cooperative synchronization in wireless networks. IEEE Trans. Signal Process. 2013, 62, 2837–2849. [Google Scholar]
- Kay, S. Fundamentals of Statistical Signal Processing, Volume I: Estimation Theory; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Leng, M.; Wu, Y.C. On clock synchronization algorithms for wireless sensor networks under unknown delay. IEEE Trans. Veh. Technol. 2010, 59, 182–190. [Google Scholar] [CrossRef]
- Abdel-Ghaffar, H.S. Analysis of synchronization algorithms with time-out control over networks with exponentially symmetric delays. IEEE Trans. Commun. 2002, 50, 1652–1661. [Google Scholar] [CrossRef]
- Moon, S.B.; Skelly, P.; Towsley, D. Estimation and removal of clock skew from network delay measurements. In Proceedings of the IEEE 18th Annual Joint Conference of the IEEE Computer and Communications Societies, New York, NY, USA, 21–25 March 1999; Volume 1, pp. 227–234.
- Paxson, V. On calibrating measurements of packet transit times. ACM SIGMETRICS Perform. Eval. Rev. 1998, 26, 11–21. [Google Scholar] [CrossRef]
- Jeske, D.R. On maximum-likelihood estimation of clock offset. IEEE Trans. Commun. 2005, 53, 53–54. [Google Scholar] [CrossRef]
- Ahmad, A.; Zennaro, D.; Serpedin, E.; Vangelista, L. A factor graph approach to clock offset estimation in wireless sensor networks. IEEE Trans. Inf. Theory 2012, 58, 4244–4260. [Google Scholar] [CrossRef]
- Jeske, D.R.; Sampath, A. Estimation of clock offset using bootstrap bias-correction techniques. Technometrics 2003, 45, 256–261. [Google Scholar] [CrossRef]
- Chaudhari, Q.M.; Serpedin, E.; Qaraqe, K. On minimum variance unbiased estimation of clock offset in a two-way message exchange mechanism. IEEE Trans. Inf. Theory 2010, 56, 2893–2904. [Google Scholar] [CrossRef]
- Leng, M.; Wu, Y.C. On joint synchronization of clock offset and skew for wireless sensor networks under exponential delay. In Proceedings of the IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 461–464.
- Chaudhari, Q.M.; Serpedin, E.; Qaraqe, K. On maximum likelihood estimation of clock offset and skew in networks with exponential delays. IEEE Trans. Signal Process. 2008, 56, 1685–1697. [Google Scholar] [CrossRef]
- Li, J.; Jeske, D.R. Maximum likelihood estimators of clock offset and skew under exponential delays. Appl. Stoch. Model. Bus. Ind. 2009, 25, 445–459. [Google Scholar] [CrossRef]
- Li, J.; Jeske, D.R.; Pettyjohn, J. Approximate and generalized pivotal quantities for deriving confidence intervals for the offset between two clocks. Stat. Methodol. 2009, 6, 97–107. [Google Scholar] [CrossRef]
- Li, J.; Jeske, D.R. Sequential Fixed Width Confidence Intervals for the Offset Between Two Network Clocks. Seq. Anal. 2009, 28, 475–487. [Google Scholar] [CrossRef]
- Pettyjohn, J.; Jeske, D.R.; Li, J. Estimation and Confidence Intervals for Clock Offset in Networks with Bivariate Exponential Delays. Commun. Stat.-Theory Methods 2013, 42, 1024–1041. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, J.; Serpedin, E.; Qaraqe, K. A robust approach for clock offset estimation in wireless sensor networks. EURASIP J. Adv. Signal Process. 2010, 2010, 19. [Google Scholar] [CrossRef]
- Pettyjohn, J.S.; Jeske, D.R.; Li, J. Least squares-based estimation of relative clock offset and frequency in sensor networks with high latency. IEEE Trans. Commun. 2010, 58, 3613–3620. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Jeske, D.R.; Chakravartty, A. Effectiveness of bootstrap bias correction in the context of clock offset estimators. Technometrics 2006, 48, 530–538. [Google Scholar] [CrossRef]
- Fujimoto, K.; Ata, S.; Murata, M. Playout control for streaming applications by statistical delay analysis. In Proceedings of the IEEE International Conference on Communications (ICC 2001), Helsinki, Finland, 11–14 June 2001; Volume 8, pp. 2337–2342.
- Loguinov, D.; Radha, H. Effects of channel delays on underflow events of compressed video over the Internet. In Proceedings of the IEEE 2002 International Conference on Image Processing, New York, NY, USA, 22–25 September 2002; Volume 2, pp. II–205–II–208.
- Ding, L.; Goubran, R.A. Speech quality prediction in VoIP using the extended E-model. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM'03), Francisco, CA, USA, 1–5 December 2003; Volume 7, pp. 3974–3978.
- Jeske, D.R. Jackknife Bias Correction of a Clock Offset Estimator. In Advances in Mathematical and Statistical Modeling; Springer: New York, NY, USA, 2008; pp. 245–254. [Google Scholar]
- Leng, M.; Wu, Y.C. Distributed clock synchronization for wireless sensor networks using belief propagation. IEEE Trans. Signal Process. 2011, 59, 5404–5414. [Google Scholar] [CrossRef]
- Du, J.; Wu, Y.C. Distributed clock skew and offset estimation in wireless sensor networks: Asynchronous algorithm and convergence analysis. IEEE Trans. Wirel. Commun. 2013, 12, 5908–5917. [Google Scholar] [CrossRef]
- Yedidia, J.S.; Freeman, W.T.; Weiss, Y. Understanding belief propagation and its generalizations. Explor. Artif. Intell. New Millenn. 2003, 8, 236–239. [Google Scholar]
- Li, Q.; Rus, D. Global clock synchronization in sensor networks. IEEE Trans. Comput. 2006, 55, 214–226. [Google Scholar]
- Giridhar, A.; Kumar, P. Distributed clock synchronization over wireless networks: Algorithms and analysis. In Proceedings of the 2006 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 4915–4920.
- Schenato, L.; Gamba, G. A distributed consensus protocol for clock synchronization in wireless sensor network. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 2289–2294.
- Zennaro, D.; Dall'Anese, E.; Erseghe, T.; Vangelista, L. Fast clock synchronization in wireless sensor networks via ADMM-based consensus. In Proceedings of the IEEE 2011 International Symposium on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks (WiOpt), Princeton, NJ, USA, 9–13 May 2011; pp. 148–153.
- Maggs, M.K.; O’Keefe, S.G.; Thiel, D.V. Consensus clock synchronization for wireless sensor networks. IEEE Sens. J. 2012, 12, 2269–2277. [Google Scholar] [CrossRef]
- Berger, A.; Pichler, M.; Klinglmayr, J.; Potsch, A.; Springer, A. Low-Complex Synchronization Algorithms for Embedded Wireless Sensor Networks. IEEE Trans. Instrum. Meas. 2015, 64, 1032–1042. [Google Scholar] [CrossRef]
- Schenato, L.; Fiorentin, F. Average TimeSynch: A consensus-based protocol for clock synchronization in wireless sensor networks. Automatica 2011, 47, 1878–1886. [Google Scholar] [CrossRef]
- Gang, X.; Shalinee, K. Analysis of distributed consensus time synchronization with Gaussian delay over wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2009, 2009. [Google Scholar] [CrossRef]
- Zennaro, D.; Ahmad, A.; Vangelista, L.; Serpedin, E.; Nounou, H.; Nounou, M. Network-wide clock synchronization via message passing with exponentially distributed link delays. IEEE Trans. Commun. 2013, 61, 2012–2024. [Google Scholar] [CrossRef]
- Luo, B.; Cheng, L.; Wu, Y.C. Fully-distributed joint clock synchronization and ranging in wireless sensor networks under exponential delays. In Proceedings of the 2014 IEEE International Conference on Communication Systems (ICCS), Macau, China, 19–21 November 2014; pp. 152–156.
- Graham, S.; Kumar, P. Time in general-purpose control systems: The control time protocol and an experimental evaluation. In Proceedings of the 43rd IEEE Conference on Decision and Control (2004 CDC), Paadise Island, Bahamas, 14–17 December 2004; Volume 4, pp. 4004–4009.
- Freris, N.M.; Graham, S.R.; Kumar, P. Fundamental limits on synchronizing clocks over networks. IEEE Trans. Autom. Control 2011, 56, 1352–1364. [Google Scholar] [CrossRef]
- Brown, D.R.; Klein, A.G. Timestamp-free network synchronization with random pairwise message exchanges. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 5754–5758.
- Dwivedi, S.; de Angelis, A.; Zachariah, D.; Handel, P. Joint Ranging and Clock Parameter Estimation by Wireless Round Trip Time Measurements. IEEE Trans. Sel. Areas Commun. 2015, 99. [Google Scholar] [CrossRef]
- Solis, R.; Borkar, V.S.; Kumar, P. A new distributed time synchronization protocol for multihop wireless networks. In Proceedings of the 2006 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 2734–2739.
- Jeske, D.R. CUSUM algorithm for detecting translations in gamma distributions. Qual. Reliab. Eng. Int. 2015, 31. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).