Abstract
In dynamic propagation environments, beamforming algorithms may suffer from strong interference, steering vector mismatches, a low convergence speed and a high computational complexity. Reduced-rank signal processing techniques provide a way to address the problems mentioned above. This paper presents a low-complexity robust data-dependent dimensionality reduction based on an iterative optimization with steering vector perturbation (IOVP) algorithm for reduced-rank beamforming and steering vector estimation. The proposed robust optimization procedure jointly adjusts the parameters of a rank reduction matrix and an adaptive beamformer. The optimized rank reduction matrix projects the received signal vector onto a subspace with lower dimension. The beamformer/steering vector optimization is then performed in a reduced dimension subspace. We devise efficient stochastic gradient and recursive least-squares algorithms for implementing the proposed robust IOVP design. The proposed robust IOVP beamforming algorithms result in a faster convergence speed and an improved performance. Simulation results show that the proposed IOVP algorithms outperform some existing full-rank and reduced-rank algorithms with a comparable complexity.
1. Introduction
Adaptive beamforming algorithms often encounter problems when they operate in dynamic environments with large sensor arrays. These problems include steering vector mismatches, high computational complexity and snapshot deficiency. Steering vector mismatches are often caused by calibration/pointing errors, and a high complexity is usually introduced by an expensive inverse operation of the covariance matrix of the received data. High computational complexity and snapshot deficiency may prevent the use of adaptive beamforming in important applications, like sonar and radar [1,2]. The adaptive beamforming techniques are usually required to have a trade-off between performance and complexity, which depends on the designer’s choice of the adaptation algorithm.
In order to overcome this computational complexity issue, adaptive versions of the linearly-constrained beamforming algorithms, such as minimum variance distortionless response (MVDR) with stochastic gradient and recursive least squares [1,2,3], have been extensively reported. These adaptive algorithms estimate the data covariance matrix iteratively, and the complexity is reduced by recursively computing the weights. However, in a dynamic environment with large sensor arrays, such as those found in radar and sonar applications, adaptive beamformers with a large number of array elements may fail in tracking signals embedded in strong interference and noise. The convergence speed and tracking properties of adaptive beamformers depend on the size of the sensor array and the eigen-spread of the received covariance matrix [2].
Regarding the steering vector mismatches often found in practical applications of beamforming, they are responsible for a significant performance degradation of algorithms. Prior work on robust beamforming design [4,5,6,7] has considered different strategies to mitigate the effects of these mismatches. However, a key limitation of these robust techniques [4,5,6,7] is their high computational cost for large sensor arrays and their suitability to dynamic environments. These algorithms need to estimate the covariance matrix of the sensor data, which is a challenging task for a system with a large array and operates in highly dynamic situations. Given this dependency on the number of sensor elements M, it is thus intuitive to reduce M while simultaneously extracting the key features of the original signal via an appropriate transformation.
Reduced-rank signal processing techniques [7,8,9,10,11,12,13,14,15,16,17] provide a way to address some of the problems mentioned above. Reduced dimension methods are often needed to speed up the convergence of beamforming algorithms and reduce their computational complexity. They are particularly useful in scenarios in which the interference lies in a low-rank subspace, and the number of degrees of freedom required to mitigate the interference through beamforming is significantly lower than that available in the sensor array. In reduced-rank schemes, a rank reduction matrix is introduced to project the original full-dimension received signal onto a lower dimension. The advantage of reduced-rank methods lies in their superior convergence and tracking performance achieved by exploiting the low-rank nature of the signals. It offers a large reduction in the required number of training samples over full-rank methods [2], which may also addresses the problem of snapshot deficiency at low complexity. Several reduced-rank strategies for processing data collected from a large number of sensors have been reported in the last few years, which include beamspace methods [7], Krylov subspace techniques [13,14] and methods of joint and iterative optimization of parameters in [15,16,17].
Despite the improved convergence and tracking performance achieved with Krylov methods [13,14], they are relatively complex and may suffer from numerical problems. On the other hand, the joint iterative optimization (JIO) technique reported in [16] outperforms the Krylov-based method with efficient adaptive implementations. However, the theoretical JIO dimensionality reduction transform matrix, Equation (63) in [16], is in fact rank-one; the column space of the JIO matrix is precisely the MVDR line. The rank selection scheme may fail to work; performance degradation is then expected. In order to address this problem, in this paper, we introduce a low-complexity robust data-dependent dimensionality reduction algorithm for reduced-rank beamforming and steering vector estimation. The proposed iterative optimization with steering vector perturbation (IOVP) design strategy jointly optimizes a projection matrix and a reduced-rank beamformer by introducing several independently-generated small perturbations of the assumed steering vector. With these vectors, the scheme updates a different column of the projection matrix in each recursion and concatenates these columns to ensure that the projection matrix has a desired rank.
The contributions of this paper are summarized as follows:
- A bank of perturbed steering vectors is proposed as candidate array steering vectors around the true steering vector. The candidate steering vectors are responsible for performing rank reduction, and the reduced-rank beamformer forms the beam in the direction of the signal of interest (SoI).
- We devise efficient stochastic gradient (SG) and recursive least-squares (RLS) algorithms for implementing the proposed robust IOVP design.
- We introduce an automatic rank selection scheme in order to obtain the optimal beamforming performance with low computational complexity.
Simulation results show that the proposed IOVP algorithms outperform existing full-rank and reduced-rank algorithms with a comparable complexity.
2. System Model
Let us consider a uniform linear array (ULA) with M sensor elements, which receive K narrowband signals where . The directionsof arrival (DoAs) of the K signals are . The received vector at the i-th snapshot (time instant) can be modelled as:
where convey the DoAs of the K signal sources. comprises K steering vectors, which are given as:
where is the wavelength and ι is the inter-element distance of the ULA. The K steering vectors are assumed to be linearly independent. The source data are modelled as , and is the noise vector, which is assumed to be zero-mean; N is assumed to be the observation size, and denotes the time instant. For full-rank processing, the adaptive beamformer output for the SoI is written as:
where the beamformer is derived according to a design criterion. The optimal weight vector is obtained by maximizing the signal-to-interference plus noise ratio (SINR) and:
where and denote the SoI and interference plus noise covariance matrices, respectively.
2.1. Minimum Variance Distortionless Response
The MVDR/SCBwas reported as the optimal design criterion of the beamformer . The MVDR criterion obtains by solving the following optimization problem:
where is the covariance matrix obtained from the sensor array, and the array response can be calculated by employing a DoA estimation procedure. By using the technique of Lagrange multipliers, the solution of (5) is easily derived as:
where R is the covariance matrix of the received signal. In practical applications, R is approximated by the sample covariance matrix , where:
with N being the number of snapshots. Larger arrays require longer duration snapshots due to the longer transit time of sound across the array. The computation of a reliable covariance matrix requires a higher number of . More snapshots are needed due to the many elements. Usually, this leads to snapshot-deficient processing [18].
2.2. Recursive Least-Squares
The matrix inversion operation in (6) requires significant computational complexity when M is large. We derive an RLS adaptive algorithm for efficient computation of the MVDR beamformer. The inverse covariance matrix can be obtained by solving the standard least-squares (LS) problem; the LS cost function with an exponential window is given by:
where is the forgetting factor. By replacing the upper equation of (5) with (8), the Lagrangian is obtained as:
Taking the gradient of (9) with respect to , equating the terms to a zero vector and solving for λ, we obtain the beamformer as:
where the estimated covariance matrix is:
By comparing Equations (6) and (10), we can see that the MVDR beamformer can be implemented in an iterative manner, and the complexity can be significantly reduced. The filter can be estimated efficiently via the RLS algorithm. However, the laws that govern their convergence and tracking behaviours imply that they depend on the number of sensor elements M and on the eigenvalue spread of the covariance matrix R. In order to estimate without matrix inversion, we use the matrix inversion lemma [2], the gain vector and the Riccati equation for the RLS algorithm given as:
The inverse correlation matrix is obtained at each step by the recursive processes for reduced computational complexity. Equation (13) is initialized by using an identity matrix where δ is a positive constant. The above-mentioned full-rank beamformers usually suffer from high complexity and low convergence speed. In the following section, we focus on the design of the proposed low-complexity reduced-dimension beamforming algorithms.
3. Problem Statement and the Dimension Reduction with IOVP
3.1. Reduced Rank Methods and the Projection Matrix
The filter in Equation (10) can be estimated efficiently via the RLS algorithm; however, the convergence and tracking behaviours depend on M and on the eigenvalue spread of R. Reduced-dimension methods are introduced to speed up the convergence of beamforming algorithms and to reduce their computational complexity [5,8]. A reduced-rank algorithm must extract the most important features of the processed data by performing dimensionality reduction. This transformation is carried out by applying a matrix on the received data as given by:
where, in what follows, we denote the D-dimensional terms with a “bar” sign. The obtained received vector is the new input to a filter given by the vector , and the resulting filter output is:
In order to design the reduced-rank filter , from Equation (6), we consider the following optimization problem:
The solution to the above problem is:
where the dimensional reduced covariance matrix is given by and the reduced-rank steering vector is obtained by , where denotes the expectation operation. The above contents show how a projection matrix can be used to perform dimensionality reduction on the received signal and resulting in improved convergence and tracking performance over the full-rank filter listed in Equations (6) and (10).
3.2. Problem Statement and the Proposed IOVP
In previous works, the JIO approach reported in [16] outperforms the Krylov-based method with efficient adaptive implementations; however, there was a problem in this approach. Specifically, the theoretical JIO dimensionality reduction transform matrix, Equation (63) in [16], is in fact rank-one. Consequently, when the reduced dimension is selected as greater than one, so that the JIO projection matrix has more than one column, pre-processing with the JIO projection matrix will yield a singular, non-invertible reduced-rank covariance matrix, which means that the reduced dimensional weights will not exist; the rank-one column space of the JIO matrix is precisely the MVDR line, and the rank selection may fail to work.
In order to address this issue, in the following, we detail a set of novel reduced-rank algorithms based on the proposed IOVP design of beamformers. The proposed IOVP design strategy jointly optimizes a projection matrix and a reduced-rank beamformer by introducing several independently-generated small perturbations of the assumed steering vector and recursively updates a different column of the projection matrix to ensure a desired rank. The bank of adaptive beamformers in the front-end is responsible for performing dimensionality reduction, which is followed by a reduced-rank beamformer, which effectively forms the beam in the direction of the SoI. This two-stage scheme allows the adaptation with different update rates, which could lead to a significant reduction in the computational complexity per update. Specifically, this complexity reduction can be obtained as the dimensionality reduction performed by the rank reduction matrix could be updated less frequently than the reduced-rank beamformer.
The principle of the proposed IOVP reduced rank scheme is depicted in Figure 1, which employs a projection matrix to perform dimensionality reduction on data vector . The rank-reduced filter processes the reduced-rank data vector to obtain a scalar estimate of the k-th desired signal.
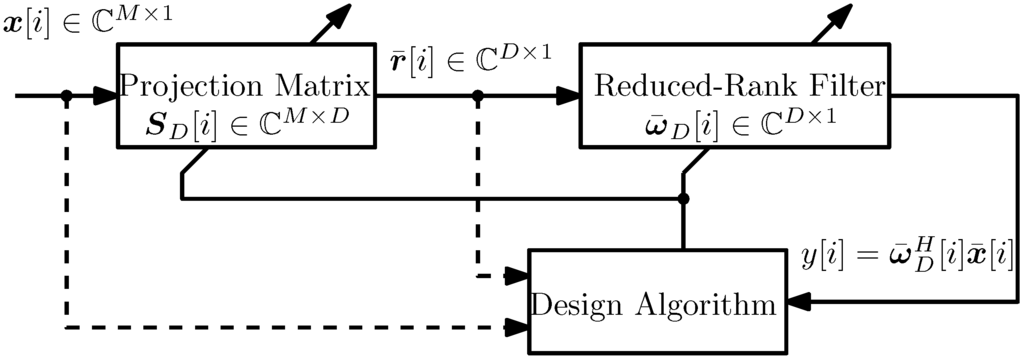
Figure 1.
Schematic of the proposed reduced-rank scheme.
Figure 1.
Schematic of the proposed reduced-rank scheme.
The design criterion of MVDR-IOVP beamformer is given by the following optimization problem:
where R is the covariance matrix obtained from sensors and vector with dimension is a zero vector except its d-th element being one. The vector is the d-th column of the projection matrix . The vectors represent the assumed steering vector and independently-generated small perturbations of the assumed steering vector. Different from the JIO approach in [16], where the columns of are jointly designed under the same criterion, the proposed IOVP approach (18) uses the vector to orthogonalize the columns of the projection matrix, and the columns can be independently updated with the perturbation vector in each recursion. The scheme updates a different column of the projection matrix in each recursion and concatenates these columns to form the projection matrix ; the concatenation procedure ensures that the projection matrix has a desired rank. According to Equation (28) in Section 3.4, an increased rank of is obtained for higher d, and the rank-one problem in [16] can be avoided. The constrained optimization problem in (18) can be solved by using the method of Lagrange multipliers [4]. The Lagrangian of the MVDR-IOVP design is expressed by:
In order to efficiently solve the above Lagrangian, in the following subsections, we introduce the stochastic gradient adaptation and the recursive least-squares adaptation methods.
3.3. Stochastic Gradient Adaptation
In this subsection, we present a low-complexity SG [2] adaptive reduced-rank algorithm for efficient implementation of the IOVP algorithm. By computing the instantaneous gradient terms of (19) with respect to and , we obtain:
where is the d-th element of the reduced-rank beamformer and the projection matrices that enforce the constraints are:
the scalar , and:
is the estimated steering vector in reduced dimension. The calculation of requires a number of complex multiplications; the computation of and requires and complex multiplications, respectively. Therefore, we can conclude that for each iteration, the SG adaptation requires complex multiplications.
3.4. Recursive Least-Squares Adaptation
Here, we derive an adaptive reduced-rank RLS [2] type algorithm for efficient implementation of the MVDR-IOVP method. The reduced-rank beamformer is updated as follows:
where:
The columns of the rank reduction matrix are updated by:
where and:
where is the forgetting factor. The inverse of the covariance matrix is obtained recursively. Equation (30) is initialized by using an identity matrix where δ is a positive constant. From Equation (28), we can see that with the proposed IOVP approach, by orthogonalizing the columns of the projection matrix , the M weights can be independently updated in each recursion, and the rank-one problem in Equation (22) of [16] can be addressed. The computational complexity of the proposed adaptive reduced-rank RLS-type MVDR-IOVP method requires complex multiplications. The MVDR-IOVP algorithm has a complexity significantly lower than a full-rank scheme if a low rank () is selected.
4. Proposed Robust Capon IOVP Beamforming
In this section, we present a robust beamforming method based on the robust capon beamforming (RCB) technique reported in [4] and the IOVP detailed in the previous section for robust beamforming applications with large sensor arrays. The proposed technique, denoted RCB-IOVP, gathers the robustness of the RCB approach [4] against uncertainties and the low complexity of IOVP techniques. Assuming that the DoA mismatch is within a spherical uncertainty set, the proposed RCB-IOVP technique solves the following optimization problem:
where is the assumed steering vector and is the updated steering vector for each iteration. The constant ϵ is related to the radius of the uncertainty sphere. The Lagrangian of the RCB-IVOP constrained optimization problem is expressed by:
where is the reduced rank covariance matrix. From the above Lagrangian, we will devise efficient adaptive beamforming algorithms in what follows.
4.1. Stochastic Gradient Adaptation
We devise an SG adaptation strategy based on the alternating minimization of the Lagrangian in (32), which yields:
where and are the step sizes of the SG algorithms, the parameter vectors and are the partial derivatives of the Lagrangian in (32) with respect to and , respectively. The recursion for is given by:
where:
and:
We denote as the difference between the updated steering vectors and the assumed one. The scalar is the d-th diagonal element of . The term denotes the d-th column vector of . The Lagrange multiplier obtained is expressed as:
4.2. Recursive Least-Squares Adaptation
We derive an RLS version of the RCB-IOVP method. The steering vector and the columns of the rank reduction matrix are updated as:
where (39) to (42) need complex multiplications, and the projection operations need a complexity of complex multiplications. It is obvious that the complexity is significantly decreased if the selected rank . The proposed RCB-IOVP RLS algorithm employs (25) and (39) to (42). The key of the RCB-IOVP RLS algorithm is to update the assumed steering vector with RLS iterations, and the updated beamformer is obtained by plugging (39) into (25) without significant extra complexity.
Note that the complexity introduced by the pseudo-inverse operation can be removed if has orthogonal column vectors; this can be achieved by incorporating the Gram–Schmidt procedure in the calculation of . Furthermore, an alternative recursive realization of the robust adaptive linear constrained beamforming method introduced by [19] can be used to further reduce the computational complexity requirement to obtain the diagonal loading terms.
5. Rank Selection
Selecting the rank number is important for the sake of computational complexity and performance. In this section, we examine the efficient implementation of two stopping criteria for selecting the rank number d. Unlike prior methods for rank selection, which utilize MSWF-based algorithms [20] or AVF-based recursions [21], we focus on an approach that jointly determines the rank number d based on the LS criterion computed by the filters and . In particular, we present a method for automatically selecting the ranks of the algorithms based on the exponentially-weighted a posteriori least-squares type cost function described by:
where α is the forgetting factor and is the reduced-rank filter with rank d. For each time interval i, we can select the rank that minimizes the cost function , and the exponential weighting factor α is required as the optimal rank varies as a function of the data record. The key quantities to be updated are the projection matrix , the reduced-rank filter , the associated reduced-rank steering vector and the inverse of the reduced-rank covariance matrix . To this end, we define the following extended projection matrix as:
and the extended reduced-rank filter weight vector as:
The extended projection matrix and the extended reduced-rank filter weight vector are updated along with the associated quantities and (only for the RLS) for the maximum allowed rank , and then, the proposed rank adaptation algorithm determines the rank that is best for each time instant i using the cost function (43). The proposed rank adaptation algorithm is then given by:
where d is an integer and and are the minimum and maximum ranks allowed for the reduced-rank filter, respectively. Note that a smaller rank may provide faster adaptation during the initial stages of the estimation procedure and a greater rank usually yields a better steady-state performance. Our studies reveal that the range for which the rank d of the proposed algorithms have a positive impact on the performance of the algorithms is limited. These values are rather insensitive to the system load and the number of array elements and work very well for all scenarios.
6. Simulations
In this section, we consider simulations for arrays with 64 and 320 sensor elements; the arrays are ULA with regular spacing between the sensor elements. The covariance matrix is obtained by time-averaging recursions with snapshots. The DoA mismatch is also considered in order to verify the robustness of various beamforming algorithms. For the robust designs, we use the spherical uncertainty set, and the upper bound is set to for 64 sensor elements and for 320 sensor elements, respectively. There are four incident signals; while the first is the SoI, the other three signals’ relative power with respect to the SoI and their DoAs in degrees are detailed in Table 1. The algorithms are trained with 120 snapshots, and the signal-to-noise ratio (SNR) is set to 10 dB for all of the simulations.

Table 1.
Interference and direction of arrival (DoA) scenario, P(dB)relative to the desired User 1/DoA (degree). SoI, signal of interest.
| Snapshots | Signal 1 (SoI) | Signal 2 | Signal 3 | Signal 4 |
|---|---|---|---|---|
| 1 to 120 | 10/90 | 20/35 | 20/135 | 20/165 |
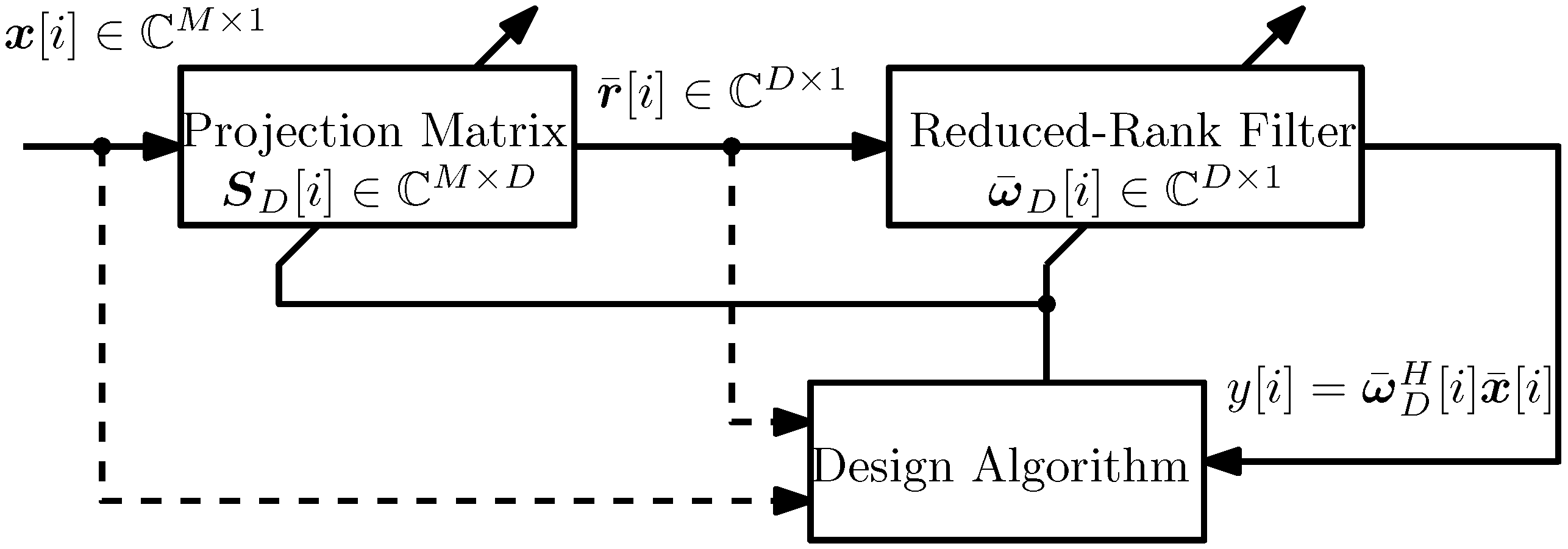
In Figure 2, we compare various beamforming techniques with a steering array of 64 elements. We introduce a maximum of two degrees of DoA mismatch, which is independently generated by a uniform random generator in each simulation run. The proposed IOVP-RLS and IOVP-SG algorithms are implemented in both non-robust MVDR [2] and robust RCB [4] schemes, respectively. The competitors including two conventional full-rank beamformers, such as MVDR-RLS and RCB-RLS, as well as two reduced-rank beamformers, such as MVDR-Krylov and RCB-Krylov [14]. In this simulation, we select for all reduced rank schemes, including MVDR-Krylov, RCB-Krylov, MVDR-IOVP-RLS/SG and RCB-IOVP-RLS/SG. A non-orthogonal Krylov projection matrix and a non-orthogonal IOVP rank reduction matrix are also generated for rank reduction. It is also important to note that the projection matrix can be initialized as , , and the inverse of the covariance matrix for each snapshot can be obtained by using the proposed RCB-IOVP-RLS algorithm.
In Figure 3, we choose a similar scenario, but without DoA mismatch. We can see from the plots that the IOVP and Krylov algorithms have a superior SINR performance to other existing methods, and this is particularly noticeable for a reduced number of snapshots. By comparing the curves in Figure 2 and Figure 3, we can see that by introducing the DoA mismatch, the conventional MVDR-RLS and RCB-Krylov-RLS schemes have about a 10-dB SINR loss; their performances are prone to steering vector mismatch. In contrast, all of the proposed IOVP reduced-rank schemes experience less than 2.5 dB of performance loss, which implies that these schemes are robust to steering vector mismatch. On the other hand, by comparing the performance of their robust rivals (such as RCB-RLS, MVDR-Krylov-RLS), the proposed schemes may provide higher SINR performance and much higher convergence speed.
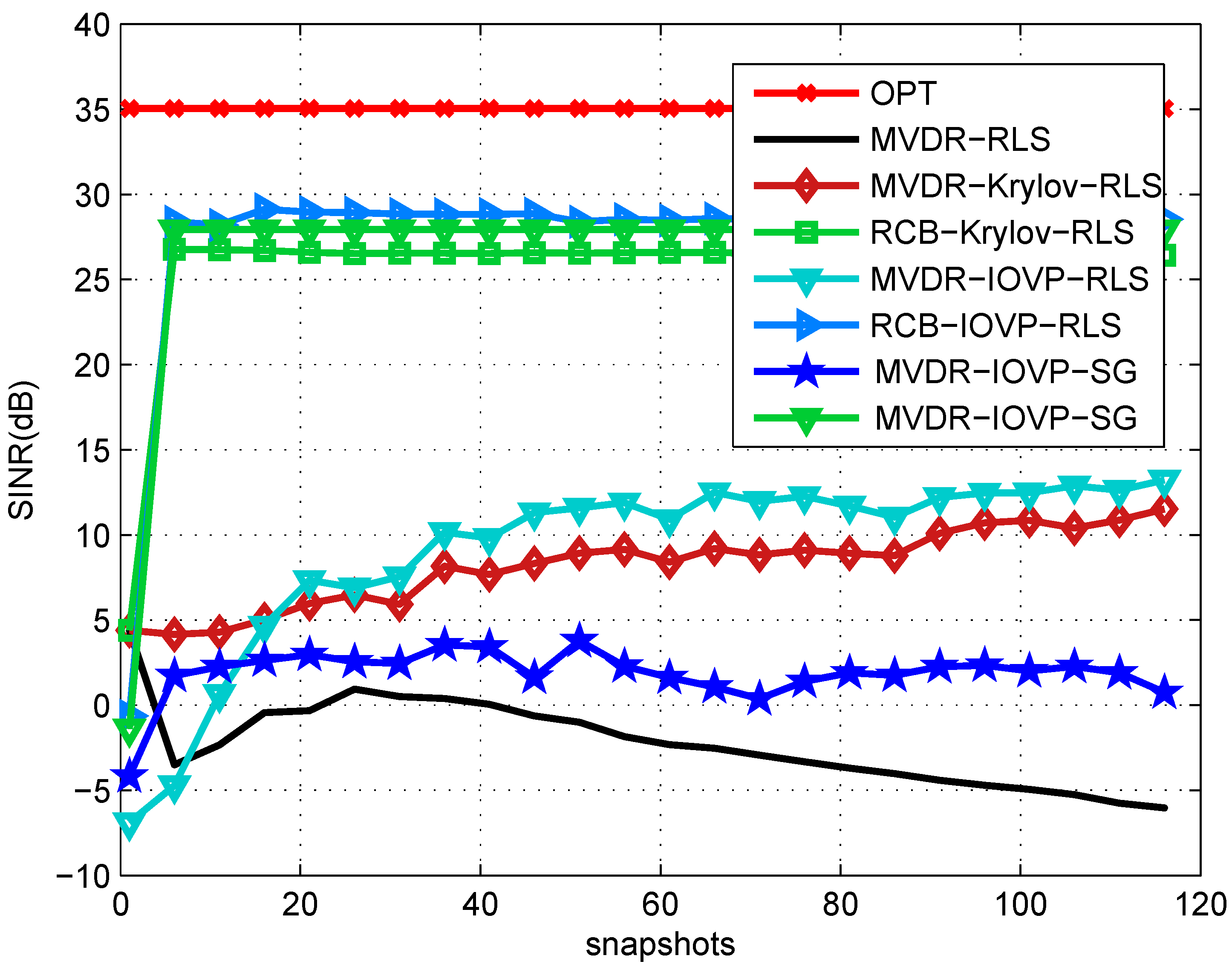
In Figure 4, we compare the output SINRs of the Krylov and the proposed IOVP rank reduction technique using a spherical constraint in the presence of steering vector errors with 320 sensor elements. We assume a DoA mismatch with two degrees and four interferences with the profile listed in Table 1. With Krylov and IOVP rank reduction, the MVDR-Krylov, MVDR-IOVP, RCB-Krylov and RCB-IOVP have superior SINR performance and a faster convergence compared to their full-rank rivals.
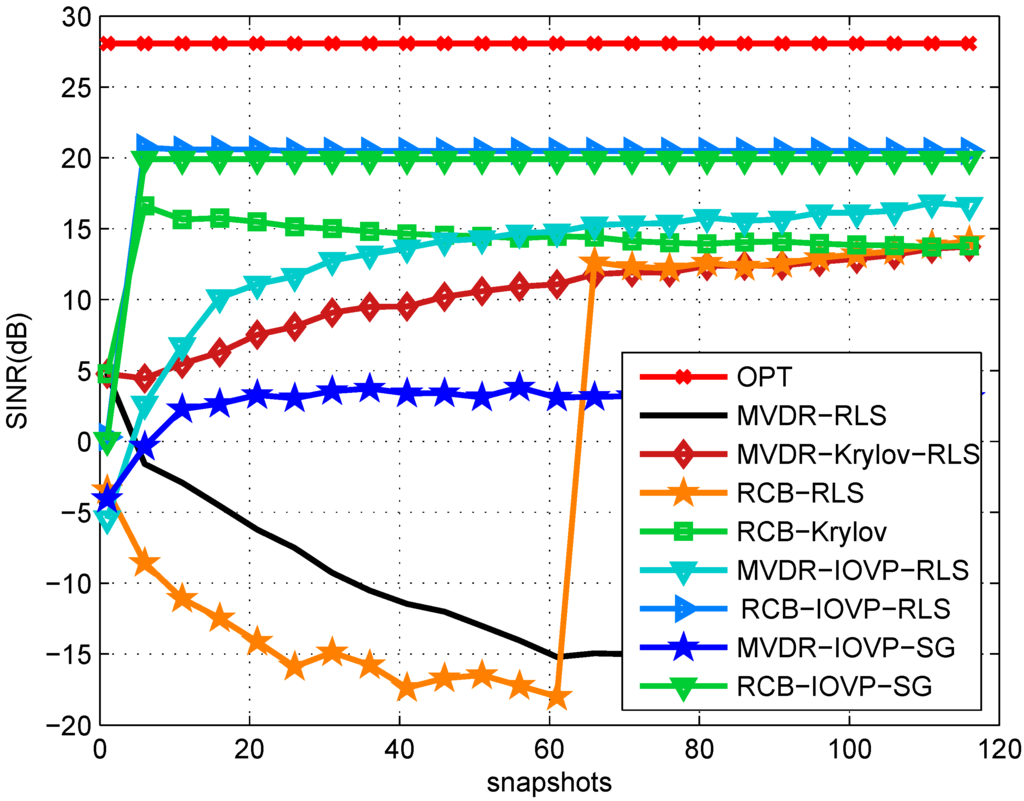
Figure 2.
Signal-to-interference plus noise ratio (SINR) performance vs. the number of snapshots, with steering vector mismatch due to 2°DoA mismatch. The spherical uncertainty set is assumed for robust beamformers (RLS indicates that the value is obtained by using RLS adaptation), non-orthogonal projection matrix.
Figure 2.
Signal-to-interference plus noise ratio (SINR) performance vs. the number of snapshots, with steering vector mismatch due to 2°DoA mismatch. The spherical uncertainty set is assumed for robust beamformers (RLS indicates that the value is obtained by using RLS adaptation), non-orthogonal projection matrix.
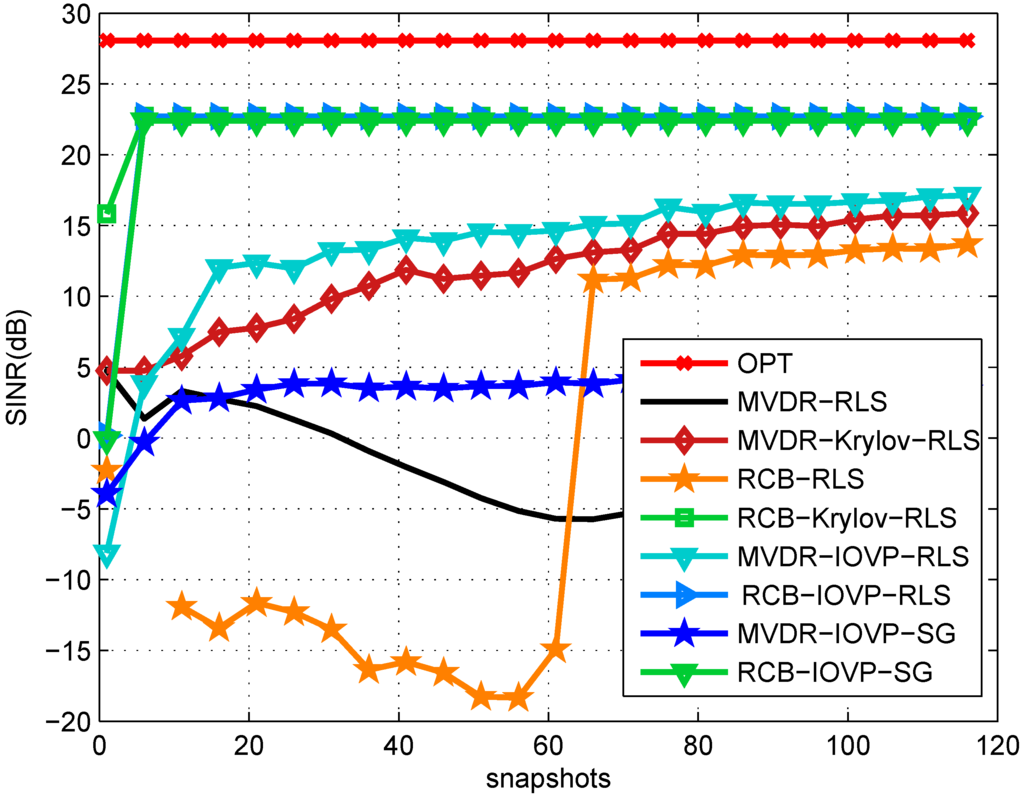
Figure 3.
SINR performance against the number of snapshots without steering vector mismatch.
Figure 3.
SINR performance against the number of snapshots without steering vector mismatch.
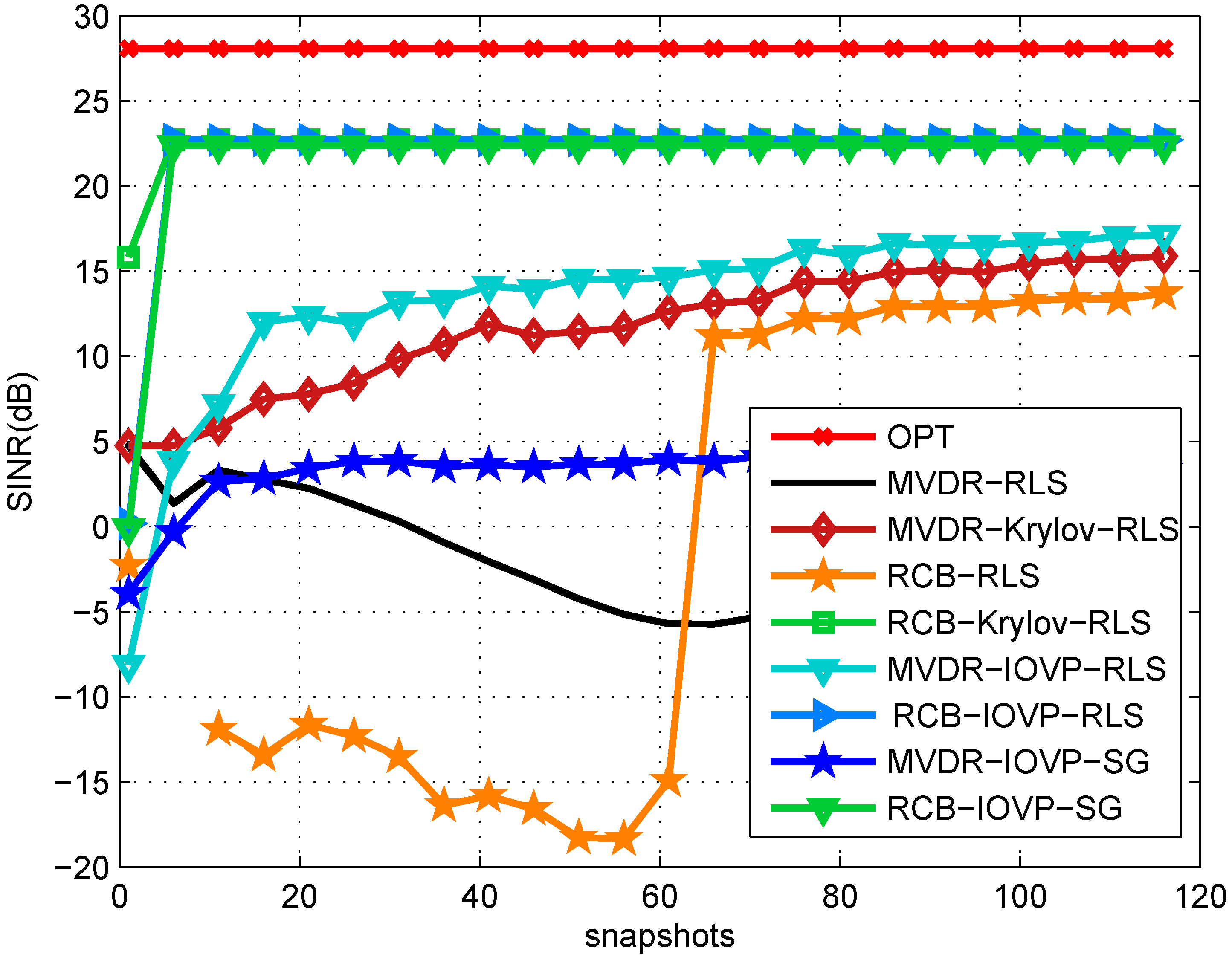
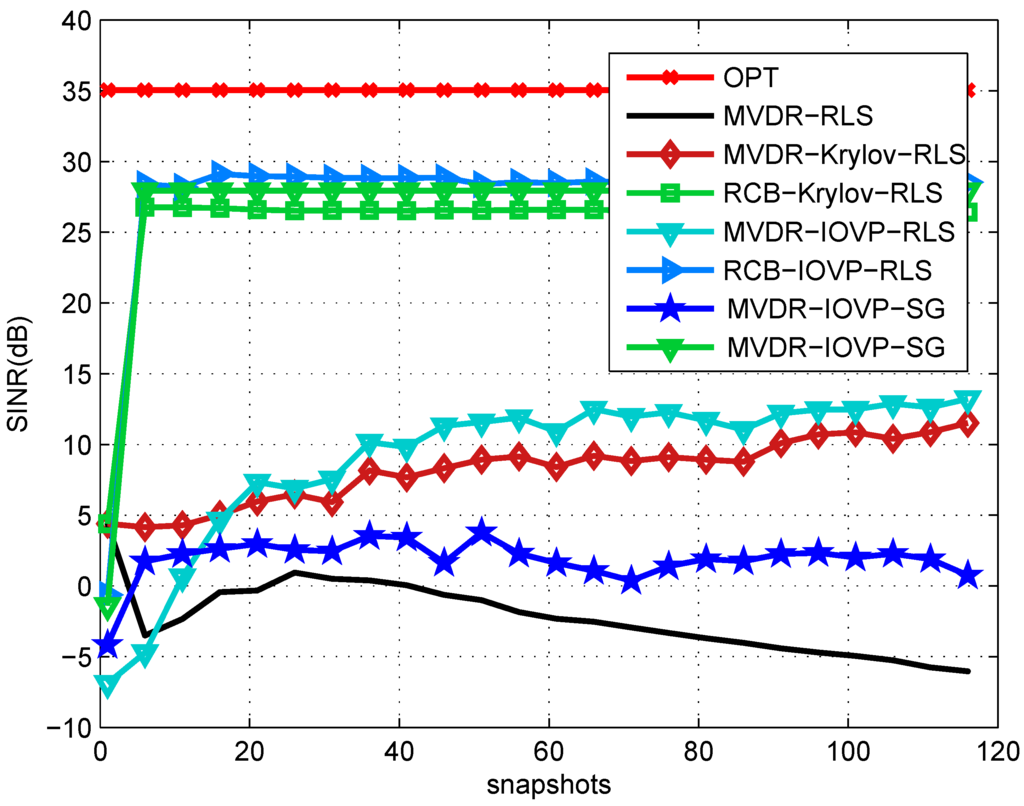
Figure 4.
SINR performance against the number of snapshots with steering vector mismatch due to 2°DoA mismatch. The spherical uncertainty set is assumed for robust beamformers with , non-orthogonal rank reduction matrix.
Figure 4.
SINR performance against the number of snapshots with steering vector mismatch due to 2°DoA mismatch. The spherical uncertainty set is assumed for robust beamformers with , non-orthogonal rank reduction matrix.
7. Conclusions
In this paper, we proposed a robust rank reduction algorithm for steering vector estimation with the method of iterative parameter optimization and vector perturbation. In this algorithm, a bank of perturbed steering vectors was introduced as candidate array steering vectors around the true steering vector. The candidate steering vectors are responsible for performing rank reduction, and the reduced-rank beamformer forms the beam in the direction of the signal of interest (SoI). The perturbation vectors and the vector were introduced in order to break the correlations among the columns of the projection matrix, and the rank number can be controlled. Additionally, we devised efficient stochastic gradient (SG) and recursive least-squares (RLS) algorithms for implementing the proposed robust IOVP design. Finally, we derived the automatic rank selection scheme in order to obtain the optimal beamforming performance with low computational complexity. The simulation results for a digital beamforming application with a large array showed that the proposed IOVP and algorithms outperformed in convergence and tracking the existing full-rank and reduced-rank algorithms at comparable complexity.
Acknowledgements
This work is supported by the Startup Foundation for Introducing Talent of NUIST.
Author Contributions
Peng Li and Rodrigo de Lamare conceived and designed the experiments; Peng Li performed the experiments; Jiao Feng analyzed the data; Peng Li and Jiao Feng wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Van Trees, H. L. Detection, Estimation, and Modulation Theory, Part IV, Optimum Array Processing; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Haykin, S. Adaptive Filter Theory; Fourth ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Li, J.; Stoica, P. Robust Adaptive Beamforming; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Li, J.; Stoica, P.; Wang, Z. On Robust Capon Beamforming and Diagonal Loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar]
- Scharf, L. L.; Tufts, D. W. Rank reduction for modeling stationary signals. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 350–355. [Google Scholar] [CrossRef]
- Vorobyov, S. A.; Gershman, A. B.; Luo, Z.-Q. Robust Adaptive Beamforming Using Worst-Case Performance Optimization: A Solution to the Signal Mismatch Problem. IEEE Trans. Signal Process. 2003, 51, 313–324. [Google Scholar] [CrossRef]
- Somasundaram, S. D. Reduced Dimension Robust Capon Beamforming for Large Aperture Passive Sonar Arrays. IET Radar Sonar Navig. 2011, 5, 707–715. [Google Scholar] [CrossRef]
- Scharf, L. L.; van Veen, B. Low rank detectors for Gaussian random vectors. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1579–1582. [Google Scholar] [CrossRef]
- Burykh, S.; Abed-Meraim, K. Reduced-rank adaptive filtering using Krylov subspace. EURASIP J. Appl. Signal Process. 2002, 12, 1387–1400. [Google Scholar] [CrossRef]
- Goldstein, J. S.; Reed, I. S.; Scharf, L. L. A multistage representation of the Wiener filter based on orthogonal projections. IEEE Trans. Inf. Theory 1998, 44, 2943–2959. [Google Scholar] [CrossRef]
- Hassanien, A.; Vorobyov, S. A. A Robust Adaptive Dimension Reduction Technique with Application to Array Processing. IEEE Signal Process. Lett. 2009, 16, 22–25. [Google Scholar] [CrossRef]
- Ge, H.; Kirsteins, I. P.; Scharf, L. L. Data Dimension Reduction Using Krylov Subspaces: Making Adaptive Beamformers Robust to Model Order-Determination. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Toulouse, France, 14–19 May 2006; Volume 4, pp. 1001–1004.
- Wang, L.; de Lamare, R. C. Constrained adaptive filtering algorithms based on conjugate gradient techniques for beamforming. IET Signal Process. 2010, 4, 686–697. [Google Scholar] [CrossRef]
- Somasundaram, S.; Li, P.; Parsons, N.; de Lamare, R. C. Data-adaptive reduced-dimension robust Capon beamforming. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013.
- De Lamare, R. C.; Sampaio-Neto, R. Adaptive reduced-rank processing based on joint and iterative interpolation, Decimation and Filtering. IEEE Trans. Signal Process. 2009, 57, 2503–2514. [Google Scholar] [CrossRef]
- De Lamare, R. C.; Wang, L.; Fa, R. Adaptive reduced-rank LCMV beamforming algorithms based on joint iterative optimization of filters: design and analysis. Signal Process. 2010, 90, 640–652. [Google Scholar] [CrossRef]
- Fa, R.; de Lamare, R. C.; Wang, L. Reduced-rank STAP schemes for airborne radar based on switched joint interpolation, decimation and filtering algorithm. IEEE Trans. Signal Process. 2010, 58, 4182–4194. [Google Scholar] [CrossRef]
- Grant, D. E.; Gross, J. H.; Lawrence, M. Z. Cross-spectral matrix estimation effects on adaptive beamformer. J. Acoust. Soc. Am. 1995, 98, 517–524. [Google Scholar] [CrossRef]
- Elnashar, A. Efficient implementation of robust adaptive beamforming based on worst-case performance optimisation. IET Signal Process. 2008, 4, 381–393. [Google Scholar] [CrossRef]
- Honig, M. L.; Goldstein, J. S. Adaptive reduced-rank interference suppression based on the multistage Wiener filter. IEEE Trans. Commun. 2002, 50, 986–994. [Google Scholar] [CrossRef]
- Haoli, Q.; Batalama, S.N. Data record-based criteria for the selection of an auxiliary vector estimator of the MMSE/MVDR filter. IEEE Trans. Commun. 2003, 51, 1700–1708. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
