One-Bit Quantization and Distributed Detection with an Unknown Scale Parameter

Abstract

We examine a distributed detection problem in a wireless sensor network, where sensor nodes collaborate to detect a Gaussian signal with an unknown change of power, i.e., a scale parameter. Due to power/bandwidth constraints, we consider the case where each sensor quantizes its observation into a binary digit. The binary data are then transmitted through error-prone wireless links to a fusion center, where a generalized likelihood ratio test (GLRT) detector is employed to perform a global decision. We study the design of a binary quantizer based on an asymptotic analysis of the GLRT. Interestingly, the quantization threshold of the quantizer is independent of the unknown scale parameter. Numerical results are included to illustrate the performance of the proposed quantizer and GLRT in binary symmetric channels (BSCs).

1. Introduction

In the context of wireless sensor networks (WSNs), the detection of unknown parameters by using a multitude of sensor nodes has been of significant interest over the past few decades (e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13] and the references therein). The widely-deployed sensors are designated to provide measurements of a given physical process (temperature, humidity, etc.), as well as to detect specific events (mobile target, acoustic source, etc.) over a region of interest. An important strategy has been followed in many studies, where a fusion center (FC) is employed to make a global decision based on original observations fromlocal sensors.

In practice, especially to meet bandwidth/energy constraints, there is a need to reduce the dimension of raw measurements from each sensor to the FC by using one-bit quantization [1,2,3,4,5,6,7,8,9,10,11]. In [4], a fixed quantization (FQ) approach was examined for distributed estimation of a mean parameter (i.e., the mean of observations). It was shown that the optimum quantization threshold depends on the unknown parameter to be estimated and is thus practically infeasible. To overcome this difficulty, a distributed adaptive quantization (AQ) approach was proposed in [5,6], where the threshold is dynamically regulated from one sensor to another, in such a way that the threshold converges to the optimum threshold.In [7], the design of the binary antisymmetric quantizer was studied by the minimization of the worst case of the Cramér–Rao bound (CRB). Using a generalized likelihood ratio test (GLRT) framework, joint estimation and detection of an unknown mean parameter based on one-bit quantization was considered in [8]. A one-bit Rao detector was introduced as a computationally-efficient alternative to the GLRTin [9]. Meanwhile, distributed estimation of both an unknown mean parameter and a scale parameter was considered in [10], where sensors are divided into two groups, each using a different threshold to generate binary observations. In situations with less stringent bandwidth/power constraints, multi-bit quantization strategies can be employed with enhanced estimation performance [11,12,13].

In this paper, we consider the problem of quantization for change detection using one-bit quantized observations collected by distributed sensors and forwarded to a FC through distortive binary symmetric channels (BSCs). The change detection problem involves an unknown change of the power, i.e., a scale parameter, of the observed signals. To deal with the unknown parameter, we employ the GLRT approach to develop a fusion rule for the FC to solve the change detection problem. We propose a one-bit quantizer based on an asymptotic analysis of the GLRT. Our analysis demonstrates that the optimum quantization thresholds for local sensors for GLRT fusion rule are identical and unrelated to the unknown scale parameter. However, the optimum quantization threshold is dependent on the cross-over error probability of the BSCs.

This paper is organized as follows. The problem is formulated in Section 2. In Section 3, the GLRT fusion rule is proposed. In Section 4, we present an asymptotic analysis of the GLRT, which is used to design the one-bit GLRT quantizers. In Section 5, the GLRT using unquantized observations in presented as a benchmark to the proposed quantization/detection schemes. Simulation results and comparisons are provided in Section 6. Finally, concluding remarks are given in Section 7.

2. Problem Formulation

We use a WSN with N spatially-distributed sensor nodes to detect a random Gaussian signal with an unknown variance ${\sigma }_1^2$. Each sensor collects an observation described as follows:

$$\left\{\begin{array}{cc}& H_0:x_n\sim 𝒩(0,{\sigma }_0^2),\hfill \\ & H_1:x_n\sim 𝒩(0,{\sigma }_1^2),\hfill \end{array}\right.n=1,2,...,N$$

(1)

Specifically, $x_n$ are independent and identically distributed (i.i.d.) Gaussian random variables with zero mean and variance ${\sigma }_i^2$ under hypothesis $H_i$, $i=0,1$, where it is assumed that the scale parameter ${\sigma }_0$ is known, whereas ${\sigma }_1$ is not. For the considered problem, the sensors are employed to monitor a sudden change of the signal power from a normal state with a known ${\sigma }_0$ to an abnormal state with anunknown ${\sigma }_1$.

There are several applications to which our formulation is relevant. One notable example is spectrum sensing (SS), where the secondary user (SU) needs to reliably detect weak licenseduser (LU) signals of possibly unknown types over a targeted frequency band in order to opportunistically use under-utilized frequency bands [14,15]. In distributed SS scenarios, multiple SUs collaborate in detecting the presence/absence of the LU [14]. The received signal at each SU is often modeled as a zero-mean Gaussian random variable with different variances under the null and alternative hypotheses, respectively (e.g., [14,15,16]). We assume the sensors are in a small neighborhood, and each of them is exposed to the same phenomenon. For the aforementioned spectral sensing problems, this implies that the collaborating secondary users are relatively close to each other, compared with their distances to the licensed user (e.g., a TV tower). As a result, their received signals have similar power.

Due to limited bandwidth/power budgets in WSNs, we consider a case where all sensor nodes quantize their local observations $\left\{x_n\right\}$ into one-bit binary data $\left\{b_n\right\}$ before transmitting them to the FC. The quantized observations $\left\{b_n\right\}$ are transmitted to the FC through some noisy wireless links, and the FC forms a global decision. The problem of interest is to design the one-bit quantizer for the sensors and the fusion rule for the FC.

3. GLRT-Based Fusion Rule

In this section, we discuss a GLRT-based fusion rule by assuming that the quantizers are known. The quantized data are transmitted to the FC over a distortion channel modeled as binary symmetric channels (BSCs) to form a global decision. The design of the quantizers will be discussed in Section 4.

3.1. One-Bit Quantization Schemes

In our study, we consider a non-regular quantizer using a pair of symmetric thresholds $\pm {\tau }_n({\tau }_n>0)$ [17] (p. 314) :

$$b_n=Q\left(x_n\right)=\left\{\begin{array}{cc}0,\hfill & \text{if}|x_n|\le {\tau }_n,\hfill \\ 1,\hfill & \text{if}|x_n|>{\tau }_n,\hfill \end{array}\right.n=1,2,\cdots ,N$$

(2)

where $x_n$ denotes the local observation at the n-th sensor and $b_n$ the quantized binary digit. To facilitate our analysis, we describe $x_n$ under $H_1$ as:

$$x_n={\sigma }_1{w}_n,n=1,2,...,N,$$

(3)

where $w_n$ denotes a random variable having the same distribution as $x_n$, but with unit variance; ${\sigma }_1$ is the unknown scale parameter to be estimated. Then, under hypothesis $H_i$, $i=0$ or 1, the probability mass function (PMF) of $b_n$ is:

$$\begin{array}{c}\hfill P_{B,i}(b_n;{\sigma }_i)={\left[2-2F_w\left(\frac{{\tau }_n}{{\sigma }_i}\right)\right]}^{b_n}{\left[2F_w\left(\frac{{\tau }_n}{{\sigma }_i}\right)-1\right]}^{1-b_n}\end{array}$$

(4)

where $F_w(·)$ denotes the cumulative distribution function (CDF) of $w_n$.

3.2. Distortion Channel: BSC

Let $b_n$ denote the binary data obtained by the quantizer (2). We assume that the distortion channels between all sensor nodes and the FC are independent, and each of them is modeled as a binary symmetric channel (BSC), i.e.,

$$y_n=\left\{\begin{array}{cc}& b_n\text{with probability}1-\tilde{p}\hfill \\ & 1-b_n\text{with probability}\tilde{p}\hfill \end{array}\right.$$

(5)

where $y_n$ denotes the received data given input $b_n$ and $\tilde{p}$ is the crossover probability of the BSC. Clearly, the PMF of the received data at the FC under $H_i$, $i=0$ or 1, is expressed as:

$$\begin{array}{c}\hfill P_{Y,i}(y_n;{\sigma }_i)=(1-\tilde{p})P_{B,i}(y_n;{\sigma }_i)+\tilde{p}{P}_{B,i}(1-y_n;{\sigma }_i)\end{array}$$

(6)

3.3. GLRT Detector

Based on the quantization scheme, due to the unknown parameter ${\sigma }_1$, we apply the GLRT [18] to solve the detection problem in (1). The GLRT detector can be obtained by replacing the unknown parameter with its maximum likelihood (ML) estimate, i.e.,

$$T_{}^{}\left(\mathbf{y}\right)=\frac{P_{\mathbf{Y},1}(\mathbf{y};{\widehat{\sigma }}_1)}{P_{\mathbf{Y},0}(\mathbf{y};{\sigma }_0)}\underset{H_0}{\overset{H_1}{\gtrless }}\eta$$

(7)

where $\mathbf{y}=[y_1^{},y_2^{},...,y_N^{}]$ contains the received data at the FC, $T_{}^{}\left(\mathbf{y}\right)$ denotes the test statistic, $P_{\mathbf{Y},i}(\mathbf{y};{\widehat{\sigma }}_i)$, $i=0$ or 1, denotes the PMF or likelihood function of y under hypothesis i corresponding to the non-regular quantization scheme, ${\widehat{\sigma }}_1$ is the ML estimate under $H_1$ and η is a detection threshold.

Specifically, since $\left\{y_n\right\}$ are independent, the likelihood function under $H_i$ is given by:

$$\begin{array}{c}\hfill P_{\mathbf{Y},i}(\mathbf{y};{\sigma }_i)=\prod _{n=1}^N{P}_{Y,i}(y_n;{\sigma }_i)\end{array}$$

(8)

The ML estimate ${\widehat{\sigma }}_1$ is obtained by maximizing the likelihood function under $H_1$, i.e.,

$${\widehat{\sigma }}_1\triangleq arg\underset{{\sigma }_1}{max}{P}_{\mathbf{Y},1}(\mathbf{y};{\sigma }_1)$$

(9)

For the considered quantizer, the ML estimate ${\widehat{\sigma }}_1$ cannot be computed in closed-form. However, it can be efficiently obtained through a one-dimensional (1D) search (e.g., gradient search). Substituting the ML estimate ${\widehat{\sigma }}_1$ in (7), we can obtain the GLRT detector.

4. Quantizer Design

This section considers the optimization of the one-bit quantizers by using an asymptotic result of the GLRT detector as our design criterion.

4.1. Asymptotic Performance Analysis

According to [18] (p. 206) , the asymptotic statistical distribution of the modified test statistic $2ln{T}^{}\left(\mathbf{y}\right)$ asymptotically follows:

$$2ln{T}^{}\left(\mathbf{y}\right)\stackrel{a}{\sim }\left\{\begin{array}{ccc}& {\chi }_1^2,\hfill & \hfill under{H}_0^{},\\ & {\chi }_1^{\text{'}2}\left(\lambda \right),\hfill & \hfill under{H}_1^{},\end{array}\right.$$

(10)

where “a” denotes an asymptotic distribution; ${\chi }_r^2$ denotes a chi-squared distribution with r degrees of freedom (DOFs); ${\chi }_r^{\text{'}2}\left(\lambda \right)$ designates a non-central chi-squared distribution with r DOFs and the non-centrality parameter λ given by:

$$\lambda ={({\sigma }_1-{\sigma }_0)}^2\text{FI}\left(\sigma \right){|}_{\sigma ={\sigma }_0}$$

(11)

where $\text{FI}\left(\sigma \right)$ denotes the Fisher information (FI) associated with the PDF under $H_1$, which is derived by taking the negative of the expectation of the second derivative with respect to σ of the logarithm of $P_{\mathbf{Y},1}(\mathbf{y};\sigma )$. Specifically, it can be shown:

$$\begin{array}{cc}\hfill \text{FI}(\sigma ;\tau )& =-E\left\{\frac{{\partial }^{2}ln{P}_{\mathbf{Y},1}(\mathbf{y};\sigma )}{\partial {\sigma }^2}\right\}=\sum _{n=1}^N{\text{Ψ}}_n(\sigma ;{\tau }_n)\hfill \end{array}$$

(12)

where $\tau =[{\tau }_1,{\tau }_2,\cdots ,{\tau }_N]$ and ${\text{Ψ}}_n(\sigma ;{\tau }_n)$ is:

$$\begin{array}{cc}\hfill {\text{Ψ}}_n(\sigma ;{\tau }_n)& =\frac{{\left(2-4\tilde{p}\right)}^2\left(\frac{{\tau }_n^2}{{\sigma }^4}\right)p_w^2\left(\frac{{\tau }_n}{\sigma }\right)}{\left[(2-3\tilde{p})-(2-4\tilde{p})F_w\left(\frac{{\tau }_n}{\sigma }\right)\right]}\hfill \\ & \times \frac{1}{\left[(-1+3\tilde{p})+(2-4\tilde{p})F_w\left(\frac{{\tau }_n}{\sigma }\right)\right]}\phantom{\frac{{\left(2-4\tilde{p}\right)}^2\left(\frac{{\tau }_n^2}{{\sigma }^4}\right){\tilde{p}}_w^2\left(\frac{{\tau }_n}{\sigma }\right)}{\left[(2-3\tilde{p})-(2-4\tilde{p})F_w\left(\frac{{\tau }_n}{\sigma }\right)\right]}}\hfill \end{array}$$

(13)

where $p_w(·)$ denotes the probability density function (PDF) of $w_n$. In light of the asymptotic statistical property of the GLRT detector presented in (10), the probability of the false alarm of the GLRT detector is given by:

$$P_{FA}=Q_{{\chi }_1^2}\left(2ln\eta \right)$$

(14)

where $Q_{{\chi }_1^2}(·)$ represents the right-tail probability of the chi-squared distribution with one DOF. The detection probability of the GLRT is calculated as:

$$P_D=Q_{{\chi }_1^{\text{'}2}\left(\lambda \right)}(2ln\eta )$$

(15)

where $Q_{{\chi }_1^{\text{'}2}\left(\lambda \right)}(·)$ denotes the right-tail probability of the noncentral chi-squared distribution with one DOF and noncentrality parameter λ.

4.2. Design Criterion of One-Bit Quantizers

We can see from (10) that given a specific false alarm probability, the larger the non-centrality parameter λ, the higher the detection probability. According to (11), the non-centrality parameter λ is proportional to FI, which is a function of the quantization threshold ${\tau }_n$. Therefore, in order to achieve the best asymptotic detection performance of the GLRT detector, we optimize the quantization threshold ${\tau }_n$ by maximizing the non-centrality parameter λ. Since $\left\{y_n\right\}$ are independent of each other, the above optimization problem decouples into a collection of N independent quantization threshold design problems. Therefore, the optimum quantization threshold is identical for all sensors. Specifically, the optimization problem is given by:

$$\underset{{\tau }_n}{max}{\text{Ψ}}_n({\sigma }_0;{\tau }_n),\forall n$$

(16)

Figure 1 illustrates the non-centrality parameter of the proposed quantization scheme versus ${\tau }_n/{\sigma }_0$, which denotes the ratio of the threshold to the standard deviation of the observation under hypothesis $H_1$. As shown in Figure 1, in both the error-free case (i.e., $\tilde{p}=0$) and BSC scenarios, the noncentrality parameter of the one-bit proposed quantization scheme is unimodal, which implies a unique maximum. Therefore, the optimum thresholds ${\tau }^{★}$ of the proposed quantizer in perfect/imperfect channels can be easily found by a conventional numerical method, and the results are reported in Table 1. The performance of the noncentrality parameter degrades rapidly as the threshold τ deviates from its maximum value (e.g., optimum value ${\tau }^{★}$) and as the crossover probability $\tilde{p}$ increases. It is noted that in the BSC scenarios (i.e., $\tilde{p}\ne 0$), the optimum threshold ${\tau }^{★}$ is different from that in the error-free case.

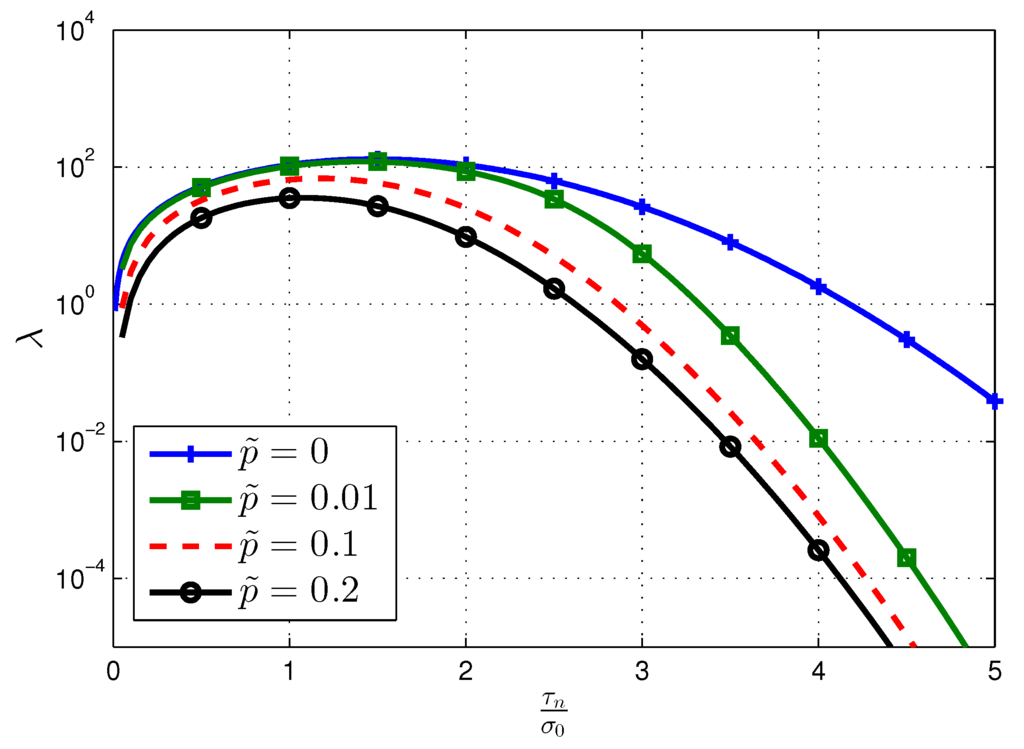
Figure 1. Non-centrality λ of the proposed quantization scheme over perfect and binary symmetric channels (BSCs) versus the normalized threshold $\frac{{\tau }_n}{{\sigma }_0}$, when the number of sensors $N=100$.

Figure 1. Non-centrality λ of the proposed quantization scheme over perfect and binary symmetric channels (BSCs) versus the normalized threshold $\frac{{\tau }_n}{{\sigma }_0}$, when the number of sensors $N=100$.

Table 1. Optimum quantization threshold in perfect/BSC channels.

Cross-Over Probability	${\tau }^{★}$
$\tilde{p}=0$	1.4821${\sigma }_0$
$\tilde{p}={10}^{-2}$	1.4109${\sigma }_0$
$\tilde{p}={10}^{-1}$	1.1736${\sigma }_0$
$\tilde{p}=0.2$	1.0785${\sigma }_0$

Table 1. Optimum quantization threshold in perfect/BSC channels.

Cross-Over Probability	${\tau }^{★}$
$\tilde{p}=0$	1.4821${\sigma }_0$
$\tilde{p}={10}^{-2}$	1.4109${\sigma }_0$
$\tilde{p}={10}^{-1}$	1.1736${\sigma }_0$
$\tilde{p}=0.2$	1.0785${\sigma }_0$

5. The Unquantized GLRT Detector

As a performance benchmark, we consider the performance of the GLRT detector, which receives the original local observations without quantization (also referred to as the unquantized GLRT detector). In this case, as shown in [18] (p. 203), the MLE of ${\sigma }_1$ is $\widehat{{\sigma }_1^2}=\frac{1}{N}{\sum }_{n=1}^N{x}_n^2$. Therefore, we conclude that the unquantized GLRT detector decides $H_1$ if:

$$\begin{array}{c}\hfill T^{\text{NQ}}\left(\mathbf{x}\right)={\left(\frac{{\sigma }_0}{{\widehat{\sigma }}_1}\right)}^{N}exp\left\{\frac{N}{2}\left(\frac{\widehat{{\sigma }_1^2}}{{\sigma }_0^2}-1\right)\right\}>\eta \end{array}$$

(17)

where the superscript ‘NQ’ is used to stand for no quantization. From an asymptotic analysis, we know that the modified test statistic $2ln{T}^{\text{NQ}}\left(\mathbf{x}\right)$ asymptotically follows:

$$2ln{T}^{\text{NQ}}\left(\mathbf{x}\right)\stackrel{a}{\sim }\left\{\begin{array}{ccc}& {\chi }_1^2,\hfill & \hfill \text{under}{H}_0^{},\\ & {\chi }_1^{\text{'}2}\left({\lambda }^{\text{NQ}}\right),\hfill & \hfill \text{under}{H}_1^{},\end{array}\right.$$

(18)

The noncentrality parameter is given by:

$${\lambda }^{\text{NQ}}=2N{\left(\frac{{\sigma }_1}{{\sigma }_0}-1\right)}^2$$

(19)

From (19), ${\lambda }^{\text{NQ}}$ is dependent on the number of sensors and standard deviations of the observations under hypotheses $H_0$ and $H_1$.

6. Simulation Results

In this section, we present computer simulation results to illustrate the performance of the proposed quantization scheme. Specifically, we use MATLAB to simulate distributed detection in a wireless sensor network with a parallel configuration, where N sensors make observations of a random Gaussian signal, and each sensor quantizes its observations into one bit of information, which is sent to the fusion center with a binary symmetric channel. The fusion center forms a global decision regarding the change of the scale parameter from ${\sigma }_0$ to ${\sigma }_1$. Our simulation is carried out with the following setups: ${\sigma }_0=1$, ${\sigma }_1=2$, $P_{FA}\in \{0.1,0,01\}$, $\tilde{p}\in \{0,0.1,0.2\}$.

Figure 2 plots the detection probabilities of the unquantized case and the one-bit GLRT detector with the optimum threshold ${\tau }^{★}$ versus the number of sensors. In the figure, a solid line and a dashed line represent the theoretical asymptotic performance, while the plus marks and circle marks represent the performance of the Monte Carlo (MC) experiments obtained by averaging over ${10}^4$ independents runs. It is observed that the theoretical asymptotic analysis provides a good approximation of the experimental performance with an increasing number of sensors. When the probability of false alarm ($P_{FA}$) is reduced, more sensors are required for the simulation to match asymptotic analysis.

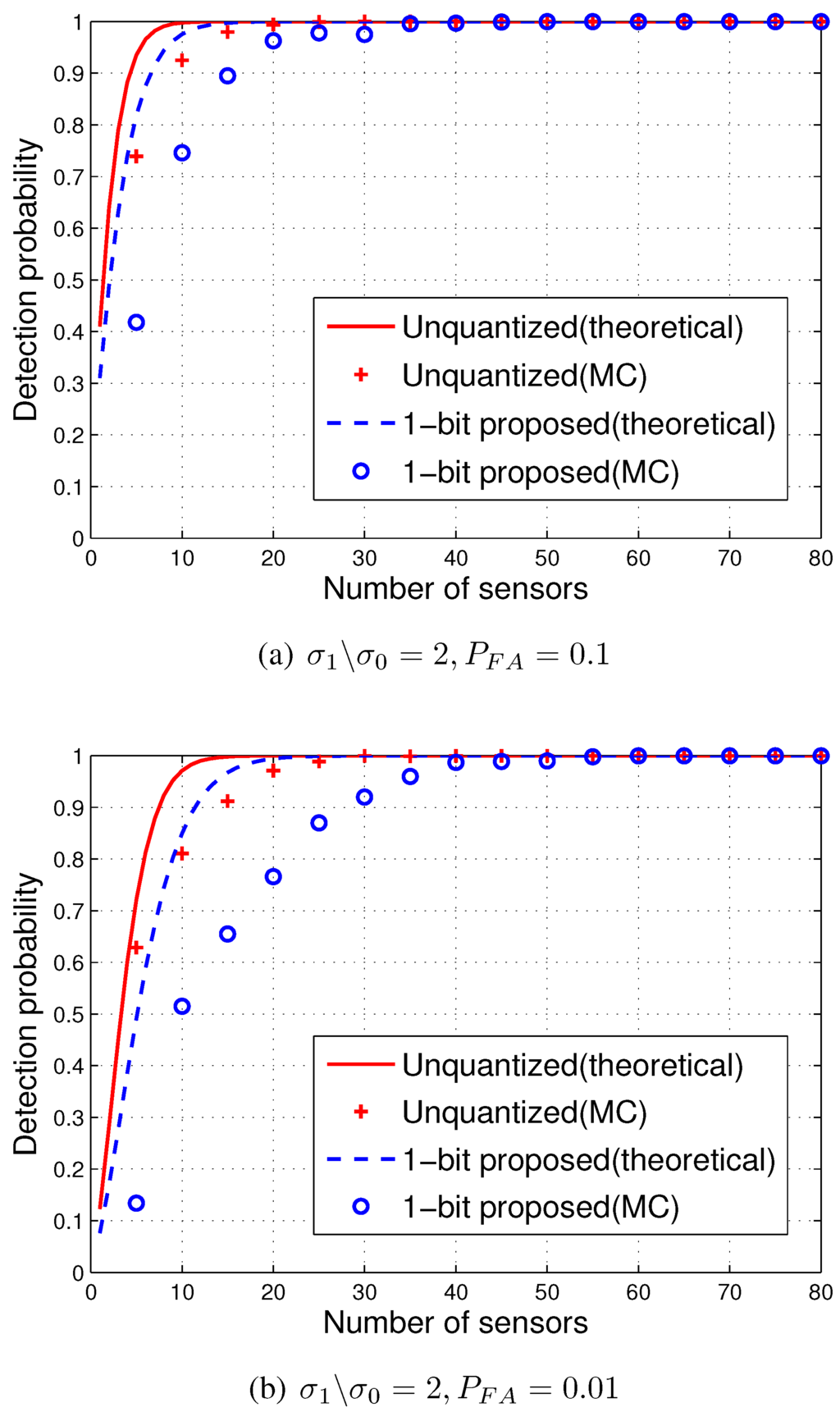
Figure 2. Performance the proposed one-bit generalized likelihood ratio test (GLRT) detector with the optimum threshold ${\tau }^{★}$ and the unquantized detector, when P_{F A} = 0.1 (a) and $0.01$ (b).

Figure 2. Performance the proposed one-bit generalized likelihood ratio test (GLRT) detector with the optimum threshold ${\tau }^{★}$ and the unquantized detector, when P_{F A} = 0.1 (a) and $0.01$ (b).

We provide simulation results to illustrate the performance of the GLRT used along with the proposed one-bit quantization scheme. Figure 3 depicts the detection probabilities of the GLRT (assuming error-free transmission between the sensors and the FC) versus the number of sensors. As a benchmark, the performance of the unquantized detector is also reported. In our simulation, for the proposed scheme, we consider three choices of the threshold, include two heuristic choices, including $\tau =0.5{\sigma }_0$ and $\tau ={\sigma }_0$, as well as the optimum threshold ${\tau }^{★}$ selected from Table 1. We assume that the standard deviation under $H_0$ and $H_1$ is ${\sigma }_0=1$ and ${\sigma }_1=2$, respectively. In the figure, the performance of the Monte Carlo (MC) experiments is obtained by averaging over ${10}^4$ independent runs. It is observed that the theoretical asymptotic analysis provides a good approximation of the experimental performance when the number of sensors is increasing. Meanwhile, the two heuristic thresholds lead to considerable performance loss.

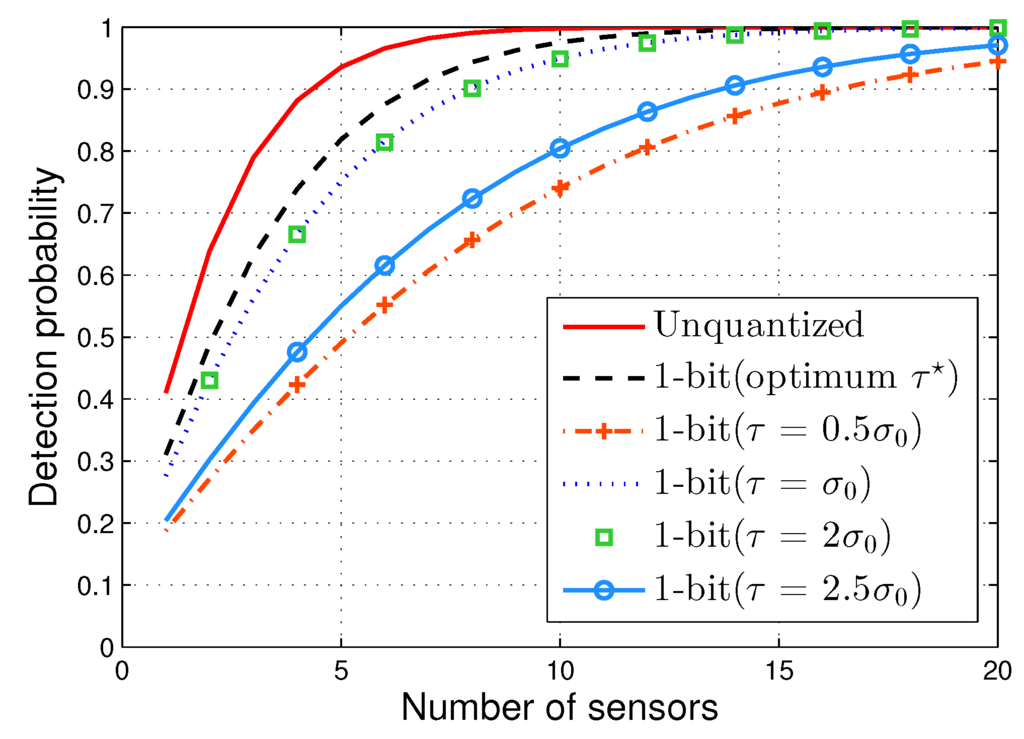
Figure 3. Performance the proposed one-bit GLRT detector with several choices of the threshold τ and the unquantized detector, when $P_{FA}=0.1$.

Figure 3. Performance the proposed one-bit GLRT detector with several choices of the threshold τ and the unquantized detector, when $P_{FA}=0.1$.

Figure Figure 4 plots the receiver operating characteristics (ROC) curves of the unquantized detector and the one-bit GLRT detector in BSC channels with several cross-over probabilities $\tilde{p}$. The unquantized case provides a reference on the optimal detection performance. It is seen that channel errors have a notable impact on the the one-bit detector.

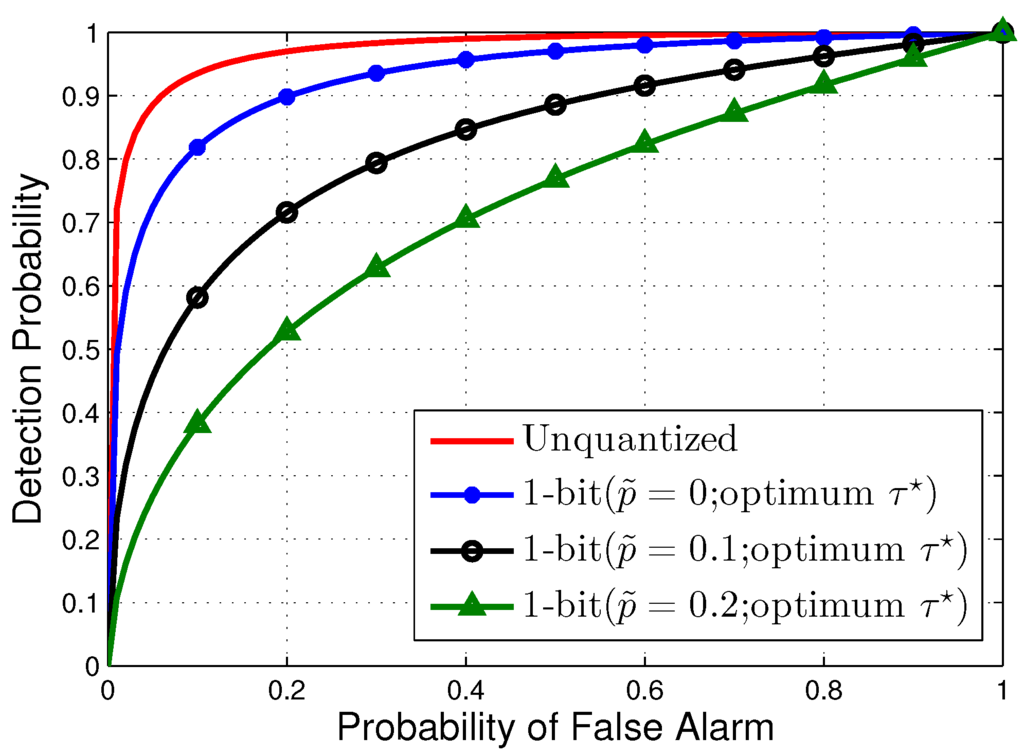
Figure 4. ROC curves of the proposed one-bit GLRT in BSC channels, when $N=5$.

Figure 4. ROC curves of the proposed one-bit GLRT in BSC channels, when $N=5$.

As shown in (13), the proposed quantization scheme requires knowledge of the crossover probability $\tilde{p}$, which needs to be estimated in practice. Let the estimated crossover probability be denoted by $\widehat{p}$. It is of interest to examine how sensitive the proposed quantization scheme is to a mismatch between $\tilde{p}$ and $\widehat{p}$. Figure 5 shows the detection probability curves as a function of the number of sensors for several estimated crossover probabilities $\widehat{p}$, where the actual crossover probability $\tilde{p}$ is 0.2. It is seen from Figure 5 that a slight mismatch (e.g., $\widehat{p}=0.1$) leads to negligible performance loss. As expected, with notable estimation error in $\widehat{p}$ (e.g., $\widehat{p}$ is away from $\tilde{p}$ by an order of magnitude), the resulting performance loss is no longer negligible.

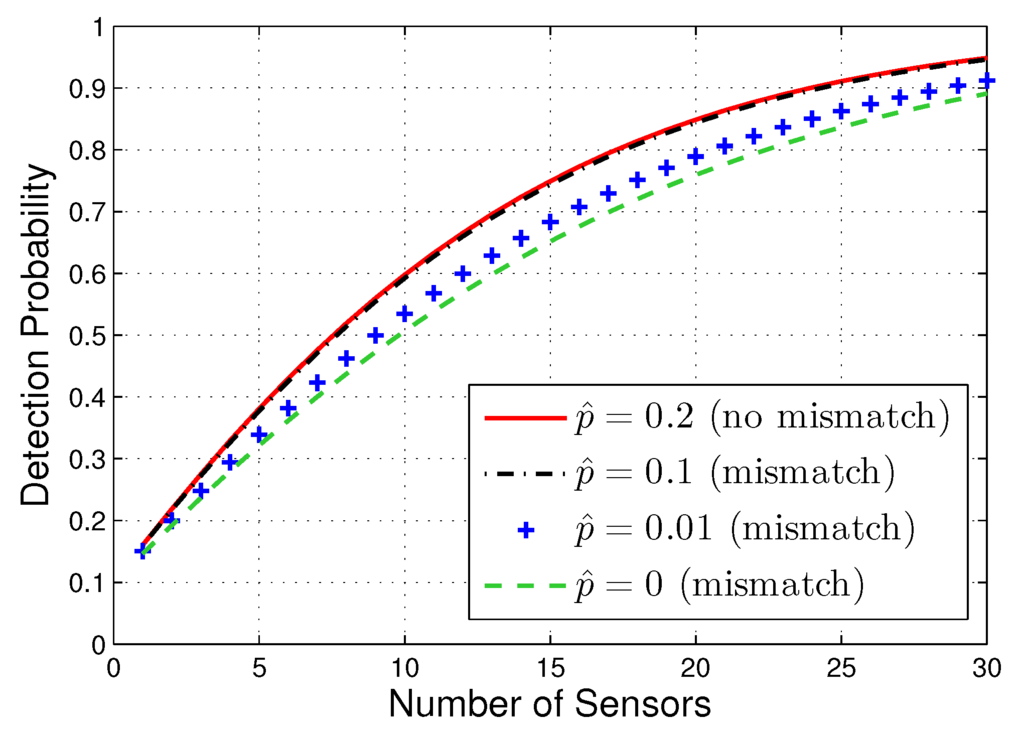
Figure 5. Performance of the proposed one-bit GLRT with several estimated values $\widehat{p}$ of the crossover probability $\tilde{p}=0.2$.

Figure 5. Performance of the proposed one-bit GLRT with several estimated values $\widehat{p}$ of the crossover probability $\tilde{p}=0.2$.

7. Conclusions

We have proposed a one-bit quantization scheme for the distributed detection of an unknown scale parameter in both the ideal and the distortion channel. Our analysis indicates that for the proposed quantization scheme, the optimum quantization thresholds are independent of the unknown variance under $H_1$ with either perfect links or binary symmetric channel between sensors and the FC. The proposed one-bit quantization scheme can achieve the same detection performance as a unquantized detector by slightly increasing the number of sensors.