Algorithm for Determining the Strong Fuzzy Grade of a Hypergroup

Abstract

In this paper, we present an algorithm for determining the strong fuzzy grade of a hypergroup, considering a particular class of hypergroups associated with genetics. A study is carried out depending on the cardinality of the initial hypergroup. The last paragraph of this paper contains the MATLAB R2018b program for the fuzzy grade for cardinals $3,4,5,6,8$.

1. Introduction

The theory of hyperstructures is a topic of algebra that is more than 90 years old and rich in applications, in particular in fuzzy, soft, and rough sets, lattices, cryptography, artificial intelligence (see [1,2]). In a hypergroupoid, the result of the “multiplication” of two elements is a set of elements rather than a single element.

The study of the connections between algebraic structures and fuzzy set theory has been a research direction since the 1970s, when Rosenfeld [3] introduced fuzzy groups. Later, algebraic hyperstructures induced by fuzzy sets were introduced and studied, as well as fuzzy hyperstructures.

First, let us present some basic definitions:

A hyperoperation on a non-empty set H is a function $\circ :H\times H\to {\mathcal{P}}^{*}\left(H\right)$, where ${\mathcal{P}}^{*}\left(H\right)$ is the set of non-empty subsets of H.

For subsets $U,V$ of H, denote $U\circ V={\bigcup }_{u\in U;v\in V}u\circ v,$ and for $z\in H$ write $z\circ U$ and $U\circ z$ for $\left\{z\right\}\circ U$ and $U\circ \left\{z\right\}$, respectively.

The structure $(H,\circ )$ is a hypergroup if for all $x,y,z$ of H we have

$$(x\circ y)\circ z=x\circ (y\circ z)\mathrm{and}z\circ H=H\circ z=H.$$

A hypergroup $(H,\circ )$ for which $x\circ y=H$ for all $x,y\in H$ is called a total hypergroup.

Various classes of hypergroups are known and studied. Regular reversible hypergroups have at least one identity and each element x has at least one inverse $x^{\prime }$, such that if $x\in y\circ z,$ then there exist the inverses $y^{\prime }$ of y and $z^{\prime }$ of z, for which $y\in x\circ z^{\prime }$ and $z\in y^{\prime }\circ x.$ Complete hypergroups form a class of hypergroups, closed to groups, in which every hyperproduct of elements is a complete part. We say that a subset A of H is a complete part of H if all hyperproducts ${\prod }_{i=1}^n{z}_i$ of elements of H which have a non-empty intersection with A are contained in $A.$ Join spaces are another important class of commutative hypergroups. A commutative hypergroup $(H,\circ )$ is a join space if for all elements $u,v,w,$$t,z$ of H,

$$u\in v\circ z,w\in t\circ z\Rightarrow u\circ t\cap v\circ w\ne \varnothing .$$

Corsini began to study the join spaces induced by fuzzy sets. He associated a join space with a fuzzy set [4] and then a fuzzy set with a hypergroupoid/join space [5], constructing in this manner a sequence of join spaces and fuzzy sets, which ends if two consecutive join spaces are isomorphic. The length of this sequence is called the fuzzy grade. This indicates a point where the structure of the spaces essentially stabilizes. In this paper, we will call it the Corsini fuzzy grade to distinguish it from the strong fuzzy grade, which will be explained later. The study of this sequence offers the possibility of studying fuzzy sets from an algebraic point of view and also provides examples of join spaces on a certain set.

Now, let us present the algorithm introduced by Corsini in [5]. First, he associated a fuzzy set with every hypergroupoid $(H,\otimes )$, as follows:

$$\forall z\in H,Q\left(z\right)=\{(x,y)\in H^2\mid z\in x\otimes y\},$$

$$q\left(z\right)= \mid Q\left(z\right)\mid ,$$

$$A\left(z\right)=\sum _{(x,y)\in Q\left(z\right)}1/\mid x\otimes y\mid ,$$

$$\mu \left(z\right)=A\left(z\right)/q\left(z\right).$$

(1)

In [6], the above fuzzy set $\mu$ was called grade fuzzy set and was denoted by $\tilde{\mu }.$

On the other hand, a join space $H_1=(H,{\circ }_{\mu })$ can be associated with the fuzzy set $\mu$ as follows:

$$x{\circ }_{\mu }y=\left\{z\right|min\{\mu \left(x\right),\mu \left(y\right)\}\le \mu \left(z\right)\le max\{\mu \left(x\right),\mu \left(y\right)\}.$$

(2)

We repeat the process and obtain a sequence of join spaces ${\left\{H_i\right\}}_i$ and a sequence of fuzzy sets ${\left\{{\mu }_i\right\}}_i$. These sequences have been studied in many contexts, for instance, in several classes of hypergroups, such as hypergroups with partial scalar identities [7], non-complete 1-hypergroups [8], and complete hypergroups [9], but also in connection with hypergraphs [10,11], multivalued functions [12], and recently, genetics [13]. Studying these sequences can be useful for analyzing the properties of join spaces, particularly their structure. Actually, the sequences are a hierarchical construction of associated join spaces, built step by step from a hypergroup or just a hypergroupoid.

In [14], the fuzzy grade is calculated for hypergroups associated with hypergraphs with the help of MATLAB. In the papers [13,14], the authors declare that they calculated the fuzzy grade of the corresponding hyperstructures, but in reality, the condition they used to stop the sequence of join spaces and fuzzy sets was that the last two join spaces had to be exactly the same or the latest two fuzzy sets had to have the same order.

The fuzzy grade of the starting hypergroup is the minimum natural number i for which $H_i\cong H_{i+1},$ while the strong fuzzy grade is the minimum natural number j for which $H_j=H_{j+1}.$ It is easy to see that for the same hyperstructure, the strong fuzzy grade $s.f.g.$ is greater than or equal to the fuzzy grade $f.g.$

According to [15], if we consider the equivalence relation $R_i$ on $H_i=(H,{\circ }_{{\mu }_i})$ defined by $x{R}_{i}y\iff {\mu }_i\left(x\right)={\mu }_i\left(y\right),$ then it follows that $R_i$ is a regular equivalence and a congruence in $H_i$. The quotient set $H_i/R_i$ consists of equivalence classes ${\left\{C_j^i\right\}}_{1\le j\le r_i}$ with cardinals $k_j$ for all $j,1\le j\le r_i.$ Therefore, with each join space $H_i$ we can associate an $r_i$-tuple $(k_1,k_2,\dots ,k_{r_i}).$ In [15], the authors established a sufficient condition in order to have two consecutive associated join spaces of a sequence be non-isomorphic. They also found a property of the quotient hypergroup determined by the join space $H_i$ and the relation associated with the fuzzy set $\tilde{\mu }$ and determined a necessary and sufficient condition for the join space $H_i$ in order for it to be a reduced hypergroup. In [9], the authors provide a method for constructing a finite hypergroup with the strong fuzzy grade equal to a given natural number.

In this paper, we consider the above construction for a class of hypergroups which has been obtained in connection with genetics (see [16,17,18]) and analyze the strong fuzzy grade of these hypergroups. This study is a continuation of the paper [13]. The last section of this paper contains the MATLAB programs for the strong fuzzy grade for cardinals $3,4,5,6,8.$

2. The Fuzzy Grade of a Genetic Hypergroup

We apply Corsini’s construction $\left(1\right)$ for the next join space, which is connected with a genetic inheritance (see [13]). This hypergroup is not complete, but it is regular and reversible.

We set $n\ge 3$ and $H=\{z_1,z_2,\dots ,z_n\}$.

We consider the hyperoperation on H given in Table 1.

Table 1. The multiplication table of ∘.

∘	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	…	${\mathit{z}}_{\mathit{n}}$
$z_1$	H	H	H	⋯	H
$z_2$	H	$\{z_2,z_3,\cdots ,z_n\}$	$\{z_2,z_3,\cdots ,z_n\}$	⋯	$\{z_2,z_3,\cdots ,z_n\}$
$z_3$	H	$\{z_2,z_3,\cdots ,z_n\}$	$\{z_3,\cdots ,z_n\}$	⋯	$\{z_3,\cdots ,z_n\}$
⋯	⋯	⋯	⋯	⋯	⋯
$z_n$	H	$\{z_2,z_3,\cdots ,z_n\}$	$\{z_3,\cdots ,z_n\}$	⋯	$\left\{z_n\right\}$

For all $1\le i\le j\le k\le n$, we have $z_i\circ (z_j\circ z_k)=(z_i\circ z_j)\circ z_k=\{z_i,z_{i+1},\cdots ,z_n\}.$

Moreover, $(H,\circ )$ is a join space. The idea of considering such a hypergroup comes from genetics; more precisely, it is associated with a type of non-Mendelian inheritance, namely Epistasis [16,18].

We have $q_1\left(z_i\right)=\left|Q_1\left(z_i\right)\right|$ for all $i\in \{1,2,\cdots ,n\}.$ By calculation, for all natural numbers $k,1\le k\le n,$

$$q_1\left(z_k\right)=2nk-k^2.$$

(3)

Indeed,

$Q_1\left(z_1\right)=\{(z_1,z),(z,z_1)\mid z\in H\}$ whence $q_1\left(z_1\right)=2n-1.$

$Q_1\left(z_2\right)=Q_1\left(z_1\right)\cup \{(z_2,z),(z,z_2)\mid z\in H\}$ whence $q_1\left(z_2\right)=4n-4.$

$Q_1\left(z_3\right)=Q_1\left(z_2\right)\cup \{(z_3,z),(z,z_3)\mid z\in H\}$ whence $q_1\left(z_3\right)=6n-9.$

$Q_1\left(z_k\right)=Q_1\left(z_{k-1}\right)\cup \{(z_k,z),(z,z_k)\mid z\in H\}$ whence $q_1\left(z_k\right)=2nk-k^2.$

Finally, $q_1\left(z_n\right)=n^2.$

For all $x\in H$, we have

$${\mu }_1\left(z\right)={\alpha }_1\left(z\right)/q_1\left(z\right).$$

(4)

Theorem 1

([13]). For $1\le i<j\le n$, we obtain ${\mu }_1\left(z_i\right)<{\mu }_1\left(z_j\right).$

For $n=2^s$, the above join space $(H,\circ )$ is an example of a hypergroup that satisfies the conditions of Theorem 6.1 [19], which states the following:

Theorem 2

([19]). Let H be the finite hypergroupoid $H=\{z_1,z_2,...,z_n\},$ with $n=2^s,$ and s a nonzero natural number, which verifies the relation

$${\mu }_1\left(z_1\right)<{\mu }_1\left(z_2\right)<\cdots <{\mu }_1\left(z_n\right),$$

i.e., the n-tuple associated with H is $(1,1,\cdots ,1).$ Then, the join space $H_{s+1}$ is a total hypergroup, and by consequence $f.g.\left(H\right)=s+1.$

In the proof of this theorem, it is checked that ${\mu }_2\left(z_i\right)={\mu }_2\left(z_{n+1-i}\right)$ for all $i\in \{1,2,\cdots ,n/2\}$ and for all $i<j\le n/2,{\mu }_2\left(z_i\right)>{\mu }_2\left(z_j\right).$ Thus, the join space $H_2=(H,{\circ }_{{\mu }_2})$ is associated with the $r_2$-tuple $(2,2,\cdots ,2)$, where $r_2=2^{s-1}$.

Continuing in this manner, the join space $H_3=(H,{\circ }_{{\mu }_3})$ is associated with the $r_3$-tuple $(4,4,\cdots ,4)$, with $r_3=2^{s-2}$, and so on. The join space $H_s=(H,{\circ }_{{\mu }_s})$ is associated with the pair $(2^{s-1},2^{s-1})$. The join space $H_{s+1}$ is a total hypergroup and $f.g.\left(H\right)=s+1.$

Example 1.

Consider $n=8=2^3$ for hypergroup $(H,\circ )$, and we obtain the following:

${\mu }_1\left(z_1\right)<{\mu }_1\left(z_2\right)<{\mu }_1\left(z_3\right)<{\mu }_1\left(z_4\right)<{\mu }_1\left(z_5\right)<{\mu }_1\left(z_6\right)<{\mu }_1\left(z_7\right)<{\mu }_1\left(z_8\right),$ corresponding to $(1,1,1,1,1,1,1,1)$,

${\mu }_2\left(z_1\right)={\mu }_2\left(z_8\right)>{\mu }_2\left(z_2\right)={\mu }_2\left(z_7\right)>{\mu }_2\left(z_3\right)={\mu }_2\left(z_6\right)>{\mu }_2\left(z_4\right)={\mu }_2\left(z_5\right),$ corresponding to $(2,2,2,2)$,

${\mu }_3\left(z_1\right)={\mu }_3\left(z_8\right)={\mu }_3\left(z_4\right)={\mu }_3\left(z_5\right)>{\mu }_3\left(z_2\right)={\mu }_3\left(z_7\right)={\mu }_3\left(z_3\right)={\mu }_3\left(z_6\right),$ corresponding to $(4,4)$,

${\mu }_4\left(z_1\right)={\mu }_4\left(z_2\right)={\mu }_4\left(z_3\right)={\mu }_4\left(z_4\right)={\mu }_4\left(z_5\right)={\mu }_4\left(z_6\right)={\mu }_4\left(z_7\right)={\mu }_4\left(z_8\right),$ corresponding to the total hypergroup.

Hence, the fuzzy grade of $(H,\circ )$ is 4.

We continue the algorithm by obtaining the join spaces $H_i$ and fuzzy functions ${\mu }_i$ in order to establish the fuzzy degree in the other situations where $n\ne 2^s.$

With $\left(2\right)$, we obtain a join space $H_1=(H,{\circ }_1)$ such that for all $z_i\in H$ we have

$z_i{\circ }_1{z}_i=\left\{z_i\right\}$ and for all $1\le i<j\le n$ we have $z_i{\circ }_1{z}_j=z_j{\circ }_1{z}_i=\{z_i,z_{i+1},\cdots ,z_j\}$.

Hence, we obtain Table 2.

Table 2. The multiplication table of ${\circ }_1$.

${\circ }_1$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	⋯	${\mathit{z}}_{\mathit{n}}$
$z_1$	$\left\{z_1\right\}$	$\{z_1,z_2\}$	$\{z_1,z_2,z_3\}$	⋯	H
$z_2$		$\left\{z_2\right\}$	$\{z_2,z_3\}$	⋯	$\{z_2,z_3,\cdots ,z_n\}$
$z_3$			$\left\{z_3\right\}$	⋯	$\{z_3,\cdots ,z_n\}$
⋯	⋯	⋯	⋯	⋯	⋯
$z_n$				⋯	$\left\{z_n\right\}$

Note that all hypergroups we consider in this paper are commutative, so we can only write in the table the elements above the main diagonal.

Applying $\left(1\right)$, we obtain the following:

$q_2\left(z_1\right)=2n-1,q_2\left(z_2\right)=4n-5,$

$q_2\left(z_3\right)=6n-13,q_2\left(z_4\right)=8n-25$ and for $1\le k\le n,$

$$q_2\left(z_k\right)=2·k·(n-k+1)-1.$$

(5)

In particular, $q_2\left(z_n\right)=2n-1=q_2\left(z_1\right),q_2\left(z_{n-1}\right)=q_2\left(z_2\right)=4(n-1)-1$

$q_2\left(z_{n-2}\right)=q_2\left(z_3\right)=2·3·(n-2)-1.$

If $n=2s$, where s is a natural number, $s\ge 2$, then

$$q_2\left(z_s\right)=q_2\left(z_{s+1}\right)=2s(s+1)-1.$$

(6)

If $n=2s+1$, where s is a natural number, $s\ge 1$, then

$$q_2\left(z_s\right)=q_2\left(z_{s+2}\right)=2s(s+2)-1$$

(7)

and

$$q_2\left(z_{s+1}\right)=2{(s+1)}^2-1.$$

(8)

For any $z\in H$ we have

$${\mu }_2\left(z\right)=A_2\left(z\right)/q_2\left(z\right).$$

(9)

Theorem 3

([13]). (i) For $n=2s$ we have the following:

$${\mu }_2\left(z_1\right)={\mu }_2\left(z_{2s}\right),{\mu }_2\left(z_2\right)={\mu }_2\left(z_{2s-1}\right),\cdots ,{\mu }_2\left(z_s\right)={\mu }_2\left(z_{s+1}\right)$$

and ${\mu }_2\left(z_1\right)>{\mu }_2\left(z_2\right)>\dots >{\mu }_2\left(z_s\right).$

(ii) 

For $n=2s+1$ we have the following:

$${\mu }_2\left(z_1\right)={\mu }_2\left(z_{2s+1}\right),{\mu }_2\left(z_2\right)={\mu }_2\left(z_{2s}\right),\cdots ,{\mu }_2\left(z_s\right)={\mu }_2\left(z_{s+2}\right)$$

and ${\mu }_2\left(z_1\right)>{\mu }_2\left(z_2\right)>\cdots >{\mu }_2\left(z_s\right)>{\mu }_2\left(z_{s+1}\right).$

Hence, for $n=2s$ the associated s-tuple is $(2,2,\cdots ,2)$, and for $n=2s+1$ the associated $(s+1)$-tuple is $(2,2,\cdots ,2,1).$

Applying $\left(2\right)$ again, we obtain the join space $H_2=(H,{\circ }_2)$, where ${\circ }_2={\circ }_{{\mu }_2}.$ For all $z_i\in H$ we have $z_i{\circ }_2{z}_i=\{z_i,z_{n+1-i}\}.$ Moreover, for all $1\le i<j\le n$ we have $z_i{\circ }_2{z}_j=z_j{\circ }_2{z}_i=\{z_i,z_{n+1-i},z_{i+1},z_{n-i},\cdots ,z_j,z_{n+1-j}\}.$

Denote $\widehat{z_i}=\{z_i,z_{n+1-i}\}.$ Hence,

$$z_i{\circ }_2{z}_i=\widehat{z_i},z_i{\circ }_2{z}_j=z_j{\circ }_2{z}_i=\widehat{z_i}\cup \widehat{z_{i+1}}\cup \cdots \cup \widehat{z_j}.$$

In what follows, we analyze separately a case where n is even and a case where n is odd.

I. Case $n=2s.$

This allows us to obtain Table 3.

Table 3. The multiplication table for $n=2s$.

${\circ }_2$	${\mathit{z}}_1$	${\mathit{z}}_2$	⋯	${\mathit{z}}_{\mathit{s}}$	${\mathit{z}}_{\mathit{s}+1}$	⋯	${\mathit{z}}_{2\mathit{s}-1}$	${\mathit{z}}_{2\mathit{s}}$
$z_1$	$\widehat{z_1}$	$\widehat{z_1}\cup \widehat{z_2}$	⋯	$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$	$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$	⋯	$\widehat{z_1}\cup \widehat{z_2}$	$\widehat{z_1}$
$z_2$		$\widehat{z_2}$	⋯	$\widehat{z_2}\cup \cdots \cup \widehat{z_s}$	$\widehat{z_2}\cup \cdots \cup \widehat{z_s}$	⋯	$\widehat{z_2}$	$\widehat{z_1}\cup \widehat{z_2}$
⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯
$z_s$				$\widehat{z_s}$	$\widehat{z_s}$	⋯	⋯	$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$
$z_{s+1}$				$\widehat{z_s}$	$\widehat{z_s}$	⋯	⋯	$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$
⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯
$z_{2s}$	$\widehat{z_1}$	$\widehat{z_1}\cup \widehat{z_2}$		$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$	$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$		$\widehat{z_1}\cup \widehat{z_2}$	$\widehat{z_1}$

We analyze the following cases:

(i)

If $s=2k$ is even, i.e., $n=4k$, then

${\mu }_3\left(z_1\right)={\mu }_3\left(z_s\right),{\mu }_3\left(z_2\right)={\mu }_3\left(z_{2k-1}\right),\dots ,{\mu }_3\left(z_k\right)={\mu }_3\left(z_{k+1}\right)$.

In this case, the associated k-tuple of $H_3$ is $(4,4,\dots ,4)=(2^2,2^2,\dots ,2^2).$

(ii)

If $s=2k+1$ is odd, i.e., $n=4k+2$, then

${\mu }_3\left(z_1\right)={\mu }_3\left(z_{2k+1}\right),{\mu }_3\left(z_2\right)={\mu }_3\left(z_{2k}\right),\dots ,{\mu }_3\left(z_k\right)={\mu }_3\left(z_{k+2}\right)$.

The associated $(k+1)$-tuple of $H_3$ is $(4,4,\dots ,4,2)=(2^2,2^2,\dots ,2^2,2).$

The cardinal 2 corresponds to ${\mu }_3\left(z_{k+1}\right)={\mu }_3\left(z_{3k+2}\right),$ since we have ${\mu }_2\left(z_{t_1}\right)={\mu }_2\left(z_{t_2}\right)$ for all $t_1,t_2,$ for which $t_1+t_2=2s+1,$ according to Theorem 2.3.

Applying (i) s times and then (ii), we obtain the following:

Theorem 4.

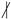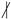Let $n=2^{s}k$ where $2$ k.

Then, the associated $k-$tuple of $H_{s+1}$ is $(2^s,2^s,\dots ,2^s)$ and the associated $(k+1)/2-$tuple of $H_{s+2}$ is $(2^{s+1},2^{s+1},\dots ,2^{s+1},2^s).$

Example 2.

For $n=6$, we have the following:

${\mu }_1\left(z_1\right)<{\mu }_1\left(z_2\right)<{\mu }_1\left(z_3\right)<{\mu }_1\left(z_4\right)<{\mu }_1\left(z_5\right)<{\mu }_1\left(z_6\right),$ corresponding to $(1,1,1,1,1,1)$,

${\mu }_2\left(z_1\right)={\mu }_2\left(z_6\right)>{\mu }_2\left(z_2\right)={\mu }_2\left(z_5\right)>{\mu }_2\left(z_3\right)={\mu }_2\left(z_4\right),$ corresponding to $(2,2,2)$,

${\mu }_3\left(z_1\right)={\mu }_3\left(z_6\right)={\mu }_3\left(z_3\right)={\mu }_3\left(z_4\right)>{\mu }_3\left(z_2\right)={\mu }_3\left(z_5\right),$ corresponding to $(4,2)$,

${\mu }_4\left(z_1\right)={\mu }_4\left(z_6\right)={\mu }_4\left(z_3\right)={\mu }_4\left(z_4\right)<{\mu }_4\left(z_2\right)={\mu }_4\left(z_5\right),$ corresponding to $(4,2)$.

Hence, the fuzzy grade of $(H,\circ )$ is 3.

Remark 1.

If in $H_i$ for all elements $z_j,z_l$ for which ${\mu }_i\left(z_j\right)<{\mu }_i\left(z_l\right)$ we have ${\mu }_{i+1}\left(z_j\right)>{\mu }_{i+1}\left(z_l\right)$, then $H_i\cong H_{i+1}.$

II. Case $n=2s+1.$

Clearly, if $n=2s+1$, then $\widehat{z_{s+1}}=\left\{z_{s+1}\right\}.$ Notice that this is the only class containing only one element.

We can thus obtain Table 4.

Table 4. The multiplication table for $n=2s+1$.

${\circ }_2$	${\mathit{z}}_1$	${\mathit{z}}_2$	⋯	${\mathit{z}}_{\mathit{s}}$	${\mathit{z}}_{\mathit{s}+1}$	${\mathit{z}}_{\mathit{s}+2}$	⋯	${\mathit{z}}_{2\mathit{s}+1}$
$z_1$	$\widehat{z_1}$	$\widehat{z_1}\cup \widehat{z_2}$	⋯	$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$	$\widehat{z_1}\cup \cdots \cup \widehat{z_{s+1}}$	$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$	⋯	$\widehat{z_1}$
$z_2$		$\widehat{z_2}$	⋯	$\widehat{z_2}\cup \cdots \cup \widehat{z_s}$	$\widehat{z_2}\cup \cdots \cup \widehat{z_{s+1}}$	$\widehat{z_2}\cup \cdots \cup \widehat{z_s}$	⋯	$\widehat{z_1}\cup \widehat{z_2}$
⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯
$z_s$				$\widehat{z_s}$	$\widehat{z_s}\cup \widehat{z_{s+1}}$	$\widehat{z_s}$	⋯	$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$
$z_{s+1}$					$\widehat{z_{s+1}}$	$\widehat{z_s}\cup {\widehat{z}}_{s+1}$	⋯	$\widehat{z_1}\cup \cdots \cup \widehat{z_s}$
⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯
$z_{2s+1}$								$\widehat{z_1}$

By calculation, we finally obtain that

$${\mu }_3\left(z_{s+1}\right)>{\mu }_3\left(z_s\right)>\dots >{\mu }_3\left(z_2\right)>{\mu }_3\left(z_1\right).$$

The associated $(s+1)$-tuple of $H_2$ is $(2,2,\dots ,2,1),$ as for $H_2.$

Example 3.

For $n=5$ we have the following (see [13]): ${\mu }_1\left(z_1\right)<{\mu }_1\left(z_2\right)<{\mu }_1\left(z_3\right)<{\mu }_1\left(z_4\right)<{\mu }_1\left(z_5\right),$ corresponding to $(1,1,1,1,1)$,

${\mu }_2\left(z_1\right)={\mu }_2\left(z_5\right)>{\mu }_2\left(z_2\right)={\mu }_2\left(z_4\right)>{\mu }_2\left(z_3\right),$ corresponding to $(2,2,1)$,

${\mu }_3\left(z_1\right)={\mu }_3\left(z_5\right)<{\mu }_3\left(z_2\right)={\mu }_3\left(z_4\right)<{\mu }_3\left(z_3\right),$ corresponding to $(2,2,1)$.

Hence, the fuzzy grade of $(H,\circ )$ is 2.

Example 4.

For $n=7$ we have the following (see [13]):

${\mu }_1\left(z_1\right)<{\mu }_1\left(z_2\right)<{\mu }_1\left(z_3\right)<{\mu }_1\left(z_4\right)<{\mu }_1\left(z_5\right)<{\mu }_1\left(z_6\right)<{\mu }_1\left(z_7\right),$ corresponding to $(1,1,1,1,1,1,1)$,

${\mu }_2\left(z_1\right)={\mu }_2\left(z_7\right)>{\mu }_2\left(z_2\right)={\mu }_2\left(z_6\right)>{\mu }_2\left(z_3\right)={\mu }_2\left(z_5\right)>{\mu }_2\left(z_4\right),$ corresponding to $(2,2,2,1)$,

${\mu }_3\left(z_2\right)={\mu }_3\left(z_6\right)<{\mu }_3\left(z_1\right)={\mu }_3\left(z_7\right)<{\mu }_3\left(z_3\right)={\mu }_3\left(z_5\right)<{\mu }_3\left(z_4\right),$ corresponding to $(2,2,2,1)$,

${\mu }_4\left(z_1\right)={\mu }_4\left(z_7\right)<{\mu }_4\left(x_2\right)={\mu }_4\left(z_6\right)<{\mu }_4\left(z_3\right)={\mu }_4\left(z_5\right)<{\mu }_4\left(z_4\right),$ corresponding to $(2,2,2,1)$.

We obtain $H_2=H_4$ and $H_3=H_5,$ but $H_2\cong H_3.$ In this case, there is no strong fuzzy grade, but $f.g.\left(H\right)=2.$

Now we will consider a new example, for $n=3$, in order to verify the results obtained using the MATLAB program of Section 3.Notice that for other values of n, the results obtained using the MATLAB program are verified through direct calculations.

Example 5.

We present the algorithm for $n=3$, starting with the Table 5:

Table 5. The multiplication table of ∘.

∘	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$
$z_1$	$\{z_1,z_2,z_3\}$	$\{z_1,z_2,z_3\}$	$\{z_1,z_2,z_3\}$
$z_2$	$\{z_1,z_2,z_3\}$	$\{z_2,z_3\}$	$\{z_2,z_3\}$
$z_3$	$\{z_1,z_2,z_3\}$	$\{z_2,z_3\}$	$\left\{z_3\right\}$

We have $H=\{z_1,z_2,z_3\}$ and $(H,\circ )$ is the starting hypergroup.

By calculation, we obtain $q_1\left(z_1\right)=5,q_1\left(z_2\right)=8,q_3\left(z_3\right)=9;$

$A_1\left(z_1\right)=5/3,A_1\left(z_2\right)=5/3+3/2,A_1\left(z_3\right)=5/3+3/2+1,$ hence

${\mu }_1\left(z_1\right)=5/15=0.333,{\mu }_1\left(z_2\right)=3.166/8=0.395,{\mu }_1\left(z_3\right)=4.166/9=0.462.$ At the second step, we obtain Table 6.

Table 6. The multiplication table of ${\circ }_1$.

${\circ }_1$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$
$z_1$	$\left\{z_1\right\}$	$\{z_1,z_2\}$	$\{z_1,z_2,z_3\}$
$z_2$	$\{z_1,z_2\}$	$\left\{z_2\right\}$	$\{z_2,z_3\}$
$z_3$	$\{z_1,z_2,z_3\}$	$\{z_2,z_3\}$	$\left\{z_3\right\}$

We obtain $q_2\left(z_1\right)=5=q_2\left(z_3\right),q_2\left(z_2\right)=7;$

$A_2\left(z_1\right)=1+2/2+2/3=2.666=A_2\left(z_3\right),A_2\left(z_2\right)=1+4/2+2/3=3.666,$ hence ${\mu }_2\left(z_1\right)=0.533={\mu }_2\left(z_3\right),{\mu }_2\left(z_2\right)=0.523.$

At the next step, we obtain ${\circ }_2$ of Table 7.

Table 7. The multiplication table of ${\circ }_2$.

${\circ }_2$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$
$z_1$	$\{z_1,z_3\}$	$\{z_1,z_2,z_3\}$	$\{z_1,z_3\}$
$z_2$	$\{z_1,z_2,z_3\}$	$\left\{z_2\right\}$	$\{z_1,z_2,z_3\}$
$z_3$	$\{z_1,z_3\}$	$\{z_1,z_2,z_3\}$	$\{z_1,z_3\}$

We obtain $q_3\left(z_1\right)=8=q_3\left(z_3\right),q_3\left(z_2\right)=5;$

$A_3\left(z_1\right)=4/2+4/3=3.333=A_3\left(z_3\right),A_2\left(z_2\right)=1+4/3=2.333,$ hence

${\mu }_2\left(z_1\right)=0.416={\mu }_2\left(z_3\right),{\mu }_2\left(z_2\right)=0.466.$

At the next step, we obtain the same hyperoperation, which means that ${\circ }_3={\circ }_2$, whence it follows that $s.f.g\left(H\right)=2.$

3. MATLAB Program for Obtaining the Strong Fuzzy Grade

In this section, we present the R2018b program used to obtain the strong fuzzy grade for a hypergroup, in particular for the hypergroup H defined in the above section. Moreover, we calculate the strong fuzzy grade for cardinals $3,4,5,6,8$ of $H.$ We use some functions to obtain this program: a function to generate the hyperoperation, then a function to obtain the fuzzy set from the given hyperoperation, then a third function to generate a new join space using the fuzzy set, and then a final function to call the first three functions. The last three functions are valid for any finite hypergroup. Only the first function is characteristic of the particular case of hypergroup studied in this paper.

The first function is used to generate a hyperoperation as described in Table 1. For example, for $n=3$ we obtain Table 8, which is isomorphic to $(\{z_1,z_2,z_3\},\circ )$ of Table 5.

Table 8. The multiplication table of ${\otimes }_3$.

${\otimes }_3$	1	2	3
1	1, 2, 3	1, 2, 3	1, 2, 3
2	1, 2, 3	2, 3	2, 3
3	1, 2, 3	2, 3	3

This table can be obtained as follows: we type

• H=generate_H(3)
• in the command window, and we can get
• >> H=generate_H(3)
• H(:,:,1) =
•    1   1   1
•    1   0   0
•    1   0   0
• H(:,:,2) =
•    2   2   2
•    2   2   2
•    2   2   0
• H(:,:,3) =
•    3   3   3
•    3   3   3
•    3   3   3
• and then we obtain the multiplication table of ${\otimes }_3$, presented in the following as Table 8.

The second function can be used to get a fuzzy set from a hyperoperation. For example, if we type

• mu=h2(H)
• in the command window, we can get
• >> mu=h2(H)
• mu =
•          0.333333333333333    0.395833333333333    0.462962962962963

The third function can be used to generate a new join space by a fuzzy set. For example, if we type

• H1 = h3(mu)
• in the command window, we can get
• >> H1 = h3(mu)
• H1(:,:,1) =
•    1   1   1
•    1   0   0
•    1   0   0
• H1(:,:,2) =
•    0   2   2
•    2   2   2
•    2   2   0
• H1(:,:,3) =
•    0   0   3
•    0   0   3
•    3   3   3

The fourth function is obtained by calling the first three functions. If we want to apply the fourth function, we first need to save the first three functions as individual m-files named generate_H.m, h2.m, and h3.m, respectively.

The results of the application of these programs can be found after the codes, from which we know that the strong fuzzy grade of H with $n=3,4,5,6,8$ is $2,3,2,3,4$, respectively, which covers the results of [13]. As for $n=7$, Leoreanu et al. showed in Example 7.4 of [13] that there is no such strong fuzzy grade.

Table 9 lists the strong fuzzy grades for H with the cardinals $3,4,5,6,8$ of Table 1, respectively.

Table 9. The strong fuzzy grades for H with the cardinals $3,4,5,6,8$ of Table 1, respectively.

the cardinality of H	3	4	5	6	8
strong fuzzy degree	2	3	2	3	4

The MATLAB programs are as follows.

%%%The first function

function H = generate_H(n)

H = zeros(n, n, n); % Initialize an all-zero 3D array

for i = 1:n

for j = 1:n

for k = 1:n

if k >= min(i, j)

H(i, j, k) = k;

end

end

end

end

end

%%%The second function

function mu=h2(H)

% Calculate the fuzzy degree of elements in H

n = size(H, 1);

mu=zeros(1,n);

for x=1:n

q=0;mu1=0;

for i=1:n

for j=1:n

flag=0;p=0;

for k=1:n

if H(i,j,k)~=0

p=p+1;

end

if x==H(i,j,k)

q=q+1;

flag=1;

end

end

if flag==1

mu1=mu1+1/p;

end

end

end

if q~=0

mu(x)=mu1/q;

end

end

%%%The third function

function H1 = h3(mu)

% to generate a new join space H1 by a fuzzy set mu

% H1(i,j,k) = k, if mu(k) is between mu(i) and mu(j); H1(i,j,k)=0,

% otherwise

if ~isvector(mu)

error(’Input mu must be a vector.’);

end

n = numel(mu);

H1 = zeros(n, n, n);

for i = 1:n

for j = 1:n

for k = 1:n

if mu(k) >= min(mu(i), mu(j)) && mu(k) <= max(mu(i), mu(j))

H1(i, j, k) = k;

end

end

end

end

end

%The fourth function

function grad = h4(n)

H = generate_H(n); %To generate H

mu = h2(H); %To generate a fuzzy set mu corresponding to H

grad = 1;

iteration = 0;

max_iterations = 50;

%%%Note 1: the following codes are designed for display the entries of H

for i = 1:size(H, 1)

for j = 1:size(H, 2)

%  Extract (i,j,:) and convert it to a row vector

slice = nonzeros(reshape(H(i,j,:), 1, []));

% Display results

fprintf(’H(%d,%d,:) = [’, i, j);

fprintf(’%d ’, slice);

fprintf(’]\n’);

end

end

%%%The end of Note 1

%To display the results of mu

fprintf(’mu1 =[ ’);

fprintf(’%.4f  ’, mu);

fprintf(’]\n’);

while iteration < max_iterations

H1 = h3(mu);

mu1 = round(h2(H1),5);  %This line can calculate %n=3,4,5,6,8

for i = 1:size(H1, 1)

for j = 1:size(H1, 2)

% Extract (i,j,:) and convert it to a row vector

slice = nonzeros(reshape(H1(i,j,:), 1, []));

% Display results

fprintf(’H%d(%d,%d,:) = [’, grad, i, j);

fprintf(’%d ’, slice);

fprintf(’]\n’);

end

end

%To display the results of all mu

fprintf(’mu%d =[ ’,grad+1);

fprintf(’%.4f  ’, mu1);

fprintf(’]\n’);

[A, ind] = sort(mu);

[B, ind1] = sort(mu1);

if ind==ind1;

break;

end

H = H1;

mu = mu1;

grad = grad + 1;

iteration = iteration + 1;

end

if iteration >= max_iterations

warning(’Reached the maximum iteration count of 50.’);

end

%To display the fuzzy grade of H

fprintf(’The fuzzy grade of H with n=%d is %d ’,size(H,1),grad);

end

    To measure the execution time of the h4 function for different values on n, we make the following program, from which we obtain Figure 1.

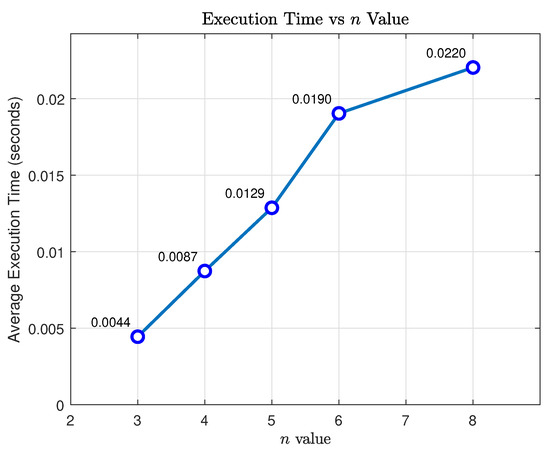
Figure 1. Execution time versus n value.

% Measure execution time of h4 function for different n values

n_values = [3, 4, 5, 6, 8];

num_trials = 5; % Number of trials for each n value

time_results = zeros(length(n_values), num_trials);

for i = 1:length(n_values)

n = n_values(i);

fprintf(’Testing n = %d...\n’, n);

for trial = 1:num_trials

tic;

[~] = evalc(’h4(n)’);

time_results(i, trial) = toc;

fprintf(’Trial %d: %.4f seconds\n’, trial, time_results(i, trial));

end

end

% Calculate average times

avg_times = mean(time_results, 2);

% Create and display results table

result_table = table(n_values’, avg_times, ...

’VariableNames’, {’n’, ’AverageTime_seconds’});

disp(result_table);

% Plot results

figure;

ax = gca;

% Set axis properties

set(ax, ’XColor’, [0 0 0], ’YColor’, [0 0 0], ...

’Color’, ’white’, ...

’GridColor’, [0.8 0.8 0.8], ...

’GridAlpha’, 0.5);

% Plot data

plot(n_values, avg_times, ’-o’, ...

’LineWidth’, 2, ...

’MarkerSize’, 8, ...

’MarkerEdgeColor’, ’b’, ...

’MarkerFaceColor’, ’w’);

% Set labels with mathematical n symbol

xlabel(’$n$ value’, ’FontSize’, 11, ’Interpreter’, ’latex’);

ylabel(’Average Execution Time (seconds)’, ’FontSize’, 11);

title(’Execution Time vs $n$ Value’, ’FontSize’, 12, ’Interpreter’, ’latex’);

% Set axis limits

xlim([2, max(n_values)+1]);

ylim([0, max(avg_times)*1.1]);

% Set x-axis ticks

set(ax, ’XTick’, 2:max(n_values));

% Add grid

grid on;

% Add data labels (removed ’s’ unit and adjusted position)

for i = 1:length(n_values)

text(n_values(i) - 0.1, avg_times(i) + max(avg_times)*0.02, ...

% Moved left by 0.1 and up by 2% of max value

sprintf(’%.4f’, avg_times(i)), ...

’FontSize’, 9, ...

’VerticalAlignment’, ’bottom’, ...

’HorizontalAlignment’, ’right’);

end

% Set figure background

set(gcf, ’Color’, ’white’);

% Save results

writetable(result_table, ’execution_times.csv’);

print(’execution_time_plot.png’, ’-dpng’, ’-r300’);

This algorithm exhibits significant bottlenecks in computational efficiency when handling large-scale problems, reflected mainly in the extremely high time complexity of the core function $h2$ of $O\left(n^4\right)$. As the size n increases, the computation time grows superlinearly, with experimental data showing a seven-fold increase in the computation time when n increases from 3 to 8. This exponential growth in complexity renders the algorithm impractical beyond certain scales, making parallel computing essential for improving computational efficiency.

GPU acceleration offers unique advantages for such problems, particularly for processing the algorithm’s regular matrix operations. Since the algorithm involves numerous independent three-dimensional/four-dimensional array operations, these computations can be perfectly mapped to a GPU’s parallel architecture. The thousands of computing cores in GPUs can simultaneously process matrix element operations, while their high-bandwidth memory effectively alleviates bottlenecks in large-scale data access. Theoretical analysis indicates that when $n>16$, the GPU solution is expected to achieve 10–100× performance improvements.

However, several challenges remain for effective GPU acceleration of this algorithm. Conditional branching statements in the algorithm may impact GPU execution efficiency, and frequent CPU–GPU data transfers introduce additional overhead. Furthermore, the current algorithm design’s memory access patterns are not fully optimized, potentially limiting the GPU’s memory bandwidth advantages. These factors require targeted optimization during implementation to achieve the desired acceleration results.

We make the following remark to interpret the obtained results: for example, $H(1,1,:)=\left[123\right]$ means that we have $1\circ 1=\{1,2,3\}$ at position (1, 1) of the multiplication table. After presenting each table corresponding to the join space $H_i$ in the sequence, the fuzzy function ${\mu }_i$ is calculated, and we indicate when the sequence stops.

The results of applying our programs are shown below.

>> h4(3);	H1(3,3,:) = [3]
H(1,1,:) = [1 2 3]	mu2 =[0.5333 0.5238 0.5333]
H(1,2,:) = [1 2 3]	H2(1,1,:) = [1 3]
H(1,3,:) = [1 2 3]	H2(1,2,:) = [1 2 3]
H(2,1,:) = [1 2 3]	H2(1,3,:) = [1 3]
H(2,2,:) = [2 3]	H2(2,1,:) = [1 2 3]
H(2,3,:) = [2 3]	H2(2,2,:) = [2]
H(3,1,:) = [1 2 3]	H2(2,3,:) = [1 2 3]
H(3,2,:) = [2 3]	H2(3,1,:) = [1 3]
H(3,3,:) = [3]	H2(3,2,:) = [1 2 3]
mu1 =[0.3333 0.3958 0.4630]	H2(3,3,:) = [1 3]
H1(1,1,:) = [1]	mu3 =[0.4167 0.4667 0.4167]
H1(1,2,:) = [1 2]	H3(1,1,:) = [1 3]
H1(1,3,:) = [1 2 3]	H3(1,2,:) = [1 2 3]
H1(2,1,:) = [1 2]	H3(1,3,:) = [1 3]
H1(2,2,:) = [2]	H3(2,1,:) = [1 2 3]
H1(2,3,:) = [2 3]	H3(2,2,:) = [2]
H1(3,1,:) = [1 2 3]	H3(2,3,:) = [1 2 3]
H1(3,2,:) = [2 3]	H3(3,1,:) = [1 3]
H3(3,2,:) = [1 2 3]	H2(2,3,:) = [2 3]
H3(3,3,:) = [1 3]	H2(2,4,:) = [1 2 3 4]
mu4 = [0.4167 0.4667 0.4167]	H2(3,1,:) = [1 2 3 4]
The strong fuzzy degree of H with	H2(3,2,:) = [2 3]
n=3 is 2.	H2(3,3,:) = [2 3]
	H2(3,4,:) = [1 2 3 4]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	H2(4,1,:) = [1 4]
	H2(4,2,:) = [1 2 3 4]
>> h4(4);	H2(4,3,:) = [1 2 3 4]
H(1,1,:) = [1 2 3 4]	H2(4,4,:) = [1 4]
H(1,2,:) = [1 2 3 4]	mu3 = [0.3333 0.3333
H(1,3,:) = [1 2 3 4]	0.3333 0.3333]
H(1,4,:) = [1 2 3 4]	H3 is the total hypergroup.
H(2,1,:) = [1 2 3 4]	mu4 = [0.2500 0.2500
H(2,2,:) = [2 3 4]	0.2500 0.2500]
H(2,3,:) = [2 3 4]	The strong fuzzy grade of H
H(2,4,:) = [2 3 4]	with n=4 is 3.
H(3,1,:) = [1 2 3 4]
H(3,2,:) = [2 3 4]	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
H(3,3,:) = [3 4]
H(3,4,:) = [3 4]	>> h4(5);
H(4,1,:) = [1 2 3 4]	H(1,1,:) = [1 2 3 4 5]
H(4,2,:) = [2 3 4]	H(1,2,:) = [1 2 3 4 5]
H(4,3,:) = [3 4]	H(1,3,:) = [1 2 3 4 5]
H(4,4,:) = [4]	H(1,4,:) = [1 2 3 4 5]
mu1 = [0.2500 0.2847	H(1,5,:) = [1 2 3 4 5]
0.3278 0.3698]	H(2,1,:) = [1 2 3 4 5]
H1(1,1,:) = [1]	H(2,2,:) = [2 3 4 5]
H1(1,2,:) = [1 2]	H(2,3,:) = [2 3 4 5]
H1(1,3,:) = [1 2 3]	H(2,4,:) = [2 3 4 5]
H1(1,4,:) = [1 2 3 4]	H(2,5,:) = [2 3 4 5]
H1(2,1,:) = [1 2]	H(3,1,:) = [1 2 3 4 5]
H1(2,2,:) = [2]	H(3,2,:) = [2 3 4 5]
H1(2,3,:) = [2 3]	H(3,3,:) = [3 4 5]
H1(2,4,:) = [2 3 4]	H(3,4,:) = [3 4 5]
H1(3,1,:) = [1 2 3]	H(3,5,:) = [3 4 5]
H1(3,2,:) = [2 3]	H(4,1,:) = [1 2 3 4 5]
H1(3,3,:) = [3]	H(4,2,:) = [2 3 4 5]
H1(3,4,:) = [3 4]	H(4,3,:) = [3 4 5]
H1(4,1,:) = [1 2 3 4]	H(4,4,:) = [4 5]
H1(4,2,:) = [2 3 4]	H(4,5,:) = [4 5]
H1(4,3,:) = [3 4]	H(5,1,:) = [1 2 3 4 5]
H1(4,4,:) = [4]	H(5,2,:) = [2 3 4 5]
mu2 = [0.4524 0.4394	H(5,3,:) = [3 4 5]
0.4394 0.4524]	H(5,4,:) = [4 5]
H2(1,1,:) = [1 4]	H(5,5,:) = [5]
H2(1,2,:) = [1 2 3 4]	mu1 = [0.2000 0.2219 0.2484
H2(1,3,:) = [1 2 3 4]	0.2799 0.3087]
H2(1,4,:) = [1 4]	H1(1,1,:) = [1]
H2(2,1,:) = [1 2 3 4]	H1(1,2,:) = [1 2]
H2(2,2,:) = [2 3]	H1(1,3,:) = [1 2 3]
H1(1,4,:) = [1 2 3 4]	0.3482 0.3067 0.3000]
H1(1,5,:) = [1 2 3 4 5]	H3(1,1,:) = [1 5]
H1(2,1,:) = [1 2]	H3(1,2,:) = [1 2 4 5]
H1(2,2,:) = [2]	H3(1,3,:) = [1 2 3 4 5]
H1(2,3,:) = [2 3]	H3(1,4,:) = [1 2 4 5]
H1(2,4,:) = [2 3 4]	H3(1,5,:) = [1 5]
H1(2,5,:) = [2 3 4 5]	H3(2,1,:) = [1 2 4 5]
H1(3,1,:) = [1 2 3]	H3(2,2,:) = [2 4]
H1(3,2,:) = [2 3]	H3(2,3,:) = [2 3 4]
H1(3,3,:) = [3]	H3(2,4,:) = [2 4]
H1(3,4,:) = [3 4]	H3(2,5,:) = [1 2 4 5]
H1(3,5,:) = [3 4 5]	H3(3,1,:) = [1 2 3 4 5]
H1(4,1,:) = [1 2 3 4]	H3(3,2,:) = [2 3 4]
H1(4,2,:) = [2 3 4]	H3(3,3,:) = [3]
H1(4,3,:) = [3 4]	H3(3,4,:) = [2 3 4]
H1(4,4,:) = [4]	H3(3,5,:) = [1 2 3 4 5]
H1(4,5,:) = [4 5]	H3(4,1,:) = [1 2 4 5]
H1(5,1,:) = [1 2 3 4 5]	H3(4,2,:) = [2 4]
H1(5,2,:) = [2 3 4 5]	H3(4,3,:) = [2 3 4]
H1(5,3,:) = [3 4 5]	H3(4,4,:) = [2 4]
H1(5,4,:) = [4 5]	H3(4,5,:) = [1 2 4 5]
H1(5,5,:) = [5]	H3(5,1,:) = [1 5]
mu2 = [0.3963 0.3822	H3(5,2,:) = [1 2 4 5]
0.3765 0.3822 0.3963]	H3(5,3,:) = [1 2 3 4 5]
H2(1,1,:) = [1 5]	H3(5,4,:) = [1 2 4 5]
H2(1,2,:) = [1 2 4 5]	H3(5,5,:) = [1 5]
H2(1,3,:) = [1 2 3 4 5]	mu4 = [0.3000 0.3067 0.3482
H2(1,4,:) = [1 2 4 5]	0.3067 0.3000]
H2(1,5,:) = [1 5]	The strong fuzzy grade of H
H2(2,1,:) = [1 2 4 5]	with n=5 is 2.
H2(2,2,:) = [2 4]
H2(2,3,:) = [2 3 4]	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
H2(2,4,:) = [2 4]
H2(2,5,:) = [1 2 4 5]	>> h4(6);
H2(3,1,:) = [1 2 3 4 5]	H(1,1,:) = [1 2 3 4 5 6]
H2(3,2,:) = [2 3 4]	H(1,2,:) = [1 2 3 4 5 6]
H2(3,3,:) = [3]	H(1,3,:) = [1 2 3 4 5 6]
H2(3,4,:) = [2 3 4]	H(1,4,:) = [1 2 3 4 5 6]
H2(3,5,:) = [1 2 3 4 5]	H(1,5,:) = [1 2 3 4 5 6]
H2(4,1,:) = [1 2 4 5]	H(1,6,:) = [1 2 3 4 5 6]
H2(4,2,:) = [2 4]	H(2,1,:) = [1 2 3 4 5 6]
H2(4,3,:) = [2 3 4]	H(2,2,:) = [2 3 4 5 6]
H2(4,4,:) = [2 4]	H(2,3,:) = [2 3 4 5 6]
H2(4,5,:) = [1 2 4 5]	H(2,4,:) = [2 3 4 5 6]
H2(5,1,:) = [1 5]	H(2,5,:) = [2 3 4 5 6]
H2(5,2,:) = [1 2 4 5]	H(2,6,:) = [2 3 4 5 6]
H2(5,3,:) = [1 2 3 4 5]	H(3,1,:) = [1 2 3 4 5 6]
H2(5,4,:) = [1 2 4 5]	H(3,2,:) = [2 3 4 5 6]
H2(5,5,:) = [1 5]	H(3,3,:) = [3 4 5 6]
mu3 = [0.3000 0.3067	H(3,4,:) = [3 4 5 6]
	H(3,5,:) = [3 4 5 6]
H(3,6,:) = [3 4 5 6]	H1(5,6,:) = [5 6]
H(4,1,:) = [1 2 3 4 5 6]	H1(6,1,:) = [1 2 3 4 5 6]
H(4,2,:) = [2 3 4 5 6]	H1(6,2,:) = [2 3 4 5 6]
H(4,3,:) = [3 4 5 6]	H1(6,3,:) = [3 4 5 6]
H(4,4,:) = [4 5 6]	H1(6,4,:) = [4 5 6]
H(4,5,:) = [4 5 6]	H1(6,5,:) = [5 6]
H(4,6,:) = [4 5 6]	H1(6,6,:) = [6]
H(5,1,:) = [1 2 3 4 5 6]	mu2 = [0.3545 0.3404
H(5,2,:) = [2 3 4 5 6]	0.3319 0.3319 0.3404 0.3545]
H(5,3,:) = [3 4 5 6]	H2(1,1,:) = [1 6]
H(5,4,:) = [4 5 6]	H2(1,2,:) = [1 2 5 6]
H(5,5,:) = [5 6]	H2(1,3,:) = [1 2 3 4 5 6]
H(5,6,:) = [5 6]	H2(1,4,:) = [1 2 3 4 5 6]
H(6,1,:) = [1 2 3 4 5 6]	H2(1,5,:) = [1 2 5 6]
H(6,2,:) = [2 3 4 5 6]	H2(1,6,:) = [1 6]
H(6,3,:) = [3 4 5 6]	H2(2,1,:) = [1 2 5 6]
H(6,4,:) = [4 5 6]	H2(2,2,:) = [2 5]
H(6,5,:) = [5 6]	H2(2,3,:) = [2 3 4 5]
H(6,6,:) = [6]	H2(2,4,:) = [2 3 4 5]
mu1 = [0.1667 0.1817	H2(2,5,:) = [2 5]
0.1994 0.2203 0.2443 0.2653]	H2(2,6,:) = [1 2 5 6]
H1(1,1,:) = [1]	H2(3,1,:) = [1 2 3 4 5 6]
H1(1,2,:) = [1 2]	H2(3,2,:) = [2 3 4 5]
H1(1,3,:) = [1 2 3]	H2(3,3,:) = [3 4]
H1(1,4,:) = [1 2 3 4]	H2(3,4,:) = [3 4]
H1(1,5,:) = [1 2 3 4 5]	H2(3,5,:) = [2 3 4 5]
H1(1,6,:) = [1 2 3 4 5 6]	H2(3,6,:) = [1 2 3 4 5 6]
H1(2,1,:) = [1 2]	H2(4,1,:) = [1 2 3 4 5 6]
H1(2,2,:) = [2]	H2(4,2,:) = [2 3 4 5]
H1(2,3,:) = [2 3]	H2(4,3,:) = [3 4]
H1(2,4,:) = [2 3 4]	H2(4,4,:) = [3 4]
H1(2,5,:) = [2 3 4 5]	H2(4,5,:) = [2 3 4 5]
H1(2,6,:) = [2 3 4 5 6]	H2(4,6,:) = [1 2 3 4 5 6]
H1(3,1,:) = [1 2 3]	H2(5,1,:) = [1 2 5 6]
H1(3,2,:) = [2 3]	H2(5,2,:) = [2 5]
H1(3,3,:) = [3]	H2(5,3,:) = [2 3 4 5]
H1(3,4,:) = [3 4]	H2(5,4,:) = [2 3 4 5]
H1(3,5,:) = [3 4 5]	H2(5,5,:) = [2 5]
H1(3,6,:) = [3 4 5 6]	H2(5,6,:) = [1 2 5 6]
H1(4,1,:) = [1 2 3 4]	H2(6,1,:) = [1 6]
H1(4,2,:) = [2 3 4]	H2(6,2,:) = [1 2 5 6]
H1(4,3,:) = [3 4]	H2(6,3,:) = [1 2 3 4 5 6]
H1(4,4,:) = [4]	H2(6,4,:) = [1 2 3 4 5 6]
H1(4,5,:) = [4 5]	H2(6,5,:) = [1 2 5 6]
H1(4,6,:) = [4 5 6]	H2(6,6,:) = [1 6]
H1(5,1,:) = [1 2 3 4 5]	mu3 = [0.2667 0.2619 0.2667
H1(5,2,:) = [2 3 4 5]	0.2667 0.2619 0.2667]
H1(5,3,:) = [3 4 5]	H3(1,1,:) = [1 3 4 6]
H1(5,4,:) = [4 5]	H3(1,2,:) = [1 2 3 4 5 6]
H1(5,5,:) = [5]	H3(1,3,:) = [1 3 4 6]
H3(1,4,:) = [1 3 4 6]	H4(3,4,:) = [1 3 4 6]
H3(1,5,:) = [1 2 3 4 5 6]	H4(3,5,:) = [1 2 3 4 5 6]
H3(1,6,:) = [1 3 4 6]	H4(3,6,:) = [1 3 4 6]
H3(2,1,:) = [1 2 3 4 5 6]	H4(4,1,:) = [1 3 4 6]
H3(2,2,:) = [2 5]	H4(4,2,:) = [1 2 3 4 5 6]
H3(2,3,:) = [1 2 3 4 5 6]	H4(4,3,:) = [1 3 4 6]
H3(2,4,:) = [1 2 3 4 5 6]	H4(4,4,:) = [1 3 4 6]
H3(2,5,:) = [2 5]	H4(4,5,:) = [1 2 3 4 5 6]
H3(2,6,:) = [1 2 3 4 5 6]	H4(4,6,:) = [1 3 4 6]
H3(3,1,:) = [1 3 4 6]	H4(5,1,:) = [1 2 3 4 5 6]
H3(3,2,:) = [1 2 3 4 5 6]	H4(5,2,:) = [2 5]
H3(3,3,:) = [1 3 4 6]	H4(5,3,:) = [1 2 3 4 5 6]
H3(3,4,:) = [1 3 4 6]	H4(5,4,:) = [1 2 3 4 5 6]
H3(3,5,:) = [1 2 3 4 5 6]	H4(5,5,:) = [2 5]
H3(3,6,:) = [1 3 4 6]	H4(5,6,:) = [1 2 3 4 5 6]
H3(4,1,:) = [1 3 4 6]	H4(6,1,:) = [1 3 4 6]
H3(4,2,:) = [1 2 3 4 5 6]	H4(6,2,:) = [1 2 3 4 5 6]
H3(4,3,:) = [1 3 4 6]	H4(6,3,:) = [1 3 4 6]
H3(4,4,:) = [1 3 4 6]	H4(6,4,:) = [1 3 4 6]
H3(4,5,:) = [1 2 3 4 5 6]	H4(6,5,:) = [1 2 3 4 5 6]
H3(4,6,:) = [1 3 4 6]	H4(6,6,:) = [1 3 4 6]
H3(5,1,:) = [1 2 3 4 5 6]	mu5 = [0.2083 0.2333 0.2083
H3(5,2,:) = [2 5]	0.2083 0.2333 0.2083]
H3(5,3,:) = [1 2 3 4 5 6]	The strong fuzzy grade of H
H3(5,4,:) = [1 2 3 4 5 6]	with n=6 is 3.
H3(5,5,:) = [2 5]
H3(5,6,:) = [1 2 3 4 5 6]	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
H3(6,1,:) = [1 3 4 6]
H3(6,2,:) = [1 2 3 4 5 6]	>> h4(8);
H3(6,3,:) = [1 3 4 6]	H(1,1,:) = [1 2 3 4 5 6 7 8]
H3(6,4,:) = [1 3 4 6]	H(1,2,:) = [1 2 3 4 5 6 7 8]
H3(6,5,:) = [1 2 3 4 5 6]	H(1,3,:) = [1 2 3 4 5 6 7 8]
H3(6,6,:) = [1 3 4 6]	H(1,4,:) = [1 2 3 4 5 6 7 8]
mu4 = [0.2083 0.2333 0.2083	H(1,5,:) = [1 2 3 4 5 6 7 8]
0.2083 0.2333 0.2083]	H(1,6,:) = [1 2 3 4 5 6 7 8]
H4(1,1,:) = [1 3 4 6]	H(1,7,:) = [1 2 3 4 5 6 7 8]
H4(1,2,:) = [1 2 3 4 5 6]	H(1,8,:) = [1 2 3 4 5 6 7 8]
H4(1,3,:) = [1 3 4 6]	H(2,1,:) = [1 2 3 4 5 6 7 8]
H4(1,4,:) = [1 3 4 6]	H(2,2,:) = [2 3 4 5 6 7 8]
H4(1,5,:) = [1 2 3 4 5 6]	H(2,3,:) = [2 3 4 5 6 7 8]
H4(1,6,:) = [1 3 4 6]	H(2,4,:) = [2 3 4 5 6 7 8]
H4(2,1,:) = [1 2 3 4 5 6]	H(2,5,:) = [2 3 4 5 6 7 8]
H4(2,2,:) = [2 5]	H(2,6,:) = [2 3 4 5 6 7 8]
H4(2,3,:) = [1 2 3 4 5 6]	H(2,7,:) = [2 3 4 5 6 7 8]
H4(2,4,:) = [1 2 3 4 5 6]	H(2,8,:) = [2 3 4 5 6 7 8]
H4(2,5,:) = [2 5]	H(3,1,:) = [1 2 3 4 5 6 7 8]
H4(2,6,:) = [1 2 3 4 5 6]	H(3,2,:) = [2 3 4 5 6 7 8]
H4(3,1,:) = [1 3 4 6]	H(3,3,:) = [3 4 5 6 7 8]
H4(3,2,:) = [1 2 3 4 5 6]	H(3,4,:) = [3 4 5 6 7 8]
H4(3,3,:) = [1 3 4 6]	H(3,5,:) = [3 4 5 6 7 8]
	H(3,6,:) = [3 4 5 6 7 8]
H(3,7,:) = [3 4 5 6 7 8]	H1(1,6,:) = [1 2 3 4 5 6]
H(3,8,:) = [3 4 5 6 7 8]	H1(1,7,:) = [1 2 3 4 5 6 7]
H(4,1,:) = [1 2 3 4 5 6 7 8]	H1(1,8,:) = [1 2 3 4 5 6 7 8]
H(4,2,:) = [2 3 4 5 6 7 8]	H1(2,1,:) = [1 2]
H(4,3,:) = [3 4 5 6 7 8]	H1(2,2,:) = [2]
H(4,4,:) = [4 5 6 7 8]	H1(2,3,:) = [2 3]
H(4,5,:) = [4 5 6 7 8]	H1(2,4,:) = [2 3 4]
H(4,6,:) = [4 5 6 7 8]	H1(2,5,:) = [2 3 4 5]
H(4,7,:) = [4 5 6 7 8]	H1(2,6,:) = [2 3 4 5 6]
H(4,8,:) = [4 5 6 7 8]	H1(2,7,:) = [2 3 4 5 6 7]
H(5,1,:) = [1 2 3 4 5 6 7 8]	H1(2,8,:) = [2 3 4 5 6 7 8]
H(5,2,:) = [2 3 4 5 6 7 8]	H1(3,1,:) = [1 2 3]
H(5,3,:) = [3 4 5 6 7 8]	H1(3,2,:) = [2 3]
H(5,4,:) = [4 5 6 7 8]	H1(3,3,:) = [3]
H(5,5,:) = [5 6 7 8]	H1(3,4,:) = [3 4]
H(5,6,:) = [5 6 7 8]	H1(3,5,:) = [3 4 5]
H(5,7,:) = [5 6 7 8]	H1(3,6,:) = [3 4 5 6]
H(5,8,:) = [5 6 7 8]	H1(3,7,:) = [3 4 5 6 7]
H(6,1,:) = [1 2 3 4 5 6 7 8]	H1(3,8,:) = [3 4 5 6 7 8]
H(6,2,:) = [2 3 4 5 6 7 8]	H1(4,1,:) = [1 2 3 4]
H(6,3,:) = [3 4 5 6 7 8]	H1(4,2,:) = [2 3 4]
H(6,4,:) = [4 5 6 7 8]	H1(4,3,:) = [3 4]
H(6,5,:) = [5 6 7 8]	H1(4,4,:) = [4]
H(6,6,:) = [6 7 8]	H1(4,5,:) = [4 5]
H(6,7,:) = [6 7 8]	H1(4,6,:) = [4 5 6]
H(6,8,:) = [6 7 8]	H1(4,7,:) = [4 5 6 7]
H(7,1,:) = [1 2 3 4 5 6 7 8]	H1(4,8,:) = [4 5 6 7 8]
H(7,2,:) = [2 3 4 5 6 7 8]	H1(5,1,:) = [1 2 3 4 5]
H(7,3,:) = [3 4 5 6 7 8]	H1(5,2,:) = [2 3 4 5]
H(7,4,:) = [4 5 6 7 8]	H1(5,3,:) = [3 4 5]
H(7,5,:) = [5 6 7 8]	H1(5,4,:) = [4 5]
H(7,6,:) = [6 7 8]	H1(5,5,:) = [5]
H(7,7,:) = [7 8]	H1(5,6,:) = [5 6]
H(7,8,:) = [7 8]	H1(5,7,:) = [5 6 7]
H(8,1,:) = [1 2 3 4 5 6 7 8]	H1(5,8,:) = [5 6 7 8]
H(8,2,:) = [2 3 4 5 6 7 8]	H1(6,1,:) = [1 2 3 4 5 6]
H(8,3,:) = [3 4 5 6 7 8]	H1(6,2,:) = [2 3 4 5 6]
H(8,4,:) = [4 5 6 7 8]	H1(6,3,:) = [3 4 5 6]
H(8,5,:) = [5 6 7 8]	H1(6,4,:) = [4 5 6]
H(8,6,:) = [6 7 8]	H1(6,5,:) = [5 6]
H(8,7,:) = [7 8]	H1(6,6,:) = [6]
H(8,8,:) = [8]	H1(6,7,:) = [6 7]
mu1 = [0.1250 0.1333	H1(6,8,:) = [6 7 8]
0.1427 0.1534 0.1657	H1(7,1,:) = [1 2 3 4 5 6 7]
0.1797 0.1950 0.2075]	H1(7,2,:) = [2 3 4 5 6 7]
H1(1,1,:) = [1]	H1(7,3,:) = [3 4 5 6 7]
H1(1,2,:) = [1 2]	H1(7,4,:) = [4 5 6 7]
H1(1,3,:) = [1 2 3]	H1(7,5,:) = [5 6 7]
H1(1,4,:) = [1 2 3 4]	H1(7,6,:) = [6 7]
H1(1,5,:) = [1 2 3 4 5]	H1(7,7,:) = [7]
H1(7,8,:) = [7 8]	H2(5,7,:) = [2 3 4 5 6 7]
H1(8,1,:) = [1 2 3 4 5 6 7 8]	H2(5,8,:) = [1 2 3 4 5 6 7 8]
H1(8,2,:) = [2 3 4 5 6 7 8]	H2(6,1,:) = [1 2 3 6 7 8]
H1(8,3,:) = [3 4 5 6 7 8]	H2(6,2,:) = [2 3 6 7]
H1(8,4,:) = [4 5 6 7 8]	H2(6,3,:) = [3 6]
H1(8,5,:) = [5 6 7 8]	H2(6,4,:) = [3 4 5 6]
H1(8,6,:) = [6 7 8]	H2(6,5,:) = [3 4 5 6]
H1(8,7,:) = [7 8]	H2(6,6,:) = [3 6]
H1(8,8,:) = [8]	H2(6,7,:) = [2 3 6 7]
mu2 = [0.2957 0.2823	H2(6,8,:) = [1 2 3 6 7 8]
0.2720 0.2672 0.2672	H2(7,1,:) = [1 2 7 8]
0.2720 0.2823 0.2957]	H2(7,2,:) = [2 7]
H2(1,1,:) = [1 8]	H2(7,3,:) = [2 3 6 7]
H2(1,2,:) = [1 2 7 8]	H2(7,4,:) = [2 3 4 5 6 7]
H2(1,3,:) = [1 2 3 6 7 8]	H2(7,5,:) = [2 3 4 5 6 7]
H2(1,4,:) = [1 2 3 4 5 6 7 8]	H2(7,6,:) = [2 3 6 7]
H2(1,5,:) = [1 2 3 4 5 6 7 8]	H2(7,7,:) = [2 7]
H2(1,6,:) = [1 2 3 6 7 8]	H2(7,8,:) = [1 2 7 8]
H2(1,7,:) = [1 2 7 8]	H2(8,1,:) = [1 8]
H2(1,8,:) = [1 8]	H2(8,2,:) = [1 2 7 8]
H2(2,1,:) = [1 2 7 8]	H2(8,3,:) = [1 2 3 6 7 8]
H2(2,2,:) = [2 7]	H2(8,4,:) = [1 2 3 4 5 6 7 8]
H2(2,3,:) = [2 3 6 7]	H2(8,5,:) = [1 2 3 4 5 6 7 8]
H2(2,4,:) = [2 3 4 5 6 7]	H2(8,6,:) = [1 2 3 6 7 8]
H2(2,5,:) = [2 3 4 5 6 7]	H2(8,7,:) = [1 2 7 8]
H2(2,6,:) = [2 3 6 7]	H2(8,8,:) = [1 8]
H2(2,7,:) = [2 7]	mu3 = [0.2262 0.2197
H2(2,8,:) = [1 2 7 8]	0.2197 0.2262 0.2262
H2(3,1,:) = [1 2 3 6 7 8]	0.2197 0.2197 0.2262]
H2(3,2,:) = [2 3 6 7]	H3(1,1,:) = [1 4 5 8]
H2(3,3,:) = [3 6]	H3(1,2,:) = [1 2 3 4 5 6 7 8]
H2(3,4,:) = [3 4 5 6]	H3(1,3,:) = [1 2 3 4 5 6 7 8]
H2(3,5,:) = [3 4 5 6]	H3(1,4,:) = [1 4 5 8]
H2(3,6,:) = [3 6]	H3(1,5,:) = [1 4 5 8]
H2(3,7,:) = [2 3 6 7]	H3(1,6,:) = [1 2 3 4 5 6 7 8]
H2(3,8,:) = [1 2 3 6 7 8]	H3(1,7,:) = [1 2 3 4 5 6 7 8]
H2(4,1,:) = [1 2 3 4 5 6 7 8]	H3(1,8,:) = [1 4 5 8]
H2(4,2,:) = [2 3 4 5 6 7]	H3(2,1,:) = [1 2 3 4 5 6 7 8]
H2(4,3,:) = [3 4 5 6]	H3(2,2,:) = [2 3 6 7]
H2(4,4,:) = [4 5]	H3(2,3,:) = [2 3 6 7]
H2(4,5,:) = [4 5]	H3(2,4,:) = [1 2 3 4 5 6 7 8]
H2(4,6,:) = [3 4 5 6]	H3(2,5,:) = [1 2 3 4 5 6 7 8]
H2(4,7,:) = [2 3 4 5 6 7]	H3(2,6,:) = [2 3 6 7]
H2(4,8,:) = [1 2 3 4 5 6 7 8]	H3(2,7,:) = [2 3 6 7]
H2(5,1,:) = [1 2 3 4 5 6 7 8]	H3(2,8,:) = [1 2 3 4 5 6 7 8]
H2(5,2,:) = [2 3 4 5 6 7]	H3(3,1,:) = [1 2 3 4 5 6 7 8]
H2(5,3,:) = [3 4 5 6]	H3(3,2,:) = [2 3 6 7]
H2(5,4,:) = [4 5]	H3(3,3,:) = [2 3 6 7]
H2(5,5,:) = [4 5]	H3(3,4,:) = [1 2 3 4 5 6 7 8]
H2(5,6,:) = [3 4 5 6]	H3(3,5,:) = [1 2 3 4 5 6 7 8]
H3(3,6,:) = [2 3 6 7]	H3(6,6,:) = [2 3 6 7]
H3(3,7,:) = [2 3 6 7]	H3(6,7,:) = [2 3 6 7]
H3(3,8,:) = [1 2 3 4 5 6 7 8]	H3(6,8,:) = [1 2 3 4 5 6 7 8]
H3(4,1,:) = [1 4 5 8]	H3(7,1,:) = [1 2 3 4 5 6 7 8]
H3(4,2,:) = [1 2 3 4 5 6 7 8]	H3(7,2,:) = [2 3 6 7]
H3(4,3,:) = [1 2 3 4 5 6 7 8]	H3(7,3,:) = [2 3 6 7]
H3(4,4,:) = [1 4 5 8]	H3(7,4,:) = [1 2 3 4 5 6 7 8]
H3(4,5,:) = [1 4 5 8]	H3(7,5,:) = [1 2 3 4 5 6 7 8]
H3(4,6,:) = [1 2 3 4 5 6 7 8]	H3(7,6,:) = [2 3 6 7]
H3(4,7,:) = [1 2 3 4 5 6 7 8]	H3(7,7,:) = [2 3 6 7]
H3(4,8,:) = [1 4 5 8]	H3(7,8,:) = [1 2 3 4 5 6 7 8]
H3(5,1,:) = [1 4 5 8]	H3(8,1,:) = [1 4 5 8]
H3(5,2,:) = [1 2 3 4 5 6 7 8]	H3(8,2,:) = [1 2 3 4 5 6 7 8]
H3(5,3,:) = [1 2 3 4 5 6 7 8]	H3(8,3,:) = [1 2 3 4 5 6 7 8]
H3(5,4,:) = [1 4 5 8]	H3(8,4,:) = [1 4 5 8]
H3(5,5,:) = [1 4 5 8]	H3(8,5,:) = [1 4 5 8]
H3(5,6,:) = [1 2 3 4 5 6 7 8]	H3(8,6,:) = [1 2 3 4 5 6 7 8]
H3(5,7,:) = [1 2 3 4 5 6 7 8]	H3(8,7,:) = [1 2 3 4 5 6 7 8]
H3(5,8,:) = [1 4 5 8]	H3(8,8,:) = [1 4 5 8]
H3(6,1,:) = [1 2 3 4 5 6 7 8]	mu4 = [0.1667 0.1667
H3(6,2,:) = [2 3 6 7]	0.1667 0.1667 0.1667
H3(6,3,:) = [2 3 6 7]	0.1667 0.1667 0.1667]
H3(6,4,:) = [1 2 3 4 5 6 7 8]	The strong fuzzy grade of H
H3(6,5,:) = [1 2 3 4 5 6 7 8]	with n=8 is 4.

4. Conclusions

In this paper, we present a MATLAB program for an algorithm that determines the strong fuzzy grade for small cardinal hypergroups: 3, 4, 5, 6, 8 For the hypergroup of cardinal 7, there is no strong fuzzy grade. In future research, we intend to obtain programs in order to calculate the strong fuzzy grade for hypergroups of large cardinals and to calculate the fuzzy grade, both for small and larger hypergroupoids, using GPU acceleration.