Accelerating Subgraph Matching Through Advanced Compression and Label Filtering

Abstract

Efficiently identifying subgraphs that match a given query graph within large-scale graphs has become a critical focus in both academic and industrial research. Subgraph matching, a fundamental problem in graph algorithms, facilitates the effective querying of graph data and is fundamentally based on the subgraph isomorphism problem, which is known to be NP-complete. Among the various stages of subgraph matching, the filtering phase is particularly crucial as it directly affects the overall efficiency of the algorithm. A robust filtering mechanism can rapidly identify candidate nodes that satisfy the query criteria, thereby significantly reducing computational costs in the subsequent stages. The analysis of existing subgraph matching techniques reveals several challenges in the filtering stage: (1) redundant enumeration of equivalent nodes; (2) incomplete filtering due to structural limitations; and (3) excessive redundant validations during the verification phase. To overcome these issues, we propose an adaptive subgraph matching (ASM) framework that integrates efficient compressed graph nodes (CGNs) and a novel label count filter (LCF) algorithm. These innovations enhance the filtering process, resulting in significant improvements in query processing performance. Experimental evaluations demonstrate that our approach achieves substantial gains, outperforming state-of-the-art subgraph search and matching algorithms by several orders of magnitude in query processing time.

1. Introduction

With the growing prominence of graph data structures in modern application domains such as social network analysis [1], bioinformatics [2], and semantic search [3], increasing research efforts and resources have been dedicated to enhancing the search performance on large-scale graphs. As one of the most important issues in the field of graph analysis is subgraph matching; given a data graph G and a query graph q, the subgraph matching problem seeks to identify all the matches of q in G [4], which is known as the NP-complete problem [5]. That is, the time complexity of matching grows exponentially in the worst case. To reduce the search space and accelerate the subgraph matching query process, various methods have been proposed to minimize the number of candidate nodes in the data graph, such as constructing indexes that store vertex-adjacent features [6] or designing effective filtering strategies [7]. However, the enumeration and storage of substructures still incur exponential time and space complexity during computation [8]. Consequently, enabling a large data graph to enumerate all query results within an efficient time frame remains a key challenge in subgraph matching research.

In

Table 1. Representative subgraph matching methods.

Community	Model	Category	Methodology	Algorithms/System
Dataset			Direct enumeration	Ullmann [10], VF2 [11], GraphQL [13]
	Exploration	Backtracking search	Offline-index	GADDI, SPath [14]
			Online-index enumeration	CFL, CECI, DPISO
	Join	Multi-way join	Pair-wise join	postgreSQL, Neo4j, GPSM [17]
			Worst-case optional join	LogicBlox, GraphFlow, EmptyHeaded

, methods for subgraph matching are broadly categorized into two groups: exploratory backtracking methods [9,10,11,12,13,14,15] and join methods [16,17]. Each algorithm has its own advantages and disadvantages. For example, the Ullmann [10] algorithm is the first subgraph isomorphic search algorithm, which does not define the matching order of the query vertices, but only utilizes the order of the input nodes of the query graph to perform sequential node-depth-first matches. The VF2 [11] algorithm selects the start node arbitrarily, and then proceeds to expand by selecting the next vertex that is connected to the query vertices that have already been matched. RapidMatch [16] for distributed environments performs queries in main memory without indexing, but is limited in scope and complex to implement. According to recent studies, the exploration backtracking method is suitable for large sparse graphs, while the join method is more suitable for small dense graphs [18]. The algorithmic studies mentioned above usually focus on analyzing and comparing the methods and performance of current algorithms [19]. Therefore, instead of trying to identify or compare differences between algorithms, we focus on current problems in subgraph matching and advanced algorithms to solve them. The problem of subgraph matching still faces several major challenges: (1) one is the repeated enumeration of equivalent nodes leading to degradation of search performance when faced with large-scale data graphs, and (2) the other is that for the generation of candidate node sets stage, the filtering conditions are incomplete and there still exists a portion of undesired candidate nodes, which leads to excessive overhead in the validation stage and affects the overall performance of the algorithm.

To address the above issues, this paper investigates the subgraph matching query problem for undirected graphs and proposes an efficient adaptive subgraph matching (ASM) algorithm. The proposed approach introduces a novel graph compression technique in the preprocessing stage, a new label count filter in the candidate node filtering stage, and an adaptive adjustment model for ultra-large-scale graphs. By reducing the size of the data graph and further filtering candidate nodes through a comprehensive filtering mechanism, the method not only improves data processing efficiency but also minimizes resource consumption.

Aiming at the above problems, the main contributions are summarized as follows:

(1)

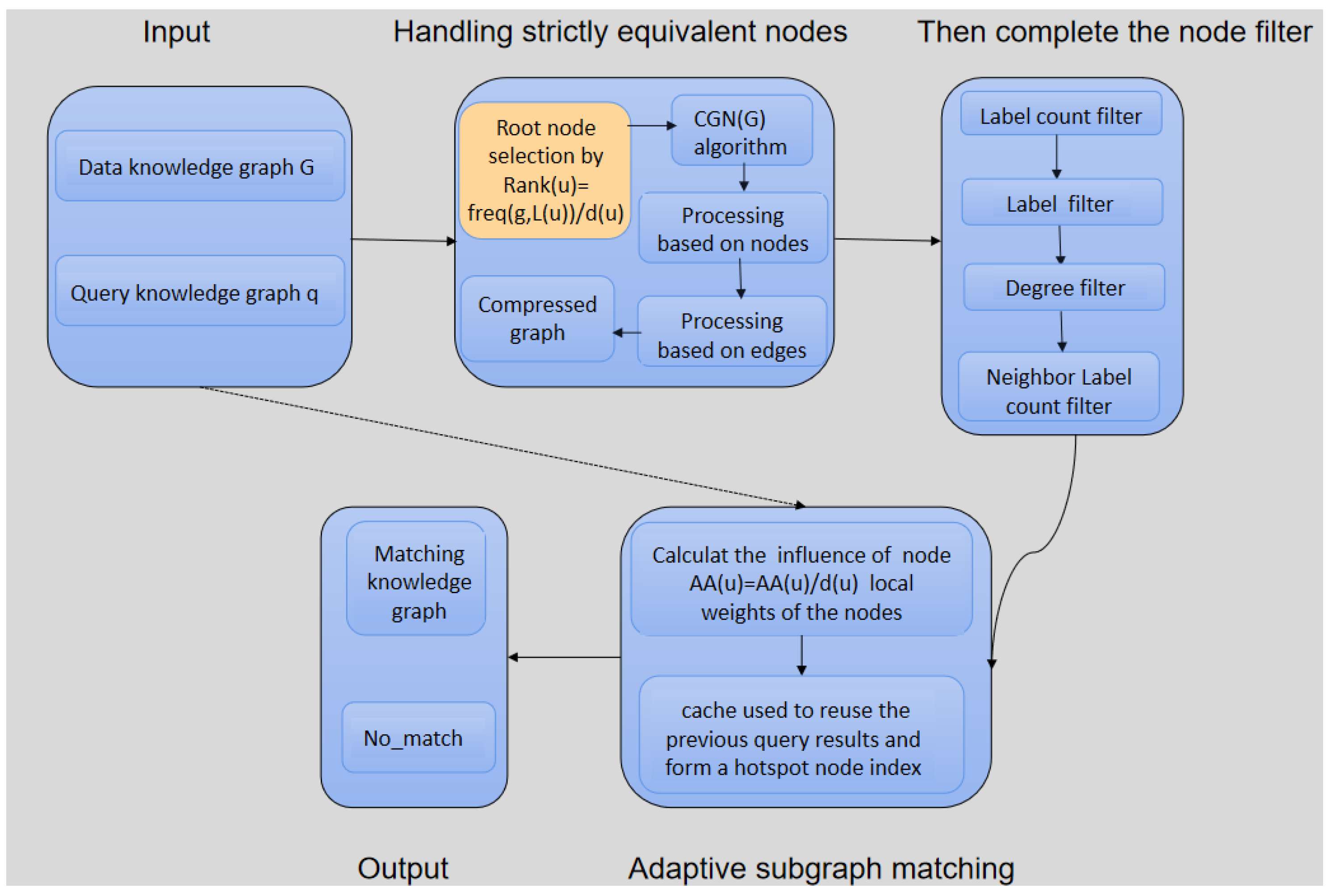
We propose a strict compressed graph node (CGN) technique to compress both the data graph and the query graph. Starting from the initial node, nodes belonging to the same equivalence class—based on their equivalence relationships—are compressed into a single node while preserving the original graph structure. This approach achieves a maximal compression of the graph data, effectively reducing the data graph to a smaller-scale representation.

(2)

We introduce a label count-based filtering (LCF) algorithm. Existing filtering methods can exclude some nodes that do not meet query conditions but often incur significant redundant validations during the subsequent verification phase, resulting in high memory overhead and extended validation times. By incorporating filtering conditions based on the labeling characteristics of dataset nodes during the filtering phase, our method further reduces the search space size, thereby enhancing overall query processing performance.

(3)

For large-scale graphs, we propose an adaptive tuning model that leverages caching to improve efficiency. This model accelerates subgraph matching (ASM) queries by reusing results from previous queries or by assessing the overall graph structure through a subset of frequently accessed (hot) nodes, forming an adaptive subgraph matching framework that dynamically adjusts according to dataset characteristics.

(4)

Extensive experiments on multiple real-world datasets have been conducted to compare the performance of ASM with three other subgraph matching algorithms, evaluating metrics such as execution time, callback counts, and average search time. Experimental results demonstrate that ASM achieves superior performance in terms of query processing time.

2. Background

2.1. Preliminaries

To enhance the readers’ understanding, we introduce several key concepts that are essential for comprehending the content of our work.

Table 2. Some necessary concepts and symbols used in our work.

Notations	Descriptions
q,G	Query graph and data graph
V(g),E(g),Σ	Vertex set, edge set, and label set of a graph g
d(u),L(u),N(u)	Degree, label, and neighbor vertex
e(u,v)	The edge between u and vs.
E(qt),E(qnt)	Tree edge and non-tree edge
Cu	Set of candidate vertices of u in C
φ and φ′	Match order and index order
$N_{-}^{{\phi }^{\prime }}\left(u\right)$, $N_{+}^{{\phi }^{\prime }}\left(u\right)$	Neighbors of u before(after) u in φ

lists the symbols that are frequently used in our work.

Theorem 1 (Graph).

In this paper, we focus on the undirected graph [20] G = (V, E, L), where V = $\left\{v_1,v_2,\dots ,v_m\right\}$ denotes the set of vertices and E = $\left\{(v_i,v_j)|v_i,v_j\in V\right\}$ denotes the set of edges. vertices denote entities and edges denote relationships between two entities. The label description L(v) (or L(e)), contains information about the current node (or edge), which comes from the label set Σ.

Theorem 2 (Subgraph Matching).

Given a data graph G = (V, E, L) and a query q = ($V_q$, $E_q$, L). A matching subgraph [21] φ(q) of q in G is defined as a subgraph in G that satisfies the mapping function φ.φ maps a point u in q to a point φ(u) in G, and an edge e = (u, v) in q to an edge φ(e) = (φ(u), φ(v)) in G.

Theorem 3 (Subgraph Isomorphism).

Given a data graph G = (V, E, L) and a query graph q = ($V_q$, $E_q$, L), q is subgraph isomorphic [22] to G if and only if there is a bijective mapping M from $V_q$ to V such that ∀u ∈ $V_q$, ∃ M(u) ∈ V: $L_V$[u] ⊆ $L_V$[M(u)] and ∀ u, $u^{\prime }$ ∈ $V_q$, ∃ (u, $u^{\prime }$) ∈ $E_q$: (M(u), M($u^{\prime }$)) ∈ E and $L_E$ [(u, $u^{\prime }$)] ⊆ $L_E$ [(M(u), M($u^{\prime }$))].

Theorem 4 (Forward (Backward) Neighbors).

Given a φ-order query vertex, the forward (backward) neighbors [23] $N_{-}^{{\phi }^{\prime }}\left(u\right)$, $N_{+}^{{\phi }^{\prime }}\left(u\right)$ of u ∈ φ are the neighbors that lie before (after) u in φ.

Theorem 5 (Knowledge Graph).

Knowledge graph (KG) can accurately semantically describe various entities and their connections in the real world [24], assigning practical meanings to nodes and edges in the graph. This practical meaning is formalized as labels for vertices and edges. Thus, a knowledge graph is formally defined as a labeled graph and is rich in semantic information [25]. A knowledge graph is formed as G = (V, E, L). Here, V is a set of vertices, L = ($L_V$ ∪ $L_E$) is a labeling function, $L_V$ assigns type-labels and attribute-labels to vertices and $L_E$ assigns relation-labels to edges.

2.2. Related Work

We summarize existing works related to the subgraph matching as follows:

Domestic and international research on subgraph matching problem has a long history and has long been proven to be an NP-complete problem, but it is still a long-lasting research hotspot for scholars at home and abroad due to its wide range of application domains and high demand for applications [26]. Whether it is the exploratory backtracking method [27], which maps query vertices to data vertices iteratively through a certain query vertex matching sequence to extend the intermediate results, or the join method, one of the two frameworks described below is used:

• Direct-enumeration framework [28]. This type of subgraph matching algorithm does not generate auxiliary index structures for preprocessing in advance, but prunes the candidate points through some filtering strategies during the enumeration process, so it directly accesses the original data graph to match the vertices and edges of the query graph during the enumeration process.
• Indexing-enumeration framework [29]. This kind of subgraph matching algorithm preprocesses the data graph and the given query graph, and generates an auxiliary indexing structure [30] to maintain the candidate vertices and edges between candidate vertices, which is accessed during the enumeration process to match the vertices and edges of the query graph. During the enumeration process, when matching the vertices and edges of the query graph, they will access this index structure instead of directly accessing the original data graph, which can reduce many invalid accesses [31]. GADDI and SPath, as representatives of Offline-index, usually build indexes on data without communicating with real-time data sources, thus facilitating the filtering of candidate sets of query variables during the actual execution of the query; however, CFL [32] and CECI [33], as representatives of Online-index, need to dynamically build and update indexes in real-time or near-real-time data streams.

In large graphs, numerous subgraphs may exist, and some of them may occur frequently or be repeatedly utilized in subsequent algorithms. To improve efficiency and simplify later computations, these subgraphs can be preprocessed. Previous studies have shown that preprocessing [34] plays a critical role in the subgraph matching problem [35], as it can significantly reduce memory usage and shorten total runtime by several orders of magnitude. By performing preprocessing, the data can be effectively organized and optimized prior to algorithm execution, thereby minimizing resource consumption and computational time in subsequent operations.

• Selection of root query node. In the process of subgraph matching, the selection of the starting node is an issue that needs to be emphasized [36]. If an appropriate matching starting node can be selected, some unmatched nodes can be excluded as early as possible, thus reducing the number of extended validations. If the starting node is not selected properly, it may cause a lot of redundant enumeration, consuming a lot of time to obtain the final correct result only through multiple extension verification. In this paper, the ranking rule is determined by the equation Rank(u) = freq(g,L(u))/d(u). Here, freq(g,L) denotes the number of nodes labeled L in the graph g, and d(u) denotes the degree of node u, i.e., the number of edges associated with node u.
• Determining the matching (visit) order. Usually, when determining the matching order in the subgraph matching process, priority is given to nodes with a smaller number of candidate nodes, i.e., nodes with smaller degrees. The advantage of this approach is that it reduces the search space and decreases the size of the intermediate result set [37]. In addition, if a wrong candidate node is found during traversal, backtracking can also be performed to explore the next node at a lower cost of trial and error.
• Generating the query tree. When a BFS traversal [38] is performed on the query graph starting from the root query node, this comes to create the query tree. The edges that appear on the query tree in the query graph are called tree edges (TEs). If an edge is on the query graph but not on the BFS tree, it is called a non-tree edge (NTE). BFS is used because, in some existing studies, it is shown that BFS minimizes the diameter of the search space [39].

3. Adaptive Subgraph Matching Architecture

In this section, we first present the compressed graph nodes (CGNs) algorithm in Section 3.1, followed by a description of the efficient filtering mechanisms in Section 3.2. Subsequently, Section 3.3 introduces the adaptive subgraph matching (ASM) algorithm, which is designed to further enhance performance.

Figure 1 illustrates the overall workflow of ASM, outlining the complete processing pipeline. The workflow consists of four primary components: input, equivalent-node compression of the knowledge graph, adaptive node filtering, and the output of the matching results. First, the data graph and query graph are loaded into memory, and root nodes are selected based on predefined formulas. The graphs then undergo strict equivalent-node compression, with edge connections updated according to the compressed nodes. The resulting compressed graph is further refined through multiple filtering stages to reduce the number of valid candidate nodes. In the adaptive module, a caching mechanism stores results from previous queries, thereby accelerating subsequent searches and improving efficiency. Finally, the matching results are generated and output based on the identified matches.

3.1. Compressed Graph Nodes (CGNs) Algorithm

In large graph databases, many nodes may share identical structures. These nodes can be small twigs within the larger graph or key nodes embedded in its core structure. Reducing the number of one-to-one node matches in the subgraph matching process is critical for improving algorithmic efficiency. To address the issue of the repetitive enumeration of equivalent nodes, we propose a strict compressed graph nodes (CGNs) algorithm for preprocessing graph data. Before the matching algorithm begins, multiple equivalent nodes in the graph are merged into a single node, thereby reducing the size of the original graph and minimizing the number of one-to-one matches required during the validation phase.

The graph compression idea is used in the existing Boost_ISO [40] algorithm. The algorithm first classifies nodes with equivalence relationships and merges those sharing the same label in the original data graph into a single node. It then examines the edges in the original graph to determine whether connecting edges exist between these merged nodes. Based on this information, the nodes with equivalence relationships are further transformed into an undirected equivalence graph.

Although this algorithm avoids the unnecessary repetitive enumeration of equivalent nodes during the subgraph isomorphism verification stage, it still contains redundant operations in the process of identifying equivalent nodes. For instance, as illustrated in Figure 2, during the verification of the path V₁-V₂-V₅, it can be determined that there is no equivalence relationship between V₁ and V₅. However, because the node has not been marked as visited, the verification of the relationship between V₁ and V₅ is repeated when processing the path V₁-V₃-V₅.

The concept related to equivalent nodes is also proposed in the literature [40] to compress the original graph. The paper proposes that two nodes are considered as equivalent nodes if they have the same parent node and the same child node after clipping the edges between them. This is an approximate node-compression technique. Although this approximate node-compression technique has been widely used, its disadvantages are obvious. This is because it is prone to produce results that cannot be returned to the original graph, thus causing the problem of over-compression.

How can it be determined whether the equivalent node is more appropriate? Our understanding will be given below: (1) Same-labeled nodes with the same father and child nodes in the case of non-prunable existing edges; and (2) Isolated nodes with the same label (nodes with degree 0).

In Algorithm 1, the main flow of the CGN algorithm for graph compression strategy is given below:

Algorithm 1 Compressed graph nodes (CGNs).

Require: Data graph g, query graph q Ensure: Compressed graph g′, q′   1:  Create the compressed graph’s vertex set V;   2:  // Creating a collection of nodes for a compressed graph   3:  for each v ∈ {v|v ∈ V(g)} do   4:        nodeExamination(v);// Examination of each node   5:  end for   6:  V0 = $\left\{v|v\in V,d(v)=0\right\}$   7:  group v ∈ V0 by labels   8:  update V = V − V0   9:  if (v == Vn ∈ V) then 10:        Vn ← v; 11:  else 12:        V ← v; 13:  end if 14:  for each v ∈ {v|v ∈ V(g)} do 15:        nodeExamination(e);// Examination of each edge 16:  end for 17:  find all edges connect to the equal points of v in g 18:  if (the begin-point is in v AND has edges between v and v′) then 19:        create an edge e between v and v′; 20:        record points in e; 21:        update the vertex number and edge number of g′; 22:  end if

First, the set of nodes of the compressed graph is created (line 1) and each node in the original graph g is examined (line 3). If an isolated node with node degree 0 is found, the processing rules for isolated nodes are used (lines 6–7), at which point the data graph nodes to be found as equivalent nodes are updated (line 8). When the first node V₁ of the original graph arrives, the set V of nodes of the compressed graph is the empty set. So add V₁ directly to the point set V. When the second node V₂ of the original graph arrives, go to the collection of nodes of the compressed graph to find out whether V₂ is equivalent to one of the recorded nodes. If V₂ is equivalent to V₁, then V₂ is added to the domain of equivalent nodes of V₁. Otherwise, V₂ will be added directly to V. Scan each node of the original graph in turn until all nodes have been visited. At this point (lines 9–11), the processing for points is finished, and the following processing for edges is carried out, which is based on the compressed node set just obtained. Nodes are selected from V in turn. We select the first equivalent node V_a of V₁. We query the neighbor table of V_a in the original graph, and if we find that there is an edge starting from V_a and its endpoint is not in the domain of equivalent nodes of V_a, we add an edge between V₁ and V_a.

The above Figure 3a is an example. We can figure out that the values of labels A, B, C, and D are 0.3, 0.5, 0.4, and 0.5, respectively, so we decide to start traversing from the label A. We start our examination at V₁, at which point the set of compressed graph nodes is V = Ø. Thus, it is straightforward to add V₁ to the point set V, denoted by $V_1^{\prime }$. At this point V = $\left\{V_1^{\prime }\right\}$ and $V_1^{\prime }$ = $\left\{V_1\right\}$. For the second node V₂, first determine the equivalence with the nodes in the set V. It is determined that V₂ is not equivalent to $V_1^{\prime }$, so V₂ is added to V. At this point V = $\left\{V_1^{\prime },V_2^{\prime }\right\}$,$V_2^{\prime }$ = $\left\{V_2\right\}$. Similarly, V₃ is added to V. At this point, V = $\left\{V_1^{\prime },V_2^{\prime },V_3^{\prime }\right\}$. When examining V₄, it is found that V₄ is equivalent to $V_3^{\prime }$ in V. Therefore, V₄ is added to the domain of equivalent nodes of the $V_3^{\prime }$. At this point, V = $\left\{V_1^{\prime },V_2^{\prime },V_3^{\prime }\right\}$ and $V_3^{\prime }$ = $\left\{V_3,V_4\right\}$. Finally, the V₅ is examined, and since there is no node that is equivalent to it, V₅ is added directly to V. At this point, V = $\left\{V_1^{\prime },V_2^{\prime },V_3^{\prime },V_4^{\prime }\right\}$ and $V_4^{\prime }$ = $\left\{V_5\right\}$.

Once the processing of the points is complete, the edges are then processed accordingly. Each node from V is selected in turn for examination. Take out $V_1^{\prime }$ first and examine each node in $V_1^{\prime }$. It is found that V₁ ∈ $V_1^{\prime }$, there is an edge from V₁ to V₃ in the original graph, and V₃ ∈ $V_3^{\prime }$. Therefore, an edge from $V_1^{\prime }$ to $V_3^{\prime }$ is added to the compressed graph. Continuing the examination, it is found that there is an edge from V₁ to V₄ and V₄ ∈ $V_3^{\prime }$. However, at this point, it will be found that an edge already exists between $V_1^{\prime }$ and $V_3^{\prime }$. Therefore there is no need to repeat the insertion of this edge. The compression completion effect is shown in Figure 4.

From the above description, it is evident that executing the CGN algorithm involves traversing the original graph. For node processing, each node in the original graph must be visited and examined, resulting in a worst-case time complexity of O(n²) for node compression. For edge processing, it is sufficient to traverse the edges of the original graph sequentially, leading to an edge-adding operation with a time complexity of O(E).

3.2. Efficiency Filtering Mechanisms

To enhance algorithm performance, the preprocessing–enumeration subgraph matching algorithm introduces a preprocessing phase prior to enumeration, aiming to reduce the size of the candidate set for each query vertex and obtain accurate statistics to optimize the matching order. Specifically, the preprocessing phase generates a complete set of candidate vertices for each query vertex. The overall process consists of three phases: candidate vertex set generation, matching order determination, and enumeration. To minimize the cost of enumeration, an effective filtering algorithm is employed to ensure that the candidate set is as small as possible while remaining complete.

Using only some looser filtering conditions leads to the existence of a large number of wrong candidate vertices and increases the computation, so the stricter the matching conditions, the better the results [27]. Since labels on both the data graph and query graph are represented by numbers, this makes the labels not only have the function of identifying nodes, but also add computational functions. We propose the concept of label count filter (LCF) for the dataset characteristics, i.e., first determine the number of nodes in the query graph, then add the label counts of all nodes to get the corresponding result, and then compare and filter with the labels of nodes with the same number of vertices in the datagram so that the LC in the datagram is equal to the LC in the query graph. The candidate nodes that pass successfully come to the label and degree filter (LDF) next, and the methods take into account the node’s label information while also incorporating the node’s degree information. Specifically, they calculate the number of labels and degree value of each node separately in the query graph, and then perform the same calculation for each node in the data graph to obtain the number of labels and degree value of all nodes in the data graph. Next, the values of the query graph are compared with the values of the data graph to filter out the set of data graph nodes that do not match and retain the nodes with exactly matching values for the combination of label and degree. Finally superimposed on the neighbor label count filter (NLCF), which is a filtering method based on the label count of neighboring nodes. Firstly, the neighbor nodes of each node are label counted to get the frequency information of the neighbor node labels. Then, this frequency information is compared with the neighbor node label counts of the corresponding nodes in the query graph. Through this comparison, the nodes whose neighbor node label counts in the data graph match those in the query graph can be filtered to achieve efficient node filtering. This helps to extract the candidate set in space and time. The main process of extracting the candidate set is as follows:

Algorithm 2 gives the process of extracting candidate sets:

First, the boundaries of the query are determined, and we generate our bounding set with the concatenated set of the parents of all nodes. For each node, we set up four filters to filter them. The first is the label count filter, as the name suggests, which uses the sum of the numbers of labels used by the nodes in the query graph to compare with the data graph to find the candidate nodes that satisfy the conditions. The next label filter (LF) collects the neighboring nodes vs. in $v_f$ with the u label, that is, nodes with different labels are removed for further filtering. The degree filter ensures that the degree (number of connected edges) of the data graph node vs. is greater than or equal to the degree of the query node u. Neighbor label count filter imposes two constraints: one is to satisfy the fact that the number of labels of the neighbors of the current node in the data graph is greater than or equal to the number of neighbor labels of the corresponding node in the query graph; rather, the labels corresponding to the same number of labels need to be the same as the kind as well. When generating the candidate set through the forward neighbor vertices, for the candidate nodes on the tree edges, if they are filtered by any of the above filters during the matching process because they do not satisfy the filtering conditions, we choose to remove their parent nodes and their corresponding child nodes in the tree edges at the same time; for the non-tree edge candidate nodes that do not satisfy the conditions, we directly remove the nodes. While generating the candidate set by backward neighboring vertices, we refine the candidate set along the opposite direction from the forward direction to get a smaller and more accurate candidate set. For the nodes that successfully pass all the filtering conditions, these are useful candidate nodes and they can be used to form the subgraph used for matching, which we store for the next step. The time complexity of Algorithm 2 is O( $\left|E\left(q\right)\right|\times \left|E\left(g\right)\right|$).

Algorithm 2 Extract candidates algorithm.

Require: Data graph g, query graph q Ensure: candidate set C   1:  for u ∈ Tq in BFS order do   2:        $u_p.\mathrm{frontiers}=\cup u_p.\mathrm{TE\_Candidate}$   3:  end for   4:  for vf ∈ up.frontiers do   5:        // label count filter   6:        LCF(N($v_f$),q);   7:        // label filter   8:        LF(N($v_f$),Lq(u));   9:        // degree filter 10:        DF(u,v); 11:        // neighbor label count filter 12:        NLCF(u,v); 13:        u.TE_candidate[$v_f$].add(v); 14:        //Forward Vertex Neighbor Generation Candidate Set 15:  end for 16:  for i ← 2 to $\left|{\phi }^{\prime }\right|$ do 17:        u ← ${\phi }^{\prime }$[i]; 18:  end for 19:  for vs. ∈ ${\bigcap }_{u^{\prime }\in N_{-}^{{\phi }^{\prime }}\left(u\right)}$ N(u′.C) do 20:        //Backward Neighborhood refined Candidate Collection 21:        for i ← $\left|{\phi }^{\prime }\right|$ to 1 do 22:              u ← ${\phi }^{\prime }$[i]; 23:              for vs. ∈ u.C and vs. $\notin {\bigcap }_{u^{\prime }\in N_{+}^{{\phi }^{\prime }}\left(u\right)}$ N(u′.C) do 24:                    remove vs. from u.C; 25:              end for 26:        end for 27:  end for

3.3. Adaptive Subgraph Matching (ASM) Algorithm

From prior research and empirical evidence, it is observed that the label characteristics of a dataset primarily influence the performance of the filtering phase, whereas the density characteristics significantly affect the performance of the sorting phase. Accordingly, the adaptive algorithm proposed in this paper evaluates the label density and adaptively selects the optimal strategy based on the dataset’s label density profile.

Given the substantial time and memory overhead required to load a mega-graph into memory, we introduce a novel concept—local weights. By partitioning the mega-graph into localized subregions, the candidate set of high-degree or “popular” nodes in the query graph can be leveraged to pinpoint approximate target regions. If isomorphic subgraphs exist, they must reside within these localized subregions, allowing subgraph isomorphism queries to be executed directly on them. This approach effectively reduces the scope of the query, thereby improving overall efficiency.

The inputs to the adaptive subgraph matching (ASM) algorithm (Algorithm 3) are a data graph g and a query graph q. The output is the result of the isomorphism of all the subgraphs of q in g. A central node that is most closely connected to other nodes is found by comparing the node influence of nodes in the query graph. Local weights consider the importance of a node relative to the entire query graph, including information such as the connectivity between nodes, and the degree of a node. Firstly, each node is assigned the same value AA_u, and the sum of AA values of all nodes is 1. During a new round of AA value calculation, node u will use the AA_u value of its own node as a weight to equally distribute to the other nodes that are connected. Nodes with no connected edges (degree 0) have unchanged AA_u values; the updated node’s AA_u value becomes the sum of the weights of all pointing nodes. Complete the above steps until the AA_u values gradually converge. The stable AA_u value of each node is finally obtained (line 8). Where N(u) is the set of all nodes pointing to node u, node vs. is a node belonging to the set N(u), and L(v) is the out-degree of node v. The local influence of a node is measured by comparing its final AA_u value.

Algorithm 3 Adaptive subgraph matching (ASM).

Require: Data graph g, query graph q Ensure: Subgraph isomorphism of all query graphs in a data graph   1:  //preprocessing process of dataset   2:  function CGN(g(v,e))   3:        for each v ∈ {v|v ∈ V(g)} do   4:              nodeExamination(v);// Examination of each node   5:              nodeExamination(e);// Examination of each edge   6:        end for   7:  end function   8:  function   9:        ExtractCandidate(LCF(N($v_f$),q),LF(N($v_f$),Lq(u)),DF(u,v),NLCF(u,v)) 10:        SCORE ← GET_GRAPH_DENSITY; 11:        $AA\left(u\right)={\sum }_{u\in N\left(u\right)}{\displaystyle \frac{AA\left(vs.\right)}{L\left(vs.\right)}}$ 12:        //The filtering method of ASM 13:        if score(G) >= scorethreshold then 14:              C ← GQL_FILTER; 15:        else 16:              C ← DAF_FILTER; 17:        end if 18:        //The ordering method of ASM 19:        π ← GenerateMatchingOrder(q,g,C,score(g)); 20:        //The enumeration method of ASM 21:        SUBGRAPHMATCH(q,g,C,score(g)); 22:  end function

The labeled density value score(g) of the nodes in the data graph is then computed. When score(g) is greater than or equal to the score_threshold (which is set empirically and artificially), we recognize the graph as dense and vice versa as sparse. Depending on the characteristics of the dataset, we can choose the appropriate algorithm at each stage, as no algorithm can overwhelm the others on all queries [18].

When subgraph matching queries are performed, a caching approach can also be used to accelerate subgraph matching queries by reusing previous query results [41]. The matching results between the query graph and the data graph are first stored in a cache. These results can be stored in an in-memory data structure, such as a hash table, a tree structure, or a database. When a new subgraph matching query is performed, it first checks whether the matching result corresponding to the current query graph exists in the cache. If so, these results can be retrieved directly from the cache without having to execute the matching algorithm again.

4. Experiments

This section presents a comprehensive analysis of the proposed method, along with a comparison of the experimental results. It begins by describing the experimental setup in Section 4.1, including hardware and software configurations as well as the specific implementation parameters. The effectiveness of the method is then validated through a series of subgraph matching experiments—a critical task in many graph-based applications—reported in Section 4.2 and Section 4.3. The evaluation provides an in-depth assessment of the method’s performance across diverse scenarios. To ensure the reliability of the results, all reported values are averaged over five independent runs, thereby reducing the influence of random fluctuations and providing a robust measure of consistency and accuracy.

4.1. Experimental Setting

This section presents a detailed description of the experimental environment, the datasets used for evaluation, and the performance metrics adopted. First, it specifies the hardware and software configurations of the experimental setup, including the computational resources employed. Next, it introduces the experimental datasets, outlining their structure, size, and relevance to the subgraph matching task. Finally, it describes the evaluation metrics used to assess the proposed method, focusing on execution time, the number of callbacks, and the average callback time measured in this study.

4.1.1. Experimental Environment

The environment configurations for the experiments in this paper are shown in

Table 3. Experimental environment.

Experimental Environment	Setting
CPU	Intel(R) Core(TM) i3-6100
Main frequency	3.70 GHz
Random access memory (RAM)	7.7 GB
Disk capacity	1 T
System type	64 bit
Operating system	Ubuntu 22.04.2 LTS
Programming environment	Microsoft VS Code1.84.1
Programming language	C++

. All the source codes are implemented in C++. Experiments are conducted on a PC running Ubuntu with Intel i3-6100 3.70 GHz CPUs, 7.7 GB memory, and 1T disk capacity. All evaluation results are averaged over five runs.

4.1.2. Datasets

In order to validate the proposed algorithm in this paper more accurately and explicitly, the experiments in this paper are mainly conducted on three real datasets, which have been widely used in previous work [30]. The dataset data are all from the Stanford Large Network Dataset Collection [42].

• Dblp Dataset: A dataset of scholarly literature in the field of computer science, containing metadata information on a large number of scholarly and conference papers in computer science, information technology, and related fields. The dataset contains 317,080 nodes and 1,049,866 edges.
• YouTube Dataset: A dataset containing user behavior and video information. Based on the videos uploaded and recommended by a user in YouTube, a relationship graph is built to get the content uploaded or recommended by other users with similar preferences to that user, and finally the content is pushed to that user. This dataset contains 1,134,890 nodes and 2,987,624 edges.
• Human Dataset: A graph dataset describing human protein interactions, where each node represents a protein entity and edges represent interactions between proteins. The dataset contains 4674 nodes and 86,292 edges.

4.1.3. Evaluation Metrics

Experiment with the subgraph matching algorithm (SUPER) designed in this paper and comparatively analyze the following existing algorithms with different indexing and sorting strategies:

• ASM: The adaptive subgraph matching algorithm we proposed in this paper contains the efficiency Compressed Graph Node (CGN) algorithm and the label filter mechanism.
• CFL [32]: One of the most advanced algorithms. Effectively reduces the search space through two phases: join filtering and locally sensitive filtering. Uses tree-structured indexing and path-based sorting strategy.
• GraphQL [13]: Employing a neighborhood signature filter and a left-depth connected sorting strategy, the method models the query as a left-depth connected tree, where the leaf nodes are the set of candidate vertices.
• CECI [33]: One of the state-of-the-art algorithms. Compact embedded clustering index is designed to sort the tree edge and non-tree edge candidate nodes using forward BFS traversal filtering and reverse BFS refinement process. Compared with the other three state-of-the-art algorithms, the proposed method demonstrates clear improvements in execution time, the number of algorithm callbacks, and the average query time during the matching process. For each dataset, results are reported for query graph node sizes ranging from 3 to 7.

Based on the method proposed in this paper, combined with the comparison algorithms used in the experiments, the overall performance of different algorithms in the experimental process is mainly measured by the following evaluation indexes to measure their effectiveness:

• Execution time: the average time for processing the query graph in the query set, excluding the time for loading data from disk, which mainly includes filtering nodes, indexing time, and enumeration time.
• Execution algorithm efficiency: the average number of callbacks and the average search time are used as metrics. In program operation, the main time overhead lies in the recursive callbacks of the algorithm, such as depth-first search, node order matching, etc. The fewer the number of callbacks or the shorter the search time, the higher the efficiency of the algorithm.

4.2. Evaluations on Execution Time

The overall performance of the algorithm compares the execution time and implementation algorithm efficiency of different datasets.

According to the experimental results shown in Figure 5a, Figure 6a and Figure 7a, different algorithms exhibit significant differences in execution time on the three datasets. The experimental results are presented according to the increasing scale of the number of nodes in the query graph, and it can be clearly seen that all the algorithms usually take more time to process larger queries. Specifically, the four algorithms, ASM, CFL, GQL, and CECI, exhibit different performances on different data graphs. Notably, the ASM algorithm consistently outperforms the other algorithms on a variety of data graphs, fully demonstrating its superior performance in terms of efficiency and stability. Whether it is a graph with a large or small amount of data, ASM demonstrates a stable execution time and superior processing power. In addition, the performance gap between these four algorithms on the Human dataset is relatively small. This phenomenon can be attributed to the fact that, although the Human dataset itself has a small amount of data, it has a large number of different labels that make the dataset relatively complex to query. A large number of labels can significantly increase the difficulty of a query. In the case of node number 6, for example, the execution time of ASM on the DBLP dataset is reduced by 75.34%, 31.27%, and 18.35% in that order.

4.3. Relative Performance Comparison Evaluation

The relative performance of the algorithm is affected by the query time: when the query time is shorter, the value of the relative performance is smaller, which represents the better performance of the algorithm. From the experimental results in Figure 5, Figure 6 and Figure 7, it can be found that ASM has the shortest or close to the shortest running time in different datasets, so the relative performance of ASM is more competitive due to the fact that there are a large number of erroneous candidate vertices in the candidate set of the other three types of algorithms and the order of generating matches is less efficient.

4.3.1. Evaluations on the Counts of Callbacks

In the experimental results shown in Figure 5b, Figure 6b and Figure 7b, we explore the number of callbacks of different algorithms on the three datasets. It can be seen that, although CECI uses more complex and stringent constraints to filter candidate nodes, it also increases the computational complexity at each step of the matching process, resulting in a significant increase in the number of combinations that satisfy all of these complex constraints. ASM obtains fewer candidates than the other algorithms on most of the datasets, which suggests that ASM has a stronger filtering capability. Since Human is dense, the effect of ASM on this datagram is more significant than that of other algorithms. In the case of node number 6, for example, ASM’s execution time on the DBLP dataset is reduced by 71.47%, 73.82%, and 75.08% in that order.

4.3.2. Evaluations on the Average Callbacks Time

The average callback times of the different algorithms on the three datasets are shown in Figure 5c, Figure 6c and Figure 7c. GQL can increase the chance of data reuse by increasing the number of nodes, which reduces the average search time. However, when the number of nodes is increased to a certain level, the complexity of the data still leads to an increase in the search time of the query due to the need to process more nodes and more data. It can be seen that ASM is able to maintain the horizontal trend under ideal conditions, and this performance is significantly better than the other algorithms. The ASM algorithm effectively reduces the number of unnecessary calculations and callbacks through its own advantages, and even when the number of nodes is increased, ASM is able to optimize the processing logic to avoid a significant increase in the search time. Again taking the case of node number 6 as an example, ASM reduces the execution time on the DBLP dataset by 90.33%, 76.5%, and 64.54% in that order. Combining the number of callbacks and callback time, we can also infer the space usage of the candidate nodes. Since the callback number and callback time directly affect the memory usage and computational overhead of the algorithm, the advantages of the ASM algorithm in these two aspects indicate that the space occupation of its candidate nodes is also relatively small. This means that, in practice, ASM cannot only process large-scale data efficiently, but also save storage space effectively, further enhancing its applicability in resource-constrained environments. In contrast, other algorithms often require more memory space to store candidate nodes and intermediate results when processing complex queries due to the high number of callbacks and the long callback time, which may lead to performance bottlenecks in large-scale data processing.

5. Conclusions

To enhance the performance of subgraph matching, we propose a strict compressed graph node (CGN) mechanism in the preprocessing stage, which processes the number of nodes and edges in both the data graph and the query graph to reduce redundant nodes. In the filtering stage, a label count filter based on dataset characteristics is employed, in combination with a label filter, a degree filter, and a neighbor label count filter. This comprehensive filtering mechanism significantly improves the efficiency of the overall subgraph matching process. Experimental results demonstrate that the preprocessing-based adaptive subgraph matching (ASM) algorithm achieves notable advantages in matching speed compared with the mainstream algorithms CFL, GQL, and CECI.