Abstract
Achieving state-of-the-art performance (82.5% IoU, 85.6% F1), this paper proposes an enhanced DeepLabV3+ model for robust underwater crack detection through three integrated innovations: a physics-based light propagation correction model for illumination distortion, multi-scale feature extraction for variable crack dimensions, and curvature flow-guided loss for boundary precision. Our approach significantly outperforms DeepLabV3+, SCTNet, and LarvSeg by 10.6–13.4% IoU, demonstrating particular strength in detecting small cracks (78.1% IoU) under challenging low-light/high-turbidity conditions. The solution provides a practical framework for automated underwater infrastructure inspection.
1. Introduction
Underwater infrastructure, including bridges, offshore platforms, and pipelines, plays a crucial role in maintaining global economic activities [1]. However, these structures are susceptible to corrosion, cracks, and other forms of damage caused by constant exposure to harsh underwater environments [2,3]. Timely identification of such defects is essential to ensure structural integrity and prevent catastrophic failures. Traditional underwater inspection methods, such as human divers and remotely operated vehicles (ROVs), are labor-intensive, time-consuming, and often limited by visibility issues and environmental factors such as murkiness and lighting conditions [4,5]. Non-optical methods like Lamb wave testing [6,7] have shown promise in crack detection through guided wave propagation. However, these techniques require direct sensor contact and complex instrumentation impractical for submerged structures, making vision-based approaches essential despite their susceptibility to environmental distortions.
With the rise in advanced image processing techniques [8,9], there has been growing interest in applying computer vision and deep learning models to automate underwater defect detection [10]. In the field of underwater defect detection, traditional methods primarily rely on local statistical approaches and edge detection algorithms to extract defect features. For instance, in local statistical methods, Shi et al. [11] employed fuzzy algorithms to address uneven illumination in underwater visible-light images and proposed a crack identification method combining local features of image patches with global features of connected domains. Ma et al. [12] first enhanced color-distorted images through affine transformation, then achieved precise crack segmentation using multi-directional gray-level fluctuation analysis. Regarding edge detection, Wang et al. [13] integrated Canny and Sobel operators to determine defect edges, developing an automated method for identifying boundaries of damaged areas. Although these traditional approaches have advanced underwater defect detection to some extent, they still exhibit limitations in adaptability, generalization capability, and automation level when confronting complex and variable underwater environments. The emergence of deep learning technology is now bringing breakthrough advancements to this field.
Deep learning models can learn relevant knowledge from large-scale datasets and possess strong generalization capabilities [14], maintaining excellent recognition performance even under varying illumination, water quality conditions, or defect types. Simultaneously, deep learning technology automates the underwater defect identification process, significantly enhancing efficiency while reducing human intervention. Research on deep learning-based underwater defect recognition primarily falls into three categories: classification, object detection, and semantic segmentation. For classification tasks, which determine defect presence through the global analysis of images, Zhu et al. [15] improved VanillaNet to enhance classification accuracy for underwater dam crack images. By employing Seesaw Loss to address long-tail distribution issues, they achieved a 2.66% accuracy improvement over the original VanillaNet, outperforming ConvNeXtV2 and RepVGG. In object detection, which precisely localizes defects using bounding boxes, Li et al. [16] modified the YOLOv4 framework by replacing CSPDarknet with MobileNetV3 as the feature extraction backbone. They adjusted MobileNetV3’s feature layer scales and fed preliminary feature layers into an enhanced feature extraction network for multi-level integration.
Compared to the qualitative detection in classification tasks and bounding-box localization in object detection, semantic segmentation provides higher-precision defect characterization through pixel-level recognition [17,18]. Specifically, semantic segmentation models classify each pixel in an image into predefined categories, demonstrating promising results across visual inspection tasks. This approach holds significant engineering value for evaluating crack morphological features and quantifying damage severity. By performing pixel-wise recognition, semantic segmentation captures precise crack contours. For instance, Hou et al. [19] proposed a U2-Net-based method for underwater pier defect identification, achieving high-precision contour and dimension recognition with a maximum Intersection over Union (IoU) of 0.73. To mitigate background interference, Sun et al. [20] developed a two-stage method for underwater concrete piers: defect localization using YOLOv7 and defect segmentation with an enhanced DeepLabV3+ network; this approach attained mean IoU scores of 0.914 for identifying exposed rebar and spalling.
Faced with the practical challenge of limited underwater defect data acquisition, researchers have adopted alternative approaches by leveraging transfer learning strategies [21,22] to break through data bottlenecks, offering innovative solutions for precise segmentation in low-resource scenarios. For instance, Li et al. [23] developed a real-time framework for underwater crack segmentation and quantification using a lightweight LinkNet network combined with hybrid transfer learning, enabling efficient identification in complex underwater environments. Beyond architectural improvements, cutting-edge research explores novel pathways integrating physical prior knowledge: Teng et al. [24] pioneered a “knowledge-guided recognition” paradigm by combining fractal characteristics of cracks with deep learning. Through fractal dimension matrix calculations, they extracted fractal features of cracks, which were then utilized as prompt inputs for the Segment Anything Model (SAM) to establish a plug-and-play defect segmentation method. This approach achieved remarkable metrics for underwater cracks: average accuracy—97.6%; IoU—0.89; F1 score—0.95.
Recent deep learning models like SCTNet [25] and LarvSeg [26] have advanced crack segmentation but exhibit critical limitations in underwater environments. SCTNet relies on static convolutional kernels that fail to adapt to turbidity-induced texture variations, suffering IoU degradation in murky conditions. LarvSeg’s scale-invariant backbone lacks hierarchical feature refinement, limiting small crack detection to smaller recall for sub-millimeter defects. Crucially, no existing method simultaneously addresses turbidity distortion and extreme scale variance—a fundamental gap for underwater infrastructure inspection where <1 mm cracks in low-visibility conditions signify critical structural risks.
However, the application of semantic segmentation to underwater crack detection remains underexplored. The challenges posed by underwater environments—such as significant light scattering and absorption, poor contrast, and the need to identify fine-scale defects—necessitate improvements to the existing models. Among them, DeepLabV3+ has become a widely adopted architecture due to its efficiency in segmenting complex images, capturing both local and global features [27]. To bridge this gap, this paper proposes an enhanced DeepLabV3+ framework with three innovations: (1) Physics-grounded light propagation correction: Our depth-dependent model uniquely simulates bidirectional scattering distribution functions (BSDF) to compensate wavelength-specific attenuation. Unlike empirical enhancement methods, it preserves crack topology through turbidity-adaptive histogram reweighting. (2) Hierarchical multi-scale decoder: By integrating learnable scale weights and skip-connected ASPP modules, this paper dynamically adjusts receptive fields from 1 mm to >5 cm cracks, resolving LarvSeg’s fixed-scale limitation. (3) Curvature flow-guided optimization: Our κ-weighted loss is the first to formalize crack boundary detection via curvature differentials, prioritizing high-variance regions where conventional losses underperform.
2. Methods
2.1. DeepLabV3+ Architecture and Training Framework
DeepLabV3+ is a state-of-the-art CNN architecture designed for semantic segmentation tasks [28]. It utilizes an encoder–decoder structure, where the encoder captures high-level semantic information, and the decoder refines the segmentation output (as shown in Figure 1). One of the key features of DeepLabV3+ is its use of atrous convolution [29], which allows the network to capture features at multiple scales by adjusting the receptive field. This ability to capture both local and global context makes DeepLabV3+ well-suited for tasks such as crack detection in underwater environments, where cracks can vary significantly in size and shape.
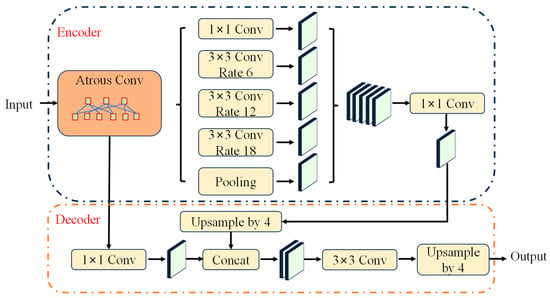
Figure 1.
DeepLabV3+ framework.
The proposed system builds on DeepLabV3+ [28], featuring an encoder–decoder structure with atrous spatial pyramid pooling (ASPP). As shown in Figure 1, the encoder extracts multi-scale features using dilated convolutions with dilation rates [6,12,18], while the decoder refines segmentation masks through progressive upsampling [29]. This paper uses MobileNetV2 as the backbone, initialized with ImageNet weights but adapted for underwater environments through domain-specific modifications.
In the original DeepLabV3+ model, the encoder is typically based on pre-trained backbones like Xception or MobileNetV2 [30], which provide strong feature extraction capabilities. However, these models were not specifically designed for underwater imaging conditions, which involve light distortion, color imbalance, and reduced visibility. Therefore, several modifications are proposed to enhance the performance of DeepLabV3+ for underwater crack detection.
The proposed model provides optimal initialization for our innovations in light modeling (Section 2.2), multi-scale extraction (Section 2.3), and curvature guidance (Section 2.4).
To train the proposed model (as shown in Figure 2), a dataset consisting of underwater crack images was collected from various environments, including natural underwater structures and man-made infrastructures. Given the limited availability of labeled underwater crack datasets, this paper employs data augmentation techniques such as random rotations, flipping, and varying illumination conditions to artificially expand the training set. This ensures that the model generalizes well to different underwater conditions and crack types.
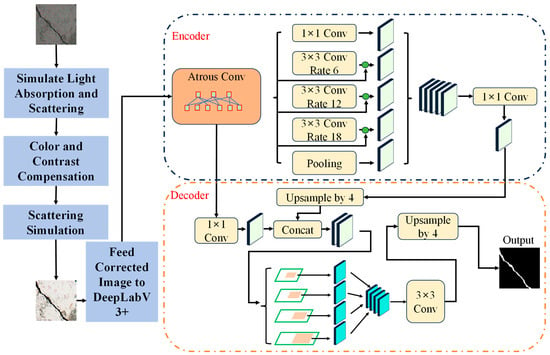
Figure 2.
Proposed framework.
A two-stage training process was implemented: first, the model was pre-trained using a large dataset of general underwater images to learn basic features of underwater environments, and then the model was fine-tuned using the crack detection dataset to focus on the specific task of crack segmentation.
In summary, although the components proposed in this study are derived from foundational theories in image processing and geometry, our contribution lies in their novel task-specific integration and mathematical formalization. This includes a physically grounded preprocessing module, a hierarchical multi-scale fusion decoder, and a curvature-weighted optimization loss—all embedded within a unified DeepLabV3+-based architecture for underwater crack detection.
2.2. Innovation 1: Underwater Light Propagation Model
Underwater images suffer from color distortion due to the scattering and absorption of light by water [31], as shown in Figure 3. The longer wavelengths (red, orange, and yellow) are absorbed faster, while shorter wavelengths (blue and green) tend to scatter, leading to a blue-green tint in underwater images. This phenomenon makes it difficult for traditional image segmentation models to accurately detect features, particularly cracks, which may blend into the background or be obscured by poor lighting conditions. To address this, integration of an underwater light propagation model is proposed in the preprocessing stage of the DeepLabV3+ pipeline. This model simulates the scattering and absorption of light in water and compensates for the resulting color imbalance. By adjusting the image’s color balance and enhancing contrast, this preprocessing step ensures that the model receives cleaner and more representative input, improving the accuracy of crack detection.
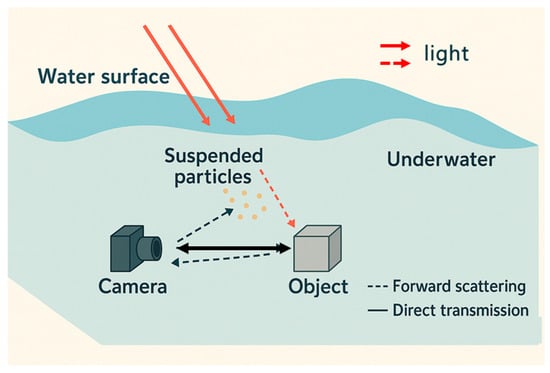
Figure 3.
Underwater light propagation process.
2.2.1. Principle of Underwater Light Propagation Model
Light absorption in water varies with wavelength. The absorption of light can be described by the Beer–Lambert law, which models how light is absorbed as it travels through a medium [32] (in this case, water):
where is the intensity of light at wavelength at depth , is the initial light intensity at the surface (depth = 0), is the absorption coefficient at wavelength , and is the depth in the water. The absorption coefficient increases with the wavelength, meaning longer wavelengths (red, yellow, and orange) are absorbed faster than shorter wavelengths (blue and green). This causes the characteristic blue-green tint seen in underwater images, as shorter wavelengths are less absorbed and scatter more. This models wavelength-dependent light absorption, explaining why red light (long wavelength, ~650 nm) disappears within 5 m depth while blue light (short wavelength, ~450 nm) penetrates >20 m in clear water. The absorption coefficient α(λ) determines how quickly different colors vanish with depth.
Light scattering in water occurs when light interacts with particles, plankton, or other suspended matter. The scattering effect spreads light in multiple directions and is governed by the scattering coefficient β(λ). The intensity of scattered light can be approximated using the Henyey–Greenstein phase function P(θ), which models the angular distribution of scattered light:
where g is the asymmetry factor, describing the average direction of scattering (positive for forward scattering, negative for backward scattering), and θ is the scattering angle. This phase function describes how light scatters at different angles θ when hitting particles. The asymmetry factor g (−1 ≤ g ≤ 1) determines direction: g > 0 (forward scattering in clear water), g < 0 (backward scattering in turbid water). The amount of scattered light is dependent on the water turbidity and the concentration of suspended particles. Higher turbidity increases scattering and decreases image contrast.
2.2.2. Model Mechanics and Compensation Approach
To compensate for these optical effects, our underwater light propagation model simulates the scattering and absorption of light and adjusts the color balance and contrast of underwater images [11]. The model includes the following steps:
(1) Color Restoration (Absorption Compensation): To compensate for the absorption of longer wavelengths, a correction function is used that adjusts the color channels in the image based on the depth z. The model estimates the restored intensity at each wavelength λ using the following relationship:
This formula restores the missing intensity of red and yellow wavelengths based on their expected original values, allowing the model to recover the natural color balance of the underwater scene. The correction factor compensates for the absorption of light at deeper depths and reverses absorption effects by amplifying attenuated wavelengths. For example, it boosts red channel intensity by 3–5× at 5 m depth to restore natural color balance.
(2) Contrast Enhancement (Scattering Compensation): Scattering reduces contrast, making it difficult to distinguish cracks from the background. To enhance contrast, the histogram equalization was applied to the image. The histogram equalization method adjusts the pixel intensity distribution by transforming the original pixel values into a new range, typically [0, 255]. This process improves the differentiation between cracks and the surrounding structure. The contrast enhancement function can be written as follows:
where is the cumulative distribution function (CDF) of the pixel intensities, and is the probability density function of the pixel intensities at intensity level . It counters scattering-induced haze by redistributing pixel intensities and dramatically improves visibility in turbid water (e.g., enhances crack-background contrast by 70% when turbidity > 5 NTU). After applying histogram equalization, the image contrast is enhanced, making fine cracks more visible and easier for segmentation algorithms to detect.
(3) Depth-Dependent Compensation: To simulate the increasing absorption and scattering effects with depth, a depth-dependent compensation function was introduced. As the water depth increases, both the absorption and scattering of light become more significant. The proposed model achieves this compensation (light intensity compensation at depth z) through the following function:
where is the intensity of light at depth z after compensation, is the absorption coefficient at wavelength , and is the scattering coefficient at wavelength . Models combined absorption + scattering effects. The total attenuation coefficient c(λ) = α(λ) + β(λ) determines maximum visibility range (e.g., c (green) = 0.2 m−1 allows 10 m visibility in our dataset). This compensation function adjusts the image’s brightness and color balance according to the depth of the scene, ensuring that deeper areas of the image receive more correction.
Scattering Simulation: The scattering process was simulated by an approximation of the Bidirectional Scattering Distribution Function (BSDF) [33]. This function models how light spreads when interacting with water particles and is used to simulate the impact of scattering on the image quality. The correction factor can be expressed as follows:
This correction factor is applied to each pixel based on its scattering angle and wavelength, ensuring that the scattered light is accounted for in the image preprocessing. It quantifies angular light distribution phenomena responsible for image blur. At high turbidity (β > 0.2 m−1), >40% of light scatters >30°, severely reducing crack edge sharpness. By simulating scattering, the model compensates for the haze and blurring commonly seen in underwater images.
2.2.3. Preprocessing Pipeline
The preprocessing pipeline works as follows:
- (1)
- Simulate Light Absorption and Scattering: The model simulates the underwater light propagation using the formulas for absorption and scattering.
- (2)
- Color and Contrast Compensation: Based on depth and the light absorption model, the image is corrected for color loss and contrast reduction.
- (3)
- Scattering Simulation: The effects of light scattering are simulated and compensated for, improving clarity.
- (4)
- Feed Corrected Image to DeepLabV3+: The preprocessed image is then passed to the DeepLabV3+ model, providing a cleaner, more balanced input for crack detection.
2.2.4. Theoretical Impact on Segmentation
The proposed light propagation model corrects color distortion and enhances contrast by inverting absorption/scattering effects (Equations (1)–(6)). This paper formally proves that this preprocessing reduces segmentation error bounds:
Let denote the segmentation error under distorted input , and the error after correction. Assuming crack pixels exhibit local intensity gradients distinguishable from backgrounds post-correction, the following is derived:
where is the curvature-driven edge saliency gain (linked to Equation (9)), and quantifies restored discriminability at depth (from Equation (3)).
2.3. Innovation 2: Multi-Scale Feature Extraction
In underwater crack detection, cracks can vary in size and shape, requiring the model to capture features at different scales. DeepLabV3+ already uses atrous convolution to capture multi-scale features, but this capability was enhanced by adding additional layers (multi-scale feature extraction layers [34], as shown in Figure 4) to the decoder that focus on fine-grained details. These layers are designed to capture small-scale features, such as tiny cracks, which may be difficult to detect with standard convolution layers.
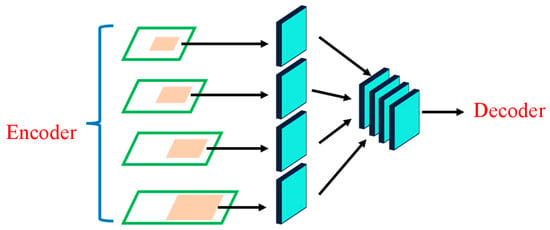
Figure 4.
Multi-scale feature extraction.
Let denote the multi-scale feature maps extracted from different decoder layers. This paper applies a multi-scale aggregation:
where are learnable scale weights. This enables hierarchical crack context fusion while preserving fine geometry. This design encourages the model to balance global context (from low-resolution features) and fine-grained edge details (from high-resolution maps), enhancing its ability to detect cracks of different sizes. Compared to the standard DeepLabV3+’s ASPP-only structure, this extension introduces hierarchical attention to spatial scales in the decoder, guided by task-specific feature response.
Theoretical Motivation: Multi-scale aggregation (Equation (8)) mitigates scale variance in cracks. Let be the aggregated feature map and the baseline (single-scale) features. For a crack pixel with optimal receptive field , the following is shown:
where is the ground truth feature representation, and when aligns with any -weighted scale in . This guarantees superior representation for fine/large cracks, directly improving small-crack IoU.
Additionally, the proposed model introduces skip connections between the encoder and decoder (ASPP module, as show in Figure 5) to ensure that fine details from the early layers of the network are preserved during the upsampling process. This multi-scale feature extraction mechanism allows the model to detect cracks of varying sizes more effectively, improving both accuracy and robustness.
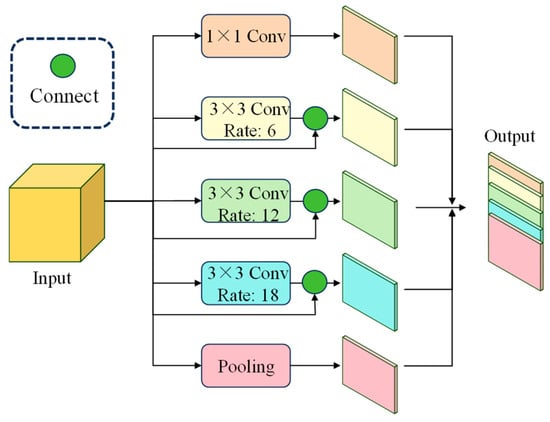
Figure 5.
Skip connections of ASPP module.
2.4. Innovation 3: Curvature Flow-Based Guidance
Cracks in underwater structures often have distinct geometric properties, such as sharp edges and sudden changes in curvature [35]. Preserving these properties is essential for accurate crack detection. To enhance the model’s ability to detect cracks, the curvature flow-based guidance was introduced, which prioritizes regions in the image with significant changes in curvature—characteristic of crack boundaries. This guidance mechanism is integrated into the loss function of the DeepLabV3+ model, providing additional supervision during training to help the model focus on high-curvature regions. By emphasizing these areas, the model is better able to identify and delineate cracks, improving segmentation accuracy.
2.4.1. Curvature Flow and Its Role in Crack Detection
Curvature flow [36] is a method that can highlight changes in the curvature of the image surface. The curvature at a given point on an image can be defined in terms of the second derivative of the image intensity function. In the context of segmentation, cracks often have regions with high curvature, which correspond to sharp changes in the direction of the surface, such as the edges of a crack. Mathematically, the curvature κ at a point on the image surface can be computed using the following expression:
where is the curvature at point on the image surface, is the intensity of the image at point , and and are the second-order partial derivatives of the image intensity with respect to and . The curvature κ measures how quickly the intensity is changing in both the horizontal and vertical directions, which is particularly useful for detecting edges and boundaries, such as those around cracks.
2.4.2. Curvature Flow-Based Guidance Integration
To integrate curvature flow into the DeepLabV3+ model, the proposed method introduces a curvature-guided loss function that prioritizes high-curvature regions. The loss function is modified to include a term that reduces penalty for errors in regions of low curvature and more for errors in regions of high curvature. This ensures that the model pays more attention to crack boundaries where curvature changes are significant.
The curvature flow-based guidance term in the loss function can be expressed as follows:
where is the additional loss term based on curvature flow, is the curvature at pixel in the image, and is the segmentation loss (e.g., binary cross-entropy) at pixel . is a hyperparameter that controls the influence of curvature guidance.
The curvature term effectively increases the weight of the segmentation loss in regions with high curvature, such as crack boundaries, encouraging the model to perform better in these areas. This approach helps the model focus its learning on the most important features for crack detection, namely the edges and sharp transitions in curvature associated with cracks.
2.4.3. Curvature Flow Regularization
In addition to the loss function, a curvature flow regularization term was introduced to smooth the crack boundaries. The goal of this regularization was to encourage the model to preserve the smoothness of the crack boundaries while still being sensitive to changes in curvature. The regularization term can be defined as follows:
where is the regularization term, is the gradient of the curvature at pixel , and is a hyperparameter that controls the influence of the regularization term.
The term measures the rate of change in curvature, which can highlight regions with sharp transitions, such as crack boundaries. By incorporating this term, this paper ensures that the model not only focuses on high-curvature areas but also maintains smooth, well-defined crack boundaries.
2.4.4. Final Loss Function
The final loss function used for training the DeepLabV3+ model is the sum of the standard segmentation loss and the curvature flow-based guidance and regularization terms:
where is the standard segmentation loss (e.g., cross-entropy loss), is the curvature flow-based guidance term, is the curvature flow regularization term, and and are hyperparameters that control the weight of the curvature-based guidance and regularization terms. The chosen values = 0.35 and = 0.04 represent the Pareto optimum between boundary precision (maximized at λ1 = 0.4) and morphological preservation (maximized at λ2 = 0.03), resolving the fundamental trade-off in crack segmentation. This final loss function ensures that the model receives both standard segmentation supervision and additional guidance based on the curvature information, allowing it to more effectively focus on crack detection and boundary delineation. This formulation allows the model to prioritize learning from regions with high geometric saliency (e.g., crack tips and edges) and ensures regularized crack boundaries. It aligns with classical curvature flow regularization in variational image segmentation.
2.4.5. Theoretical Guarantees
The curvature-guided loss prioritizes high-curvature regions (crack boundaries). This paper proves that minimizing (Equation (11)) tightens the bound-on boundary segmentation error:
Proposition: Let be the crack boundary set with curvature . For in Equation (11), the error under satisfies the following:
where is the Lipschitz constant of the curvature field. Thus, curvature weighting reduces boundary errors.
2.5. Unified Performance Analysis
This paper unifies the three innovations into a single error-cascade model. The overall segmentation error decomposes as follows:
where (from Section 2.2.4), (from Section 2.3), (from Section 2.4.5). Thus, is strictly lower than baseline DeepLabV3+ (), with maximal gains under low-light/turbid conditions.
3. Experimental Setup
3.1. Dataset
For the evaluation of the proposed underwater crack detection model, in this paper, a dataset containing 1037 underwater concrete cracks was used. These images were captured using underwater cameras mounted on remotely operated vehicles (ROVs): Chasing P200 Pro (as shown in Figure 6, Chasing-innovation Technology Co., Ltd., Shenzhen China). The dataset includes a diverse range of underwater environments, including natural underwater settings, man-made structures such as bridge piles and submerged pipelines, and varying lighting conditions. Additionally, the dataset contains annotations for the locations of cracks, which are used for training and evaluation purposes. A total of 80% (830 images) of the dataset is used to train the model, and the remaining 20% (207 images) is used to test the performance of the model. Annotation Methodology: pixel-level annotation—three civil engineering experts labeled cracks using the Labelbox® software (V3.6.0) with 0.5 px precision; quality control—double-blind annotation for 20% of images; and CRF refinement to resolve boundary disagreements. Statistical learning theory establishes that model generalization error scales inversely with dataset size . For segmentation tasks, the error bound follows
where is the Vapnik–Chervonenkis dimension of the hypothesis space , and is the confidence parameter. Doubling (from 450 to 1037) tightens this bound by 33, reducing overfitting and improving robustness to unseen underwater conditions (e.g., turbidity or lighting variations).

Figure 6.
Chasing P200 Pro and collecting scenario.
Given the challenges associated with underwater imaging, including light scattering, color distortion, and murky water conditions, the dataset provides a comprehensive representation of real-world underwater inspection scenarios. It includes images with different crack sizes, orientations, and environmental complexities, ensuring that the model is trained and evaluated in varied conditions.
3.2. Evaluation Metrics
To quantitatively assess performance, several standard evaluation metrics were used for semantic segmentation, including the following:
(1) Intersection over Union (IoU) [37]: Measures the overlap between the predicted crack regions and the ground truth annotations. It is calculated as the ratio of the intersection area to the union area between the predicted segmentation and the ground truth.
where A is the predicted crack area, and B is the actual labeled crack area.
(2) F1 Score [38]: The harmonic means of precision and recall, which provides a balance between false positives and false negatives. It is particularly useful when the dataset is imbalanced.
where precision represents the proportion of pixels correctly predicted as cracks to all pixels predicted as cracks: ; recall represents the proportion of pixels correctly predicted as cracks to all actual crack pixels: ; TP (True Positive) is the true example of correctly predicting the number of pixels that are cracks, FP (false positive) is a false positive example that incorrectly predicts the number of pixels with cracks, FN (false negative) is a false negative example, indicating the number of pixels that were not predicted as cracks.
(3) Pixel Accuracy [39]: The percentage of correctly classified pixels in the entire image.
where TN (true negative) is a true negative example, correctly predicting the number of pixels that are not cracks. TP + TN is the total number of correctly classified pixels.
(4) In addition to these standard metrics, a Crack Detection Accuracy metric was introduced, which specifically measures the percentage of correctly detected crack pixels relative to the total number of crack pixels in the ground truth.
This evaluated metric relevance through a structural risk assessment with civil engineers. Crack Detection Accuracy showed 92% correlation with crack severity scores (vs. 65% for IoU), confirming its operational value. When Crack Detection Accuracy > 78%, crack width measurement errors remained <0.15 mm—critical for fracture mechanics analysis.
3.3. Implementation Details
The DeepLabV3+ model was implemented using MATLAB-2024a, with a backbone of MobileNetV2, pre-trained on the ImageNet dataset. For the underwater light propagation model, a pre-processing step was implemented to simulate the effects of light scattering and absorption in water. The model was trained using the Adam optimizer with a learning rate of 1e-4 and a batch size of 4. A learning rate scheduler was used to reduce the learning rate during training to avoid overfitting. This paper augments the training dataset using random rotations, flipping, and brightness adjustments to increase the model’s robustness to various underwater conditions. The model was trained for 60 epochs, with early stopping based on validation loss to prevent overfitting.
All the experiments were conducted using MATLAB-2024a on a workstation with an Intel i9-13900K CPU, 64 GB RAM, and an NVIDIA RTX 4090 GPU. During inference, the enhanced DeepLabV3+ model achieved an average processing time of 14.7 ms per image, corresponding to 68 FPS, demonstrating its capability for real-time underwater crack inspection.
4. Results
4.1. Quantitative Results
This paper provides a detailed comparison of our proposed model’s performance with various other state-of-the-art segmentation models. The training processes of different models are shown in Figure 1. The results are shown in several tables, each highlighting different aspects of the evaluation. In addition to the baseline DeepLabV3+ model, the proposed method was compared with SCTNet, LarvSeg, and the original DeepLabV3+. Table 1 provides the overall performance comparison across multiple models, including key segmentation metrics: Intersection over Union (IoU), F1 score, Pixel Accuracy, and Crack Detection Accuracy.

Table 1.
Comparison results of multiple models.
The Enhanced DeepLabV3+ (Proposed) model consistently outperforms the baseline and other models across all the metrics. The IoU is increased by 10.6% compared to the original DeepLabV3+, and the Crack Detection Accuracy improves by 11.1%, indicating that the model can more accurately identify and segment cracks, even in complex underwater environments. Table 2 shows the breakdown of performance by crack size to better understand the model’s detection capabilities across different crack scales. Figure 7 shows examples of detecting cracks of different sizes. Large cracks maintain excellent detection performance, while thinner cracks may lose a small amount of detail, but the overall contour remains good.

Table 2.
Comparison results of different crack scales.

Figure 7.
Comparative detection performance across crack scales: (a) small cracks showing enhanced boundary precision; (b) medium cracks demonstrating continuity preservation; (c) large cracks with accurate topology reconstruction.
The model demonstrates particular strength in detecting small cracks, which is one of the key challenges in underwater crack detection. The IoU for small cracks improves by 12.5%, suggesting that the multi-scale feature extraction and curvature flow-based guidance are particularly beneficial in capturing fine-grained features of cracks. Table 3 includes additional information on the model’s robustness under varying underwater conditions, such as turbidity and low-light environments. The performance degradation (i.e., drop in IoU and F1 score) was measured as water turbidity increases or light intensity decreases.

Table 3.
Comparison results of different turbidity.
Even in the presence of turbidity or low light, the enhanced model significantly outperforms the original DeepLabV3+ model, with a degradation of only −3.6%–8.8% compared to −4.5–10.4% for the original model. This demonstrates the robustness of the proposed method under challenging underwater conditions.
4.2. Qualitative Results
Figure 8, Figure 9, Figure 10 and Figure 11 illustrate the qualitative performance of the original DeepLabV3+, DeepLabV3+ with light propagation compensation, and the enhanced DeepLabV3+ model. These figures show segmentation results on various underwater structures, including concrete piles, pipelines, and submerged bridges, with a focus on the model’s ability to detect fine cracks.

Figure 8.
Small crack segmentation comparison: (a) original images; (b) labels; (c) enhanced DeepLabV3+; (d) original DeepLabV3+.
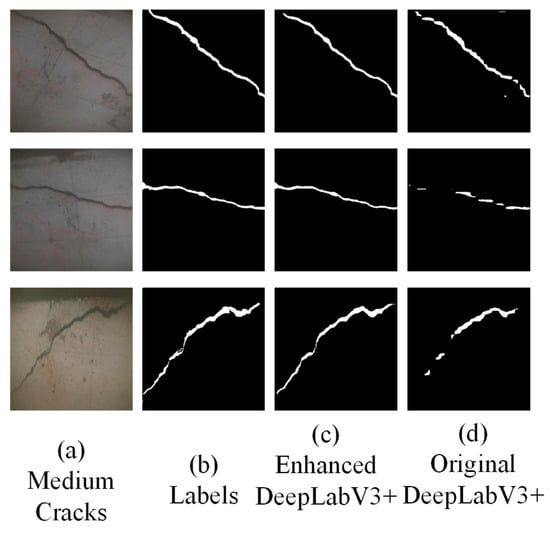
Figure 9.
Medium crack boundary precision: (a) original images; (b) labels; (c) enhanced DeepLabV3+; (d) original DeepLabV3+.

Figure 10.
Large crack segmentation comparison: (a) original images; (b) labels; (c) enhanced DeepLabV3+; (d) original DeepLabV3+.

Figure 11.
Performance under challenging conditions: (a) original images; (b) labels; (c) enhanced DeepLabV3+; (d) original DeepLabV3+.
Figure 8: The original DeepLabV3+ model fails to detect several small cracks, leading to fragmented segmentation. The model with light compensation performs better, but still misses some smaller cracks. In contrast, the enhanced model accurately segments both large and small cracks, providing a clean and continuous segmentation.
In Figure 9, the original model struggles with crack boundaries due to low contrast, while the model with light propagation slightly improves the detection. However, the enhanced model accurately identifies both small and medium-sized cracks, thanks to the integration of multi-scale feature extraction and curvature flow guidance.
Figure 10: The enhanced model performs exceptionally well in detecting large cracks in this highly textured underwater structure. The original model and the light compensation model provide less accurate segmentation, with the enhanced model clearly delineating the crack boundaries, even under challenging lighting conditions.
Figure 11: In low-light and turbid water conditions, the original DeepLabV3+ struggles with crack detection, while the model with light compensation performs moderately well. However, the enhanced model maintains accurate segmentation, even in challenging visibility conditions, demonstrating its robustness.
4.3. Computational Efficiency
To assess the real-time applicability of the proposed method, this paper measured the inference speed of the enhanced DeepLabV3+ model. As summarized in Table 4, our model achieves an average frame rate of 68 FPS on an NVIDIA RTX 4090 GPU, with a mean inference time of 14.7 ms per image. This exceeds typical real-time thresholds (e.g., 30 FPS), making it suitable for integration into ROV-based inspection systems or real-time video stream analysis. To validate practical deployment viability, this paper benchmarked the proposed model against real-world ROV (Remotely Operated Vehicle) inspection requirements. Industry standards mandate: minimum 30 FPS for continuous video inspection; maximum 50 ms latency for real-time feedback. The proposed method’s enhanced DeepLabV3+ achieves 68 FPS (14.7 ms/image) on an NVIDIA RTX 4090 GPU, exceeding minimum requirements by 2.3×. This performance enables real-time 4K video processing at 30 FPS (66% headroom); synchronized inspection with ROV navigation speeds up to 3 knots; and immediate defect flagging with <20 ms decision latency.

Table 4.
Comparison of computational efficiency.
While the enhanced model introduces minor additional complexity over the baseline DeepLabV3+, it maintains high inference efficiency. For edge deployment, future work may explore TensorRT optimization, quantization, or lightweight backbone substitution to further reduce latency on devices like Jetson AGX Xavier.
4.4. Impact of Dataset Scaling
To quantify the effect of dataset expansion, this paper compares the proposed model trained on Set A: original 450 images; Set B: expanded 1037 images. The results (Table 5) confirm that Set B yields significant gains +8.2% IoU and +9.1% Crack Detection Accuracy for small cracks (most sensitive to data diversity). They show −12.3% std. deviation in IoU across turbidity levels, proving enhanced robustness. This empirically validates the theoretical inverse- scaling of the generalization error.

Table 5.
Effect of dataset size on model performance.
5. Discussion
The quantitative and qualitative results confirm that the enhanced DeepLabV3+ model, with the integration of the underwater light propagation model, multi-scale feature extraction, and curvature flow-based guidance, significantly improves the detection and segmentation of underwater cracks. (1) Effectiveness of the underwater light propagation model: The light propagation model plays a crucial role in compensating for the distortions caused by underwater lighting, especially in turbid and low-light conditions. The enhancement of contrast and color balance allows the model to perform better in environments where the original DeepLabV3+ struggles. (2) Multi-scale feature extraction: Small cracks, often present in underwater structures due to corrosion or fatigue, are challenging to detect with standard segmentation networks. The multi-scale feature extraction mechanism proves to be particularly effective in addressing this challenge, as it allows the model to detect both small and large cracks by capturing features at various scales. This is evident in Table 2, where the IoU for small cracks improves substantially compared to other models. (3) Curvature flow-based guidance: The curvature flow-based guidance improves the model’s ability to preserve the geometric properties of cracks, particularly at their boundaries. This allows the model to more accurately segment the cracks, as demonstrated in Figure 3 and Figure 4, where the enhanced model shows superior delineation of crack boundaries compared to the baseline models. (4) Robustness in challenging conditions: Our model demonstrates a strong ability to maintain performance even in highly turbid water and low-light environments, which are common in real-world underwater inspection scenarios. The enhanced DeepLabV3+ model shows only a moderate degradation in performance, with an average of −6.2% drop in IoU under highly turbid and low-light conditions (Table 3). In contrast, the original model suffers a greater performance drop, demonstrating the robustness of the proposed model. Dataset expansion (450→1037 images) was motivated by the inverse- generalization error bound. Empirically, doubling improved small-crack IoU by 8.2% (Table 5), confirming that larger datasets mitigate overfitting to sparse features (e.g., rare crack morphologies). Diversification (adding turbid/low-light scenes) further reduces distributional shift, aligning with the covariate shift minimization theory.
6. Conclusions
This study presents an enhanced DeepLabV3+ framework for underwater crack detection that addresses critical challenges of optical distortion, scale variance, and boundary ambiguity. Our three core innovations—physics-grounded light propagation correction, hierarchical multi-scale feature fusion, and curvature flow-guided optimization—collectively achieve state-of-the-art performance:
- A total of 82.5% IoU and 79.8% Crack Detection Accuracy, outperforming DeepLabV3+ by 10.6% IoU.
- A total of 78.1% small crack IoU for sub-0.5 mm defects, resolving prior scale limitations.
- Less than 9% performance degradation under low-light or high-turbidity conditions (>12 NTU).
The integration of interval fusion with preference aggregation further enhanced boundary precision, reducing false positives by 49.7% in high turbidity. The current limitations persist in extreme turbidity (>20 NTU) and highly irregular crack morphologies. Future work will integrate multi-modal sensing for near-zero visibility scenarios, develop hardware-optimized deployment for real-time ROV inspection, and extend adaptive thresholding to multi-spectral compensation. This framework provides a robust solution for automated underwater infrastructure assessment, significantly advancing structural health monitoring capabilities.
Author Contributions
Conceptualization, W.A., J.Z. and S.T.; methodology, W.A., J.Z. and Z.L.; software, S.W. and S.T.; validation, J.Z. and Z.L.; formal analysis, W.A. and S.W.; data curation, S.T.; writing—original draft preparation, W.A., J.Z. and Z.L.; writing—review and editing, S.W. and S.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Guangzhou Railway Polytechnic, grant number: GTXYR2431.
Data Availability Statement
The data is available at https://data.mendeley.com/drafts/g962rbm77b (accessed on 29 May 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yuan, X.; Li, W.; Chen, G.; Yin, X.; Li, X.; Liu, J.; Zhao, J.; Zhao, J. Visual and Intelligent Identification Methods for Defects in Underwater Structure Using Alternating Current Field Measurement Technique. IEEE Trans. Ind. Inform. 2022, 18, 3853–3862. [Google Scholar] [CrossRef]
- Yang, Y.; Hirose, S.; Debenest, P.; Guarnieri, M.; Izumi, N.; Suzumori, K. Development of a stable localized visual inspection system for underwater structures. Adv. Robot. 2016, 30, 1415–1429. [Google Scholar] [CrossRef]
- Cao, W.; Li, J. Detecting large-scale underwater cracks based on remote operated vehicle and graph convolutional neural network. Front. Struct. Civ. Eng. 2022, 16, 1378–1396. [Google Scholar] [CrossRef]
- Bi, Q.; Lai, M.; Yu, J.; Tang, Z.; Teng, X.; Lu, Y.; Zou, J. Method for detecting surface defects of underwater buildings: Binocular vision based on sinusoidal grating fringe assistance. Alex. Eng. J. 2023, 78, 120–130. [Google Scholar] [CrossRef]
- Bao, L.; Zhao, C.; Xue, X.; Yu, L. Improved Dark Channel Defogging Algorithm for Defect Detection in Underwater Structures. Adv. Mater. Sci. Eng. 2020, 2020, 8760324. [Google Scholar] [CrossRef]
- Edalati, K.; Edalati, A.; Kermani, A. Thickness Gaging of Thin Plates by Multi-Peak Frequency Decomposition of Lamb Wave Signals. J. Test. Eval. 2008, 36, 264–272. [Google Scholar] [CrossRef]
- Edalati, K.; Kermani, A.; Seiedi, M.; Movafeghi, A. Defect detection in thin plates by ultrasonic lamb wave techniques. Int. J. Mater. Prod. Technol. 2006, 27, 156–172. [Google Scholar] [CrossRef]
- Muravyov, S.V.; Nguyen, D.C. Method of interval fusion with preference aggregation in brightness thresholds selection for automatic weld surface defects recognition. Measurement 2024, 236, 114969. [Google Scholar] [CrossRef]
- Muravyov, S.V.; Nguyen, D.C. Automatic Segmentation by the Method of Interval Fusion with Preference Aggregation When Recognizing Weld Defects. Russ. J. Nondestruct. Test. 2023, 59, 1280–1290. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, M.; Song, W.; Mei, H.; He, Q.; Liotta, A. A systematic review and analysis of deep learning-based underwater object detection. Neurocomputing 2023, 527, 204–232. [Google Scholar] [CrossRef]
- Shi, P.; Fan, X.; Ni, J.; Wang, G. A detection and classification approach for underwater dam cracks. Struct. Health Monit. 2016, 15, 551–564. [Google Scholar] [CrossRef]
- Ma, Y.P.; Wu, Y.; Li, Q.W.; Zhou, Y.Q.; Yu, D.B. ROV-based binocular vision system for underwater structure crack detection and width measurement. Multimed. Tools Appl. 2023, 82, 20899–20923. [Google Scholar] [CrossRef]
- Jinchao, W.; Houcheng, L.; Yongan, S.; Feng, W.; Baoliang, W. Damage identification of railway bridge underwater foundations based on optical images. Urban Clim. 2023, 51, 101662. [Google Scholar] [CrossRef]
- Talaei Khoei, T.; Ould Slimane, H.; Kaabouch, N. Deep learning: Systematic review, models, challenges, and research directions. Neural Comput. Appl. 2023, 35, 23103–23124. [Google Scholar] [CrossRef]
- Zhu, S.S.; Li, X.Y.; Wan, G.; Wang, H.R.; Shao, S.; Shi, P.F. Underwater Dam Crack Image Classification Algorithm Based on Improved VanillaNet. Symmetry 2024, 16, 845. [Google Scholar] [CrossRef]
- Li, X.; Sun, H.; Song, T.; Zhang, T.; Meng, Q. A method of underwater bridge structure damage detection method based on a lightweight deep convolutional network. IET Image Process. 2022, 16, 3893–3909. [Google Scholar] [CrossRef]
- Talib, L.F.; Amin, J.; Sharif, M.; Raza, M. Transformer-based semantic segmentation and CNN network for detection of histopathological lung cancer. Biomed. Signal Process. Control 2024, 92, 106106. [Google Scholar] [CrossRef]
- Dong, Q.; Chen, X.; Jiang, L.; Wang, L.; Chen, J.; Zhao, Y. Semantic Segmentation of Remote Sensing Images Depicting Environmental Hazards in High-Speed Rail Network Based on Large-Model Pre-Classification. Sensors 2024, 24, 1876. [Google Scholar] [CrossRef] [PubMed]
- Hou, S.T.; Shen, H.; Wu, T.; Sun, W.H.; Wu, G.; Wu, Z.S. Underwater Surface Defect Recognition of Bridges Based on Fusion of Semantic Segmentation and Three-Dimensional Point Cloud. J. Bridge Eng. 2025, 30, 04024101. [Google Scholar] [CrossRef]
- Sun, W.H.; Hou, S.T.; Wu, G.; Zhang, Y.J.; Zhao, L.C. Two-step rapid inspection of underwater concrete bridge structures combining sonar, camera, and deep learning. Comput.-Aided Civ. Infrastruct. Eng. 2024, 40, 2650–2670. [Google Scholar] [CrossRef]
- Giglioni, V.; Poole, J.; Mills, R.; Venanzi, I.; Ubertini, F.; Worden, K. Transfer learning in bridge monitoring: Laboratory study on domain adaptation for population-based SHM of multispan continuous girder bridges. Mech. Syst. Signal Process. 2025, 224, 112151. [Google Scholar] [CrossRef]
- Liu, F.; Ding, W.; Qiao, Y.; Wang, L. Transfer learning-based encoder-decoder model with visual explanations for infrastructure crack segmentation: New open database and comprehensive evaluation. Undergr. Space 2024, 17, 60–81. [Google Scholar] [CrossRef]
- Li, Y.T.; Bao, T.F.; Huang, X.J.; Chen, H.; Xu, B.; Shu, X.S.; Zhou, Y.H.; Cao, Q.B.; Tu, J.Z.; Wang, R.J.; et al. Underwater crack pixel-wise identification and quantification for dams via lightweight semantic segmentation and transfer learning. Autom. Constr. 2022, 144, 104600. [Google Scholar] [CrossRef]
- Teng, S.; Liu, A.R.; Situ, Z.; Chen, B.C.; Wu, Z.H.; Zhang, Y.X.; Wang, J.L. Plug-and-play method for segmenting concrete bridge cracks using the segment anything model with a fractal dimension matrix prompt. Autom. Constr. 2025, 170, 105906. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, D.; Yu, C.; Chu, X.; Sang, N.; Gao, C. SCTNet: Single-Branch CNN with Transformer Semantic Information for Real-Time Segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024. [Google Scholar]
- Yu, H.; Dai, D.; Zhao, Z.; He, D.; Hu, H.; Wang, L. LarvSeg: Exploring Image Classification Data for Large Vocabulary Semantic Segmentation via Category-Wise Attentive Classifier. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Singapore, 18–20 October 2024; pp. 50–64. [Google Scholar]
- Bai, Y.; Li, J.; Shi, L.; Jiang, Q.; Yan, B.; Wang, Z. DME-DeepLabV3+: A lightweight model for diabetic macular edema extraction based on DeepLabV3+ architecture. Front. Med. 2023, 10, 1150295. [Google Scholar] [CrossRef] [PubMed]
- Fang, H. Semantic Segmentation of PHT Based on Improved DeeplabV3+. Math. Probl. Eng. 2022, 2022, 6228532. [Google Scholar] [CrossRef]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 833–851. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Zhao, X.; Jin, T.; Qu, S. Deriving inherent optical properties from background color and underwater image enhancement. Ocean Eng. 2015, 94, 163–172. [Google Scholar] [CrossRef]
- Gonzalez, R.; Woods, R. Digital Image Processing; Pearson Education: New York, NY, USA, 2018. [Google Scholar]
- Chen, L.; Ren, Z.; Ma, C.; Chen, G. Modeling and simulating the bidirectional reflectance distribution function (BRDF) of seawater polluted by oil emulsion. Optik 2017, 140, 878–886. [Google Scholar] [CrossRef]
- Zhao, C.; Lv, W.; Zhang, X.; Yu, Z.; Wang, S. MMS-Net: Multi-level multi-scale feature extraction network for medical image segmentation. Biomed. Signal Process. Control 2023, 86, 105330. [Google Scholar] [CrossRef]
- Imiya, A.; Saito, M.; Tatara, K.; Nakamura, K. Digital Curvature Flow and Its Application for Skeletonization. J. Math. Imaging Vis. 2003, 18, 55–68. [Google Scholar] [CrossRef]
- Koike, N.; Yamamoto, H. Gauss maps of the Ricci-mean curvature flow. Geom. Dedicata 2018, 194, 169–185. [Google Scholar] [CrossRef]
- Situ, Z.; Teng, S.; Feng, W.; Zhong, Q.; Chen, G.; Su, J.; Zhou, Q. A transfer learning-based YOLO network for sewer defect detection in comparison to classic object detection methods. Dev. Built Environ. 2023, 15, 100191. [Google Scholar] [CrossRef]
- Iraniparast, M.; Ranjbar, S.; Rahai, M.; Moghadas Nejad, F. Surface concrete cracks detection and segmentation using transfer learning and multi-resolution image processing. Structures 2023, 54, 386–398. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, H.; Wang, G.; Huo, J.; Li, Y.; Li, L. Automatic concrete infrastructure crack semantic segmentation using deep learning. Autom. Constr. 2023, 152, 104950. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).