Incremental Delayed Subgradient Method for Decentralized Nonsmooth Convex–Concave Minimax Optimization

Abstract

In this paper, we propose an incremental-type subgradient scheme for solving a nonsmooth convex–concave minimax optimization problem in the setting of Euclidean spaces. We investigate convergence results by deriving an upper bound for the absolute value of the difference between the function value of the averaged iterates and the saddle value, provided that the step size is a constant. By assuming that the step-size sequence is diminishing, we prove the convergences of both the averaged sequence of function values and the sequence of function values of averaged iterates to the saddle value. Finally, we also show some numerical examples for illustrating the obtained theoretical result.

1. Introduction

In this work, we focus on developing an iterative method for solving a finite-sum nonsmooth convex–concave minimax optimization problem in a decentralized setting:

$${\displaystyle \underset{\mathbf{u}\in \mathcal{X}}{min}\underset{\mathbf{v}\in \mathcal{Y}}{max}\sum _{i=1}^m{F}_i(\mathbf{u},\mathbf{v}),}$$

(1)

where the component coupling function $F_i:{\mathbb{R}}^p\times {\mathbb{R}}^r\to \mathbb{R}$ for each $i=1,\cdots ,m$ is a convex–concave function and the constrained sets $\mathcal{X}\subset {\mathbb{R}}^p$ and $\mathcal{Y}\subset {\mathbb{R}}^r$ are compact convex sets. The convex–concave optimization problem (1) has been extensively studied, with numerous methods proposed in the literature. It arises in various areas of convex optimization. In addition, it has been widely applied in multiple fields, namely, generative adversarial networks (GANs) [1,2], adversarial robust learning [3], classification [4,5,6], and image processing [7,8].

When $m=1$, the gradient descent–ascent method, a well-known approach introduced by Arrow, Hurwicz, and Uzawa [9], is commonly used to solve the problem in the smooth case. Furthermore, for cases where the coupling function is not necessarily smooth, Nedić and Ozdaglar [10] proposed the subgradient method, which uses subgradient computation in the place of gradient computation. Since the coupling objective function is a convex–concave real-valued function, the existence of subgradients for both variables is guaranteed. A common difficulty with gradient or subgradient methods for convex optimization is that while subgradients exist, they are often hard to compute. To address this issue, the concept of delay techniques for calculating subgradients was introduced [11,12,13,14]. Specifically, the next iteration can be updated using information from stale iterates rather than computing the subgradient in the current iterate, which saves computational runtime. Recently, Arunrat and Nimana [15] proposed a method based on the subgradient method, together with the delayed technique to give more strategies in order to calculate the subgradient for solving problem (1) when $m=1$. In this approach, the iterates are updated simultaneously using delayed subgradients at stale iterates of their respective variables, combined with the current iterates of the other variable. The method is referred to as the delayed subgradient method and can be explicitly formulated as follows: For a current iterate $\left(\mathbf{u}\right[k],\mathbf{v}[k\left]\right)\in \mathcal{X}\times \mathcal{Y}(k\ge 0)$, compute

$$\mathbf{u}[k+1]:=P_{\mathcal{X}}\left[\mathbf{u}\left[k\right]-\gamma {\tilde{\nabla }}_{\mathbf{u}}F\left(\mathbf{u}[k-{\tau }_k],\mathbf{v}\left[k\right]\right)\right],$$

and

$$\mathbf{v}[k+1]:=P_{\mathcal{Y}}\left[\mathbf{v}\left[k\right]+\gamma {\tilde{\nabla }}_{\mathbf{v}}F\left(\mathbf{u}\left[k\right],\mathbf{v}[k-{\mu }_k]\right)\right],$$

where ${\tilde{\nabla }}_{\mathbf{u}}F(\mathbf{u}[k-{\tau }_k],\mathbf{v}\left[k\right])$ is a subgradient of F with respect to $\mathbf{u}$ at a stale iterate $\mathbf{u}[k-{\tau }_k]$; ${\tilde{\nabla }}_{\mathbf{v}}F(\mathbf{u}\left[k\right],\mathbf{v}[k-{\mu }_k])$ is a subgradient of F with respect to $\mathbf{v}$ at a stale iterate $\mathbf{v}[k-{\mu }_k]$; and $P_{\mathcal{X}}$ and $P_{\mathcal{Y}}$ are metric projections on $\mathcal{X}$ and $\mathcal{Y}$, respectively. In some situations, the objective functions can be expressed as a finite sum or within a stochastic setting. Focusing on each coordinate individually rather than on the entire function can often yield better results. Several methods were also developed to address this type of convex–concave optimization problem [16,17,18,19,20].

On the other hand, many authors are interested in studying convex minimization problems where the objective function is expressed as a finite sum. This problem is known as the additive convex optimization problem. Specifically, let $m\ge 1$; for all $i=1,\dots ,m$, let $F_i:{\mathbb{R}}^n\to \mathbb{R}$ be a convex function and let $\mathcal{X}\subset {\mathbb{R}}^n$ be a nonempty closed and convex set. The additive convex optimization problem is defined as follows:

$$\begin{array}{c}{\displaystyle \mathrm{minimize}\sum _{i=1}^m{F}_i\left(\mathbf{u}\right)}\hfill \\ {\displaystyle \mathrm{subject}\mathrm{to}\mathbf{u}\in \mathcal{X}.}\hfill \end{array}$$

In 2001, Nedić and Bertsekas proposed the so-called incremental subgradient methods [21,22] to address this problem. At each iteration, the solution is updated based on the subgradient of a single component of the objective function. The method is essentially structured as follows: $\mathbf{u}\left[k\right]\in \mathcal{X}$ is the vector obtained after k cycles, and the vector $\mathbf{u}[k+1]\in \mathcal{X}$ is updated by initializing with ${\mathbf{u}}_1\left[k\right]:=\mathbf{u}\left[k\right]$, where we compute

$$\begin{array}{c}{\mathbf{u}}_{i+1}\left[k\right]:=P_{\mathcal{X}}\left({\mathbf{u}}_i\left[k\right]-{\gamma }_k\tilde{\nabla }{F}_i\left({\mathbf{u}}_i\left[k\right]\right)\right),\hfill \end{array}$$

and generate $\mathbf{u}[k+1]\in \mathcal{X}$ after one more cycle of m steps as

$$\mathbf{u}[k+1]:={\mathbf{u}}_{m+1}\left[k\right],$$

where $\tilde{\nabla }{F}_i\left({\mathbf{u}}_i\left[k\right]\right)$ is a subgradient of $F_i$ at ${\mathbf{u}}_i\left[k\right]$, and ${\gamma }_k$ is a positive step size. These components can be selected either cyclically or randomly at each step. These methods are well suited for large-scale problems, as they reduce the memory and computational requirements compared with batch methods. Furthermore, this approach eliminates the need for a central user to collect all the data from each component. We notice that the delay technique has not yet been applied to the incremental subgradient method for solving problem (1).

In this work, we propose the incremental delayed subgradient method for solving the decentralized nonsmooth convex–concave minimax problem (1). This approach updates the next iterates incrementally by incorporating delayed subgradients from past iterates of their respective variables while using the current iterates of the other variable. We provide a detailed characterization of the fundamental relations required to analyze the behavior of the generated sequences. Furthermore, we establish convergence results for both constant and diminishing step-size sequences. Finally, we present numerical examples to demonstrate the effectiveness of the proposed method.

The following sections are structured as follows: In Section 2, we review essential concepts and important results related to convex–concave coupling functions and the min–max optimization problem. Section 3 introduces the incremental delayed subgradient method, outlines the assumptions, and provides relevant discussions. In addition, this section includes an analysis of the convergence properties of the proposed method. Section 4 presents numerical experiments on simple convex–concave functions to demonstrate the effectiveness of the proposed method. Finally, the concluding section summarizes our findings and provides closing remarks.

2. Preliminaries

In this section, we recall some definitions and useful facts used in this work. We denote the symbols $\mathbb{R}$ as the set of real numbers and ${\mathbb{N}}_0$ as the set of nonnegative integers. Let $\mathbf{u}=(x_1,x_2,\cdots ,x_p)$ and $\mathbf{v}=(y_1,y_2,\cdots ,y_p)$ in ${\mathbb{R}}^p$; the $\mathit{inner}\mathit{products}$ of $\mathbf{u}$ and $\mathbf{v}$, denoted by $⟨\mathbf{u},\mathbf{v}⟩$, is defined by $⟨\mathbf{u},\mathbf{v}⟩:={\sum }_{i=1}^p{x}_i{y}_i$. Moreover, the $\mathit{norm}$ of $\mathbf{u}$, denoted by $\parallel \mathbf{u}\parallel$, is defined by $\parallel \mathbf{u}\parallel :=\sqrt{⟨\mathbf{u},\mathbf{u}⟩}$. If $\mathcal{X}$ is a bounded set in ${\mathbb{R}}^p$, then we denote the diameter of $\mathcal{X}$ by $D_{\mathcal{X}}:=sup\{\parallel \mathbf{u}-\mathbf{v}\parallel :\mathbf{u},\mathbf{v}\in \mathcal{X}\}$.

Let $\mathcal{X}\subset {\mathbb{R}}^p$ and $\mathcal{Y}\subset {\mathbb{R}}^r$ be nonempty sets and $F:\mathcal{X}\times \mathcal{Y}\to \mathbb{R}$ be a function. We say that F is a convex–concave function if the function $F(·,\mathbf{v}):\mathcal{X}\to \mathbb{R}$ is a convex function for each fixed $\mathbf{v}\in \mathcal{Y}$, that is,

$$F(\alpha \mathbf{x}+(1-\alpha )\mathbf{y},\mathbf{v})\le \alpha F(\mathbf{x},\mathbf{v})+(1-\alpha )F(\mathbf{y},\mathbf{v})\mathrm{for}\mathrm{all}\mathbf{x},\mathbf{y}\in \mathcal{X}\mathrm{and}\alpha \in (0,1),$$

and $F(\mathbf{u},·):\mathcal{Y}\to \mathbb{R}$ is a concave function for each fixed $\mathbf{u}\in \mathcal{X}$, that is,

$$F(\mathbf{u},\alpha \mathbf{w}+(1-\alpha \left)\mathbf{z}\right)\ge \alpha F(\mathbf{u},\mathbf{w})+(1-\alpha )F(\mathbf{u},\mathbf{z})\mathrm{for}\mathrm{all}\mathbf{w},\mathbf{z}\in \mathcal{Y}\mathrm{and}\alpha \in (0,1).$$

A vector pair $({\mathbf{u}}^{*},{\mathbf{v}}^{*})\in \mathcal{X}\times \mathcal{Y}$ is said to be a saddle point of F on $\mathcal{X}\times \mathcal{Y}$ (with respect to minimizing in $\mathbf{u}$ and maximizing in $\mathbf{v}$) if

$$F({\mathbf{u}}^{*},\mathbf{v})\le F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\le F(\mathbf{u},{\mathbf{v}}^{*}),\mathrm{for}\mathrm{all}\mathbf{u}\in \mathcal{X},\mathbf{v}\in \mathcal{Y}.$$

We call the value $F^{*}:=F({\mathbf{u}}^{*},{\mathbf{v}}^{*})$ the saddle value. Note that if $\mathcal{X}$ and $\mathcal{Y}$ are nonempty closed bounded convex sets and $F:\mathcal{X}\times \mathcal{Y}\to \mathbb{R}$ is a convex–concave function, then F has a saddle point on $\mathcal{X}\times \mathcal{Y}$ (see [23], Corollary 37.6.2).

Let $f:{\mathbb{R}}^p\to \mathbb{R}$ be a function and let $\mathbf{u}\in {\mathbb{R}}^p$. A vector $\tilde{\nabla }f\left(\mathbf{u}\right)\in {\mathbb{R}}^p$ is called a $\mathit{subgradient}$ of f at $\mathbf{u}$ if

$$f\left(\mathbf{v}\right)\ge ⟨\tilde{\nabla }f\left(\mathbf{u}\right),\mathbf{v}-\mathbf{u}⟩+f\left(\mathbf{u}\right)\mathrm{for}\mathrm{all}\mathbf{v}\in {\mathbb{R}}^p.$$

We denote the set of all subgradients of f at $\mathbf{u}$ by $\partial f\left(\mathbf{u}\right)$ and refer to it as the subdifferential of f. The function f is called subdifferentiable at $\mathbf{u}\in {\mathbb{R}}^p$ if $\partial f\left(\mathbf{u}\right)\ne \varnothing$. Note that if $f:{\mathbb{R}}^p\to \mathbb{R}$ is a convex function and $\mathbf{u}\in {\mathbb{R}}^p$, then f is subdifferentiable at $\mathbf{u}$. If $f:{\mathbb{R}}^p\to \mathbb{R}$ is a concave function, a vector $\tilde{\nabla }f\left(\mathbf{u}\right)\in {\mathbb{R}}^p$ is called a $\mathit{supergradient}$ of f at $\mathbf{u}$ if

$$f\left(\mathbf{v}\right)\le ⟨\tilde{\nabla }f\left(\mathbf{u}\right),\mathbf{v}-\mathbf{u}⟩+f\left(\mathbf{u}\right)\mathrm{for}\mathrm{all}\mathbf{v}\in {\mathbb{R}}^p.$$

The set of all supergradients of f at $\mathbf{u}$ is denoted by $\overline{\partial }f\left(\mathbf{u}\right)$ and is called the superdifferential of f. For simplicity, we also refer to them as the subgradient and subdifferential sets. Furthermore, we note that $\overline{\partial }f\left(\mathbf{u}\right)=-\partial (-f)\left(\mathbf{u}\right)$. Moreover, since $-f$ is a convex function, we also have that f is subdifferentiable at $\mathbf{u}$.

Let $F:{\mathbb{R}}^p\times {\mathbb{R}}^r\to \mathbb{R}$ be a convex–concave function. Following the above definition of a subgradient for a convex function, we extend this concept to define the subgradients of a convex–concave function as follows. And, for a fixed $\mathbf{v}\in {\mathbb{R}}^r$ and $\overline{\mathbf{u}}\in {\mathbb{R}}^p$, we call a vector ${\tilde{\nabla }}_{\mathbf{u}}F(\overline{\mathbf{u}},\mathbf{v})\in {\mathbb{R}}^p$ a subgradient of the convex function $F(·,\mathbf{v})$ with respect to $\mathbf{u}$ at the point $\overline{\mathbf{u}}$ if

$$⟨{\tilde{\nabla }}_{\mathbf{u}}F(\overline{\mathbf{u}},\mathbf{v}),{\mathbf{u}}^{\prime }-\overline{\mathbf{u}}⟩+F(\overline{\mathbf{u}},\mathbf{v})\le F({\mathbf{u}}^{\prime },\mathbf{v}),\mathrm{for}\mathrm{all}{\mathbf{u}}^{\prime }\in {\mathbb{R}}^p.$$

And for a fixed $\mathbf{u}\in {\mathbb{R}}^p$ and let $\overline{\mathbf{v}}\in {\mathbb{R}}^r$, we call a vector ${\tilde{\nabla }}_{\mathbf{v}}F(\mathbf{u},\overline{\mathbf{v}})\in {\mathbb{R}}^r$ a subgradient of the concave function $F(\mathbf{u},·)$ with respect to $\mathbf{v}$ at the point $\overline{\mathbf{v}}$ if

$$⟨{\tilde{\nabla }}_{\mathbf{v}}F(\mathbf{u},\overline{\mathbf{v}}),{\mathbf{v}}^{\prime }-\overline{\mathbf{v}}⟩+F(\mathbf{u},\overline{\mathbf{v}})\ge F(\mathbf{u},{\mathbf{v}}^{\prime }),\mathrm{for}\mathrm{all}{\mathbf{v}}^{\prime }\in {\mathbb{R}}^r.$$

Let $\mathcal{X}\subset {\mathbb{R}}^p$ be a nonempty subset and $\mathbf{u}\in {\mathbb{R}}^p$. If there is a point $\mathbf{v}\in \mathcal{X}$ such that

$$\parallel \mathbf{u}-\mathbf{v}\parallel \le \parallel \mathbf{u}-\mathbf{z}\parallel ,$$

for all $\mathbf{z}\in \mathcal{X}$, then $\mathbf{v}$ is said to be a metric projection of $\mathbf{u}$ onto $\mathcal{X}$ and we usually symbolize it by writing $P_{\mathcal{X}}\left(\mathbf{u}\right)$. Note that if $\mathcal{X}\subset {\mathbb{R}}^p$ is a nonempty closed convex set, then for each $\mathbf{u}\in {\mathbb{R}}^p$, there exists a unique metric projection $P_{\mathcal{X}}\left(\mathbf{u}\right)$.

3. Incremental Delayed Subgradient Method

In this section, we present the incremental delayed subgradient method (in short, IDSM), which is the main algorithm of this work. After that, we state the technical lemmata that is used in the convergence results.

To begin with, we need the following delay bound assumption.

Assumption 1.

The delay sequences ${\left\{{\tau }_i^k\right\}}_{k=0}^{\infty },{\left\{{\mu }_i^k\right\}}_{k=0}^{\infty }\subset {\mathbb{N}}_0$ are bounded, that is, there exists a non-negative integer ${\tau }_{max}$ such that

$$0\le {\tau }_i^k,{\mu }_i^k\le {\tau }_{max},\mathit{for}\mathit{all}k\ge 0\mathit{and}i=1,\dots ,m.$$

We are in a position to present the incremental delayed subgradient method in Algorithm 1 as follows.

Algorithm 1 Incremental Delayed Subgradient Method (in short, IDSM)

Initialization: Given the step-size sequence ${\left\{{\gamma }_k\right\}}_{k=0}^{\infty }\subset (0,\infty )$ of real numbers, choose initial points $\mathbf{u}\left[0\right],\mathbf{u}[-1],\dots ,\mathbf{u}[-{\tau }_{max}]\in \mathcal{X}$ and $\mathbf{v}\left[0\right],\mathbf{v}[-1],\dots ,\mathbf{v}[-{\tau }_{max}]\in \mathcal{Y}$ arbitrarily.

Iterative Step: For an iterate $\left(\mathbf{u}\right[k],\mathbf{v}[k\left]\right)\in \mathcal{X}\times \mathcal{Y}$ ($k\ge 0$), starting with $${\mathbf{u}}_1\left[k\right]:=\mathbf{u}\left[k\right]\mathrm{and}{\mathbf{v}}_1\left[k\right]:=\mathbf{v}\left[k\right].$$

For each $i=1,\dots ,m$, compute $${\mathbf{u}}_{i+1}\left[k\right]:=P_{\mathcal{X}}\left[{\mathbf{u}}_i\left[k\right]-{\gamma }_k{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])\right],$$ and $${\mathbf{v}}_{i+1}\left[k\right]:=P_{\mathcal{Y}}\left[{\mathbf{v}}_i\left[k\right]+{\gamma }_k{\tilde{\nabla }}_{\mathbf{v}}{F}_i(\mathbf{u}\left[k\right],\mathbf{v}[k-{\mu }_i^k])\right],$$ where ${\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])$ is a subgradient of $F_i$ with respect to $\mathbf{u}$ at stale iterate $\mathbf{u}[k-{\tau }_i^k]$, and ${\tilde{\nabla }}_{\mathbf{v}}{F}_i(\mathbf{u}\left[k\right],\mathbf{v}[k-{\mu }_i^k])$ is a subgradient of $F_i$ with respect to $\mathbf{v}$ at stale iterate $\mathbf{v}[k-{\mu }_i^k]$.

Compute $$\mathbf{u}[k+1]:={\mathbf{u}}_{m+1}\left[k\right]\mathrm{and}\mathbf{v}[k+1]:={\mathbf{v}}_{m+1}\left[k\right].$$

Update $k:=k+1$.

To make the analysis of the convergence results of the Algorithm 1 more straightforward, we assume throughout this work that

$$\mathbf{u}\left[0\right]=\mathbf{u}[-1]=\cdots =\mathbf{u}[-{\tau }_{max}]\hspace{1em}\mathrm{and}\hspace{1em}\mathbf{v}\left[0\right]=\mathbf{v}[-1]=\cdots =\mathbf{v}[-{\tau }_{max}].$$

Remark 1.

If the number $m=1$, the proposed IDSM reduces to the method proposed by Arunrat and Nimana [15]. Furthermore, if, additionally, the delays have vanished, that is ${\tau }_{max}=0$, the IDSM is the subgradient method proposed by Nedić and Ozdaglar [10].

3.1. Technical Lemmata

The boundedness assumption of the constraint sets $\mathcal{X}$ and $\mathcal{Y}$, along with the fact that the subgradient of a real-valued convex function is uniformly bounded over any bounded subset, leads to the boundedness property as the following lemma.

Lemma 1.

There is a real constant $B>0$ such that for all $(\mathbf{u},\mathbf{v})\in \mathcal{X}\times \mathcal{Y}$ and for all $i=1,\dots ,m$,

$$\begin{array}{c}\hfill max\left\{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u},\mathbf{v})\parallel ,\parallel {\tilde{\nabla }}_{\mathbf{v}}{F}_i(\mathbf{u},\mathbf{v})\parallel \right\}\le B.\end{array}$$

Next, we focus on characterizing the fundamental repeated relations of the iterative sequences $\mathbf{u}\left[k\right]$ and $\mathbf{v}\left[k\right]$ and points $\mathbf{u}\in \mathcal{X}$ and $\mathbf{v}\in \mathcal{Y}$, respectively, which are utilized in the next steps of the convergence results. For the simplicity of the notation, we denote the following:

$$F(\mathbf{u},\mathbf{v}):=\sum _{i=1}^m{F}_i(\mathbf{u},\mathbf{v})\hspace{1em}\mathrm{for} \mathrm{all} (\mathbf{u},\mathbf{v})\in {\mathbb{R}}^p\times {\mathbb{R}}^r.$$

Lemma 2.

Let ${\left\{\mathbf{u}\left[k\right]\right\}}_{k=0}^{\infty }$ and ${\left\{\mathbf{v}\left[k\right]\right\}}_{k=0}^{\infty }$ be sequences generated by the IDSM, and $a\in (0,1)$ be a real number. The following statements are true:

(i) 

For all $\mathbf{u}\in \mathcal{X}$ and for all integers $k\ge 0$,

$$\begin{array}{ccc}\hfill {\parallel \mathbf{u}[k+1]-\mathbf{u}\parallel }^2& \le & {\parallel \mathbf{u}\left[k\right]-\mathbf{u}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1\right)\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +8B^2{\gamma }_k^{2-a}{m}^3+2{\gamma }_k(F(\mathbf{u},\mathbf{v}\left[k\right])-F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m}}({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2.\hfill \end{array}$$

(ii) 

For all $\mathbf{v}\in \mathcal{Y}$ and for all integers $k\ge 0$,

$$\begin{array}{ccc}\hfill {\parallel \mathbf{v}[k+1]-\mathbf{v}\parallel }^2& \le & {\parallel \mathbf{v}\left[k\right]-\mathbf{v}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1\right)\sum _{i=1}^m{\parallel {\mathbf{v}}_{i+1}\left[k\right]-{\mathbf{v}}_i\left[k\right]\parallel }^2\hfill \\ & & +8B^2{\gamma }_k^{2-a}{m}^3+2{\gamma }_k(F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u}\left[k\right],\mathbf{v}))\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m}}({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{v}[k-j+1]-\mathbf{v}[k-j]\parallel }^2.\hfill \end{array}$$

Proof. 

We present only the proof of (i). Since the proof of (ii) trivially follows the line of reasoning of the proof of (i) by replacing the convexity by the concavity of $F_i(\mathbf{u},·)$ for all $\mathbf{u}\in \mathcal{X}$, we omit it here.

Let $\mathbf{u}\in \mathcal{X}$ and $k\ge 0$ be given. For every $i=1$ to m, by using the definition of $\mathbf{u}[k+1]$ and the property of metric projection, we note that

$$\begin{array}{ccc}\hfill 0& \le & ⟨{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]+{\gamma }_k{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}-{\mathbf{u}}_{i+1}\left[k\right]⟩\hfill \\ & =& ⟨{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right],\mathbf{u}-{\mathbf{u}}_{i+1}\left[k\right]⟩+{\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}-\mathbf{u}[k-{\tau }_i^k]⟩\hfill \\ & & +{\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}[k-{\tau }_i^k]-{\mathbf{u}}_{i+1}\left[k\right]⟩.\hfill \end{array}$$

(2)

Let us arrange the terms on the right-hand side of the inequality above. Now, the first term can be arranged as

$$⟨{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right],\mathbf{u}-{\mathbf{u}}_{i+1}\left[k\right]⟩={\displaystyle \frac{1}{2}}\parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2-{\displaystyle \frac{1}{2}}\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i{\left[k\right]\parallel }^2-{\displaystyle \frac{1}{2}}{\parallel {\mathbf{u}}_{i+1}\left[k\right]-\mathbf{u}\parallel }^2.$$

(3)

Since ${\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])$ is the subgradient of a convex function $F_i(·,\mathbf{v}\left[k\right])$ at $\mathbf{u}[k-{\tau }_i^k]$, we obtain that the second term can be bounded as

$${\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}-\mathbf{u}[k-{\tau }_i^k]⟩\le {\gamma }_k(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])).$$

(4)

Regarding the last term in the inequality above, we begin by noting that

$$\begin{array}{ccc}\hfill ⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}[k-{\tau }_i^k]-{\mathbf{u}}_{i+1}\left[k\right]⟩& =& ⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1]⟩\hfill \\ & & +⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]⟩.\hfill \end{array}$$

(5)

By using the facts that the constant $a\in (0,1)$ and the number $m\ge 1$, we note that

$$\begin{array}{ccc}\hfill 0& \le & {\parallel m{\gamma }_k^{{\displaystyle \frac{2-a}{2}}}{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])-{\displaystyle \frac{1}{2m}}{\gamma }_k^{{\displaystyle \frac{a}{2}}}(\mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1])\parallel }^2\hfill \\ & =& m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])\parallel }^2-{\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1]⟩\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1]\parallel }^2,\hfill \end{array}$$

which implies that

$$\begin{array}{ccc}\hfill {\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1]⟩& \le & m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1]\parallel }^2.\hfill \end{array}$$

(6)

Using the same technique for deriving (6), we also have

$$\begin{array}{ccc}\hfill {\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]⟩& \le & m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]\parallel }^2.\hfill \end{array}$$

(7)

Thus, by applying the obtained inequalities (6) and (7), inequality (5) becomes

$$\begin{array}{ccc}\hfill {\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]),\mathbf{u}[k-{\tau }_i^k]-{\mathbf{u}}_{i+1}\left[k\right]⟩& \le & 2m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1]\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]\parallel }^2.\hfill \end{array}$$

(8)

By applying inequalities (3), (4) and (8) in inequality (2), we obtain

$$\begin{array}{ccc}\hfill 0& \le & {\displaystyle \frac{1}{2}}\parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2-{\displaystyle \frac{1}{2}}\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i{\left[k\right]\parallel }^2-{\displaystyle \frac{1}{2}}{\parallel {\mathbf{u}}_{i+1}\left[k\right]-\mathbf{u}\parallel }^2\hfill \\ & & +{\gamma }_k(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]))+2m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}\parallel \mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1]{\parallel }^2+{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]\parallel }^2\hfill \\ & =& {\displaystyle \frac{1}{2}}\parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2-{\displaystyle \frac{1}{2}}\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i{\left[k\right]\parallel }^2-{\displaystyle \frac{1}{2}}{\parallel {\mathbf{u}}_{i+1}\left[k\right]-\mathbf{u}\parallel }^2\hfill \\ & & +{\gamma }_k(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))+{\gamma }_k(F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]))\hfill \\ & & +2m^2{\gamma }_k^{2-a}\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]){\parallel }^2+{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1]\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]\parallel }^2.\hfill \end{array}$$

(9)

Now, we apply the subgradient inequality for a convex function $F_i(·,\mathbf{v}\left[k\right])$ at $\mathbf{u}\left[k\right]$ and $\mathbf{u}[k+1]$ to obtain

$$\begin{array}{ccc}\hfill {\gamma }_k(F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]))& =& {\gamma }_k(F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F_i(\mathbf{u}[k+1],\mathbf{v}\left[k\right]))\hfill \\ & & +{\gamma }_k(F_i(\mathbf{u}[k+1],\mathbf{v}\left[k\right])-F_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]))\hfill \\ & \le & {\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]),\mathbf{u}\left[k\right]-\mathbf{u}[k+1]⟩\hfill \\ & & +{\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k+1],\mathbf{v}\left[k\right]),\mathbf{u}[k+1]-\mathbf{u}[k-{\tau }_i^k]⟩.\hfill \end{array}$$

(10)

Using the same technique to derive inequality (6), we can obtain the following inequalities:

$$\begin{array}{ccc}\hfill {\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]),\mathbf{u}\left[k\right]-\mathbf{u}[k+1]⟩& \le & m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}\left[k\right]-\mathbf{u}[k+1]\parallel }^2,\hfill \end{array}$$

(11)

and

$$\begin{array}{ccc}\hfill {\gamma }_k⟨{\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k+1],\mathbf{v}\left[k\right]),\mathbf{u}[k+1]-\mathbf{u}[k-{\tau }_i^k]⟩& \le & m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k+1],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k+1]-\mathbf{u}[k-{\tau }_i^k]\parallel }^2.\hfill \end{array}$$

(12)

From inequalities (11) and (12), along with (10), it follows that inequality (9) becomes

$$\begin{array}{ccc}\hfill 0& \le & {\displaystyle \frac{1}{2}}\parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2-{\displaystyle \frac{1}{2}}\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i{\left[k\right]\parallel }^2-{\displaystyle \frac{1}{2}}{\parallel {\mathbf{u}}_{i+1}\left[k\right]-\mathbf{u}\parallel }^2\hfill \\ & & +{\gamma }_k(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))+m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}\left[k\right]-\mathbf{u}[k+1]\parallel }^2+m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k+1],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}\parallel \mathbf{u}[k+1]-\mathbf{u}[k-{\tau }_i^k]{\parallel }^2+2m^2{\gamma }_k^{2-a}{\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{4m^2}}\parallel \mathbf{u}[k-{\tau }_i^k]-\mathbf{u}[k+1]{\parallel }^2+{\displaystyle \frac{{\gamma }_k^a}{4m^2}}{\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]\parallel }^2,\hfill \end{array}$$

and it is organized as

$$\begin{array}{ccc}\hfill \parallel {\mathbf{u}}_{i+1}{\left[k\right]-\mathbf{u}\parallel }^2& \le & \parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}-1\right){\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +2{\gamma }_k(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])+2{\gamma }_k^{2-a}{m}^2(\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i{(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])\parallel }^2\hfill \\ & & +\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i{(\mathbf{u}[k+1],\mathbf{v}\left[k\right])\parallel }^2+2\parallel {\tilde{\nabla }}_{\mathbf{u}}{F}_i(\mathbf{u}[k-{\tau }_i^k],\mathbf{v}\left[k\right]){\parallel }^2)\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{2m^2}}{\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2+{\displaystyle \frac{{\gamma }_k^a}{m^2}}{\parallel \mathbf{u}[k+1]-\mathbf{u}[k-{\tau }_i^k]\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{2m^2}}{\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]\parallel }^2\hfill \\ & \le & \parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}-1\right){\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +2{\gamma }_k(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))+8B^2{\gamma }_k^{2-a}{m}^2+{\displaystyle \frac{{\gamma }_k^a}{2m^2}}{\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m^2}}\parallel \mathbf{u}[k+1]-\mathbf{u}[k-{\tau }_i^k]{\parallel }^2+{\displaystyle \frac{{\gamma }_k^a}{2m^2}}{\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]\parallel }^2,\hfill \end{array}$$

(13)

where the constant B is the bound of the subgradients given in Lemma 1. We observe that the term $\parallel \mathbf{u}[k+1]-\mathbf{u}[k-{\tau }_i^k]{\parallel }^2$ in inequality (13) above can be written as

$$\begin{array}{ccc}\hfill \parallel \mathbf{u}[k+1]-\mathbf{u}[k-{\tau }_i^k]{\parallel }^2& =& {({\tau }_i^k+1)}^2{∥\sum _{j=0}^{{\tau }_i^k}{\displaystyle \frac{\mathbf{u}[k-j+1]-\mathbf{u}[k-j]}{{\tau }_i^k+1}}∥}^2\hfill \\ & \le & ({\tau }_i^k+1)\sum _{j=0}^{{\tau }_i^k}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2\hfill \\ & \le & ({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2.\hfill \end{array}$$

Thus, using this inequality in (13), we have

$$\begin{array}{ccc}\hfill \parallel {\mathbf{u}}_{i+1}{\left[k\right]-\mathbf{u}\parallel }^2& \le & \parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}-1\right){\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +2{\gamma }_k(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))+8B^2{\gamma }_k^{2-a}{m}^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{2m^2}}{\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2+{\displaystyle \frac{{\gamma }_k^a}{2m^2}}{\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}\left[k\right]\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m^2}}({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2.\hfill \end{array}$$

(14)

Now, we investigate the terms ${\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2$ and $\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}{\left[k\right]\parallel }^2$ in inequality (14) as follows. By using the convexity of ${\parallel ·\parallel }^2$, we note that

$$\begin{array}{ccc}\hfill {\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2& =& {∥\sum _{i=1}^m({\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right])∥}^2\hfill \\ & =& m^2{∥\sum _{i=1}^m{\displaystyle \frac{{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]}{m}}∥}^2\le m\sum _{i=1}^m{∥{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]∥}^2.\hfill \end{array}$$

(15)

With the same technique as above, the term $\parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}{\left[k\right]\parallel }^2$ is bounded as

$$\begin{array}{ccc}\hfill \parallel \mathbf{u}[k+1]-{\mathbf{u}}_{i+1}{\left[k\right]\parallel }^2& =& {∥\sum _{j=i+1}^m({\mathbf{u}}_{j+1}\left[k\right]-{\mathbf{u}}_j\left[k\right])∥}^2\hfill \\ & =& {(m-i)}^2{∥\sum _{j=i+1}^m{\displaystyle \frac{({\mathbf{u}}_{j+1}\left[k\right]-{\mathbf{u}}_j\left[k\right])}{m-i}}∥}^2\hfill \\ & \le & m\sum _{j=1}^m\parallel {\mathbf{u}}_{j+1}\left[k\right]-{\mathbf{u}}_j{\left[k\right]\parallel }^2=m\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2.\hfill \end{array}$$

(16)

Therefore, by applying inequalities (15) and (16) in inequality (14), we obtain that

$$\begin{array}{ccc}\hfill \parallel {\mathbf{u}}_{i+1}{\left[k\right]-\mathbf{u}\parallel }^2& \le & \parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}-1\right){\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +2{\gamma }_k(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))+8B^2{\gamma }_k^{2-a}{m}^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{2m}}\sum _{i=1}^m{∥{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]∥}^2+{\displaystyle \frac{{\gamma }_k^a}{2m}}\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m^2}}({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2\hfill \\ & =& \parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}-1\right){\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +2{\gamma }_k(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))+8B^2{\gamma }_k^{2-a}{m}^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m^2}}({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m}}\sum _{i=1}^m{∥{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]∥}^2.\hfill \end{array}$$

(17)

By adding inequality (17) over $i=1,\cdots ,m$, we obtain

$$\begin{array}{ccc}\hfill \sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-\mathbf{u}\parallel }^2& \le & \sum _{i=1}^m\parallel {\mathbf{u}}_i{\left[k\right]-\mathbf{u}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}-1\right)\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +2{\gamma }_k\sum _{i=1}^m(F_i(\mathbf{u},\mathbf{v}\left[k\right])-F_i(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))+8B^2{\gamma }_k^{2-a}{m}^3\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m}}\sum _{i=1}^m\sum _{i=1}^m{∥{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]∥}^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m^2}}({\tau }_{max}+1)\sum _{i=1}^m\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2,\hfill \end{array}$$

and then

$$\begin{array}{ccc}\hfill {\parallel \mathbf{u}[k+1]-\mathbf{u}\parallel }^2& \le & {\parallel \mathbf{u}\left[k\right]-\mathbf{u}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}-1\right)\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +2{\gamma }_k(F(\mathbf{u},\mathbf{v}\left[k\right])-F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))+8B^2{\gamma }_k^{2-a}{m}^3\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m^2}}({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}\sum _{i=1}^m{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2\hfill \\ & & +{\gamma }_k^a\sum _{i=1}^m{∥{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]∥}^2,\hfill \end{array}$$

implying that

$$\begin{array}{ccc}\hfill {\parallel \mathbf{u}[k+1]-\mathbf{u}\parallel }^2& \le & {\parallel \mathbf{u}\left[k\right]-\mathbf{u}\parallel }^2+\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1\right)\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +2{\gamma }_k(F(\mathbf{u},\mathbf{v}\left[k\right])-F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right]))+8B^2{\gamma }_k^{2-a}{m}^3\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m}}({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2,\hfill \end{array}$$

as desired. □

3.2. Bounds for Constant Step Size

Before proposing the lemma below, we define the notations in the case of a constant step size, where we write the averaged iterates $\widehat{\mathbf{u}}\left[N\right]$ and $\widehat{\mathbf{v}}\left[N\right]$ as

$$\widehat{\mathbf{u}}\left[N\right]:={\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^N\mathbf{u}\left[k\right]\mathrm{and}\widehat{\mathbf{v}}\left[N\right]:={\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^N\mathbf{v}\left[k\right],\mathrm{for}\mathrm{all}N\ge 0.$$

The proof of the following lemma can be carried out in the same manner as the proof of Lemma 4.2 in [15] by using Lemma 2 with ${\gamma }_k=\gamma$.

Lemma 3.

Let ${\left\{\mathbf{u}\left[k\right]\right\}}_{k=0}^{\infty }$ and ${\left\{\mathbf{v}\left[k\right]\right\}}_{k=0}^{\infty }$ be sequences generated by the IDSM, and $a\in (0,1)$ be a real number. Suppose that the step-size constant $\gamma \in \left(0,{\left({\displaystyle \frac{1}{\frac{1}{2m^2}+1+{({\tau }_{\max }+1)}^2}}\right)}^{1/a}\right)$. The following statements are true:

(i) 

For all $\mathbf{u}\in \mathcal{X}$ and for all integers $N\ge 0$,

$${\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u},\widehat{\mathbf{v}}\left[N\right])\le {\displaystyle \frac{{\parallel \mathbf{u}\left[0\right]-\mathbf{u}\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a}.$$

(18)

(ii) 

For all $\mathbf{v}\in \mathcal{Y}$ and for all integers $N\ge 0$,

$${\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\widehat{\mathbf{u}}\left[N\right],\mathbf{v})\ge -{\displaystyle \frac{{\parallel \mathbf{v}\left[0\right]-\mathbf{v}\parallel }^2}{2\gamma (N+1)}}-4B^2{m}^3{\gamma }^{1-a}.$$

(19)

Next, we determine the upper bound for the minimax gap of the averaged iterates $\widehat{\mathbf{u}}\left[N\right]$ and $\widehat{\mathbf{v}}\left[N\right]$ by using the obtained results in Lemma 3 as follows:

Theorem 2.

Let ${\left\{\mathbf{u}\left[k\right]\right\}}_{k=0}^{\infty }$ and ${\left\{\mathbf{v}\left[k\right]\right\}}_{k=0}^{\infty }$ be sequences generated by the IDSM, and $a\in (0,1)$ be a real number. Suppose that the step-size constant $\gamma \in \left(0,{\left({\displaystyle \frac{1}{\frac{1}{2m^2}+1+{({\tau }_{\max }+1)}^2}}\right)}^{1/a}\right)$. Then, for all $N\ge 0$ and any saddle point $({\mathbf{u}}^{*},{\mathbf{v}}^{*})\in \mathcal{X}\times \mathcal{Y}$, we have

$$0\le F(\widehat{\mathbf{u}}\left[N\right],{\mathbf{v}}^{*})-F({\mathbf{u}}^{*},\widehat{\mathbf{v}}\left[N\right])\le {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (N+1)}}+8B^2{m}^3{\gamma }^{1-a}.$$

Proof. 

Let $\mathbf{u}={\mathbf{u}}^{*}$ and $\mathbf{v}={\mathbf{v}}^{*}$ in inequalities (18) and (19), respectively. For each $N\ge 0$, we have

$${\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F({\mathbf{u}}^{*},\widehat{\mathbf{v}}\left[N\right])\le {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a},$$

and

$$F(\widehat{\mathbf{u}}\left[N\right],{\mathbf{v}}^{*})-{\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])\le {\displaystyle \frac{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}{\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a}.$$

Therefore, by combining these two inequalities, we can conclude that

$$0\le F(\widehat{\mathbf{u}}\left[N\right],{\mathbf{v}}^{*})-F({\mathbf{u}}^{*},\widehat{\mathbf{v}}\left[N\right])\le {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (N+1)}}+8B^2{m}^3{\gamma }^{1-a},$$

The proof is completed. □

Furthermore, we can derive the upper bound for the difference in the function values of the averaged iterates $F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])$ and the saddle value $F^{*}$ as the following theorem.

Theorem 3.

Let ${\left\{\mathbf{u}\left[k\right]\right\}}_{k=0}^{\infty }$ and ${\left\{\mathbf{v}\left[k\right]\right\}}_{k=0}^{\infty }$ be sequences generated by the IDSM, and $a\in (0,1)$ be a real number. Suppose that the step-size constant $\gamma \in \left(0,{\left({\displaystyle \frac{1}{\frac{1}{2m^2}+1+{({\tau }_{max}+1)}^2}}\right)}^{1/a}\right)$. Then, for all $N\ge 0$ and any saddle point $({\mathbf{u}}^{*},{\mathbf{v}}^{*})\in \mathcal{X}\times \mathcal{Y}$, we have

$$\begin{array}{ccc}\hfill -{\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-\widehat{\mathbf{u}}{\left[N\right]\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (N+1)}}-8B^2{m}^3{\gamma }^{1-a}& \le & F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\hfill \\ & \le & {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-\widehat{\mathbf{v}}\left[N\right]\parallel }^2}{2\gamma (N+1)}}\hfill \\ & & +8B^2{m}^3{\gamma }^{1-a}.\hfill \end{array}$$

(20)

Proof. 

For any $N\ge 0$, we set $\mathbf{u}={\mathbf{u}}^{*}$ and $\mathbf{v}={\mathbf{v}}^{*}$ in (18) and (19), respectively, where we have that

$${\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F({\mathbf{u}}^{*},\widehat{\mathbf{v}}\left[N\right])\le {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a},$$

(21)

and

$${\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\widehat{\mathbf{u}}\left[N\right],{\mathbf{v}}^{*})\ge -{\displaystyle \frac{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}{\parallel }^2}{2\gamma (N+1)}}-4B^2{m}^3{\gamma }^{1-a}.$$

(22)

Since $\widehat{\mathbf{u}}\left[N\right]\in \mathcal{X}$ and $\widehat{\mathbf{v}}\left[N\right]\in \mathcal{Y}$ for all $N\ge 0$, the saddle-point relation implies that

$$F({\mathbf{u}}^{*},\widehat{\mathbf{v}}\left[N\right])\le F({\mathbf{u}}^{*},{\mathbf{v}}^{*}),$$

and

$$F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\le F(\widehat{\mathbf{u}}\left[N\right],{\mathbf{v}}^{*}).$$

We invoke these two results with inequalities (21) and (22), respectively, which are

$${\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\le {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a},$$

(23)

and

$$F({\mathbf{u}}^{*},{\mathbf{v}}^{*})-{\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])\le {\displaystyle \frac{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}{\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a}.$$

(24)

Now, by combining inequalities (23) and (24), we obtain

$$\begin{array}{ccc}\hfill -{\displaystyle \frac{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}{\parallel }^2}{2\gamma (N+1)}}-4B^2{m}^3{\gamma }^{1-a}& \le & {\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\hfill \\ & \le & {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a}.\hfill \end{array}$$

(25)

In addition, by using $\mathbf{u}={\widehat{\mathbf{u}}}_N$ and $\mathbf{v}={\widehat{\mathbf{v}}}_N$ in (18) and (19), respectively, we derive that

$${\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])\le {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-\widehat{\mathbf{u}}{\left[N\right]\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a},$$

and

$${\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])\ge -{\displaystyle \frac{m\parallel \mathbf{v}\left[0\right]-\widehat{\mathbf{v}}{\left[N\right]\parallel }^2}{2\gamma (N+1)}}-4B^2{m}^3{\gamma }^{1-a}.$$

Next, we combine the two obtained relations and multiply by $-1$ on both sides of the inequality to obtain that

$$\begin{array}{ccc}\hfill -{\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-\widehat{\mathbf{u}}{\left[N\right]\parallel }^2}{2\gamma (N+1)}}-4B^2{m}^3{\gamma }^{1-a}& \le & F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])-{\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])\hfill \\ & \le & {\displaystyle \frac{\parallel \mathbf{v}\left[0\right]-\widehat{\mathbf{v}}{\left[N\right]\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a}.\hfill \end{array}$$

(26)

Finally, we sum up inequalities (25) and (26) to obtain

$$\begin{array}{ccc}\hfill -{\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-\widehat{\mathbf{u}}{\left[N\right]\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (N+1)}}-8B^2{m}^3{\gamma }^{1-a}& \le & F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\hfill \\ & \le & {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-\widehat{\mathbf{v}}\left[N\right]\parallel }^2}{2\gamma (N+1)}}\hfill \\ & & +8B^2{m}^3{\gamma }^{1-a},\hfill \end{array}$$

which completes the proof. □

By noticing the proving lines of Theorem 3, we can derive the complexity upper bound of the IDSM as the following remark.

Remark 2.

Let $({\mathbf{u}}^{*},{\mathbf{v}}^{*})\in \mathcal{X}\times \mathcal{Y}$ be a saddle point of problem (1) and $N\ge 0$. According to (25), we have

$$\begin{array}{ccc}\hfill -{\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (N+1)}}-4B^2{m}^3{\gamma }^{1-a}& \le & {\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\hfill \\ & \le & {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a},\hfill \end{array}$$

which yields the upper bound on the average of function values ${\displaystyle \frac{1}{(N+1)}}{\sum }_{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])$ for the saddle value $F^{*}$ as

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\right|\le {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a}.\end{array}$$

Notice that by choosing a small step size γ so that the term ${\gamma }^{1-a}$ is small allows for a small error level, as required. To obtain an ε-optimal solution to problem (1), we now want to know how many iterations N are required. Now, let $\epsilon >0$ be so that

$$\left|{\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\right|\le \epsilon .$$

Note that finding the nonnegative integer N for which

$$\begin{array}{c}\hfill {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a}\le \epsilon ,\end{array}$$

is achieved in the same manner as

$$\begin{array}{c}\hfill N\ge {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (\epsilon -4B^2{m}^3{\gamma }^{1-a})}}-1.\end{array}$$

Let us fix a length $\{0,1,\dots ,N\}$. By putting the positive real number $a>0.5$ and committing over this length, we may choose the constant step size $\gamma ={\displaystyle \frac{\epsilon }{{(N+1)}^{1/2(1-a)}}}$ for some constant $\epsilon \in \left(0,{\left({\displaystyle \frac{1}{\frac{1}{2m^2}+1+{({\tau }_{max}+1)}^2}}\right)}^{1/a}\right)$ so that

$$\begin{array}{ccc}& & {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\gamma (N+1)}}+4B^2{m}^3{\gamma }^{1-a}\hfill \\ & =& {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\epsilon {(N+1)}^{1-(1/2(1-a\left)\right)}}}+{\displaystyle \frac{4B^2{m}^3{\epsilon }^{1-a}}{{(N+1)}^{1/2}}}\hfill \\ & \le & \left({\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\epsilon }}+4B^2{m}^3{\epsilon }^{1-a}\right){\displaystyle \frac{1}{{(N+1)}^{1-(1/2(1-a\left)\right)}}}.\hfill \end{array}$$

Since we know that ${\displaystyle \frac{1}{2+{({\tau }_{max}+1)}^2}}\le 1$ and $a<1-a$, we have ${\left(2+{({\tau }_{max}+1)}^2\right)}^{-(1-a)/a}\le 1$. Now, by particularly putting $\epsilon :={\displaystyle \frac{1}{{(2+{({\tau }_{max}+1)}^2)}^{1/a}}}={\displaystyle \frac{1}{{({\tau }_{max}^2+2{\tau }_{max}+3)}^{1/a}}}$, we obtain the above constant bound:

$$\begin{array}{ccc}& & {\displaystyle \frac{\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+{\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}\parallel }^2}{2\epsilon }}+4B^2{m}^3{\epsilon }^{1-a}\hfill \\ & =& {\displaystyle \frac{(\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}{\parallel }^2){({\tau }_{max}^2+2{\tau }_{max}+3)}^{1/a}}{2}}\hfill \\ & & +4B^2{m}^3{({\tau }_{max}^2+2{\tau }_{max}+3)}^{-(1-a)/a}\hfill \\ & \le & {\displaystyle \frac{(\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}{\parallel }^2){({\tau }_{max}^2+2{\tau }_{max}+3)}^{1/a}}{2}}\hfill \\ & & +4B^2{m}^3.\hfill \end{array}$$

Therefore, we obtain the complexity upper bound within a fixed length $\{0,1,\dots ,N\}$ and a constant $a\in (0,0.5)$ as

$$\begin{array}{ccc}& & \left|{\displaystyle \frac{1}{(N+1)}}\sum _{k=0}^{N}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\right|\hfill \\ & \le & \left({\displaystyle \frac{(\parallel \mathbf{u}\left[0\right]-{\mathbf{u}}^{*}{\parallel }^2+\parallel \mathbf{v}\left[0\right]-{\mathbf{v}}^{*}{\parallel }^2){({\tau }_{max}^2+2{\tau }_{max}+3)}^{1/a}}{2}}+4B^2{m}^3\right){\displaystyle \frac{1}{{(N+1)}^{1-(1/2(1-a\left)\right)}}}.\hfill \end{array}$$

3.3. Convergences of Function Values

For notation simplicity, we write the averaged iterates $\overline{\mathbf{u}}\left[N\right]$ and $\overline{\mathbf{v}}\left[N\right]$ as

$$\overline{\mathbf{u}}\left[N\right]:={\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_k\mathbf{u}\left[k\right]}{{\sum }_{k=0}^N{\gamma }_k}}\mathrm{and}\overline{\mathbf{v}}\left[N\right]:={\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_k\mathbf{v}\left[k\right]}{{\sum }_{k=0}^N{\gamma }_k}},\mathrm{for}\mathrm{all}N\ge 0.$$

Lemma 4.

Let ${\left\{\mathbf{u}\left[k\right]\right\}}_{k=0}^{\infty }$ and ${\left\{\mathbf{v}\left[k\right]\right\}}_{k=0}^{\infty }$ be sequences generated by the IDSM, and $a\in (0,1)$ be a real number. Suppose that the step-size sequence ${\left\{{\gamma }_k\right\}}_{k=0}^{\infty }\subset \left(0,{\left({\displaystyle \frac{1}{\frac{1}{2m^2}+1+{({\tau }_{max}+1)}^2}}\right)}^{1/a}\right)$ is non-increasing.

(i) 

For all $x\in \mathcal{X}$ and for all integers $N\ge 0$,

$${\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F(\mathbf{u},\overline{\mathbf{v}}\left[N\right])\le {\displaystyle \frac{D_{\mathcal{X}}^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}.$$

(27)

(ii) 

For all $y\in \mathcal{Y}$ and for all integers $N\ge 0$,

$${\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F(\overline{\mathbf{u}}\left[N\right],\mathbf{v})\ge {\displaystyle \frac{-D_{\mathcal{Y}}^2-8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}.$$

(28)

Proof. 

(i) Let $x\in \mathcal{X}$ be given. Taking into account Lemma 2 (i), we note that for all $k\ge 0$,

$$\begin{array}{ccc}\hfill 2{\gamma }_k(F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u},\mathbf{v}\left[k\right]))& \le & {\parallel \mathbf{u}\left[k\right]-\mathbf{u}\parallel }^2-{\parallel \mathbf{u}[k+1]-\mathbf{u}\parallel }^2\hfill \\ & & +\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1\right)\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\gamma }_k^a}{m}}({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2\hfill \\ & & +8B^2{\gamma }_k^{2-a}{m}^3.\hfill \end{array}$$

For a fixed integer $N\ge 0$, by summing this relation over k from 0 to N, we obtain

$$\begin{array}{ccc}\hfill 2\sum _{k=0}^N{\gamma }_k(F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u},\mathbf{v}\left[k\right]))& \le & {\parallel \mathbf{u}\left[0\right]-\mathbf{u}\parallel }^2-{\parallel \mathbf{u}[N+1]-\mathbf{u}\parallel }^2+8B^2{m}^3\sum _{k=0}^N{\gamma }_k^{2-a}\hfill \\ & & +\sum _{k=0}^N\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1\right)\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_{i+1}\left[k\right]\parallel }^2\hfill \\ & & +{\displaystyle \frac{({\tau }_{max}+1)}{m}}\sum _{k=0}^N{\gamma }_k^a\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2.\hfill \end{array}$$

(29)

For the last term of the above inequality, the non-increasing property of the step-size sequence ${\left\{{\gamma }_k\right\}}_{k=0}^{\infty }$ implies that

$$\begin{array}{ccc}\hfill \sum _{k=0}^N\sum _{j=0}^{{\tau }_{max}}{\gamma }_k^a{\parallel \mathbf{u}[k-j+1]-\mathbf{u}[k-j]\parallel }^2& =& \sum _{j=0}^{{\tau }_{max}}\sum _{k=-j}^{N-j}{\gamma }_{k+j}^a{\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2\hfill \\ & =& \sum _{j=0}^{{\tau }_{max}}\sum _{k=0}^{N-j}{\gamma }_{k+j}^a{\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2\hfill \\ & \le & \sum _{j=0}^{{\tau }_{max}}\sum _{k=0}^{N-j}{\gamma }_k^a{\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2\hfill \\ & \le & \sum _{j=0}^{{\tau }_{max}}\sum _{k=0}^N{\gamma }_k^a{\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2\hfill \\ & =& ({\tau }_{max}+1)\sum _{k=0}^N{\gamma }_k^a{\parallel \mathbf{u}[k+1]-\mathbf{u}\left[k\right]\parallel }^2\hfill \\ & \le & m({\tau }_{max}+1)\sum _{k=0}^N{\gamma }_k^a\sum _{i=1}^m{∥{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]∥}^2.\hfill \end{array}$$

(30)

By applying this obtained inequality in inequality (29), we have

$$\begin{array}{ccc}& & 2\sum _{k=0}^N{\gamma }_k(F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u},\mathbf{v}\left[k\right]))\hfill \\ & \le & {\parallel \mathbf{u}\left[0\right]-\mathbf{u}\parallel }^2-{\parallel \mathbf{u}[N+1]-\mathbf{u}\parallel }^2+8B^2{m}^3\sum _{k=0}^N{\gamma }_k^{2-a}\hfill \\ & & +\sum _{k=0}^N\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1\right)\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2\hfill \\ & & +{({\tau }_{max}+1)}^2\sum _{k=0}^N{\gamma }_k^a\sum _{i=1}^m{∥{\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]∥}^2\hfill \\ & \le & {\parallel \mathbf{u}\left[0\right]-\mathbf{u}\parallel }^2+8B^2{m}^3\sum _{k=0}^N{\gamma }_k^{2-a}\hfill \\ & & +\sum _{k=0}^N\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1+{\gamma }_k^a{({\tau }_{max}+1)}^2\right)\sum _{i=1}^m{\parallel {\mathbf{u}}_{i+1}\left[k\right]-{\mathbf{u}}_i\left[k\right]\parallel }^2.\hfill \end{array}$$

Now, the condition of the step-size sequence ${\left\{{\gamma }_k\right\}}_{k=0}^{\infty }$ implies that ${\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1+{\gamma }_k^a{({\tau }_{max}+1)}^2<0$ for all $k\ge 0$, and so

$$2\sum _{k=0}^N{\gamma }_k(F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u},\mathbf{v}\left[k\right]))\le {\parallel \mathbf{u}\left[0\right]-\mathbf{u}\parallel }^2+8B^2{m}^3\sum _{k=0}^N{\gamma }_k^{2-a},$$

implying that

$${\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-{\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u},\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}\le {\displaystyle \frac{{\parallel \mathbf{u}\left[0\right]-\mathbf{u}\parallel }^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}.$$

As a result of the concavity of the function $F(\mathbf{u},·)$, it follows that

$$F(\mathbf{u},\overline{\mathbf{v}}\left[N\right])\ge {\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u},\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}},$$

which means that the above inequality becomes

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F(\mathbf{u},\overline{\mathbf{v}}\left[N\right])& \le & {\displaystyle \frac{{\parallel \mathbf{u}\left[0\right]-\mathbf{u}\parallel }^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}\hfill \\ & \le & {\displaystyle \frac{D_{\mathcal{X}}^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}.\hfill \end{array}$$

(ii) Let $y\in \mathcal{Y}$ be given. By utilizing Lemma 2 (ii), we have that for all $k\ge 0$,

$$\begin{array}{ccc}\hfill 2{\gamma }_k(F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u}\left[k\right],\mathbf{v}))& \ge & {\parallel \mathbf{v}[k+1]-\mathbf{v}\parallel }^2-{\parallel \mathbf{v}\left[k\right]-\mathbf{v}\parallel }^2\hfill \\ & & -\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1\right)\sum _{i=1}^m{\parallel {\mathbf{v}}_{i+1}\left[k\right]-{\mathbf{v}}_i\left[k\right]\parallel }^2\hfill \\ & & -{\displaystyle \frac{{\gamma }_k^a}{m}}({\tau }_{max}+1)\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{v}[k-j+1]-\mathbf{v}[k-j]\parallel }^2\hfill \\ & & -8B^2{\gamma }_k^{2-a}{m}^3.\hfill \end{array}$$

We sum up the above inequality from $k=0$ to a fixed number $N\ge 0$ and we obtain that

$$\begin{array}{ccc}\hfill 2\sum _{k=0}^N{\gamma }_k(F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u}\left[k\right],\mathbf{v}))& \ge & {\parallel \mathbf{v}[N+1]-\mathbf{v}\parallel }^2-{\parallel \mathbf{v}\left[0\right]-\mathbf{v}\parallel }^2-8B^2{m}^3\sum _{k=0}^N{\gamma }_k^{2-a}\hfill \\ & & -\sum _{k=0}^N\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1\right)\sum _{i=1}^m{\parallel {\mathbf{v}}_{i+1}\left[k\right]-{\mathbf{v}}_i\left[k\right]\parallel }^2\hfill \\ & & -{\displaystyle \frac{({\tau }_{max}+1)}{m}}\sum _{k=0}^N{\gamma }_k^a\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{v}[k-j+1]-\mathbf{v}[k-j]\parallel }^2.\hfill \end{array}$$

(31)

In a similar technique to inequality (30), we also obtain

$$\sum _{k=0}^N{\gamma }_k^a\sum _{j=0}^{{\tau }_{max}}{\parallel \mathbf{v}[k-j+1]-\mathbf{v}[k-j]\parallel }^2\le m({\tau }_{max}+1)\sum _{k=0}^N{\gamma }_k^a\sum _{i=1}^m{\parallel {\mathbf{v}}_{i+1}\left[k\right]-{\mathbf{v}}_i\left[k\right]\parallel }^2.$$

Invoking this relation in inequality (31), we have

$$\begin{array}{ccc}\hfill 2\sum _{k=0}^N{\gamma }_k(F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u}\left[k\right],\mathbf{v}))& \ge & {\parallel \mathbf{v}[N+1]-\mathbf{v}\parallel }^2-{\parallel \mathbf{v}\left[0\right]-\mathbf{v}\parallel }^2-8B^2{m}^3\sum _{k=0}^N{\gamma }_k^{2-a}\hfill \\ & & -\sum _{k=0}^N\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1\right)\sum _{i=1}^m{\parallel {\mathbf{v}}_{i+1}\left[k\right]-{\mathbf{v}}_i\left[k\right]\parallel }^2\hfill \\ & & -{({\tau }_{max}+1)}^2\sum _{k=0}^N{\gamma }_k^a\sum _{i=1}^m{\parallel {\mathbf{v}}_{i+1}\left[k\right]-{\mathbf{v}}_i\left[k\right]\parallel }^2\hfill \\ & \ge & {-\parallel \mathbf{v}\left[0\right]-\mathbf{v}\parallel }^2-8B^2{m}^3\sum _{k=0}^N{\gamma }_k^{2-a}\hfill \\ & & -\sum _{k=0}^N\left({\displaystyle \frac{{\gamma }_k^a}{2m^2}}+{\gamma }_k^a-1+{\gamma }_k^a{({\tau }_{max}+1)}^2\right)\hfill \\ & & \sum _{i=1}^m{\parallel {\mathbf{v}}_{i+1}\left[k\right]-{\mathbf{v}}_i\left[k\right]\parallel }^2.\hfill \end{array}$$

Again, by applying the condition of the step-size sequence ${\left\{{\gamma }_k\right\}}_{k=0}^{\infty }$, we obtain

$$2\sum _{k=0}^N{\gamma }_k(F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])-F(\mathbf{u}\left[k\right],\mathbf{v}))\ge -{\parallel \mathbf{v}\left[0\right]-\mathbf{v}\parallel }^2-8B^2{m}^3\sum _{k=0}^N{\gamma }_k^{2-a},$$

and then

$${\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-{\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v})}{{\sum }_{k=0}^N{\gamma }_k}}\ge {\displaystyle \frac{{-\parallel \mathbf{v}\left[0\right]-\mathbf{v}\parallel }^2-8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}.$$

Furthermore, since we know that $F(·,\mathbf{v})$ is a convex function for a fixed $\mathbf{v}\in \mathcal{Y},$ we also have

$$F(\overline{\mathbf{u}}\left[N\right],\mathbf{v})\le {\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v})}{{\sum }_{k=0}^N{\gamma }_k}}.$$

Finally, we can conclude that

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F(\overline{\mathbf{u}}\left[N\right],\mathbf{v})& \ge & {\displaystyle \frac{{-\parallel \mathbf{v}\left[0\right]-\mathbf{v}\parallel }^2-8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}\hfill \\ & \ge & {\displaystyle \frac{-D_{\mathcal{Y}}^2-8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}},\hfill \end{array}$$

as desired. □

Theorem 4.

Let ${\left\{\mathbf{u}\left[k\right]\right\}}_{k=0}^{\infty }$ and ${\left\{\mathbf{v}\left[k\right]\right\}}_{k=0}^{\infty }$ be sequences generated by the IDSM, and $a\in (0,1)$ be a real number. Suppose that the step-size sequence ${\left\{{\gamma }_k\right\}}_{k=0}^{\infty }\subset \left(0,{\left({\displaystyle \frac{1}{\frac{1}{2m^2}+1+{({\tau }_{max}+1)}^2}}\right)}^{1/a}\right)$ is non-increasing and satisfies ${lim}_{k\to \infty }{\gamma }_k=0$ and ${\sum }_{k=0}^{\infty }{\gamma }_k=\infty$. Then, the averaged sequence of function values ${\left\{{\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}\right\}}_{k=0}^{\infty }$ and the sequence of function values of averaged iterates ${\left\{F(\overline{\mathbf{u}}\left[N\right],\overline{\mathbf{v}}\left[N\right])\right\}}_{N=0}^{\infty }$ both converge to $F^{*}$.

Proof. 

Let $\mathbf{u}={\mathbf{u}}^{*}$ and $\mathbf{v}={\mathbf{v}}^{*}$ in (27) and (28), respectively. We obtain that for all $N\ge 0$,

$${\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F\left({\mathbf{u}}^{*},\overline{\mathbf{v}}\left[N\right]\right)\le {\displaystyle \frac{D_{\mathcal{X}}^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}.$$

(32)

and

$${\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F(\overline{\mathbf{u}}\left[N\right],{\mathbf{v}}^{*})\ge {\displaystyle \frac{-D_{\mathcal{Y}}^2-8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}.$$

(33)

For all $N\ge 0$, since the sets $\mathcal{X}$ and $\mathcal{Y}$ are convex, we have that $\overline{\mathbf{u}}\left[N\right]\in \mathcal{X}$ and $\overline{\mathbf{v}}\left[N\right]\in \mathcal{Y}$. This, together with the saddle-point relation of $({\mathbf{u}}^{*},{\mathbf{v}}^{*})\in \mathcal{X}\times \mathcal{Y}$, implies that

$$F\left({\mathbf{u}}^{*},\overline{\mathbf{v}}\left[N\right]\right)\le F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\le F(\overline{\mathbf{u}}\left[N\right],{\mathbf{v}}^{*}).$$

(34)

Now, applying inequalities (32) and (33) with the saddle-point relation (34), we obtain that for all $N\ge 0$,

$${\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\le {\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F\left({\mathbf{u}}^{*},\overline{\mathbf{v}}\left[N\right]\right)\le {\displaystyle \frac{D_{\mathcal{X}}^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}},$$

and

$${\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\ge {\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F(\overline{\mathbf{u}}\left[N\right],{\mathbf{v}}^{*})\ge {\displaystyle \frac{-D_{\mathcal{Y}}^2-8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}.$$

Therefore, we have that for all $k\ge 0$,

$$-{\displaystyle \frac{D_{\mathcal{Y}}^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}\le {\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F({\mathbf{u}}^{*},{\mathbf{v}}^{*})\le {\displaystyle \frac{D_{\mathcal{X}}^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}.$$

(35)

Next, by the condition that ${\sum }_{k=0}^{\infty }{\gamma }_k=\infty$, we obtain

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}{\displaystyle \frac{D_{\mathcal{X}}^2}{2{\sum }_{k=0}^N{\gamma }_k}}=\underset{N\to \infty }{lim}{\displaystyle \frac{D_{\mathcal{Y}}^2}{2{\sum }_{k=0}^N{\gamma }_k}}=0.\end{array}$$

(36)

Since ${lim}_{k\to \infty }{\gamma }_k^{1-a}=0$, we have

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}{\displaystyle \frac{8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k\left({\gamma }_k^{1-a}\right)}{2{\sum }_{k=0}^N{\gamma }_k}}=0.\end{array}$$

(37)

By using these two results with inequality (35), we arrive at the conclusion that

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}{\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}=F^{*}.\end{array}$$

(38)

Again, by setting $\mathbf{u}=\overline{\mathbf{u}}\left[N\right]$ and $\mathbf{v}=\overline{\mathbf{v}}\left[N\right]$ in (27) and (28), respectively, we have that for all $N\ge 0$,

$$-{\displaystyle \frac{D_{\mathcal{Y}}^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}}\le {\displaystyle \frac{{\sum }_{k=0}^N{\gamma }_{k}F(\mathbf{u}\left[k\right],\mathbf{v}\left[k\right])}{{\sum }_{k=0}^N{\gamma }_k}}-F\left(\overline{\mathbf{u}}\left[N\right],\overline{\mathbf{v}}\left[N\right]\right)\le {\displaystyle \frac{D_{\mathcal{X}}^2+8B^2{m}^3{\sum }_{k=0}^N{\gamma }_k^{2-a}}{2{\sum }_{k=0}^N{\gamma }_k}},$$

Combining this with inequalities (36)–(38), it becomes

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}F\left(\overline{\mathbf{u}}\left[N\right],\overline{\mathbf{v}}\left[N\right]\right)=F^{*},\end{array}$$

as desired. □

4. Numerical Examples

In this section, we consider the numerical examples of the proposed method (IDSM) for solving the distributed matrix game problem of the following form:

$${\displaystyle \underset{\mathbf{u}\in {\Delta }_p}{min}\underset{\mathbf{v}\in {\Delta }_r}{max}\sum _{i=1}^m{F}_i(\mathbf{u},\mathbf{v}),}$$

where the constrained sets ${\Delta }_p\subset {\mathbb{R}}^p$ and ${\Delta }_r\subset {\mathbb{R}}^r$ are standard simplices in ${\mathbb{R}}^p$ and ${\mathbb{R}}^r$, respectively, and the component coupling function $F_i:{\mathbb{R}}^p\times {\mathbb{R}}^r\to \mathbb{R}$ for each $i=1,\cdots ,m$ is given by

$${\displaystyle F_i(\mathbf{u},\mathbf{v})=⟨\mathbf{u},{\mathbf{A}}_i\mathbf{v}⟩+\frac{1}{2}{\parallel \mathbf{u}\parallel }^2-\frac{1}{2}{∥\mathbf{v}-\frac{1}{m}{\mathbf{1}}_r∥}^2,}$$

where ${\mathbf{1}}_r$ is the vector in ${\mathbb{R}}^r$, all of whose components are 1. We generated $p\times r$ matrices ${\mathbf{A}}_i$ for each $i=1,\dots ,m$ randomly, where its entries were independently and uniformly distributed in the interval $(-10,10)$. We compared the IDSM with the existing methods NO-09 and AN-23. We set the delay sequences with the cyclic order delays ${\tau }_i^k={\mu }_i^k=kmod({\tau }_{max}+1)$ for all $k\ge 0$ and $i=1,\dots ,m$, with the delay bounds ${\tau }_{max}=0,5$, and 10 for both the IDSM and AN-23. We set the step-size constant as ${\left({\displaystyle \frac{1}{2+{(\tau +1)}^2}}\right)}^{1/0.99}$ for the IDSM and ${\left({\displaystyle \frac{2}{1+2{(\tau +1)}^2}}\right)}^{1/0.99}$ for AN-23 and NO-09. We performed 100 independent random tests and terminated all tested methods when the number of iterations reached 100. We examined the considered problem in various problem sizes $p\times r$, as detailed below.

4.1. The Case $p=10$

In Figure 1a–c, we consider the behavior of the average of 100 independently sampled function values with a fixed $p=10$. We observed that for all values r, all methods tended to converge to the saddle values.

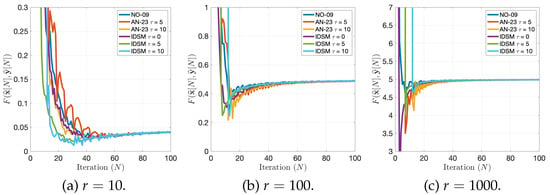
Figure 1. Behaviors of the average of 100 independent values $F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])$ performed by NO-09, AN-23, and the IDSM for the cases $p=10$ and $r=10,100$, and 1000.

According to Figure 2, which shows the behaviors of the relative errors of the function value for each problem size, we noticed that the IDSM with an appropriate delay bound selection, particularly for a fixed delay bound of $\tau =10$, provided the most accurate results with the lowest relative error across all sizes. Additionally, for fixed delay bounds of $\tau =5$ and $\tau =0$, it still exhibited lower relative error values when compared with the AN-23 and NO-09 methods.

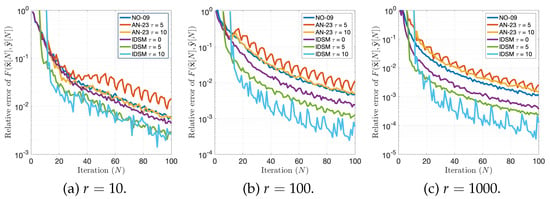
Figure 2. Behaviors of the average of 100 independent relative errors of values $F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])$ performed by NO-09, AN-23, and the IDSM for the cases $p=10$ and $r=10,100$, and 1000.

4.2. The Case $p=100$

It can be observed from Figure 3 that for all values r, all methods tended to converge to the saddle values.

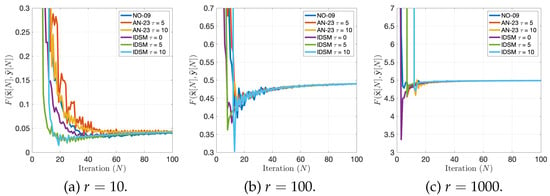
Figure 3. Behaviors of the average of 100 independent values $F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])$ performed by NO-09, AN-23, and the IDSM for the cases $p=100$ and $r=10,100$, and 1000.

In Figure 4, we observed that when $r=10$, the relative error with a fixed delay bound of $\tau =10$ for the IDSM exhibited the lowest relative error values. In contrast, for $r=100$ and $r=1000$, the IDSM with a fixed delay bound of $\tau =5$ provided the most accurate results, showing the lowest relative error. Moreover, we found that the IDSM, in the case of fixed delay bounds, gave lower relative errors than both the AN-23 and NO-09 methods under the same fixed delay bounds.

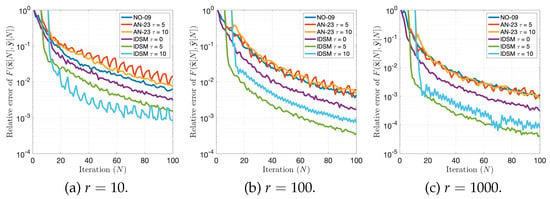
Figure 4. Behaviors of the average of 100 independent relative errors of values $F(\widehat{\mathbf{u}}\left[N\right],\widehat{\mathbf{v}}\left[N\right])$ performed by NO-09, AN-23, and the IDSM for the cases $p=100$ and $r=10,100$, and 1000.

5. Conclusions

In this work, we introduce the so-called incremental delayed subgradient method (in short, IDSM) to solve the saddle-point problem. We characterize the relations associated with the IDSM for use in the next crucial theorem. Moreover, we prove the convergence results, which are divided into two parts. In the part concerning the constant step size, we provide an upper bound for the absolute value of the difference between the function value of the averaged iterates and the saddle value. We also derive the complexity upper bound within a fixed time length. For the case of the diminishing step-size sequence, we prove the convergence results by demonstrating the convergences of both the averaged sequence of function values and the sequence of function values of averaged iterates to the saddle value. We finally showed numerical examples for matrix game problems. Even if the IDSM with delay effects yielded a better convergence behavior than those of NO-09 and AN-23, we noticed that the selection of appropriate delay bounds for some particular problems will be an interesting research direction.