Abstract
Mobile robots are increasingly integral to diverse applications, with path-planning algorithms being essential for efficient and secure mobile robot navigation. Mobile robot path planning is defined as the design of the least time-consuming, shortest-distance, and most collision-free path from the starting point to the endpoint for the mobile robot’s autonomous movement. This study investigates and assesses two widely used algorithms in artificial intelligence (AI)—Improved Particle Swarm Optimization (IPSO) and Improved Genetic Algorithm (IGA)—for path planning of mobile robot navigation problems. In this work Manhattan movements are proposed as a distance formula to modify both algorithms in the path planning of the mobile robot navigation problem. Unlike the traditional GA and PSO, which can use horizontal search, the proposed algorithm relies on vertical search, which gives us an advantage. The results demonstrate the effectiveness of these modified algorithms in barrier detection and obstacle avoidance. Six different experiments were run using both improved algorithms to show their ability to achieve their goal and avoid obstacles in various scenarios with different complexities. Across various scenarios, the tested AI algorithms performed effectively, regardless of the map scale and complexity. This paper proposes a complete comparison between the two improved algorithms in different scenarios. The results show that the algorithms’ performance is influenced more by the density of walls and obstacles than by the size or complexity of the map.
1. Introduction
The field of robotics has garnered significant attention in both the research and industrial domains, with applications in manufacturing, medicine, service provision, exploration, and transportation. However, future robotic systems require enhanced autonomy and intelligence. Mobile robots are a type of robot that can perform specific tasks independently in complex environments and do not depend on human guidance. Autonomous navigation of mobile robots is essential across various industries [1], including mining [2], military operations [3], rescue missions [4], space exploration [5], agriculture [6], and entertainment [7]. Path planning is a critical part of a mobile robot system that bridges the robot’s information perception and motion control. Path planning involves finding the shortest and safest path [8] from the initial point to a designated destination, taking into account factors such as distance, time, energy efficiency [9,10], safety, and the smoothness of the journey. Algorithms for path planning can be categorized as online or offline, depending on the availability of data to the robot. Offline planning relies on pre-existing information, while online planning utilizes real-time sensor data to assess the robot’s environment. Path-searching methodologies [11] are employed to identify optimal routes based on environmental modeling and optimization objectives. Earlier path-planning approaches [12] largely focused on distance minimization, whereas more recent research has begun to incorporate safety, robustness, and continuity. Safety constraints are critical for both the robot and its environment. However, pursuing smoother trajectories can lead to increased resource utilization and extended execution times. This study conducted multifaceted experiments using complex designs to evaluate the efficacy of motion-planning algorithms in diverse settings. Our experiments utilized a grid map as the foundational framework, consisting of intersecting horizontal and vertical lines to pinpoint locations. This map, derived from sensor measurements, assumes a known robot pose. For simplicity, our experiments assumed a known map without uncertainty, employing grid maps as a straightforward representation. The experimental setup emulated the operating environment of Automated Guided Vehicles (AGVs) [13] by defining a fixed dimension for the occupancy map (30 × 40). Each iteration specified coordinates for the starting point and destination, simulating the AGV’s operational terrain with a grid map filled with obstacles. We employed eight distinct grid maps of increasing complexity, characterized by varying obstacle densities. This paper emphasizes the importance of selecting appropriate path parameters, such as the Manhattan distance. The distance and time taken to transport a robot from the starting point to the ending position are considered in determining the optimal route. Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO) are utilized to account for these factors and select the best course of action. This research presents a novel and unique contribution to the field of path planning by introducing improved versions of two well-established metaheuristic algorithms: Particle Swarm Optimization (PSO) and the Genetic Algorithm (GA). Unlike conventional implementations found in the literature, the improvements proposed in this study aim to overcome known limitations such as premature convergence, local minima entrapment, and slow adaptation to dynamic environments. To the best of the authors’ knowledge, no previous work has proposed or directly compared these specific improved variants under controlled, grid-based conditions using Manhattan movement. The significance of this work lies in its dual impact—scientifically, it advances the optimization capabilities of PSO and GA in constrained environments; and practically, it opens up new possibilities for real-world applications such as autonomous robotics, smart logistics, and intelligent transportation systems. The proposed improvements were carefully tested and validated against benchmark scenarios to demonstrate their effectiveness and potential for real-time deployment.
The organization of this paper is as follows: Section 2 gives a detailed background on all of the technical aspects used in this research. Section 3 provides a literature survey on different research articles on the path planning problem for mobile robots. Section 4 introduces the main methodology of the proposed work. Section 5 presents the experiments and results. Section 6 shows the additional experiments performed in this research in more detail, so as to draw more conclusions from the research. Finally, Section 7 concludes the article and discusses future directions in this field of research.
2. Background
2.1. Types of Distance Formula
Different types of distance formula are employed in this study, including Euclidean distance, Hamming range, Manhattan distance, Chebyshev distance, and Minkowski distance. The focus is on the Manhattan distance.
In this study, Manhattan movements—restricting motion to the four cardinal directions (up, down, left, and right)—were adopted as the basis for path planning. This decision was made for several key reasons. Firstly, it simplifies the search space, allowing for clearer and more consistent comparisons between informed and uninformed algorithms. Many real-world applications, such as grid-based robotic navigation, warehouse automation, and 2D game environments, naturally follow this movement model. Secondly, the Manhattan movement aligns seamlessly with the Manhattan distance heuristic, which is both admissible and consistent in such settings, making it ideal for evaluating heuristic-based algorithms like A*. By limiting the movement options, the contrast in efficiency, optimality, and search behavior between algorithms such as Dijkstra’s (uninformed) and A* or Greedy Best First Search (informed) becomes more pronounced and measurable. Finally, the use of Manhattan movements allows for intuitive visualizations and simplifies performance analysis, especially in environments with obstacles, where diagonal shortcuts are often unrealistic. This modeling choice enhances the experimental clarity and strengthens the reliability of the comparative results presented here.
2.2. Basics of Manhattan Distance
Manhattan distance, also known as the L1 norm or L1 metric, was first conceptualized by Hermann Minkowski and has since found widespread application in diverse fields like regression analysis and frequency distribution. Manhattan distance exhibits several key characteristics:
- Multiple finite paths exist between two points, each with a length equal to the Manhattan distance.
- Two steps can be taken along a straight line of the exact length of the Manhattan distance.
- Movement is constrained to one horizontal direction.
- The other point lies within a square at a specific Manhattan distance.
Directions: Manhattan distance utilizes four primary directions, as shown in Figure 1 (right), while diagonal distance incorporates eight directions, as shown in Figure 1 (left). As shown in Figure 2, algorithms are modified to pass through any dimensions rather than being limited to specific directions. When applying Manhattan movement from point (S) to point (G), six scenarios—(a–f)—arise, each with identical step counts and costs. However, the calculations differ due to rotation incurring higher costs than forward movement. Only two paths, (a) and (b), achieve the best path with minimal rotation, while the other four paths, (c–f), add additional costs. Path planning begins by selecting parameters such as the angle of motion, distance, and heading. Two types of path parameters are distinguished: the four directions of motion shown in Figure 1 (left), and eight directions for Figure 1 (right). Optimizing the path involves considering both distance and time metrics to determine the most efficient route.
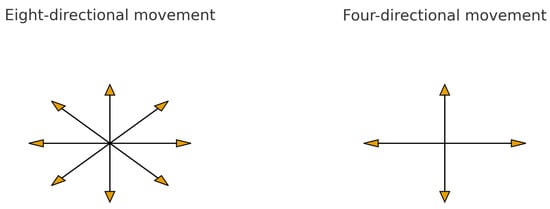
Figure 1.
Different directions of Manhattan distance.
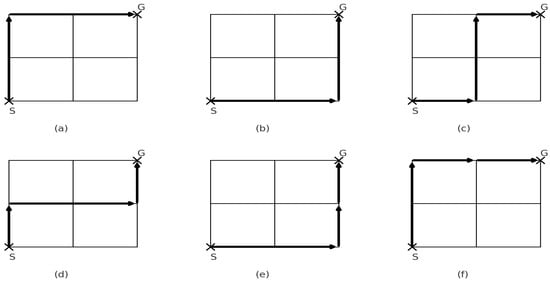
Figure 2.
Different ways to reach from point to point using Manhattan movement. (a–f) subfigures show different ways to reach the goal from starting point.
2.3. Artificial Intelligence Algorithms
In this work, modified Genetic Algorithms and Particle Swarm Optimization algorithms are examined and compared for the path-planning problem of mobile robots. In this section, the needed background information about the two algorithms and how they are applied in the path-planning problem is introduced.
2.3.1. Genetic Algorithm
The Genetic Algorithm (GA), conceptualized by John Holland and colleagues in the 1970s, integrates principles of “survival of the fittest”, “random search”, and “parallel evaluation” to form resilient stochastic search algorithms [14]. The GA manipulates a set of alternatives to solve problems, where each alternative represents a unique sequence of binary values, characters, or numbers constituting a chromosome. The fitness score of each chromosome indicates its performance relative to others in the population. The GA begins with a random pool of chromosomes, employing genetic operators like crossover and mutation to generate novel chromosomes. Parental chromosomes, selected based on fitness, produce progeny, which completely replace the previous generation at each generational iteration. Over time, the population evolves to improve its solution to the problem. Proposed Algorithm: The preparatory steps for defining the path-planning problem in a form suitable for a GA include the following:
- (a)
- Using a grid map to represent the search environment.
- (b)
- Selecting only necessary nodes on the grid map for the robot’s navigation.
- (c)
- Assigning each location on the grid map a corresponding identifier.
- (d)
- Identifying the number of static obstacles in the search area.
- (e)
- Determining the critical path if the source and destination nodes are known.
- (f)
- Tuning the hyperparameters of the GA.
Algorithm 1 shows the complet steps of the proposed improved GA algorithm.
| Algorithm 1: Improved Genetic Algorithm (IGA) for robot path planning |
 |
2.3.2. Particle Swarm Optimization
Particle Swarm Optimization (PSO) is a population-based optimization algorithm inspired by the behavior of a bird flock or a fish school. The algorithm was first introduced by James Kennedy and Russ Eberhart in 1995 [15]. This algorithm is designed to solve complex optimization problems by simulating the intelligence found in groups of animals (e.g., birds, fish) found in nature. In PSO, particles (potential solutions) move through the search space influenced by their own best-known position and the best-known positions of the neighboring particles. Each particle adjusts its velocity and position depending on its own experience and the experience of the group (called a swarm). After a number of iterations, this cooperation allows the swarm to reach optimal solutions.
The algorithm is known for its simplicity and computational efficiency. PSO has been successfully applied to a wide range of optimization problems, including biomedical engineering [16], wind farm layout [17], and disease prediction [18].
In [19], the authors proposed an approach for modeling the mobile path-planning problem as a PSO problem. In a network-based model featuring a mobile robot environment, immobile obstacles are represented in a two-dimensional square grid. The route’s uniqueness is depicted through the variability of each cell. The swarm size, defined by the swarm X and swarm Y axes, indicates the number of intermediate nodes that the swarm must traverse to reach its destination. Multiple iterations reflect the number of attempts that the particle swarm makes to select the optimal value, considering barriers along the path. The robot’s working area encompasses starting and ending points, with coordinates determining potential barriers. Each possible location undergoes evaluation to identify potential barriers, with replacement points selected based on the best fit. The total distance traveled by the robot between the starting and ending points is determined iteratively, with comparisons made to identify the optimal location globally. Particle movement is guided by calculating velocity in two dimensions (X and Y) and updating the positions accordingly. The process iterates until the optimal global position aligns with the desired location, concluding with the presentation of the optimal solution.
Proposed Algorithm: The preparatory steps for defining the path-planning problem in a form suitable for PSO include the following:
- Particle Starting Point: Marks the initial phase of the particle trajectory, with positions and velocities initially generated randomly within search boundaries.
- Checking for Obstacles: Particles evaluate potential obstructions in the pursuit space, updating positions based on conditional statements.
- Evaluating Fitness Function: Particle fitness is assessed based on spatial incorporation and problem parameters.
- Finding the Best Global Particle Location: Each particle’s optimal position is determined by averaging distance appreciation over known regions.
- Calculating New Velocity and Position: Particle positions and velocities are updated iteratively to seek the best solution.
- Checking and Modifying Infeasible Paths: Conditional statements determine the feasibility of paths, allowing for adjustments if obstacles are encountered.
- Modification of Path-Planning Algorithm: This study focuses on modifying the PSO algorithm to move as Manhattan movements, ensuring efficient movement with minimal rotation. The research compares and evaluates various algorithms across different maps with varying obstacle densities to achieve successful path planning.
Algorithm 2 shows the improved PSO algorithm.
| Algorithm 2: Manhattan-based PSO (IPSO) for robot path planning |
 |
In the proposed IPSO, the correction by Manhattan distance is not an algebraic modification of the velocity equation but, rather, a discretization process that enforces the robot’s movement constraints.
In the standard Particle Swarm Optimization (PSO), the velocity and position of each particle are updated according to
where and denote the velocity and position of particle i at iteration t, respectively; is the inertia weight; and are the cognitive and social acceleration coefficients, respectively; and are random values in ; is the personal best position of particle i; and g is the global best position among all particles.
For grid-based path planning, continuous motion is unsuitable because the robot moves in discrete grid cells. Therefore, in the proposed Improved PSO (IPSO), the conventional Euclidean movement is replaced with grid-constrained motion using the Manhattan distance:
which restricts the motion to the four orthogonal directions only (up, down, left and right).
The corresponding implementation is
- vq = sign(v_i);
- step = min(abs(v_i), D_man(x_i, g));
- x_new = x_old + vq .* step;
This modification enables PSO to operate effectively in a discrete search space and ensures that each particle generates feasible, collision-free paths.
3. Literature Survey
Path planning for mobile robots has been an active area of research for the past several years. Various algorithms and techniques have been proposed to address the challenge of efficient and secure navigation. In this section, a literature review is provided that examines the key developments and advancements in this area, with a focus on the utilization of Improved Particle Swarm Optimization (IPSO) and Improved Genetic Algorithms (IGAs) for path planning.
Particle Swarm Optimization has become a widely used algorithm for path planning in mobile robot navigation tasks. PSO is inspired by the social behavior of bird flocks, where individuals adjust adjust their positions based on their own experiences and the experiences of their neighbors [19]. Several studies have explored the application of the PSO algorithm for mobile robot path planning, investigating its ability to find optimal or near-optimal paths while considering certain constraints (such as obstacles) and minimizing energy requirements [20]. In [21], an Improved Particle Swarm Optimization (PSO) algorithm is proposed to solve the local trapping and premature convergence challenges. In this modified PSO, an adaptive fractional-order velocity is introduced to enforce some disturbances on the particle swarm. This modification enhances its capability of jumping out of local minima and exploring the search space more effectively. The GA has also been widely employed for mobile robot path planning, demonstrating its effectiveness in finding feasible and optimal paths in complex environments [22,23]. Researchers have proposed various modifications and hybridization to enhance the performance of both algorithms. Jawad and Hadi [24] introduced a comparative study of intelligent algorithms, including modified versions of PSO and GAs, for mobile robot path planning. Their results showed that the modified algorithms were capable of effectively navigating complex environments and avoiding obstacles. Raja and Pugazhenthi [25] conducted a review of optimal path-planning techniques for mobile robots, highlighting the potential of PSO and GAs in addressing the challenge. They emphasized the importance of considering factors such as distance, time, and energy efficiency in the path-planning process. Rafai, Adzhar, and Jaini [26] presented a comprehensive review on path planning and obstacle avoidance algorithms for autonomous mobile robots, including a discussion on the applications of PSO and GAs. They underscored the need for robust and adaptable path-planning algorithms to handle the complexities of real-world environments. Another recent research direction in this area is multi-robot path navigation. Unlike single-robot path planning, where the primary objective is to find the optimal path from a start point to a goal, MRPP must address additional challenges arising from the interactions among multiple robots. In [27], the authors propose using multi-objective Particle Swarm Optimization for multi-robot path planning. The authors introduce a new method called Multi-Robot Particle Swarm Optimization (MPSO). In this method the robot decides the movement direction based on information gathered from sensors only. In [28], the authors propose using a Genetic Algorithm for a multi-robot path-planning application. In this work, a global map for the environment is first created using the SLAM algorithm. The problem after that is formed as a multiple traveling salesman problem with a Genetic Algorithm to solve. The literature also showcases the integration of AI techniques with other approaches, such as the use of Manhattan distance and grid-based representations, to improve the efficiency and effectiveness of path planning. For instance, Liu et al. [29] conducted a review on path-planning techniques for mobile robots, highlighting the potential of incorporating Manhattan distance and grid-based models to enhance the performance of AI-based algorithms. The integration of these AI techniques with other methodologies, such as Manhattan distance and grid-based representations, has shown promising results in navigating complex environments and achieving efficient and secure navigation for autonomous mobile robots. Overall, there are major limitations in the literature, including that PSO research articles suffer from premature convergence and poor obstacle avoidance. On the other hand, the regular GA has a high computation time. This justifies the motivation and need for Improved Particle Swarm Optimization (IPSO) and Improved Genetic Algorithms (IGAs) in addressing the challenges of mobile robot path planning.
4. Methodology
Operating Environment
This study simplifies the use of grid maps by representing a network of vertical and horizontal lines to identify points at certain locations. The experimental setup simulates the operating environment of an Automated Guided Vehicle (AGV) by establishing a dimension for the map of (30 × 40). The maps include a starting location, a destination, and obstacles of varying complexity. The experiments involve eight occupancy version maps, as shown in Figure 3, which are used to test the algorithms’ ability to find paths from the start to the endpoint while avoiding obstacles.
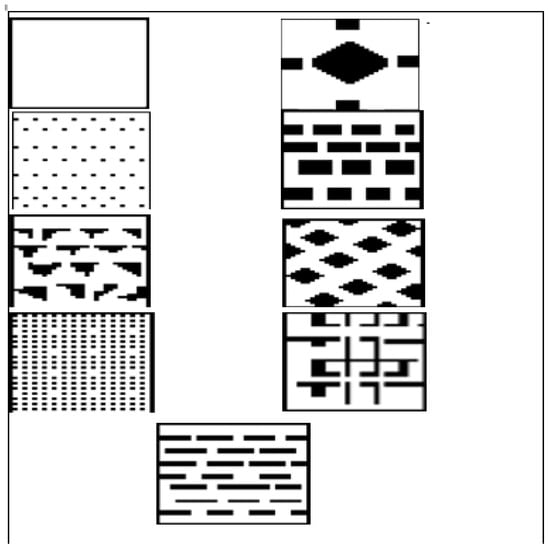
Figure 3.
Eight different environments used in experimental simulations.
5. Experiments and Results
Nine different experiments were conducted, wherein both Particle Swarm Optimization (PSO) and the Genetic Algorithm (GA) were modified to mimic Manhattan movements. Processing time gains, path length, cost, violation, and iteration counts were computed for the IPSO and IGA. Table 1 outlines the defined parameters representing the proposed algorithms. Furthermore, the working area in algorithm variables was transformed into a maze of search challenges, with obstacles represented by black squares on the graph. Purple circles denoted the starting point, green circles the target point, blue circles the pivots, and green lines the path length, as exemplified in Figure 4. The algorithms were optimized to find the shortest feasible route for the robot without encountering obstacles. The combination of IPSO and IGA enabled the robots to navigate previously challenging terrain efficiently and successfully.

Table 1.
Fixed parameters for all subsequent experiments.
5.1. Experiment Zero [20]
The purpose of this experiment was to show that traditional AI methods like A* and Dijkstra can solve path-planning problems. However, the remaining experiments concentrated on metaheuristic algorithms. Figure 4 shows the results of four experiments for this experiment, along with a grid background for the user to understand the mobile robots’ movements.
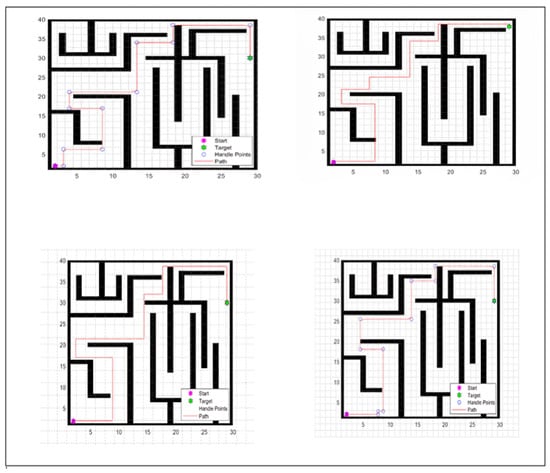
Figure 4.
Four results of experiment zero.
5.2. Experiment One
In the initial experiment, both the IPSO and IGA began with fixed points for the initial and target points. The number of pivots chosen was based on the anticipated rotations necessary to reach the goal. For instance, if only one pivot was chosen, both algorithms would fail to reach the goal point, as the number of pivots needs to match or exceed the number of obstacles (which is four) to avoid all obstacles and reach the goal. Table 2 outlines the parameters for IPSO, starting with a population size of ten and identical values for c1 and c2. Other parameters remained constant across all experiments. Table 3 summarizes the parameters utilized in the IGA during the initial experiment, along with the corresponding results. Table 4 shows the relationship between the pivot number and success rate.

Table 2.
IPSO’s initial parameters in the first experiment.

Table 3.
GA parameters and results in the first experiment.

Table 4.
PSO’s relationship between pivot numbers and successful runs in the first experiment.
A correlation was observed between the difficulty level and the number of turns required to navigate each obstacle. Additionally, the number of successful attempts to reach the target point was correlated with the number of pivots used.
Both the IPSO and IGA successfully reached the goal point with four pivots chosen. All results for both algorithms achieved successful runs for the specified parameters. Figure 5 illustrate successful operations during the first experiment.
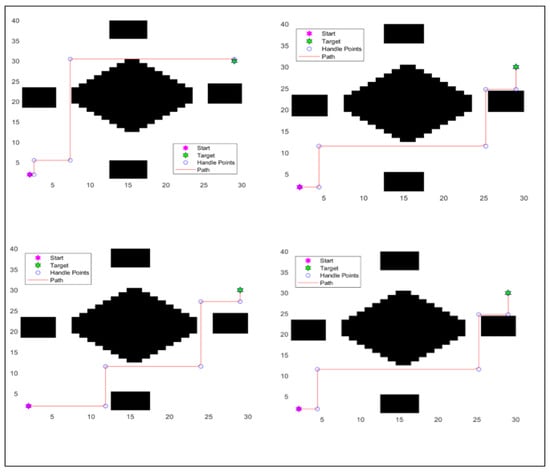
Figure 5.
First experiment’s results across multiple runs.
5.3. Experiment Two
In the second experiment, when the same parameters as in the first experiment were applied, the number of successful runs decreased to 3–4 out of 100 runs (4%). This prompted an investigation into the relationships between parameters to enhance the success rate. Table 5 shows the relationship between the number of populations and the number of pivots for IPSO. Experimentation with different pivot numbers revealed that the maximum number of successful runs occurred with ten pivots. Table 6 shows the results of particle swarm optimization for the second experiment. The relation between the pivot number and successful runs can be clearly noticed from these results. Table 7 shows the parameters of the Genetic Algorithm for the second experiment.

Table 5.
Relation between the number of population and number of pivots.

Table 6.
Results of Particle Swarm Optimization for the second experiment and relation between the number of pivots and successful runs.

Table 7.
Genetic Algorithm parameters for the second experiment.
Table 6 shows results of Improved PSO for second experiment and shows the relation between the number of pivots and successful runs.
Figure 6 shows the second experiment’s results across multiple runs.
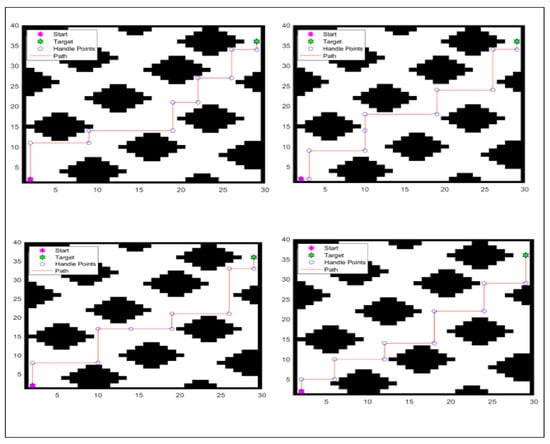
Figure 6.
Second experiment’s results across multiple runs.
5.4. Experiment Three
As shown in the first and second experiments, satisfactory results were not achieved with shared parameter values. Therefore, different settings for c1 and c2 were tested to improve the results. Table 8 and Table 9 outline the parameters and results for the IPSO and IGA in the third experiment. The minimum number of pivots required for success was determined to be eight. Figure 7 shows the results of third experiment.

Table 8.
PSO’s initial parameters in the third experiment.

Table 9.
GA parameters and results in the third experiment.

Figure 7.
Third experiment’s results across multiple runs.
6. Additional Experiments (Experiments Four to Eight)
In all of the remaining experiments, parameters similar to those of the previous experiments were applied. The population size was increased to 100 to enhance the success rates. Table 10 displays the parameters and results for IPSO in the fourth experiment, with the minimum number of pivots required being eight. Figure 8 showcase samples of successful operations during the fourth experiment.

Table 10.
Fourth experiment’s results.

Figure 8.
Fourth experiment’s results across multiple runs.
Figure 9 shows the Fifth experiemt’s results.
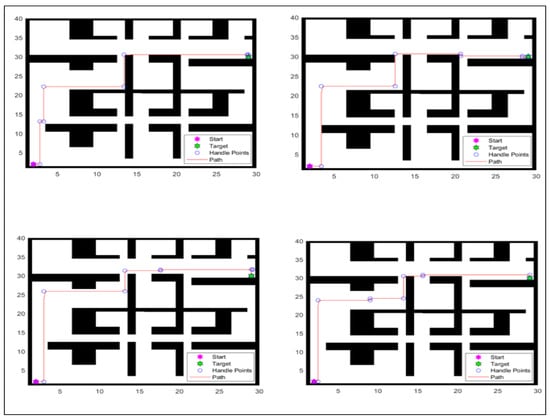
Figure 9.
Fifth experiment’s results across multiple runs.
Figure 10 shows the Sixth experiment’s results.
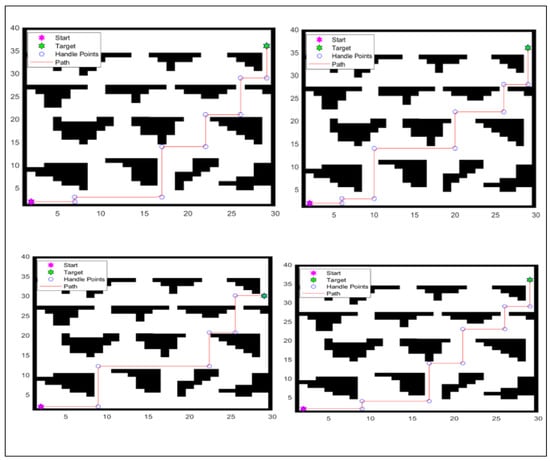
Figure 10.
Sixth experiment’s results across multiple runs.
Figure 11 shows the seventh experiement’s results across multiple runs.
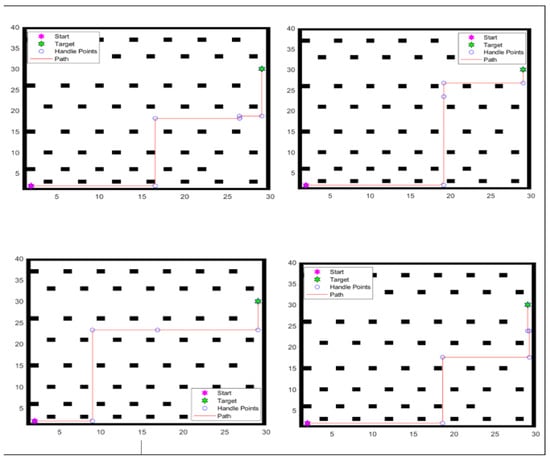
Figure 11.
Seventh experiment’s results across multiple runs.
Figure 12 shows the Eighth Experiment’s results across mutiple runs.
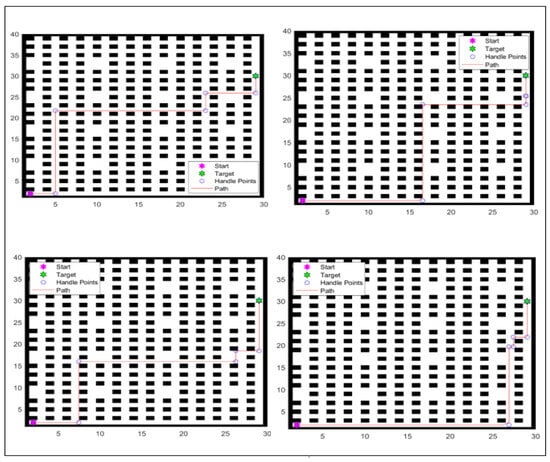
Figure 12.
Eighth experiment’s results across multiple runs.
6.1. Fourth Experiment’s Results
Observation: The number of successful runs is zero when four pivots are used, and the success rate increases as the number of pivots increases.
Minimum Number of Pivots: The minimum number of pivots required for this experiment to achieve a reasonable success rate is eight pivots. For fewer pivots (e.g., four or six), the success rate significantly drops.
Trend: As the number of pivots increases, the success rate improves, and at ten pivots, all runs are successful.
6.2. Fifth Experiment’s Results
Table 11 shows the results of the fifth experiment.

Table 11.
Fifth experiment’s Particle Swarm Optimization results.
Table 12 shows the Eighth experiments’ PSO results with different numbers of pivots.

Table 12.
Sixth–Eighth experiments’ PSO results with different numbers of pivots.
7. Conclusions and Future Work
Path planning is crucial for ensuring safe and optimal routes. This study explored the effectiveness of Improved Particle Swarm Optimization (IPSO) and Improved Genetic Algorithms (IGAs) in barrier detection for autonomous mobile robot navigation. This study employed multifaceted experiments to evaluate the efficacy of motion-planning algorithms across diverse settings. Path-planning methods including map representation using various distance formulae were employed, with a focus on Manhattan distance. Improved Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO) were utilized to optimize the paths, considering distance and time metrics. The proposed algorithm for path planning in a network-based model featuring a mobile robot environment involves using a grid map, selecting only necessary nodes, assigning each location a corresponding identifier, identifying static obstacles, and determining the critical path. The robot’s working area encompasses starting and ending points, with coordinates determining potential barriers. The combination of IPSO and IGA enabled the robots to navigate previously challenging terrain efficiently and successfully. This study proposes a cost-effective strategy for achieving collision-free step planning for mobile robots, demonstrating consistent performance regardless of map scale. The results prove the ability of the proposed algorithms (IGA and IPSO) for efficient path planning of mobile robots in different scenarios with different complexities. This study also reports the optimal hyperparameters for both algorithms to achieve effective path planning. Finally, this study contributes valuable insights into the optimization of navigation strategies for mobile robots, offering a foundation for developing more sophisticated and effective path-planning algorithms that can address the complexities of real-world environments. This research has some limitations, as the scope of the research was limited to proving the superior performance of the proposed modifications. However, further testing could enhance this work and enable statistical testing. Future work may involve further testing and statistical testing, leveraging AI, modern mathematics, and bio-mimetic algorithms to create more efficient algorithms. The computational cost of AI algorithms depends on factors like pivot number, population size, and map complexity. The modifications aim to enhance their ability to solve complex maps.
Author Contributions
Conceptualization, M.A. and A.B.; methodology, M.A., A.I. and H.R.; software, M.A. and A.Y.; validation, M.A., H.R. and A.I.; formal analysis, M.A., A.B. and H.R.; investigation, M.A. and A.Y.; resources, M.A. and H.R.; data curation, M.A. and A.Y.; writing—original draft preparation, M.A., H.R. and A.I.; writing—review and editing, A.Y. and H.R.; visualization, A.I. and H.R; supervision, A.B., H.R. and A.I.; project administration, A.B., M.A., A.I. and H.R.; funding acquisition, M.A. and A.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
There was no dataset needed for this project.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| MPSO | Manhattan-Based Particle Swarm Optimization |
| MGA | Manhattan-Based Genetic Algorithm |
| MRPP | Mobile Robot Path Planning |
| AMR | Autonomous Mobile Robot |
| AGV | Automated Guided Vehicle |
| SLAM | Simultaneous Localization and Mapping |
| Manhattan Distance Metric | |
| Number of Pivot Nodes in the Planned Path | |
| Mutation Rate | |
| Inertia Weight (PSO Parameter) | |
| Cognitive and Social Acceleration Constants | |
| Objective (Cost) Function for a Candidate Path | |
| Collision and Penalty Weight Coefficients | |
| SD | Standard Deviation |
| CI | Confidence Interval |
References
- Marques, B.; Junqueira, G.; Alves, J.; Pedrosa, E. Mobile Robots Meet Augmented Reality Technologies: Transforming Human-Robot Interaction in Industry 4.0 Scenarios. In Proceedings of the Companion of the 2024 ACM/IEEE International Conference on Human-Robot Interaction, Boulder, CO, USA, 11–15 March 2024; pp. 740–744. [Google Scholar]
- Pachayapan, K.; Abdulsalam, I.; Subramanian, S.; Sudhakaran, S.; Suresh, Y. Gas detecting robot for mining operations. In Proceedings of the AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2024; Volume 3042. [Google Scholar]
- Kurniawan, J.; Syafaat, M.; Kasiyanto, K.; Widiatmoko, D.; Maulana, R.; Putra, Z.N. Omni wheel robot movement exploration using a control system for military surveillance with integrated sensor. TEKNOSAINS J. Sains Teknol. Inform. 2025, 12, 110–121. [Google Scholar] [CrossRef]
- Schwaiger, S.; Muster, L.; Novotny, G.; Schebek, M.; Wöber, W.; Thalhammer, S.; Böhm, C. Semi-Autonomous Mobile Search and Rescue Robot for Radiation Disaster Scenarios. arXiv 2024, arXiv:2406.14385. [Google Scholar] [CrossRef]
- Wang, M.; Cong, M.; Du, Y.; Zhong, H.; Liu, D. Bio-inspired mobile robot design and autonomous exploration strategy for underground special space. Robot. Intell. Autom. 2024, 44, 382–393. [Google Scholar] [CrossRef]
- Huang, A.; Kim, W.Y.; Chen, T.; Jang, J.; Lee, K.H. Pitch Angle Control of the Self-Balancing Cargo Platform in an Agricultural Mobile Robot Using a 3-RPS Parallel Mechanism. Precis. Agric. Sci. Technol. 2024, 6, 151–164. [Google Scholar]
- Lyu, H. Entertainment robot simulation in interactive art process based on deep learning algorithms and gesture recognition. Entertain. Comput. 2025, 52, 100827. [Google Scholar] [CrossRef]
- Abdallaoui, S.; Aglzim, E.H.; Chaibet, A.; Kribèche, A. Thorough review analysis of safe control of autonomous vehicles: Path planning and navigation techniques. Energies 2022, 15, 1358. [Google Scholar] [CrossRef]
- Farooq, M.U.; Eizad, A.; Bae, H.K. Power solutions for autonomous mobile robots: A survey. Robot. Auton. Syst. 2023, 159, 104285. [Google Scholar] [CrossRef]
- Soori, M.; Arezoo, B.; Dastres, R. Optimization of energy consumption in industrial robots, a review. Cogn. Robot. 2023, 3, 142–157. [Google Scholar] [CrossRef]
- Rajchandar, K.; Kothandaraman, D.; Manoharan, G.; Kabanda, G. Robotics and its Navigation Techniques: The Present and Future Revelations. In Handbook of Artificial Intelligence and Wearables; CRC Press: Boca Raton, FL, USA, 2024; pp. 189–204. [Google Scholar]
- Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A comparative review on mobile robot path planning: Classical or meta-heuristic methods? Annu. Rev. Control 2020, 50, 233–252. [Google Scholar] [CrossRef]
- Kopp, T.; Baumgartner, M.; Seeger, M.; Kinkel, S. Perspectives of managers and workers on the implementation of automated-guided vehicles (AGVs)—A quantitative survey. Int. J. Adv. Manuf. Technol. 2023, 126, 5259–5275. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 7 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Suriyan, K.; Nagarajan, R. Particle swarm optimization in biomedical technologies: Innovations, challenges, and opportunities. In Emerging Technologies for Health Literacy and Medical Practice; IGI Global: Hershey, PA, USA, 2024; pp. 220–238. [Google Scholar]
- Zhang, Z.; Li, J.; Lei, Z.; Zhu, Q.; Cheng, J.; Gao, S. Reinforcement learning-based particle swarm optimization for wind farm layout problems. Energy 2024, 313, 134050. [Google Scholar] [CrossRef]
- Yi, J.; Yu, P.; Huang, T.; Xu, Z. Optimization of Transformer heart disease prediction model based on particle swarm optimization algorithm. In Proceedings of the 2024 6th International Conference on Frontier Technologies of Information and Computer (ICFTIC), Qingdao, China, 8–10 November 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1109–1113. [Google Scholar]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Mohamed, A.; Bahgat, A.; Rashad, H.; Ibrahim, A. Comparison of Path Planning between Improved Informed and Uninformed Algorithms for Mobile Robot. Int. J. Adv. Comput. Sci. Appl. 2022, 13. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Ab Wahab, M.N.; Nazir, A.; Khalil, A.; Ho, W.J.; Akbar, M.F.; Noor, M.H.M.; Mohamed, A.S.A. Improved genetic algorithm for mobile robot path planning in static environments. Expert Syst. Appl. 2024, 249, 123762. [Google Scholar] [CrossRef]
- Lamini, C.; Benhlima, S.; Elbekri, A. Genetic algorithm based approach for autonomous mobile robot path planning. Procedia Comput. Sci. 2018, 127, 180–189. [Google Scholar] [CrossRef]
- Jawad, M.M.; Hadi, E.A. A Comparative study of various intelligent algorithms based path planning for Mobile Robots. J. Eng. 2019, 25, 83–100. [Google Scholar] [CrossRef]
- Raja, P.; Pugazhenthi, S. Optimal path planning of mobile robots: A review. Int. J. Phys. Sci. 2012, 7, 1314–1320. [Google Scholar] [CrossRef]
- Rafai, A.N.A.; Adzhar, N.; Jaini, N.I. A review on path planning and obstacle avoidance algorithms for autonomous mobile robots. J. Robot. 2022, 2022, 2538220. [Google Scholar] [CrossRef]
- Thabit, S.; Mohades, A. Multi-robot path planning based on multi-objective particle swarm optimization. IEEE Access 2018, 7, 2138–2147. [Google Scholar] [CrossRef]
- Sun, R.; Tang, C.; Zheng, J.; Zhou, Y.; Yu, S. Multi-robot path planning for complete coverage with genetic algorithms. In Proceedings of the International Conference on Intelligent Robotics and Applications, Shenyang, China, 8–11 August 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 349–361. [Google Scholar]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path planning techniques for mobile robots: Review and prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).