Experimental Structural Template on Tensegrity and Textile Architecture Integrating Physical and Digital Approaches
Abstract
1. Introduction
1.1. Efficiency of Structure
1.2. Case Study
1.2.1. Frei Otto and His Model Studies
- Soap Film Models: Otto used soap films to explore tensile equilibrium and minimal surfaces, creating forms optimized for material efficiency and structural performance.
- Hanging Chain Models: Inspired by Gaudí [26], Otto employed hanging chains to study compression-free forms, later inverting these models to develop self-supporting geometries suitable for large-span structures.
1.2.2. Heinz Isler and Physical Model Validation
- Shell Structures: Isler’s primary focus was on compression-only forms, which he developed using hanging membrane models. These models, when inverted, produced structurally efficient shells optimized for minimal material use.
- Buildability Testing: Isler’s method demonstrated that physical models could serve not only as form-finding tools but also as engineering validation frameworks, ensuring the constructability of the proposed forms.
1.2.3. Munich Olympic Stadium: Integration of Tension and Compression
1.2.4. Key Insights from Physical Models
- Natural Force Paths: Physical models allow designers to visualize force distribution intuitively, revealing tension and compression zones in a tangible way;
- Material Efficiency: These models inherently encourage minimal material use, ensuring structural optimization without excess weight or waste;
- Practical Feasibility: Before the advent of advanced computational tools, physical prototypes provided the primary method for validating form-finding processes and structural performance.
2. Methodology
2.1. Research Objectives
- Exploring Knitting Techniques
- 2.
- Concept Model Development
- 3.
- Validation of Buildability at 1:5 Scale
- 4.
- Digital Analysis for Structural Performance
- 5.
- Critical Evaluation and Refinement
2.2. PolRe as a Material
- An internal support structure made of a moderately flexible polyethylene terephthalate (PET) [27];
- An external fabric coating, whose primary function is to protect the PET core from heat and UV-induced aging.
2.3. Knitting as the Optimal Approach
3. Results
3.1. Physical Models
3.1.1. Conceptual Physical Models
- Knitted Mesh for Tensile member
- 2.
- Structural unit and Form generation
- 3.
- Architectural Application Prototype development
3.1.2. Scaled Model Built up with Manual Knitting Machine
3.1.3. Knitting Process
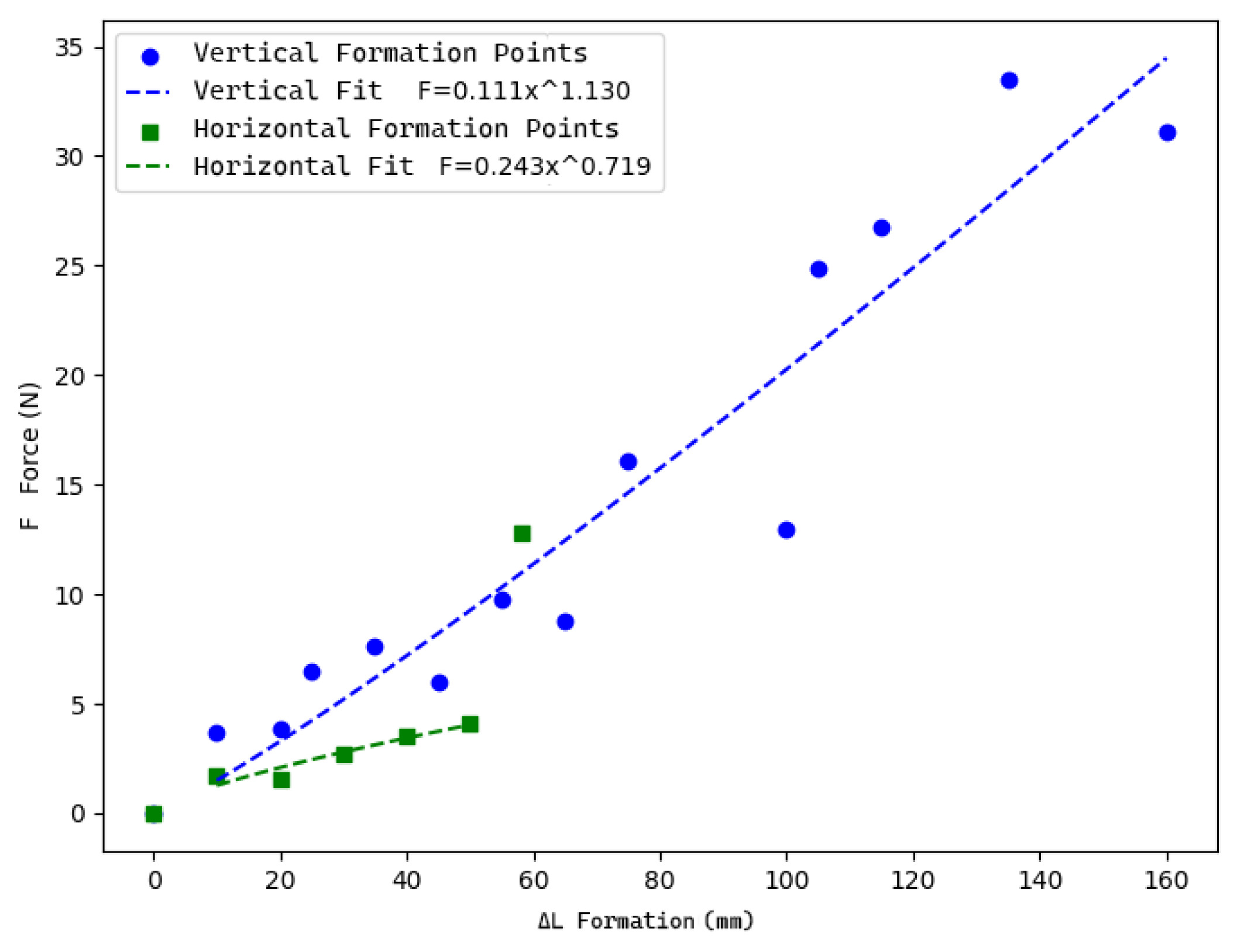
3.2. Digital Simulation
4. Discussion
4.1. Scaled Physical Model Node Refinements
- Simple Solution on the physical model
- 2.
- Crochet-Based Node
- 3.
- Final Node Design
4.2. Implications and Challenges
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Wolf, C.; Pomponi, F.; Moncaster, A. Measuring embodied carbon dioxide equivalent of buildings: A review and critique of current industry practice. Energy Build. 2017, 140, 68–80. [Google Scholar] [CrossRef]
- Barozzi, M.; Lienhard, J.; Zanelli, A.; Monticelli, C. The Sustainability of Adaptive Envelopes: Developments of Kinetic Architecture. Procedia Eng. 2016, 155, 275–284. [Google Scholar] [CrossRef]
- Boller, G.; Chilton, J.C. Heinz Isler’s Experimental Approach to Form Finding. In Heinz Isler and His Architectural Legacy; Birkhäuser: Basel, Switzerland, 2020. [Google Scholar] [CrossRef]
- Goldsmith, N. The physical modeling legacy of Frei Otto. Int. J. Space Struct. 2016, 31, 25–30. [Google Scholar] [CrossRef]
- Boller, G.; Schwartz, J. Modelling the form. Heinz Isler, Frei Otto and their approaches to form-finding. In Proceeding of the 7th Annual Conference on Construction History (2020) (Virtual), Cambridge, UK, 4–5 April 2020; pp. 565–576. [Google Scholar]
- Juan, S.; Mirats-Tur, J. Tensegrity frameworks: Static analysis review. Mech. Mach. Theory 2008, 43, 859–881. [Google Scholar] [CrossRef]
- Snelson, K. Continuous Tension, Discontinuous Compression. U.S. Patent No. 3,169,611; U.S. Patent and Trademark Office, 16 February 1965. Available online: https://www.freepatentsonline.com/3169611.html (accessed on 20 February 2025).
- Wu, J.; Zhang, L.; He, Z.; Yan, Z. Comparative Analysis of Two Tensegrity Grids Considering Slack and Rupture of Cables. AIAA J. 2020, 58, 2321–2329. [Google Scholar] [CrossRef]
- Sultan, C.; Skelton, R.E. Deployment of tensegrity structures. Int. J. Solids Struct. 2003, 40, 4637–4657. [Google Scholar] [CrossRef]
- Gupta, S.S.; Tan, Y.Y.; Chia, P.Z.; Pambudi, C.P.; Quek, Y.H.; Yogiaman, C.; Tracy, K.J. Prototyping knit tensegrity shells: A design-to-fabrication workflow. SN Appl. Sci. 2020, 2, 1062. [Google Scholar] [CrossRef]
- Schling, E.; Barthel, R.; Ihde, A.; Tutsch, J.; Huth, S. Bending-Activated Tensegrity. In Proceedings of the IASS Annual Symposia, Amsterdam, The Netherlands, 17–20 August 2015. [Google Scholar]
- Wit, A.; Riether, G. Underwood Pavilion. In Proceedings of the 20th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA 2015), Daegu, Republic of Korea, 20–22 May 2015. [Google Scholar] [CrossRef]
- Lee, S. Analysis of electrical and comfort properties of conductive knitted fabrics based on blending ratio of silver-coated yarns for smart clothing. J. Eng. Fibers Fabr. 2022, 17, 3. [Google Scholar] [CrossRef]
- Cirio, G.; Lopez-Moreno, J.; Otaduy, M.A. Yarn-Level Cloth Simulation with Sliding Persistent Contacts. In Proceedings of the IEEE Transactions on Visualization and Computer Graphics, Los Angeles, CA, USA, 18–22 March 2017; Volume 23, pp. 1152–1162. [Google Scholar] [CrossRef]
- Hörteborn, E. Knitted Architecture and Wind: Designing Loosely Fitted Architectural Textiles for Interaction with Wind; Chalmers Tekniska Hogskola: Göteborg, Sweden, 2023; p. 9. [Google Scholar] [CrossRef]
- Zanelli, A.; Monticelli, C.; Viscuso, S. Closing the Loops in Textile Architecture: Innovative Strategies and Limits of Introducing Biopolymers in Membrane Structures. In Advances in Architecture and Building Technology; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Yadav, P.; Ismail, N.; Essalhi, M.; Tysklind, M.; Athanassiadis, D.; Tavajohi, N. Assessment of the environmental impact of polymeric membrane production. J. Membr. Sci. 2021, 622, 118987. [Google Scholar] [CrossRef]
- SO-IL; Veenendaal, D.; Popescu, M. Common Thread. Summum Engineering. 2024. Available online: https://www.summum.engineering/portfolio/common-thread/ (accessed on 20 February 2025).
- Kaiser, R.; Bridgens, B.; Elsacker, E.; Scott, J. BioKnit: Development of mycelium paste for use with permanent textile formwork. Front. Bioeng. Biotechnol. 2023, 11, 1229693. [Google Scholar] [CrossRef]
- Thomsen, M.; Šinke, Y.; Monteiro, F.; Lienhard, J.; La Magna, R.; Tamke, M. Systems for transformative textile structures in CNC knitted fabrics—Isoropia. Text. Struct. 2019, 2019, 3245–3250. [Google Scholar] [CrossRef]
- Tamke, M.; Šinke, Y.; Monteiro, F.; Lienhard, J.; La Magna, R.; Thomsen, M. Computational knit—Design and fabrication systems for textile structures with customised and graded CNC knitted fabrics. Archit. Eng. Des. Manag. 2020, 17, 175–195. [Google Scholar] [CrossRef]
- Thomsen, M.R.; Tamke, M.; Deleuran, A.H.; Tinning IK, F.; Evers, H.L.; Gengnagel, C.; Schmeck, M. Hybrid Tower, Designing Soft Structures. In Modelling Behaviour: Design Modelling Symposium 2015; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Cui, Z.; Zhang, S.; Viscuso, S.; Zanelli, A. Weaving Octopus: An Assembly–Disassembly-Adaptable Customized Textile Hybrid Prototype. Buildings 2023, 13, 2413. [Google Scholar] [CrossRef]
- Jenett, B.; Cameron, C.; Tourlomousis, F.; Rubio, A.P.; Ochalek, M.; Gershenfeld, N. Discretely assembled mechanical metamaterials. Sci. Adv. 2020, 6, eabc9943. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Li, Z.; Zeng, K.; Guo, Z.; Wang, Z.; Yu, X.; Li, X.; Cheng, L. All-in-One: An Interwoven Dual-Phase Strategy for Acousto-Mechanical Multifunctionality in Microlattice Metamaterials. Adv. Funct. Mater. 2024, 34, 2420207. [Google Scholar] [CrossRef]
- Tomlow, J. Gaudí’s reluctant attitude towards the inverted catenary. Proc. ICE-Eng. Hist. Herit. 2011, 164, 219–233. [Google Scholar] [CrossRef]
- Olam, M. Mechanical and Thermal Properties of HDPEPET Microplastics, Applications, and Impact on Environment and Life; IntechOpen: London, UK, 2023. [Google Scholar] [CrossRef]
- Wikipedia Contributors. Spool Knitting. Wikipedia. Available online: https://en.wikipedia.org/wiki/Spool_knitting (accessed on 3 January 2024).
- Zhang, Z.; Chen, J. Smart Knitted Surface—TARP Textile Architecture Research Paths—Theoretical and Experimental Understanding of Membranes and Shells in Architecture and Construction. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2024. Available online: https://www.politesi.polimi.it/handle/10589/222721?mode=complete (accessed on 16 July 2024).





















| Chemical Formula | C10H8O4 |
|---|---|
| Density (g/cm3) | 1.38–1.56 |
| Flammability | Self-extinguishing |
| Freezing resistance (°C) | −50 |
| Usable max. Temperature (°C) | 70 |
| Tensile strength (MPa) | 40–60 |
| Young’s modulus (MPa) | 1000–3500 |
| Flexural strength (MPa) | 55–100 |
| Elongation at break (%) | 19–46 |
| Flexural modulus (MPa) | 2000–3500 |
| Hardness (Shore-A) | 96 |
| Model and Type | Description | Advantages | Disadvantages |
|---|---|---|---|
| Figure 8a: Type e | A continuous mesh spans from the bottom to the top, integrated with isolated compression rods. | The entire structure is wrapped in textile, limiting accessibility to the interior space. | |
| Figure 8b: Type d + Type e | Based on Model, but incorporates an isolated tensegrity unit at the bottom with openings on each side. | Although this approach introduces openings, the fabric pieces at the bottom act as tensile members that hinder entry. Moreover, unnecessary separation disrupts the overall aesthetic coherence. | |
| Figure 8c: Type c + Type e | A continuous mesh with openings. The mesh does not provide vertical tension, so additional cables serve as tensile members in place of the mesh in that direction. | The addition of rigid cables results in a redundant design language, and the risk of progressive collapse remains. Furthermore, the full potential of the tensile mesh is not realized. | |
| Figure 8d: Type d + Type e | A continuous mesh with bespoke opening shape that provides tension throughout the entire system | The tensile members carry only tension, while the rods handle compression alone. This clarifies the design language of the structural form, creating a clean tension–compression system. | Because of the uniform knitting pattern, the ground level is looser than the upper levels, rendering it less stable than the original model. Possible solutions involve reinforcing the knitting pattern or adding extra joint elements for better stability. |
| Figure 8e: Type c + Type d + Type e | Building on Model d, additional cables are added to reinforce the tension within the system. | Offers a strong, stable base at ground level, enhancing the structure’s load-bearing capacity and overall robustness. | Incorporates redundant components that add unnecessary complexity to the design language. |
| Figure 8f: Type b + Type e | A rigid cable delivers tension for the first unit, and from the second unit onward, a continuous mesh system is used. | Provides a slender, floating appearance, contributing a distinctive aesthetic quality to the structure while maintaining functional integrity. | Does not effectively address the progressive collapse concern. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Viscuso, S.; Zanelli, A.; Chen, J. Experimental Structural Template on Tensegrity and Textile Architecture Integrating Physical and Digital Approaches. Materials 2025, 18, 1721. https://doi.org/10.3390/ma18081721
Zhang Z, Viscuso S, Zanelli A, Chen J. Experimental Structural Template on Tensegrity and Textile Architecture Integrating Physical and Digital Approaches. Materials. 2025; 18(8):1721. https://doi.org/10.3390/ma18081721
Chicago/Turabian StyleZhang, Zhiyuan, Salvatore Viscuso, Alessandra Zanelli, and Jinghan Chen. 2025. "Experimental Structural Template on Tensegrity and Textile Architecture Integrating Physical and Digital Approaches" Materials 18, no. 8: 1721. https://doi.org/10.3390/ma18081721
APA StyleZhang, Z., Viscuso, S., Zanelli, A., & Chen, J. (2025). Experimental Structural Template on Tensegrity and Textile Architecture Integrating Physical and Digital Approaches. Materials, 18(8), 1721. https://doi.org/10.3390/ma18081721






