Abstract
Magnetic inductive heating (MIH) has been a topic of great interest because of its potential applications, especially in biomedicine. In this paper, the parameters characteristic for magnetic inductive heating power including maximum specific loss power (SLPmax), optimal nanoparticle diameter (Dc) and its width (ΔDc) are considered as being dependent on magnetic nanoparticle anisotropy (K). The calculated results suggest 3 different Néel-domination (N), overlapped Néel/Brownian (NB), and Brownian-domination (B) regions. The transition from NB- to B-region changes abruptly around critical anisotropy Kc. For magnetic nanoparticles with low K (K < Kc), the feature of SLP peaks is determined by a high value of Dc and small ΔDc while those of the high K (K > Kc) are opposite. The decreases of the SLPmax when increasing polydispersity and viscosity are characterized by different rates of d(SLPmax)/dσ and d(SLPmax)/dη depending on each domination region. The critical anisotropy Kc varies with the frequency of an alternating magnetic field. A possibility to improve heating power via increasing anisotropy is analyzed and deduced for Fe3O4 magnetic nanoparticles. For MIH application, the monodispersity requirement for magnetic nanoparticles in the B-region is less stringent, while materials in the N- and/or NB-regions are much more favorable in high viscous media. Experimental results on viscosity dependence of SLP for CoFe2O4 and MnFe2O4 ferrofluids are in good agreement with the calculations. These results indicated that magnetic nanoparticles in the N- and/or NB-regions are in general better for application in elevated viscosity media.
1. Introduction
MIH of magnetic nanoparticles (MNPs) while exposed to an alternating magnetic field (AFM) has attracted a lot of attention due to its potential applications in various domains, in particular cancer hyperthermia treatment and drug delivery. In cancer hyperthermia, it uses MIH on the principle that the cancer cells can be killed due to their higher thermal sensitivity than that of healthy ones [1,2,3,4,5,6,7,8,9,10,11]. For drug delivery, the MIH can be used to trigger remotely or on-site release of drug molecules being tagged to the MNPs [1,2,3,8,11,12,13]. Recently, new interesting biomedical applications were proposed including tuning the cellular gate for regulation of plasma glucose [14], biomaterials devitrification [15,16,17] and determination of MNPs accumulation in various organs [18]. In order to optimize the amount of MNPs used in the MIH, many studies focused on the conditions for maximizing heating efficiency, which is described theoretically by SLP or experimentally by specific absorption rate (SAR). The MIH power of MNPs has been known to consist of 3 main contributions: magnetization hysteresis, Néel relaxation generated by changing direction of the magnetic moments, and Brownian relaxation due to physical movement of MNPs. According to the linear response theory (LRT) [19,20], the Néel and Brownian relaxation processes are the main mechanisms to generate heat by the fluid containing superparamagnetic nanoparticles (NPs). Similar to other physical properties, the MIH power depends strongly on the diameter (D) of MNPs. Finding optimal particle diameter at which the SLP exhibits maximum value is frequently the purpose of both theoretical and experimental MNPs-MIH research.
Theoretical calculations indicated that, as a result of the competition between Néel and Brownian dissipation processes, the SLP versus D curve exhibits a peak shape with maximum value (SLPmax) at a characteristic particle diameter Dc for different material parameters and field conditions [21,22,23,24,25,26]. From the studies of various Fe3O4 (FO) MNPs with different size at frequency f = 376 kHz, the maximum SLPmax was found for a 16 nm (size standard deviation, σ = 0.175) sample [27,28,29]; for iron oxide nanocubes at f = 520 kHz, it is 19 ± 3 nm [30,31]. An analysis of various data after taking a normalization of field factor gave an elevation of SLP in the diameter range from 14–18 nm [25]. For γ-Fe2O3, elevation of SLP for 5 sample sizes from 5.3 nm to 16.5 nm (σ = 0.19–0.43) is in agreement with the theoretical prediction for the peak appearance at Dc = 14.5 nm [22]. Although these results have confirmed the existence of optimal particle size Dc of MNPs in MIH, finding the value of Dc is not a simple task in experimental works because of the impact of other parameters such as the magnetic anisotropy, viscosity of fluid, and the size distribution.
Firstly, while the magnetic anisotropy of MNPs can be considered as a constant in theoretical works, it depends strongly on the particle size. Additionally, it was showed that the SLPmax and Dc decreases monotonically with increasing anisotropy [23,24]. It is noted that, due to the difference in morphology, the synthesized MNPs of the same material can have quite different polydispersity, anisotropy K values (e.g., FO MNPs having K ranging from about 20 to 550 kJ/m3 [32,33]) which can influence the SLPmax and Dc parameters. Secondly, the value of SLPmax was found to reduce with expansion of size distribution [22]. In practice, there will be some size distribution of the MNPs regardless of the synthesis method and producing MNPs with a sufficiently narrow size distribution is a difficult task. Thus far there have been few reports on experimental verification of calculated optimal D which would require the ability to synthesize MNPs with high monodispersity and to tune D precisely [22,25,28,34]. Thirdly, there might be some relationships between the value of Dc and SAR and ferrofluid viscosity. The size dependences of heating power with some variations of D and ferrofluid viscosity was studied experimentally and theoretically which showed for example for γ-Fe2O3 and CoFe2O4 MNPs SAR decreased about 20% and 80% with an increase of the viscosity, respectively [22]. To be able to obtain MNPs with optimal heating power, it is desirable to develop a complete correlation of SLP versus D and to consider impacts of different parameters, e.g., size distribution and shape of the NPs [20,21,22].
In this work, assessments of the impact of K on overall behavior of the heating power quantity have been systematically analyzed. The characteristics of SLP versus D for different MNPs have been studied by considering the impacts of two experimental parameters of the MNPs ferrofluid: σ and media viscosity (η). The different shapes of SLP(D) or the different rates of d(SLPmax)/dσ and d(SLPmax)/dη for FO MNPs with various anisotropy have been studied and explained as a result of the competition between Néel and Brownian dissipation processes. Here, the experimental results of MNPs of manganese ferrite (MFO), and cobalt ferrite (CFO) are considered as representative of low K (Néel domination) N type, and high K (Brownian domination) B type, which have confirmed the theoretical predictions.
2. Theoretical Basis
The SLP of the MNPs can be calculated as follows [4,20,21,22,23,24,25,26]:
where Φ is the volume fraction (%), ρ the mean mass density (g/m3) and P the loss power density (W/m3). The calculations were carried out for particles with size standard deviation (or size polydispersity) parameter σ = 0–0.5, and viscosity η = 1–10 mPa·s, assuming the volume fraction Φ = 0.1% and the surface ligand layer thickness of 1 nm.
For the superparamagnetic NPs, it is generally known that Néel and Brownian relaxation losses mainly contribute to the MIH of materials. The Néel relaxation loss is originated from relaxation effects of magnetization in a magnetic field, the Brownian relaxation loss is due to the rotation of the NPs as a whole in a ferrofluid. In the LRT, χ is assumed to remain constant with increasing H. This approach was shown to be valid for small magnetic fields. Based on theoretical results, it was found that the condition of validity for the LRT is χ < 1. The dimensionless parameter, ξ, can be given by ref. [19]:
Therefore, LRT based on Néel and Brownian relaxation losses is suitable for superparamagnetic NPs or H << HC [19]. The correlation between SLP (based on LRT), the field amplitude (H), frequency (f) and the MNPs imaginary susceptibility (χ”) is ref. [20,24]:
with μ0 being the permeability of free space; where
The effective relaxation time (τ) can be determined from the compositional relaxation of Néel (τN) and Brownian (τB) processes [20,24]:
with
where V and VH are the volume of the core magnetic, and the whole capped particle, respectively.
For monodisperse superparamagnetic NPs (σ = 0), the value of SLP is calculated based on above equations. Considering the impact of particle size deviation (σ > 0), the mean loss power density can be described as ref. [20]:
with
and g(D) the distribution function
3. Results and Discussion
3.1. Characteristics of Optimal Parameters in Domination Regions of Néel or Brownian Relaxations
Magnetite is one of the extensively studied and important in a wide range of medical applications because of its biocompatibility. The anisotropy value of FO MNPs was reported between a few tens to higher than 500 kJ/m3 [32,33]. The calculations are, therefore, made for different K up to 50 kJ/m3 and the results of SLP versus particle diameter at K equal to 9 kJ/m3, 20 kJ/m3, 41 kJ/m3 are presented in Figure 1.
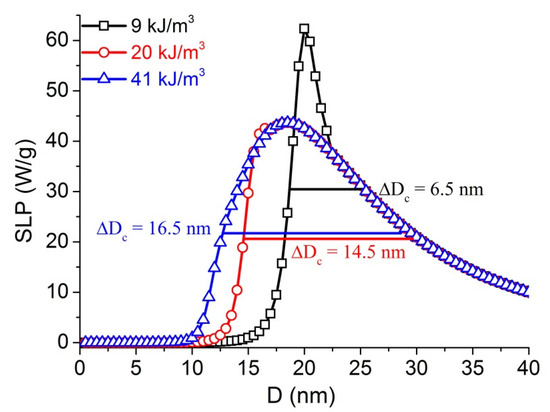
Figure 1.
SLP versus D, calculated at f = 100 kHz, H = 5.18 kA/m, σ = 0, η = 1 mPa⋅s for monodispersive FO MNPs with 3 different K of 9, 20, and 41 kJ/m3. The bars denote the (full-width-half-maximum (FWHM)) ΔDc.
The typical peak behaviors of the calculated SLP against D obtained for FO MNPs can be seen in Figure 1. Here, the difference in the SLP (D) graph shape of FO MNPs depends on the value of K [20,23]. We have introduced full-width-half-maximum (FWHM) ΔDc for describing the peaks. The Dc, ΔDc and SLPmax obtained at f = 100 kHz, H = 5.18 kA/m (65 Oe), σ = 0, η = 1 mPa⋅s for monodisperse FO ferrofluids with different anisotropy K are listed in Table 1.

Table 1.
Dc, ΔDc, SLPmax, τN, τB, and τ obtained for monodisperse FO ferrofluids with different anisotropy constant K. (f = 100 kHz, H = 5.18 kA/m, σ = 0, η = 1 mPa⋅s).
The results showed that the high K (50 kJ/m3) FO sample (18.5 nm) has much smaller value of Dc compared with that of the low K (3 kJ/m3) one (28.5 nm). In contrast, there is a large increase in the value of FWHM ΔDc when the value of K goes from 3 kJ/m3 (3.5 nm) to 50 kJ/m3 (16.5 nm). The fact that the SLP peak is narrow for low K but broad for high K can be attributed to Néel or Brownian domination, respectively [9,20,22,24].
Based on Equation (5), it is clear that the effective relaxation time is dominated by the shorter of the two components. For example, A. E. Deatsch et al. found that the Brownian relaxation becomes more significant at 13 nm for high anisotropy particles (40 kJ/m3) [25]. We calculated the value of relaxation times at Dc for all samples. As can be seen in Table 1, the value of effective relaxation time is approximately equal to the Brownian relaxation time at Dc when the value of K is higher than 19 kJ/m3. The calculations indicated that the Brownian relaxation dominated at Dc when the value of K is higher than 19 kJ/m3. Therefore, the difference in peak behaviors of the SLP against D depends on the domination of Néel or Brownian relaxations. As can be seen in Table 1, the value of Dc changes with an increase of K from 3 kJ/m3 to 20 kJ/m3, because the Néel relaxation loss still affects this parameter. When the value of K for FO is higher than 20 kJ/m3, Dc and SLPmax are unchanged due to the domination of Brownian relaxation loss. Therefore, it changes abruptly at some critical anisotropy Kc = 20 kJ/m3.
Changes of characteristic parameters, SLPmax, Dc and ΔDc as a function of K for f = 100 kHz, η = 1 mPa⋅s are presented in Figure 2, where it suggests 3 different regions. In the lowest K (region I: K ≤ 5 kJ/m3): SLPmax, Dc and ΔDc decrease with increasing K. The middle region (region II: 5 kJ/m3 ≤ K ≤ 20 kJ/m3) is characterized by a tendency of the decrease of Dc to slow down while ΔDc starts to increase with increasing K. In the high K region (region III: K > 20 kJ/m3), all the 3 parameters become almost constant. Relating to the dissipation mechanisms, the regions I, II and III can be correspondingly assigned as Néel-domination (N-region), Néel/Brownian overlap (NB-region) and Brownian-domination (B-region). While the transition from N- to NB-region is quite smooth, the transition to the B region is distinctly of the first order and in case of FO MNPs it corresponds to a critical anisotropy value Kc of about 20 kJ/m3.
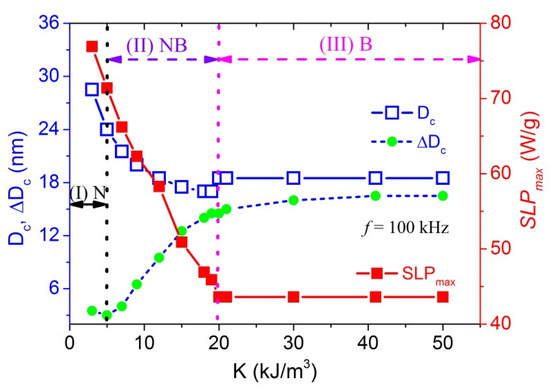
Figure 2.
Changes of characteristic parameters, SLPmax, Dc and ΔDc from Néel-domination to Brownian-domination region calculated for frequency f = 100 kHz, viscosity η = 1 mPa⋅s.
3.2. Dependence of Critical Anisotropy Kc on Frequency (f)
Based on LRT, the value of SLP reaches the maximum SLPmax at the optimal particle size Dc when the condition ωτ = 1 is satisfied. Therefore, the anisotropy boundary of the transition from NB- to B-region might depend on the frequency of AMF.
Based on the data of FO MNPs at η = 1 mPa⋅s for the expanded K range and at various frequencies, the SLP was calculated and results of Dc versus K are presented in Figure S1a. For frequencies up to 1000 kHz can be seen an abrupt change of Dc at Kc associated with the transition to the Brownian domination region (for example with f = 500 kHz, the value of Kc is about 60 kJ/m3, and the three N, NB and B regions are presented in Figure S1b. The dependence of the critical anisotropy Kc on the field frequency is presented in Figure 3, which follows the function:
where A = 214.63 kJ/m3, B = 0.0000814 ms, and f0 = 81.27 kHz are fitting constants.
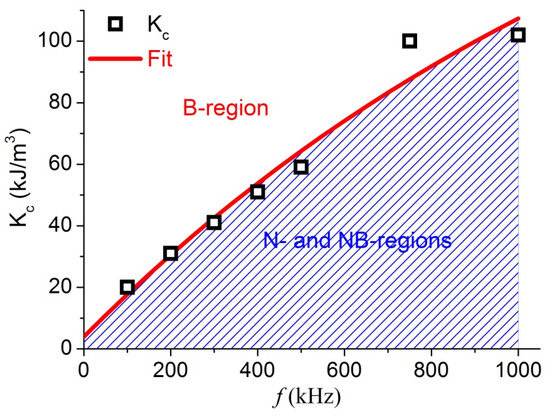
Figure 3.
Kc versus f at η = 1 mPa⋅s, the fitting gave R2 = 0.94121.
The values of critical anisotropy Kc at different frequencies for fluids with various viscosities are listed in Table 2. For MFO fluid with K = 3 kJ/m3, the Brownian relaxation dominates when η = 1 mPa⋅s and f = 100 kHz (low frequency) but it becomes the Néel relaxation domination when η ≥ 1 mPa⋅s or f ≥ 100 kHz. For CFO fluid, the Néel relaxation dominates when η ≥ 4 mPa⋅s or f ≥ 500 kHz, but it is the Brownian relaxation domination when η ≤ 2 mPa⋅s or f ≤ 1000 kHz.

Table 2.
Values of Kc at different frequencies for fluids with various viscosities (η (mPa⋅s)).
3.3. Orientations to Choose Proper Regions in Biomedical Applications
For biomedical applications, the size distribution and the viscosity of ferrofluid must be considered. In the above calculation of the relaxation times and MIH power of MNPs, the particles were assumed to have the same size, in other words the MNPs are monodispersive with σ = 0. However, in reality, this assumption cannot be satisfied because usually there would exist some size distribution of the NPs regardless of the synthetic method used. In practice, producing monodisperse MNPs (σ = 0) is almost impossible task. For example, J. P. Fortin et al. synthesized 16.5 nm γ-Fe2O3 with σ = 0.43, which could be reduced to 0.19 (d = 5.3 nm) after size sorting by successive phase separations [22]. M.P. Pileni et al. synthesized 2–5 nm CoFe2O4 with 30% polydispersity in size distribution by using functionalized surfactants [35]. When A. K. Gupta et al. compared the different characteristic features of the iron oxide NPs fabricated through different methods, they were always polydisperse NPs with narrow or broad size distributions [3]. Therefore, the assumption (σ = 0) appears not to be realized. In fact, in the synthesis of MNPs using seed mediated-growth or size sorting route, the common value of σ was reported in between 0.3–0.5 but sometime it can reduce to 0.15–0.2 [2,22,36,37]. The polydispersity characterized by the σ of MNPs can give rise to the reduction of SLP [20]. For γ-Fe2O3 MNPs, σ in the range of 0.08–0.15 could result in a decrease of SLPmax to half of the monodispersive value [22,24]. Calculations were carried out for various anisotropy (K) and standard deviation (σ) of FO MNPs at f = 100 kHz, H = 5.18 kA/m, η = 1 mPa⋅s and the results of relative SLPmax(σ)/SLPmax(σ = 0) are represented in Figure 4.
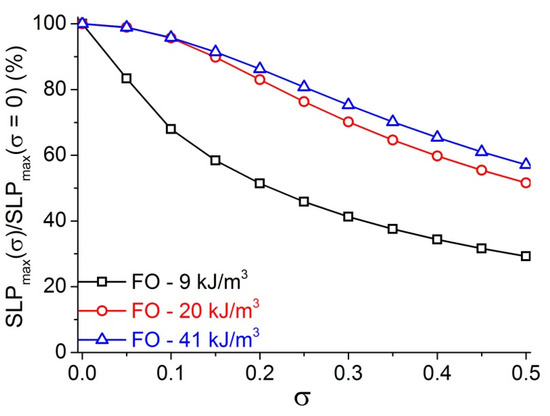
Figure 4.
SLPmax(σ)/SLPmax(σ = 0) calculated at f = 100 kHz, H = 5.18 kA/m, η = 1 mPa⋅s for FO samples with K = 9, 20, and 41 kJ/m3.
The change of heating power behavior with varying K has been reflected clearly also in the dependence of relative SLP on size standard variation. It can be seen that the domination region strongly influences the behavior of SLP besides material composition and particle size. Our results in Figure 4 indicate that, in all the curves, the SLPmax decreases with increasing σ and there is a clear trend of increasing relative SLPmax when the value of K changes from the NB-region (9 kJ/m3) to Kc (20 kJ/m3) and then the B-region (41 kJ/m3). In other words, for the similar polydispersity degree σ, the MNPs in the B-region would have higher heating power than that of those in the NB-region. These results indicated that the monodispersity requirement for getting the same heating power is much less strict for the MNPs in B-region as compared with the case of MNPs in N- or NB-region. Quantitatively, the polydispersity-caused SLP reduction for iso-dispersity of σ = 0.2 FO MNPs and σ50 (defined as at the position of ½ SLPmax) with various anisotropies at f = 100 kHz, H = 5.18 kA/m, η = 1 mPa⋅s are listed in Table 3. The parameter σ50 is seen to increase from 0.21 to 0.58 with K from 9 to 32 kJ/m3, then becomes constant for K ≥ 36 kJ/m3 indicating that the monodispersity requirement for obtaining the same heating power is much less strict for the high K as compared with the case of low K MNPs. The results in Table 3 also show that the polydispersity-caused SLP reduction decreased with an increase of magnetic anisotropy. From the slope of the SLP graph in Figure S2, it is estimated that an increase of K by about 4 times can result in saving as much as 35% of the heating power. These results seem to be consistent with the observation on cubic-shaped FO MNPs of about 20 nm (K = 180 kJ/m3) having higher heating power than spherical ones (K = 20 kJ/m3) [32]. The improvement of heating power by increasing K is an interesting topic and it has been recently reported for different materials, while the elevation of K was possible by various approaches including surface morphology, exchange-bias or stacking of particles in chains [32,33,36,37,38,39].

Table 3.
Polydispersity-caused SLP reduction for iso-dispersity σ = 0.2 FO MNPs and σ50, defined as at the position of ½ SLPmax, with various anisotropy K (f = 100 kHz, H = 5.18 kA/m, η = 1 mPa⋅s).
The medium in which MNPs are dispersed also can affect the heating efficacy of MNPs. Based on Equations (3)–(7), Rosensweig’s calculations demonstrated a dependence of the heating rate ΔT/Δt on the medium viscosity at 3 different frequencies [20]. We performed systematic calculations of SLPmax in the viscosity range from 1 mPa⋅s to 10 mPa⋅s for MNPs with various K. The results of the relative SLPmax(η)/SLPmax(η = 1 mPa⋅s) for the fluid of FO MNPs are presented in Figure 5. As can be seen in Figure 5, for FO MNPs with the value of K in NB-region (9 kJ/m3), SLPmax decreases very little with increasing η. In contrast, there is a large decrease in the SLPmax when the value of η is going from 1 kJ/m3 to 4 mPa⋅s for 20 kJ/m3, and 41 kJ/m3 FO MNPs. It is noted that the value of critical anisotropy at 4 mPa⋅s for the field frequency of 100 kHz is 60 kJ/m3 (Table 2). Therefore, the decrease of SLPmax with increasing η might occur when the value of anisotropy is smaller than Kc. In other words, this behavior happens when the K of FO MNPs is in the B-region. These calculations indicated that the FO MNPs with the K in the N- or NB-regions are much better for MIH applications in highly viscous conditions. The observation of weak and strong decrease of the heating power with increasing viscosity, will be discussed as compared with experimental results in the following section.
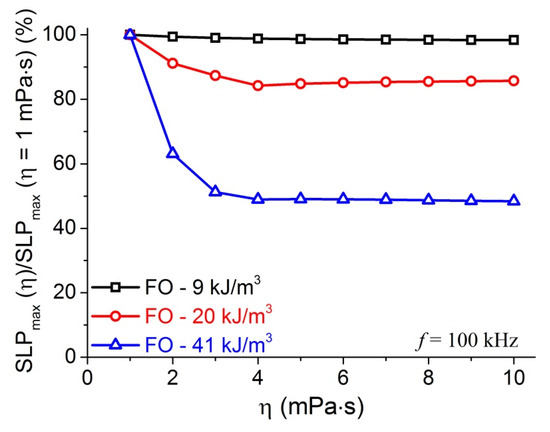
Figure 5.
SLPmax(η)/SLPmax(η = 1 mPa⋅s) calculated at f = 100 kHz, H = 5.18 kA/m for FO samples with K = 9, 20, and 41 kJ/m3.
3.4. A Comparison with Experimental Results
To compare the results from the experiments with the theoretical ones in a simple way, we have investigated SLP of the same MNPs but varying viscosity. Previously we reported the SAR measurements carried out at the field of 178 kHz and 5.18 kA/m (65 Oe) for bare CFO and MFO MNPs suspended in water fluid with added agar forming media with viscosity up to about 2 mPa⋅s, and observed strong and weak decrease of SAR with an increase of η, respectively for CFO and MFO, which is in agreement with the LRT prediction [40]. For comparing the results from the experiments with the theoretical ones, we studied two ferrofluids of 20 nm low-K MnFe2O4 and 15 nm high-K CoFe2O4 MNPs coated with chitosan. They were prepared by co-precipitation. To create the magnetic fluids with different viscosity, the MNPs suspension was mixed with various agar concentrations. The value of viscosity extended up to about 8 mPa⋅s by adding more agar amounts. The fabrication of samples with various viscosities as well as the method of viscosity measurement were described earlier [40] as were the experimental details of the synthesis and the coating procedure by chitosan [41]. As discussed in our previous reports, chitosan has been widely used in biomedicine due to its biocompatibility and biodegradability [41]. Based on the measured magnetization curves shown in Figure S3, the thickness of chitosan coating layer was estimated to be around 4 nm. The value of MS, HC and Keff for MFO and CFO NPs (shown details in Supplementary Section S3) are presented in Table 4.

Table 4.
Values of Kc at different frequencies for fluids with various viscosities (η (mPa⋅s)).
In addition to the field of 178 kHz, 5.18 kA/m (provided by a commercial generator RDO HFI 5 kW [40]), the calorimetric measurements were additionally conducted at two fields of the same amplitude of 15.9 kA/m (200 Oe) with frequencies of 340 kHz and 450 kHz (provided by a commercial generator UHF-20A [42]), to seek evidence of SAR behavior changing with increasing field frequency. The temperature elevation with time, T(t), was monitored by using the same commercial optical sensor (GaAs-Opsens) for both MIH sets up.
The heating curves, measured at the lower field, for the two series of MFO and CFO samples in solutions of various agar concentrations are presented in Figure 6. The values of were calculated from the fitting of the temperature rising curves T(t) for the whole time range following the method described in reference [40].
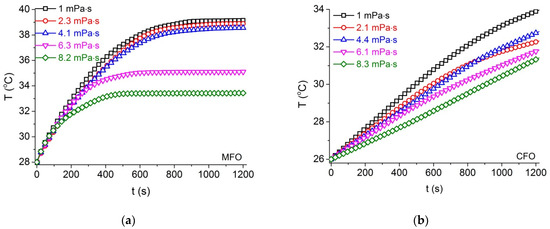
Figure 6.
Hyperthermia curves measured at field frequency f = 178 kHz, H = 5.18 kA/m for (a) MFO and (b) CFO ferrofluids of various viscosities.
In order to compare the experimental and theoretical SAR, we calculated the Néel-Brownian relaxation experimental by using the Equation:
where is the SAR contribution by hysteresis mechanism, whose estimation is described in Supplementary Section S3, similarly to the approach reported in [42]. The results of calculated obtained from the measurements at 340 kHz and 450 kHz. They are gathered in Supplementary Section S4. As can be seen, for the MFO samples with K = 11 kJ/m3 and Hc were close to or smaller than the AFM amplitudes, the contribution of is less than 2.5% of the whole heating power. However, for the CFO samples with K = 62 kJ/m3 and Hc much larger than the field amplitude used, the maximum contributions were 17%, 16% and 9% for 178, 340 and 145 kHz, respectively.
In order to discuss about the impact of AFM frequency on the SAR characteristics relevant to the relaxation mechanisms, we calculated the ratio of SAR(η)/SAR(η = 1 mPa⋅s) for all the MFO and CFO samples of various viscosities measured at the 3 frequencies (see also Tables S1–S3), the dependences of which are shown in Figure 7.
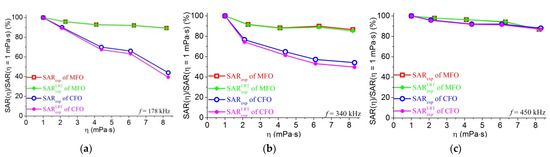
Figure 7.
Relative and measured at field of (a) 5.18 kA/m, 178 kHz; (b) 15.9 kA/m, 340 kHz; and (c) 15.9 kA/m, 450 kHz.
Firstly, it can be noted that the decrease of SAR with increasing viscosity is experimentally observed in all the cases, so that the impact of the hysteresis contribution is insignificant.
Secondly, Figure 7a,b suggest that the strong and weak decrease of SAR with increasing viscosity, depicted respectively for CFO and MFO, confirm our previous experiment reported for η ≤ 2.12 mPa⋅s [40] and the agreement with the LRT theory prediction shown in Figure 5. While such a behavior is natural for the case of the field (178 kHz, 65 Oe) with the parameter ξ of about 0.7, it is worth noting that such behavior ‘survived’ to the field of 340 kHz and 15.9 kA/m with ξ of about 2. The trend of decreasing SAR with increasing viscosity η in our experiments is also in agreement with the observation for γ-Fe2O3 (D = 7.1 nm, σ = 0.37) and CoFe2O4 (D = 9.7 nm, σ = 0.35) MNPs where SAR decreased, respectively, about 20% and 80% when the viscosity increased from 0.75 to 335 mPa⋅s [22]. In fact, it was found that SLP value from MNPs dispersed in water is higher than in glycerol for the same type of MNPs, MNP dose, and AMF condition [43]. A similar phenomenon was observed in the cellular environment as well, in which the measured SLP value decreased by half associated with attenuation of the Brownian relaxation in cellular conditions [44]. Thirdly, while the MFO ferrofluids remain almost not impacted by the field frequency used, it is interesting to observe for CFO samples a clear shift from high K toward low-K characteristic behavior when the used field frequency increases from 178 kHz to 450 kHz. In particular, Figure 7c for the case of f = 450 kHz indicates that the relative SAR versus η for the CFO MNPs approaches to the type of very weak decrease of the heating power with increasing the media viscosities, similarly to that of MFO MNPs. This observation is in good agreement with the scheme shown in Figure S7, according to which the MFO MNPs of K = 11 kJ/m3 are predicted to exhibit the SAR contributed mainly from the Neel or overlapped Neel-Brownian relaxation losses depending not on the used field frequency, and the dissipation mechanism contributing to the SAR for the CFO MNPs with K = 62 kJ/m3 belongs to the pure Brownian region for AMF with f below about 460 kHz and changes to the Neel-Brown or Neel type above this frequency.
4. Conclusions
In summary, in addition to the peak position Dc and its amplitude SLPmax, we have introduced a peak width ΔDc and performed systematic analyses of the three parameters against the magnetic anisotropy of MNPs, fluid viscosities and the frequency of the alternating magnetic field. High K MNPs have been shown to exhibit domination of Brownian loss while it becomes that of Néel loss in low K ones. To the best of our knowledge, our results have demonstrated for the first time the transition from Néel to Brownian loss region not to occur in a continuous way, but at critical anisotropy Kc which increases with the frequency of the alternating magnetic field and the viscosity of the ferrofluid. We have pointed out that, for a given material, fabrication of MNPs with higher anisotropy up to Kc can improve the heating power as much as 35% thanks to the offsetting of the polydispersity-caused reduction. From the calculation and experimental results, it appears that low K MNPs are in general better for MIH applications in highly viscous conditions than those of high K ones.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/ma14081875/s1, Figure S1: (a) Dc versus K for various AMF frequencies. (b) The width ΔDc, and Dc versus K at f = 500 kHz showing 3 characteristic N, NB and B regions; Figure S2: Polydispersity-caused SLP reduction calculated at f = 100 kHz for iso-dispersity σ = 0.2 FO MNPs as a function of anisotropy K, Figure S3: Magnetization curves measured for as-synthesized and chitosan coated (a) MFO, and (b) CFO MNPs; Figure S4: The initial magnetization curves of MFO and CFO MNPs. The solid lines represent the fitting curve assuming “the law of approach to saturation”; Figure S5: Hyperthermia curves measured at fields of frequency f = 340 kHz, H = 15.9 kA/m (200 Oe) for (a) MFO and (b) CFO ferrofluids of various viscosities; Figure S6: Hyperthermia curves measured at fields of frequency f = 450 kHz, H = 15.9 kA/m for (a) MFO and (b) CFO ferrofluids of various viscosities; Figure S7: Illustration scheme for the MIH experiments for CFO and MFO MNPs, Table S1: Values of , , , and at 5.18 kA/m, 178 kHz; Table S2: Values of , , , and at 15.9 kA/m, 340 kHz; Table S3: Values of , , , and at 15.9 kA/m, 450 kHz.
Author Contributions
All authors discussed and agreed upon the idea, and made scientific contributions: conceptualization, N.T.K.T and N.X.P.; writing—original draft preparation, L.D.T., L.H.N. and N.X.P.; experiment designing, P.H.N, D.H.M. and P.T.P.; experiment performing, L.H.N. and P.H.N.; data analysis, D.H.M, L.H.N., P.T.P. and N.X.P.; discussion, review and editing, L.D.T., N.T.K.T. and N.X.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Engineering and Physical Sciences Research Council, EPSRC (EP/M015157/1 and EP/M018016/1), Asian Office of Aerospace R&D, AOARD (FA2386-17-1-4042 award).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article or Supplementary Materials.
Acknowledgments
We are grateful to the financial support by AOARD under FA2386-17-1-4042 award. N. T. K. Thanh thanks EPSRC (EP/M015157/1 and EP/M018016/1) for funding.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Pankhurst, Q.A.; Thanh, N.T.K.; Jones, S.K.; Dobson, J. Progress in Applications of Magnetic Nanoparticles in Biomedicine. J. Phys. D 2009, 42, 224001. [Google Scholar] [CrossRef]
- Kumar, C.S.S.R.; Mohammad, F. Magnetic nanomaterials for hyperthermia-based therapy and controlled drug delivery. Adv. Drug Deliv. Rev. 2011, 63, 789–808. [Google Scholar] [CrossRef]
- Gupta, A.K.; Guptab, M. Synthesis and surface engineering of iron oxide nanoparticles for biomedical applications. Biomaterials 2005, 26, 3995–4021. [Google Scholar] [CrossRef] [PubMed]
- Hergt, R.; Dutz, S.; Muller, R.; Zeisberger, M. Magnetic particle hyperthermia: Nanoparticle magnetism and materials development for cancer therapy. J. Phys. Condens. Matter 2006, 18, S2919–S2934. [Google Scholar] [CrossRef]
- Thuy, T.T.; Maenosono, S.; Thanh, N.T.K. Next Generation Magnetic Nanoparticles for Biomedical Applications. In Magnetic Nanoparticles: From Fabrication to Clinical Applications, 1st ed.; Thanh, N.T.K., Ed.; CRC Press: New York, NY, USA, 2012; pp. 99–128. [Google Scholar]
- Gavilán, H.; Brollo, M.E.F.; Gutiérrez, L.; Veintemillas-Verdaguer, S.; Morales, M.D.P. Controlling the Size and Shape of Uniform Magnetic Iron Oxide Nanoparticles for Biomedical Applications. In Clinical Applications of Magnetic, 1st ed.; Thanh, N.T.K., Ed.; CRC Press: New York, NY, USA, 2018; pp. 3–24. [Google Scholar]
- Obaidat, I.M.; Issa, B.; Haik, Y. Magnetic properties of magnetic nanoparticles for efficient hyperthermia. Nanomaterials 2015, 5, 63–89. [Google Scholar] [CrossRef]
- Hilger, I. In vivo applications of magnetic nanoparticle hyperthermia. Int. J. Hyperth. 2013, 29, 828–834. [Google Scholar] [CrossRef] [PubMed]
- Jeun, M.; Kim, Y.J.; Park, K.H.; Paek, S.H.; Bae, S. Physical Contribution of Néel and Brown Relaxation to Interpreting Intracellular Hyperthermia Characteristics Using Superparamagnetic Nanofluids. J. Nanosci. Nanotechnol. 2013, 13, 5719–5725. [Google Scholar] [CrossRef]
- Lin, M.; Huang, J.; Sha, M. Recent Advances in Nanosized Mn-Zn Ferrite Magnetic Fluid Hyperthermia for Cancer Treatment. J. Nanosci. Nanotechnol. 2014, 14, 792–802. [Google Scholar] [CrossRef] [PubMed]
- Hedayatnasab, Z.; Abnisa, F.; Daud, W.M.A.W. Review on magnetic nanoparticles for magnetic nanofluid hyperthermia application. Mater. Des. 2017, 123, 174–196. [Google Scholar] [CrossRef]
- Derfus, A.M.; Maltzahn, G.V.; Harris, T.J.; Duza, T.; Vecchio, K.S.; Ruoslahti, E.; Bhatia, S.N. Remotely triggered release from magnetic nanoparticles. Adv. Mater. 2007, 19, 3932–3936. [Google Scholar] [CrossRef]
- Brazel, S.C. Magnetothermally-responsive nanomaterials: Combining magnetic nanostructures and thermally-sensitive polymers for triggered drug release. Pharm. Res. 2009, 26, 644–656. [Google Scholar] [CrossRef]
- Stanley, S.A.; Gagner, J.E.; Damanpour, S.; Yoshida, M.; Dordick, J.S.; Friedman, J.M. Radio-Wave Heating of Iron Oxide Nanoparticles Can Regulate Plasma Glucose in Mice. Science 2012, 336, 604–608. [Google Scholar] [CrossRef]
- Etheridge, M.L.; Xu, Y.; Rott, L.; Choi, J.; Glasmcher, B.; John, C.; Bischof, R.F. Heating of magnetic nanoparticles improves the thawing of cryopreserved biomaterials. Technology 2014, 2, 229–242. [Google Scholar] [CrossRef]
- Manuchehrabadi, N.; Gao, Z.; Zhang, J.; Ring, H.L.; Shao, Q.; Liu, F.; McDermott, M.; Fok, A.; Rabin, Y.; Brockbank, K.G.M.; et al. Improved Tissue Cryopreservation using Inductive Heating of Magnetic Nanoparticles. Sci. Transl. Med. 2017, 9, eaah4586. [Google Scholar] [CrossRef]
- Manuchehrabadi, N.; Shi, M.; Roy, P.; Han, Z.; Qiu, J.; Xu, F.; Lu, T.J.; Bischof, J. Ultrarapid Inductive Rewarming of Vitrified Biomaterials with Thin Metal Forms. Ann. Biomed. Eng. 2018, 46, 1857–1869. [Google Scholar] [CrossRef]
- Pham, H.N.; Pham, T.H.G.; Nguyen, D.T.; Phan, Q.T.; Le, T.T.H.; Ha, P.T.; Do, H.M.; Hoang, T.M.D.; Nguyen, X.P. Magnetic inductive heating of organs of mouse models treated by copolymer coated Fe3O4 nanoparticles, Adv. Nat. Sci. Nanosci. Nanotechnol. 2017, 8, 025013. [Google Scholar] [CrossRef]
- Carrey, J.; Mehdaoui, B.; Respaud, M. Simple models for dynamic hysteresis loops calculation: Application to hyperthermia optimization. J. Appl. Phys. 2011, 109, 083921. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Maenosono, S.; Saita, S. Theoretical Assessment of FePt Nanoparticles as Heating Elements for Magnetic Hyperthermia. IEEE Trans. Magn. 2006, 42, 1638–1642. [Google Scholar] [CrossRef]
- Fortin, J.P.; Wilhelm, C.; Servais, J.; Menager, C.; Bacri, J.C.; Gazeau, F. Size-Sorted Anionic Iron Oxide Nanomagnets as Colloidal Mediators for Magnetic Hyperthermia. J. Am. Chem. Soc. 2007, 129, 2628–2635. [Google Scholar] [CrossRef] [PubMed]
- Habib, A.H.; Ondeck, C.L.; Chaudhary, P.; Bockstaller, M.R.; McHenry, M.E. Evaluation of Iron-cobalt/ferrite core-shell nanoparticles for cancer thermotherapy. J. Appl. Phys. 2008, 103, 07A307. [Google Scholar] [CrossRef]
- Phong, P.T.; Nguyen, L.H.; Manh, D.H.; Lee, I.J.; Phuc, N.X. Computer simulations of contributions of Néel and Brown relaxation to Specific Loss Power of magnetic fluids in Hyperthermia. J. Electron. Mater. 2017, 46, 2393–2405. [Google Scholar] [CrossRef]
- Deatsch, A.E.; Evans, B.A. Heating efficiency in magnetic nano particle hyperthermia. J. Magn. Magn. Mater. 2014, 354, 163–172. [Google Scholar] [CrossRef]
- Suto, M.; Hirota, Y.; Mamyiya, H.; Fujita, A.; Kasuya, R.; Tohji, K.; Jeyadevan, B. Heat dissipation mechanism of magnetite nanoparticles in magnetic fluid hyperthermia. J. Magn. Magn. Mater. 2009, 321, 1493–1496. [Google Scholar] [CrossRef]
- Gonzales-Weimuller, M.; Zeisberge, M.; Krishnan, K.M. Size-dependent heating rates of iron oxide nanoparticles for magnetic fluid hyperthermia. J. Mag. Magn. Mater. 2009, 321, 1947–1950. [Google Scholar] [CrossRef]
- Krishnan, K.M. Biomedical nanomagnetics: A spin through possibilities in imaging, diagnostics, and therapy. IEEE Trans. Mag. 2010, 46, 2523–2558. [Google Scholar] [CrossRef]
- Khandhar, A.P.; Ferguson, R.M.; Simon, J.A.; Krifhnan, K.M. Tailored magnetic nanoparticles for optimizingmagnetic fluid hyperthermia. J. Biomed. Mater. Res. Part A 2012, 100A, 728–737. [Google Scholar] [CrossRef]
- Lartigue, L.; Innocenti, C.; Kalaivani, T.; Awwad, A.; Sanchez-Duque, M.; Guari, Y.; Larionova, J.; Guerin, C.; Montero, J.L.; Barragan-Montero, V.; et al. Water-dispersible sugar-coated iron oxide nanoparticles: An evaluation of their relaxometric and magnetic hyperthermia properties. J. Am. Chem. Soc. 2011, 133, 10459–10472. [Google Scholar] [CrossRef]
- Guardia, P.; Corato, R.D.; Lartigue, L.; Wilheim, C.; Espinosa, A.; Garcia-Hernandez, M.; Gazeau, F.; Manna, L.; Pellegrino, T. Water-soluble Iron Oxide Nanocubes with High Values of Specific Absorption Rate for Cancer Cell Hyperthermia Treatments. ACS Nano 2012, 6, 3080–3091. [Google Scholar] [CrossRef]
- Vreeland, E.C.; Watt, J.; Schober, G.B.; Hance, B.G.; Austin, M.J.; Price, A.D.; Fellows, B.D.; Monson, T.C.; Hudak, N.S.; Maldonado-Camargo, L.; et al. Enhanced nanoparticles size control by extending Lamer’s Mechanism. Chem. Mater. 2015, 27, 6059–6066. [Google Scholar] [CrossRef]
- Khurshid, H.; Alonso, J.; Nemati, Z.; Phan, M.H.; Mukherjee, P.; Fdez-Gubieda, M.L.; Barandiarán, J.M.; Srikanth, H. Anisotropy effects in magnetic hyperthermia: A comparison between spherical and cubic exchange-coupled FeO/Fe3O4 nanoparticles. J. Appl. Phys. 2015, 117, 17A337. [Google Scholar] [CrossRef]
- Gonzalez-Fernandez, M.A.; Torres, T.E.; Andres-Verges, M.; Costo, R.; dela Presa, P.; Serna, C.J.; Morales, M.P.; Marquina, C.; Ibarra, M.R.; Goya, G.F. Magnetic nanoparticles for power absorption: Optimizing size, shape and magnetic properties. J. Solid State Chem. 2009, 182, 2779. [Google Scholar] [CrossRef]
- Pileni, M.P.; Moumen, N.; Hochepied, J.H.; Bonville, P.; Veiller, P. Control of the size of cobalt ferrite nanoparticles: Synthesis and properties. J. Phys. Fr. 1997, 7, C1-505–C1-508. [Google Scholar] [CrossRef]
- Lahiri, B.B.; Ranoo, S.; Muthukumaran, T.; Philip, J. Magnetic hyperthermia in water based ferrofluids: Effects of initial susceptibility and size polydispersity on heating efficiency. AIP Conf. Proc. 2018, 1942, 040019. [Google Scholar]
- Levy, M.; Quarta, A.; Figuerola, A.; Wilheim, C.; Garcia-Hermandez, M.; Genovese, A.; Falcui, A.; Alloyseau, D.; Buonsanti, R.; Cozzoli, P.D.; et al. Correlating magneto-structural properties to hyperthermia performance of highly monodisperse iron oxides nanoparticles prepared by a seeded-growth route. Chem. Mater. 2011, 23, 4170–4180. [Google Scholar] [CrossRef]
- Lee, J.H.; Jang, J.T.; Choi, J.S.; Moon, S.H.; Noh, S.H.; Kim, J.W.; Kim, J.G.; Kim, I.S.; Park, K.I.; Cheon, J.W. Exchange-coupled Magnetic Nanoparticles for Efficient Heat Induction. Nanotechnology 2011, 6, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Baubeta, C.; Simeonidis, K.; Makridis, A.; Angelakaris, M.; Iglesias, O.; Guardia, P.; Cabot, A.; Yeadra, L.; Estrade, S.; Peiro, F.; et al. Learning from Nature to Improve the Heat Generation of Iron-Oxide Nanoparticles for Magnetic Hyperthermia Applications. Sci. Rep. 2013, 3, 1652–1659. [Google Scholar] [CrossRef]
- Phong, P.T.; Nguyen, L.H.; Phong, L.T.H.; Nam, P.H.; Manh, D.H.; Lee, I.J.; Phuc, N.X. Study of specific loss power of magnetic fluids with various viscosities. J. Magn. Magn. Mater. 2017, 428, 36–42. [Google Scholar] [CrossRef]
- Mai, T.T.T.; Ha, P.T.; Pham, H.N.; Le, T.T.H.; Pham, H.L.; Phan, T.B.H.; Tran, D.L.; Nguyen, X.P. Chitosan and O-carboxymethyl chitosan modified Fe3O4 for hyperthermic treatmenmt. Adv. Nat. Sci. Nanosci. Nanotechnol. 2012, 3, 015006. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Oanh, V.T.K.; Nam, P.H.; Doan, D.H.; Truong, N.X.; Ca, N.X.; Phong, P.T.; Hong, L.V.; Lam, T.D. Increase of magnetic hyperthermia efficiency due to optimal size of particles: Theoretical and experimental results. J. Nanopart. Res. 2020, 258, 1–16. [Google Scholar] [CrossRef]
- Kalambur, V.S.; Han, B.; Hammer, B.E.; Shield, T.W.; Bischof, J.C. In vitro characterization of movement, heating and visualization of magnetic nanoparticles for biomedical applications. Nanotechnology 2005, 16, 1221. [Google Scholar] [CrossRef]
- Di Corato, R.; Espinosa, A.; Lartigue, L.; Tharaud, M.; Chat, S.; Pellegrino, T.; Menager, C.; Gazeau, F.; Wilhelm, C. Magnetic hyperthermia effciency in the cellular environment for different nanoparticle designs. Biomaterials 2014, 35, 6400–6411. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).