Strain Range Dependent Cyclic Hardening of 08Ch18N10T Stainless Steel—Experiments and Simulations
Abstract
1. Introduction
2. Experiments
2.1. Experimental Setup
2.2. Experimental Program
3. Constitutive Model with Strain Range Dependency
3.1. Cyclic Plasticity and Memory Surface
3.2. Isotropic Hardening
3.3. Kinematic Hardening
3.4. Modification for Torsional Loading
4. Identification of Material Parameters
5. FE Simulations
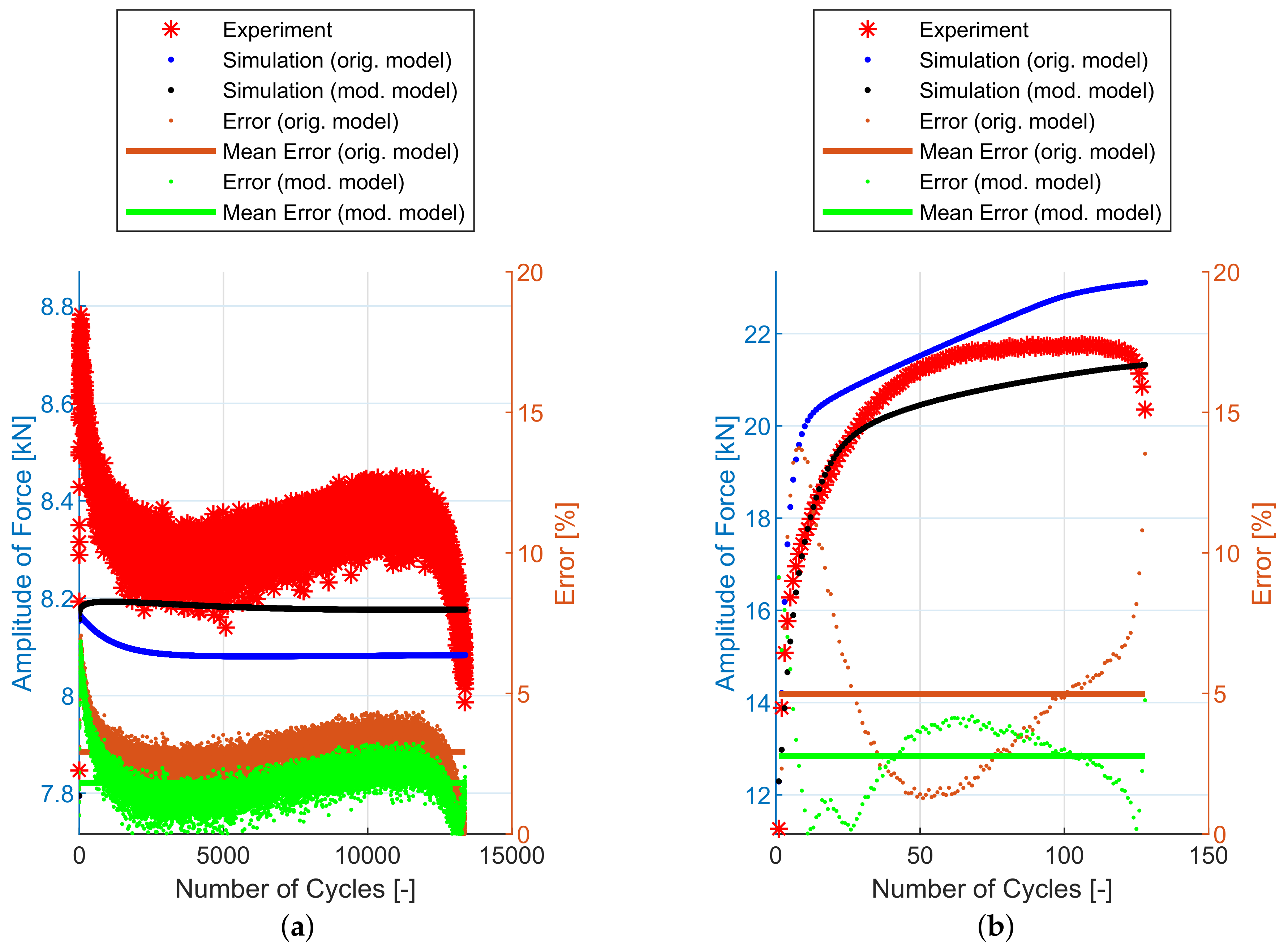
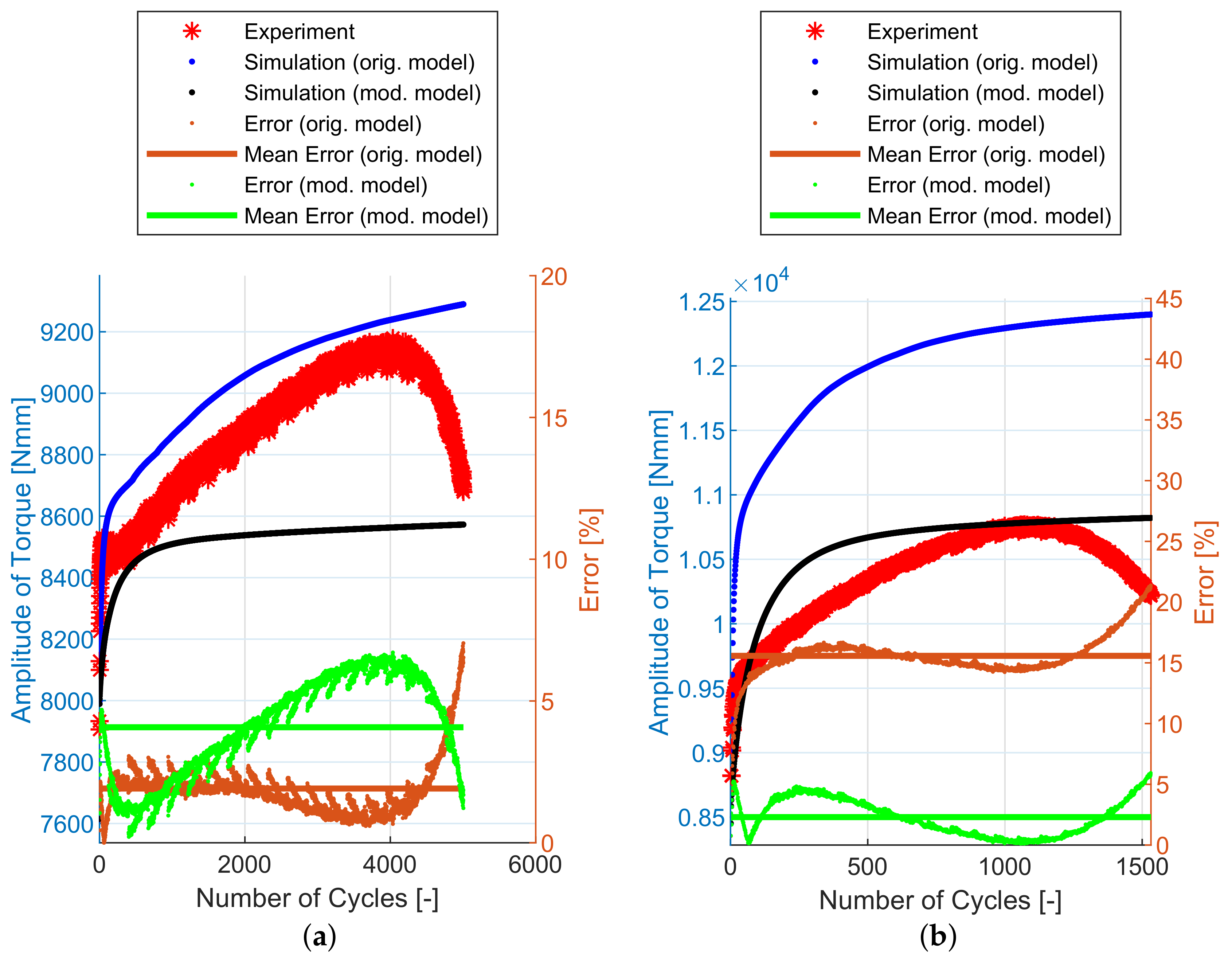
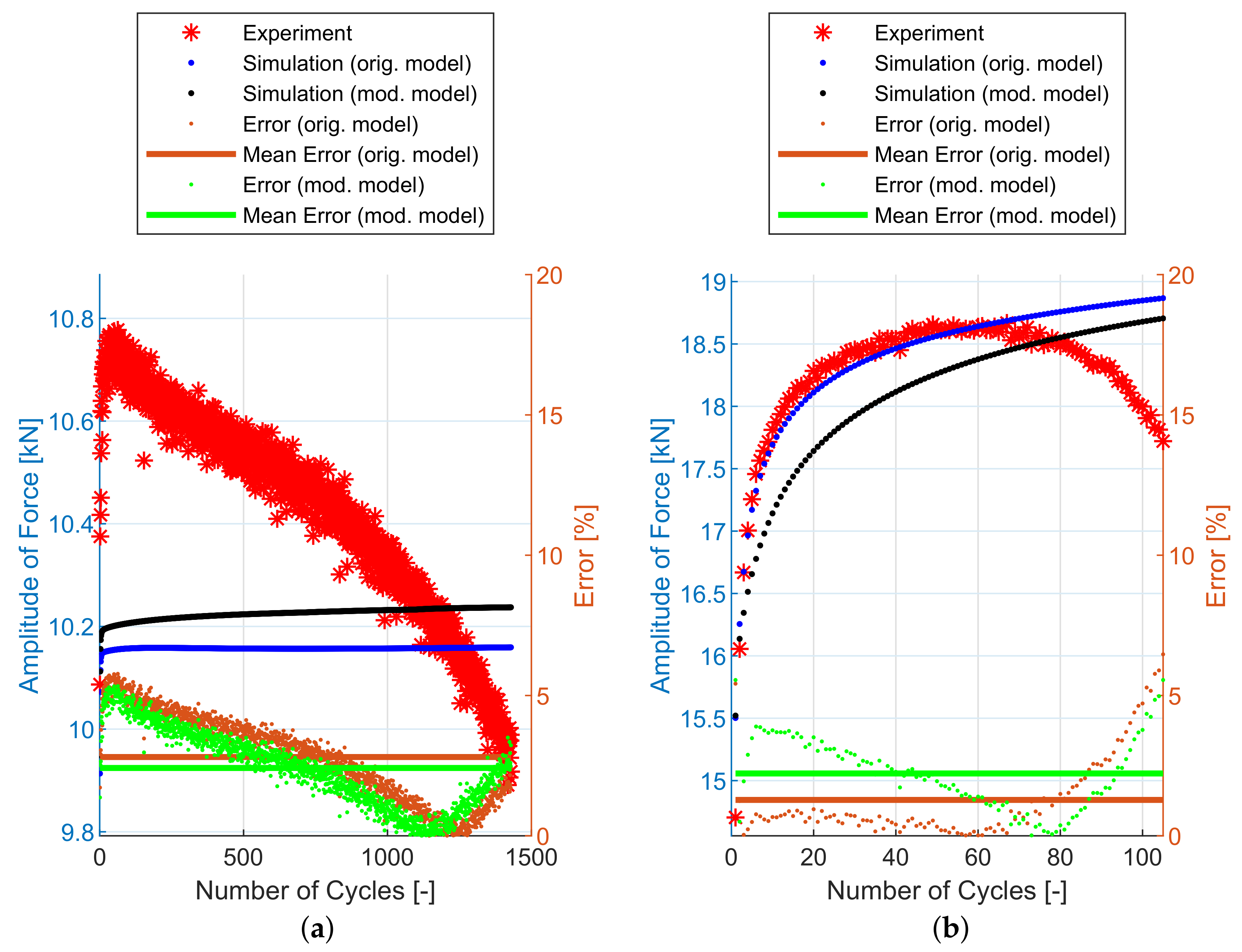
6. Experimental and Simulation Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DIC | digital image correlation |
| IDF | identification specimen series |
| FE | finite element |
| FEM | finite element method |
| UG | uniform-gage |
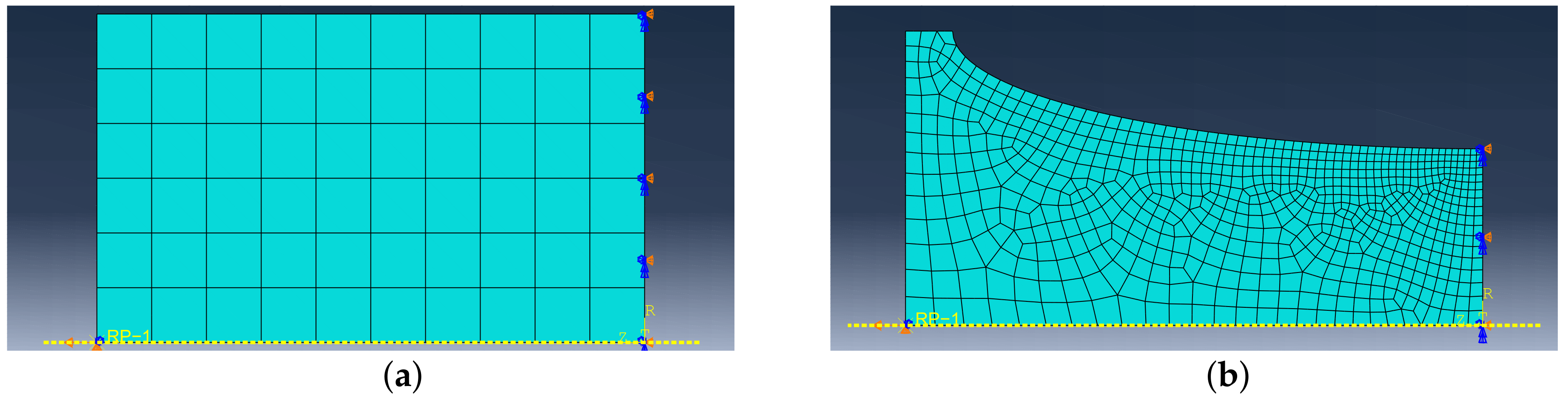
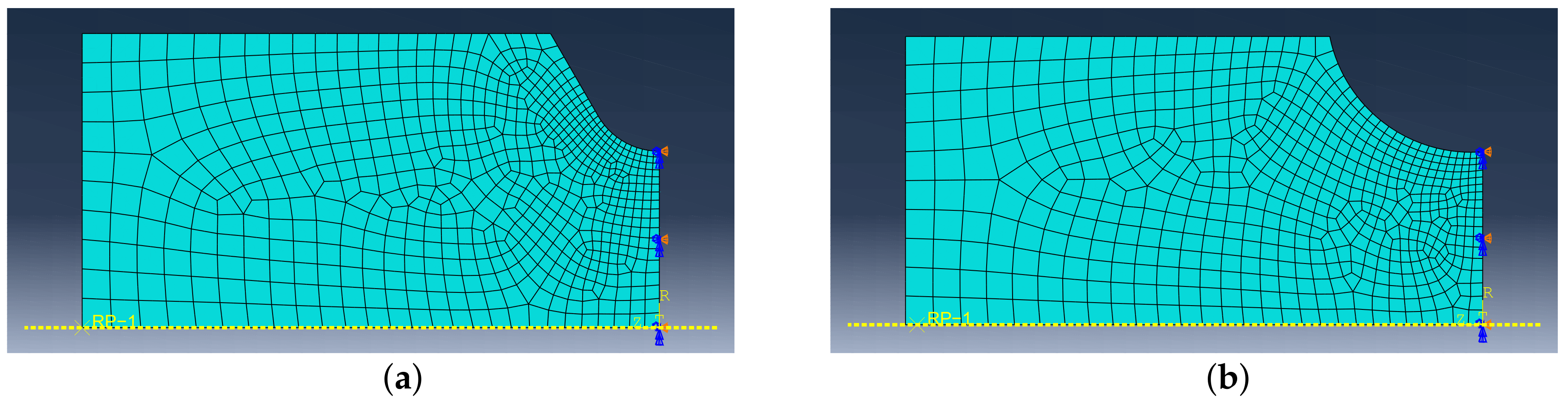
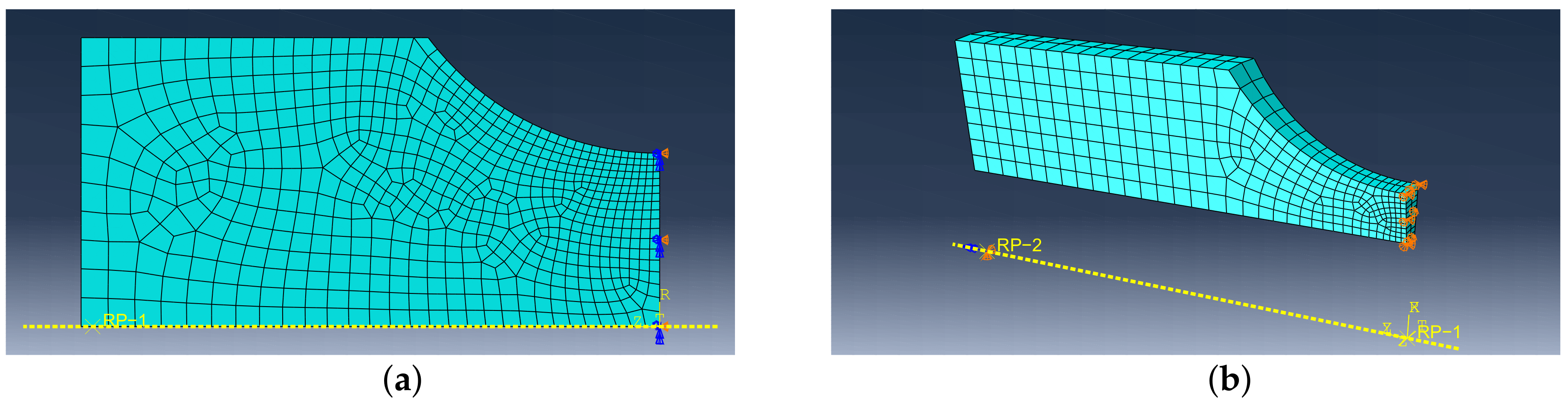
Appendix A. Boundary Conditions of Simulations
| Specimen Name | Geometry Type | ||
|---|---|---|---|
| IDF-1 | UG | 0.030 | 37509 |
| IDF-2 | UG | 0.050 | 4285 |
| IDF-3 | UG | 0.075 | 916 |
| IDF-4 | UG | 0.100 | 580 |
| IDF-5 | UG | 0.125 | 254 |
| IDF-6 | E9 | 0.132 | 159 |
| IDF-7 | E9 | 0.154 | 381 |
| IDF-8 | E9 | 0.176 | 370 |
| IDF-9 | E9 | 0.198 | 161 |
| IDF-10 | E9 | 0.245 | 156 |
| IDF-11 | E9 | 0.264 | 124 |
| IDF-12 | E9 | 0.353 | 93 |
| Specimen Name | Geometry Type | ||
|---|---|---|---|
| E9-1 | E9 | 0.0447 | 13382 |
| E9-2 | E9 | 0.0446 | 15104 |
| E9-3 | E9 | 0.0662 | 4053 |
| E9-4 | E9 | 0.0662 | 3887 |
| E9-5 | E9 | 0.0881 | 1529 |
| E9-6 | E9 | 0.0880 | 1853 |
| E9-7 | E9 | 0.1100 | 1158 |
| E9-8 | E9 | 0.1100 | 631 |
| E9-9 | E9 | 0.1320 | 748 |
| E9-10 | E9 | 0.1540 | 546 |
| E9-11 | E9 | 0.1770 | 406 |
| E9-12 | E9 | 0.1980 | 332 |
| E9-13 | E9 | 0.2200 | 253 |
| E9-14 | E9 | 0.2420 | 181 |
| E9-15 | E9 | 0.2420 | 195 |
| E9-16 | E9 | 0.2640 | 220 |
| E9-17 | E9 | 0.3520 | 128 |
| Specimen Name | Geometry Type | ||
|---|---|---|---|
| NT-1 | NT | 0.8703 | 5006 |
| NT-2 | NT | 0.8694 | 6894 |
| NT-3 | NT | 1.1423 | 2222 |
| NT-4 | NT | 1.1414 | 2289 |
| NT-5 | NT | 1.4031 | 2045 |
| NT-6 | NT | 1.3772 | 1532 |
| NT-7 | NT | 1.6554 | 1170 |
| NT-8 | NT | 2.1492 | 925 |
| Specimen Name | Geometry Type | ||
|---|---|---|---|
| R1.2-1 | R1.2 | 0.0245 | 1429 |
| R1.2-2 | R1.2 | 0.0246 | 946 |
| R1.2-3 | R1.2 | 0.0326 | 715 |
| R1.2-4 | R1.2 | 0.0406 | 523 |
| R1.2-5 | R1.2 | 0.0407 | 490 |
| R1.2-6 | R1.2 | 0.0489 | 290 |
| R1.2-7 | R1.2 | 0.0485 | 356 |
| R1.2-8 | R1.2 | 0.0560 | 241 |
| R1.2-9 | R1.2 | 0.0563 | 256 |
| R1.2-10 | R1.2 | 0.0639 | 134 |
| R1.2-11 | R1.2 | 0.0642 | 202 |
| R1.2-12 | R1.2 | 0.0721 | 171 |
| R1.2-13 | R1.2 | 0.0718 | 164 |
| R1.2-14 | R1.2 | 0.0794 | 112 |
| R1.2-15 | R1.2 | 0.0868 | 145 |
| R1.2-16 | R1.2 | 0.0869 | 114 |
| R1.2-17 | R1.2 | 0.0945 | 96 |
| R1.2-18 | R1.2 | 0.0944 | 105 |
| Specimen Name | Geometry Type | ||
|---|---|---|---|
| R2.5-1 | R2.5 | 0.0228 | 5875 |
| R2.5-2 | R2.5 | 0.0341 | 1245 |
| R2.5-3 | R2.5 | 0.0340 | 1041 |
| R2.5-4 | R2.5 | 0.0454 | 607 |
| R2.5-5 | R2.5 | 0.0454 | 761 |
| R2.5-6 | R2.5 | 0.0568 | 378 |
| R2.5-7 | R2.5 | 0.0567 | 429 |
| R2.5-8 | R2.5 | 0.0718 | 242 |
| R2.5-9 | R2.5 | 0.0679 | 346 |
| R2.5-10 | R2.5 | 0.0794 | 265 |
| R2.5-11 | R2.5 | 0.0791 | 212 |
| R2.5-12 | R2.5 | 0.0904 | 210 |
| R2.5-13 | R2.5 | 0.0903 | 221 |
| R2.5-14 | R2.5 | 0.1015 | 205 |
| R2.5-15 | R2.5 | 0.1015 | 163 |
| R2.5-16 | R2.5 | 0.1126 | 189 |
| R2.5-17 | R2.5 | 0.1126 | 156 |
| R2.5-18 | R2.5 | 0.1237 | 132 |
| R2.5-19 | R2.5 | 0.1237 | 129 |
| R2.5-20 | R2.5 | 0.1419 | 106 |
| R2.5-21 | R2.5 | 0.1346 | 114 |
| Specimen Name | Geometry Type | ||
|---|---|---|---|
| R5-1 | R5 | 0.0308 | 4427 |
| R5-2 | R5 | 0.0461 | 1700 |
| R5-3 | R5 | 0.0457 | 1072 |
| R5-4 | R5 | 0.0603 | 733 |
| R5-5 | R5 | 0.0589 | 953 |
| R5-6 | R5 | 0.0727 | 623 |
| R5-7 | R5 | 0.0747 | 527 |
| R5-8 | R5 | 0.0893 | 342 |
| R5-9 | R5 | 0.0869 | 543 |
| R5-10 | R5 | 0.1050 | 297 |
| R5-12 | R5 | 0.1010 | 374 |
| R5-13 | R5 | 0.1154 | 264 |
| R5-14 | R5 | 0.1156 | 290 |
| R5-15 | R5 | 0.1146 | 228 |
| R5-16 | R5 | 0.1287 | 152 |
| R5-17 | R5 | 0.1276 | 272 |
| R5-18 | R5 | 0.1418 | 179 |
| R5-19 | R5 | 0.1467 | 155 |
| R5-20 | R5 | 0.1403 | 177 |
| R5-21 | R5 | 0.1540 | 163 |
| R5-22 | R5 | 0.1531 | 174 |
| R5-23 | R5 | 0.1663 | 144 |
| R5-24 | R5 | 0.1685 | 189 |
| R5-25 | R5 | 0.1652 | 163 |
Appendix B. Abaqus USDFLD Subroutine
Appendix B.1. Full Fortran Code of Abaqus USDFLD Subroutine
C Material model by Miro Fumfera C
C version 2019-11-10 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C USDFLD Subroutine for 08Ch18N10T Austenitic Stainless Steel
C Original modely by Radim Halama
C modified by Miro Fumfera for 08Ch18N10T
SUBROUTINE USDFLD(FIELD,STATEV,PNEWDT,DIRECT,T,CELENT,
1 TIME,DTIME,CMNAME,ORNAME,NFIELD,NSTATV,NOEL,NPT,LAYER,
2 KSPT,KSTEP,KINC,NDI,NSHR,COORD,JMAC,JMATYP,MATLAYO,LACCFLA)
INCLUDE 'ABA_PARAM.INC'
CHARACTER*80 CMNAME,ORNAME
CHARACTER*3 FLGRAY(15)
DIMENSION FIELD(NFIELD),STATEV(NSTATV),DIRECT(3,3),T(3,3),TIME(2)
DIMENSION ARRAY(15),JARRAY(15),JMAC(*),JMATYP(*),COORD(*)
parameter ZERO=0D0,ONE=1D0,TWO=2D0,THREE=3D0,TOLER=1D-12,
+ NTENS=6 !NTENS=4 for Axisymetric, NTENS=6 for 3D
real*8 RMused,RM,RMmax,RMmin,oRM,dRM, RMRused,RMR,oRMR,dRMR,
+ heavisideG,DDP,G,DirVec(NTENS),DirVecR(NTENS)
real*8 ALPHAv(NTENS),dALPHA1v(NTENS),ALPHA1v(NTENS),
+ dALPHA2v(NTENS),ALPHA2v(NTENS),dALPHA3v(NTENS),ALPHA3v(NTENS),
+ dALPHAv(NTENS),oALPHAv(NTENS),magALPHAv
real*8 ALPHAr(NTENS),dALPHA1r(NTENS),ALPHA1r(NTENS),
+ dALPHA2r(NTENS),ALPHA2r(NTENS),dALPHA3r(NTENS),ALPHA3r(NTENS),
+ dALPHAr(NTENS),oALPHAr(NTENS),magALPHAr
real*8 EPLAS(NTENS),oEPLAS(NTENS),dEPLAS(NTENS),EQPLAS,oEQPLAS,
+ dEQPLAS,FLOW(NTENS)
real*8 R,oR,dR,AR,BR,CR,ER
real*8 PhiInfty,dPHIcyc,PHIcyc,oPHIcyc,PHI0,PHI
real*8 AInfty,BInfty,CInfty,DInfty,EInfty
real*8 AOmega,BOmega,COmega
real*8 KShear
real*8 C1,GAMMA1,C2,GAMMA2,C3,GAMMA3
integer K1,iEPLAS,iALPHA1v,iALPHA2v,iALPHA3v,iEQPLAS,iRM,iPHI,
+ iPHIcyc,iALPHAv,iR,iFIELD1,iFIELD2,iALPHA1r,iALPHA2r,iALPHA3r,
+ iRMR,iALPHAr
parameter(iEPLAS=7,iALPHA1v=31,iALPHA2v=37,iALPHA3v=43,iEQPLAS=49,
+ iR=50,iRM=51,iPHI=52,iPHIcyc=53,iPhiInfty=54,iRMR=61,iALPHA1r=71,
+ iALPHA2r=77,iALPHA3r=83,iRMRused=95,iRMused=96,iALPHAv=97,
+ iALPHAr=94,iFIELD1=98,iFIELD2=99)
C Material parameters
C1 = 6.339971e+04
GAMMA1 = 1.485569e+02
C2 = 9.999778e+03
GAMMA2 = 9.113512e+02
C3 = 2000
GAMMA3 = 0
SYIELD = 150
PHI0 = 2.317802e+00
AInfty = -1.312737e-09
BInfty = 1.798138e-06
CInfty = -8.670490e-04
DInfty = 1.667770e-01
EInfty = -1.060028e+01
RMmin = 1.305410e+02
RMmax = 5.065918e+02
BR = 3.011316e-01
CR = 1.486489e-01
ER = 1.181843e-02
AOmega = 0
BOmega = 2.002387e-13
COmega = -4.859126e+00
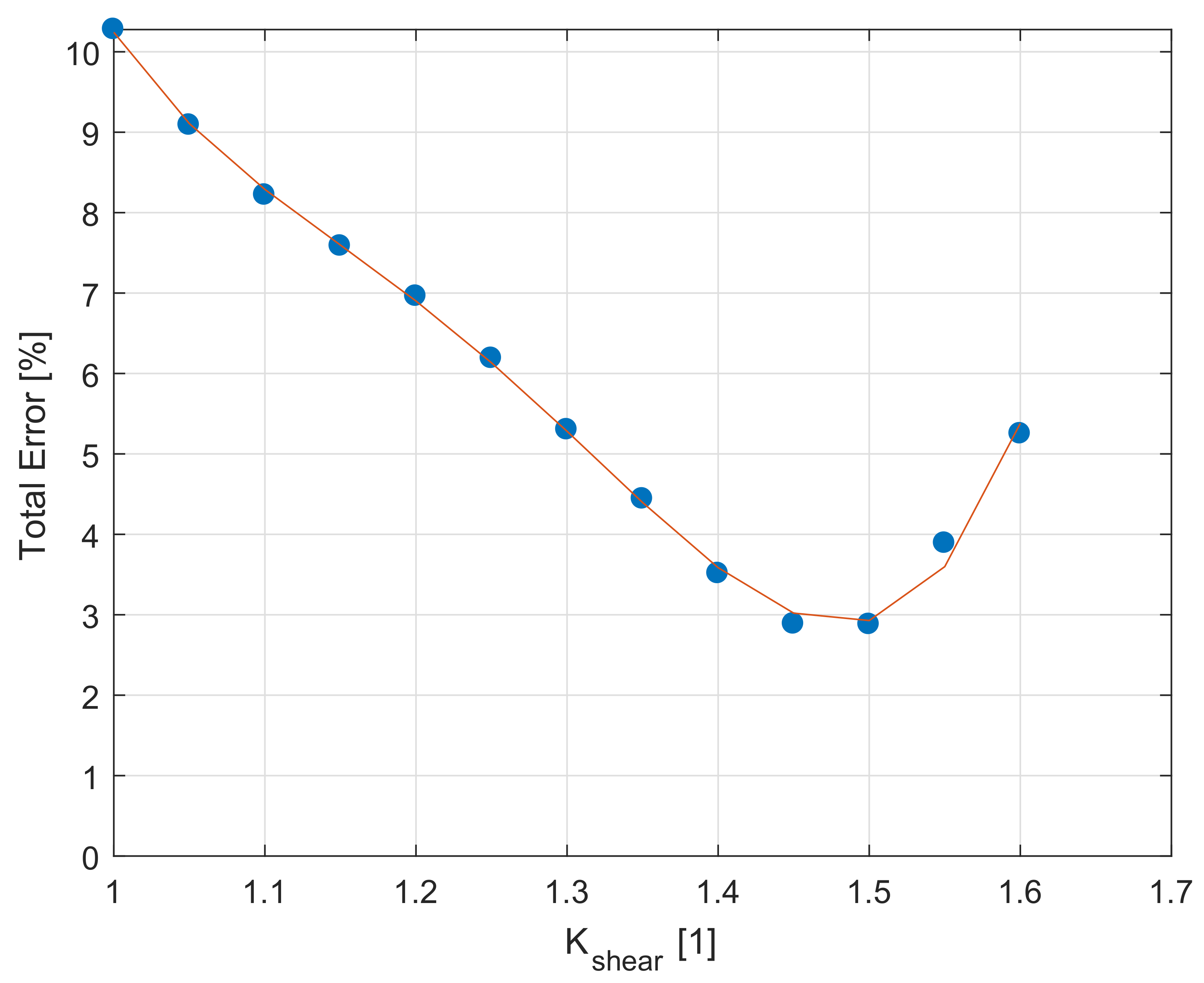
KShear = 1.50
C get PE components
call GETVRM('PE',ARRAY,JARRAY,FLGRAY,JRCD,JMAC,JMATYP,
+ MATLAYO,LACCFLA)
C EQPLAS
EQPLAS = ARRAY(7)
oEQPLAS = STATEV(iEQPLAS)
dEQPLAS = EQPLAS - oEQPLAS
C get PE
do K1=1,NTENS
oEPLAS(K1) = STATEV(iEPLAS-1+K1)
EPLAS(K1) = ARRAY(K1)
dEPLAS(K1) = EPLAS(K1) - oEPLAS(K1)
enddo
C get ALPHAv
do K1=1,NTENS
ALPHA1v(K1) = STATEV(iALPHA1v-1+K1)
ALPHA2v(K1) = STATEV(iALPHA2v-1+K1)
ALPHA3v(K1) = STATEV(iALPHA3v-1+K1)
oALPHAv(K1) = STATEV(iALPHAv-1+K1)
ALPHA1r(K1) = STATEV(iALPHA1r-1+K1)
ALPHA2r(K1) = STATEV(iALPHA2r-1+K1)
ALPHA3r(K1) = STATEV(iALPHA3r-1+K1)
oALPHAr(K1) = STATEV(iALPHAr-1+K1)
enddo
C get FLOW vector
if(dEQPLAS.gt.ZERO) then
do K1=1,NDI
FLOW(K1) = dEPLAS(K1)/dEQPLAS
enddo
do K1=NDI+1,NTENS
FLOW(K1) = dEPLAS(K1)/TWO/dEQPLAS
enddo
else
do K1=1,NTENS
FLOW(K1) = ZERO
enddo
endif
C RM
RM = STATEV(iRM)
oRM = RM
C dALPHAv
do K1=1, NDI
dALPHA1v(K1) = (TWO/THREE*C1*dEQPLAS*FLOW(K1) -
+ GAMMA1*ALPHA1v(K1)*dEQPLAS)/(ONE+GAMMA1*dEQPLAS)
dALPHA2v(K1) = (TWO/THREE*C2*dEQPLAS*FLOW(K1) -
+ GAMMA2*ALPHA2v(K1)*dEQPLAS)/(ONE+GAMMA2*dEQPLAS)
dALPHA3v(K1) = (TWO/THREE*C3*dEQPLAS*FLOW(K1) -
+ GAMMA3*ALPHA3v(K1)*dEQPLAS)/(ONE+GAMMA3*dEQPLAS)
ALPHAv(K1) = (ALPHA1v(K1)+dALPHA1v(K1)) +
+ (ALPHA2v(K1)+dALPHA2v(K1)) + (ALPHA3v(K1)+dALPHA3v(K1))
!dALPHAv(K1) = ALPHAv(K1)-oALPHAv(K1)
dALPHAv(K1) = dALPHA1v(K1) + dALPHA2v(K1) + dALPHA3v(K1)
enddo
do K1=NDI+1, NTENS
dALPHA1v(K1) = (TWO/THREE*C1*dEQPLAS*FLOW(K1) -
+ GAMMA1*KShear*ALPHA1v(K1)*dEQPLAS)/(ONE+GAMMA1*dEQPLAS)
dALPHA2v(K1) = (TWO/THREE*C2*dEQPLAS*FLOW(K1) -
+ GAMMA2*KShear*ALPHA2v(K1)*dEQPLAS)/(ONE+GAMMA2*dEQPLAS)
dALPHA3v(K1) = (TWO/THREE*C3*dEQPLAS*FLOW(K1) -
+ GAMMA3*KShear*ALPHA3v(K1)*dEQPLAS)/(ONE+GAMMA3*dEQPLAS)
ALPHAv(K1) = (ALPHA1v(K1)+dALPHA1v(K1)) +
+ (ALPHA2v(K1)+dALPHA2v(K1)) + (ALPHA3v(K1)+dALPHA3v(K1))
!dALPHAv(K1) = ALPHAv(K1)-oALPHAv(K1)
dALPHAv(K1) = dALPHA1v(K1) + dALPHA2v(K1) + dALPHA3v(K1)
enddo
do K1=1, NTENS
ALPHA1v(K1) = ALPHA1v(K1) + dALPHA1v(K1)
ALPHA2v(K1) = ALPHA2v(K1) + dALPHA2v(K1)
ALPHA3v(K1) = ALPHA3v(K1) + dALPHA3v(K1)
ALPHAv(K1) = ALPHA1v(K1) + ALPHA2v(K1) + ALPHA3v(K1)
enddo
C magALPHAv
magALPHAv = ZERO
do K1=1, NDI
magALPHAv = magALPHAv + ALPHAv(K1)**2
enddo
do K1=NDI+1, NTENS
magALPHAv = magALPHAv + TWO*ALPHAv(K1)**2
enddo
magALPHAv = sqrt(THREE/TWO*magALPHAv)
C G function
G = magALPHAv - RM
if(magALPHAv.gt.ZERO) then
do K1 = 1, NTENS
DirVec(K1)=ALPHAv(K1)/magALPHAv
enddo
else
do K1 = 1, NTENS
DirVec(K1) = ZERO
enddo
endif
C double dot product DDP
DDP = ZERO
do K1 = 1, NDI
DDP = DDP+DirVec(K1)*dALPHAv(K1)
enddo
do K1 = NDI+1, NTENS
DDP = DDP+TWO*DirVec(K1)*dALPHAv(K1)
enddo
C heaviside function of G
if (G.gt.ZERO) then
heavisideG = ONE
elseif (abs(G).lt.TOLER) then
heavisideG = ONE/TWO
else
heavisideG = ZERO
endif
C memory surface RM
dRM = heavisideG*abs(DDP)
RM = oRM + dRM
if (RM.lt.RMmin) then
RMused = RMmin
elseif (RM.gt.RMmax) then
RMused = RMmax
else
RMused = RM
endif
C RMR
RMR = STATEV(iRMR)
oRMR = RMR
do K1=1, NDI
dALPHA1r(K1) = (TWO/THREE*C1*dEQPLAS*FLOW(K1) -
+ GAMMA1*ALPHA1r(K1)*dEQPLAS)/(ONE+GAMMA1*dEQPLAS)
dALPHA2r(K1) = (TWO/THREE*C2*dEQPLAS*FLOW(K1) -
+ GAMMA2*ALPHA2r(K1)*dEQPLAS)/(ONE+GAMMA2*dEQPLAS)
dALPHA3r(K1) = (TWO/THREE*C3*dEQPLAS*FLOW(K1) -
+ GAMMA3*ALPHA3r(K1)*dEQPLAS)/(ONE+GAMMA3*dEQPLAS)
ALPHAr(K1) = (ALPHA1r(K1)+dALPHA1r(K1)) +
+ (ALPHA2r(K1)+dALPHA2r(K1)) + (ALPHA3r(K1)+dALPHA3r(K1))
!dALPHAr(K1) = ALPHAr(K1)-oALPHAr(K1)
dALPHAr(K1) = dALPHA1r(K1) + dALPHA2r(K1) + dALPHA3r(K1)
enddo
do K1=NDI+1, NTENS
dALPHA1r(K1) = (TWO/THREE*C1*dEQPLAS*FLOW(K1) -
+ GAMMA1*KShear*ALPHA1r(K1)*dEQPLAS)/(ONE+GAMMA1*dEQPLAS)
dALPHA2r(K1) = (TWO/THREE*C2*dEQPLAS*FLOW(K1) -
+ GAMMA2*KShear*ALPHA2r(K1)*dEQPLAS)/(ONE+GAMMA2*dEQPLAS)
dALPHA3r(K1) = (TWO/THREE*C3*dEQPLAS*FLOW(K1) -
+ GAMMA3*KShear*ALPHA3r(K1)*dEQPLAS)/(ONE+GAMMA3*dEQPLAS)
ALPHAr(K1) = (ALPHA1r(K1)+dALPHA1r(K1)) +
+ (ALPHA2r(K1)+dALPHA2r(K1)) + (ALPHA3r(K1)+dALPHA3r(K1))
!dALPHAr(K1) = ALPHAr(K1)-oALPHAr(K1)
dALPHAr(K1) = dALPHA1r(K1) + dALPHA2r(K1) + dALPHA3r(K1)
enddo
do K1=1, NTENS
ALPHA1r(K1) = ALPHA1r(K1) + dALPHA1r(K1)
ALPHA2r(K1) = ALPHA2r(K1) + dALPHA2r(K1)
ALPHA3r(K1) = ALPHA3r(K1) + dALPHA3r(K1)
ALPHAr(K1) = ALPHA1r(K1) + ALPHA2r(K1) + ALPHA3r(K1)
enddo
C magALPHAr
magALPHAr = ZERO
do K1=1, NDI
magALPHAr = magALPHAr + ALPHAr(K1)**2
enddo
do K1=NDI+1, NTENS
magALPHAr = magALPHAr + TWO*ALPHAr(K1)**2
enddo
magALPHAr = sqrt(THREE/TWO*magALPHAr)
C G function
G = magALPHAr - RMR
if(magALPHAr.gt.ZERO) then
do K1 = 1, NTENS
DirVecR(K1)=ALPHAr(K1)/magALPHAr
enddo
else
do K1 = 1, NTENS
DirVecR(K1) = ZERO
enddo
endif
C double dot product DDP
DDP = ZERO
do K1 = 1, NDI
DDP = DDP+DirVecR(K1)*dALPHAr(K1)
enddo
do K1 = NDI+1, NTENS
DDP = DDP+TWO*DirVecR(K1)*dALPHAr(K1)
enddo
C heaviside function of G
if (G.gt.ZERO) then
heavisideG = ONE
elseif (abs(G).lt.TOLER) then
heavisideG = ONE/TWO
else
heavisideG = ZERO
endif
C memory surface RMR
dRMR = heavisideG*abs(DDP)
RMR = oRMR + dRMR
if (RMR.lt.RMmin) then
RMRused = RMmin
elseif (RMR.gt.RMmax) then
RMRused = RMmax
else
RMRused = RMR
endif
C R
oR = STATEV(iR)
AR = CR*exp(ER*RMRused)
dR = AR*((EQPLAS+dEQPLAS)**BR-EQPLAS**BR)
R = oR + dR;
C PHIinfty
PhiInfty = AInfty*RMused**4 + BInfty*RMused**3 +
+ CInfty*RMused**2 + DInfty*RMused + EInfty
C Omega
OMEGA∼= AOmega+BOmega*(RMused)**-COmega
C PHIcyc
oPHIcyc = STATEV(iPHIcyc)
dPHIcyc = OMEGA*(PhiInfty-oPHIcyc)*DEQPLAS
PHIcyc = oPHIcyc + dPHIcyc
C PHI
PHI = PHI0 + PHIcyc
C save STATEV
STATEV(iEQPLAS) = EQPLAS
do K1=1,NTENS
STATEV(iEPLAS-1+K1) = EPLAS(K1)
STATEV(iALPHA1v-1+K1) = ALPHA1v(K1)
STATEV(iALPHA2v-1+K1) = ALPHA2v(K1)
STATEV(iALPHA3v-1+K1) = ALPHA3v(K1)
STATEV(iALPHAv-1+K1) = ALPHAv(K1)
STATEV(iALPHA1r-1+K1) = ALPHA1r(K1)
STATEV(iALPHA2r-1+K1) = ALPHA2r(K1)
STATEV(iALPHA3r-1+K1) = ALPHA3r(K1)
STATEV(iALPHAr-1+K1) = ALPHAr(K1)
STATEV(120+K1) = dALPHAv(K1)
enddo
STATEV(iR) = R
STATEV(iRM) = RM
STATEV(iRMR) = RMR
STATEV(iRMused) = RMused
STATEV(iRMRused) = RMRused
STATEV(iPHIcyc) = PHIcyc
STATEV(iPHI) = PHI
STATEV(iPhiInfty) = PhiInfty
STATEV(127) = SYIELD+R
STATEV(128) = DDP
C FIELD(1)
FIELD(1) = SYIELD+R
STATEV(iFIELD1) = FIELD(1)
C FIELD(2)
FIELD(2) = PHI
STATEV(iFIELD2) = FIELD(2)
RETURN
END
Appendix B.2. Material Parameters Definition in the Abaqus Input File
*Material, name=Material-1
*Depvar
128
*Elastic
210000.0,0.3
*Plastic, dependencies=2, hardening=COMBINED, datatype=PARAMETERS,
number backstresses=3
** Material data as∼a∼function of FIELD1 and∼FIELD2 follows:
SYIELD,C1,GAMMA1,C2,GAMMA2,C3,GAMMA3,FIDEL1,FIELD2
%%
** Material data as∼a∼function of FIELD1 and∼FIELD2 follows: ** ... 250.0,63399.70889,222.83539,9999.77788,1367.02686,2000.0,0.0,250.0,1.5 150.0,63399.70889,237.69108,9999.77788,1458.16199,2000.0,0.0,150.0,1.6 151.0,63399.70889,237.69108,9999.77788,1458.16199,2000.0,0.0,151.0,1.6 ** ...
References
- Halama, R.; Sedlák, J.; Šofer, M. Phenomenological Modelling of Cyclic Plasticity. In Numerical Modelling; Miidla, P., Ed.; IntechOpen: Rijeka, Croatia, 2012; pp. 329–354. [Google Scholar]
- Halama, R.; Fumfera, J.; Gál, P.; Kumar, T.; Makropulos, A. Modeling the Strain-Range Dependent Cyclic Hardening of SS304 and 08Ch18N10T Stainless Steel with a Memory Surface. Metals 2019, 9, 832. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, J. Benchmark experiments and characteristic cyclic plastic deformation behavior. Int. J. Plast. 2008, 24, 1481–1515. [Google Scholar] [CrossRef]
- Facheris, G.; Janssens, K.G.F.; Foletti, S. Multiaxial fatigue behavior of AISI 316L subjected to strain-controlled and ratcheting paths. Int. J. Fatigue 2014, 68, 195–208. [Google Scholar] [CrossRef]
- Kim, C. Nondestructive Evaluation of Strain-Induced Phase Transformation and Damage Accumulation in Austenitic Stainless Steel Subjected to Cyclic Loading. Metals 2018, 8, 14. [Google Scholar] [CrossRef]
- Borodii, M.; Shukayev, S. Additional cyclic strain hardening and its relation to material structure, mechanical characteristics, and lifetime. Int. J. Fatigue 2007, 29, 1184–1191. [Google Scholar] [CrossRef]
- Jin, D.; Tian, D.J.; Li, J.H.; Sakane, M. Low-cycle fatigue of 316L stainless steel under proportional and nonproportional loadings. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 850–858. [Google Scholar] [CrossRef]
- Xing, R.; Dunji, Y.; Shouwen, S.; Xu, C. Cyclic deformation of 316L stainless steel and constitutive modeling under non-proportional variable loading path. Int. J. Plast. 2019, 120, 127–146. [Google Scholar] [CrossRef]
- Srnec Novak, J.; Benasciutti, D.; De Bona, F.; Stanojevic, A.S.; De Luca, A.; Raffaglio, Y. Estimation of Material Parameters in Nonlinear Hardening Plasticity Models and Strain Life Curves for CuAg Alloy. IOP Conf. Ser. Mater. Sci. Eng. 2016, 119, 012020. [Google Scholar] [CrossRef]
- Benallal, A.; Marquis, D. Constitutive Equations for Nonproportional Cyclic Elasto-Viscoplasticity. J. Eng. Mater. Technol. 1987, 109, 326–336. [Google Scholar] [CrossRef]
- Tanaka, E. A nonproportionality parameter and a cyclic viscoplastic constitutive model taking into account amplitude dependences and memory effects of isotropic hardening. Eur. J. Mech. A/Solids 1994, 13, 155–173. [Google Scholar]
- Jiang, Y.; Sehitoglu, H. Modeling of cyclic ratchetting plasticity, part I: Development of constitutive relations. J. Appl. Mech. 1996, 63, 720–725. [Google Scholar] [CrossRef]
- ASTM Standard E606-92. Standard Practise for Strain-Controlled Fatigue Testing; ASTM International: West Conshohocken, PA, USA, 1998. [Google Scholar]
- Fumfera, J.; Halama, R.; Kuželka, J.; Španiel, M. Strain-Range Dependent Cyclic Plasticity Material Model Calibration for the 08Ch18N10T Steel. In Proceedings of the 33rd Conference with International Participation on Computational Mechanics, Špičák, Czech Republic, 6–8 November 2017. [Google Scholar]
- Abdel-Karim, M.; Ohno, N. Kinematic hardening model suitable for ratchetting with steady-state. Int. J. Plast. 2000, 16, 225–240. [Google Scholar] [CrossRef]
- Peč, M.; Šebek, F.; Zapletal, J.; Petruška, J.; Hassan, T. Automated calibration of advanced cyclic plasticity model parameters with sensitivity analysis for aluminium alloy 2024-T351. Adv. Mech. Eng. 2019, 11, 1–14. [Google Scholar] [CrossRef]
- Halama, R.; Pagáč, M.; Paška, Z.; Pavlíček, P.; Chen, X. Ratcheting Behaviour of 3D Printed and Conventionally Produced SS316L Material. In Proceedings of the ASME 2019 Pressure Vessels & Piping Conference PVP2019, San Antonio, TX, USA, 14–19 July 2019. Paper Number PVP2019-93384. [Google Scholar]

| 210,000 | 0.3 | 150 | 63,400 | 148.6 | 10,000 |
| 911.4 | 2000 | 0 | |||
| 130.54 | |||||
| 0 | −4.8591 | 506.59 | 2.3178 | 1.5 |
| Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] | Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] |
|---|---|---|---|---|---|
| E9-1 | 2.9226 | 1.8207 | E9-10 | 7.8144 | 8.8757 |
| E9-2 | 2.3311 | 1.2756 | E9-11 | 2.5028 | 3.9003 |
| E9-3 | 2.4027 | 1.1938 | E9-12 | 4.3523 | 6.5915 |
| E9-4 | 1.6977 | 0.7773 | E9-13 | 4.0929 | 3.4343 |
| E9-5 | 8.0687 | 7.0447 | E9-14 | 2.1610 | 3.8515 |
| E9-6 | 8.8658 | 7.4521 | E9-15 | 2.9195 | 2.9485 |
| E9-7 | 11.7310 | 10.4229 | E9-16 | 1.8601 | 2.7524 |
| E9-8 | 3.8241 | 3.9171 | E9-17 | 4.9766 | 2.7579 |
| E9-9 | 9.8245 | 9.5508 |
| Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] | Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] |
|---|---|---|---|---|---|
| NT-1 | 1.9100 | 4.0682 | NT-5 | 14.2137 | 1.3947 |
| NT-2 | 0.8367 | 5.9823 | NT-6 | 15.5549 | 2.2815 |
| NT-3 | 11.2048 | 1.3797 | NT-7 | 13.1168 | 1.5014 |
| NT-4 | 11.1021 | 1.0934 | NT-8 | 8.8054 | 4.7887 |
| Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] | Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] |
|---|---|---|---|---|---|
| R1.2-1 | 2.8075 | 2.4172 | R1.2-10 | 1.6518 | 1.7538 |
| R1.2-2 | 3.7011 | 3.1679 | R1.2-11 | 2.0827 | 2.2332 |
| R1.2-3 | 2.2438 | 2.2027 | R1.2-12 | 3.9411 | 3.2028 |
| R1.2-4 | 2.8530 | 2.7056 | R1.2-13 | 2.5308 | 3.1540 |
| R1.2-5 | 2.8984 | 2.7105 | R1.2-14 | 1.4521 | 1.8444 |
| R1.2-6 | 4.7877 | 4.4405 | R1.2-15 | 3.6781 | 2.6435 |
| R1.2-7 | 1.4888 | 1.4897 | R1.2-16 | 1.5820 | 1.9106 |
| R1.2-8 | 7.1382 | 6.7943 | R1.2-17 | 1.6089 | 2.5930 |
| R1.2-9 | 2.4171 | 2.2355 | R1.2-18 | 1.2789 | 2.2219 |
| Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] | Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] |
|---|---|---|---|---|---|
| R2.5-1 | 7.3714 | 7.1025 | R2.5-12 | 2.1944 | 1.6489 |
| R2.5-2 | 8.1586 | 7.6327 | R2.5-13 | 1.2466 | 1.0057 |
| R2.5-3 | 9.1468 | 8.6587 | R2.5-14 | 8.7778 | 9.1473 |
| R2.5-4 | 6.8139 | 6.8130 | R2.5-15 | 2.6624 | 3.0678 |
| R2.5-5 | 6.6714 | 6.6118 | R2.5-16 | 1.4643 | 1.3563 |
| R2.5-6 | 9.9838 | 9.1708 | R2.5-17 | 0.9873 | 1.5697 |
| R2.5-7 | 4.3249 | 3.4860 | R2.5-18 | 1.4020 | 1.4515 |
| R2.5-8 | 3.8551 | 3.8250 | R2.5-19 | 1.6099 | 2.6423 |
| R2.5-9 | 1.0034 | 0.9027 | R2.5-20 | 0.9634 | 2.4069 |
| R2.5-10 | 4.7921 | 4.9816 | R2.5-21 | 4.1944 | 3.2605 |
| R2.5-11 | 1.9673 | 2.1464 |
| Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] | Specimen Name | Orig. Model Mean Err. [%] | Mod. Model Mean Err. [%] |
|---|---|---|---|---|---|
| R5-1 | 2.1303 | 1.4186 | R5-13 | 6.7479 | 6.8700 |
| R5-2 | 2.0673 | 1.8112 | R5-14 | 5.1055 | 5.4414 |
| R5-3 | 0.7021 | 0.8284 | R5-15 | 1.3043 | 1.4251 |
| R5-4 | 0.9757 | 0.9284 | R5-16 | 1.1829 | 1.3661 |
| R5-5 | 1.4847 | 1.4209 | R5-17 | 3.6903 | 3.6048 |
| R5-6 | 1.7435 | 1.6993 | R5-18 | 3.1399 | 2.9518 |
| R5-7 | 2.9066 | 2.7548 | R5-19 | 6.1649 | 6.1226 |
| R5-8 | 5.3372 | 5.4106 | R5-20 | 2.8263 | 2.6683 |
| R5-9 | 4.9004 | 4.5530 | R5-21 | 1.0485 | 1.2882 |
| R5-10 | 2.3623 | 2.6227 | R5-22 | 8.2167 | 7.6119 |
| R5-11 | 7.0110 | 6.8065 | R5-23 | 2.2011 | 1.6441 |
| R5-12 | 2.3912 | 3.1025 | R5-24 | 3.5803 | 3.1425 |
| Geometry | The Original Nodel [2] Total Error [%] | The Modified Model Total Error [%] |
|---|---|---|
| E9 | 4.84 | 4.61 |
| NT | 9.60 | 2.85 |
| R1.2 | 2.79 | 2.76 |
| R2.5 | 4.27 | 4.23 |
| R5 | 3.30 | 3.23 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fumfera, J.; Halama, R.; Procházka, R.; Gál, P.; Španiel, M. Strain Range Dependent Cyclic Hardening of 08Ch18N10T Stainless Steel—Experiments and Simulations. Materials 2019, 12, 4243. https://doi.org/10.3390/ma12244243
Fumfera J, Halama R, Procházka R, Gál P, Španiel M. Strain Range Dependent Cyclic Hardening of 08Ch18N10T Stainless Steel—Experiments and Simulations. Materials. 2019; 12(24):4243. https://doi.org/10.3390/ma12244243
Chicago/Turabian StyleFumfera, Jaromír, Radim Halama, Radek Procházka, Petr Gál, and Miroslav Španiel. 2019. "Strain Range Dependent Cyclic Hardening of 08Ch18N10T Stainless Steel—Experiments and Simulations" Materials 12, no. 24: 4243. https://doi.org/10.3390/ma12244243
APA StyleFumfera, J., Halama, R., Procházka, R., Gál, P., & Španiel, M. (2019). Strain Range Dependent Cyclic Hardening of 08Ch18N10T Stainless Steel—Experiments and Simulations. Materials, 12(24), 4243. https://doi.org/10.3390/ma12244243






