Research Progress on Heat Transfer of Herringbone Plate Heat Exchangers Under Single-Phase/Two-Phase Flow

Abstract

Against the backdrop of the “dual carbon” strategy, enhancing energy utilization efficiency and promoting low-carbon urban heating have become key directions for energy system transformation. Due to the compact structure, high heat transfer efficiency, and strong adaptability, herringbone plate heat exchangers have emerged as critical intermediate heat exchange equipment in long-distance heating systems. This paper reviews research on the heat transfer performance of herringbone plate heat exchangers, systematically examining fluid flow patterns within plate heat exchangers and the mechanisms influencing thermohydraulic performance under single-phase and two-phase flow conditions, along with recent advancements. First, factors affecting fluid flow within herringbone corrugated plates are introduced. Subsequently, recent experimental and numerical simulation advancements under single-phase and two-phase conditions are presented, along with corresponding performance correlation equations. In contrast, two-phase heat transfer mechanisms are more complex, with relatively insufficient research and a lack of universally applicable theoretical models and performance correlations. This paper argues that future efforts should focus on strengthening research into two-phase flow heat transfer mechanisms and developing more universal and predictive performance models to support the efficient application of plate heat exchangers in low-carbon heating and industrial energy conservation.

1. Introduction

The global energy structure is undergoing profound transformation. The widespread reliance on conventional fossil fuels has not only led to serious environmental degradation but also intensified global climate change, driving nations to speed up their shift toward cleaner energy sources. Against this backdrop, enhancing energy efficiency and reducing carbon emissions have become a global consensus. District heating, particularly the long-distance transportation of heat utilizing waste heat from power plants, is emerging as a highly efficient and clean energy utilization method. It is increasingly becoming a key direction for optimizing urban energy systems [1,2,3,4,5].

As a major energy consumer, China has continuously optimized its power generation mix in recent years, with the installed capacity of non-fossil energy sources steadily increasing [1,6,7]. However, coal-fired power generation still accounts for a significant proportion [8,9,10,11,12,13]. Efficient utilization of waste heat from power plants can not only ensure power supply but also improve the overall efficiency of the entire energy system [14,15,16,17,18]. Long-distance district heating systems have emerged in response to this need [19,20,21,22,23]. By transporting heat generated from thermal power plants or other industrial waste heat sources through extensive pipeline networks to various urban heat consumption terminals, these systems enable efficient allocation and sharing of thermal energy resources across regions [24,25,26,27,28,29]. However, such systems face numerous operational challenges, including long transmission distances, significant heat loss, and complex operational control [30,31]. To maintain stable temperature and pressure within the heating network during transmission and enable flexible regulation between different zones, intermediate heat exchange stations have become indispensable components of the system [32]. These stations not only perform heat exchange and pressure regulation but must also exhibit excellent thermal response capabilities and operational stability. Plate heat exchangers are favored for intermediate stations in long-distance heating systems because they pack large heat-transfer capacity into a small, highly adaptable footprint [33,34,35,36]. Corrugated metal plates are stacked to create slim channels; hot and cold streams flow in opposite directions on either side, exchanging heat efficiently. Their performance comes from a high surface-area-to-volume ratio, large heat-transfer coefficients, and the ability to react quickly to temperature changes, so they cope with a broad range of duties [37,38,39].

Long-distance heating systems serve as a vital means for achieving low-carbon urban heating, and their efficient operation relies heavily on intermediate heat exchange equipment [40,41,42,43,44]. The remarkable heat transfer capacity and optimized structure of herringbone corrugated plate heat exchangers make them indispensable core components within these systems [45,46,47,48,49]. As urban heating systems demand ever-higher levels of energy efficiency, stability, and intelligence, research and optimization of plate heat exchanger performance face increasingly stringent requirements [40,41,42,43,44,45,46,47]. Exploring the influence of structural parameters on heat transfer and pressure drop performance in detail is not only of great theoretical value but also offers essential practical guidance for engineering [41,42,43,44,45,46,47,48,49,50].

Since the birth of the first thin-plate stamped plate heat exchanger, this equipment has been widely applied across multiple fields including chemical engineering, food processing, pharmaceuticals, and HVAC [51,52,53,54,55]. Its development journey has also witnessed the continuous advancement of heat transfer technology. The earliest plate heat exchanger was invented by Germans in the 1880s [55,56]. In 1930, the UK developed the channel-type plate heat exchanger. Subsequently, the emergence of stainless steel materials and rubber seal structures established the fundamental configuration of modern plate heat exchangers. Research on plate heat exchangers in China began relatively late, starting in the 1960s when the Lanzhou Petrochemical Machinery Factory developed the first domestically produced plate heat exchanger [57,58,59,60]. After over 50 years of development, China has achieved significant progress in the design, manufacturing, and application of plate heat exchangers [61,62,63,64]. These devices consist of multiple parallel thin plates—known as heat transfer plates—stacked together. The plates are stamped from metal sheets, typically rectangular in shape with an aspect ratio of approximately 2.7 to 3.3 with a thickness of approximately 0.6 mm to 0.8 mm [51,52,53,54]. The surface features corrugations, with a hole at each corner. Between the holes and corrugations lies a flow-guiding zone equipped with flow-guiding grooves. Positioning holes are located at both ends of the plate. The plates are connected and positioned by guide rods. Removable plate heat exchangers feature sealing gasket grooves pressed around the plate periphery and outside the corner holes [61,62,63,64,65]. Sealing gaskets, typically made of rubber or asbestos (differing primarily in temperature tolerance), are installed within these grooves. These gaskets form flow channels between plates and control the opening/closing of corner holes [66,67,68]. By flowing on opposite sides of the plates, the hot and cold media enable heat exchange through the temperature difference [69]. The plates are secured together by a clamping plate and bolts, ensuring tight contact between the plates and gaskets to prevent fluid leakage, as shown in Figure 1.

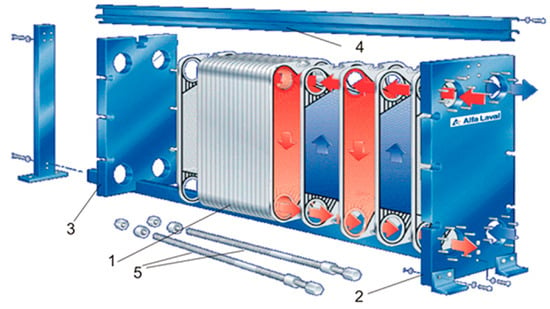
Figure 1. Plate-and-frame PHE (construction scheme): 1—stack of plates with gaskets; 2—fixed-frame plate; 3—moving plate of frame; 4—carrying bar; 5—tightening bolts (courtesy of OAO Alfa Laval Potok, Korolev, Moscow region, Russian Federation) [69].

The core component of plate heat exchangers is the corrugated plate, whose surface typically features various corrugation patterns such as chevron, sawtooth, or washboard designs [70], as shown in Figure 2. Chevron corrugations are among the most commonly used plate designs, thanks to their excellent heat transfer efficiency and favorable hydrodynamic properties.

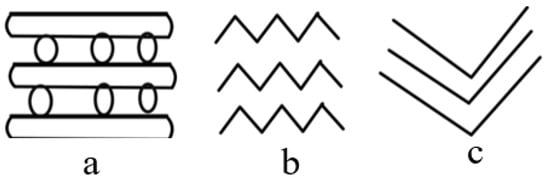
Figure 2. Common types of plate corrugations. (a): washboard, (b): zigzag, (c): chevron or herringbone.

The chevron corrugation induces intense turbulence in the fluid flow, disrupting the thermal boundary layer and enhancing heat transfer efficiency [70,71]. Simultaneously, its structure reduces flow resistance to a certain extent, achieving a favorable balance between heat transfer and resistance. The herringbone plate heat exchanger’s special corrugated pattern enhances fluid heat transfer, generally leading to a much higher heat transfer coefficient than traditional shell-and-tube designs [33]. Plate heat exchangers are generally divided into two categories according to their construction: detachable gasketed types and welded types, as shown in Figure 3. Detachable types are more widely used in long-distance heating systems due to their ease of maintenance and adaptability [71,72]. Plate materials are predominantly corrosion-resistant metals like stainless steel and titanium alloys, while gaskets are selected from rubber or asbestos based on medium temperature and chemical properties. The sealing structure between plates not only defines fluid flow paths but also directly impacts the equipment’s pressure-bearing capacity and operational safety.

Figure 3. Plate heat exchangers are categorized as: (a) Removable plate heat exchanger [72], (b) brazed plate heat exchanger [69], (c) brazed plate heat exchanger [69].

In summary, as a vital means for achieving low-carbon heating in urban areas, the efficient operation of long-distance heating systems relies heavily on intermediate heat exchange equipment [9,10,11,12]. Plate heat exchangers, particularly herringbone corrugated plate heat exchangers, have become key core components in these systems due to their outstanding heat transfer performance and structural advantages. As urban heating systems demand ever-higher levels of energy efficiency, stability, and intelligence, research and optimization of plate heat exchanger performance face increasingly stringent requirements. Thus, exploring the impact of structural parameters on heat transfer and pressure drop performance is crucial both from a theoretical standpoint and for providing valuable insights for engineering practice [13,14,15,16,17].

2. Materials and Methods

The fluid flow between the corrugated plates is a critical factor in herringbone plate heat exchangers, as it directly influences the effectiveness of heat exchange, the resistance to flow, and the overall performance of the system [13,14,15,16]. The non-linear corrugated structure significantly disturbs fluid flow: as fluid flows along the plate surface, it not only changes direction along the corrugation path but also generates intense secondary flows and vortices in the convex and concave regions of the corrugations. However, the quality of fluid flow characteristics is not solely determined by the corrugation structure alone. By varying the number of channels, the velocity field, and the degree of flow uniformity, the overall structure of the heat exchanger and the configuration of fluid paths jointly determine its thermal and hydraulic performance.

2.1. Heat Exchanger Layout

The layout of flow channels is a major determinant of the thermal efficiency and hydraulic resistance in corrugated plate heat exchangers. The primary configurations are single-pass and multi-pass layouts, each with distinct characteristics suited for different applications.

The most fundamental arrangement involves both fluids passing through only once, maintaining the same flow direction throughout the entire path, commonly referred to as the “single-pass configuration.” Within the heat exchanger, the fluid follows a single path: entering through the inlet, passing through only one plate channel, and exiting through the outlet. In this arrangement, each fluid (hot and cold) exchanges heat within its own dedicated channel. Its primary advantage lies in the ability to centralize all inlet and outlet connections on the fixed end plate. During maintenance or cleaning, only the plates need to be removed, eliminating the need to modify piping. This configuration is the most commonly used and is also known as the U-pattern arrangement. Another single-pass variant is the Z-pattern arrangement, where fluids enter and exit through opposite end plates.

Multi-channel arrangement refers to the division of a fluid into multiple streams within the heat exchanger, which then flow simultaneously through several parallel plate channels [71]. This configuration is employed in most practical industrial applications of plate heat exchangers. The hot and cold fluids pass through alternately arranged channels to facilitate heat transfer. Single-channel and multi-channel arrangements are illustrated in Figure 4.

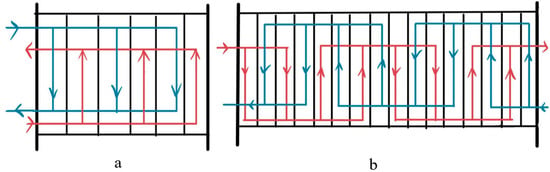
Figure 4. Arrangements of PHE. (a) U-arrangement. (b) Multi-pass PHE.

By increasing the number of channels, larger fluid flow rates can be handled to meet industrial production demands. The fluid is diverted into multiple channels, with each channel maintaining a relatively low flow velocity. This effectively reduces the overall pressure drop across the heat exchanger and decreases the power consumption of the pumping system. In summary, single-channel and multi-channel configurations represent two fundamental structural design philosophies for corrugated plate heat exchangers. Single-channel designs prioritize precision control and experimental research, while multi-channel configurations focus on meeting industrial production demands for high flow rates, efficiency, and low pressure drop. In practical applications, multi-channel layouts are more prevalent, overcoming inherent challenges through optimized plate design and fluid distribution.

2.2. Flow Path

By altering the arrangement of plate heat exchangers, the fluid flow path can be modified. Among these, vertical flow and diagonal flow represent two common fluid flow path designs, each exerting distinct effects on heat transfer efficiency, pressure drop, and fluid distribution uniformity, as illustrated in Figure 5. In corrugated plate heat exchangers, vertical flow typically refers to fluid entering and exiting along the plate’s length (usually vertically) and maintaining flow in this direction within the plate channels [60,61,62,63]. This flow pattern can be understood as: Flow Path Direction: Fluid enters from one end (e.g.; bottom) of the heat exchanger, flows upward or downward through the channels between plates, and exits from the other end (e.g.; top). Diagonal flow, often termed cross-flow or herringbone flow in plate heat exchanger design, describes a scenario where the fluid does not simply flow along the plate’s length. Instead, the corrugated plate design guides the fluid at an angle (diagonally) through the plate channels, or the two fluids exchange heat in a cross-flow configuration. Herringbone corrugated plates are the typical structure used to achieve this flow pattern.

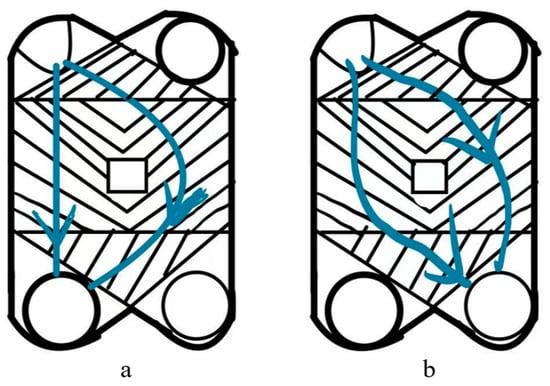
Figure 5. (a) Vertical flow plate. (b) Diagonal flow plate.

Additionally, the contact points between corrugated plates form a multi-point support structure, endowing the plates with excellent mechanical stability under pressure and enabling them to withstand high operating pressures. From the perspective of heat transfer mechanisms, the heat transfer process in chevron corrugated plate heat exchangers primarily involves three mechanisms: conduction, convective heat transfer, and turbulent mixing [60,61,62,63,64,65]. The corrugated structure enhances thermal conductivity efficiency by increasing the contact area between the fluid and the plate surface. Simultaneously, the induced turbulent flow intensifies momentum and energy exchange within the fluid, further boosting overall heat transfer performance. Moreover, the meandering flow channels between corrugated plates cause the fluid to undergo multiple redirects and redistributions during flow, increasing the flow path length. This prolongs the heat exchange duration, thereby enhancing heat transfer effectiveness. For decades, extensive research has focused on the design and optimization of chevron-patterned PHEs, where the geometric parameters of the chevron corrugations play a critical role. Based on practical application requirements, numerous experimental and numerical studies have either investigated the impact of geometric parameters on thermohydraulic performance or addressed multi-objective optimization problems concerning these parameters [62,63,64,65,66].

This chapter focuses on fluid flow within herringbone plate heat exchangers. First, it analyzes the structural characteristics, applicable scenarios, and impact on flow performance of two core channel configurations: single-channel and multi-channel layouts. Subsequently, it explores the design principles of typical flow paths such as vertical flow and diagonal flow, along with their correlation mechanisms with heat transfer and resistance. This aims to establish a flow analysis foundation for subsequent thermal-hydraulic performance studies under single-phase and two-phase flow conditions, while providing theoretical support for structural optimization and engineering selection of heat exchangers.

3. Single-Phase Flow

Single-phase flow is a fundamental concept in fluid dynamics, referring to the movement of a substance in a single-phase state (such as liquid, gas, or solid particles) through a pipeline, channel, or open environment within an entire flow system. It does not involve phase transitions or the mixing of multiple phase states. Although single-phase flow does not involve phase changes, its research findings often lay the foundation for understanding more complex multiphase flow phenomena, such as boiling heat transfer and condensation [17].

3.1. Experimental Research

Under single-phase flow conditions, heat transfer between the fluid and the wall surface primarily relies on convective heat transfer mechanisms [73,74]. Corrugated structures effectively enhance heat transfer efficiency by inducing turbulence, increasing fluid disturbance, and disrupting the thermal boundary layer. Recent experimental findings are summarized in Table 1.

Table 1. Current Research Status of Geometric Structures in Single-Phase Heat Transfer.

Authors	Parameter	Key Finding(s)
Kılıç and İpek [75]	β = 30°, 60°	The corrugated chevron plate heat exchanger with a β angle of 60° exhibits superior thermal performance and achieves a higher heat transfer rate compared with other configurations.
Kitti Nilpueng et al. [76]	Surface roughness(μm):0.95–2.75 β = 30°, 60°	The plate heat exchanger achieves its best thermal performance when the chevron angle is 30°, the surface roughness is highest, and the Reynolds number is lowest.
Yang et al. [77]	An ethylene glycol (EG) and water mixture’s β = 27°, 46°, 65°	The findings indicate that the herringbone angle exerts the greatest influence on heat transfer.
Krishnan et al. [78]	25° < β < 75°; 0.13 < h/p < 0.36	The peak heat transfer performance is achieved at corrugation angles of approximately 42°, 60°, and 70°, corresponding to h/p ratios of 0.14, 0.20, and 0.27, respectively.
Yubin Du et al. [79]	The depth varies between 1.2 mm and 2.0 mm, while the pitch lies between 5.2 mm and 7.6 mm.	At constant Reynolds number, the heat transfer coefficient rose by up to 40% and 80% when the dimple depths ranged from 0.7 to 2.0 mm and the pitches from 2.8 to 6.0 mm.
Yi Zhong et al. [80]	β = 130°, h = 2 mm, p = 7.6 mm	Flow resistance reduces with increasing corrugation height, while larger corrugation spacing can negatively impact the flow state within the heat exchanger.
Khan et al. [81]	β = 30°/30° or 60°/60° or 30°/60°	The chevron angle and Reynolds number significantly affect the heat transfer coefficient, according to the experimental results.
Zahrani et al. [82]	This study investigates the thermal performance of two newly developed modified FPHEs.	At different Reynolds numbers, the temperature gradient severity and average temperature inside the middle thermal plate were calculated.
M. Bobič et al. [83]	The counterflow plate heat exchanger’s dynamic behavior is investigated.	Thermal imaging results give a more detailed understanding of the temperature distribution and the movement of its transient front through the fluid flow channels.
Panday and Singh [84]	The steady-state performance of a PHE in a Z-type flow arrangement is investigated for four pass setups: 1–1, 2–2, 3–3, and 4–4.	It is shown that increasing the number of passes and velocity may have a counterproductive effect on effectiveness and Nusselt number enhancement, despite maintaining the same mass flow rate.
Kumar et al. [85]	β = 60°/60°, 60°/30°, 30°/30°	A larger chevron angle in the plates negatively affects the hydraulic performance of a PHE, as it results in higher pressure drops.
Gulenoglu et al. [86]	The Reynolds numbers (300–5000) and Prandtl numbers vary for all the plates that have 30° of chevron angle	Nusselt number and friction factor correlations are obtained for each plate from the experimental data
Nguyen et al. [87]	The effect of electrochemical etching parameters on SUS304 specimens was first examined, along with its application to a commercial plate heat exchanger.	Electrochemical etching leads to significant changes in the PHE’s surface properties, which consequently affect its fouling behavior.

Kılıç and İpek [75] experimentally tested corrugated plate heat exchangers with 30° and 60° corrugation angles. Their findings revealed that the β = 60° herringbone plate heat exchanger demonstrated the highest effectiveness and heat transfer rate. They also assessed the pressure drop for various herringbone angles, noting the best heat transfer rate occurred at a flow velocity of 0.390 kg/m²·min and β = 60°.

Kitti Nilpueng et al. [76]. studied the combined effects of corrugation angle and surface roughness on heat transfer performance in single-phase water flow. They tested heat transfer coefficients and pressure drop characteristics for corrugation angles of 30° and 60°, with surface roughness levels ranging from 0.95–2.75 μm, across Reynolds numbers from 1200 to 3500. The findings showed that the heat transfer coefficient and pressure drop at a 30° angle were 2.51 and 1.87 times higher than at 60°, respectively. Under conditions of low Reynolds number and high roughness, the 30° chevron angle exhibited superior thermal performance.

Yang et al. [77] conducted experiments on single-phase heat transfer in brazed plate heat exchangers with nine different geometric parameters, specifically for high Prandtl number flows. Their results showed that the herringbone angle is the most influential factor on heat transfer. Additionally, they found that both the geometric dimensions and the herringbone angle together play a significant role in heat transfer.

Krishnan et al. [78] studied the heat transfer and pressure drop characteristics of triangular cross-corrugated flow channels in a small-scale test setup, focusing on corrugation angles between 25° and 75° and depth-to-pitch ratios from 0.13 to 0.36. They identified the corrugation angle, pattern, and depth-to-pitch ratio as the primary geometric parameters influencing heat transfer and pressure drop in these channels.

Dimpled plate heat exchangers, which include continuous curved surfaces between adjacent dimples, are attracting interest for their lower material requirements and smaller internal volume compared to traditional herringbone plate heat exchangers. Yubin Du et al. [79] conducted comprehensive experimental analysis of the thermal performance of dimples with three distinct parameter sets. Preliminary findings identified peripheral flow and symmetric vortices between dimples within herringbone corrugated channels based on different combinations of dimple depth and pitch.

Wciślik [88] investigates the impact of the Nusselt number correlation on the efficiency (e) and exergy efficiency, ηex, of a chevron-type gasketed plate heat exchanger used in a typical small solar installation for single-family houses. The laboratory bench is shown in Figure 6.

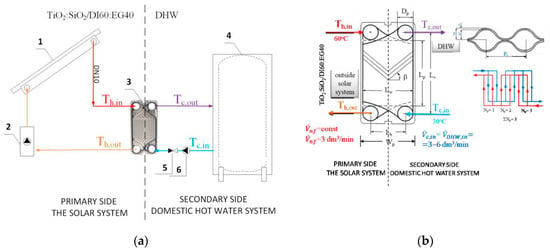
Figure 6. (a) The hydraulic layout of the solar system, including the plate heat exchanger and its operating conditions [88]; (b) initial system conditions and key dimensions of the chevron-type PHE, including cross-sectional dimensions perpendicular to the trough direction [88].

Yi et al. [80] experimentally investigated the hydraulic characteristics of seven types of herringbone BPHEs. The results indicate a power-law relationship between f and Re: it exhibits a similar trend but with different amplitudes for different plates, and the power-law exponent can be approximated as a constant.

Khan et al. [81] conducted experiments on water-to-water single-phase flow in commercial plate heat exchangers using 30°/30°, 60°/60°, and hybrid 30°/60° chevron plates. For Reynolds numbers ranging from 500–2500 and Prandtl numbers between 3.5–6.5, they observed that both chevron angle and flow conditions play major roles in determining heat transfer coefficients.

Zahrani et al. [82] analyzed the efficiency of two newly modified FPHEs in terms of thermal performance. Results were compared with conventional corrugated and flat plate PHEs. However, this study primarily aimed to validate the numerical model implemented in the experiments.

M. Bobič et al. [83] investigated the dynamic behavior of counter-current plate heat exchangers. A series of system tests using infrared thermal imaging technology experimentally validated the predicted transients. Analysis indicated good agreement between the proposed model and experiments. Thermal imaging measurements provided a clearer understanding of how temperature varied and propagated through the flow.

Panday and Singh [84] experimentally investigated the thermohydraulic performance of PHEs under steady-state conditions at isothermal and non-isothermal conditions across four distinct channel arrangements: 1–1, 2–2, 3–3, and 4–4. Results indicate that under identical mass flow conditions, increasing the number of passes may prove counterproductive, as higher velocity enhances efficiency and increases the Nusselt number.

Kumar et al. [85] investigated the effect of geometric parameters on fluid dynamics and heat transfer within PHEs through a series of experiments. They observed that increasing the herringbone angle from (60°/30°) to (60°/60°) improved PHE efficiency by approximately 22.05%. Furthermore, increasing the herringbone angle reduces pressure drop.

Gulenoglu et al. [86] utilized a test rig for herringbone gasketed plate heat exchangers to investigate the thermal and hydraulic characteristics of three distinct plate geometries. Experiments were conducted with varying plate counts, multiple flow velocities, and inlet/outlet temperature values. Using the experimental data, equations for the Nusselt number and friction factor per plate were established.

Nguyen et al. [87] employed an etching method to enhance the surface roughness and contact angle of herringbone-patterned PHE steel surfaces, improving thermal performance coefficients. Damir [89] conducted research on single-phase visualization techniques, using them to investigate the influence of velocity on fluid flow and validating his findings through numerical simulations. He dissolved methyl blue in a glycerol/water mixture as the working fluid.

Single-phase flow, as the most fundamental and widely applied heat transfer condition in V-shaped plate heat exchangers (PHEs), has been systematically investigated through experimental studies. These investigations elucidated the impact of geometric and operating parameters on system performance, pinpointed optimization focuses, and established core experimental support for numerical validation and design development.

3.2. Numerical Simulation

Recently, the application of CFD in the study of herringbone corrugated plate heat exchangers has primarily focused on elucidating flow mechanisms, optimizing geometric parameters, exploring complex operating conditions, and integrating with other technologies. Regarding numerical simulation methods, research has largely relied on commercial CFD software, with an emphasis on experimentally validating simulation results. Recent research findings are summarized in Table 2.

Table 2. Recent numerical simulation results of single-phase heat transfer.

Authors	Parameter	Key Finding(s)
Jonghyeok Lee and Kwansoo Lee [90]	30° ≤ β ≤ 60° and 2.0 ≤ p/h ≤ 4.4	An increase in the chevron angle β, and a reduction in the pitch-to-height ratio and a reduction in the pitch-to-height ratio p/h decreased led to higher values for both f and j.
Xiaowei Zhu [91]	18° ≤ β ≤ 72°	For low Reynolds numbers, a higher β results in a significant heat transfer enhancement, while at high Reynolds numbers, the improvement is less pronounced.
Yubin Du et al. [79]	20 ≤ G ≤465, 0.7 ≤ h ≤ 1.5, 2.8 ≤ p ≤ 7.6	The results showed that the heat transfer coefficient increased by up to 40% and 80% at the same Reynolds number, corresponding to dimple depths ranging from 0.7 to 2.0 mm and pitches from 2.8 to 6.0 mm, respectively.
Yi Zhong et al. [80]	β = 130°, h = 2 mm, p = 7.6 mm	Numerical results show that the pressure drop Δp is positively correlated with the corrugated angle and spacing but negatively correlated with the corrugated height.
Chen Su et al. [92]	An LR35GB-corrugated plate heat exchanger	The phenomenon of flow distribution bias and its influence on heat transfer performance are elucidated.
Zhigang Liu [93]	The straight channel printed circuit heat exchanger (PCHE)	Provide a theoretical basis for the optimization design of the oil-water heat exchange system
Zahrani et al. [82]	The thermal performance of two newly developed modified FPHEs have been investigated in this study.	Considering all the factors, FPHEm1 shows poor thermal efficiency, closely resembling that of FPHEC.
M. Bobič et al. [83]	The dynamic behaviour of a counterflow plate heat exchanger is studied.	The numerical findings indicated that different fluid flow arrangements notably impact the transient temperature behavior, overall temperature reduction, and heat transfer rate as the fluid moves from the inlet to the outlet on the hot side of the plate heat exchanger during the cooling process.
Sarraf et al. [94]	Re ≈ 200, BPHE	The analysis indicates that flow structures are influenced not only by the chevron angle but also by the mass flow rate.
Liu et al. [95]	The geometric dimensions, corrugation height, and corrugation inclination of each plate remain the same, while the diameter of the variable vortex generator columns is different.	Simulation results indicate that the flow baffle can reduce the flow regions with lower velocities on both sides of the channel, thereby making heat transfer more uniform. In addition, the pressure loss at the channel outlet with built-in flow baffles is very small.

Lee et al. [90] performed a numerical study employing the Large Eddy Simulation (LES) technique to explore the unsteady flow behavior in a chevron plate heat exchanger. They found that β = 30° should be used when the flow is laminar, while β = 60° provides optimal performance under turbulent flow conditions. Regardless of the Reynolds number, p/h = 2.0 delivers optimal performance. Lee et al. applied periodic boundary conditions in both the flow and spanwise directions.

Yubin Du et al. [79] numerically simulated three types of pitted plate heat exchangers. Results showed that under identical Reynolds numbers, heat transfer coefficients increased by up to 40% and 80% for pits with depths ranging from 0.7–2.0 mm and spacings from 2.8–6.0 mm, respectively. The flow transitioned from laminar to turbulent at a Reynolds number near 300.

Yi Zhong et al. [80] explored the hydraulic behavior of seven herringbone BPHEs using numerical simulations, highlighting the effect of structural parameters on hydraulic performance. Pressure drop Δp showed positive correlations with corrugation angle and spacing, and negative correlations with corrugation height. Hydraulic performance studies are crucial for optimizing BPHE design.

Chen Su et al. [92] employed CFD methods to reveal flow non-uniformity and heat transfer enhancement mechanisms in corrugated plate heat exchangers, demonstrating that numerical simulations can capture intricate internal flow details. Some simulation results are shown in Figure 7.

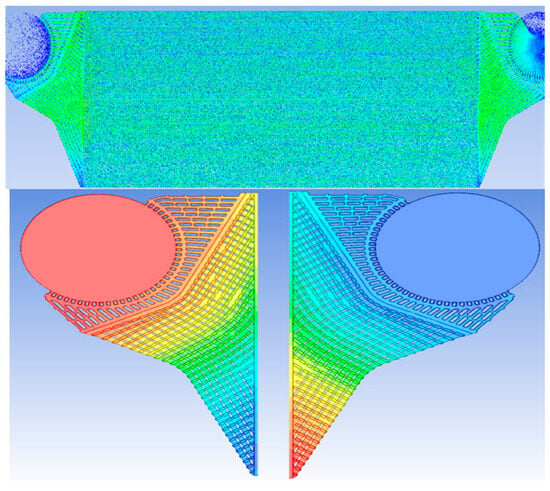
Figure 7. Numerical simulation diagram [92].

Zahrani et al. [82] studied the heat transfer efficiency of two newly modified FPHEs. All four heat exchangers shared identical dimensions and were tested under identical physical conditions. FPHE_m1 exhibited poorer thermal performance, closely resembling that of the FPHE, while FPHEC demonstrated the most superior thermal performance, making it a potential replacement for similar products.

Korobiichuk et al. [96] constructed three-dimensional models of three different types of cavity geometries formed between two heat exchange plates (flat plate, herringbone plate, and plate with conical stamping). The channels formed by the three types of plates were simulated using finite element analysis in ANSYS. Some simulation results are shown in Figure 8.

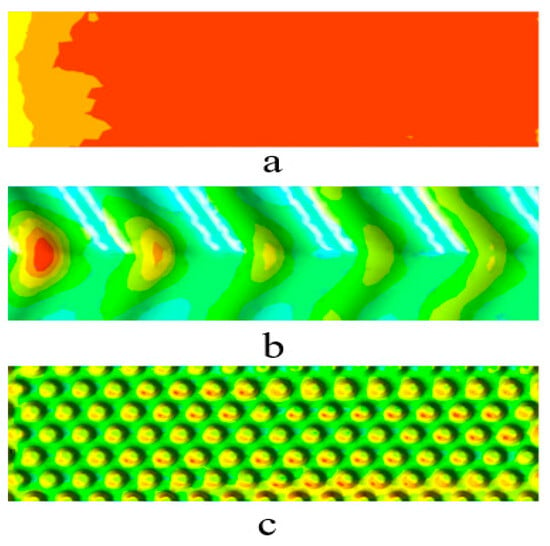
Figure 8. Contours illustrating the heat transfer coefficients: (a) flat heat exchanger plate [96], (b) chevron plate [96], (c) conical stamped plate [96].

Giunti et al. [97] investigated the performance of brazed plate heat exchangers using CFD, focusing on the pressure drop in single-phase flow across the entire channel of plates with recessed corrugations. Their work aims to bridge gaps in the literature, particularly in areas related to port behavior, and to create a framework for future conjugate heat transfer studies. Some simulation results are shown in Figure 9.

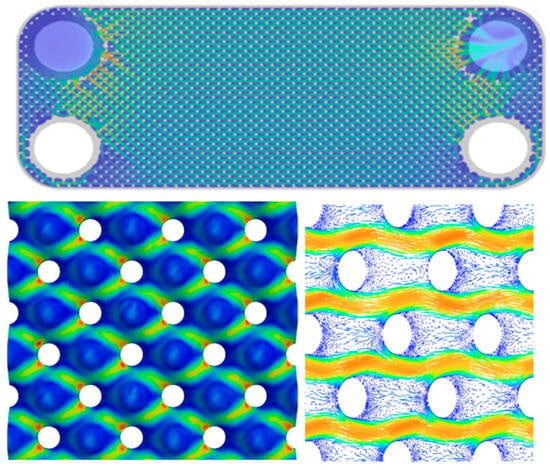
Figure 9. Numerical simulation diagram [97].

M. Bobič et al. [83] investigated the dynamic behavior of counterflow plate heat exchangers to understand their transient response to inlet temperature perturbations under different fluid flow configurations. The numerical findings suggest that different fluid flow configurations greatly affect the transient temperature behavior, total temperature decrease, and heat transfer rate during the cooling process of the fluid from inlet to outlet on the hot side of the plate heat exchanger.

Sarraf et al. [94] conducted numerical simulations to examine heat and mass transfer characteristics in single-phase flow inside brazed plate heat exchangers. The analysis revealed that flow patterns exhibit sensitivity not only to the herringbone angle but also to mass flow rates.

Liu et al. [95] investigated multiphysics phenomena (fluid flow and temperature) in a dual-channel hot/cold model via numerical simulation. Results indicate that turbulent columns reduce low-velocity flow regions on both sides of the channel, thereby promoting more uniform temperature transfer. Additionally, pressure loss at the outlet of channels incorporating turbulent columns is minimal.

Kurose et al. [98] selected HFC-134a and HFO-1234ze(E) as working refrigerants and developed a CFD model to predict heat transfer at the supercritical pressure of a PHE. Their simulation results validated the mechanism by which the heat transfer coefficient reaches its maximum value when the enthalpy is slightly above the pseudo-critical point.

3.3. Performance Correlation

Accurate and rapid estimation of heat transfer coefficients and pressure losses is vital in the development and optimization of plate heat exchangers for engineering design and operational regulation. Due to the highly three-dimensional flow and complex turbulent structures within chevron-shaped corrugated channels, traditional empirical formulas for circular tubes or straight channels prove inadequate. Consequently, researchers have progressively developed a “family of performance correlation equations” covering laminar-transitional-turbulent flow regimes based on extensive experimental and numerical simulations. This framework continues to evolve toward broader parameter coverage, lower uncertainty, and enhanced interpretability. Selected research outcomes are presented in Table 3.

Table 3. Performance Correlation under Single-Phase Heat Transfer.

Authors	Parameter	Formula
Krishnan et al. [78]	Nu, f	$\begin{array}{c}{f}_p=44.60{\left[{\left({\displaystyle \frac{\beta {\left(h_{ch}/P_{ch}\right)}^2}{Re}}\right)}^{9.32}+{\displaystyle \frac{1}{{\left(\frac{2505\theta }{Re}\right)}^{16.2}}}\right]}^{0.066}\\ N{u}_p=0.205{\left(0.276R{e}^{3/4}{f}^{1/2}\right)}^{5/4}P{r}^{1/3}\end{array}$
Zhu [91]	Nu, Re	$\begin{array}{c}N{u}_l=2.56\cos {\beta }^{1.23}R{e}^{(1-0.9\sqrt{\cos \beta })}P{r}^{1/3}\\ N{u}_t=\left({\displaystyle \frac{0.578}{\sqrt{\cos \beta }}}-0.561\right)R{e}^{(0.6+0.22\cos \beta )}P{r}^{1/3}\end{array}$
Yang et al. [77]	Nu, Re	$\begin{array}{c}Nu=\left(-1.342\times {10}^{-4}\cdot {\beta }^2+1.808\times {10}^{-2}\cdot \beta -0.0075\right)\\ \cdot R{e}^{(-7.956\times {10}^{-5}\cdot {\beta }^2+9.687\times {10}^{-3}\cdot \beta +0.3155)}\cdot R{e}^{\varphi /\beta }\cdot R{e}^{\gamma /\beta }\cdot P{r}^{1/3}\cdot {\left({\displaystyle \frac{\mu }{{\mu }_{\omega }}}\right)}^{0.14}\end{array}$
Khan et al. [81]	Nu, Re	$Nu=\left(0.0161{\displaystyle \frac{\beta }{{\beta }_{\max }}}+0.1298\right)R{e}^{\left(0.198{\displaystyle \frac{\beta }{{\beta }_{\max }}}+0.6398\right)}P{r}^{0.35}{\left({\displaystyle \frac{\mu }{{\mu }_w}}\right)}^{0.14}$
Yubin Du et al. [79]	Nu, Re	$Nu=\left\{\begin{array}{c}{C}_{1}R{e}^{m_1}P{r}^{n_1}{\gamma }^{k_1}{\left(\mu /{\mu }_{\mathrm{wall}}\right)}^{0.14} Re\le 300\\ C_{2}R{e}^{m_2}P{r}^{n_2}{\gamma }^{k_2}{\left(\mu /{\mu }_{\mathrm{wall}}\right)}^{0.14} Re>300\end{array}\right.$
Yi Zhong et al. [80]	f, Re	$f=a^{\ast }R{e}^{-0.67}$
Zahrani et al. [82]	Nu, f	$\begin{array}{c}Nu=0.14311R{e}^{0.71}P{r}^{1/3}{\left({\displaystyle \frac{\mu }{{\mu }_w}}\right)}^{0.14}\\ f=3.444R{e}^{-0.2255}\end{array}$
Panday and Singh [84]	f, Re	$\begin{array}{c}f=a\times R{e}^b\\ \mathrm{where}, 339\le Re\le 2850.\end{array}$
Gulenoglu et al. [86]	Δp, f	$\mathsf{\Delta }P=4f\left(L_{eff}{N}_p/D_h\right)\left(G_c^2/2\rho \right){\left({\mu }_b/{\mu }_w\right)}^{-0.17}$
Luan et al. [99]	Nu, Re	$Nu=\left\{\begin{array}{l}0.16R{e}^{0.65}P{r}^{0.33}{\left({\displaystyle \frac{\mu }{{\mu }_w}}\right)}^{0.14}Num.\hfill \\ 0.27R{e}^{0.60}P{r}^{0.33}{\left({\displaystyle \frac{\mu }{{\mu }_w}}\right)}^{0.14}Exp.\hfill \end{array}\right.$
Cao et al. [100]	Nu, Re	$\begin{array}{c}Nu=4.56R{e}^{0.38}P{r}^{0.4}{\left({\displaystyle \frac{\pi \beta }{180}}\right)}^{0.20}(H{\mathrm{0.300.32}}_w^{0.14}{z}_z{h}_h)\end{array}$
Nilpueng et al. [87]	Nu, Re	$\begin{array}{c}Nu=0.343R{e}^{0.604}P{r}^{0.33}{(R/d_{\mathrm{hyd}})}^{0.133}{(\beta /30)}^{-1.327}\end{array}$
Nilpueng and Wongwises [101]	Nu, Re	$Nu=0.061R{e}^{0.831}P{r}^{0.333}{\left(R/d_{\mathrm{hyd}}\right)}^{0.122}$
Mutumba et al. [102]	Nu, Re	$Nu=0.0488R{e}^{0.89}P{r}^{0.333}$
Zhang et al. [103]	Nu, Re	$Nu=0.655R{e}^{0.581}P{r}^{0.317}$

Early correlation equations primarily focused on fitting experimental data, employing power-law forms to express the Nusselt number (Nu) and friction factor (f) as functions of parameters such as Reynolds number (Re), corrugation angle (β), and corrugation depth-to-pitch ratio (h/p). For instance, the generalized correlation for Nu and f proposed by Krishnan et al. achieves prediction errors within ±15% across the ranges 25° ≤ β ≤ 75° and 0.13 ≤ h/p ≤ 0.36, providing a reliable tool for engineering design. However, such empirical models exhibit high sensitivity to geometric parameters, poor extrapolation capability, and fail to elucidate the physical mechanisms underlying heat transfer enhancement through flow pattern modifications.

With the advancement of computational fluid dynamics, large eddy simulation has been introduced to capture unsteady turbulent structures within corrugated channels. Based on LES data, Zhu et al. established relationships between Nu and f with respect to Re, β, and the surface expansion factor φ, proposing a segmented flow regime model. This revealed that Nu exhibits insensitivity to Re and β in laminar regions, while significantly intensifying with increasing β in turbulent regions. This model achieves over 90% prediction accuracy in laminar regions and maintains errors below 20% in turbulent regions, marking the first transition from “empirical fitting” to “data-driven physical modeling.” However, its limitations include dependence on specific geometric configurations and boundary conditions, with applicability to complex two-phase/three-phase flows yet to be validated.

To balance engineering versatility and prediction accuracy, Yang et al. proposed the generalized Nu correlation for ACRC based on 22 different plate types and plate width ranges (including ethylene glycol-water mixtures). This work pioneered the integration of the V-angle, amplification factor, and corrugation aspect ratio into a unified expression, making it applicable to various plate heat exchangers. However, its prediction accuracy is only 50%. Inconsistent definitions of geometric parameters and significant variations in projected area treatment methods remain major obstacles to its widespread adoption. Additionally, for predicting performance in mixed chevron structures,

Khan et al. proposed a simplified Nu correlation. Within the range of Re = 500–2500 and Pr = 3.5–6, the error was controlled within ±4%, validating the mixed-angle structure’s favorable balance between heat transfer enhancement and pressure drop control. However, this model remains limited to specific operating conditions and structural configurations, lacking generalization capabilities for variable conditions and structures.

Although Table 3 collects more than a dozen single-phase correlations, most of them were regressed from fewer than three chevron plates with water or water–glycol mixtures; their reported error bands are ±5% (Khan, 2010 [81]) to ±15% (Krishnan, 2021 [78]) only within 500 < Re < 2500, 25° ≤ β ≤ 75° and plate-surface enlargement φ ≤ 1.35. Once the fluid viscosity ratio exceeds 2, or mixed-chevron (30°/60°) plates and high-φ surfaces (>1.4) are used, the deviation of Nu and f can rise to 20–30% and the overall pressure drop is often under-predicted by a similar margin because port and distribution losses are not included. Consequently, for water-like media engineers can adopt Krishnan’s or Yang’s set with confidence, but for high-viscosity oil or wide-φ packs a 20% safety factor on Δp should be added and CFD-assisted header correction is advised.

This chapter systematically reviews experimental studies, numerical simulations, and performance correlation equations under single-phase flow conditions. It has established a comprehensive research framework—“experimental quantification of patterns -numerical revelation of mechanisms—correlation-based performance prediction”—which not only clarifies the regulatory mechanisms of geometric parameters and operating conditions on thermohydraulic performance but also provides robust theoretical and data support for subsequent two-phase flow research and industrial equipment optimization. However, it should be noted that existing research still has limitations, such as insufficient adaptability studies for multi-component mixed working fluids and extreme operating conditions (e.g.; high-viscosity fluids). Future work should further expand the parameter range and working fluid types to enhance the universality of single-phase flow research, thereby better supporting the efficient operation of industrial energy-saving and low-carbon heating systems.

4. Two-Phase Flow

In practical applications, particularly within high-efficiency heat exchange systems, plate heat exchangers are employed not only for single-phase fluid heat transfer but also extensively in complex two-phase heat transfer processes involving phase changes—such as boiling and condensation—across numerous industrial scenarios. The mechanisms governing phase-change heat transfer are significantly more complex and multifaceted than those of single-phase heat transfer [104,105,106,107,108]. They involve not only convective heat exchange within the fluid but are also strongly influenced by the phase-change processes themselves—including bubble nucleation, growth, detachment, and coalescence, as well as the formation, flow, and breakup of condensate films. These microscopic phase-change phenomena interact intricately with the geometric parameters of the heat transfer surface, particularly the angle of the chevron corrugations. The governing mechanisms of heat transfer and pressure loss in two-phase flow often display significant variations when compared to single-phase flow. The core of two-phase heat transfer lies in the phase change occurring within the fluid during heat exchange (liquid absorbs heat to evaporate into gas, or gas releases heat to condense into liquid), which greatly enhances the heat transfer efficiency per unit volume of fluid.

4.1. Experimental Research

Recent experimental studies have consistently focused on in-depth analysis of its enhanced heat transfer mechanisms, continuous optimization of key design parameters, systematic evaluation of its performance under diverse operating conditions, and active exploration of the application potential of novel heat transfer fluids alongside cutting-edge testing and analysis methods. Selected recent experimental findings are summarized in Table 4.

Table 4. Current Status of Geometric Structure Research in Two-Phase Heat Transfer.

Authors	Parameter	Keys
Longo and Gasparella [109]	The BPHE tested consists of 10 plates, 72 mm in width and 310 mm in length; β = 65°	The heat transfer coefficients are significantly influenced by heat flux and outlet conditions, but only slightly affected by saturation temperature.
Arima et al. [110]	A vertical flat PHE (a plate heat exchanger)	Results from the measurements show an increase in local boiling heat transfer coefficients with higher vapor quality.
Táboas et al. [104]	Regarding the flow boiling of ammonia and water in a plate heat exchanger.	In the new correlation, a transition criterion divides the boiling process into two regions: an apparent nucleate boiling zone, where pure convective boiling does not occur, and a zone with a competition between both mechanisms.
Eungchan Lee et al. [105]	The heat transfer and pressure drop performance of water during flow boiling in the PHX for FWGs was experimentally investigated under low mass flux conditions.	The two-phase frictional pressure drop increased with increasing mean vapor quality and mass flux because it was proportional to the kinetic energy per unit volume.
Mancin et al. [106]	Heat transfer coefficients for the partial condensation of R407C and R410A were measured in two different BPHE prototype designs.	A key finding from the experiments is that the condensation heat transfer coefficient in both BPHEs exhibits a positive correlation with vapor quality and a negative correlation with the temperature difference.
Longo et al. [107]	A collection of 251 previously established experimental data points forms the basis for investigating Brazed Plate Heat Exchangers.	The proposed model incorporates distinct correlations for nucleate and convective boiling mechanisms and can be extended to accommodate scenarios involving outlet vapor superheating.
Khan et al. [108]	An asymmetric chevron corrugation with angles of 30° and 60°.	In the experiments, the heat flux was set to vary from 21 to 44 kW m−2, while the saturation temperature varied from −25 to −2 °C.
Huang et al. [111]	A study on the thermal-hydraulic performance (heat transfer and pressure drop) of diverse zeotropic mixtures, their heat transfer deterioration, and parameters influencing the degradation.	Compared to pure-component fluids, the mixtures exhibited heat transfer deterioration as high as 34%. The extent of this degradation was inversely correlated with heat transfer performance, manifesting most significantly under less efficient working conditions.

A schematic diagram of the commonly used plates in the experiment is shown in Figure 10.

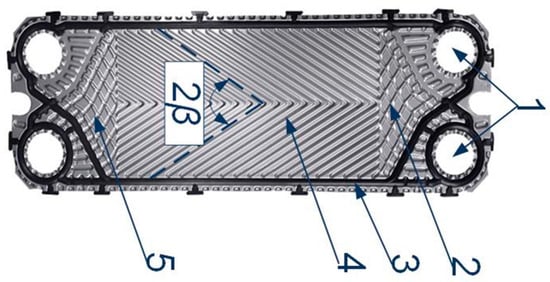
Figure 10. A typical commercial GPHE plate comprises: 1. inlet/outlet ports, 2 & 5. flow distribution zones, 3. sealing gasket, and 4. main heat transfer area [59].

Longo and Gasparella [109] experimentally studied the vaporization of R134a in a small brazed plate heat exchanger, measuring heat transfer coefficients and pressure drops under varying heat flux, refrigerant mass flux, saturation temperature, and outlet conditions. The results indicated that the heat transfer coefficient was strongly influenced by heat flux and outlet conditions but only marginally affected by saturation temperature. In addition, the frictional pressure drop showed a linear relationship with the kinetic energy per unit volume of the refrigerant flow.

Arima et al. [110] investigated ammonia boiling heat transfer in a vertical flat plate heat exchanger, reporting that the local heat transfer coefficient increased with higher vapor quality. Their study also detailed the influences of saturation pressure, mass flux, and heat flux on the boiling performance.

Táboas et al. [104] established a novel correlation for flow boiling in plate heat exchangers using experimental data from water-vapor mixture tests. This correlation effectively captures the transition mechanism from nucleate to convective boiling and demonstrates high predictive accuracy, with 98% of the heat transfer coefficient estimates falling within a ±20% error band relative to the measured values.

Eungchan Lee et al. [105] conducted an experimental study on the flow characteristics, boiling heat transfer, and pressure drop of water in plate heat exchangers (PHX) under low mass flux conditions. Their results demonstrated that the two-phase frictional pressure drop increases with higher average vapor quality and mass flux, which was attributed to its proportionality to the kinetic energy per unit volume. In contrast, the effect of heat flux on the two-phase frictional pressure drop was found to be negligible.

Mancini et al. [106] performed condensation experiments using R407C and R410A refrigerants with 15 K superheating in two brazed plate heat exchanger (BPHE) prototypes that differed in geometric configuration, plate design, and aspect ratio. The condensation heat transfer coefficients were evaluated under constant saturated inlet temperatures of 41.8 °C for R407C and 36.5 °C for R410A. The results revealed that, in both types of BPHEs, the condensation heat transfer coefficient rises with increasing vapor mass flux but declines as the temperature difference grows.

Longo et al. [107] developed a novel model to characterize refrigerant boiling processes within brazed plate heat exchangers (BPHEs). This model integrates distinct formulations for nucleate and convective boiling mechanisms and is further applicable to scenarios involving outlet vapor superheating.

Khan et al. [108] studied the evaporation of refrigerants with miscible oil in a flooded corrugated plate heat exchanger (PHE) featuring three different chevron angle configurations: 30°, 60°, and a mixed 30°/60° pattern. Their results showed that the boiling heat transfer coefficient increased with both larger chevron angles and higher saturated temperatures.

Huang et al. [111] explores the effects of working fluid properties, on two-phase flow in V-shaped PHEs, operating conditions, and geometric structures. It preliminarily reveals key patterns in two-phase thermohydraulic performance, providing indispensable experimental support for subsequent numerical simulation validation, mechanism modeling, and engineering applications.

Zakaria and Mahmoud [112] conducted a comprehensive energy and exergy analysis to evaluate the effects of injecting submillimeter air bubbles into both the cold and hot water streams upstream of a ten-plate corrugated plate heat exchanger (C-PHE) operating in a counterflow configuration. The laboratory bench and the plate shape are shown in Figure 11.

Figure 11. Experimental setup components consist of (1) CWB, (2) HWB, (3) C-PHE, and (4) corrugated plate channel of PHE [112].

Tao et al. [113], Santos et al. [114], and Lee et al. [115] employed visualization techniques to study flow patterns and heat transfer characteristics in herringbone-type plate heat exchangers. Through detailed analysis of the observed flow behaviour, they further investigated the associated heat transfer performance.

Current experimental studies on two-phase flow in V-shaped PHEs have systematically explored the effects of working fluid properties, operating conditions, and geometric structures. These investigations have preliminarily revealed key patterns governing the thermal-hydraulic performance of two-phase flow, providing indispensable experimental support for subsequent numerical simulation validation, mechanism modeling, and engineering applications.

4.2. Numerical Simulation

FLUENT and ANSYS are the most commonly used software for numerical simulation of herringbone corrugated plate heat exchangers [116]. They provide powerful meshing, solver, and post-processing capabilities, enabling researchers to efficiently conduct complex fluid dynamics and heat transfer analyses. Recent research findings are summarized in Table 5.

Table 5. Recent Numerical Simulation Results of Two-Phase Heat Transfer.

Authors	Parameter	Method
Huashan Su [116]	A two-dimensional two-channel model	Simulated the evolution of the phase-change heat transfer process in the corrugated plate channel of a plate heat exchanger
Fulin Kong et al. [117]	Change the four parameters: plate spacing, corrugation depth, corrugation spacing, and herringbone angle.	The performance of a corrugated plate heat exchanger (CPHE) is significantly influenced by the chevron angle and corrugation depth, with an optimal corrugation pitch existing to balance the heat transfer coefficient (HTC) and flow resistance.
Zhao Yuqing [118]	The plate heat exchanger serves as a primary component within the heat pump circuit.	A strong correlation was observed between the simulation and experimental results. The computed average error rates for the condenser and evaporator stood at 5.75% and 1.13%.
Almalfi et al. [119]	To quantify the impact of plate geometry on thermal-hydraulic behavior, a sensitivity analysis of the predictive models was carried out.	Evaluation of principal geometrical parameters via sensitivity analysis, comparison of multiple two-phase correlations, and discussion of dominant performance trends.
Abed et al. [120]	The working fluid is water. The investigation focuses on low mass flux conditions and examines a range of vapor qualities for inlet streams of both subcooled and saturated liquid.	The heat transfer coefficient is enhanced under conditions of higher mass flux and lower wall and inlet flow temperatures.
Mudhafar [121]	The K050 chevron PHE	A comparative analysis investigates the influence of an inflow distributor on two-phase flow distribution across the channels of a plate heat exchanger.

Research on the effects of two-phase flow in herringbone corrugated plate heat exchangers has been relatively scarce, not because of its insignificance, but due to the immense complexity of two-phase flow, the significant challenges in research methodologies, and the current focus in both research and application. Nevertheless, some researchers have made considerable efforts in this area.

Su et al. [116] simulated phase change heat transfer within corrugated plate channels using a two-dimensional dual-channel model, analyzing the evolution of the average Nusselt number and average heat flux. Although their study employed a two-dimensional model, it provides a foundation for understanding how corrugated structures influence phase change processes. Some simulation results are shown in Figure 12.

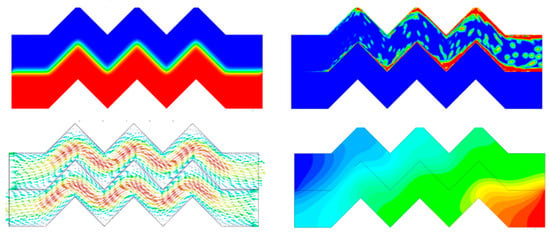
Figure 12. Some simulation results [116].

Fulin Kong et al. [117]. evaluated how plate spacing, corrugation depth, pitch, and chevron angle influence flow and transfer processes. Their analysis revealed that corrugation depth and chevron angle have a pronounced impact on performance, noting an optimal spacing that maximizes thermal-hydraulic efficiency. They also concluded that the effect of these geometric parameters on flow boiling is distinct from their effect on single-phase heat transfer.

Mudhafar [121] also employed the same three-dimensional model, but his research focused on the influence of multi-channel Reynolds number on gas–liquid distribution.

Across two studies, empirical correlations were developed to predict flow boiling performance in plate heat exchangers. Amalfi et al. [119] utilized multi-regression analysis, while Abed et al. [120] conducted similar work with a focus on water as the working fluid to model heat transfer and pressure drop.

Current numerical simulations of two-phase flow in V-shaped PHEs have systematically explored model development, parameter optimization, and system adaptation. This work has established a research framework centered on “model validation–mechanism analysis–performance prediction,” providing crucial support for deepening understanding of two-phase flow and guiding heat exchanger structural optimization.

4.3. Performance Correlation

It is noteworthy that existing performance correlations primarily focus on single-phase flow conditions. For complex two-phase/three-phase flows involving boiling, condensation, and phase transitions, there remains a lack of universally applicable, high-accuracy prediction models. Although some studies have attempted to establish local heat transfer models based on the VOF or Euler-Euler frameworks, challenges in capturing phase interfaces and the scarcity of experimental data have prevented the development of two-phase/three-phase Nu and f correlations suitable for engineering applications. Recent research results are summarized in Table 6.

Table 6. Performance Correlation under Two-Phase Heat Transfer.

Authors	Parameter	Formula
Khan et al. [108]	Nu, Re	$\mathrm{N}{\mathrm{u}}_{\mathrm{tp}}=129.26{(\mathrm{R}{\mathrm{e}}_{\mathrm{eq}}B{o}_{\mathrm{eq}})}^{-0.079}{(P^{\ast })}^{0.33}$
Arima et al. [110]	h	$\mathrm{h}=16.4h_{l,eq}{\left({\displaystyle \frac{1}{X_{vv}}}\right)}^{1.08}$
Táboas et al. [104]	h	$\begin{array}{c}\mathrm{If} u_{\mathrm{SV}}<-111.88\cdot u_{\mathrm{S}\mathrm{L}}+11.848\left[{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}\right]\Rightarrow h_{\mathrm{T}\mathrm{P}}=5\cdot B{o}^{0.15}\cdot h_{\mathrm{lo}}\\ \mathrm{If} u_{\mathrm{SV}}>-111.88\cdot u_{\mathrm{SL}}+11.848\left[{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}\right]\\ h_{TP} \mathrm{the} \mathrm{greater} \mathrm{of} \left\{\begin{array}{c}{h}_{\mathrm{nb}}=5\cdot B{o}^{0.15}\cdot h_{\mathrm{lo}}\\ h_{\mathrm{cb}}={\left({\varphi }_{\mathrm{Chisholm}}^2\right)}^{0.2}\cdot h_{\mathrm{lo}}\end{array}\right.\end{array}$
Eungchan Lee et al. [105]	Nu	$\begin{array}{l}\mathrm{N}{\mathrm{u}}_{\mathrm{tp},\mathrm{pred}}=98.7{(\mathrm{R}{\mathrm{e}}_g/\mathrm{R}{\mathrm{e}}_f)}^{-0.0848}\mathrm{B}{\mathrm{o}}^{-0.0597}{x}_{\mathrm{tt}}^{0.0973}\\ \mathrm{for}\mathrm{R}{\mathrm{e}}_g/\mathrm{R}{\mathrm{e}}_f<9.0\\ \mathrm{N}{\mathrm{u}}_{\mathrm{tp},\mathrm{pred}}=234.9{(\mathrm{R}{\mathrm{e}}_g/\mathrm{R}{\mathrm{e}}_f)}^{-0.576}\mathrm{B}{\mathrm{o}}^{-0.275}{\mathrm{X}}_{\mathrm{tt}}^{0.660}\\ \mathrm{for}\mathrm{R}{\mathrm{e}}_g/\mathrm{R}{\mathrm{e}}_f>9.0\end{array}$
Longo et al. [107]	H, Re	$h_{\mathrm{s}}=0.277({\lambda }_{\mathrm{s}}/d_{\mathrm{h}}){\mathrm{R}{\mathrm{e}}_{\mathrm{s}}}^{0.766}{\mathrm{P}{\mathrm{r}}_{\mathrm{s}}}^{0.333}$
Mancin et al. [106]	h	$\mathrm{h}=\left(h_{Nu}^2\right)+h_{shear}^2{)}^{1/2}\left[\begin{array}{c}1.074(T_{sat}\end{array}\right]-{\left.T_w\right)}^{-0.386}$
Amalfi et al. [119]	Nu	$N{u}_{tp}=982\cdot {\beta }^{{\ast }^{1.101}}W{e}_m^{0.315}B{o}^{0.320}{\rho }^{{\ast }^{-0.224}}$
Eungchan Lee et al. [105]	f, Re	$f_{tp,pred}\mathrm{R}{\mathrm{e}}^{0.4074}=49.13\mathrm{R}{\mathrm{e}}_{eq}^{-0.4386}$

The two-phase correlations listed in Table 6 were almost exclusively built from pure R134a, R410A or water data acquired on 30° or 60° single-chevron test sections at 50 < G < 150 kg m⁻² s⁻¹ and 0.1 < x < 0.8, giving an apparent ±20% scatter; when they are extrapolated to low-GWP zeotropic mixtures the experimental HTC is systematically under-predicted by 15–25% and the dry-out quality is shifted by ≈0.1. Moreover, header pressure loss and flow maldistribution are absent in these equations, so in commercial stacks (>30 plates) the real overall Δp can exceed the predicted value by 30–50%. Therefore Longo or Amalfi should be limited to pure refrigerants with x ≤ 0.8, whereas for mixed refrigerants the HTC should be scaled up by 1.2 and the calculated pressure drop augmented by 30%; three-dimensional VOF simulations of the inlet header are strongly recommended whenever the plate count rises above fifty.

Current systematic research on two-phase heat transfer in herringbone corrugated plate heat exchangers remains in an exploratory development phase, facing numerous challenges. To advance this field, future efforts should focus on the following key directions:

(1)

Interface capture models: Developing accurate and efficient interface tracking methods (e.g.; VOF, Level Set, or coupled models) is essential to capture the dynamic behavior of vapor–liquid interfaces, particularly in complex corrugated geometries.

(2)

Multi-scale simulation: Integrating micro-scale bubble dynamics with macro-scale flow and heat transfer behavior through multi-scale modeling approaches can provide deeper insights into the coupling mechanisms between phase change and surface structure.

(3)

Experimental visualization techniques: High-resolution visualization tools—such as high-speed imaging, infrared thermography, and tomographic techniques—should be further developed to enable real-time observation of flow patterns, phase distribution, and local heat transfer phenomena.

These directions will not only enhance the fundamental understanding of two-phase transport mechanisms but also support the development of more accurate and universally applicable performance correlations for engineering applications.

5. Conclusions

Against the backdrop of the “dual carbon” strategy driving the transformation of urban low-carbon heating and energy systems, herringbone corrugated plate heat exchangers (PHEs) have emerged as critical intermediate heat transfer equipment in long-distance heating systems and industrial energy conservation applications. This is due to their compact structure, high heat transfer efficiency, and strong adaptability. This paper systematically reviews research progress on the influence of the chevron corrugation structure on fluid flow and heat transfer performance under single-phase and two-phase flow conditions. Unlike previous review papers that only focused on single-phase heat transfer enhancement or listed geometric parameters in isolation, this work provides a comprehensive and up-to-date atlas of single-phase correlations, covering studies published after 2020, and benchmarks their error ranges and applicability. It offers designers a quick ‘range selection’ tool rather than a single uncertain equation. This paper also provides a critical synthesis of two-phase flow mechanisms (nucleate boiling, film condensation, uneven flow distribution), highlights knowledge gaps in bubble–surface interactions, and quantifies deviations (20–40%) of existing HTC correlations when using zeotropic mixtures or low-GWP refrigerants. Key findings include:

(1)

The structural design of chevron corrugated plates is central to determining the heat exchanger’s flow and heat transfer performance. Regarding arrangement configurations: single-channel layouts facilitate maintenance and suit precise control/experimental studies but only accommodate low flow rates. Multi-channel layouts reduce single-channel velocity through flow splitting, enabling high-flow heat exchange while effectively lowering pressure drop—making them the mainstream industrial configuration. Regarding flow paths, vertical flow along the plate length offers simplicity but weak turbulence. Diagonal flow induces strong secondary flows and vortices through corrugations, disrupting thermal boundary layers to extend heat transfer paths while enhancing mechanical stability via multi-point support at plate contact points—a key flow pattern design for high-efficiency heat transfer.

(2)

Under single-phase flow conditions, the heat transfer performance of herringbone PHEs has established clear influencing patterns and a well-defined research framework. Experimental studies have confirmed the dominant role of geometric parameters, while numerical simulations have deepened understanding of flow mechanisms. Integrating both approaches has further explored enhanced heat transfer measures and related performance correlations for herringbone corrugated plate heat exchangers, laying groundwork for future optimization.

(3)

Due to phase transition processes, the heat transfer mechanism in two-phase flow is far more complex than in single-phase flow. While current research has achieved phased progress, significant limitations remain. Compared to single-phase flow studies, two-phase flow research is more intricate and yields relatively fewer findings. Experimental studies have revealed key influencing patterns: the two-phase heat transfer coefficient exhibits strong sensitivity to heat flux and steam mass fraction, but weak sensitivity to saturated temperature; friction pressure drop exhibits linear correlation with fluid kinetic energy per unit volume, with negligible influence from heat flux. Numerical simulations have preliminarily explored phase-change mechanisms: three-dimensional simulations based on VOF interface capture and the Lee mass transfer model reveal that ripple depth and β significantly affect two-phase heat transfer performance, with an optimal ripple spacing existing to balance heat transfer coefficient and flow resistance. Current two-phase studies lack universal mechanistic models, making it difficult to accurately describe the effects of geometric parameters on bubble dynamics and liquid film behavior. Generic performance correlation equations are scarce, and existing models heavily depend on specific working fluids and operating conditions, failing to cover complex industrial scenarios.

The efficient application of herringbone PHEs in low-carbon heating and industrial energy conservation is currently undergoing rapid evolution through the stages of “concept validation-parametric optimization-regional topology optimization-multi-physics topology optimization”. Future topological optimization of herringbone corrugated plate heat exchangers will advance along a three-pronged approach of “multi-physics-multi-scale-smart manufacturing”: Conducting collaborative optimization across the entire scale range—from μm level surface folds to cm level flow channel distribution—while incorporating manufacturing constraints such as roll forming and diffusion welding into the optimization loop. This approach ultimately yields a “manufacturable” optimal topology ready for direct production, enabling the design of a new generation of plate heat exchangers characterized by high efficiency, lightweight construction, and extended service life.