Coordinated Strategy to Improve Post-Fault Characteristics of Hybrid Multi-Infeed HVDC Transmission System

Abstract

The characteristics of the dynamic reactive power demand of a hybrid multi-infeed HVDC transmission system during the post-fault recovery period are analyzed and a coordinated control strategy to improve the fault recovery characteristics of the hybrid multi-infeed HVDC transmission system is proposed in this paper. During the process of fault recovery, the LCC-HVDC adopts a progressive staggering recovery strategy. At the same time, according to the reactive power shortage of LCC-HVDC, the dynamic power limiter is used to adjust the upper and lower limit values of the outer loop power controller of VSC-HVDC, and the reactive power generated by the VSC-HVDC can be rapidly adjusted. Therefore, the problem of excessive reactive power demand during the recovery process can be solved and the reactive power demand can be satisfied with the proposed strategy. Moreover, the ability of VSC-HVDC to provide reactive power support can be fully utilized. Finally, a simulation model of a hybrid tri-infeed HVDC system is built using PSCAD/EMTDC (Version 4.6.2) software to verify the effectiveness of the proposed control strategy.

1. Introduction

Line-commutated-converter-based high-voltage direct-current (LCC-HVDC) transmission technology, which relies on the AC grid for commutation, offers advantages such as large power transfer capacity, long transmission distance, and low overall cost. It plays a critical role in addressing the reverse geographical distribution of energy resources and load centers in China and serves as a key technical support for the national “West-to-East Power Transmission” strategy, accounting for more than 50% of the total transmitted capacity [1]. Compared with LCC-HVDC, voltage source converter-based high-voltage direct-current (VSC-HVDC) transmission features greater control flexibility, eliminates the need for reactive power compensation, and is free from commutation failure issues, which has led to its rapid development in recent years [2]. With the continuous construction of VSC-HVDC projects, hybrid multi-infeed HVDC transmission systems—where multiple LCC-HVDC and VSC-HVDC links coexist within the same AC network—have gradually emerged [3,4]. The East China and Guangdong power grids represent the most densely concentrated multi-infeed HVDC systems worldwide. In 2020, the Wudongde HVDC project, the tenth HVDC link terminating in Guangdong, was officially commissioned, transforming the Guangdong power grid into a hybrid multi-infeed HVDC transmission system [5,6]. In 2022, the Baihetan–Jiangsu ±800 kV ultra-high voltage direct current (UHVDC) transmission project was completed and put into operation, becoming the first HVDC project employing a hybrid cascaded configuration of LCC and VSC technologies [7,8].

Although multi-infeed HVDC systems enhance operational flexibility and expand transmission capacity, they also increase structural complexity, thereby exacerbating challenges related to system security and stability. When the receiving-end system is subjected to a large disturbance, the converter will consume a large amount of reactive power, especially for the receiving-end system with multiple HVDC converters. The AC system must be strong enough to support the operation of multiple HVDC links. Furthermore, the strong electrical coupling between the converter stations makes the commutation bus voltage drops correspondingly during the fault of the receiving-end grid, which may lead to continuous commutation failure or multiple HVDC links’ simultaneous commutation failure, bringing large dynamic reactive power demand during the recovery process, and the problems of voltage stability will be quite serious [9,10,11,12]. Fortunately, VSC-HVDC can compensate for the dynamic reactive power demand in real time and improve the voltage stability of the receiving-end system after a large disturbance. The problems of how to slow down the interaction between HVDCs during the recovery period and speed up the recovery of active power at the same time, and what strategies are used to coordinate and orderly recover the hybrid multi-infeed HVDC transmission system after fault clearing, need to be further researched.

The post-fault recovery characteristics of LCC-HVDC and MMC-HVDC have been investigated by establishing the transient simulation models [13,14]. The simulation study of Chu-Sui UHVDC shows that the peak value of reactive power demand of the inverter station will not be affected by the severity of commutation bus fault if commutation failure occurs [15]. It is revealed that the voltage interactions among converter stations in multi-infeed HVDC systems are an important factor triggering commutation failures in [16]. A coordinated and progressive recovery strategy for a multi-infeed HVDC system is proposed in [17,18] by setting a first-order lag loop after the VDCOL (Voltage-Dependent Current Order Limiter) of each HVDC system and by controlling the time constant, thus staggering the peak value of reactive power demand of HVDC converters during the post-fault recovery process. A regulation method for the additional current proportional coefficient is proposed in [19], which enables the stronger DC system to recover more rapidly, thereby facilitating a faster restoration of the overall system voltage and transmitted power. An “autonomous coordination” strategy is proposed to decompose the coordinated optimization in [20], taking into account short-term voltage stability constraints and optimal HVDC power recovery, in order to achieve dynamic reactive power support. A control strategy based on a constant extinction area for suppressing commutation failure is proposed in [21]. It also proposes a VSC-HVDC dynamic power limiting regulation control, but its limiting regulation can only be adjusted in segments. It is concluded that harmonics are one of the reasons for continuous commutation failure during HVDC post-fault recovery, and a hybrid HVDC continuous commutation failure suppression strategy based on harmonic voltage compensation is proposed in [22]. A correlation model among the extinction angle and DC current of LCC-HVDC inverter and the output reactive power of VSC-HVDC is deduced to optimize the control within the controllable range of commutation failure in [23]. A reactive power priority control method is proposed to enhance the reactive power output capability of VSC converter stations in [24], allowing them to provide additional reactive power for voltage support during system faults. A control method is proposed to effectively regulate the reactive power of MMC-HVDC in hybrid parallel HVDC systems, which can support the inverter-side AC bus voltage and improve the overall fault recovery performance of the system in [25]. The above-mentioned references only consider the improvement of LCC-HVDC or VSC-HVDC control strategies but do not make full use of the recovery characteristics of the two HVDCs for coordinated control. Therefore, designing a coordinated control strategy that integrates the dynamic reactive power regulation capability of VSC-HVDC into the peak-shifting restoration strategy of LCC-HVDC to achieve precise, bidirectional regulation of reactive power supply and demand during the restoration process has become a critical issue for enhancing the post-fault characteristics of hybrid multi-feed systems.

Based on the analysis of the characteristics of dynamic reactive power during the post-fault recovery period of a hybrid multi-infeed HVDC transmission system, a coordinated control strategy to improve the post-fault recovery characteristics of the hybrid multi-infeed HVDC transmission system is proposed from two aspects: (a) dynamic reactive power demand; and (b) dynamic reactive power supply. The main idea is to reduce the reactive power demand peak value by using a peak staggering recovery strategy for LCC-HVDC and, at the same time, adopt a dynamic adaptive current limiting strategy for VSC-HVDC to provide dynamic reactive power and smooth the reactive power demand during the post-fault recovery process.

The remainder of this paper is organized as follows. The characteristics of dynamic reactive power during the post-fault recovery period are presented in Section 2. Section 3 provides the multi-infeed HVDC transmission system progressive peak staggering recovery strategy. Section 4 proposes a post-fault recovery characteristic improvement strategy for a hybrid multi-infeed HVDC transmission system and its implementation process of VSC-HVDC coordinated control strategy. In Section 5, verification of the effectiveness of the control strategy proposed in this paper is implemented. Finally, conclusions are drawn in Section 6.

2. The Characteristics of Inverter Dynamic Reactive Power Demand After Large Disturbance of Hybrid Multi-Infeed HVDC Transmission System

To reflect the mutual interaction between LCC-HVDCs under large disturbances and the supporting role of VSC-HVDC for LCC-HVDC, this paper employs a hybrid multi-infeed HVDC transmission system model. This model is shown in Figure 1. It consists of two LCC-HVDCs and one VSC-HVDC system. There is an electrical distance between the three receiving converter stations. The line impedance values Z₁₂, Z₁₃, and Z₂₃ can be set according to the actual situation.

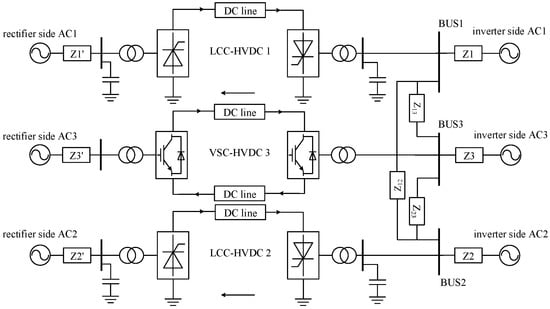
Figure 1. The structure of a hybrid multi-infeed HVDC transmission system.

The dynamic reactive power demand at the receiving end during the recovery period after a large disturbance is bigger than that under a small disturbance, which is even more detrimental to the system voltage stability. This section focuses on the dynamic reactive power characteristics of inverters under large disturbances. In this paper, a large disturbance refers to a serious symmetrical three-phase short-circuit fault occurring at the receiving-end grid, which is serious enough to cause commutation failure and require the rectifier station to adopt the minimum current control during the post-fault period.

2.1. Model of HVDC Control System in Recovery Period After Large Disturbance

The control mode adopted by the converter is a combination of several basic control modes [26], and the switching logic of the control mode is shown in Figure 2. The DC current, DC voltage on rectifier sides, DC voltage on inverter sides, and the extinction angle measured values are I_d,mes, U_dr,mes, U_di,mes, and γ_mes, respectively; the setting values are I_d,ref, U_dr,ref, U_di,ref, and γ_ref, respectively; and the deviation values are I_d,err, U_dr,err, U_di,err, and γ_err, respectively. The selection logic of the control mode increases the difficulty of establishing the mathematical model, and the control mode can be determined according to the values of the operating electric variables during the post-fault recovery period.

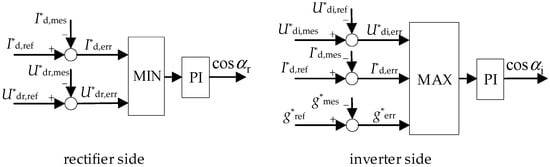
Figure 2. Selection logic of LCC-HVDC control mode.

At the initial stage after fault clearance, as the voltage setting value on the rectifier side is constant, the current setting value increases from the minimum DC current I_L to 1 (p.u.) under the action of the VDCOL, and the DC voltage deviation is larger than the current deviation, leading the rectifier side to adopt constant current control. While the DC voltage does not reach the value constant DC voltage control during the post-fault recovery period, the DC voltage deviation is smaller than that decided by the extinction angle, so the inverter side adopts constant extinction angle control.

After the control mode is determined, the control block diagram of the HVDC system can be shown as Figure 3. The HVDC system mainly consists of the DC current setting control, the secondary system of PI control [27], the primary system, the measurement linking the primary system with the secondary system to complete the signal transmission, and the converters. The first-order measurement is ignored to reduce the order of the equation.

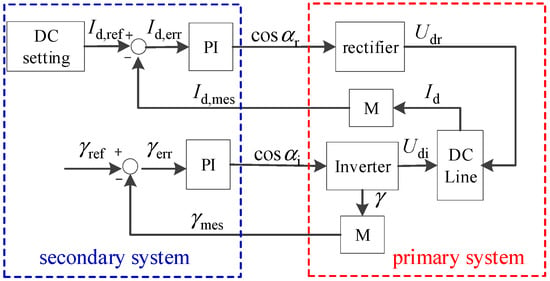
Figure 3. Control block of the LCC-HVDC system.

After the three-phase short-circuit fault is cleared, the primary system can be represented by a quasi-steady-state model [28,29].

$$\begin{array}{l}{I}_{\mathrm{d}}(t)={\displaystyle \frac{1.35n{E}_{\mathrm{r}}(t)\cos {\alpha }_{\mathrm{r}}(t)+1.35n{E}_{\mathrm{i}}(t)\cos {\alpha }_{\mathrm{i}}(t)}{R_{\mathrm{cr}}+R_{\mathrm{L}}+R_{\mathrm{ci}}}}\\ \gamma (t)=\arccos [{\displaystyle \frac{\sqrt{2}{X}_{\mathrm{ci}}{I}_{\mathrm{d}}(t)}{E_{\mathrm{i}}(t)}}-\cos {\alpha }_{\mathrm{i}}(t)]\end{array}$$

(1)

In the formula, α_r(t) and α_i(t) are the firing angles of the sending end and receiving end, respectively, and their cosine values are the input of the primary system, whereas the DC current I_d(t) and extinction angle γ(t) are the output of the primary system. The parameters of the primary system include the number of 6-pulse converters in the converter station n, DC line resistance R_L, equivalent commutation resistance R_cr at the sending end and R_ci at the receiving end, commutation reactance X_ci at the receiving end, and commutation bus voltages E_r(t) and E_i(t).

2.2. Characteristics of Dynamic Reactive Power Demand of Inverter After Large Disturbance

As shown in Figure 3, for an LCC-HVDC system with parameters determined, the dynamic reactive power curve in the fault recovery process is well-determined by the system input (I_d,ref, γ_ref), boundary conditions (firing angle of rectifier and inverter station at the moment of fault clearance), and time-varying parameters in the system (E_r(t) and E_i(t)). After the disturbance of different magnitudes occurs at the receiving-end system, if the above parameters are close to each other, the reactive power demand during the recovery period will be relatively fixed.

2.2.1. Time-Varying Parameters in a System

The bus voltages E_r(t) and E_i(t) are the time-varying parameters of the system. At the fault-clearing moment, the DC transmission active power begins to climb, the converter consumes little reactive power, and the filter bank provides excessive reactive power. Even with different magnitudes of disturbance, usually the AC voltage can quickly recover to the rated value, and the fault severity has little effect on the commutation bus voltage. As the converter consumption reactive power increases to the peak and then decreases, the bus voltage first drops to the valley and then returns to the rated value. Therefore, after the fault clearance, if the system voltage is stable, the AC voltage will fluctuate around the rated voltage. Ignore the AC voltage fluctuation during the recovery period, and take E_r(t) and E_i(t) as the rated operating values.

2.2.2. System Boundary Conditions

During the fault period of the commutation bus at the inverter side, due to the commutation failure of the inverter, the leading firing angle β increases to its upper limit value β_max. Therefore, the constant β control is adopted on the inverter side, and the constant minimum current control is adopted on the rectifier side at the moment of fault clearance. The firing angle of the converter station at the time t₀ of fault clearance is:

$$\left\{\begin{array}{l}\cos {\alpha }_{\mathrm{i},t_0}=\cos ({180}^{°}-{\beta }_{\max })=-\cos {\beta }_{\max }\\ \cos {\alpha }_{\mathrm{r},t_0}={\displaystyle \frac{I_{\mathrm{L}}{I}_{\mathrm{d},\mathrm{base}}-k_3\cos {\alpha }_{\mathrm{i},t_0}}{k_2}}\end{array}\right.$$

(2)

At steady state, the firing angle is:

$$\left\{\begin{array}{l}\cos {\alpha }_{\mathrm{i},\mathrm{s}}=k_5{I}_{\mathrm{d},\mathrm{s}}{I}_{\mathrm{d},\mathrm{base}}-\cos {\gamma }_{\mathrm{ref}}\\ \cos {\alpha }_{\mathrm{r},\mathrm{s}}={\displaystyle \frac{I_{\mathrm{d},\mathrm{s}}{I}_{\mathrm{d},\mathrm{base}}-k_3\cos {\alpha }_{\mathrm{i},\mathrm{s}}}{k_2}}\end{array}\right.$$

(3)

Assuming that the AC voltage is the rated value, where k₂ = 1.35nE_r/R_all, R_all = R_cr + R_d + R_ci, k₃ = 1.35nE_i/R_all, k₅ = $\sqrt{2}$X_ci/E_i, I_d,base is the reference value of DC current, and I_d,s is the steady-state value of the DC current. After major perturbations of varying severity, the system’s boundary conditions remain largely unchanged.

2.2.3. System Input

System input I_d,ref is a nonlinear function of the internal variable DC voltage of the system, as shown in Figure 4, where I_d,VDCOL is the current setting value output by VDCOL, and I_d,HMI is the current instruction value.

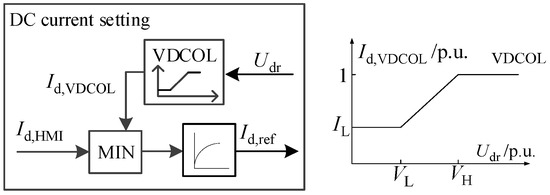
Figure 4. Control scheme of DC current reference.

If the rise time of the DC voltage is not taken into account, let V_H = 0, V_L = 0, I_d,VDCOL jump from the minimum current I_L to the rated value after the fault clearance. Considering the inertia element in the control system, the current setting value under different fault conditions has nothing to do with the disturbance severity, i.e.,

$$I_{\mathrm{d},\mathrm{ref}}=I_{\mathrm{d},\mathrm{base}}[1-(1-I_{\mathrm{L}})e^{-(t-t_0)/T}]$$

(4)

where T is the time constant of the inertial element. The faster the rate of DC voltage rise, the smaller the influence of I_d,ref. During the post-fault recovery period, the AC voltage rises rapidly due to the excess reactive power injection of the filter bank; correspondingly, the DC voltage also rises at a fast rate, and I_d,ref is less affected by the fault severity.

Usually, the commutation bus voltage will recover quickly; therefore, the system input, the system boundary value conditions, and the time-varying parameters in the system are less affected by the severity of the fault, and the difference in dynamic reactive power demand is also small during the recovery process. Since the actual AC voltage fluctuates around the rated voltage and the DC voltage rises quickly after the fault clearance, a curve similar to the dynamic reactive power characteristics after different magnitudes of disturbance can be obtained by replacing the AC voltage with the rated value, as well as ignoring the DC voltage rise time.

2.3. Calculation of Dynamic Reactive Power Demand in the Recovery Process After Large Disturbance

According to the above section, E_r(t) and E_i(t) are set as rated operating values, the setting value of DC current is shown in (5), and the maximum dynamic reactive power demand under different magnitudes of disturbance can be obtained. Equation (1) can be simplified into a linear expression if we replace arccos(x) by −π(x − 1)/2 approximately:

$$I_{\mathrm{d}}(t)={\displaystyle \frac{1.35n{E}_{\mathrm{r}}\cos {\alpha }_{\mathrm{r}}(t)+1.35n{E}_{\mathrm{i}}\cos {\alpha }_{\mathrm{i}}(t)}{R_{\mathrm{cr}}+R_{\mathrm{L}}+R_{\mathrm{ci}}}}$$

(5)

$$\gamma (t)=-{\displaystyle \frac{\pi }{2}}[{\displaystyle \frac{\sqrt{2}{X}_{\mathrm{ci}}{I}_{\mathrm{d}}(t)}{E_{\mathrm{i}}}}-\cos {\alpha }_{\mathrm{i}}(t)-1]$$

(6)

By combining (4)–(6) and selecting x₁ and x₂ in Figure 5 as state variables, a second-order differential equation can be obtained.

Figure 5. Partial control components of rectifiers and inverters.

For a simple solution, it is approximately considered that the cosα_i(t) in (5) and the I_d(t) in (6) are equal to the cosα_i,s and I_d,s in the steady-state operation of the system. Then, the original second-order differential equation can be changed into two first-order differential equations:

$$\begin{array}{l}{\displaystyle \frac{\mathrm{d}{x}_1}{\mathrm{d}t}}={\displaystyle \frac{k_1}{T_1}}[I_{\mathrm{d},\mathrm{ref}}-k_3\cos {\alpha }_{\mathrm{i},\mathrm{s}}-k_2(x_1+T_1{\displaystyle \frac{\mathrm{d}{x}_1}{\mathrm{d}t}})]\\ {\displaystyle \frac{\mathrm{d}{x}_2}{\mathrm{d}t}}={\displaystyle \frac{k_4}{T_2}}[({\gamma }_{\mathrm{ref}}-{\displaystyle \frac{\pi }{2}})-k_6(k_5{I}_{\mathrm{d},\mathrm{s}}-x_2-T_2{\displaystyle \frac{\mathrm{d}{x}_2}{\mathrm{d}t}})]\end{array}$$

(7)

In the above formula, k₁, T₁, and k₄, T₂ are PI parameters on both sides, respectively, and k₆ = −π/2. The approximation used in (6) is accurate within the range where x approaches 1, corresponding to the typical operating range of the trigger angle α_i during recovery. Considering that the inverter operates in fixed-switching-angle control mode, cosα_i(t) varies within a range near its steady-state value, resulting in a small calculated Q_di error.

According to (7) and boundary value conditions (2) and (3), the reactive power characteristic curve can be obtained.

The cosine of the firing angle of the rectifier side is:

$$\begin{array}{c}\cos {\alpha }_{\mathrm{r}}={\displaystyle \frac{I_{\mathrm{d},\mathrm{s}}{I}_{\mathrm{d},\mathrm{base}}-k_3{k}_5{I}_{\mathrm{d},\mathrm{s}}{I}_{\mathrm{d},\mathrm{base}}+k_3\cos {\gamma }_{\mathrm{ref}}}{k_2}}+{\displaystyle \frac{k_1{I}_{\mathrm{d},\mathrm{base}}(I_{\mathrm{d},\mathrm{s}}-I_{\mathrm{L}})(T-T_1)}{T_1+k_1{k}_2{T}_1-k_1{k}_{2}T}}{e}^{-{\displaystyle \frac{(t-t_0)}{T}}}\\ +({\displaystyle \frac{I_{\mathrm{d},\mathrm{base}}(I_{\mathrm{L}}-I_{\mathrm{d},\mathrm{s}}+k_3{k}_5{I}_{\mathrm{d},\mathrm{s}})}{k_2}}+{\displaystyle \frac{k_3(\cos {\beta }_{\max }-\cos {\gamma }_{\mathrm{ref}})}{k_2}}-{\displaystyle \frac{k_1{I}_{\mathrm{d},\mathrm{base}}(I_{\mathrm{d},\mathrm{s}}-I_{\mathrm{L}})(T-T_1)}{T_1+k_1{k}_2{T}_1-k_1{k}_{2}T}})e^{{\displaystyle \frac{-k_1{k}_2}{T_1\left(1+k_1{k}_2\right)}}(t-t_0)}\end{array}$$

(8)

The cosine of the firing angle of the inverter station is:

$$\cos {\alpha }_{\mathrm{i}}=(-\cos {\beta }_{\max }-k_5{I}_{\mathrm{d},\mathrm{s}}{I}_{\mathrm{d},\mathrm{base}}+\cos {\gamma }_{\mathrm{ref}})e^{{\displaystyle \frac{k_4{k}_6(t-t_0)}{T_2\left(1-k_4{k}_6\right)}} }+(k_5{I}_{\mathrm{d},\mathrm{s}}{I}_{\mathrm{d},\mathrm{base}}-\cos {\gamma }_{\mathrm{ref}})$$

(9)

Substituting (8) and (9) into (10), the dynamic reactive power demand curve Q_di of the inverter after a large disturbance can be obtained.

$$Q_{\mathrm{di}}=1.35n{E}_{\mathrm{i}}\left(k_2\cos {\alpha }_{\mathrm{r}}+k_3{k}_5{I}_{\mathrm{d},\mathrm{s}}{I}_{\mathrm{d},\mathrm{base}}-k_3\cos {\gamma }_{\mathrm{ref}}\right)\sqrt{1-{[(k_5{I}_{\mathrm{d},\mathrm{s}}{I}_{\mathrm{d},\mathrm{base}}-2\cos {\alpha }_{\mathrm{i}})/2]}^2}$$

(10)

The analytical expression for the reactive power demand Q_di of the converter after a fault is shown in (10). By differentiating Q_di and setting it to zero, the maximum value of reactive power demand during fault recovery can be obtained. Analysis indicates that when the inertia time constant T of the current reference value I_d,ref varies, the timing at which the reactive power demand reaches its peak also changes accordingly.

For multi-infeed DC transmission systems, simultaneous restoration of multiple LCC-HVDC lines may result in a combined reactive power peak exceeding the AC grid’s capacity. The theoretical analysis indicates that by deliberately setting different time constants T_d for each line, the reactive power peaks of individual DC systems during fault restoration can be temporally staggered. This peak-spreading approach effectively reduces the maximum instantaneous reactive power demand on the AC system, thereby mitigating voltage sags during restoration and suppressing the risk of subsequent commutation failures. The above describes the principle of the coordinated interleaved recovery control strategy.

3. Multi-Infeed HVDC Transmission System Progressive Peak Staggering Recovery Strategy

According to the analysis of the dynamic reactive power demand of LCC-HVDC during the fault recovery process in the previous section, there is a peak value of dynamic reactive power demand during the fault recovery process. Therefore, for a multi-feed DC system composed of conventional DC, if the conventional DC control strategy is maintained for each LCC-HVDC during the fault recovery period, there will be continuous commutation failures, the dynamic reactive power demand of each HVDC reaches the peak at the same time, and the total reactive power demand is relatively large. According to the change in T in the previous section, the moment when each HVDC reaches the maximum value during the fault recovery period can be staggered. Therefore, a staggering recovery strategy [17,18] was proposed to smooth the reactive power demand of a multi-infeed HVDC transmission system and reduce the reactive power peak value in the recovery process.

As shown in Figure 6, a first-order delay and a small link after the voltage-dependent current order limit (VDCOL) are set for each LCC-HVDC to realize the staggering recovery strategy of the multi-infeed HVDC transmission system. The small link can guarantee that the first-order delay only works when the current increases, adjusts the recovery speed of the DC current, and achieves the purpose of coordinating the orderly recovery of each HVDC line’s current. Moreover, the time constant T_d of the first-order delay is positively correlated with the recovery speed of the DC current. The larger the time constant, the slower the DC recovery speed, and the longer it takes for the DC current to return to a steady state. Therefore, the recovery speed of each HVDC line after a fault can be adjusted by changing the time constant.

Figure 6. Structure of a staggering recovery strategy for a hybrid multi-infeed HVDC transmission system.

The control effect of DC current under the staggering recovery strategy of each HVDC is shown in Figure 7. Curve 0 is the current characteristic when the time constant of the small link is 0 (equal to the original curve). Curve 1 and Curve 2 are the current characteristics when the time constant is T_d1 and T_d2, respectively, where T_d1 < T_d2.

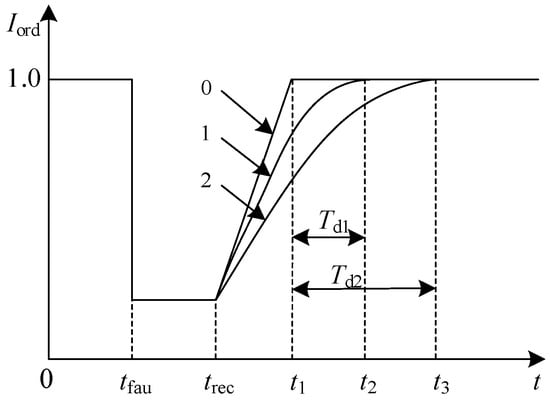
Figure 7. Current characteristics under different time constants.

To determine the optimal value of this critical parameter T_d, an optimization process was implemented using the Multiple Run feature in PSCAD/EMTDC, based on the index mentioned in reference [17]. The procedure was as follows: First, calculate the progressive peak-shaving recovery factor DIR for each DC circuit based on the content of reference [17], and rank the recovery sequence of each DC circuit according to its magnitude. Next, multiple compensation settings for the time constant T_d are established within the range of 0–60 ms at 10 ms intervals. Using the multiple-run capability in PSCAD/EMTDC (Version 4.6.2) software, calculations are performed to observe the reactive demand curve and active power delivery curve during the restoration process under different T_d values. The following two metrics are comprehensively evaluated: (1) minimum peak total reactive demand; and (2) shortest time required for line active power delivery to recover to 0.9 p.u. The T_d value achieving the optimal coordination of these two metrics is ultimately selected as the staggered restoration time constant adopted in this study.

This systematic approach ensured that the selected T_d values effectively staggered the reactive power peaks while maintaining satisfactory active power recovery speed. Building upon this optimized staggering recovery of LCC-HVDCs, the following section introduces the coordinated control strategy with VSC-HVDC to further enhance the overall post-fault characteristics.

4. Coordinated Control Strategy for Hybrid Multi-Feed DC Transmission Systems

In order to improve the fault recovery characteristics of a hybrid multi-infeed HVDC transmission system and make full use of the fast dynamic response of VSC-HVDC, this paper proposes a fault recovery performance improvement strategy for a hybrid multi-infeed HVDC transmission system. The basic idea of this strategy is that, in the process of fault recovery, a progressive peak staggering recovery is adopted between LCC-HVDCs. VSC-HVDC adopts an adaptive current limiting strategy; at the same time, VSC-HVDC considers the coordinated reactive power control of each HVDC system, which dynamically adjusts the upper and lower limit value of the VSC-HVDC q-axis reactive power outer loop output i_q^* according to the reactive power shortage of LCC. A schematic diagram of the absorbed reactive power of the converter station under different control strategies is shown in Figure 8.

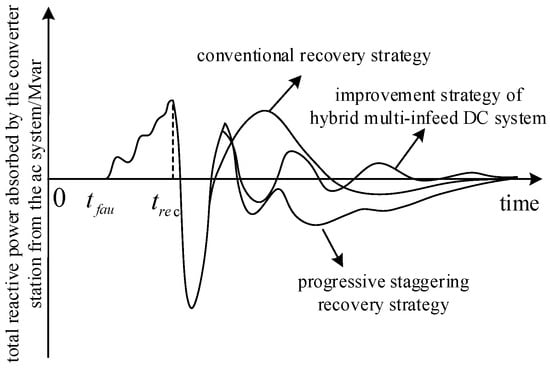
Figure 8. Schematic diagram of absorbed reactive power of the converter station.

In Figure 8, as for the traditional simultaneous recovery control strategy, when the AC voltage at the receiving-end system is restored to near the rated value, the AC voltage will remain basically constant. While the VSC-HVDC control strategy adopts a constant AC voltage, this will lead to weak regulation of the reactive power at this stage. On the contrary, the DC current of each LCC-HVDC increases rapidly, and the arc extinction angle is still at a larger level. At this point, LCC-HVDC will reach the peak reactive power demand almost at the same time, so the first peak reactive power demand is larger in this case. For the progressive peak staggering recovery strategy, the core is to stagger the DC current recovery process of each LCC-HVDC, which reflects that multiple peaks will be formed on the reactive power waveform, but the biggest peak will be smaller than that of the simultaneous recovery strategy. However, this strategy has little effect on the AC voltage of the receiving end, so it still fails to exert the reactive power regulation ability of VSC-HVDC at this stage. As for the hybrid multi-infeed HVDC transmission system improvement strategy proposed in this paper, the reactive power regulation ability of the VSC-HVDC can be adequately utilized. On the basis of the progressive peak staggering recovery, VSC-HVDC will provide more reactive power at the valley of reactive power demand and less at the peak of reactive power demand, so that the total reactive power absorbed during the fault recovery process is closest to its steady-state operating value.

4.1. Dynamic Power Limiting Regulation Strategy

The dynamic power limiting regulation strategy is the core of the coordinated control strategy for a hybrid multi-infeed HVDC transmission system, which is based on the adaptive current limit [30] (the logic diagram of adaptive current limit control is shown in Figure 9).

Figure 9. The logic diagram of adaptive current limit control.

According to the reactive power shortage of LCC-HVDC, the strategy dynamically adjusts the upper and lower limit values of the VSC-HVDC q-axis reactive power outer loop output i_q^*, so that the steady-state operating point of the VSC-HVDC can be changed during the fault period. The specific control logic diagram is shown in Figure 10. The outputs i_{qlim max1} and i_{qlim min1} serve as the upper and lower limits of the reactive current for the adaptive current limiting controller.

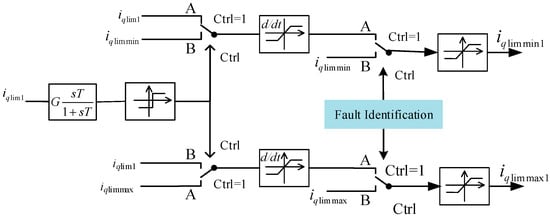
Figure 10. Specific control logic diagram of VSC-HVDC.

In Figure 10, i_qlim1 is calculated according to the instantaneous power theory, and the formula is:

$$i_{q\lim 1}={\displaystyle \frac{Q_{LCC}/S_b+v_{oq}{i}_{od}}{v_{od}}}$$

(11)

where Q_LCC is the reactive power absorbed by the LCC from the AC system, S_b is the reference value of system capacity, and v_od and v_oq are the dq axis components of the AC voltage at the receiving end, respectively. According to the phase-locked loop control theory, v_od = 1 and v_oq = 0, and the final i_qlim1 can be calculated by:

$$i_{q\lim 1}={\displaystyle \frac{Q_{LCC}}{S_b}}$$

(12)

The dynamic power limiting regulation strategy includes the following parts:

• Selection of upper and lower limits

According to the calculated reference value of i_qlim1, calculate its slope. When the slope is positive, modify the lower limit value of i_q^* and select as i_qlim1; otherwise, select as i_qlimmin. On the contrary, when the slope is negative, modify the upper limit value of i_q^* and select as i_qlim1, or otherwise as i_qlimmax, where i_qlimmin and i_qlimmax are the static reactive power limiting values.

2.

Slope limitation

Considering the fast regulation speed of VSC-HVDC, the slope controller is added to limit the rate of change in reactive power so as to avoid the continuous commutation failure of LCC caused by the rapid fluctuation of reactive power.

3.

Control enable

Control the operation of the control strategy. The enabling signal is selected as the output signal of the fault identification module. When a fault is identified, the output signal is set to 1 and maintained until the system recovers to near the steady-state value. A detailed control logic block diagram can be found in reference [31].

Through the synergy effects of the above control strategies, VSC-HVDC can quickly compensate for the reactive power shortage of LCC-HVDC and ease the reactive power demand of the converter station on the receiving-end system during the process of fault recovery.

4.2. Implementation Process of VSC-HVDC Coordinated Control Strategy

The coordinated control strategy of the VSC-HVDC mainly includes the adaptive current limiting strategy and the dynamic power limiting regulation strategy. The output of the dynamic power limiting regulation strategy provides the input parameters for the reactive current limiting in the adaptive current limiting strategy. The dynamic power limiting regulation strategy is to limit the reactive current reference value i_q^*, while the adaptive current limiting strategy is to use the remaining capacity as a limit to i_d^* on the basis of satisfying the demand of the reactive current. The flowchart of the coordinated control strategy for the VSC-HVDC is shown in Figure 11, and the specific steps are as follows:

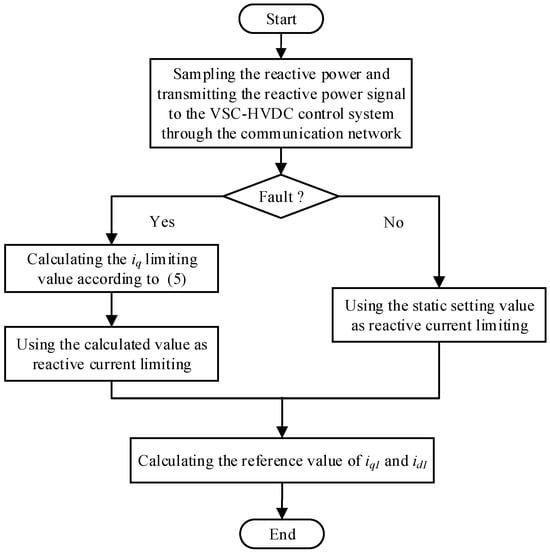
Figure 11. The flowchart of the VSC-HVDC coordinated control strategy.

(1)

Sample the reactive power absorbed from the AC system by each LCC-HVDC receiving end converter station and transmit it to the VSC-HVDC control system through the communication network. Use the single-phase to ground short-circuit fault and three-phase short-circuit fault criteria of commutation failure predictive control to determine whether the fault occurs. If the result is yes, skip to step 2; otherwise, skip to step 4.

(2)

Sum the reactive power shortage value of each converter station and calculate the limiting value i_qlim1 of i_q by Equation (12).

(3)

Send the limit value of i_q obtained in the previous step to the dynamic power limiting adjustment controller to calculate the upper and lower limit values of the final signal i_q and use it as the upper and lower limits i_qlimmin1 and i_qlimmax1 of the reactive current limits output by the outer loop of the adaptive current limiting controller. Then, skip to step 5.

(4)

Use the static setting values i_qlimmin and i_qlimmax as the upper and lower limits of the reactive current limits output by the outer loop of the adaptive current limiting controller.

(5)

Use the adaptive current limit controller as shown in Figure 9 to calculate i_q1^* and i_d1^* by i_qlimmin1 and i_qlimmax1 obtained in the previous step.

5. Experimental Verification

To verify the improvement effect of the control strategy proposed in this paper, a hybrid tri-infeed HVDC transmission system is established in the PSCAD/EMTDC (Version 4.6.2) simulation software. The rated firing angle α_N of the inverter side is 142°, the minimum extinguishing angle γ_min is 7°, and the line impedance value of three AC lines (L1-2, L1-3, and L2-3) is Z₁₃ = Z₂₃ = Z₁₂/2 = 1.8 + j4.15(Ω). The main parameters of LCC-HVDC and VSC-HVDC are shown in Table 1 and Table 2. The transmission power of each line under initial steady-state conditions is shown in Table 3.

Table 1. Specific parameters of the LCC-HVDC system.

LCC-HVDC Parameters	Rectifier Side	Inverter Side
AC voltage class	330 kV	220 kV
DC voltage class	±500 kV	±500 kV
AC equivalent impedance	47.655∠84° Ω	8.833∠75° Ω
reactive compensation capacity	626 MVar	626 MVar
transformer capacity	603.7 MVA	591.8 MVA
transformer leakage reactance	0.18 p.u.	0.18 p.u.
transformer ratio	345/213.5 kV	209.2/230 kV

Table 2. Specific parameters of the VSC-HVDC system.

VSC-HVDC Parameters	Rectifier Side	Inverter Side
AC voltage class	220 kV	220 kV
DC voltage class	±320 kV	±320 kV
transformer capacity	1000 MVA	1000 MVA
transformer leakage reactance	0.15 p.u.	0.15 p.u.
transformation ratio	230/370 kV	370/230 kV
number of submodules	200	200
submodule capacitance	10 mF	10 mF
bridge arm reactance value	29 mH	29 mH

Table 3. Power transmitted by each line under initial steady-state conditions.

DC Line Name	Active Power	Reactive Power
LCC-HVDC1	928.9 MW	−75 Mvar
LCC-HVDC2	928.9 MW	−75 Mvar
VSC-HVDC	999.6 MW	0

Three groups of different cases for comparative analysis are set as follows:

Case 1: Both LCC-HVDCs and VSC-HVDC adopt the traditional control strategy.

Case 2: A progressive peak staggering recovery strategy is adopted between LCC-HVDCs, whereas a traditional control strategy is adopted for VSC-HVDC.

Case 3: The fault recovery improvement strategy proposed in this paper is applied.

In all cases, the contingency faults are applied to the simulation model: after the system stabilizes, a three-phase short-circuit fault is applied at the receiving end commutation bus at 5.0 s. The fault lasts 100 ms, and the simulation runs from 4.9 s to 5.9 s. The time domain simulation waveform comparison diagram of three cases is shown in Figure 12.

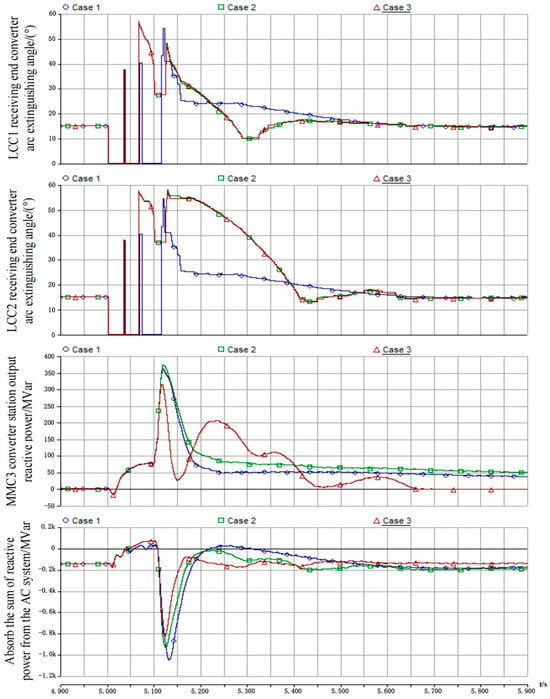
Figure 12. Comparison of simulation waveforms with different T_d.

As shown in Figure 12, when the progressive peak staggering recovery strategy between LCC-HVDCs is adopted, from the perspective of the commutation failure duration (the time of duration when γ is below 7.2° [32]), LCC can return to normal commutation 0.04 s earlier than the non-adopted one. It can be seen that the progressive peak staggering recovery can improve the ability of LCC-HVDC to resist continuous commutation failure to some extent. Case 2 and case 3 show that there is little difference in extinction angle between the two cases during the process of fault recovery. From this point, we can know that the proposed VSC dynamic power limiting strategy primarily affects the total reactive power of the converter station. Further comparison of the two cases of VSC output reactive power waveform shows that using a dynamic power limiting regulation control strategy can give full play to the ability of VSC to adjust reactive power quickly. VSC-HVDC can rapidly reduce its output reactive power and reduce the surplus reactive power of the system in the process of voltage recovery after fault clearance. At the same time, the VSC can increase the reactive power output at the peak of the LCC consumption reactive power during the process of fault recovery and reduce the reactive power output at the valley. The speed of reactive power recovery to the pre-fault level in case 3 is better than the traditional control strategy or just adopting the progressive peak staggering recovery strategy.

Some evaluation indexes are given in Table 4. It can be seen that among the three cases, case 3 has the best fault recovery characteristics, with the advantages of a smaller reactive power peak value, faster fault recovery speed, and smaller reactive power fluctuation. Therefore, the fault recovery characteristic improvement strategy proposed in this paper is better than the traditional control strategies, and this strategy gives full play to the ability of the reactive power support of VSC-HVDC.

Table 4. Fault recovery evaluation index data under different recovery strategies.

Evaluation Index	Case 1	Case 2	Case 3
duration of commutation failure/s	0.1123	0.067	0.067
peak value of total absorbed reactive power during recovery/MVar	23.34	−19.2	−81.68
peak value of total output reactive power during recovery/MVar	−1050	−933	−826
time for system reactive power level to return to steady state/s	1.745	2.166	0.62

The data in Table 3 indicate that despite the strategy employed in case 2 successfully reducing the peak reactive power demand, it results in a longer total recovery time. This is an inherent and expected trade-off. The strategy intentionally slows down the current recovery of one (or more) LCC-HVDC lines by assigning it a larger time constant T_d, thereby staggering the reactive power peaks. While this progressive recovery strategy effectively alleviates the instantaneous stress on the AC voltage, it inevitably extends the duration for the entire system to return to its pre-fault steady-state power level. Case 3 demonstrates how this trade-off can be mitigated. By integrating the VSC-HVDC’s dynamic reactive power support, the proposed coordinated strategy not only maintains the benefit of reduced peak demand but also significantly accelerates the overall recovery process, achieving a superior performance on both metrics.

6. Conclusions

In this paper, the characteristics of the dynamic reactive power demand of the inverter after a large disturbance are analyzed, and the method of determining the dynamic reactive power demand curve Q_di of the inverter after a large disturbance is illustrated. Based on the research of reactive power demand, a strategy is proposed to improve the fault recovery characteristics of the hybrid multi-infeed HVDC transmission system, which is a control strategy that combines the progressive peak staggering recovery strategy between the LCC-HVDCs and the dynamic adaptive limiting strategy of VSC-HVDC. The strategy can reduce the reactive power peak value during the process of fault recovery and improve the ability of LCC-HVDC to resist continuous commutation failure by controlling the recovery sequence of each LCC and staggering the time of the reactive power peak value. By adopting the control strategy of dynamic power limiting regulation, the ability of fast reactive power regulation of VSC-HVDC can be fully utilized, the impact of reactive power during the fault recovery process on the receiving-end AC system can be reduced, and the system stability can be adequately improved.

It is worth noting that the proposed coordinated strategy relies on communication between the LCC-HVDC and VSC-HVDC controllers to transmit reactive power information. In practical applications, communication delays may exist. Excessive delays could desynchronize the VSC’s reactive support from the LCC’s instantaneous demand, potentially diminishing the effectiveness of peak shaving and recovery acceleration. Future work will investigate the robustness of the strategy to such delays and explore compensation methods or alternative local measurement-based coordination schemes to mitigate this dependency.