Moisture Condition Assessment of Oil–Paper Insulation Based on Frequency-Domain Dielectric Spectroscopy and Relaxation Time Distribution

Abstract

The Debye model and its modified forms are widely applied to interpret relaxation polarization processes in dielectric media. However, these models generally require prior assumptions regarding the number of polarization branches, which makes it difficult to construct an equivalent circuit model that accurately reflects the real relaxation characteristics. In this work, frequency-domain dielectric spectra of oil–paper insulation samples with different moisture contents were measured and analyzed. A distributed Debye model considering the probabilistic distribution of relaxation branches was established, and the corresponding relaxation time distribution was obtained using discretization and regularization techniques. Based on this, an accurate moisture condition assessment method for oil–paper-insulated bushings is proposed. The results indicate that, with increasing moisture content, both the real and imaginary parts of the complex capacitance increase significantly in the low-frequency region, while remaining nearly constant at high frequencies. Meanwhile, the peak of the imaginary part shifts toward higher frequencies. By applying the proposed discretization and regularization method to the measured dielectric spectra, the relaxation time distribution function can be accurately derived. As the moisture content increases, the relaxation time constant corresponding to the third relaxation peak gradually decreases. The constructed assessment model exhibits high accuracy, with a maximum error below 2.66%.

1. Introduction

Oil–paper insulation materials are widely used in high-voltage electrical equipment such as transformers, switchgear, and bushings. Prolonged exposure to strong electric fields and complex environmental conditions gradually degrades the dielectric properties of oil–paper insulation, reducing equipment reliability and operational stability. Therefore, condition monitoring of oil–paper insulation is essential to ensure the safe and stable operation of power systems [1,2]. Conventional diagnostic techniques—including partial discharge detection, infrared thermography, and oil sample analysis—can provide preliminary condition assessments of oil–paper-insulated equipment [3]. However, these techniques depend heavily on long-term monitoring and environmental variations, making rapid on-site diagnosis difficult. Consequently, developing diagnostic methods capable of real-time reflection of dielectric performance variations in oil–paper insulation systems has become a key research focus [4,5].

Time–frequency dielectric response analysis has recently emerged as a promising approach for evaluating insulation defects [6,7]. Among these, frequency-domain spectroscopy (FDS) effectively characterizes insulation performance by measuring dielectric spectra over a wide frequency range. Compared with conventional techniques, FDS can capture the polarization behavior of materials, thereby revealing internal defects and degradation levels [8]. Numerous studies have demonstrated that FDS enables accurate assessment of insulation conditions in oil–paper systems [9,10]. In spectral analysis, Morsalin and Phung [11] characterized insulation conditions by extracting the dielectric loss factor (tan δ) from FDS data. However, subsequent studies reported that FDS measurements often include significant conductivity components, which obscure pure polarization information. To mitigate this issue, researchers have proposed the dielectric modulus method, which analyzes the reciprocal of complex permittivity to minimize conductivity interference [12,13]. Although this approach improves the separation between polarization and conductivity effects, it cannot completely eliminate conductivity influence. Recently, the extended logarithmic-derivative spectroscopy (LDS) method was introduced to achieve full extraction of polarization information without conductivity interference [14,15].

Beyond spectral analysis, modeling studies of relaxation polarization mechanisms have received extensive attention. The Debye model, proposed in the 1930s, describes relaxation polarization in homogeneous dielectrics. Daning Zhang et al. [16] obtained extended Debye parameters from transformer tests and used MATLAB 2024a simulations to analyze the influence of paperboard insulation parameters on FDS curves. Mingze Zhang et al. [17] conducted FDS tests on oil–paper samples with varying aging and moisture levels under different voltages, revealing nonlinear variations in FDS curves and constructing a model for periodic ion motion losses. Lin Du et al. [18] investigated the influence of temperature and moisture content on extended Debye parameters, extracting characteristic quantities to assess moisture conditions. The results showed exponential and linear relationships between these parameters and moisture content. However, researchers later found that the extended Debye model poorly fits experimental results, leading to the development of improved variants such as the Cole–Cole, Davidson–Cole, and Havriliak–Negami (H–N) models. These models introduce correction parameters to enhance fitting accuracy. Nevertheless, most FDS-based studies still rely on the Debye family of models, which share a fundamental limitation: they are a priori assumption models requiring a predefined number of relaxation processes in the dielectric. This simplification assumes only a finite set of polarization mechanisms, whereas real dielectric systems exhibit multiple overlapping relaxation processes with a continuous distribution of relaxation times. As a result, previously proposed moisture-assessment methods often yield inconsistent evaluation results.

To address these limitations, the distribution of relaxation time (DRT) approach has been introduced to decompose microscopic dielectric relaxation processes with different time constants in the time domain, thereby identifying additional relaxation mechanisms. Ronglun Zhang et al. [19] derived DRT curves for oil–paper insulation samples with varying aging degrees using polarization–depolarization current data and developed an aging assessment model based on the most probable relaxation time constant. However, few studies have applied DRT to investigate moisture conditions in oil–paper insulation.

To fill this research gap, this paper proposes an analytical framework combining frequency-domain dielectric spectroscopy (FDS) and distribution of relaxation time (DRT) analysis to investigate polarization characteristics under varying moisture conditions. Characteristic parameters are extracted from DRT curves, and quantitative relationships between moisture content and these parameters are established using polynomial fitting. The resulting assessment model is experimentally validated. From a physical perspective, the proposed method overcomes the low accuracy caused by the fixed-branch assumption in traditional extended Debye models. The relaxation time distribution function exhibits clear physical significance and a strong correlation between dielectric parameters and insulation condition. Hence, this approach enables accurate moisture assessment of oil–paper insulation bushings and offers new insights for reliability evaluation of power equipment.

2. Sample Preparation and FDS Testing Analysis

2.1. Preparation of Samples with Different Moisture Contents

Cable paper used for winding high-voltage capacitor cores typically has a thickness of 0.08–0.15 mm. In this study, circular insulating paperboard samples with a thickness of 0.15 mm and a diameter of 80 mm were selected to prepare and analyze specimens with different defect conditions. Transformer oil No. 25 (naphthenic mineral insulating oil) was used.

Initially, both the insulating paperboard and transformer oil were vacuum-dried at 90 °C for 72 h in a vacuum oven, yielding dry insulating paperboard (moisture content < 0.5%) and insulating oil (moisture content < 20 × 10⁻⁶). The paperboard was then vacuum-impregnated with the dried insulating oil for 48 h. For oil–paper-insulated transformers, the typical oil-to-paper mass ratio ranges from 1:6 to 1:10. However, the main insulation in oil–paper capacitor bushings contains minimal oil. To simulate the actual bushing structure, an oil-to-paper mass ratio of 1:15 was adopted, resulting in dry oil–paper insulation samples.

The moisture-conditioning process is illustrated in Figure 1. The dried insulating paperboard was placed on an electronic balance and exposed to ambient air for natural moisture absorption. Based on the balance readings, changes in moisture content were roughly estimated. When the mass approached the target value, samples were taken and measured using a moisture analyzer (balance range 1–60 g, precision 0.001 g; analyzer accuracy 0.01%). The measured value was recorded as the paperboard’s moisture content. Immediately afterward, the paperboard was immersed in the dried insulating oil and sealed at room temperature for 48 h to achieve complete impregnation.

Figure 1. Moisture sample preparation flowchart.

By controlling the natural moisture absorption time, oil–paper insulation samples with moisture contents of 0.96%, 1.98%, 2.84%, 3.51%, and 4.06% were prepared. The overall preparation process and final samples are shown in Figure 1 and Figure 2, respectively.

Figure 2. Moisture oil–paper samples.

2.2. FDS Testing Principles and Measurements

The dielectric polarization process can be examined by measuring the amplitude and phase of the current under sinusoidal excitation. For a single frequency, the current–voltage relationship can be expressed as follows:

$$\begin{array}{ll}I(\omega )& =j\omega C_0\left\{{\epsilon }_{\infty }+{\chi }^{\prime }(\omega )-j\left[{\displaystyle \frac{{\sigma }_0}{{\epsilon }_0\omega }}+{\chi }^{″}(\omega )\right]\right\}U(\omega )\\ & =j\omega C_0\epsilon (\omega )U(\omega )\\ & =j\omega \left\{C^{\prime }(\omega )-j{C}^{″}(\omega )\right\}U(\omega )=j\omega C(\omega )U(\omega )\end{array}$$

(1)

where C(ω) is the complex capacitance of the dielectric, U(ω) is the driving voltage applied across the dielectric, ε∞ is the optical permittivity, ε₀ is the vacuum permittivity, σ₀ is the dielectric conductivity, χ′(ω) and χ″(ω) are the real and imaginary parts of the complex polarizability, and C₀ is the geometric capacitance determined by the specimen dimensions.

If C₀ is known, the complex permittivity can be derived from the phase and amplitude of the response current. The frequency-domain dielectric loss factor is defined as follows:

$$tan \delta ={\displaystyle \frac{{\epsilon }^{″}(\omega )}{{\epsilon }^{\prime }(\omega )}}={\displaystyle \frac{\frac{{\sigma }_0}{{\epsilon }_0\omega }+{\chi }^{″}(\omega )}{{\epsilon }_{\infty }+{\chi }^{\prime }(\omega )}}$$

(2)

where ε′(ω) and ε″(ω) denote the real and imaginary parts of the complex permittivity, respectively. The real component describes the dielectric’s ability to store bound charges, while the imaginary component reflects dielectric loss. Both capacitance C and loss factor tan δ are frequency-dependent and influenced by aging, temperature, and moisture content. Therefore, analyzing the variation of ε or C with frequency provides richer diagnostic information than power-frequency dielectric loss, enabling a more comprehensive evaluation of insulation condition.

FDS measurements were conducted on the five groups of oil–paper samples with different moisture contents using a broadband, temperature-controlled dielectric impedance spectrometer capable of covering a frequency range from 3 μ Hz to 20 M Hz. To optimize measurement efficiency, the experimental frequency range was set to 0.01 Hz–10 M Hz. All tests were performed at room temperature with an applied voltage of 1 V. Copper electrodes with a diameter of 30 mm were used as measurement electrodes for the paper specimens. To ensure reliability, the FDS measurement for each moisture level was repeated three times. The complex capacitance spectra showed excellent repeatability, with a coefficient of variation of less than 3% across the measured frequency range, confirming the stability of the measurement system and the prepared samples.

2.3. Influence of Sample Moisture Content on FDS Curve Characteristics

The FDS characteristic curves of oil–paper insulation samples with different moisture contents are shown in Figure 3. Figure 3a presents the real component (C′) of the complex capacitance as a function of frequency. For all samples, C′ decreases with increasing frequency, with the most pronounced differences observed in the low-frequency region. As the moisture content increases, C′ values at low frequencies rise significantly, indicating that moisture enhances the polarization capability of the oil–paper system. This effect is most evident at low frequencies, where interfacial polarization dominates. At higher moisture levels, water molecules form hydrogen bonds with cellulose chains and increase the free-ion concentration, promoting charge accumulation at interfaces and thus intensifying interfacial polarization, which elevates low-frequency C′ values. As frequency increases, polarization mechanisms gradually shift from interfacial to dipolar polarization. The polarization response can no longer follow rapid field variations, causing the C′ curves for samples with different moisture contents to converge in the high-frequency range [20,21]. Figure 3b illustrates the imaginary component (C″) of the complex capacitance. With increasing moisture content, the peak positions of C″ shift toward higher frequencies, and the low-frequency values increase notably. This behavior indicates that moisture has a strong influence on dielectric loss. In the low-frequency region, moisture promotes ionic conduction and interfacial polarization, leading to higher C″ values. In the low-frequency region (<10 Hz), the imaginary capacitance (C″) generally increases with moisture content. However, the sample with the highest moisture content (4.06%) exhibits a slightly lower C″ value than the 3.51% sample at the very lowest frequencies, which may be attributed to the saturation of interfacial polarization or competing ion migration effects at extremely high moisture levels. The overall trend of increasing dielectric loss with moisture content remains clear. As the moisture content rises, polarization effects become more pronounced, further enhancing dielectric loss. The interaction between water molecules and cellulose facilitates ion migration and interfacial charge accumulation, resulting in greater dielectric losses at low frequencies. At higher frequencies, the polarization response cannot keep pace with the applied field, and the imaginary component tends to stabilize.

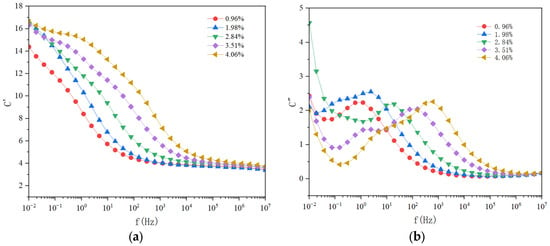
Figure 3. (a) Real component curves and (b) Imaginary component curves of complex capacitance for oil–paper samples with different moisture contents.

In summary, moisture content exerts a significant influence on the dielectric characteristics of oil–paper insulation, particularly in the low-frequency range, where the effects of moisture are most dominant.

3. Principles of DRT

3.1. Mathematical Fundamentals of DRT

The distribution of relaxation times (DRT) method was originally developed in the field of electrochemistry and, in the early 21st century, was introduced into solid oxide fuel cell (SOFC) research to distinguish between different electrochemical processes within the cell. In this study, the DRT method is applied to insulating materials to separate and characterize multiple polarization processes. Owing to its superior modeling capability, DRT enables comprehensive extraction of polarization characteristics, thereby facilitating accurate assessment of moisture conditions in oil–paper insulation systems [22].

Previous studies have shown that dielectric relaxation in complex dielectric systems involves multiple polarization types. The DRT method is particularly powerful in separating such overlapping processes. To capture these phenomena more accurately, this study assumes that the relaxation time constant τ_i takes continuous values over the range (0, ∞). Accordingly, the real and imaginary components of the complex permittivity can be expressed as follows:

$${\epsilon }_{DRT}^{\prime }(\omega )={\epsilon }_{\infty }+({\epsilon }_s-{\epsilon }_{\infty }){\int }_0^{\infty } {\displaystyle \frac{f(\tau )}{1+{\omega }^2{\tau }^2}}d\tau$$

(3)

$${\epsilon }_{DRT}^{″}(\omega )=i({\epsilon }_s-{\epsilon }_{\infty }){\int }_0^{\infty } {\displaystyle \frac{\omega \tau f(\tau )}{1+{\omega }^2{\tau }^2}}d\tau$$

(4)

where i is the imaginary unit, and f(τ) is the relaxation time distribution function satisfying the normalization condition:

$${\int }_0^{\infty } f(\tau )d\tau =1$$

(5)

The equivalent circuit of oil–paper insulation, shown schematically in Figure 4, can be represented by a large number of parallel RC branches, each corresponding to a distinct polarization process of unknown quantity and intensity. This configuration provides a realistic approximation of the actual polarization behavior in oil–paper insulation systems and effectively avoids the a priori assumption limitation of the Debye model.

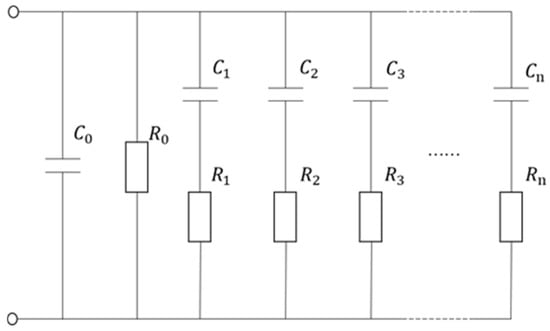
Figure 4. Equivalent circuit diagram.

Since FDS test frequencies are typically sampled at equal intervals in the logarithmic domain, Equations (3) and (4) can be rewritten in logarithmic domain form for subsequent calculations. By setting x = ln τ, then dx = d(ln τ) = dτ/τ, and τ = e^x. Accordingly,

$${\epsilon }_{DRT}^{\prime }(\omega )={\epsilon }_{\infty }+({\epsilon }_s-{\epsilon }_{\infty }){\int }_{-\infty }^{\infty } {\displaystyle \frac{{\gamma }^{\prime }(x)}{1+{\omega }^2{e}^{2x}}}dx$$

(6)

$${\epsilon }_{DRT}^{″}(\omega )=i({\epsilon }_s-{\epsilon }_{\infty }){\int }_{-\infty }^{\infty } {\displaystyle \frac{\omega e^x{\gamma }^{\prime }(x)}{1+{\omega }^2{e}^{2x}}}dx$$

(7)

where γ′(x) is the relaxation time distribution function in the logarithmic domain, with γ′(x) = γ(e^x) = γ(τ) = τ$f(\tau )$.

3.2. Solution Method for Relaxation Time Distribution Function

Since the number of data points in FDS is typically limited while γ′(x) is continuous, solving for γ′(x) becomes challenging. Solving for large numbers of unknowns with limited available information is an ill-posed problem in mathematics that cannot be solved through conventional mathematical methods. Various methods have been proposed to accurately obtain γ′(x), including the Fourier transform [23], maximum entropy [24], Monte Carlo sampling, genetic programming, operational calculus, and regularization methods [25]. In this study, the regularization method is adopted, consisting of two main steps: (1) discretization of γ′(x) and (2) solving the discrete system via regularization.

First, γ′(x) must be discretized. The selection of discretization basis functions is crucial and can effectively reduce approximation errors. Considering curve smoothness, this paper adopts Gaussian basis functions as the discrete basis for γ′(x):

$${\gamma }^{\prime }\left(x\right)=\sum _{m=1}^M a_m\phi \left(x\right) , \phi (x)=exp\left[-{\left(\mu (x-x_m)\right)}^2\right]$$

(8)

where μ is the shape factor (μ = 0.5 in this paper), a_m is the weight coefficient, and x_m is the center of the m-th basis function. The shape factor μ controls the width of the Gaussian basis functions. A value of μ = 0.5 was selected after preliminary trials, as it provided an optimal balance between resolution (the ability to distinguish close relaxation peaks) and smoothness of the resulting DRT curve. A smaller μ value would lead to broader basis functions, smearing out fine details, while a larger μ value would make the basis functions too narrow, potentially introducing spurious oscillations and increasing sensitivity to noise.

Substituting Equation (8) into Equations (6) and (7) yields the following:

$${\epsilon }_{DRT}^{\prime }(\omega )={\epsilon }_{\infty }+({\epsilon }_s-{\epsilon }_{\infty })\sum _{m=1}^M a_m{\int }_{-\infty }^{\infty } {\displaystyle \frac{\mathit{exp}\left[-(x-x_m{)}^2\right]}{1+{\omega }^2{e}^{2x}}}dx$$

(9)

$${\epsilon }_{DRT}^{″}(\omega )=i({\epsilon }_s-{\epsilon }_{\infty })\sum _{m=1}^M a_m{\int }_{-\infty }^{\infty } {\displaystyle \frac{\omega e^x\mathit{exp}\left[-(x-x_m{)}^2\right]}{1+{\omega }^2{e}^{2x}}}dx$$

(10)

By letting y = x − x_m, then x = y + x_m, dx = dy. The above relationships can be written in a matrix form:

$${\epsilon }_{DRT}^{\prime }(f_n)={\epsilon }_{\infty }+({\epsilon }_s-{\epsilon }_{\infty })\sum _{m=1}^M A_{nm}^{\prime }{a}_m$$

(11)

$${\epsilon }_{DRT}^{″}(f_n)=i({\epsilon }_s-{\epsilon }_{\infty })\sum _{m=1}^M A_{nm}^{″}{a}_m$$

(12)

where A′_nm and A″_nm are integral matrices as follows, with x_m = ln τ_m = −lnf_m and ω_n = 2πf_n:

$$A_{nm}^{\prime }={\int }_{-\infty }^{\infty } {\displaystyle \frac{e^{-y^2}}{1+4{\pi }^2{e}^{2\left(y+ln{f}_n-ln{f}_m\right)}}}dy$$

(13)

$$A_{nm}^{″}={\int }_{-\infty }^{\infty } {\displaystyle \frac{2\pi e^{y+ln{f}_n-ln{f}_m-y^2}}{1+4{\pi }^2{e}^{2\left(y+ln{f}_n-ln{f}_m\right)}}}dy$$

(14)

Equations (11) and (12) establish the mathematical correspondence between FDS data and DRT representation.

After completing the discretization of γ′(x), DRT is solved by fitting the calculated ${\epsilon }_{DRT}(f_n)$ to the experimentally measured ${\epsilon }_{EXP}(f_n)$, minimizing the following error function:

$$S(x)=\sum _{n=1}^N \left[{\left({\epsilon }_{EXP}^{\prime }\left(f_n\right)-{\epsilon }_{DRT}^{\prime }\left(f_n\right)\right)}^2+{\left({\epsilon }_{EXP}^{″}\left(f_n\right)-{\epsilon }_{DRT}^{″}\left(f_n\right)\right)}^2\right]$$

(15)

To prevent overfitting and enhance the model’s robustness against noise, a regularization term is incorporated:

$$S(x)=\sum _{n=1}^N \left[{\left({\epsilon }_{EXP}^{\prime }\left(f_n\right)-{\epsilon }_{DRT}^{\prime }\left(f_n\right)\right)}^2+{\left({\epsilon }_{EXP}^{″}\left(f_n\right)-{\epsilon }_{DRT}^{″}\left(f_n\right)\right)}^2\right]+\lambda P(x),\lambda \ge 0$$

(16)

where λ is the regularization parameter and P(x) is the penalty function. To achieve smoother constructed function curves and enhance model noise resistance, this paper takes P(x) = ${‖Lx‖}_2^2$, where L is the first-order derivative differential matrix of γ′(x).

The inversion of the DRT from FDS data is an ill-posed problem, sensitive to noise in the experimental data. The discretization using Gaussian basis functions and the introduction of Tikhonov regularization (Equation (16)) are essential for stabilizing the solution and ensuring computational stability. The sensitivity of the solution to the key parameter (the regularization parameter λ) is systematically analyzed in Section 4.1. The choice of the shape factor μ for the basis functions also influences the result, and its selection is based on a balance between resolution and smoothness.

4. Moisture Condition Assessment Model

4.1. Influence of Regularization Parameter λ on DRT

Prior to solving and analyzing the DRT, the regularization parameter λ must be properly selected, as it directly influences the quality of the DRT results. An excessively large λ value leads to over-smoothing, which may filter out critical information; conversely, an excessively small λ value results in overfitting and oscillatory behavior of the reconstructed function.

To investigate the influence of λ, the real part of the complex capacitance data for an oil–paper sample with a 0.96% moisture content was used. Regularization parameters of λ = 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², and 10⁻¹ were tested. The corresponding DRT results are shown in Figure 5.

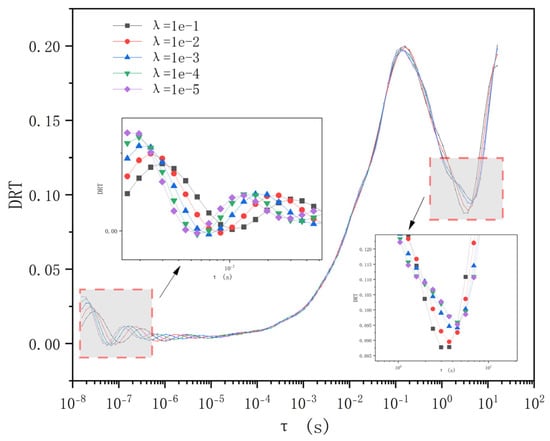
Figure 5. DRT of the 0.96% moisture sample under different λ values derived from the experimental spectra.

Figure 5 illustrates the DRT curves obtained from the same experimental data (C′ of the 0.96% sample) under different regularization parameters λ. The goal is to select a λ that produces a physically plausible, smooth DRT without overfitting the experimental noise. At very small λ (e.g., 10⁻⁵), the solution is under-smoothed, resulting in sharp, likely artifactual peaks at short relaxation times. At very large λ (e.g., 10⁻²), the solution is over-smoothed, erasing meaningful structural details. A value of λ = 10⁻³ was selected as it yields a smooth curve while retaining the distinct relaxation peaks, representing the best trade-off between fidelity to the data and suppression of noise [22].

4.2. Influence of Moisture Content on DRT

Following the procedure outlined in Section 3, the relaxation time distribution functions for oil–paper samples with different moisture contents were derived from the real and imaginary parts of the complex capacitance, as illustrated in Figure 6. As the moisture content increases from 0.96% to 4.06%, the peak of the relaxation time distribution clearly shifts toward shorter relaxation times (i.e., smaller τ values). This indicates that moisture accelerates both polarization and depolarization processes in oil–paper insulation, resulting in reduced relaxation times. Physically, this behavior arises because water molecules enhance ionic mobility within the cellulose–oil matrix, promoting faster polarization formation and dissipation. The variation in DRT curves is particularly evident in the short-relaxation time region, where moisture has the strongest influence on polarization kinetics. At higher moisture levels, hydrogen bonding between water molecules and cellulose chains forms structures that are more easily polarized, thereby facilitating charge accumulation and release over shorter timescales. Consequently, the dielectric relaxation becomes faster as the moisture content increases.

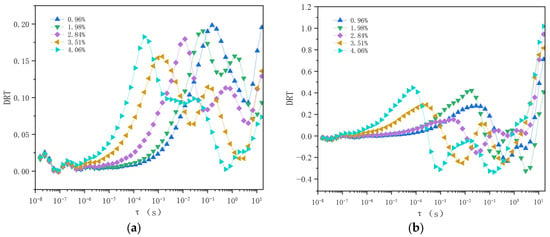
Figure 6. DRT of oil–paper insulation samples with different moisture contents derived from (a) C′ and (b) C″ components (calculated from the measured FDS data).

Comparing Figure 6a,b, it can be observed that when the imaginary part of permittivity (C″) is used in the analysis, the DRT results exhibit poorer regularity. This deviation is primarily caused by the conductivity component present in the imaginary capacitance, which introduces bias into the inversion process. Therefore, in this study, the real part of complex capacitance (C′) was employed as the basis for DRT analysis and subsequent model development.

4.3. Moisture Condition Assessment Model Based on DRT

As shown in Figure 6, multiple dielectric relaxation processes can be observed in the DRT curves of oil–paper insulation. These are manifested as three distinct relaxation peaks, corresponding to three primary polarization mechanisms. Conventional multi-branch extended Debye models fail to accurately capture such complex relaxation behavior. Among these peaks, the third relaxation peak exhibits a strong and consistent correlation with the sample moisture content. Specifically, as the moisture content increases, the relaxation time corresponding to the third peak decreases monotonically.

Based on this observation, the relationship between the third peak relaxation time (τ) and moisture content (H) was extracted, as illustrated in Figure 7.

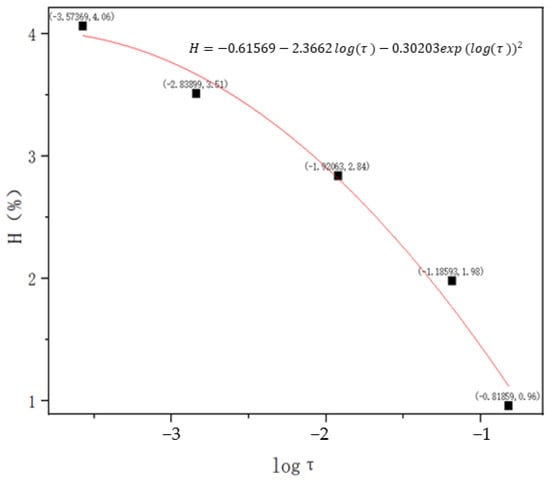
Figure 7. Relationship curve between the third peak relaxation time and the moisture content.

Using the least squares fitting method, a polynomial model was established, yielding an empirical expression with a coefficient of determination (R²) = 0.983, as given in Equation (17):

$$H=-0.61569-2.3662\mathit{log}\left(\tau \right)-0.30203exp(\mathit{log}\left(\tau \right){)}^2$$

(17)

To verify the predictive accuracy and generalization capability of the proposed model, two additional oil–paper samples with moisture contents of 1.09% and 2.78% were prepared independently, following the same procedures described in Section 2.1. These samples were not used in the model development presented in Figure 6. Their relaxation time distribution functions were obtained through FDS testing and DRT calculation, as shown in Figure 8. The third peak relaxation times were determined to be 0.01518 s and 0.012 s, respectively. Substituting these values into Equation (17) produced estimated moisture contents of 1.119% and 2.814%, corresponding to relative errors below 2.66%. The relative error was calculated along the Y-axis (moisture content) with reference to the following formula:

$$\mathit{Relative} \mathit{Error}(\%)={\displaystyle \frac{|H_{actual}-H_{predicted}|}{H_{actual}}}\times 100\%$$

(18)

where $H_{actual}$ is the measured moisture content, and $H_{predicted}$ is the value estimated by the model (Equation (17)). These results demonstrate that the proposed DRT-based moisture assessment model provides high-precision evaluation of the moisture condition in oil–paper insulation systems. The maximum relative error for the independent validation samples was below 2.66%, demonstrating the high consistency and accuracy of the proposed assessment model. It is noted that the validation samples exhibit minor structural differences in the DRT at longer relaxation times compared to the calibration samples in Figure 6a. Model validation results using independent samples in Table 1. These variations are likely attributable to inherent microstructural differences in the cellulose paper or subtle variations in the impregnation process, which predominantly affect slower polarization processes. Crucially, the position of the third relaxation peak, which is the key feature for moisture assessment, remains consistent and follows the established trend.

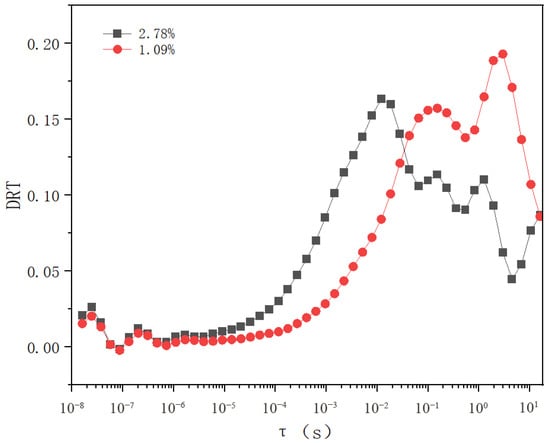
Figure 8. DRT (derived from C′) of the independent validation samples with moisture contents of 1.09% and 2.78%, which were not used for model calibration.

Table 1. Model validation results using independent samples.

Sample	τ (s)	Hactual (%)	Hpredicted (%)	Relative Error (%)
1	0.01518	1.09	1.119	2.66%
2	0.01200	2.78	2.814	1.22%

To further validate the superiority of the proposed DRT-based method, its performance was compared with a conventional approach that uses the magnitude of the complex capacitance at 0.01 Hz as the moisture indicator [8]. For the validation samples, the conventional method yielded estimation errors of 8.5% and 12.5%, respectively, which are significantly higher than the errors below 2.66% achieved by the proposed DRT method. This demonstrates the enhanced accuracy of utilizing the relaxation time distribution feature over a single frequency-point parameter.

In summary, the relaxation time distribution function quantitatively reflects the contribution of different polarization processes in dielectric relaxation based on probability density. Compared with the traditional extended Debye model, the DRT approach offers superior analytical accuracy, allowing for finer separation of microscopic relaxation mechanisms with distinct time constants in the time domain.

5. Conclusions

This study investigated a quantitative moisture assessment approach for oil–paper insulation used in transformer bushings, based on the distribution of relaxation time (DRT) derived from frequency-domain dielectric spectroscopy (FDS) measurements and distributed Debye model parameters.

By applying discretization and regularization techniques, the DRT function was accurately reconstructed, enabling detailed characterization of polarization processes within the insulation system. A moisture condition assessment model was subsequently established using the relaxation time corresponding to the third DRT peak as the key characteristic parameter. Experimental analysis revealed that as the moisture content increased, the third relaxation peak shifted toward shorter relaxation times, while its amplitude remained nearly constant. The developed model demonstrated high predictive accuracy, with an average estimation error of less than 2.66%, confirming its reliability and effectiveness for evaluating the moisture condition of oil–paper insulation in transformer bushings. Overall, the proposed DRT-based diagnostic approach offers a physically meaningful and analytically precise method for assessing insulation health, providing valuable guidance for the monitoring, maintenance, and lifespan evaluation of high-voltage power equipment.

While accurate under laboratory conditions, this method has limitations: temperature effects, aging byproducts, and multi-stress aging were not considered. Future work requires temperature compensation, robustness evaluation against interference, and validation with field equipment for practical application.