Thermodynamic Cycle Model for Ammonia–Ionic Liquid in High Temperature Absorption Heat Pumps—Ionic Liquids Parameters

Abstract

This article evaluates and develops a thermodynamic steady-state model, analyzing the thermodynamic properties of ammonia–ionic liquid (NH₃–IL) working pairs for use in high-temperature (>100 °C) absorption heat pumps. Given the increasing need for energy savings and reductions in greenhouse gas emissions, this is becoming an important consideration in the context of industrial facilities. Prior work on ammonia–ionic liquid (IL) pairs has largely focused on lower supply temperatures and offers no quantitative criteria connecting IL properties to high-temperature (>100 °C) cycle design. This article presents calculations based on correlations in the literature to determine the vapor pressures of pure ionic liquids using a modified Redlich–Kwong equation of state; the vapor–liquid equilibrium (VLE) of NH₃/[emim][SCN] and NH₃/H₂O mixtures in the NRTL model; the specific heats of pure ionic liquids (ILs); the specific heat capacities of NH₃–IL and NH₃–H₂O mixtures; and the excess enthalpy (HE) for NH₃/[emim][SCN] and NH₃/[emim][EtSO₄] as a function of temperature and composition, using a combination of NRTL + Gibbs–Helmholtz and Redlich–Kister polynomials. The calculations confirm the practically zero volatility of ionic liquids in the generator. This preserves the high purity of the ammonia vapor above the NH₃/[emim][SCN] solution (y₁ ≥ 0.997 over a wide range of temperatures and concentrations) and enables the rectification process in the generator to be omitted. The specific heat capacity of pure ionic liquids (ILs) has been shown to be 52–63% lower than that of water. Mixtures of ammonia (NH₃) and ILs with a mass fraction of 0.5/0.5 have a specific heat at 120 °C that is 34–37.5% lower than that of the ammonia–water (NH₃–H₂O) solution. This directly translates into a reduction in the power required in the generator. Excess enthalpy results show moderate or strongly negative values within the useful temperature and concentration range, indicating the exothermic nature of the mixture. At the same time, the NH₃/[emim][EtSO₄] mixture is characterized by a decrease in enthalpy with increasing temperature, suggesting that benefits for the COP of the system can be obtained. Based on these calculations, criteria for selecting ionic liquids for use in high-temperature absorption pumps were formulated: negligible volatility, a low specific heat capacity for the mixture, and a strongly negative excess enthalpy, which decreases with temperature, at the operating temperatures of the absorber and generator.

1. Introduction

The introduction of various European Union regulations aimed at lowering carbon dioxide emissions has had a significant impact on the energy and heat-generation industries serving residential, domestic, and industrial applications across the European Union [1]. Based on the European Green Deal and sustainability directives, enterprises must not only limit greenhouse gas emissions but also gradually phase out fossil fuels [2]. This creates a growing need to introduce energy-efficient and environmentally friendly solutions. One promising area is the use of ionic liquids in the field of high-temperature absorption heat pumps (AHPs).

To this date, an expanding body of literature addresses the use of ionic liquids as alternatives to conventional working fluids in absorption heat pumps [3,4,5]. Thus far, investigations have focused mainly on low-capacity devices delivering supply temperatures in the 45–65 °C range [4,5]. Kühn et al. [3] conducted a review of ionic liquids as novel absorbents for thermally driven chillers and heat pumps. The review emphasized the negligible vapor pressure and tunability of solvent–solute interactions. Wang and Infante Ferreira conducted an analysis of NH₃–IL absorption cycles, emphasizing that the majority of prior implementations target ≤ 65 °C delivery and offering guidance on IL selection at the cycle level. Wang’s monograph serves to further consolidate the fundamentals and applications [4,5]. The experimental and correlative foundations for NH₃ + IL mixtures were established by Yokozeki and Shiflett. VLE measurements were provided, and Redlich–Kwong/EOS treatments were modified, enabling cycle modeling at elevated temperatures [6,7,8]. Concurrently, Ren et al. reported vapor pressures, excess enthalpies, and heat capacities for IL-containing binaries [9]. It is evident that researchers have not considered the impact of increasing the temperature of hot water. Additionally, previous work on AHP with ammonia–ionic liquids does not provide quantitative, verifiable criteria for selecting ionic liquids for use at high temperatures (>100 °C). In particular, there is a lack of correlation between the properties of ionic liquids and the three key design requirements of eliminating rectification, reducing generator power due to the low specific heat capacity of the mixture, and maintaining exothermicity in the absorption process within a useful concentration and temperature range. Analyzing fast-growing energy demands, particularly in the industrial sector, it is necessary to extend these studies to higher-capacity devices capable of delivering supply temperatures above 100 °C. This kind of solution can be pivotal in the industry, where heat demand is high and there is simultaneous pressure to reduce emissions and limit fossil-fuel consumption. In this context, the present study establishes a steady-state thermodynamic model of the NH₃–IL cycle for a heating system operating at temperatures above 100 °C. This is achieved by using well-established property frameworks from the literature to quantitatively define IL selection criteria, such as negligible volatility, low solution Cp, and a strongly negative excess enthalpy at absorber temperatures. The study also benchmarks literature-reported ILs against the NH₃–H₂O pair, providing practical guidance on selecting an absorbent for industrial applications.

The deployment of absorption heat pumps in industrial facilities and factories is particularly important due to the increasingly constrained availability of electricity. With global electricity demand rising, the industry faces difficulties in securing additional electricity supply. Moreover, many plants experience grid congestion, which limits the addition of electrically driven systems. Consequently, absorption heat pumps in which the mechanical compressor is replaced with a thermally driven sorption compressor are an attractive alternative. They can be driven by an existing heat source, such as a steam boiler, which is advantageous from a capital expenditure perspective. This solution, combined with an absorption heat pump, does not significantly burden the power grid, which is an essential consideration for sustainable development.

Traditionally, the absorption heat pumps considered in this paper have ammonia–water and lithium bromide–water as the working pairs. The NH₃–H₂O system, which is commonly used and is considered as a base for this paper, has several limitations that are particularly significant at high-temperature heating systems. The volatility of water means that vapors leaving the generator must be purified, generating internal heat/cooling cycles, exergy losses, and a practical limit on the purity of the medium. This narrows the possible temperature difference and the achievable temperature in the absorber/condenser. The thermodynamics of the NH₃–H₂O equilibrium generate high solution circulation ratios: the solubility of NH₃ in water decreases sharply with temperature. Therefore, maintain the required vapor purity, large flows of strong/weak solution must be circulated. This increases the size of the exchangers and pumping costs. The high heat capacity of the water–ammonia solution results in a large proportion of sensible heat in the generator and absorber, thereby increasing the required heat. Consequently, at water-heating temperatures above 100 °C, NH₃–H₂O systems incur significant losses and design limitations, prompting the search for alternative absorbents. Nevertheless, the ionic liquids under discussion in this paper, as outlined in the existing literature, have the potential to offer a number of advantages over conventional solutions based on standard working pairs. A principal property that could be considered an advantage is that they can be engineered to meet specific physicochemical and thermodynamic requirements, thereby affording engineers and scientists greater flexibility in tailoring parameters to the needs of a given process. Moreover, it has been demonstrated that the maintenance of high thermal stability and low vapor pressure of ionic liquids is a possibility, which could in turn allow operation at higher temperatures. These parameters could be of critical importance for industrial processes that necessitate elevated water-supply temperatures for process equipment.

At the same time, further research is needed to optimize or find proper ionic liquids for achieving the highest possible coefficient of performance (COP), especially in high-temperature applications. The potential of ionic liquids in this area is promising; however, satisfactory results have so far only been achieved in systems with relatively low supply temperatures—for domestic usage. This article presents the possibilities, methods, and proposals for employing ionic liquids in high-temperature absorption heat pumps. The optimal physicochemical parameters of these liquids are also considered to ensure their effectiveness in industrial processes while minimizing energy use and CO₂ emissions.

2. Materials and Methods

2.1. General

All quantitative analyses were performed in custom Microsoft Excel workbooks developed by the authors. Input parameters were taken exclusively from papers, standards, and technical documents listed in the References. When multiple sources reported the same quantity, priority was given to primary literature and international/industry standards; secondary sources were used only for cross-checks. When sources provided ranges, the mid-point was used for central estimates. No stochastic or machine-learning methods were used; all results arise from deterministic spreadsheet calculations.

Generative artificial intelligence (GenAI) was used solely to render publication quality figures from the precomputed Excel/CSV table. Figures have been generated by programs written in Python (version 3.14) language. Figure 1 and Figure 2 were drawn by the authors using Autodesk AutoCAD software (version 2025). There are no restrictions on material availability beyond standard licensing of third-party sources cited in the References.

All parameters for ionic liquids were taken from peer-reviewed correlations within their reported T-x validity ranges. The parameters have not been fitted. From a design standpoint, for a high-temperature absorption heat pump, the following requirements have been targeted: absorbents with negligible vapor pressure, low mass-based heat capacity and strongly negative excess enthalpy, and NRTL parameterizations that yield ammonia-strong vapor at generator temperatures. The selected ILs meet these criteria.

2.2. Example Model Validation

2.2.1. VLE

The NRTL-based predictions for VLE were overlaid with experimental VLE from Yokozeki & Shiflett [6]. According to this, Mean Absolute Percentage Error has been calculated to 4.71%, which shows

Table 1. Validation of VLE model (example for NH₃/[emim][SCN]).

Temperature	Pressure by [6]	Molar Fraction of Absorbate	Pressure Calculated in This Study	MAPE
T (K)	P (Mpa)	x1 (%)	P (Mpa)	(%)
283.2	0.214	40	0.191	4.71
	0.244	45.1	0.226
	0.364	65.2	0.367
	0.447	73.1	0.422
	0.502	78.6	0.460
	0.547	81.9	0.482
	0.590	87.6	0.519
298.1	0.256	40	0.280
	0.307	44.4	0.329
	0.536	64.2	0.571
	0.672	72.3	0.675
	0.747	78.1	0.748
	0.815	81.5	0.790
322.6	0.501	40	0.482
	0.535	41.6	0.513
	0.961	61.8	0.985
	1.241	70.4	1.217
	1.420	76.6	1.389
	1.562	80.4	1.493
	1.777	86.9	1.667
348	0.917	40	0.850
	0.840	37.8	0.780
	1.553	58.1	1.564
	2.045	67.3	2.013
	2.419	74.1	2.374
	2.711	78.4	2.609
	3.174	85.8	3.014
372.8	1.519	40	1.420
	1.149	34	1.133
	2.144	54.2	2.253
	2.958	63.3	2.916
	3.576	70.8	3.541
	4.120	75.4	3.955
	5.007	83.9	4.757

.

2.2.2. Specific Heat Capacity

The Group additivity method and Linear T-correlation method predictions for specific heat capacity were overlaid with experimental SHC data from ILThermo [10]. According to this, Mean Absolute Percentage Error has been calculated to 1.06% for Group additivity method as shown in [11] and 0.22% for Linear T-correlation method as shown in [4]. Values which are the base for this calculation are shown in

Table 2. Validation of Specific Heat Capacity Model (example for [bmim][PF6]).

Temperature	Group Additivity Method	Linear T-Correlation Method	Experimental Data	MAPE for Group Additivity Method	MAPE for Linear T-Correlation Method
T (K)	Cp (J kmol−1 K−1)	Cp (J kmol−1 K−1)	Cp (J kmol−1 K−1)	(%)	(%)
300.05	417.693	408.923	409.200	1.06	0.22
330	431.230	428.501	428.300
360.05	444.813	446.269	445.300
390.09	458.391	462.154	462.100
403.13	464.285	468.465	472.000

.

2.3. Limitation of the Present Study

This work presents a steady-state thermodynamic cycle model for a high-temperature ammonia–ionic liquid absorption heat pump, based on property frameworks from the literature (NRTL for vapor–liquid equilibrium (VLE), modified Redlich–Kwong for vapor pressures, and group-contribution heat capacities). The main limitations are as follows:

Data and models: The model parameters (NRTL/EOS/Cp) were obtained from correlations in the literature, with limited validity with respect to temperature and composition. The quantitative model form and parameter uncertainties were not propagated to the cycle metrics.

Scope of fluids: The research covers a set of ILs used as a base for other studies (e.g., [emim][SCN], [emim][EtSO₄], [bmim][PF₆]). Some EOS parameters are incomplete due to lack of information in the literature.

Cycle idealizations: Pressure drops, heat losses, rectifier behavior, and dynamic mass-transfer resistances are assumed as neglected. Boundary conditions are fixed to representative industrial temperatures—parameters are assumed to be constant.

Mixture thermodynamics: Excess enthalpy is computed from simplified correlations; composition-dependent Cp is approximated by mass-weighted averages.

Engineering aspects: No hydraulic design, viscosity impact, material compatibility, IL stability/degradation, environmental, safety, or cost considerations are quantified.

Parameters out of scope: circulation ratio, COP, and flow rates have not been calculated.

2.4. Thermodynamic Model Structure

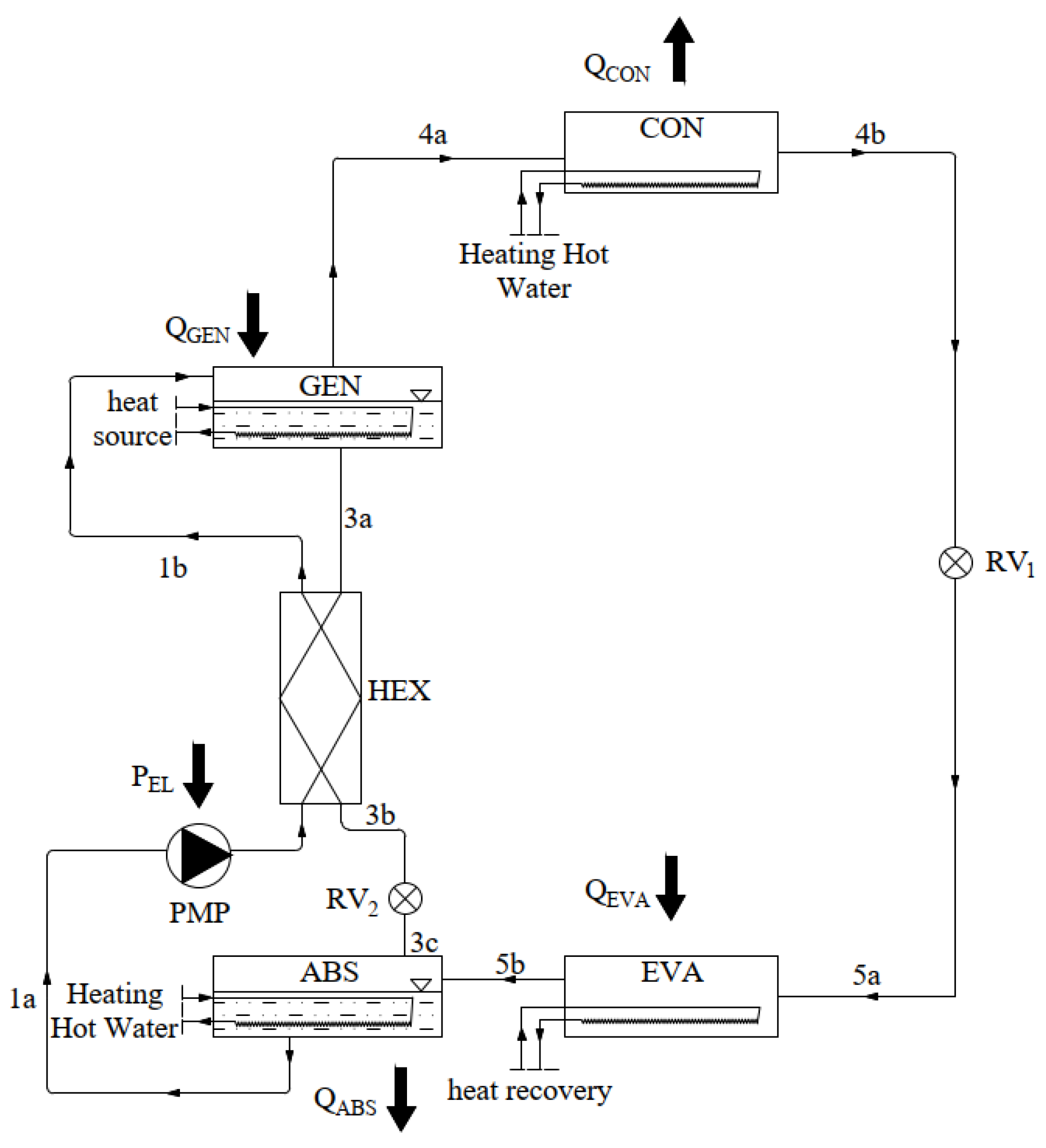
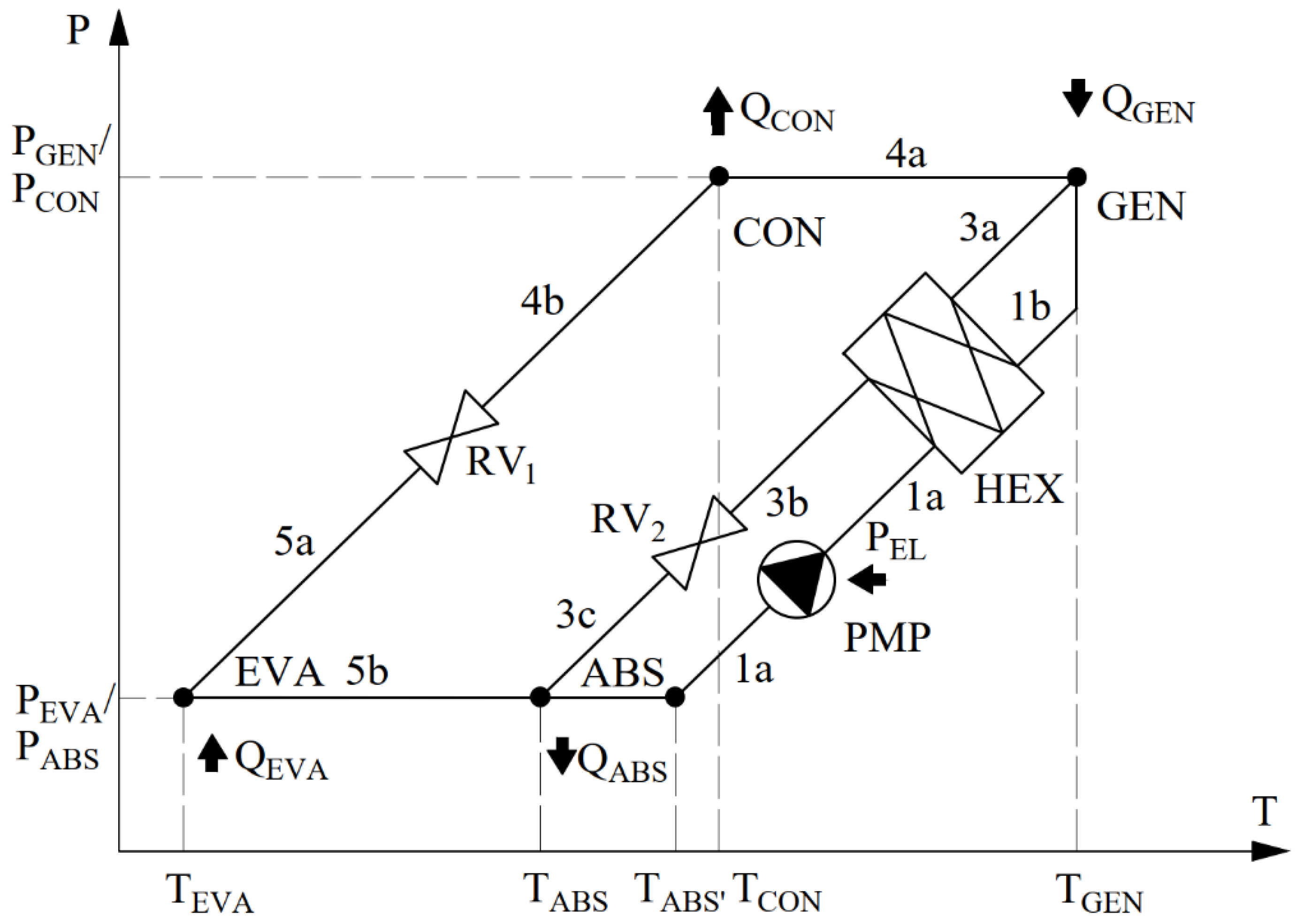
This study analyzes an absorption heat pump system operating in a conventional configuration, comprising an absorber (ABS), a generator (GEN), a condenser (CON), an evaporator (EVA), circulation pumps (PMP), and a heat exchanger (HEX).

The description of the individual components of the absorption heat pump is as follows. In the analysis below, processes occurring in the rectifying section (KOR) are omitted.

Absorber (ABS): In the absorber, refrigerant vapor returning from the evaporator (EVA) is absorbed by the weak solution, forming a strong solution. This solution is then conveyed via line (1a) by the circulation pumps (PMP) to the heat exchanger (HEX) and subsequently to the generator (GEN). Absorption of the refrigerant by the weak solution in the absorber releases heat (QABS—an exothermic process), which is used to heat the heating water via a heat exchanger located within the absorber; this is essential for proper system operation.

Generator (GEN): The strong solution transported from the absorber (1b) is heated in a heat exchanger supplied with energy from an external heat source (QGEN). In practice, steam or hot flue gases from combustion processes are commonly used as heating media; electric heaters or other high-temperature sources are also possible. Heat exchange between the high-temperature source and the strong solution results in desorption (evaporation) and significant heating of the refrigerant (e.g., ammonia), a constituent of the working pair. Consequently, the solution splits into two streams: a vapor (refrigerant) and a liquid (weak absorbent solution). The refrigerant is directed to the condenser (4a–CON), while the weak solution returns to the absorber via the heat exchanger (3a, 3b–HEX) and the expansion valve (3c–RV2).

Heat Exchanger (HEX): A typical liquid–liquid heat exchanger connected to the absorber and generator via piping. The weak solution returning from the generator (3a) transfers heat to the strong solution (1a), thereby preheating it prior to further heating in the generator.

Condenser (CON): The refrigerant vapor separated from the strong solution in the generator is cooled and condensed in the condenser, transferring heat to the heating medium (e.g., heating hot water). The condensed refrigerant is then routed to the evaporator (4b) via the expansion valve (RV1).

Evaporator (EVA): In the evaporator, the refrigerant is re-evaporated by heat from the low-temperature heat source (e.g., process cooling water). The evaporated refrigerant returns via line (5b) to the absorber, where the cycle restarts.

2.5. Thermodynamic Aspects of the Model

The thermodynamic model of this system is based on an absorption cycle, in which heat is turned from a lower to a higher temperature with minimal mechanical-energy input, in contrast to electrically driven compressor heat pumps [12]. Using ionic liquids as the absorbent—i.e., as part of the working pair—can enable higher efficiency and higher heating-water temperatures owing to favorable physicochemical properties (e.g., high chemical and thermal stability) and the ability to adapt liquid parameters to the specific requirements of the process. In this system, ammonia acts as the refrigerant and the ionic liquid acts as the absorbent. Together, they form strong solutions. Since ammonia boils at −33.35 °C at atmospheric pressure [13], it is assumed to be more volatile than the ionic-liquid component of the working pair. The process is depicted in the p–t diagram below.

In what follows, the system is analyzed primarily from the standpoint of the highest achievable heating-water temperatures. To provide a detailed discussion of the thermodynamic processes, we treat them on a component-by-component basis of the absorption heat pump.

Generator (GEN)

Thermophysical parameters of the fluids: The conditions in the generator should enable the heating water to reach a high supply temperature (>100 °C); the following assumptions are adopted:

• A heating medium at 135 °C is supplied to the generator heat exchanger; the temperature of the fluid in the generator is 130 °C. It was assumed that the differential temperature between the heating medium in the generator and the strong solution should be at least 5 °C. A temperature of 130 °C was selected to maximize overheating heat gains in ammonia. The temperature of this element is determined by commercially available heat exchange devices, and can be increased if the permissible temperature of each generator element exceeds the design temperature.
• The circulation pump (PMP) raises the pressure from the absorber to the target liquid pressure in the generator; the pressure is further affected by the heat supplied to the generator. After ammonia evaporation, isochoric heating increases its pressure. If only pure ammonia—or a mixture with similar thermophysical properties—was evaporated, the vapor would have to be compressed to about 72.83 bar, the saturation pressure corresponding to 108 °C. The pressure in this component has been selected to enable the transfer of heat from the condensation of ammonia to the high-temperature heating-water system (>100 °C). It is imperative that the differential temperature between the heating-water system and the condensation temperature of ammonia is a minimum of 8 °C. A reduction in the quantity may be possible (to 5 °C), although this would result in an increase in the size of the condenser.

Process description: The strong solution—a stable mixture of ammonia and an ionic liquid—is pumped by the circulation pump (PMP) into the generator. For correct operation and to avoid rectification, one component—here, ammonia—should evaporate at a lower temperature than the ionic liquid [12], which is assumed based on the current knowledge of ionic liquids [14]. Upon heat addition, the strong solution undergoes distillation and splits into two independent fluids; the evaporated refrigerant (ammonia vapor) carries away heat. To ensure evaporation of the cleanest possible refrigerant (ammonia) and eliminate rectification, the ionic liquid must have a much lower volatility than ammonia and remain liquid at the generator’s pressure and temperature. Saturation vapor-pressure parameters for the ammonia/ionic-liquid system are given in Section 4.2. After refrigerant evaporation in the generator and its appropriate purification (i.e., removal of the ionic-liquid fraction from the vapor), the AHP cycle divides into two independent streams: the weak solution and the refrigerant.

Heat Exchanger (HEX)

Thermophysical parameters of the fluids:

• The weak solution, consisting predominantly of the ionic liquid, is at a high temperature attained in the generator. For analysis, 130 °C at the HEX inlet and 90 °C at the outlet are assumed. The liquid pressure follows the generator pressure; its exact value depends on the ionic liquid used and its thermophysical properties. The temperature of the weak solution has been taken directly from that of the fluid in the generator. It is assumed that the fluid in pipeline connecting HEX and GEN will not exhibit any cooling. The outlet temperature of the weak solution in the heat exchanger is assumed to be directly proportional to the differential temperature between the weak solution outlet and the strong solution inlet. It was hypothesized that this differential temperature would be a of 7 °C.
• The strong solution—a stable mixture of ionic liquid and ammonia—enters the HEX at a temperature determined by the processes in the absorber and the physicochemical characteristics of that component. The temperature of 83 °C is taken directly from the strong solution outlet of the absorber. It is assumed that the fluid in pipeline connecting HEX and ABS will not exhibit any cooling. Additionally, it is assumed that upon leaving the HEX, the strong solution’s temperature is 10 °C below the weak solution inlet temperature, i.e., 120 °C. A decrease in differential temperature will result in an increase in the size of the HEX. The liquid pressure follows the circulation pump discharge and thus the generator pressure (GEN).

Process description: The weak solution is routed to the HEX, where it transfers heat to the strong solution, thereby reducing its own temperature. To quantify the heat transferred to the strong solution, the ionic liquid’s physicochemical and thermodynamic properties are required—specifically, specific heat, thermal conductivity, kinematic viscosity, enthalpy, and density (or specific volume). These parameters and their determination are discussed in the next section. After passing through the HEX, the weak solution (liquid) reaches the expansion valve, where its pressure is reduced to the absorber pressure.

The strong solution is transported by the circulation pump to the HEX and then to the generator. Partial ammonia evaporation from the strong solution may occur in the HEX; however, it is essential to maximize recovery of the heat contained in the ionic liquid (weak solution) discharged to the absorber. To correctly describe heat exchange between the ionic liquid and the ionic-liquid–ammonia mixture, the properties of the considered solution must be known; as with the ionic liquid, the required parameters are specific heat, thermal conductivity, kinematic viscosity, enthalpy, and specific volume.

Condenser (CON)

Thermophysical parameters of the fluids:

• The refrigerant (ammonia) enters the condenser as a vapor at the high temperature (130 °C) and pressure established in the generator. Any pressure loss or temperature decrease is assumed to occur in the pipelines between GEN and CON. While transferring heat to the heating water, the ammonia condenses at the saturation temperature corresponding to the high-side pressure (Tcond > 100 °C), thereafter, the condensate may be subcooled to about 90 °C. For subsequent analysis, the condenser outlet ammonia is taken as 90 °C (subcooled liquid) at a pressure equal to the generator (high-side) pressure. It is assumed that the differential temperature between the heating water inlet and the ammonia outlet should be at least 10 °C. Note that, to meet the heating-water requirements, the high-side pressure must not be lower than the saturation pressure, which corresponds to a temperature of not less than 104 °C.
• The heating water changes from 80 °C to 100 °C across the condenser. The inlet temperature is taken directly from the outlet temperature of the heating water in the absorber. The outlet temperature in the condenser must be at least 100 °C to fulfill the hypothesis of this paper. The pressure of the heating water is not analyzed in the present paper and is therefore omitted.

Process description:

In the condenser, high-temperature, high-pressure ammonia vapor transfers heat to the heating water, raising its temperature from 80 °C to 100 °C. Condensation occurs at the saturation temperature T_cond > 100 °C, followed by possible subcooling of the liquid to about 90 °C.

Evaporator (EVA)

Thermophysical parameters of the fluids:

• Immediately after leaving the condenser, the refrigerant passes the expansion valve (RV1), where its pressure is reduced to a value that enables evaporation by heat from the low-temperature source. An evaporation pressure of 11.36 bar, corresponding to 30 °C, is assumed and used in subsequent analyses. The temperature and pressure of ammonia are assumed to be 5 °C lower in any part of the evaporator than in the heat-recovery water flowing through it. It is assumed that with heat supplied from the low-temperature source, the refrigerant fully evaporates to dry saturated vapor (no superheat).
• The heat-recovery water flowing through the evaporator heat exchanger is cooled from 40 °C to 35 °C. The temperature of the heat-recovery system is set at 40 °C, which is the standard return temperature for cooling systems in the beverage industry. Pressure of heat-recovery water is not analyzed in the present paper and is therefore omitted.

Process description:

After throttling at the expansion valve between the condenser and the evaporator to the evaporation pressure, the refrigerant enters the evaporator and absorbs heat from the low-temperature source. As heat is absorbed, ammonia evaporates to saturated vapor, which is routed to the absorber.

Absorber (ABS)

Thermophysical parameters of the fluids:

• The refrigerant, in the vapor phase, enters the absorber directly from the evaporator. Its temperature and pressure are assumed to be unchanged at 30 °C and 11.36 bar—any pressure loss or temperature decrease or increase is assumed to occur in the pipelines between EVA and ABS.
• The weak solution, as a liquid, entering the absorber immediately after the expansion valve is assumed to be at 90 °C and 11.36 bar. To prevent ammonia from flashing out of the strong solution in the absorber, the absorbent (ionic liquid) must markedly depress the ammonia vapor pressure at the absorber temperature.
• The mixture temperature (strong solution) after absorption and heat removal is assumed to be 83 °C, with the pressure remaining 11.36 bar. It is hypothesized that the temperature differential between the weak solution outlet and the heating hot water inlet must be a minimum of 8 °C. It is hypothesized that lower values could be impacted by an increase in absorbers.
• The heating water across the absorber’s heat exchanger changes from 75 °C to 80 °C. It is assumed that the inlet temperature will be maintained at a differential temperature of 20–25 °C between the supply and return flow in a heating-water system. Its pressure is not material in the present analysis and is omitted.

Process description:

In the absorber, the weak solution (liquid) contacts the ammonia vapor from the evaporator. Absorption is exothermic; the absorber is therefore cooled by the returning heating water, raising its temperature from 75 °C to 80 °C. The absorber is the first element where heat is transferred from the working fluid to the heating loop [12].

3. Physicochemical and Thermodynamic Properties of Ionic Liquid

To correctly describe all processes in the AHP, it is essential to determine selected physicochemical and thermodynamic properties. As indicated earlier, several critical parameters are needed to establish the utility of these liquids in the present case.

3.1. Specific Heat Capacity

A key parameter indicating whether a liquid can be applied in the device under consideration is its specific heat capacity.

Specific heat is defined in numerous ways by monographs and articles [9,11,15]. It is justified to consider the specific heat as the heat (energy) required to change the temperature of a given mass of the substance. For absorption heat pump systems, specific heat at constant pressure (p = const.) is pertinent. Although AHP components are structurally tight, providing constant working volumes in sections; from a thermodynamic perspective, they constitute control volumes with flow and intensive interphase mass transfer. Sensible heat, given that the system is quasi-isobaric, solution composition is not constant, phase changes often occur, and enthalpy is the appropriate property for energy balances, is associated with derivative (1).

$${\left({\displaystyle \frac{\partial h}{\partial T}}\right)}_p=c_p$$

(1)

where h is enthalpy of the substance (kJ kg⁻¹), T is temperature (K), and cp is specific heat (kJ kg⁻¹K⁻¹).

Specific heat may also be calculated from (2):

$$c_p={\displaystyle \frac{\mathsf{\Delta }Q}{m·\left(t_k-t_p\right)}}$$

(2)

where ΔQ is heat supplied to the fluid (J), m is mass (kg), t_k is final fluid temperature (K), and t_p is initial fluid temperature (K)

From (2), experimental determination of a liquid’s specific heat capacity requires precise measurement of the amount of heat supplied to a closed system and the temperature difference before and after the process. This necessitates an appropriate instrument capable of determining these quantities with high accuracy. For solids and liquids, measurements should be performed using an adiabatic calorimeter [16]. In this apparatus, a hermetically sealed sample is heated with a precisely quantified heat input, and its temperature rise is observed. To minimize environmental influences, the device employs a high vacuum and thermally insulated barriers. The measuring temperature range must permit testing the sample from −30 °C to 150 °C.

To compute the specific heat capacity of ionic liquids, numerous empirical correlations exist; two representative correlations are given below [4,11]. The first is taken from [4] (Meng Wang, Carlos A. Infante Ferreira) and is given as follows:

$$C_p\hspace{0.17em}=\left|c_0\right|+|c_1\hspace{0.17em}T|$$

(3)

where c₀, c₁ are correlation parameters (related to molar mass) determined experimentally; T is temperature (K), and C_p is specific heat capacity (kJ kmol⁻¹ K⁻¹).

The second is derived from Růžička V, Domalski E.S., as adapted for ionic liquids by Gardas and Coutinho [11]:

$$C_{p,L}\left(T\right)\hspace{0.17em}=|R\left[A+B\left({\displaystyle \frac{T}{100}}\right)+D{\left({\displaystyle \frac{T}{100}}\right)}^2\right]|$$

(4)

where R is the gas constant (8.314472 J mol⁻¹ K⁻¹), T is temperature (K), and C_p,L(T) is specific heat capacity (J mol⁻¹ K⁻¹). Parameters A, B, D are calculated from the following:

$$A =\sum _{i=1}^k{n}_i{a}_i$$

(5)

$$B=\sum _{i=1}^k{n}_i{b}_i$$

(6)

$$D=\sum _{i=1}^k{n}_i{d}_i$$

(7)

where a_i, b_i, and d_i are group-contribution values for cations and anions, selected individually for each ionic liquid, and n_i is group multiplicity. Using these relations, one can calculate the specific heat of any ionic liquid for which cation/anion group values are available, in the 196.36–663.10 K temperature range [11].

3.2. Enthalpy

Enthalpy is a thermodynamic function equal to the sum of internal energy and the product of pressure and volume. This function could be described as below:

$$H =U +pV$$

(8)

where H is enthalpy (J), U is internal energy (J), p is absolute pressure (Pa), and V is total system volume (m³).

For simplicity, the foregoing can be expressed in differential form per 1 kg of fluid (specific properties), which will be used in further relations [4]:

$$dh =du+dpV$$

(9)

where h is specific enthalpy (J kg⁻¹).

Values of enthalpy for commonly used substances (denoted in the formulae as XY), i.e., water or ammonia, are widely known and available. At the same time, the enthalpy values of ionic liquids (denoted in the formulae as CJ), owing to their properties and the very broad range of design possibilities, are parameters that must be calculated or determined. To determine this parameter, and given the specific heat values of these liquids, the enthalpy can be calculated from the following formula [4]:

$$h_{CJ}\left(T\right)=h_0\left(T_0\right)+{\int }_{T_0}^T{C}_p^{CJ}dT$$

(10)

where T₀ is the reference temperature [K] and h₀ is the reference enthalpy (J kg⁻¹). The reference enthalpy at T₀ = 273.15 K is taken, in accordance with the IIR, as h = 200 kJ/kg [6].

It should be noted that, in absorption heat pumps, in addition to the pure ionic liquid (CJ) constituting the weak solution, a mixture composed of the ionic liquid and another liquid of known enthalpy will also be employed. The enthalpy of the saturated solution at equilibrium can be calculated by means of the following formula [4]:

$$h^{mie}\left(T,P,w_{XY}\right)=h_{row}^{mie}=w_{XY}{h}_{XY}\left(T\right)+w_{CJ}{h}_{CJ}\left(T\right)+h^E\left(T,P,w_{XY}\right)$$

(11)

where w is the mass fraction (the ratio of the component mass to the mass of the mixture).

The enthalpies of the individual substances are the sum of the reference enthalpy and the integral of the specific heat capacity over temperature T. This computation is straightforward. Another essential step is to determine the value of the excess enthalpy. The value of this parameter is very important for calculating the value of COP and for analyzing energy balances. Negative values suggest the possibility of substantial energy release during the absorption of ammonia into the ionic liquid in the absorber. The excess enthalpy for systems composed of ionic liquids and ammonia can be calculated using several approaches [6,7,9,17,18,19], two of which are listed below.

The first approach to calculating the excess enthalpy is based on the Redlich–Kister equation [17,18,20] illustrated below:

$$H^E=x_1{x}_2\sum _{i=1}^4{A}_i\times (2{x_1-1)}^{i-1}$$

(12)

where H^E is the excess enthalpy (kJ mol⁻¹), x₁ and x₂ are the mole fractions of the respective components of the mixture, and A_i are the regression parameters of the Redlich–Kister polynomial determined experimentally. The approach based on the above formula faces a difficulty due to the very limited amount of data for ammonia-based mixtures. Accordingly, in many cases an alternative approach is required.

Another equation for determining the excess enthalpy is a relation based on the NRTL (Non-Random Two-Liquid) method and the Gibbs–Helmholtz equation [19]. As a first step, one should begin with the calculation of the excess Gibbs energy, which is described below:

$${\displaystyle \frac{g^E}{RT}}=x_1{x}_2\left({\displaystyle \frac{{\tau }_{21}{G}_{21}}{x_1+x_2{G}_{21}}}+{\displaystyle \frac{{\tau }_{12}{G}_{12}}{x_2+x_1{G}_{12}}}\right)$$

(13)

where G^E is the excess Gibbs energy, x₁ and x₂ are the mole fractions of the respective components of the mixture, and τ and G are parameters calculated on the basis of the NRTL model discussed in Section 4.4.

In the next step, one should consider the formula that enables conversion of the relationship between Gibbs energy and enthalpy. This is provided by the following equation:

$${\left({\displaystyle \frac{\partial \left(G^E/T\right)}{\partial T}}\right)}_{P,x}=-\hspace{0.17em}{\displaystyle \frac{H^E}{T^2}}$$

(14)

The following expression for the excess enthalpy of a binary mixture is obtained by combining the foregoing relations:

$$H^E= -R\left({\displaystyle \frac{x_1{x}_2{b}_{21}{G}_{21}\left[x_1\left({\alpha }_{21}{\tau }_{21}-1\right)-x_2{G}_{21}\right]}{{\left(x_1+x_2{G}_{21}\right)}^2}} + {\displaystyle \frac{x_1{x}_2{b}_{12}{G}_{12}\left[x_2\left({\alpha }_{12}{\tau }_{12}-1\right)-x_1{G}_{12}\right]}{{\left(x_2+x_1{G}_{12}\right)}^2}}\right)$$

(15)

The individual quantities necessary to determine H^E are calculated from the following equations taken from [19]:

$${\tau }_{12}={\tau }_{12}^{\left(0\right)}+{\displaystyle \frac{{\tau }_{12}^{\left(1\right)}}{T+273.15}}+e_{12}\hspace{0.17em}\mathit{ln}\left(T +273.15\right)+f_{12}\hspace{0.17em}\left(T +273.15\right)$$

(16)

$${\tau }_{21}={\tau }_{21}^{\left(0\right)}+{\displaystyle \frac{{\tau }_{21}^{\left(1\right)}}{T+273.15}}+e_{21}\hspace{0.17em}\mathit{ln}\left(T+273.15\right)+f_{21}\hspace{0.17em}\left(T+273.15\right)$$

(17)

$${\alpha }_{12}=c_{12}+d_{12}\hspace{0.17em}T,{ \alpha }_{21}=c_{21}+d_{21}\hspace{0.17em}T$$

(18)

It is important to note that the excess enthalpy, as well as other parameters related to the proper determination of the parameters of ionic liquids and of mixtures of ionic liquids with ammonia, can be determined by means of equations of state. An outline of these solutions is presented in Section 4.4.

3.3. Vapor–Liquid Equilibrium (VLE)

Vapor–liquid equilibrium in an absorption heat pump is the thermodynamic state in which the rate of evaporation of the refrigerant equals its rate of condensation in the absorbent solution; under these conditions, at a given temperature, pressure, and composition, the vapor pressure and the partitioning of the refrigerant between phases are established. The position of this equilibrium determines the operating parameters of the generator and the absorber and the concentration difference between the rich and weak solutions, and thus determines the solution circulation, the heat demand, and the system efficiency. The liquid–vapor equilibrium is determined, inter alia, by means of the NRTL (Non-Random Two-Liquid) method. The necessary equations [4,20,21] for calculating the liquid–vapor equilibrium by this method are given below:

$$P = {\gamma }_1{x}_1{P}_1^{sat}+{\gamma }_2{x}_2{P}_2^{sat}$$

(19)

$$\mathit{ln}{\gamma }_1=x_2^2\left[{\tau }_{21}{\left({\displaystyle \frac{G_{21}}{x_1+x_2{G}_{21}}}\right)}^2+{\displaystyle \frac{G_{12}{\tau }_{12}}{{\left(x_2+x_1{G}_{12}\right)}^2}}\right]$$

(20)

$$\mathit{ln}{\gamma }_2=x_1^2\left[{\tau }_{12}{\left({\displaystyle \frac{G_{12}}{x_2+x_1{G}_{12}}}\right)}^2+{\displaystyle \frac{G_{21}{\tau }_{21}}{{\left(x_1+x_2{G}_{21}\right)}^2}}\right]$$

(21)

$$G_{12}=e^{-\alpha {\tau }_{12}}$$

(22)

$$G_{21}={ e}^{-\alpha {\tau }_{21}}$$

(23)

$${\tau }_{12}={\tau }_{12}^{\left(0\right)}+{\displaystyle \frac{ {\tau }_{12}^{\left(1\right)}}{T}}$$

(24)

$${\tau }_{21}={\tau }_{21}^{\left(0\right)}+{\displaystyle \frac{{\tau }_{21}^{\left(1\right)}}{T}}$$

(25)

On the basis of the above equations, and given the parameters ${\tau }_{12}^{\left(0\right)}$, ${\tau }_{12}^{\left(1\right)}$, ${\tau }_{21}^{\left(0\right)}$, ${\tau }_{21}^{\left(1\right)}$ and α, which are determined experimentally, one can determine the vapor pressure of any mixture of two liquids. For a complete analysis, however, it is also necessary to determine the vapor pressure of each component of the mixture, the determination of which is described in Section 3.4.

At the same time, it should be noted that the above equations taken from [4] do not coincide with those indicated in [19]. This follows from the fact that in [4], the authors consider that an accurate prediction of the excess enthalpy (H^E) from the NRTL model is difficult due to the need to evaluate the temperature derivative, and the relations in activity-coefficient models are purely empirical. Consequently, a different method is used to determine H^E, and the determination of τ₁₂ and τ₂₁ is carried out without introducing extended temperature-dependent terms, which are necessary when determining the excess enthalpy. Therefore, it should be borne in mind that the method of determining the NRTL model parameters described in the above section should be used only for VLE determination, whereas H^E should be determined using the methods described in Section 4.2.

3.4. Equations of State

An equation of state is an element describing the relationship between the parameters of a thermodynamic system. It typically describes parameters such as pressure, density, temperature, entropy, and/or the energy of the system. At the same time, it should be noted that standard equations of state, e.g., the Van der Waals equation, due to the structure and composition of ionic liquids, cannot serve as the basis for the above-mentioned analyses [22]. Accordingly, in many studies, attempts have been made to determine appropriate equations of state for ionic liquids, as well as for mixtures of ionic liquids with other substances. One modification is presented in [22], where a method of modifying the Van der Waals equation is indicated in order to best determine the parameters of ionic liquids. The formula takes the following form:

$$\left[P_r+\tau {\rho }_r^{2}A\left({\rho }_r,T_r\right)\right]·[1-v{\rho }_{r}B\left({\rho }_r{T}_r\right)]=\zeta {\rho }_r{T}_r$$

(26)

The above formula, derived in [22], is based on reduced variables, which was a deliberate procedure enabling the determination of temperature dependencies from the fundamental Van der Waals equation. On the basis of the aforesaid formula and the values of the individual parameters, i.e., τ, A, B—whose dependencies are given in [22]—one can compute with high accuracy the parameters for ionic liquids, such as pressure, temperature, and density.

Another relation, based on an equation of state and this time allowing the calculation of several quantities, including the vapor pressure of pure ionic liquids, the vapor pressure of mixtures, and the enthalpy of mixing of ionic liquids and ammonia, was presented in the works of Yokozeki and Shiflett [6,7]. For this purpose, they modified the Redlich–Kwong equation [6,7,8]. The equation takes the following form:

$$P = {\displaystyle \frac{RT}{V-b}}-{\displaystyle \frac{a\left(T\right)}{V\left(V+b\right)}}$$

(27)

$$a\left(T\right)=0.427480\cdot {\displaystyle \frac{R^2{T}_c^2}{P_c}}\cdot \alpha \left(T\right)$$

(28)

$$b=0.08664\cdot {\displaystyle \frac{R{T}_c}{P_c}}$$

(29)

where the principal modifying term is based on an empirical expression for α(T) shown below:

$$\alpha \left(T\right)=\sum _{k=0}^3{\beta }_k{\left({\displaystyle \frac{1}{T_r}}-T_r\right)}^k,\mathrm{ }\left(T_r\equiv {\displaystyle \frac{T}{T_c}}\right)$$

(30)

The coefficients β_k are experimentally determined quantities and are specific to each substance. The above equations enable determination of the parameters of the individual substances and are used primarily for this purpose in the present work.

4. Results

To verify the feasibility of using selected ionic liquids in the working mixtures of high-temperature absorption heat pumps, a series of calculations were performed as indicated in the subsections below. The parameters of the individual ionic liquids analyzed are shown in

Table 3. Parameters of the substances analyzed in the calculations of the vapor pressure of the pure components of the mixture [4,6,10,23].

Substance	Molar Mass	Tc (K)	Pc (kPa)	Viscosity	Fluid Density	Parameters of the Modified Redlich–Kwong Equation
	(g mol−1)			cP	g/cm3	β0 (–)	β1 (–)	β2 (–)
Ammonia (NH3)	17.03	406.15	11,424	0.15	0.6	1.00027	0.45689	−0.05772
Water (H2O)	18.02	647.1	22,064	0.89	1	1.00236	0.54254	−0.08667
[emim][SCN]	169.25	1001.1	4102	24.7	1.12	1	0.7236	0
[emim][EtSO4]	236.29	1067.5	4050	99	1.24	ND	ND	ND
[bmim][PF6]	226.02	719.4	1730	274	1.37	ND	ND	ND
[hmim][NTf2]	447.42	ND	ND	70.1	1.37	ND	ND	ND

ND—No Data.

,

Table 4. Parameters of the mixtures analyzed in the calculations of the vapor pressure of absorption heat pump (AHP) working fluids [4].

Solution	NRTL Model Parameters for Determining Liquid–Vapor Equilibrium (VLE)
	α (–)	${\mathit{\tau }}_{12}^{\left(0\right)}$ (–)	${\mathit{\tau }}_{12}^{\left(1\right)}$ (–)	${\mathit{\tau }}_{21}^{\left(0\right)}$ (–)	${\mathit{\tau }}_{21}^{\left(1\right)}$ (–)
Ammonia (NH3)/[emim][SCN]	−0.27082	−10.66	3120.01	5.6	−1967.71
Ammonia (NH3)/Water (H2O)	−0.24355	24.17	−18,636.4	7.26	−3370.4

,

Table 5. Parameters of the substances analyzed in the calculations of the specific heat of pure ionic liquids using the method indicated in [4].

Substance	Correlation Parameters for Determining Cp Using the Method Indicated in [4]
	c0 (–)	c1 (–)
[emim][SCN]	116.474	0.547
[emim][EtSO4]	245.526	0.462
[bmim][PF6]	282.07	0.452

,

Table 6. Computed parameters of the substances analyzed in calculating the specific heat of pure ionic liquids by the method indicated in [11].

Substance	Parameters for Determining Cp Using the Method Indicated in [9]
	A	B	D
[emim][EtSO4]	33.132	5.073	−0.321
[bmim][PF6]	13.205	15.744	−1.251

and

Table 7. Parameters of the mixtures analyzed in the calculations of the excess enthalpy of absorption heat pump (AHP) working fluids [11].

Solution	Parameters of NRTL Model for Determining Excess Enthalpy (HE)
	a12 (–)	a21 (–)	b12 (–)	b21 (–)	e12 (–)	e21 (–)	f12 (–)	f21 (–)	c (–)	d (–)
Ammonia (NH3)/[emim][SCN]	−0.0545	−0.8702	178.418	−516.44	0	0	0	0	0.3	0.0004
Ammonia (NH3)/[emim][EtSO4]	−0.9204	2.2626	2457.8	−1665	−0.6979	0.6749	0.0015	−0.0071	0.3	0.0058

. In Table 3, viscosity and density parameters have been selected for a temperature of 25 °C and atmospheric pressure of 101.3 kPa. The determination of the vapor pressure of the ionic liquid was carried out on the basis of the works of Yokozeki and Shiflett [6,7,8]. Liquid–vapor equilibrium was implemented using the equations of the NRTL model. The specific heat of the ionic liquids was determined according to the formulas indicated in the article by Meng Wang and Carlos A. Infante Ferreira [4], and a modification of the approach of Ruzicka V., Domalski E. S., as indicated in [11] by Ramesh L. Gardas and Joao A. P. Coutinho. The excess enthalpy was determined from two relations, namely the NRTL (Non-Random Two-Liquid) method with the Gibbs–Helmholtz relation [19] and the Redlich–Kister equation [17,18]. Each set of results is shown in comparison with water, which, together with ammonia, constitutes the classical working mixture used in absorption heat pump systems. The parameters of the ionic liquids for the calculations were taken from the respective sources, i.e., [4,6,9,11]. The ionic liquids which have been considered in this paper are as follows: 1-ethyl-3-methylimidazolium thiocyanate ([emim][SCN]), 1-ethyl-3-methylimidazolium ethyl sulfate ([emim][EtSO₄]), 1-butyl-3-methylimidazolium hexafluorophosphate ([bmim][PF₆]), 1-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([hmim][NTf₂]). These liquids are well known, and information about their properties can easily be found in a wide range of publications. This is why they have been selected for this research project.

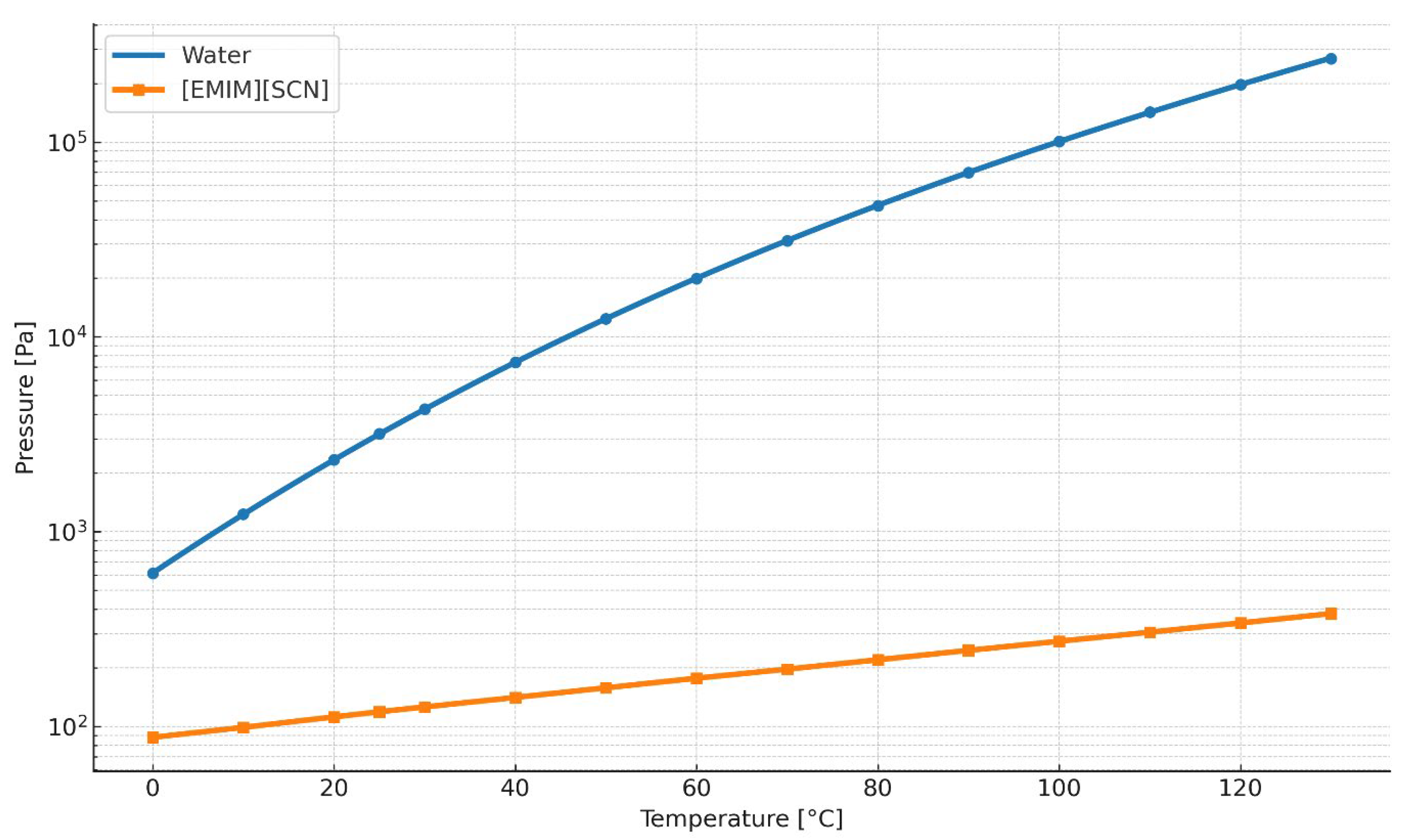
4.1. Vapor Pressure of Pure Ionic Liquids

For the analysis of the vapor pressure of ionic liquids, the substance 1-Ethyl-3-methyl-imidazolium-thiocyanate [emim][SCN] was considered. The calculation results are given in

Table 8. Results of the vapor-pressure calculations for water and the ionic liquid [emim][SCN] using the modified Redlich–Kwong equation [6,7,8].

Operating Temperature		H2O (Water)	[emim][SCN] (Ionic Liquid)
T (°C)	T (K)	P (Pa)	P (Pa)
0	273.15	611	88
10	283.15	1229	99
20	293.15	2346	112
25	298.15	3180	119
30	303.15	4261	126
40	313.15	7404	141
50	323.15	12,370	158
60	333.15	19,950	177
70	343.15	31,160	197
80	353.15	47,290	220
90	363.15	69,930	246
100	373.15	101,000	274
110	383.15	142,700	305
120	393.15	197,800	340
130	403.15	269,200	380

and illustrated in Figure 3.

Accordingly, it may be stated unequivocally that the vapor pressure of ionic liquids is virtually zero, which implies that, over the entire range of engineering applications, a vacuum would be required to induce evaporation of this substance.

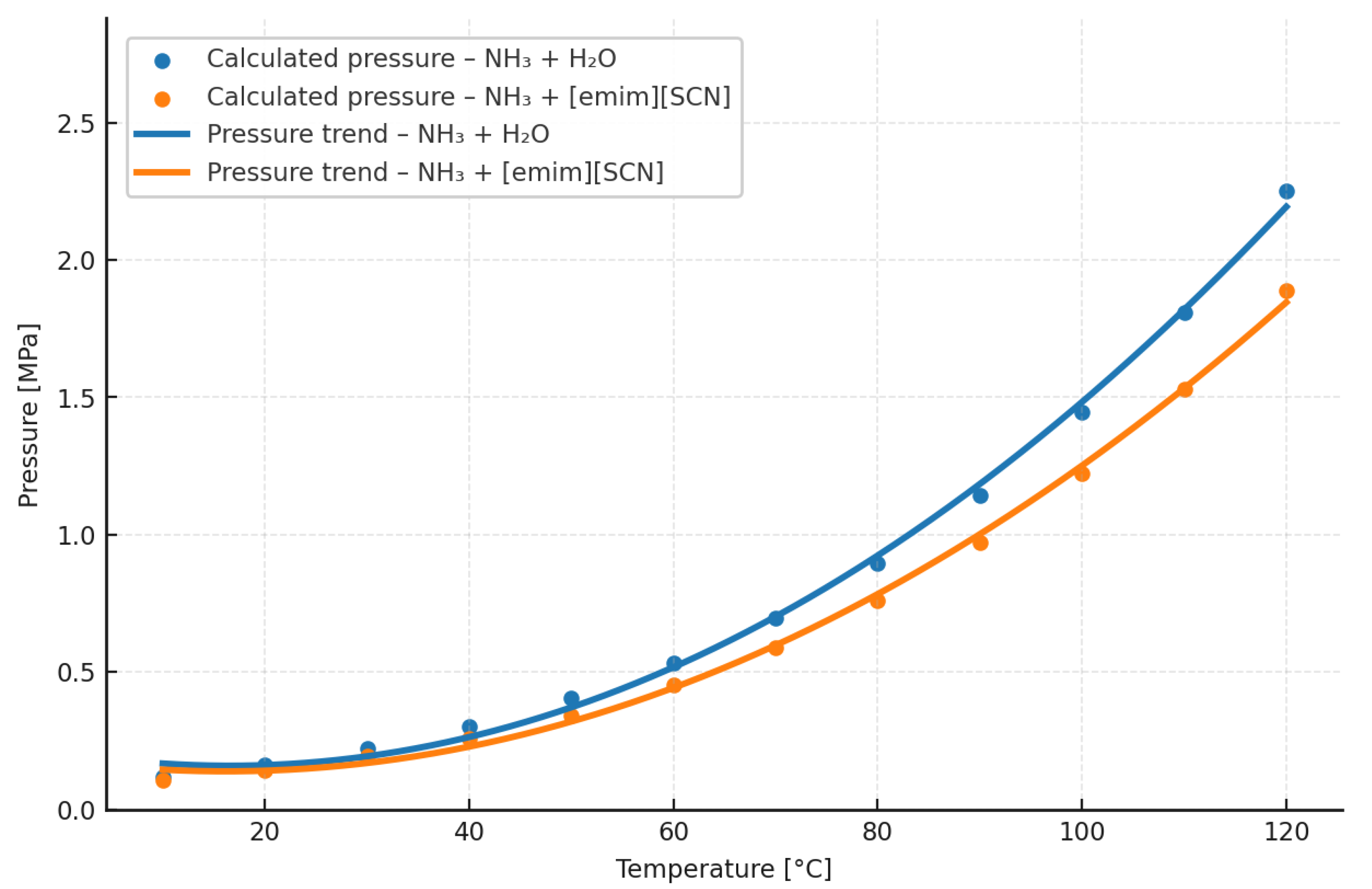
4.2. Vapor Pressure of Working-Fluid Solutions

For the analysis of the vapor pressure of working-fluid mixtures with ionic liquids, the substance 1-Ethyl-3-methyl-imidazolium-thiocyanate [emim][SCN] in mixture with ammonia was considered. A mole fraction of ammonia x₁ = 0.4 was assumed. The calculation results are presented in

Table 9. Results of the vapor-pressure calculations for the ammonia–ionic-liquid [emim][SCN] mixture using the NRTL model [4] for mole fractions x₁ = 0.4, x₂ = 0.6.

Operating Temperature	Ammonia (NH3)/[emim][SCN]
	Coefficients γ of Model NRTL		Vapor Pressure
T (K)	γ1 (–)	γ2 (–)	P (Pa)
283.15	0.8029	0.8467	191,502
293.15	0.7306	0.8290	251,150
303.15	0.6769	0.8146	307,606
313.15	0.6377	0.8033	397,124
323.15	0.6099	0.7948	483,932
333.15	0.5914	0.7886	618,114
343.15	0.5803	0.7846	750,749
353.15	0.5755	0.7822	951,061
363.15	0.5760	0.7814	1,152,035
373.15	0.5810	0.7818	1,449,858
383.15	0.5899	0.7833	1,752,431
393.15	0.6024	0.7856	2,195,919

and illustrated in Figure 4.

Based on the results from Table 9 and

Table 10. Results of the vapor-pressure calculations for the ammonia–water mixture using the NRTL model [4] for mole fractions x₁ = 0.4, x₂ = 0.6.

Operating Temperature	Ammonia (NH3)/Water (H2O)
	Coefficients γ of Model NRTL		Vapor Pressure
T (K)	γ1 (–)	γ2 (–)	P (Pa)
283.15	0.6091	0.5061	145,619
293.15	0.5965	0.5260	205,735
303.15	0.5880	0.5482	268,541
313.15	0.5833	0.5721	365,757
323.15	0.5823	0.5974	466,359
333.15	0.5845	0.6235	618,315
343.15	0.5897	0.6501	774,891
353.15	0.5974	0.6767	1,006,317
363.15	0.6072	0.7030	1,244,069
373.15	0.6189	0.7285	1,588,641
383.15	0.6318	0.7528	1,941,357
393.15	0.6456	0.7755	2,445,195

and Figure 4, it can be inferred that the vapor pressure of the ammonia–IL mixture, in the operating temperature range from 283.15 K to 323.15 K, is greater than the vapor pressure of the ammonia–water working fluid used in absorption heat pumps. Above 323.15 K, the pressure of the IL-based working fluid is lower than that of the water-based one. At the same time, it should be noted that the higher pressure of the ammonia (NH₃)/[emim][SCN] mixture at low temperatures mainly results from the high values of γ₁ and γ₂ calculated by the NRTL model.

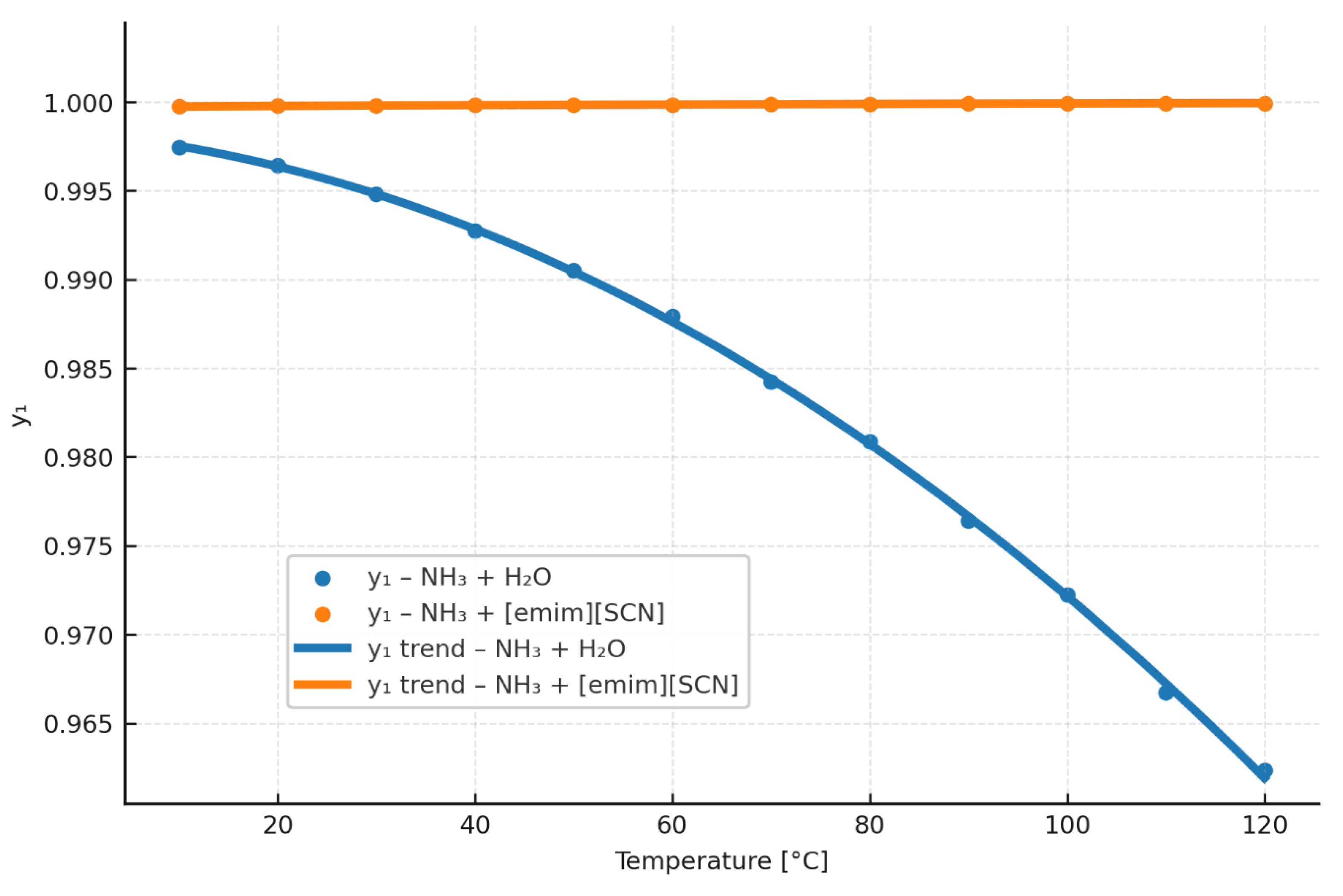
4.3. Vapor–Liquid Equilibrium (VLE)

According to the calculations presented in Section 4.2, the differences in vapor pressure for the NH₃/[emim][SCN] mixture and for NH₃/H₂O [23] are relatively small. However, a more pertinent parameter from the standpoint of high-temperature absorption heat pumps is the composition of the vapor observed above the working-liquid mixture in the GEN. According to Figure 5, the vapor above the working fluid consisting of [emim][SCN] and ammonia is practically pure ammonia. These results indicate that, in AHP systems based on an NH₃/IL mixture, it is reasonable to forgo the rectification process even at high temperatures in the generator, which are required in high-temperature absorption heat pumps. By eliminating rectification, the system increases its COP, and it does not decline appreciably with increasing generator temperature.

Table 11. Molar fraction of absorbate in vapor.

Substance	Temperature	Molar Fraction of Absorbate in Liquid
		x1 = 0.1; x2 = 0.9	x1 = 0.4; x2 = 0.6	x1 = 0.5; x2 = 0.5	x1 = 0.9; x2 = 0.1
		Molar Fraction of Absorbate in Vapor
	T (K)	y1 (–)
Ammonia (NH3)/[emim][SCN]	283.15	0.999989	0.999737	0.999850	0.997074
	313.15	0.999997	0.999829	0.999912	0.997785
	343.15	0.999999	0.999876	0.999939	0.998531
	373.15	1.000000	0.999911	0.999956	0.999104
	403.15	1.000000	0.999931	0.999965	0.999413
Ammonia (NH3)/Water (H2O)	283.15	0.819796	0.997439	0.998848	0.999950
	313.15	0.732596	0.993072	0.996898	0.999919
	343.15	0.669840	0.984295	0.992690	0.999932
	373.15	0.647411	0.972129	0.986194	0.999984
	403.15	0.640450	0.957191	0.977343	0.999999

contains a wide range of data for the molar content of ammonia (y₁) in the vapor in the GEN.

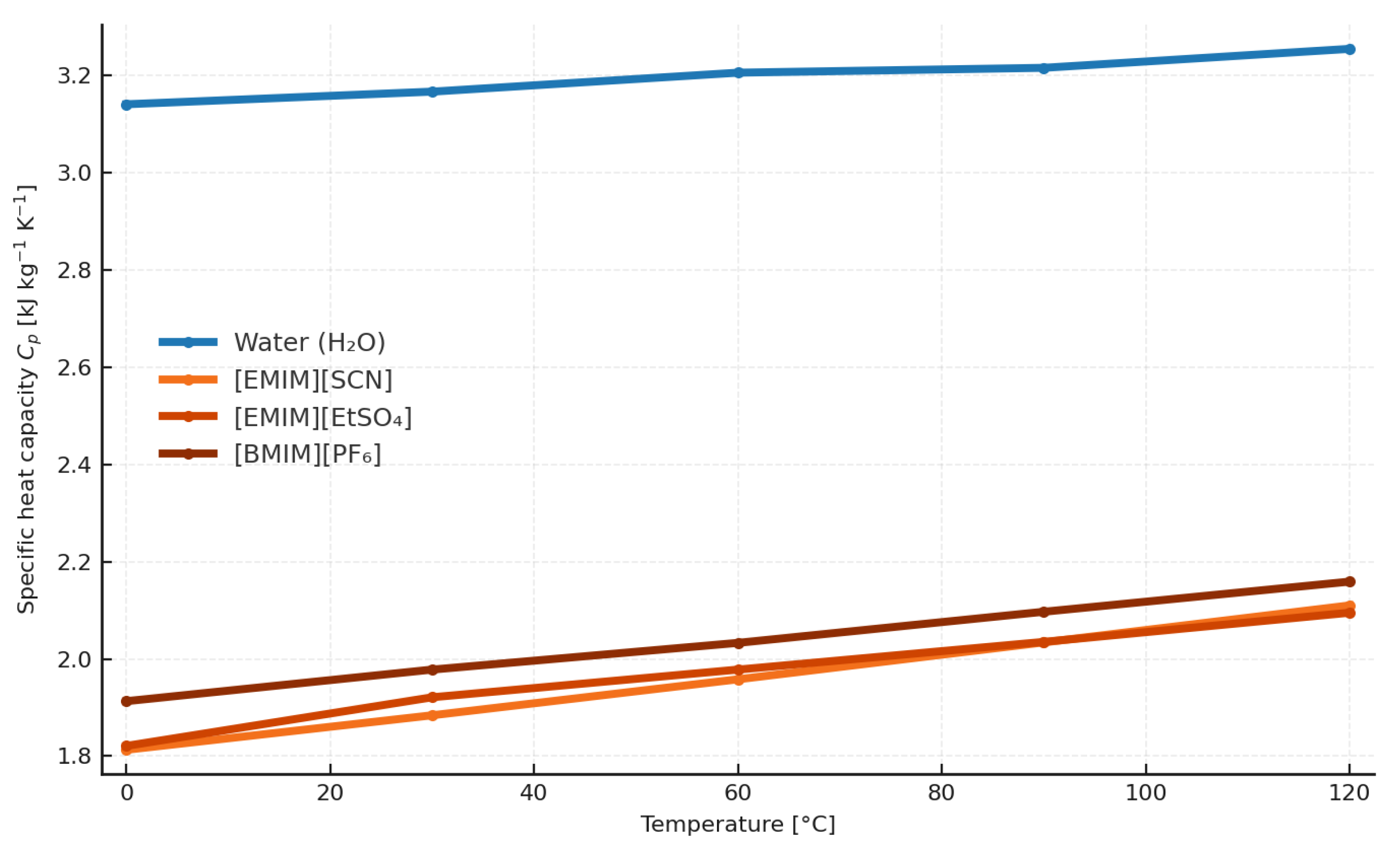
4.4. Specific Heat Capacity of Ionic Liquids

The specific heat capacity of an ionic liquid is a parameter defined primarily on the basis of experimental studies. Based on experimental data [24], it has been assessed that the specific heat capacity depends on the liquid temperature and, to a very small extent, on its pressure. Characteristic, interpolated values as a function of pressure are given in

Table 12. Specific heat capacity values of the ionic liquid [hmim][NTf₂] as a function of pressure at T = 381.15 K.

Operating Temperature	[hmim][NTf2] (Ionic Liquid)
	Pressure	Specific Heat Capacity [Cp]
T (K)	P (Mpa)	Cp (J kg−1 K−1)
381.15	0.1	1527.74
	0.3	1527.6678
	0.5	1527.5955
	0.7	1527.5233
	0.9	1527.451
	1.1	1527.3788
	1.3	1527.3065
	1.5	1527.2343
	1.7	1527.162
	1.9	1527.0898

. At the same time, the determination of specific heat can be performed using empirical computational models based on the structure presented in Section 3.1. The results of calculations using the method indicated in the article by Meng Wang and Carlos A. Infante Ferreira [4] are shown in

Table 13. Calculated specific heat values, on a molar basis, for ionic liquids using methods [4,11].

Substance	Temperature	Group Additivity Method According to [11]	Linear T-Correlation Method According to [4]	Specific Heat Capacity of Water
	T (K)	Cp (kJ kmol−1 K−1)	Cp (kJ kmol−1 K−1)	Cp (kJ kmol−1 K−1)
[emim][SCN]	273.15	265.887	ND	75.983
	303.15	282.297	ND	75.318
	333.15	298.707	ND	75.343
	363.15	315.117	ND	75.780
	393.15	331.527	ND	76.526
[emim][EtSO4]	273.15	371.721	370.775	75.983
	303.15	385.581	378.814	75.318
	333.15	399.441	386.373	75.343
	363.15	413.301	393.452	75.780
	393.15	427.161	400.050	76.526
[bmim][PF6]	273.15	405.534	389.748	75.983
	303.15	419.094	411.036	75.318
	333.15	432.654	430.452	75.343
	363.15	446.214	447.995	75.780
	393.15	459.774	463.667	76.526

ND—No Data.

. Calculations based on the formula of Ruzicka V., Domalski E. S., as adapted by Ramesh L. Gardas and Joao A. P. Coutinho [11], are also shown in Table 13 and in Figure 6.

Based on the results, it can be stated unequivocally that, in calculating the specific heat of ionic liquids, variations in this parameter due to pressure changes are negligible.

Accordingly, it follows that the two methods proposed in this article for use in thermodynamic calculations for determining specific heat capacity are equivalent and provide similar results over the temperature range 273.15–393.15 K. The maximum observed difference in results is 6.78%. Relative to water, the specific heat of ionic liquids on a molar basis is 350% to 600% higher than that of water. By contrast, the specific heat capacity of the analyzed substances on a mass basis (per gram) is 63% to 52% lower than that of water.

4.5. Specific Heat Capacity of Working-Fluid Solutions with Ionic Liquids

The specific heat capacity of solutions of an ionic liquid and ammonia could be calculated using the formula below [4], which takes the mass fraction of the given substance into account. This value is necessary for calculating the enthalpy of the mixture including mixtures with ionic liquids.

$$C_p=w_{xy}\times C_p^{xy}+\left(1-w_{xy}\right)\times C_p^{CJ}$$

(31)

The calculated values for the ammonia–ionic-liquid mixtures (for each ionic liquid) and for ammonia–water are given in

Table 14. Specific heat of ammonia–ionic-liquid and ammonia–water mixtures at a 0.5/0.5 mass ratio.

Substance	Temperature	Specific Heat Capacity
	T (K)	Cp (kJ kg−1 K−1)
Ammonia (NH3)/[emim][SCN]	273.15	3.093
	303.15	3.249
	333.15	3.488
	363.15	4.111
	393.15	6.639
Ammonia (NH3)/[emim][EtSO4]	273.15	3.095
	303.15	3.231
	333.15	3.451
	363.15	4.055
	393.15	6.564
Ammonia (NH3)/[bmim][PF6]	273.15	3.205
	303.15	3.342
	333.15	3.563
	363.15	4.167
	393.15	6.677
Ammonia (NH3)/Water (H2O)	273.15	4.417
	303.15	4.505
	333.15	4.697
	363.15	5.283
	393.15	7.784

. A 50/50 mass solution is considered, and the specific heat (C_p) parameters are assumed without considering the mixture

From the calculated data, illustrated in Figure 6, it can be concluded with certainty that ionic-liquid-based mixtures have a significantly lower specific heat at the same mass fraction.

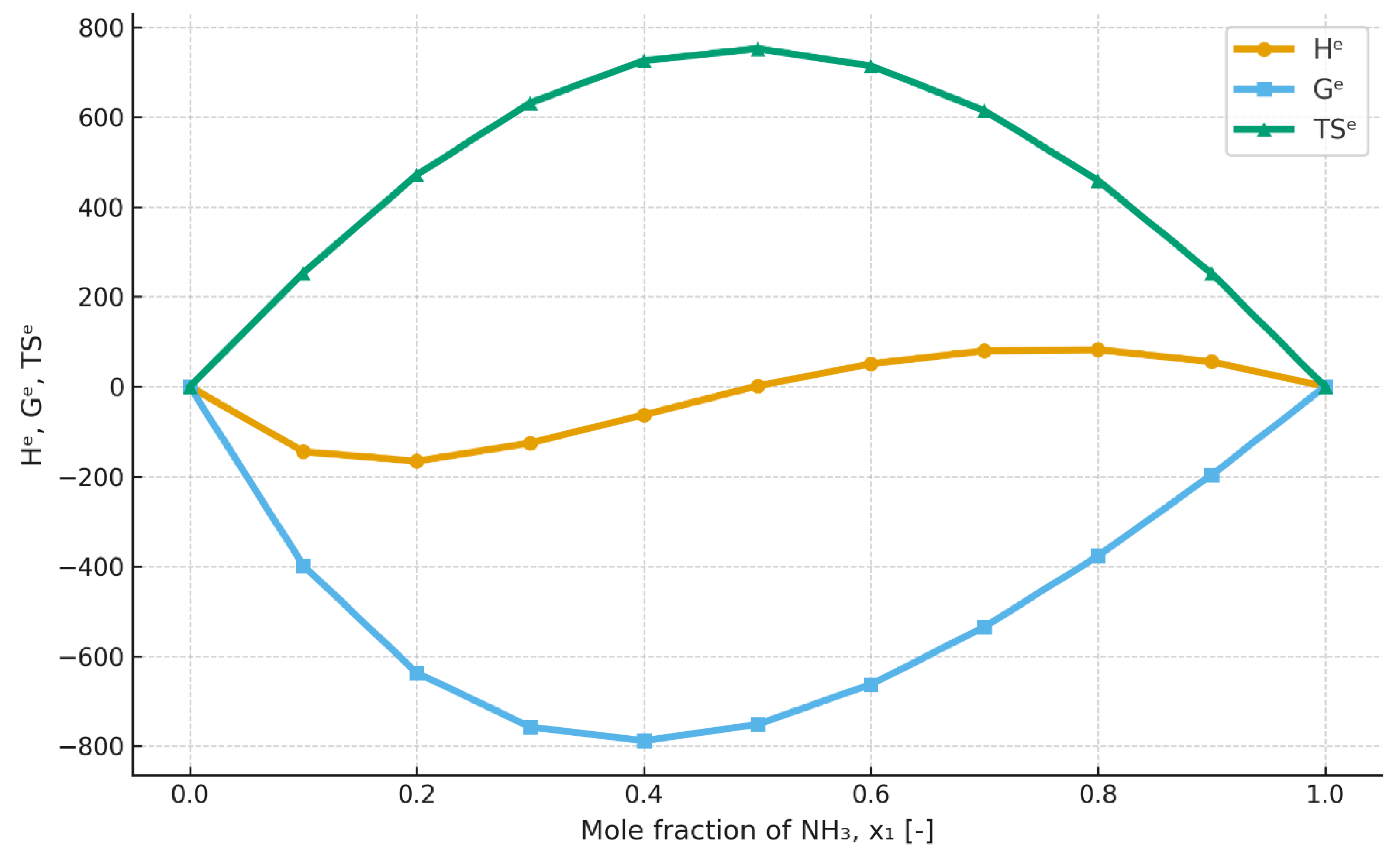
4.6. Excess Enthalpy

The excess enthalpy is a key thermodynamic parameter for working mixtures used in absorption heat pumps, because it enters directly into the generator heat balance and thus determines the required generator duty (Q_GEN) and the achievable COP.

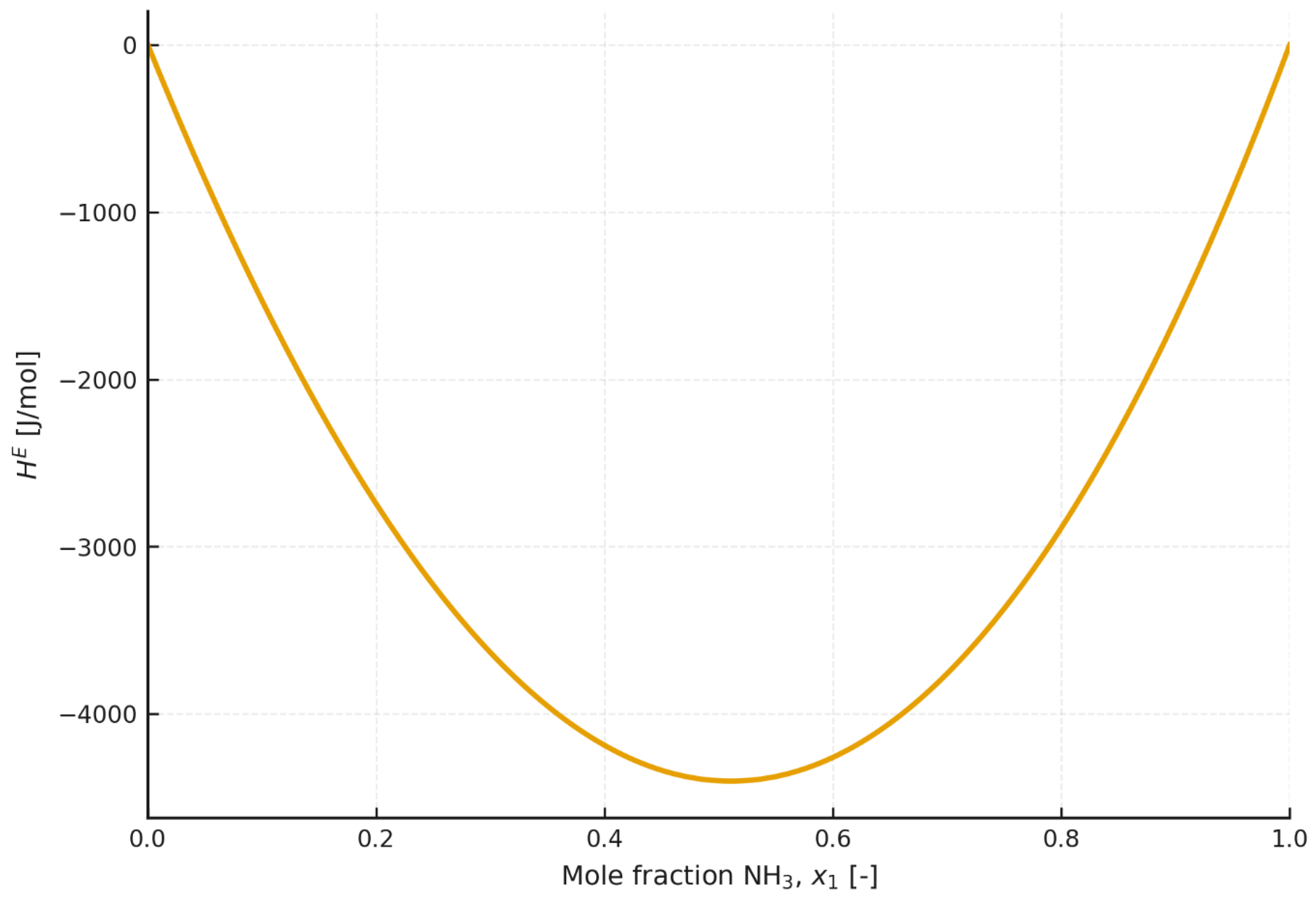
According to Figure 7, it can be inferred that, for the [emim][SCN]–ammonia mixture at 403.15 K, the excess enthalpy is negative for every ammonia mole fraction. For 303.15 K, in accordance with Figure 8, the excess enthalpy for the ammonia–[emim][SCN] mixture is negative up to an ammonia mole fraction of approximately 0.5. Above this value, the excess enthalpy becomes positive, which indicates an endothermic process and, at the same time, points to a significant reduction in the suitability of such a working-fluid composition for use in an absorption heat pump.

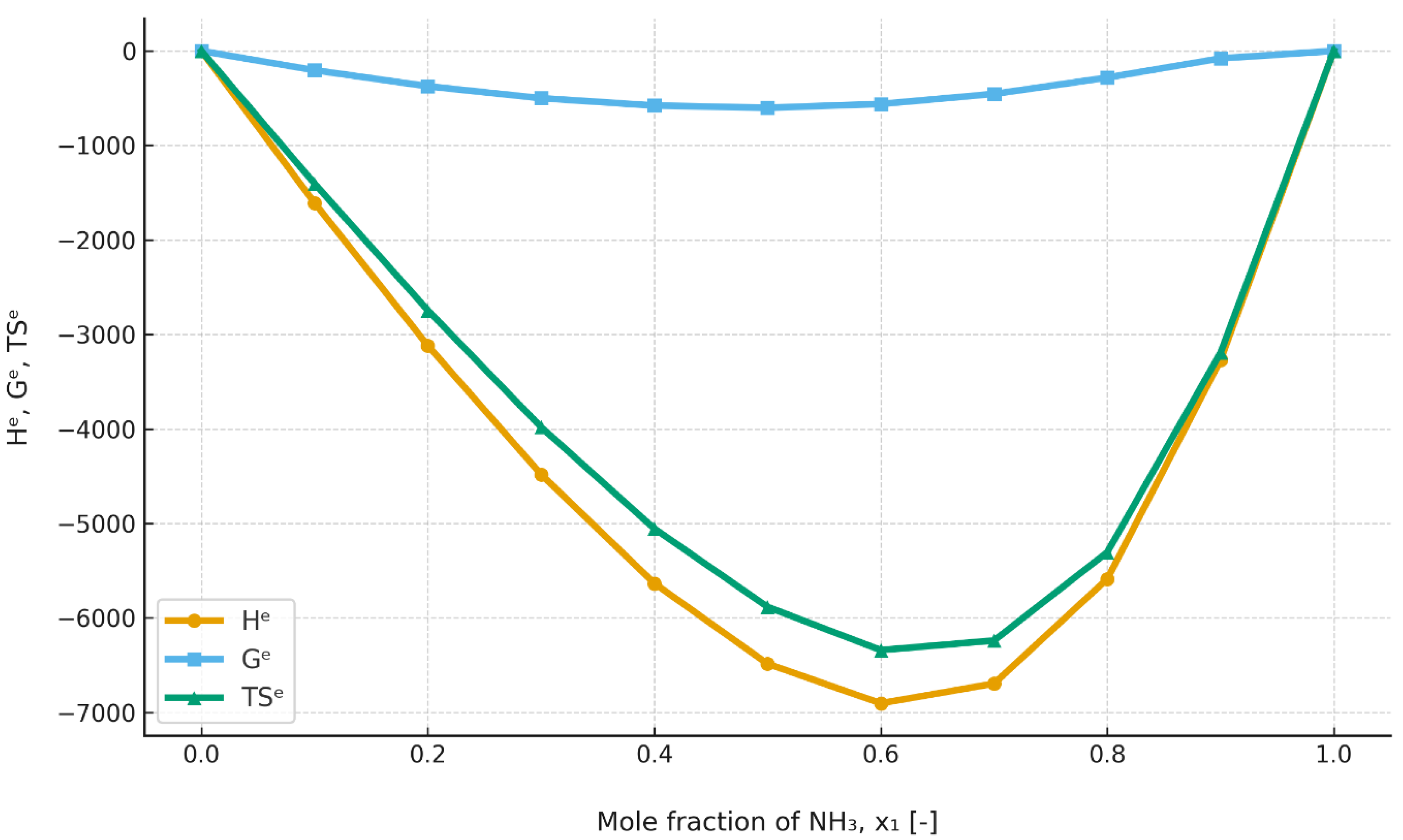
For the ammonia–ionic-liquid [emim][EtSO₄] mixture, the excess enthalpy values at 403.15 K, shown in Figure 9, are significantly negative over the entire range and are, at the same time, decidedly more negative than in the case of [emim][SCN]. At 303.15 K, which indicated in Figure 10, the excess enthalpy increases slightly; however, it retains the same characteristic behavior.

The excess enthalpy results indicate that the mixing process of ammonia and ionic liquids should, in principle, be exothermic over all or part of the concentration range. In addition, it should be noted that the excess enthalpy exhibits different temperature dependence for different mixtures. For [emim][SCN], the excess enthalpy decreases markedly with increasing temperature, whereas for mixtures based on [emim][EtSO₄], it increases only slightly with increasing temperature. Considering that mixing of the components in an absorption heat pump takes place in the absorber, it may be assumed that, when high heating-water temperatures are considered, the excess enthalpy will be negative for every composition and system.

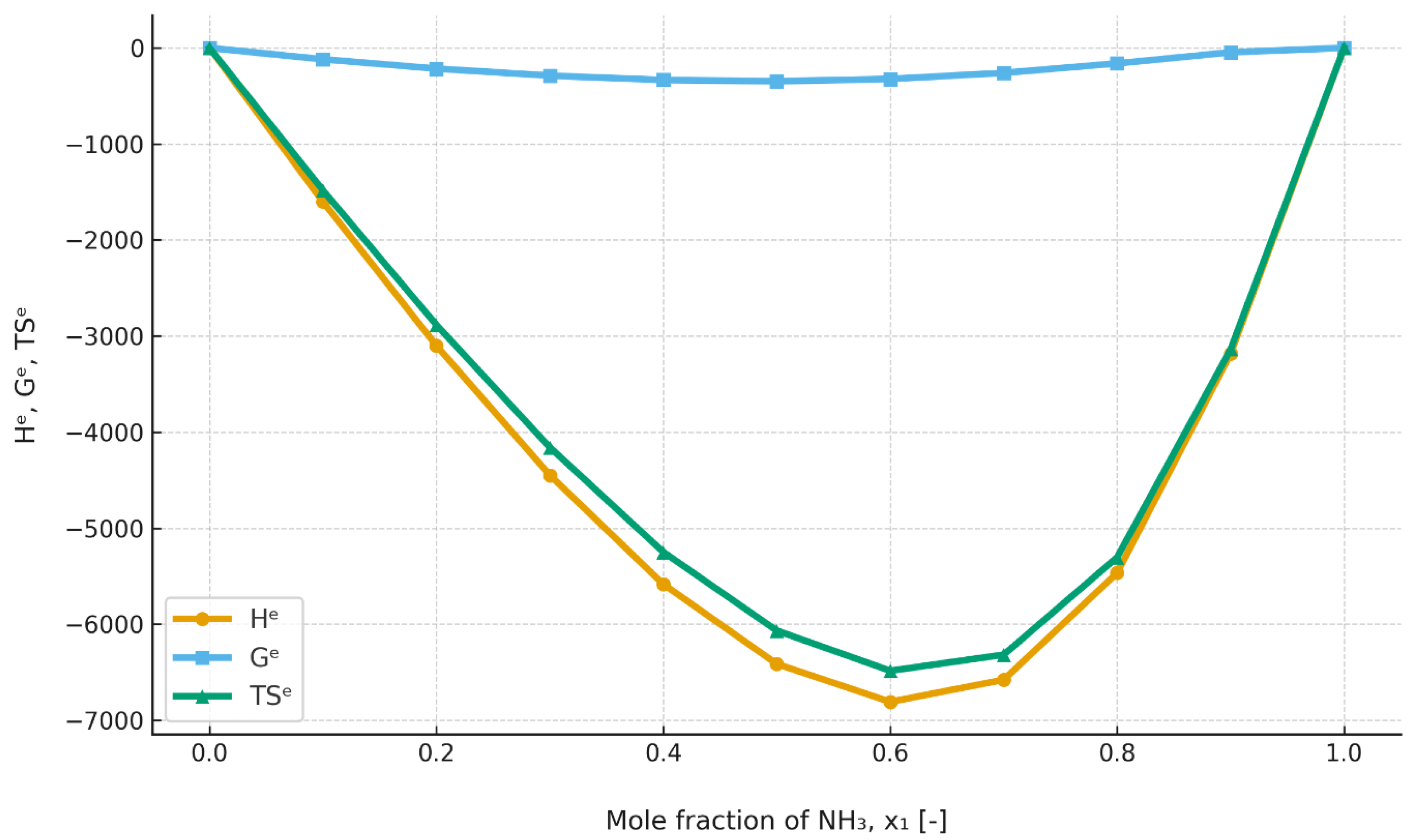
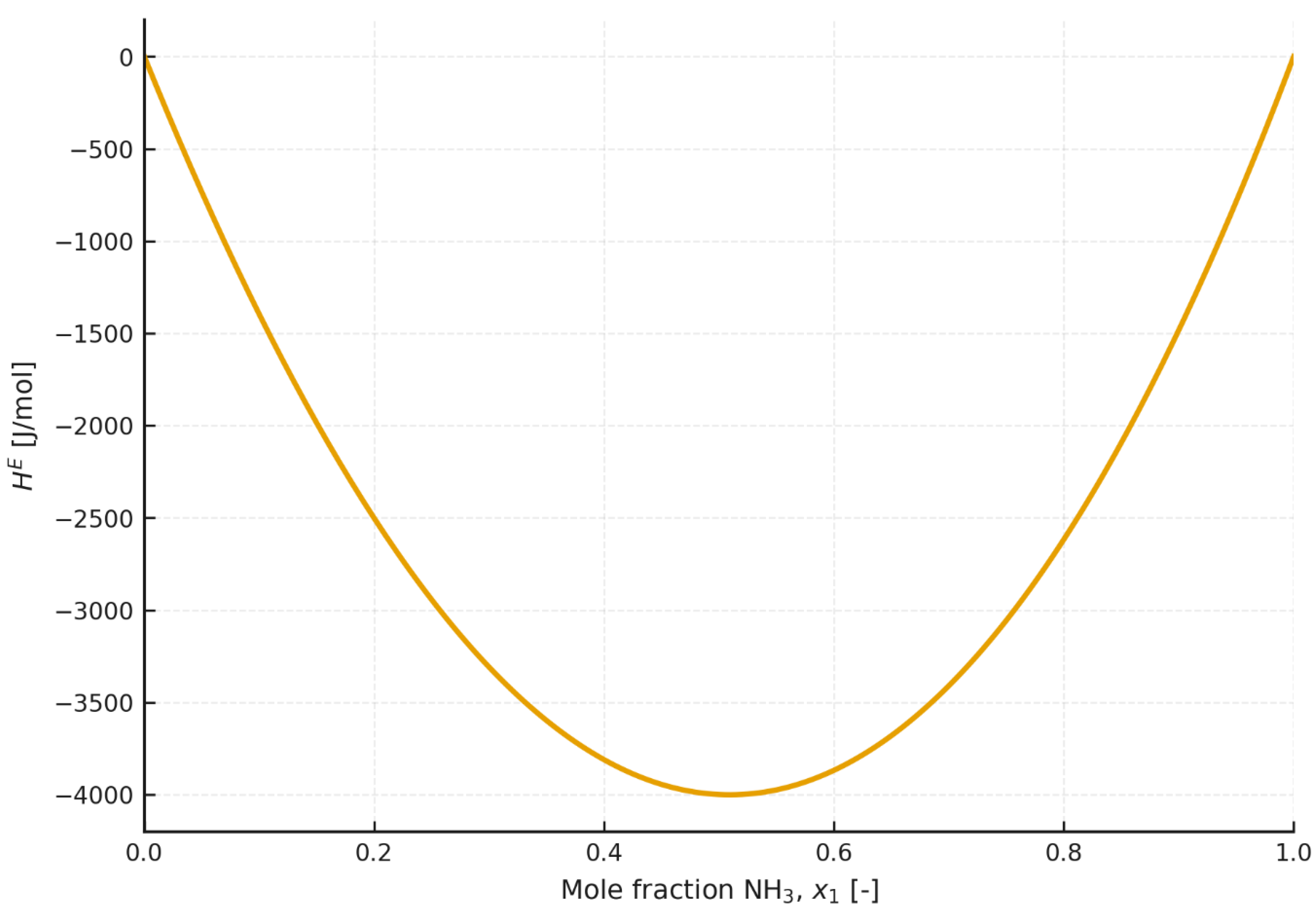
Figure 11 and Figure 12 have been added for comparison, providing data on the excess enthalpies of the ammonia/water mixture.

5. Discussion

5.1. General

The Results section demonstrates several relationships that are pertinent to the design of high-temperature absorption heat pumps. In order to achieve heating-water temperatures in excess of 100 °C, it is necessary for the thermodynamic parameters of the working pair to be capable of supporting operation at such elevated conditions Consequently, the working pair should ensure low operating pressure in the generator–condenser section, almost pure ammonia vapor exiting the generator, a low specific heat capacity of the rich solution, and exothermic mixing (negative excess enthalpy) over the relevant composition range.

5.2. Sensitivity to IL Composition

In the present study, the cycle was evaluated for representative strong and weak solution compositions within the solubility limits of the NH₃–IL pairs. Nevertheless, the primary conclusions demonstrate only a negligible degree of sensitivity to variations in the ammonia mole fraction. For NH3/[emim][SCN], VLE calculations over x₁ = 0.1–0.9 and 283–403 K show vapor compositions y1 > 0.997 (see Table 11, Figure 5). In addition, the excess enthalpy curves (see Figure 7, Figure 8, Figure 9 and Figure 10) remain in a negative trend within the x₁ ≈ 0.2–0.6 range for both the NH3/[emim][SCN] and NH3/[emim][EtSO4] mixtures. Furthermore, the mixture heat capacities exhibit a continuous and smooth variation in response to composition, remaining lower than those observed for the NH3-H₂O system. Consequently, variations in strong/weak concentrations primarily effect absolute COP and generator power requirements, whilst maintaining the ranking of IL candidates and the qualitative design implications. Consequently, a comprehensive optimization with respect to composition is identified as a future research objective.

5.3. Critical Parameters Values

The VLE of the working-fluid mixture of an absorption heat pump is one of the most important parameters from the standpoint of achieving high heating-water temperatures. By employing ionic liquids, the vapor pressure of the mixture with ammonia can be slightly reduced (reflected in Table 9 and Table 10, Figure 4). It has been determined that at an operative temperature of 120 °C, the vapor pressure of a working fluid containing ammonia and ionic liquid ([emim][SCN]) is 11.2% lower than that of a conventional working fluid containing ammonia and water.

More important, however, is the fact that, owing to the very low vapor pressure of ionic liquids, their content in the vapor present in the absorber is practically zero (reflected in Table 11, Figure 5). As demonstrated in Table 11, it is evident that the molar fraction of the absorbate in the vapor, denoted as y₁, exhibits a consistent range, irrespective of the molar content of ammonia in the working fluid, Ammonia (NH3)/[emim][SCN]. This range extends from y₁ = 0.997074 to y₁ = 1.000000. It is important to note that, in contrast to a conventional mixture comprising ammonia and water, the molar content of the absorbate in the vapor increases with temperature. This is a highly advantageous phenomenon from the perspective of high-temperature absorption heat pumps. To illustrate this, consider the molar content of ammonia at 0.4 at a temperature of 130 °C. It can be concluded that the molar content of ammonia in the vapor above the working fluid, ammonia/[emim][SCN], is 4.27 percentage points lower than in a mixture based on ammonia and water. This fact also has a significant impact on the energy performance of the system and reduces its costs owing to the possibility of dispensing with the rectification process.

Ionic liquids, compared with water, are also characterized by lower specific heat, which directly affects the amount of heat that must be supplied to the generator to evaporate the liquid. As demonstrated in Table 14, the specific heat at 120 °C for working mixtures based on ionic liquids is lower from 14.12% (for ionic liquid [bmim][PF6]) to 14.70% (for ionic liquid [emim][EtSO₄]), which is lower comparing to the specific heat of conventional systems. In accordance with the following equation, this is beneficial by reducing the required generator duty (Q_GEN). The above follows directly from Equations (10) and (11) and from Equation (31) for the COP of the absorption heat pump:

$$COP = 1 + {\displaystyle \frac{Q_{EVA}}{Q_{GEN}}}$$

(32)

Another parameter that favorably affects the feasibility of employing ionic liquids in mixture with ammonia in high-temperature absorption heat pumps is the excess enthalpy. For certain ionic-liquid mixtures ([emim][EtSO₄]) with ammonia, the excess enthalpy decreases with increasing temperature. It is important to note that the COP of an absorption heat pump is determined by the excess enthalpy difference between the temperature of the absorber and the temperature of the generator. The COP is known to increase in proportion to the exothermicity of the absorber in comparison to that of the generator. The following formula illustrates this relationship:

$${\left[-H^E\right]}_{T_{ABS}} >{ \left[-H^E\right]}_{T_{GEN}} ⟺ || H^E\left(T_{ABS}\right) <{ H}^E\left(T_{GEN}\right)$$

(33)

This relationship is satisfied by the ionic liquid [emim][EtSO₄], which is characterized by higher excess enthalpy at lower temperatures (see Figure 9 and Figure 10).

5.4. Thermodynamic Limits for Ammonia–IL Mixtures

The applicability of ammonia–ionic-liquid (NH₃-IL) working pairs is constrained by several intrinsic thermodynamic limits that delineate the feasible operating window for high-temperature absorption heat pumps.

Generator pressure limit:

• At elevated temperatures, the total pressure of NH₃–IL mixtures is governed by the saturation pressure of ammonia. While ionic liquids (ILs) eliminate rectification, resulting in a vapor that is almost entirely ammonia (NH₃), transferring all the heat from the ammonia condensation process in the condenser to the high-temperature heating-water system requires a pressure of over 72 bar. This results in significant design limitations. This effect cannot be eliminated by ILs.

Excess enthalpy limits

• Negative excess enthalpy (HE) is required in the absorber for effective absorption. However, for some ILs (e.g., [emim][SCN]), the HE becomes more positive or less negative at high NH₃ content or lower temperatures. This imposes a strict thermodynamic limit on feasible compositions.

Heat capacity limit of the rich solution

• As the mixture Cp approaches the intrinsic Cp of the IL, there is a reduction in the required power of the generator. Beyond this point, further concentration changes do not provide thermodynamic benefit.

6. Conclusions

Absorption heat pumps in which the working fluid consists of mixtures of ionic liquids and ammonia constitute a promising technological solution in the energy sector. The present article posits that the parameter values that may allow the utilization of ionic liquids in high-temperature absorption heat pumps while ensuring favorable COP values are as follows.

Vapor–Liquid Equilibrium

• VLE and volatility of NH₃–IL mixtures are of particular significance in this context. The negligible IL vapor pressure and almost pure ammonia vapor leaving the generator allows rectification to be omitted and strongly reduces internal heat loads. The calculations showed that the refrigerant vapor produced in the generator is approximately 5% purer than in the classical ammonia–water system.

Specific heat capacity

• Secondary critical assumption associated with ionic liquids concerns the optimization of their physicochemical parameters, including specific heat/heat capacity (Cp). The use of ionic liquids with a significantly lower specific heat than the other component of the mixture can markedly reduce the amount of heat that must be supplied to evaporate the mixture in the generator [GEN]. Accordingly, one should seek ionic liquids with the lowest possible heat capacity [14].

Excess enthalpy

• Research has demonstrated that the sign and magnitude of the enthalpy excess between ammonia and an ionic liquid are pivotal indicators of cycle efficiency. The process of strong exothermic mixing, characterized by a substantial negative enthalpy excess, has been shown to stabilize the rich solution in the absorber. Concurrently, it has been demonstrated that certain ionic liquids are distinguished by both a negative excess enthalpy value and a decline in excess enthalpy with rising temperature. Consequently, in systems utilizing such liquids, the generator requires a reduced amount of heat per unit of heat produced, thereby directly increasing the COP.

Attention should also be paid to the thermodynamic properties of ionic liquids, such as density and viscosity, which are crucial for their effective application. Parameters such as density can be determined from scientific studies such as Mäki-Arvela, Päivi [26]. Ionic liquids used in absorption systems should exhibit the lowest possible viscosity which could be crucial in the designing and construction process.