Abstract
The issue of solar curtailment and generation limitations, driven by insufficient grid absorption capacity, is becoming increasingly severe, significantly reducing the capacity factor and economic returns of photovoltaic (PV) power plants. The present study proposes a scenario-based simulation framework, developed using PVsyst software (version 7.4), with a view to investigating the impact of collaborative optimisation using different energy storage capacities on PV integration. The construction of an optimisation model is undertaken with the dual objectives of minimising curtailment losses and maximising the capacity factor. Through the implementation of scenario simulations, a coordinated control strategy is devised for divergent storage capacities, incorporating a charging approach during periods of photovoltaic over-generation and a discharging approach during instances of under-generation. Such an approach is coupled with marginal benefit analysis to simulate system performance under a range of technical conditions. The findings of the present study demonstrate that the implementation of storage coordination optimisation has the potential to result in a substantial reduction in curtailment losses and enhancement of the capacity factor. As energy storage capacity increases from 0 MWh to 10 MWh, curtailment losses decrease by approximately 52%, and capacity factors improve by about 11%. However, as storage capacity increases, the marginal benefits decrease. When storage capacity reaches 9 MWh, and the marginal rate of return exhibits a distinct critical point with increasing storage capacity per unit. The most critical parameter influencing the MRR (Marginal Rate of Return) is the Power Curtailment, which is the primary source of losses, and increasing the Power curtailment can immediately liberate substantial amounts of high-value, otherwise-curtailed solar energy.
1. Introduction
The global energy landscape is undergoing a rapid transition towards decarbonisation, with solar photovoltaic (PV) power emerging as a pivotal renewable energy technology, as evidenced by the continuously rapid growth in installed capacity [1]. However, in regions with high photovoltaic (PV) penetration, the inherent intermittency, volatility, and forecasting uncertainties of solar power create a fundamental mismatch with grid flexibility as deployment scales up. This phenomenon is especially pronounced in regions where the capacity to reduce peak demand and the transmission capabilities are inadequate to manage the variable nature of PV generation. In response to this issue, a significant number of system operators have implemented limitations on the grid injection power of photovoltaic (PV) systems, resulting in substantial solar curtailment. This phenomenon results in substantial energy wastage and economic losses, thereby hindering the sustainable development of the PV industry [2,3,4,5].
In order to address the issue of solar curtailment, the deployment of energy storage systems is recognised as a viable technical solution. A substantial body of research is currently focused on the utilisation of energy storage for the purpose of facilitating spatiotemporal energy transfer. This is intended to enhance the grid’s capacity to accommodate photovoltaic (PV) generation.
Some researchers have pursued performance improvements through optimizing multi-energy and storage coordination. Liu et al. [6] developed a term coordinated scheduling model for the wind-solar-hydro hybrid pumped storage (WSHPS) system with peak shaving operation. The results showed that compared with the wind-solar-hydro hybrid (WSH) system, the total power generation of the WSHPS system in the dry, normal, and wet year increased by 10.69%, 11.40%, and 11.27%, respectively. The solar curtailment decreased by 68.97%, 61.61%, and 48.43%, respectively. Du et al. [7] developed proposed methodology for the purpose of enhancing the efficiency of a photovoltaic-battery-hydrogen coupled system (PBHS), with particular consideration given to the temporal variation in electricity tariffs. A non-dominated sorting genetic algorithm based on elite strategy (NSGA-II) was introduced as an effective tool for solving mathematical models, the proposed plan achieved a significant reduction of 7.7% in annual investment costs and a 15.16% reduction in annual carbon emissions. Bazdar et al. [8] investigated the synergistic co-optimisation of economy and resilience for distributed hybrid energy systems (HES) that integrate limited renewable energy sources with hybrid energy storage. The focus was specifically on the combination of adiabatic compressed air energy storage (A-CAES) and batteries. The proposal of a two-stage sizing-dispatch model was intended to facilitate the determination of the optimal configuration. The findings indicated that by optimizing sizing and integrating storage, a substantial annual enhancement in resilience, amounting to approximately 41.1%, can be accomplished. Jiang et al. [9] proposed a wind farm energy storage capacity optimisation model with the objective of maximising wind energy utilisation while reducing storage infrastructure costs. Particle swarm optimisation results demonstrated that this model can smooth wind energy output at lower cost and with greater utilisation efficiency.
Others have advanced system sizing and configuration methodologies. Ibrahim et al. [10] presented a modified sizing algorithm based on the Golden Section Search method and the objective was to enhance the efficiency of the energy storage unit by optimizing the number of batteries. Ruan et al. [11] proposed an optimal configuration model for hybrid energy storage systems in scenarios with high renewable energy penetration. The model considered multiple constraints, including power flow, unit commitment, and storage operation. Based on these constraints, it determined the optimal configuration of storage systems. Makhubele et al. [12] proposed a hybrid energy system. The system included rooftop PV installations, lithium-ion storage, and connection to the national grid. A techno-economic analysis was conducted over a 25-year project lifespan to evaluate energy cost, payback period, net present cost, and carbon dioxide emissions. The results showed that the levelized cost of energy (LCOE) was USD 0.0071/kWh. Liu et al. [13] proposed a novel energy management strategy that accounts for battery cycle ageing, grid mitigation, and local time-of-use pricing. Single-criterion optimisation has been demonstrated to exhibit superior performance in comparison to existing scenarios for the target building across a range of metrics, including energy supply, battery storage, grid, and system-wide considerations. Multi-criterion optimisation considering all performance indicators reveals that photovoltaic self-consumption and efficiency can be enhanced by 15.0% and 48.6%, respectively. Sleptchenko et al. [14] presented a generalized optimization model for cost minimization in combined energy production and storage facilities. The model can incorporate any combination of dynamic supply, storage, and energy-intensive product demand.
Furthermore, several contributions focused on grid integration. Chen et al. [15] proposed a distributed energy storage (DES) optimization allocation strategy based on transmission betweenness and source-network-load synergy in active distribution networks. And an optimal siting calculation method for energy storage based on the node transmission betweenness was proposed. The results showed that the system’s renewable energy consumption rate reached 98.29%. Additionally, Li et al. [16] proposed an optimization strategy for energy storage, and aimed to improve system performance within current group control system. A bilevel coordinated planning model for distributed energy storage (DESS)was developed. The result showed that the proposed strategy significantly enhanced the network’s ability to absorb photovoltaic energy. Li et al. [17] investigated the coordination and optimisation of multi-site distributed battery energy storage systems participating in grid demand response. Furthermore, it proposed a strategic analysis framework for multi-site distributed battery energy storage systems engaging in demand response.
However, extant research predominantly employs conditional optimisation analysis, aiming to identify a single optimal solution for a specific set of conditions. While this approach is indeed effective, it fails to reveal the dynamic evolution of economic benefits during the expansion of energy storage capacity. In the event of external parameter alteration, solutions founded upon obsolescent conditions may become invalid. The present study employs a marginal analysis framework to address these limitations. The examination of the evolution of marginal benefits (MCF, MCL, MRR) provides a comprehensive economic analysis of capacity allocation. This approach identifies critical points of benefit maximisation and provides a dynamic basis for risk assessment.
The article’s organisation is as follows: Section 1 (introduction) outlines the current research progress, limitations, knowledge gaps, objectives, and rationale; Section 2 discusses systems modelling and research methods; Section 3 presents the results and analysis; Section 4 discusses the major findings and future work; and Section 5 summarises the key findings of the study.
2. Systems Modelling and Research Methods
2.1. Case Overview
This study selected the city of Golmud in China’s Qinghai Province as the simulation site. Situated in the heart of the Qinghai-Tibetan Plateau, it has an average elevation of 2780 m and an annual total solar radiation of 7000–8000 MJ/m2, as shown in Table 1. The city is classified as a Category I solar energy region, characterised by abundant solar resources [18].

Table 1.
Solar energy resource zones in China.
2.2. System Model
In the PVsyst software, a 10 MW solar PV installation capacity was set, with power curtailment limits (PVlimit) configured sequentially at 6 MW, 7 MW and 8 MW, in order to simulate scenarios involving power constraints during periods of peak PV output.
Building upon the aforementioned PV plant model, an energy storage system was introduced. To analyse the impact of varying storage capacities on system performance, this study designed continuous capacity scenarios ranging from 2 MWh to 10 MWh. The specific configuration schemes are detailed in Table 2.

Table 2.
Energy storage configuration plan.
2.3. Cooperative Optimisation Control Strategy
To maximize the absorption of curtailed power losses and ensure the normal operation of energy storage batteries, this system uses the charge-discharge control strategy shown in Figure 1. The core objective is to stabilize the grid-connected power output of the power station near the curtailment threshold by implementing an operational strategy of ‘shaving peaks and filling troughs’.
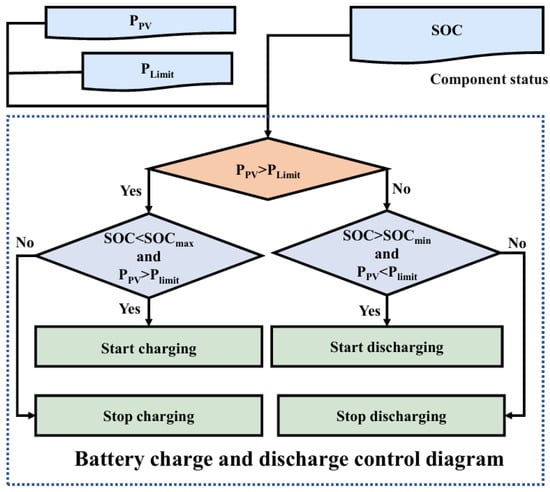
Figure 1.
Charge and discharge control strategy for energy storage batteries.
2.3.1. Charging Phase
The system monitors the output power of the photovoltaic array (PPV) continuously when PPV exceeds PVlimit and the battery’s state of charge (SOC) has not reached its maximum charge capacity (SOCmax), the portion of the photovoltaic array’s output power that exceeds the power curtailment limit () is used for charging batteries in energy storage systems, and the process has the expression as shown in Equation (1).
2.3.2. Discharge Phase
When PPV is less than PVlimit, and the battery’s state of charge (SOC) exceeds the preset minimum safety threshold (SOCmin), the energy storage system battery begins discharging, with the discharge power () objective being to compensate for the difference between the PV output and the curtailment power, and the process expression is shown in Equation (2) and Figure 1.
2.4. Performance Evaluation Metrics
A quantitative analysis is conducted based on the following key performance indicators to evaluate the synergistic optimisation effect of energy storage systems on grid-connected photovoltaic power plants under power curtailment.
2.4.1. Capacity Factor
Capacity Factor (CF) is a key metric used to evaluate the operational efficiency of power plants. It is characterised by the ratio of the actual annual grid-connected electricity generation (Eactual) to the theoretical maximum annual generation (Etheo)which is expressed by Equations (3) and (4).
where Prate is Photovoltaic Array Power, the unit is W.
2.4.2. Curtailment Loss
Curtailment Loss (CL) is a physical quantity used to measure the energy lost due to curtailment during photovoltaic grid connection. The unit is kWh, as shown in Equation (5).
where is annual photovoltaic array electricity output, the unit is KWh.
2.4.3. Curtailment Loss Rate
Curtailment Loss Rate (CLR) is a physical quantity that reflects the degree to which curtailment issues have been mitigated, as expressed in Equation (6).
2.5. Definition of Marginal Metrics
This paper employs marginal analysis, an economic decision-making method centred on examining how marginal benefits (the additional gain from a unit change in a decision variable) and marginal costs (the additional cost incurred by such a change) evolve. The subsequent section defines several key marginal parameters that are most pertinent to the system in question.
2.5.1. Marginal Capacity Factor
Marginal Capacity Factor (MCF) denotes the marginal increase in the system’s capacity factor for each unit of additional energy storage capacity added. This represents the marginal optimisation capability of expanding energy storage in terms of the utilisation rate of photovoltaic equipment, as described in Equation (7).
In the formula, is the system capacity factor corresponding to an energy storage capacity of n. is the system capacity factor corresponding to an energy storage capacity of n + 1. represents the unit increase in energy storage capacity, measured in MWh.
2.5.2. Marginal Curtailment Loss
Marginal Curtailment Loss (MCL) denotes the reduction in curtailment losses for each additional unit of energy storage capacity, representing the marginal absorption capacity of expanded energy storage for curtailed solar power generation, as described in Equation (8).
In the formula, represents the system curtailment loss corresponding to an energy storage capacity of n, represents the system curtailment loss corresponding to an energy storage capacity of n + 1, measured in kWh.
2.5.3. Marginal Rate of Return
This section assumes fixed electricity prices and maintenance costs.
Marginal Rate of Return (MRR) represents the ratio of the annualized incremental revenue per unit of additional energy storage capacity to the corresponding incremental investment, as described in Equation (9).
In Equation (9), represents the incremental revenue, measured in yuan per year. represents incremental investment, measured in yuan. m is the number of years the unit has been in continuous operation.
Among these, is primarily influenced by changes in grid-connected electricity output resulting from variations in configured energy storage capacity and can be calculated using Equation (10).
In the formula, represents the grid-connected electricity generated by increasing the unit energy storage capacity, measured in kWh. w denotes the unit electricity price, expressed in yuan per kWh. primarily includes the increased cost of energy storage equipment (), installation and operation/maintenance costs (), and land infrastructure allocation (), calculated through Equation (11).
3. Results and Analysis
3.1. Analysis of Baseline Scenario Results
Power Curtailment Scenarios for Non-Energy Storage Power Plants Only
Figure 2 shows the relationship between daily solar irradiance per square metre and power generation. As shown in Figure 2a, the graph shows that the two variables generally correlate linearly. In Figure 2b, the output power of the photovoltaic array and the actual electricity generation follow the same monthly variation trend. Below is a correlation analysis of the output power of the photovoltaic array and the actual grid-connected power. The linear correlation between the two variables is measured using the Pearson correlation coefficient (rxy).
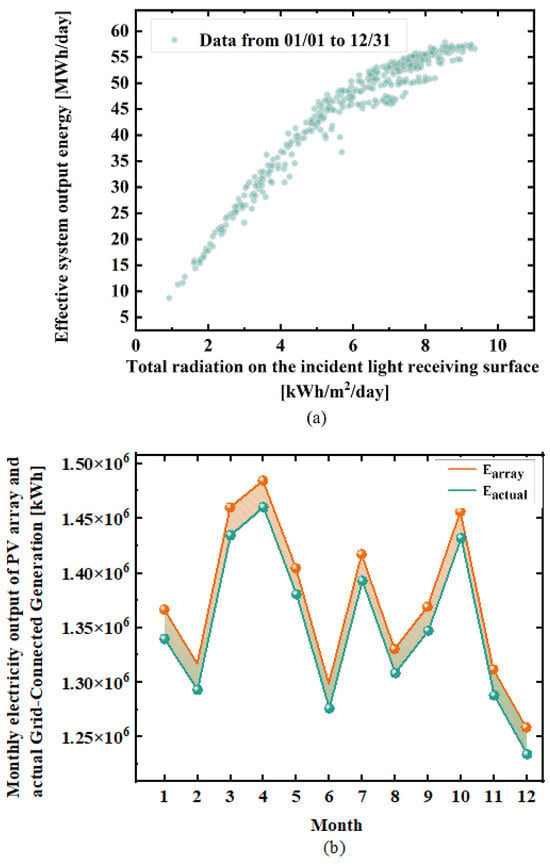
Figure 2.
(a) Daily input/output energy chart for the system; (b) Output power of the photovoltaic array and actual electricity generation.
This paper denotes the monthly photovoltaic array output as Exi and the monthly grid-connected electricity as Eyi, as described in Equation (12).
In the formula, represents the average monthly output of the photovoltaic array, represents the average grid-connected electricity generation across all months, where n = 12.
As shown in Table 3, the Pearson correlation coefficient is 0.999827 under the scenario of power plants with no energy storage and limited electricity generation only. This indicates an extremely strong positive correlation between the photovoltaic array’s electricity output and electricity generation, proving that there is no significant distortion in the data throughout the entire process, from power generation to grid connection. This validates the rationality of the established system. Additionally, under these operating conditions, the three-performance metrics are as follows: CF is 0.184814372, CL is 3,388,529, and CLR is 0.173090349.

Table 3.
Results of three performance metrics.
3.2. Annual Electricity Generation Analysis
In order to compare the impact of energy storage battery capacity on curtailment issues directly, this section selects S2 as the small-capacity battery, S5 as the medium-capacity battery and S10 as the large-capacity battery. The energy storage batteries are configured on small, medium and large scales in order to compare the system’s monthly electricity output.
As shown in Figure 3, where 0 MWh represents the monthly output of electricity of the system without energy storage participation, the monthly electricity output shows a significant increase as the energy storage capacity increases from 0 MWh to 2 MWh. Furthermore, the annual total generation demonstrates a consistent upward trend as the energy storage capacity is incrementally raised from the base level to 5 MWh and further to 10 MWh.
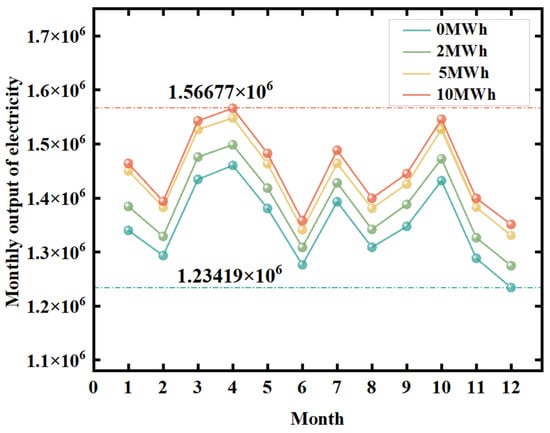
Figure 3.
Actual monthly output of electricity with different energy storage capacities.
Photovoltaic power stations equipped with energy storage systems can store excess solar power that was previously curtailed in energy storage batteries. As storage capacity increases, the absorption rate of the system improves further. The energy stored in these systems can be released during periods of low irradiation, effectively generating power. In essence, the storage system shifts curtailed midday power to the evening when solar output is low, thereby overcoming grid curtailment constraints.
3.3. CF, CL, CLR Analysis
Energy storage capacity is a key parameter that influences CF, CL and CLR. As illustrated in Figure 4a, the energy storage configuration increases from 0 MWh to 10 MWh, the system capacity factor rises steadily from 0.1848 to 0.2050. A small energy storage capacity in the system can restrict the number of charge-discharge cycles that the storage units can perform, resulting in a low capacity factor. However, when capacity increases, the storage units can respond more flexibly to grid demands, extending the regulation duration and enabling them to cover morning and evening load peaks and troughs. This confirms the value of flexible regulation of storage units for photovoltaic power plants, further improving the utilisation rate of photovoltaic equipment over time.
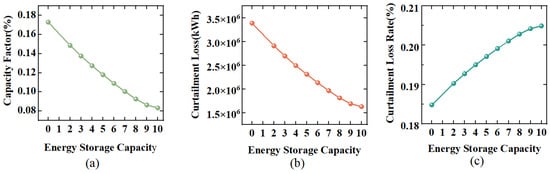
Figure 4.
Variation of Different Parameters with Energy Storage Capacity (a) CF; (b) CL; (c) CLR.
Figure 4b demonstrates the impact of energy storage on curtailed solar power. When the storage capacity is 0 MWh, the annual curtailed power is 3,388,529 kWh. Increasing the storage capacity to 2 MWh reduces the annual curtailed power output sharply to 2,910,126 kWh, and scaling it up to 10 MWh lowers it further to 1,628,894 kWh. This demonstrates that energy storage can directly absorb excess power from curtailed PV generation. This enables the system to transition from ‘immediate PV absorption’ to a more flexible operational mode, which significantly enhances the flexibility of the power generation system.
Figure 4c shows that as the energy storage capacity increases from 0 MWh to 10 MWh, the curtailment loss rate decreases from 0.1731 to 0.0832, which corresponds to the direct absorption effect of energy storage on curtailed electricity shown in Figure 4b. This indicates that deploying energy storage systems to accommodate more renewable energy directly reduces the output share of conventional power units. As their output decreases, the ‘relative proportion’ of curtailment also declines.
Together, these three factors demonstrate how energy storage capacity improves the regulatory capabilities of photovoltaic power generation systems in the event of curtailment. Improving storage utilisation efficiency directly reduces curtailed electricity and indirectly optimises the entire power generation system, making it a key driver for increasing PV integration.
3.4. Marginal Benefit Analysis
As demonstrated in Figure 5a,b, both MCF and MCL demonstrate a downward trend with each unit increase in energy storage capacity. It is evident that when the storage capacity is increased from 8 MWh to 9 MWh, there is a marked decline in both MCF and MCL. This finding suggests that the enhancement in system capacity factor, attributable to each unit of additional storage capacity, exhibits a progressive decline. The amount of curtailed solar power that can be captured and utilised per unit of new capacity diminishes progressively, exhibiting diminishing marginal returns. This suggests that as energy storage capacity continues to expand, the performance gains per unit of new capacity and the reduction in curtailed solar generation may be associated with saturated equipment utilisation and system regulation capabilities, as well as the fragmented absorption of curtailed solar power by newly added storage capacity.

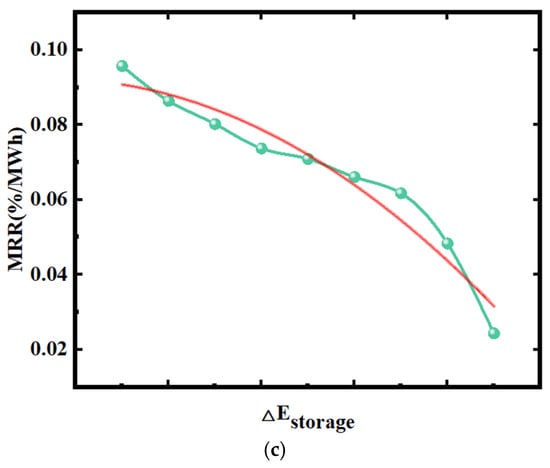
Figure 5.
The broken lines and fitted lines of marginal benefit (a) Relationship between unit energy storage capacity increment and MCF decay; (b) Relationship between unit energy storage capacity increment and MCL decay; (c) Relationship between unit energy storage capacity increment and MRR decay.
As shown in Figure 5c, the MRR demonstrates a declining trend with each unit increase in energy storage capacity. Especially, when storage capacity increases from 8 MWh to 9 MWh, the MRR experiences a precipitous decline. It is evident that an augmentation in capacity, in excess of 9 MWh, results in the MRR approaching zero. This indicates a critical point for the MRR with respect to unit energy storage capacity increases.
This critical point indicates an economic capacity ceiling for energy storage expansion. Beyond this threshold, the revenue mechanism becomes ineffective, and the sharp decline in MRR may stem from an imbalance between incremental revenue and incremental investment costs. The declining returns of MCF and MCL indicate that the available capacity has almost reached its limit in terms of absorbing reduced solar power, resulting in negligible additional benefits and the unit cost of energy storage continues to present a challenge in terms of reduction in the short term, consequently giving rise to persistently high incremental investment costs. The preceding analysis demonstrates that the MRR threshold delineates the economic boundary for energy storage capacity planning. Beyond this threshold, the economic viability is significantly diminished.
3.5. Sensitivity Analysis
To assess the impact of key parameter uncertainties on the economic viability of energy storage systems, this section conducts single-factor sensitivity analyses for five core parameters. The basic settings for these five parameters are shown in Table 4. Power Curtailment (PC) is the grid-connected power limitation during photovoltaic power generation grid connection. Unit Energy Storage Cost (UESC) refers to the incremental investment cost resulting from increased unit energy storage capacity. Curtailment Reduction (CR) is a key performance indicator used to quantify how energy storage systems enhance the grid integration capacity of PV power. It specifically refers to the reduction in annual curtailment loss between two scenarios with different energy storage configurations. Unit Electricity Price (UEP) is the price of electricity per kWh, and Inverter Efficiency (IE) is the ratio of input DC power converted to AC power by the inverter. These five parameters were selected as sensitivity factors. Each parameter varied by 20% from its baseline value to study the corresponding changes in Marginal Return Rate (MRR). This analysis aims to identify key drivers affecting the economic viability of energy storage investments and provide direction for system optimization.

Table 4.
Parameters for sensitivity analysis: baseline values and ranges.
As shown in Figure 6, varying different parameters have different effects on MRR. The impact of PC on MRR is found to be significant, while the effect of IE on MRR is found to be negligible. Conversely, UESC, CL, and UEP have been shown to exert considerable influence on MRR.
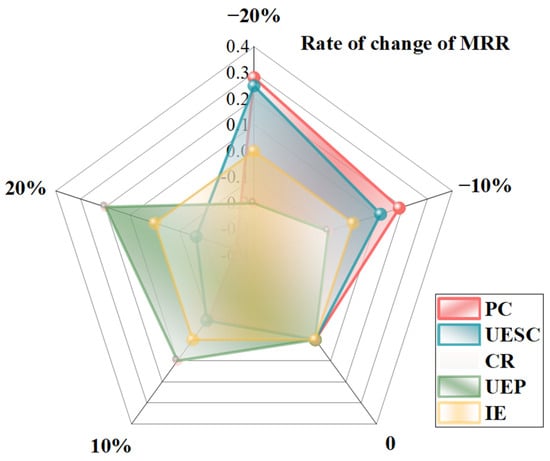
Figure 6.
Sensitivity analysis results.
It is evident that among these, PC has the most extensive coverage area, thereby signifying that its fluctuations exert the most substantial impact on MRR. The theoretical upper limit of system revenue is defined by PC. In regions where photovoltaic (PV) penetration is high, curtailment is identified as the primary source of losses. When the PC threshold is relaxed from 6 MW to 6.5 MW, a significant amount of high-value curtailed energy is immediately released. This energy can be converted into revenue at a negligible marginal cost, thereby significantly boosting MRR. Conversely, the imposition of further PC restrictions would precipitate a precipitous decline in MRR. The CR and UEP models demonstrate considerable overlap, exhibiting consistent impacts on MRR. For UESC and UEP, both factors directly determine project economic viability. It is evident that an increase in electricity prices will result in a linear rise in the value of all generated electricity. Furthermore, it has been demonstrated that this will enhance incremental revenue from curtailment mitigation via energy storage. It is evident that since storage investment constitutes the most substantial incremental cost of the system, fluctuations in its cost directly impact the rate of return, thereby exerting a considerable influence on MRR. With regard to IE, its comparatively negligible impact on MRR change may be attributed to the restricted revenue variation it engenders. In comparison with substantial incremental investments, such as energy storage, its marginal contribution ratio remains negligible.
Based on the above analysis, it is imperative to prioritise the enhancement of PC through technological or policy measures. Subsequent to this, there is a necessity to pursue higher UEP and to select energy storage systems that are more cost-effective.
4. Discussion and Future Work
4.1. Limitations
Although this study effectively revealed the marginal benefit patterns of capacity configuration for photovoltaic-storage systems using the PVsyst simulation framework, certain limitations must be acknowledged. Firstly, the meteorological databases integrated into the PVsyst software (such as Meteonorm) have inherent time lags and may therefore fail to reflect the latest local climate change trends accurately. This may affect the accuracy of long-term performance predictions. Secondly, as PVsyst is a system-level simulation tool focused on energy balance, it employs simplified models for components such as batteries, which fail to precisely simulate their internal dynamic characteristics.
4.2. Policy and Practical Implications
Research findings indicate that moderately relaxing power curtailment thresholds is a more cost-effective way of enhancing PV integration capacity than solely deploying large-capacity energy storage systems. Grid companies are therefore recommended to prioritise enhancing regional grid flexibility and transmission capacity.
4.3. Adaptability to Larger and Hybrid Energy Systems
This study employs an optimisation framework based on marginal benefits, extending beyond the specific case of individual photovoltaic-storage power stations. The core principles of the system demonstrate high adaptability and can be effectively scaled to larger and hybrid energy systems for the purpose of evaluating the value of energy storage.
4.3.1. Applied to a Larger Grid
When the system is expanded to encompass regional or national grids, the system boundary is extended from single-point interactions to the entire grid. Consequently, key parameters require corresponding adjustments.
Power curtailment limits will no longer represent constraints at individual substations, but will instead reflect transmission capacity bottlenecks along critical corridors or the grid’s overall capacity to accommodate variable renewable energy sources.
The Curtailment Loss would be quantified as the total wasted renewable energy across the entire grid region, often referred to as system-wide curtailment.
At this scale, the framework’s ability to identify the marginal value of storage becomes crucial for grid planning. It can answer questions such as whether it is more cost-effective to invest in a large-scale, centralized storage facility to relieve a transmission constraint or to deploy distributed storage at multiple grid congestion points.
4.3.2. Applied to Hybrid Energy Systems
The framework can be extended to model hybrid systems comprising wind, solar, batteries, and even hydrogen storage.
When adapting to hybrid systems, new component models, such as wind power output data and hydrogen storage, must be incorporated. The objective shifts from minimising curtailed generation to either minimising the system-wide cost or maximising renewable energy utilisation.
4.4. Future Work
Despite the utilisation of multi-scenario simulations and sensitivity analyses in this paper, which serve to mitigate certain uncertainties, it should be noted that the meteorological data within PVsyst is not updated in real time. Future research utilise higher-precision measured data in order to enhance the model’s accuracy and generalisation capability.
The present study principally focuses on technical and economic considerations; future work may incorporate environmental benefits to achieve multi-objective optimisation.
The transition from deterministic to probabilistic analysis is a significant development in the field. For instance, employing Monte Carlo simulations and defining key parameters as probability distributions is able to generate a range of potential outcomes for metrics such as net present value. This would directly quantify investment risk.
5. Conclusions
To address the severe curtailment challenges faced by high-penetration photovoltaic power plants, this study proposes a solution based on synergistic optimisation and energy storage. The present study employs systematic simulation and model analysis to validate the effectiveness of the proposed approach. The analysis focuses on the impact of three parameters—the capacity factor, curtailment losses, and curtailment loss rate—as storage capacity varies. Furthermore, it elucidates patterns of economic benefit as storage scale changes, thus providing clear guidance for optimising core parameter configurations. The study’s main conclusions are as follows.
- Energy storage enables PV stations to alleviate grid constraints by storing and shifting curtailed power over time. Larger storage capacities allow for more effective utilisation.
- Energy storage capacity is a key parameter influencing the system. As the energy storage configuration increases from 0 MWh to 10 MWh, the system capacity factor undergoes an improvement of 10.9%. Energy storage capacity is a key parameter, with an increase from 0 MWh to 10 MWh resulting in a 10.9% improvement in the system capacity factor, a 51.9% direct reduction in annual curtailed energy, and a decrease in the curtailment rate from 0.1731 to 0.0832.
- As storage capacity increases, the pattern of diminishing marginal returns becomes apparent. The amount of curtailed energy captured per additional unit declines, reducing the system’s performance increment.
- When energy storage capacity reaches 9 MWh, the MRR displays a distinct critical threshold for increases in energy storage capacity per unit. This threshold indicates an economic upper limit for storage capacity expansion, beyond which the revenue mechanism becomes almost ineffective. The MRR threshold delineates the economic boundary for energy storage capacity planning.
- Reducing Power Curtailment (PC) through technical or policy measures is important for improving project economics, as it is the element that most strongly influences marginal income.
Author Contributions
Conceptualization, Y.J. and F.A.; Methodology, Y.Y.; Software, Y.Y.; Formal analysis, Y.Y.; Data curation, Y.Y.; Writing—original draft, Y.Y.; Writing—review & editing, Y.J.; Visualization, Y.J.; Supervision, Y.J.; Project administration, Y.J. and F.A.; Funding acquisition, F.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research is conducted under the initiative of Jilin Province Science and Technology Development Plan Project (Research on Coordinated Operation Methods for “Vehicle-Grid-Storage” Dispatch and Control in Power Systems with High Penetration of Renewable Energy).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| PVlimit | Power Curtailment Limits (MW) |
| PPV | Output Power of Photovoltaic Array (kW) |
| SOC | Battery’s State of Charge |
| CF | Capacity Factor |
| rxy | Pearson correlation coefficient |
| CR | Curtailment Reduction (kWh/year) |
| UEP | Unit Electricity Price (CNY/kWh) |
| UESC | Unit Energy Storage Cost (CNY/kWh) |
| CL | Curtailment Loss (kWh) |
| CLR | Curtailment Loss Rate |
| MCF | Marginal Capacity Factor |
| MCL | Marginal Curtailment Loss |
| MRR | Marginal Rate of Return |
| PC | Power Curtailment (MW) |
| IE | Inverter Efficiency |
References
- Jäger-Waldau, A. Snapshot of photovoltaics-February 2024. EPJ Photovolt. 2024, 15, 9. [Google Scholar] [CrossRef]
- Zhao, H.L.; Cui, C.; Zhang, Z.B. Assessing the dynamics of power curtailment in China: Market insights from wind, solar, and nuclear energy integration. Int. J. Hydrogen Energy 2025, 118, 209–216. [Google Scholar] [CrossRef]
- van Eldik, R.; van Sark, W. Firm wind and solar photovoltaic power with proactive curtailment: A European analysis. Energy Conv. Manag. 2026, 347, 25. [Google Scholar] [CrossRef]
- Micheli, L.; Soria-Moya, A.; Talavera, D.L.; Abbasi, B.; Fernández, E.F. Energy and economic implications of photovoltaic curtailment: Current status and future scenarios. Sustain. Energy Technol. Assess. 2025, 81, 10. [Google Scholar] [CrossRef]
- Newbery, D.M.; Biggar, D.R. Marginal curtailment of wind and solar PV: Transmission constraints, pricing and access regimes for efficient investment. Energy Policy 2024, 191, 8. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Zhang, H.; Guo, P.C.; Li, C.X.; Wu, S. Optimal Scheduling of a Cascade Hydropower Energy Storage System for Solar and Wind Energy Accommodation. Energies 2024, 17, 2734. [Google Scholar] [CrossRef]
- Du, Q.; Guo, W.H.; Mo, S.Q.; Wang, Y.A.; Qin, T.F.; Zhu, B.X.; Zheng, H.B. Feasibility study on rooftop photovoltaic hydrogen production: Multi-objective optimization and energy scheduling strategy considering time-of-use pricing. Renew. Energy 2025, 245, 10. [Google Scholar] [CrossRef]
- Bazdar, E.; Nasiri, F.; Haghighat, F. Resilience-centered optimal sizing and scheduling of a building-integrated PV-based energy system with hybrid adiabatic-compressed air energy storage and battery systems. Energy 2024, 308, 25. [Google Scholar] [CrossRef]
- Jiang, Z.; Feng, J.X.; Sun, Y.D.; Sun, B.H.; Wu, N.H. Wind Farm Energy Storage Capacity Optimization Based on PSO. In Proceedings of the 9th International Conference on Natural Computation (ICNC), Shenyang, China, 23–25 July 2013; pp. 590–594. [Google Scholar]
- Ibrahim, T.; Kerekes, T.; Sera, D.; Lashab, A.; Stroe, D.I. Lithium-Ion Supercapacitors and Batteries for Off-Grid PV Applications: Lifetime and Sizing. Batteries 2024, 10, 42. [Google Scholar] [CrossRef]
- Ruan, P.; Su, Q.L.; Zhang, L.L.; Luo, J.; Diao, Y.P.; Xie, L.; Zheng, H. Optimal Siting and Sizing of Hybrid Energy Storage Systems in High-Penetration Renewable Energy Systems. Energies 2025, 18, 2196. [Google Scholar] [CrossRef]
- Makhubele, W.J.; Thango, B.A.; Ogudo, K.A. Evaluating Rooftop Solar Photovoltaics and Battery Storage for Residential Energy Sustainability in Benoni, South Africa. Processes 2025, 13, 1828. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Yang, H.X.; Li, Y.T. Energy storage and management system design optimization for a photovoltaic integrated low-energy building. Energy 2020, 190, 20. [Google Scholar] [CrossRef]
- Sleptchenko, A.; Sgouridis, S. Joint Optimization of Energy Production & Storage. In Proceedings of the 6th IEEE International Conference on Industrial Engineering and Applications (ICIEA), Tokyo, Japan, 12–15 April 2019; pp. 913–917. [Google Scholar]
- Chen, W.; Hao, P.H.; Wei, Z.H.; Chen, L.K. Study on the optimization allocation method of distributed energy storage in an active distribution network taking into account transmission betweenness and source-network-load synergy. Electr. Power Syst. Res. 2025, 247, 13. [Google Scholar] [CrossRef]
- Li, J.L.; Zhao, Y.; Cheng, X.; Yao, Y.C.; Li, C.X.; Jian, X.D.; He, P.W. Energy storage planning strategies for multi-scenario photovoltaic energy storage collaborative cluster control systems. Electr. Eng. 2025, 107, 12999–13013. [Google Scholar] [CrossRef]
- Li, Y.J. Research on Optimal Control Operation of Energy Storage System Considering Demand Response. In Proceedings of the 4th International Conference on Automation Electronics and Electrical Engineering, Shenyang, China, 19–21 November 2021; pp. 105–108. [Google Scholar]
- Si, L.J.; Wang, P.Y.; Cao, D.Q. Towards sustainable development goals: Assessment of wind and solar potential in northwest China. Environ. Res. 2024, 252, 14. [Google Scholar] [CrossRef] [PubMed]
- Gerber, D.L.; Bruce, N.; Richard, B.; Jason, P. Cost analysis of distributed storage in AC and DC microgrids. Appl. Energy 2023, 344, 121218. [Google Scholar] [CrossRef]
- Aksu, İ.Ö.; Ghaemi, S.; Moghaddam, A.A. A two-stage deep learning approach for accurate day-ahead electricity price forecasting. Eng. Appl. Artif. Intell. 2026, 163, 112721. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).