An Integrated Optimization Method for Multiuser Energy Storage Configuration and Leasing in Campus Energy Systems

Abstract

With respect to the current campus energy systems, the research on energy storage deployment has focused mostly on single users or a single metric, making it difficult to accommodate diverse multiuser needs while efficiently utilizing the available resources. This results in narrow evaluation dimensions and underutilized storage assets. To address this issue, an integrated method for multiuser energy storage, optimal sizing and leasing is proposed in this paper; the method is aimed at improving the economics and utilization of storage. First, we construct a campus energy system architecture that includes an energy storage service provider and develop a storage sizing model that minimizes the average daily total cost, yielding the optimal power ratings and capacities for different users. Second, we construct a comprehensive evaluation framework from both economic and technical perspectives and apply quantitative methods to select the best configuration scheme. On this basis, we propose a multicriteria optimization-based storage leasing mechanism that enables resource sharing among users and maximizes the revenue received by the service provider. Simulation results reveal that across five typical user scenarios, the proposed method outperforms the traditional single-configuration models: the overall storage utilization rate increases by 3.84%, the cost-reduction rates for some users exceed 16%, and the investment payback period decreases by approximately one year. Compared with configuration-only approaches, the proposed integrated configuration–leasing framework simultaneously enhances user-side economics and the profitability of the service provider. The integrated sizing and leasing method not only demonstrates solid economic and technical feasibility but is also applicable to multiuser campuses, shared storage cases, and cloud storage scenarios, providing a reference path for future multidimensional value extraction processes and commercial operations.

1. Introduction

The urgency of the global energy transition and climate change mitigation is driving the widespread adoption of distributed renewable energy sources, such as wind and photovoltaic power, within campus and community energy systems [1]. However, the inherent intermittency and variability of renewable energy, coupled with the diversity and dynamic nature of multiuser energy demands, pose significant challenges to the stable operation of power networks and the optimal economic dispatching of resources [2,3].

To ensure reliability and economic efficiency, an effective coordination mechanism between generation, load, and storage is essential. Energy storage systems, with their energy time-shifting and rapid regulation capabilities, have emerged as key technologies for enhancing the energy efficiency and supply reliability levels of integrated energy systems [4]. Nevertheless, the existing research has focused primarily on single-user scenarios or isolated performance metrics and lacks comprehensive configuration and evaluation methods that are tailored to diverse user demands and complex operational environments [5]. Furthermore, the underutilization of storage resources and the extended payback periods for investment constrain the adoption of these approaches within industrial parks [6]. This reveals the need for systematic configuration and evaluation frameworks that can balance both technical performance and economic feasibility under differentiated user requirements.

Consequently, the configuration and evaluation of energy storage systems have emerged as central research topics involving modern energy systems, with their effectiveness highly dependent on scientifically sound strategies and systematic assessment methods [7,8]. Optimal solutions demand a balance between capacity and power levels, ensuring both technical and economic viability and comparability across diverse user scenarios [9,10]. Recent literature has made progress in model development, yet several gaps remain in addressing multi-user coordination and integrated evaluation.

For instance, reference [11] proposed a robust energy storage capacity configuration model for distribution networks that considers renewable energy uncertainties; the aim of this work was to optimize microgrid storage planning, day-ahead scheduling, and renewable energy utilization processes, although the economic performance of the developed system was not comprehensively addressed. Reference [12] developed an optimal user-side energy storage configuration model for microgrids in industrial parks with multiple transformers, maximizing annual profits, reducing electricity and demand charges, and improving the degree of photovoltaic integration by optimizing the capacity and location of the storage system; however, they did not consider diverse user requirements. Reference [13] introduced a demand-aware, multitimescale optimization method for user-side energy storage configuration, targeting the gap in systematic models regarding differing user needs and scenarios to enhance the level of renewable integration in modern power systems; however, a comprehensive evaluation of the optimized configurations is lacking. These studies indicate that while various optimization techniques exist, few frameworks integrate configuration and evaluation for heterogeneous user demands within industrial parks.

The scientific evaluation of energy storage configuration schemes is a key step for ensuring rational investment decisions. Common evaluation methods include the analytical hierarchy process (AHP), fuzzy comprehensive evaluation, data envelopment analysis, and their combined applications [14,15]. Among these methods, the AHP is widely adopted because of its ability to effectively integrate expert judgments with quantitative analyses, demonstrating strong applicability in terms of addressing complex multiobjective decision-making problems. Reference [16] investigated an integrated evaluation technique for configuring energy storage based on the AHP, addressing challenges in user-side energy management and demand response tasks; however, the proposed scaling method lacks adaptability to dynamic multiuser environments. Building upon this, reference [17] introduced a capacity configuration and economic evaluation method for photovoltaic energy storage stations (PESSs) based on game theory and the AHP; their aim was to optimize the overall economic performance of PESSs under trajectory planning scenarios, with the objectives of minimizing curtailed photovoltaic power and maximizing the net revenue received by the PESSs. However, this method does not deeply analyze dynamic changes in practical operating environments. Overall, these studies have established comprehensive indicator systems, but further research is needed to couple configuration optimization with evaluation processes in multiuser contexts.

Although configuring energy storage can effectively reduce the energy costs incurred by users, storage resources are often not fully utilized. With the development of internet technology, the concept of the sharing economy has gradually been applied to energy storage, leading to the concepts of “shared energy storage” (SES) and “cloud energy storage” (CES) [18,19]. SES primarily refers to providing on-demand storage services to multiple electricity users or grid entities by shifting from storage that is dedicated to a single entity to a shared model, thereby enabling the centralized allocation and efficient utilization of resources. The main idea of CES is to integrate and repurpose dispersed user-side storage resources and replace the physical storage on the user side with virtual storage capacity to reduce installation costs and improve the utilization of storage resources [20].

The existing studies generally agree that shared energy storage (SES) and cloud energy storage (CES) can effectively alleviate the high costs, low utilization rates, and demand mismatches that are associated with traditional storage systems. However, a persistent tradeoff remains between energy efficiency and fairness in benefit allocation decisions, which can be addressed through emerging technologies such as blockchain and multienergy coordination [18,20]. At the system level, CES is regarded as a “shared benefit pool” in distributed power systems, where resource aggregation and optimal siting can enable economies of scale and provide improved overall efficiency [21]. In addition, the virtual energy storage sharing model virtualizes centralized physical storage as tradable capacities, thereby significantly reducing investment risks and user costs and offering a novel pathway for commercialization [22]. Moreover, scholars have proposed various market-based operation mechanisms. For instance, market-clearing models for SES can coordinate transactions between renewable generation schemes and idle storage capacity, which not only increases the renewable energy consumption level but also increases the returns of investors and generators [23]. On the user side, CES enables the clustering and scheduling of dispersed small-scale storage devices, achieving peak shaving, valley filling, and maximum renewable energy absorption, thereby providing improved utilization efficiency and reducing the incurred operational costs [24]. Nevertheless, the engagement of multiple stakeholders raises profit distribution challenges. To address this, an asymmetric Nash bargaining framework was developed; this framework minimizes social costs while enhancing the fairness and feasibility of benefit allocation [25]. Building on this, game-theoretic approaches have been further incorporated into business model designs. A Stackelberg game-based time-pricing strategy has been shown to achieve win–win outcomes between operators and users, not only increasing the revenue received by operators but also optimizing user-side energy behaviors [26].

To address the aforementioned limitations, this study is focused on the differentiated needs of multiple users within industrial parks, and a system architecture that incorporates energy storage service providers, storage configuration and commercial leasing into a unified framework is established. The proposed approach emphasizes the technoeconomic tradeoffs in configuration tasks by optimizing the allocation of storage capacity and power. Additionally, a multidimensional evaluation index system is introduced to systematically assess the configuration outcomes, ensuring the comparability and flexibility of the resulting solutions. On this basis, the evaluation process is further integrated with the leasing mechanism to create a coordinated model for both configuration and operation purposes, thereby providing improved storage utilization efficiency and investment returns. Finally, the feasibility and practical value of the proposed method are validated through a representative industrial park-based case study. The novelty of this study lies in an integrated optimization framework that jointly addresses multiuser energy storage sizing and commercial leasing. By combining an AHP-based configuration evaluation with a multiobjective leasing optimization model, the proposed approach coordinates the technical configuration stage with the subsequent economic operation process.

2. Baseline Architecture of an Industrial Park System with an Energy Storage Service Provider

This study is focused on the assessment and leasing of energy storage resources on the user side of an industrial park. The objective is to minimize the energy consumption costs incurred by users and maximize the utilization of energy storage resources through configuration and leasing. The relationships among the various entities of the park system are illustrated in Figure 1.

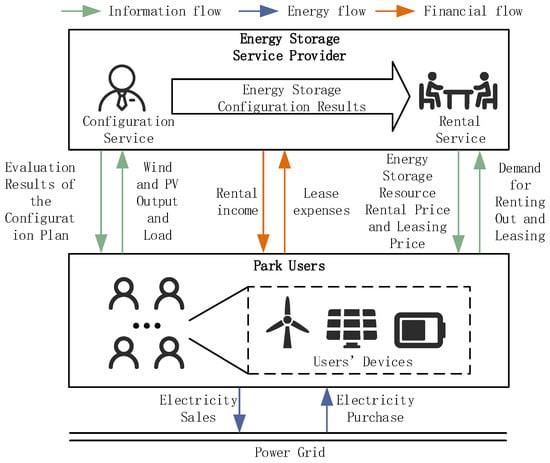
Figure 1. Relationships among the various entities of the park system.

The architecture consists of three main types of core units: diversified user loads; distributed renewable generation units, including wind and solar; and an energy storage system. These units are electrically connected through the park-level grid and are interconnected with the upstream main grid, enabling bidirectional power exchanges.

In the information and management layer, the energy storage service provider performs two main functions: technical configuration and commercial leasing. First, the provider collects each park user’s historical and real-time energy consumption data, renewable generation outputs, and grid electricity price information through the information platform. These multi-source data form the information flow, which serves as the input for the energy storage configuration optimization model. Based on the optimization and evaluation results, the provider designs user-specific configuration schemes and conducts a comprehensive techno-economic assessment with comparative ranking to provide a quantitative basis for leasing decisions.

The energy flow represents the actual electricity exchange between users, the grid, and the storage facilities, while the financial flow corresponds to the cost and revenue transactions during leasing.

Finally, the provider publishes the optimized leasing options through the management platform. According to the announced pricing and matching strategies, users can choose to lease storage resources or make their own storage available for leasing, thereby satisfying their energy needs while reducing total energy costs.

3. Optimal Energy Storage Configuration and Evaluation Model Considering Multiple Users

3.1. Energy Storage Configuration Optimization Model

The optimal energy storage configuration model for each typical user is consistent. The core objective is to minimize the average comprehensive daily cost within the planning period (usually 1 year), including the investment cost, operation and maintenance cost and purchase and sale revenue. Moreover, the power balance constraint, purchase and sale power constraints and energy storage operation constraints are considered to economically and efficiently determine the optimal installation capacity and power level of the energy storage system.

3.1.1. Objective Function

$$\min C=C_{\mathrm{invest}}+C_{\mathrm{o}\text{\&}\mathrm{m}}-R_{\mathrm{grid}}$$

(1)

where $C_{\mathrm{invest}}$ is the investment cost, $C_{\mathrm{o}\text{\&}\mathrm{m}}$ is the operation and maintenance cost, and $R_{\mathrm{grid}}$ is the revenue derived from electricity purchase and sales.

$$C_{\mathrm{invest}}=(c_{\mathrm{p}}\cdot P_{\mathrm{ess}}^{\mathrm{rat}}+c_{\mathrm{e}}\cdot E_{\mathrm{ess}}^{\mathrm{rat}})\cdot r/D$$

(2)

$$r={\displaystyle \frac{e\cdot {\left(1+e\right)}^y}{{\left(1+e\right)}^y-1}}$$

(3)

where $P_{\mathrm{ess}}^{\mathrm{rat}}(\mathrm{kW})$ is the power capacity of the energy storage system and $E_{\mathrm{ess}}^{\mathrm{rat}}(\mathrm{kW})$ is the energy capacity of the energy storage system. $c_{\mathrm{p}}$ represents the cost per unit of power, and $c_{\mathrm{e}}$ represents the cost per unit of energy. $r$ is the annualized interest rate, $e$ is the discount rate, $y$ is the energy storage lifespan, and $D$ is the number of days in a year (365 days).

$$C_{\mathrm{o}\text{\&}\mathrm{m}}=(c_{\mathrm{o}\text{\&}\mathrm{m}}\cdot P_{\mathrm{ess}}^{\mathrm{rat}})\cdot r/D$$

(4)

where $c_{\mathrm{o}\text{\&}\mathrm{m}}$ is the operational cost coefficient per unit of charging/discharging capacity.

$$R_{\mathrm{grid}}=\sum _{t=1}^T\left[c_{\mathrm{buy}}\left(t\right)\cdot P_{\mathrm{buy}}\left(t\right)-c_{\mathrm{sell}}\left(t\right)\cdot P_{\mathrm{sell}}\left(t\right)\right]\cdot \mathrm{\Delta }t$$

(5)

where $P_{\mathrm{buy}}\left(t\right)$ is the power purchased from the grid during period $t$, $P_{\mathrm{sell}}\left(t\right)$ is the power sold to the grid during period $t$, and $c_{\mathrm{buy}}\left(t\right)$ and $c_{\mathrm{sell}}\left(t\right)$ are the corresponding time-of-use electricity rates for period $t$.

3.1.2. Constraints

(1)

Power balance constraint

In any scheduling period $t$, the output of all the power sources (including grid power purchases, energy storage discharges, and distributed generation outputs) must be equal to all the load requirements (including the user load, energy storage charging, and grid power sales); that is,

$$P_{\mathrm{load}}\left(t\right)+P_{\mathrm{ch}}\left(t\right)+P_{\mathrm{sell}}\left(t\right)=P_{\mathrm{dg}}\left(t\right)+P_{\mathrm{disch}}\left(t\right)+P_{\mathrm{buy}}\left(t\right)$$

(6)

where $P_{\mathrm{load}}\left(t\right)$ is the user load within the park, $P_{\mathrm{dg}}\left(t\right)$ is the distributed renewable energy power generated during period $t$, $P_{\mathrm{ch}}\left(t\right)$ is the charging power of the energy storage system during period $t$, and $P_{\mathrm{disch}}\left(t\right)$ is the discharge power during period $t$.

(2)

Electricity purchase and sale constraints

$$\left\{\begin{array}{c}0\le P_{\mathrm{buy}}\left(t\right)\le P_{\max ,\mathrm{grid}}\\ 0\le P_{\mathrm{sell}}\left(t\right)\le P_{\max ,\mathrm{grid}}\end{array}\right.$$

(7)

where $P_{\max ,\mathrm{grid}}$ is the maximum value of the power exchanged with the grid.

(3)

Charge and discharge power constraints of the energy storage system

The charge and discharge power of the energy storage cannot exceed its rated power; that is,

$$\left\{\begin{array}{c}0\le P_{\mathrm{ch}}\left(t\right)\le P_{\mathrm{ess}}^{\mathrm{rat}}\cdot u_{\mathrm{ch}}\left(t\right)\\ 0\le P_{\mathrm{disch}}\left(t\right)\le P_{\mathrm{ess}}^{\mathrm{rat}}\cdot u_{\mathrm{disch}}\left(t\right)\\ u_{\mathrm{ch}}\left(t\right)+u_{\mathrm{disch}}\left(t\right)\le 1\end{array}\right.$$

(8)

where $u_{\mathrm{ch}}\left(t\right)$ and $u_{\mathrm{disch}}\left(t\right)$ denote integer variables ranging from 0–1 that represent the charging and discharging states, respectively.

(4)

State-of-charge (SOC) constraints

$$S\left(t+1\right)=S\left(t\right)+\left({\eta }_{\mathrm{ch}}\cdot P_{\mathrm{ch}}\left(t\right)-P_{\mathrm{disch}}\left(t\right)/{\eta }_{\mathrm{disch}}\right)\cdot \mathrm{\Delta }t/E_{\mathrm{ess}}^{\mathrm{rat}}$$

(9)

$$S_{\min }\le S\left(t\right)\le S_{\max }$$

(10)

where ${\eta }_{\mathrm{ch}}$ is the charging efficiency and ${\eta }_{\mathrm{disch}}$ is the discharging efficiency. $S_{\min }$ is the minimum value of the dispatchable energy capacity of the storage system, and $S_{\max }$ is the maximum value of the dispatchable energy capacity of the system. To prevent overcharging and overdischarging and extend battery lives, the SOC must be strictly confined within the permissible range. $S\left(t\right)$ is the state of charge at the end of period $t$.

3.2. An AHP-Based Comprehensive Evaluation Model for Energy Storage Configuration Schemes

After determining numerous energy storage configuration schemes for different user types, how to select the technically and economically optimal scheme becomes a key decision-making problem. In view of the multidimensionality of the evaluation criteria and the possible contradictions among them, the AHP, a semiquantitative and systematic multicriteria decision-making method, is used in this study to comprehensively evaluate and rank five typical user energy storage configuration schemes. The AHP method can decompose complex decision-making problems into objectives, criteria, schemes and other levels. The relative weight of each criterion is calculated through pairwise comparisons, and the comprehensive priority of each scheme is finally synthesized, which effectively addresses the problem of combining qualitative judgments with quantitative data.

3.2.1. Evaluation Indices

(1)

Cost reduction rate ($C_{\mathrm{red}}$)

The cost reduction rate reflects the direct economic benefits that users gain from deploying energy storage; it quantifies the percentage savings achieved in electricity costs achieved through such a deployment. As a benefit-oriented metric where higher values indicate greater effectiveness, its calculation formula is as follows:

$$C_{\mathrm{red},i}={\displaystyle \frac{C_{\mathrm{base},i}-C_{\mathrm{ess},i}}{C_{\mathrm{base},i}}}\times 100\%$$

(11)

where $C_{\mathrm{base},i}$ is the total electricity cost of the system before energy storage is implemented and $C_{\mathrm{ess},i}$ is the total system cost after user $i$’s energy storage configuration plan is adopted.

(2)

Energy storage investment payback period ($PBP$)

The energy storage payback investment period is measured as the speed at which the initial investments are recovered, and the number of years required to recoup the initial investment in energy storage is calculated. As a cost-based metric, a lower value of $PBP$ indicates better performance. Its calculation formula is as follows:

$$PB{P}_i={\displaystyle \frac{C_{\mathrm{invest},i}+C_{\mathrm{o}\text{\&}\mathrm{m},i}}{C_{\mathrm{base},i}-C_{\mathrm{ess},i}}}$$

(12)

where $C_{\mathrm{invest},i}$ and $C_{\mathrm{o}\text{\&}\mathrm{m},i}$ represent the energy storage investment cost and the operation and maintenance cost, respectively, incurred after adopting user $i$’s energy storage configuration plan.

(3)

Energy storage utilization rate ($U_{\mathrm{ess}}$)

This metric measures the capacity utilization efficiency of the energy storage system during a typical day, indicating the extent to which its investment benefits are realized. It is a performance-oriented indicator where higher values represent better outcomes, and its calculation formula is as follows:

$$U_{\mathrm{ess},i}={\displaystyle \frac{{\displaystyle \sum _{t=1}^{24}}S\left(t\right)}{24}}$$

(13)

where the average daily operating hours of the energy storage system are 24 h.

3.2.2. AHP Evaluation Process Modeling

(1)

Constructing a hierarchical structure and judgment matrix

The hierarchical structure of the evaluation model is divided into three layers. The highest layer (the target layer) is the optimal user energy storage configuration scheme. The middle layer (the criterion layer) consists of three core evaluation indicators proposed by users, namely, the cost reduction rate, the investment payback period of energy storage and the energy storage utilization rate, and the criterion set is defined as $C=\left\{\begin{array}{c}{C}_{\mathrm{red}},PBP,U_{\mathrm{ess}}\end{array}\right\}$. The bottom layer (the scheme layer) consists of the five specific configuration schemes to be evaluated.

Experts are invited to use the Saaty 1–9 scale method to compare the criteria in pairs and construct a judgment matrix $\mathit{A}$:

$$\mathit{A}={\left(a_{ij}\right)}_{k\times k}=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right)$$

(14)

where $a_{ij}$ indicates the importance of criterion $i$ relative to criterion $j$ and $k$ is the number of indicators; $k=3$ in this paper.

(2)

Calculating the weight vector and performing a consistency test

The maximum eigenvalue ${\lambda }_{\max }$ of matrix $\mathit{A}$ is calculated to ultimately determine the weight vector $\mathit{W}=\left(\begin{array}{c}{w}_1,w_2,w_3\end{array}\right)$ for the three criteria, where $w_1$, $w_2$, and $w_3$ correspond to the weightings for the cost reduction rate, energy storage investment payback period, and energy storage utilization rate, respectively. To verify the consistency of the judgment logic, the consistency ratio $CR$ must be calculated using the following formula:

$$\left\{\begin{array}{c}CR={\displaystyle \frac{CI}{RI}}\\ CI={\displaystyle \frac{{\lambda }_{\max }-k}{k-1}}\end{array}\right.$$

(15)

It should be noted that the AHP weighting procedure employed in this study is based on expert judgment using the Saaty 1–9 scale. As a subjective weighting method, the resulting criterion weights do not involve statistical confidence intervals, where $CI$ is the consistency index and $RI$ is the average random consistency index. If $CR<0.1$, the consistency of the judgment matrix is considered acceptable, and the weight distribution is reasonable.

(3)

Constructing a normalized decision matrix

The original data obtained for the five schemes under the three criteria are standardized to generate a standardized matrix $\mathit{Z}={\left(z_{ij}\right)}_{m\times n}$ to eliminate dimensional differences. Moreover, let the original decision matrix be $\mathit{X}={\left(x_{ij}\right)}_{m\times n}$, where $x_{ij}$ is the original value of scheme $i$ under criterion $j$.

For the benefit index $(C_{\mathrm{red}},U_{\mathrm{ess}})$, positive standardization is adopted, and the associated calculation formula is as follows:

$$z_{ij}={\displaystyle \frac{x_{ij}-\min \left(x_j\right)}{\max \left(x_j\right)-\min \left(x_j\right)}}$$

(16)

For the cost index $\left(PBP\right)$, negative standardization is adopted, and the corresponding calculation formula is as follows:

$$z_{ij}={\displaystyle \frac{\max \left(x_j\right)-x_{ij}}{\max \left(x_j\right)-\min \left(x_j\right)}}$$

(17)

(4)

Calculating the comprehensive scores and scheme rankings

The comprehensive score $S{C}_i$ of each scheme is determined by the weighted sum of its standardized score vector and criterion weight vector. The calculation formula is as follows:

$$S{C}_i=\sum _{j=1}^n{w}_j\cdot z_{ij},i=1,2,\dots ,m$$

(18)

In accordance with the calculated comprehensive scores $S{C}_i$, the five schemes are arranged in descending order, and the highest score corresponds to the energy storage configuration scheme with the best comprehensive performance under the given criterion weight.

4. Multiobjective Optimization Model for User Energy Storage Leasing

In this chapter, an energy storage leasing model is built on the basis of the configuration results presented in Section 3, with the objective of enhancing the aforementioned indicators and improving the benefits received by users.

4.1. User Energy Consumption Model

4.1.1. Objective Function

$$\min C=C_{\mathrm{invest}}+C_{\mathrm{o}\text{\&}\mathrm{m}}-R_{\mathrm{grid}}-C_{\mathrm{v}}+C_{\mathrm{r}}$$

(19)

$$\left\{\begin{array}{l}{C}_{\mathrm{v}}=\alpha \left(E_{\mathrm{ess}}^{\mathrm{v}}\cdot {\pi }_{\mathrm{E}}^{\mathrm{v}}+P_{\mathrm{ess}}^{\mathrm{v}}\cdot {\pi }_{\mathrm{P}}^{\mathrm{v}}\right)\\ C_{\mathrm{r}}=\left(1-\alpha \right)\left(E_{\mathrm{ess}}^{\mathrm{r}}\cdot {\pi }_{\mathrm{E}}^{\mathrm{r}}+P_{\mathrm{ess}}^{\mathrm{r}}\cdot {\pi }_{\mathrm{P}}^{\mathrm{r}}\right)\end{array}\right.$$

(20)

where $C_{\mathrm{v}}$ denotes the revenue obtained by the user from leasing out their energy storage resources; $C_{\mathrm{r}}$ denotes the expenditure incurred by the user for leasing energy storage resources; $\alpha$ is the leasing parameter, which equals 1 when the user leases out their energy storage resources and 0 when the user leases energy storage resources; $E_{\mathrm{ess}}^{\mathrm{v}}$ and $P_{\mathrm{ess}}^{\mathrm{v}}$ represent the capacity and power of the storage leased out by the user, respectively; $E_{\mathrm{ess}}^{\mathrm{r}}$ and $P_{\mathrm{ess}}^{\mathrm{r}}$ represent the capacity and power of the storage leased by the user; ${\pi }_{\mathrm{E}}^{\mathrm{v}}$ and ${\pi }_{\mathrm{P}}^{\mathrm{v}}$ are the unit capacity price and unit power price for leasing out storage resources, respectively; and ${\pi }_{\mathrm{E}}^{\mathrm{r}}$ and ${\pi }_{\mathrm{P}}^{\mathrm{r}}$ are the unit capacity price and unit power price for leasing storage resources, respectively.

4.1.2. Constraints

Similar to the constraints described earlier, the users are also subject to the power balance constraint, electricity purchase and sales constraints, the charging and discharging power constraints of the energy storage system, and the state-of-charge constraint. The difference is that the rated power and rated capacity of a user are modified after they participate in leasing, as shown below:

$$\left\{\begin{array}{l}{P}_{\mathrm{ess}}^{\mathrm{rat}\prime }=\alpha \left(P_{\mathrm{ess}}^{\mathrm{rat}}-P_{\mathrm{ess}}^{\mathrm{v}}\right)+\left(1-\alpha \right)\left(P_{\mathrm{ess}}^{\mathrm{rat}}+P_{\mathrm{ess}}^{\mathrm{r}}\right)\\ E_{\mathrm{ess}}^{\mathrm{rat}\prime }=\alpha \left(E_{\mathrm{ess}}^{\mathrm{rat}}-E_{\mathrm{ess}}^{\mathrm{v}}\right)+\left(1-\alpha \right)\left(E_{\mathrm{ess}}^{\mathrm{rat}}+E_{\mathrm{ess}}^{\mathrm{r}}\right)\end{array}\right.$$

(21)

In addition, to improve the indicator values, the following indicator-related constraints are introduced:

$$z_{ij}>z_{ij}^{*}$$

(22)

where $z_{ij}^{*}$ is the indicator value obtained from the configuration scheme for the target user.

4.2. Energy Storage Leasing Model

The energy storage service provider integrates and matches user demands and earns profits by capturing the price differences between users. Its revenue is given as follows:

$$W_{\mathrm{plat}}={\displaystyle {\sum }_{i=1}^m{C}_{\mathrm{i},\mathrm{r}}}-{\displaystyle {\sum }_{i=1}^m{C}_{\mathrm{i},\mathrm{v}}}$$

(23)

To ensure that the service provider makes a profit and that the price of energy storage resources remains within an appropriate range, the following constraints are imposed:

$$\left\{\begin{array}{l}0<{\pi }_{\mathrm{E}}^{\mathrm{v}}<{\pi }_{\mathrm{E}}^{\mathrm{r}}\\ 0<{\pi }_{\mathrm{P}}^{\mathrm{v}}<{\pi }_{\mathrm{P}}^{\mathrm{v}}\end{array}\right.$$

(24)

To maximize the benefits received by both the users and the service provider, the objective function of the energy storage leasing model is formulated as follows:

$$\max W=W_{\mathrm{plat}}+{\displaystyle {\sum }_{i=1}^m{W}_i}$$

(25)

$$W_i=C_i^{*}-C_i$$

(26)

where $W_i$ denotes the benefit received by the user after they participate in energy storage leasing and $C_i^{*}$ and $C_i$ represent the energy consumption costs incurred by the user before and after they participate in energy storage leasing, respectively.

4.3. Matching Rules

After determining the available energy storage capacity and energy storage demand for upload, the cloud energy storage service platform must match resources based on each user’s specific requirements. Unlike conventional commodities, energy storage resource matching is complex because maximum capacity is coupled with maximum charge/discharge power, making simple capacity-based matching insufficient. Considering these constraints, this paper designs a matching mechanism that targets maximizing transaction value.

Assuming the idle energy storage capacity submitted by supply-side users is

$$Supply=\left\{Suppl{y}_1,Suppl{y}_2,Suppl{y}_3,\cdots ,Suppl{y}_m\right\},$$

(27)

the energy storage demand submitted by demand-side users is

$$Demand=\left\{Deman{d}_1,Deman{d}_2,Deman{d}_3,\cdots ,Deman{d}_n\right\}$$

(28)

where $m$ represents the number of supply-side users and $n$ represents the number of demand-side users. For the supply-side user $i\left(1\le i\le m\right)$, the amount of idle energy storage capacity they submit is $Suppl{y}_i=\left\{E_{i.\mathrm{ess}}^{\mathrm{v}},P_{i.\mathrm{ess}}^{\mathrm{v}}\right\}$. For the demand-side user $j\left(1\le j\le n\right)$, the energy storage demand they submit is $Deman{d}_j=\left\{E_{j.\mathrm{ess}}^r,P_{j.\mathrm{ess}}^r\right\}$.

Sum the idle energy storage capacity and the energy storage demand:

$$E_{\mathrm{all}}^{\mathrm{v}}=E_{1.\mathrm{ess}}^{\mathrm{v}}+E_{2.\mathrm{ess}}^{\mathrm{v}}+E_{3.\mathrm{ess}}^{\mathrm{v}}+\cdots +E_{m.\mathrm{ess}}^{\mathrm{v}}$$

(29)

$$E_{\mathrm{all}}^{\mathrm{r}}=E_{1.\mathrm{ess}}^{\mathrm{r}}+E_{2.\mathrm{ess}}^{\mathrm{r}}+E_{3.\mathrm{ess}}^{\mathrm{r}}+\cdots +E_{n.\mathrm{ess}}^{\mathrm{r}}$$

(30)

Step 1: Convert the amount of idle energy storage capacity into the required energy storage capacity. The result of this conversion is $Suppl{y}_{i.\mathrm{Con}}=\left\{E_{i.\mathrm{ess}}^{\mathrm{v}},{\displaystyle \frac{E_{i.\mathrm{ess}}^{\mathrm{v}}}{P_{i.\mathrm{ess}}^{\mathrm{v}}}}\right\}$, $Deman{d}_{j.\mathrm{Con}}=\left\{E_{j.\mathrm{ess}}^r,{\displaystyle \frac{E_{j.\mathrm{ess}}^r}{P_{j.\mathrm{ess}}^r}}\right\}$.

Step 2: Sort both idle energy storage capacity and demand by their respective values ${\displaystyle \raisebox{1ex}{$E$}\!\left/ \!\raisebox{-1ex}{$P$}\right.}$, arranging them in ascending order (if identical values occur, further sort by capacity in descending order). This sorting logic is based on the principle that smaller ${\displaystyle \raisebox{1ex}{$E$}\!\left/ \!\raisebox{-1ex}{$P$}\right.}$ supply-side users with faster charging speeds for their idle storage resources can more readily meet the high-power charging/discharging demands of demand-side users. For identical users, those submitting larger amounts of idle storage capacity or demand exhibit greater economies of scale, stronger market competitiveness, and greater potential to drive market development. Such users should be prioritized. This sorting mechanism effectively incentivizes supply-side users to provide higher-quality idle storage resources, thereby boosting market participation.

Step 3: Match energy storage resources. Supply-side users with higher priority are matched first with demand-side users of corresponding priority, and so on, until either the unused storage capacity of supply-side users or the storage demand of demand-side users is fully matched.

5. Solution Flowchart

The YALMIP toolbox is used in MATLAB R2023a to solve the model by the Gurobi solver and the particle swarm optimization algorithm. The specific solution process is shown in Figure 2, where the number of particles is 500, the maximum number of iterations is 300, and the spatial dimensionality is 4.

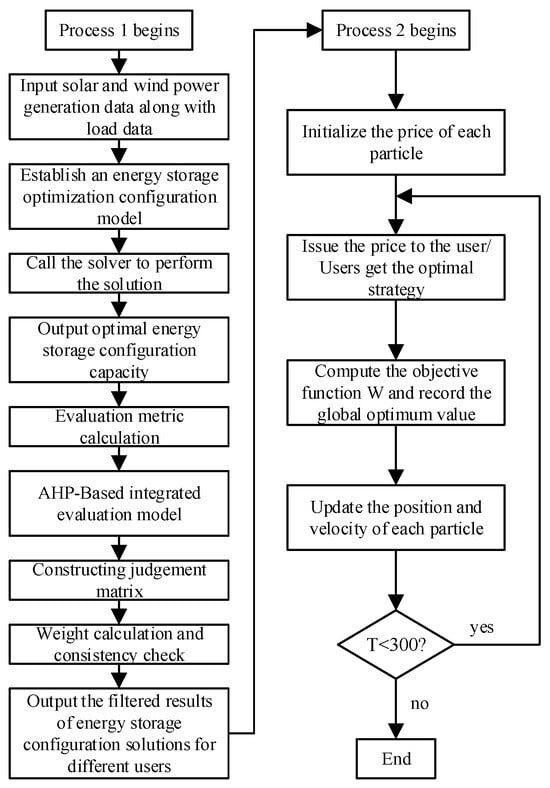
Figure 2. Solution flowchart.

(1)

First, the characteristics of the basic data are analyzed. The data include the historical data concerning the distributed photovoltaic and wind power output in the park, as well as the load data of five users. The peak–valley characteristics of the user loads and the differences between the power consumption patterns of user pairs, as well as the volatility and temporal correlation of the wind and solar outputs, are analyzed.

(2)

The basic data are input into the energy storage configuration optimization model, the Gurobi commercial solver is used to determine the energy storage configuration optimization results, and the original values of the three key indicators for are calculated for the subsequent evaluation.

(3)

According to the calculated evaluation index values of multiple schemes, a comprehensive evaluation model for the energy storage configuration scheme is constructed based on the AHP, and a judgment matrix is constructed as well. The eigenvector of the matrix is calculated to determine the weight of each criterion, and a consistency test is passed. Afterward, according to the score levels, the ranking and screening results of the energy storage configuration schemes developed for different users are output.

6. Case Study Simulation

6.1. Basic Data

To validate the proposed energy storage configuration and evaluation model, a high-tech industrial park in China is selected as a case study in this work. The park is equipped with photovoltaic (PV) arrays and wind turbines and includes five representative user types with markedly different load profiles. The load curves of the five user categories on a typical day are shown in Figure 3; Figure 4 shows the PV output curve, whose peak occurs at approximately noon and coincides with the peak load periods of some users; Figure 5 depicts the wind turbine output curve, which exhibits intermittency and a certain peak shaving (anti-peak) characteristic. The photovoltaic and wind power data used in this study are based on the typical day operation data of the selected industrial park, which are used to reflect representative generation characteristics. It should be noted that the typical-day load and renewable generation profiles used in this case study aim to reflect representative operating characteristics; however, they cannot capture the full temporal variability and uncertainties present in real-world industrial park operation.

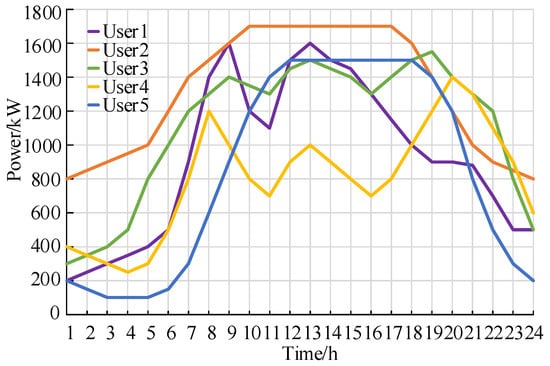
Figure 3. Load curves of five types of users.

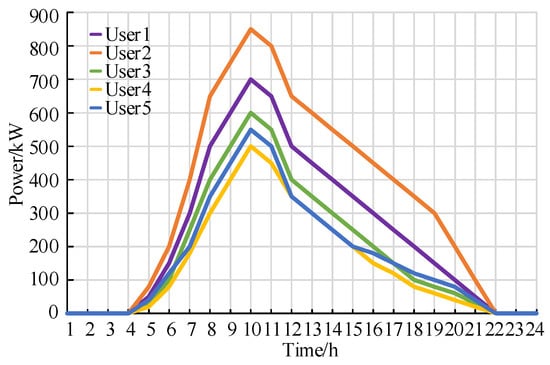
Figure 4. Photovoltaic output curves of five types of users.

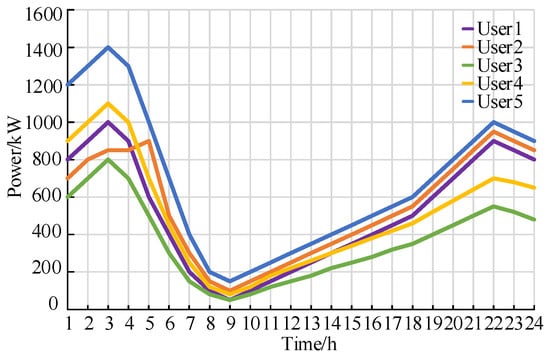
Figure 5. Wind turbine output curves of five types of users.

The time-of-use (TOU) electricity pricing policy that is currently implemented in the regional power grid is adopted in this study, as shown in Table 1. The electricity price is highest during peak periods, followed by flat periods, and it is lowest during valley periods. The selling price of electricity is lower than the purchase price, reflecting the price spread encountered in grid transactions.

Table 1. Time-of-use electricity price table.

Period	Time Interval	Power Price (CNY/kWh)
		Purchase Price	Selling Price
Peak	7:00–9:00 13:00–14:00 18:00–20:00	1.2	0.9
Flat	10:00–12:00 15:00–17:00 21:00–22:00	0.8	0.5
Valley	23:00–06:00 (next day)	0.3	0.2

The unit power cost of the energy storage system $c_{\mathrm{p}}$ is set to 3500 CNY/kW, the unit capacity cost $c_e$ is set to 1000 CNY/kWh, and the unit operation and maintenance (O&M) cost $c_{\mathrm{o}\text{\&}\mathrm{m}}$ is set to 40 CNY/kW. The charging/discharging efficiency is ${\eta }_{\mathrm{ch}}={\eta }_{\mathrm{disch}}=90\%$, and the SOC operating range is limited to $\left[\begin{array}{c}0.1,0.9\end{array}\right]$. The service life of the storage system is assumed to be 8 years, with a discount rate of 3%.

6.2. Analysis of the Energy Storage Configuration Optimization Results Produced for Different Users

On the basis of the typical daily load curves of the five user categories, the wind and solar output curves shown in Figure 3, Figure 4 and Figure 5, the time-of-use (TOU) pricing structure specified in Table 1, and the given technoeconomic parameters of the energy storage paradigm, these inputs are substituted into the storage configuration model developed in Section 3 to obtain a solution. As a result, different optimal storage configuration schemes for the five user categories, along with the original values of their corresponding indicators, are obtained. The detailed results are summarized in Table 2 and Table 3.

Table 2. Results of the energy storage configuration schemes produced for different users.

Users	Rated Power/kW	Rated Capacity/kWh	Daily Average Comprehensive Cost/CNY
			Before Configuration	After Configuration
User 1	650	4387	7154.00	6785.64
User 2	700	4725	10,101.00	9771.78
User 3	890	6007	13,973.00	13,282.90
User 4	520	3510	6458.00	5949.69
User 5	682	4608	5924.00	5504.75

Table 3. Evaluation indices of the energy storage configuration scheme.

Users	Cost Reduction Rate	Payback Period/Years	Storage Utilization Rate
User 1	5.15%	7.1	36.09%
User 2	3.26%	8.5	42.59%
User 3	4.94%	5.2	44.33%
User 4	7.87%	4.1	43.11%
User 5	7.08%	6.5	49.66%

The configuration results clearly reveal the direct influences of the complex interactions among the user load characteristics, the temporal features of self-owned renewable energy output, and the time-of-use (TOU) pricing mechanism on the optimal scale of the energy storage configuration scheme.

User 3 exhibits a high load peak and sustained high-load operations. Their daytime load curve largely coincides with the peak pricing periods, making the deployment of a large-scale storage system (890 kW/6007 kWh) highly economical; the daily net revenue received from buying and selling electricity is the highest at this point, reaching 9708.57 CNY. Although user 4’s maximum load is lower, their load volatility complements their PV output curve well. With a medium-scale storage configuration (520 kW/3510 kWh), user 4 achieves the highest cost reduction rate (7.87%). Users 1 and 2 fall between these two cases. User 2 has a relatively high and persistent load and is configured with a large storage capacity (700 kW/4725 kWh); however, owing to their relatively flat load curve, their arbitrage space is limited, resulting in the lowest cost reduction rate (3.26%). User 1 exhibits a pronounced bimodal load profile that aligns closely with the peak pricing periods, thus enabling effective storage arbitrage and yielding a 5.15% cost reduction rate. User 5’s load curve exhibits typical residential characteristics: their nighttime loads are high and coincide with the wind generation peaks. The configured storage system (682.8 kW/4608.9 kWh) primarily stores abundant low-priced wind power at night and releases it during high-priced daytime periods, achieving good economic performance (7.08% cost reduction) with a relatively high storage utilization rate.

6.3. Analysis of the Evaluation Results Obtained for Different Energy Storage Configuration Schemes

Before conducting the AHP-based evaluation, it should be noted that the five con-figuration schemes analyzed in this section are derived from the optimal energy storage configuration results obtained for the five user categories in Section 6.2. The de-tailed rated power, rated capacity, and techno-economic performance indicators of these schemes are summarized in Table 2 and Table 3, which serve as the basis for the sub-sequent comprehensive evaluation. On the basis of the AHP evaluation model developed in Section 2, a comprehensive evaluation of the five developed configuration schemes is conducted. Three experts in the energy field are invited to perform pairwise comparisons among the criteria, thereby constructing a judgment matrix and calculating the weights. The weights of the criterion layer are obtained as shown in Table 4. The consistency ratio (CR) of the judgment matrix is calculated to be $CR=0.0332<0.1$, which passes the consistency test.

Table 4. Criterion layer weights.

Indicator	$\mathbf{Cos}\mathbf{t}\mathbf{Reduction}\mathbf{Rate}{\mathit{w}}_1$	$\mathbf{Payback}\mathbf{Period}{\mathit{w}}_2$	$\mathbf{Storage}\mathbf{Utilization}\mathbf{Rate}{\mathit{w}}_3$
Weight	0.6370	0.1047	0.2583

In accordance with the attributes of the indicators, the original data in Table 3 are standardized. Combined with the weights in Table 4, the comprehensive scores of each scheme are calculated. The normalized comprehensive scores are illustrated in Figure 6.

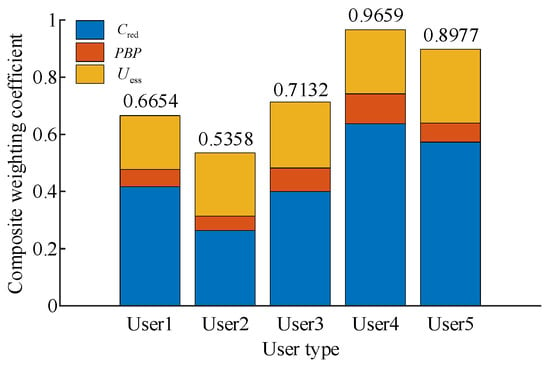
Figure 6. Comprehensive scores of the evaluation indices achieved by each scheme.

By converting the evaluation results into a 100-point scale, the screening criteria determined for the comprehensive scores are presented in Table 5. On this basis, user 4 achieves the highest comprehensive score, reaching the “Excellent” level. This is attributed mainly to their highest cost reduction rate and shortest payback period, indicating that deploying storage on this user’s side yields the best economic performance. Although user 3 has a short payback period and a high storage utilization rate, their relatively low cost reduction rate places them second overall, at the “Good” level. Compared with user 4, users 1 and 5 obtain similar comprehensive scores, both falling into the “Fair” category. User 5 achieves the highest storage utilization rate but a lower cost reduction rate, whereas user 1 demonstrates relatively balanced performance across all the indicators. User 2 performs poorly in all respects—particularly with the lowest cost reduction rate and the longest payback period—resulting in the lowest comprehensive score (at the “Fail” level); thus, storage deployment is not recommended for user 2.

Table 5. Rating criteria.

Evaluation	Excellent	Good	Fair	Pass	Fail
Interval	[90, 100)	[80, 90)	[70, 80)	[60, 70)	[0, 60)

6.4. Analysis of the Energy Storage Leasing Results

After 100 simulation runs, the results of users participating in energy storage leasing are obtained, as shown in Table 6.

Table 6. User rental results.

Demand Users/(kWh, kW)	Supply Users/(kWh, kW)
	User 1	User 3	User 4	User 5
User 2	{1688, 250}	{386, 57}	{405, 60}	{559, 83}

The energy storage leasing results reveal that user 1 provides the greatest amount of storage resources for leasing, approximately 3–4 times that of the other supply-side users. This is because, among the users with comprehensive scores exceeding 60, user 1 has the lowest score, just meeting the qualification threshold, and has the lowest storage utilization rate, resulting in the greatest amount of idle storage resources.

According to the solution results, the benefits received by the users and the service provider are obtained as shown in Table 7.

Table 7. Benefits received by the users and service providers.

	Cost Before Leasing/CNY	Cost After Leasing/CNY	Benefit/CNY
User 1	6785.64	6726.40	59.24
User 2	10,101.00	10,063.05	37.95
User 3	13,282.90	13,265.69	17.21
User 4	5949.69	5937.07	12.62
User 5	5504.75	5487.79	16.96
Provider	0	−42.17	42.17
Total	41,623.98	41,437.83	186.15

Table 7 shows that the users’ energy costs decrease after they participate in energy storage resource leasing. Among them, users 1 and 2 achieve the greatest reductions, by 59.24 CNY and 37.95 CNY, respectively. User 1’s high benefit arises because they lease out the largest amount of storage resources—approximately 3–4 times that of the other supply-side users—and thus their benefit is also 3–4 times those of the other users. User 2’s high benefit is derived from the fact that they originally had no storage installed; after the storage resources are leased from the service provider, their own energy cost is effectively reduced.

Although the incremental daily profit appears small, it reflects the efficiency gain achieved by the leasing mechanism on a typical day. When aggregated over an annual operation period, this benefit becomes economically meaningful. Additionally, the leasing model enhances energy storage utilization and system flexibility, providing long-term value beyond daily profit.

6.5. Comparative Analysis of Indicators

A comparison among the user indicators produced before and after participating in energy storage resource leasing is shown in Table 8.

Table 8. Index comparison results.

Indicator		Before Leasing	After Leasing	Improvement Rate
Cost Reduction Rate	User 1	5.15%	5.98%	16.12%
	User 2	\	0.38%	\
	User 3	4.94%	5.06%	2.43%
	User 4	7.87%	8.07%	2.54%
	User 5	7.08%	7.36%	3.95%
Payback Period/years	User 1	7.09	6.08	16.61%
	User 2	\	\	\
	User 3	5.18	5.03	2.98%
	User 4	4.11	3.99	3.01%
	User 5	6.54	6.26	4.47%
Storage Utilization Rate	User 1	36.09%	38.82%	7.56%
	User 2	\	43.49%	\
	User 3	44.33%	44.37%	0.09%
	User 4	43.11%	47.19%	9.46%
	User 5	49.66%	50.10%	0.89%

As shown in the table, the energy storage leasing model has positive effects on both the economic performance and the resource utilization efficiency of users. In terms of cost, most users experience varying degrees of improvement after leasing, with user 1 showing the most significant savings, achieving an improvement rate of 16.12%. This is partly because user 1 leases out a larger amount of their storage resources and partly because of their relatively low baseline value, which together lead to a marked effect. Furthermore, the payback period is generally shortened; for example, the payback period of user 1 decreases from 7.09 years to 6.08 years, representing a reduction of 16.61%. These findings demonstrate that the energy storage leasing model can effectively accelerate capital recovery and enhance the feasibility of investment.

With respect to storage utilization, the users exhibit a certain degree of improvement. User 4 achieves the greatest increase (9.46%), followed by user 1 (7.56%), highlighting the advantage of the energy storage leasing model in optimizing the resource utilization rate. Users 3 and 5 show limited gains because their baseline storage utilization rates are already high. Moreover, for user 2, the utilization rate of the proposed (self-owned) configuration is 42.59%, whereas the utilization rate of the leased storage resources is 43.49%, reflecting an improvement of 2.11%. Therefore, by leasing storage resources, user 2 can not only save installation and O&M costs but also improve their utilization rate.

In addition, the overall storage utilization rate of the users increases from 43.47% to 45.14%, representing an improvement of 3.84%. The specific SOC profile of the storage system is illustrated in Figure 7. The total capacity of the storage system used in the simulation is 23,237 kWh, corresponding to the sum of the rated capacities of the five users listed in Table 2. In Figure 7, the SOC is expressed in terms of energy (kWh) to better reflect the variation in total stored energy among multiple users. As shown, the storage resources store more electricity during periods with low loads and release more electricity during peak load periods, thereby achieving the purposes of peak shaving and valley filling and alleviating the stress imposed on the power grid.

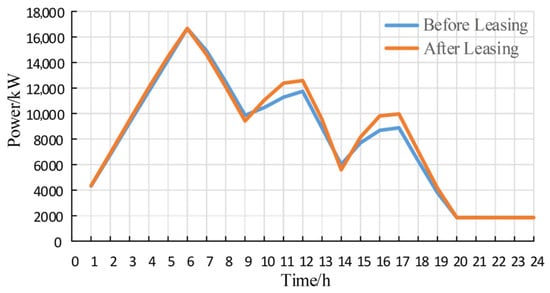
Figure 7. Overall energy storage (SOC) diagram of the users.

7. Conclusions

In this paper, a systematic study covering optimal configurations, a comprehensive evaluation, and energy storage resource leasing is conducted. The conclusions are as follows.

(1)

An energy storage configuration optimization model that considers the different load characteristics of multiple users is constructed. Unlike the conventional studies that treated the target park as a single load or considered only a single type of user, this paper analyzes the diverse characteristics of different users and ultimately provides optimal storage configuration schemes that are tailored to each user.

(2)

A comprehensive evaluation and decision-making framework for multiuser energy storage configuration schemes is proposed based on the analytic hierarchy process (AHP). A multidimensional evaluation index system encompassing both economic and technical aspects is constructed, thus overcoming the limitations of single-indicator evaluations and providing decision makers with a clear and reliable basis for selecting the optimal schemes that are most suitable for specific users from among multiple feasible alternatives.

(3)

A user energy storage leasing model based on multiobjective optimization is proposed; this model explores the value of user storage from multiple dimensions and provides additional benefits for both energy storage service providers and users.

Although this study provides a complete configuration–evaluation–leasing framework under deterministic typical-day conditions, it does not incorporate uncertainties arising from wind/solar forecasting errors or stochastic load variations. Future work will introduce uncertainty optimization theory—such as robust optimization or stochastic programming—to develop configuration schemes with enhanced resilience to renewable energy variability and demand fluctuations. Moreover, the AHP-based evaluation framework adopted in this study is subject to inherent expert subjectivity and does not provide statistical confidence intervals for the derived criterion weights. Future work will consider uncertainty-aware extensions such as fuzzy AHP, interval AHP, or stochastic multi-criteria decision-making methods to improve the robustness and reliability of the evaluation process. And we will further incorporate fairness mechanisms such as Stackelberg game or asymmetric Nash bargaining to achieve both equitable profit distribution and overall system efficiency.