Abstract
Fuel Cell Hybrid Electric Vehicles (FCHEVs) offer a promising path toward sustainable transportation, but their operational economy and component durability are highly dependent on the energy management strategy (EMS). Conventional deep reinforcement learning (DRL) approaches to EMS often suffer from training instability and are typically reactive, failing to leverage predictive information such as upcoming road topography. To overcome these limitations, this paper proposes a proactive, slope-aware EMS based on an expert-guided DRL framework. The methodology integrates a rule-based expert into a Soft Actor-Critic (SAC) algorithm via a hybrid imitation–reinforcement loss function and guided exploration, enhancing training stability. The strategy was validated on a high-fidelity FCHEV model incorporating component degradation. Results on the dynamic Worldwide Harmonized Light Vehicles Test Cycle (WLTC) show that the proposed slope-aware strategy (DRL-S) reduces the SOC-corrected overall operating cost by a substantial 14.45% compared to a conventional rule-based controller. An ablation study confirms that this gain is fundamentally attributed to the utilization of slope information. Microscopic analysis reveals that the agent learns a proactive policy, performing anticipatory energy buffering before hill climbs to mitigate powertrain stress. This study demonstrates that integrating predictive information via an expert-guided DRL framework successfully transforms the EMS from a reactive to a proactive paradigm, offering a robust pathway for developing more intelligent and economically efficient energy management systems.
1. Introduction
The global imperative to mitigate climate change and reduce carbon emissions has catalyzed a paradigm shift in the transportation sector, with a significant focus on the electrification of vehicle powertrains []. Among various alternative solutions, Fuel Cell Hybrid Electric Vehicles (FCHEVs) have emerged as a particularly promising technology, especially for heavy-duty applications such as city buses [,]. They combine the long-range and rapid refueling advantages of conventional vehicles with the zero-emission benefits of electric propulsion [].
The core challenge in optimizing an FCHEV lies in its complex powertrain, which comprises at least two distinct energy sources: a fuel cell system as the primary source and a power battery as a secondary source and energy buffer. An intelligent energy management strategy (EMS) is therefore crucial for coordinating the power flow between these components []. The primary objectives of an EMS are often conflicting: minimizing hydrogen consumption, mitigating the degradation of key components (i.e., the fuel cell and battery) to prolong lifespan, and maintaining the battery’s State of Charge (SOC) within a sustainable range [].
Numerous EMS approaches have been proposed in the literature. Conventional rule-based (RB) strategies, such as thermostat and power-following controllers, are widely used due to their simplicity and robustness, but they are inherently suboptimal, as they cannot adapt to varying driving conditions []. Optimization-based methods, including Dynamic Programming (DP) [] and Model Predictive Control (MPC) [], can achieve near-optimal performance. However, DP suffers from the curse of dimensionality and requires non-causal knowledge of the entire driving cycle, limiting it to offline benchmarking. MPC, while causal, depends heavily on the accuracy of short-term predictions and imposes a significant online computational burden [].
In recent years, deep reinforcement learning (DRL) has shown great potential for developing adaptive, self-learning EMSs that do not require a priori knowledge of the driving cycle []. However, the application of standard DRL algorithms to complex, safety-critical systems like vehicles faces two major hurdles: (1) low sample efficiency and potential instability during the initial training phases, and (2) the purely reactive nature of most DRL frameworks, which typically only use current and past state information. This reactive limitation precludes the use of predictable future information, such as upcoming road topography (slope), which represents a significant missed opportunity for proactive energy optimization.
To address these limitations, this paper proposes an expert-guided, slope-aware DRL-based EMS for an FCHEV.
The primary contributions of this work are threefold:
- 1.
- We propose a novel synergistic DRL framework that uniquely integrates expert guidance with slope-aware perception. This hybrid approach simultaneously solves two of the key challenges of DRL: it enhances training stability via imitation, while enabling a proactive policy via slope anticipation.
- 2.
- We demonstrate, through both macroscopic and microscopic analysis, the emergent intelligent behavior of the learned policy. We reveal the “anticipatory energy buffering” and “powertrain stress mitigation” mechanisms that our agent learns, moving beyond a reactive paradigm.
- 3.
- We provide rigorous validation of this slope-aware, expert-guided approach. Our method achieves a substantial 14.45% reduction in overall operating cost on the dynamic WLTC cycle, and we use an ablation study (DRL-NS) to definitively prove that this performance gain is fundamentally attributed to the agent’s learned ability to leverage topographical information.
2. Literature Review
The development of EMS for FCHEVs has evolved through three primary paradigms: rule-based, optimization-based, and learning-based approaches. Rule-based strategies, while simple and robust, are inherently suboptimal, as they lack adaptability to diverse driving conditions [,]. Optimization-based methods like DP can compute globally optimal solutions offline but are non-causal and computationally prohibitive for real-time application []. This has led to a surge in research on data-driven, learning-based methods, with DRL at the forefront.
DRL offers a powerful model-free framework for developing adaptive EMSs that can learn control policies through interaction with the environment. Early studies demonstrated the viability of applying foundational DRL algorithms, such as Deep Q-Networks (DQNs) and Deep Deterministic Policy Gradient (DDPG), to the energy management problem, showing promising results compared to RB strategies [,]. More recent works have adopted advanced, state-of-the-art DRL algorithms like Twin-Delayed DDPG (TD3) and Soft Actor-Critic (SAC), which offer improved stability and sample efficiency, further closing the gap to optimal solutions [,].
Despite these advancements, the practical application of standard DRL still faces fundamental limitations as extensively documented in recent reviews [,]. The first challenge is the “curse of dimensionality” and low sample efficiency, where reliance on random exploration leads to slow convergence and instability, particularly for multi-objective problems involving component degradation []. The second limitation is that most DRL frameworks are inherently reactive, making decisions based solely on the current state. This fails to leverage predictable future information (e.g., road topography and traffic), which is critical for proactive and strategic energy planning [].
To address the second limitation, a significant research trend has focused on making DRL agents “prescient” by incorporating predictive information into the state space. Researchers have successfully integrated future velocity predictions, traffic conditions, and, most relevant to this work, upcoming road topographical information (e.g., slope) to develop predictive EMSs [,]. These studies have consistently shown that providing the agent with even short-term preview information can lead to substantial improvements in fuel economy by enabling more strategic energy planning.
To tackle the first limitation of sample inefficiency, another research direction has focused on integrating expert knowledge to guide the DRL agent’s learning process. This paradigm, often referred to as imitation learning or learning from demonstrations, uses a pre-existing controller (e.g., a rule-based or MPC-based expert) to provide high-quality action samples. Techniques such as pre-training the DRL agent on expert data [,], enriching the replay buffer with expert transitions [], and directly blending expert and agent actions via methods like rule-interposing [] have been shown to significantly accelerate convergence and improve the final policy’s performance.
While both predictive control and expert guidance have demonstrated individual merits, a synergistic framework that combines the proactive planning capability afforded by slope information with the enhanced training stability and efficiency provided by expert guidance remains an area ripe for exploration. This paper aims to fill this gap by proposing an expert-guided, slope-aware DRL strategy. Our approach is designed not only to learn a forward-looking policy by perceiving the road topography but also to ensure a stable and efficient learning process through a novel integration of a rule-based expert. By simultaneously addressing the reactive nature and the sample inefficiency of standard DRL, we hypothesize that our method can achieve superior performance in complex, multi-objective energy management tasks that consider both fuel economy and long-term component health [,].
3. Knowledge-Guided DRL Methodology
This section details the comprehensive methodology employed in this study. It begins by formally formulating the energy management task as a Markov Decision Process (MDP). Subsequently, it elaborates on the core of our proposed method: the development of the rule-based expert strategy and the advanced Soft Actor-Critic (SAC) algorithm. Finally, it presents the novel knowledge-guided framework that synergistically integrates the expert strategy into the DRL agent to enhance training stability and overall performance.
3.1. Problem Formulation as a Markov Decision Process
The sequential decision-making process of energy management is formally cast as a continuous Markov Decision Process (MDP), defined by the tuple . The objective of the DRL agent is to learn an optimal policy that maximizes the expected cumulative discounted reward over time.
- State Space (): The state provides a comprehensive snapshot of the vehicle’s condition. For the proposed slope-aware strategy, a 5-dimensional state vector is defined aswhere is the battery SOC, is the motor power demand, is the previous FC power, is the FC power change rate, and is the current road slope.
- Action Space (): The action is a continuous variable representing the normalized requested FC power, , which is then scaled to the physical range .
- Reward Function (): The reward function is designed to reflect the minimization of the overall operating cost. It is a weighted sum of the costs of hydrogen consumption (), FC degradation (), and battery degradation (), plus a penalty for SOC deviation from a target value ():where are weighting coefficients.
3.2. The Expert Strategy: Proportional-Thermostat Controller
To provide foundational knowledge and stabilize the DRL agent’s exploration, a rule-based expert strategy, , is designed. This strategy, while not globally optimal, provides a stable and reasonable baseline for FCHEV operation, reflecting common industry practice.
Specifically, the strategy is a Proportional-Thermostat Controller. It determines the fuel cell power request, , based solely on the deviation of the current SOC from a predefined target, (set to 0.5). The control law is formulated as
where is the proportional gain, is the minimum power (0 kW), and is the maximum FC power (60 kW). Based on heuristic tuning to ensure robust charge-sustaining behavior, was set to 200. This strategy ensures the FC is activated proportionally to the SOC deficit, providing a simple and stable baseline. The output is then normalized to (and subsequently mapped to ) to serve as the expert action for the DRL framework.
3.3. The Core Algorithm: Soft Actor-Critic (SAC)
The backbone of our learning agent is the Soft Actor-Critic (SAC) algorithm, a state-of-the-art off-policy DRL method renowned for its high sample efficiency and stability in continuous control tasks [].
The defining feature of SAC is its maximum entropy objective. Unlike traditional RL algorithms that solely aim to maximize the cumulative reward, SAC aims to maximize a weighted sum of the expected return and the policy’s entropy. The objective for the policy is given by
where is the entropy of the policy at state , and is a temperature parameter that determines the importance of the entropy term. This entropy maximization encourages broader exploration by penalizing policies that are overly deterministic, which helps to prevent convergence to sharp, suboptimal local optima and enhances the overall robustness of the learned policy.
The SAC framework is implemented using an actor-critic architecture with three main neural networks:
- Stochastic Policy (Actor): The actor network, , learns a policy that maps states to a probability distribution over actions. It is trained to maximize the soft Q-value, effectively learning to choose actions that are not only high value but also maintain high entropy.
- Soft Q-Functions (Critics): SAC employs two separate critic networks, and , to learn the soft Q-value function. The critics are trained by minimizing the soft Bellman error, and the smaller of the two Q-values is used during the policy update (the clipped double-Q trick) to mitigate Q-value overestimation.
- Tunable Temperature (): The temperature parameter is a crucial hyperparameter that balances the reward and entropy terms. In modern SAC implementations, is not a fixed value but is automatically tuned by formulating a separate optimization problem, aiming to constrain the policy’s entropy to a target value.
3.4. Knowledge Integration: The Expert-Guided Framework
While SAC is powerful, its initial random exploration can be inefficient. To accelerate and stabilize the learning process, we propose an expert-guided framework that integrates the knowledge from the Proportional-Thermostat Controller () into the SAC algorithm in two synergistic ways.
- 1.
- Imitation Loss: We augment the actor’s loss function with an imitation term that encourages the DRL policy to stay close to the expert’s behavior. This is formulated as the Mean Squared Error (MSE) between the mean action of the stochastic DRL policy, , and the expert’s action, . The final hybrid policy objective is a weighted combination of the SAC objective and this imitation loss:where is a hyperparameter that balances the reinforcement and imitation objectives, guiding the agent’s exploration towards the reasonable regions defined by the expert.
- 2.
- Guided Exploration: During data collection, we employ a mixed-action strategy. Periodically (e.g., every 20 steps), an action is sampled from the expert policy and executed, and the resulting transition is stored in the replay buffer. This technique injects high-quality, stable transitions into the buffer, providing the agent with better data to learn from, especially in the early stages of training.
This dual-guidance mechanism ensures that the DRL agent explores the vast state–action space efficiently while being anchored by a stable, common-sense baseline, leading to faster convergence and a more robust and performant final policy.
4. System Modeling and Experimental Setup
4.1. FCHEV System Modeling
The energy management strategy is developed for a high-fidelity model of a fuel cell hybrid electric bus, the system topology of which is illustrated in Figure 1. The key parameters for the vehicle and its components, summarized in Table 1, are adopted from the high-fidelity and experimentally validated model presented in []. This ensures that our study is conducted on a realistic and representative model of the target 13.5-ton FCHEV.
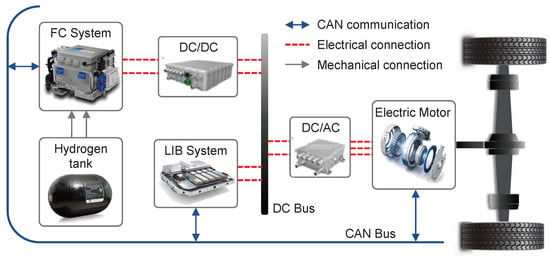
Figure 1.
System topology of the simulated Fuel Cell Hybrid Electric Vehicle (FCHEV).

Table 1.
Key parameters of the studied FCHEV.
4.1.1. Vehicle Dynamics and Energy Flow
The longitudinal dynamics of the vehicle are governed by the tractive force required at the wheels, which is calculated as follows:
where m is the vehicle mass, g is the gravitational constant, is the road slope, is the air density, and are the vehicle’s instantaneous velocity and acceleration, respectively, and and are the rolling and air resistance coefficients, respectively. The required motor power, , is supplied concurrently by the fuel cell and the battery. The power balance equation for the powertrain is thus defined as
where and are the output power of the LIB and FC systems, respectively. The objective of the EMS is to determine the optimal at each time step.
4.1.2. Fuel Cell (FC) System Model
The FC system is modeled as a Proton Exchange Membrane Fuel Cell (PEMFC). Its hydrogen consumption and degradation characteristics are based on quasi-static empirical models derived from experimental data [].
- Hydrogen Consumption: The instantaneous hydrogen consumption rate, , is determined via a lookup map based on the FC output power , as shown in Figure 2.
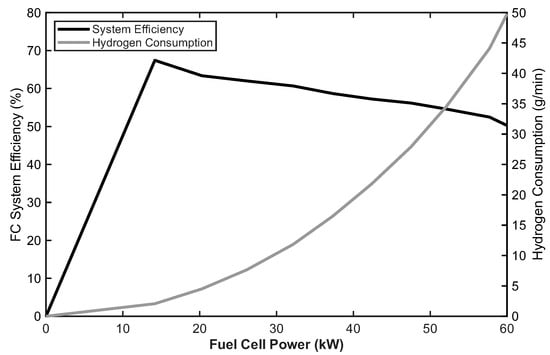 Figure 2. Fuel cell system characteristics: hydrogen consumption rate and system efficiency as a function of FC power.
Figure 2. Fuel cell system characteristics: hydrogen consumption rate and system efficiency as a function of FC power. - Degradation Model: The aging of the FC system is quantified by the decay rate of its stack voltage, . This decay is modeled as a function of start–stop events, low-power operation (), high-power operation (), and the power change rate ():where are experimentally determined coefficients, and are binary indicators for operation below 20% or above 80% of the rated power, respectively. This model allows for the quantification of the FC aging cost within the EMS objective function.
4.1.3. Battery (LIB) System Model
The LIB system is modeled using an R-int equivalent circuit model for its electrical behavior and a throughput-based model for aging []:
- Electrical Model: The battery terminal voltage and current are determined by its open-circuit voltage () and ohmic internal resistance (), which are both functions of SOC as depicted in Figure 3. The change in SOC is then calculated by integrating the current over time:
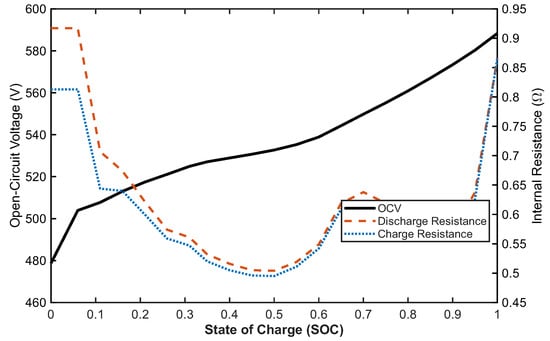 Figure 3. Open-circuit voltage and internal resistance of the battery as a function of SOC.
Figure 3. Open-circuit voltage and internal resistance of the battery as a function of SOC. - Aging Model: The battery’s capacity degradation is described by its State-of-Health (SOH), where the rate of SOH decay is a function of the total charge throughput, C-rate (), and temperature as formulated in []. This allows for the calculation of the LIB aging cost.
4.1.4. Electric Motor Model
The electric motor is the sole propulsion component. Its performance is characterized by an experimentally determined efficiency map, , which defines the motor’s electrical efficiency as a function of its torque and speed as shown in Figure 4. The required electrical power is calculated based on this map and the mechanical power demand from the driveline.
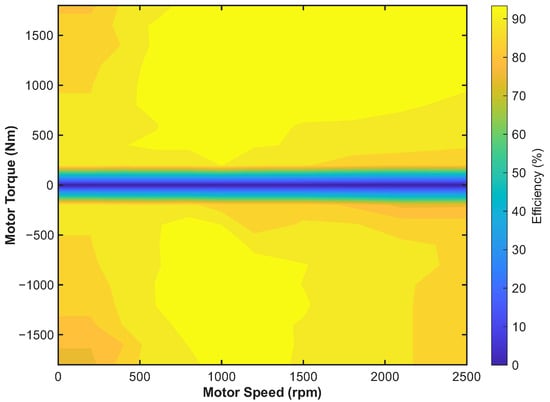
Figure 4.
Electric motor efficiency map.
4.2. Experimental Setup
To validate the effectiveness of the proposed energy management strategy, a series of simulation experiments were conducted. The simulation environment, modeling a 13.5-ton fuel cell hybrid bus, was developed in Python. The performance of the proposed strategy is benchmarked against two other controllers on two distinct driving cycles.
4.2.1. Driving Cycles
Two driving cycles with synthesized, time-aligned road slope information were utilized to evaluate the strategies’ performance and generalization capabilities. The velocity and slope profiles for both cycles are depicted in Figure 5. The training cycle, a modified China City Driving Cycle (CCDC) shown in Figure 5a, is characterized by frequent start–stop events and lower average speeds, representing typical urban bus operation. For evaluation, the Worldwide Harmonized Light Vehicles Test Cycle (WLTC), shown in Figure 5b, was employed. Its dynamic nature, encompassing distinct low-, medium-, and high-speed phases, serves as a comprehensive test case to assess the generalization capability of the trained policies on an unseen cycle.
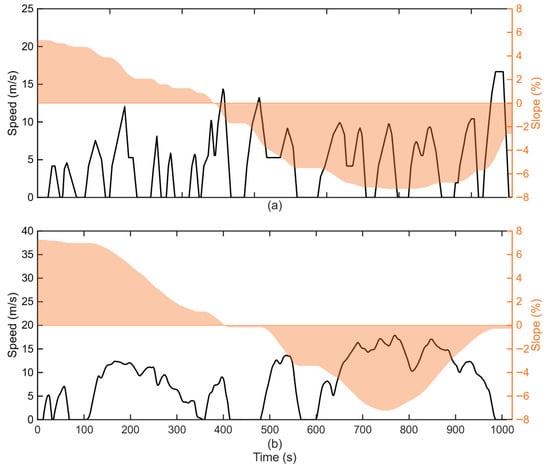
Figure 5.
Velocity and slope profiles of the driving cycles used for training and testing. (a) The modified China City Driving Cycle (CCDC) used for training, characterized by frequent start–stop events. (b) The Worldwide Harmonized Light Vehicles Test Cycle (WLTC) used for testing, featuring more dynamic and higher-speed phases.
- Training Cycle: The deep reinforcement learning agents were trained on a modified China City Driving Cycle. This cycle is characterized by low average speeds and frequent start–stop events, which is representative of typical urban bus operating conditions.
- Testing Cycle: For evaluation, the Worldwide Harmonized Light Vehicles Test Cycle (WLTC) was employed. Its dynamic nature, encompassing low-, medium-, high-, and extra-high-speed phases, serves as a challenging and comprehensive test case to assess the generalization capability of the trained policies on an unseen cycle.
4.2.2. Compared Strategies
Three distinct energy management strategies were implemented for a comprehensive comparison:
- Rule-Based (RB): A conventional rule-based controller serves as the baseline. It operates on a simple thermostat logic, activating the fuel cell at a fixed power level when the battery State of Charge (SOC) drops below a predefined threshold and deactivating it when the SOC exceeds an upper threshold. This represents a widely used, non-predictive industry benchmark.
- DRL-NoSlope (DRL-NS): To perform an ablation study and rigorously quantify the value of slope information, a DRL agent without slope awareness was trained. This agent utilizes the identical expert-guided SAC algorithm as the proposed method but is provided with a reduced, 4-dimensional state representation , which deliberately excludes the road slope.
- Proposed (DRL-S): The proposed strategy is the expert-guided SAC agent that receives the full, 5-dimensional state representation, including the current road slope . This enables the agent to learn and exploit the temporal correlations between the driving state and road topography.
4.2.3. DRL Strategies Configuration and Training
The proposed DRL-S agent and the DRL-NS baseline agent were implemented in Python using the PyTorch framework. Both agents share an identical neural network architecture and set of hyperparameters to ensure a fair comparison. The actor (policy) network and the critic (Q-value) networks are both simple multi-layer perceptrons (MLPs). The training was conducted for 100 episodes on the CCDC training cycle. The imitation loss weight was set to 0.5, balancing the exploratory SAC objective with the expert guidance. All key hyperparameters used for training are detailed in Table 2.

Table 2.
DRL hyperparameter configuration.
5. Results and Analysis
5.1. Training Process Analysis
The DRL agents, both the proposed DRL-S and the ablation DRL-NS, were trained for 100 episodes on the China City Driving Cycle. The training was facilitated by the expert-guided Soft Actor-Critic (SAC) algorithm, designed to enhance learning stability and accelerate convergence. The evolution of the cumulative reward during the training process for both agents is presented in Figure 6.
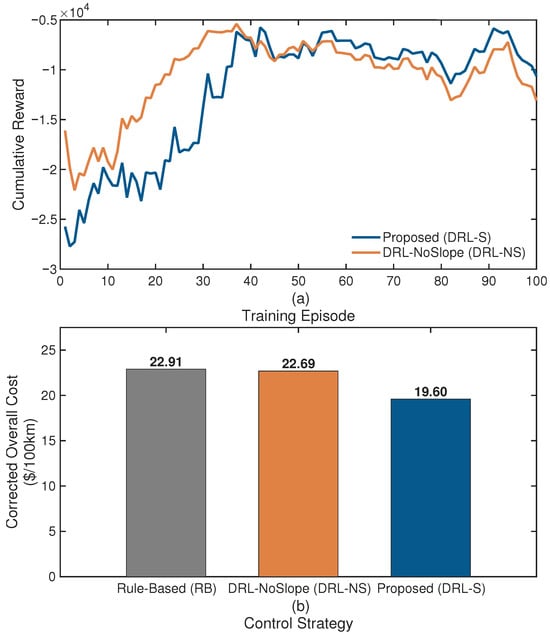
Figure 6.
Cumulative reward curves for the proposed DRL-S and the DRL-NS strategies during the training process. The solid lines represent the moving average of the episodic rewards, illustrating the overall learning trend.
As illustrated in Figure 6a, the reward curves for both agents exhibit a clear and stable upward trend, eventually converging to a high-reward plateau. This convergence demonstrates the efficacy of the expert-guided SAC framework in navigating the complex, high-dimensional state–action space of the energy management problem. The initial phase of rapid reward increase can be attributed to the agent quickly learning fundamental policies, guided by the imitation loss from the expert rules. Subsequently, the learning rate gradually decreases as the agents fine-tune their policies through exploration to maximize the long-term objective function. Notably, the proposed DRL-S strategy consistently achieves a slightly higher level of cumulative reward upon convergence compared to its DRL-NS counterpart. This observation provides an initial indication that by leveraging road slope information, the DRL-S agent is capable of discovering a more optimal policy, a hypothesis that will be rigorously validated through comparative performance analysis in the subsequent section. Likewise, according to Figure 6b, the overall cost of the proposed DRL-S strategy in the training process is superior to two baselines, which is aligned with the reward metric.
5.2. Comparative Performance Analysis
The comprehensive quantitative performance of the three control strategies was evaluated on both the CCDC training cycle and the unseen WLTC testing cycle. The final SOC-corrected results, summarized in Table 3, reveal a nuanced but powerful insight into the capabilities of the proposed slope-aware strategy.

Table 3.
Overall performance comparison of all strategies on different driving cycles.
A striking observation from Table 3 is the performance disparity of the proposed DRL-S agent between the two cycles. On the unseen and highly dynamic WLTC, the DRL-S agent demonstrates its profound superiority, achieving a corrected overall cost of 19.60 USD/100 km—a substantial 14.45% reduction compared to the RB controller. However, on the CCDC, which it was trained on, its performance is comparable to the baseline strategies.
This seemingly paradoxical result is not an indication of failure but rather strong evidence of the agent’s successful generalization of a fundamental physical principle, rather than simple overfitting to the training data. If the agent had merely overfitted to the specific patterns of the CCDC, it would have excelled on the CCDC and performed poorly on the unseen WLTC. The observed outcome is precisely the opposite, which can be explained by the intrinsic characteristics of the driving cycles.
The CCDC represents a low-energy-demand regime. Characterized by low average speeds and frequent start–stop events, the vehicle’s power demand is dominated by inertial forces during acceleration, while the power required to overcome aerodynamic drag () and grade resistance () remains relatively small. In this context, the potential for long-term energy savings through slope anticipation is minimal, as the planning horizon is constantly interrupted. Consequently, the performance of a sophisticated predictive strategy converges with that of simpler reactive strategies like RB and DRL-NS.
In contrast, the WLTC features higher speeds and more sustained driving events, representing a high-energy-demand regime. In this scenario, the energy impact of aerodynamic drag and grade resistance becomes significant, and at times, dominant. This creates a high-stakes optimization problem where the ability to anticipate and prepare for prolonged, high-power events like hill climbs offers a substantial opportunity for cost reduction. It is precisely in this challenging environment that the proposed DRL-S agent’s learned, forward-looking policy unlocks its true potential. The agent applies the general principles of anticipatory energy management—learned during its CCDC training—to a new condition where those principles yield far greater returns.
Therefore, the results validate that the proposed slope-aware strategy provides its most significant advantage in the complex and dynamic driving scenarios where it is most needed, showcasing its robust generalization and practical value beyond the confines of its training data. To understand how the DRL-S agent achieves these quantitative gains on the WLTC, a detailed microscopic analysis of its control behavior is presented in the following section.
5.3. In-Depth Analysis of Control Strategy Behavior
To elucidate the underlying mechanism behind the superior performance of the proposed DRL-S strategy, a microscopic analysis of the control actions was conducted on a representative and challenging segment (550–700 s) of the WLTC test cycle. This segment, illustrated in Figure 7, is partitioned into three distinct phases based on the critical changes in road slope to facilitate the analysis. It is crucial to note that the emergent anticipatory behavior of the DRL-S agent is not the result of being explicitly provided with future information. Rather, it is a sophisticated, forward-looking policy learned by the value-based reinforcement learning algorithm, which inherently optimizes for long-term cumulative rewards by recognizing the temporal correlations within the driving cycle.
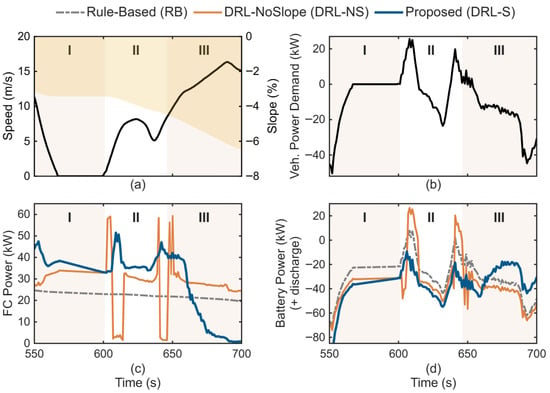
Figure 7.
Microscopic behavior comparison of the three strategies over a challenging segment of the WLTC. (a) Driving conditions, including vehicle speed (left axis) and road slope (right axis). (b) The resulting vehicle power demand at the axle. (c) The control actions of the fuel cell (FC) power. (d) The corresponding response of the battery power, where positive values indicate discharging.
As depicted in Figure 7a,b, the vehicle first decelerates and then begins to accelerate during the preparatory Phase I (550–606 s), where the power demand is low. In this phase, the DRL-S agent exhibits a remarkable proactive energy buffering strategy. It elevates the fuel cell (FC) power output to approximately 40 kW (Figure 7c), actively charging the battery at a high rate in anticipation of the upcoming high-power demand event (Figure 7d). In stark contrast, the DRL-NS agent, being unaware of the impending incline, maintains a low, reactive FC output, while the rule-based (RB) strategy holds a static, non-adaptive power level of around 25 kW.
The significant performance divergence occurs in Phase II (606–642 s), which contains the steepest section of the incline and a corresponding sharp peak in vehicle power demand. The proactive energy buffering in Phase I enables the DRL-S agent to implement an effective “peak shaving” strategy for the battery. It orchestrates a smooth, coordinated response from both the FC and the pre-charged battery, thereby mitigating the peak battery discharge power significantly. Conversely, the DRL-NS agent responds with aggressive, high-frequency power spikes from both the FC (to its maximum limit) and the battery, inducing substantial stress on the powertrain components. The inflexible RB strategy is the least effective; its static FC output forces the battery to single-handedly absorb the entire dynamic load, resulting in the highest stress and deepest discharge.
Finally, in the recovery Phase III (642–700 s), after the power demand peak has passed, the DRL-S agent intelligently curtails its FC output to near zero. This allows it to maximize the capture of regenerative braking energy. In summary, the detailed analysis reveals that the proposed DRL-S strategy transforms the energy management paradigm from being purely reactive to proactively predictive. This learned, forward-looking behavior—characterized by anticipatory energy buffering and powertrain stress mitigation—directly translates into the superior overall operating economy demonstrated in the macroscopic analysis.
5.4. Statistical Distribution Analysis of Component Operation
To further validate the underlying reasons for the performance gains on a global scale, a statistical analysis of the key powertrain components’ operating points over the entire WLTC was conducted. Figure 8 provides a holistic view of how each strategy utilizes the fuel cell and the battery.
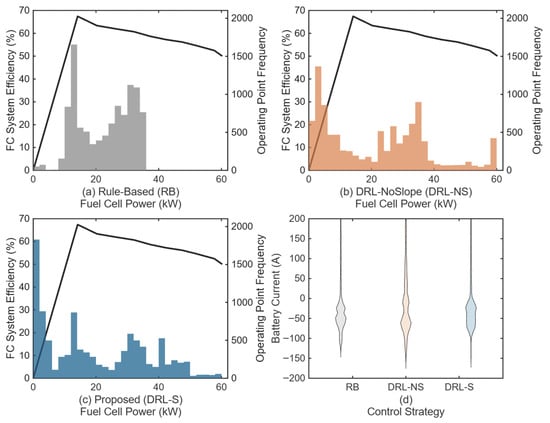
Figure 8.
Statistical distributions of component operation over the entire WLTC. (a–c) show the fuel cell operating point frequency distributions for the RB, DRL-NS, and DRL-S strategies, respectively, overlaid on the FC system efficiency curve (black line). (d) Violin plots showing the probability density of the battery current for each strategy.
Figure 8 provides a global statistical validation of the behaviors observed in the microscopic analysis. Figure 8a–c illustrate the frequency distribution of the fuel cell operating points, overlaid on the system efficiency curve. The three strategies exhibit fundamentally different utilization philosophies.
The rule-based (RB) strategy (Figure 8a) primarily operates the FC at a static power level near 15 kW, which is a suboptimal efficiency region. This inflexible approach fails to adapt to the varying power demands.
The DRL-NoSlope (DRL-NS) strategy (Figure 8b) displays a highly scattered distribution, with a significant number of operating points falling in the high-power (> 45 kW) region. This high-load zone is notoriously inefficient and is also known to accelerate FC degradation, which directly explains the high FC aging cost for this strategy seen in Table 3.
In contrast, the Proposed (DRL-S) strategy (Figure 8c) demonstrates a highly intelligent control pattern. It successfully concentrates the vast majority of its operating points within the peak efficiency “sweet spot” of the FC map, primarily between 15 kW and 45 kW. This strategic placement of operating points is the direct cause of the superior fuel economy (lowest H2 cost) documented in Table 3.
Furthermore, Figure 8d presents the probability density of the battery current. A detailed examination of these distributions reveals a critical distinction. Both the DRL-NS and RB strategies exhibit significant probability density in the positive (discharge) current region; the DRL-NS plot is also visibly wider, signifying greater overall current variance and frequent high-rate discharge events. In stark contrast, the violin plot for the proposed DRL-S strategy, while also centered in the charging (negative) region, displays a significantly suppressed positive tail. This shape provides clear statistical evidence that the DRL-S policy is highly effective at mitigating high-rate battery discharge, thereby protecting the battery from accelerated degradation. This statistical finding globally corroborates the “peak shaving” behavior observed in the time-series analysis (Section 5.4) and is the direct cause of the DRL-S strategy achieving the lowest battery degradation cost as documented in Table 3.
6. Conclusions
In this paper, an expert-guided, slope-aware energy management strategy based on deep reinforcement learning was proposed and validated for a fuel cell hybrid electric bus. The proposed DRL-S strategy integrates topographical information into its state representation and leverages an expert-guided SAC algorithm to ensure stable and efficient training.
A comprehensive set of simulation experiments was conducted, and the results lead to several key conclusions. On a dynamic and unseen WLTC testing cycle, the proposed DRL-S strategy demonstrated a remarkable performance, achieving a corrected overall operating cost of 19.60 USD/100 km, which constitutes a significant 14.45% improvement over a conventional rule-based (RB) controller. An ablation study confirmed that this performance gain is fundamentally attributed to the utilization of slope information, as a DRL agent without slope awareness (DRL-NS) offered only marginal improvements. Microscopic and statistical analyses revealed that the DRL-S agent learned a truly proactive control policy, performing anticipatory energy buffering before hill climbs and effectively mitigating powertrain stress. This forward-looking behavior, learned implicitly through the value-based optimization of long-term rewards, allows the agent to maintain components in higher-efficiency operating regions and reduce degradation.
The findings of this study confirm that combining expert guidance with DRL is an effective approach for developing robust control policies for complex hybrid powertrains. More importantly, it validates the significant potential of incorporating predictive information, even as simple as the current road slope, to transform the EMS from a reactive to a proactive paradigm, unlocking substantial gains in real-world operating economy.
Future work will aim to extend this framework by incorporating a wider range of preview information, such as traffic flow data. Furthermore, we acknowledge limitations inherent to this study, including the challenges of bridging the simulation-to-reality (‘Sim2Real’) gap for onboard hardware deployment and the sensitivity of DRL performance to hyperparameter selection. A valuable future study would also involve benchmarking the proposed model-free agent against advanced model-based controllers to comprehensively evaluate the trade-offs between computational cost, model dependency, and optimality.
Author Contributions
Conceptualization, S.Z. and H.H.; Methodology, H.H. and J.W.; Software, S.Z. and J.W.; Formal analysis, S.Z.; Investigation, S.Z.; Writing—original draft, S.Z.; Writing—review and editing, H.H. and J.W.; Visualization, S.Z.; Supervision, H.H.; Funding acquisition, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China grant number 52172377.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Sheng Zeng was employed by the company Beijing Institute of Technology, Zhengzhou Yutong Bus Co. Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
Nomenclature
| CCDC | China City Driving Cycle |
| DRL | Deep Reinforcement Learning |
| DRL-NS | Deep Reinforcement Learning—No Slope (Ablation Strategy) |
| DRL-S | Deep Reinforcement Learning—Slope (Proposed Strategy) |
| EMS | Energy Management Strategy |
| FC | Fuel Cell |
| FCHEV | Fuel Cell Hybrid Electric Vehicle |
| LIB | Lithium-Ion Battery |
| MDP | Markov Decision Process |
| MPC | Model Predictive Control |
| RB | Rule-Based |
| SAC | Soft Actor-Critic |
| SOC | State of Charge |
| WLTC | Worldwide Harmonized Light Vehicles Test Cycle |
References
- Zhang, F.; Wang, L.; Coskun, S.; Pang, H.; Cui, Y.; Xi, J. Energy management strategies for hybrid electric vehicles: Review, classification, comparison, and outlook. Energies 2020, 13, 3352. [Google Scholar] [CrossRef]
- Min, D.; Song, Z.; Chen, H.; Wang, T.; Zhang, T. Genetic algorithm optimized neural network based fuel cell hybrid electric vehicle energy management strategy under start-stop condition. Appl. Energy 2022, 306, 118036. [Google Scholar] [CrossRef]
- Yu, P.; Li, M.; Wang, Y.; Chen, Z. Fuel cell hybrid electric vehicles: A review of topologies and energy management strategies. World Electr. Veh. J. 2022, 13, 172. [Google Scholar] [CrossRef]
- Khalatbarisoltani, A.; Zhou, H.; Tang, X.; Kandidayeni, M.; Boulon, L.; Hu, X. Energy management strategies for fuel cell vehicles: A comprehensive review of the latest progress in modeling, strategies, and future prospects. IEEE Trans. Intell. Transp. Syst. 2023, 25, 14–32. [Google Scholar] [CrossRef]
- Sorlei, I.S.; Bizon, N.; Thounthong, P.; Varlam, M.; Carcadea, E.; Culcer, M.; Iliescu, M.; Raceanu, M. Fuel cell electric vehicles—A brief review of current topologies and energy management strategies. Energies 2021, 14, 252. [Google Scholar] [CrossRef]
- Hu, H.; Yuan, W.W.; Su, M.; Ou, K. Optimizing fuel economy and durability of hybrid fuel cell electric vehicles using deep reinforcement learning-based energy management systems. Energy Convers. Manag. 2023, 291, 117288. [Google Scholar] [CrossRef]
- Dong, H.; Hu, Q.; Li, D.; Li, Z.; Song, Z. Predictive Battery Thermal and Energy Management for Connected and Automated Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2025, 26, 2144–2156. [Google Scholar] [CrossRef]
- An, L.N.; Tuan, T.Q. Dynamic programming for optimal energy management of hybrid wind–PV–diesel–battery. Energies 2018, 11, 3039. [Google Scholar] [CrossRef]
- Pereira, D.F.; da Costa Lopes, F.; Watanabe, E.H. Nonlinear model predictive control for the energy management of fuel cell hybrid electric vehicles in real time. IEEE Trans. Ind. Electron. 2020, 68, 3213–3223. [Google Scholar] [CrossRef]
- Tang, X.; Chen, J.; Pu, H.; Liu, T.; Khajepour, A. Double deep reinforcement learning-based energy management for a parallel hybrid electric vehicle with engine start–stop strategy. IEEE Trans. Transp. Electrif. 2021, 8, 1376–1388. [Google Scholar] [CrossRef]
- Fayyazi, M.; Sardar, P.; Thomas, S.I.; Daghigh, R.; Jamali, A.; Esch, T.; Kemper, H.; Langari, R.; Khayyam, H. Artificial intelligence/machine learning in energy management systems, control, and optimization of hydrogen fuel cell vehicles. Sustainability 2023, 15, 5249. [Google Scholar] [CrossRef]
- Luca, R.; Whiteley, M.; Neville, T.; Shearing, P.R.; Brett, D.J. Comparative study of energy management systems for a hybrid fuel cell electric vehicle-A novel mutative fuzzy logic controller to prolong fuel cell lifetime. Int. J. Hydrogen Energy 2022, 47, 24042–24058. [Google Scholar] [CrossRef]
- Chatterjee, D.; Biswas, P.K.; Sain, C.; Roy, A.; Ahmad, F. Efficient energy management strategy for fuel cell hybrid electric vehicles using classifier fusion technique. IEEE Access 2023, 11, 97135–97146. [Google Scholar] [CrossRef]
- Sun, W.; Zou, Y.; Zhang, X.; Guo, N.; Zhang, B.; Du, G. High robustness energy management strategy of hybrid electric vehicle based on improved soft actor-critic deep reinforcement learning. Energy 2022, 258, 124806. [Google Scholar] [CrossRef]
- Li, D.; Hu, Q.; Jiang, W.; Dong, H.; Song, Z. Integrated power and thermal management for enhancing energy efficiency and battery life in connected and automated electric vehicles. Appl. Energy 2025, 396, 126213. [Google Scholar] [CrossRef]
- Lian, R.; Tan, H.; Peng, J.; Li, Q.; Wu, Y. Cross-type transfer for deep reinforcement learning based hybrid electric vehicle energy management. IEEE Trans. Veh. Technol. 2020, 69, 8367–8380. [Google Scholar] [CrossRef]
- Zhou, J.; Xue, S.; Xue, Y.; Liao, Y.; Liu, J.; Zhao, W. A novel energy management strategy of hybrid electric vehicle via an improved TD3 deep reinforcement learning. Energy 2021, 224, 120118. [Google Scholar] [CrossRef]
- Xu, D.; Cui, Y.; Ye, J.; Cha, S.W.; Li, A.; Zheng, C. A soft actor-critic-based energy management strategy for electric vehicles with hybrid energy storage systems. J. Power Sources 2022, 524, 231099. [Google Scholar] [CrossRef]
- Ganesh, A.H.; Xu, B. A review of reinforcement learning based energy management systems for electrified powertrains: Progress, challenge, and potential solution. Renew. Sustain. Energy Rev. 2022, 154, 111833. [Google Scholar] [CrossRef]
- Sidharthan Panaparambil, V.; Kashyap, Y.; Vijay Castelino, R. A review on hybrid source energy management strategies for electric vehicle. Int. J. Energy Res. 2021, 45, 19819–19850. [Google Scholar] [CrossRef]
- Tang, X.; Chen, J.; Qin, Y.; Liu, T.; Yang, K.; Khajepour, A.; Li, S. Reinforcement learning-based energy management for hybrid power systems: State-of-the-art survey, review, and perspectives. Chin. J. Mech. Eng. 2024, 37, 43. [Google Scholar] [CrossRef]
- Teimoori, Z.; Yassine, A. A review on intelligent energy management systems for future electric vehicle transportation. Sustainability 2022, 14, 14100. [Google Scholar] [CrossRef]
- Hu, T.; Li, Y.; Zhang, Z.; Zhao, Y.; Liu, D. Energy Management Strategy of Hybrid Energy Storage System Based on Road Slope Information. Energies 2021, 14, 2358. [Google Scholar] [CrossRef]
- Hou, Z.; Guo, J.; Chu, L.; Hu, J.; Chen, Z.; Zhang, Y. Exploration the route of information integration for vehicle design: A knowledge-enhanced energy management strategy. Energy 2023, 282, 128809. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Y.; Yang, H.; Huang, Z.; Lv, C. Human-guided reinforcement learning with sim-to-real transfer for autonomous navigation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 14745–14759. [Google Scholar] [CrossRef]
- Zare, A.; Boroushaki, M. A knowledge-assisted deep reinforcement learning approach for energy management in hybrid electric vehicles. Energy 2024, 313, 134113. [Google Scholar] [CrossRef]
- Wu, J.; Yang, H.; Yang, L.; Huang, Y.; He, X.; Lv, C. Human-guided deep reinforcement learning for optimal decision making of autonomous vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 6595–6609. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Z.; Chen, Z. Development of energy management system based on a rule-based power distribution strategy for hybrid power sources. Energy 2019, 175, 1055–1066. [Google Scholar] [CrossRef]
- Huang, Y.; Kang, Z.; Mao, X.; Hu, H.; Tan, J.; Xuan, D. Deep reinforcement learning based energymanagement strategy considering running costs and energy source aging for fuel cell hybrid electric vehicle. Energy 2023, 283, 129177. [Google Scholar] [CrossRef]
- Zhang, D.; Cui, Y.; Xiao, Y.; Fu, S.; Cha, S.W.; Kim, N.; Mao, H.; Zheng, C. An improved soft actor-critic-based energy management strategy of fuel cell hybrid vehicles with a nonlinear fuel cell degradation model. Int. J. Precis. Eng.-Manuf.-Green Technol. 2024, 11, 183–202. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Li, X.; He, H.; Wu, J. Knowledge-guided deep reinforcement learning for multiobjective energy management of fuel cell electric vehicles. IEEE Trans. Transp. Electrif. 2024, 11, 2344–2355. [Google Scholar] [CrossRef]
- Ebbesen, S.; Elbert, P.; Guzzella, L. Battery State-of-Health Perceptive Energy Management for Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2012, 61, 2893–2900. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).