Numerical Simulations of Forced Ignition and Flame Dynamics in an Ammonia/Air Mixing Layer

Abstract

This work explores NH₃/air non-premixed combustion in a mixing layer, with the objective of quantifying the influence of key parameters on ignition and flame dynamics. A series of two-dimensional simulations were conducted with forced ignition. The evolutions of the Damköhler number (Da) and flame stretch at the peak heat release rate for cases with successful/unsuccessful ignition were examined. It was found that for the cases with successful ignition, the Damköhler number is always larger than unity, the flame stretch maintains a positive value, and the tangential diffusion consistently dominates the normal diffusion all the time. On the contrary, for the cases with unsuccessful ignition, the Damköhler number gradually becomes less than unity, and the value of the flame stretch changes from positive to negative as time advances. During flame quenching, the value of the normal diffusion term becomes larger than that of the tangential diffusion term. The effects of mixing layer thickness on the ignition kernel evolution were assessed. It was shown that a thicker mixing layer promotes ignition kernel development. The ignition process is also influenced by the location of the spark in the mixture fraction space. Finally, the flame dynamics were analyzed in terms of scalar dissipation rate ($\chi$), displacement speed $S_d$, and flame stretch ($\kappa$) for various cases. The results showed that the $S_d$ is negatively correlated with the $\kappa$ and $\chi$. The Markstein length was evaluated, and it does not differ between the cases with varying mixing layer thickness.

1. Introduction

Ammonia (NH₃) is a promising hydrogen carrier because of its well-known manufacturing, reliable large-scale storage, and convenience in transport. It serves as a carbon-free fuel in applications such as internal combustion engines, industrial furnaces, and fuel cells [1]. Its low reactivity, however, makes the ignition of ammonia/air mixtures challenging [2], which adversely affects flame kernel development and subsequent combustion [3]. Elucidating the fundamental mechanisms controlling the ignition process in these systems is therefore critical.

Given the challenges in measuring key parameters in reacting flows, numerical simulation with detailed reaction mechanisms has emerged as a primary method for ignition studies. There are several methods to model ignition, such as imposing a high-temperature zone [4] or burnt gas [5] locally, as well as setting a spark through the addition of a source term in the energy conservation equation [6]. The approach using an electric spark has been shown to be reliable and robust [7]. Various factors that influence the ignition process with an electric spark have been investigated numerically [8,9]. Owston et al. [10] assessed the effect of initial spark placement within the flammability limits of hydrogen/air mixture, and it was found that the location of ignition did not appreciably affect the flame displacement speed. Han et al. [11] determined the quenching distance and explored the effects of equivalence ratio, electrode gap distance, and electrode radius on minimum ignition energy (MIE) using detailed chemical kinetics of methane/air combustion. The results showed that the size of the electrodes significantly affects the MIE within the quenching distance but does not affect it above the quenching distance. Later, Wang et al. [12] investigated the influences of ignition kernel size, mixing layer thickness, and location of ignition kernel in a dimethyl ether (DME)/air mixing layer. The authors found that the increased mixing layer thickness leads to a shorter ignition time. The mixture fraction range covered by the ignition kernel has a great impact on subsequent flame initiation. Chen et al. [6] identified heat loss to the electrodes as a key inhibitor of hydrogen/air ignition. Their work demonstrated that ignition propensity, particularly for large Lewis number mixtures, can be enhanced by increasing the electrode gap to reduce this thermal quenching. Richardson et al. [13] attributed ignition failure in methane/air mixtures to the interplay between excessive dissipation and local mixture flammability. They observed that regions with very low scalar dissipation may lack sufficient fuel, while conversely, flammable regions can experience quenching from excessively high dissipation rates.

In the studies mentioned above, traditional hydrocarbon and hydrogen fuels were considered. As a zero-carbon fuel, the ignition process of ammonia is less well-understood. Lesmana et al. [14] investigated ammonia/air premixed combustion to determine the influence of spark gap and duration on the minimum ignition energy across different equivalence ratios. Both spark gap and duration significantly influence the MIE, with the energy first decreasing and then increasing as these parameters are raised. In a typical non-premixed system, separately injected fuel and an oxidizer form a triple flame upon ignition, which propagates consistently [15,16]. As for the non-premixed combustion of ammonia/air, Fatehi and Renzi [17] investigated a novel combustor design for non-premixed ammonia combustion and found that a staged rich-lean strategy achieved a threefold reduction in ${\mathrm{NO}}_x$ emissions while maintaining high combustion efficiency. Tang et al. [18] evaluated chemical kinetic models against their NO measurements in non-premixed NH₃/H₂ flames and discovered substantial uncertainties, with models overpredicting peak NO levels by more than 1000 ppm. To the best of our knowledge, the ignition process in ammonia/air mixing layers has not been studied in the literature, and the propagation characteristics of a triple flame in ammonia/air mixing layers remain unclear.

Based on the above discussion, this work performs a set of two-dimensional numerical simulations to investigate the forced ignition and flame dynamics in an ammonia/air diffusion combustion mixing layer. The study systematically evaluates the effects of ignition energy, mixing layer thickness, and spark location on ignition success. Furthermore, flame behavior is characterized by analyzing how flame displacement speed responds to variations in flame stretch and scalar dissipation rate for various cases.

2. Model and Numerical Methods

2.1. Configuration

In the present work, a configuration of ammonia/air combustion in a mixing layer is considered. Figure 1 shows a schematic of the computational domain. As can be seen, air and ammonia are in the oxidizer stream and fuel stream, respectively. The size of the computational domain is 25 mm and 60 mm in the x and y directions, respectively. Outlet boundary conditions are used in all directions. A uniform mesh is used with a grid spacing of 50 μm. The velocity field is zero under ambient conditions of 298 K and 1 bar. A hyperbolic tangent function [12,15] is adopted to describe the initial distribution of the fuel along the x-direction in the mixing layer:

$$Y_{{\mathrm{NH}}_3}={\displaystyle \frac{1}{2}}\left(1+tanh\left({\displaystyle \frac{x-x_o}{\Delta h/4}}\right)\right),$$

(1)

where $x_o$ is the center. The mass fractions of ${\mathrm{O}}_2$ and ${\mathrm{N}}_2$ can be expressed as $Y_{{\mathrm{O}}_2}=0.233(1-Y_{{\mathrm{NH}}_3})$ and $Y_{{\mathrm{N}}_2}=0.767(1-Y_{{\mathrm{NH}}_3})$. $\Delta h$ represents the mixing layer thickness, which is a function of the flame thickness $\delta$, defined as [19]:

$$\delta ={\displaystyle \frac{D_{th}}{S_L}}={\displaystyle \frac{\lambda }{{\rho }_u{c}_p{S}_L}},$$

(2)

where $D_{th}$ is thermal diffusivity. $\lambda$ is the thermal conductivity. ${\rho }_u$ and $c_p$ are the density and specific heat, respectively. $S_L$ is the laminar flame speed at stoichiometric condition with $S_L$ = 0.072 m/s. The resultant flame thickness is 0.36 mm.

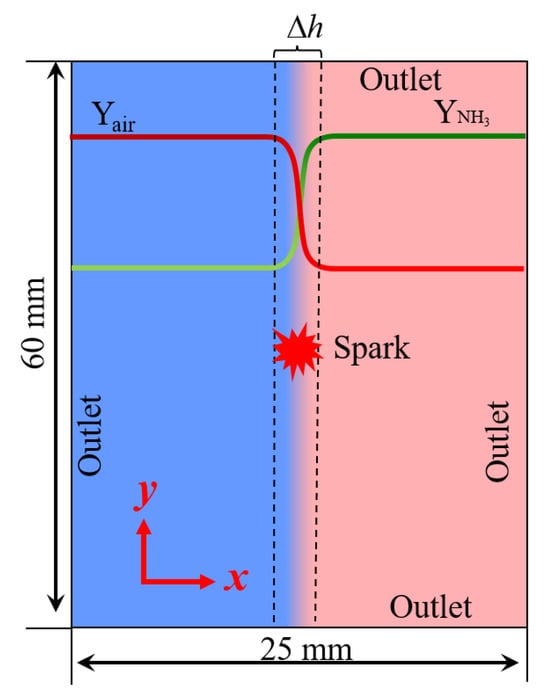
Figure 1. Schematic of computational domain.

The mixture is ignited by a spark, implemented as an energy source at the domain center over a specified duration [20]:

$$q_{\mathrm{ig}}(r,t)=\left\{\begin{array}{cc}{\displaystyle \frac{E_{\mathrm{ig}}}{\pi r_{\mathrm{ig}}^2{\mathrm{\tau }}_{\mathrm{ig}}}\exp \left(-{\left(\frac{r}{r_{\mathrm{ig}}}\right)}^2\right)}\hfill & \mathrm{if}t\le {\mathrm{\tau }}_{\mathrm{ig}}\hfill \\ 0\hfill & \mathrm{if}t>{\mathrm{\tau }}_{\mathrm{ig}}\hfill \end{array}\right.$$

(3)

where $E_{\mathrm{ig}}$ is the total input energy of ignition. ${\mathrm{\tau }}_{\mathrm{ig}}$ and $r_{\mathrm{ig}}$ are the ignition duration time and the ignition kernel size, respectively.

The two-dimensional simulations were conducted to obtain the characteristics of ignition and to evaluate the effects of mixing layer thickness, ignition energy, and ignition position. The parameters are summarized in Table 1. $Z_0$ represents the mixture fracture at the center of the spark. Bilger’s method is used to calculate the mixture fraction [21]. For ammonia/air combustion, the stoichiometric mixture fraction ($Z_{st}$) is 0.142.

Table 1. Simulation parameters.

Cases	${\mathit{E}}_{\mathbf{ig}}$ (J/m)	$\mathbf{\Delta }\mathit{h}$/$\mathit{\delta }$	${\mathit{Z}}_0$
Case 1	5.2	5	0.142
Case 2	5.5	5	0.142
Case 3	5.8	5	0.142
Case 4	5.8	1	0.142
Case 5	5.8	3	0.142
Case 6	5.8	5	0.012
Case 7	5.8	5	0.298

2.2. Governing Equations

The numerical framework integrates the open-source computational fluid dynamics platform OpenFOAM [22] with the chemical kinetics library Cantera [23]. Cantera handles the evaluation of transport properties, while OpenFOAM solves the governing equations for reacting flow using a structured grid. The governing equations are written as [22,24]

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla ·\left(\rho \mathit{u}\right)=0,$$

(4)

$${\displaystyle \frac{\partial \rho \mathit{u}}{\partial t}}+\nabla ·\left(\rho \mathit{uu}\right)=-\nabla \mathit{p}+\nabla ·\mathit{t},$$

(5)

$${\displaystyle \frac{\partial \rho Y_k}{\partial t}}+\nabla ·\left(\rho \mathit{u}{\mathit{Y}}_{\mathit{k}}\right)={\dot{\mathit{w}}}_{\mathit{k}}-\nabla ·{\mathit{j}}_{\mathit{k}},$$

(6)

$${\displaystyle \frac{\partial \left(\rho h\right)}{\partial t}}+\nabla ·\left(\rho \mathit{u}h\right)=-\nabla ·\dot{\mathit{q}}+{\displaystyle \frac{\partial \mathit{p}}{\partial \mathit{t}}}-\sum _{\mathit{k}}{\mathit{h}}_{\mathit{k}}^{\mathit{o}}{\dot{\mathit{w}}}_{\mathit{k}}+{\mathit{q}}_{\mathrm{ig}},$$

(7)

where $\rho$ is the density, $\mathit{u}$ is the fluid velocity, p is the pressure, $\mu$ is the dynamic viscosity, $Y_k$ is the mass fraction of species k, $\mathit{t}$ is the viscous stress tensor, and ${\dot{w}}_k$ is the reaction rate. ${\mathit{j}}_{\mathit{k}}$ is the diffusion mass flux for the mixture-averaged model and is calculated as ${\mathit{j}}_{\mathit{k}}=-\rho D_k\nabla Y_k$. $D_k$ is the diffusion coefficient of species i and is computed based on the Chapman–Enskog solution of the Boltzmann equations [25]. $\mathit{h}$ is the total sensible enthalpy, and ${\mathit{h}}_{\mathit{k}}^{\mathit{o}}$ is the standard enthalpy of the formation. $q_{\mathrm{ig}}$ is a source term modeling the spark. $\dot{q}$ is the energy diffusion, which calculated as

$$\dot{q}=-{\displaystyle \frac{\lambda }{c_p}}\nabla h_s+\sum _{\mathit{k}}({\displaystyle \frac{\lambda }{c_p}}{h}_{s,k}\nabla Y_k)+\sum _{\mathit{k}}(h_{s,k}\nabla {\mathit{j}}_{\mathit{k}}),$$

(8)

where $\lambda$ is the heat conductivity, and $h_{s,k}$ is the sensible enthalpy of the kth species.

2.3. Numerical Methods

The simulations employ Okafor’s detailed chemical kinetic mechanism for ammonia combustion [26], which comprises 59 species and 356 elementary reactions. This mechanism has demonstrated good predictive capability for flammability limits and laminar flame speeds, showing consistent agreement with experimental measurements [27].

The numerical simulations utilize the Crank–Nicolson scheme for time integration and a fourth-order interpolation scheme for spatial discretization. Pressure–velocity coupling is handled with the PIMPLE algorithm. A time step of 5 ×${10}^{-6}$ s is adopted, ensuring a maximum convective CFL number below 0.1. For the evaluation of detailed transport properties, the solver is interfaced with the open-source Cantera library [23], employing a mixture-averaged diffusion model [28].

The solver was validated through a one-dimensional laminar premixed ammonia/air flame simulation at stoichiometric conditions ($\varphi$ = 1), with an initial temperature of 298 K and atmospheric pressure, utilizing the Okafor chemical mechanism. The agreement of the laminar flame profiles of various quantities between the present solve and the open-source library Cantera is excellent, as can be seen in Figure 2.

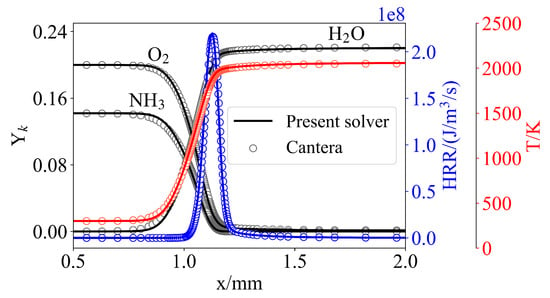
Figure 2. One-dimensional flame results compared to a reference solution computed with Cantera. Open symbols represent the Cantera data, while solid lines denote the simulation results of the present solver.

3. Results and Discussion

3.1. Effect of Ignition Energy on Ignition Process

First, the effect of ignition energy on the ignition process is examined by comparing the results of case 1 ($E_{ig}$ = 5.2 J/m), case 2 ($E_{ig}$ = 5.5 J/m), and case 3 ($E_{ig}$ = 5.8 J/m). Figure 3 shows the evolution of the heat release rate (HRR) for different cases. The red, blue, and yellow lines represent the iso-lines of the stoichiometric mixture fraction ($Z_{st}$ = 0.142), the lean flammability limits ($Z_{lean}$ = 0.101) and the rich ($Z_{rich}$ = 0.164) flammability limits, respectively. Successful ignition is marked by the formation of two counter-propagating triple flames, while failed ignition is indicated by flame contraction and continuously decaying HRR. As can be seen, case 1 and case 2, with low ignition energies, result in failed ignition, while case 3, with a high ignition energy, ignites successfully.

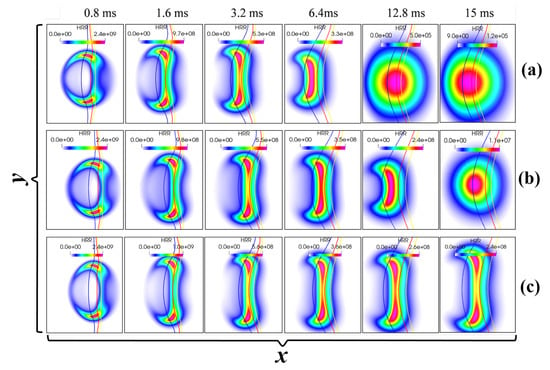
Figure 3. Temporal evolution of HRR field for fixed $r_{\mathrm{ig}}$ = 0.5 mm, ${\mathrm{\tau }}_{\mathrm{ig}}$ = 0.6 ms, and $\Delta h$ = 5$\delta$ but different input energies: (a) $E_{\mathrm{ig}}$ = 5.2 J/m, (b) $E_{\mathrm{ig}}$ = 5.5 J/m, and (c) $E_{\mathrm{ig}}$ = 5.8 J/m. Here, the blue, red, and yellow lines represent $Z_{lean}$, $Z_{st}$ and $Z_{rich}$, respectively (units: HRR: J/m³/s).

The evolutions of the maximum HRR and temperature in the computational domain are shown in Figure 4a and Figure 4b, respectively. The ignition process can be divided into two stages. The first stage is characterized by external energy deposition and intense exothermic reactions within a localized zone, leading to a rapid increase in both heat release rate and temperature. Concurrently, dual triple flames form and propagate bidirectionally along the Z = 0.12 mixture fraction contour. After the transient effects of the spark have completed, the ignition process experiences the second stage, during which, for case 1 and case 2, the two triple flames contract and move closer to each other. Subsequently, the maximum values of HRR and temperature decrease rapidly following energy input cessation and thermal dissipation. However, for case 3, the two triple flames continue to propagate in a self-sustained manner, and the values of the maximum HRR and temperature level off.

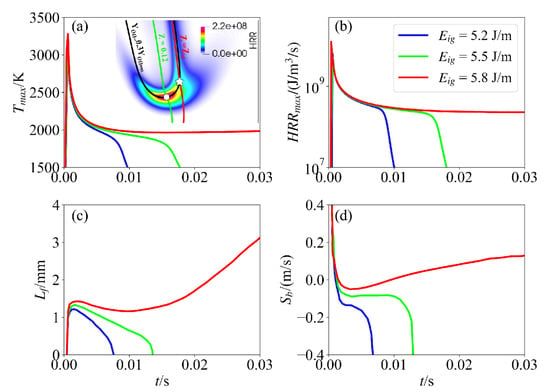
Figure 4. Evolution of (a) maximum temperature, (b) maximum HRR, (c) flame location, and (d) flame propagation speed as time at different ignition energies for unsuccessful ($E_{\mathrm{ig}}$ = 5.2 and 5.5 J/m) and successful ($E_{\mathrm{ig}}$ = 5.8 J/m) ignition.

To quantify the flame propagation, the location of the leading point with the maximum HRR along the y direction, denoted as $L_f$, is tracked, as shown in Figure 4c. The flame propagation speed, defined as $S_b=d{L}_f/dt$, is presented in Figure 4d. It is seen that the flame propagation speed varies non-monotonically in time. In particular, it initially decreases with time due to the termination of the ignition energy deposition. During this period, the flame is over-driven by the ignition energy. Afterwards, the trend of $S_b$ reverses, and its value increases after reaching a minimum value for the case with successful ignition (case 3). In contrast, the value of $S_b$ plateaus for a while and then decreases rapidly due to unsuccessful ignition for case 1 and case 2. A similar behavior was also observed in previous theoretical analyses and experiments [20,29].

The Damköhler number measures the relative importance between the kinetics and dissipation for combustion [30]. In the present work, the local Damköhler number is defined as the absolute value of the ratio of the reaction term to the diffusion term in the transport equation of the ${\mathrm{H}}_2\mathrm{O}$ mass fraction ($Y_P$):

$$Da=\left|{\displaystyle \frac{{\dot{w}}_{H_{2}O}}{\nabla ·(\rho D_{H_{2}O}\nabla Y_{H_{2}O})}}\right|,$$

(9)

where $\rho$ is the density, and $\dot{w_{H_{2}O}}$ is the reaction source term. $D_{H_{2}O}$ is the diffusion coefficient of the P, and $Y_{H_{2}O}$ is the $H_{2}O$ mass fraction.

There is a significant difference in the flame surface area between the successful and unsuccessful ignition cases. Therefore, the flame stretch is used to quantitatively compare the cases with successful/unsuccessful ignition. By definition, the flame stretch $\kappa$ is expressed as [31]

$$\kappa =a_t+S_{d}K,$$

(10)

where K is the flame curvature, which is computed as $K=\nabla ·\mathit{n}$. Here, $\mathit{n}=-\nabla Y_{H_{2}O}/\left|\nabla Y_{H_{2}O}\right|$ is the flame normal vector. $a_t$ is the tangential strain rate, and $S_d$ is the flame displacement speed, which can be expressed as follows:

$$a_t=\nabla ·\mathit{u}-a_n,$$

(11)

$$S_d={\displaystyle \frac{-{\dot{w}}_{H_{2}O}-\frac{\partial }{\partial x_j}\left(D_{H_{2}O}\frac{\partial Y_{H_{2}O}}{\partial x_j}\right)}{\rho \left|\nabla Y_{H_{2}O}\right|}},$$

(12)

where $a_n$ is the normal strain rate given by $a_n=n_i{S}_{ij}{n}_j$, $n_i$ is ith component of the flame normal vector $\mathit{n}$, and $S_{ij}$ is the strain rate tensor component, defined as follows:

$$S_{ij}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right).$$

(13)

The evolutions of the Damköhler number and flame stretch for the cases with various ignition energies at the position of maximum HRR are presented in Figure 5. Several observations can be made. First, external energy deposition activates chemical reactions, rendering the reaction term dominant over diffusion. Therefore, the Damköhler number is greater than unity. Second, the Damköhler number approaches unity as ignition energy deposition terminates. Moreover, the flame stretch also decreases sharply and approaches zero. Finally, for case 1 and case 2, the Damköhler number is less than unity after a critical time, which means that the diffusion term dominant over the reaction term and the flame propagation cannot self-sustain. However, for case 3, the Damköhler number is close to unity, and a balance between the reaction term and diffusion term is achieved. The flame stretch also maintains a positive level. Therefore, it is suggested that the Damköhler number can be used as an indicator for assessing the ignition result. The Damköhler number should be larger than unity for the mixture to successfully ignite.

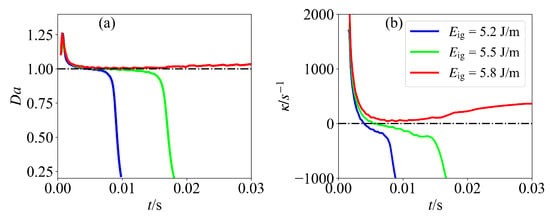
Figure 5. Temporal evolution of (a) Damköhler numbers and (b) flame stretch for various ignition energies at the position of maximum HRR.

For flame modeling applications, the respective contributions of normal ($D_n$) and tangential ($D_t$) diffusion to the total diffusion term are evaluated [12]:

$$D_n=\mathit{n}·\nabla (\rho D_{H_{2}O}\mathit{n}·\nabla Y_{H_{2}O}),$$

(14)

$$D_t=-D_{H_{2}O}K\rho \left|Y_P\right|$$

(15)

Figure 6 plots the temporal evolution of $D_n$ and $D_t$ at the leading point, as well as the total diffusion term for various cases. It is seen that $D_n$ is smaller than $D_t$ for all cases at the beginning of the ignition process, implying that the tangential diffusion is the dominant contributor. However, once the ignition fails, a reversal in the trend between $D_n$ and $D_t$ occurs, with $D_n$ becoming larger. Therefore, the normal diffusion term plays a more crucial role than the tangential diffusion term for the cases with unsuccessful ignition (case 1 and case 2).

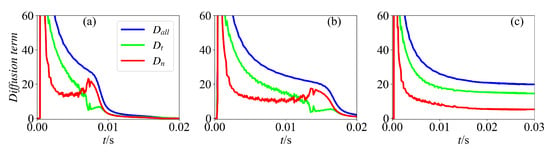
Figure 6. Temporal evolution of tangential diffusion and normal diffusion for H₂O molecule for various ignition energies: (a) $E_{\mathrm{ig}}$ = 5.2 J/m, (b) $E_{\mathrm{ig}}$ = 5.5 J/m, and (c) $E_{\mathrm{ig}}$ = 5.8 J/m.

3.2. Effect of Mixing Layer Thickness on Ignition Process

Figure 7 shows the effects of $\Delta h$ on the ignition process, where the ignition process for the cases with three mixing layer thicknesses of $\Delta h$ = $\delta$ (case 4), 3$\delta$ (case 5), and 5$\delta$ (case 3) is compared. It is seen that two triple flames are formed initially for all cases. Then, the burning area for the case with narrow mixing layers becomes smaller, and eventually, the flame extinguishes. To explain this phenomenon, the evolutions of the Damköhler number, scalar dissipation rate, and flame stretch at the location of the maximum HRR are shown in Figure 8. The scalar dissipation rate, $\chi$, which measures the rate of molecular mixing, is calculated as [32]

$$\chi =2D_{th}{\left|\nabla Z\right|}^2.$$

(16)

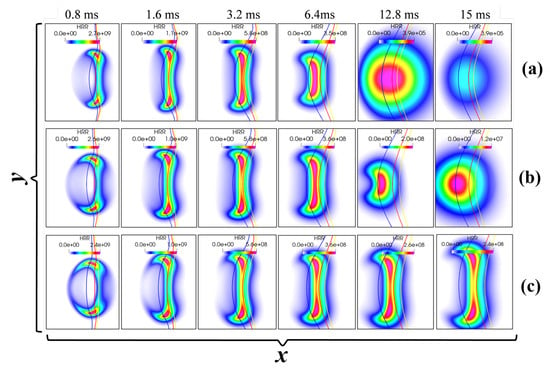
Figure 7. Temporal evolution of HRR for fixed $r_{\mathrm{ig}}$ = 0.5 mm, ${\tau }_{\mathrm{ig}}$ = 0.6 ms, and $E_{\mathrm{ig}}$ = 5.8 J/m but different mixing layer thicknesses: (a) $\Delta h$ = $\delta$, (b) $\Delta h$ = 3$\delta$, and (c) $\Delta h$ = 5$\delta$ (Units: HRR: J/m³/s). Here, the blue, red, and yellow lines represent $Z_{lean}$, $Z_{st}$, and $Z_{rich}$, respectively.

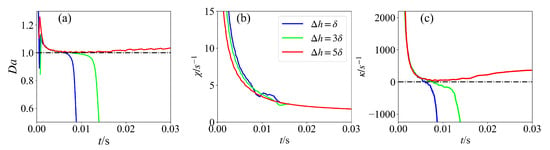
Figure 8. Temporal evolution of (a) Damköhler numbers, (b) scalar dissipation rate, and (c) flame stretch for H₂O atom for various mixing layer thicknesses at maximum HRR.

In Figure 8, for the case with $\Delta h$ = $\delta$, the scalar dissipation rate is larger, and the ignition process is more susceptible to dissipative loss of heat and radicals, resulting in quick flame quenching. Meanwhile, the corresponding Damköhler number of this case becomes less than unity, and the value of the flame stretch also changes from positive to negative. A similar process occurs for the case with $\Delta h$ = 3$\delta$. It is interesting to observe that the profile of scalar dissipation rate fluctuates evidently when the flame quenches. For the case with $\Delta h$ = 5$\delta$, the profile of the scalar dissipation rate is smooth consistently. The Damköhler number of this case is always larger than unity, and the flame stretch maintains a positive value. It is suggested that a high scalar dissipation rate can locally weaken the reactions due to heat and species loss, and hence, the ignition is retarded. Low scalar dissipation rate, in contrast, allows the species and temperature to accumulate during the induction time, which leads to ignition. Overall, it is indicated that increasing the mixing layer thickness can promote ignition kernel development.

3.3. Effect of Spark Position on Ignition Process

Attention is now turned to the effect of the spark position on the ignition process. Three ignition locations are selected at coordinates (0,0), (−0.00042,0), and (0.00037,0), corresponding to spark placements in lean (case 6), stoichiometric (case 3), and rich (case 7) mixtures, respectively.

Figure 9 shows the evolution of the HRR for different cases. Compared to the case with the spark located at the iso-line of the stoichiometric mixture fraction (baseline case), the ignition becomes more difficult when the spark position is placed in the lean or rich mixture. This behavior is attributed to the spark’s mixture fraction coverage. The spark spans over a wide range in the mixture fraction space for the baseline case, and thus, the high temperature induced by the spark can ignite the mixture successfully. However, for the case with the spark placed in the lean/rich side, the heat generated by the spark first results in a high-temperature area; then, the ignition is unsuccessful due to the weak reaction rate.

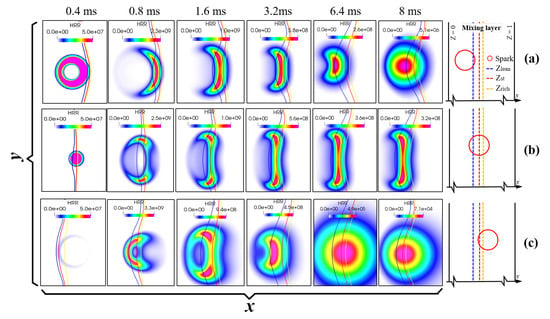
Figure 9. Temporal evolution of HRR field for fixed $r_{\mathrm{ig}}$ = 0.5 mm, ${\tau }_{\mathrm{ig}}$ = 0.6 ms, $E_{\mathrm{ig}}$ = 5.8 J/m, and $\Delta h$ = 5$\delta$ but different positions of ignition; the spark is placed at (a) $Z_0$ = 0.012 (lean mixture), (b) $Z_0$ = 0.142 ($Z_{st}$), and (c) $Z_0$ = 0.298 (rich mixture) (units: HRR: J/m³/s). Here, the blue, red, and yellow lines represent $Z_{lean}$, $Z_{st}$, and $Z_{rich}$, respectively. The schematic diagrams on the right show the initial location of the spark.

To further understand the effect of the spark position on the ignition process, the evolutions of the Damköhler number, scalar dissipation rate, and flame stretch at the maximum HRR location for various cases are shown in Figure 10. It is readily seen that the Damköhler number is larger than unity, and the flame stretch is positive initially for all cases. However, later, the Damköhler number for the case with the spark placed in the rich mixture becomes less than unity, and the flame stretch becomes negative. This is because the scalar dissipation rate of this case is the highest, which leads to quick flame quenching. The ignition also fails for the case with the spark placed in the lean mixture, despite the low scalar dissipation rate. The reason for this is that the spark covers only a narrow mixture fraction range; therefore, the reaction rate is too low for the flame to survive. The Lewis number could be discussed to explain the results of ignition. The Lewis number of ammonia is about 0.9, which indicates faster mass diffusion than thermal diffusion and enhances flame propagation toward higher reactant concentrations. For the spark located at the rich mixture, this promotes propagation into fuel-rich zones while suppressing development toward lean zones, causing local oxidizer deficiency and extinction. For the spark located at the lean mixture, the same mechanism drives flames toward even leaner regions, accelerating heat loss to excess air while insufficient fuel diffusion from rich zones leads to kernel cooling and failure, thus connecting ammonia’s transport properties directly to its distinctive ignition behavior.

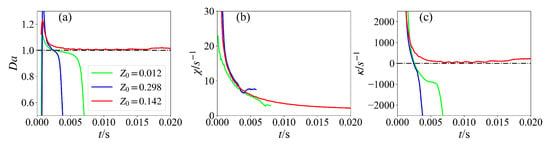
Figure 10. Temporal evolution of (a) Damköhler numbers, (b) scalar dissipation rate, and (c) flame stretch for various ignition positions at maximum HRR.

3.4. Flame Dynamics During Flame Propagation

The flame dynamics at the leading edge of triple flames has been investigated extensively in previous studies with traditional fuels [12]. However, the dynamics of triple flames in ammonia/air mixing layers are not well understood yet. In this subsection, the flame dynamics for the cases with various mixing layer thicknesses are analyzed. Note that $E_{ig}$ of these cases are increased to 6.9 J/m so that all these cases can successfully ignite. Figure 11 illustrates the flame propagation process following successful ignition at a mixing layer thickness of $\Delta h=3\delta$. As can be seen, a typical triple flame structure forms after ignition, characterized by a prominent non-premixed branch and weak premixed branches. Compared to methane and hydrogen triple flames [4,33], the ammonia triple flame exhibits a significantly weaker rich-premixed branch but a relatively stronger diffusion branch. This occurs because ammonia undergoes thorough pyrolysis in the high-temperature burned gas region where the diffusion branch is anchored. The active intermediates generated from pyrolysis then participate in further rapid oxidation reactions, releasing substantial heat that significantly enhances both the intensity and stability of the diffusion branch. This contrast highlights the unique structure of the NH₃/air triple flame. Subsequently, the flame propagates toward the unburned mixture along $Z_{st}$. The lean premixed branch gradually strengthens, whereas the rich premixed branch remains weak. This behavior exhibits notable differences compared to triple flames of methane and hydrogen.

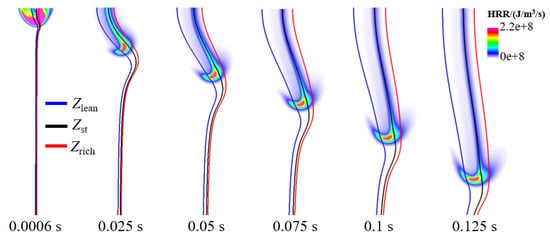
Figure 11. Temporal evolution of flame for the case with mixing layer thickness of $\Delta h=3\delta$.

The leading edge, defined as the location of peak HRR, is used to track flame variables. Figure 12 shows its propagation speed for different mixing layer thicknesses. It is seen that the flame propagation speed changes significantly initially, due to the effect of the initial spark, and at the end of the simulations, due to the boundary effect. A linear quasi-steady propagation regime is clearly observed during $t=$ 0.06∼0.14 s for all cases. The same trend was observed in the ignition process of premixed combustion [34]. In the following, the flame dynamics is analyzed based on the data in the quasi-steady regime.

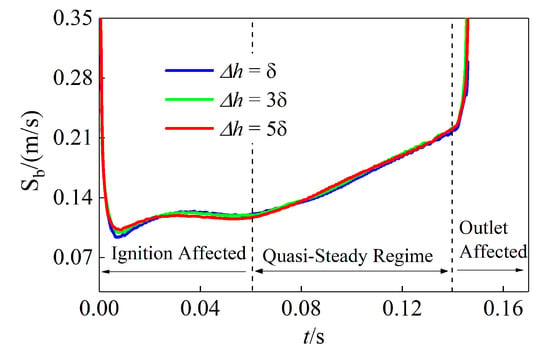
Figure 12. Temporal evolution of flame propagation speed at the leading edge for the cases with different mixing layer thicknesses.

The linear dependence of laminar flame speed on flame stretch in weakly stretched flames is widely adopted in combustion research to obtain the unstretched laminar flame speed [34,35]. Here, the theory is employed to analyze the dynamics of triple flames:

$$S_d^{*}=S_L-L\kappa ,$$

(17)

where $S_d^{*}$ is the density-weighted flame displacement speed, which is calculated as $S_d^{*}=\rho S_d/{\rho }_u$. The Markstein length L is obtained from the negative slope of the $S_d^{*}-\kappa$ curve, where $\kappa$ denotes the flame stretch and $S_L$ the unstretched laminar flame speed.

Figure 13a shows the $S_d^{*}-\kappa$ curves at the leading edge for different mixing layer thicknesses. As can be seen, $S_d^{*}$ exhibits an approximately linear, monotonic decrease with increasing $\kappa$. This result is also consistent with the results reported in Ref. [4] regarding propagating partially premixed DME/air flames. Figure 13a also indicates that the displacement speed is not sensitive to the mixing layer thickness. As a measure of local mixing timescales, the scalar dissipation rate dictates chemical reaction rates and consequently governs triple-flame dynamics. Figure 13b shows the $S_d^{*}-\chi$ curves at the leading edge, illustrating the influence of scalar dissipation rate on triple-flame dynamics. During flame propagation, $\chi$ decreases as a result of transverse diffusion in the y direction. A lower $\chi$ indicates a longer mixing time and more complete chemical reaction, which raises $S_d^{*}$. Thus, flame displacement speed increases with decreasing scalar dissipation rate, showing a consistent negative correlation. This trend remains the same across all cases and is unaffected by mixing layer thickness.

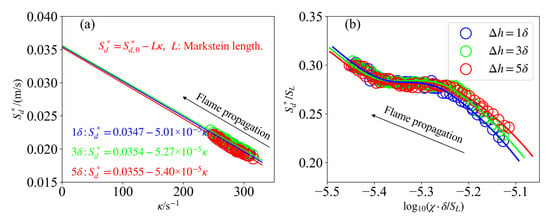
Figure 13. The response of (a) $S_d^{*}$ with $\kappa$ and (b) normalized $S_d^{*}$ with $\chi$ for the cases with different mixing layer thicknesses. The symbols represent simulation results. The solid lines represent linear fitting.

4. Conclusions

This work presents two-dimensional simulations of NH₃/air non-premixed combustion in a mixing layer. The effects of the mixing layer thickness, ignition energy, and ignition position on the ignition process were analyzed. Moreover, the flame dynamics were analyzed. The main conclusions are summarized as follows:

For the case with successful ignition, the Damköhler number exceeds unity, the flame stretch has a positive value, and the tangential diffusion term plays a more important role. However, once ignition fails, the normal diffusion term will be larger than that of the tangential diffusion term. The mixing layer thickness was found to significantly influence the ignition process, as increasing the thickness reduces the scalar dissipation rate and thereby promotes ignition kernel development.The spark position significantly affects ignition outcomes. For the case with the spark placed in the rich mixture, the high scalar dissipation rate causes the flame to quench quickly. For the case with the spark placed in the lean mixture, despite a low scalar dissipation rate, the spark spans over a small range in the mixture fraction space; therefore, the reaction rate is too low for the flame to survive. Flame displacement speed exhibits a negative correlation with both flame stretch and scalar dissipation rate, a trend that remains consistent across all mixing layer thicknesses investigated.

This study provides key insights for designing ammonia-fueled combustion systems like gas turbines and internal combustion engines. First, thicker mixing layers promote ignition by reducing scalar dissipation, suggesting combustion chambers should allow for adequate fuel-air mixing time and space before ignition through optimized nozzle flow and injection. Second, since ignition success strongly depends on spark location, the igniter should be placed where mixtures are near-stoichiometric with low scalar dissipation to ensure robust flame kernel formation. Overall, this work clarifies ignition mechanisms in ammonia–air non-premixed layers, providing a foundation for analyzing ammonia combustion in practical turbulent environments.