A Compact Integrated Equalizer Based on Multi-Stacked Buck-Boost Converter for Large-Scale Energy Storage System

Abstract

Traditional symmetric voltage multiplier-based structures offer low current stress and high scalability. However, the equalization current flowing into each energy storage cell must overcome four diode voltage drops per switching cycle, significantly degrading energy transfer efficiency. A compact integrated equalizer based on multi-stacked buck-boost converters for large-scale energy storage systems is proposed. By replacing diodes with inductors, the design achieves high-efficiency cell balancing even at low cell voltages. The integrated design leverages the boost circuit’s inherent current ripple for driving the balancing system, eliminating extra switches and minimizing size and cost. Additionally, it provides independent balancing channels for each cell, eliminating equalization current superposition. This reduces cell current stress while enabling large-scale system balancing. Experimental validation on an eight-cell setup demonstrated successful balancing with 87.5% system efficiency.

1. Introduction

Large-scale battery energy storage systems (LS-BESS) are pivotal for integrating renewable energy and enhancing grid flexibility [1,2]. However, the LS-BESS performance, lifespan, and safety are fundamentally constrained by cell inconsistencies, which arise from manufacturing variations and operational conditions [3]. The presence of voltage imbalances among cells can trigger overcharging or over-discharging, which in turn accelerates cell degradation and introduces significant safety risks [3]. Thus, advanced battery management, particularly efficient equalization techniques, is critical to ensuring the reliability and economic viability of such systems.

Retired lithium batteries (RLB) from electric vehicles offer the advantages of lower cost and higher energy density compared to traditional lead-acid battery packs [4]. RLB is extensively utilized in “low-intensity” usage scenarios such as electric bicycles, 5G base station energy storage systems, and home energy storage systems [5]. However, even with RLBs undergoing capacity sorting or consistency screening, differences persist among individual cells in terms of lifespan, cycle count, charge–discharge current rates, operating temperatures, and internal resistances [6]. Operationally, the “weakest link” phenomenon dictates that the lowest-capacity cell sets the usable limit for the entire battery pack. Capacity variations give rise to a reduction in overall pack performance and can drive individual cells into abusive operational states (overcharging/discharging), thereby causing accelerated degradation and potential safety incidents, including fire. Therefore, the implementation of a battery equalization system is paramount to ensure the safe and stable functioning of RLB [7].

In the passive balancing approach [8], resistors are configured in parallel with cells at higher voltages to divert and dissipate surplus charge, thus establishing system balance. However, the passive balance method can only ensure cell balance and cannot increase battery pack capacity. Additionally, the passive balance method has lower balancing current and system efficiency. Active balance methods include switch-capacitor [9,10,11], switch-inductor [12,13], multi-winding transformer [14,15,16,17,18], switch-matrix [19,20], voltage multiplier [21,22,23], and wireless power transfer [24,25,26]. The active balance method allocates energy to low-voltage cells, achieving system balance with higher efficiency and a larger balancing current.

Utilizing a network of switches and capacitors, the switched-capacitor equalizer operates by transferring energy from higher-voltage cells to their lower-voltage counterparts. A fundamental limitation of this method is that its balancing current exhibits a strong correlation with the voltage disparity among cells, consequently yielding low efficiency during the final stages of balancing when voltages converge [27]. To address the need for higher balancing currents, Ye et al. developed a method capitalizing on LC resonance through switched-resonant capacitors [28]. Building upon this, Shang et al. further improved the energy transfer pathway with a star-structured switched-capacitor equalizer [29]. This topology enables direct, parallel energy transfer from high-voltage to low-voltage cells, significantly boosting the energy transfer rate.

The switch-inductor-based equalizer is proposed to increase balancing currents, which operate on the same principle as a buck-boost converter [30]. The balancing current can be precisely controlled by modulating the duty cycle of the MOSFET. Conversely, conventional switched-inductor equalizers can only shift energy between immediately neighboring batteries. For superior performance in energy transfer, Xu et al. introduced a novel integrated balancing method based on inductive coupling, which facilitates direct energy exchange between adjacent batteries [13]. A key feature of this design is the use of separate buck-boost converters and coupled inductors for each cell, allowing energy to be shuttled efficiently from high-voltage to low-voltage cells and leading to a markedly improved energy transfer rate.

To minimize the switch count in equalization circuits, a balanced structure utilizing multi-winding transformers has been proposed. Larger balancing currents flow through low-voltage cells using secondary windings with the same number of turns to output the same voltage. To address scalability in large battery packs, Shang et al. introduced an innovative balancing architecture using a modularized multi-winding transformer, employing forward converters within modules to balance individual cells and flyback converters between modules to achieve inter-module balancing [14], eliminating residual magnetism within the transformer. Xu et al. leveraged the Zeta circuit to create an integrated balancing structure. This topology utilizes the circuit’s inherent switches to achieve simultaneous balancing between supercapacitors and the battery pack [31]. Integrated multi-winding transformers leverage additional balancing circuits inherent in DC-DC converters, thereby avoiding the addition of extra switches and resulting in a more compact and cost-effective system.

Uno et al. proposed an integrated balancing structure based on voltage multipliers [32], utilizing the voltage multiplier to output the same voltage at each port, thus achieving battery pack balancing. Uno also improved the multi-stacked buck-boost converters and star-structured switched-capacitor equalizers integrated balancing system to realize balancing functionality without additional switches [33]. An integrated, self-modularized design was introduced by Tan et al., which combines a battery equalizer with a supercapacitor charger to enhance the scalability of voltage multipliers in hybrid electric applications. The battery equalization structure and the supercapacitor charging equalizer are integrated into a circuit with only two switches, three inductors, several energy storage capacitors, and diodes. This integration effectively reduces both the size and cost of the system. Uno et al. first proposed the multi-stacked super buck-based equalization structure, which utilizes inductors instead of diodes to achieve battery pack equalization, effectively improving system efficiency [26]. His subsequent work introduced transformer-less, single-switch integrated chargers, achieving system and circuit simplification through the integration of the charger and equalizer into a single unit [34].

However, as the number of series-connected cells in energy storage systems increases, the traditional voltage multipliers balancing circuit causes high current stress on intermediate cells during balancing, as all balancing current flows through them.

In the realm of balancing circuits, recent advancements are predominantly centered on wireless power transfer and their integrated applications. A notable contribution comes from Zhang et al., who employed a multi-winding transformer in a wireless power transfer-based design to balance numerous voltage multipliers, thereby effectively enhancing system scalability [25,26,34]. Further innovations include the switch-based strategy at receiving ports by Cai et al. for anti-misalignment charging [35], and the multi-layer voltage multiplier topology by Liu et al. for improved transfer efficiency [36]. Nevertheless, all these circuits share a fundamental drawback: the inherent use of voltage multipliers results in significant current stress on individual cells.

To mitigate current stress in cells, Yang et al. [23] presented a voltage equalizer that combines a boost full-bridge input cell with a symmetric VM circuit for long battery packs, thereby alleviating stress on the energy storage units. Owing to its symmetric architecture, energy is transferred directly through individual cells, making the system compatible with both battery and supercapacitor applications. A key drawback of this symmetrical VM system is its doubled voltage drop per cycle. The accumulation of more diode forward voltages per cycle directly undermines its efficiency relative to other topologies at the same cell voltage [37]. This inefficiency is particularly pronounced in real-world scenarios, where the inherently low voltage of individual cells is further diminished by the current being subjected to two diode drops every switching cycle [38], compounding the inherent inefficiency.

This work therefore presents a compact, integrated equalizer based on a multi-stacked buck-boost converter for large-scale energy storage systems. In this design, a boost DC-DC circuit efficiently channels energy into the multi-stacked buck-boost converter. Key contributions of this study include the following:

(1)

The system requires only one transformer, and the additional balancing system does not necessitate extra switches, effectively reducing system volume.

(2)

Employing a symmetric structure ensures that balancing on Bn2 does not pass through Bn1, mitigating issues of uneven current stress that can lead to premature aging in hierarchical battery packs compared to existing structures.

(3)

The proposed equalizer improves the overall energy transfer efficiency of the system by replacing diodes with inductors.

2. Operation Analysis

In the voltage equalizer structure combining a boost full-bridge inverter with a symmetrical voltage multiplier, the balancing current must pass through four diodes during a single operating cycle. This path entails a substantial diode voltage drop, which consequently diminishes the system’s energy transfer efficiency. The schematic diagram of the traditional voltage equalizer based on a boost full-bridge inverter and symmetrical voltage multiplier is presented in Figure 1. To overcome these limitations, a compact integrated equalizer based on a multi-stacked buck-boost converter is proposed for large-scale energy storage systems, as illustrated in Figure 2. By replacing diodes with inductors, the energy transfer efficiency can be effectively improved during the energy transmission process.

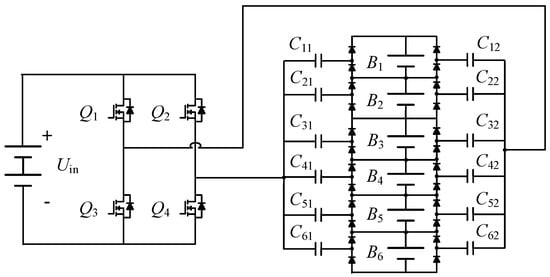
Figure 1. The structure of the voltage equalizer based on boost full-bridge inverter and symmetrical voltage multiplier.

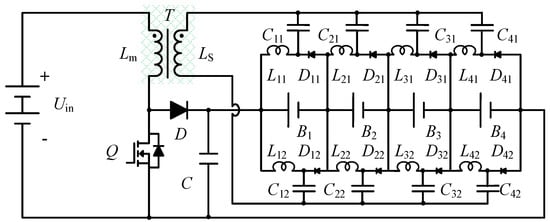
Figure 2. The structure of the symmetric multi-boost-buck based equalizer, and the green part is the drive transformer.

Figure 1 shows the circuit topology of the conventional symmetric VM designed for long battery packs. The DC power supply uses an inverter to power the symmetric VM balance structure, driving the symmetric VM with alternating current. The symmetrical VM is mainly composed of diodes D_n1–D_n4 and transfer capacitors C_n1 and C_n2. The working process of the VM can be categorized into two distinct modes.

Mode I (t₀ − t₁) i_{C1_I} flows into UC₁ through the transmission capacitors C₁₁ and C₁₂ and diodes D₁₁ and D₁₄. i_{C2_I} flow into UC₂ through the transmission capacitors C₂₁ and C₂₂ and diodes D₂₁ and D₂₄, as shown in Figure 3.

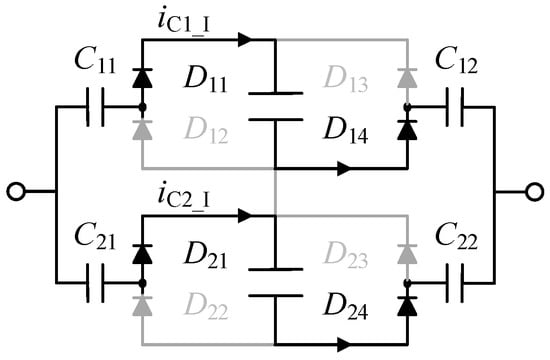
Figure 3. The working process of the symmetric VM in mode I.

Mode II (t₁ − t₂) i_{C1_II} flows into UC₂ through the transmission capacitors C₁₁ and C₁₂ and diodes D₁₂ and D₁₃. i_{C2_II} flows into UC₂ through the transmission capacitors C₂₁ and C₂₂ and diodes D₂₂ and D₂₃, as shown in Figure 4.

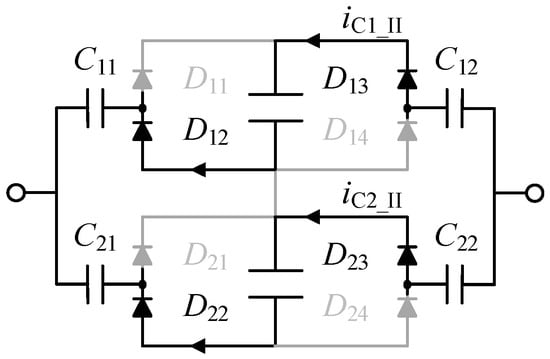
Figure 4. The working process of the symmetric VM in mode II.

Figure 3 and Figure 4 demonstrate that the current path flows through two diodes, thereby ensuring a consistent path length under both positive and negative input voltages. Given a diode forward voltage drop of 0.53 V and a cell voltage of 2.5 V, the power loss solely from the diode accounts for nearly 29.7% in one cycle. When a cell voltage is 3.65 V, the power loss solely from the diode accounts for nearly 22.5% in one cycle, resulting in low energy transfer efficiency for the system.

To improve the equalization efficiency of symmetric VM at low voltage, a multi-Boost-Buck based equalizer is proposed. To avoid double voltage drops in one cycle, a diode is replaced by one inductor in the proposed structure. The working process of the VM is categorized into two distinct modes, presented in Figure 5 and Figure 6.

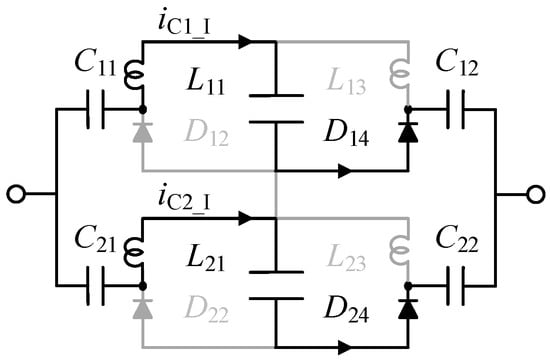
Figure 5. The working process of the symmetric multi-boost-buck based equalizer in mode I.

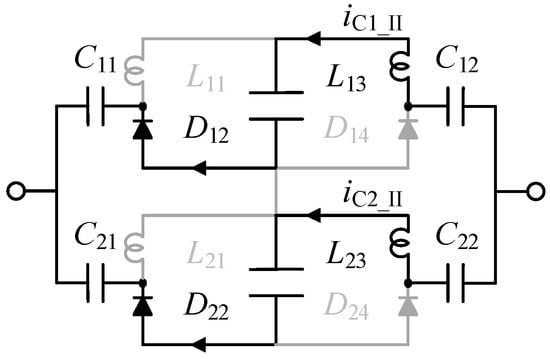
Figure 6. The working process of the symmetric multi-boost-buck based equalizer in mode II.

Therefore, the amount of electricity flowing into the capacitor C_n1 is equal to the amount of electricity flowing out during each cycle.

As shown in Figure 5 and Figure 6, energy flow passes through one diode regardless of whether the input voltage is positive or negative. Given a diode forward voltage drop of 0.53 V and a cell voltage of 2.5 V, the power loss solely from the diode accounts for nearly 17.5% in one cycle. When a cell voltage of 3.65 V, the power loss solely from the diode accounts for nearly 12.6% in one cycle.

Compared to the traditional symmetric VM equalizer, the proposed topology effectively mitigates the detrimental impact of diode voltage drops on system efficiency. Therefore, the proposed equalizer achieves a 10–12% gain in balancing efficiency within large-scale energy storage systems. While inductors were not considered in this simplified analysis, their nature as energy storage components means that, their parameters can be optimized to further enhance system performance.

Design of the Proposed Integrated Equalizer

A scalable, multi-stacked buck-boost topology is introduced for voltage equalization in energy storage systems, as illustrated in Figure 7. The core balancing mechanism employs a symmetrical buck-boost converter design, where the equalizing current is confined to flow solely through its respective cell. The circuit incorporates transfer capacitors (C₁₁–C_nm), a transformer secondary winding (L_S), transfer inductors (L₁₁–L_nm), and diodes (D₁₁–D_nm). Battery units B₁ through B₄, with respective voltages U_B1–U_B4, are connected to the system. Additionally, a boost converter is formed by switch Q, diode D, the main inductor L_m, and capacitor C.

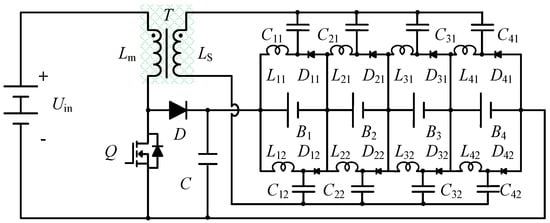
Figure 7. The structure of the proposed equalizer, and the green part is the drive transformer.

Mode I [t₀ − t₁, Figure 8]: As depicted in Figure 8, when switch Q is turned on, the boost converter is activated, energizing inductor L_m. A voltage is then induced in the secondary winding L_S, driving a current (i_{n_I}) that flows through batteries B₁ to B₄. This current loop is completed back to inductor L_m via components C_n2, L_n1, D_n2, and C_n1. Simultaneously, the current i_{Ln_I} through inductor L_n2 continues to conduct via battery B_n and diode D_n2.

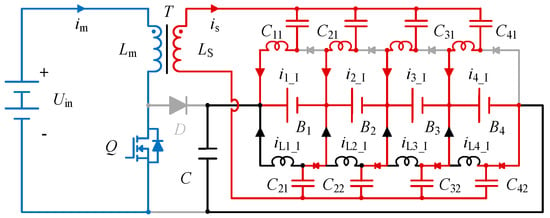
Figure 8. Operating phases of the proposed equalizer at Mode I. The blue part is the battery charging circuit, and the red part is the balancing circuit.

The equation for the freewheeling current i_{n_I} is as follows:

$$i_{nm\_1}(t)=-I_{nm\_1}+{\displaystyle \frac{V_{Bn}}{L_{n1}}}(t-t_0)$$

(1)

where I_{Ln_I} is the initial current of the L_n2.

Mode II [t₁ − t₂, Figure 9]: As depicted in Figure 9, when switch S remains on, the current i_{Ln_I} becomes 0. The boost converter is activated, energizing inductor L_m. This current (i_{n_I}) is completed back to inductor L_m via components C_n2, L_n1, D_n2, and C_n1.

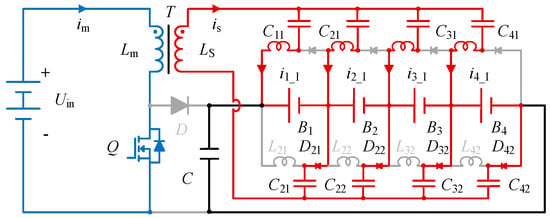
Figure 9. Operating phases of the proposed equalizer at Mode II. The blue part is the battery charging circuit, and the red part is the balancing circuit.

When the power source energizes the inductor L_m, the charging current i_m increases. This current drives the transformer, and the voltage at the multi-winding ports is given by the following:

$$V_{\mathrm{LS}}={\displaystyle \frac{V_{\mathrm{Lm}}}{N}}={\displaystyle \frac{V_{\mathrm{in}}}{N}}$$

(2)

where N is the winding turns ratio of the transformer.

The voltage of the V_Lm satisfies the following:

$${\displaystyle \frac{V_{\mathrm{L}m}}{N}}=\left({\mathrm{V}}_{\mathrm{C}n2}-{\mathrm{V}}_{\mathrm{C}n1}\right)+V_{\mathrm{B}n}+L_{n1}\cdot {\displaystyle \frac{d{i}_{n\_\mathrm{I}}}{dt}}+V_{\mathrm{D}nm}+r_n\cdot i_{n\_\mathrm{I}}$$

(3)

where r_n is the equivalent resistance of the balance circuit loop, and V_Dnm is the voltage drop of the D_nm. V_Cn1 and V_Cn2 represent the voltages across capacitors C_n1 and C_n2, respectively.

Balancing current i_{Ln_I} is given by the following:

$$i_{n\_\mathrm{I}}(t)={\displaystyle \frac{\frac{V_{\mathrm{L}m}}{N}-V_{\mathrm{B}n}-V_{\mathrm{D}n1}}{r_n}}\cdot \left(1-e^{-{\displaystyle \frac{r_n}{L_{n1}}}(t-t_1)}\right)$$

(4)

Balance current I_{Ln_I} is given by the following:

$$\begin{array}{ll}{I}_{n\_\mathrm{I}}& ={\displaystyle \frac{1}{T}}{\displaystyle {\int }_{t_0}^{t_2}\frac{\frac{V_{\mathrm{in}}}{N}-V_{\mathrm{B}n}-V_{\mathrm{D}n2}}{r_n}\cdot \left(1-e^{-\frac{r_n}{L_{n1}}(t-t_0)}\right)dt}\\ & ={\displaystyle \frac{\frac{V_{\mathrm{in}}}{N}-V_{\mathrm{B}n}-V_{\mathrm{D}n2}}{r_n}}\left[(t_2-t_0)+{\displaystyle \frac{L_{n1}}{r_n}}(e^{-{\displaystyle \frac{r_n}{L_{n1}}}{D}_{\mathrm{on}}T}-1)\right]\end{array}$$

(5)

Mode III [t₂ − t₃, Figure 10]: When switch Q is turned off, the boost converter enters the discharging phase, where the combined energy from the DC source and inductor L_m is delivered to charge the battery pack. During this period, a current ripple is observed in inductor L_m. Simultaneously, a reverse voltage is induced in the secondary winding L_S, generating a current i_{1_II}. This current flows out to charge the series-connected batteries B₁ through B₄ and subsequently passes through components C_n2, L_n2, B_n, and D_n1, before returning to inductor L_S via C_n1. Meanwhile, inductor L_n1 maintains its current circulation through B_n and D_n1.

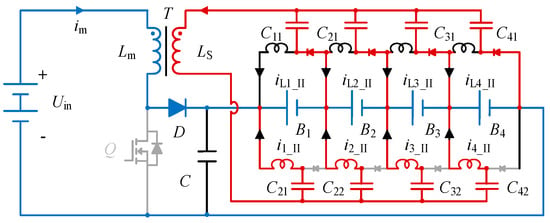
Figure 10. Operating phases of the proposed equalizer at Mode III. The blue part is the battery charging circuit, and the red part is the balancing circuit.

Therefore, the continuous current equation for i_{n_II}.

$$i_{n\_I}(t)=-I_{n\_I}+{\displaystyle \frac{V_{Bn}}{L_{n1}}}(t-t_2)$$

(6)

where I_{n_I} is the initial current of the L_n1. Therefore, upon completion of this phase, the current i_{n_I} will drop to zero.

Mode IV [t₃ − t₄, Figure 11]: When switch Q remains off, this current flows out to charge the series-connected batteries B₁ through B₄ and subsequently passes through components C_n2, L_n2, B_n, and D_n1, before returning to inductor L_S via C_n1.

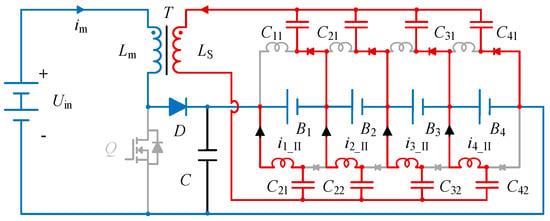
Figure 11. Operating phases of the proposed equalizer at Mode IV. The blue part is the battery charging circuit, and the red part is the balancing circuit.

During the charging of inductor L_m by the power source, the rising magnetizing current i_m drives the transformer. The voltage it establishes across the multi-winding ports can be defined by the following:

$$V_{\mathrm{LS}}={\displaystyle \frac{V_{\mathrm{Lm}}}{N}}={\displaystyle \frac{V_{\mathrm{B}}-V_{\mathrm{in}}}{N}}$$

(7)

The voltage of the V_Lnm is given by the following expression:

$${\displaystyle \frac{V_{\mathrm{B}}-V_{\mathrm{in}}}{N}}=\left(V_{\mathrm{C}n1}-V_{\mathrm{C}n2}\right)+V_{\mathrm{B}n}+L_{n2}\cdot {\displaystyle \frac{d{i}_{n\_\mathrm{II}}}{dt}}+V_{\mathrm{D}n1}+r_n\cdot i_{n\_\mathrm{II}}$$

(8)

Balancing current i_nm is given by the following:

$$i_{n\_\mathrm{II}}(t)={\displaystyle \frac{\frac{V_{\mathrm{B}}-V_{\mathrm{in}}}{N}-V_{\mathrm{B}n}-V_{\mathrm{D}n1}}{r_n}}\cdot \left(1-e^{-{\displaystyle \frac{r_n}{L_{n2}}}(t-t_0)}\right)$$

(9)

Balance current I_{n_II} is given by the following:

$$\begin{array}{ll}{I}_{n\_\mathrm{II}}& ={\displaystyle \frac{1}{T}}{\displaystyle {\int }_{t_2}^{t_4}\frac{\frac{V_{\mathrm{B}}-V_{\mathrm{in}}}{N}-V_{\mathrm{B}n}-V_{\mathrm{D}n1}}{r_n}\cdot \left(1-e^{-\frac{r_n}{L_{n2}}(t-t_0)}\right)dt}\\ & ={\displaystyle \frac{\frac{V_{\mathrm{B}}-V_{\mathrm{in}}}{N}-V_{\mathrm{B}n}-V_{\mathrm{D}n1}}{r_n}}\left[(t_4-t_2)+{\displaystyle \frac{L_{n2}}{r_n}}(e^{-{\displaystyle \frac{r_n}{L_{n2}}}{D}_{\mathrm{off}}T}-1)\right]\end{array}$$

(10)

From (10), the current flowing into the battery over one cycle can be expressed as follows. The higher the actual voltage V_Bn, the greater the balancing current I_{n_I} and I_{n_II}. When V_Bn is smaller, the balance current is larger. Thus, the system enables battery charge balancing.

For the proposed topology, the reference directions for all currents and voltages are defined as follows (Figure 12):

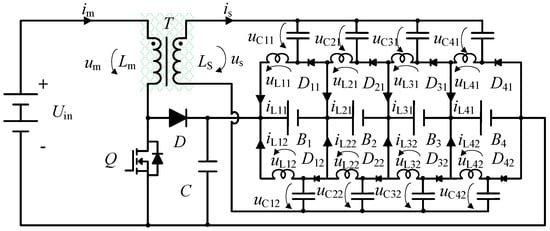
Figure 12. Reference directions of currents and voltages in the proposed topology, and the green part is the drive transformer.

For the loop formed by L_s,C_i1, L_i1, L_i2, and C_i2, the Kirchhoff’s voltage equation is given by:

$$u_{\mathrm{S}}=U_{\mathrm{C}i1}+u_{\mathrm{L}i1}-u_{\mathrm{L}i2}+U_{\mathrm{C}i2}$$

(11)

where u_Li1 represents the voltage across inductor L_i1, u_Li2 denotes the voltage across inductor L_i2, U_Ci1 is the average voltage across capacitor C_i1, and U_Ci2 is the average voltage across capacitor C_i2. According to the volt-second balance principle, the average value of the inductor voltage over one switching period must be zero under steady-state conditions to ensure proper core reset of the magnetic components. Therefore, the averaged form of Equation (11) is derived as follows:

$$U_{\mathrm{S}}=U_{\mathrm{C}i1}+U_{\mathrm{L}i1}-U_{\mathrm{L}i2}+U_{\mathrm{C}i2}=U_{\mathrm{C}i1}+U_{\mathrm{C}i2}=0$$

(12)

Substituting the above expression into Equation (11) yields the following:

$$u_{\mathrm{S}}=u_{\mathrm{L}i1}-u_{\mathrm{L}i2}$$

(13)

For Mode 1, the current flow direction in the circuit is illustrated in Figure 9 below when the circuit operates in DCM.

For the charging loop formed by L_s, C_i1, L_i1, B_i, D_i2, C_i2, the corresponding Kirchhoff’s voltage equation can be written as follows:

$$-u_{\mathrm{S}}+U_{\mathrm{C}i1}+u_{\mathrm{L}i1}+u_{\mathrm{B}i}+U_{\mathrm{D}i2}+U_{\mathrm{C}i2}=0$$

(14)

Substituting the above into Equation (14) gives the following:

$$u_{\mathrm{L}i1}=u_{\mathrm{S}}-U_{\mathrm{B}i}-U_{\mathrm{D}i2}$$

(15)

Since the MOSFET is turned on at this stage, it follows that:

$$\left\{\begin{array}{c}{U}_{\mathrm{in}}=u_{\mathrm{m}}\\ u_{\mathrm{s}}={\displaystyle \frac{u_{\mathrm{m}}}{N}}\end{array}\right.$$

(16)

Substituting this equation back into Equation (15) results in the following:

$$\left\{\begin{array}{l}{u}_{\mathrm{L}i1}={\displaystyle \frac{U_{\mathrm{in}}}{N}}-U_{\mathrm{B}i}-U_{\mathrm{D}i2}\hfill \\ u_{\mathrm{m}}=U_{\mathrm{in}}\hfill \end{array}\right.$$

(17)

Assuming the converter duty cycle is D, the final values of the inductor currents i_Lm.I, i_Li1.I, and i_Li2.I at the end of Mode 1 are given by the following:

$$\left\{\begin{array}{l}{i}_{\mathrm{L}i1.I}={\displaystyle \frac{(\frac{U_{\mathrm{in}}}{N}-U_{\mathrm{B}i}-U_{\mathrm{D}i2})}{L_{i1}}}D{T}_s+I_{\mathrm{L}i.\mathrm{DCM}}\hfill \\ \begin{array}{l}{i}_{Li2.I}=0\hfill \\ i_{\mathrm{Lm}.I}={\displaystyle \frac{U_{\mathrm{in}}}{L_{\mathrm{m}}}}D{T}_s+I_{\mathrm{Lm}.\mathrm{DCM}}\hfill \end{array}\hfill \end{array}\right.$$

(18)

If the turn-off time of the MOSFET prior to Mode 1 is sufficiently long, diodes D_i1 and D_i2 are both off before Mode 1 begins. Thus, in discontinuous conduction mode (DCM), the currents i_Lm.DCM, i_Li1.DCM and i_Li2.DCM are zero.

For Mode 2, the current flow direction in the circuit is shown in Figure 10.

Applying the same method, the KVL equation for the charging loop formed by L_s, C_i1, L_i2, B_i, D_i1, C_i2, can be written as follows:

$$-u_{\mathrm{S}}+U_{\mathrm{C}i1}-U_{\mathrm{D}i1}-U_{\mathrm{B}i}-u_{\mathrm{L}i2}+U_{\mathrm{C}i2}=0$$

(19)

This leads to the following:

$$u_{\mathrm{L}i2}=-u_{\mathrm{S}}-U_{\mathrm{D}i1}-U_{\mathrm{B}i}$$

(20)

At this stage, since the MOSFET is turned off the following:

$$\left\{\begin{array}{l}{U}_{\mathrm{in}}=u_{\mathrm{m}}+U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}\hfill \\ u_{\mathrm{m}}=N{u}_{\mathrm{s}}\hfill \end{array}\right.$$

(21)

Substituting into Equation (20) gives the following:

$$u_{\mathrm{L}i2}={\displaystyle \frac{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}{N}}-U_{\mathrm{D}i1}-U_{\mathrm{B}i}$$

(22)

Meanwhile, the voltage across inductor L_i1 satisfies the following:

$$u_{\mathrm{L}i1}=-U_{\mathrm{D}i1}-U_{\mathrm{B}i}$$

(23)

Therefore, the final current values at the end of this mode can be given by the following:

$$\left\{\begin{array}{l}{i}_{\mathrm{L}i1.II}={\displaystyle \frac{-U_{\mathrm{D}i1}-U_{\mathrm{B}i}}{L_{i1}}}{D}_{\mathrm{a}1}{T}_s+I_{\mathrm{L}i1.I}\hfill \\ \begin{array}{l}{i}_{\mathrm{L}i2.II}={\displaystyle \frac{\frac{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}{N}-U_{\mathrm{D}i1}-U_{\mathrm{B}i}}{L_{i2}}}{D}_{\mathrm{a}2}{T}_s+I_{\mathrm{L}i2.I}\hfill \\ i_{\mathrm{Lm}.II}=-{\displaystyle \frac{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}{L_{\mathrm{m}}}}{D}_{\mathrm{a}2}{T}_s+I_{\mathrm{Lm}.I}\hfill \end{array}\hfill \end{array}\right.$$

(24)

where D_a1 is the ratio of the time required for the current in inductor L_i1 to decrease from i_Li1.I to zero to the switching period in DCM, and D_a2 is the corresponding ratio for the primary winding inductor current decreasing from i_Lm.I to zero. Setting i_Li1.II and i_Lm.II to zero and combining Equations (18) and (24), we obtain the following:

$$\left\{\begin{array}{l}{D}_{\mathrm{a}1}={\displaystyle \frac{(\frac{U_{\mathrm{in}}}{N}-U_{\mathrm{B}i}-U_{\mathrm{D}i2})}{U_{\mathrm{D}i1}+U_{\mathrm{B}i}}}D\hfill \\ \begin{array}{l}{D}_{\mathrm{a}2}={\displaystyle \frac{U_{\mathrm{in}}}{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}}D\hfill \\ i_{\mathrm{L}i2.II}={\displaystyle \frac{\frac{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}=i}}-U_{\mathrm{in}}}{N}-U_{\mathrm{D}i1}-U_{\mathrm{B}i}}{L_{i2}}}\cdot {\displaystyle \frac{U_{\mathrm{in}}}{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}}D{T}_{\mathrm{s}}\hfill \end{array}\hfill \end{array}\right.$$

(25)

After the inductor current i_Li2.II in DCM 2 drops to zero, inductor L_i2 freewheels through the battery and diode, resulting in the following:

$$i_{Li2.III}={\displaystyle \frac{-U_{\mathrm{D}i2}-U_{\mathrm{B}i}}{L_{i2}}}{D}_{\mathrm{a}3}{T}_{\mathrm{s}}+I_{\mathrm{L}i2.II}$$

(26)

Setting the final current i_Li2.III to zero gives the following:

$$D_{\mathrm{a}3}={\displaystyle \frac{\frac{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}{N}-U_{\mathrm{D}i1}-U_{\mathrm{B}i}}{U_{\mathrm{D}i2}+U_{\mathrm{B}i}}}\cdot {\displaystyle \frac{U_{\mathrm{in}}}{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}}D$$

(27)

When the current in inductor L_i2 decreases to zero, the current in the loop becomes discontinuous, and i_Lm.DCM, i_Li1.DCM and i_Li2.DCM are all zero.

Thus, the average currents of the respective inductors can be solved as follows:

$$\left\{\begin{array}{l}{I}_m={\displaystyle \frac{1}{2}}(D_{\mathrm{a}2}+D)I_{\mathrm{Lm}.I}\hfill \\ \begin{array}{l}{I}_{\mathrm{L}i1}={\displaystyle \frac{1}{2}}(D_{\mathrm{a}1}+D)I_{\mathrm{L}i1.I}\hfill \\ I_{\mathrm{L}i2}={\displaystyle \frac{1}{2}}(D_{\mathrm{a}2}+D_{\mathrm{a}3})I_{\mathrm{L}i2.II}\hfill \end{array}\hfill \end{array}\right.$$

(28)

From this, the following can be derived:

$$\left\{\begin{array}{l}{I}_m={\displaystyle \frac{1}{2}}({\displaystyle \frac{U_{\mathrm{in}}}{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}}+1){\displaystyle \frac{U_{\mathrm{in}}}{L_{\mathrm{m}}}}{D}^2{T}_s\hfill \\ \begin{array}{l}{I}_{\mathrm{L}i1}={\displaystyle \frac{1}{2}}({\displaystyle \frac{(\frac{U_{\mathrm{in}}}{N}-U_{\mathrm{B}i}-U_{\mathrm{D}i2})}{U_{\mathrm{D}i1}+U_{\mathrm{B}i}}}+1)\cdot {\displaystyle \frac{(\frac{U_{\mathrm{in}}}{N}-U_{\mathrm{B}i}-U_{\mathrm{D}i2})}{L_{i1}}}{D}^2{T}_s\hfill \\ I_{\mathrm{L}i2}={\displaystyle \frac{1}{2}}({\displaystyle \frac{U_{\mathrm{in}}}{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}}+{\displaystyle \frac{K}{U_{\mathrm{D}i2}+U_{\mathrm{B}i}}}){\displaystyle \frac{K}{L_{i2}}}{D}^2{T}_s\hfill \end{array}\hfill \end{array}\right.$$

(29)

where K is given by:

$$K={\displaystyle \frac{U_{\mathrm{in}}}{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{\mathrm{in}}}}\cdot {\displaystyle \frac{U_{\mathrm{D}}+{\displaystyle \sum _{i=1}^4{U}_{\mathrm{B}i}}-U_{in}}{N}}-U_{\mathrm{D}i1}-U_{\mathrm{B}i}$$

(30)

Based on the average current levels of inductors L_m, L_i1, and L_i2, the required inductor parameters can be calculated.

The duty cycle is controlled to regulate both the input and charging voltages. The resulting relationship between the input and output voltage is derived as follows:

$$\left(1-D\right)V_{\mathrm{B}}=U_{\mathrm{in}}$$

(31)

where D is the duty cycle.

A feedback control loop, utilizing the battery current (I_B) and voltage (V_B) as inputs, adjusts the duty cycle D of switch Q (see Figure 13). This mechanism guarantees that the boost circuit operates in constant-current or constant-voltage charging modes as required.

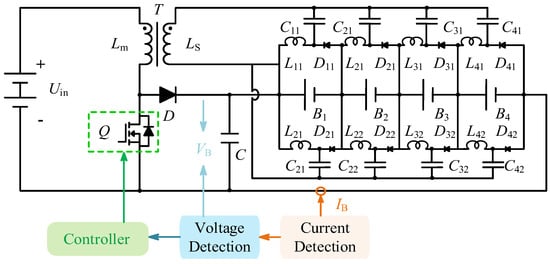
Figure 13. Control block of the proposed method.

3. Implementation and Experimental Results

To demonstrate the proposed voltage equalizer, an experimental platform was built with eight WTGR7V55F00Z ultracapacitor cells (5 F, 0–7.5 V operating range per cell), as shown in Figure 14. The transformer utilizes an iron oxide toroidal core. The key parameters of the proposed design are listed in Table 1.

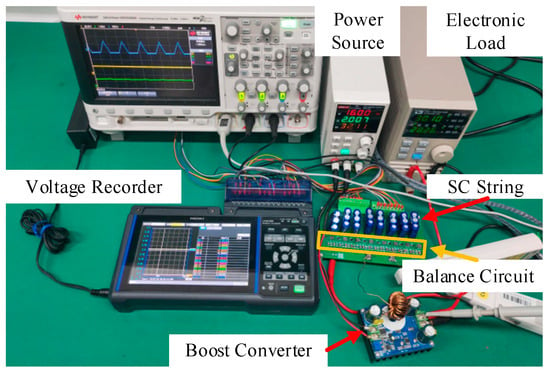
Figure 14. Photograph of the experimental prototype for the eight-series UC modularized equalizer.

Table 1. Specifications of the multi-stacked buck-boost based equalizer.

Symbol	Parameter	Value	Unit
f	Charging Frequency	150	kHz
VE	Input Voltage	16	V
VBnm	Ultracapacitor Voltage	0–7.5	V
C	Stabilizing capacitor	940	μF
VD	Voltage Drop	0.22	V
Lm	Primary Inductance	33.25	μH
L1	Secondary Inductance	12.31	μH
N	21/9	-	-

Figure 15 shows the balance current i_LS in the secondary coil L_S of the balancing transformer. The boost output voltage u_B, and the boost output current i_B.

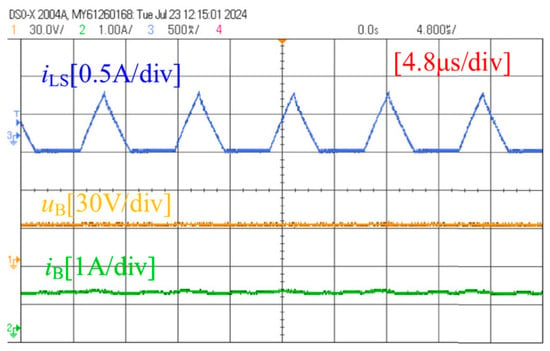
Figure 15. The experimental waveforms currents i_L, V_B, and i_B.

The inherent low capacity of the UC cell rules out single-cycle balancing. Therefore, verification was conducted by paralleling an electronic load (set to constant voltage mode) with the UC string and performing a series of tests under three different voltage distributions.

Case 1: Figure 16 demonstrates a notable convergence in the voltages of the eight UCs. Starting from a highly unbalanced state (3.6140, 3.4655, 3.4200, 3.3580, 4.0195, 3.8990, 3.7685, 3.6980 V), a 100 s balancing process effectively equalized the voltages to 3.6465, 3.6575, 3.6600, 3.6555, 3.6735, 3.6585, 3.6455, and 3.6375 V. This successfully narrowed the maximum voltage gap from 0.6615 V down to 0.036 V.

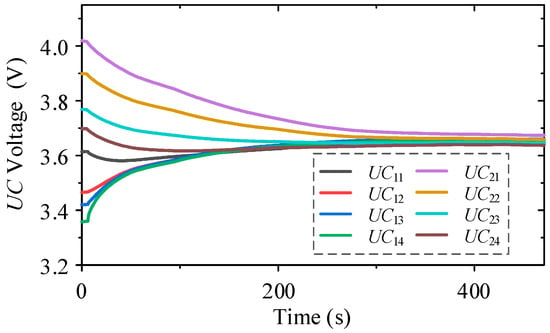
Figure 16. The Multi-stacked buck-boost based equalizer balance eight series-connected UCs in Case 1.

Case 2: Figure 17 demonstrates a marked voltage convergence for the eight UCs. Starting from a significant imbalance (3.6670, 3.7870, 3.9140, 4.0320, 3.3430, 3.4105, 3.4985, 3.5880 V), a 350 s equalization phase successfully brought the voltages to 3.6485, 3.6655, 3.6660, 3.6650, 3.6645, 3.6485, 3.6390, and 3.6355 V. The result was a drastic reduction in the maximum voltage difference, from an initial 0.6890 V to a final 0.030 V.

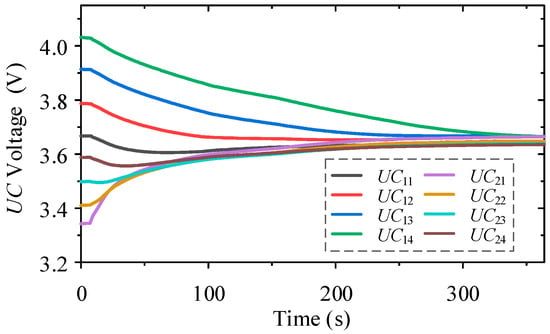
Figure 17. The multi-stacked buck-boost based equalizer balance eight series-connected UCs in Case 2.

Case 3: The voltage change in the batteries during charging is shown in Figure 18. The UC cells’ initial voltages are 3.5650, 3.9750, 3.8560, 3.6550, 3.3830, 3.7615, 3.4590, and 3.5835V, respectively. After about 1000s of charging balance, the voltages become 3.6425, 3.6725, 3.6640, 3.6585, 3.6655, 3.6520, 3.6390, and 3.6375V. The maximum voltage difference reduces from 0.5920V to 0.035 V. The results show that the voltages gradually tend to be consistent.

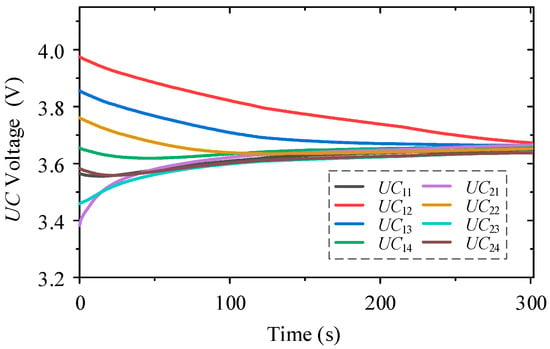
Figure 18. The multi-stacked buck-boost based equalizer balance eight series-connected UCs in Case 3.

The measured system efficiency is illustrated in Figure 19. When the output power is 10–35 W, the system efficiency is about 87.5%.

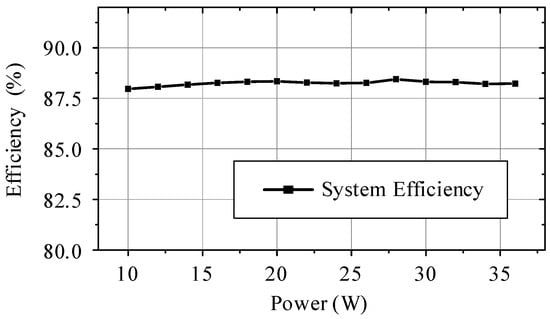
Figure 19. The multi-stacked buck-boost based equalizer balance eight series-connected UCs in Case 4.

4. Comparison with Conventional Voltage Equalizers

This study models an 8-cell series string. The bidirectional switches, each combining two MOSFETs in inverse parallel, are driven by a single circuit. Since all battery systems require a charger/discharger as an essential component, Table 2 compares only the number of additional components needed for the balancing circuit. Components required for the charge/discharge system itself are excluded from this count. The component requirements, such as the number of MOSFETs, inductors, and capacitors, of the proposed design are benchmarked against prior equalizers in Table 2.

Table 2. Comparison of proposed equalizer in terms of components.

Equalizer	Component
	MOS	Driver	Inductor	Capacitor	Diode	Transformer	Resistor
Passive Equalizer [8]	8	8	0	0	0	0	8
Series SC [9]	16	16	0	8	0	0	0
Two-Mode SC [11]	31	16	1	9	1	0	0
L2C3 Resonant [19]	36	20	2	3	0	1	0
Forward-Flyback [14]	10	10	0	0	0	2	0
PS Modulation [16]	16	16	0	16	0	1	0
Modular EA-VM [33]	4	4	2	12	16	2	0
BCI-VM [23]	0	0	1	16	32	0	0
Proposed Equalizer	0	0	17	16	16	0	0

The performance evaluation framework in Table 3 encompasses five comparison categories: control logic (CL), balance speed (BS), scalability, current stress, and system efficiency. A brief description of each characteristic is provided below.

Table 3. Performance comparison between the multi-stacked buck-boost based equalizer and existing.

Balance Methods	CL	BS	Scalability	Current Stress	Efficiency
Passive Equalizer [8]	VB	S	G	S	0%
Series SC [9]	Auto	F	M	M	93.6%
Two-Mode SC [11]	VB	M	G	S	91.1%
L2C3 Resonant [19]	VB	M	E	S	90.1%
Forward-Flyback [14]	Auto	VF	G	M	93.15%
PS Modulation [16]	VB	F	G	M	90%
Modular EA-VM [33]	Auto	VF	E	L	85.6%
BCI-VM [23]	Auto	F	E	S	85%
Proposed Equalizer	Auto	F	E	S	87.5%

• Control Logic: The control logics are primarily classified into two categories. The first method (VB) involves activating the balancing function by controlling switch conduction based on measured cell voltages. The second method (Auto) achieves automatic cell voltage convergence by utilizing either a fixed-frequency/pulse-width PWM signal or the inherent ripple current from the charging process as the driving mechanism.
• Balance Speed: This refers to the convergence speed of a balancing system under a given voltage difference. A faster balance speed enables the system to reach its balancing target more quickly. Balance speeds are typically classified into several grades: Very Fast (VF), Fast (F), Medium (M), and Slow (S).
• Scalability: This refers to the system’s capability to be cost-effectively adapted for use with a long battery string while maintaining its balancing functionality. Scalability is typically classified into several grades: Excellent (E), Good (G), and Medium (M).
• Current Stress: Current stress refers to the current stress on individual cells during the series battery cell equalization process. Whether in integrated or self-equalizing circuits, the impact of charging current must be considered. Scalability is generally categorized into several levels: Large (L), Medium (M), and Small (S).
• Efficiency: The balancing efficiency of a self-balancing circuit refers to the effectiveness of the conversion and transfer process during which “balancing energy” is delivered from higher-energy cells to lower-energy ones. The integrated balancing efficiency refers to the effectiveness of energy distribution from the power source to each individual cell.

5. Conclusions

A symmetric multi-boost-buck circuit for an integrated equalizer is proposed. Derived from the principle of current ripple in a boost converter, the symmetric structure ensures that each cell has an independent current path during balancing, which minimizes the current stress on individual cells. Additionally, the use of inductors instead of diodes significantly boosts the equalization efficiency under low voltage conditions. The proposed integrated equalization circuit was experimentally validated under various voltage distributions, with results demonstrating good voltage convergence performance.

A key challenge for future research is to extend this topology to long battery strings while maintaining the current voltage and current ratings of the components, in order to achieve effective charging balance and discharging balance.