Abstract
This study addresses the problem of minimizing cable costs in Standardized Photovoltaic Power Units (SPPUs) by proposing an integrated inverter placement optimization framework. A high-precision economic model is first established to quantify the cost of both direct current (DC) and low-voltage alternating-current (LV-AC) cables as a function of inverter location. To improve solution accuracy and efficiency, an enhanced particle swarm optimization algorithm, termed the Adaptive Classification Method PSO (ACM-PSO), is developed, featuring population classification strategies as well as adaptive inertia weighting and neighborhood learning strategies. The optimization process incorporates hierarchical trench planning, dynamic combiner-unit partitioning, and multi-scheme layout generation, ensuring that both spatial and economic factors are systematically considered. A case study on Unit 19 of a 350 MW flat-ground PV plant in Xinjiang, China, demonstrates that the proposed method reduces total cable investment to CNY 292,945, achieving a cost saving of 2.3–3.8% compared with conventional layouts. These results confirm not only the methodological innovation of ACM-PSO for constrained nonlinear PV layout problems, but also its practical generalizability, offering a replicable and scalable design paradigm for large-scale PV plants.
1. Introduction
1.1. Background
With the explosive growth of both population and global economic activity, world energy consumption is projected to increase by more than 50% over the next 25 years [1]. Over the past five decades, excessive dependence on fossil fuels has led to a 164.96% increase in carbon dioxide emissions, causing profound climate change and severe environmental challenges [2]. As a result, the large-scale deployment of clean and sustainable energy sources has become one of the central tasks of the energy sector in recent years.
In China, the western regions possess abundant solar resources, and photovoltaic (PV) power generation has attracted strong governmental support due to its inherent advantages of renewability, environmental friendliness, and low maintenance costs. With the rapid expansion of PV plant capacity and installation density, plant-level economic performance has increasingly become a decisive factor in determining project investment returns [3].
Previous studies have shown that, among balance-of-system components, cables represent one of the most expensive cost drivers, typically accounting for 12–18% of the initial capital investment in PV plants [4]. Since the inverter serves as the central energy conversion hub of a PV plant, its placement directly determines the routing and total length of both the direct current (DC) and low-voltage alternating-current (LV-AC) cables [5]. Yet, rule-of-thumb, experience-driven layouts often result in redundant cabling and significant economic losses [6,7]. Field data indicate that misplanned cable paths can inflate total project costs by roughly 8.6% in mountainous installations [8] and by more than 5% in desert, flat-ground projects [9]. Such cost penalties underscore the need for a joint optimization of inverter placement and cable routing to achieve the PV industry’s objectives of cost reduction and efficiency improvement [10,11].
1.2. Literature Review
Most existing PV design optimization studies focus on isolated aspects of the system rather than an integrated inverter-cabling layout [12]. For example, some researchers target higher inverter power density [13,14] or seek the optimal DC/AC sizing ratio [15]. Others evaluate the economics of cable selection or refine the array layout configuration for better performance [16,17]. Tan et al. [18] developed a refined design framework for string inverters but did not quantify the relationship between cable costs and layout variables. Similarly, Xia et al. [19] proposed a tiered cable-selection strategy for desert sites that did not consider dynamic inverter placement. In other international efforts, Monte Carlo simulations and differential-evolution algorithms have been applied to PV layout optimization [20]. Ekici et al. [21] investigated thermal losses across various PV system components and reported that cable losses alone could account for up to 1.7% of the total. Narasimhan et al. [22] proposed an optimization framework for cable selection that simultaneously considered both cost and thermal losses, effectively reducing installation expenses while preserving system efficiency. Similarly, Khan et al. [23] examined cabling constraints under different PV system configurations by developing a cable-length estimation model coupled with a cost evaluation function, and validated the model’s reliability through case studies.
To date, however, two critical gaps remain: (I) the influence of inverter placement on cable-routing economics and its mathematical modeling have rarely been investigated, and (II) intelligent optimization methods specifically targeting inverter deployment in PV systems have scarcely been reported.
1.3. Novelty and Contributions
The optimization of inverter deployment in PV systems is essentially a nonlinear programming problem with multiple strong constraints. Such problems place stringent demands on modeling accuracy as well as on the efficiency and stability of intelligent algorithms. To address these challenges, the main innovations and contributions of this study are as follows:
- High-precision cost modeling: A mathematical model is developed that explicitly quantifies cable installation costs as a function of inverter placement.
- Algorithmic enhancement: An improved adaptive particle swarm optimization (ACM-PSO) algorithm is introduced, significantly enhancing both the accuracy and efficiency of problem solving.
- Generalizable solution framework: A systematic optimization framework for inverter placement in PV systems is established and shown to exhibit strong generalization capability, making it applicable to large-scale PV plant design.
- Practical validation: The proposed method is validated in a large-scale PV project in Xinjiang, where it achieved a 2.3–3.8% reduction in cable installation costs compared with conventional layout approaches.
1.4. Paper Organization
This paper investigates the impact of inverter deployment on cable installation costs in PV systems and proposes an optimization framework based on an improved adaptive particle swarm optimization (ACM-PSO) algorithm. Section 1 introduces the research background and current state of optimization studies in PV systems, highlighting the key problem addressed in this work. Section 2 presents the methodology, including the enhancement strategies for the particle swarm algorithm, the mathematical modeling of cable costs with respect to inverter placement, and the overall optimization framework. Section 3 details the technical validation conducted on a large-scale PV project in Xinjiang. Section 4 discusses the implementation results, and Section 5 concludes this study with the main findings and outlines directions for future research.
2. Methodology
2.1. Modified Particle Swarm Optimizer
Given the well-established rapid convergence capability of particle swarm optimization (PSO) [24], this study applies an enhanced PSO variant termed the Adaptive Classification Method PSO (ACM-PSO) [25], characterized by improved convergence efficiency and solution accuracy.
A large amount of research has demonstrated that although the traditional particle swarm optimization (PSO) algorithm exhibits excellent search speed, it suffers from poor stability, mainly due to the abrupt loss of population diversity in the middle and late stages of the search [26,27]. To preserve population diversity throughout all search phases while simultaneously enhancing algorithmic performance, we introduced a population classification and adaptive control strategy as an improvement to the conventional PSO. In the improved algorithm, the search process divides the population into three categories based on the distribution of particles: leader, elite, and explorer. Different categories of particles use distinct strategies for updating position and velocity. Specifically, particles that discover a new global optimal position during an iteration are called leaders (if no new optimal position is found during an iteration, the leadership remains vacant). Particles with higher objective function values are considered elites, while the remaining particles are classified as explorers.
Benchmark evaluations using basic benchmark functions [28] and the CEC2014 test suite [29] demonstrate that ACM-PSO attained the highest accuracy for over 42.5% of test functions and consistently ranked among the top five algorithms across more than 75% of the repeated test cases.
2.1.1. Leader
In the searching process of ACM-PSO, particles that find a new global optimal position in an iteration are called leaders (if no new global optimal position is found, the leader particle remains vacant). The position of the leader particle is updated not using the traditional update strategy, but instead using a Gaussian mutation strategy, as shown in Equation (1).
where x represents the position information; j is the dimensional index; t is the iteration number; Gaussian is the Gaussian mutation operator; and stands for the standard deviation of the Gaussian distribution, which is updated using Equation (2).
where .
2.1.2. Elite
Elite particles are those with the best fitness in each iteration. The update strategy for these particles is designed to strengthen the algorithm’s local exploitation capability, thereby improving the precision and effectiveness of the algorithm’s overall search process. To further enhance the search efficiency of the algorithm while maintaining stability, an adaptive design has been applied to the position update strategy of the elite particles. As shown in Equation (3), during the global search phase, an accelerated search strategy is employed [30], whereas during the local exploration phase, the traditional position update strategy is used.
where x is the position of particles, v is the velocity information, i is the particle index, r donates a random number in range [−1, 1], R refers to the residual of the iteration, which is calculated by the Formula (4), and ω is a special acceleration factor, which updates using the Formula (5).
where f(·) is the objective function, and u is the mean fitness of the whole population in the t iteration.
The velocity updating strategy for elite particles are given in Equation (6) [31].
where χ is the constriction coefficient, w is the inertia factor, c1 represents the local acceleration coefficient, c2 is the global acceleration coefficient, r1 and r2 donate random values in range [−1, 1], pbest is the individual best position, and gbest is the historical best position of the population.
Compared with the conventional particle swarm optimization algorithm, the constriction factor, inertia weight, and acceleration coefficients in Equation (6) are all adaptively adjusted. The parameters are adaptively adjusted based on the Euclidean distance d between the particle and the global optimum, as calculated by Formula (7).
Specifically,
where χmin = 0.72, and χmax and dmax are calculated using Formulas (9) and (10), respectively.
For the inertia weight, it is updated by Formula (11).
where wmax = 1.2 and wmin = 0.4.
For the acceleration factors, c1 is calculated by Formula (12), and c2 is updated using Formula (13).
where c1,max = 2.5 and c1,min = 0.5.
where c2,max = 3.0 and c2,min = 0.6.
Meanwhile, Zhan et al. [32] demonstrated that the sum of the individual acceleration factor c1 and the global acceleration factor c2 should not exceed 4, as exceeding this value can hinder the stability of the population. Therefore, in the variant proposed in this chapter, if the sum of c1 and c2 exceeds 4, it will be reset to 2, as shown below.
2.1.3. Explorer
The velocity update strategy for explorer particles aims to balance the algorithm’s global search capability with its local exploration ability. Since explorer particles make up the majority of the population, their information update method also needs to maintain population diversity. In ACM-PSO, the position update for explorer particles follows the traditional position update method. The velocity update strategy, as shown in Equation (15) [33], employs a multi-leader strategy to reduce the influence of local positions on the explorer particles.
where is the average value of the personal best position; r is a random value in the range of [−1, 1]; and the update strategy for the inertia weight w is the same as that for elite particles, as shown in Equation (11), but its maximum and minimum values are adjusted to 1.0 and 0.1, respectively. The update strategies for the learning factors c1 and c2 are also the same as those for elite particles, as indicated in Equations (12) and (13).
2.2. Modeling Method for Standardized PV Power Units
2.2.1. Design of Main Cable Trenches and Extraction of String Information
(1) Core Design Parameters of Photovoltaic Power Units
Core parameters of standardized PV power units serve as essential inputs for designing and modeling PV systems. These parameters primarily encompass the geometric layout of the PV arrays, the number of inverters, the total number of PV strings, the road design, and the location of the pad-mounted transformer. By integrating this information, a topological model of the PV generation unit can be developed, which provides essential data support for subsequent cable routing and inverter placement optimization. Typically, the pad-mounted transformer is positioned at the center of the PV array to minimize cable transmission losses.
(2) Main Cable Trench Layout
With the transformer at its center, main cable trenches are arranged in a radial pattern, extending outward in the east, west, south, and north directions to reach the outermost PV strings at the array edges. These main trenches accommodate low-voltage alternating-current (LV-AC) cables that connect the inverters to the transformer. The four-directional radial configuration effectively balances cable lengths, reducing the risk of localized cable congestion and laying a solid foundation for the optimized design of auxiliary cable trenches.
(3) Relationship between Strings and Racks
The number of strings per rack, denoted as M, is a critical variable influencing auxiliary cable trench design. Based on the total number of strings, inverter quantity, and DC/AC sizing ratio within a standardized PV unit, the number of strings connected to each inverter can be calculated as
where Nparallel is the number of strings connected to each inverter, Nstring stands for the total number of strings within a standardized PV power unit, and Ninverter represents the total number of inverters. This parameter directly determines the scale of inverter-combiner units.
2.2.2. Auxiliary Cable Trenches and String Numbering Design
(1) Array Partitioning and Calculation of Auxiliary Cable Trenches
The standardized PV generation unit is divided into two symmetrical sub-arrays, using the array access road as the dividing line. Taking a north–south-oriented PV plant road as an example, the string layout within these sub-arrays can be expressed as
where Arraywest and Arrayeast represent the string layouts of the west and east sub-arrays, respectively; Rw and Cw are the numbers of rows and columns in the west sub-array, respectively; and Re and Ce are the numbers of rows and columns in the east sub-array, respectively. Considering adjacent racks may share a common cable trench, the total number of auxiliary cable trenches for each sub-array can be further determined based on the number of strings (M) installed per rack, as shown below
where FLOOR denotes the rounding-down function, and Nwest and Neast are the numbers of auxiliary cable trenches for the west and east sub-arrays, respectively.
(2) Photovoltaic String Numbering Scheme
This paper adopts a structured string-numbering approach, following a priority rule of “left-to-right, top-to-bottom,” to uniquely index each PV string within the standardized generation unit. Specifically, the numbering can be expressed by Equation (19).
where ai,j and bi,j denote the string identifiers for the west and east sub-arrays, respectively. This systematic numbering convention not only simplifies the spatial positioning of PV strings, but also provides structured data support for combiner-unit partitioning.
2.2.3. Economic Metrics Model
Based on the cable trench layouts and the inverter-combiner-unit partitioning results described previously, the total number of possible inverter installation positions for each inverter-combiner unit equals Nparallel. Specifically, each string within an inverter-combiner unit can serve as a potential installation site. The inverter installation information is thus defined as
where I represents possible inverter information, including installation position (x, y) and connected strings (N).
Subsequently, the length of DC cables from each string to the inverter and the length of low-voltage AC cables from the inverter to the transformer are calculated for each inverter-combiner configuration. An economic indicator model based on total cable cost is defined as
where Eu(ai,j) is the total cable cost associated with inverter installation at position ai,j under scheme u; Lv,DC represents the total DC cable length connecting all strings to the inverter for the corresponding inverter-combiner unit; PDC is the unit price of DC cable; Lv,AC denotes the length of the low-voltage AC cable from the inverter to the transformer; and PAC is the unit price of low-voltage AC cable.
2.3. Optimization Procedure
In summary, the inverter layout optimization problem for standardized PV power units aimed at minimizing cable costs can be formulated as a nonlinear programming problem, as shown in Equation (22). The objective function is to minimize the cabling cost (as defined in Equation (21)), and the decision variables are the characteristics of each inverter (i.e., the number of units it controls and its spatial coordinates), as defined in Equation (20). The optimization solving process based on the improved swarm intelligence algorithm is illustrated in Figure 1.
where g(I) is several performance metric constraints and Ω is the decision domain.
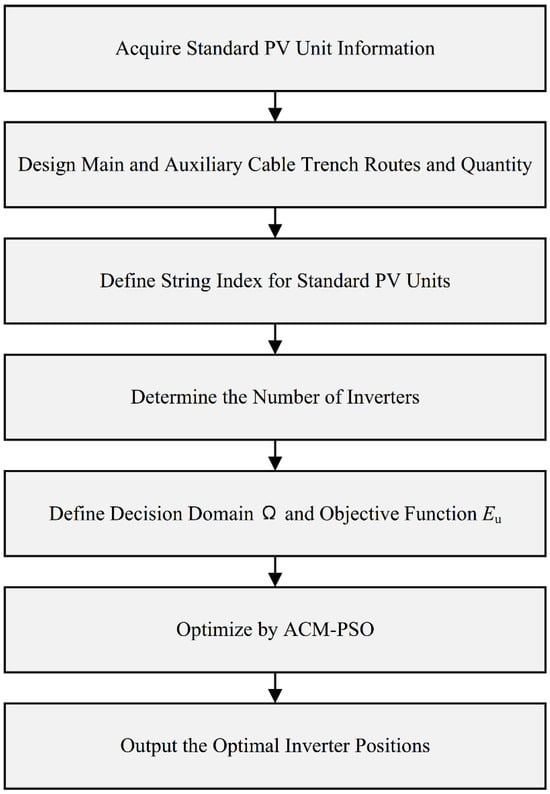
Figure 1.
Procedure of inverter layout optimization using ACM-PSO.
3. Case Validation
The empirical analysis in this study is based on a 350 MW ground-mounted PV project located in Xinjiang, China. The project site features flat terrain with minimal topographical constraints on cable routing, making it representative of standardized PV generation units. Unit #19 was selected as a typical case study. This unit has a rated capacity of 3.3 MW and is equipped with 11 string inverters rated at 300 kW each, and one 3300 kVA pad-mounted transformer. It employs N-type monocrystalline bifacial dual-glass 550 Wp PV modules.
The unit consists of 304 PV strings—four inverters are connected to 27 strings each, while the remaining seven inverters are connected to 28 strings each. The array layout is divided into two symmetrical sub-arrays (west and east) by a central north–south access road, with each sub-array containing 154 strings arranged in 11 rows by 14 columns. The transformer is located at the geometric center of the array, and each mounting rack supports two PV strings. The layout of Unit #19 is illustrated in Figure 2.
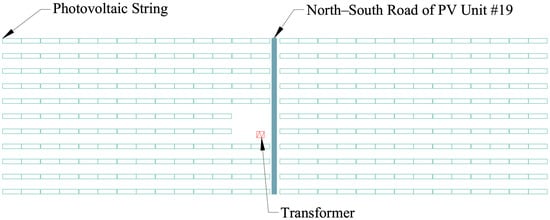
Figure 2.
Layout of #19 standard PV unit.
3.1. Main and Auxiliary Cable Trench Design
Based on the central positioning of the pad-mounted transformer, four main cable trenches are planned to extend radially toward the east, west, south, and north, forming a cross-shaped (“+”) trunk corridor that connects to the outermost PV strings at the array boundary.
For the auxiliary cable trenches, a hierarchical planning strategy is adopted. Using the central north–south access road as the dividing line, the west and east sub-arrays are treated independently, and the number of auxiliary trenches for each is calculated using Equation (18). Substituting the parameters Cw = Ce = 14 and M = 2, the number of auxiliary trenches is determined as Nwest = Neast = 3. Accordingly, three auxiliary cable trenches are assigned to each sub-array, as shown in Figure 3.
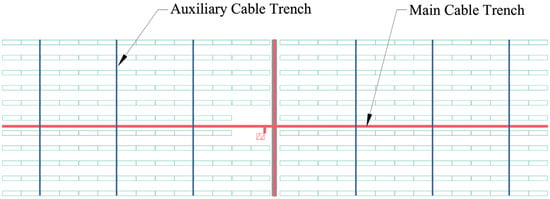
Figure 3.
Cable trench of unit #19.
The spacing between auxiliary trenches is dynamically adjusted according to the PV string layout to ensure that adjacent mounting racks share the same trench path, thereby reducing redundant cable routes and improving layout efficiency.
3.2. Inverter Combiner-Unit Partitioning Scheme
The string numbering results for Photovoltaic Power Unit #19, obtained according to Equation (19), are shown in Equation (23).
3.3. Economic Metrics Model Parameters
The DC cable model adopted in this project is GF-WDZCEER23-125-DC1800V−2 × 4 mm2, and the low-voltage AC cable model is ZRC-YJLHY23-1.8/3 kV-3 × 240 mm2. Both cable types comply with design specifications and voltage drop requirements. The unit prices are PDC = 9 CNY/m for DC cables and PAC = 80 CNY/m for low-voltage AC cables. These parameters are applied in the economic indicator model established in Equation (21).
4. Results and Discussions
4.1. Cable Cost Comparison Across Different Schemes
The improved ACM-PSO algorithm was employed to optimize the objective function. For performance evaluation, the four lowest-cost schemes identified during the optimization process were selected for comparative analysis, as summarized in Table 1.

Table 1.
Comparison of the four lowest-cost schemes.
As shown in the table, Scheme 1 achieves the lowest total cable cost of CNY 292,945 with a combination of 17,705 m of DC cables and 1670 m of LV-AC cables, representing the optimal economic performance. Compared with the second-best Scheme 2, the cost reduction reaches 2.3%, and compared with Scheme 4 (CNY 304,353), the saving rate further increases to 3.8%. It is worth noting that although Scheme 2 shortens LV-AC cable length to 1393 m, its DC cable length increases by 18.3% relative to Scheme 1, resulting in only the second-best overall cost.
In summary, the cost variation pattern highlights the importance of parameter coordination in multi-objective optimization. The cost differences between schemes primarily stem from the nonlinear trade-off between DC and LV-AC cable lengths.
4.2. Spatial Layout Analysis of the Optimal Scheme
Figure 4 presents the array layout of Unit #19 under Scheme 1. The defining feature of this configuration is the concentration of inverters at the intersections of main and auxiliary cable trenches, which optimizes DC and LV-AC cable lengths in a coordinated manner—embodying the core logic of cable cost minimization and significantly reducing overall cable expenditure. The analysis reveals the following:
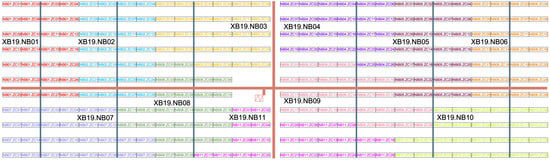
Figure 4.
The inverter positions of the optimal scheme for #19 standard PV power unit. Note: The different colors in the figure indicate the sub-units assigned to different inverters.
(1) Axial linear distribution of inverters—Inverters are arranged along the axes of the main and auxiliary cable trenches, with an average distance of 152 m from the transformer. This layout leverages the radial topology of the trench network to position inverters along the primary LV-AC transmission corridors, effectively minimizing cross-zone LV-AC cable routing requirements.
(2) Block-continuous string layout within combiner units—Strings in each inverter-combiner unit are arranged in contiguous blocks, avoiding non-contiguous jumps between strings. This allows DC cables to follow straight-line paths, reducing their average length by 22 % compared with traditional staggered layouts. For example, the first inverter-combiner unit (28 strings) has a total DC cable length of only 1526 m.
(3) Hierarchical trench planning as structural support—The “+” shaped main trench skeleton (Figure 3) balances DC and LV-AC cabling requirements, while the dynamic configuration of auxiliary trenches (shared between adjacent racks) accommodates the continuous-string wiring pattern. Statistical results indicate that this coordinated mechanism reduces total trench length by 15% and lowers routing conflict rates to below 2%, thereby achieving global optimization of the cable network’s efficiency.
5. Conclusions
5.1. Main Conclusions
This study presents a cable cost–oriented inverter placement method for standardized photovoltaic (PV) generation units. By integrating hierarchical cable trench planning, dynamic combiner-unit partitioning, and a multi-objective cost optimization model, the proposed approach systematically addresses the long-standing issues of cable redundancy and economic inefficiency in conventional PV unit design. Based on empirical validation using Unit #19 of a 350 MW flat-ground PV project in Xinjiang Province, China, the following conclusions are drawn:
(1) Cable Cost Reduction. The optimal scheme yields a total cable cost of CNY 292,945, representing a 2.3% reduction compared to the suboptimal Scheme 2 and a 3.8% saving over Scheme 4. The results confirm that joint optimization of main/auxiliary trench planning and inverter siting has a decisive impact on minimizing both DC and LV-AC cable lengths.
(2) Spatial Layout Characteristics. The optimal configuration showed distinct features of axial convergence and string continuity. Specifically, 63% of inverters were located along auxiliary cable trenches with an average transformer distance of 165 m, reducing LV-AC cable length by 14.6–19.2%. A contiguous string layout within combiner units further shortened average DC cable length, while hierarchical trench coordination reduced total trench length and routing conflicts.
(3) Indicative generalizability. Although validated through a single case study, the framework highlights a systematic approach that could be adapted to different site conditions. Nevertheless, its broader applicability requires further testing across diverse PV plant scales and terrains before definitive generalizations can be made.
5.2. Limitations and Future Works
(1) Robust, multi-objective optimization. Future works should extend ACM-PSO to handle chance-constraints and robustness (e.g., cable-price volatility, demand uncertainty), jointly optimizing cost, reliability (N-1 inverter redundancy), constructability, and environmental impact. They should explore hybrids with DE/CMA-ES and topology-aware warm starts, plus GPU-parallel implementations.
(2) Learning-augmented solvers. Future works should train surrogate models (Kriging/XGBoost) and graph neural networks to rapidly predict DC/LV-AC lengths and trenching effort, and use active learning to refine surrogates during searches. They should investigate reinforcement learning for adaptive operator selection within ACM-PSO.
(3) Lifecycle economics and O&M. Future works should move beyond CAPEX to include cable losses, degradation, thermal derating, failure/repair logistics, and carbon cost, enabling true LCOE-driven placement with sensitivity/uncertainty analyses.
Author Contributions
Conceptualization, M.Z. and J.W.; methodology, M.Z. and X.G.; software, M.Z.; validation, R.T., Y.W. and L.C.; formal analysis, M.Z.; investigation, M.Z. and J.W.; resources, Y.W. and L.C.; data curation, M.Z. and J.W.; writing—original draft preparation, M.Z. and X.G.; writing—review and editing, J.P. and Q.H.; visualization, M.Z.; supervision, Q.H. and J.P.; project administration, Q.H.; funding acquisition, Q.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Project of Power China Guiyang Engineering Corporation Limited, grant number YJ2022-13; Guizhou Provincial Science and Technology Program Project, Achievement Transformation and Industrialization Program [2025] General 003; Guizhou Provincial Science and Technology Program Project, Science and Technology Support Program [2025] General 098.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Authors Meng Zhang, Jixuan Wei, Rong Tang, Qin Hu, Yang Wang and Li Chang are employed by the company Power China Guiyang Engineering Corporation Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Xu, Y.; Gan, X.; Pei, J.; Wang, W.; Chen, J.; Yuan, S. Applications of Artificial Intelligence and Computational Intelligence in Hydraulic Optimization of Centrifugal Pumps: A Comprehensive Review. Eng. Appl. Comput. Fluid Mech. 2025, 19, 2474675. [Google Scholar] [CrossRef]
- Gan, X.; Pei, J.; Pavesi, G.; Yuan, S.; Wang, W. Application of Intelligent Methods in Energy Efficiency Enhancement of Pump System: A Review. Energy Rep. 2022, 8, 11592–11606. [Google Scholar] [CrossRef]
- Ding, M.; Xu, Z.; Wang, W.; Wang, X.; Song, Y.; Chen, D. A Review on Chinaߣs Large-Scale PV Integration: Progress, Challenges and Recommendations. Renew. Sustain. Energy Rev. 2016, 53, 639–652. [Google Scholar] [CrossRef]
- Cheng, R.; Zhou, Q.; Wang, S. Comparison of Cable Costs in PV Power Stations. Sol. Energy 2023, 1, 18–26. [Google Scholar]
- Gao, Z.; Li, S.; Zhou, X.; Ma, Y. An Overview of PV System. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; IEEE: New York, NY, USA, 2016; pp. 587–592. [Google Scholar]
- Zhong, Q.; Tong, D. Spatial Layout Optimization for Solar Photovoltaic (PV) Panel Installation. Renew. Energy 2020, 150, 1–11. [Google Scholar] [CrossRef]
- Xu, S. Research on Modeling and Design Optimization Techniques for Large Photovoltaic Power Station. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2024. [Google Scholar]
- Wang, R. Design Optimization of PV Power Station with Complex Terrain—A Case Study of Mountain PV Project in Shanxi. Eng. J. Wuhan Univ. 2023, 56, 279–283. [Google Scholar]
- Wang, Y.; Liu, B.; Xing, Y.; Peng, H.; Wu, H.; Zhong, J. Ecological Construction Status of Photovoltaic Power Plants in China’s Deserts. Front. Environ. Sci. 2024, 12, 1406546. [Google Scholar] [CrossRef]
- Ding, H.; He, X.; Jing, H.; Wu, X.; Weng, X. Design Method of Primary Structures of a Cost-Effective Cable-Supported Photovoltaic System. Appl. Sci. 2023, 13, 2968. [Google Scholar] [CrossRef]
- Nascimento, E.O.; Monteiro, P.R.D.; Borges, T.T. Optimization of Cables in a Solar Power Plant Using Genetic Algorithms. Int. J. Adv. Eng. Technol. 2023, 16, 608–625. [Google Scholar]
- Khatib, T.; Mohamed, A.; Sopian, K. A Review of Photovoltaic Systems Size Optimization Techniques. Renew. Sustain. Energy Rev. 2013, 22, 454–465. [Google Scholar] [CrossRef]
- Li, Y.; Liu, R.; Liang, C. Comprehensive Benefit Optimization Method for Photovoltaic Inverters Participating in Distribution Network Loss Reduction by Reactive Compensation. Front. Energy Res. 2024, 12, 1502053. [Google Scholar] [CrossRef]
- Vlahinić, S.; Franković, D.; Komen, V.; Antonić, A. Reactive Power Compensation with PV Inverters for System Loss Reduction. Energies 2019, 12, 4062. [Google Scholar] [CrossRef]
- Scarabelot, L.T.; Rambo, C.R.; Rampinelli, G.A. A Relative Power-Based Adaptive Hybrid Model for DC/AC Average Inverter Efficiency of Photovoltaics Systems. Renew. Sustain. Energy Rev. 2018, 92, 470–477. [Google Scholar] [CrossRef]
- Freitas, S.; Serra, F.; Brito, M.C. Pv Layout Optimization: String Tiling Using a Multi-Objective Genetic Algorithm. Sol. Energy 2015, 118, 562–574. [Google Scholar] [CrossRef]
- Mignoni, N.; Carli, R.; Dotoli, M. Layout Optimization for Photovoltaic Panels in Solar Power Plants via a MINLP Approach. IEEE Trans. Autom. Sci. Eng. 2025, 22, 18148–18161. [Google Scholar] [CrossRef]
- Tan, J.; Wang, X.; Zhang, S. Refinement Design of Photovoltaic Power Generation System Based on String Inverter. Rural Electrif. 2023, 1, 55–59+66. [Google Scholar]
- Xia, X.; Peng, Y.; Zhang, N.; Li, J.; Zhu, L. Research on Cable Selection for PV Power Stations in Desert Areas. Sol. Energy 2023, 11, 12–17. [Google Scholar]
- Yao, Y.; Wang, Y.; Jia, H.; Mu, Y. A Novel Differential Evolution Method with a Hierarchical Decoder for the Photovoltaic Layout Optimization Problem. Int. J. Electr. Power Energy Syst. 2025, 164, 110397. [Google Scholar] [CrossRef]
- Ekici, S.; Kopru, M.A. Investigation of PV System Cable Losses. Int. J. Renew. Energy Res. 2017, 7, 807–815. [Google Scholar] [CrossRef]
- Narasimhan, A. Qualitative Assessment of PV System Cable Loss and Practical Cost Optimization. In Proceedings of the 2020 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 2–4 July 2020; pp. 1–6. [Google Scholar]
- Khan, F.U.; Murtaza, A.F.; Sher, H.A.; Al-Haddad, K.; Mustafa, F. Cabling Constraints in PV Array Architecture: Design, Mathematical Model and Cost Analysis. IEEE Access 2020, 8, 182742–182754. [Google Scholar] [CrossRef]
- Nayak, J.; Swapnarekha, H.; Naik, B.; Dhiman, G.; Vimal, S. 25 Years of Particle Swarm Optimization: Flourishing Voyage of Two Decades. Arch. Comput. Methods Eng. 2023, 30, 1663–1725. [Google Scholar] [CrossRef]
- Gan, X.; Xu, Y.; Pei, J.; Wang, W.; Yuan, S. Approaching a Modified Adaptive Swarm Intelligence to Energy Efficiency Enhancement of an Inline Pump. Energy 2025, 325, 136207. [Google Scholar] [CrossRef]
- Freitas, D.; Lopes, L.G.; Morgado-Dias, F. Particle Swarm Optimisation: A Historical Review Up to the Current Developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Tan, D.; Liu, L. Particle Swarm Optimization Algorithm: An Overview. Soft Comput 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary Programming Made Faster. IEEE Trans. Evol. Computat. 1999, 3, 82–102. [Google Scholar] [CrossRef]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2014 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization; Technical Report 201311; Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2013. [Google Scholar]
- Chen, K.; Zhou, F.; Liu, A. Chaotic Dynamic Weight Particle Swarm Optimization for Numerical Function Optimization. Knowl.-Based Syst. 2018, 139, 23–40. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimization. In Proceedings of the 2000 Congress on Evolutionary Computation. CEC00 (Cat. No.00TH8512), La Jolla, CA, USA, 16–19 July 2000; IEEE: New York, NY, USA, 2000; Volume 1, pp. 84–88. [Google Scholar]
- Zhan, Z.H.; Zhang, J.; Li, Y.; Chung, H.S. Adaptive Particle Swarm Optimization. IEEE Trans. Syst. Man Cybern. B 2009, 39, 1362–1381. [Google Scholar] [CrossRef]
- Liu, P.; Liu, J. Multi-Leader PSO (MLPSO): A New PSO Variant for Solving Global Optimization Problems. Appl. Soft Comput. 2017, 61, 256–263. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).