Computational and Experimental Investigation of Additively Manufactured Lattice Heat Sinks for Liquid-Cooling Railway Power Electronics ^†

Abstract

This study investigates the performance of lattice-structured heat sinks based on BCCz unit cells in comparison to conventional straight-fin and pin-fin designs. Various lattice configurations were explored. Numerical simulations and experimental evaluations were carried out to analyze thermal resistance, pressure drop, and temperature distribution under different operating conditions. Among the designs, the BCCz configuration with a circular cross-section was identified as the most promising candidate for integration into the final heat sink demonstrator, offering reliable and consistent performance. A prototype using the BCCz lattice structure was additively manufactured, alongside a conventional design for comparison. The results highlight the superior heat dissipation capabilities of lattice structures, achieving up to a 100% improvement in thermal performance at high flow rates and up to 300% at low flow rates compared to a conventional straight-fin heat sink. However, the pressure drop generated by the lattice structures remains a challenge that must be addressed. This work underscores the potential of optimized lattice-based heat exchangers to meet the severe thermal management requirements of railway power electronics.

1. Introduction

The railway industry is undergoing a major transformation driven by the demand for high-speed, energy-efficient, and environmentally sustainable transportation. This evolution relies heavily on power electronics, which are essential to critical systems such as traction drives, converters, and auxiliary units. The shift toward electric and hybrid railway systems further underscores the need for efficient and reliable power electronics, making effective thermal management a central enabler of technological progress and operational sustainability [1,2,3]. Maintaining these components within their optimal temperature ranges is crucial, as inadequate heat dissipation can lead to overheating, performance degradation, and potentially catastrophic failure [1,4]. These challenges are intensified by high-power loads, harsh operating conditions, and compact configurations typical of railway applications. Moreover, the increasing power density of modern systems amplifies thermal constraints, requiring advanced and efficient cooling strategies to ensure the safety and reliability of railway operations [5].

Various cooling methods are used to manage thermal loads in power electronics, each with specific characteristics that make them suitable for different applications. In addition, heat sinks play a crucial role in dissipating heat from power electronics by increasing the surface area for heat transfer to the surrounding coolant. Liquid cooling has emerged as a viable solution for high-power railway power electronics due to its superior heat transfer capabilities compared to traditional air-cooled systems [6,7,8,9,10].

Conventional heat sinks often feature straight fins, which are relatively simple to manufacture and provide a basic increase in surface area for convective heat transfer [11,12]. Pin-fin heat sinks, characterized by an array of featured pins, offer a further increase in surface area and can be more effective in turbulent flow conditions [13]. Porous structures, particularly metal foams, have been explored for their high surface-area-to-volume ratio, which can lead to enhanced heat transfer in compact applications [14]. However, the adoption of liquid cooling requires the development of heat sinks with enhanced performance, reduced weight, and optimized designs to meet the severe operational requirements of railway systems [15].

Additive manufacturing (AM), commonly referred to as 3D printing, has revolutionized the design and production of heat sinks across multiple industries, including aerospace, automotive, and energy systems [16,17]. The application of additive manufacturing offers significant potential for addressing mentioned challenges by enabling the production of complex heat sink geometries [15,18,19,20] that are otherwise unattainable using conventional manufacturing techniques. Laser Powder Bed Fusion (LPBF) is widely used to fabricate intricate metal lattice structures (LSs) with high surface-to-volume ratios, which are essential for achieving efficient heat transfer by maximizing fluid interaction and heat dissipation while minimizing pressure drop [16,21].

LSs have emerged as a promising alternative to traditional foam structures for heat sink applications, especially with the progress in additive manufacturing technologies [20,22,23,24] that allow for the creation of complex and intricate geometries. They consist of periodic arrangements of unit cells, designed to achieve specific mechanical or thermal properties, such as high surface-area-to-volume ratio, improved fluid mixing, and high design flexibility. Despite these advantages, challenges remain in the widespread adoption of additively manufactured heat sinks. Key limitations include scalability (additive manufacturing processes can be slow and expensive, particularly when large-scale components are required [25]) and surface roughness (the inherent surface roughness of additively manufactured parts can impede fluid flow and increase pressure drop, requiring additional post-processing [26]).

A wide variety of LS topologies exists, each of them with distinct geometric features that influence their thermal and mechanical properties. Examples include BCC (Body Centered Cubic), BCCz (a variant of BCC with additional strut in z direction), FCC (Face Centered Cubic), FCCz (a variant of FCC with additional strut in z direction), and OTL (Octet-Truss Lattice), as well as others like gyroid, diamond, and cube [24,27]. The choice of topology depends on the specific application requirements, considering factors such as the desired heat transfer rate, allowable pressure drop, and mechanical strength.

Porosity, which refers to the ratio of void volume to the total volume of the LS, is a critical design parameter that directly affects both the surface area for heat transfer and the resistance to fluid flow [28]. Optimizing the porosity is essential to achieve a balance between maximizing heat dissipation and minimizing the pumping power required in liquid cooling systems. Different lattice topologies and design parameters, such as strut diameter and cell size, influence the overall pressure loss associated with fluid flow through the structure. Therefore, careful consideration of these factors is necessary to ensure efficient cooling without excessive energy consumption.

Various materials are suitable for additive manufacturing of lattice structure heat sinks. Aluminum alloys and copper alloys are commonly used metals due to their thermal properties [19,29,30,31]. Thermally conductive polymers are also emerging as potential materials for lightweight and electrically insulating heat sinks [32]. The selection of the material depends on the specific performance requirements of the railway power electronics being cooled and the operational environment.

This study extends existing research to evaluate the computational and experimental performance of additively manufactured lattice heat sinks for liquid cooling in railway power electronics. The primary aim is to design and experimentally assess a full scale LS heat sink. The research approach includes:

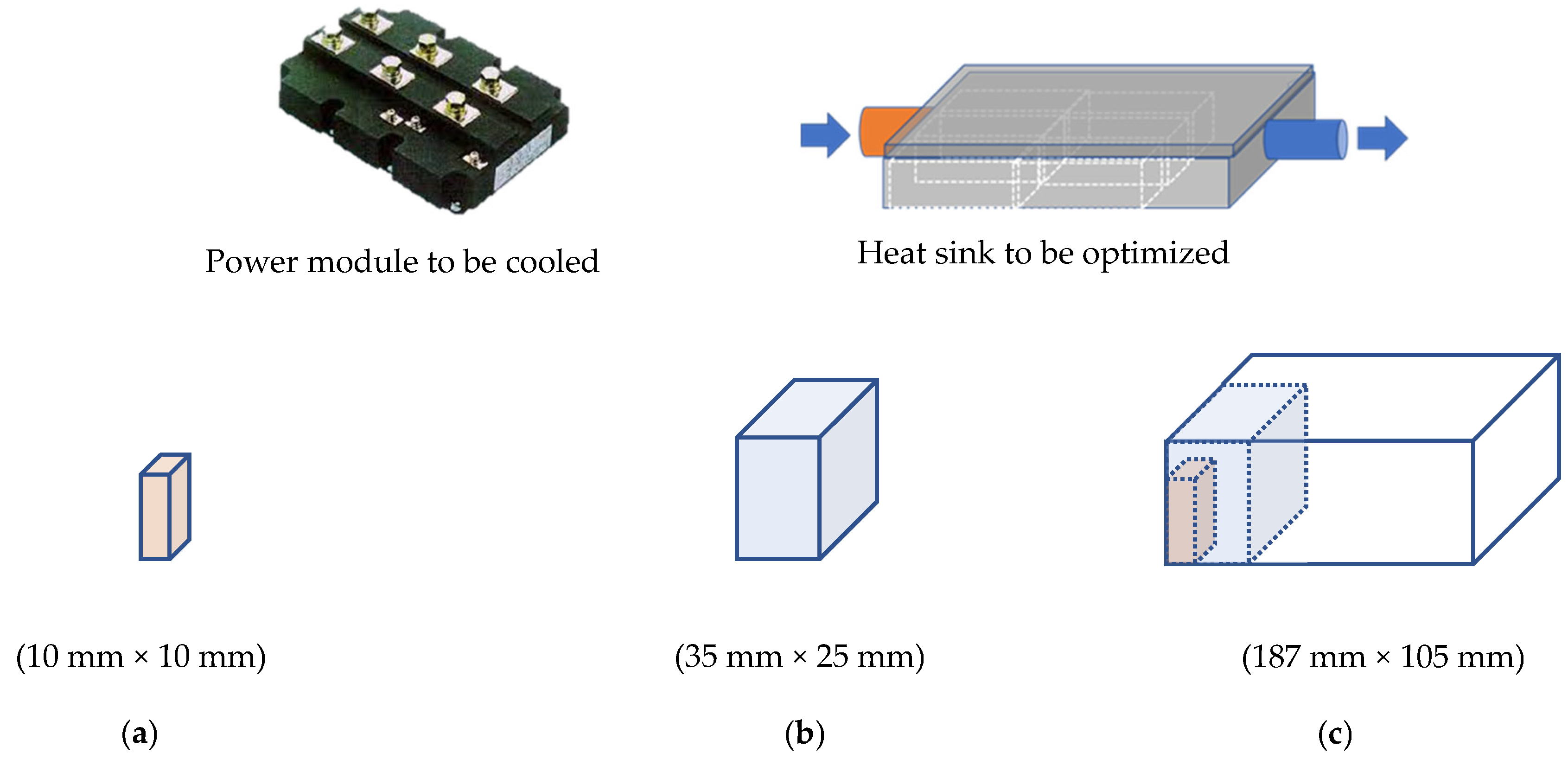
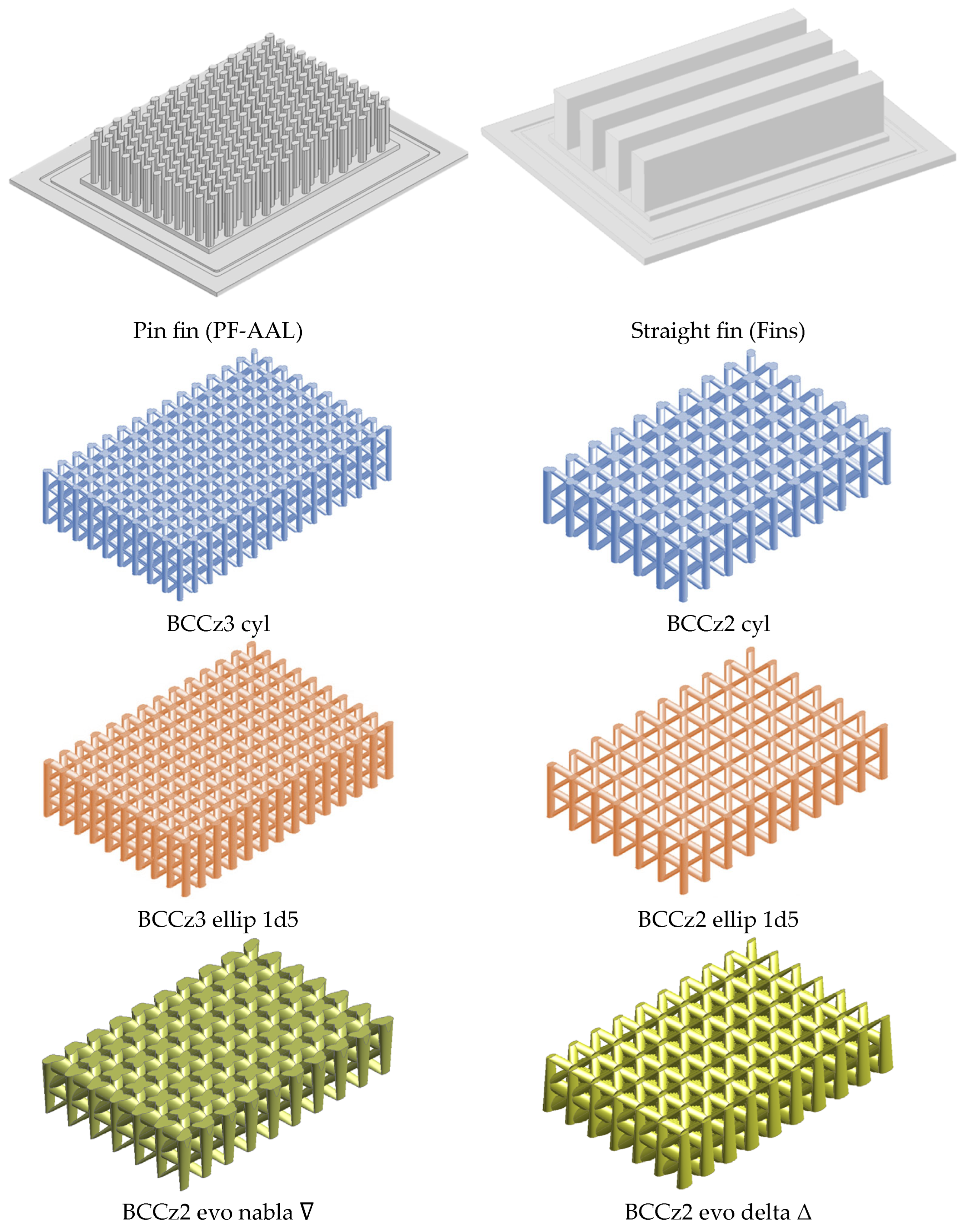
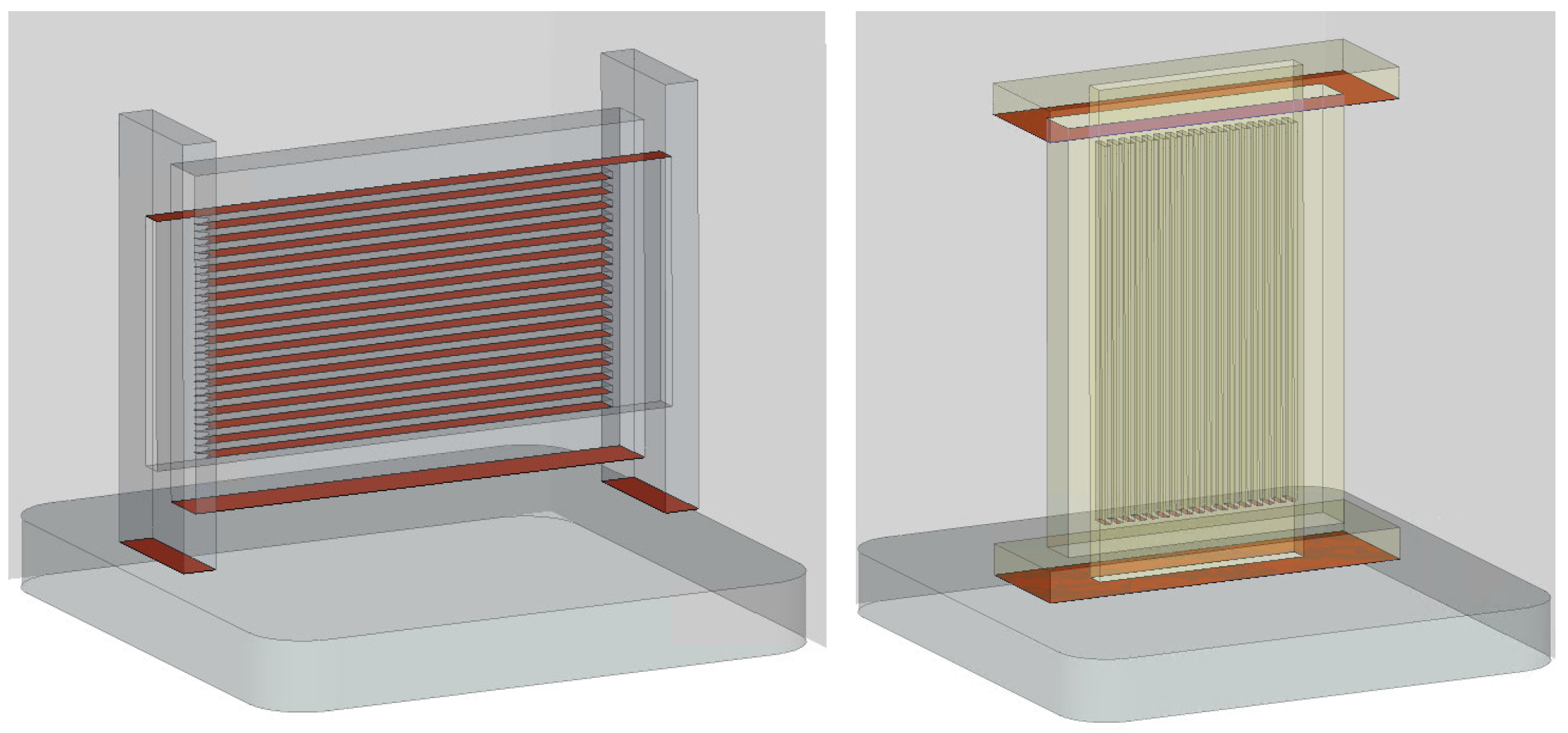
• Evaluating Lattice Topologies: Initial investigations focused on the thermal and hydraulic performance of various LS topologies using a simplified elementary structure (ES) heat sink (Figure 1a) to identify the most efficient topology for further analysis.
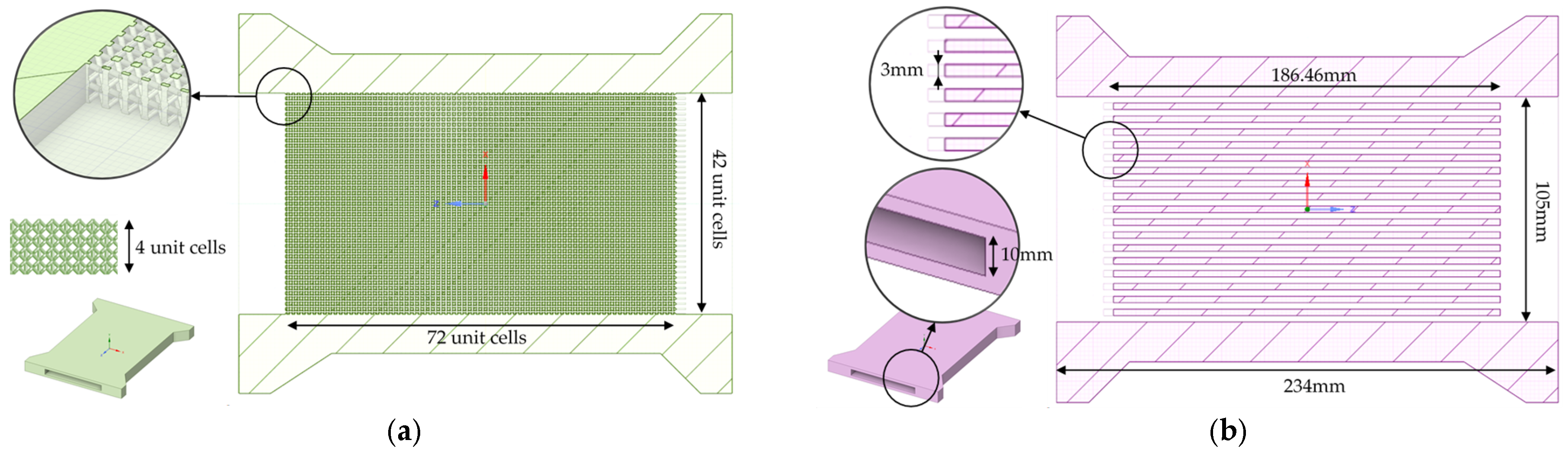
• Detailed Computer Fluid Dynamics (CFD) and Experimental Studies: The selected topology, a BCCz LS, is subjected to extensive CFD simulations and experimental validation. The investigations involve testing a reduced structure (RS) heat sink (Figure 1b) under varying flow rates and inlet temperatures. Comparative performance analyses with conventional straight-fin heat sinks are conducted based on metrics such as thermal resistance, pressure drop, and temperature distribution. Geometrical modification effects on performance were evaluated.
• Full Scale Demonstrator (FSD): The final phase involved designing and manufacturing a FSD heat sink (Figure 1c) using the optimized lattice configurations identified earlier. Its performance is benchmarked against conventional straight-fin demonstrator on a real power module.

The study aims to provide an in-depth understanding of the advantages and constraints of lattice-based heat sinks for railway power electronics cooling. The results contribute to developing innovative thermal management solutions that address the operational and environmental challenges in the railway sector.

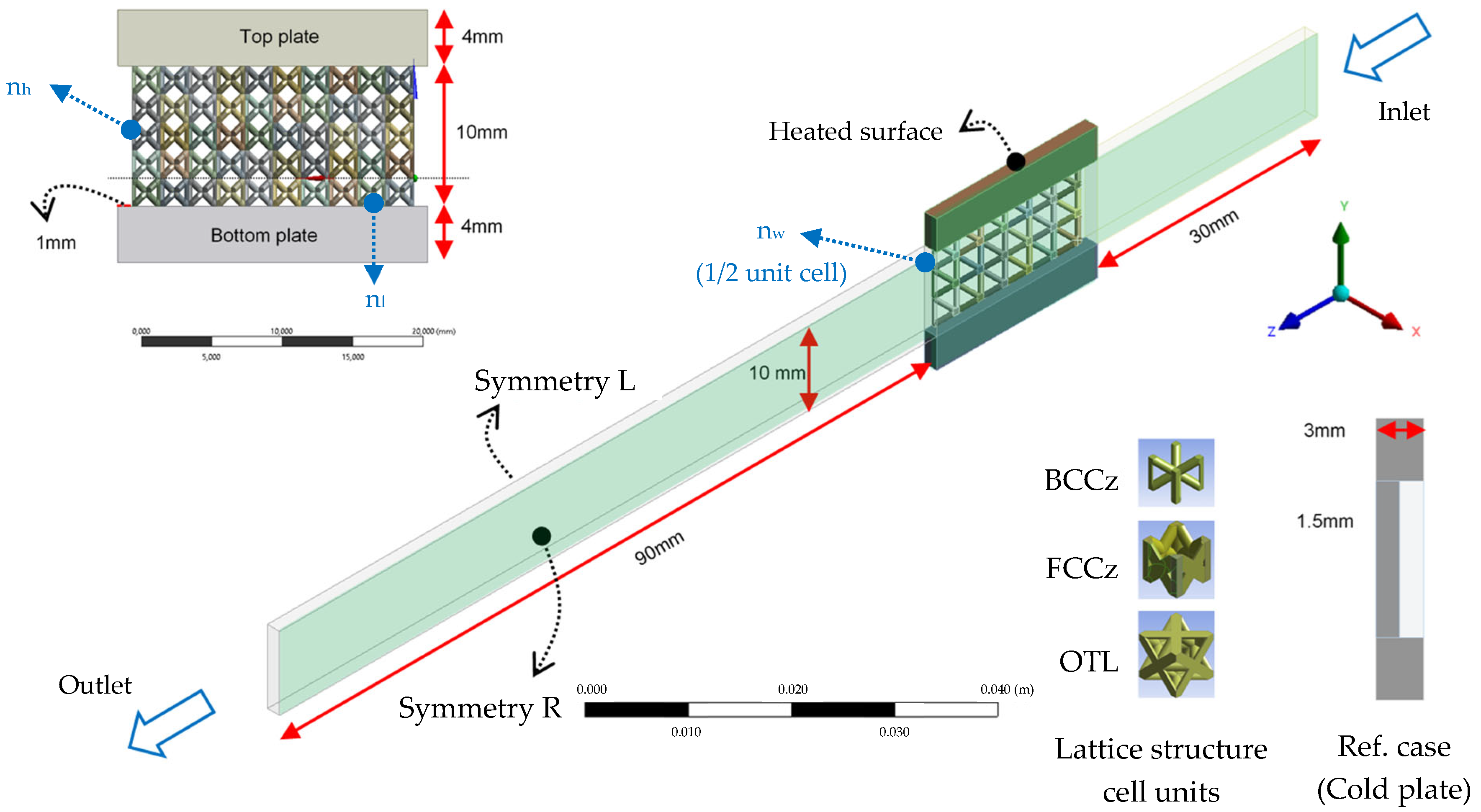
2. Initial Investigation of the Lattice Structure Topologies

First, a comprehensive parametric numerical CFD study using Ansys Fluent (from 2020R1 to 2022R2) was undertaken on an elementary structure (1/2 cell width) to investigate potential lattice configurations for the purpose of enhancing heat transfer in power electronics. Three LS topologies, namely BCCz, FCCz, and OTL, have been selected for evaluation. The primary objective is to identify a lattice configuration that aligns with the railway application requirements. A simplified geometry of a typical cold plate module has been proposed as a reference case for comparison against the new lattice cold plate. Figure 2 shows the details of the numerical model which has been validated against the work of Yun et al. in [23] using both laminar and k-ω SST turbulent models to check their effect on results. To reduce the computational cost, two symmetry planes were considered on either side of the computational domain with a LS composed of a half unit cell along the width (between the symmetry planes). Compared to the complete model, deviations of approximately 3% for temperatures and pressure drop have been obtained. The deviation for velocity is higher at 17% due to the restricted volume of fluid between the two symmetries. However, these deviations are considered acceptable considering the substantial 89% reduction in computation time, making it suitable for the parametric study.

The working fluid is water at V_in = 1 m/s, Tin = 70 °C and P_out = 1.01325 × 10⁵ Pa. A constant heat flux of 120 kW/m² is imposed at the heated surface. In addition, the effect of the heat sink geometrical parameters (strut diameter) was considered, and

Table 1. Geometrical details of parametric study.

Topology nw × nh × nl	BCCz		FCCz		OTL
	d (mm)	Porosity (-)	d (mm)	Porosity (-)	d (mm)	Porosity (-)
1/2 × 4 × 8	0.5	0.8	0.5	0.82	0.5	0.68
	0.6	0.72	0.6	0.77	0.55	0.63
	0.7	0.65	0.7	0.71	0.6	0.57
	0.8	0.56	-	-	-	-
1/2 × 3 × 6	0.6	0.83	0.6	0.82	0.5	0.8
	0.7	0.78	0.7	0.78	0.6	0.74
	0.8	0.73	0.8	0.73	0.7	0.66
1/2 × 2 × 4	1	0.8	1	0.84	0.8	0.78
	1.2	0.72	1.2	0.78	0.9	0.74
	1.4	0.65	1.4	0.72	1	0.68
1/2 × 1 × 2	1.5	0.95	1.5	0.89	1	0.88
	2	0.81	2	0.81	1.5	0.78
	2.5	0.73	2.5	0.78	2	0.65

shows the considered configurations where (n_w × n_h × n_l) in the Topology column represents the number of unit cells along the width, height, and length of the LS, respectively. The flow field is considered as steady.

Figure 3 shows the equivalent thermal resistance (Rth, defined later in Equation (1)) and pressure drop (ΔP) as functions of the porosity for the considered cases, and compares them to the reference case (indicated by the red line). Evidently, increasing the porosity (by decreasing the strut diameter) helps reduce the pressure drop, but inversely leads to an increase in the equivalent thermal resistance. Considering the reference case, the goal is to minimize both thermal resistance and pressure drop for efficient thermal management in the system. Most of the investigated cases exhibit a lower equivalent thermal resistance than the reference case. However, this improvement comes at the cost of a higher pressure drop, which varies depending on the specific topology. To gain a deeper understanding of the trade-off between these two parameters, the performance points (Rth vs. ΔP) are presented in Figure 4.

In Figure 4, the BCCz configurations demonstrate a significant improvement over the reference case by achieving lower thermal resistance while maintaining an acceptable pressure drop. Specifically, configurations like BCCz1/2 × 3 × 6 and BCCz1/2 × 2 × 4 exhibit thermal resistance values below the reference case (~6 K/W) and are positioned on the lower-left region of the graph, indicating superior heat dissipation capabilities. In comparison, the FCCz topologies exhibit slightly higher thermal resistance values than the BCCz ones, with almost similar pressure drop. On the other hand, the OTL configurations achieve lower thermal resistance drops than both BCCz and FCCz but at the cost of higher pressure drops.

When compared to the reference case, the BCCz topology emerges as the best choice, offering a balanced trade-off between thermal and hydraulic performances. Its ability to reduce thermal resistance significantly, coupled with the flexibility of additive manufacturing, positions it as the most efficient solution for enhancing heat dissipation in this preliminary study. To confirm this trend, additional simulations were conducted on BCCz topology to explore the impact of reducing coolant velocity. As shown in the results in Figure 5, the reduction to 50% (0.5 m/s) demonstrated a significant decrease in pressure drop (around 60%), accompanied by a small increase in thermal resistance (approximate 10%). These results once again highlight the effectiveness of BCCz for the intended application.

3. Experimental and Computational Study on BCCz LS-Based Reduced Structure

In this section, an in-depth analysis of the selected topology, a BCCz LS, will be presented through extensive CFD simulations and experimental validation. The study systematically evaluates the thermal and hydrodynamic performance of a reduced-structure heat sink under a range of operating conditions, including varying flow rates and inlet temperatures. Comparative analyses will be conducted against conventional straight-fin heat sinks, utilizing key performance metrics such as thermal resistance, pressure drop, and temperature distribution.

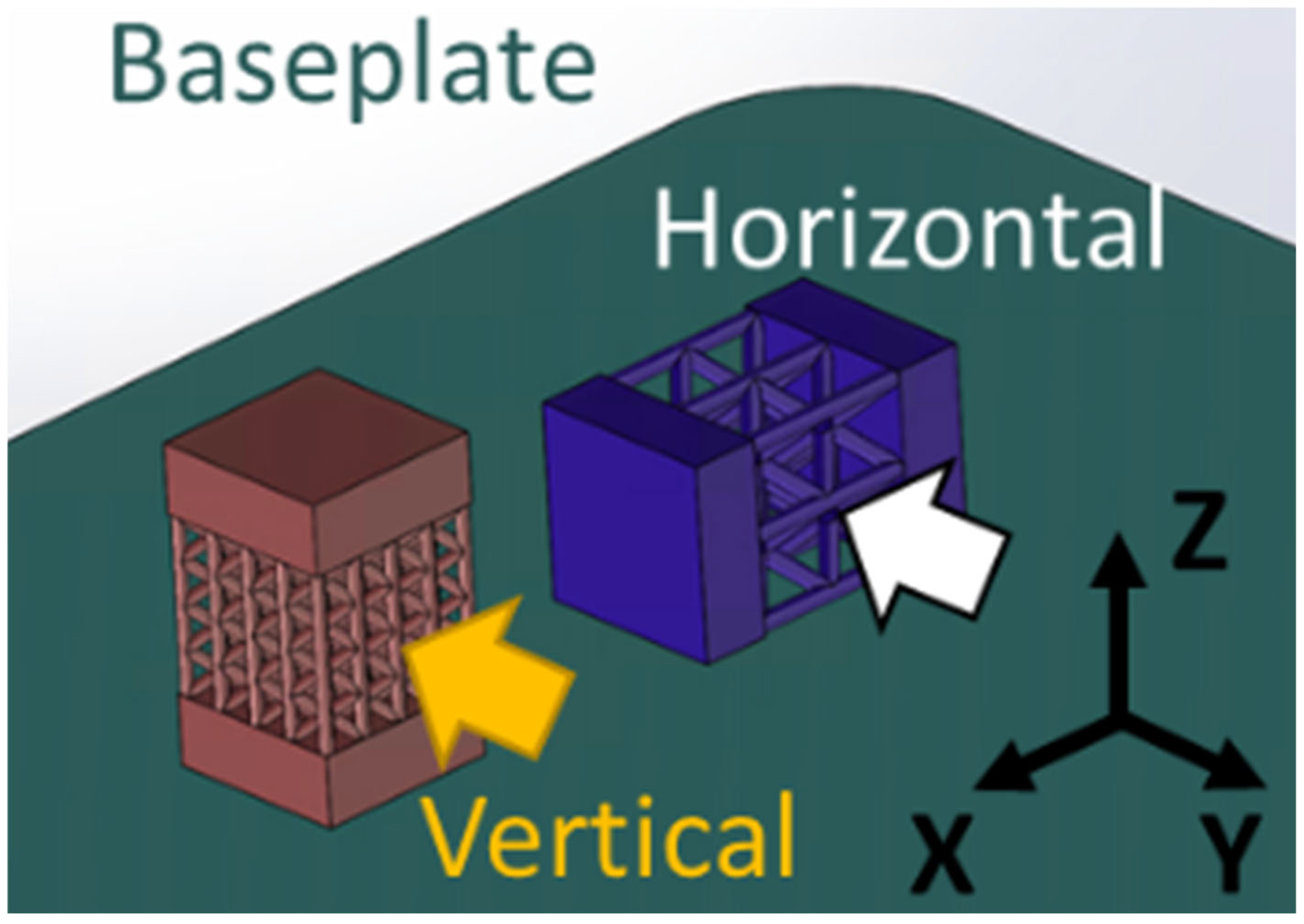
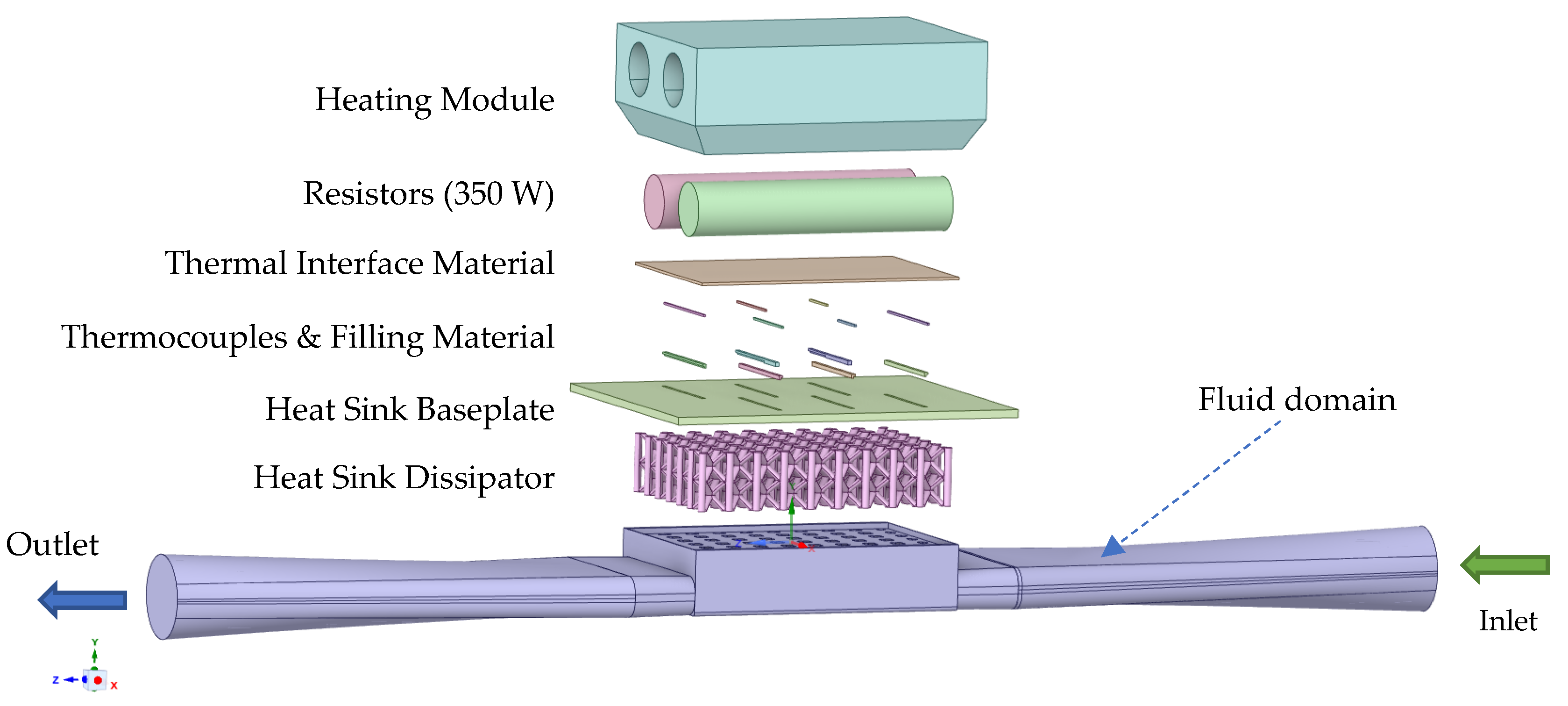
3.1. Reduced Structure Test Bench Design

An experimental test bench was designed and built to evaluate the performance of all heat sinks (Figure 6). It is composed of the following components: a heating module (HM) heated by two resistors (350 W), a thermal interface material (TIM) to ensure good contact between the HM and the heat sink baseplate, and finally, the coolant channel. The upper face of the baseplate of the heat sink (TIM side surface) contains six grooved channels to host six thermocouples. A glycol water 50% is used as coolant with temperature dependent properties. The volume flow rates are between 2.8 and 7 L/min. The inlet temperatures are 20 °C and 70 °C, which are chosen according to industrial needs. A differential pressure sensor is used to measure the pressure drop between the inlet and the outlet of the heat sink. In addition to the additively manufactured LS heat sinks, a machined pin-fin heat sink (well characterized previously [33]) is tested in the same environment in order to validate the CFD numerical model. Its thermal performance served as a benchmark for comparison with all LS configurations. In order to properly assess the impact of the manufacturing method on the performance of heat sink, an additively manufactured pin-fin heat sink is also manufactured and studied. Both the machined reference pin-fin (denoted PF-MAL) and the additively manufactured pin-fin (denoted PF-AAL) heat sinks are made of aluminum, Al7075 and AlSi7Mg0.6, respectively, with temperature dependent conductivities of 115–133 W/(m·K) for Al7075 (Data sheet) and 135–149 W/(m·K) for AlSi7Mg0.6 measured by hot-disk method. The lattice heat sink material is also made of AlSi7Mg0.6

An uncertainty analysis was conducted to quantify the reliability of the experimental results. The uncertainty in temperature measurements was estimated at ±0.4 °C. This value was determined by comparing the mean thermocouple readings for the baseplate (T_baseplate) and inlet fluid (T_in) temperatures in the absence of heat flux across the investigated temperature range. Consequently, the uncertainty on the equivalent thermal resistance was calculated using the following relation: ΔRth = Rth × 0.4/(T_baseplate − T_in). This results in a maximum relative error of 1.32% for T_in = 20 °C and 1.71% for Tin = 70 °C. For pressure drop measurements, an uncertainty of ±65 Pa was considered, based on the specifications provided by the pressure sensor manufacturer.

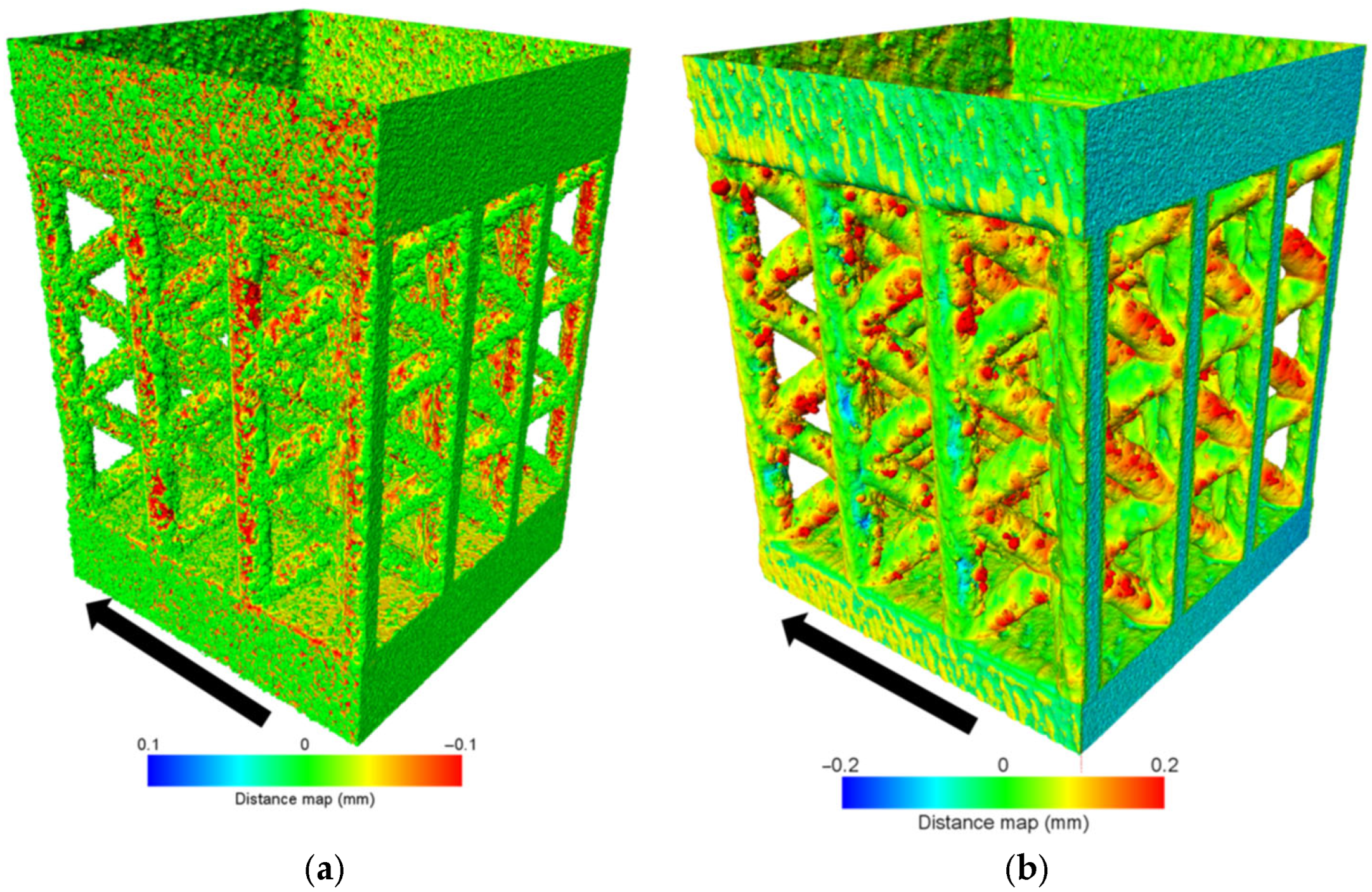
3.2. Reduced Structure Additive Manufacturing

3.2.1. Alloy and Additive Manufacturing Technology

Copper and copper alloys can be considered as the standard material for heat exchanger applications. Nevertheless, additive manufacturing of copper-based alloys was not mature enough at the beginning of the study. For this reason, AlSi7Mg0.6, a widespread aluminum alloy was chosen for this project. This alloy presents more elevated specific mechanical properties when compared to other aluminum alloys for additive manufacturing, allowing lightweight and strong structures. Among the additive manufacturing technologies, the LPBF has been selected because it is the most mature, the most extended, and also indicated for building small and complex geometries such as LS.

Table 2. Comparison of density and thermal conductivity as well as advantages/disadvantages of potential materials for heat exchangers.

Material	Density (kg/m3)	Thermal Conductivity (W/m·K)	Advantages	Disadvantages
Copper alloys	8960	210–400	- Potentially, the highest thermal conductivity	- Low maturity in LPBF. - LPBF as-built parts show thermal conductivity much lower than standard copper alloys. - Increasing thermal conductivity requires high-temperature heat treatments. - Residual stresses can lead to significant deformations during high temperature heat treatment.
Aluminum alloys	2710	110–250	- Low weight. - High maturity in LPBF. - Thermal heat treatment at low temperature enhances thermal conductivity. - Best thermal conductivity by density ratio. - Corrosion and wearing properties of LPBF as-built parts are better than traditional manufactured counterparts.	- Only for low temperature heat exchangers. - LPBF as-built parts show thermal conductivity lower than standard aluminum alloys.
Stainless Steel	8000	16	- High maturity in LPBF. - High resistance to corrosion and wearing.	- Worst thermal conductivity by density ratio. - Low conductivity.

compares the density and thermal conductivity as well as the advantages/disadvantages of copper alloys, aluminum alloys, and stainless steel.

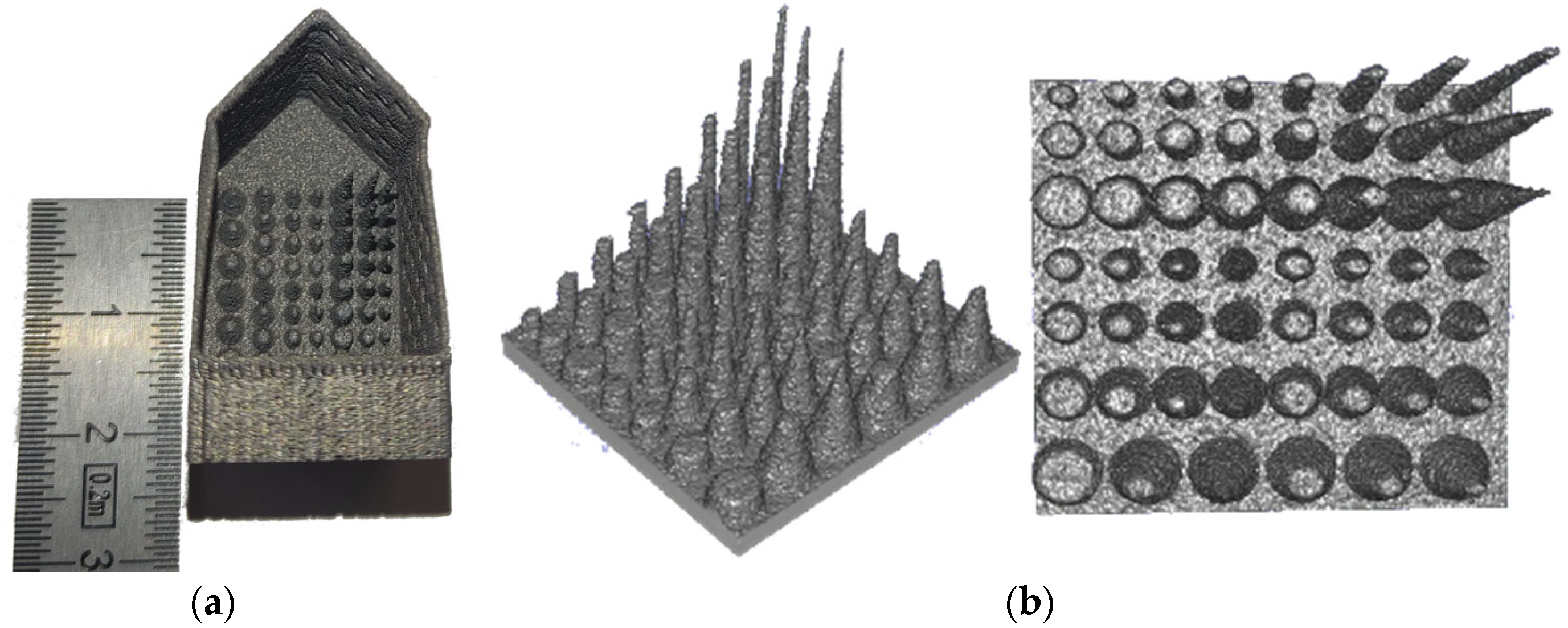
3.2.2. Feasibility Study

The LPBF process is controlled by hundreds of parameters which have an impact on the microstructure, material health, surface roughness, geometrical accuracy, geometrical distortions due to residual stresses, and design limits (e.g., maximal horizontal hang-off, minimum struts diameter, maximum manufacturing angles, etc.). In the present work, two different parameter sets were available. In order to evaluate the most adapted parameter for our purpose and for a first feasibility assessment, all the lattice configurations identified from the state-of-the-art and those used in the preliminary thermo-fluidic simulation were built. Representative LSs were reproduced in a 10 mm × 10 mm × 10 mm cubic volume. These structures were built with both parameter sets and in two directions, Figure 7. It is worth noting that all the structures were correctly built, so design constraints could not be defined with this feasibility exploration. To choose the best for the use case, they were lately characterized by optical microscopy, confocal microscopy (roughness), and some of them by Contrast Tomography 3D Scan (geometrical distortions).

Roughness: A mosaic acquisition was achieved with a Zeiss LSM800 confocal microscopy (Carl Zeiss Microscopy Gmbh, Jena, Germany) using a ×5 objective on the faces indicated by the white arrow in Figure 7. Roughness difference is qualitatively observed by the flattened 2D surface reconstruction and the 3D view, Figure 8. One parameter set creates a mild rough surface, mainly due to trapped powder particles on the surface, and the other creates a much smoother surface which reveals the layer-by-layer manufacturing approach. Surface roughness descriptors have been extracted for a quantitative comparison from flat surfaces observed with a ×20 objective. The descriptors were obtained from analysis of a 1.2 × 1.7 mm² surface from each parameter set samples. The results are gathered in

Table 3. Surface roughness.

Parameter Set	Roughness Indicators
	Ra [µm]	Rz [µm]	Sa [µm]	Sz [µm]
A	19.6	186	19.4	205
B	12.1	89.9	11.9	140

.

Geometry: Geometric distortion from CAD can reduce heat exchanger performance by altering the desired flow behavior. A first qualitative assessment was performed by optical microscopy using a Keyence VHX7000 (Keyence Corporation, Malines, Belgium) and a 3D mosaic acquisition protocol, Figure 9. This technique allows us to have a high resolution and no out-of-focus points. By comparing regions of the same lattice configurations, and superposing them to the theoretical CAD contours (blue and red lines on the zooms), the first trend appears: Parameter set A better respects the geometric tolerances than Parameter set B. This is more evident in lattice configuration containing small size cells and thin struts (red-highlighted structure). In this case, some channels of the LSs built with Parameter set B seem to be blocked by melted material, which can entail powder removal difficulties and strongly modify fluid flow. To quantitatively confirm that Parameter set A entails lower geometrical distortions, one of the lattice configurations built with each parameter set underwent CT scan. The obtained volume was compared with the nominal CAD, and the deviations are shown in Figure 10.

In conclusion, no geometrical design limitation was found after this feasibility study. Nevertheless, it allowed us to select a manufacturing set of parameters and further expand the design space for heat exchangers. Parameter set A was chosen for the rest of parts, as it allowed better reproduction of the CAD geometry.

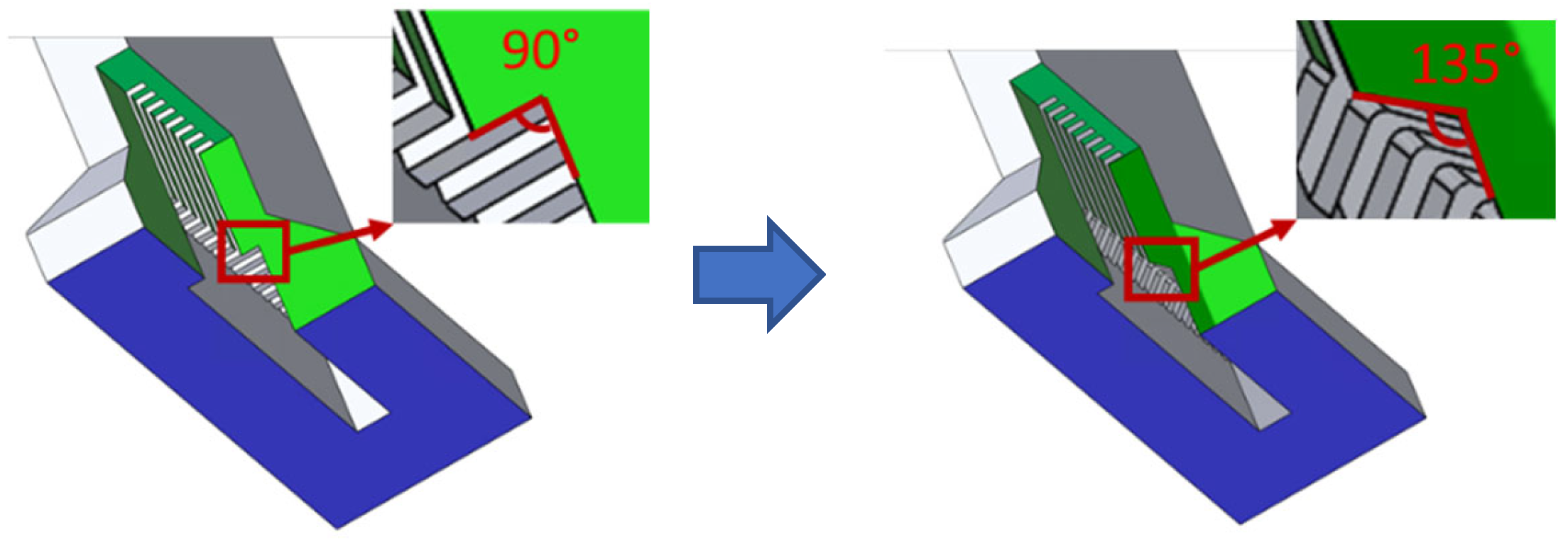
3.2.3. Further Design Limits Explorations

Once the parameter set was fixed, an extensive exploration of the manufacturing limits was initiated. The aim of this study was to define the thinnest struts that can be reproductively built depending on its section, length, inclination with respect to the building direction, and other parameters, as shown in Figure 11. For this purpose, small cages containing the struts were built at different angles ranging from 0° (vertical) to 80°. These building angles, along with the different lengths of the struts, cover the building configurations of a single strut for a wide range of lattice unit cells sizes and shapes (e.g., elongated or contracted along the baseplate direction). Struts with circular and elliptical evolving cross-section diameters were also built. Those elements increased confidence in the advanced heat exchanger geometries presented in this document.

No major issues were detected, except that struts thinner than 0.3 mm diameter (short diameter for elliptical sections) were not consistently built. Progressive struts sections could lead to different local porosity values to those explored until now. These regions can be observed on advanced heat exchangers in Figure 12.

Powder removal issues can also arise. To explore powder removal limits of LSs, cubic volume cages with one open face were built and filled with LS, as shown in Figure 13. The LSs were designed in such a way that different channel diameters for powder removal were created. After an ultrasound cleaning of about 10 min, the opposite side to the free face was removed by polishing and then optical observations were performed with transmitted light so clogged channels could be easily detected. Channels smaller than 400 µm present some difficulties for correct powder removal, mainly associated with local collapse of horizontal struts and surfaces that represents the worst configuration possible, as shown in Figure 13. The advanced geometries shown in this communication satisfy powder removal constraints and are considered as fully feasible by additive manufacturing when considering both the struts geometries and for the powder removal constraints.

Nevertheless, it is also possible to observe that some fused material can remain attached to the lattice and block the fluid, as seen in Figure 14. Eventually, this artifact could be liberated by the force applied by the fluid flow during operation. This raises concerns about fluid contamination, filtering needs, and surface post-treatment. Chemical etching, for example, could play an important role both in the roughness of the LS and also in the removal of this kind of obstacles to the fluid. These aspects should be explored in further studies.

3.2.4. Corrosion Behavior

Corrosion test on as-built AlSi10Mg shows that LPBF parts exhibit better corrosion resistance than the same alloys fabricated by traditional methods [34]. In the as-built microstructure, this can be explained by the silicon (Si) network acting as corrosion barrier. Heat treatments (annealing or homogenization) break this network, reducing its corrosion resistance. Direct or artificial aging heat treatment could be a compromise to achieve superior mechanical and thermal properties while maintaining corrosion resistance. Surface roughness, controlled by process parameters, also appears to be an important feature that reduces or increases corrosion rates and pitting. For applications with liquids, cavitation erosion was studied for AlSi10Mg [35]. The results showed that additively manufactured parts differ significantly from the wrought reference sample. Although, in the first seconds of the test, the erosion rate was higher for LPBF parts (phenomena related to roughness and pores), the erosion rate entered a steady state with low erosion rate. For LPBF parts, surface did not present large and deep craters, unlike wrought parts. The as-built finer grain structure produced by LPBF provides good sliding wear resistance, with mass loss rates much lower than those of cast or extruded parts [36]. Process parameters, which affect hardness and porosity, have a direct impact on the wear rate. The wear mechanism is abrasive for higher hardness materials, but can evolve towards adhesion as the hardness decreases. Annealing treatment can cause mechanical softening, thus increasing the wear rate.

3.3. Computational Configuration

In this study, the CFD model was developed using ANSYS Fluent with a pressure-based solver, with geometric and flow conditions selected to closely replicate the experimental configuration. Figure 15 shows the computational model built after the experimental test bench design. The working fluid was a 50% glycol–water mixture, modeled with temperature-dependent thermophysical properties. Identical volume flow rates and inlet temperatures as utilized in the experimental study are applied in this numerical model, with an outlet pressure set at 1 bar absolute. The CFD model was validated using experimental measurements obtained from the reference machined pin-fin (PF-MAL) heat sink. For all simulations, convergence of the governing equations was ensured, and mass and heat flux balances were verified.

The Reynolds number, based on the inlet diameter, ranged from 1433 to 14,231. The k–ω SST turbulence model was selected for its enhanced accuracy in predicting flow separation and near-wall behavior in transitional and turbulent flows [23,37,38].

A grid independence study was conducted to determine the best mesh resolution, ensuring that the numerical results were independent of the mesh density. The study compared numerical results obtained using three different hybrid mesh densities: a reference mesh with approximately 80 million cells, a second mesh with approximately 56 million cells, and a third mesh with approximately 26 million cells. The investigation spanned four different operational conditions defined by varying flow rates and fluid inlet temperatures (a. Qv = 2.8 L/min; Tin = 20 °C, b. Qv = 7 L/min; Tin = 20 °C, c. Qv = 2.8 L/min; T_in = 70 °C and d. Qv = 7 L/min; T_in = 70 °C). The primary parameters for assessing grid independence were the temperature field across the heat sink’s baseplate and the temperatures recorded at specific thermocouple locations. Comparing temperature contours across the baseplate (Figure 16) revealed no significant discrepancies among the three mesh densities for any of the study configurations. Figure 17 shows thermocouple temperatures recorded on the baseplate of the reference machined pin-fin heat sink (PF-MAL) as a function of mesh density for the four different configurations. The percentage difference in thermocouple temperatures between all mesh densities (26, 56, and 80 million cells) is generally very small. For configurations (a), (b), and (d), the difference is very low and insignificant (less than 0.3% as absolute difference), while configuration (c) exhibited slightly larger difference for the 26 million and 56 million cell meshes (e.g., thermocouple TC6 absolute differences were 2% and 1.85% for the 56 and 26 million cell cases, respectively). Consequently, the mesh with approximately 26 million cells was selected for subsequent simulations to optimize computational resources without compromising result accuracy. It is worth noting that, for the selected mesh density, the maximum element size allowed in the fluid domain was set to 0.2 mm. This value, also used for the other lattice structure heat sinks, led to a higher cell count due to the increased geometric complexity of the model.

The numerical study was carried out on six different BCCz LS heat sinks based on the BCCz3 and BCCz2 with changing the cross-section shape.

Table 4. All LS configurations considered in the reduced structure study.

Configuration Name	N° of Unit Cells H × W × L	Porosity	Strut Cross-Section Shape
BCCz3 cyl	3 × 9 × 14	0.74	Circular
BCCz2 cyl	2 × 6 × 9	0.74	Circular
BCCz3 ellip 1d5	3 × 9 × 14	0.62	Elliptical-Ratio = 1.5
BCCz2 ellip 1d5	2 × 6 × 9	0.79	Elliptical-Ratio = 1.5
BCCz2 evo nabla ∇	2 × 6 × 9	0.56	Evolutive and Elliptical-Ratio = 3
BCCz2 evo delta Δ	2 × 6 × 9	0.56	Evolutive and Elliptical-Ratio = 3

and

Table 5. All LS configurations geometrical details in the reduced structure study.

Configuration Name	LS Total Volume (mm3)	Fluid–Lattice Contact Surface (mm2)	Baseplate–Fluid Contact Surface (mm2)	Baseplate–Lattice Contact Surface (mm2)
BCCz3 cyl	1736.90	10,184.37	660.71	188.63
BCCz2 cyl	1568.50	6504.57	695.51	153.53
BCCz3 ellip 1d5	2284.30	10,396.02	715.05	133.98
BCCz2 ellip 1d5	1227.60	6129.74	783.68	65.36
BCCz2 evo nabla ∇	2804.20	7008.95	501.18	347.45
BCCz2 evo delta Δ	2806.90	7314.97	801.98	47.03

show the details of all LS configurations considered, while Figure 18 shows their geometries. Both “BCCz2 cyl” and “BCCz3 cyl” configurations have a circular cross-section, whereas the remaining four configurations possess an elliptical cross-section, with a radius ratio of 1.5 for the “ellip 1d5” configurations and that of 3 for “evolutive” cross-section configurations.

For thermal performance comparison among all heat sinks, the equivalent thermal resistance is calculated in the following manner,

Rth = (T_baseplate − T_ref)/Φ,

(1)

where Φ is heating power (W), T_ref is reference temperature (K) equal to T_in, and T_baseplate is average temperature on the heat sink baseplate (K).

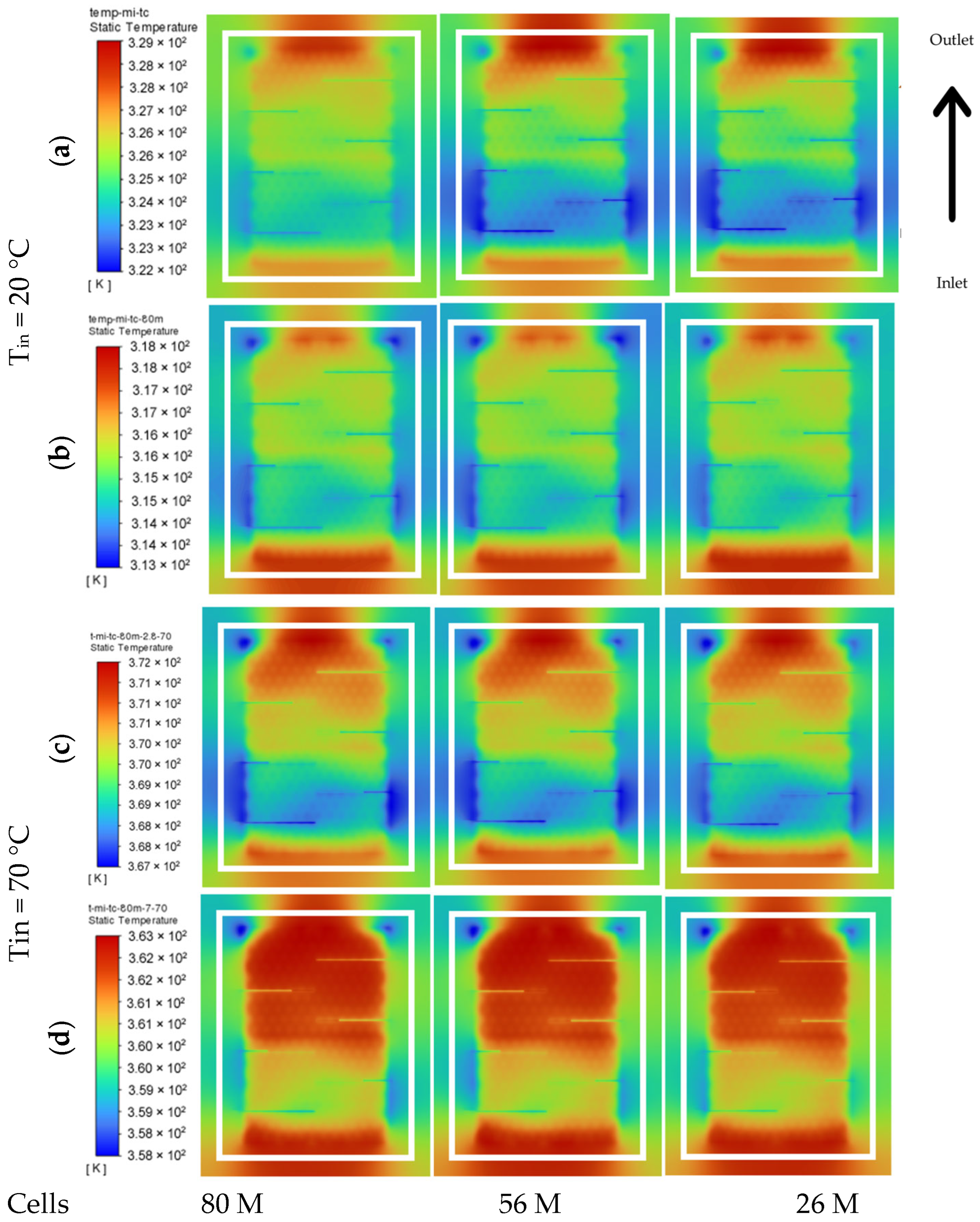
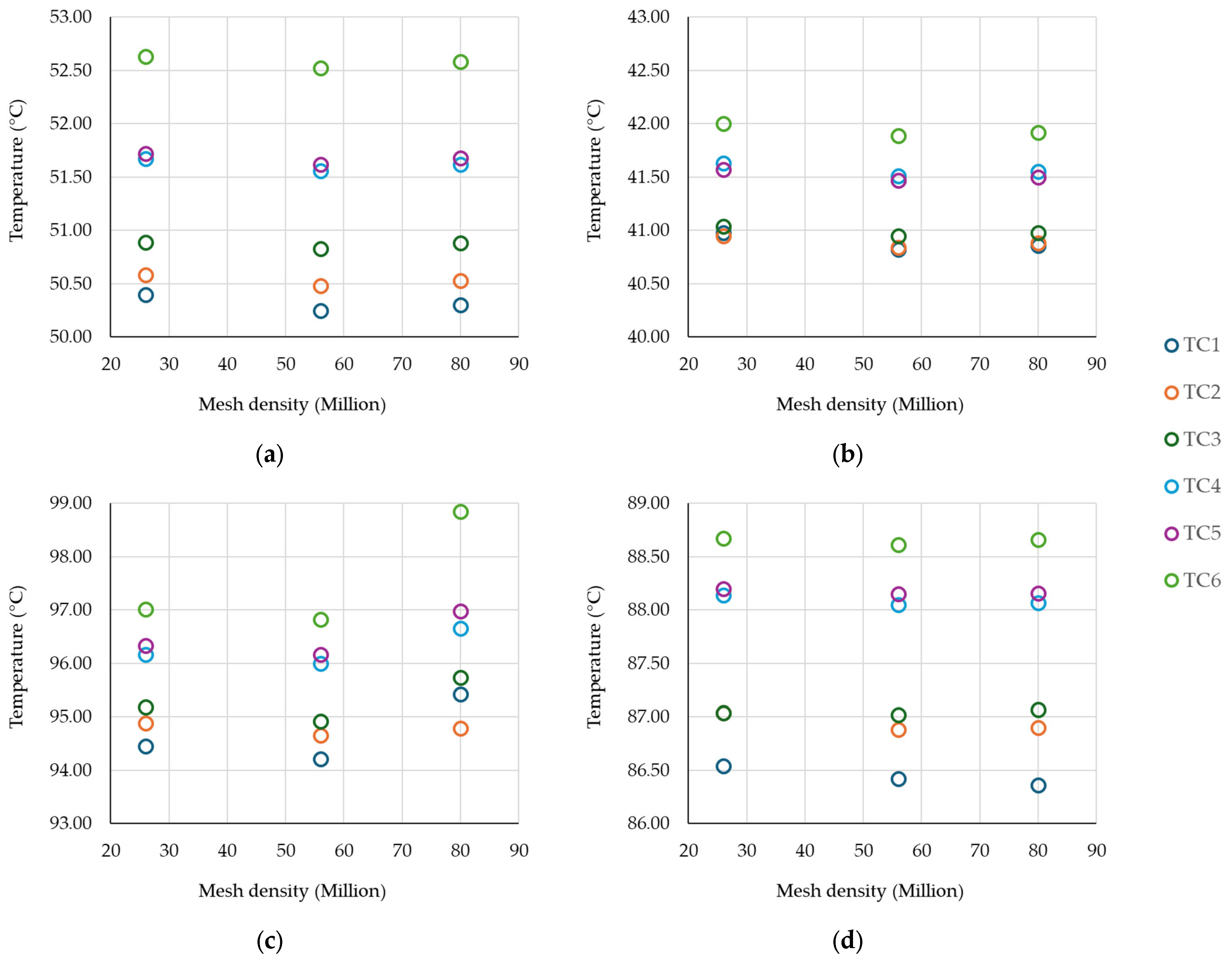
3.4. Reduced Structure—Results and Discussion

In the following, the first section compares conventional straight-fin (Fins) and pin-fin (PF-MAL, PF-AAL) heat sinks with LS (BCCz3 cyl and BCCz2 cyl) heat sinks. The second section expands the analysis to all LS (BCCz3 cyl, BCCz2 cyl, BCCz3 ellip 1d5, BCCz2 ellip 1d5, BCCz2 evo nabla ∇, and BCCz2 evo delta Δ) heat sinks. The goal is to identify the best-performing heat sink configuration in terms of thermal resistance and pressure drop.

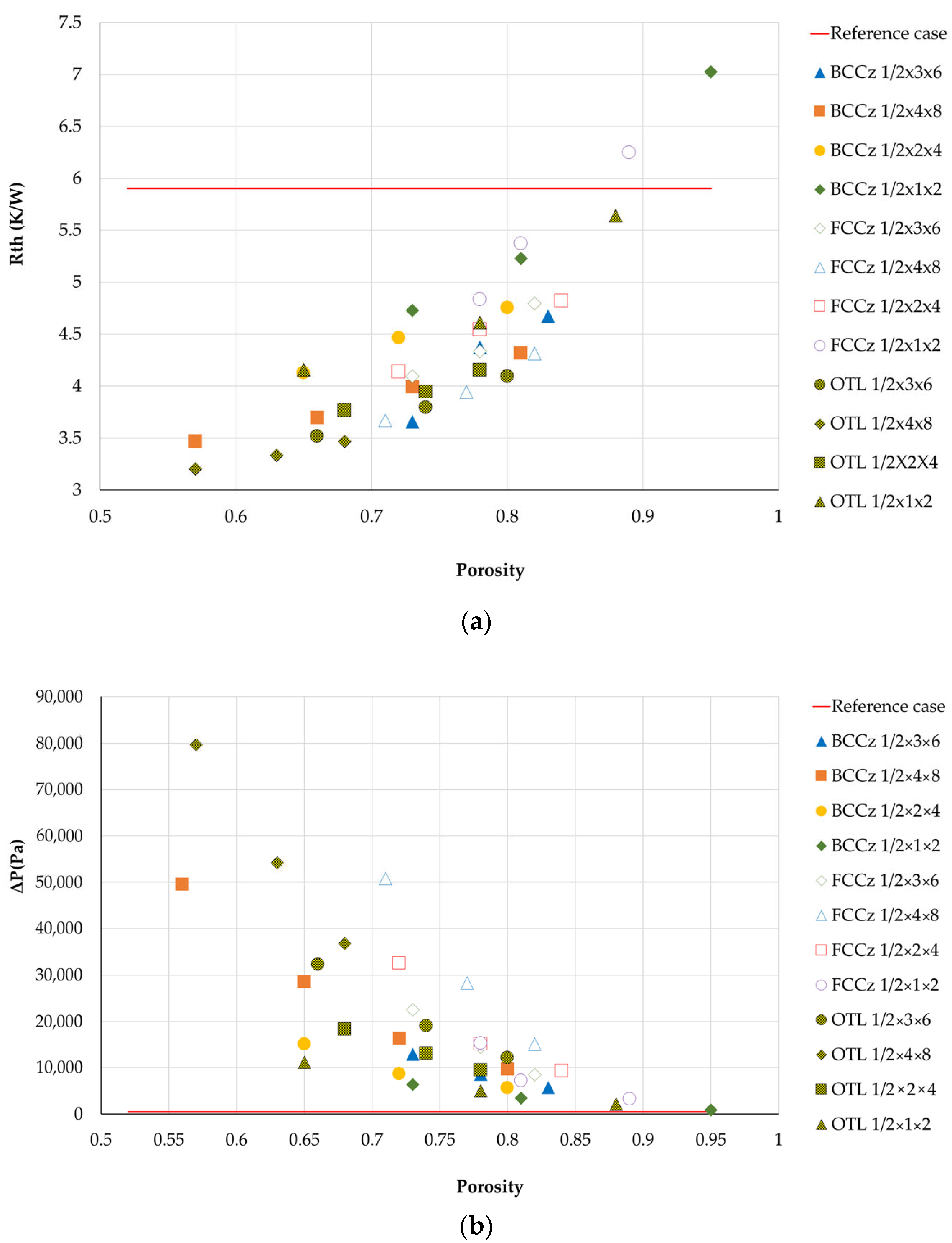
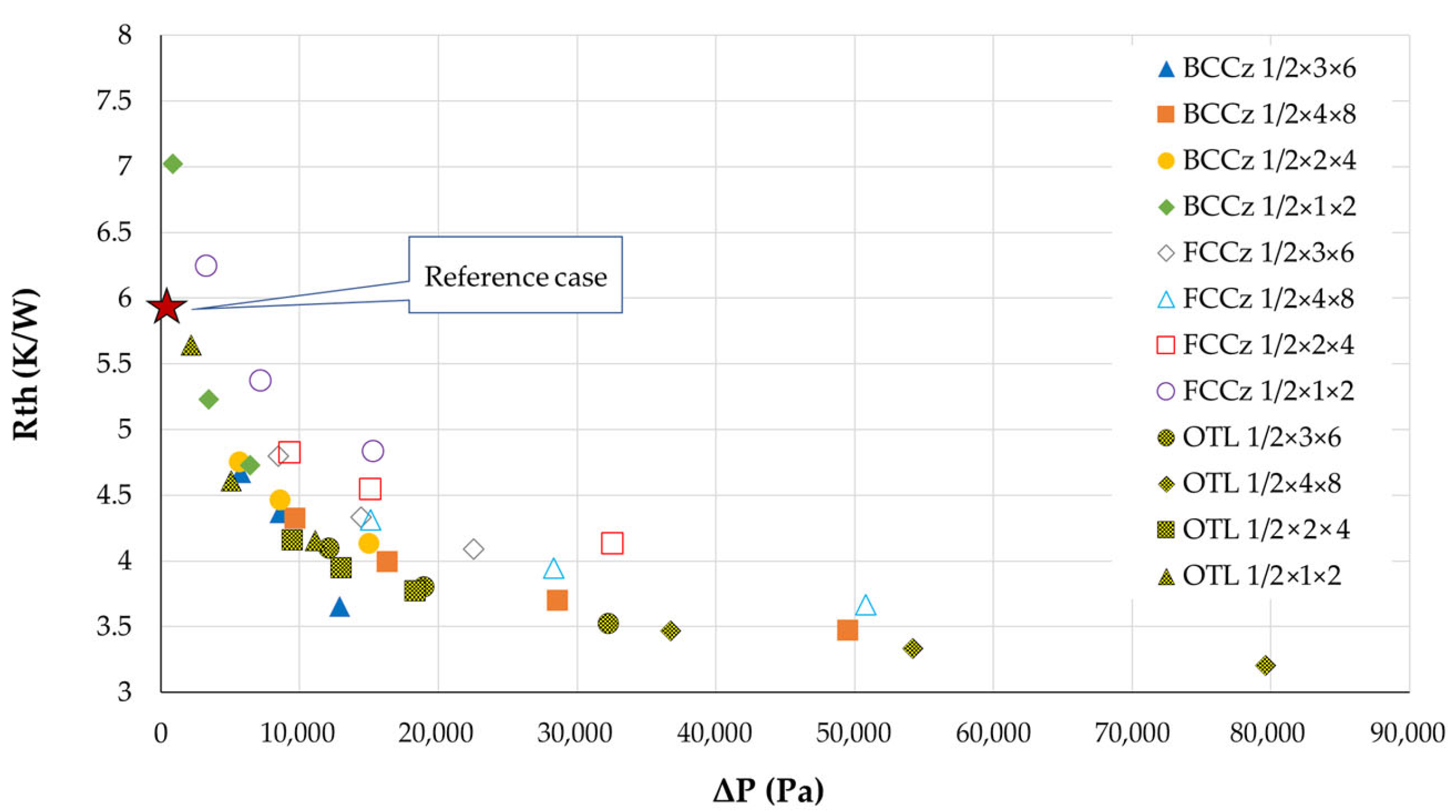
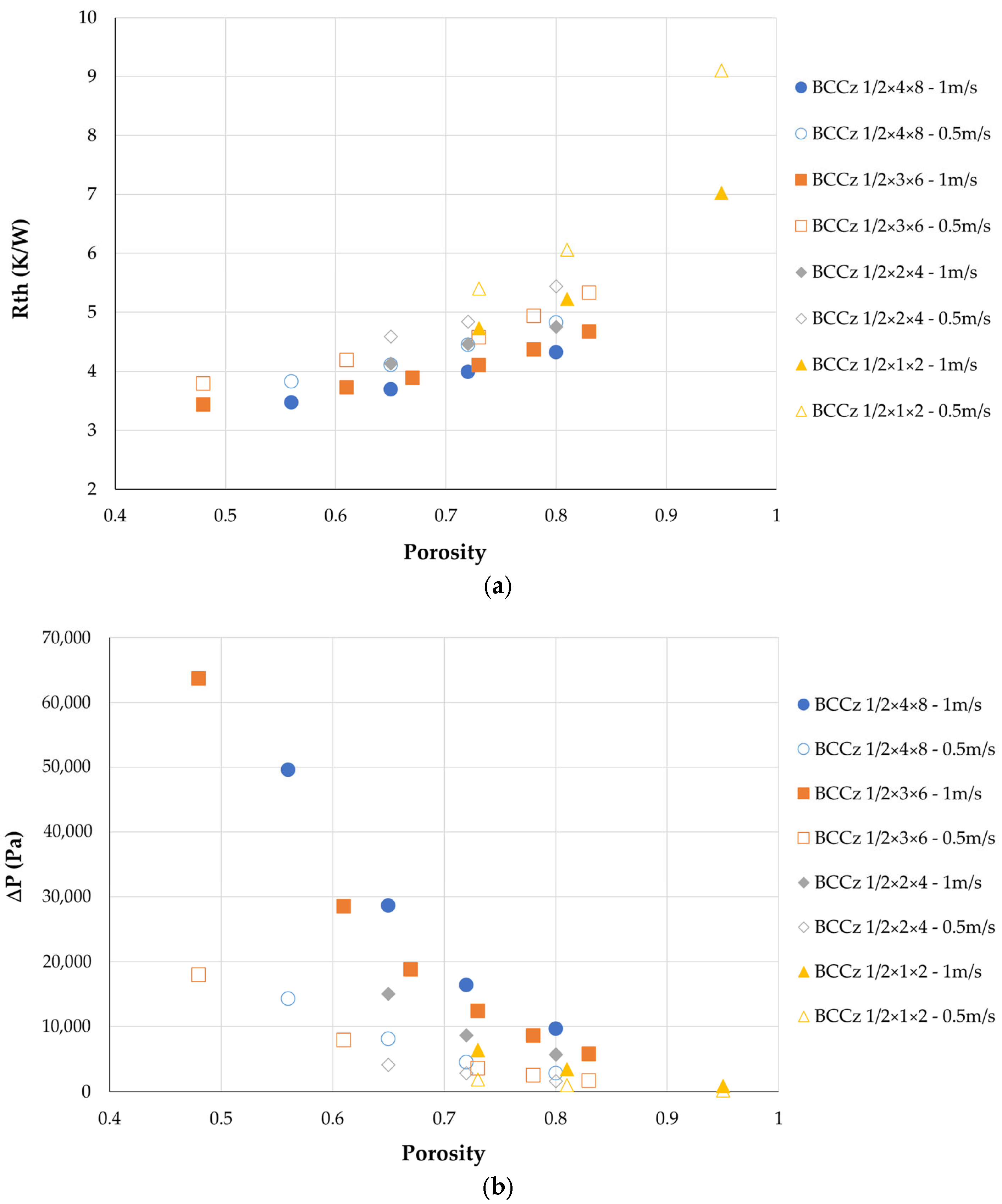
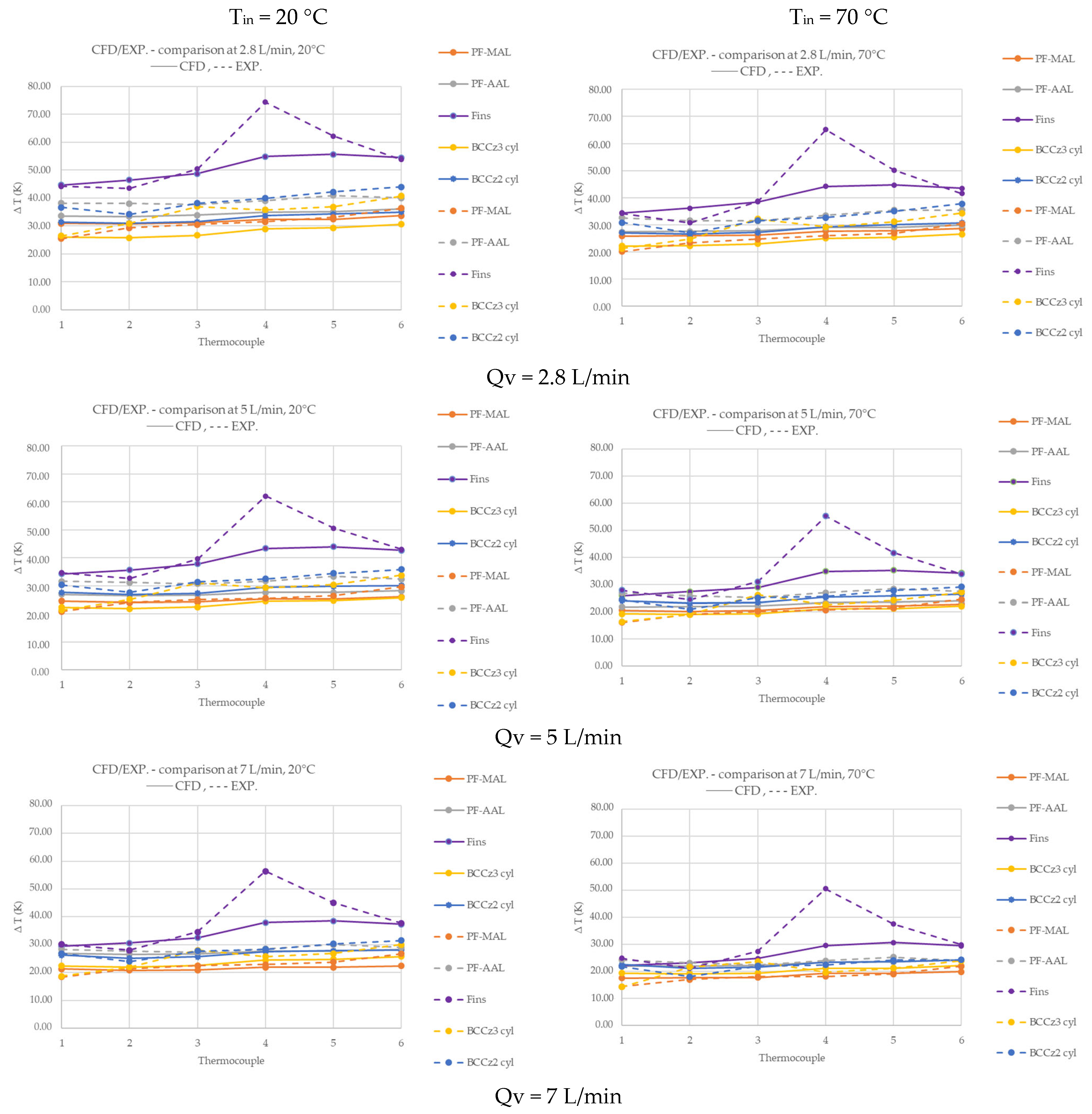
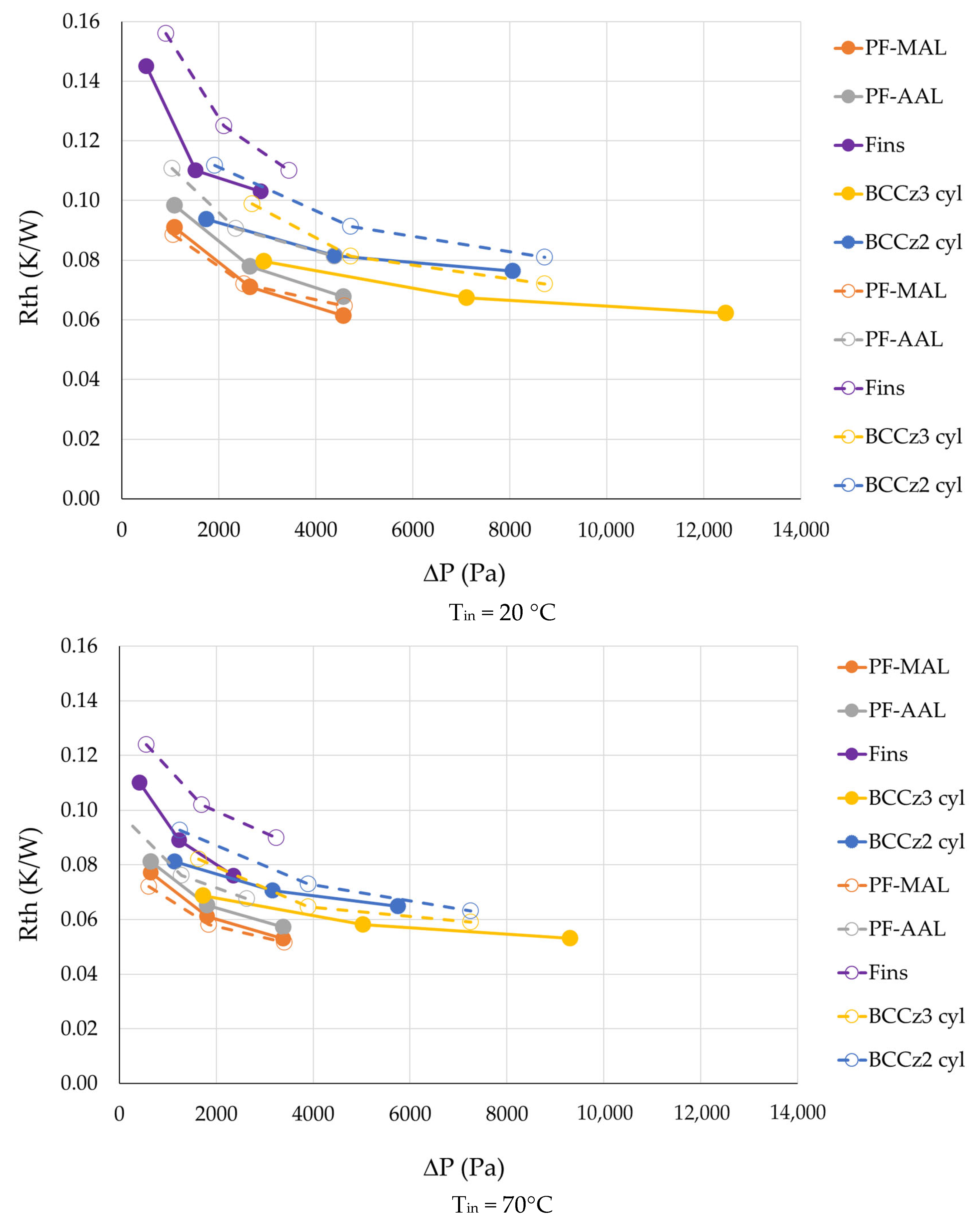
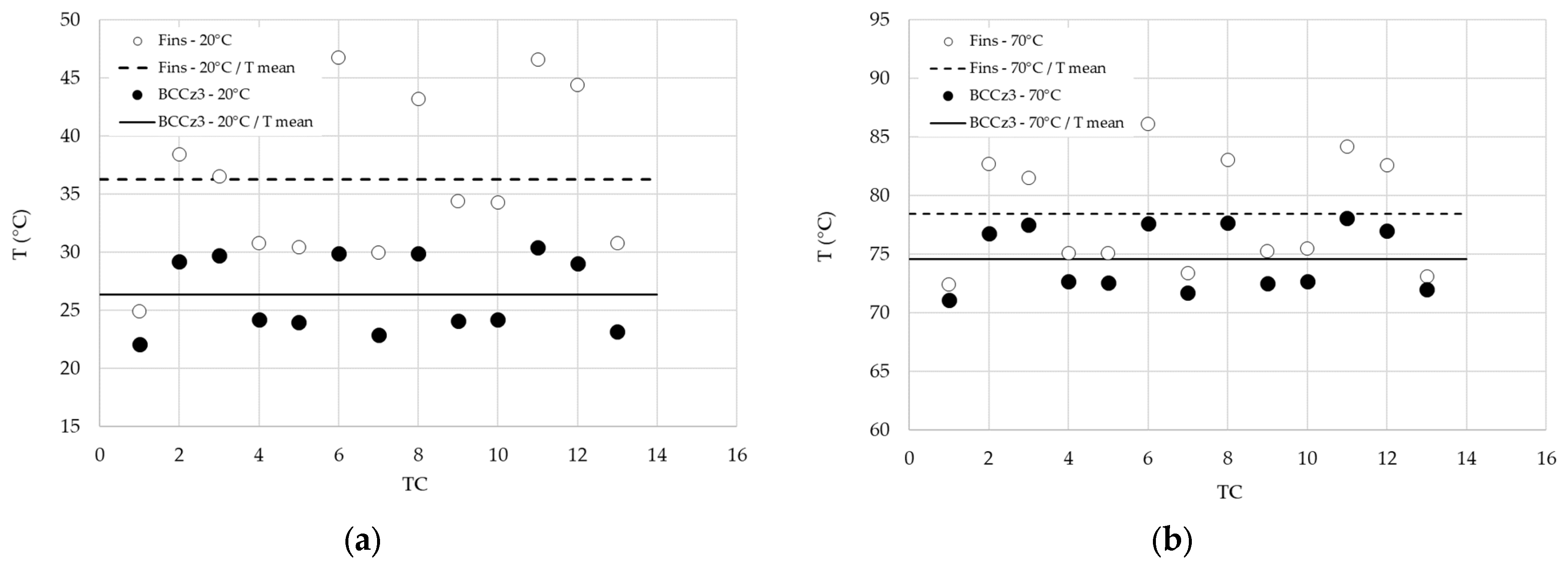
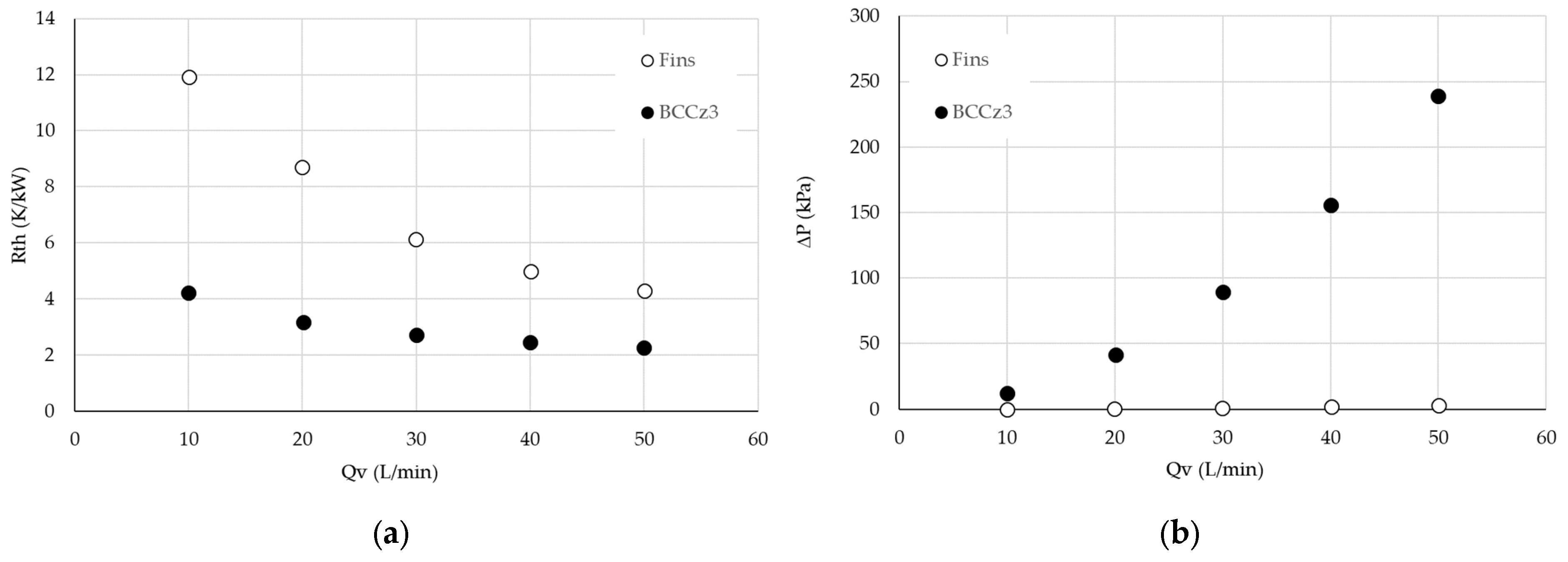
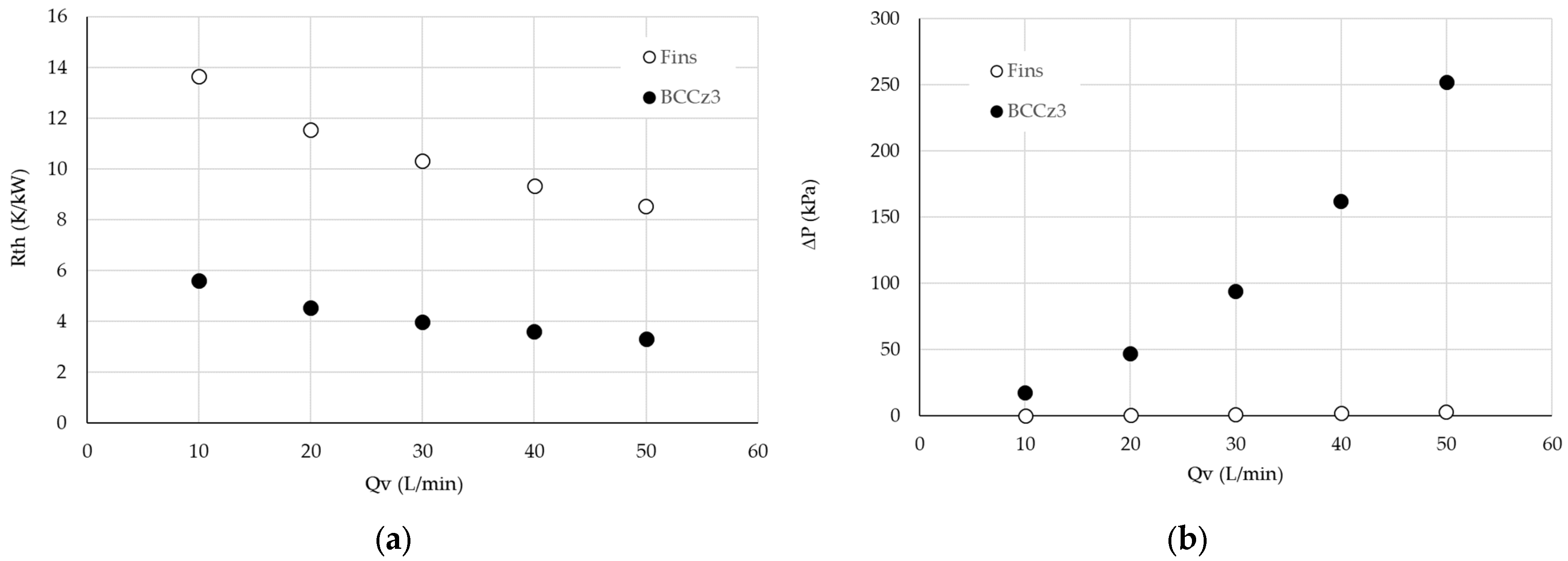
3.4.1. Comparison of Conventional Heat Sink and LS Heat Sinks

Figure 19 presents a comparative analysis of temperature variations on heat sink baseplate expressed as temperature differences (ΔT = T_TC − T_in), where T_TC is the measured temperature on baseplate, under different inlet flow rates and temperatures. The comparison includes both numerical and experimental data. Three flow rates are considered—2.8 L/min, 5 L/min, and 7 L/min—along with two inlet temperatures of 20 °C and 70 °C. The results demonstrate a consistent trend in which increasing the flow rate leads to a systematic reduction in the temperature difference (ΔT) across all heat sink configurations. This behavior is expected since a higher flow rate enhances convective heat transfer, leading to improved cooling efficiency and a lower baseplate temperature. Increasing inlet temperature slightly reduces temperature difference (ΔT) measured on baseplate. It is worth noting that the temperature value measured by temperature thermocouple no. 4 for the Fins configuration is likely overestimated due to an integration issue with the baseplate, which was resolved in the other tested configurations.

To know more about the thermohydraulic performance of these configurations, Figure 20 compares performance curves of the RS heat sinks: straight-fin and pin-fin configurations with BCCz3 and BCCz2 cylindrical LSs. Across both inlet temperatures, PF-MAL exhibits the lowest equivalent thermal resistance, demonstrating superior heat dissipation performance. This is expected since pin-fin structures generally provide a high surface area for heat transfer while maintaining efficient fluid distribution. The “Fins” configuration, however, shows the highest Rth values, indicating poor thermal efficiency compared to the other conventional designs. The LS heat sinks (BCCz3 cyl and BCCz2 cyl) exhibit intermediate performance. BCCz3 cyl’s equivalent thermal resistance (Rth) was marginally higher than the PF-MAL heat sink but considerably lower than the “Fins” configuration. As expected, the pressure drops for BCCz3 cyl and BCCz2 cyl increase with flow rate, but their thermal resistance remains competitive, particularly at lower flow rates (Qv) values.

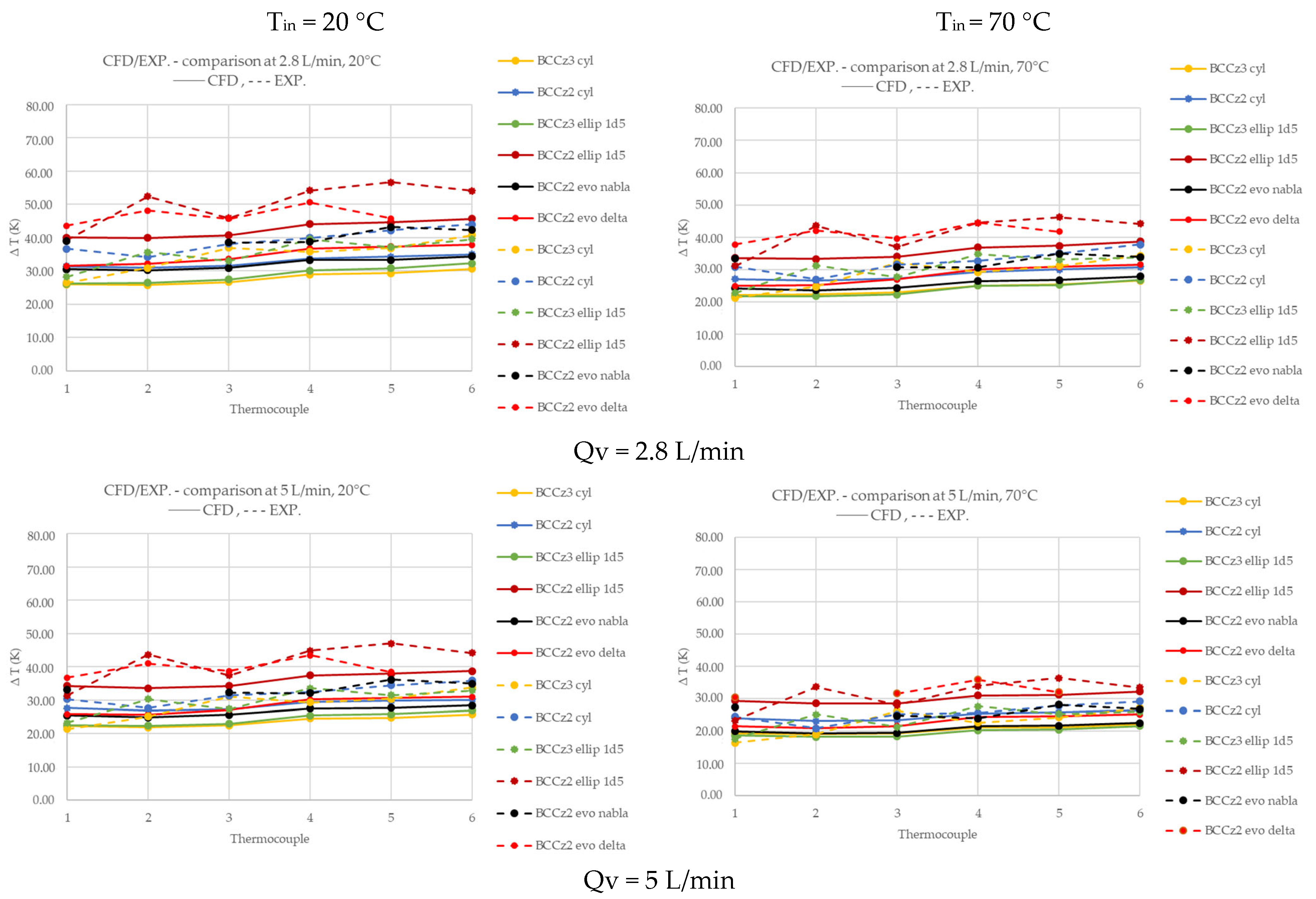
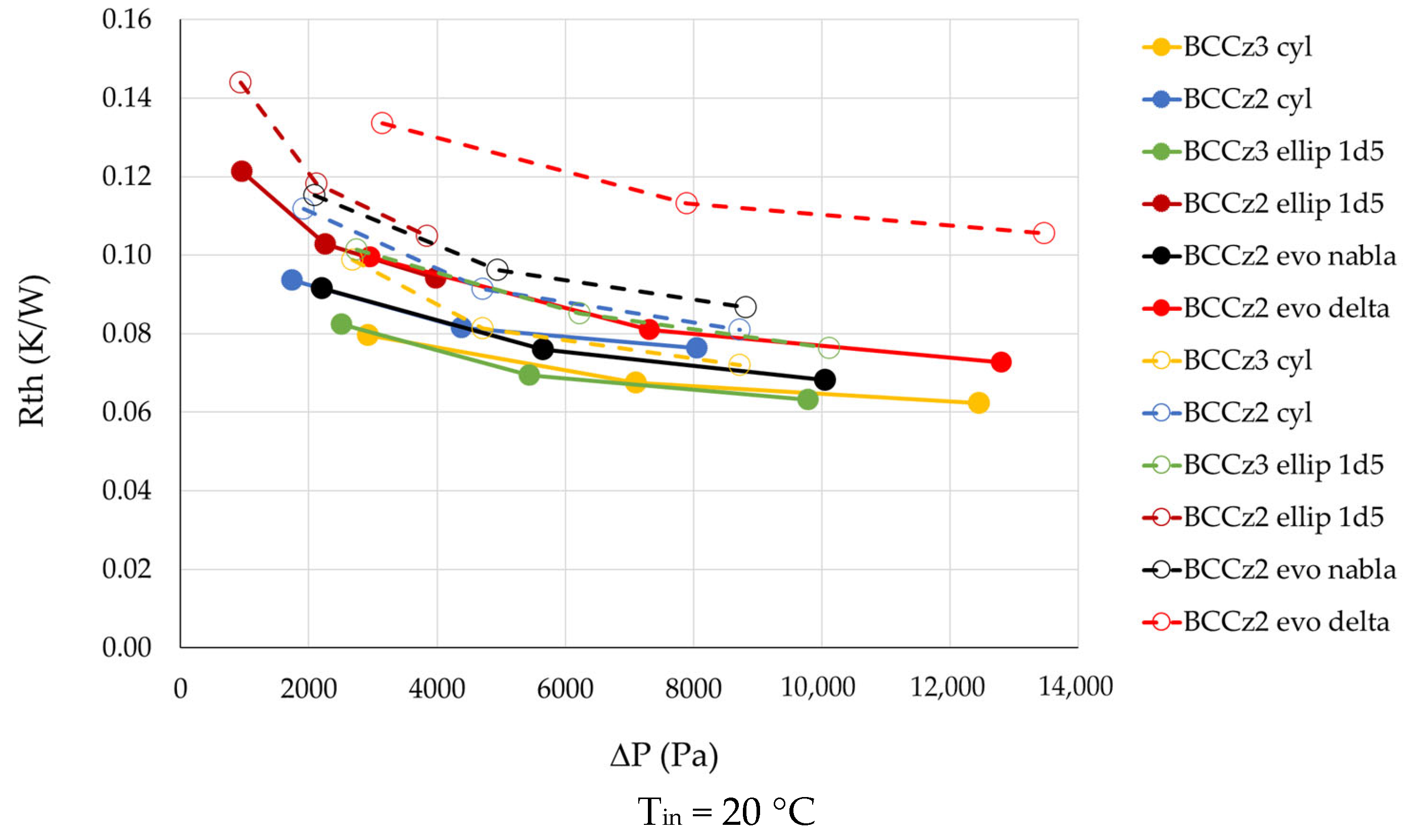
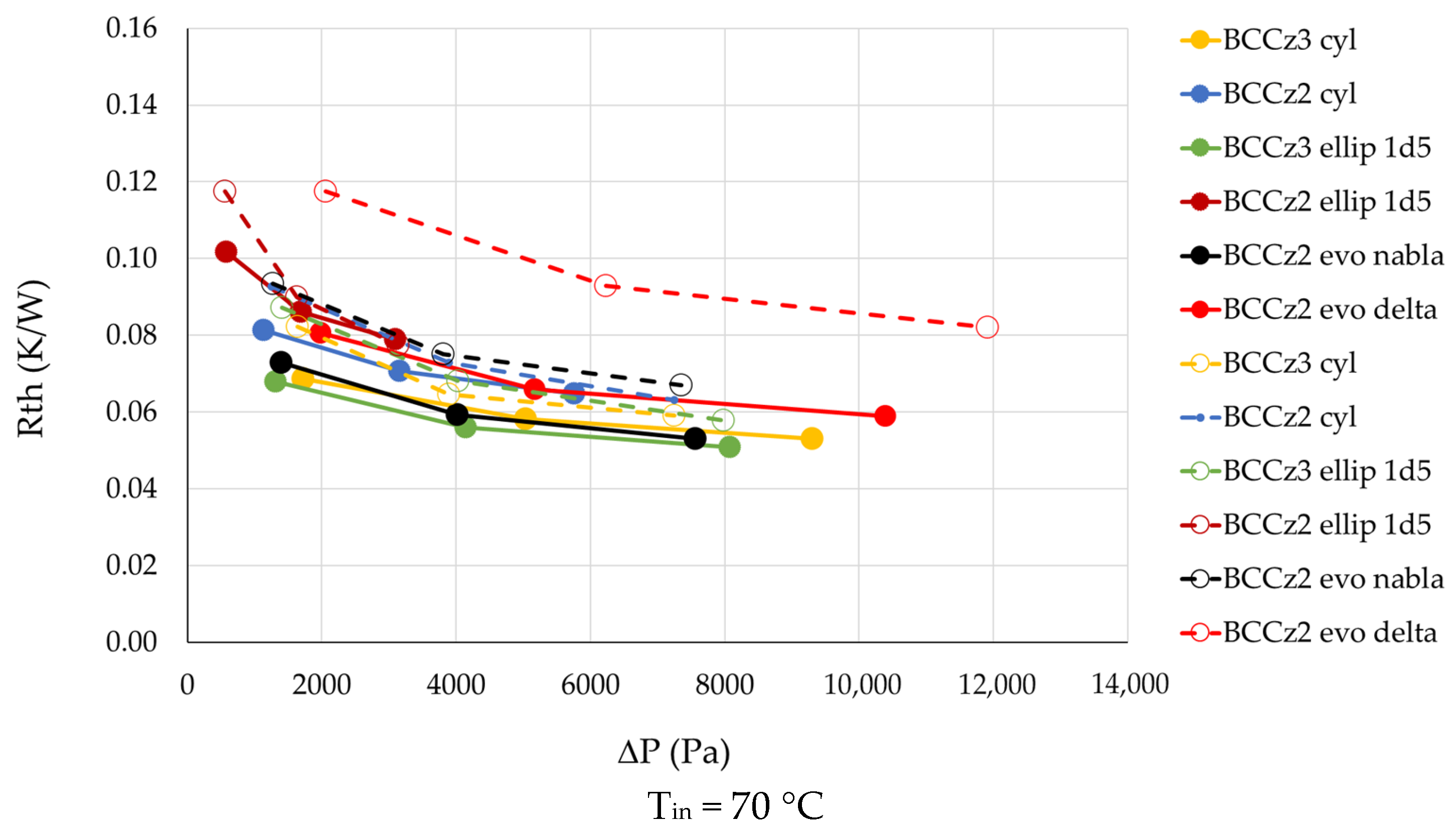
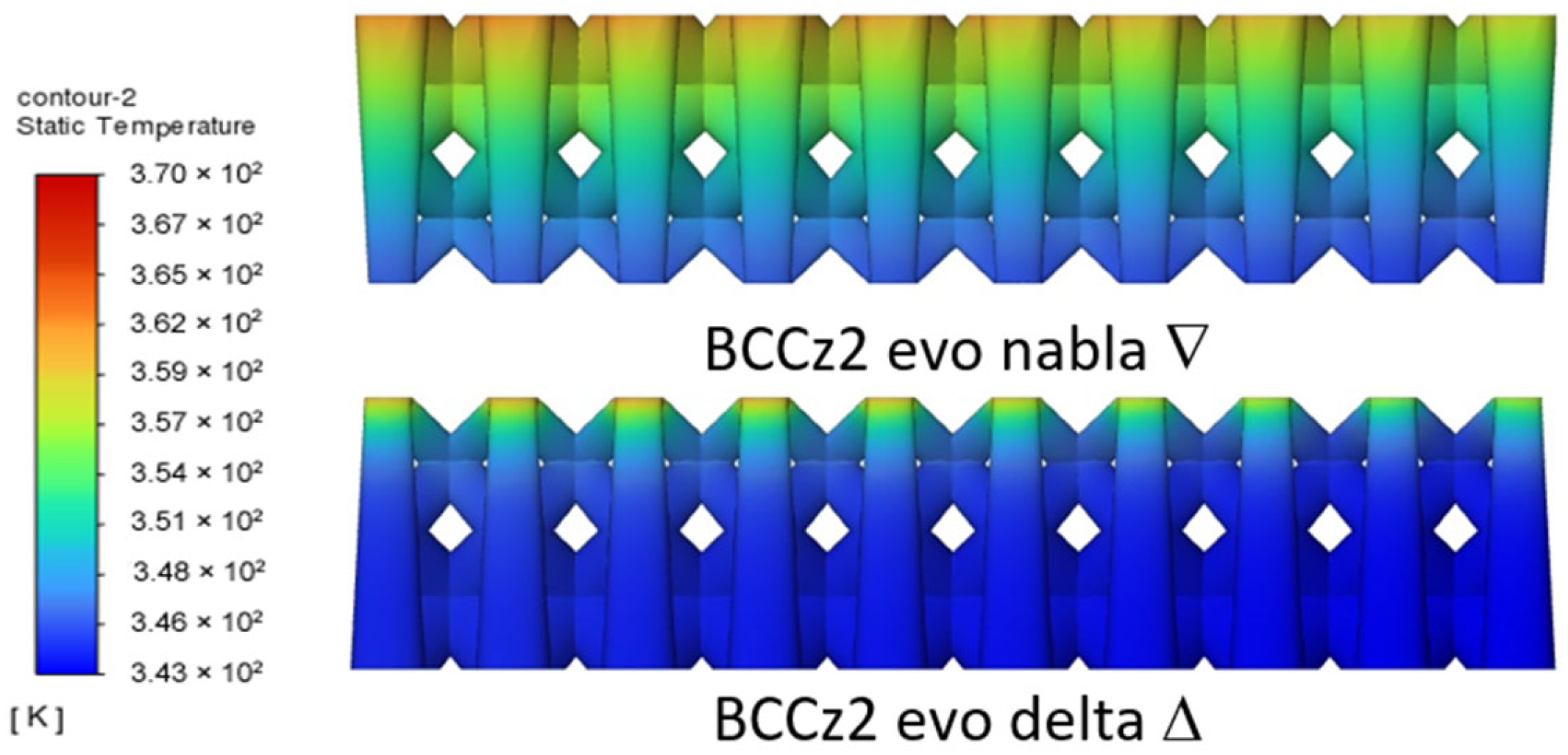
3.4.2. Comparison Between LS Heat Sinks

Figure 21 presents a comparative analysis of temperature differences (ΔT) measured on the baseplate of all LS heat sinks. The comparison includes both numerical and experimental data to assess the thermal performance of different LS geometries.

The first observation concerns the performance of the elliptical cross-section (BCC2 ellip 1d5, BCC3 ellip 1d5) compared to the cylindrical LSs (BCC2 cyl, BCC3 cyl). Across all cases, the experimental and numerical results show good agreement, with CFD predictions following the general trends of experimental data. However, some deviations exist at specific thermocouple positions, suggesting potential uncertainties in measurement or numerical assumptions. For both flow rates and inlet temperatures, the regular elliptical cross-section exhibits lower ΔT values than the cylindrical structure. At higher flow rates (Qv = 7 L/min), the difference between elliptical and cylindrical cross-sections diminishes.

A closer analysis of the evolutive cross-sections (BCC2 evo nabla, BCC2 evo delta) reveals a distinct trend in thermal behavior. These structures are designed with gradual cross-section variations to enhance thermal spreading and fluid mixing. The “delta” cross-section (BCC2 evo delta) consistently shows the highest ΔT values. This trend is particularly noticeable in the experimental data, where the “delta” structure exhibits significant temperature peaks, especially at the middle thermocouple positions. This suggests that the “delta” cross-section creates localized thermal resistance on the baseplate side due to the small contact area between the baseplate and the LS, leading to inefficient cooling performance. In contrast, the “nabla” cross-section performs better than “delta” and shows relatively uniform ΔT distribution across the thermocouple positions.

Figure 22 shows the performance curves of all LS heat sinks. The BCCz3 and BCCz2 cylindrical structures continue to show strong performance, with BCCz3 exhibiting the lowest Rth values among all designs. The elliptical cross-section (BCCz3 ellip 1d5 and BCCz2 ellip 1d5) shows a noticeable reduction in Rth compared to the cylindrical versions, particularly at lower pressure drops. This suggests that the elliptical shape enhances convective heat transfer by improving flow dynamics. In contrast, the evolutive cross-sections (“nabla” and “delta”) show mixed results. The “delta” design exhibits the highest Rth values, indicating inefficient heat dissipation compared to the other designs. The “nabla” design performs better but still does not surpass the standard cylindrical and elliptical designs. These results suggest that while geometric evolution can influence thermo-hydraulic behavior, not all modifications lead to improved performance.

To find out more about thermal behavior, the temperature distribution in both evolutive structures obtained by the CFD is considered. Figure 23 shows the temperature contours for the two BCCz2 LS evolutive designs (nabla and delta) under a volume flow rate (Qv) of 2.8 L/min and an inlet temperature (Tin) of 70 °C. The “nabla” design clearly exhibits a more uniform temperature distribution throughout the structure. In fact, the limited coolant movement around the top end of this structure is insufficient to extract heat, so heat diffuses by conduction within the structure towards the base. This promotes more efficient heat dissipation through the LS strut surfaces. In contrast, the “delta” design shows a localized temperature variation on the baseplate side of the structure, suggesting less effective heat removal from the LS strut surfaces.

3.5. Conclusion on the Elementary Structure Heat Sink Study

At this stage, experimental and numerical analysis confirm that BCCz3 cyl is the most suitable LS for the full scale demonstrator heat sink. It provides a well-balanced compromise between thermal efficiency and fluidic resistance, outperforming BCCz2 and other lattice geometries. While elliptical cross-sections offer marginal improvements, their complexity may not justify the trade-off in manufacturability. Evolutive designs, particularly “delta,” do not offer sufficient thermal benefits and introduce higher resistance. Therefore, BCCz3 cyl stands out as the best candidate for integration into the final heat sink design, offering reliable performance across various flow rates and inlet temperatures. However, the configuration BCCz2 evo nabla deserves further investigation in a future study.

4. Experimental and Computational Study on Full Scale Demonstrator

4.1. Demonstrators’ Design and Description

Based on the latest findings, a full scale demonstrator heat sink was designed using a lattice structure adhering to the BCCz topology. As illustrated in Figure 24a, the design comprises 72 unit cells in length, 42 unit cells in width, and 4 unit cells in height. With a circular strut diameter of 0.7 mm, the resulting porosity is approximately 0.7.

A simple straight-fin heat sink was also designed as a reference case. This conventional heat sink consists of 17 parallel fins, each 3 mm wide, with a 3 mm gap between consecutive fins, as shown in Figure 24b. The design replicates the dimensions of the actual heat sink used in railway applications to cool one of the six power converter modules located between the catenary and the motor of a high-speed train.

To ensure a uniform velocity profile at the heat sink inlet, two transition sections (a divergent section at the inlet and a convergent section at the outlet) were designed and additively manufactured using Multi Jet Fusion technology with HP PA12 material. Figure 25 shows the CAD drawing of these adapters, which were applied to both sides of the heat sinks.

4.2. Full Scale Demonstrator Test Bench Design

A new experimental test bench was designed and constructed to evaluate the performance of the FSD heat sinks under realistic conditions (Figure 26). A real HVIGBT Mitsubishi CM1500HC-66 power module (Mitsubishi Electric Semiconductor, Tokyo, Japan), including Si IGBTs and diodes, was utilized to simulate realistic dissipated power. The upper surface of the baseplate for both heat sinks, on the thermal interface material (TIM) contact side, features 13 grooved channels designed to accommodate 13 thermocouples, as shown in Figure 27. A filling material was used to securely position the thermocouples (type K, calibrated) and ensure reliable measurements. A 50% glycol–water mixture was used as the coolant, with the volume flow rate varied between 10 and 50 L/min. The flow rate was measured using a Coriolis Flowmeter (EMERSON Micro Motion Series F with F100S sensor, Boulder, CO, USA), while the inlet temperatures were maintained at 20 °C and 70 °C. Additionally, a differential pressure sensor (Rosemount 2051C, Cluj, Romania) was used to measure the pressure drop across the heat sink section.

The uncertainty associated with the equivalent thermal resistance values (ΔRth) remained consistent with the methodology described in Section 3 (page 10) and was calculated using the following relation: ΔRth = Rth × 0.4/(T_baseplate − T_in). This results in a maximum relative error of 6.34% for T_in = 20 °C and 9.23% for Tin = 70 °C. However, the uncertainty in the pressure drop (ΔP) measurements differs: it was estimated to be ±39 Pa for the conventional straight-fin heat sink and ±260 Pa for the LS BCCz heat sink, based on the specifications of the respective pressure sensors used during the tests.

4.3. Full Scale Demonstrator Additive Manufacturing

Although additive manufacturing allows more freedom in design than traditional manufacturing processes, some constraints exist and need to be integrated into the heat exchanger design. This design must also account for finishing steps that may be required, such as machining of interfaces.

Thickening and envelop simplifications for machining of interface surfaces: Due to the thermal shrinkage of the part after building, holes for bolts are filled in the preform design. These modifications prevent potential eccentricity of the hole centers with respect to their nominal positions. The surface in contact with the heat exchanger (red surface in Figure 28) must also be machined to ensure flatness and minimal surface roughness. To accommodate this machining step, an extra 2 mm thickness has been added, increasing the height of the central section from 18 mm to 22 mm. The same approach has been applied to the inlet/outlet contact surfaces where O-rings are needed to ensure watertightness (blue surface in Figure 28). An extra 3 mm has been added to these interfaces.

Orientation choice in the build plate: MSC Simufact Additive 2024 software was used to gain insight into the best part orientations within the build space, considering the amount of support needed and the manufacturing risks. Two orientations appeared to offer good trade-offs among the different parameters considered in the orientation study (Figure 29). Nevertheless, the first orientation included many internal surfaces with a high risk or a need for internal supports that could not be removed after manufacturing. Therefore, the second orientation was chosen, and design modifications were implemented in the regions highlighted in red to reduce risk and ensure manufacturability. A chamfer was created on the inlet/outlet surfaces that will be machined during the finishing step, eliminating the risk in these regions through a smooth transition. This simple solution was also applied to the internal fins, as seen in Figure 30.

4.4. Full Scale Demonstrator—Results and Discussion

The experimental study involved a wide range of operating conditions, including flow rates from 10 to 50 L/min, inlet temperatures of 20 °C and 70° C, and heating powers from 900 to 2000 W.

Figure 31 compares the temperature distribution along the baseplate of both heat sinks under two different inlet temperature conditions (20 °C and 70 °C) while maintaining a constant flow rate of 50 L/min and heating power of 1905 W. The x-axis represents the temperature thermocouple number (TC) (see Figure 27), and the y-axis indicates the temperature (°C). Results indicate an inconsistent temperature distribution along the baseplate for both fin and BCCz configurations, suggesting non-uniform power dissipation at the module level due to die repartition. A clear trend emerges when comparing the two configurations: the BCCz LS steadily demonstrates lower temperatures than the fins configuration, regardless of the inlet temperature. This indicates superior heat dissipation capabilities for the BCCz heat sink. The mean temperature line further emphasizes this difference, with the BCCz configuration maintaining a lower average temperature throughout the baseplate (4 to 10 °C for Tin = 20 °C and 70 °C, respectively), highlighting the significant improvement in heat dissipation achieved by the BCCz heat sink.

Figure 32 shows the temperature distribution on the baseplate for Fins and BCCz3 configurations under varying flow rates (50, 30, and 10 L/min). The temperature increases with decreasing flow rate for both configurations. The mean temperature, represented by horizontal lines, also increases with decreasing flow rate. Both result sets reveal a clear distinction between the thermal performance of the fins and BCCz heat sinks. The BCCz configuration regularly exhibits lower temperatures compared to the fins configuration across all flow rates.

Figure 33 shows a comparison of experimental thermal resistance (Rth) and pressure drop (ΔP) variation versus flow rate between the fins (◯) and BCCz (●) configurations with the inlet temperature of 70 °C and heating power of 1905 W. The results suggest that using the BCCz LS results in a 100% improvement in thermal performance at a flow rate of 50 L/min and a 300% improvement at a flow rate of 10 L/min. On the other hand, the use of the BCCz leads to a decrease in hydraulic performance. The pressure drop increases with the flow rate from 12 kPa for 10 L/min up to 239 kPa for 50 L/min.

Similar conclusions can be drawn for an inlet temperature of 20 °C, as depicted in Figure 34 although with minor variations.

The results of this experimental study can be summarized in three points:

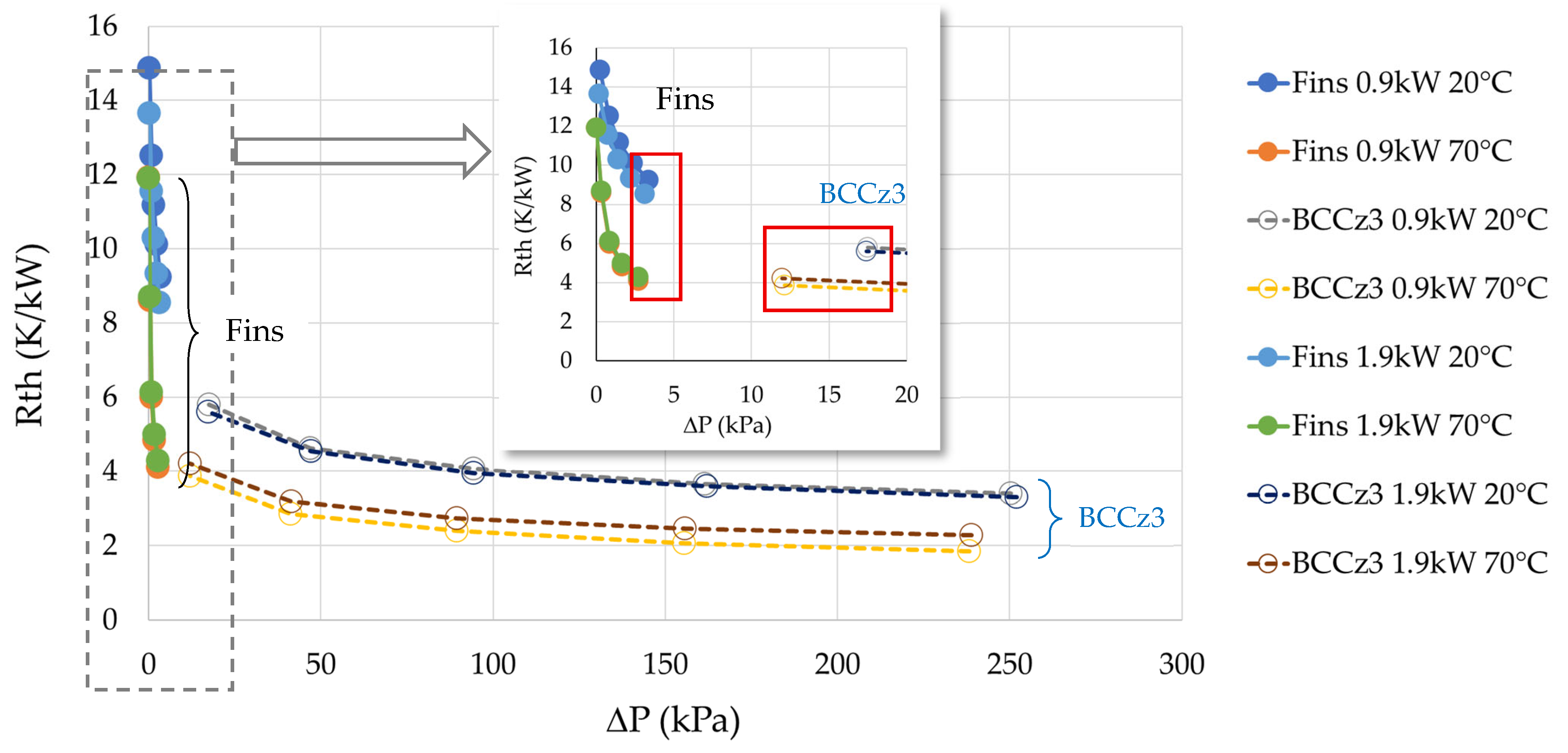
• Improved thermal performance: The implementation of a LS represents a significant step forward in improving the thermal performance of the heat sink, especially compared to traditional straight-fin heat sinks. The LS allows for more efficient heat dissipation.
• Optimization of hydraulic performance: although thermal performance is experiencing substantial improvement, optimizing the hydraulic performance of such LSs is a crucial challenge that requires careful consideration.
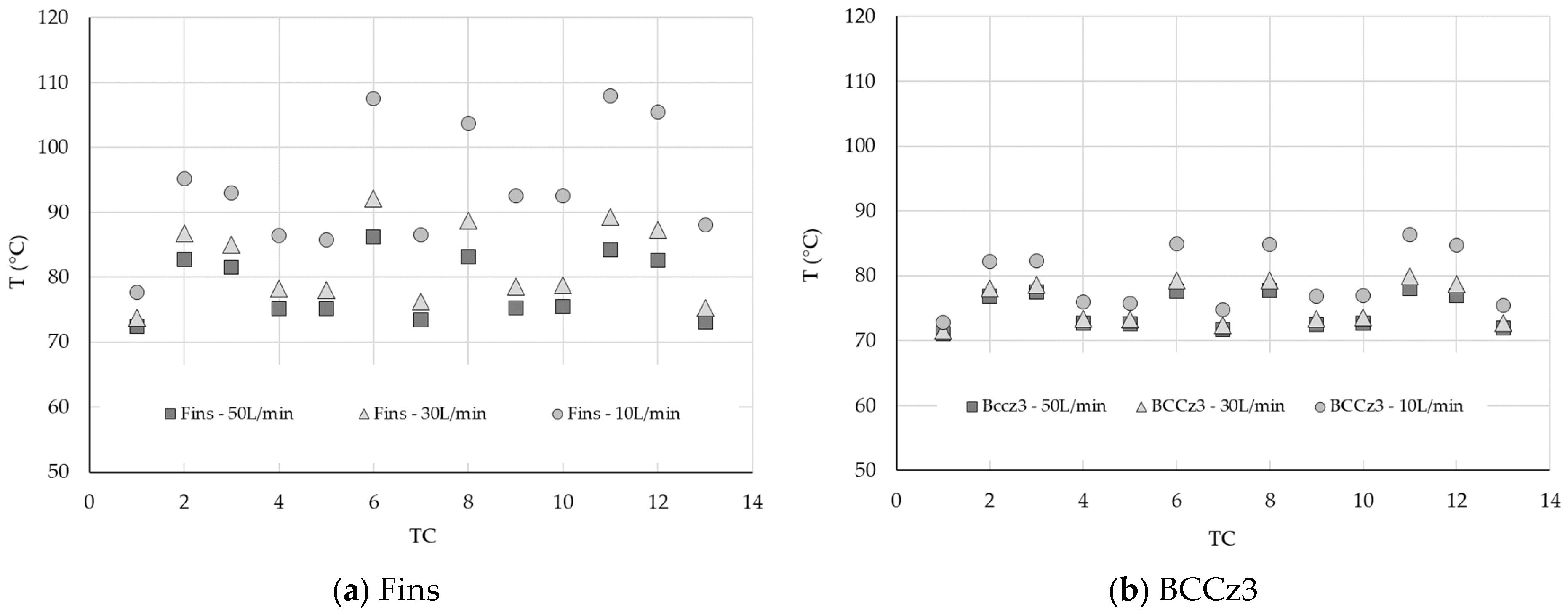
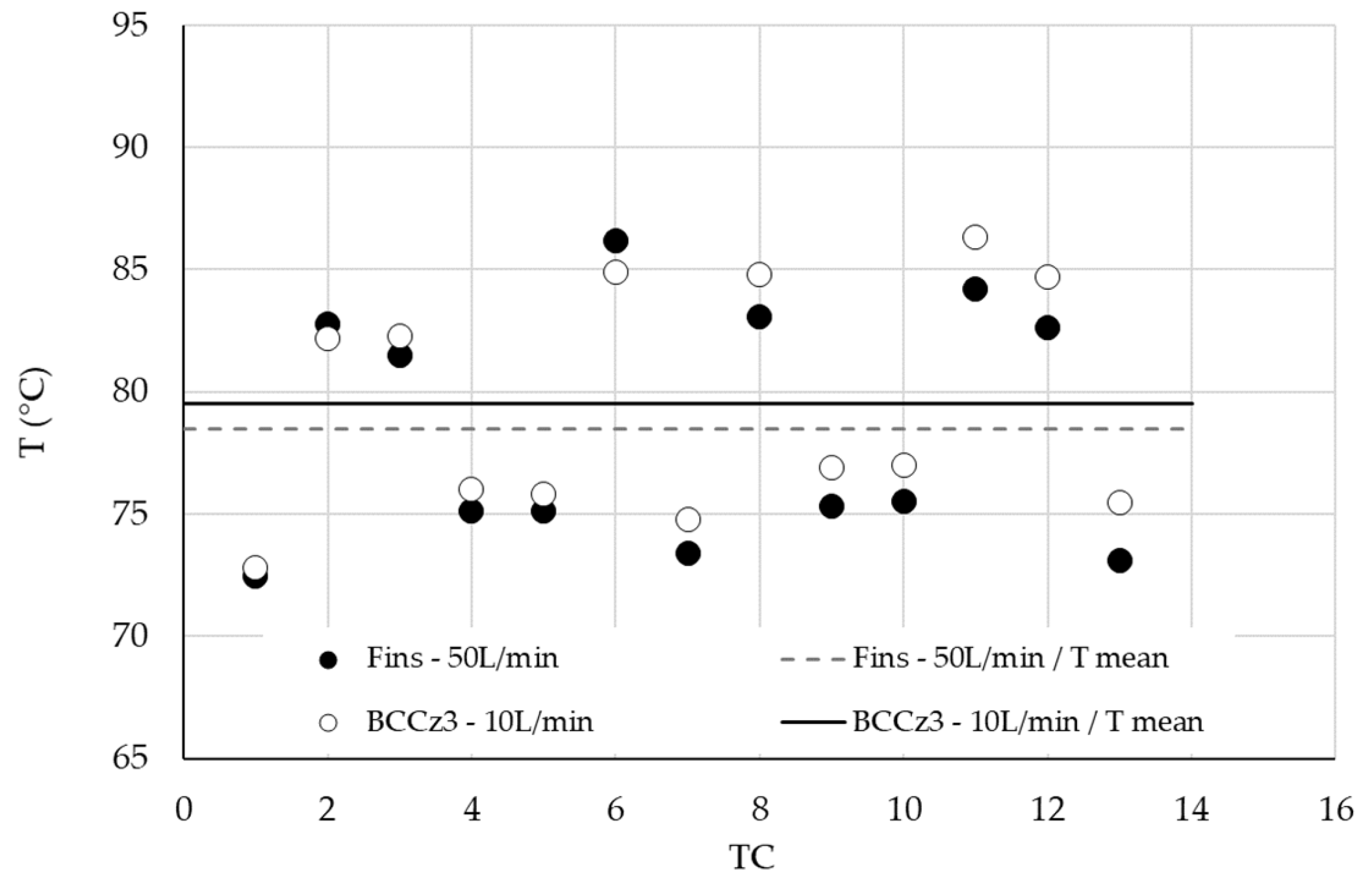
• Impact on flow rate: A notable observation is that by reducing the flow rate in the BCCz configuration, it is possible to maintain comparable thermal performance while keeping the pressure drop at an acceptable level, resulting in a greater operating flexibility. Figure 35 compares the baseplate temperature distribution for the Fins configuration at 50 L/min with that of the BCCz configuration at 10 L/min. The performance of these two cases can be reviewed in Figure 36, focusing on the framed data points.

Experimental baseplate temperatures for the BCCz configuration (with Qv = 10 L/min) and Fins configuration (with Qv = 50 L/min) at T_in = 70 °C and a heating power of 1905 W.

5. Final Conclusions

This study demonstrates the strong potential of additively manufactured lattice heat sinks for enhancing the thermal management of power electronics in railway applications. Through a comprehensive numerical and experimental investigation, lattice structures based on the BCCz unit cell topology were shown to significantly outperform conventional straight-fin and pin-fin heat sinks, achieving lower thermal resistance while maintaining acceptable pressure drops. The BCCz3 with circular strut cross-section, in particular, emerged as the most effective design, offering an optimal balance between thermal efficiency and fluidic resistance. The full scale demonstrator further confirmed that lattice-based heat sinks enable up to a 300% improvement in heat dissipation compared to conventional heat sinks, even at significantly reduced flow rates—achieving the same thermal performance with up to five times lower coolant flow. This demonstrates enhanced operational flexibility without compromising thermal efficiency. While challenges remain in optimizing hydraulic behavior (high pressure drop) and managing manufacturing complexity, this work highlights the viability and advantages of leveraging additive manufacturing to tailor lattice geometries for demanding cooling applications. These findings position additively manufactured lattice heat sinks as a promising solution for the next generation of railway power electronic systems, where efficiency, reliability, and compactness are critical.

6. Suggestions for Further Research

Roughness of the LS surface effect: The effect of the divergence between the actual geometry of the lattice structure heat sink obtained by additive manufacturing and the original CAD geometry on the thermal and hydraulic performance should be considered in a detailed, dedicated study. The scanned geometry files obtained by tomography have a huge number of facets and must be corrected and simplified carefully, which is a major challenge. This will allow evaluating the impact of manufacturing errors on thermal performance numerically as well as experimentally.

Hydraulic optimization: Future work could build on the recent MDO study in [39] to develop design rules to reduce pressure drops in heat sinks, balancing thermal efficiency with acceptable hydraulic performance.

Economic Considerations: Although optimizing hydraulic behavior and managing manufacturing complexity remain challenges, this work highlights the feasibility and benefits of additive manufacturing for adapting lattice geometries to demanding cooling applications. However, their larger-scale industrial adoption depends not only on performance but also on economic viability. According to this study, LPBF lattice heat sinks currently cost between EUR 4000 and EUR 5000 per module, and are approximately ten times more expensive than conventional machined or brazed cold plates. Although this price gap is significant, it could be reduced through the use of multi-laser LPBF systems, which have demonstrated cost reductions of up to three times, as well as by optimizing production volume and flow [40,41]. Beyond manufacturing efficiency, the economic case for additive manufacturing is significantly strengthened when it enables multifunctional integration at the system level [42]. For instance, lattice heat sinks can be directly integrated into power substrates or structural components, combining thermal management, structural support, and even fluid routing into a single part. This reduces assembly steps, minimizes interfaces, and simplifies maintenance. Such integrated designs allow for efficient thermal performance with reduced coolant flow requirements and enhanced operational reliability. These benefits underscore the importance of conducting a dedicated economic viability assessment when considering the adoption of multifunctional lattice heat sinks in the rail industry.