Degradation Prediction of Proton Exchange Membrane Fuel Cell Based on Multi-Head Attention Neural Network and Transformer Model
Abstract
1. Introduction
2. Degradation Prediction Model
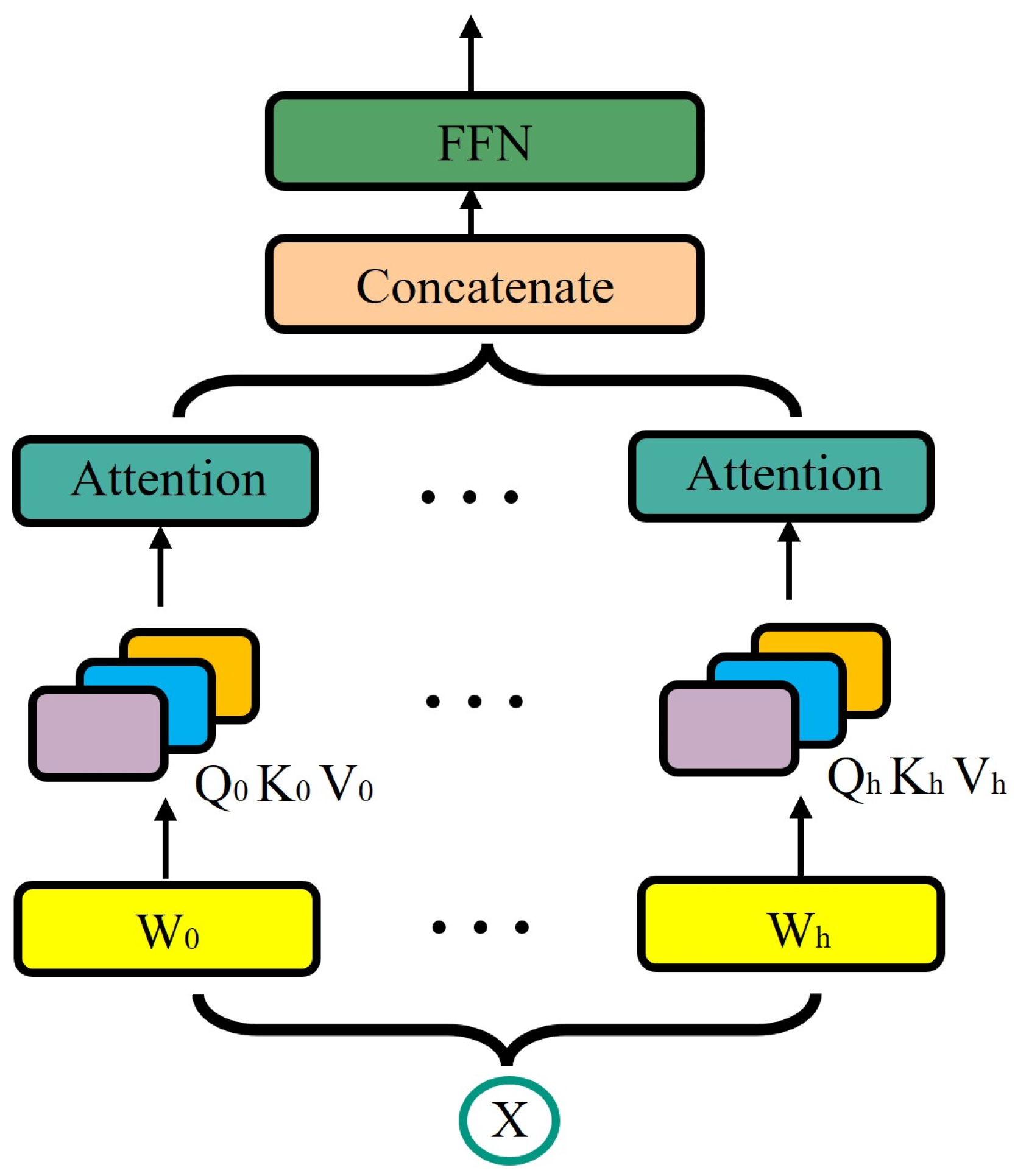
2.1. Multi-Head Attention with Class Token Model
2.1.1. Attention Mechanism
2.1.2. Multi-Head Attention with Feedforward Network
2.1.3. Class Token
2.2. Transformer Encoder Model
2.2.1. Position Encoding
2.2.2. Residual Connection and Layer Normalization
2.2.3. Training Optimization Strategies
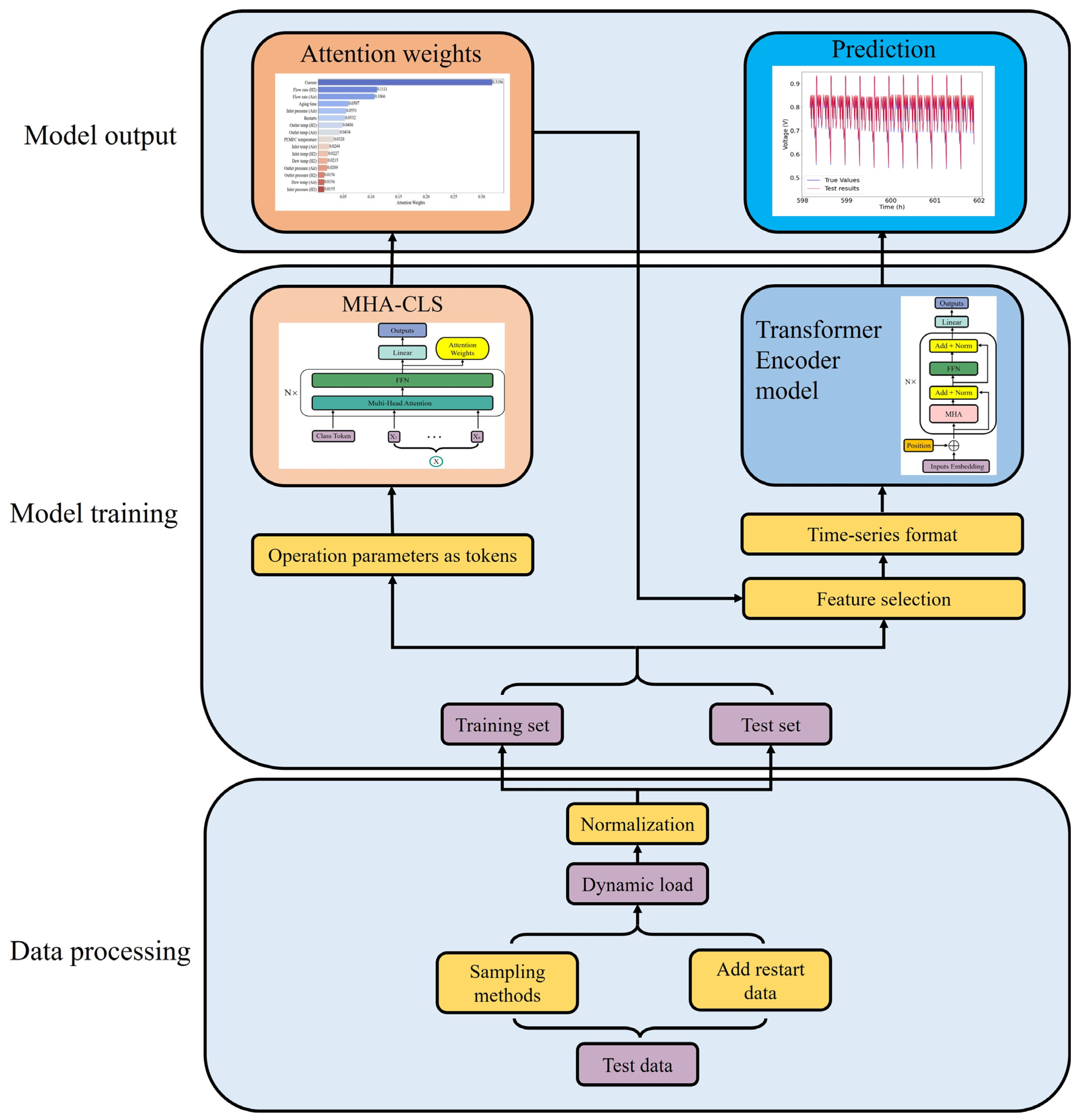
3. Data Processing and Experimental Design
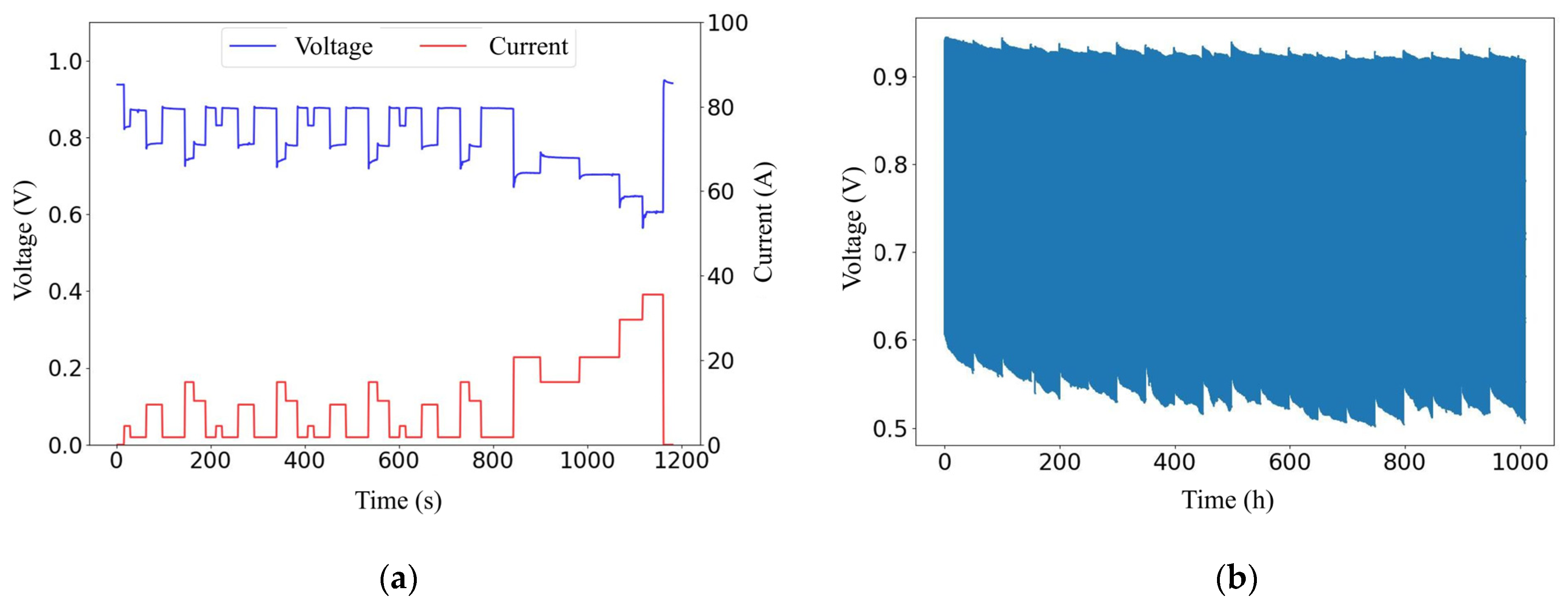
3.1. Data Processing
3.2. Implementation of the Model
- Data processing: To analyze the performance of the PEMFC under dynamic load cycle operating conditions, the dynamic cycle dataset is employed in this study. The data preprocessing methods used in this study are detailed in Section 3.1. The dynamic cycle dataset then undergoes normalization processes to ensure consistency.
- Designing the structure of MHA-CLS and Transformer Encoder models: The basic architecture of both models is determined based on their respective purpose. For the MHA-CLS, the model is structured to treat each operational parameter as an individual token to identify the contribution of each parameter to the prediction. The Transformer Encoder model is designed to process the time-series data in a sequence, leveraging its ability to capture long-range dependencies and temporal patterns for degradation prediction.
- Models training; After preprocessing, the dynamic cycle dataset is divided into a training set and a testing set with a predefined ratio. The models are trained by feeding them the dynamic cycle dataset, and the training process involves the optimizer and the evaluation criteria. In addition, various hyperparameters are set to optimize model performance.
- Performance prediction: Upon training completion, the trained MHA-CLS model is used to analyze the impact of varying operational parameters on performance, while the Transformer Encoder model predicts the aging trends of the PEMFC over time using selected operating parameters.
4. Simulation Results and Discussion
4.1. Evaluation Methods of Prediction Performance
4.2. Simulation Results for MHA-CLS
4.3. Prediction Results for Transformer Encoder Model
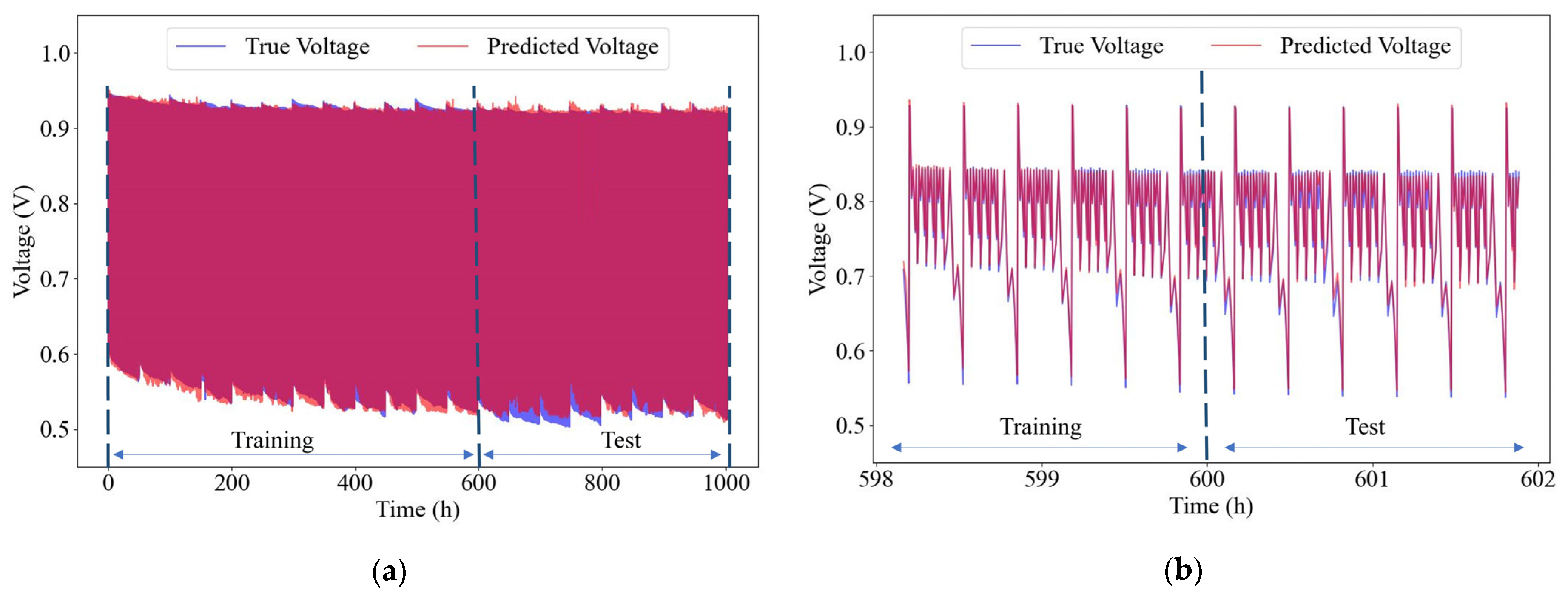
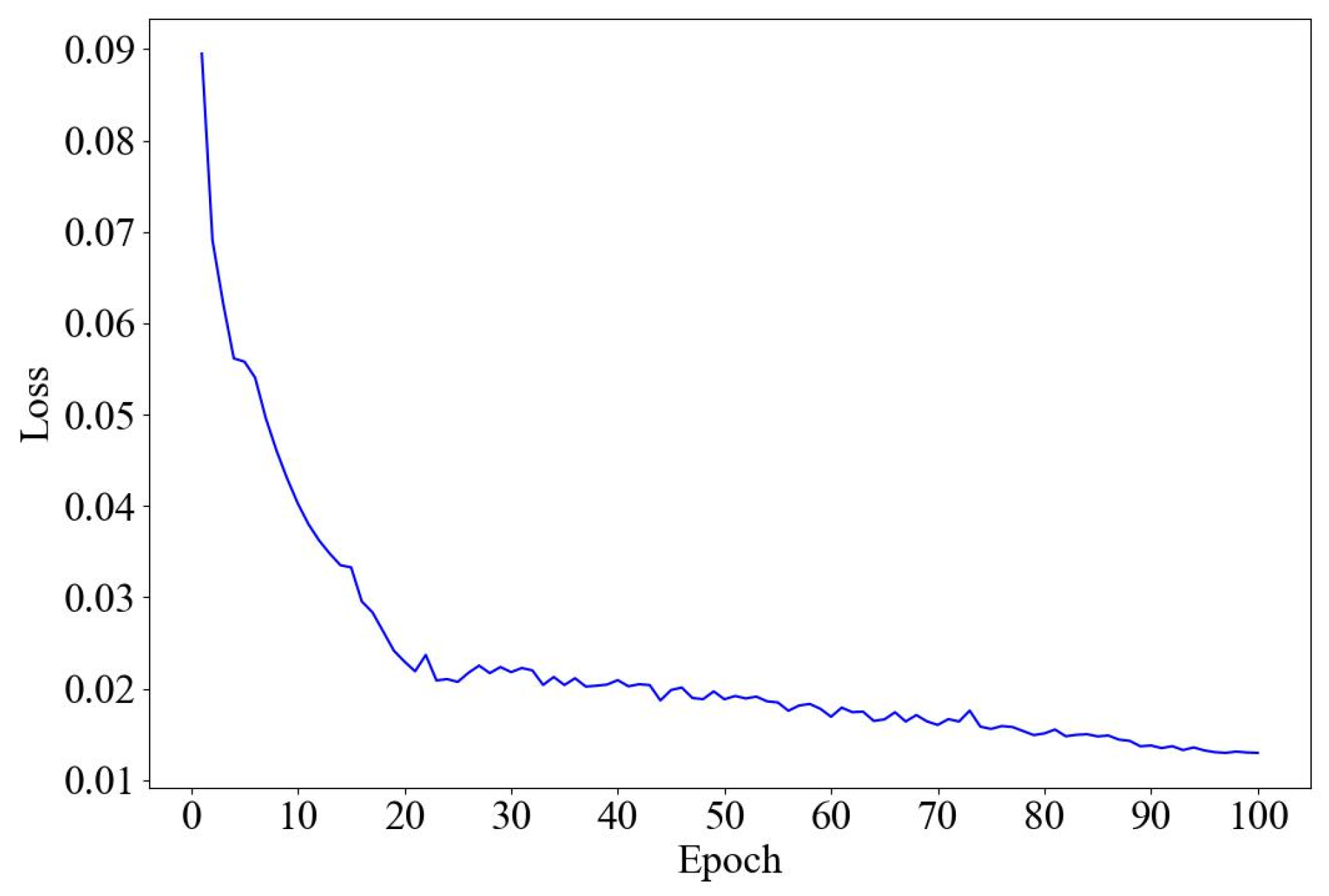
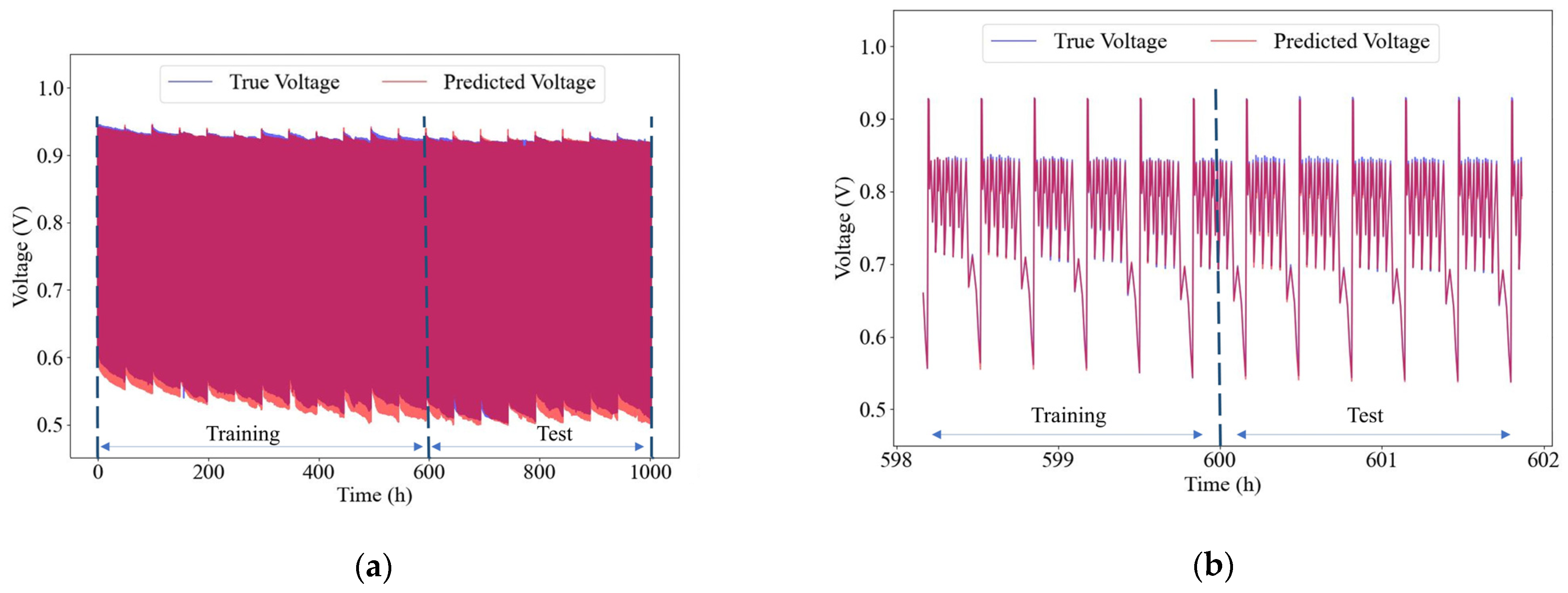
4.3.1. Prediction Performance with All Operational Parameters
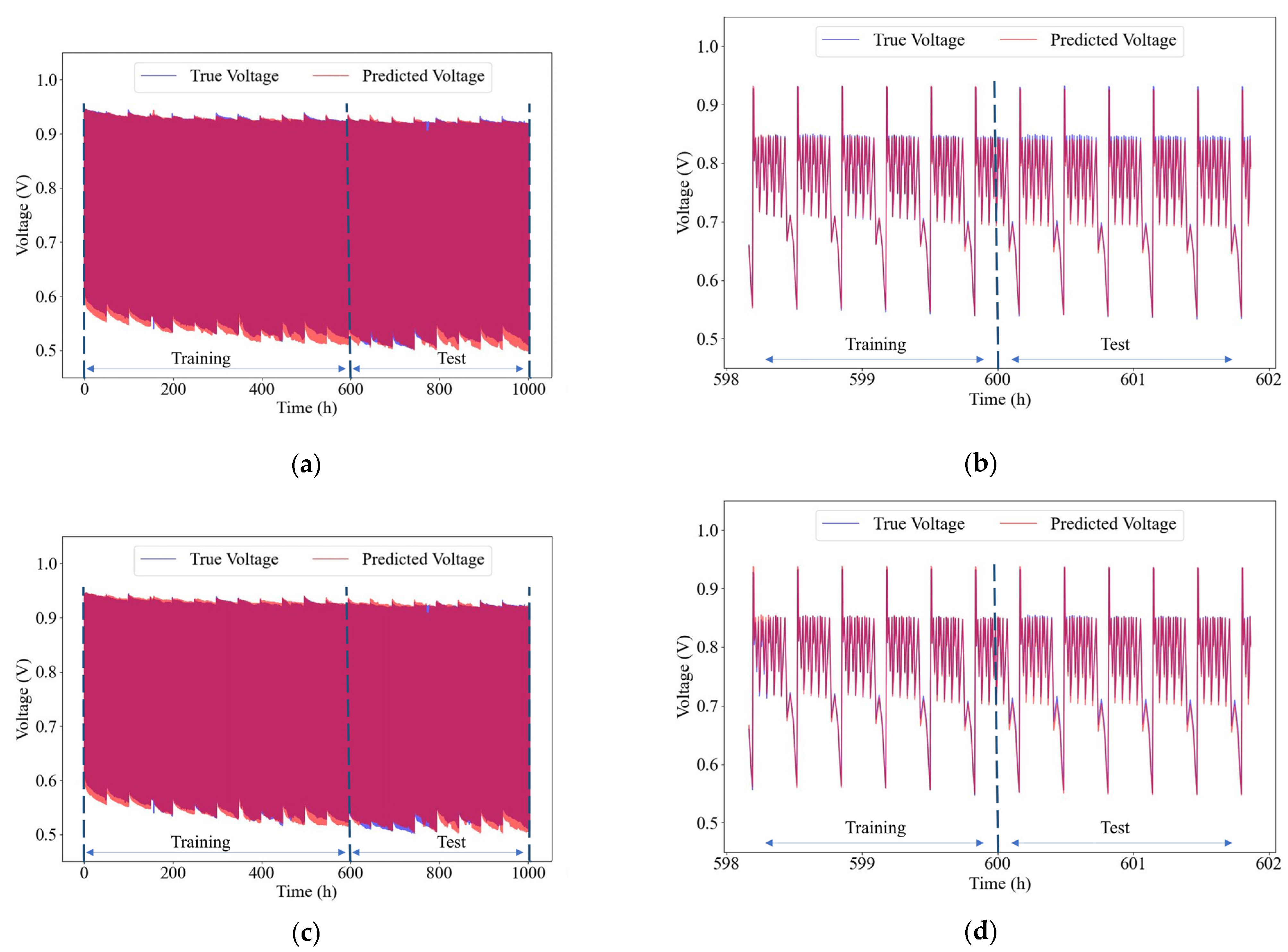
4.3.2. Prediction Performance with Selected Operational Parameters
4.3.3. Comparison with Other Works
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PEMFC | Proton exchange membrane fuel cell |
| FCEVs | Fuel cell electric vehicles |
| ANN | Artificial neural network |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| CNN | Convolutional Neural Network |
| ESN | Echo state network |
| MGU | Minimal Gated Unit |
| NARX | Nonlinear autoregressive exogenous |
| MHA | Multi-head attention |
| MHA-CLS | Multi-Head Attention with Class Token Model |
| FFN | Feedforward Network |
| ViT | Vision Transformer |
| Adam | Adaptive moment estimation |
| FC-DLC | Fuel Cell Dynamic Load Cycle |
| MSE | Mean squared error |
| MAE | Mean absolute error |
| RMSE | Root mean squared error |
References
- Abe, J.O.; Popoola, A.; Ajenifuja, E.; Popoola, O.M. Hydrogen Energy, Economy and Storage: Review and Recommendation. Int. J. Hydrogen Energy 2019, 44, 15072–15086. [Google Scholar] [CrossRef]
- Staffell, I.; Scamman, D.; Abad, A.V.; Balcombe, P.; Dodds, P.E.; Ekins, P.; Shah, N.; Ward, K.R. The Role of Hydrogen and Fuel Cells in the Global Energy System. Energy Environ. Sci. 2019, 12, 463–491. [Google Scholar] [CrossRef]
- Khalili, S.; Rantanen, E.; Bogdanov, D.; Breyer, C. Global Transportation Demand Development with Impacts on the Energy Demand and Greenhouse Gas Emissions in a Climate-Constrained World. Energies 2019, 12, 3870. [Google Scholar] [CrossRef]
- Cano, Z.P.; Banham, D.; Ye, S.; Hintennach, A.; Lu, J.; Fowler, M.; Chen, Z. Batteries and Fuel Cells for Emerging Electric Vehicle Markets. Nat. Energy 2018, 3, 279–289. [Google Scholar] [CrossRef]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Aminudin, M.; Kamarudin, S.; Lim, B.; Majilan, E.; Masdar, M.; Shaari, N. An Overview: Current Progress on Hydrogen Fuel Cell Vehicles. Int. J. Hydrogen Energy 2023, 48, 4371–4388. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, X.Z.; Martin, J.J.; Wang, H.; Zhang, J.; Shen, J.; Wu, S.; Merida, W. A Review of PEM Fuel Cell Durability: Degradation Mechanisms and Mitigation Strategies. J. Power Sources 2008, 184, 104–119. [Google Scholar] [CrossRef]
- Tanç, B.; Arat, H.T.; Baltacıoğlu, E.; Aydın, K. Overview of the next Quarter Century Vision of Hydrogen Fuel Cell Electric Vehicles. Int. J. Hydrogen Energy 2019, 44, 10120–10128. [Google Scholar] [CrossRef]
- Raeesi, M.; Changizian, S.; Ahmadi, P.; Khoshnevisan, A. Performance Analysis of a Degraded PEM Fuel Cell Stack for Hydrogen Passenger Vehicles Based on Machine Learning Algorithms in Real Driving Conditions. Energy Convers. Manag. 2021, 248, 114793. [Google Scholar] [CrossRef]
- Ahmadi, P.; Torabi, S.H.; Afsaneh, H.; Sadegheih, Y.; Ganjehsarabi, H.; Ashjaee, M. The Effects of Driving Patterns and PEM Fuel Cell Degradation on the Lifecycle Assessment of Hydrogen Fuel Cell Vehicles. Int. J. Hydrogen Energy 2020, 45, 3595–3608. [Google Scholar] [CrossRef]
- Pei, P.; Chen, H. Main Factors Affecting the Lifetime of Proton Exchange Membrane Fuel Cells in Vehicle Applications: A Review. Appl. Energy 2014, 125, 60–75. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S. Degradation Mechanisms of Proton Exchange Membrane Fuel Cell under Typical Automotive Operating Conditions. Prog. Energy Combust. Sci. 2020, 80, 100859. [Google Scholar] [CrossRef]
- Nguyen, H.L.; Han, J.; Nguyen, X.L.; Yu, S.; Goo, Y.-M.; Le, D.D. Review of the Durability of Polymer Electrolyte Membrane Fuel Cell in Long-Term Operation: Main Influencing Parameters and Testing Protocols. Energies 2021, 14, 4048. [Google Scholar] [CrossRef]
- Strahl, S.; Gasamans, N.; Llorca, J.; Husar, A. Experimental Analysis of a Degraded Open-Cathode PEM Fuel Cell Stack. Int. J. Hydrogen Energy 2014, 39, 5378–5387. [Google Scholar] [CrossRef]
- Dhimish, M.; Vieira, R.G.; Badran, G. Investigating the Stability and Degradation of Hydrogen PEM Fuel Cell. Int. J. Hydrogen Energy 2021, 46, 37017–37028. [Google Scholar] [CrossRef]
- Song, K.; Ding, Y.; Hu, X.; Xu, H.; Wang, Y.; Cao, J. Degradation Adaptive Energy Management Strategy Using Fuel Cell State-of-Health for Fuel Economy Improvement of Hybrid Electric Vehicle. Appl. Energy 2021, 285, 116413. [Google Scholar] [CrossRef]
- Hahn, S.; Braun, J.; Kemmer, H.; Reuss, H.-C. Optimization of the Efficiency and Degradation Rate of an Automotive Fuel Cell System. Int. J. Hydrogen Energy 2021, 46, 29459–29477. [Google Scholar] [CrossRef]
- Zuo, B.; Cheng, J.; Zhang, Z. Degradation Prediction Model for Proton Exchange Membrane Fuel Cells Based on Long Short-Term Memory Neural Network and Savitzky-Golay Filter. Int. J. Hydrogen Energy 2021, 46, 15928–15937. [Google Scholar] [CrossRef]
- Chandesris, M.; Vincent, R.; Guetaz, L.; Roch, J.-S.; Thoby, D.; Quinaud, M. Membrane Degradation in PEM Fuel Cells: From Experimental Results to Semi-Empirical Degradation Laws. Int. J. Hydrogen Energy 2017, 42, 8139–8149. [Google Scholar] [CrossRef]
- Mayur, M.; Strahl, S.; Husar, A.; Bessler, W.G. A Multi-Timescale Modeling Methodology for PEMFC Performance and Durability in a Virtual Fuel Cell Car. Int. J. Hydrogen Energy 2015, 40, 16466–16476. [Google Scholar] [CrossRef]
- Pei, P.; Chang, Q.; Tang, T. A Quick Evaluating Method for Automotive Fuel Cell Lifetime. Int. J. Hydrogen Energy 2008, 33, 3829–3836. [Google Scholar] [CrossRef]
- Ou, M.; Zhang, R.; Shao, Z.; Li, B.; Yang, D.; Ming, P.; Zhang, C. A Novel Approach Based on Semi-Empirical Model for Degradation Prediction of Fuel Cells. J. Power Sources 2021, 488, 229435. [Google Scholar] [CrossRef]
- Vichard, L.; Harel, F.; Ravey, A.; Venet, P.; Hissel, D. Degradation Prediction of PEM Fuel Cell Based on Artificial Intelligence. Int. J. Hydrogen Energy 2020, 45, 14953–14963. [Google Scholar] [CrossRef]
- Napoli, G.; Ferraro, M.; Sergi, F.; Brunaccini, G.; Antonucci, V. Data Driven Models for a PEM Fuel Cell Stack Performance Prediction. Int. J. Hydrogen Energy 2013, 38, 11628–11638. [Google Scholar] [CrossRef]
- Huo, W.; Li, W.; Zhang, Z.; Sun, C.; Zhou, F.; Gong, G. Performance Prediction of Proton-Exchange Membrane Fuel Cell Based on Convolutional Neural Network and Random Forest Feature Selection. Energy Convers. Manag. 2021, 243, 114367. [Google Scholar] [CrossRef]
- Ming, W.; Sun, P.; Zhang, Z.; Qiu, W.; Du, J.; Li, X.; Zhang, Y.; Zhang, G.; Liu, K.; Wang, Y.; et al. A Systematic Review of Machine Learning Methods Applied to Fuel Cells in Performance Evaluation, Durability Prediction, and Application Monitoring. Int. J. Hydrogen Energy 2023, 48, 5197–5228. [Google Scholar] [CrossRef]
- Chen, K.; Badji, A.; Laghrouche, S.; Djerdir, A. Polymer Electrolyte Membrane Fuel Cells Degradation Prediction Using Multi-Kernel Relevance Vector Regression and Whale Optimization Algorithm. Appl. Energy 2022, 318, 119099. [Google Scholar] [CrossRef]
- Wilberforce, T.; Biswas, M. A Study into Proton Exchange Membrane Fuel Cell Power and Voltage Prediction Using Artificial Neural Network. Energy Rep. 2022, 8, 12843–12852. [Google Scholar] [CrossRef]
- Sahajpal, K.; Rana, K.P.S.; Kumar, V. Accurate Long-Term Prognostics of Proton Exchange Membrane Fuel Cells Using Recurrent and Convolutional Neural Networks. Int. J. Hydrogen Energy 2023, 48, 30532–30555. [Google Scholar] [CrossRef]
- Zuo, J.; Lv, H.; Zhou, D.; Xue, Q.; Jin, L.; Zhou, W.; Yang, D.; Zhang, C. Deep Learning Based Prognostic Framework towards Proton Exchange Membrane Fuel Cell for Automotive Application. Appl. Energy 2021, 281, 115937. [Google Scholar] [CrossRef]
- Yu, Y.; Yu, Q.; Luo, R.; Chen, S.; Yang, J.; Yan, F. A Predictive Framework for PEMFC Dynamic Load Performance Degradation Based on Feature Parameter Analysis. Int. J. Hydrogen Energy 2024, 71, 1090–1103. [Google Scholar] [CrossRef]
- Li, S.; Luan, W.; Wang, C.; Chen, Y.; Zhuang, Z. Degradation Prediction of Proton Exchange Membrane Fuel Cell Based on Bi-LSTM-GRU and ESN Fusion Prognostic Framework. Int. J. Hydrogen Energy 2022, 47, 33466–33478. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y.; Zhou, S.; Li, H.; Zhu, W.; Liu, Y.; Xie, C.; Zhang, R. Degradation Prediction of Proton Exchange Membrane Fuel Cell Based on Mixed Gated Units under Multiple Operating Conditions. Int. J. Hydrogen Energy 2024, 67, 268–281. [Google Scholar] [CrossRef]
- Ramesh, A.S.; Vigneshwar, S.; Vickram, S.; Manikandan, S.; Subbaiya, R.; Karmegam, N.; Kim, W. Artificial Intelligence Driven Hydrogen and Battery Technologies–A Review. Fuel 2023, 337, 126862. [Google Scholar] [CrossRef]
- Pan, R.; Yang, D.; Wang, Y.; Chen, Z. Performance Degradation Prediction of Proton Exchange Membrane Fuel Cell Using a Hybrid Prognostic Approach. Int. J. Hydrogen Energy 2020, 45, 30994–31008. [Google Scholar] [CrossRef]
- Lv, L.; Pei, P.; Ren, P.; Wang, H.; Wang, G. Exploring Performance Degradation of Proton Exchange Membrane Fuel Cells Based on Diffusion Transformer Model. Energies 2025, 18, 1191. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; Volume 30. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-Training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Lu, J.; Batra, D.; Parikh, D.; Lee, S. Vilbert: Pretraining Task-Agnostic Visiolinguistic Representations for Vision-and-Language Tasks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2019; Volume 32. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.-H. Restormer: Efficient Transformer for High-Resolution Image Restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5728–5739. [Google Scholar]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A Transformer-Based Framework for Multivariate Time Series Representation Learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Online, 14–18 August 2021; pp. 2114–2124. [Google Scholar]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jégou, H. Training Data-Efficient Image Transformers & Distillation through Attention. In Proceedings of the International Conference on Machine Learning, PMLR, Online, 18–24 July 2021; pp. 10347–10357. [Google Scholar]
- Zuo, J.; Lv, H.; Zhou, D.; Xue, Q.; Jin, L.; Zhou, W.; Yang, D.; Zhang, C. Long-Term Dynamic Durability Test Datasets for Single Proton Exchange Membrane Fuel Cell. Data Brief 2021, 35, 106775. [Google Scholar] [CrossRef]
- Tang, X.; Shi, L.; Li, M.; Xu, S.; Sun, C. Health State Estimation and Long-Term Durability Prediction for Vehicular PEM Fuel Cell Stacks Under Dynamic Operational Conditions. IEEE Trans. Power Electron. 2025, 40, 4498–4509. [Google Scholar] [CrossRef]
- Nagulapati, V.M.; Kumar, S.S.; Annadurai, V.; Lim, H. Machine Learning Based Fault Detection and State of Health Estimation of Proton Exchange Membrane Fuel Cells. Energy AI 2023, 12, 100237. [Google Scholar] [CrossRef]





| Parameter | Physical Meaning |
|---|---|
| Time | Aging time (s) |
| Current | The operating current (A) |
| Voltage | PEMFC output voltage (V) |
| Pressure anode inlet, pressure anode outlet | Inlet and outlet pressure of H2 (kPa) |
| Pressure cathode inlet, pressure cathode outlet | Inlet and outlet pressure of air (kPa) |
| Temp anode inlet, temp anode outlet | Inlet and outlet temperature of H2 (°C) |
| Temp cathode inlet, temp cathode outlet | Inlet and outlet temperature of air (°C) |
| Temp anode dewpoint water | Dewpoint water temperature of H2 (°C) |
| Temp cathode dewpoint water | Dewpoint water temperature of air (°C) |
| Total anode stack flow | Total stack flow of H2 (NLPM) |
| Total cathode stack flow | Total stack flow of air (NLPM) |
| Temp endplate | Operating temperature of PEMFC (°C) |
| Metric | RMSE | MSE | MAE | |
|---|---|---|---|---|
| Training Phase | 0.01517550 | 0.00023029 | 0.00998576 | 0.99375892 |
| Test Phase | 0.01784608 | 0.00031848 | 0.01170215 | 0.99026889 |
| Metric | RMSE | MSE | MAE | |
|---|---|---|---|---|
| Training Phase | 0.00497314 | 0.00002751 | 0.00387942 | 0.99925697 |
| Test Phase | 0.00895497 | 0.00008019 | 0.00659059 | 0.99035249 |
| Metric | Training Phase | Test Phase | ||||
|---|---|---|---|---|---|---|
| 16-Dim | 8-Dim | 11-Dim | 16-Dim | 8-Dim | 11-Dim | |
| RMSE | 0.00497314 | 0.00578862 | 0.00466829 | 0.00895497 | 0.00924553 | 0.00878816 |
| MSE | 0.00002751 | 0.00003351 | 0.00002179 | 0.00008019 | 0.00009468 | 0.00007723 |
| MAE | 0.00387942 | 0.00441970 | 0.00345508 | 0.00659059 | 0.00717803 | 0.00645769 |
| 0.99925697 | 0.99911760 | 0.99944786 | 0.99035249 | 0.98701987 | 0.99070856 | |
| Dataset | Method | Training Phase | Test Phase |
|---|---|---|---|
| Dynamic drive cycle dataset (0.6–0.95 V) | ANN [47] | 0.0429 | |
| SVM [47] | 0.0294 | ||
| LSTM [30] | 0.011066 | 0.017637 | |
| GRU [30] | 0.015873 | 0.018260 | |
| LSTM attention [30] | 0.008542 | 0.016409 | |
| AT-MIXGU [33] | 0.009975 | 0.011049 | |
| Transformer Encoder(11-dim) | 0.004668 | 0.008788 | |
| Transformer Encoder(16-dim) | 0.004973 | 0.008954 | |
| 2500 h durability test dataset (210–365 V) | Informer [46] | 0.75 | |
| Improved Informer [46] | 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Huang, X.; Li, Y.; Ma, H.; Zhang, K.; Song, K. Degradation Prediction of Proton Exchange Membrane Fuel Cell Based on Multi-Head Attention Neural Network and Transformer Model. Energies 2025, 18, 3177. https://doi.org/10.3390/en18123177
Tang Y, Huang X, Li Y, Ma H, Zhang K, Song K. Degradation Prediction of Proton Exchange Membrane Fuel Cell Based on Multi-Head Attention Neural Network and Transformer Model. Energies. 2025; 18(12):3177. https://doi.org/10.3390/en18123177
Chicago/Turabian StyleTang, Yikai, Xing Huang, Yanju Li, Haoran Ma, Kai Zhang, and Ke Song. 2025. "Degradation Prediction of Proton Exchange Membrane Fuel Cell Based on Multi-Head Attention Neural Network and Transformer Model" Energies 18, no. 12: 3177. https://doi.org/10.3390/en18123177
APA StyleTang, Y., Huang, X., Li, Y., Ma, H., Zhang, K., & Song, K. (2025). Degradation Prediction of Proton Exchange Membrane Fuel Cell Based on Multi-Head Attention Neural Network and Transformer Model. Energies, 18(12), 3177. https://doi.org/10.3390/en18123177





