Abstract
This paper addresses the increasingly severe issue of exceeding short-circuit current limits brought about by the rapid development of large power grids. It investigates the principles of short-circuit current control and methods to limit short-circuit current through the modification of grid equipment. Building on the current state of research, this study introduces different types of impedances to analyze their effects on the control of short-circuit currents, thereby exploring the principles of short-circuit current control based on the composition of actual grid short-circuit currents. Regarding the issue of controlling short-circuit current levels in large power grids, a detailed analysis is conducted of the operational principles, advantages, and disadvantages of five types of modified grid equipment for limiting short-circuit current: high-impedance generators, high-impedance transformers, current-limiting reactors, fault current limiters (FCLs), and a generator–transformer–line group unit. This study identifies the applicable conditions for each short-circuit current-limiting measure and presents specific engineering simulation cases to validate their effectiveness in limiting short-circuit currents, thus determining the control effects of each limiting measure. The results indicate that this research plays an important role in controlling short-circuit currents in power systems, maintaining the safe and stable operation of power systems, and improving the structural framework of power systems.
1. Introduction
With the rapid growth of China’s economy, electricity demand has been continuously rising, leading to the ongoing expansion of the grid structure. In this process, the complexity and scale of the power system have made the issue of short-circuit currents increasingly prominent. Short-circuit current refers to the current that flows through the fault point when a short-circuit fault occurs in the power system, and its magnitude directly affects the safe and stable operation of electrical equipment. With the increase in the number of generating units and the extension of transmission lines, particularly the integration of large generating equipment, the risk of excessive short-circuit currents has become more apparent. This may lead to equipment damage and the instability of the power system, posing severe challenges for protection device design and power system operation. In AC power grids, a rapid increase in short-circuit currents can prevent protection devices from operating correctly within the set time, resulting in cascading failures within the power system. An excess of short-circuit currents also increases safety hazards in the system, raising the likelihood of accidents. Thus, there is an urgent need to implement effective measures to limit short-circuit currents to address this issue. By effectively reducing short-circuit currents through these measures, the safe and reliable operation of the power system can be ensured, providing a solid guarantee for the sustainable development of the economy and the efficient utilization of energy.
For many years, scholars both domestically and internationally have conducted extensive research on how to solve the problem of excessive short-circuit currents.
Surya, A. et al. suggest that increasing the impedance value of transformers to 45% can effectively reduce short-circuit currents in high-voltage power systems, thereby minimizing the risk of transformer damage [1]. Li, J. et al. propose that transformers with variable impedance can reduce short-circuit currents and overvoltages through novel suppression measures, enhancing the safety and economic value of the power grid [2]. Xu, C. et al. have put forward a current-limiting strategy for modular inverter systems under asymmetric short-circuit faults, which is simpler and more effective than existing methods, ensuring reliable power supply [3]. Varetsky, Y. et al. point out that current-limiting reactors in industrial power grids may be damaged due to peak currents, necessitating the careful selection of grid locations, equipment start-up currents, and potential grid configurations [4]. Gouda, O. et al. introduced a novel air-core current-limiting reactor that effectively limits fault currents in medium- and low-voltage systems without causing harmonic issues [5]. Ren, H. et al. argue that current-limiting reactors can effectively limit short-circuit currents in 500 kV power systems but may increase the transient recovery voltage steepness during circuit breaker interruptions [6]; they also proposed that adding current-limiting reactors on 500 kV transmission lines can reduce temporary overvoltages by altering positive- and zero-sequence impedance parameters [7]. Wang, P. et al. introduced a DC solid-state current limiter with adaptive current-limiting capability, which effectively suppresses the rapid rise in DC fault currents in power systems, reducing the impact on the dynamic characteristics of reactors [8]. Wang, Z. et al. contend that current-limiting reactors can effectively reduce peak-to-peak short-circuit fault currents in DC distribution systems, minimizing damage and ensuring system safety [9].
Lyu, H. et al. proposed an improved hybrid DC circuit breaker with adaptive fault current-limiting capabilities, which effectively restrains fault currents, maintains system stability, and reduces requirements for protection and surge arrester capacity [10]. Han, B. et al. proposed a dynamic breaker that combines changes in system structure with dynamically adjusting system topology during faults in Reference [11]. In Reference [12], Wang, Z. et al. proposed a hybrid direct-current circuit breaker with current-limiting capabilities, which exhibits better breaking performance and lower costs compared to traditional topologies, solving the problem of excessive short-circuit currents in branch grids. The fault current limiter (FCL) is a novel current-limiting solution. Wu, S. studied several representative fault current limiters, including those under development, with a focus on Thyristor-Protected Series Capacitor (TPSC)-based short-circuit current limiters (SCCLs). The research also introduced a demonstration project of fault current limiters in the East China 500 kV grid, detailing the main circuit diagram and using overvoltage protection control, as well as summarizing the development trends of fault limiters in the literature [13]. In Reference [14], Yan, Z. researched TPSC-based short-circuit current limiters with externally connected series reactors, effectively addressing excessive short-circuit currents in high-voltage transmission systems, enhancing reliability and availability. Ming, Z. believes that fault current limiters provide zero or low impedance under normal conditions and high-impedance during short-circuit faults, offering a multifunctional solution for various applications [15]. In Reference [16], Zhang, Q. et al. proposed an AC fast-recovery superconducting fault current limiter, which can effectively suppress short-circuit currents and increase system stability by over three times. Amini, M. et al. proposed a novel fault current limiter based on hollow variable series reactors, which can effectively limit fault currents in a short time while minimizing voltage drop and reactive power loss during normal operation [17]. In Reference [18], Mujie, Z. et al. proposed that a 550 kV fault current limiter with fast switching and a large capacity can effectively limit short-circuit currents, improving the distance protection performance of power grid lines. Akin, F. et al. contend that hollow reactors in solid-state fault current limiters can effectively limit fault currents during grid failures while carrying nearly the entire current of the network under normal conditions [19]. Zhang, K. et al. argue that fast-switching fault current limiters can effectively limit short-circuit currents in extra-high-voltage transmission lines without significantly impacting the overvoltage during automatic reclosing [20]. Meanwhile, in Reference [21], Gan, Y. et al. also pointed out that fault current limiters and flexible current-limiting technologies show broad prospects in AC power supply systems, but further research on equipment topology and configuration is needed to improve economic viability.
Regarding the topic of how to limit short-circuit currents in large power grids, we have previously conducted some research and published two manuscripts. In Ref. [22], we briefly described the advantages and disadvantages of more than a dozen current-limiting measures, as well as their applicable conditions and installation locations, focusing on the optimal selection methods when multiple solutions are available for the same short-circuit current exceedance issue [22]. Subsequently, we shifted our research focus to the current-limiting measures themselves, categorizing the measures outlined in Ref. [22] into two main categories based on structural changes to the power grid and the renovation of grid equipment. Therefore, in Ref. [23], we provided a detailed discussion of the principles and related simulations of current-limiting measures that involve changing the grid structure, while the current manuscript addresses the other major category of current-limiting measures, namely, measures related to renovating grid equipment, including principles and simulation studies, to complete our research framework.
In practical engineering, the selection of short-circuit current-limiting measures is often based on engineering experience. However, there is relatively little systematic research that thoroughly examines the principles, advantages, and disadvantages of various measures, specifies the applicable conditions for each, and conducts actual grid simulations to validate their effectiveness in limiting current.
This paper focuses on researching measures and methods to limit short-circuit currents through the renovation of grid equipment. It provides a detailed analysis of the working principles, advantages, disadvantages, and applicable conditions of each measure, which is of significant importance for the evaluation and selection of current-limiting measures based on actual engineering needs. Furthermore, for each current-limiting measure, real grid data are used for simulation analysis, allowing for a comparison of short-circuit currents before and after the implementation of the limiting measures. This clearly illustrates the effectiveness of the current-limiting measures studied in this paper. Additionally, this paper elaborates in detail on the existing gaps in current research and conducts simulations, contributing valuable insights into addressing the issue of exceeding short-circuit current limits.
This paper primarily focuses on the issue of exceeding short-circuit current limits in the 500–220 kV high- and low-voltage electromagnetic ring networks present in China’s large power grids. In Section 2, the composition and control principles of short-circuit currents in the grid are examined. Section 3 places emphasis on analyzing the mechanisms, applicable conditions, advantages, and disadvantages of short-circuit current-limiting measures that involve renovating grid equipment. In Section 4, a simulation analysis of the current-limiting effects of each short-circuit current-limiting measure, using a specific grid as a case study, is conducted. Finally, Section 5 presents a summary of the research findings and discusses the limitations of this study.
2. Principle of Short-Circuit Current Control
In mainland China, common issues of excessive short-circuit currents often occur in the 500–220 kV electromagnetic ring network, as illustrated in the schematic diagram shown in Figure 1.
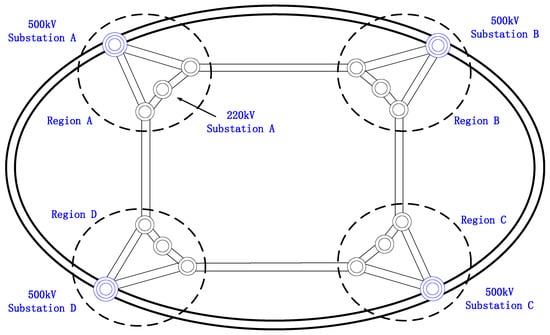
Figure 1.
Schematic diagram of the 500–220 kV electromagnetic ring network.
As the most severe type of short-circuit fault, it is essential to study the control principles of three-phase short-circuit currents. The magnitude of three-phase short-circuit currents depends on the self-impedance of the short-circuit point, which physically represents the electrical distance between the short-circuit point and other points in the network. The tighter the network structure, the smaller the node self-impedance and the electrical distance, resulting in higher levels of short-circuit currents; conversely, the opposite is also true.
To investigate the mechanisms behind excessive short-circuit currents in substations, the positive-sequence equivalent circuit diagram of any 500 kV substation connected to any 220 kV substation is depicted in Figure 2.
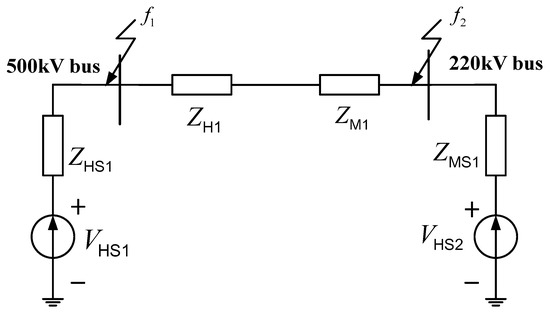
Figure 2.
Positive-sequence equivalent circuit diagram of 500 kV substation and its connected 220 kV substation.
In Figure 2, represents the positive-sequence equivalent impedance of the 500 kV bus to ground, characterizing the transfer impedance associated with all 500 kV substations connected to this bus. The more 500 kV lines connected to it, the tighter the 500 kV network, resulting in a smaller value of . and are the positive-sequence equivalent impedances of the transformer T configuration circuit. denotes the positive-sequence equivalent impedance of the 220 kV bus to ground, which characterizes the transfer impedance associated with all 220 kV substations (including power plants) connected to this bus. The more 220 kV lines connected and the more power plants connected to the bus, the smaller this value becomes.
From Figure 2, it can be noted that when a three-phase short circuit occurs on the 500 kV side, the self-impedance is given by
Let be the voltage before the three-phase short circuit on the 500 kV side; then, the three-phase short-circuit current on the 500 kV side is
The self-impedance during a three-phase short circuit on the 220 kV side is
Let be the voltage before the three-phase short circuit on the 220 kV side; then, the three-phase short-circuit current on the 220 kV side is
From Equations (2) and (4), it can be seen that to control the short-circuit current of the 500–220 kV electromagnetic ring network, it is necessary to start with increasing the impedance values of , , and . The commonly used technical measures for controlling short-circuit current in engineering are also based on the principle of increasing impedance.
Since the formats of Equations (2) and (4) are consistent, if we continue by making , then the three-phase short-circuit current at this point is
In this equation, represents the ground equivalent impedance of the bus under study for the short circuit. represents the ground equivalent impedance of the upstream or downstream bus connected to the short-circuit bus through the transformer.
To investigate the degree of impact that impedance changes have on the short-circuit current, the short-circuit current from Equation (5) is taken as the function value, with the three impedances as independent variables. The partial derivatives are then calculated as
From Equation (6), it can be seen that the first-order partial derivatives of the short-circuit current with respect to the three impedances are all negative. This indicates that increasing the impedance will result in a decrease in the short-circuit current. To investigate the shape of the first-order partial derivative curves, let the second-order partial derivatives be
From Equation (7), it can be observed that the second-order partial derivatives are all positive, indicating that , , and are all monotonically increasing functions over the interval . The limits of the three first-order partial derivatives at the endpoints of the interval are calculated as
Based on the above derivation, the curves of the three-phase short-circuit current with respect to the partial derivatives of the three components of impedance in the system can be plotted as shown in Figure 3.
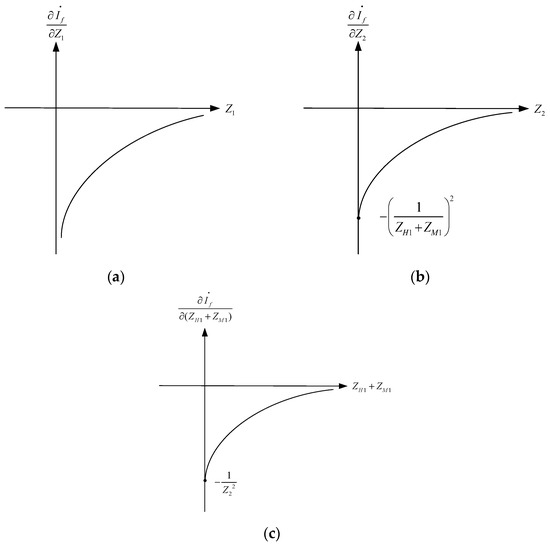
Figure 3.
(a) The partial derivative curve of with respect to the same-level equivalent impedance; (b) the partial derivative curve of with respect to the non-same-level equivalent impedance; (c) the partial derivative curve of with respect to the transformer’s equivalent impedance.
From Figure 3, it can be seen that the values of the three partial derivatives are all negative within the defined domain. As the impedance decreases, the partial derivatives become smaller, indicating that the slope of the short-circuit current becomes larger. This means that the short-circuit current monotonically decreases as the three components of impedance increase. When the impedance increases arithmetically to limit the short-circuit current, the smaller the impedance value, the more significant the effect of increasing the impedance on limiting the short-circuit current; conversely, the larger the impedance value, the weaker the effect of further increasing the impedance to limit the short-circuit current.
Additionally, and both have limits at the zero point of impedance, which indicates that the control effect on the short-circuit current achieved by changing the non-same-level equivalent impedance and the transformer’s equivalent impedance is limited. Furthermore, the limit of at the zero point approaches negative infinity, indicating that the short-circuit current is most influenced by the same-level equivalent impedance to ground. Therefore, most current-limiting measures for short-circuit currents are based on increasing the same-level equivalent impedance at the short-circuit point.
3. Current-Limiting Measures for Renovating Power Grid Equipment
To address the issue of exceeding short-circuit current limits, one option is to replace circuit breakers with those that have a larger interrupting capacity. However, due to the technical conditions for manufacturing circuit breakers and the engineering conditions for connecting circuit breakers to the power grid, the maximum interrupting capacity of circuit breakers at each voltage level is limited. This limit represents the upper limit of the short-circuit current that should be controlled at that voltage level. The upper limits of short-circuit currents for various voltage levels are shown in Table 1 [23].

Table 1.
The upper limit of short-circuit current for each voltage level.
In this paper, current-limiting measures are categorized into two types based on the different categories of network equipment being modified: the addition of large high-reactance equipment and increasing line impedance.
3.1. The Addition of Large High-Reactance Equipment
3.1.1. Install a High-Impedance Generator
Synchronous motors are the most widely used generators in the power systems of our country. They can be classified into two types based on the structure of their main magnetic poles: salient pole generators and non-salient pole generators. Non-salient pole generators have a uniform air gap, and the direct-axis and quadrature-axis synchronous reactances are equal. Ignoring magnetic circuit saturation, the electromotive force equation for non-salient pole synchronous generators is given by
In this equation, represents the terminal voltage of the armature stator winding, is the resistance voltage drop for the one-phase winding of the armature, denotes the leakage reactance of the stator winding, is the armature reaction reactance, and is the synchronous reactance of the non-salient pole synchronous motor. The vector diagram of the non-salient pole generator is shown in Figure 4.
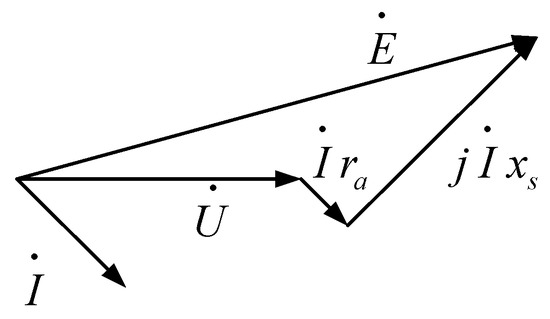
Figure 4.
Vector diagram of the non-salient pole generator.
The electromotive force equation for salient pole generators is given by
In this equation, is the direct-axis synchronous reactance of the synchronous motor, and is the quadrature-axis synchronous reactance of the synchronous motor. The vector diagram of the salient pole generator is shown in Figure 5.
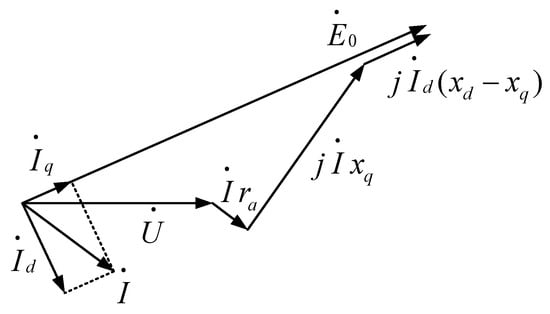
Figure 5.
Vector diagram of the salient pole generator.
The short-circuit ratio of a generator is defined as the ratio of the short-circuit current during a three-phase steady-state short circuit at the rated voltage with no load to the rated current. Increasing the synchronous reactance of the generator will lead to a corresponding reduction in the air gap and the size of the equipment, decrease the amount of copper used in the rotor, lower the cost of the motor, increase the electrical distance of the system, and correspondingly reduce the short-circuit current. This has a certain impact on controlling the short-circuit current, especially in large-capacity units entering the grid, which can cause serious short-circuit current exceedance in the area. However, increasing the impedance of the generator may also lead to a decrease in the generator’s short-circuit ratio, increasing the impact of load changes on the generator voltage, resulting in a rise in reactive power loss during normal operation, which is not conducive to voltage stability in the system. This could also increase the phase angle difference between high-impedance generators and other motors in parallel with the system, negatively affecting the static stability of the system.
Therefore, when controlling the impedance of a generator and reducing the short-circuit current in a system, it is also important to consider the generator’s short-circuit ratio, balancing the operational performance and cost requirements of the motor. Currently, the short-circuit ratio of turbine non-salient pole generators in China is generally between 0.47 and 0.63, while that for hydraulic salient pole generators is typically between 1.0 and 1.4.
3.1.2. Install a High-Impedance Transformer
When studying an ideal transformer, it is generally assumed that the winding resistance is zero and the magnetic permeability of the core is infinitely large, and leakage flux is neglected. The schematic diagram of an ideal transformer is shown in Figure 6.
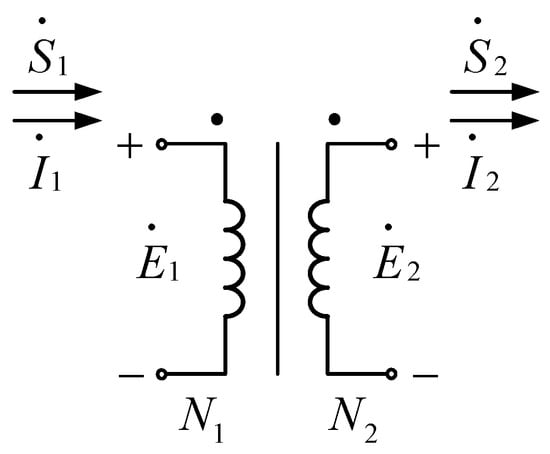
Figure 6.
Schematic diagram of ideal dual-winding transformer.
The turns ratio is defined as
Then, the basic relationship for the voltage and current of an ideal dual-winding transformer is given by
The complex power flowing into the primary winding is denoted as
Substituting Equations (12) and (13) into Equation (14), we obtain the complex power flowing out of the secondary winding as
From Equation (15), it can be concluded that an ideal transformer does not have active and reactive losses.
In practical applications, dual-winding transformers should take into consideration winding resistance and leakage flux based on the ideal transformer model. The permeability of the core in real dual-winding transformers is a finite value. The resistances and are connected in series on both sides of Figure 6, representing the winding resistances of the primary and secondary sides, respectively. The reactances and are also connected in series on both sides of Figure 6, representing the leakage reactance of the primary and secondary sides.
Since the magnetizing current is typically less than 5% of the rated current, it can generally be neglected. The equivalent circuit diagram of a real dual-winding transformer after removing the parallel branches in the circuit is shown in Figure 7.
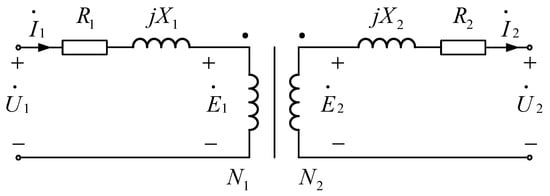
Figure 7.
Equivalent circuit of a dual-winding transformer ignoring magnetizing current.
Due to the presence of resistance, the transformer experiences active loss. Due to the presence of leakage reactance, the transformer experiences reactive loss. The components on the secondary side of the diagram can be directed back to the primary side through
resulting in the simplified equivalent circuit diagram shown in Figure 8.
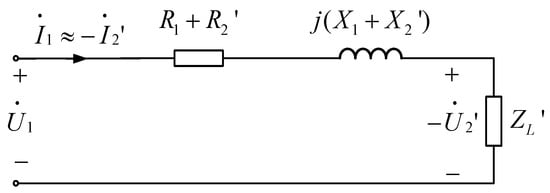
Figure 8.
Simplified equivalent circuit diagram of double-winding transformer.
In the figure, is the load impedance directed to the primary side. At this time, the transformer’s short-circuit impedance is defined as
In engineering practice, to control the excessive short-circuit current in certain areas—especially the short-circuit current transmitted to a lower-voltage-level grid from an adjacent higher-voltage-level grid through transformers—using high-impedance transformers is one feasible method. The principle is to adjust the short-circuit impedance value of the transformer as indicated in Equation (18). For large power transformers with a rated capacity over 500 kVA, the winding resistance is typically less than the leakage reactance. Therefore, in general practice, it is common to control the excessive short-circuit current by adjusting the equivalent leakage reactance, or short-circuit reactance . High-impedance transformers effectively limit the short-circuit current on the low-voltage side while also reducing the amount of steel used, decreasing no-load losses, lowering the probability of damage caused by electric power shocks to the transformer, minimizing interference with and harm to adjacent communication lines, facilitating the selection of circuit breakers and other electrical equipment, and significantly enhancing the power supply capacity on the low-voltage side. However, high-impedance transformers may also introduce some issues, primarily concerning self-loss and system stability: increasing impedance requires extending the transformer windings, which leads to increased copper usage, corresponding increases in active loss, larger transformer sizes, and higher equipment costs. As the transformer impedance voltage increases, the fluctuations of secondary voltage with varying loads become greater, impacting the stable operation of the system.
Therefore, when using high-impedance transformers, it is also necessary to be constrained by equipment parameter selection and manufacturing technology, as well as by system stability conditions. The transformer’s short-circuit impedance should not be excessively high, given the need to satisfy requirements for the dynamic stability, thermal stability, and interruption capacity of the secondary bus distribution device while also meeting the requirements for short-circuit impact forces on the transformer.
3.2. Increasing Line Impedance
3.2.1. Install a Current-Limiting Reactor
The manufacturing technology for current-limiting reactors is mature, and their current-limiting effect is good, making them a common measure for current limitation. Ordinary three-phase reactors consist of three single-phase hollow coils. Due to the absence of a core structure, the resistance of the coil leads is relatively low, resulting in minimal active loss; in engineering, they can be considered to serve primarily as reactance. Based on their installation locations and modes of action, such reactors can be categorized into two types: bus bar reactors and line reactors, shown in Figure 9.
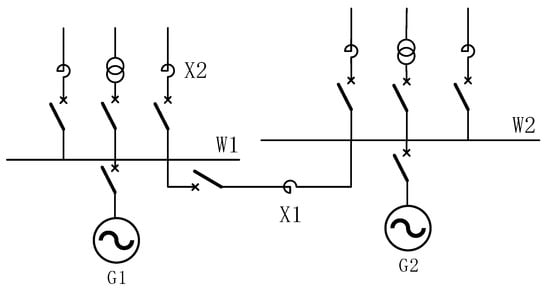
Figure 9.
Schematic diagram of installation position of reactor.
Bus bar reactors are installed at sections of bus bars, as indicated by position X1 in the figure; line reactors are installed at the output segments of cable lines, as indicated by position X2 in the figure. It is assumed that the series-connected reactor limits the short-circuit current at node 1, as shown in Figure 10.
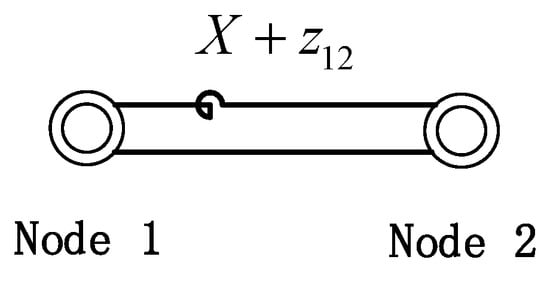
Figure 10.
Schematic diagram of series connection of reactance.
Using the principle of constructing an impedance matrix via the addition method, we can set the voltages of all nodes before the fault to 1. The effect of the series-connected reactor on limiting the short-circuit current at Node 1 can be calculated in two steps:
- (1)
- Disconnect Line 1 between Node 1 and Node 2.
Add a “chain branch” by inserting a branch with impedance between the two points, and update the elements of the admittance matrix for the first time as
- (2)
- Add Line 3 between Node 1 and Node 2.
Insert a “chain branch” by connecting another branch with impedance between the two points, and perform a second update of the admittance matrix elements to obtain the admittance matrix elements for calculating the short-circuit current at Node 1, which is represented as
Thus, the change in short-circuit current at Node 1 before and after the series-connected reactor is given by
After the reactor is connected to the system, while it increases the electrical distance and reduces the short-circuit current, its purely reactive characteristic will increase the reactive power loss in the system, which may further lead to a certain degree of voltage drop at nearby nodes. If the voltage drop is significant, it will affect the voltage level of the system. The power factor of the transmission line, the impedance of the reactor, and the magnitude of the line current will all affect the amount of voltage drop. Generally speaking, the larger the power factor and the greater the reactor impedance, the larger the voltage drop.
3.2.2. Install a Fault Current Limiter
The operating principle and installation location of fault current limiters are almost the same as those of reactors. The difference lies in that the fault current limiter relies on its own power electronic devices and detection and control systems, achieving the goal of allowing the inserted reactance to operate only during short-circuit faults without affecting the steady-state operation of the system.
Common types of fault current limiters include series resonance, parallel resonance, and impedance switching fault current limiters. The circuit schematic of the series resonance-type fault current limiter is shown in Figure 11.
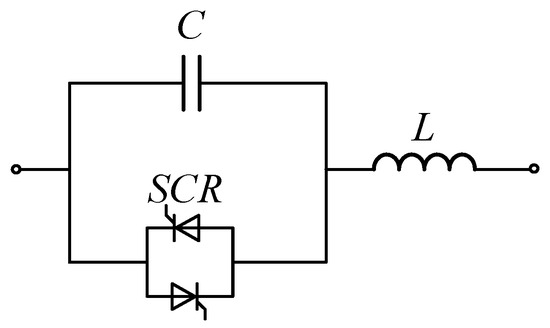
Figure 11.
The series resonance-type fault current limiter.
In the series resonance-type fault current limiter, when no fault occurs in the system, the thyristor SCR is in the off state, effectively placing the capacitor C and the inductor L in series, which results in , and there is
Under the condition that the component parameters satisfy the above requirements, the capacitor C and the inductor L are in a series resonance state, presenting zero impedance to the outside, not altering the phase angle difference of the original voltage and current, and not consuming reactive power, thereby having no impact on the steady-state operation of the system. When the monitoring system detects that the line current exceeds a preset threshold, the control system sends a signal to the thyristor SCR to turn it on. At this point, the capacitor C will be short-circuited, and the inductor L will function to limit the current.
The schematic diagram of the parallel resonance-type fault current limiter is shown in Figure 12.
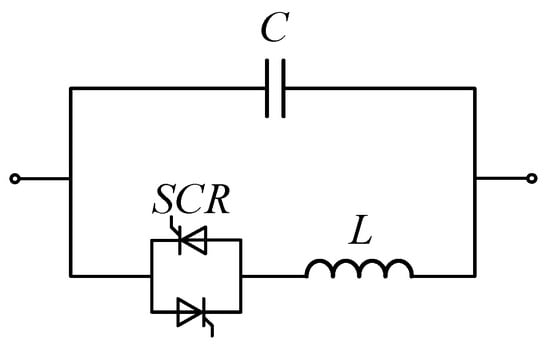
Figure 12.
The parallel resonance-type fault current limiter.
During the normal operation of the system, the parallel resonance-type fault current limiter can adjust the parameters of the capacitor C and the inductor L to bring them into an out-of-tune state. It can then be adjusted to a capacitive or inductive state as required by the system, functioning as a compensation component. After a short-circuit fault occurs, the control system adjusts the parameters of the capacitor C and the inductor L to make them enter a parallel resonance state, and there is
at which point the device impedance is
In the parallel resonance state, the component exhibits an infinite impedance characteristic to the outside, effectively limiting the short-circuit current.
The circuit schematic of the impedance switching-type fault current limiter is shown in Figure 13.
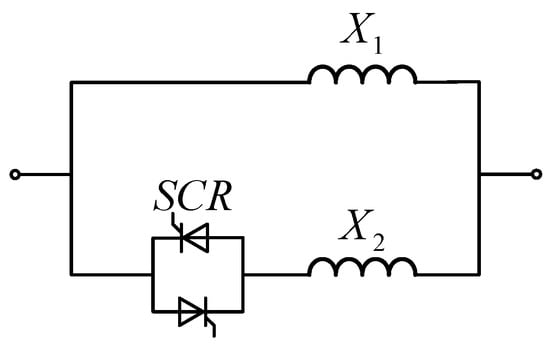
Figure 13.
The impedance switching-type fault current limiter.
In this component, the impedance is a very small value. During the normal operation of the power system, the thyristor SCR is in the conducting state, and at this time, the parallel total impedance of impedances and is also a very small value, with the impedance relationship being
When a short-circuit fault occurs, the thyristor SCR turns off, and impedance is effectively inserted into the system, achieving the purpose of current limiting.
The installation locations of the fault current limiter are similar to those of current-limiting reactors, and they can be categorized based on the location of the short-circuit current to be limited, such as at system interconnections or bus connections, system incoming lines, and system outgoing lines.
Fault current limiters can limit short-circuit currents without negatively impacting the system; however, they require advanced manufacturing technology, and their manufacturing costs and operational maintenance expenses are also high. Therefore, they cannot be used on a large scale in power systems. They may be deployed for one or two points in the system where short-circuit currents exceed standards, especially when other measures cannot meet engineering requirements.
3.2.3. Generator–Transformer–Line Group Unit
The generator is the source of short-circuit current in the power system, and the generator’s output voltage is typically boosted through a step-up transformer before being fed into the grid. The connection of grid units is the simplest form of wiring without a bus, and it is also one of the simplest, most basic forms among all primary connection schemes. The unit connection structure is straightforward, with fewer switching devices, easy operation, and no generator-voltage-level bus, which reduces the probability of short-circuit faults on the low-voltage side of the generator connected to the step-up transformer and decreases the short-circuit current. The generator–double-winding transformer connection scheme is widely used in large units, with the wiring schematic shown in Figure 14.
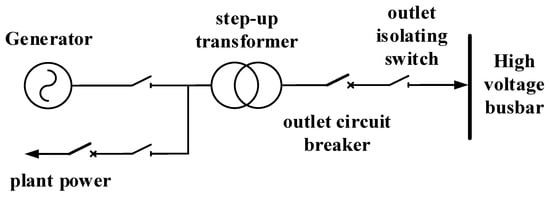
Figure 14.
Schematic diagram of generator–transformer unit wiring.
When the impedance of the generator and step-up transformer is a fixed value, the contribution of a single generator to the short-circuit current of the grid after passing through the step-up transformer is also a fixed value. In the case of large units entering the grid causing excess short-circuit current, when the above conditions are fixed, the control of the short-circuit current can only be achieved by adjusting the wiring of the high-voltage bus and lines. The connection structure of the aforementioned generator is modified to a generator–transformer–line group unit format, eliminating the step-up substation bus and connecting the generator–transformer output circuit breaker directly to the nearby hub substation through a short line. The wiring schematic of the generator–transformer–line group unit is shown in Figure 15.
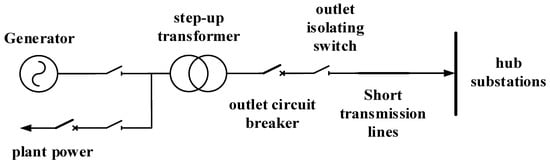
Figure 15.
Schematic diagram of generator–transformer–line group unit wiring.
Under this modified wiring structure, electrical energy first passes through a short line before entering the grid, effectively increasing the electrical distance and lowering the system’s short-circuit current levels. By eliminating the step-up distribution device, the power plant can directly transmit energy to the nearby hub substation or switch station, making the plant structure compact and saving land area while also addressing pollution issues related to dust and cooling tower vapor affecting the distribution devices in thermal power plants to some extent.
However, this measure may also cause some loss of stability in the grid, and the connected lines should not be excessively long. Additionally, this connection involves numerous issues related to grid system planning and layout, power plant layout and investment, and how to draw on standby power sources during power plant start-up, which need to be carefully evaluated in specific projects to decide whether to implement it.
In summary, the conditions for selecting the current-limiting measures included in this paper are summarized as shown in Table 2.

Table 2.
Brief description of selection criteria for short-circuit current-limiting measures.
4. Simulation Analysis of Current-Limiting Cases
The simulation analysis is completed by using the software PSD-BPA (3.1, 2023) developed by China Electric Power Research Institute, the data used are all the data of the Chongqing power grid, the calculation standard is set to the national standard in 2013, and all the faults are set to three-phase symmetrical short circuits.
4.1. Simulation and Calculation of Measures for Addition of Large High-Reactance Equipment
The 220 kV grid structure in a specific region is shown in Figure 16. There are a total of 12,220 kV substations in this area, among which the Shengquan 220 kV substation serves as the connection point to the higher-level 500 kV station and is linked by three 500/220 kV transformers. The Luohuang power plant provides power support for this region. The short-circuit current levels at the substations in this area before implementing current-limiting measures are shown in Table 3.
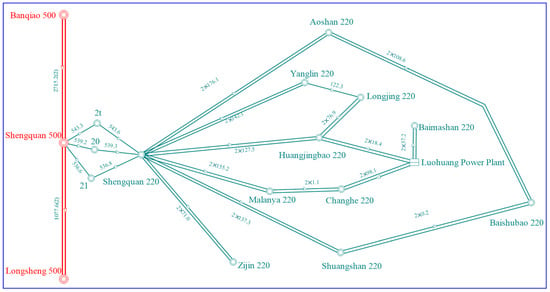
Figure 16.
Structure of 220 kV power grid in a specific region.

Table 3.
Short-circuit current level of substations in the area before taking measures.
Current-limiting measures are now implemented:
- (1)
- The Luohuang power plant replaces high-impedance generators; the direct-axis transient reactance is increased to 0.072 pu (per unit value, the ratio of the actual value to the reference value), and the quadrature-axis transient reactance is increased to 0.1 pu. The short-circuit current levels after the modification are shown in Table 4.
 Table 4. The short-circuit current level of the substation in the area after increasing the impedance of the generator.
Table 4. The short-circuit current level of the substation in the area after increasing the impedance of the generator. - (2)
- The 500/220 kV transformer of the Shengquan station is replaced with a high-impedance transformer; the leakage reactance of the Shengquan 2t transformer is increased from −0.0163 to −0.0001. The short-circuit current levels after this replacement are shown in Table 5.
 Table 5. The short-circuit current level of the substation in the area after increasing the impedance of the transformer.
Table 5. The short-circuit current level of the substation in the area after increasing the impedance of the transformer.
A comparison of short-circuit currents before and after measures are taken is illustrated in Figure 17.
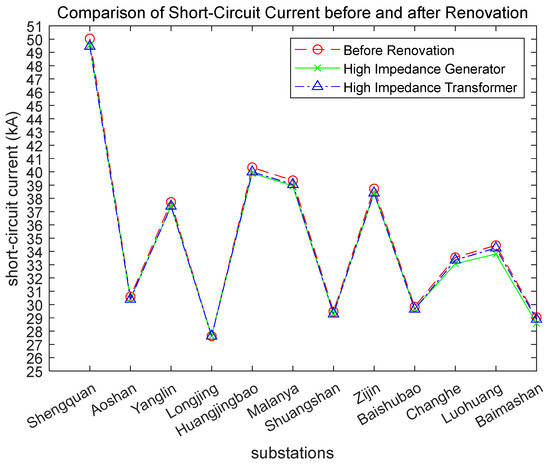
Figure 17.
Comparison of short-circuit current levels before and after the transformation of high-impedance equipment.
From Figure 17, it can be seen that modifying the generators to high-impedance can effectively reduce the short-circuit currents at the power plant (Luohuang) and nearby substations (such as Changhe and Huangjingbao). Additionally, implementing high-impedance modifications on the interconnecting transformers between the higher and lower voltage levels can significantly reduce the short-circuit currents at both the upper and lower connecting substations (Shengquan) and their nearby stations (such as Huangjingbao and Zijin). The effectiveness of the short-circuit current limitation is related to the new impedance values set.
Overall, these measures involve the high-impedance reconstruction of generators and transformers. High-impedance generators can effectively address the issue of excessive short-circuit current caused by the integration of the power plant into the grid. On the other hand, high-impedance transformers mainly limit the contribution of short-circuit currents from high-voltage grids to lower-voltage grids by modifying transformer equipment.
The effectiveness of these measures varies based on the impedance of the new equipment; however, excessively high-impedance can lead to issues with power system stability and excessive losses, wasting electrical energy. Conversely, low impedance may result in negligible current-limiting effects, making the cost of replacing the equipment unjustifiable. Therefore, it is necessary to calculate suitable impedance values through practical assessments to comprehensively evaluate the balance between effectiveness and cost before considering equipment modifications.
4.2. Simulation and Calculation of Measures for Increasing Line Impedance
We continue with the simulation calculations using the example of the Shengquan area power grid shown in Figure 16. The short-circuit current data before any measures were taken are shown in Table 3.
The proposed current-limiting measures are as follows:
- (1)
- Current-limiting reactor: Current-limiting reactors will be connected in series on the Shengquan–Huangjingbao dual-circuit line to limit the short-circuit current at the Shengquan substation. After the modification, the impedance of both circuits will be set to 0.1 pu. The short-circuit current levels after this modification are listed in Table 6.
 Table 6. Short-circuit current level of the substation in the area after series connection of reactance.
Table 6. Short-circuit current level of the substation in the area after series connection of reactance.
To compare the effect of the current-limiting reactors in limiting the current, a comparative chart is shown in Figure 18.
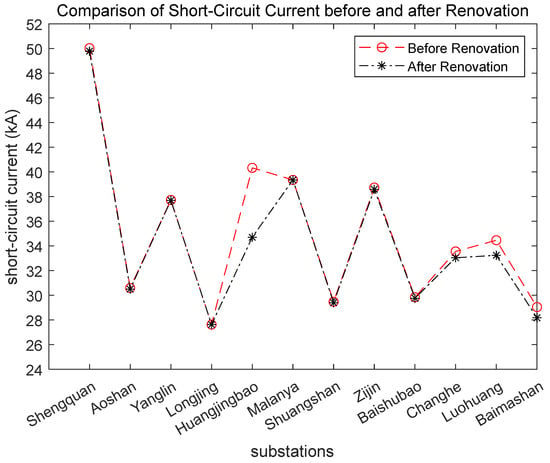
Figure 18.
Comparison diagram of current-limiting effect of current-limiting reactors.
As seen in Figure 18, the series connection of current-limiting reactors can effectively limit the current at the modified nearby substation (Huangjingbao).
- (2)
- Fault current limiter: A fault current limiter will be installed on the “Shengquan 20” transformer branch, with an impedance value set to 15 Ω. During the system’s steady-state operation, the series resonance results in an impedance value that is nearly zero. When a fault occurs, it will operate to limit the current. The principle of current limitation is the same as that of a conventional series reactor, so the short-circuit current values at each station will not be elaborated on; only the transient waveform of the current for the branch with the current-limiting device will be presented to illustrate its current-limiting effect during a fault. The short-circuit current waveform of the “Shengquan 20” transformer branch during a fault at Shengquan substation before the installation of the fault current limiter is shown in Figure 19.
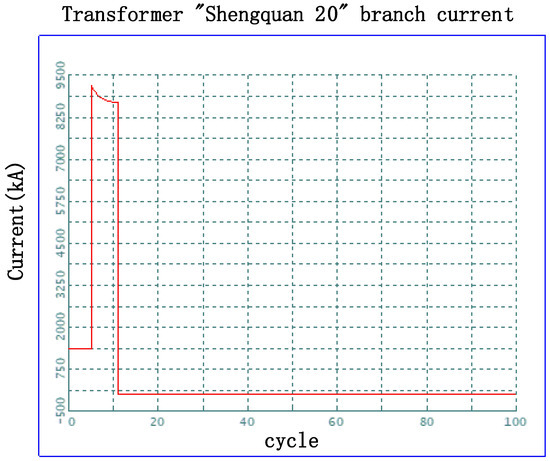 Figure 19. Fault current waveform of the branch before being connected to the fault current limiter in series.
Figure 19. Fault current waveform of the branch before being connected to the fault current limiter in series.
In terms of setting the fault condition, the FCL becomes effective when the current in this branch reaches 6 kA, at which point the reactor is engaged in limiting the current. The FCL will disengage once the current decreases below 5 kA for more than 2 s. The fault initiation time is set to 5 cycles, and after 6 cycles, the bus protection devices will operate to cut off all outgoing feeders, effectively clearing the fault. The positive-sequence current curve of the branch after the bus fault is shown in Figure 20.
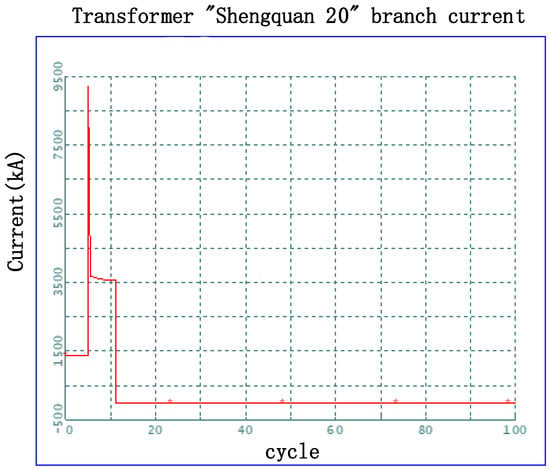
Figure 20.
Fault current waveform of the branch after being connected to the fault current limiter in series.
From Figure 20, it can be seen that at the start of the fault at 5 cycles, the short-circuit current for this line reaches up to 9.2 kA. After the 15 Ω FCL is activated, it limits the current to 3.6 kA, maintaining this stable level until the fault is cleared at 11 cycles. This means that the 15 Ω fault current limiter reduces the current on this line by approximately 5.6 kA.
- (3)
- Generator–transformer–line group unit connection to the grid: The Luohuang power plant has two generating units, which are connected to the 220 kV bus “Luohuang power plant” through step-up transformers. The connection to this bus is now canceled, and the output voltage of the units is increased and directly connected to the Huangjingbao, Changhe, and Baimashan substations. A structural diagram of the substations in this area after the modification is shown in Figure 21, and the short-circuit currents at the three substations are listed in Table 7.
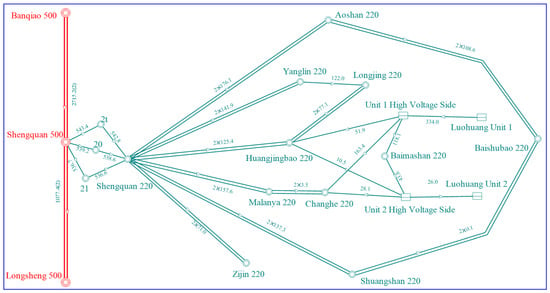 Figure 21. A structural diagram of the power grid after the transformation of the generator–transformer–line group unit.
Figure 21. A structural diagram of the power grid after the transformation of the generator–transformer–line group unit. Table 7. Short-circuit current levels of relevant substations before and after the transformation of the generator–transformer–line group unit.
Table 7. Short-circuit current levels of relevant substations before and after the transformation of the generator–transformer–line group unit.
From Table 7, it can be seen that using the generator–transformer–line group unit approach to connect the power plant units to the grid can effectively reduce the short-circuit currents at the point of integration into the grid.
Overall, these measures are aimed at cases where individual branches contribute significantly to the short-circuit currents at nearby substations, and where it is inconvenient to directly disconnect the lines. By increasing the line reactance, the current contributed by these branches during short-circuit conditions is reduced. Compared to directly disconnecting the lines, the current-limiting effect is somewhat weaker and may require the installation of new equipment; therefore, there are cost considerations. However, it remains the preferred solution in most situations where direct line disconnection is not feasible.
Based on the above research and Table 3, Table 4, Table 5, Table 6 and Table 7, a summary of the current-limiting methods discussed in this paper is presented in Table 8.

Table 8.
Comparison of each short-circuit current-limiting measure discussed in this paper.
5. Conclusions
This paper addresses the increasingly severe issue of excessive short-circuit current brought about by the rapid development of large power grids. It studies the principles of short-circuit current control and commonly used measures to limit short-circuit current, and conducts a simulation analysis of current-limiting effects through specific case studies. The findings are as follows:
- (1)
- The equivalent impedance of the power grid can be divided into three categories: non-same-level equivalent impedance, the transformer’s equivalent impedance, and same-level equivalent impedance. The control effect of short-circuit current achieved by changing non-same-level equivalent impedance and the transformer’s equivalent impedance is limited; however, theoretically, the control effect of the same-level equivalent impedance on short-circuit current is infinite. Therefore, the limiting principle of most short-circuit current limitation measures is to increase the same-level equivalent impedance at the short-circuit point.
- (2)
- The smaller the equivalent impedance, the more significant the effect of limiting short-circuit current. As current-limiting measures are added, when the equivalent impedance increases in an arithmetic progression, the limiting effect becomes increasingly weak.
- (3)
- High-impedance generators can effectively control the short-circuit current provided by power sources, primarily reflected in the substations where power plants connect to the grid and their nearby substations. High-impedance transformers can effectively control the short-circuit current delivered from the power source to the lower-level grid; however, both come with issues related to cost, losses, and stability.
- (4)
- Installations of current-limiting reactors and fault current limiters are effective measures aimed at specifically limiting short-circuit currents in certain substations within the grid: Current-limiting reactors have a wide range of applicable conditions and mature technology, making them a preferred choice when other measures are not feasible, although they can cause some losses. On the other hand, fault current limiters can compensate for the shortcomings of current-limiting reactors, as they can limit short-circuit currents without impacting the normal operation of the grid; however, their technical conditions are not yet fully mature, and they are expensive, limiting their large-scale usage. The generator–transformer–line group unit connection method does not have a generator-voltage-level bus, which reduces the probability of short-circuit faults on the low-voltage side of the step-up transformer and decreases short-circuit currents. This effectively lowers the short-circuit currents at the power plant connection points and nearby substations without adding new equipment, but longer transmission lines can result in a loss of stability in the grid.
- (5)
- Each current-limiting measure, while effectively limiting short-circuit current, can also bring corresponding issues to grid operation. Therefore, in addition to short-circuit calculations, stability calculations, power flow calculations, and economic costs should be comprehensively considered. After a thorough comparison and evaluation, the optimal solution for addressing the issue of excessive short-circuit current can be obtained.
Although this paper has achieved certain research outcomes, there are still areas that can be improved. For instance, the differences between the equipment parameters used in this study and those in actual operational applications have not been considered. Additionally, the development direction of new multifunctional FCLs is another important issue that should be addressed.
Author Contributions
Conceptualization, S.S. and G.Z.; methodology, G.Z.; software, Z.L.; validation, G.Z. and Y.Z.; formal analysis, Z.Y.; investigation, Y.Z.; resources, Y.Z. and Z.L.; data curation, G.Z. and Z.L.; writing—original draft preparation, G.Z., S.S. and Z.L.; writing—review and editing, G.Z., S.S. and X.T.; visualization, X.T. and S.S.; supervision, Z.L. and Y.Z.; project administration, S.S.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Chinese Academy of Engineering Strategic Research and Advisory Project (JL2024-13) and Jilin University Teaching Research Project (2023CGP009).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Yuguang Zhou was employed by the Dandong Jinshan Thermal Power Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Surya, A.; Gumilar, L.; Habibi, M.; Kusumawardana, A.; Afandi, A.N. Increase in High Impedance Value of Transformer to Reduce Short Circuit Fault Currents in High Voltage Networks. In Proceedings of the 2022 11th Electrical Power, Electronics, Communications, Controls and Informatics Seminar (EECCIS), Malang, Indonesia, 23–25 August 2022; pp. 51–55. [Google Scholar]
- Li, J.; Zheng, M.; Cao, H.; Zhao, Z.; Gu, Y.; Li, T.; Li, Z.; Sun, Y.; Liu, Y.; Ai, S.; et al. Current limiting ability and overvoltage analysis of variable impedance transformer. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 557–560. [Google Scholar]
- Xu, C.; Cai, J.; Wu, F.; Hu, D.; Lu, Z.; Liao, J.; Gong, J.; Pan, S. A Current Limiting Method with Sequence-Separated Control Strategy for Modular Inverter System under Asymmetrical Short Circuit Faults. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 4448–4453. [Google Scholar]
- Varetsky, Y.; Gajdzica, M. Study of Short Circuit and Inrush Current Impact on the Current-Limiting Reactor Operation in an Industrial Grid. Energies 2023, 16, 811. [Google Scholar] [CrossRef]
- Gouda, O.; Afifi, Z.; Awaad, M. A Novel Air Core Current Limiter Reactor for Medium and Low Voltage Systems. Electr. Power Syst. Res. 2023, 217, 109114. [Google Scholar] [CrossRef]
- Ren, H.; Zhang, Y. Analysis of Transient Recovery Voltage of 500 kV Line Considering Current Limiting Reactor. J. Phys. Conf. Ser. 2023, 2488, 012036. [Google Scholar] [CrossRef]
- Ren, H.; Wei, X.; Wu, H. Influence of line current limiting reactor on temporary overvoltage of 500 kV transmission line. J. Phys. Conf. Ser. 2023, 2592, 012062. [Google Scholar] [CrossRef]
- Wang, P.; Zhou, Y.; Wei, W.; Hao, X.; Mao, Z.; Wang, W.; Xu, D. A DC Solid-State Current Limiter with Adaptive Current-Limiting Ability. IEEE Trans. Ind. Appl. 2023, 59, 970–980. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, S.; Liu, Q.; Zhang, C.; Zhao, Q.; Mu, H. Influence Analysis of Current Limiting Reactor on Pole-to-Pole Short Circuit Fault in DC Distribution System. E3S Web Conf. 2021, 256, 01032. [Google Scholar] [CrossRef]
- Lyu, H.; He, J.; Li, B.; Li, Y.; Spier, D.; Prieto-Araujo, E.; Gomis-Bellmunt, O. An Improved Hybrid DC Circuit Breaker with Self-Adaptive Fault Current Limiting Capability. IEEE Trans. Power Electron. 2022, 37, 4730–4741. [Google Scholar] [CrossRef]
- Han, B.; Jin, Y.; Ni, Q.; Xiang, Z.; Zhou, J.; Wang, Q.; Yu, Y. Study on the impact of dynamic adjustment of system topology on transient characteriscs of short circuit current. In Proceedings of the 2021 International Conference on Power System Technology (POWERCON), Haikou, China, 8–9 December 2021; pp. 2270–2274. [Google Scholar]
- Wang, Z.; Peng, L.; Yan, L.; Wu, Y.; Wu, Y.; Zhuang, W.; Dai, H.; Bai, Y. A Current-Limiting Hybrid DC Circuit Breaker. In Proceedings of the 2023 3rd International Conference on Electrical Engineering and Control Science (IC2ECS), Hangzhou, China, 29–31 December 2023; pp. 469–473. [Google Scholar]
- Wu, S.; Jing, P.; Dai, C.; Jin, X. Fault Current Limiting Measures and Their Recent Progress. Power Syst. Technol. 2008, 32, 23–32. [Google Scholar]
- Yan, Z. Short-circuit current limiter based on TPSC. East China Electr. Power 2005, 33, 41–42. [Google Scholar]
- Ming, Z. Review for short-circuit current limiters. East China Electr. Power 2008, 43–46. Available online: https://consensus.app/papers/review-for-shortcircuit-current-limiters-ming/14873448352151918ddcfe786bc91d9b/ (accessed on 1 May 2025).
- Zhang, Q.; Song, M.; Li, L.; Xiang, B.; Tang, Z.; Li, H.; Yuan, Z.; Du, H.; Geng, Y.; Liu, Z.; et al. Current limiting and recovery characteristics of an AC fast recovery superconducting fault current-limiting breaker. Supercond. Sci. Technol. 2023, 36, 115026. [Google Scholar] [CrossRef]
- Amini, M.; Aliabad, A.; Amiri, E. Design and Analysis of Fault Current Limiter Based on Air Core Variable Series Reactor. IEEE Access 2021, 9, 166129–166136. [Google Scholar] [CrossRef]
- Mujie, Z.; Junbo, F.; Dejun, S.; Hao, L.; Pan, X.; Yukun, W. Research on the Influence of 500 kV Fault Current Limiter on Line Distance Protection. In Proceedings of the 2023 8th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 22–25 September 2023; pp. 38–43. [Google Scholar]
- Akin, F.; Arikan, O.; Kucukaydin, B. Multi-physics modelling and performance analysis of an air-core reactor in the framework of solid-state fault current limiters. Electr. Power Syst. Res. 2024, 231, 110313. [Google Scholar] [CrossRef]
- Zhang, K.; Hu, J.; Lu, X.; Peng, Z.; Ma, P.; Gao, F. Influence of fast switching fault current limiter on electromagnetic transient of extra-high voltage transmission line. J. Phys. Conf. Ser. 2024, 2903, 012007. [Google Scholar] [CrossRef]
- Gan, Y.; Wu, J.; Lyu, H.; Chen, J.; Yuan, J.; Chen, L.; Tang, J. Review of Fault Current Limiting Measures in AC Power Systems. In Proceedings of the 2023 2nd Asian Conference on Frontiers of Power and Energy (ACFPE), Chengdu, China, 20–22 October 2023; pp. 367–373. [Google Scholar]
- Sun, S.; Zhou, G.; Song, Y.; Tang, X.; Yuan, Z.; Qi, X. Research on Optimization Method of Short-Circuit Current-Limiting Measures Based on Combination Assignment. Energies 2024, 17, 5724. [Google Scholar] [CrossRef]
- Sun, S.; Zhou, G.; Song, Y.; Tang, X.; Zhou, Y.; Yuan, Z. Research on Measures to Limit Short-Circuit Current by Changing the Structure of the Power Grid. Energies 2025, 18, 2098. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).