Abstract
There is some risk of power quality disturbances at many stages of production, transformation, distribution, and energy consumption. The cornerstone for dealing with power quality problems is the characterization of power quality disturbances (PQDs). However, past research has focused on a narrow topic: noise disruption, overfitting, and training time. A new strategy is suggested to address this problem that combines efficient one-dimensional dataset compression with the convolutional neural network (CNN) classification algorithm. First, three types of compression algorithms: wavelet transform, autoencoder, and CNN, are proposed to be evaluated. According to the IEEE-1159 standard, the synthetic dataset was built with fourteen different PQD types. Furthermore, the PQD classification procedure integrated compressed data with the CNN classification algorithm. Finally, the suggested method demonstrates that combining CNN compression and classification methods can efficiently recognize PQDs. Even in noisy environments, PQD signal processing achieved up to 98.25% accuracy and managed the overfitting.
1. Introduction
Energy is a multidisciplinary topic that addresses not only technical but also social and economic factors. The amazing beneficial effect of energy on the quality of life in all nations provides optimism for the future [1]. The high dependence on sustainable energy necessitates improved power quality (PQ) in electricity generation, power transmission, and established distribution networks. The quality of power is becoming a more important element, particularly as the concept of smart grids, for defining future electricity businesses, is on the horizon around the world. Customers and electric power utilities are expected to achieve ideal electrical current and voltage waveforms at the recommended power frequency [2]. Yet, one among the biggest contributors of problems related to PQ is distributed energy generation [3]. To attain good PQ, it is essential to eradicate the source of distractions, hence lowering consumer damages.
Power quality is strongly related to the energy usage of electrical equipment. This is an essential problem, since electronic equipment’s life expectancy is occasionally falling [4]. The quality of electricity is characterized by electrical harmonics, low power factor, voltage insufficiency, and disruptive power output, whereas the typical current or voltage behavior, when it impairs the proper functioning of the power systems, is to be regarded as a power quality disturbance (PQD) [5]. A wide range of electromagnetic disturbances occur at various places throughout the system, affecting the amount of energy delivered to various demand sites. Some of the most frequent system disruptions in alphabetical order are flickers, harmonics, interruptions, sags, swells, and transients [6].
These occurrences have technical consequences, involving machine heat damage and insulation decline, among other things, that have a negative influence on electrical and electronic devices, particularly harm to industrial utilities, software for computers, and hardware [7]. Moreover, electrical devices can create chaotic behavior. However, recent research has effectively showed how chaotic phenomena permits addressing energy transmission in networks [8]. Based on the preceding, it is critical to recognize these types of disturbances to determine which measures should be taken to minimize these occurrences. Thus far, classification and detection of disturbances have been recognized as keyways to maintain the quality of electricity. In terms of the smart electrical grid, it is viable to build an Internet of Things (IoT)-based power quality system and place it throughout the line of distribution, with the purpose of transmitting consumption and interruptions information onto utilities over a two-way communications network [9]. A general smart grid structure is presented in Figure 1.
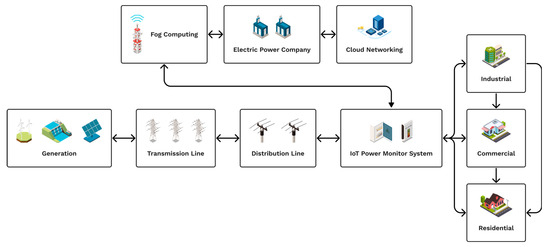
Figure 1.
General smart grid system.
Under these conditions, the most essential factor to consider for achieving real-time data transfer is the computing power of the method used for categorizing and detecting disturbance; in a nutshell, the speed of computation has to match the data transfer speed and bandwidth. The smart grid will be constructed of numerous components. Before the system can be completely operational, all infrastructure, including technology, must be perfected, and tested thoroughly. With government support, this development might take around a decade.
Considering the problems mentioned earlier, the paper’s key contributions are as follows:
- To examine the most efficient compression approach for PQD datasets. Since a high compression ratio for any technique does not guarantee the optimum solution for all data kinds, several compression methods and algorithms are available for each data format. Many variables affect which compression technique is suited for each data type. Hence, the data compression algorithm selected will impact the categorization model’s performance. Therefore, it is critical to determine the best dataset compression method utilized as a benchmark to achieve high accuracy in the classification process.
- There is no doubt that the effectiveness of characteristics retrieved by CNNs is far superior to that of artificial classification techniques. CNNs, on the other hand, are commonly employed for image categorization. This is one of the research gaps that must be examined for appropriateness for 1D PQD applications.
Considering points 1 and 2, we assumed that combining appropriate compression and classification algorithms can accurately identify PQDs.
- 3.
- Due to the tremendous learning capabilities of CNNs, there is a substantial risk of overfitting in PQD classification. This study proposes principles training methodologies, such as improved optimizers and assessing methods, to overcome overfitting.
- 4.
- To validate the proposed CNN classification approach, this study performs a detailed comparison of training time, accuracy, and model parameter utilizing three compression algorithms, including wavelet transform, autoencoder, and CNN algorithms.
The paper is structured as follows: Section 2 presents an analysis of the scientific research to provide evidence for the suggested approach. Section 3 discusses the definition of PQD classification, the method of creating the artificial PQD dataset, and the structure of three dataset compression models. Section 4 presents and discusses the experimental method and the outcomes. Section 5 created a conclusion for the optimum compression model performance.
2. Review of Related Works
Statistical information, spatial-temporal factors, and the stationary and non-stationary patterns of PQ signals are utilized to characterize areas with power quality problems [10]. Many articles have investigated the potential of deep learning approaches for defining and categorizing various PQDs in smart grids [11]. Deep learning algorithms are currently considered to have the inherent capacity to learn optimum features from raw input data, therefore avoiding time-consuming feature engineering. Different designs such as convolutional neural network (CNN) [12], recurrent neural network (RNN) [13], identity-recurrent neural network (IRNN) [14], and long short-term memory (LSTM) have been explored in deep power studies, to comprehend the efficacy of different deep learning processes [15]. Furthermore, power quality problems in smart grids have been reliably identified and described by utilizing hybrid architectures that integrate CNN–LSTM [16].
The Hilbert–Huang transform technique was used to identify PQDs, then classified using a multi-layer perceptron neural network (MLPNN) approach [17]. Other research converted signal events into pictures and supplied them into a multi-layer CNN (MLCNN) framework [18]. Simultaneously, some researchers used a 1D deep CNN (dCNN) to assess variables that cause PQDs in microgrids [19].
The following paper proposes a novel technique for detecting and classifying PQDs based on improved principal component analysis (IPCA) and 1-dimensional CNN (1D-CNN). The authors presented a new approach for classifying PQDs by combining principal component analysis (PCA) and the 1D-CNN method. This technique is used in the wind-grid distribution network, which is a wind energy-based energy source technology created and built to supply power to the network [20]. However, because of the enormous quantity of data, the problem of training time is a restricted topic in prior research. Because of the high sample rate and quantity of measuring endpoints in PQ tracking, massive files of data are generated [21]. To address this matter, a data compression technique is necessary to reduce calculation time within the stage of training [22]. Signal methods for compression were proposed with the aim of limiting the quantity of data that must be kept.
Academics have previously performed research on PQD data compression with wavelet transform (WT) [23]. Another study provided a classifier for the successful classification of PQ concerns using a MLPNN. The wavelet transform and sensitivity analysis were utilized to extract features and minimize dimensionality. With 99.81% categorization accuracy, the improved classifier accurately recognized the six fundamental PQ abnormalities [24].
The following study used wavelet packet transform (WPT), in conjunction with threshold modification, to compress transient disturbance data. Wavelet packet transform divided a signal into multiple frequency bands, and it also selected frequency bands flexibly to address the limitations of the WT. Data compressions for voltage sag and transient pulses were generated, and the reduction results using WT demonstrated their feasibility and efficacy. To improve the preceding technique, a method combining the supported orthogonal wavelet db4 with the threshold estimation approach of the minimax theorem to compress PQDs signals was applied. The suggested approach produced a decent compression result through the correct selection of the decomposition layer [25].
In addition, combining the discrete wavelet transform (DWT) and WPT, a new compression approach for PQDs data was proposed. The data compression paved the way for remote power protection and PQ monitoring. The results of data compression obtained by employing the appropriate wavelet filter revealed that the compression ratios were less than 11% and decreased to over 50% of that percentage value by adopting extra lossless compression [26].
Although the WT method achieved good results in detecting power disturbances, it could also perform multi-resolution time–frequency analysis and successfully minimize the size of the disruption dataset collection; however, it exhibited some drawbacks, such as the reliance of its accuracy on the choice of mother wavelet, as well as the effectiveness in classification being, likewise, highly dependent on choosing features and associated classifiers [27]. Furthermore, the method was sensitive to noisy signal interference and had a high computational cost [28]. As a result, a novel signal processing method with a wide range of applications and anti-noise capabilities should be devised.
Deep learning (DL) and other data mining techniques have been used to compress signals. Deep stacked autoencoders (DSAE) were employed to compress data from smart meter. The nonlinear compressor achieved fewer data losses and elevated compression rates [29]. CNN compression has also recently received some scientific attention. A work [30] proposed replacing standard linear projecting on the fully connected layer with circle projection, saving storage space and allowing fast Fourier transform to expedite computation. Another study [31] aimed to minimize the overall quantity of parameters and processes across the network. The pruning strategy described resulted in a significant reduction in parameter size and computing workload.
Even with the reviewed compression algorithm above, there is still another problem with PQD qualification. The quality of the classification results offers information about the weights of the input characteristics but does not affect their extraction. Due to the lack of extracted characteristics, recognizing distinct PQDs may not always be advantageous and may even be detrimental, particularly when the sampling dataset shows noise. Instead of using prior methods to classify PQD, a novel analytical framework should be employed, to shorten the analytical process and improve accuracy.
Deep learning applied to power quality disturbance problems can increase the accuracy of classification, reduce time, and simplify operations. Ref. [32] contains a method that can be used to convert the PQD data input into a 2-dimensional matrix, comparable to visual data, and determine the PQD categories using a conventional 2-dimensional CNN. The PQD data in this study, on the other hand, are a 1-dimensional time series, while the 2-dimensional CNN was developed for image analysis. As a result, it is not entirely appropriate for the PQD problem. Ref. [16] performed a useful comparison of various common CNN models and recurrent neural networks in PQD classification. However, the research did not discuss the training duration, variable number, model size, and characteristics of such DNNs. Furthermore, previous studies did not consider the overfitting problem, which could substantially impair DNN performance. Therefore, further data acquisition verification is required to validate the efficacy of deep learning algorithms.
3. Proposed Framework
3.1. Generating the Dataset of Artificial Power Quality Disturbances
This study was designed using 14 types of PQD, which represent the IEEE Preferred Procedure for Electric Power Quality Monitoring, namely transient, short duration root mean square variation (i.e., sag), swell, long duration voltage variation (i.e., interruption), unbalance, voltage fluctuation, and waveform distortion (i.e., harmonic and notch). It is very representative in terms of ensuring the quality of electricity supply during regular operation. These considerations are supported by earlier research findings indicating the eight most prevalent PQ distortions are flicker, harmonics, interrupts, notch, oscillatory transients, sags, spikes, and swells [33]. Using only eight PQD criteria, the implemented approach achieved a precision percentage of 94.6. Based on these findings, this study hypothesized that utilizing more criteria will better represent the primary types of power quality problems while also investigating the effectiveness of classification algorithms in mapping more patterns of PQDs.
The parameter descriptions are shown below.
- ▪
- The time (t1 and t2) and intensity (α) parameters for normal, sag, swell, interruption, transient, notch, sag with harmonic, swell with harmonic, interruption with harmonic, flicker with harmonic, and flicker with swell;
- ▪
- Intensity parameter (λ) for flicker and flicker with swell;
- ▪
- Intensity parameter (β) for transient oscillation;
- ▪
- The flicker frequency (ff) for flicker disturbance;
- ▪
- The harmonics intensity (α1, α3, α5, α7) at a waveform for harmonic disturbance;
- ▪
- T is the period of the fundamental wave.
The synthetic dataset was created using fourteen different forms of PQDs, all of which are widely recognized in the literature, namely flicker (f), f-harmonic, f-sag, f-swell, harmonic, interruption (i), i-harmonic, normal, notch, sag (sa), s-harmonic, swell (sw), sw-harmonic, and transient oscillation. The kind of disturbances and their distinctive mathematical models and typical parameters corresponded to the IEEE-1159 standard [34], and the suggested characteristic formulas were utilized in other publications.
The sample frequency variable was set at 3200 Hz in the initial configuration. The fundamental frequency was set to 60 Hz, and each set of samples consisted of ten repetitions (533 points). Every disturbance included 10,000 data training samples, in order to attain the learning dataset’s quality. As a consequence, 140,000 samples were employed for data training, with 80% used for learning and 20% used for validation. In addition, every category acquired 1000 testing data points, totalling 14,000 testing data points spread across 14 categories. In this study, data were gathered twice. The first collection utilized the original synthetic dataset (no noise), while the second used a dataset corrupted by Gaussian white noise (GWN) with variable signal–noise ratio (SNR) values of 40 dB and 20 dB [35]. As indicated in Table 1, datasets were generated by implementing the PQD mathematical model in the MATLAB program (R2023a). The randn function in MATLAB was used to generate GWN, which was a series of independent samples generated from the same probability distribution that follows a Gaussian distribution.

Table 1.
Mathematical models of PQD.
3.2. Proposed Dataset Compression Algorithm
Compression is a means of representing various types of data, which can include numerical, written content, visual content, audio, or any kind of information, with a minimum data size, as specified in a general data compression scheme, as shown in Figure 2. There are two types of compression, namely lossy compression and lossless compression. Lossy compression indicates that the decompressed data differ from the original, whereas lossless compression implies that the original and decompressed data are identical. The type of information that needs to be compressed will determine which of the two compression techniques or algorithms is used. Lossy compression, for example, is preferable for compressing video, audio, and image data, due to its high accuracy and compression ratio. The original files are too huge to transmit otherwise. Because decompression requires equivalent data, it is preferable to employ lossless compression for written content and numerical or symbols. Since PQD data are exclusively in numeric and text format, lossless data compression is the optimum solution for PQD data processing.
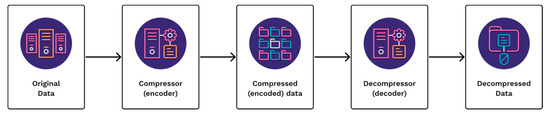
Figure 2.
General data compression scheme.
This study will provide insight into three data compression algorithms, namely wavelet transform, CNN, and autoencoder, to provide reliable data compression algorithm performance testing statistics, as each of the aforementioned algorithms has its own set of advantages for analyzing one-dimensional time series data. The wavelet transform is able to evaluate rapid changes in frequency, whereas autoencoders are able to acquire complex nonlinear transform functions. CNNs can analyze vast volumes of data and make extremely accurate predictions.
3.2.1. Wavelet Transform
The WT was used to compress the disturbance signal in this study, as it was in the approach of [36]. The wavelet decomposition approach was selected to identify and locate the signal disruption. To stretch and shift the waveform, the mother wavelet in (1) was initially used, as follows:
where a and b represent scale and shift parameters. To implement the WT in the digital system, the discrete wavelet transform (DWT) shown in (2) is utilized, as follows:
where represents the scale and represents the time-shift. The mother Daubechies wavelet (Db4) was used in this experiment. The decomposition level was set to four, and the threshold value was fixed to 62.91 [37]. The data compression process contained the following steps to achieve efficient compression outcomes, as illustrated in Figure 3.
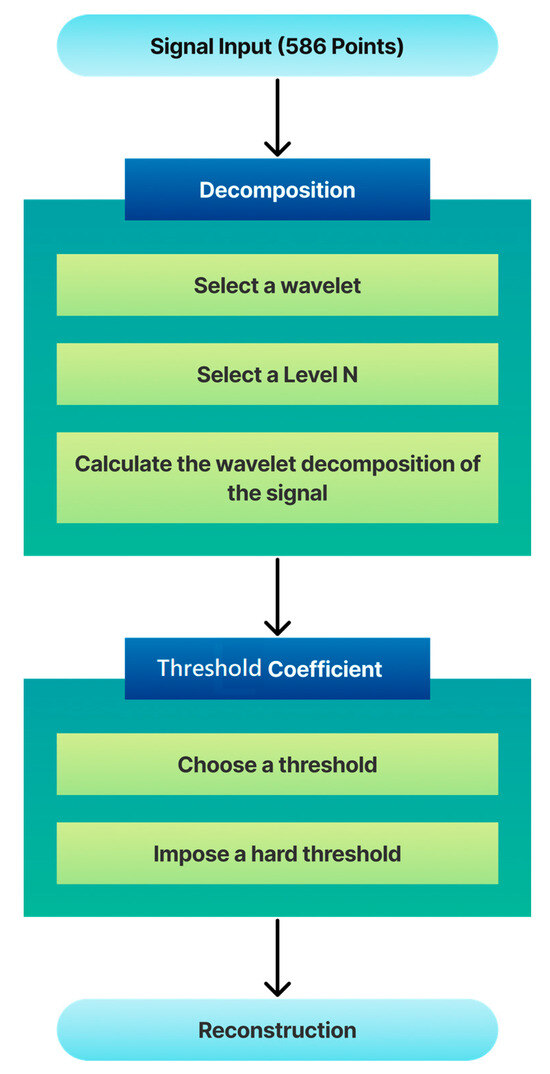
Figure 3.
Stages of data compression, utilizing the wavelet transform algorithm.
3.2.2. Basic Autoencoder
An autoencoder (AE) is essentially a feed-forward artificial neural network (ANN) that attempts to reproduce the input data layer onto its output layer. The linkage of the two networks, as illustrated in Figure 4, determined the structure of the autoencoder. The encoder oversees the transformation of a high-dimensional spatial characteristic to low-dimensional spatial information. The decoder reassembles the initial signal from the code. Using this design, the two networks underwent training concurrently by modifying the decoder weights first, followed by the encoder weights. The primary goal of this design is to minimize the gap between reconstruction (the output) and original signal (the input). Alternatively, the number of nodes in the hidden layer was substantially smaller than the number of nodes in the input layer, allowing the encoder to effectively represent the input data.
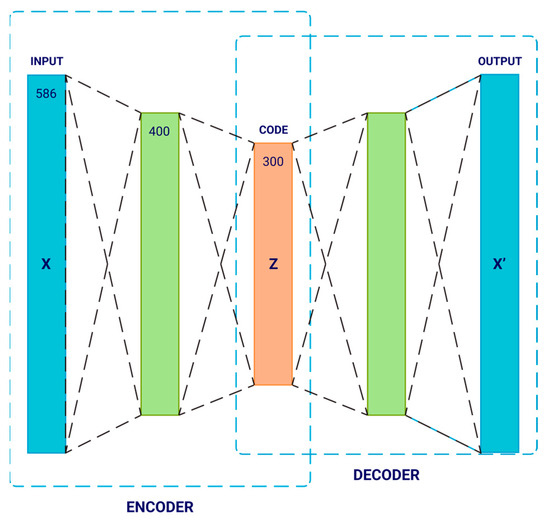
Figure 4.
Representation of a fundamental autoencoder.
For an input vector , the encoder provides a nonlinear representation of the input information for calculating the encoded features , as follows:
where and signify the weights and biases, respectively, and denote the chosen activation function. The encoded values are then decoded in order to recreate the initial input data using the following:
Where and denote the decoder’s weight and bias values. The error function is reduced during the training stage by altering , as follows:
In this scenario, represents the cost function, which can be specified as the squared of error or the cross-entropy functional, amongst other things [38]. Implementation of the autoencoders in Keras will employ a vector of 586 numbers between [0, 1], 400 nodes in the hidden layer, and a code-size of 300.
3.2.3. Convolutional Neural Network
Compressing data using the CNN compression technique requires two CNNs, one for encoding and one for decoding. Figure 5 depicts a high-level overview of CNN architecture. The sequential model type will be used to build the CNN compression model in Keras. The first two layers are Conv1D layers. These convolutional layers will deal with the input, seen as 1-dimensional metrices. In the first and second layers, (16, 4) are the number of nodes in each layer. ReLU is the activation function used for the first two layers. The first layer also takes in an input shape for 586 numbers. Between the Conv1D layers and the dense layer, there are MaxPooling and Flatten layers. MaxPooling is used to down-sample an input representation, lowering its dimensionality and allowing assumptions about features included in the binned sub-regions. Flatten layers transform the shape of the data from a vector of 1D matrices (or nD matrices, actually) into the right structure for a dense layer to comprehend. Dense is the standard layer type used for the output layer, and the activation is ReLU. There are 300 nodes in the output layer.

Figure 5.
Architecture of the CNN compression algorithm.
3.3. Structure of Classification Model
This section discusses the benefits and usefulness of employing a deep CNN to solve PQD problems. The deep CNN classification model algorithm will be presented individually in this section. Finally, some efficient overfitting reduction approaches will be described. The deep CNN network is designed with three PQD variables in mind: the beginning, when PQDs occur, and, last, at random. As a result, deep CNN should be capable of monitoring during the input period. Second, PQD characteristics are variable; particularly, disruptions of the identical type differ greatly. As a result, the trained network should be capable of robust generalization. Noise resistance is crucial, since noise is constantly relevant to real signals. Finally, some disturbances present a significant number of detail characteristics at short sample periods, necessitating the capacity of the network to concentrate on both localized and general features.
Details of the proposed framework of 1D deep CNN classification architecture are illustrated in Figure 6. This model is similar to the one provided in [39]. However, the improved technique includes a data compression stage that compresses the dataset using wavelet transform, autoencoder, and CNN algorithm before transferring it to the CNN classification model through the network layer, whereas the previous model directly passed the original dataset.

Figure 6.
Reprinted from Ref. [40]: proposed framework. Full Connected Layer—FCL.
The network structure is divided into two main parts: the feature extraction layers and the classification layers [41].
- ▪
- Feature Extraction
This section presents the important properties of the training data set and is divided into the following three types of layers: input layers, including the pre-processing data layer, convolutional layers, and pooling layers. Each layer is defined in detail below. The model’s input is handled in the first layer by the input layer. This starts with the input layer receiving the one-dimensional signal data. The data consist of the original 14 types of PQD data and PQD noise-contaminated data. Both data are compressed by three compression algorithms, as mentioned above. As a result, there are six categories of datasets in total. If all the training sets are in the appropriate format, it will be delivered directly to the convolutional layers of the feature learning phase; otherwise, it will be prepared at the pre-processing data layer. This layer converts several data formats to make our system more versatile and capable of handling data from multiple sources. A common square matrix format represents tensors in the convolution parts. If the supplied data are not in an appropriate square form with dimensions, padding will change it to the common form as needed.
The convolutional layers control feature learning and apply convolution to the incoming data. There are four numbers of convolutional layers. Each layer consists of ten filter numbers, three Kernel sizes, and one stride, and is equipped by ReLU as an activator. In this model, the pooling layer adopts maximum pooling, five Kernel sizes, one stride, and includes ReLU as an activator to highlight classifier information.
- ▪
- Classification
This section indicates class labels from the training data, using feature learning in the earlier part of convolutional layers. It is divided into three sections: the reshape layer, the class prediction layer, and the output layer. Before being sent into the prediction phase, the input must be in the form of a vector required by the next layer. This task is executed in the reshape layer. The primary function of this layer is to predict the class. The fully connected layer, consisting of a dense layer with ReLU activation, a dense layer with softmax activation, and a flatten layer, is used in this section. During the training step, the layer parameters are modified to produce the best fitting model. Figure 7 summarizes the details of each layer.
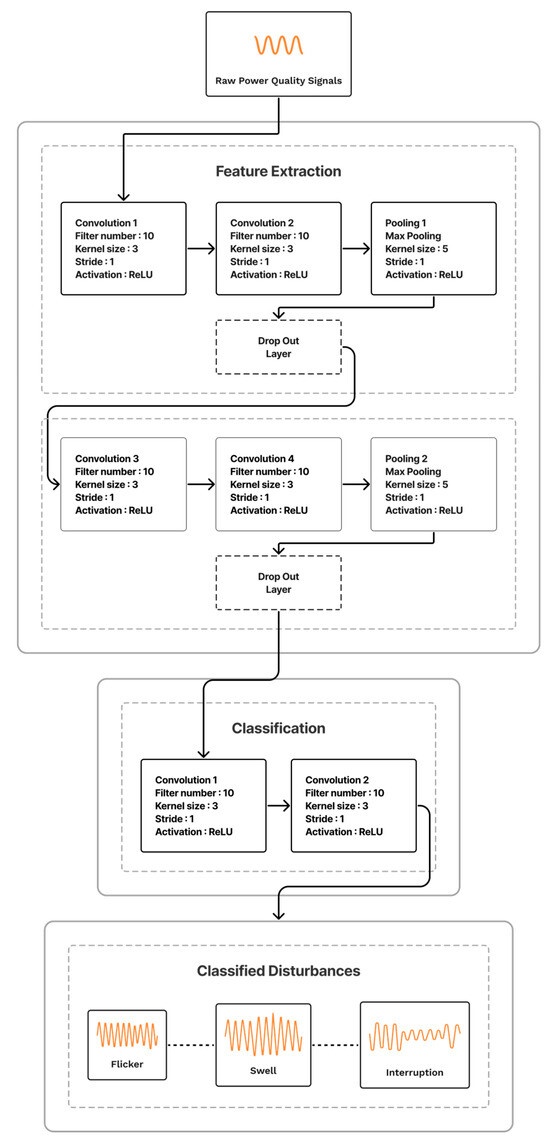
Figure 7.
Parameter specifications for each layer.
3.4. Deep Convolutional Neural Network Layer Descriptions
This part comprises a comprehensive layer description of the proposed deep learning CNN architecture for 1-D PQD classification.
- Convolutional layers in one dimension: Local connectivity and weight sharing are the fundamental concepts of the convolutional layer [42]. Convolutional layers are used to build filters using shared weights and a limited receptive field. The layer of l-th contains Fl filters, and Xi is the input of the 1-dimensional matrix (n x1). K (k x1) denotes the filter kernel. The output of the convolutional layer by the fl-th filter is stated as follows:
The activation function is denoted by the symbol f(x), whereas m = n − k + 1. It simulates the action of a neuron from input to output. In deep learning, the rectified linear unit (ReLU) is used in the convolutional layer, which is speedier than the tanh function. As follows:
- 2.
- A pooling layer: After convolution, the pooling layer scales and maps the data to minimize the data dimension and emphasize classifier information. The pooling layer serves the same function as a fuzzy filtration system; average pooling and maximum pooling provide the average and maximum value of activations, respectively. In the PQD waveform, average pooling is more vulnerable to noise. In this scenario, maximum pooling outperforms average pooling. As a result, the pooling layer employs maximum pooling:
- 3.
- Dropout layers: Dropout is an approach for simulating the parallel training of multiple neural networks with diverse topology. Several layer outputs are removed while training. A new hyperparameter is provided for calculating the probability of dropping the gradient outputs or the inverse probability of retaining the gradient outputs. A common number for keeping the output of each node in a hidden layer is 0.5, and a value close to 1.0, such as 0.8, for maintaining inputs from the visible layer.
- 4.
- Dense layer or a fully connected layer: D is a parameter of the l-th dense layer that can be learned. The output value can be represented as follows:
- 5.
- Softmax activation function: The softmax value represents the possibility of a sample from the associated class being input. Therefore, the neurons in the hidden layer should be the same as the category set and output the group with the greatest probability ratio. The length of an array Z is given by j. i represents the array index; i = 1, 2, …, j. The following is the softmax value of Si:
3.5. Resolvation of Overfitting
Overfitting is an irreversible problem in supervised learning. It occurs when a model fails to extrapolate from a visible dataset to an invisible dataset. Overfitting causes the model to perform flawlessly on the training set while fitting badly on the test set. This is due to the difficulty overfitting models have in dealing with information in the test set that differs from that in the training set. Over-fitted models, on the other hand, prefer to memorize all the data, including the inevitable noise on the training set, rather than learning the discipline concealed behind the data [43]. Overfitting is a major concern with this study, especially in experimental research using noised dataset. An advanced structure of network and training techniques are used to minimize overfitting, as follows.
- Dropout: Configurations of neural networks with varied model configurations have been shown to prevent overfitting. However, it typically suffers the added computational cost of training and maintaining numerous models. These include halting training as soon as performance on a validation set begins to deteriorate, introducing weight penalties of various types, such as L1 and L2 regularization, and gentle weight sharing [44]. A single model is utilized in this paper to simulate having a massive number of distinct network designs by removing nodes at random during training, known as a dropout. It provides a computationally cheap and highly effective regularization strategy for reducing overfitting and adaptation errors in DNNs of all types. Furthermore, dropout enhanced neural network performance on supervised learning tasks in vision, voice recognition, document classification, bioinformatics, and various benchmark data sets.
- Powerful optimizer: In the training period, the weight of every single layer is modified using a feature known as an optimizer, which can be stochastic gradient descent (SGD) [45], Adagrad, Adadelta, RMSProp, Adam, or NAdam. Although recent research indicates that the NAdam can collaborate with the early stop classification during the training phase to minimize overfitting significantly [46], the Adam optimizer outperforms the NAdam optimizer in computing efficiency in this work.
4. Results and Discussion
4.1. Data Pre-Processing Stage
Two criteria datasets were supplied into the model, as shown in Figure 8. The first dataset contained the original synthetic PQD signals, while the second dataset comprised noise-corrupted synthetic PQD signals. A synthetic PQD was initially built by applying the PQD mathematical model in the MATLAB application to obtain both criteria for the dataset. Since the original synthetic or noise-free data were generated using mathematical procedures, the collected data were very similar to the ideal conditions for the features of each PQD category. Data that had been distorted by noise were generated to produce data that resembled the actual conditions of the power distribution and transmission network, which were defined as sag, swell, interruption, harmonics, flicker, notch, and transient. Sag is a voltage or current magnitude variance of 0.1 to 0.9 pu at the power frequency for the time interval T to 9T seconds. Swell is defined as an increase in voltage or current magnitude between 0.1 and 0.8 pu at the power frequency across the time period T to 9T seconds. Interruption is defined as a voltage or current magnitude deviation ranging from 0.9 to 1 pu at the power frequency for a time period of T to 9T seconds. Harmonics are the frequencies in a sinusoid of currents or voltage that occur in integer multiples. Flicker is a voltage magnitude variation over time that causes an unstable impression in visual sensations induced by light impulses. Notch is described as shifting interference of a pure power voltage sinusoidal frequency happens less than half a cycle. A transient is a problem that varies between two successive steady states in a short time period, compared to the time scale of relevance.
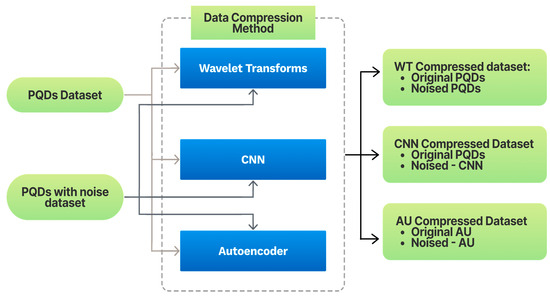
Figure 8.
Framework for generating compressed data.
Each synthetic signal sample was then compressed separately using the wavelet transform, CNN, and autoencoder algorithms. The compression operation generated six types of compressed data, which were subsequently employed in the classification model.
The dataset was then used to assess the model performance for 14 different categories of PQD classification. The following rules determined the distribution of data in this study to avoid overlapping data. The model learning procedure utilized 140,000 samples, with 80% for learning and 20% for validation. This process provided the value of loss and accuracy validation, implying how poorly or well a model behaved after each optimization iteration. In addition, each category received 1000 testing data points, for 14,000 testing data points spread throughout 14 categories. The total number of data samples was 154,000 for each type of data. Table 2 provides a summary of the synthetic data.

Table 2.
Datasets utilized during the examination.
In emulation, the epoch numbers were set from 100 to 500 to obtain the lowest possible inaccuracy. The batch size was set to 500, and the learning rate was set at 0.02. The Adam method was used to optimize the model, and the argmax function in the testing model was utilized to determine the class with the greatest prediction. The learning technique and model testing were performed using Google Collab, with GPU (Graphics Processing Unit) acceleration and an internet connection through an 802.11ax Wi-Fi 6 wireless network. At the same time, the CNN architecture in 1-D was constructed using the Keras framework. The hardware used is a MacBook Air with the following technical specifications: 8 GB of RAM, an M1 chip including an 8-core CPU with four performance cores and four efficiency cores, a 7-core GPU, and a 16-core Neural Engine. The M1 CPU is reported to be 3.5 times faster than the previous Intel processor, with up to five times higher graphics processing capabilities [47]. Furthermore, when compared to using Google Collab with an accelerated CPU, in this study, the training time was eight times faster using the GPU, with an average of 36 s every epoch. In contrast, the CPU consumed 303 s per epoch. Experimental studies for PQD classification in datasets were carried out separately using CNNs in 1-D models. In the CNN model, the process was repeated many times, depending on two dataset criteria and three data compression techniques.
4.2. Comparison of Three Compression Algorithms
As indicated in Table 3, this section compares the compression algorithm and its performance in the CNN classification model for PQDs using the free-noise dataset in model learning. The first experiment demonstrated that the CNN compression classification process achieved 99.74% accuracy in just three epochs, or one minute and forty-three seconds. Using a wavelet transform approach, the model achieved 99.52% accuracy after twenty-six episodes in fifteen minutes and six seconds. Meanwhile, the model could only attain 99.03 percent accuracy in the 24th minute at the 59th epoch when applying the autoencoder compression approach.

Table 3.
Model learning performance of CNN classification.
Furthermore, the time spent testing for the categorization of one disturbance pattern revealed that the autoencoder was superior by an average of 6.9 ms per step, followed by CNN at 7.7 ms per step and wavelet transform at 9.4 ms per step. However, the CNN compression algorithm showed faster data robustness during the learning process.
Among the three compression techniques, CNN, as a compression algorithm, is extremely suitable to be used in conjunction with the CNN classification model. The experimental findings demonstrated that the combination of compression and classification algorithms significantly reduced training times, being 15 to 24 times faster than using wavelet transform and autoencoder as compression algorithms on the CNN classification algorithm network.
Figure 9 compares the training processes of the three algorithms on the CNN classification model. In contrast, loss and accuracy are determined for each epoch in the training set and validation.

Figure 9.
Training process of three compression algorithms.
This demonstrates that CNN reached high accuracy in less time and thrive in these conditions. The wavelet transform produced nearly the same training model, but it took longer to achieve the highest accuracy value. This confirms that the CNN model compression method included simplifying the structure of deep learning algorithms by employing fewer model parameters, which reduced computation and boosted inference time in deep learning architectures. Meanwhile, wavelet transform required several processes, including filtering, sampling, and convolution, that were time- and space-consuming. Autoencoder, on the other hand, exhibited unstable or fluctuating performances during the learning process.
4.3. Performance Comparison before and after Adding the Dropout Layer
In a variety of conditions, the PQDs in the field may be subjected to noise pollution. The noise effect is critical to PQD compressions, as they may result in the overfitting of the model, because the algorithm conceptualized noise or random disturbances in the training dataset. The learning curve in Figure 10a depicts the overfit model of the PQD dataset, specifically a stage during which training losses continue to diminish with experience, while validation losses have decreased to a minimal level and will rise. Since overfit cannot be removed, Figure 10b indicates that overfitting is corrected after applying methodological training approaches, such as optimizer enhancement and hyperparameter set-up, in the model system.
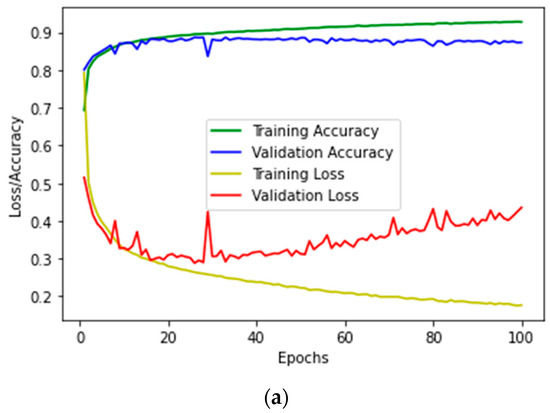
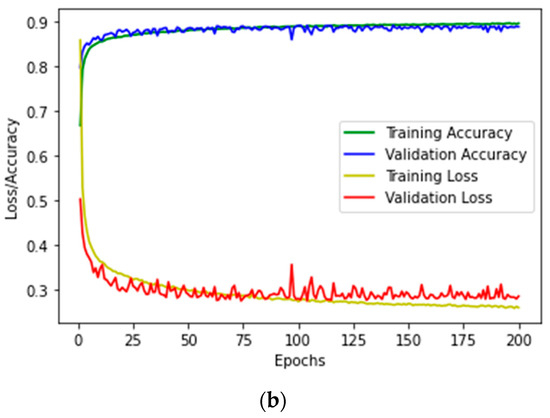
Figure 10.
(a) PQD dataset with a SNR of 40 dB: overfitting dataset. (b) PQD dataset with a SNR of 40 dB: reducing overfitting dataset.
This study presents experimental results of relevant strategies to consider when employing dropout, to prevent overfitting in neural networks in practice. The appropriate dropout rate in this experiment was set to 0.5 for the hidden layer and close to 1.0 for the input layer, as recommended in the original dropout paper [48]. However, this study began with a small dropout value of 20% to 50% neurons, with 20% giving a reasonable beginning point. Generally, a low probability had little effect, whereas a large value caused the network to under-learn. By randomly removing units, the neural network was forced to develop a more robust representation of the data and was prevented from making predictions based on a single neuron. This regularization strategy increased the neural network’s ability to generalize and perform effectively on data, enhancing its accuracy.
4.4. Accuracy-Based Comparison
Some frequently used metrics were performed, to evaluate the model on test data comprehensively. These were accuracy, recall, precision, and F1-score criteria. Accuracy is commonly regarded as the primary way of evaluating PQDs. In the experiment, three compression algorithms were applied to six datasets using a CNN classifier. The accuracy of the classifiers for each data compression strategy is shown in Table 4. In terms of the free-noised dataset, CNN achieved the highest accuracy of 99.96%, followed by WT and autoencoder at 99.93% and 99.91%, respectively. In comparison to the noised data with a SNR of 40 dB and a SNR of 20 dB, CNN performed exceptionally well, achieving a value of 98.67% and 98.25%, respectively.

Table 4.
Detail performance of compression algorithms.
4.5. Recall-Based Comparison
Recall is an important quality matrix because it is necessary to correctly classify 14 different types of PQDs. Regarding free noised signal, autoencoder had the lowest recall score of 99.41%, while CNN had the greatest recall score of 99.74%. Using the CNN compression method, the noised data classifier obtained a maximum recall score of 90.50%. WT and autoencoder both had recall rates of 88.91% and 88.74%, respectively.
4.6. Precision-Based Comparison
Precision is another performance evaluation matrix that assesses the performance of categorization models. For noised data, the WT compression, in conjunction with the CNN classifier, had the lowest precision score of 89.11%, while the CNN had the best precision score of 90.67%. When employing a free noised dataset, CNN compression outperformed WT and autoencoder. The CNN compression produced a maximum precision of 99.74%, while the autoencoder compression reached a minimum precision of 99.42%.
4.7. F1 Score-Based Comparison
The F1-score is the harmonic mean of precision and recall. In the free noised dataset, the autoencoder compression method achieved a very low F1-score of 99.41%, while CNN achieved the best F1-score of 99.74% and the WT algorithm obtained an F1-score of 99.52%. The autoencoder compression achieved the lowest F1-score of 88.73% for noised datasets, whereas CNN compression achieved the greatest F1-score of 90.45%.
4.8. Classification Error Comparison
Although each method performed admirably in general, the amount of incorrectly classified instances also determined the efficiency of the classification process. Figure 11 demonstrates in considerable detail, using a bar chart, that wavelet transform had the highest number of classification errors, particularly in seven class labels from fourteen PQD classification categories. This is due to the WT method’s reliance on the appropriate mother wavelet for accuracy, and classification performance depended highly on feature selection and the connected classifier. Furthermore, autoencoder had the most significant number of misclassifications in the following classes: flicker, flicker sag, and flicker swell. Primarily, this is because autoencoder is an unsupervised technique that learns from its data rather than from labels applied by humans. As a result, the autoencoder frequently required a huge amount of clean data to obtain relevant findings. It could produce contradictory answers if the dataset was insufficiently large, unclean, or noisy. CNN, on the other hand, had the fewest incorrectly classified instances. However, some classes, like interruption, normal, sag, and swell had a slightly higher error count than both algorithms.
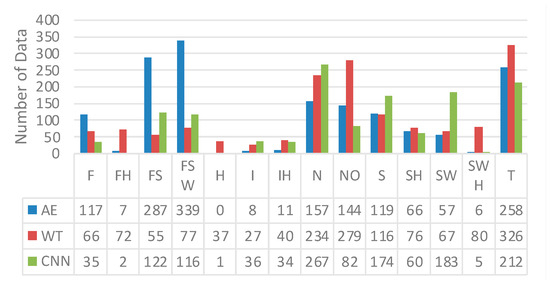
Figure 11.
Mapping of incorrect instances.
5. Conclusions
This paper proposed a framework for combining 1-dimensional dataset compression with the CNN classification. After evaluating three types of compression algorithms, namely wavelet transform, autoencoder, and CNN, the CNN classification model with the CNN compression algorithm outperformed the other two compression algorithms tested on the 1-dimensional PQDs, in terms of accuracy, recall, precision, and F1 score, with the following values: 98.25%, 98.21%, 98.28%, and 98.28% for data with noise and more than 99% for the original data. The model also had the shortest test time and the fewest error-classified instances.
Compared to the classification model before adding the dropout layer, using the dropout layer in the DCNN reduced overfitting and effectively sped up training, especially when dealing with noise-contaminated data. This finding supports the initial hypothesis of this study that the CNN compression algorithm is appropriate for the PQDs dataset and is highly recommended to be used in conjunction with the 1D-CNN classification model to achieve satisfactory performance on system requirements.
The authors recommend that future studies be conducted utilizing actual data acquired from installed power sources and predictive algorithms, for instance time series analysis, to ensure the application can forecast the PQDs that will occur based on disrupting the proper functioning of the power systems on the smart grid network.
Author Contributions
Conceptualization, Y.-C.C., M.S. and S.S.B.; data curation, S.S.B. and M.S.; methodology, Y.-C.C., M.S. and C.-I.C.; software, M.S. and S.S.B.; validation, Y.-C.C. and C.-I.C.; formal analysis, Y.-C.C. and M.S.; resources, M.S. and S.S.B.; writing—original draft preparation, M.S. and C.-I.C.; writing—review and editing, M.S. and C.-I.C.; supervision, Y.-C.C. and C.-I.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology of Taiwan, grant number MOST 111-2628-E-008-004-MY3, and the National Science and Technology Council of Taiwan, grant number NSTC 112-2218-E-008-011.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors gratefully acknowledge the helpful comments and suggestions of the reviewers for improving the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fortuna, L.; Buscarino, A. Sustainable Energy Systems. Energies 2022, 15, 9227. [Google Scholar] [CrossRef]
- Elbasuony, G.S.; Aleem, S.H.A.; Ibrahim, A.M.; Sharaf, A.M. A unified index for power quality evaluation in distributed generation systems. Energy 2018, 149, 607–622. [Google Scholar] [CrossRef]
- Khokhar, S.; Zin, A.A.B.M.; Mokhtar, A.S.B.; Pesaran, M. A comprehensive overview on signal processing and artificial intelligence techniques applications in classification of power quality disturbances. Renew. Sustain. Energy Rev. 2015, 51, 1650–1663. [Google Scholar] [CrossRef]
- Andrei, H.; Cepisca, C.; Grigorescu, S. Power quality and electrical arc furnaces. In Power Quality; IntechOpen: London, UK, 2011; pp. 77–100. [Google Scholar]
- Singh, R.; Mohanty, S.R.; Kishor, N.; Thakur, A. Real-time implementation of signal processing techniques for disturbances detection. IEEE Trans. Ind. Electron. 2018, 66, 3550–3560. [Google Scholar] [CrossRef]
- Berutu, S.S.; Chen, Y.-C. Power Quality Disturbances Classification Based on Wavelet Compression and Deep Convolutional Neural Network. In Proceedings of the 2020 International Symposium on Computer, Consumer and Control (IS3C), Taichung City, Taiwan, 13–16 November 2020; pp. 327–330. [Google Scholar]
- Schael, M.; Sourkounis, C. Influences of power supply quality on electric equipment in production processes. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 2081–2086. [Google Scholar]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L. Chaos addresses energy in networks of electrical oscillators. IEEE Access 2021, 9, 153258–153265. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Syamsudin, M.; Berutu, S.S. Pretrained Configuration of Power-Quality Grayscale-Image Dataset for Sensor Improvement in Smart-Grid Transmission. Electronics 2022, 11, 3060. [Google Scholar] [CrossRef]
- Pérez-Ortiz, M.; Jiménez-Fernández, S.; Gutiérrez, P.A.; Alexandre, E.; Hervás-Martínez, C.; Salcedo-Sanz, S. A review of classification problems and algorithms in renewable energy applications. Energies 2016, 9, 607. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Zia, M.F.; Benbouzid, M.; El Hani, S. Overview of Signal Processing and Machine Learning for Smart Grid Condition Monitoring. Electronics 2021, 10, 2725. [Google Scholar] [CrossRef]
- Binsha, P.; Kumar, S.S.; Soman, K. Power quality signal classification using convolutional neural network. Int. J. Comput. Technol. Appl. 2016, 9, 8033–8042. [Google Scholar]
- Gal, Y.; Ghahramani, Z. A theoretically grounded application of dropout in recurrent neural networks. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Barcelona, Spain, 5–10 December 2016; pp. 1027–1035. [Google Scholar]
- Le, Q.V.; Jaitly, N.; Hinton, G.E. A simple way to initialize recurrent networks of rectified linear units. arXiv 2015, arXiv:1504.00941. [Google Scholar]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Mohan, N.; Soman, K.; Vinayakumar, R. Deep power: Deep learning architectures for power quality disturbances classification. In Proceedings of the 2017 International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 21–23 December 2017; pp. 1–6. [Google Scholar]
- Rodriguez, M.A.; Sotomonte, J.F.; Cifuentes, J.; Bueno-López, M. Classification of power quality disturbances using hilbert huang transform and a multilayer perceptron neural network model. In Proceedings of the 2019 International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; pp. 1–6. [Google Scholar]
- Sindi, H.; Nour, M.; Rawa, M.; Öztürk, Ş.; Polat, K. A novel hybrid deep learning approach including combination of 1D power signals and 2D signal images for power quality disturbance classification. Expert Syst. Appl. 2021, 174, 114785. [Google Scholar] [CrossRef]
- Dash, P.; Prasad, E.N.; Jalli, R.K.; Mishra, S. Multiple power quality disturbances analysis in photovoltaic integrated direct current microgrid using adaptive morphological filter with deep learning algorithm. Appl. Energy 2022, 309, 118454. [Google Scholar] [CrossRef]
- Mengi, O.O.; Altas, I.H. A new energy management technique for PV/wind/grid renewable energy system. Int. J. Photoenergy 2015, 2015, 356930. [Google Scholar] [CrossRef]
- He, S.; Tian, W.; Zhang, J.; Li, K.; Zhang, M.; Zhu, R. A high efficient approach for power disturbance waveform compression in the view of heisenberg uncertainty. IEEE Trans. Ind. Inform. 2018, 15, 2580–2591. [Google Scholar] [CrossRef]
- Shen, Y.; Abubakar, M.; Liu, H.; Hussain, F. Power quality disturbance monitoring and classification based on improved PCA and convolution neural network for wind-grid distribution systems. Energies 2019, 12, 1280. [Google Scholar] [CrossRef]
- Eristi, B.; Yildirim, O.; Eristi, H.; Demir, Y. A new embedded power quality event classification system based on the wavelet transform. Int. Trans. Electr. Energy Syst. 2018, 28, e2597. [Google Scholar] [CrossRef]
- Chen, S.; Zhu, H.Y. Wavelet transform for processing power quality disturbances. EURASIP J. Adv. Signal Process. 2007, 2007, 47695. [Google Scholar] [CrossRef]
- Gao, R.X.; Yan, R. Wavelet packet transform. In Wavelets; Springer: Berlin/Heidelberg, Germany, 2011; pp. 69–81. [Google Scholar]
- Dekhandji, F.Z. Detection of power quality disturbances using discrete wavelet transform. In Proceedings of the 2017 5th International Conference on Electrical Engineering-Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 October 2017; pp. 1–5. [Google Scholar]
- Wang, J.; Xu, Z.; Che, Y. Power quality disturbance classification based on DWT and multilayer perceptron extreme learning machine. Appl. Sci. 2019, 9, 2315. [Google Scholar] [CrossRef]
- Weeks, M.; Bayoumi, M. Discrete wavelet transform: Architectures, design and performance issues. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2003, 35, 155–178. [Google Scholar] [CrossRef]
- Huang, X.; Hu, T.; Ye, C.; Xu, G.; Wang, X.; Chen, L. Electric load data compression and classification based on deep stacked auto-encoders. Energies 2019, 12, 653. [Google Scholar] [CrossRef]
- Lu, Y.; Kumar, A.; Zhai, S.; Cheng, Y.; Javidi, T.; Feris, R. Fully-adaptive feature sharing in multi-task networks with applications in person attribute classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5334–5343. [Google Scholar]
- Yang, T.-J.; Chen, Y.-H.; Sze, V. Designing energy-efficient convolutional neural networks using energy-aware pruning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5687–5695. [Google Scholar]
- Balouji, E.; Salor, O. Classification of power quality events using deep learning on event images. In Proceedings of the 2017 3rd International Conference on Pattern Recognition and Image Analysis (IPRIA), Shahrekord, Iran, 19–20 April 2017; pp. 216–221. [Google Scholar]
- Igual, R.; Medrano, C. Research challenges in real-time classification of power quality disturbances applicable to microgrids: A systematic review. Renew. Sustain. Energy Rev. 2020, 132, 110050. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Mitra, M.; Sengupta, S. Electric power quality. In Electric Power Quality; Springer: Berlin/Heidelberg, Germany, 2011; pp. 5–12. [Google Scholar]
- Chen, Y. Improved energy detector for random signals in Gaussian noise. IEEE Trans. Wirel. Commun. 2010, 9, 558–563. [Google Scholar] [CrossRef]
- Ning, J.; Wang, J.; Gao, W.; Liu, C. A wavelet-based data compression technique for smart grid. IEEE Trans. Smart Grid 2010, 2, 212–218. [Google Scholar] [CrossRef]
- Chen, C.-I.; Berutu, S.S.; Chen, Y.-C.; Yang, H.-C.; Chen, C.-H. Regulated Two-Dimensional Deep Convolutional Neural Network-Based Power Quality Classifier for Microgrid. Energies 2022, 15, 2532. [Google Scholar] [CrossRef]
- Wang, S.; Chen, H.; Wu, L.; Wang, J. A novel smart meter data compression method via stacked convolutional sparse auto-encoder. Int. J. Electr. Power Energy Syst. 2020, 118, 105761. [Google Scholar] [CrossRef]
- Baloglu, U.B.; Talo, M.; Yildirim, O.; San Tan, R.; Acharya, U.R. Classification of myocardial infarction with multi-lead ECG signals and deep CNN. Pattern Recognit. Lett. 2019, 122, 23–30. [Google Scholar] [CrossRef]
- Syamsudin, M. Implementasi Algoritma Kompresi Data untuk Meningkatkan Kinerja Pendeteksian Gangguan Kualitas Daya Listrik. Med. Tek. J. Tek. Elektromedik Indones. 2023, 5, 30–38. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Syamsudin, M.; Berutu, S. Regulated 2D Grayscale Image for Finding Power Quality Abnormalities in Actual Data. J. Phys. Conf. Ser. 2022, 2347, 012018. [Google Scholar] [CrossRef]
- Huang, C.; Ni, S.; Chen, G. A layer-based structured design of CNN on FPGA. In Proceedings of the 2017 IEEE 12th International Conference on ASIC (ASICON), Guiyang, China, 25–28 October 2017; pp. 1037–1040. [Google Scholar]
- Ying, X. An overview of overfitting and its solutions. Proc. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Hinton, G.E.; Nowlan, S. Preface to “Simplifying Neural Networks by Soft Weight Sharing”. In The Mathematics of Generalization; CRC Press: Boca Raton, FL, USA, 2018; pp. 369–371. [Google Scholar]
- Gueorguieva, N.; Valova, I.; Klusek, D. Solving Large Scale Classification Problems with Stochastic Based Optimization. Procedia Comput. Sci. 2020, 168, 26–33. [Google Scholar] [CrossRef]
- Dozat, T. Incorporating Nesterov Momentum into Adam. 2016. Available online: https://openreview.net/forum?id=OM0jvwB8jIp57ZJjtNEZ (accessed on 6 January 2024).
- Fojtik, R. New Processor Architecture and Its Use in Mobile Application Development. In Proceedings of the 2018 International Conference on Digital Science, Budva, Montenegro, 19–21 October 2018; pp. 545–556. [Google Scholar]
- Ha, C.; Tran, V.-D.; Van, L.N.; Than, K. Eliminating overfitting of probabilistic topic models on short and noisy text: The role of dropout. Int. J. Approx. Reason. 2019, 112, 85–104. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).