State of Charge Prediction of Mine-Used LiFePO₄ Battery Based on PSO-Catboost

Abstract

The accurate prediction of battery state of charge (SOC) is one of the critical technologies for the safe operation of a power battery. Aiming at the problem of mine power battery SOC prediction, based on the comparative experiments and analysis of particle swarm optimization (PSO) and Categorical Boosting (Catboost) characteristics, the PSO-Catboost model is proposed to predict the SOC of a power lithium iron phosphate battery. Firstly, the classification model based on Catboost is constructed, and then the particle swarm algorithm is used to optimize the Catboost hyperparameters to build the optimal model. The experiment and comparison show that the optimized model’s prediction accuracy and average precision are superior to other comparative models. Compared with the Catboost model, the Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) values of the PSO-Catboost model decreased by 12.4% and 25.4% during charging and decreased by 5.5% and 12.2% during discharging. Finally, the Random Forest (RF) and Extreme Gradient Boosting (XGBoost) models, both ensemble learning models, are selected and compared with PSO-Catboost after being optimized via PSO. The experimental results show that the proposed model has a better performance. In this paper, experiments show that the optimization model can select parameters more intelligently, reduce the error caused by artificial experience to adjust parameters, and have a better theoretical value and practical significance.

1. Introduction

Mines’ demand for electric drives is increasing year by year. As an essential power source, the safe and efficient operation of a mine power battery pack is necessary. The mine power battery pack mainly comprises lithium iron phosphate batteries [1] (referred to as lithium batteries from now on), which have a stable chemical composition, are safer to use in high temperatures and other environments, and reduce potential safety hazards. Lithium batteries are not resistant to deep discharge or overcharging; if left in this state for a long time, they will suffer irreparable damage. Therefore, the battery management system (BMS) is needed to regulate the lithium battery to improve its operational safety and prolong its service life [2,3]. The BMS monitors the battery’s state of charge (SOC) to ensure it is not overcharged or over-discharged during operation.

The SOC of a lithium-ion battery cannot be measured directly but can be predicted by analyzing the characteristic factors during its operation, including voltage, current, and temperature. At the same time, lithium-ion batteries are highly nonlinear and time-varying systems, and it is difficult to fit a model that can accurately estimate the charge and discharge state of the battery using traditional methods. The application of artificial intelligence theory based on machine learning to solve the problems of nonlinear systems has a good performance. Because machine learning is highly nonlinear, fault-tolerant, and self-learning, it can be trained with known samples to obtain the internal law of nonlinear systems. Therefore, the method can solve the battery state of charge prediction problem without considering the internal details of the battery [4].

The machine learning (ML) method establishes the mapping relationship between battery state information and SOC, which avoids establishing a complex battery model. It consists of three parts: the input, model, and output. The input and output can train the ML model without physical constraints by optimizing the algorithm and training data. Machine learning methods, such as support vector machines (SVM) [5], neural networks (NNs) [6], and Gaussian process regression (GPR) [7], are often used in SOC prediction. A joint SOC and SOH estimation framework has been proposed in the literature [8], utilizing both data-driven and model-based approaches. For the first part, the proposed method applies a least squares support vector machine (LS-SVM) to identify the dynamics of the cell and then creates a state-space model in which an odorless particle filter (UPF) is used to estimate the SOC of the cell. The 2.2 Ah NMC 18650 cell was tested on the NEWARE BTS3000N battery cycle machine, and the results show that the maximum SOC estimation error is less than 2%, and the RMSE of SOH estimation is less than 4%. Gaussian process regression (GPR) models were proposed in the literature [9]. First, the input dataset related to SOC is combined with the feature extraction strategy. Data preprocessing, correlation analysis, and principal component analysis were used. The exponential square kernel function optimizes the feature weights via the automatic association determination method. Finally, the autoregressive GPR model is constructed to improve the estimation accuracy and confidence further. The battery pack, consisting of 177 Ah NMC cells, was tested on a Digatron EVT 300–600 battery tester and had an estimated error of less than 3.9%. The above work is based on the single model to obtain the SOC value, but the performance of the single model is limited and can only be met in some cases.

The ensemble learning model is a kind of model used in machine learning. The ensemble learning model combines multiple individual models to optimize its prediction results, which can further improve the accuracy of SOC prediction. Ensemble learning methods have superior nonlinear fitting ability and can reduce computational complexity via parallel computing. In the literature [10], the differential search optimization RF (DSA-RF) algorithm is used to predict the SOC of electric vehicle batteries, and two different types of lithium-ion battery data, LiNCA and LiNMC, are used. The robustness of the algorithm is further verified under various temperature conditions. The RMSE and MAE were lower than 1% and 0.5% in the DST and FUDS cycles at different temperatures. In the HPPC test, the proposed algorithm achieves high SOC accuracy in LiNCA and LiNMC batteries, with RMSE of 0.508% and 0.382%, respectively. The literature [11] uses support vector regression (SVR) and XGBoost to predict SOC, and both models are validated on the University of Maryland Cycle battery dataset. By comparison, it is found that XGBoost is faster and more accurate. This paper uses a new classification and promotion algorithm (Catboost) [12] to predict the SOC of mine power batteries. The model optimized via the particle swarm optimization algorithm has achieved good prediction results.

2. SOC Prediction Model

Catboost (Categorical Boosting) is an improved GBDT (Gradient Boosting Decision Trees) algorithm [13]. It is an ensemble learning algorithm based on a symmetric decision tree, which can deal with data with different characteristics and is enormously robust. Catboost can effectively deal with the problems of gradient deviation and prediction offset, reduce overfitting occurrence, and have good accuracy and versatility.

2.1. GBDT Algorithm

The GBDT algorithm is a framework algorithm for ensemble learning. Its basic idea is to use the primary weak learner to obtain the strong learner through current reinforcement and iteration. The GBDT algorithm is an ensemble learning algorithm based on a boosting algorithm composed of a gradient lifting algorithm and a decision tree algorithm. The model is additive, and the basis function is a decision tree (CART). The iterative process of the algorithm is to obtain the gradient of the current model based on the same dataset and to obtain the weak learner based on the gradient training.

Given a training dataset ${\left\{\left(x_i,y_i\right)\right\}}_{i=1}^n$, $x_i$ is a sample and $y_i$ is the label of sample $x_i$. Let $f\left(x\right)$be the prediction model, and GBDT aims to learn an optimal model $f\left(x\right)$. Formally, at each iteration t of the gradient GBDT algorithm, the model $f\left(x\right)$ is updated in the following manner:

$$f^t\left(x\right)=f^{t-1}\left(x\right)+ϵh^t\left(x\right)$$

(1)

In the formula, $f^{t-1}$ is the model built in the previous iteration, $h^t$ is a weak learner selected from the function $H$, and ϵ is the learning rate. Select the weak learner $h^t\in H$. The output fits the loss function according to the orientation of the negative gradient of the current model as follows:

$$g^t\left(x,y\right)={\displaystyle \frac{\partial L\left(y,s\right)}{\partial s}}{|}_{s=F^{t-1}\left(x\right)}$$

(2)

$$h^t={argmin}_{h\in H}{\displaystyle \frac{1}{n}}\sum _{k=1}^n{\left[-g^t\left(x_k,y_k\right)-h\left(x_k\right)\right]}^2$$

(3)

In the formula, $h^t$ represents the newly generated weak learner, $-g^t$ is the negative gradient of the loss function, and $L$ is the loss function where n indicates the number of iterations, and n = 1, 2, …, N.

2.2. Catboost Algorithm

The significant advantage of the Catboost algorithm is that the classification data can be processed during the model training process rather than during the data preprocessing process. Hypothetical dataset $D=\left\{\left(X_i,Y_i\right)i=1,\dots ,n\right\}$, of which $X_i=\left(x_{i,1},\dots ,x_{i,m}\right)$, is a vector containing both numeric and categorical features; m is the number of features; and $Y_i\in R$ is the corresponding label. First, the data are randomly arranged. Then, for each sample, the average of the labels of the samples with the same class value in the permutation is calculated. The set $\sigma ={\sigma }_1,\dots ,{\sigma }_n$ represents a permutation. Then, observations of the permutation $x_{i,k}$ are replaced with $x_{{\sigma }_{\rho },k}$. The calculation formula is as follows:

$${\sigma }_{p,k}={\displaystyle \frac{\sum _j^{p-1}\left[x_{{\sigma }_j,\mathrm{k}}=x_{{\sigma }_i,k}\right]·Y_{{\sigma }_j}+\alpha ·P}{\sum _j^{p-1}\left[x_{{\sigma }_j,k}=x_{{\sigma }_i,k}\right]+\alpha }}$$

(4)

where $\left[x_{{\sigma }_j,\mathrm{k}}=x_{{\sigma }_i,k}\right]=1$ if $x_{{\sigma }_j,k}=x_{{\sigma }_i,k}$, and otherwise, 0. $P$ is the prior value and α is the corresponding weight value. The initial is the average label value of the regression and the prior probability that the label used for classification encounters a positive label. Adding the prior helps reduce the noise of the secondary class. On the one hand, the method uses all the data for training; conversely, it avoids the overfitting problem by performing random permutations.

Like the traditional standard GBDT algorithm, Catboost constructs a new tree structure to approximate the gradient of the current model. However, almost all enhancement algorithms have the problem of overfitting due to the estimation of the offset gradient. In some GBDT-derived algorithms, there are two ways to construct a new tree: one is to select the tree structure after the tree structure is fixed, and the other is to set the values in the leaves. Catboost, to overcome the partial gradient problem in the traditional enhancement algorithm, proposes a new mode of leaf value calculation when the tree structure is selected. Specifically, suppose that $F^i$ represents a built model and $g^i\left(X_k,Y_k\right)$ represents the gradient value of the kth training sample after constructing i trees. To keep the gradient unbiased, for each sample $X_k$, a separate model is mis-trained, which does not need to be updated with the gradient estimate, and each$M_k$ has the same structure. Use $M_k$ to estimate the gradient on $X_k$, then score the resulting tree based on the estimation. The model update process is shown in the following Algorithm 1:

Algorithm 1: Updating the models and calculating model values for gradient estimation

In addition, Catboost uses the forgetting tree as the primary learner of prediction. Each tree uses the same segmentation criteria in this tree structure, which makes the overall structure of the algorithm balanced and not prone to overfitting. This symmetry has a regularization effect on the constraints of the tree structure. More importantly, it allows the Catboost model to have a speedy inference process. In tree prediction, each feature segmentation is independent of the priority order, and multiple samples can be predicted together. To summarize, Catboost has unique advantages for the model learning of multi-type feature datasets.

2.3. Particle Swarm Optimization

The machine learning models usually have default parameters, typically set by the author after some consideration when the model is proposed, to perform well on general problems and datasets. However, these default parameters may not be optimal for a particular situation, dataset, or application scenario. In this paper, the factors that need to be considered in predicting SOC for specific data are complex, and the default parameters may not be the most suitable. Therefore, model tuning is one of the critical steps to optimize the performance of machine learning models.

To improve the performance of the Catboost model, this paper uses particle swarm optimization (PSO) to enhance its performance [14]. Particle swarm optimization algorithm has the characteristics of self-organization, evolution, and strong global search ability. Particle swarm can iterate to find the optimal initial parameters of the Catboost model. The particle swarm optimization algorithm is to find the optimal solution through cooperation and information sharing between individuals in the group, and its implementation process is roughly similar to the process of birds foraging. Assuming that each possible solution is a particle, the optimal solution is obtained by adjusting the position and velocity of the particle according to the mutual information and the fitness value in the D-dimensional space.

Assume that there are n particles in the population, which is expressed as $x=\left(x_1,x_2,\dots ,x_n\right)$; each particle is iteratively searched in the solution space according to the set rules, and two extreme values are generated at the end of each particle; $P_{id}$ is the optimal solution searched by the particle itself; $P_{gd}$ is the current optimal solution of the whole population. Adapt the current position according to these two extreme values. The velocity of the ith particle is assumed to be $v_i=\left(v_{i1},v_{i2},\dots ,v_{in}\right),i=\mathrm{1,2},\dots ,m$. The position is expressed as $x_i=\left(x_{i1},x_{i2},\dots ,x_{in}\right),i=\mathrm{1,2},\dots ,m$, and the updated equation is

$$v_{id}\left(t+1\right)=\omega v_{id}\left(t\right)+c_1{rand}_1\left(t\right)\left[p_{id}-z_{id}\left(t\right)\right]+c_2{rand}_2\left(\mathrm{t}\right)\left[p_{gd}-z_{id}\left(t\right)\right]$$

(5)

$$x_{id}\left(t+1\right)=x_{id}\left(t\right)+v_{id}\left(t+1\right)$$

(6)

where $t$ is the number of population iterations, d is the dimension of population space, ω is the inertia weight,$rand\left(\right)$ is a random number distributed over (0, 1), and $c_1$ and $c_2$ are learning factors. $c_1$ is a cognitive learning factor, representing a coefficient for adjusting to the optimal position, and $c_2$ is a social learning factor, representing a coefficient for the entire population to move to the optimal position.

When the PSO optimization algorithm is used to optimize the Catboost model, the position of each particle in the PSO algorithm represents the optimization parameters required by the Catboost model. Appropriate initial parameters accelerate the Catboost model to obtain the prediction results.

2.4. PSO-Catboost Model

For machine learning algorithms, hyperparameter tuning is crucial to the model’s performance, which directly controls the behavior of the training algorithm. Some simple methods for hyperparameter tuning include random search (RS), grid search (GS), and so on. However, these methods have shortcomings, such as a complex search space, more time required for each iteration, and high variance. The PSO algorithm is a population-based meta-heuristic optimization technology that is simple to implement and can quickly search for the optimal solution close to the actual value in a multi-dimensional space. In this study, the PSO method is used to optimize the hyperparameters of the Catboost algorithm. The PSO model parameter setting is conducted as follows: in the method proposed in this paper, the learning factor $c_1=0.9$, $c_2=0.7$, the number of iterations $T_{max}=100$, the population size pop = 20, and the inertia weight ${\omega }_{max}=0.8$, ${\omega }_{min}=0.5$. Randomly initialize a group of particles; the parameters are shown.

The flow of the PSO-Catboost model is shown in the Figure 1. The model-building process is as follows:

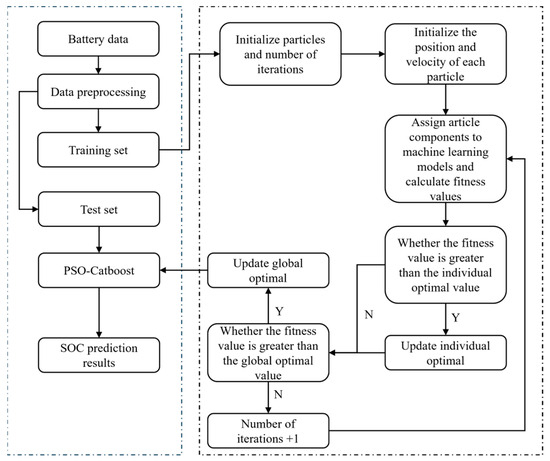
Figure 1. PSO-Catboost Model Flow.

(1)

Data preprocessing and dividing the dataset into training and test sets.

(2)

Each particle component is initialized according to the value range of the parameter range.

(3)

Start the iterative calculation and update each particle’s velocity and position components according to Equations (5) and (6).

(4)

Fit value comparison. Firstly, whether the fitness value is more excellent than the individual optimum is judged, and if the fitness value is more excellent than the individual optimum, the model is updated; otherwise, the individual optimum remains unchanged. Secondly, whether the fitness value is more excellent than the global optimum is judged and the model is updated if the fitness value is greater than the global optimum; otherwise, the global variable remains unchanged.

(5)

Determining whether to terminate the iteration according to the iteration termination condition and performing the following operation if the iteration is terminated; otherwise, continue to iterate.

(6)

Finally, output the predicted SOC result.

3. Dataset

In the vehicle driving condition data acquisition experiment, we used the mine explosion-proof vehicle as a platform for dynamic data acquisition. The experimental vehicle is shown in Figure 2. The test vehicle is equipped with 176 single 60 Ah lithium iron phosphate batteries. The specifications of the battery pack are shown in Table 1.

Figure 2. Vehicle Test Platform.

Table 1. Battery Pack Specifications.

Project	Content
Model	3.2 V 60 Ah
Battery type	Lithium iron phosphate battery
Rated capacity	60 Ah
Rated voltage	562.3 V
Charge and discharge cut-off voltage	492.8 V~633.6 V
Operating temperature	Charge: 0–65 °C/Discharge: −20–65 °C

To evaluate the battery pack’s performance under actual use, we conducted a 1-month experiment, including charge–discharge and rest periods. Driving a vehicle on a closed road includes all phases of realistic driving: starting, stopping, accelerating, decelerating, constant speed, etc., with five different driving periods. The temperature of the experimental environment is about 10 °C. The experimental process is as follows:

(1)

Fully charge the battery. The criterion of full charge is that when a single battery in the battery pack reaches the limited voltage value (3.5 V), the system sends an instruction to stop charging.

(2)

Drive the vehicle to a designated closed road for a driving test at a speed not exceeding 25 km/H. The test road is a circular route with a slight slope.

(3)

In the driving process, the SOC is reduced by 10%, the vehicle is stopped for 0.5 h, and the voltage of the single battery is sampled and measured.

(4)

When the SOC value drops below 30%, stop the test and return to charging.

The test data are stored in an Excel format, and the battery voltage (Figure 3a), current (Figure 3b), and temperature (Figure 3c) during charging and discharging are extracted as characteristic data to predict the battery pack’s SOC. The reference SOC value is calculated using the ampere-hour integration method, and the calculation formula is as follows:

$$\mathrm{S}\mathrm{O}\mathrm{C}={\mathrm{S}\mathrm{O}\mathrm{C}}_0-{\displaystyle \frac{1}{\mathrm{C}}}{\int }_0^{\mathrm{T}}\mathrm{I}\mathrm{d}\mathrm{t}$$

(7)

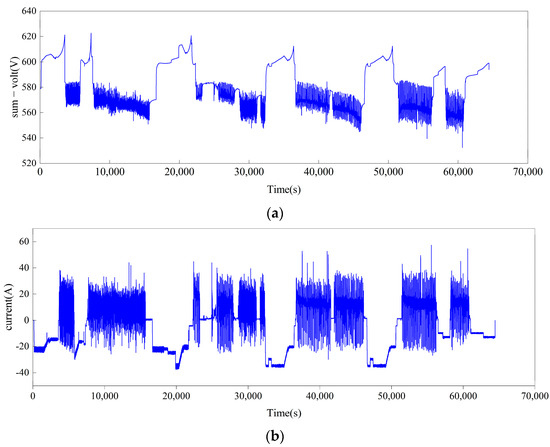
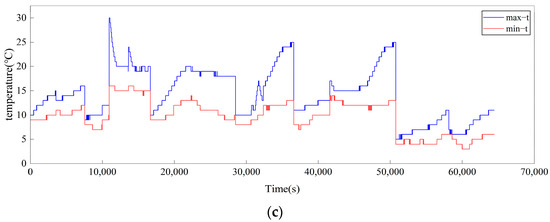
Figure 3. Battery data curve (a) voltage, (b) current, and (c) temperature.

The formula ${\mathrm{S}\mathrm{O}\mathrm{C}}_0$ is the battery’s initial SOC value, T is the discharge time, I is the discharge current, and C is the battery capacity.

After the data are acquired, the data are normalized, and normalizing the input data before the training process is the key to obtaining good results. In a feature, there is usually a significant difference between the maximum and the minimum. For example, at 0.01 and 1000, the magnitude of the value is scaled to a relatively small value when normalization is performed. Assume that for some feature x, x′ is the normalized value, then the min–max normalization is calculated as shown in Equation (8), where$min\left(x\right)$ is the minimum value of $x$ and $max\left(x\right)$ is the maximum value:

$$x^{\prime }={\displaystyle \frac{x-\mathit{min}\left(x\right)}{\mathit{max}\left(x\right)-\mathit{min}\left(x\right)}}$$

(8)

4. Accuracy Standard

The Relative Absolute Error (MAE), Root Mean Square Error (RMSE), and linear regression coefficient of determination (R²) are used to evaluate the estimation effect of different models on a power battery’s SOC. The three indicators confirm the accuracy of various models and assess the deviation between the SOC value of the power battery predicted using different models and the actual value from other dimensions.

4.1. Mean Absolute Error—MAE

The mean absolute error of the model is the average of the absolute value of each prediction error over all instances of the test dataset. The prediction error is the difference between that instance’s actual and predicted values. The $MAE$ formula is as follows:

$$MAE={\displaystyle \frac{1}{N}}\sum _{i=1}^n\left|{\widehat{Y}}_i-Y_i\right|$$

(9)

4.2. Root Mean Square Error—RMSE

The Root Mean Square Error (RMSE) quantifies the average disparity between the predicted and actual values of the statistical model. It evaluates the magnitude of error in the regression or other statistical models. A value of 0 signifies an exact match between the predicted and actual values, though this scenario is seldom observed in practical applications. A low $RMSE$ value signifies a well-fitted model with more accurate predictions. Conversely, a higher value indicates a more significant error and reduced prediction accuracy.

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^n{\left({\widehat{Y}}_i-Y_i\right)}^2}$$

(10)

4.3. Coefficient of Determination of Linear Regression—R²

The Coefficient of Determination for Linear Regression, commonly used as R², is an indicator used to assess the degree of fit of a linear regression model R². The value range is between 0 and 1. The closer to 1, the better the model fits, and the closer to 0, the worse the model fits. R²’s calculation formula is as follows

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{\left(Y_i-{\widehat{Y}}_i\right)}^2}{{\sum }_{i=1}^n{\left(Y_i-{\overline{Y}}_i\right)}^2}}$$

(11)

In the above formula, $n$ represents the number of values in the dataset. $Y_i$ represents a true value, ${\widehat{Y}}_i$ represents a predicted value, and ${\overline{Y}}_i$ represents the average of the true values.

5. Results and Analysis

5.1. Comparison with the Catboost Model

The PSO-Catboost algorithm is an optimization algorithm that uses the particle swarm algorithm to search for the optimal parameters. Randomly initialize a group of particles; the parameters are shown to verify its feasibility. The Catboost algorithm selects general parameters for comparison. Table 2 shows the default parameters of the Catboost algorithm and the range of PSO optimization search parameters.

Table 2. Hyperparameter configuration before and after Catboost optimization.

Hyperparameter	Description	Catboost	PSO-Catboost
iterations	The number of trees	500	(50, 1000)
learning_rate	Learning rate	0.1	(0.01, 0.5)
depth	Maximum depth of the tree	10	(1, 16)
l2_leaf_reg	The weight of the L2 regularization term	5	(1, 10)

Figure 4 compares prediction results and errors between the Catboost algorithm and PSO-Catboost. Figure 4a,c show that the model captures the degradation trajectory of battery power before and after optimization. Figure 4b,d show that the prediction error before and after optimization fluctuates around 0, and the error is less than 5%.

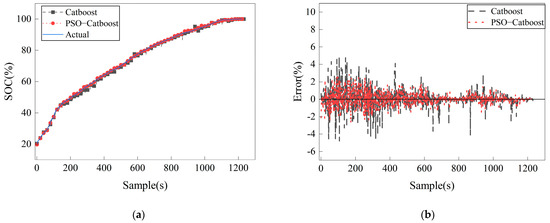
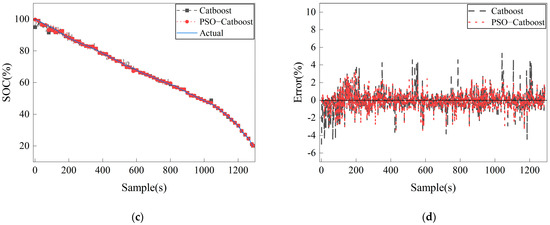
Figure 4. Comparison of charge–discharge prediction and error before and after optimization of the Catboost algorithm. (a) Charge SOC prediction. (b) Charge SOC prediction error. (c) Discharge SOC prediction. (d) Discharge SOC prediction error.

Table 3 compares the prediction accuracy between the PSO-Catboost and Catboost algorithms. The MAE and RMSE values predicted with Catboost are 0.3451 and 0.5602 in the charging process and 0.4712 and 0.7430 in the discharging process. The MAE and RMSE values of PSO-Catboost are 0.3023, 0.4452, and 0.6524, respectively. After optimization, the values of MAE and RMSE are reduced by 12.4% and 25.4%, and 5.5% and 12.2%, respectively, and the R² of the optimized algorithm is improved. PSO-Catboost performs slightly better than the ordinary Catboost algorithm in charging and discharging processes. This indicates that the particle swarm optimization algorithm may optimize the model parameters more effectively for this particular task, thereby improving the prediction performance.

Table 3. Comparison of charge and discharge prediction performance before and after Catboost optimization.

	Algorithm	MAE	RMSE	R2
Charge	Catboost	0.3451	0.5602	0.9980
	PSO-Catboost	0.3023	0.4179	0.9985
Discharge	Catboost	0.4712	0.7430	0.9941
	PSO-Catboost	0.4452	0.6524	0.9956

5.2. Comparison with Other Models

To further verify the superior performance of the PSO-Catboost algorithm model in predicting battery SOC, based on the existing data, two different methods, PSO-Random Forest and PSO-XGBoost, are compared with PSO-Catboost. Catboost, RF, and XGBoost are integrated algorithms, and XGBoost and Catboost are derivative models of GBDT architecture. RF and Catboost are ensemble algorithms with decision trees as weak learners, but their structures differ. The optimization range of PSO-Catboost is shown in Table 2, and the parameter ranges of PSO-XGBoost and PSO-RF are shown in the following Table 4.

Table 4. Hyperparameter range of XGBoost and RF algorithms optimized with PSO.

Algorithm	Hyperparameters	Description	Range
PSO-XGBoost	learning_rate	Learning rate	(0.01, 0.3)
	n_estimators	The number of trees	(10, 1000)
	max_depth	Maximum depth of the tree	(1, 100)
	colsample_bytree	Proportion of features used when training each tree	(0, 1)
	min_child_weight	Minimum sum of weights among child nodes	(1, 6)
	subsample	Proportion of samples used when training each tree	(0.5, 1)
	gamma	Controls the growth of the tree. Higher values are more conservative	(0, 1)
PSO-RF	max_features	Maximum number of features considered when each node is split	(0.1, 1)
	n_estimators	The number of trees	(10, 1000)
	max_depth	Maximum depth of the tree	(1, 100)
	min_samples_split	Minimum number of samples required for point splitting	(2, 20)
	min_samples_leaf	Minimum number of samples required for leaf nodes	(1, 20)

Figure 5 compares the three optimized models’ SOC prediction results and errors. It can be seen from Figure 5a,c that the prediction sequence of all models is above the test sample sequence, indicating that the three optimization models have a good fit with the observed values. In Figure 5b,d, the prediction errors of the three optimization models all fluctuate around the 0 value, and the fluctuation range is between (−5% and 5%). Compared with other methods, the PSO-Catboost model proposed in this paper is closer to the actual value, and the error fluctuation is more minor.

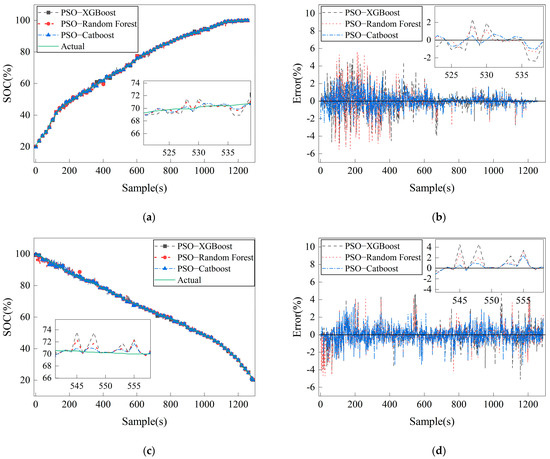
Figure 5. Comparison of SOC prediction of different models optimized with PSO. (a) Charge SOC prediction. (b) Charge SOC prediction error. (c) Discharge SOC prediction. (d) Discharge SOC prediction error.

Table 5 compares the three algorithms’ performance after particle swarm optimization. It can be seen from Table 5 that the SOC prediction method proposed in this paper performs better and has higher prediction accuracy. During charging and discharging, the MAE values of the PSO-Catboost model are 0.3023 and 0.4452, and the RMSE values are 0.4179 and 0.6524, significantly lower than those of the other two models. Overall, the PSO-CatBoost algorithm performs well in both processes, with a lower prediction error and a higher degree of fit, followed by PSO-RF, while PSO-XGBoost is relatively poor.

Table 5. Comparison of charge and discharge prediction performance of different models optimized via PSO.

	Algorithm	MAE	RMSE	R2
Charge	PSO-Catboost	0.3023	0.4179	0.9985
	PSO-RF	0.3263	0.5035	0.9966
	PSO-XGBoost	0.4488	0.6542	0.9934
Discharge	PSO-Catboost	0.4452	0.6524	0.9956
	PSO-RF	0.4928	0.7848	0.9899
	PSO-XGBoost	0.4970	0.7582	0.9923

6. Conclusions

Improving the prediction accuracy of mine power battery SOC is essential in battery applications. The Catboost model can be effectively applied to multi-feature classification problems, and the particle swarm algorithm can obtain the approximate optimal solution faster. This study proposes a particle swarm optimization algorithm to optimize the Catboost model, which is used to complete the SOC prediction of mine power lithium batteries. Through experiments and comparisons, the following conclusions are drawn:

(1)

The cat boost model optimized via PSO can obtain a prediction value close to the actual value, and the SOC prediction accuracy and robustness of the optimized model are better than those of the unoptimized single model.

(2)

PSO optimized the Catboost, RF, and XGBoost models to predict the SOC values of the battery charge and discharge process, and the performance of different integrated models was compared horizontally. Through the experiment and comparison, the PSO-Catboost model performed better and better matched the actual value. The comparison results of the R² values are PSO-CatBoost > PSO-XGBoost > PSO-RF.

(3)

The experimental results show that the optimization model can select the parameters more intelligently, reduce the error caused by artificial experience when adjusting the parameters, and have better theoretical value and practical significance.