Emergency Capability Evaluation of Port-Adjacent Oil Storage and Transportation Bases: An Improved Analytic Hierarchy Process Approach

Abstract

The large-scale storage and stable supply of oil products are essential for national energy security and economic development. As the economy expands and energy demands rise, centralized storage and supply systems become increasingly vital for ensuring the efficiency and reliability of oil product distribution. However, large oil storage depots present substantial safety risks. In the event of fires, explosions, or other accidents, emergency response efforts face stringent demands and challenges. To enhance the emergency response capabilities of oil storage and transportation bases (OSTBs), this paper proposes an innovative approach that integrates the improved analytic hierarchy process (IAHP) with the Entropy Weight Method (EMW) to determine the combined weights of various indices. This approach reduces the subjective bias associated with the traditional analytic hierarchy process (AHP). The emergency response capabilities of OSTBs are subsequently evaluated through fuzzy comprehensive analysis. An empirical study conducted on an OSTB in the Zhoushan archipelago quantitatively assesses its emergency preparedness. The results show that the base excels in pre-incident prevention, demonstrates robust preparedness and response capabilities, and exhibits moderate recovery abilities after incidents. These findings provide a theoretical foundation for reducing the likelihood of accidents, enhancing emergency response efficiency, and mitigating the severity of consequences. Practical recommendations are also offered based on the results.

1. Introduction

Amidst the rapid social and economic development, China’s demand for energy is increasing, making sufficient energy supply a critical condition for national economic progress [1,2]. As a major form of fossil energy, oil is also crucial to industrial development and energy security [3]. In 2000, China began deliberating the construction of strategic oil reserves, with their operation officially commencing in 2007 [4]. By 2021, oil consumption accounted for 18.9% of the national energy consumption. Petroleum derivatives have become integral across various sectors, providing essential support and driving development in multiple fields [5]. The stable supply of oil is related to national energy security, stable economic development, and even national security [6]. As China’s economic entities have expanded and intensified their development processes, the structure of petrochemical enterprises has been optimized and adjusted [7]. The 14th Five-Year Plan has steered petrochemical projects into designated industrial parks, promoting high-level agglomerated development and encouraging the optimization and reorganization of these enterprises [8]. This strategic direction has resulted in the formation of centralized and integrated development models within the petrochemical industry. Consequently, expanding oil depot reserves has become a key focus, with various sizes of oil storage and transportation bases (OSTBs) being established nationwide to manage the supply, storage, and transfer of oil [9]. However, hazards during the transportation processes at these bases can easily lead to compound disasters that are difficult to predict and control, thereby expanding the scope of disasters and increasing associated risks [10]. This poses significant challenges to the safe and sustainable development of China’s oil storage and transportation infrastructure.

Recent incidents underscore the inherent risks associated with oil storage and transportation [11]. For example, on 15 October 2017, an explosion occurred on an oil drilling platform in Louisiana, USA. Similarly, on 29 May 2021, a flash explosion took place in the pipeline area of the cracking furnace in the No. 2 ethylene old area of Shanghai Petrochemical Company. These incidents highlight the critical need for robust safety measures and risk management strategies to ensure the secure operation of OSTBs.

Accident case data collection is very important for accident prevention and research. Cui et al. [12] analyzed 136 domino effect accidents of atmospheric storage tanks and used the event tree analysis method to achieve relative probability. Based on the accident probability, an analysis model was proposed to analyze the event chain and determine the network structure. Based on the Bayesian network, Sun et al. [13] used a random forest algorithm to learn the structure of 1610 traffic collision accidents involving dangerous materials from 2013 to 2017 and completed the construction of the Bayesian network structure. Based on expert experience and accident investigation, Li et al. [14] constructed a fault tree to clarify the causal relationship and realized the probability analysis of aluminum production explosion accidents by transforming the fault tree into a Bayesian network. Gong and Sun [15] constructed a national oil security assessment index system based on five main factors (resource, political, economic, transportation, and military factors) that affect oil security and selected 16 indicators. Ang and Choong [16] used the Delphi method to construct the oil security index system, but the system is only limited to the comprehensive evaluation method. They analyzed the shortcomings of China’s oil security evaluation index system through a review and put forward corresponding suggestions.

There are many complex factors affecting the safety of oil storage and transportation [10]. The existing safety evaluation index system has strong subjectivity and lacks systematic problems. In view of the risk of OSTBs being affected by many factors, this paper uses a fuzzy comprehensive analysis method and analytic hierarchy process, improved analytic hierarchy process, and Entropy Weight Method (EWM) to evaluate their emergency capability [17]. Firstly, the index system of emergency capability is established [18]. Secondly, based on the above methods, an emergency capability evaluation model is constructed. Finally, through the above-listed methods for practice and case analysis, according to the final membership degree and combination weight analysis, we point out the shortcomings of the OSTBs and put forward suggestions for improvement [19].

2. Emergency Capability Index

2.1. Principles of Index System Construction

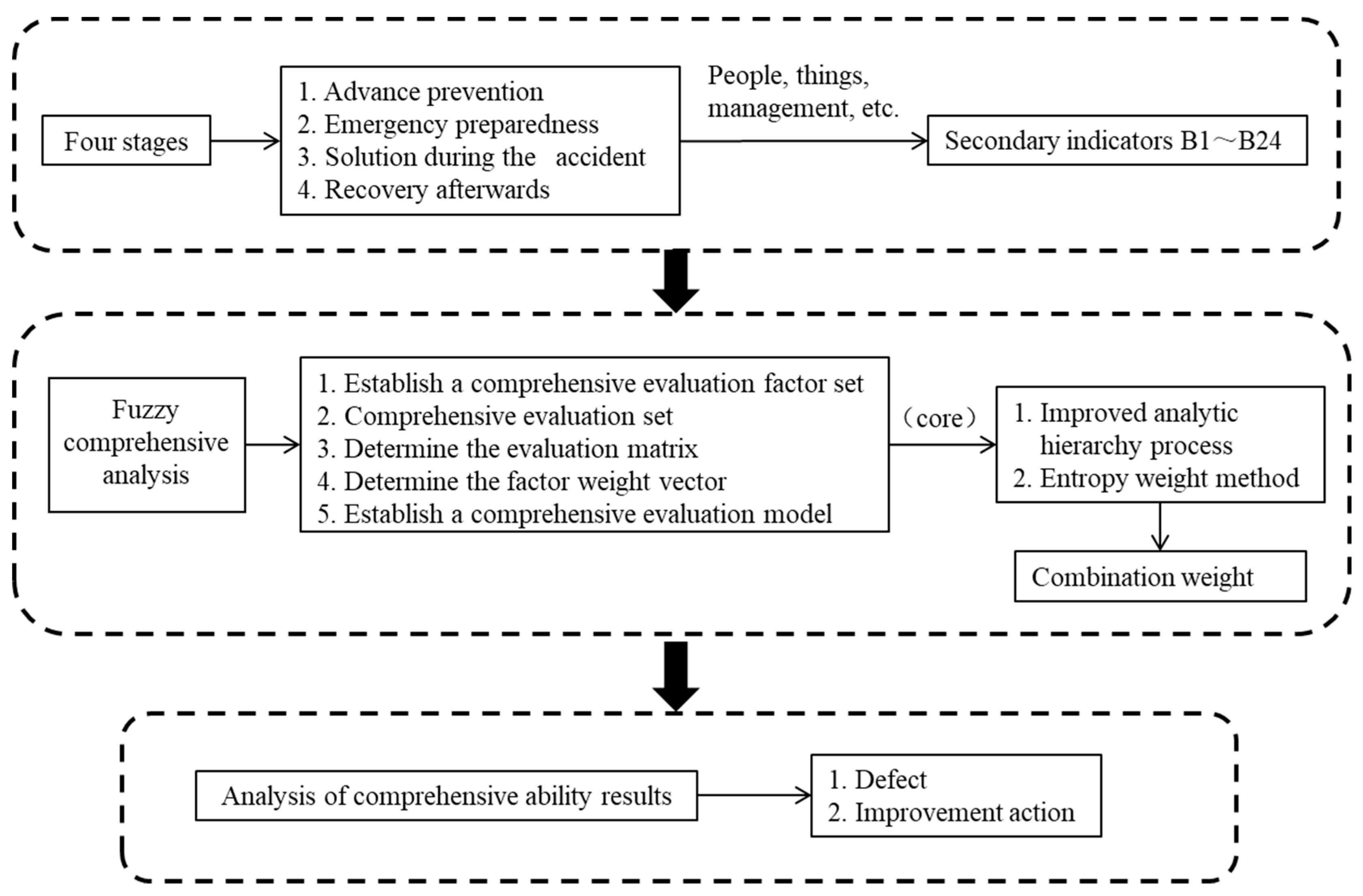
The evaluation of the emergency management capability of OSTBs is affected by many factors and levels, so the evaluation system is a complex dynamic system [20]. Among them, three principles are followed: a completeness principle, quantitative and qualitative combination, and system optimization. This paper evaluates the emergency capability of an OSTB through a structured analysis process comprising three key stages: the delineation of emergency capability indices, the calculation of combined weights via the fuzzy comprehensive analysis method, and the final assessment of comprehensive capability outcomes [21]. The detailed process is depicted in Figure 1.

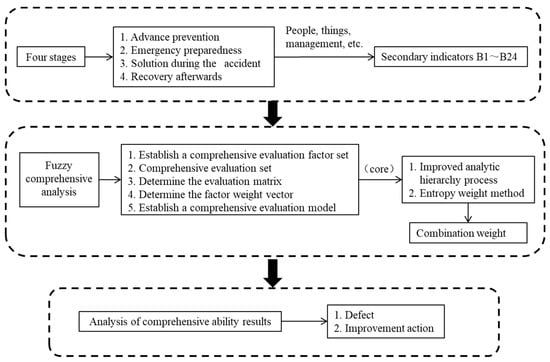
Figure 1. Emergency capability analysis flowchart.

2.2. Construction of Emergency Capability Index System

The emergency management system is an open complex giant system [22]. Based on the types and quantities of hazard sources, the emergency capability evaluation of OSTBs is the evaluation of the whole complex system, including the self-management of each module in the base and the comprehensive emergency management of the base, which needs to consider the integrity of the base [23]. For an enterprise or unit containing dangerous chemicals, any problem in any link may lead to a chain reaction, thus giving the possibility of further expansion of the accident. Therefore, the selection of the OSTBs of the emergency capacity evaluation system focused on the actual situation of the base of emergency management [24].

Based on the selection principle of the emergency response capability index described above, this paper, on the basis of a large number of relevant studies, combined with the ‘Guidelines for the Investigation and Treatment of Safety Risks in Hazardous Chemical Enterprises’, ‘Guidelines for Safety Risk Assessment of Oil and Gas Storage Enterprises (Trial)’, and ‘Guidelines for Emergency Preparedness for Production Safety Accidents in Hazardous Chemical Enterprises’ promulgated by the emergency management department, from the perspective of time, is divided into the four stages of pre-prevention, emergency preparedness, in-process disposal, and post-recovery, and then each stage is analyzed [25]. Considering the people, objects, and management in the OSTBs, the emergency indicators of each stage are preliminarily determined. Through the analysis of the overlap between the indicators and the expert interviews, the evaluation system of the emergency response capacity of the oil reserve base is finally determined [26]. The detailed content of the system is shown in Table 1.

Table 1. Evaluation index system of emergency capacity of OSTBs.

First-Grade Indices	Second Index
Advance prevention A1	Monitoring and early warning capabilities B1
	Hidden danger management situation B2
	Safety education situation B3
	Enterprise risk source identification ability B4
	Emergency training situation B5
	Emergency drills B6
	Safety inspections B7
Emergency preparedness A2	Emergency organization situation B8
	Emergency material situation B9
	Capital investment situation B10
	Emergency plan situation B11
	Emergency shelter situation B12
	The formulation of emergency laws and regulations B13
Solution during the accident A3	Emergency team capacity B14
	Command coordination ability B15
	Communication and information support capabilities B16
	Situation assessment ability B17
Solution during the accident A3	Emergency evacuation capacity B18
	Fault treating ability B19
	Medical rescue capability B20
	Public opinion response ability B21
Recovery afterwards A4	Aftercare ability B22
	Summary evaluation ability B23
	Management improvement ability B24

After determining the emergency capability evaluation system of the OSTBs, the appropriate model is selected to comprehensively evaluate the emergency capability of the base.

3. Construction of Emergency Capability Evaluation Model

At present, the common evaluation models are the chromatographic analysis, weighted Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), principal component analysis, gray correlation analysis, and Fuzzy Comprehensive Evaluation Method (FCEM) [27].

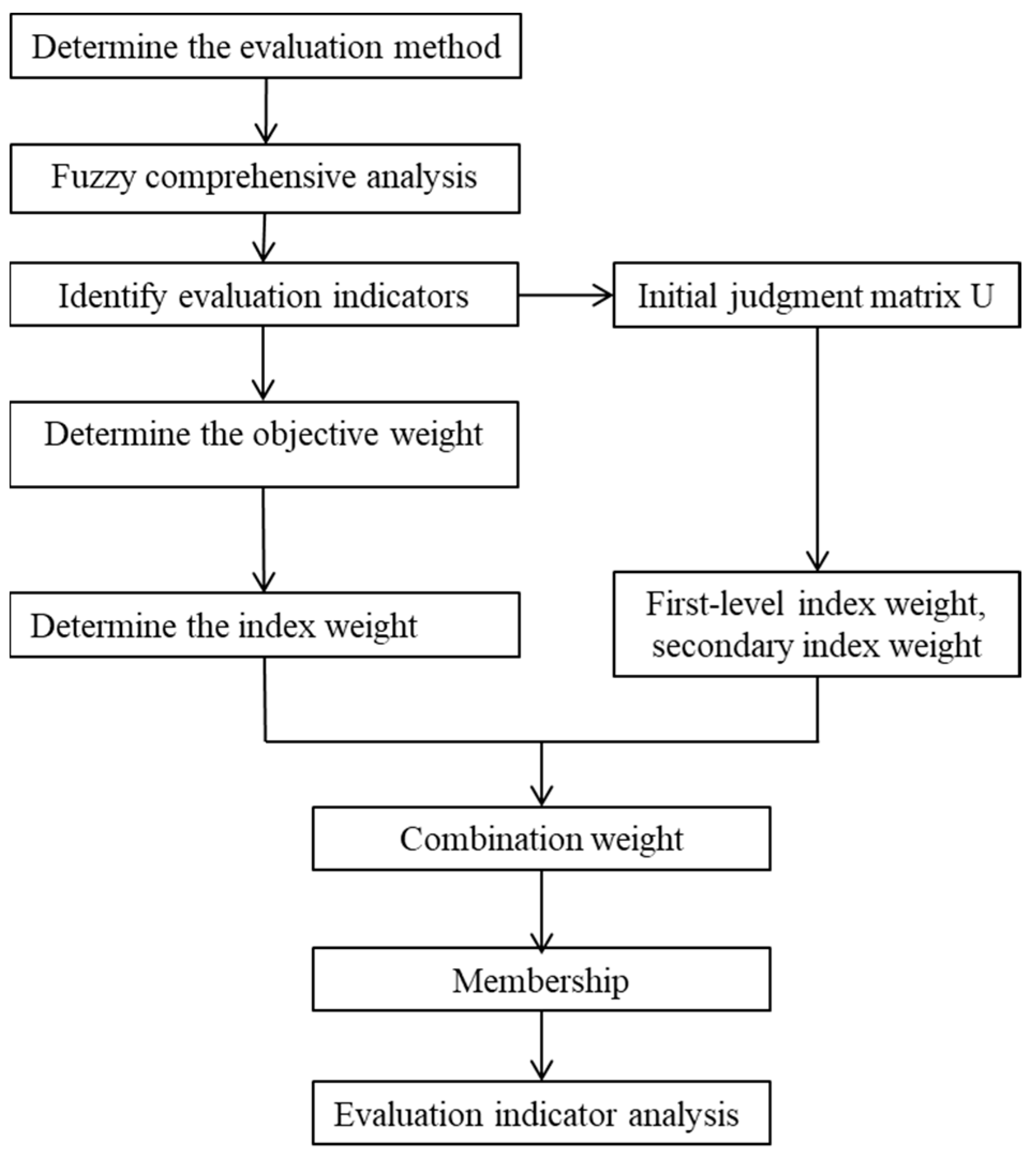
In the evaluation index of OSTBs, there is no way to perform an evaluation with actual data in the evaluation process, such as whether the emergency organization is perfect and whether the evaluation ability is complete [24]. At present, most of them rely on expert experience to judge, so there is a certain ambiguity in the evaluation [28]. In this paper, the fuzzy comprehensive analysis method is used to evaluate the emergency response capability of the base. The specific analysis steps are shown in Figure 2.

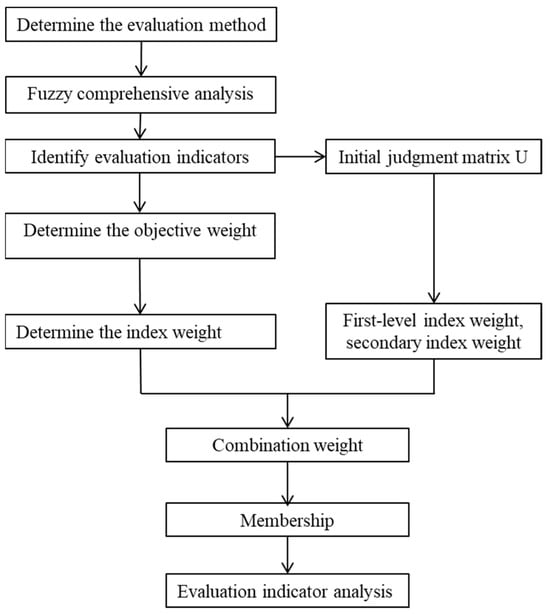
Figure 2. Frame diagram of emergency capability evaluation model.

3.1. FCEM

FCEM, a comprehensive analysis method based on fuzzy theory, was proposed by American automatic control scholar Lotfi Zadeh in 1965 and has been widely applied to various research fields since then [29].

The FCEM is mainly divided into the following steps.

(1) Establish a Comprehensive Evaluation Factor Set

Determine the evaluation index system of the analysis object, that is, the evaluation index related to the evaluation object. There are many factors related to the evaluation object. After selecting the appropriate factors, these factors can form a common set, that is, the comprehensive evaluation factor set. Use A to represent the factor set.

$$A=\left\{A_1,A_2,\cdots A_n\right\}$$

In the formula, A_n(n = 1,2,…n) represents the influencing factors of the accident disaster of the OSTBs, which has certain ambiguity [30].

(2) Comprehensive Evaluation Set

Comprehensively consider the evaluation indicators and finally give a comprehensive evaluation result. The evaluation results are divided into different levels. These many evaluation levels form an evaluation set, that is, a comprehensive evaluation set. C represents the comprehensive evaluation set.

$$C=\left\{c_1,c_2,\cdots c_n\right\}$$

In the formula, C_n(n = 1,2,…n) represents the comprehensive evaluation results made by the decision maker when the influencing factors of the disaster accident of the OSTBs occur. Through the FCEM, the corresponding comprehensive evaluation results of the evaluation object at the present stage can be obtained.

(3) Determine the Evaluation Matrix

Suppose that the nth evaluation index of the evaluation index factor set A is $A_n$, and the membership degree of the nth evaluation index of the evaluation set C is $c_n$, then the comprehensive evaluation result of $A_n$ can be represented by set $Q_n$.

$$D=\left(\begin{array}{c}{D}_1\\ D_2\\ ⋮\\ D_n\end{array}\right)=\left(\begin{array}{cccc}{d}_{11}& d_{12}& \cdots & d_{1n}\\ d_{21}& d_{22}& \cdots & d_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ d_{n1}& d_{n2}& \cdots & d_{nn}\end{array}\right)$$

(1)

(4) Determine the Factor Weight Vector

The weight represents the degree of influence of each evaluation index on the evaluation object, which is expressed as ${\omega }_i$, where i = 1,2,..., n, and the weight satisfies the normalization principle, that is, ${\displaystyle \sum {\omega }_i}=1$, the weight of each evaluation index constitutes the weight vector W.

$$W=\{{\omega }_1,{\omega }_2,\cdots ,{\omega }_n\}$$

The greater the weight value, the greater the impact of this factor on the comprehensive evaluation of the evaluation object. The smaller the weight value, the smaller the impact of this factor on the comprehensive evaluation of the evaluation object.

(5) Establish a Comprehensive Evaluation Model

$$R_i=W_i\times D_i$$

(2)

In the formula, $R_i$ represents the result of the i-th comprehensive evaluation. After the step-by-step operation, $R_i=W_i\times D_i=\left\{r_1,r_2,\cdots ,r_i\right\}$ is obtained.

Finally, based on the principle of maximum membership degree, select the corresponding evaluation level $\underset{1\le i\le n}{\max }\left\{r_i\right\}$ as the comprehensive evaluation result of the evaluation object. The maximum membership principle is one of the basic principles of fuzzy mathematics [31]. It is a direct method for model identification using fuzzy set theory. For n actual models, it can be expressed as n fuzzy subsets A₁, A₂,..., A_n, x₀ ∈ X on the domain X. If there is i₀ ≤ n, A_i0 (x₀) = max (A₁(x₀), A₂(x₀),..., A_n(x₀)), then x₀ is considered relative to A_i0, which is the maximum membership principle.

3.2. Index Weight

As the core step of the FCEM, the appropriate weight is the core of the FCEM [32]. The following is a brief introduction to some index weighting methods, as shown in Table 2.

Table 2. Partial weight analysis model.

Comprehensive Evaluation Model	Principle	Merit	Defect
AHP	The evaluation object system is hierarchical. The importance of influencing factors was analyzed by pairwise comparison.	Systematic: the object as the whole system, according to the comprehensive logic of hierarchical analysis Practicality: the combination of quantitative and qualitative can effectively solve the problem Simplicity: simple calculation, clear results	Only the existing schemes can be analyzed, and new schemes cannot be provided. The reliability of qualitative data is not high, and the quantitative cost is too small.
EWM	Using calculation, the dispersion degree of the influencing factors of the evaluation object is evaluated, and based on this, the importance degree is evaluated.	Adaptability: high degree of harmony, can be combined well with other methods Objectivity: compared with the subjective weighting method, the accuracy is higher	There is a lack of horizontal comparison between the indicators. Largely dependent on the sample.
Principal Component Analysis	The variables are simplified by the method of variable transformation, and the comprehensive score is obtained. The weight is determined according to the proportion of each factor in the comprehensive score.	The factors of complex systems can be simplified To a certain extent, it reduces the influence of subjective factors on the evaluation results	Has a certain sample limit. There are certain limitations. When the factor load is positive or negative, the evaluation significance is low.
G1 Method	The weight is determined by experts to evaluate and compare the importance of each factor in the system.	The amount of calculation is relatively small The applicability and operability are strong, and there is no need to construct a judgment matrix and conduct a consistency test	The subjectivity is too strong.

In the process of weight determination, considering the subjective and objective factors, this paper selects the combined weight analysis method combining the improved analytic hierarchy process and the EWM to determine the importance of the evaluation index related to the disaster emergency response capacity of the OSTBs.

3.2.1. AHP

AHP, a method for determining the importance of the index factors of the analysis object, was proposed by the famous American operational research scholar Satie in the 1970s [33]. The main steps of AHP are as follows:

(1) Establishment of Hierarchical Structure

The evaluation index system of the disaster emergency capability of OSTBs mainly includes four aspects: pre-prevention, emergency preparation, in-process disposal, and post-recovery. The hierarchical structure of the evaluation index system of base disaster emergency capability is shown in Table 1.

(2) Construct a Pairwise Comparison Matrix

As an example, the ‘1–5’ scale method is used to compare and assign the importance of the indicator elements bi and bj at the same level. Similarly, the importance of the same layer of elements relative to the previous layer of elements is obtained. Finally, from the initial judgment matrix $P={\left(p_{ij}\right)}_{n\times n}$, $p_{ij}$ is obtained, which represents the proportional scale of the importance of the elements bi and bj relative to the previous level elements. The proportional scale is shown in Table 3.

Table 3. The ‘1–5’ scale method.

Scale	Definition
1	Both are of the same importance
3	One of them is obviously important
5	One is of strong importance
2, 4	Above median value

(3) Determine the Index Weight

For the constructed judgment matrix P, the product M_i of each row element is calculated, and then the n-th root of m_i(i = 1, 2, n) is obtained. Finally, the m_i is normalized, the feature vector ${\beta }_i^{\text{'}}$(i = 1, 2, n) is solved by the root method, and the feature vector set ${\beta }^{\text{'}}=\left({\beta }_1^{\text{'}},{\beta }_2^{\text{'}},\cdots ,{\beta }_n^{\text{'}}\right)$ of the judgment matrix P can be obtained. The specific calculation formula is as follows:

$$M_i={\displaystyle \prod _{j=1}^n{P}_{ij}}$$

(3)

$$m_i=\sqrt[n]{M_i}$$

(4)

$${\beta }_i^{\text{'}}={\displaystyle \frac{m_i}{{\displaystyle \sum _i^n{m}_i}}}$$

(5)

(4) Consistency Check

In general, when CR < 0.1, it means that the evaluation matrix conforms to the consistency test. The test formula is shown in Formulas (6) and (7):

$$CI={\displaystyle \frac{{\lambda }_{\max }-n}{n-1}}$$

(6)

$$CR={\displaystyle \frac{CI}{RI}}$$

(7)

The parameters of the judgment matrix in the formula: n, order; λ_max, maximum feature vector; CI, general consistency index; RI, mean random consistency index (the detailed values of RI are shown in Table 4); CR, random consistency ratio.

Table 4. Random consistency RI value.

n	Value of RI	n	Value of RI
1	0	7	1.36
2	0	8	1.41
3	0.58	9	1.45
4	0.89	10	1.49
5	1.12	11	1.52
6	1.26	12	1.54

3.2.2. IAHP

From the above, we know that the analytic hierarchy process is based on the subjective thinking of human beings, and human thinking is quantified by the scale method [34]. However, there are too many grades in the original scale method, and there is no clear boundary between the importance judgment of each factor. When the decision maker makes a multi-level evaluation of the index only through subjective experience, it may increase the error of the result. When there are too many indicators, it may occur that A is more important than B, B is more important than C, but C is more important than A, which leads to the inconsistency of the chromatographic analysis method. In the process of determining the index weight, the index matrix needs to meet the consistency test. If it does not match, it needs to be replaced. The process is relatively complex.

The traditional analytic hierarchy process usually adopts the 1–9 scale method, but it is difficult to operate in the actual scoring process, and there are many affected factors, which may make the judgment matrix not accurate enough, thus affecting the final weight calculation. The improved analytic hierarchy process uses a simpler and clearer scoring method, that is, direct comparison between the two [35]. There are three values in the improved analytic hierarchy process: 0, 1, and 2. Taking A and B as examples, three values indicate the importance of A and B. Among them, 0 means B is important, 1 means equally important, and 2 means A is important. The improved analytic hierarchy process is used to obtain the initial judgment matrix, and the method of calculating the relative importance is as follows.

$$r_{ij}={\displaystyle \sum _{j=1}^n{a}_{ij}}$$

(8)

In the formula, i and j represent the natural number.

The construction of the initial judgment matrix is shown in Formula (9).

$$\left\{\begin{array}{c}{a}_{ij}=r_i-r_j+1\hspace{1em}{r}_i\ge r_j\\ a_{ij}={(r_j-r_i+1)}^{-1}\hspace{1em}{r}_i\le r_j\end{array}\right.$$

(9)

Then, calculate the weight.

$$w_i={\displaystyle \frac{\overline{w_i}}{{\displaystyle \sum _{i=1}^n\overline{w_i}}}}$$

(10)

The approximate weight is calculated by the above formula, where

$$\overline{w_i}=\sqrt[n]{{\displaystyle \prod _{j=1}^n{a}_{ij}}}$$

(11)

3.2.3. EWM

EWM, an objective assignment method, is a method used to determine the index weight according to the amount of information provided by the survey data of each index [36]. It can truly and effectively reflect the evaluation results. It has been widely used in various research fields. The steps to determine the importance of the index are as follows.

Step 1: Count the number of accidents u_i,j caused by the risk factors of people, things, technology, environment, and management, where j = n = 12 represents the month. For the ith subsystem, the probability of an accident in the jth month is

$$p_{ij}={\displaystyle \frac{u_{ij}}{{\displaystyle \sum _j{u}_{ij}}}}$$

(12)

Step 2: Calculate the weight of the subsystem accident.

(1) Standardization.

$$r_{ij}={\displaystyle \frac{{\left(u_{ij}\right)}_{\max }-u_{ij}}{{\left(u_{ij}\right)}_{\max }-{\left(u_{ij}\right)}_{\min }}}$$

(13)

In the formula, $r_{i,j}$ is the value after standardization; ${\left(u_{i,j}\right)}_{max}$ and ${\left(u_{i,j}\right)}_{min}$ are the initial maximum and minimum values, respectively.

The entropy value e_ij and information utility d_ij of the system are calculated.

$$e_i={\displaystyle \frac{-{\displaystyle \sum _{j=1}^n\left(f_{ij}\times \ln \left(f_{ij}\right)\right)}}{\ln n}}$$

(14)

$$f_{ij}={\displaystyle \frac{r_{ij}}{{\displaystyle \sum _{j=1}^n{r}_{ij}}}}$$

(15)

$$d_{ij}=1-e_{ij}$$

(16)

When f_i,j = 0, let f_i,j × Inf_i,j = 0.

(2) Determine the index weight.

The entropy weight is calculated by using the entropy value of the i-th seed system.

$${\omega }_i^{\text{'}}={\displaystyle \frac{1-e_i}{m-{\displaystyle \sum _{i=1}^m{e}_i}}}$$

(17)

Step 3: Calculate the coupling degree.

$$C_j={\displaystyle \frac{m{\left({\displaystyle \prod p_{ij}}\right)}^{1/m}}{{\displaystyle \sum p_{ij}}}}$$

(18)

Step 4: Calculate the comprehensive coordination index of the accident probability in month j.

$$T_j={\displaystyle \sum _{i=1}^m{p}_{ij}\times {\omega }_i^{\text{'}}}$$

(19)

Step 5: Calculate the coupling coordination degree of the OSTBs system in month j.

$$D_j=\left|\sqrt{C_j\times T_j}\right|$$

(20)

Considering the subjective deviation of the analytic hierarchy process, this paper uses the EWM to properly de-subjectivize the weight and make the weight determination method more accurate. Finally, Formula (20) is used to synthesize the subjective and objective weights to obtain the combined weights.

$$W_i^{\text{'}}={\displaystyle \frac{W_i\times {\omega }_i}{{\displaystyle \sum _{i=1}^n{W}_i\times {\omega }_i}}}$$

(21)

In the formula, $W_i^{\text{'}}$ represents the combined weight of the i-th index; i represents the objective weight value of the i-th index; and W_i represents the subjective weight value of the i-th index.

4. Case Analysis

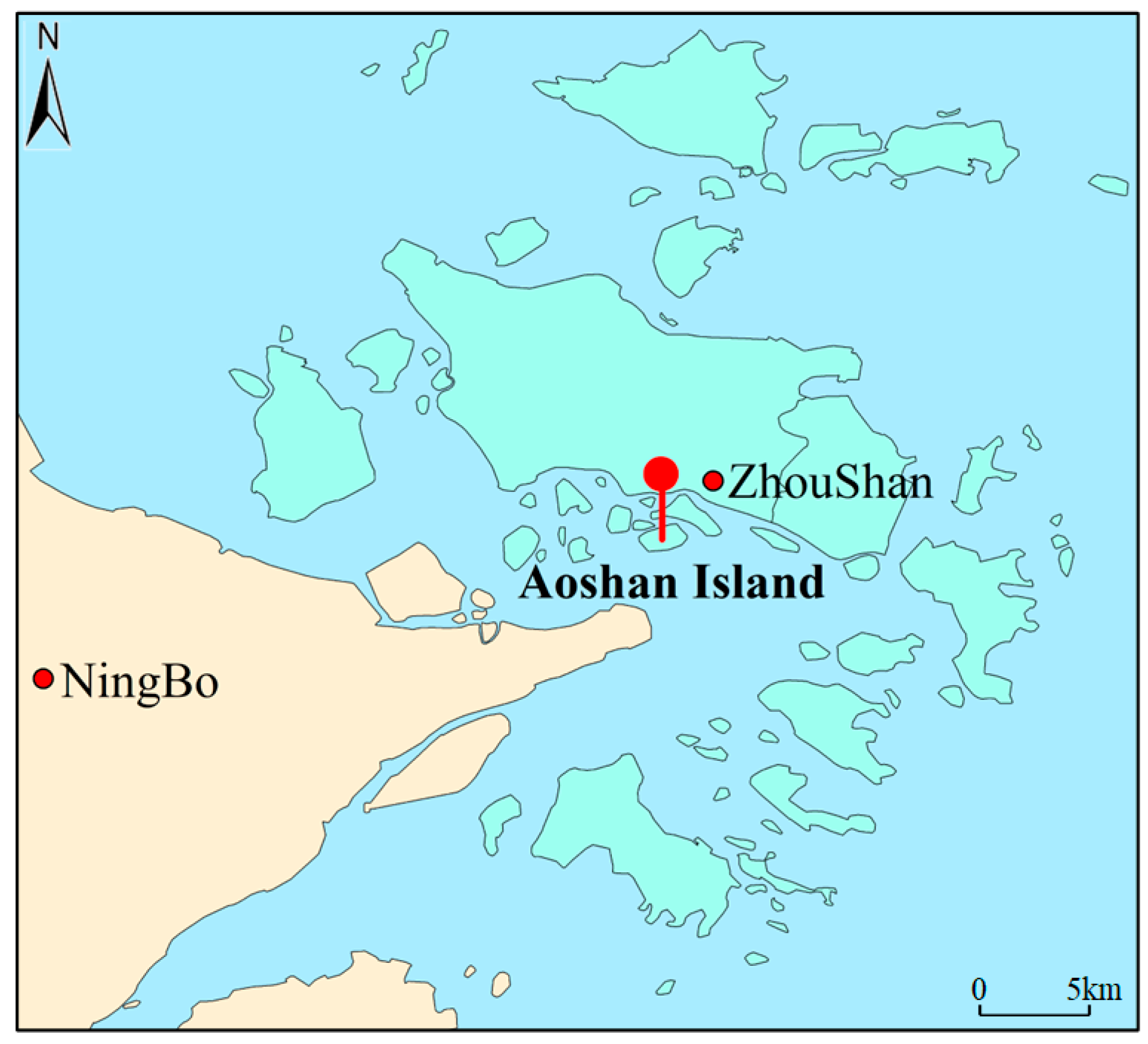
Zhonghua Xingzhong’s Aoshan Oil Storage and Transportation Base, one of the largest in China, is situated in Zhoushan City, Zhejiang Province. The facility boasts a total storage tank capacity of 2.97 million cubic meters, with a bonded tank capacity amounting to 1.895 million cubic meters. Comprising six oil terminals, it caters to capacities ranging from 3000 to 300,000 tons, with a collective design capacity of 42.205 million tons. The precise geographical location of this OSTB is illustrated in Figure 3. This section employs the Sino-chem Aoshan OSTB as a case study to validate the fuzzy comprehensive evaluation model introduced in this paper.

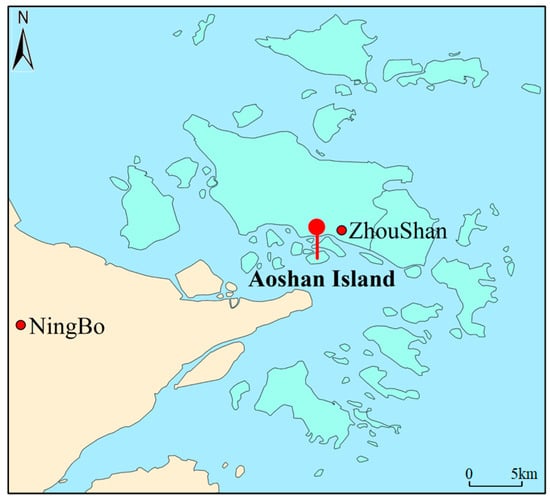
Figure 3. OSTB location.

4.1. Weight Determination of Evaluation Index System

4.1.1. Subjective Weight Determination Based on IAHP

An expert questionnaire on the disaster emergency capabilities of OSTBs was developed, incorporating the evaluation index system tailored specifically for this purpose. A total of ten experts from relevant fields were invited to participate in this endeavor, utilizing the ‘0–2 scaling method’ to assign weights to each level of indicators, with each expert contributing equally to the overall evaluation. Consequently, a pairwise comparison judgment matrix was constructed. As an illustrative example, the scores assigned by these ten experts to the first-level indicators were aggregated by averaging their respective scoring tables, and the consolidated results are presented in Table 5.

Table 5. Expert assessment of emergency response capacity of OSTBs.

	Advance Prevention	Emergency Preparedness	Solution During the Accident	Recovery Afterwards	${\mathit{r}}_{\mathit{i}}$
Advance prevention	1.0	0.0	0.4	1.2	2.6
Emergency preparedness	2.0	1.0	1.2	1.6	5.8
Solution during the accident	1.6	0.8	1.0	1.6	5.0
Recovery afterwards	0.8	0.4	0.4	1.0	2.6

Then, according to the above initial matrix, the improved analytic hierarchy process is used to establish the judgment matrix U.

$$U=\left[\begin{array}{cccc}1.00& 0.24& 0.29& 1.00\\ 4.20& 1.00& 1.80& 4.20\\ 3.40& 0.56& 1.00& 3.40\\ 1.00& 0.24& 0.29& 1.00\end{array}\right]$$

According to Formulas (8)–(10), the weight of the first-level index determined by the scoring table given by the experts is shown in Table 6.

Table 6. Weight of first-level index of disaster emergency capacity of OSTBs.

	Advance Prevention	Emergency Preparedness	Solution During the Accident	Recovery Afterwards
Weight	0.1028	0.4751	0.3193	0.1028

The initial matrix of the secondary index is as follows:

$$\begin{array}{c}{A}_1=\left[\begin{array}{ccccccc}1.00& 1.20& 0.80& 1.40& 0.60& 1.00& 1.20\\ 0.80& 1.00& 0.80& 1.20& 0.80& 0.20& 1.40\\ 1.20& 1.20& 1.00& 0.80& 1.00& 1.20& 0.80\\ 0.60& 0.80& 1.20& 1.00& 0.60& 1.00& 0.60\\ 1.40& 1.20& 1.00& 1.40& 1.00& 1.20& 0.80\\ 1.00& 1.80& 0.80& 1.00& 0.80& 1.00& 0.60\\ 0.80& 0.60& 1.20& 1.40& 1.20& 1.40& 1.00\end{array}\right];\\ A_2=\left[\begin{array}{cccccc}1.00& 1.40& 0.80& 1.20& 1.00& 1.00\\ 0.60& 1.00& 0.60& 0.40& 1.00& 1.00\\ 1.20& 1.40& 1.00& 1.20& 1.60& 0.80\\ 0.80& 1.60& 0.80& 1.00& 1.00& 1.20\\ 1.00& 1.00& 0.40& 1.00& 1.00& 1.20\\ 0.60& 1.00& 1.20& 0.80& 0.80& 1.00\end{array}\right];\\ A_3=\left[\begin{array}{cccccccc}1.00& 1.20& 0.30& 1.10& 1.00& 0.60& 1.00& 1.20\\ 0.60& 1.00& 1.10& 0.90& 0.60& 1.10& 1.10& 0.70\\ 1.70& 0.90& 1.00& 1.10& 1.40& 0.80& 1.20& 0.70\\ 0.90& 1.10& 0.90& 1.00& 0.70& 1.10& 1.20& 0.80\\ 1.00& 1.40& 0.60& 1.30& 1.00& 1.50& 1.10& 0.80\\ 1.40& 0.90& 1.20& 1.00& 0.50& 1.00& 1.00& 1.60\\ 1.00& 0.90& 0.80& 0.80& 0.90& 1.00& 1.00& 1.10\\ 0.80& 1.30& 1.30& 1.20& 1.20& 0.40& 0.90& 1.00\end{array}\right];\\ A_4=\left[\begin{array}{ccc}1.00& 0.90& 1.10\\ 1.10& 1.00& 0.80\\ 0.90& 1.20& 1.00\end{array}\right].\end{array}$$

Using the same methodology, the scoring tables provided by 10 experts were calculated individually, and the final actual weights were derived, as presented in Table 7. The experts primarily consist of experienced frontline engineering and technical personnel from enterprises, as well as researchers from relevant research institutions.

Table 7. Subjective weight of disaster emergency capacity index of OSTBs.

First-Level Indicators	Weight	Second-Level Indicators	Weight	Subjective Weights
Advance prevention A1	0.1028	Monitoring and early warning capabilities B1	0.1485	0.0153
		Hidden danger management situation B2	0.1160	0.0119
		Safety education situation B3	0.1514	0.0156
		Enterprise risk source identification ability B4	0.1192	0.0123
		Emergency training situation B5	0.1676	0.0172
		Emergency drills B6	0.1415	0.0146
		Safety inspections B7	0.1558	0.0160
Emergency preparedness A2	0.4751	Emergency organization situation B8	0.1829	0.0836
		Emergency material situation B9	0.1260	0.0576
		Capital investment situation B10	0.2039	0.0932
		Emergency plan situation B11	0.1802	0.0824
		Emergency shelter situation B12	0.1540	0.0704
		The formulation of emergency laws and regulations B13	0.1530	0.0670
Solution during the accident A3	0.3193	Emergency team capacity B14	0.1113	0.0355
		Command coordination ability B15	0.1120	0.0358
		Communication and information support capabilities B16	0.1378	0.0440
		Situation assessment ability B17	0.1235	0.0394
		emergency evacuation capacity B18	0.1362	0.0435
		fault treating ability B19	0.1333	0.0426
		Medical rescue capability B20	0.1213	0.0387
		Public opinion response ability B21	0.1245	0.0397
Recovery afterwards A4	0.1028	Aftercare ability B22	0.3343	0.0344
		Summary evaluation ability B23	0.3215	0.0330
		Management improvement ability B24	0.3442	0.0354

4.1.2. Objective Weight Determination Based on EWM

Eight experts were invited to score the disaster emergency response capacity of the OSTBs at all levels in the form of a questionnaire survey. The score was based on the percentage system. The higher the score, the greater the impact factor of the factor on the target layer. The expert scoring results are shown in Table 8.

Table 8. Expert scoring table of disaster and accident emergency capability.

Index	Expert Estimation
	1	2	3	4	5	6	7	8
B1	80	92	91	95	90	85	89	93
B2	95	90	85	89	83	84	80	81
B3	84	84	79	81	85	80	84	87
B4	60	70	74	62	68	74	80	67
B5	82	90	86	82	84	80	88	92
B6	76	72	75	74	78	83	70	84
B7	74	69	76	80	65	73	68	69
B8	79	70	68	72	77	86	69	80
B9	79	76	80	70	84	86	83	78
B10	74	82	73	76	70	86	72	87
B11	69	74	70	75	81	71	78	77
B12	75	85	81	82	77	81	84	76
B13	84	77	81	68	76	80	82	86
B14	83	80	80	88	81	86	85	79
B15	73	80	70	79	73	71	82	84
B16	80	76	86	80	82	82	88	90
B17	68	66	59	55	60	65	78	67
B18	80	72	73	71	74	76	79	84
B19	78	83	81	85	82	90	85	75
B20	70	80	74	73	71	66	69	64
B21	68	66	70	72	70	74	77	76
B22	77	78	75	79	84	78	88	81
B23	74	83	77	70	81	76	83	75
B24	75	79	83	81	74	80	72	78

The information entropy of each index is obtained after standardizing the recovered expert questionnaire, as shown in Table 9.

Table 9. Information entropy of disaster emergency capacity index of OSTBs.

Index	Information Entropy	Index	Information Entropy
Monitoring and early warning	0.300798	Emergency laws and regulations formulated	0.974148
Hidden danger treatment	0.876816	Emergency team	0.964251
Safety education	0.982414	Command and coordination	0.978542
Enterprise risk source identification	0.984866	Communication and information assurance	0.905676
Emergency training	0.877007	Assessment of issues	0.991365
Emergency exercise	0.965936	Emergency evacuation	0.986350
Safety inspection	0.979332	Incident management	0.900636
Emergency organization	0.954634	Medical rescue	0.981244
Emergency materials	0.954927	Public opinion response	0.991401
Funding	0.950252	Aftermath handling	0.943035
Emergency plan	0.984520	Summary evaluation	0.978831
Emergency shelter	0.976330	Management improvement	0.975680

The weight of each index is calculated as shown in Table 10.

Table 10. Objective weight of disaster emergency capacity index of OSTBs.

Index	Objective Weights	Index	Objective Weights
Monitoring and early warning	0.4261	Emergency laws and regulations formulated	0.0158
Hidden danger treatment	0.0751	Emergency team	0.0218
Safety education	0.0107	Command and coordination	0.0131
Enterprise risk source identification	0.0092	Communication and information assurance	0.0575
Emergency training	0.0749	Assessment of issues	0.0053
Emergency exercise	0.0208	Emergency evacuation	0.0083
Safety inspection	0.0126	Incident management	0.0606
Emergency organization	0.0276	Medical rescue	0.0114
Emergency materials	0.0275	Public opinion response	0.0052
Funding	0.0303	Aftermath handling	0.0347
Emergency plan	0.0094	Summary evaluation	0.0129
Emergency shelter	0.0144	Management improvement	0.0148

Then, the combination weight and the specific combination weight are calculated as shown in Table 11.

Table 11. Combined weight of emergency capacity index of OSTBs.

Index	Combination Weight	Index	Combination Weight
Monitoring and early warning	0.0156	Emergency laws and regulations formulated	0.0684
Hidden danger treatment	0.0122	Emergency team	0.0363
Safety education	0.0159	Command and coordination	0.0366
Enterprise risk source identification	0.0126	Communication and information assurance	0.0449
Emergency training	0.0176	Assessment of issues	0.0402
Emergency exercise	0.0149	Emergency evacuation	0.0444
Safety inspection	0.0163	Incident management	0.0435
Emergency organization	0.0854	Medical rescue	0.0395
Emergency materials	0.0588	Public opinion response	0.0405
Funding	0.0952	Aftermath handling	0.0351
Emergency plan	0.0842	Summary evaluation	0.0337
Emergency shelter	0.0719	Management improvement	0.0362

4.2. Comprehensive Evaluation of Disaster Emergency Capability of OSTBs

The emergency response capability of OSTBs is quantitatively evaluated. In order to make the quantitative results more intuitive, this paper divides the index system into five grades, as shown in Table 12.

Table 12. Scoring criteria for emergency response capacity of OSTBs.

0–20	20–40	40–60	60–80	80–100
Bad	Average bad	Average	Average good	Good

In this section, 10 experts are invited to evaluate and score the disaster emergency response capacity of the OSTBs. The membership degree of the experts is shown in Table 13.

Table 13. Expert scoring subordination degree of emergency response capability of OSTBs.

First-Level Indicators	Second-Level Indicators	Evaluation Grade
		Bad	Average Bad	Average	Average Good	Good
Advance prevention	Monitoring and early warning	0	0	0	0.2	0.8
	Hidden danger treatment	0	0	0.1	0.2	0.7
	Safety education	0	0	0	0.2	0.8
	Enterprise risk source identification	0	0.1	0.1	0.6	0.2
	Emergency training	0	0	0.2	0.5	0.3
	Emergency exercise	0	0	0.3	0.6	0.1
	Safety inspection	0	0	0.4	0.5	0.1
Emergency preparedness	Emergency organization	0	0	0.5	0.4	0.1
	Emergency materials	0	0	0	0.4	0.6
	Funding	0	0	0.2	0.6	0.2
	Emergency plan	0	0.1	0.5	0.4	0
	Emergency shelter	0	0	0	0.3	0.7
	Emergency laws and regulations formulated	0	0	0.3	0.6	0.1
Solution during the accident	Emergency team	0	0	0	0.4	0.6
	Command and coordination	0	0.1	0.2	0.7	0
	Communication and information assurance	0	0	0.1	0.6	0.3
	Assessment of issues	0	0	0.3	0.6	0.1
	Emergency evacuation	0	0	0	0.2	0.8
	Incident management	0	0	0.3	0.5	0.2
	Medical rescue	0	0	0.3	0.6	0.1
	Public opinion response	0	0	0	0.9	0.1
Recovery afterwards	Aftermath handling	0	0	0.5	0.5	0
	Summary evaluation	0	0	0.6	0.4	0
	Management improvement	0	0.1	0.6	0.4	0

According to the above formula, the fuzzy comprehensive evaluation R_i is calculated:

$$R_i=\left(0,0.0158,0.2654,0.4794,0.2424\right)$$

According to the principle of maximum membership degree:

Max R_i = 0.4794.

Therefore, the analysis shows that the emergency capability level of the OSTBs is good, but there are some improvements. For example, it is necessary to increase the investment of funds and the arrangement of personnel work and improve the emergency organization, the formulation of emergency plans, and the treatment after the accident. Among them, the areas with large shortcomings need to be continuously improved with time in order to improve the comprehensive emergency response capability of the base and minimize losses as much as possible when disasters and accidents occur.

4.3. Analysis of Comprehensive Evaluation Results of Disaster Emergency Capability of OSTBs

The evaluation result table of each index factor is obtained by calculation, as shown in Table 14.

Table 14. Evaluation results of accident and disaster factors in OSTBs.

Evaluation Result	Bad	Average Bad	Average	Average Good	Good
Advance prevention	0.0000	0.0006	0.0108	0.0307	0.0340
Emergency preparedness	0.0000	0.0099	0.1599	0.2424	0.1018
Solution during the accident	0.0000	0.0023	0.0457	0.1677	0.1066
Recovery afterwards	0.0000	0.0030	0.0491	0.0386	0.0000

(1)

Advance Prevention

The maximum membership degree for pre-prevention is 0.0340, indicating a moderate level of pre-prevention ability. An analysis of the pre-prevention module evaluation table reveals that the enterprise’s risk source identification capabilities require enhancement. The majority of oil constituents are hydrocarbons, which are inherently volatile. In instances where storage and transportation conditions are suboptimal, these volatile compounds can infiltrate the atmosphere or be discharged into environments such as oceans, leading to the degradation or pollution of natural ecosystems. Consequently, it is crucial to optimize the daily management of oil storage and transportation practices.

Furthermore, deficiencies exist in the implementation of emergency drills and safety inspections. Conducting regular ‘training for war’ is vital to mitigate chaos during emergency situations. In peacetime, it is imperative to intensify rescue drills tailored to specific scenarios. Additionally, bolstering safety inspections of equipment across various regions is essential to achieving genuine prevention measures.

(2)

Emergency Preparedness

The maximum membership degree of emergency preparedness is 0.2424, indicating a moderate level of preparedness. An assessment of the emergency preparedness module reveals that the base’s emergency plan is deficient, failing to meet the established standards, necessitating substantial enhancements. Additionally, the emergency organizational structure is inadequate, with multiple departments remaining on paper, resulting in overlapping personnel responsibilities and a lack of clarity.

(3)

Solution During the Accident

The maximum membership degree of the disposal in the matter is 0.1677, indicating a relatively satisfactory level of performance. However, an examination of the evaluation table for the disposal module reveals that the base’s emergency command and coordination abilities are inadequate. Specifically, the base fails to fully leverage the benefits of unified command, coordination, and personnel dispatch across various departments, thereby hindering its ability to achieve optimal emergency response levels. Furthermore, there is a need to enhance the base’s capacity to predict disaster accident scenarios, scientifically identify risks, and effectively prevent and control them. This will help minimize the losses caused by accidents and prevent the occurrence and escalation of secondary disasters and risks.

(4)

Recovery Afterwards

The maximum membership degree observed post-recovery is 0.0491, indicating a general level of recovery. Analysis of the post-recovery module evaluation table highlights the necessity to reinforce the post-experience summary and management improvement at the base. To enhance resilience, it is crucial to identify existing issues through the examination of historical accidents, validate them, and implement improvements accordingly.

4.4. Discussion

As a critical component of the energy supply chain, petroleum storage and transportation facilities, due to their extensive storage of hazardous materials, are highly susceptible to domino effects that can lead to major accidents, resulting in severe economic losses and casualties. Therefore, conducting quantitative assessments of emergency response capabilities, based on comprehensive risk evaluation, is crucial. This approach aims to scientifically predict and mitigate potential risks, reducing the likelihood of accidents and minimizing losses when incidents occur, thereby ensuring the safe and stable operation of these facilities.

To address the issue of subjective bias in weight assignment inherent in the traditional AHP, this study proposes an improved strategy by integrating AHP with the EWM. By incorporating objective data through EWM, the influence of subjective judgment is diminished, leading to a more scientifically accurate and reasonable determination of weights. This enhancement improves the reliability and credibility of the assessment results, providing a more robust foundation for decision-making in the risk management of petroleum storage and transportation facilities.

Additionally, strengthening the development of emergency response teams through systematic training and practical drills enhances their response speed and on-site handling capabilities, effectively controlling the progression of emergencies and mitigating disaster impacts. Furthermore, the introduction of advanced risk monitoring and early warning systems enables real-time monitoring of equipment conditions and the working environment, facilitating the rapid identification of potential risk factors and thereby significantly improving the safety and stability of these facilities.

Finally, emergency drills, as a vital tool for testing the effectiveness of emergency plans, must be given considerable attention. Regularly conducting realistic simulation exercises ensures that employees are familiar with emergency procedures and can respond swiftly and accurately in the event of an incident, preventing ineffective plan execution. This is not only crucial for safeguarding personnel safety but also reflects the enterprise’s commitment to fulfilling its social responsibilities and upholding national energy security.

5. Conclusions

(1) By conducting a comprehensive analysis of relevant literature and expert knowledge, this study adheres to principles of systematic, scientific, and practical framework construction in developing an emergency capability indicator system. This system includes four primary indicators and twenty-four secondary indicators for evaluating emergency response capabilities in oil storage and transportation bases, thus forming a comprehensive assessment model for disaster accident emergency capabilities in such facilities.

(2) To determine the weights of the indicators scientifically, this study employs a combination of the IAHP and EWM. The improved AHP is used to address complex decision-making problems by structuring hierarchical models, while the EWM objectively evaluates the importance of each indicator through information entropy calculations. By integrating these methods, the study utilizes fuzzy comprehensive evaluation to systematically assess emergency response capabilities in oil storage and transportation bases, ensuring the precision and objectivity of the weight determination.

(3) Using a case study of an oil storage and transportation base in Zhoushan, the assessment indicates that the base’s emergency capability is relatively good. To further enhance this capability, it is recommended that (i) the emergency response teams and command personnel receive advanced professional training to improve their comprehensive skills and overall system response capability; (ii) the base enhance its risk identification and assessment abilities by thoroughly examining potential risks associated with equipment and environmental factors; and (iii) emergency plans be refined and regularly practiced to improve personnel’s practical response skills, ensuring effective implementation of emergency measures during disaster incidents.