Optimizing EV Battery Management: Advanced Hybrid Reinforcement Learning Models for Efficient Charging and Discharging

Abstract

This paper investigates the application of hybrid reinforcement learning (RL) models to optimize lithium-ion batteries’ charging and discharging processes in electric vehicles (EVs). By integrating two advanced RL algorithms—deep Q-learning (DQL) and active-critic learning—within the framework of battery management systems (BMSs), this study aims to harness the combined strengths of these techniques to improve battery efficiency, performance, and lifespan. The hybrid models are put through their paces via simulation and experimental validation, demonstrating their capability to devise optimal battery management strategies. These strategies effectively adapt to variations in battery state of health (SOH) and state of charge (SOC) relative error, combat battery voltage aging, and adhere to complex operational constraints, including charging/discharging schedules. The results underscore the potential of RL-based hybrid models to enhance BMSs in EVs, offering tangible contributions towards more sustainable and reliable electric transportation systems.

1. Introduction

Effective energy management is not just a theoretical concept but a practical necessity for lithium-ion batteries. It plays a pivotal role in optimizing the battery’s capacity, thereby enhancing performance by maintaining a stable state of charge (SOC) and state of health (SOH) [1]. Furthermore, it maximizes energy output and minimizes losses during charging and discharging cycles. Importantly, it serves as a key tool in mitigating battery degradation, which can occur due to cycling, temperature variations, and overcharging. Implementing smart energy management systems (EMSs) can significantly slow down degradation rates, prolonging battery lifespan [2]. Lastly, optimal energy management is critical in ensuring lithium-ion batteries’ safety and reliability. It acts as a preventive measure against issues such as overcharging, over-discharging, overheating, and thermal runaway, thereby reducing the risks of malfunctions and safety hazards [3]. This emphasis on safety should reassure the audience about the reliability of lithium-ion batteries when managed effectively.

Additionally, efficient energy management maximizes the economic value of lithium-ion batteries by extending their lifespan and optimizing performance, reducing the frequency of replacements, lowering overall operational costs [4], and lessening their environmental impact. This aligns with sustainability goals by maximizing renewable energy sources and minimizing waste [5]. This emphasis on the economic benefits of efficient energy management underscores the practical value of our research.

Lithium-ion batteries are pivotal in various sectors, including electric vehicles (EVs), renewable energy storage systems, and portable electronics. Effective energy management enables the seamless integration of these batteries into larger energy systems, promoting grid stability and facilitating smoother energy transitions [6]. Understanding the fundamental working principles and components of lithium-ion batteries, which operate based on electrochemical principles involving the movement of ions between two electrodes through an electrolyte, is essential [7].

The evolution of artificial intelligence (AI) techniques in battery management has been transformative, paralleling advancements in AI and battery technology [8]. Initially, battery management employed basic computational methods, such as rule-based control systems and simple mathematical models, which lacked the adaptability and predictive capabilities needed for optimal management in complex scenarios [9,10]. However, the advent of machine learning (ML) techniques, including regression, decision trees, and support vector machines, revolutionized battery management systems (BMSs), enabling them to process large datasets and enhance state estimation accuracy for SOC and SOH [8].

The subsequent integration of neural networks and deep learning architectures marked a significant shift, with these techniques developing sophisticated models capable of discerning intricate patterns from massive datasets for SOC prediction, battery health monitoring, and fault detection. Including predictive analytics and prognostics has further enabled the estimation of battery degradation and remaining useful life (RUL), fostering proactive maintenance strategies and informed decision-making about battery replacement or refurbishment.

Recent advances have seen the use of evolutionary algorithms, genetic algorithms, and particularly reinforcement learning (RL) for optimizing charging/discharging cycles, managing thermal conditions, and maximizing battery performance. RL has been instrumental in developing adaptive control strategies through real-time interaction with the battery system. This study highlights the integration of RL-based AI techniques for optimizing the charging and discharging of lithium-ion batteries. It underscores the transformative potential of AI-driven strategies on the efficiency, reliability, and sustainability of energy storage systems, sparking excitement about the future of battery management.

This study introduces novel hybrid RL models that optimize lithium-ion batteries’ charging and discharging processes in EVs, significantly advancing current BMSs. Unlike previous research, which primarily focused on singular aspects of battery management or employed conventional RL methods, this paper integrates two advanced RL techniques—deep Q-learning (DQL) and active-critic learning—to create a synergistic model that leverages the strengths of both algorithms. This hybrid approach enhances the efficiency and performance of battery operations. It extends battery lifespan through adaptive learning that intelligently considers complex variables such as the SOH, battery voltage aging, and operational constraints under varying charging and discharging schedules. The contributions of this work are substantiated through rigorous simulation and experimental validation, demonstrating the hybrid model’s superiority in maintaining optimal battery conditions and improving overall vehicle sustainability and reliability. By offering a comprehensive solution that integrates advanced AI strategies, this research paves the way for more effective integration of RL techniques in real-time BMS applications, setting a new standard for AI-driven energy management in EVs.

The paper is structured as follows: Section 2 provides an overview of the related works and the unique contributions of this study; Section 3 details the materials and methods used in the research; Section 4 and Section 5 delve into the results and discussion, comprehensively presenting the findings; and Section 6 concludes with recommendations for future directions based on the study’s findings, offering valuable insights for further research and development.

2. Related Works

Ye et al. (2022) [11] and Mhaisen et al. (2020) [12] conducted studies on EV charging scheduling using RL techniques, incorporating a sole charging rate and functionality. These RL models offer users a schedule for both charging and discharging. Ye et al. (2022) proposed that the RL method performs better than the baseline model predictive control [11]. However, Mhaisen et al. (2020) aimed to lower user charging expenses with their RL model, contrasting the goal of maximizing the charging station’s profits [12]. Furthermore, Liang et al. (2021) [13] employed RL to orchestrate a fleet of EVs charging within a mobility-on-demand framework. The model encompasses charge scheduling, vehicle re-balancing, and order dispatching, all represented through a Markov decision process. By leveraging deep reinforcement learning (DRL) and binary linear programming (BLP), the researchers sought to derive a solution closely approaching optimality for the model. The RL model determines EV actions, including accepting an order, re-balancing to a specific position, or charging. These actions are predicated on evaluating the state value across various locations, temporal instances, and SOCs. Dabbaghjamanesh et al. (2021) [14] investigated Q-learning techniques for load forecasting within an EV charging station. The researchers in [14] introduced a methodology to anticipate the anticipated loads of EVs at a charging station to pre-emptively manage potential adverse grid impacts, such as amplified power overloads and losses. Study [14] revealed the model’s proficiency in accurately predicting future loadings across three distinct charging scenarios: uncoordinated, coordinated, and smart. In another study, Chu et al. (2022) [15] investigated the use of federated RL models to minimize charging expenses, where each user generates their own RL model, combining these models to create a universal model for all users. Additionally, Li et al. (2022) [16] explored the application of deep RL to minimize user charging expenses amid uncertainties in electricity pricing. They utilized a long short-term memory (LSTM) method to extract temporal features from the electricity price signal. These models effectively meet their objectives by reducing user charging expenses. In a study, Kang et al. (2023) [17] proposed a bi-level RL model for battery energy storage systems (BESSs), accounting for uncertainty within an energy-sharing community. This model aimed to optimize two strategies: (i) A short-term scheduling model designed for optimizing electricity flows, considering operational goals such as the self-sufficiency rate (SSR), peak load management, and economic profitability. (ii) A long-term planning model focused on determining the optimal BESS plan, including decisions related to installation, replacement, and disuse, while also considering the selection between new and reused batteries. Shibl et al. (2023) [18] introduce a charging management solution for EVs based on RL. It considers fast, conventional, and Vehicle-to-Grid (V2G) operations to meet user and utility requirements. DRL techniques are applied to model the behaviors of EV chargers and EV users. In this scenario, the EV chargers serve as the RL environment, while the EV users function as the RL agents. Subsequently, the system underwent testing using various case studies employing real-life EV charging data. These tests confirmed the system’s effectiveness and reliability in safeguarding the distribution grid and fulfilling the charging needs of EV users. Plug-in hybrid EVs (PHEVs) offer a viable solution to the growing concerns surrounding energy shortages [19,20,21].

Nevertheless, the current limitations of existing battery technologies constrain widespread PHEV adoption. For instance, the prevalent lithium-ion battery suffers relatively high capital costs and degradation over its operational lifespan. In this way, the study [22] explores the potential application of a novel lithium–sulfur (Li–S) battery featuring bilateral solid electrolyte interphases in PHEVs. In contrast to metals like cobalt and nickel, commonly found in conventional lithium-ion batteries, sulfur, utilized in Li–S batteries, presents advantages due to its cost-effectiveness and more straightforward manufacturing process. The enhanced energy density of the new Li-S battery also translates to an extended driving range for PHEVs. Ref. [22] investigates the use of new bilateral solid electrolyte interphase (SEI) Li–S batteries in both Light-Duty Vehicles (LDVs) and Heavy-Duty Vehicles (HDVs). The power output of the Electric Motor (EM) adapts based on factors such as the driver’s power needs, battery SOC, and driving conditions. At high battery SOC levels, the vehicle operates primarily on electric power from the battery. To preserve the battery’s lifespan, the Internal Combustion Engine (ICE) charges the battery during low SOC levels. During rapid acceleration, both the ICE and EM contribute to meeting power demands. At the same time, during deceleration, the system regenerates energy, with the EM functioning as a generator to charge the battery.

Li et al. (2022) [23] employed a hybrid data-driven approach to analyze battery capacity. Initially, raw capacity data were processed using ensemble empirical mode decomposition and Hurst exponent-based methods to extract two local fluctuation components and one long-term memory feature component. Gaussian process regression (GPR) was used to predict the local fluctuation components, while a long short-term memory (LSTM) neural network was responsible for predicting the long-term memory feature. Prediction errors and uncertainties were quantified using the GPR training error, and these predictions were integrated to provide future capacity values along with their 95% confidence intervals. Lipu et al. (2022) [24] investigated key implementation factors of deep learning (DL) methods, including data types, features, size, preprocessing, algorithm operations, functions, hyperparameter adjustments, and performance evaluations. Additionally, the authors examined the limitations and challenges of DL in BMSs, encompassing issues related to batteries, algorithms, and operations. Lin et al. (2023) [25] focused on energy efficiency as a measure of battery performance in energy conversion, quantified using the ratio of energy output to input during charging and discharging cycles. They calculated energy efficiency systematically throughout the battery’s lifespan, observing primarily linear trends in efficiency trajectories, which the Mann–Kendall trend test confirmed. A linear model was proposed to describe efficiency degradation, revealing that ambient temperature, discharge current, and cutoff voltage uniquely impact energy efficiency. Meng et al. (2023) [26] presented an innovative battery prognostics method that utilizes random charging curve segments to enhance flexibility and practical applicability. The method began with partial incremental capacity analysis within defined voltage ranges, generating features for SOH estimation and prognostics. An LSTM network, guided by Bayesian optimization, was introduced to adjust hyperparameters and automatically achieve precise SOH estimation outcomes. Yao et al. (2024) [27] proposed a mechanistic empowerment-based method to assess the health of lithium-ion batteries by analyzing cell performance degradation mechanisms from internal processes. Using discharge operational data and data-driven principles, a mechanism empowerment characteristic curve was reconstructed. To streamline feature inputs and eliminate redundancy, interval voltage segmentation and the Max-Relevance and Min-Redundancy (MRMR) algorithms were employed. These optimized inputs were then used with four machine learning algorithms, achieving a SOH estimation with a Root Mean Square Error (RMSE) of less than 3% for all models.

Many heat transfer applications employ genetic algorithms (GAs) or soft computing methods for thermal optimization, but battery thermal management lags. So, Afzal (2021) [28] explored a unique approach, combining GAs with an in-house finite volume method (FVM) code to optimize key parameters of lithium-ion battery cells in EVs: the average Nusselt number, friction coefficient, and maximum temperature. Usseglio-Viretta et al. (2023) [29] introduced a genetic algorithm to determine optimal patterns, utilizing a cost-effective proxy distance-based model. It examines wetting in coin–cell and pouch–cell configurations, each with its electrolyte infiltration method. Optimal hexagonal and mud-crack-like fast charging and wetting patterns are identified and compared with simpler, pre-defined patterns. Schneider et al. (2014) [30] introduced an EV routing problem with time windows and recharging stations (E-VRPTW). It allows vehicles to recharge at available stations using suitable schemes. Additionally, it addresses constraints like limited freight capacities and customer time windows, which are crucial in real logistics scenarios.

Quintana et al. (2022) [31] presented a model addressing the robust bus charging location problem, considering system vulnerabilities. It includes a safeguard mechanism enabling buses to access backup charging stations if primary ones fail. A mixed-integer programming (MIP) model is proposed to minimize disruptions in eBus operations. Additionally, an extensive neighborhood search framework is introduced for efficient problem-solving. Sassi and Oulamara (2017) [32] focus on the EV scheduling and optimal charging problem, addressing a fleet of both EVs and combustion engine vehicles (CEVs). The goal is to optimize vehicle assignments to tours and minimize EV charging costs while considering operational constraints like charger availability, grid capacity, and EV driving range. The problem’s NP-hardness is established, and an MIP formulation is presented.

Burzyński and Kasprzyk (2021) [33] introduced a novel approach to model the SOH of cyclically operated lithium-ion batteries using Gaussian process regression. This method enables the estimation of LIB degradation across different load patterns during an equivalent duty cycle.

Aljohani et al. (2021) [34] proposed a real-time, data-driven optimization framework for EV routing to minimize energy consumption. The framework employs a Double Deep Q-learning Network (DDQN) to learn the optimal travel policy for the EV agent. Through training, the policy model estimates the agent’s best action based on reward signals and Q-values derived from feasible routing options. Energy requirements on the road are evaluated using a Markov Chain Model (MCM), where each Markov unit step represents the average energy consumption, accounting for various driving patterns, environmental factors, road conditions, and constraints.

Doan et al. (2023) [35] introduced a battery management algorithm designed to optimize the lifespans of retired lithium batteries with varying health states within a battery energy storage system. Such systems enable the utilization of retired batteries for backup power in various settings, like homes and data centers. In these systems, battery packs comprise multiple retired batteries connected in parallel or series to meet power demands. Due to differences in capacity levels among retired batteries, a scheduling strategy is essential to efficiently manage battery cells within the pack, prolonging the secondary lifespans of these retired batteries.

Shahriar et al. (2022) [36] presented a novel approach for estimating battery SOC, which combines CNN and gated recurrent unit-long short-term memory (GRU-LSTM) networks. This hybrid RNN model incorporates explainable artificial intelligence (EAI) to synchronize cell parameters with SOC estimation. By leveraging DL techniques, the model comprehensively understands the complex relationship between monitoring signals such as current, voltage, temperature, and battery SOC.

Tang et al. (2021) [37] introduced a novel framework for energy management in power-split hybrid electric vehicles (HEVs) under naturalistic driving conditions, integrating battery health awareness and DRL. Firstly, driving scenarios reflecting diverse patterns and behaviors are established using real traffic data. Next, expert knowledge is incorporated into the deep deterministic policy gradient (DDPG) algorithm to enhance convergence speed while ensuring vehicle performance. Finally, using different weight coefficients, the framework optimizes the balance between fuel consumption, battery aging cost, and SOC sustainability penalty. Comparison with state-of-the-art strategies, including DQN and dynamic programming (DP), validates the superiority of the proposed control strategy.

3. Materials and Methods

Battery management is crucial in various applications, especially EVs and renewable energy systems. Maintaining excellent battery performance, longevity, and safety is essential. AI-based optimal control strategies have emerged as a promising approach to achieve this. These strategies use AI algorithms that optimize battery usage, improve efficiency, and extend battery lifespan. Various AI-based approaches tailored explicitly for battery management are proposed, including DRL with Q-learning and actor–critic methods integrated with machine learning techniques. DRL algorithms enable batteries to learn optimal control policies through interactions with their environment, maximizing performance based on rewards and penalties. This section discusses the dataset used in this study and presents the recent advances in optimal battery charging and discharging techniques that leverage RL algorithms.

3.1. The Definition of Remaining Useful Life (RUL)

The lithium-ion battery undergoes continuous electrochemical changes over time [38]. Each charge and discharge cycle gradually diminishes its performance, reducing its lifespan. The aging process is influenced by various physical and chemical factors, including thermal and mechanical stresses, side reactions, and complex operational conditions, as documented in Ref. [39]. Critical contributors to battery degradation encompass the dissolution of electrode material, the decomposition of the electrolyte, the formation of the solid electrolyte interphase (SEI) film, overcharging, depth of discharge, and ambient temperature. These factors collectively lead to a gradual decline in battery performance, significantly impacting the reliability of operations and safety in EVs. As a result, accurately monitoring and predicting lithium-ion batteries’ remaining useful life (RUL) presents significant challenges. The RUL of the battery is denoted as $Q_{rul}$ and can be defined as follows:

$$Q_{rul}=Q_{cap-i}-Q_{cur-i}$$

(1)

where $Q_{cap-i}$ signifies the battery life derived from the battery life experiment, while $Q_{cur-i}$ represents the current usage time of the battery. An alternative way to represent the RUL is described as follows:

$$Q_{rul-i}=\frac{C_i-C_e}{C_n-C_e}\ast 100$$

(2)

where $C_i$ denotes the current capacity while $C_n$ signifies the nominal capacity and $C_e$ stands for the end-of-life capacity.

3.2. The Battery Degradation Model

When balancing model precision and computational intricacy, the double exponential empirical model matched the battery degradation process [38].

$$Q_{cap-i}=a_i\exp \left(b_i.i\right)+c_i\exp \left(d_i.i\right)$$

(3)

Herein, the model parameters $a_i$, $b_i$, $c_i$, and $d_i$ are indicative of specific model characteristics. Initial parameter estimations can be calculated using MATLAB’s cftool (MATLAB R2016a). The state transition and observation equation for the double-exponential empirical degradation model are as follows [40]:

$$x_k={[a_k b_k c_k d_k]}^T$$

(4)

$$\left\{\begin{array}{c}{a}_i=a_{i-1}+w_a w_a~N(0,{\sigma }_a)\\ b_i=b_{i-1}+w_b w_b~N(0,{\sigma }_b)\\ c_i=c_{i-1}+w_c w_c~N(0,{\sigma }_c)\\ d_i=d_{i-1}+w_d w_d~N(0,{\sigma }_d)\end{array}\right.$$

(5)

$$Q_{cap-i}=a_i\exp \left(b_i.i\right)+c_i\exp \left(d_i.i\right), h_i~N\left(0,{\sigma }_n\right)$$

(6)

where $x_i$ represents the state vector, encompassing $a_i$ and $c_i$ parameters associated with internal impedance, while $b_i$ and $d_i$ relate to the aging rate. The variables $w_a$, $w_b$, $w_c$, and $w_d$ denote the process noise, and $h_i$ signifies the observed noise.

Mathematical models for predicting aging effects on charging/discharging time in lithium-ion batteries often consider various degradation mechanisms such as capacity fade, resistance increase, and changes in electrochemical kinetics.

One approach to modeling capacity fades over time $t$ Is to use an empirical decay function:

$$Q\left(t\right)=Q_{0}x{e}^{-kt}$$

(7)

where $Q\left(t\right)$ represents the battery capacity at the time $t$, $Q_0$ is the initial capacity of the battery, and $k$ is the capacity fade rate constant.

The resistance increase over cycles can be modeled using a similar empirical decay function:

$$R\left(t\right)=R_{0}x{e}^{-kt}$$

(8)

where $R\left(t\right)$ is the internal resistance at the time $t$, $R_0$ is the initial internal resistance, and $k$ is the resistance increase rate constant.

The changes in electrochemical kinetics during charging/discharging can be described using a combination of Butler–Volmer kinetics and mass transport equations. These equations typically involve partial differential equations governing ion diffusion, charge transfer, and solid-state reactions. The resulting model predicts how changes in electrode morphology, electrolyte composition, and kinetics of response affect charging/discharging time over cycles.

An integrated aging model combines the above components to predict overall charging/discharging time changes over cycles. This model considers the interactions between capacity fade, resistance increase, and changes in electrochemical kinetics. It may involve solving a system of coupled differential equations or using numerical simulation techniques to predict the time evolution of battery performance parameters.

3.3. Dataset

This section discusses the datasets used in the study, which are publicly available. The dataset used in the study was developed collaboratively by Stanford University and the Massachusetts Institute of Technology (MIT) [41]. We used 80% of the data for training, 10% for testing, and the remaining 10% for validation.

All cells in the dataset undergo either one-step or two-step fast charging, following a policy denoted as “C1(Q1)-C2”. Here, C1 and C2 represent the first and second constant-current steps, with Q1 indicating the state-of-charge (SOC, %) at which the current transitions. Charging continues at 1C CC-CV after the second step until reaching 80% SOC, adhering to manufacturer specifications with upper and lower cutoff potentials set at 3.6 V and 2.0 V, respectively. Despite these fixed potentials, cells may occasionally surpass the upper limit during fast charging, triggering significant constant-voltage charging. Discharge occurs at 4C.

The dataset is segmented into three “batches”, comprising approximately 48 cells, and distinguished by a “batch date”, signifying the test initiation date. Irregularities specific to each batch are outlined on their respective pages. Data are provided in two formats: a MATLAB struct for each batch and raw data CSV files for individual cells. The MATLAB structure simplifies data accessibility and is compatible with MATLAB and Python via the h5py package, facilitating Pandas data frame generation. Note that occasional errors in test and step times, such as mid-cycle resets to zero, are rectified within the structs. Temperature measurements are conducted using Type T thermocouples attached with thermal epoxy (OMEGATHERM 201) and Kapton tape to the exposed cell can after stripping a portion of the plastic insulation. However, the reliability of these measurements varies due to potential thermal contact inconsistencies and occasional loss of thermocouple contact during cycling. Internal resistance measurements are obtained by averaging ten pulses of ±3.6C, with a pulse width of either 30 ms (on dates 12 May 2017 and 30 June 2017) or 33 ms (on date 12 April 2018), during charging at 80% SOC.

3.4. Actor–Critic Learning of the Proposed Scheme

This section discusses limitations in existing techniques for battery charging due to high computational costs, algorithm complexity, and uncertainties. To overcome these issues, an approach is presented using a model-free multistage constant current technique based on DRL. This technique ensures battery safety, decreases degradation, and optimizes charging profiles. The method employs a Proximal Policy Optimization (PPO) algorithm [42] to train the DRL agent, which learns a reliable control policy by interacting with the battery using a comprehensive reward function. This confirms the effectiveness of this method through a comparison with a 6CCCV profile designed for rapid charging while also evaluating its resilience to changes in electrode thicknesses and porosity. 6CCCV likely refers to a charging method used for lithium-ion batteries, where the charging process consists of three distinct phases: constant current (CC), constant voltage (CV), and trickle charge (C). Within the charging process, the PPO functions like an actor–critic, on-policy, policy-gradient RL algorithm, drawing inspiration from Trust Region Policy Optimization (TRPO) [43]. Leveraging TRPO’s notable performance, robustness, and stability, the PPO algorithms optimize a clipped surrogate objective function, employing it as the loss function denoted by Formula (9).

$$L^{clp}\left(\theta \right)={\widehat{E}}_t\left[\min \left(r_t\left(\theta \right){\widehat{A}}_t,clip\left(r_t\left(\theta \right), 1-\epsilon ,1+\epsilon \right){\widehat{A}}_t\right)\right]$$

(9)

where $r_t\left(\theta \right)$ represents the probability ratio defined as Formula (10).

$$r_t\left(\theta \right)=\frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{old}}\left(a_t|s_t\right)}$$

(10)

The probability ratio $r_t\left(\theta \right)$ is restricted within the range [1 −$\epsilon$, 1 +$\epsilon$], ensuring periodic updates of the old policy align with the new one. Studies have demonstrated that PPO exhibits superior overall performance in contrast to the divergence of TRPO [40]. Algorithm 1 depicts the PPO algorithm.

Algorithm 1: The PPO algorithm with Actor–Critic Style

1: for $i$ = 1 to $I_{max}$ do 2: for $j$ $=1 \mathrm{to} N$ do 3:   Execute the policy ${\pi }_{{\theta }_{old}}$ $\mathrm{in} \mathrm{environment} \mathrm{for} T$ timesteps 4:   $\mathrm{Calculate} \mathrm{advantage} \mathrm{predictions} {\widehat{A}}_1, {\widehat{A}}_2,\dots .., {\widehat{A}}_T$ 5: end for 6:   Optimize the surrogate $L$ $\mathrm{wrt} \theta$$, \mathrm{with} I_{max}$ $\mathrm{epochs} \mathrm{and} \mathrm{minibatch} \mathrm{size} M\le NT$ 7:   ${\theta }_{old}\leftarrow \theta$ 8: end for

As depicted in Figure 1A, the actor–critic approach facilitates continuous state/action spaces utilizing a function approximator, for instance, a neural network. Both in RL and Dynamic Programming (DP) [42], actions are taken by a policy to maximize the anticipated total discounted reward. Following a specific policy and processing rewards, one estimates the expected return given states using the value function. In the actor–critic approach, the actor refines the policy based on the value function estimated by the critic. Illustrated in Figure 1B [44], during the charging phase, the Li-ions within the cathode electrode undergo deintercalation, dissolve into the electrolyte, and diffuse to the anode electrode by traversing through the separator [45]. The finite element is built along the x-direction and comprises the negative, separator, and positive electrodes. Within each finite element, active particles are present, facilitating spherical lithium intercalation.

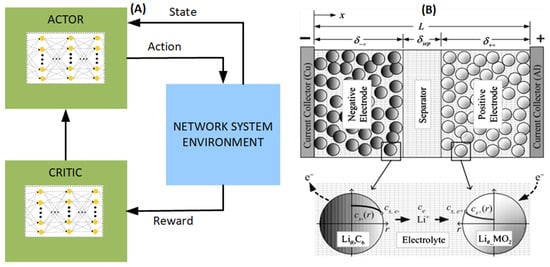
Figure 1. (A) Actor-critic approach in Continuous State/Action spaces. (B) Lithium-ion Movement During Battery Charging [44].

A DRL agent interacts with a simulated environment through Pybamm instead of real-world interaction. This agent can learn the most effective approach to minimize battery charging duration while adhering to safety constraints. The environmental states within this framework will encompass the $SOC$ represented as ${\mathrm{S}\mathrm{O}\mathrm{C}}_t$, determined through Coulomb counting, along with the cell voltage $V_t$ and the cell temperature $T_t$. Here, $s_t$ = (${\mathrm{S}\mathrm{O}\mathrm{C}}_t, V_t$,$T_t$)$\in S\subset {\mathbb{R}}^3$. The definition of $SOC$ can be articulated as follows [46]:

$${\mathrm{S}\mathrm{O}\mathrm{C}}_t=\frac{Q_{rm}}{Q_{rt}}$$

(11)

where $Q_{rm}$ denotes the current remaining capacity of the battery while $Q_{rt}$ signifies the battery’s rated capacity. With the current state $s_t$ at hand, the agent executes an action within the environment, obtaining a scalar reward along with the new state $s_{t+1}$. This updated state encapsulates ample information about the environment. The framework protocol necessitates two parameters per step: the C rate and the duration time. Hence, the action vector can be depicted as $a_t=(C{r}_t,△(t)\in A)$, where $C{r}_t\in (1C to mC)$ is the $C$ rate and $△\left(t\right)\in (1 Minutes to nMinutes)$ is the charging period, with $m, n$ $\in \mathbb{N}$. The reward function, denoted as $R$, involves assigning the reward $r_{t+1}$ after transitioning from state st to $s_{t+1}$ upon taking action $a_t$. Three primary components are as follows: firstly, ensuring adherence to safety constraints; secondly, minimizing the duration of each charging stage; and thirdly, rmulti, which penalizes the agent for using the same C rate as previously to maintain a multistage profile. Lastly, a component addresses the disparity between the $SOC$ at time $‘t’$ and the desired $SOC$ (${\mathrm{S}\mathrm{O}\mathrm{C}}_t$), guiding the policy to meet the final $SOC$ condition [47].

Figure 2 depicts the consecutive phases within an episode throughout the training procedure, emphasizing the dynamic interplay between the agent and its surroundings. To adequately prepare the DRL agent, it is imperative to establish a range of parameters encompassing the environmental factors pertinent to training and the hyperparameters specific to the agent.

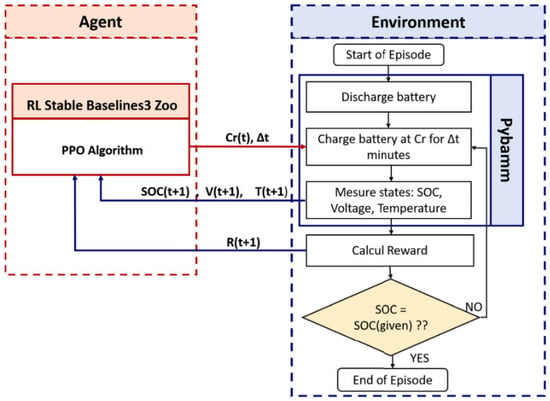
Figure 2. A flow diagram depicting the training process for the DRL charging technique [43].

3.5. Deep Q-Network Model of the Proposed Scheme

An RL is usually employed to develop optimal charging and discharging strategies [45]. RL algorithms denoted as DRL [46], such as DQN [47], PPO [42], or deep actor–critic learning [48], learn optimal policies by interacting with the battery system and observing rewards or penalties based on its actions. These algorithms aim to find charging/discharging profiles that maximize energy storage, minimize degradation, and balance performance metrics like SOC, power output, and efficiency [49,50]. The main concept focuses on attaining maximum returns or particular goals through acquiring strategies via interactions between an agent and its environment, thereby empowering the agent to make optimal choices. Introducing the Markov decision process (MDP) simplifies the modeling intricacies in RL across diverse environments. The following is a breakdown of its components: Action (Agent): This represents the entity performing actions within an environment to attain rewards. Environment: This signifies the scenario faced by the agent. Reward: Instantaneous return provided to the agent for specific actions or tasks. State: This represents the present condition conveyed by the environment. The main goal in RL is to maximize the total rewards, where the future path of rewards affects computations. Total reward is characterized as the weighted addition of rewards from time $‘t’$ until the completion of the learning process, articulated mathematically [49].

$$R_t={\sum }_{t^{\prime }=t}^T{\mathcal{o}}^{t^{\prime }-t_{r_t}}$$

(12)

The constant $\mathcal{o}$, the discount coefficient, which belongs to the range [0,1], assesses how future rewards impact the overall cumulative rewards.

The function $Q_{\pi } (s, a)$ depicts the action $a$ taken within the current state $s$, persisting throughout the learning process based on the strategy $\pi$. The overall return achieved by the agent can be formulated as follows:

$$Q_{\pi } (s, a)=\mathbb{E}[R_t |s_t=s, a_t=a,\pi ]$$

(13)

If, for all combinations of states and actions, the anticipated return attained by a strategy ${\pi }^{\ast }$ surpasses or equals that of other strategies, then that strategy is regarded as the optimal choice. It should be emphasized that several optimal strategies could possess identical state–action functions.

$$Q^{*}\left(s, a\right)={max}_{\pi }\mathbb{E}[R_t |s_t=s, a_t=a,\pi ]$$

(14)

The state–action function referred to as the optimal function adheres to the Bellman optimality equation, expressed as follows:

$$Q^{*}\left(s, a\right)={\mathbb{E}}_{s^{\prime }}~s[r+\mathcal{o}{max}_{a^{\prime }}Q(s^{\prime },a^{\prime }\left)\right|s,a]$$

(15)

In principle, solving the Q-value function involves iterative Bellman equations. Nevertheless, practical applications often employ neural networks and linear functions to estimate the function representing the value of state–action pairs. This approximation facilitates the integration of deep learning and RL, thus propelling the advancement of DRL.

The DQN has been widely deployed to tackle challenges related to charging and discharging in user-side battery energy storage systems. In some instances, its effectiveness has rivaled that of human experts. However, adjusting the storage priority in experience memory is often delayed compared to updating Q-network parameters. To tackle the need for efficient management of battery charging and discharging, this enhancement focuses on prioritizing the update of sequence samples and improving the training performance of the deep neural network (DNN). By doing so, the enhancement aims to reduce the cost associated with charging and discharging actions and decrease energy depletion within the facility. The approach considers real-time electricity prices, battery status, and time as critical factors. The approach formulates the state of energy consumption, behavior for charging and discharging, reward function, and structure of neural networks to facilitate the flexible scheduling of strategies for charging and discharging, ultimately optimizing the advantages of battery energy storage. Figure 3 provides a visual representation of the network architecture of the DQN.

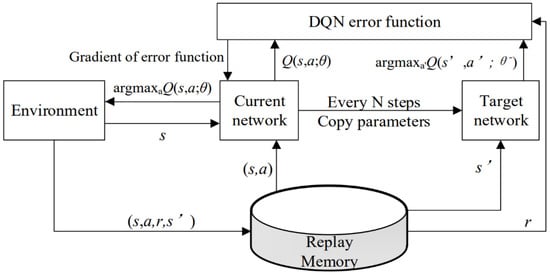
Figure 3. An architecture of the DQN [49].

The loss function in the DQN algorithm is defined as the variance between the predicted value and the target value, expressed as follows:

$$L_f=\mathbb{E}\left[{r+\mathcal{o}{max}_{a^{\prime }}Q\left(s^{\prime },a^{\prime },{\theta }^{-}\right)-Q\left(s,a,\theta \right)}^2\right]$$

(16)

Figure 4 represents a scheme for RUL estimation based on the DNN model. Figure 4A,B demonstrate a schematic file of RUL estimation based on AI-driven techniques such as DNN and prediction performance results, respectively. Ensuring the BMS’s dependable functioning and timely maintenance heavily relies on these assessments. Previous researchers have proposed numerous valuable methods for prognosticating lithium-ion batteries’ health and future behavior.

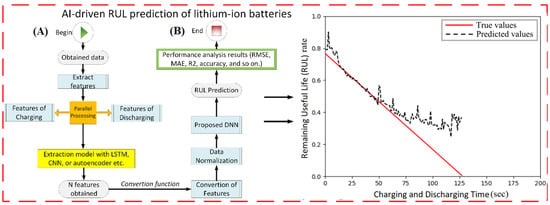
Figure 4. (A) A framework for RUL prediction based on the DNN method. (B) The results of RUL prediction versus charging/discharging times.

Initially, the target network is kept static after several training steps. Subsequently, at regular intervals of every $N$ steps, the current value network parameters are copied to the target value network parameters [49]. This process aims to stabilize the training procedure, facilitating easier model convergence. To address the drawbacks found in the traditional DQN algorithm, such as the overestimation of the Q-value, inadequate directivity, and instability, various enhanced DQN methods have been introduced [50]. To achieve the optimal control of charging and discharging in energy storage batteries, the study employs DQN and its enhanced algorithms [51]. The objective is to secure excellent performance for energy storage batteries within intricate operational settings while minimizing power consumption costs within the facility. The algorithm utilizes the ε-greedy approach to find an equilibrium between exploring novel actions and capitalizing on optimal ones and employs a strategy. During the exploration phase, the algorithm picks the action with the highest Q-value with a probability of 1 − ε, while other actions are selected with a probability of ε. Initially, during the training phase, ε may be set to a higher value to encourage thorough exploration of actions. As training progresses, the exploration rate ε gradually decreases with each iteration, leading to a preference for actions with the highest Q-value to achieve better convergence. After training, the method directly picks the action with the highest Q-value [52].

4. Experimental Setup and Results

In order to execute the applications of the study, a Windows 10 computer equipped with an Intel R-Core i7 processor, 16 GB of RAM, and an Nvidia Geforce 4 GB graphics card was utilized. The Python programming language and its associated libraries were employed for this purpose. The experimental setup involved fine-tuning hyperparameters based on techniques established in prior studies with similar objectives. The Adam optimizer facilitated the learning of the DRL weights. The optimal configuration and hyperparameters for each algorithm were fine-tuned using Ray Tuner 2.24.0 [53]. Key parameters included a discount factor of 0.95, a batch size of 64, and a learning rate of 0.001. The models were implemented using Python 3.12.4 and TensorFlow.

The experiment was designed with real-world relevance in mind, utilizing 140 lithium batteries, divided into two categories: half allocated for UPS emergency power and the other half designated for energy storage. The charging strategy aimed to maintain battery SOC within the 20% to 80% range, which aligns with consumer concerns about range and addresses safety and degradation issues associated with rapid charging at full battery capacity. To ensure the experiments aligned with real-world conditions, the measurable states were limited, imposing a maximum C rate of 7C to prevent degradation, which tends to increase with higher C rates.

During the training phase, the DRL agent underwent an extensive regimen spanning 336 h. The study focused on how the agent adjusted its learning patterns in response to environmental changes, particularly assessing the agent’s sensitivity to modifications in design parameters. This was carried out by systematically varying the values of key hyperparameters and observing the resulting changes in the agent’s learning patterns. Among the various experiments conducted, the most significant findings concerning electrode thickness related to the learning curve. Given the focus of numerous studies on electrode microstructure and the pursuit of advanced architectures to minimize charging duration, this research explored the impact of electrode thickness and porosity on the performance of the DRL agent in reducing charge times using the previously described framework.

4.1. Assessing DRL Performances through Benchmarking

Before presenting the scheduling outcomes proposed here, we provide a concise overview of DRL as background information. We evaluate the effectiveness of the suggested approaches by employing diverse DRL variants.

4.1.1. Double Deep Q-Learning (DDQN)

In Q-learning, a critic network is employed alongside the Q-function to derive an optimal policy based on the state–action pair [53]. The action-value function, denoted by $Q_{\pi } (s, a)$, reflects the efficacy of actions taken in respective states. The optimal $Q_{{\pi }^{*}}^{*}$ $(s, a)$ represents the highest cumulative reward attainable for action $a_t$ in state $s_t$. The action-value Q($s_t, a_t$) undergoes updates utilizing the following equation:

$$Q_{{\pi }^{*}}^{*}\left(s, a\right)\leftarrow \left(1-\theta \right)Q\left(s_t , a_t\right)+\theta [r_t+\gamma max Q\left(s_{t+1} , a_{t+1}\right)]$$

(17)

where $\theta$ denotes the rate of learning, influencing how much the new reward impacts the existing $Q\left(s_t\right)$ value. On the other hand, $\gamma$ serves as the discount factor, weighing the importance of immediate and future rewards [54].

4.1.2. Deep Deterministic Policy Gradients (DDPG)

The DDPG belongs to the category of actor–critic off-policy methods, constituting a model-free algorithm derived from DPG, capable of functioning within continuous state and action spaces [55]. This approach relies on DNNs to establish two approximation functions stemming from the actor–critic framework. The actor network operates as a policy function $\mu \left(s\right|{\theta }^{\mu })$, deterministically mapping states to actions, while the critic Q($s$,$a$) is trained using the Bellman equation. Throughout the agent’s training, updates to the critic and actor network weights are consistently made based on observed rewards at each time step. For smoother training, duplicate networks are created: an actor target network ${\mu }^{\prime }$ with parameters ${\theta }^{\mu \prime }$ and a critic target network $Q^{\prime }$ with parameters ${\theta }^{Q^{\prime }}$. A loss function, denoted as $L$, is computed as the mean squared error between the target value and the critic’s estimated Q-value, expressed as follows:

$$L\left({\theta }^Q\right)=\frac{1}{M}{\sum }_{i=1}^M(y_i-Q\left(s_t , a_t|{\theta }^Q\right))$$

(18)

where M represents the magnitude of the experience mini-batch and $y_i$ is derived through the application of Q-learning. The parameters ${\theta }^Q$ of the critic network undergo updates by minimizing $L$ throughout the mini-batch of experiences extracted from the replay buffer.

4.1.3. Soft Actor–Critic (SAC)

Traditional model-free DRL methods encounter two primary challenges: heightened sampling complexity and inadequate convergence, both of which hinge on parameter adjustment. In a bid to enhance sample efficiency, off-policy algorithms like DDPG have been proposed; however, their efficacy is heavily contingent upon hyperparameter settings. Hence, the cutting-edge off-policy DRL algorithm, SAC, is introduced, which is grounded on maximum entropy [56,57]. Similar to DDPG, SAC adopts an actor–critic architecture and employs an experience replay buffer to facilitate an off-policy formulation. Diverging from DDPG, SAC’s principal feature lies in entropy regularization. The algorithm operates based on maximum entropy within the RL framework, aiming to maximize both expected rewards and entropy concurrently. This objective is articulated as follows [47]:

$${\pi }^{*}={argmax}_{\pi }=E_{\pi }\left[{\sum }_{t=0}^{\propto }{\gamma }^t\left(r_t+\alpha H_t^{\pi }\right)\right]$$

(19)

where $H$ denotes the Shannon entropy component, reflecting the agent’s inclination toward adopting various actions while $\alpha$ serves as a regularization factor signifying the significance of the entropy term concerning rewards. Traditionally, within typical DRL algorithms, $\alpha$ is often set to 0. Maximizing this objective function closely relates to the trade-off between exploration and exploitation, guaranteeing the agent’s deliberate encouragement to explore new policies while mitigating the risk of suboptimal outcomes. Consequently, SAC ensures robust learning and efficient sampling.

4.1.4. Model Predictive Control (MPC)

In industry, MPC is extensively employed as an efficient method for managing complex multivariate constraint control challenges [58]. The MPC model is utilized alongside the proposed DRL model for performance evaluation. MPC operates by iteratively resolving an online constrained optimization problem to select control actions, aiming to minimize a performance index over a finite prediction horizon based on system model predictions. The objective function for operational/aging costs and associated constraints are formulated within the same environmental model employed in DRL. Unlike precomputed offline computations, MPC computes control inputs online for each stage at each sampling interval. The system state is updated, an optimal control problem is solved online, and the controller’s time window is shifted back by one step.

4.2. The Performance Results of the Hybridization DRL Methods

Figure 5a,b [43] illustrate the deviations in states and the learning curves related to the thickness of the anode and cathode electrodes, respectively. The DRL agent demonstrated the capability to adapt its charging strategy for both types of electrodes, facilitating swift and, in some instances, ultra-fast charging while maintaining battery safety.

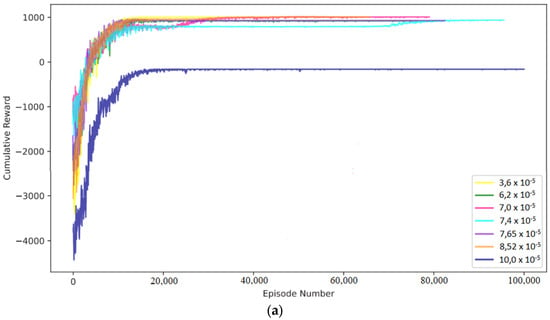
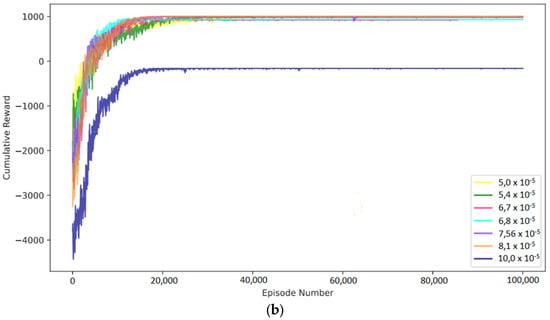
Figure 5. DRL agent testing performance for different (a) anode and (b) cathode thicknesses of the lithium-ion battery, [43]. (Reproduced with permission from [43], Elsevier: 2024).

The training outcomes of the DRL model networks are illustrated in Figure 6. These DRL agents underwent training over 7000 episodes, each employing different DRL methodologies, which produced distinct cost curves as shown in the figure. Figure 6 captures the progression of network performance throughout the training phase of the proposed DRL models. Notably, the DDQN, DDPG, and SAC algorithms operate off-policy, utilizing random sampling from the replay buffer for training purposes. DDQN encountered challenges in attaining an optimized policy until the replay buffers were adequately populated. Its performance plateaued beyond 5000 episodes without further improvement. In comparison, DDPG displayed superior performance to DDQN but exhibited a slower learning rate than SAC. SAC demonstrated continual policy enhancement within the initial 5000 episodes, after which it stabilized with negligible reward improvement.

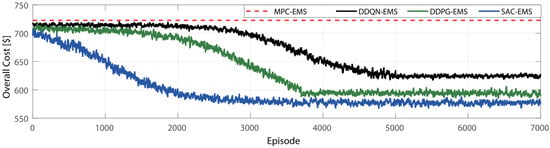
Figure 6. The total daily operating cost assessed for the analyzed DRL techniques.

In Figure 7, we present the outcomes of the experimental trials conducted with the proposed DRL scheduling methods. The results are visualized as follows: the red dotted line illustrates the charging/discharging system scheduling employing MPC based on Time-of-Use (TOU); the black dotted line represents charging/discharging scheduling utilizing DDQN; the green dotted line portrays charging/discharging scheduling employing DDPG; and the blue solid line illustrates charging/discharging scheduling employing SAC. While the primary framework for charging/discharging scheduling methods relies on TOU, additional adjustments are made based on deviations in supply and demand.

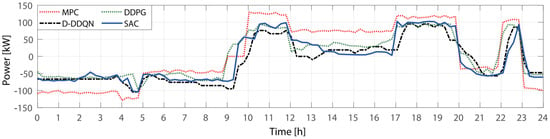
Figure 7. The charging/discharging scheduling results of the DRL methods.

Figure 8 depicts the outcomes of tests conducted to evaluate optimized charging/discharging schedules on battery health, specifically focusing on the impact of DOD on battery longevity. After each scheduling iteration, a complete discharge was performed every 50 cycles to assess the remaining capacity, revealing variations in SOH and capacity fade. Following 500 cycles, the MPC-EMS experienced a capacity loss of approximately 17.37%. In contrast, the DDQN-EMS and the DDPG-EMS losses were 15.81% and 11.47%, respectively. Notably, the SAC-EMS scheduling demonstrated the lowest capacity loss, measuring only 3.41%. The MPC-EMS approach exhibited accelerated capacity reduction, primarily due to higher DOD levels. In contrast, the DRL methods achieved slower capacity degradation by maintaining a more consistent SOC and avoiding deep discharge thresholds. These experimental findings underscore that maintaining a high DOD with a narrow SOC range can significantly diminish battery lifespan and escalate degradation costs.

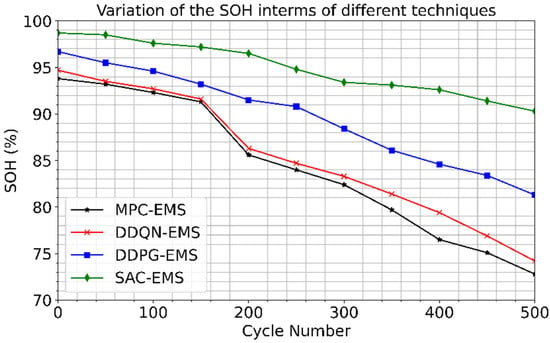
Figure 8. The variations in the SOH of battery packs employ the presented techniques.

Figure 9 illustrates the percentage of SOC relative error resulting from hyperparameter optimization during the training and testing phases for the lithium-ion battery circuit voltage parameters. The SAC-EMS, DDPG-EMS, and DDQN-EMS algorithms demonstrated superior performance among the models considered. Generally, excluding outliers, errors for these algorithms were bounded between −1% and 1%, which is promising. The DDPG-EMS showed slightly larger errors, ranging from −0.15% to 0.15%. Conversely, the DDQN-EMS exhibited larger errors, ranging from −2% to 2%, while the Model Predictive Control (MPC)-EMS displayed the highest error range, from −2.25% to 2.25%.

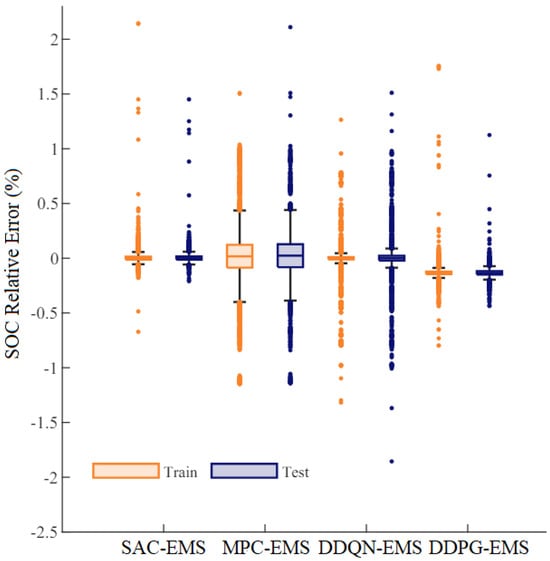
Figure 9. The SOC relative errors with the presented techniques.

Table 1 presents the results of the adaptive test study, which includes data on rewards, state violations, and average charging time. The study simulates battery aging by incrementally increasing the film resistance in the anode every 100 cycles up to a total of 1000 cycles. Battery aging, a slow process compared to battery dynamics, requires numerous cycles to observe clearly. Among various aging phenomena, the growth of resistance during cycling is particularly notable. This study evaluates the adaptability of an output-based learning policy by introducing perturbations to an internal electrochemical parameter, which influences voltage and temperature measurements. Notably, the same results were also obtained in Ref. [59], where these findings were reproduced to compare different reinforcement learning (RL) methods for the readers.

Table 1. The results of the adaptive test study are also shown in Ref. [59].

Test Parameters	The Data on Rewards	Cycle Number
		200	400	600	800	1000
Cumulative Return [-]	AOF	0	0	0	−246	−241
	SOF	−223	−435	−753	−1142	−1344
	$R_f^{-}\left[\Omega \right]$	0.026	0.078	0.121	0.153	0.178
Temperature Violation [°C]	AOF	−2.35	−0.07	−2.41	0	0.01
	SOF	2.33	4.23	5.87	7.28	7.52
	$R_f^{-}\left[\Omega \right]$	0.027	0.077	0.101	0.146	0.169
Voltage Violation [V]	AOF	0	0.06	0.38	0.17	0.16
	SOF	0.03	0.42	0.16	0.24	0.32
	$R_f^{-}\left[\Omega \right]$	0.024	0.068	0.104	0.141	0.174
Time [min]	AOF	32.3	32.7	36.4	38.7	46.8
	SOF	25.7	26.9	27.7	28.3	30.5
	$R_f^{-}\left[\Omega \right]$	0.028	0.053	0.102	0.152	0.179

AOF: Adaptive output feedback; SOF: Static output feedback; $R_f^{-}\left[\Omega \right]$: Resistance.

Initially, both static and adaptive RL policies yield similar returns for the first 100 cycles. However, as the battery ages, the static policy begins to falter, while the adaptive policy adjusts its control strategies through continuous learning, as illustrated in Table 1, and despite the battery reaching its voltage and temperature thresholds more quickly with aging, shown in Figures. The adaptive policy consistently outperforms the static policy. This improvement is attributed to the adaptive policy’s capability to update its actor–critic parameters based on received rewards. By cycle 1000, the average charging time due to battery aging has increased from 23.4 to 40.1 min, as depicted in Table 1. This indicates a substantial lengthening of the time required to charge the battery over repeated use cycles. The observed increase in charging time reflects the progressive degradation of the battery’s performance characteristics, such as capacity and internal resistance, which are inherent to lithium-ion batteries as they undergo repeated charging and discharging cycles. As the battery ages, these degradation mechanisms decrease charge acceptance and efficiency, resulting in longer charging times to achieve the same charge level as in earlier cycles. This trend underscores the importance of understanding and mitigating battery aging effects to maintain optimal performance and prolong the lifespan of lithium-ion batteries in practical applications.

5. Discussion

The provided analysis offers a detailed examination of the research outcomes concerning the application of DRL in optimizing battery management strategies for EVs. The training outcomes of the DRL model networks, as depicted in Figure 6, provide insights into the performance progression of various DRL methodologies over 7000 episodes. Notably, the study observes distinct learning curves for different algorithms, with some algorithms encountering challenges in achieving optimized policies until adequate data were available in the replay buffers. Despite variations in learning rates and performance stabilization, the study effectively evaluates the efficacy of different DRL methodologies in enhancing battery management.

Figure 7 presents the outcomes of experimental trials conducted with the proposed DRL scheduling methods. The results highlight the adaptability and effectiveness of DRL algorithms in optimizing charging/discharging scheduling, with additional adjustments made based on supply and demand variations. This underscores the potential of DRL techniques in addressing dynamic real-world conditions and enhancing scheduling accuracy.

Figure 8 provides insights into the impact of optimized charging/discharging schedules on battery health, mainly focusing on DOD and SOH. The experimental findings emphasize the importance of maintaining a consistent SOC to mitigate capacity loss and prolong battery lifespan. By evaluating the trade-offs between DOD levels and capacity degradation, the study underscores the significance of optimized charging/discharging strategies in minimizing battery degradation costs.

Figure 9 analyzes the percentage of SOC relative error resulting from hyperparameter optimization during the training and testing phases. The study evaluates the performance of different DRL algorithms in SOC estimation, with promising results observed for specific methodologies. These findings contribute to the ongoing refinement and optimization of DRL techniques for battery management applications.

Finally, the results in Table 1 show insights into an adaptive test study evaluating the adaptability of output-based learning policies in mitigating resistance growth caused by battery aging. By incrementally increasing film resistance in the anode and introducing perturbations to internal electrochemical parameters, the study assesses the adaptability of DRL algorithms to aging phenomena. The observed improvement in policy performance over extended cycling periods underscores the potential of adaptive learning strategies in enhancing battery management effectiveness.

DRL techniques offer powerful tools for optimizing energy management in EV fleets, but their computational intensity presents challenges for real-time implementation and scalability, particularly in large-scale fleet applications. The complexity of DRL algorithms, such as DQL or policy gradient methods, often requires significant computational resources for training and inference. This computational burden can limit their feasibility for real-time decision-making in EVs, where quick responses to changing driving conditions are essential. Additionally, scaling DRL to large fleets introduces further challenges as the computational requirements grow exponentially with the number of vehicles. Efficient implementation strategies, such as distributed computing or hardware acceleration, may be necessary to overcome these scalability limitations and enable the widespread adoption of DRL-based energy management solutions in EV fleets. Furthermore, research into lightweight DRL architectures and algorithmic optimizations could help alleviate computational constraints, making DRL more accessible for real-world applications at scale.

In summary, the analysis provides a comprehensive evaluation of the research outcomes, highlighting the potential of DRL techniques in optimizing battery management strategies for EVs. The findings contribute to advancing electric transportation systems’ efficiency, reliability, and sustainability, underscoring the importance of ongoing research and development in this field.

6. Conclusions

This research illustrates the potential of hybrid RL models in optimizing the charging and discharging processes of lithium-ion batteries in EVs. By combining DQL and active-critic learning, the study has effectively utilized the strengths of these techniques to improve both battery performance and lifespan. The study’s rigorous simulations and experimental validations confirm that these hybrid RL models can achieve optimal management strategies, overcoming challenges such as battery SOH, voltage aging, power scheduling, and operational constraints. The presented benchmarking methods were used to analyze the relative errors of SOC. The SAC-EMS, DDPG-EMS, and DDQN-EMS algorithms performed the best among tested models. The SAC-EMS algorithm had good accuracy, with errors between −1 and 1. The DDPG-EMS algorithm had errors ranging from −0.15 to 0.15, while the DDQN-EMS algorithm had errors ranging from −2 to 2. The MPC-EMS algorithm had the most significant errors, ranging from −2.25 to 2.25.

These findings highlight the potential of RL-based hybridization models in advancing BMSs for EVs, ultimately leading to the improved efficiency, reliability, and sustainability of electric transportation systems. As the industry evolves, it is essential to continue refining and expanding upon RL techniques in battery management. Future research should focus on further innovations and practical implementations to meet the growing demands of the EV market, ultimately leading to more robust and eco-friendly transportation solutions.