Abstract
This paper presents the application of a numerical approach known as proper generalized decomposition (PGD) to calculate the per-unit length (PUL) ac resistance of rectangular conductors. PGD has been successfully used in areas such as fluid mechanics and biomedical applications. It solves a partial differential equation (PDE) by decomposing the answer into a set of unknown one-dimensional (1D) functions in an iterative approach until it reaches a predetermined convergence. In this paper, a frequency-dependent meshing scheme is employed in the PGD technique at each frequency to properly take skin and proximity effects into account. One of the main advantages of PGD over traditional numerical approaches such as finite element or finite difference methods is that it confines the answers within a set of one-dimensional functions, which require fewer computational resources. Different examples of single and multiple rectangular conductors are considered to study skin and proximity effects. The PGD results are compared with those obtained using a commercial finite element method (FEM) software to verify the accuracy of the model. This approach can be used in applications such as white box modeling of transformers, EMC analysis, hairpin winding design used in electric vehicles, and busbar simulation.
1. Introduction
Rectangular conductors are commonly used in various industrial applications. Their rectangular shape offers several advantages over other conductor shapes, such as efficiency and space utilization, easy implementation, and higher current-carrying capacity. These features make them a popular choice in applications such as multiconductor planar transmission line structures [1,2,3,4,5,6], motors and generators [7], hairpin windings used in electric vehicle applications [8], transformer production, and industrial busbars [9,10]. The proper utilization of conductors requires precise design methodologies. The damping coefficient is a significant parameter that must be considered to achieve a precise design. An example of an application in which precise damping calculation is crucial is the insulation design for high voltage transformers [11]. Voltage calculation is a critical aspect of insulation design and requires accurate calculations of ac resistance and damping. Furthermore, the calculation of ac resistance in rectangular conductors is influenced by skin, proximity, and edge effects. The complexity of analytically calculating the ac resistance of rectangular conductors makes it challenging to accomplish.
There are many approximations for the calculation of the ac resistance of single rectangular conductors, such as one- and two-dimensional calculations [12,13], the circular cross-section formula [13] used for rectangular conductors [14,15,16], and the Ametani formula [17,18,19]. The shortcomings of these approaches have been discussed in [20], and a quasi-analytical approach has been developed for the calculation of ac resistance of single rectangular conductors taking skin and edge effects into account [20]. However, the proximity effect is also important in a system of multiple conductors, but the approach presented in [20] cannot be used for multiple conductors or proximity effect calculations. The main obstacle in the analytical calculation of the ac resistance of rectangular conductors is that it is difficult to define accurate boundary conditions. There is a semi-analytical approach based on thin wire approximation used for cylindrical conductors [21]. This approach is not computationally efficient for a higher number of conductors such as electrical machines’ windings. Moreover, it cannot take the edge-effect of rectangular conductors into account. One of the original approaches developed over the past few decades is the partial element equivalent circuit (PEEC) [22,23,24,25]. PEEC revolves around utilizing integral equation formulations to characterize geometric properties, which are then mapped onto circuit elements to model complex electromagnetic interactions. One of the main challenges of PEEC is computational complexity due to high-density meshing requirements [26,27,28].
There are traditional two-dimensional (2D) numerical methods such as finite difference time domain (FDTD) [19] and finite element methods (FEM) [29] to calculate the per-unit length (PUL) resistance of rectangular conductors. The 2D FEM has been used for PUL parameter or eddy current loss calculations of ac machines while heavy computation is the main drawback of the approach [30,31]. In many applications of 2D FEM for machine windings, the effect of neighbouring turns or proximity effect has been neglected due to the complexity of the computation [32,33,34,35]. The main drawback of 2D numerical methods is that they are more computationally demanding [36,37,38,39,40]. When it comes to skin and proximity effects, a very fine mesh size is needed due to small skin depth at higher frequencies. This makes the 2D matrices large, demands more memory, and makes the computation less efficient.
In this paper, proper generalized decomposition (PGD) technique has been implemented for the calculation of the ac resistance of a 2D system of rectangular conductors in the frequency domain, taking into account skin, edge, and proximity effects. Proper generalized decomposition is a numerical approach used in mathematics, biomedical, and fluid mechanic applications [36,38,39,40,41]. In the PGD technique, the unknown answer is decomposed into one-dimensional (1D) functions [37,42], which makes the computation more efficient while maintaining accuracy. There are some recent applications of PGD pertinent to electrical systems, such as high dimensional parametric solutions for synchronous machines [43], impedance calculation of rectangular conductors [44,45], solving magnetostatic problems [46], magnetic simulation of soft magnetic composite (SMC) microstructures [47], and time-domain modeling of frequency-dependent transmission lines [48]. In [46], PGD has been used to effectively overcome the computational challenges posed by a coupled nonlinear magnetostatic problem and circuit equations. The PGD approach has successfully been used for solving fluid mechanic problems with considerable CPU time saving in comparison to a standard solver [49]. PGD has been employed in [50], enabling the decomposition of the high-order parametric modeling of piezoelectric energy harvesters into lower-order 1D problems while preserving high accuracy. The PGD technique has demonstrated remarkable effectiveness in facilitating parametric sweeping of frequency domain full-wave problems [51]. Reference [52] utilizes the space variable-separated PGD technique to mitigate the computational complexity associated with the 3D capacitance extraction of interconnects in integrated circuits. PGD has been used in material applications to solve the 3D elasticity problems [53]. To mitigate the computational burden associated with solving a finite element (FE) model for magnetostatic problems characterized by variable geometric parameters, the PGD model has been applied successfully [54]. In light of these distinct advantages, the present research incorporates the employment of the PGD technique, further enhancing its capabilities by integrating frequency-dependent meshing into its core features.
In existing literature where PGD is employed for skin and proximity effect calculations (e.g., [44,45]), the frequency dependence is considered as a function with only one mesh size for the whole frequency range. However, this results in inaccuracies where the skin depth is small compared to the smaller dimension of the conductor. In this paper, the existing PGD method is augmented with the addition of a frequency dependent meshing, which overcomes this drawback. Specifically, a distinct meshing strategy is employed at each frequency, with coarser mesh size being selected at lower frequencies. Moreover, an extremely fine mesh size is adopted for skin depth region, a finer mesh size for the remaining of the conductor, and a coarse mesh size for the far air boundary.
2. Proper Generalized Decomposition (PGD)
This section describes the main features of the PGD technique and it has been employed for solving magnetic vector potential of perfectly straight conductors in free space in two dimensions (2D). PGD is a popular numerical method used in computational engineering to solve partial differential equations (PDEs) [36,42]. It works by constructing the solution of a PDE as the sum of unknown one-dimensional functions (known as modes) without prior knowledge of the solution. One of the main advantages of the PGD approach, compared to traditional computational approaches such as finite element and finite difference, is its ability to handle high-dimensional systems with relatively low computational costs. For example, if M number of meshes were required in each direction in a two dimensional problem, number of meshes is needed for traditional computational approaches while around is needed for PGD technique [37,42]. When it comes to complex systems with smaller mesh size (e.g., ), the PGD with meshes is more efficient than traditional approaches with meshes [37,42].
Consider a problem defined in a D-dimensional space for the unknown field . In this context, each coordinates represents the typical coordinate associated with physical space, time, or frequency defined over a domain of . Additionally, these coordinates may include problem parameters, such as boundary conditions or material parameters. PGD approximates the solution for in the separated form as [42]
in which both the number of terms N and the functions are unknown. The approximate solution is considered as u for simplicity. For calculating the ith term of the 1D function , an arbitrary initial value is considered, and the final terms are calculated in an iterative approach. More details are provided in the following sections. In the following, without loss of generality, the main features of PGD is explained for a two-dimensional Poisson equation on a rectangular domain.
2.1. Solving Poisson Equation Using PGD
Consider the Poisson equation in a two-dimensional rectangular domain as [42]
where is the unknown and is the source term. A Dirichlet boundary condition is considered at the far enough boundary, e.g., . The purpose is to approximate u using N number of functions X and Y in the form of
Additional terms and should be calculated in each step until convergence is achieved. The two-dimensional is approximated using the one-dimensional functions and , which require less computational effort. Using an appropriate test function , the weighted residual form of (2) can be written as
At the nth step of calculating u, the first terms of X and Y have already been calculated. The next step is to calculate and in an iterative approach, say p iterations, to obtain the PGD solution [42]
where and are the unknowns at step n and iteration p. Of the several different techniques for calculating and , alternating direction strategy is commonly used [42] and is discussed below.
2.2. Alternating Direction Strategy
In this approach, is calculated from , and then is calculated from the calculated . At each step n, an arbitrary guess is selected and the process continues until reaching a fixed point with acceptable tolerance [42],
in which is an appropriate norm.
2.2.1. Calculating from
In this case, (5) can be written as [42]
where only is unknown. The test function can be defined as [42]
Combining (7), (8) and (4) yields [42],
where all functions of y are known and can be calculated numerically using trapezoidal rule as [42]
Incorporating constant coefficients , , , and calculated from (10) to (9), Equation (9) then becomes [42]
which is the weighted residual form of a one-dimensional problem over and can be solved using any numerical method such as finite element or finite difference. Alternatively, a corresponding strong form of (11) can be written as [42]
which is a second-order one-dimensional ordinary differential (ODE) equation that is solved using the finite element method for calculating . is calculated using discretization in the x-direction. A detailed step-by-step meshing approach used for discretization is explained in Section 3.3. Using the PGD, the 2D integrals of (9) are decomposed to 1D integrals of (10) and (11) to obtain the unknown such that different meshings (i.e., on x and y axis) are not involved at the same time. In fact, there are only 1D integrals of y in (10) and 1D integrals of x in (11) which need less computational resources.
2.2.2. Calculating from Calculated
Following the same approach applied for calculating and using the calculated , a second-order one-dimensional ODE can be derived for , and can be solved using the finite element method. is calculated using discretization in the y-direction following the meshing approach explained in Section 3.3. The details of the calculation can be found in [42]. The iteration would continue until the error (6) is reduced to an acceptable value.
2.3. Stopping Criterion
The process of finding a new term should be continued until an acceptable convergence is satisfied. Generally speaking, the higher the number of terms, the higher the accuracy of the answer. Typical stopping criteria are summarized as follows:
- The norm of the new calculated term with respect to the whole PGD expansion [42]:
- The norm of the new calculated term with respect to the first term, which is computationally less expensive but less accurate than (13) [42]:
- Residue approximation obtained from combining PGD expansion into Poisson equation, which is more appropriate and used in this paper [42]:
Since the PGD decomposes the 2D system into a series of 1D functions, all these error estimation calculations lead to one-dimensional integrals [42]. This is more computationally efficient than 2D matrix calculation. This paper uses (6) for the internal calculation of each step n. For the stopping criterion, (15) or maximum N should be met to end adding a new term n. If the stopping criteria has not been met, a new term n will be added. This new term is calculated in an iterative way, p iterations, using (7)–(12) until (6) has been met. Then, the stopping criteria (15) will be rechecked. For more details about error estimation, the following papers can be considered [55,56,57,58].
3. Skin Effect
Skin effect is a phenomenon in which ac current distributes with more concentration near the surface of a conductor due to the interaction between the internal magnetic field and the electric current of the conductor. When it comes to rectangular conductors, the edge effect should also be considered [20,59]. PGD is a suitable technique for rectangular conductors since mesh selection is easy and straightforward in Cartesian coordinates. Hence, it covers the edges very well. The magnetic vector potential and, consequently, the current density distribution is calculated by solving the diffusion equation [29]
In (16), , , and are angular frequency, conductivity, permeability, and the z component of the external current density, respectively, and f is the frequency. goes to zero at infinity. To solve (16), the Dirichlet boundary condition (i.e., ) at a far enough boundary is employed (i.e., truncating the outer boundary at a distance much larger than a conductor size) [20,29,44]. In this section, (16) is solved at each frequency using the PGD approach and approximated as
Since the skin depth is smaller at higher frequencies, meshing should be frequency-dependent such that a smaller mesh size is considered at higher frequencies [20]. More details are provided in Section 3.3.
In some existing literature employing PGD for skin and proximity effect calculation, the frequency is considered as a separate function as [44,45]
where is a function of frequency. The main advantage of (18) is that one meshing is used for all frequencies [44,45]. In other words, X and Y functions are calculated only once for all frequencies. However, the drawback is that due to the nonlinear behaviour of the skin effect, (18) only works at lower frequencies. In fact, using the same X and Y functions is not accurate for two frequencies where the current distribution across the conductor cross section is uniform at one frequency (i.e., low frequency) and nonuniform at the other frequency (i.e., high frequency). This is exemplified in the following where (16) has been solved assuming the proper external current density, representing each case study.
3.1. Case 1: Single Rectangular Conductor
A square conductor with a side length of , conductivity , and a constant real value of external current density A/m2 is considered in free space. The size of the free space is considered as with a Dirichlet boundary condition, i.e., , at the outermost boundary of the air around the conductor. This boundary condition is considered for the rest of the paper. Equation (16) is solved using PGD where is approximated as given in (17). Once (16) is solved, the current density distribution at the cross section of the conductor at and is calculated using [13]
and is shown in Figure 1. In (19), is the total current density distribution and is the source current density or external current density [20]. As shown in Figure 1a, current distributes almost evenly at while it tends to flow with more concentration near the conductor’s surface at due to the skin effect, as in Figure 1b.
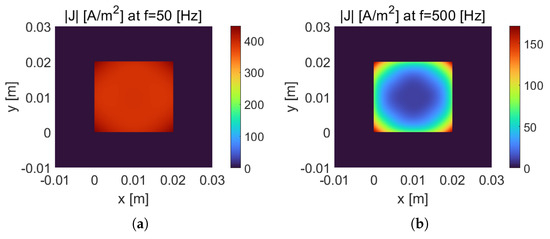
Figure 1.
Magnitude of current density distribution of a single square conductor at (a) and (b) . The total currents of these two cases are different and calculated as follows: A, and A.
Current density distribution at on and are shown for PGD and FEM in Figure 2, and match very well. As can be seen in Figure 1b and Figure 2, the current concentrates more on the edges of the conductor and also near the surface of the conductor due to the skin effect.
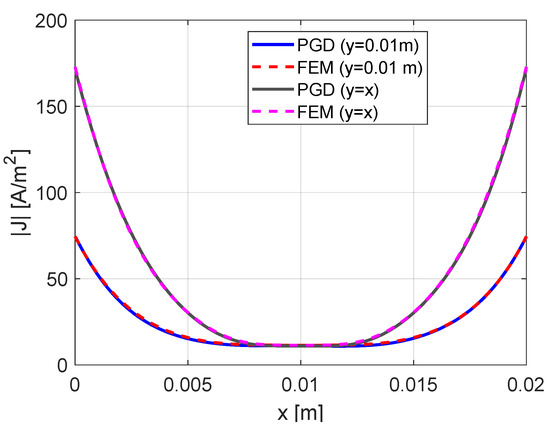
Figure 2.
Current density distribution at the cross section of the square conductor at and for both PGD and FEM at 500 Hz.
The effect of the number of terms N on the error estimation (15) at is shown in Figure 3. The PUL ac resistance of the conductor versus the number of terms is plotted in Figure 4 at . PGD reached the predetermined threshold of at , i.e., . The PUL ac resistance calculated using PGD is , which matches well with FEM with an error of . (See [29] for details of the resistance calculation.) Selecting a smaller threshold may lead to a more accurate result as more terms are used (see Figure 4). The convergence of the current density distribution as the number of terms N increases in (17) along at Hz is plotted in Figure 5 for the square conductor. As shown in the figure, with the increase in the number of terms N, the current density distribution converges to the FEM solution.
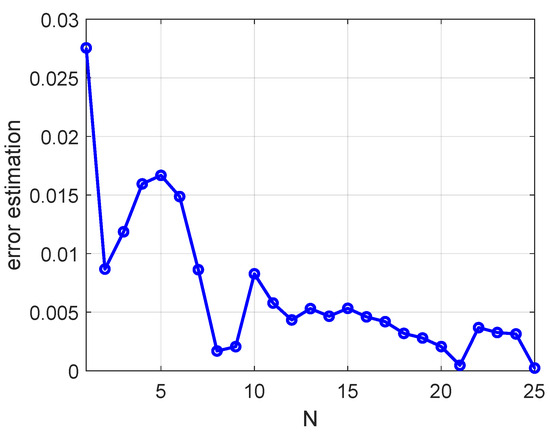
Figure 3.
Error estimation (15) vs. the number of terms N for square conductor, Hz.
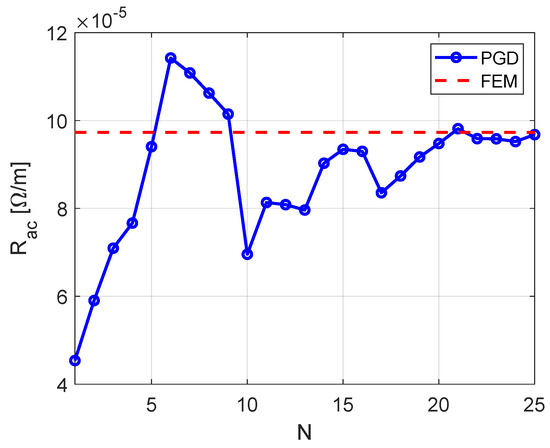
Figure 4.
Ac resistance change of square conductor vs. the number of terms in (17), Hz.
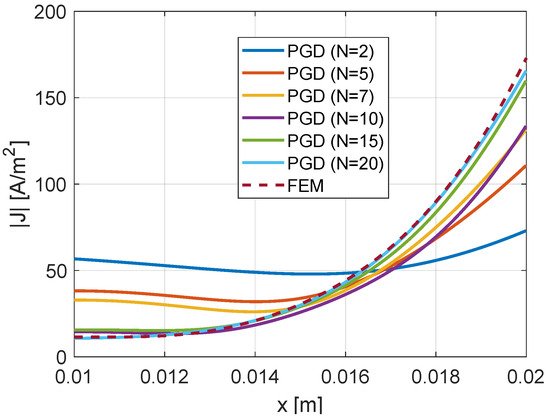
Figure 5.
Current density distribution of square conductor for different number of terms N in (17) along at Hz.
3.2. Effect of Considering Frequency as a Function
One of the strengths of the PGD approach is that it can consider different parameters as functions, such as those that appear in the PDE formula and boundary conditions. For instance, Dirichlet and Neumann boundary conditions can be considered as separate functions [42]. Moreover, frequency has been considered as a separate function for skin effect calculations, as shown in (18) [44,45]. The advantage of using (18) in skin and proximity effect calculation is that one-time meshing is needed for the whole frequency range. However, using the PGD technique proposed in this paper, i.e., (17), a separate meshing is selected at each frequency, which provides a much higher accuracy at higher frequencies.
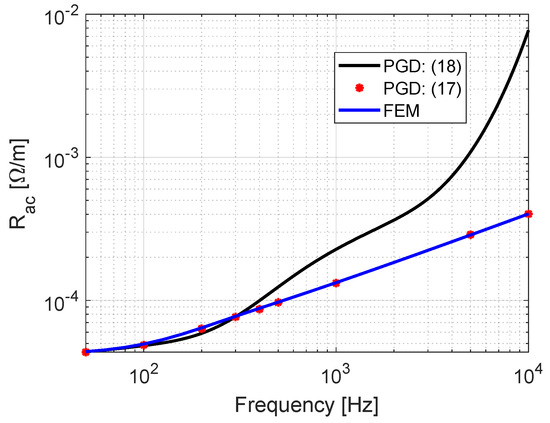
To make a comparison between these two approaches, i.e., using (17) or (18), the single rectangular conductor studied in Section 3.1 is selected. The PUL ac resistance is calculated for both approaches in the frequency range of 50 Hz–10 kHz. The results are compared with FEM and shown in Figure 6. According to the figure, (18) is accurate up to . That is because skin depth is comparable to the conductor dimension at lower frequency range; hence current distributes more evenly, and in turn, it is possible for (18) to have the same X and Y functions for the lower frequency range. However, at higher frequencies such as , the current tends to concentrates more near the surface of the conductor with less current distribution at the middle of the conductor. As a consequence, it is not possible to have the same X and Y functions for low and high frequencies. Therefore, (18) does not work for this broad range of frequency and is not considered for the rest of the paper. Moreover, in other publications employing (18), only a low frequency range, e.g., up to 500 Hz, is considered [44,45]. The calculated using PGD (17) and FEM in the frequency range of 50 Hz–100 kHz is shown in Figure 7. Figure 6 and Figure 7 verify the accuracy of (17).
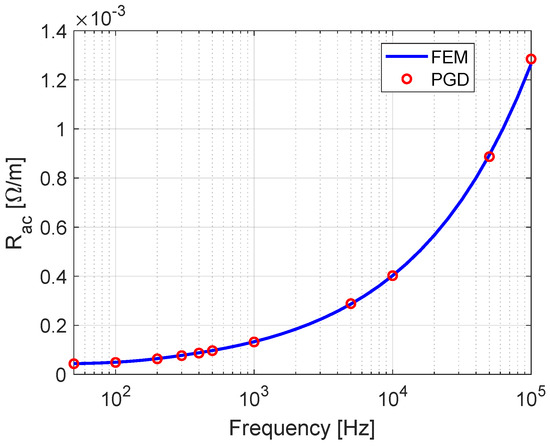
Figure 7.
Comparison between FEM and PGD approach (17) for the square conductor of Case 1.
3.3. Meshing
One of the main challenges for skin and proximity effects calculations is appropriate meshing selection. Since the skin depth becomes smaller at higher frequencies, a very small mesh size is required at those frequencies, and as a consequence, more computational effort is needed. Overestimating the size of the mesh increases computational effort and underestimating it decreases accuracy. Therefore, it is essential to choose the appropriate meshing to decrease CPU time while maintaining accuracy. In this section, three different meshing approaches are studied where the PUL of the square conductor of Case 1 is calculated.
3.3.1. Approach 1, Frequency-Dependent Meshing Linearly Spaced over the Entire Domain
Due to smaller skin depth at higher frequencies, the mesh size is reduced as the frequency increases. Inappropriate meshing can lead to inaccuracy or computational inefficiency. To show this, different linearly spaced meshing is selected over the entire domain for both 50 Hz and 500 Hz. A general schematic of the linearly spaced meshing is plotted in Figure 8. Table 1 shows the effect of mesh size on CPU time requirement, , and the percentage error calculated for the square conductor using the PGD (17). The percentage error is calculated using the determined by FEM that are and at 50 and 500 Hz, respectively. According to the table, overestimating the meshing at 50 Hz, i.e., using mesh size instead of , increases the CPU time from 1008 to 9501 seconds with negligible change in accuracy. On the other hand, underestimating the mesh size at 500 Hz, i.e., using a mesh size of instead of , increases the error by . Therefore, choosing an appropriate frequency-dependent meshing would save CPU time while maintaining accuracy.
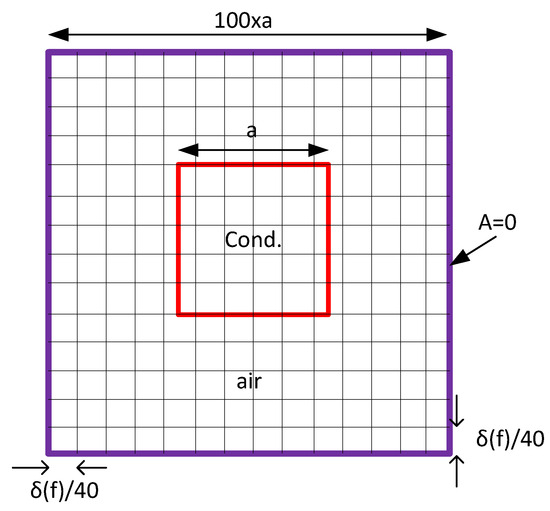
Figure 8.
Schematic of the linearly spaced meshing with mesh size (approach 1).

Table 1.
Approach 1: CPU time, and percentage error of PGD (17) using frequency dependent linearly spaced meshing. Note: This approach either results in lower accuracy or an increased CPU time. This issue has been resolved using approaches 2 and 3.
3.3.2. Approach 2, Finer Mesh Size for the Conductor and Coarser Mesh Size for the Rest of the Domain
As explained in Section 3.1, the air domain around the conductor is , while most of the field variation is concentrated around the conductor. Considering the same mesh size for the conductor and the rest of the domain is not computationally efficient. Therefore, in addition to frequency-dependent meshing, a finer mesh size is selected for the conductor and a coarser mesh size for the rest of the domain, as shown in Figure 9. The CPU time requirement, calculated using PGD (17) and the percentage error are shown in Table 2 for approach 2 of meshing. Due to the change in meshing selection from approach 1 to approach 2, the CPU time decreased from 1008 to s at 50 Hz and from 10,664 to 90 s at 500 Hz, with negligible change in accuracy.
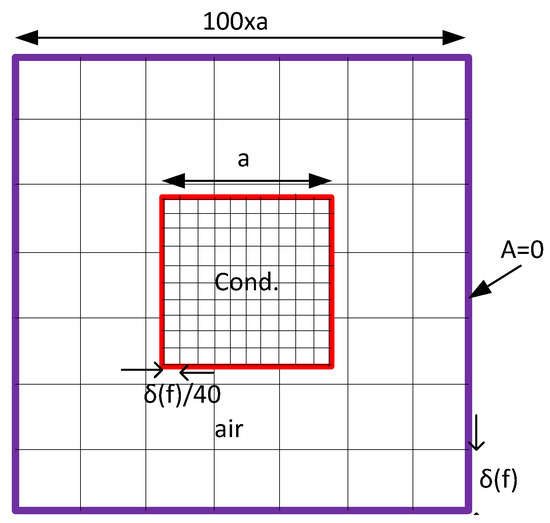
Figure 9.
Schematic of approach 2 meshing.

Table 2.
CPU time, and percentage error of PGD (17) using meshing approach 2.
3.3.3. Approach 3, Adaptive Meshing
At higher frequencies, most of the current is distributed in a very small layer, known as skin depth, and a negligible current is distributed in the rest of the conductor [20]. Hence, it is computationally more efficient to consider a very fine mesh size for the skin depth, a fine mesh size for the rest of the conductor, and a coarse mesh size for the rest of the domain. To accomplish this, a layer with thickness is considered at each side of the skin depth with mesh size ; see the red area in Figure 10. A fine mesh size for the rest of the conductor (i.e., the green area in Figure 10) and a coarse mesh size for the rest of the domain (i.e., the white area in Figure 10) are selected.
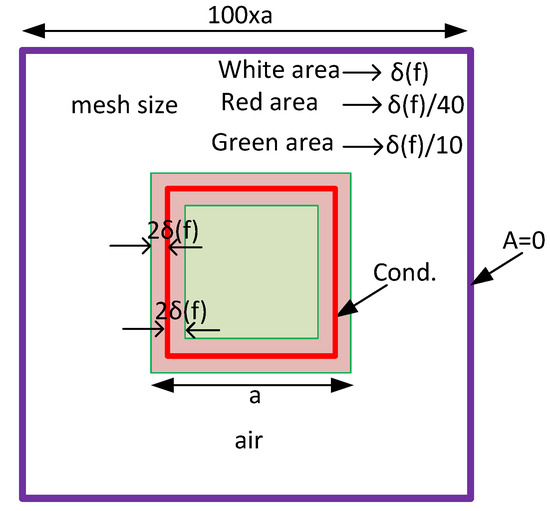
Figure 10.
Schematic of approach 3 meshing.
Table 3 shows a comparison between the meshing approaches 2 and 3 at 500 and 5000 Hz. of FEM at 5000 Hz is calculated as for comparison. According to Table 3, the CPU time decreases in approach 3 by three times when compared to approach 2, with negligible effect on percentage error. Since meshing approach 3 is computationally more efficient while maintaining accuracy, it has been selected for the rest of the paper. It should be noted that none of these three meshing approaches are applicable to the existing PGD approach (18).

Table 3.
CPU time, and percentage error of PGD (17) using meshing approach 2 and approach 3.
4. Proximity Effect
When there is more than one current-carrying conductor, in addition to the skin effect of the conductor itself, current density distribution also gets affected by the magnetic field of the nearby conductors. This phenomenon is known as the proximity effect [19,29]. Due to the proximity effect, there is more resistive loss because of the change in the distribution of current, resulting in a higher ac resistance. Due to the edge effect and lack of accurate boundary conditions, a quasi-analytical approach has been developed for calculation of single rectangular conductors [20]. When it comes to multiple rectangular conductors, the proximity effect further complicates the calculation of . Hence, numerical approaches should be used. Using traditional two-dimensional numerical approaches such as the finite element method demands more computational effort since 2D meshing is required. However, PGD decomposes the results into one-dimensional functions (i.e., uses 1D meshing), requiring fewer computational resources. In this section, different cases of proximity effect calculations using PGD (17) are studied by solving (16) to show the validity of the approach.
4.1. Case 2O: Two Rectangular Conductors with Current in Opposite Directions
Two parallel square conductors with dimensions and material equal to Case 1 and a separation distance of , carrying currents of opposite directions at , are considered in free space. The diffusion equation (16) is solved using PGD, and a final answer in the form of (17) is considered. The magnitude of the current density distribution and magnetic vector potential are shown in Figure 11. According to Figure 11a, the current density distribution of the conductors is affected by both the internal and the external magnetic fields, namely skin and proximity effects, respectively. The ac resistance calculated for one of the conductors using both PGD and FEM is provided in Table 4. According to the table, increases with frequency due to skin and proximity effects. The results of the PGD match well with FEM.
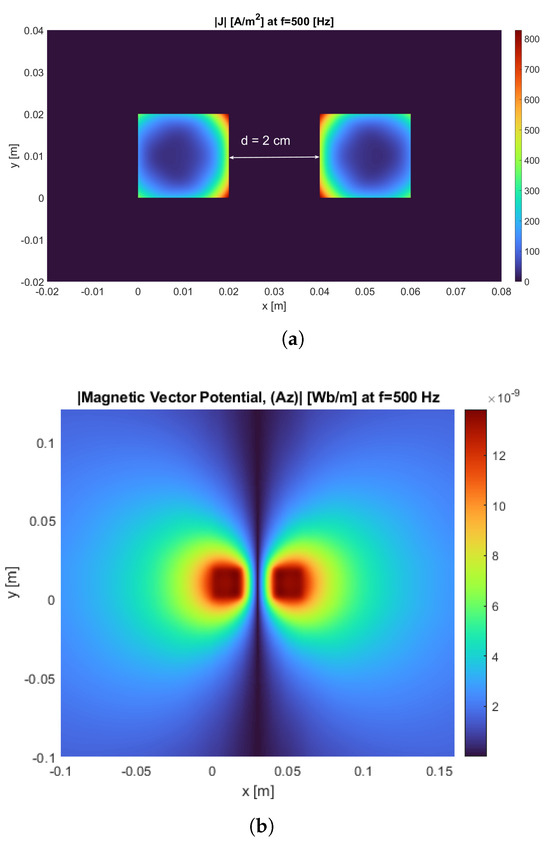
Figure 11.
Case 2O: (a) magnitude of current density distribution and (b) magnitude of magnetic vector potential of two parallel rectangular conductors with opposite current directions at using PGD.

Table 4.
in for one of the conductors of Case 2O.
4.2. Case 2S: Two Rectangular Conductors with Current in Same Direction
The same two parallel rectangular conductors as in Case 2O are considered but with currents in the same direction. The current density distribution and magnetic vector potential calculated using PGD are shown in Figure 12. of one of the conductors of Case 2S calculated using both PGD and FEM approaches in the frequency range of 50–10,000 Hz are provided in Table 5. As expected, in Case 2O, the current distribution is higher at the near edges of the conductors, whereas in Case 2S, the far edges of the conductors see a higher current distribution. The increase in ac resistance for Case 2S and Case 2O is due to skin and proximity effects, whereas in Case 1, the increase in the ac resistance with frequency is due to the skin effect only. The proximity effect is more pronounced at higher frequencies and when the conductors are closer to each other [29].
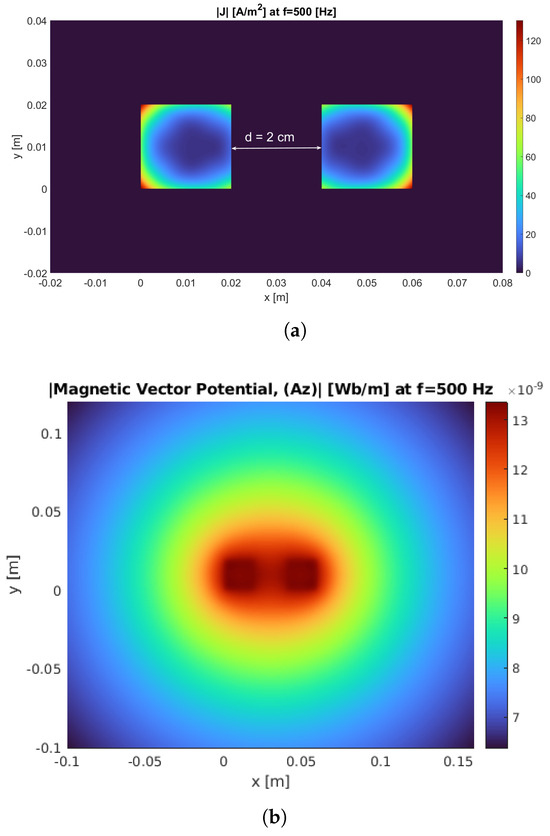
Figure 12.
Case 2S: Magnitude of (a) current density distribution and (b) magnetic vector potential of two parallel rectangular conductors with the same current directions at using PGD.

Table 5.
in for one of the conductors of Case 2S.
The effect of decreasing the distance between conductors (d in Figure 12a) on is shown in Table 6 at . The closer the conductors to each other, the more proximity effect they have on each other, which results in higher .

Table 6.
Variation of of the conductors of Case 2S as function of separation d at .
4.3. Case 2N: Two Rectangular Conductors with Only One Carrying a Current
In this case, two parallel conductors are considered where the first one has an external current density ( A/m2, and the second one has external current density . Due to the proximity effect, a current is induced in the second conductor in the opposite direction of the current of the first conductor. Moreover, the distribution of current in conductor 1 also changes due to the proximity effect. The magnitude of the current density distribution and magnetic vector potential of both conductors at Hz are shown in Figure 13. of conductor 1 is calculated as and using PGD and the FEM, respectively. The current density distribution in conductor 1 on and is shown in Figure 14 for both PGD and FEM. Unlike the single conductor, which only has the skin effect, the current distribution is not symmetric due to the proximity effect. These results confirm that the PGD technique is accurate and can handle more complex situations.
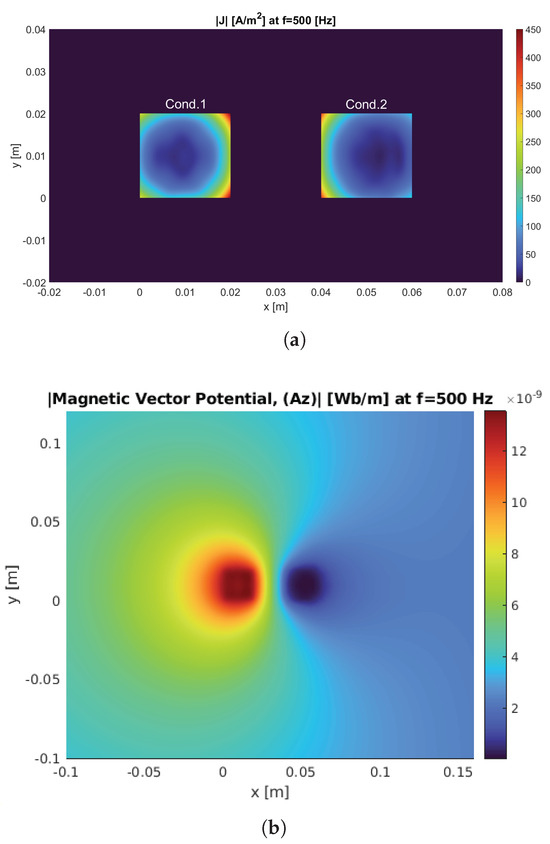
Figure 13.
Case 2N: Magnitude of (a) current density distribution and (b) magnetic vector potential of two parallel rectangular conductors at using PGD when A/m2 and A/m2.
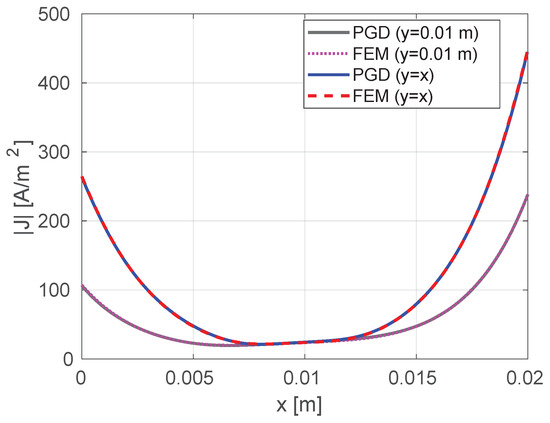
Figure 14.
Current density distribution of conductor 1 of Case 2N on and at Hz.
4.4. Case 3: Array of Conductors
An array of conductors is considered to further analyze the validity of the PGD approach. A array of conductors with a conductor size of , conductivity , and frequency is considered. The current density distribution is calculated at the cross section of conductors using PGD in two cases:
- All conductors have external current with the same current directions, A/m2,
- Only one conductor has an external current, A/m2, and the rest of the conductors have zero external currents, .
4.4.1. Case 3S-All Conductors Have Current with the Same Direction
The magnitude of the current density distribution at the cross-section of the conductors determined using PGD is shown in Figure 15. Due to the proximity effect of conductors on each other, the current density distribution is affected. In fact, the current density is the highest at the edges of the array, and the whole array behaves similar to a single conductor.The change in the current density distribution would cause more loss at higher frequencies and, in turn, higher ac resistance. of conductor 1 is calculated as and at 500 Hz using the PGD and the FEM, respectively. The current density distribution in conductor 1 on is calculated using PGD and FEM at 500 Hz and shown in Figure 16.
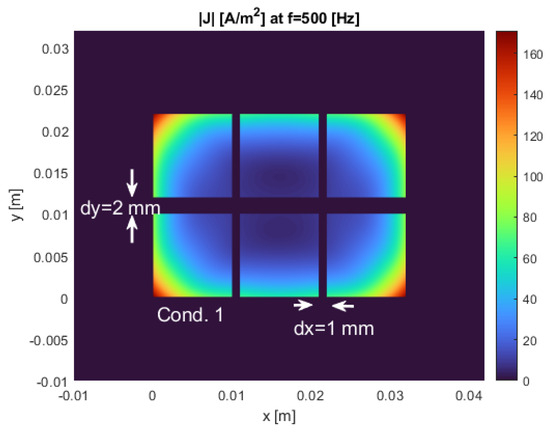
Figure 15.
Array of conductors with the same current direction.
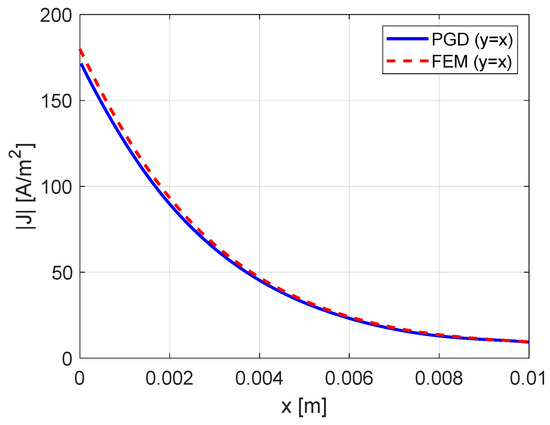
Figure 16.
Current density distribution of conductor 1 of Case 3S on at 500 Hz.
4.4.2. Case 3N-Only One Conductor Has Current
In this case, only conductor one has an external current density A/m2 while the other conductors have zero external current density. Figure 17 shows the current density distribution at the cross section of conductors solved using the PGD approach. There is induced current or proximity current only at the conductors in the vicinity of conductor 1, while the rest of the conductors have negligible induced current. of conductor 1 is calculated as and at 500 Hz using the PGD and the FEM, respectively. Moreover, current density distribution in conductor 1 on is calculated using PGD and FEM at 500 Hz and is shown in Figure 18. These results verify the validity of the PGD approach.
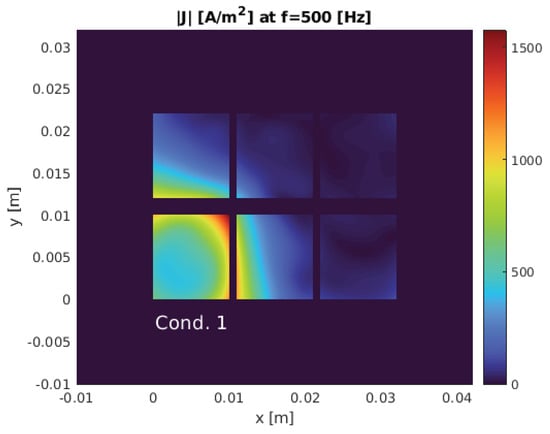
Figure 17.
Array of conductors with one conductor carrying current.
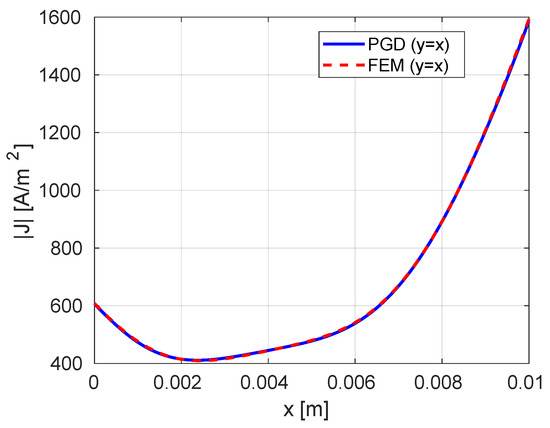
Figure 18.
Current density distribution of conductor 1 of Case 3N on at 500 Hz.
5. Conclusions
The proper generalized decomposition (PGD) technique was used for studying the skin and proximity effect of rectangular conductors. Magnetic vector potential was calculated as a set of 1D functions at each frequency, which needs less computational resources than traditional 2D numerical approaches while still maintaining good accuracy. To improve the accuracy of the PGD method over a wide range of frequencies and to reduce the required memory, three different frequency-dependent meshing approaches were employed. The ac resistance, magnetic vector potential, and current density distribution of a single rectangular conductor were calculated, and the results were compared with a commercial FEM software with great accuracy. It was shown that the existing PGD approach, that considered just one meshing for the entire frequency range with frequency as a function, was only accurate at lower frequencies where current distributes almost evenly at the cross section of conductors. However, the PGD approach considered in this paper considered separate meshing at each frequency, and had great accuracy over a wide frequency range. For proximity effect studies, different scenarios were considered to show the validity of the approach. First, two parallel conductors were considered in three different cases, with the same and opposite external current directions, and when one of the conductors does not have an external current. Depending on the current direction and the distance between conductors, the proximity effect would change the current distribution. The PGD was able to accurately calculate this. An array of conductors were studied in two different situations where all conductors carry an external current with the same direction, and when just one of the conductors carried an external current. The PGD results were as accurate as the FEM results but with less computational effort. The simulated scenarios could resemble busbars or transformer winding, and can be applied to a higher number of conductors with fewer computational resources.
Author Contributions
Conceptualization, B.T., A.M.G. and B.K.; methodology, B.T., A.M.G. and B.K.; software, B.T.; validation, B.T., A.M.G. and B.K.; formal analysis, B.T., A.M.G. and B.K.; investigation, B.T., A.M.G. and B.K.; resources, A.M.G. and B.K.; data curation, B.T.; writing—original draft preparation, B.T.; writing—review and editing, B.T., A.M.G. and B.K.; visualization, B.T.; supervision, A.M.G. and B.K.; project administration, A.M.G. and B.K.; funding acquisition, A.M.G. and B.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Sciences and Engineering Research Council of Canada (NSERC).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ac | Alternating current |
| EMC | Electromagnetic compatibility |
| FDTD | Finite difference time domain |
| FEM | Finite element method |
| 1D | One-dimensional |
| ODE | Ordinary differential equation |
| PDE | Partial differential equations |
| PEEC | Partial element equivalent circuit |
| PUL | Per unit length |
| PGD | Proper generalized decomposition |
| SMC | Soft magnetic composites |
| 2D | Two-dimensional |
References
- Holloway, C.L.; Kuester, E.F. DC Internal Inductance for a Conductor of Rectangular Cross Section. IEEE Trans. Electromagn. Compat. 2009, 51, 338–344. [Google Scholar] [CrossRef]
- Holloway, C.L.; Kuester, E.F.; Ruehli, A.E.; Antonini, G. Partial and Internal Inductance: Two of Clayton R. Paul’s Many Passions. IEEE Trans. Electromagn. Compat. 2013, 55, 600–613. [Google Scholar] [CrossRef]
- Holloway, C.L.; Kuester, E.F. Net and Partial Inductance of a Microstrip Ground Plane. IEEE Trans. Electromagn. Compat. 1998, 40, 33–46. [Google Scholar] [CrossRef]
- Williams, D.F.; Holloway, C.L. Transmission-line parameter approximation for digital simulation. IEEE Trans. Electromagn. Compat. 2001, 43, 466–470. [Google Scholar] [CrossRef]
- Antonini, G.; Orlandi, A.; Paul, C. Internal impedance of conductors of rectangular cross section. IEEE Trans. Microw. Theory Tech. 1999, 47, 979–985. [Google Scholar] [CrossRef]
- Antonini, G.; Orlandi, A.; Pignari, S.A. Review of Clayton R. Paul studies on multiconductor transmission lines. IEEE Trans. Electromagn. Compat. 2013, 55, 639–647. [Google Scholar] [CrossRef]
- Wang, Y.; Pries, J.; Zhou, K.; Hofmann, H.; Rizzo, D. Computationally Efficient AC Resistance Model for Stator Winding with Rectangular Conductors. IEEE Trans. Magn. 2020, 56, 1–9. [Google Scholar] [CrossRef]
- Choi, M.; Choi, G. Modeling, Investigation, and Mitigation of AC Losses in IPM Machines with Hairpin Windings for EV Applications. Energies 2021, 14, 8034. [Google Scholar] [CrossRef]
- Piatek, Z.; Baron, B.; Jablonski, P.; Kusiak, D.; Szczegielniak, T. Numerical Method of Computing Impedances. Prog. Electromagn. Res. B 2013, 51, 135–156. [Google Scholar] [CrossRef][Green Version]
- Labridis, D.; Dokopoulos, P. Electromagnetic forces in three-phase rigid busbars with rectangular cross-sections. IEEE Trans. Power Deliv. 1996, 11, 793–800. [Google Scholar] [CrossRef]
- CIGRE. Brochure, 577a. Electrical Transient Interaction between Transformers and the Power System-Part 1: Expertise, Joint Working Group a2/c4. 39. CIGRE April 2014. p. 176. Available online: https://www.e-cigre.org/publications/detail/577a-electrical-transient-interaction-between-transformers-and-the-power-system-part-1-expertise.html (accessed on 19 April 2024).
- Lammeraner, J.; Stafl, M. Eddy Currents; Iliffe Books Ltd.: London, UK, 1966. [Google Scholar]
- Stoll, R.L. The Analysis of Eddy Currents; Oxford University Press: Oxford, UK, 1974. [Google Scholar]
- de Leon, F.; Semlyen, A. Detailed modeling of eddy current effects for transformer transients. IEEE Trans. Power Deliv. 1994, 9, 1143–1150. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Tang, W.H.; Ji, T.Y.; Wu, Q.H. Finite-element modeling for analysis of radial deformations within transformer windings. IEEE Trans. Power Deliv. 2014, 29, 2297–2305. [Google Scholar] [CrossRef]
- Shintemirov, A.; Tang, W.H.; Wu, Q.H. A hybrid winding model of disc-type power transformers for frequency response analysis. IEEE Trans. Power Deliv. 2009, 24, 730–739. [Google Scholar] [CrossRef]
- Ametani, A.; Fuse, I. Approximate method for calculating impedance of multiconductor with arbitrary cross-section. Electr. Eng. Jpn. 1991, 111, 896–902. [Google Scholar] [CrossRef]
- Ametani, A.; Ohno, T. Transmission Line Theories for the Analysis of Electromagnetic Transients in Coil Windings. In Electromagnetic Transients in Transformer and Rotating Machine Windings; Su, Q., Ed.; IGI Global: Hershey, PA, USA, 2013; pp. 1–44. [Google Scholar]
- Asada, T.; Baba, Y.; Nagaoka, N.; Ametani, A.; Mahseredjian, J.; Yamamoto, K. A Study on Basic Characteristics of the Proximity Effect on Conductors. IEEE Trans. Power Deliv. 2017, 32, 1790–1799. [Google Scholar] [CrossRef]
- Tabei, B.; Ametani, A.; Gole, A.M.; Kordi, B. Quasi-Analytical Calculation of Frequency-Dependent Resistance of Rectangular Conductors Considering the Edge Effect. Energies 2022, 15, 503. [Google Scholar] [CrossRef]
- Pagnetti, A.; Xemard, A.; Paladian, F.; Nucci, C.A. An improved method for the calculation of the internal impedances of solid and hollow conductors with the inclusion of proximity effect. IEEE Trans. Power Deliv. 2012, 27, 2063–2072. [Google Scholar] [CrossRef]
- Ruehli, A.E. Equivalent circuit models for three-dimensional multiconductor systems. IEEE Trans. Microw. Theory Tech. 1974, 22, 216–221. [Google Scholar] [CrossRef]
- Antonini, G.; Cristina, S.; Orlandi, A. PEEC modeling of lightning protection systems and coupling to coaxial cables. IEEE Trans. Electromagn. Compat. 1998, 40, 481–491. [Google Scholar] [CrossRef]
- Mei, S.; Ismail, Y.I. Modeling skin and proximity effects with reduced realizable RL circuits. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2004, 12, 437–447. [Google Scholar]
- Bednarz, C.; Schreiber, H.; Leone, M. Efficient multiport equivalent circuit for skin and proximity effect in parallel conductors with arbitrary cross sections. IEEE Trans. Electromagn. Compat. 2018, 60, 2053–2056. [Google Scholar] [CrossRef]
- Chen, H.; Du, Y. Proximity effect modelling for cables of finite length using the hybrid partial element equivalent circuit and artificial neural network method. IET Gener. Transm. Distrib. 2018, 12, 3876–3882. [Google Scholar] [CrossRef]
- Kovacevic-Badstuebner, I.; Romano, D.; Lombardi, L.; Grossner, U.; Ekman, J.; Antonini, G. Accurate calculation of partial inductances for the orthogonal PEEC formulation. IEEE Trans. Electromagn. Compat. 2020, 63, 82–92. [Google Scholar] [CrossRef]
- Paul, C.R. Analysis of Multiconductor Transmission Lines; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Tabei, B.; Ametani, A.; Gole, A.M.; Kordi, B. Study of Skin and Proximity Effects of Conductors for MTL-Based Modeling of Power Transformers Using FEM. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- McLaren, P.; Oraee, H. Multiconductor transmission-line model for the line-end coil of large AC machines. IEE Proc. B (Electr. Power Appl.) 1985, 132, 149–156. [Google Scholar] [CrossRef]
- Morisco, D.P.; Rapp, H.; Iepure, I.L.; Möckel, A. Extended modelling approach of hairpin winding eddy current losses in high power density traction machines. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; Volume 1, pp. 874–880. [Google Scholar]
- De Gersem, H.; Muetze, A. Finite-element supported transmission-line models for calculating high-frequency effects in machine windings. IEEE Trans. Magn. 2012, 48, 787–790. [Google Scholar] [CrossRef]
- Krings, A.; Paulsson, G.; Sahlén, F.; Holmgren, B. Experimental investigation of the voltage distribution in form wound windings of large AC machines due to fast transients. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1700–1706. [Google Scholar]
- Toudji, M.; Parent, G.; Duchesne, S.; Dular, P. Determination of winding lumped parameter equivalent circuit by means of finite element method. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Mihaila, V.; Duchesne, S.; Roger, D. A simulation method to predict the turn-to-turn voltage spikes in a PWM fed motor winding. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1609–1615. [Google Scholar] [CrossRef]
- Ammar, A.; Chinesta, F.; Cueto, E.; Doblaré, M. Proper generalized decomposition of time-multiscale models. Int. J. Numer. Methods Eng. 2012, 90, 569–596. [Google Scholar] [CrossRef]
- Chinesta, F.; Leygue, A.; Bordeu, F.; Aguado, J.V.; Cueto, E.; González, D.; Alfaro, I.; Ammar, A.; Huerta, A. PGD-based computational vademecum for efficient design, optimization and control. Arch. Comput. Methods Eng. 2013, 20, 31–59. [Google Scholar] [CrossRef]
- Croft, T.L.D. Proper Generalised Decompositions: Theory and Applications. Ph.D. Thesis, Cardiff University, Cardiff, UK, 2015. [Google Scholar]
- Ammar, A.; Mokdad, B.; Chinesta, F.; Keunings, R. A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modeling of complex fluids. J. Non-Newton. Fluid Mech. 2006, 139, 153–176. [Google Scholar] [CrossRef]
- Ammar, A.; Mokdad, B.; Chinesta, F.; Keunings, R. A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modelling of complex fluids: Part II: Transient simulation using space-time separated representations. J. Non-Newton. Fluid Mech. 2007, 144, 98–121. [Google Scholar] [CrossRef]
- Zou, X.; Conti, M.; Díez, P.; Auricchio, F. A nonintrusive proper generalized decomposition scheme with application in biomechanics. Int. J. Numer. Methods Eng. 2018, 113, 230–251. [Google Scholar] [CrossRef]
- Chinesta, F.; Keunings, R.; Leygue, A. The Proper Generalized Decomposition for Advanced Numerical Simulations: A Primer; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Sancarlos, A.; Ghnatios, C.; Duval, J.L.; Zerbib, N.; Cueto, E.; Chinesta, F. Fast computation of multi-parametric electromagnetic fields in synchronous machines by using pgd-based fully separated representations. Energies 2021, 14, 1454. [Google Scholar] [CrossRef]
- Pineda-Sanchez, M.; Sapena-Baño, A.; Perez-Cruz, J.; Martinez-Roman, J.; Puche-Panadero, R.; Riera-Guasp, M. Internal inductance of a conductor of rectangular cross-section using the proper generalized decomposition. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 2007–2021. [Google Scholar] [CrossRef]
- Sancarlos-González, A.; Pineda-Sanchez, M.; Puche-Panadero, R.; Sapena-Bano, A.; Riera-Guasp, M.; Martinez-Roman, J.; Perez-Cruz, J.; Roger-Folch, J. Computation of the impedance of rectangular conductors as a function of the frequency using a parametric proper generalized decomposition. In Proceedings of the 2017 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF) Book of Abstracts, Lodz, Poland, 14–16 September 2017; pp. 1–2. [Google Scholar]
- Henneron, T.; Clenet, S. Application of the PGD and DEIM to solve a 3-D non-linear magnetostatic problem coupled with the circuit equations. IEEE Trans. Magn. 2015, 52, 1–4. [Google Scholar] [CrossRef][Green Version]
- Henneron, T.; Benabou, A.; Clenet, S. Nonlinear proper generalized decomposition method applied to the magnetic simulation of a SMC microstructure. IEEE Trans. Magn. 2012, 48, 3242–3245. [Google Scholar] [CrossRef][Green Version]
- Malik, M.H.; Borzacchiello, D.; Chinesta, F.; Diez, P. Inclusion of frequency-dependent parameters in power transmission lines simulation using harmonic analysis and proper generalized decomposition. Int. J. Numer. Model. Electron. Netw. Devices Fields 2018, 31, 1–16. [Google Scholar] [CrossRef]
- Dumon, A.; Allery, C.; Ammar, A. Proper general decomposition (PGD) for the resolution of Navier–Stokes equations. J. Comput. Phys. 2011, 230, 1387–1407. [Google Scholar] [CrossRef][Green Version]
- Qin, Z.; Talleb, H.; Yan, S.; Xu, X.; Ren, Z. Application of PGD on parametric modeling of a piezoelectric energy harvester. IEEE Trans. Magn. 2016, 52, 1–11. [Google Scholar] [CrossRef]
- Yan, S.; Xu, X.; Lyu, P.; Ren, Z. Application of POD and PGD for efficient parameter sweeping in frequency-domain full-wave problems. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Li, Y.; Yan, S.; Xu, X.; Lyu, P.; Ren, Z. 3-D IC interconnect parasitic capacitance extraction with a reformulated PGD algorithm. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Kazemzadeh-Parsi, M.J.; Chinesta, F.; Ammar, A. Proper Generalized Decomposition for Parametric Study and Material Distribution Design of Multi-Directional Functionally Graded Plates Based on 3D Elasticity Solution. Materials 2021, 14, 6660. [Google Scholar] [CrossRef]
- Boumesbah, A.; Tomezyk, J.; Henneron, T. Metamodel of Parametric Geometric Magnetostatic Problem Based on PGD and RBF Approaches. IEEE Trans. Magn. 2022, 59, 1–10. [Google Scholar] [CrossRef]
- Ammar, A.; Chinesta, F.; Diez, P.; Huerta, A. An error estimator for separated representations of highly multidimensional models. Comput. Methods Appl. Mech. Eng. 2010, 199, 1872–1880. [Google Scholar] [CrossRef]
- Bouclier, R.; Louf, F.; Chamoin, L. Real-time validation of mechanical models coupling PGD and constitutive relation error. Comput. Mech. 2013, 52, 861–883. [Google Scholar] [CrossRef]
- Ladeveze, P.; Chamoin, L. On the verification of model reduction methods based on the proper generalized decomposition. Comput. Methods Appl. Mech. Eng. 2011, 200, 2032–2047. [Google Scholar] [CrossRef]
- de Almeida, J.M. A basis for bounding the errors of proper generalised decomposition solutions in solid mechanics. Int. J. Numer. Methods Eng. 2013, 94, 961–984. [Google Scholar] [CrossRef]
- Tabei, B.; Ametani, A.; Gole, A.M.; Kordi, B. A Study on AC Resistance Calculation of Single Rectangular Conductors. In Proceedings of the 2021 IEEE Electrical Power and Energy Conference (EPEC), Toronto, ON, Canada, 22–31 October 2021; pp. 459–462. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).