Investigations on Bi Doped Cu₂Se Prepared by Solid State Reaction Technique for Thermoelectric Applications

Abstract

The influence of Bi doping on the structural and thermoelectric properties of Cu₂Se is presented in this work. Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) samples were prepared using conventional solid-state reaction techniques. According to room temperature XRD results, Cu_2−xBi_xSe samples have a monoclinic crystal structure. Doping Bi to the Cu site acts as a donor, lowering the hole concentration, except for the sample with x = 0.004. The resistivity of the Cu_2−xBi_xSe sample increases with an increase in Bi content. Seebeck coefficient data confirm that the holes are the charge carriers in Cu_2−xBi_xSe samples. At 700 K, the Cu_1.988Bi_0.012Se sample has the highest power factor of 1474 μWm⁻¹K⁻², showing great potential in developing high-performance Cu₂Se based thermoelectric materials.

1. Introduction

The increasing demand for energy caused by the expanding global population places extreme strain on the available energy supplies. Due to the finite supply of fossil fuels and their detrimental effects on the environment, the research community is exploring sustainable energy harvesting techniques to satisfy the world's current energy needs. The globe paradoxically faces a shortage of renewable energy resources on the one hand. On the other side, a tremendous quantity of heat is produced by our industrial operations, car exhaust, and building heating systems, which is wasted in the environment. Such waste heat may be converted into energy (electricity) to assist us in satisfying our energy needs while also preserving the environment [1]. Thermoelectric materials can directly convert temperature differences to electricity, making them a viable solution to energy problems and pollution [2]. Thermoelectric devices are solid-state devices with no moving parts, and they have the benefits of cheap maintenance, high dependability, and exceptional scalability. The thermoelectric (TE) devices emit no greenhouse gases, making them environmentally beneficial. The scientific world has been attracted to thermoelectric materials for decades due to all their unique properties. Nevertheless, TE devices are insufficient when compared to their traditional counterparts due to their low efficiency. For the scientific community, creating TE materials with greater efficiency has remained a challenging part [1]. In the mid-1990s, theoretical predictions suggested that nanostructure engineering might considerably improve thermoelectric efficiency, prompting experimental efforts to demonstrate proof-of-principle and high-efficiency materials [3]. Thermoelectric materials convert heat into electricity through Seebeck effect. Utilizing the Peltier effect, they act as cooling devices when they are used in a reverse manner.

The power factor, $PF=S^2\sigma$, is used to evaluate the efficiency of thermoelectric materials where σ and S are electrical conductivity, and the Seebeck coefficient respectively [4]. Because of their potential for good thermoelectric performance, many materials have been investigated. Bi-Te alloys [5,6], Half-Heusler compounds [7,8], PbTe [9,10], SnSe [11,12], and skutterudites [13] are a few of the most well-known. Cu₂Se-based compounds have recently received much attention because of their low thermal conductivity, toxicity, earth abundance, and cheapness [14]. Recent years have seen the development of a number of novel methods, including Phonon-Glass-Electron-Crystal (PGEC) paradigm, the use of band resonant states to enhance the density of states, formation of bulk nano-composite structures, increasing the band degeneracy by prompting band convergence by varying the composition or temperature, using ultrafast solidification techniques, seeking material with extreme anharmonicity of lattice vibration and even Phonon-Liquid-Electron Crystal (PLEC) concepts have all been proposed to enhance the efficiency of thermoelectric materials. It seems to work well in super-ionic compounds such as Cu_2−xX (X = S, Se, Te). Although having a straightforward chemical formula, copper chalcogenides have a very complicated crystal structure. Heyding was the first to report on the structure and phase diagram of Cu₂Se; various groups thereafter conducted thorough structural investigations [15].

Cu₂Se has two distinct crystal structures: the α-phase at low temperatures and the β-phase at high temperatures. Doping is one of the most significant methods for improving a material's thermoelectric characteristics. Several dopants have been suggested to improve the chemical stability, the Seebeck coefficient, or the electrical conductivity of copper selenide to improve its thermoelectric performance [14]. Many researches were done on doping different dopants like Mg [16], Na [17], Ni [14], Te [1], K [18], etc in Cu₂Se system. The power factor of Cu_1.99Mg_0.01Se ~ 1200 μWm⁻¹K⁻² [16], Cu_1.96Na_0.04Se ~ 900 μWm⁻¹K⁻² [17], Cu₂Se ~ 1100 μWm⁻¹K⁻² [2], Cu_1.99K_0.01Se~900 μWm⁻¹K⁻² [18] at 700 K. Heavy-element dopants have piqued our interest, implying that doping heavy-element is a viable technique to increase the complexity system [2]. Recently Liao et al. [19] studied Bi-doped α-Cu₂Se near room temperature, and Lisha Xue et al. studied the impact of Bi doping on the thermoelectric characteristics of Cu₂Se materials [2]. Bismuth is doped into Cu₂Se to enhance its electrical property.

The fabrication of pure copper selenide and doped material has been proposed using various techniques, such as high-temperature, high-pressure technology, mechanical alloying, melting followed by spark plasma sintering, and the conventional solid-state sintering method [1,2,14,19,20]. S. Mangavati et al. used a solid-state reaction technique to prepare Te-doped Cu₂Se and obtained a power factor of ~ 800 μWm⁻¹K⁻² at 350 K [1]. Zhiming Geng et al. used the solid-state reaction technique to prepare Cu₂Se and obtained a power factor of ~ 780 μWm⁻¹K⁻² at 350K [20]. The present work uses the solid-state reaction technique to synthesize Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) samples. The effects of Bi doping on electrical, structural, and other thermoelectric properties of Cu₂Se are investigated.

2. Experiment Details

Material Synthesis

Polycrystalline Cu₂Se and Bi-doped Cu_2−xBi_xSe samples were produced using a standard solid-state reaction approach. Cu (99.7%, Loba Chemie, Mumbai, India), Se (99%, Molychem, Mumbai, India), and Bi (99%, Molychem, Mumbai, India) powders were taken and mixed using a mortar pestle according to stoichiometric ratios. The powders were compressed into rectangular pellets using a hydraulic press with a 5 MPa pressure. These pellets were sealed in quartz tubes under a high vacuum (10⁻⁶ mBar). The sealed quartz tube was placed in furnace at 973 K for 72 h. Later, the furnace was allowed to cool to room temperature naturally. Further, the obtained pellets were ground, pelletized, vacuum sealed, and sintered at 473 K for 48 h. Two-step sintering was performed to obtain more homogeneous compounds. Figure 1 shows the schematic representing the synthesis process of Cu_2−xBi_xSe samples.

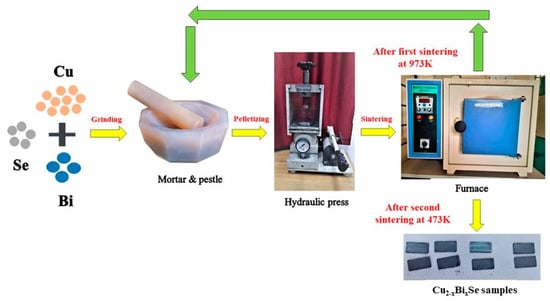
Figure 1. Schematic representing the synthesis process of Cu_2−xBi_xSe samples.

To examine the crystallographic details of the prepared samples, X-ray diffraction (Rigaku miniflex 600) using wavelength of Cu K_α (λ = 1.5406 Å) studies at room temperature were performed. Rietveld refinement technique with the Fullproof program was used to acquire crystallographic information. To study the morphology of the compound Scanning Electron microscope (SEM) (JEOL, JSM-7610FPlus) micrographs were taken. Energy Dispersive X-ray Spectroscopy (EDS) analysis was carried out to study the chemical composition of the prepared sample. The room-temperature Hall effect measurement was carried out using Ecopia HMS—5500 system to determine the carrier concentration and mobility using a field strength of 0.5 T. High-temperature electrical resistivity and thermopower are measured simultaneously using the Linseis LSR—3 system.

3. Results and Discussion

3.1. X-ray Diffraction (XRD) Analysis

The powder X-ray diffraction studies of the Cu_2−xBi_xSe (x = 0,0.004,0.008,0.012) samples show that all the materials are polycrystalline in nature. The structure of the undoped sample is found to be monoclinic with the space group of Cm. Also, all the doped samples exhibited monoclinic structure with the space group P2₁/c [1]. The Rietveld refinement technique with the Fullprof program was used to acquire the crystallographic information of pure and Bi-doped Cu₂Se samples. The XRD pattern of the Rietveld refined graph is represented in Figure 2. Vertical lines are used to represent all permitted peaks, and blue lines are used to depict the difference between the observed and fitted patterns for each peak. For all the four samples the major peak is located at θ = 44º. From the Rietveld refinement technique the values of lattice parameters, χ² and other goodness of fitting parameters (R_p, R_wp, R_exp) are estimated. Table 1 lists the values of several parameters of Cu_2−xBi_xSe samples calculated from the refinement. Here, a, b and c are the lattice parameters. Since the Cu_2−xBi_xSe samples are monoclinic a ≠ b ≠ c, and α = β = 90°, γ = 101°. The obtained χ² value of Cu₂Se is 1.995, Cu_1.996Bi_0.004Se is 2.289, Cu_1.992Bi_0.008Se is 1.538, Cu_1.988Bi_0.012Se is 1.531.

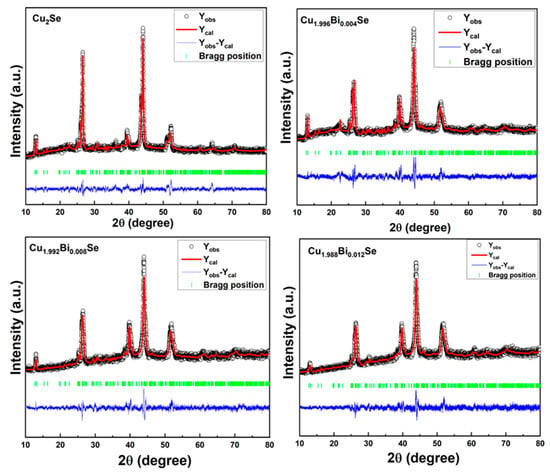
Figure 2. Rietveld refinement X-ray plots of Cu_2−xBi_xSe samples.

Table 1. Rietveld refined crystallographic parameters and fitting parameters for Cu_2−xBi_xSe samples.

Compositions	x = 0.000	x = 0.004	x = 0.008	x = 0.012
a (Å)	7.2095 ± 0.0003	7.1292 ± 0.0008	7.1477 ± 0.0009	7.1550 ± 0.0007
b (Å)	4.1058 ± 0.0001	4.1098 ± 0.0004	4.1223 ± 0.0004	4.1261 ± 0.0003
c (Å)	13.8195 ± 0.0015	13.7745 ± 0.0013	13.7836 ± 0.0020	13.7900 ± 0.0015
α = γ (°)	90.000	90.000	90.000	90.000
β (°)	101.490	101.290	101.325	101.341
V (${\mathsf{\AA }}^3$)	400.870 (0.050)	395.775 (0.069)	398.224 (0.083)	399.157 (0.030)
Rp	35.7	35.7	29.8	31.6
Rwp	28.0	30.9	27.3	28.5
Rexp	19.8	20.4	22.0	23.0
${\chi }^2$	1.995	2.289	1.538	1.531
GoF-index	1.4	1.5	1.2	1.2

XRD data was further analyzed to understand the effect of crystallite size and strain on the physical characteristics of the examined samples. It is widely known that the strain and crystallite size within the unit cell affects the XRD peak broadening. To distinguish the contribution of both effects multiple approaches, including Scherrer, modified Scherrer, and size strain plot (SSP), were used to identify the contribution of both effects, which are described in the following sections.

3.1.1. Scherrer Method

The peak broadening with crystallite size and lattice strain resulting from dislocation may be assessed using the straightforward and effective XRD peak profile analysis. Based on the Scherrer equation, the average crystallite size was determined from the XRD peak [21],

$$D=\frac{K\lambda }{\beta cos\theta }$$

(1)

where β is full width at half maximum, D is crystallite size, θ is diffraction angle, K is shape factor (here the value of K is taken as 0.9), λ = 1.5406 Å. The crystallite size varies from 16 nm to 36 nm, tabulated in Table 2. Dislocation density (δ), defined as the length of dislocation per unit volume of crystal, represents the number of flaws in the sample. The equation for calculating dislocation density is as follows [21]:

$$\delta =\frac{1}{D^2}$$

(2)

Table 2. Crystallite size, dislocation density, and strain of the sample calculated from Scherrer, modified Scherrer method, and size strain plot.

Bi Content, x	Crystallite Size, D (nm)			Dislocation Density, δ (1015 Lines/m2)			Strain, ε
	SSP	Modified Scherrer	Scherrer	SSP	Modified Scherrer	Scherrer	SSP	Scherrer
0.000	32 ± 3	43 ± 4	36 ± 4	1.00	0.54	0.77	0.007	0.001
0.004	63 ± 6	64 ± 6	51 ± 5	0.25	0.25	0.38	0.003	0.007
0.008	21 ± 2	21 ± 2	17 ± 2	2.22	2.29	3.38	0.014	0.002
0.012	17 ± 2	17 ± 2	17 ± 2	3.55	3.44	3.60	0.003	0.002

the strain (ε) is estimated using the following equation:

$$\epsilon =\frac{\beta cos\theta }{4}$$

(3)

3.1.2. Modified Scherrer Method

The modified Scherrer formula is based on the concept that applying the least square approach reduces the source of error, and one can obtain the average values of D through all the peaks. The equation used in the modified Scherrer method is [22],

$$\ln \beta =\ln \frac{K\lambda }{D}+\ln \frac{1}{\cos \theta }$$

(4)

hence the plot of lnβ versus ln(1/cosθ) for all or part of the specified peaks can be linear, as presented in Figure 3. The value of ln(Kλ/D) can be calculated from the intercept after establishing the best linear plot. The value of crystallite size is calculated using the equation given below [23],

$$D=\frac{{\mathrm{e}}^{\left(\mathrm{intercept}\right)}}{K\lambda }$$

(5)

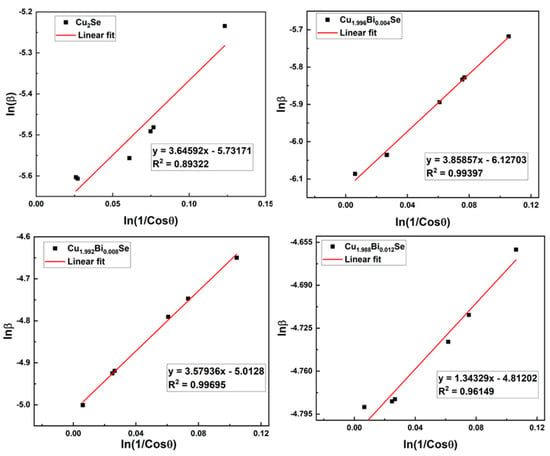
Figure 3. Modified Scherrer plots of Cu_2−xBi_xSesamples.

In modified Scherrer method the crystallite size varies between 17–64 nm and the dislocation density vary from 0.5 to 4 × 10¹⁵ lines/m².

3.1.3. Size-Strain Plot (SSP)

The role of strain for broadening is excluded in Scherrer and modified Scherrer methods. As a result, SSP is used to compute the crystallite size, which considers both size and strain contributions. One of the advantages of this strategy is that data from the high-angle reflections are given less weightage, where precision is typically low [21]. The strain profile is expected to be explained by the Gaussian function and crystallite size profile by the Lorentzian function and is given by [21],

$${\left(d\beta cos\theta \right)}^2=\frac{K\lambda }{D}{d}^2\beta cos\theta +\frac{{\epsilon }^2}{4}$$

(6)

and a graph of ${\left(d\beta cos\theta \right)}^2$ versus $d^2\beta cos\theta$ is plotted as shown in Figure 4. Slope and intercept were obtained from this graph which was further used to calculate crystallite size and strain respectively. The slope and intercept were obtained from this graph. The crystallite size is evaluated by,

$$D=\frac{K\lambda }{\mathrm{Slope}}$$

(7)

the Strain is estimated by the following Equation [21],

$$\epsilon =2\sqrt{\mathrm{Intercept}}$$

(8)

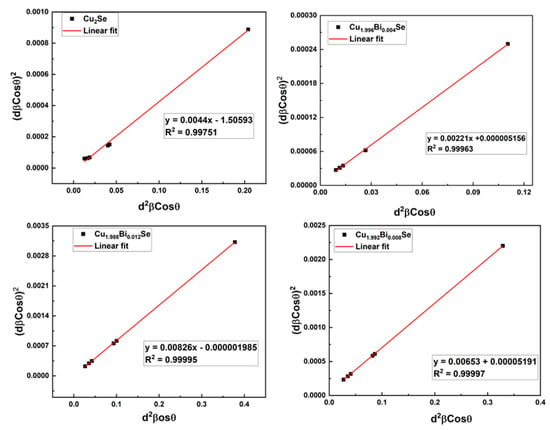
Figure 4. Size-Strain plots of Cu_2−xBi_xSe samples.

In SSP method, the crystallite size varies from 17–32 nm. Figure 4 displays a better fit, where all the data points are in a straight line. The conclusion drawn from the various approaches is that the crystallite size and micro-strain measurements acquired using the SSP are more accurate than those made using the other two methods for the materials used in the current study.

3.2. SEM and EDS Analysis

Figure 5A shows the SEM images of Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) samples. All the samples exhibit polycrystalline nature with randomly oriented grains. Due to the low dopant concentration, all samples have a similar morphology. Since sintering was performed at low temperatures, the examined samples do not exhibit clear grain development. Less porosity is observed in all the examined samples implying that the synthesized samples are dense, and grains are well connected. A high grain density can increase the number of grain boundaries in the material, which can act as a barrier to the movement of charge carriers (electrons or holes) and increase their scattering. This, in turn, can increase the Seebeck coefficient of the material. The presence of small grains between larger grains indicates grain size non-uniformity, which could scatter phonons and lower lattice heat conductivity [1].

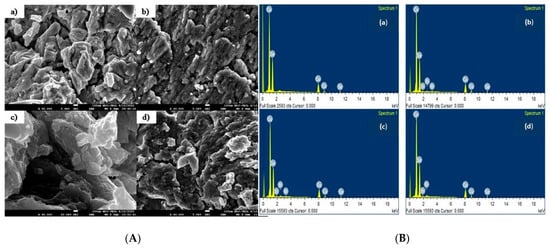
Figure 5. (A) SEM images of (a) Cu₂Se, (b) Cu_1.996Bi_0.004Se, (c) Cu_1.992Bi_0.008Se, (d) Cu_1.988Bi_0.012Se samples. (B) EDS spectrum of (a) Cu₂Se, (b) Cu_1.996Bi_0.004Se, (c) Cu_1.992Bi_0.008Se, (d) Cu_1.988Bi_0.012Se samples.

The chemical composition of the prepared sample is estimated using Energy Dispersive X-ray Spectroscopy (EDS). EDS spectra of Cu_2−xBi_xSe are shown in Figure 5B, and corresponding results are tabulated in Table 3. EDS data reveals that the chemical composition of prepared samples is close to the nominal composition within experimental limits. Figure 6a–d shows the elemental composition of Cu_2−xBi_xSe samples.

Table 3. EDS results of Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) samples.

Nominal Composition	Cu (At%)	Se (At%)	Bi (At%)
Cu2Se	68.41	31.59	0.0
Cu1.996Bi0.004Se	68.92	30.94	0.14
Cu1.992Bi0.008Se	68.54	30.87	0.59
Cu1.988Bi0.012Se	68.35	31.01	0.65

Figure 6. EDS map of (a) Cu₂Se, (b) Cu_1.996Bi_0.004Se, (c) Cu_1.992Bi_0.008Se, (d) Cu_1.988Bi_0.012Se.

3.3. Electrical and Thermelectric Transport Properties

3.3.1. Hall Measurement

The room temperature mobility and carrier concentration of all the samples is given in Table 4. The positive sign of the carrier concentration indicates that pristine and Bi-doped samples are p-type semiconductors. The plot of carrier concentration and mobility versus Bi content is shown in Figure 7. It is observed that carrier concentration and mobility follow the opposite trend except for x = 0.012. The carrier concentration of the pristine Cu₂Se sample is 18 × 10²⁰ cm⁻³. Bi acts as an electron donor [16]. It reduces the carrier concentration up to x = 0.008. After that, it significantly increases. This is due to the incorporation of trivalent Bismuth compensating for the Cu deficiency. The solubility of Bi is low in the Cu-Se matrix; hence after x = 0.008, it can regenerate the Cu deficiency, thereby enhancing the carrier concentration for x = 0.012 [19].

Table 4. Carrier concentration and mobility of Cu_2−xBi_xSe samples.

Bi Content x	Carrier Concentration (1020 cm−3)	Mobility (cm2V−1s−1)
0.00	18	128
0.004	32	22
0.008	6	23
0.012	8	38

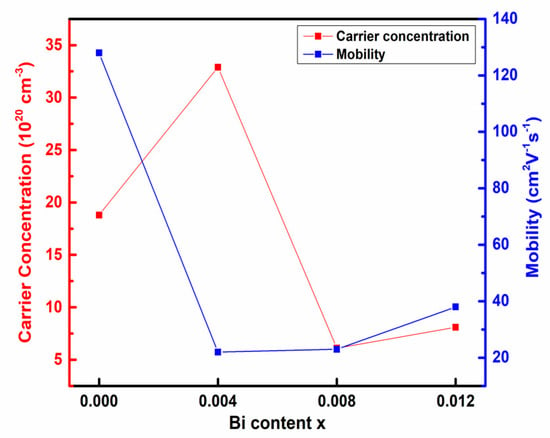
Figure 7. Plot of mobility and carrier concentration at 300K as a function of Bi doping content.

3.3.2. Resistivity Measurement

The electrical resistivity of Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) is carried out in the temperature range 300–700 K. The corresponding plot is shown in Figure 8a. The resistivity of all the samples increases linearly with temperature, indicating highly degenerate semiconducting characteristics. In comparison with the pristine, addition of Bi content has increased the resistivity in the measured temperature range. The obtained values in the range of 4.6 to 12.9 μΩ-m which agrees with the reported values [2,24]. At 700 K, an increase in the resistivity is observed with an increase in Bi content as represented in Figure 8b. This is attributed to electron donor behavior of Bi⁺³, which results in recombination of charge carriers thereby reducing the carrier concentration and hence increase the resistivity. Also, the increased resistivity for the doped samples could be a result of increased boundary scattering of the carriers leading to reduction in the mobility (See Figure 7) [25]. The pristine and doped samples exhibited a phase transition from α-phase to β-phase at about 350 K which is due to the transition of crystal structure from low temperature monoclinic to high temperature cubic [26]. The resistivity of the Cu_2−xBi_xSe sample at 300 K is given in Table 5. We attempted to study the behavior of electrical resistivity by various models. At high temperature region we attempted to fit the small polaron hopping (SPH) model. However, we observed that it was not valid for the presently investigated system. But the power law could well describe the resistivity data, as represented by Equation (9), for temperatures ranging from 400 K to 700 K [1]. The power-law fit is exhibited in Figure 9 and the parameters attained from the fit are tabulated in Table 6. Figure 8b shows the comparison of the resistivity of the synthesized composition with existing literature on Cu2Se with different dopants. From this graph, we can understand that the prepared samples of Cu2−xBixSe (x = 0.00, 0.004, 0.008, 0.012) have low resistivity compared to reported materials, which is one of the important criteria to get a high-power factor.

$$\rho \left(T\right)=a{T}^b$$

(9)

where T is the characteristic temperature.

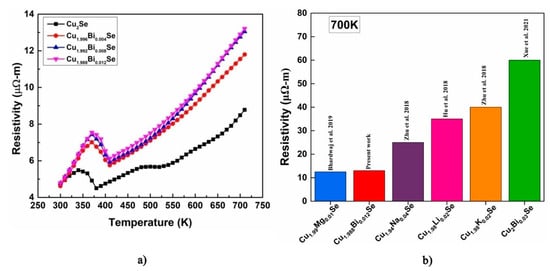
Figure 8. (a) Temperature-dependent resistivity plot of Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) samples, (b) comparison of resistivity of the synthesized composition with existing literature on Cu₂Se with different dopants [2,16,17,18,27].

Table 5. Value of Resistivity, Seebeck coefficient, Power factor for Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) samples at 300 K.

Bi Content (x)	Resistivity (μΩ-m)	Seebeck Coefficient (μV/K)	Power Factor (ΩWm−1K−2)
0.00	4.71	49.5	520
0.004	4.62	57.2	707
0.008	4.78	55.9	653
0.012	4.79	53.9	607

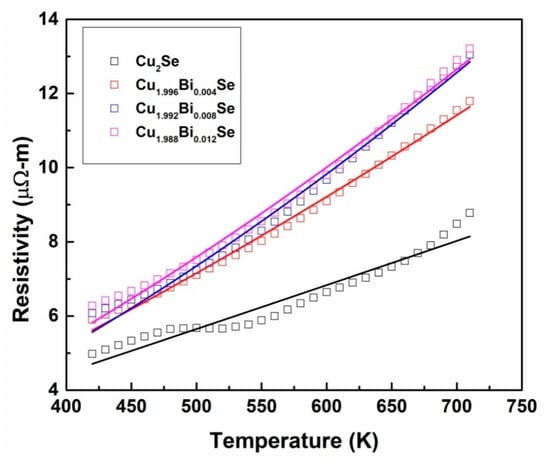
Figure 9. Resistivity data fitted with Power law (Equation (9)).

Table 6. Parameters obtained from power law (Equation (9)).

Bi Content x	a	b
0.000	0.00856	1.04451
0.004	0.00128	1.38871
0.008	0.00036	1.59499
0.012	0.00059	1.52026

3.3.3. Seebeck Coefficient

The temperature-dependent Seebeck coefficient for Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) is measured in the temperature range 300–700 K. The variation is shown in Figure 10a. The positive sign of the Seebeck coefficient indicates that holes as dominant charge carriers which is confirmed with Hall measurements. It indicates that all the prepared samples are p-type semiconductors. The Seebeck coefficient of all the samples increases as the temperature rises, indicating the behavior of heavily doped semiconductors. With an increase in Bi concentration, the material's Seebeck coefficient increases due to the reduction in carrier concentration (See Figure 7) thereby verifying the Mott’s relation [28]. This trend is in agreement with the resistivity data. It shows that the dependency of carrier concentration is reflected in the nature of both the electrical resistivity and Seebeck coefficient. At room temperature, Seebeck coefficient for pristine sample is obtained as 49.5 μV/K which is in agreement with the reported values [29,30]. Room temperature Seebeck coefficient values of all the samples are listed in Table 5. Maximum Seebeck coefficient of 142 μV/K is obtained for the sample x = 0.012 at 700 K. Figure 10b represents comparison of Seebeck coefficient of synthesized Cu_1.988Bi_0.012Se to existing research on Cu₂Se with various dopants.

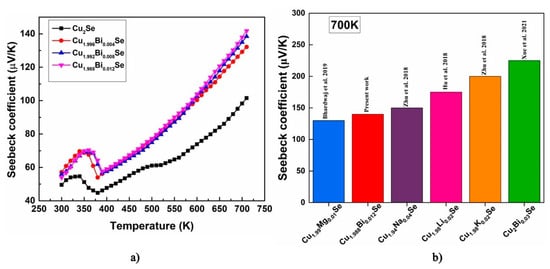
Figure 10. (a) Temperature-dependent Seebeck coefficient for Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) samples, (b) comparison of Seebeck coefficient of the synthesized composition with existing literature on Cu₂Se with different dopants [2,16,17,18,27].

3.3.4. Power Factor

The power factor of the Cu_2−xBi_xSe is calculated in the temperature range 300–700 K by using the formula $PF=\frac{S^2}{\rho }$ and represented in Figure 11a. The power factor of Cu_2−xBi_xSe increases with an increase in Bi content. Enhancement in the thermopower is reflected in the power factor. It shows an increasing trend with increasing temperature. The highest power factor of 1474 μWm⁻¹K⁻² is observed at 700 K for the Cu_1.988Bi_0.012Se sample which is 30% higher than the pristine sample at 700 K. The power factor for the Cu_2−xBi_xSe sample at 300 K is given in Table 5, and it can be observed that for Bi content x = 0.004 has the maximum power factor at room temperature. Due to high power factor Cu_2−xBi_xSe can be considered as promising thermoelectric material. Comparison of power factor of the synthesized compound with existing research on Cu₂Se with different dopants is represented in Figure 11b. It is observed that compared to other synthesized compounds present study has gained remarkable power factor.

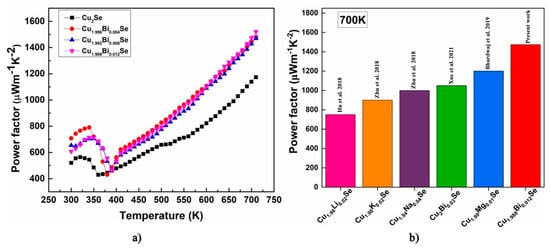
Figure 11. (a) Temperature-dependent Power factor for Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) samples, (b) comparison of power factor of the synthesized composition with existing literature on Cu₂Se with different dopants [1,16,17,18,27].

The comparison of power factors obtained from the current study and some previously studied compounds is given in Table 7. It provides the information about the power factor of various compounds which are prepared by different methods like solid state reaction technique, spark plasma sintering, hydrothermal method, high pressure synthesis, ball milling method etc. at 300 K and 700 K. The current study produced better outcomes than similar studies that have been published.

Table 7. Comparing the power factor of various compounds.

SI.No.	Compound	Year	Method	Power Factor~ (μWm−1K−2)		References
				At 300 K	At 700 K
1	Cu1.988Bi0.012Se		Solid state reaction technique	607	1474	Present work
2	Cu2Se	2021	High pressure synthesis	-	1100	[2]
3	Cu1.99Mg0.01Se	2019	Single step synthesis	-	1200	[16]
4	Cu2Se	2022	Solid state reaction technique	550	-	[1]
5	Cu1.99K0.01Se	2018	Hydrothermal method	-	900	[18]
6	Cu1.982Bi0.006Se	2019	Spark plasma sintering	700	-	[19]
7	Cu2SnSe2.96	2020	Solid state reaction technique	35	-	[27]
8	Pb0.96Bi0.04S	2021	Hydrothermal method	-	10	[31]
9	Sn0.89Mn0.08Bi0.03Te	2021	Solid state reaction technique	-	18	[32]
10	Cu2.85Ag0.15Sb0.985Bi0.015Se4	2021	Vacuum melting and hot pressing	-	1200	[33]
11	Li0.03Cu1.81Bi0.04Se	2021	Ball milling method	-	10	[34]

4. Conclusions

Cu_2−xBi_xSe (x = 0.00, 0.004, 0.008, 0.012) samples were prepared using the solid-state reaction technique with conventional sintering. From XRD data it is confirmed that Cu_2−xBi_xSe has a monoclinic crystal structure and the space group changes from Cm to P2₁/c for pristine and doped samples respectively. All the samples exhibited less porous structures indicated the presence of well-connected grains. The resistivity of all the samples revealed phase transition at 350 K indicates the change in the structure from low temperature monoclinic to high temperature cubic. The positive value of Seebeck data confirms the p-type semiconductor nature with holes being the majority charge carriers. The resistivity and Seebeck coefficient of the sample increase with an increase in Bi content clearly indicates the dependency of carrier concentration. At 700 K, Cu_1.988Bi_0.012Se sample has the highest power factor of 1474 μWm⁻¹K⁻², which is 30% higher than the pristine sample at that temperature indicating that Bi-doped Cu₂Se can be used as promising thermoelectric material for the thermoelectric applications.