Abstract
Adiabatic Compressed Air Energy Storage (ACAES) is regarded as a promising, grid scale, medium-to-long duration energy storage technology. In ACAES, the air storage may be isochoric (constant volume) or isobaric (constant pressure). Isochoric storage, wherein the internal pressure cycles between an upper and lower limit as the system charges and discharges is mechanically simpler, however, it leads to undesirable thermodynamic consequences which are detrimental to the ACAES overall performance. Isobaric storage can be a valuable alternative: the storage volume varies to offset the pressure and temperature changes that would otherwise occur as air mass enters or leaves the high-pressure storage. In this paper we develop a thermodynamic model based on expected ACAES and existing CAES system features to compare the effects of isochoric and isobaric storage. Importantly, off-design compressor performance due to the sliding storage pressure is included by using a second degree polynomial fit for the isentropic compressor efficiency. For our modelled systems, the isobaric system round-trip efficiency (RTE) reaches 61.5%. The isochoric system achieves 57.8% even when no compressor off-design performance decrease is taken into account. This fact is associated to inherent losses due to throttling and mixing of heat stored at different temperatures. In our base-case scenario where the isentropic compressor efficiency varies between and , the isochoric system RTE is approximately 10% lower than the isobaric. These results indicate that isobaric storage for CAES is worth further development. We suggest that subsequent work investigate the exergy flows as well as the scalability challenges with isobaric storage mechanisms.
1. Introduction
There are two heat-based categories of Compressed Air Energy Storage (CAES): systems which use a supplementary heat input to heat the air prior to expansion, most often denoted Diabatic CAES (DCAES) systems; and systems which do not require a supplementary fuel, most commonly denoted Adiabatic CAES (ACAES) [1]. Isothermal (or more accurately near-isothermal) systems have also been proposed, however these are also adiabatic in the sense that, as a whole, the systems aims to minimise the net heat loss to the ambient over a charge–discharge cycle. Diabatic CAES is largely irrelevant to Net Zero agendas unless the fuel used is a low-carbon option. The challenges with low-carbon diabatic systems are, therefore, common with the use of low-carbon fuels for power generation (i.e., low-carbon hydrogen or ammonia in gas turbines) and largely distinct from the challenges in designing a successful adiabatic system [2]. In this article, we focus on ACAES systems and the mechanism of air storage, which can be either constant volume (isochoric), or constant pressure (isobaric).
Isochoric air storage (Figure 1a) is used in both the utility scale DCAES plants that operate today (Huntorf in Germany and McIntosh in the USA [3]). Both of these plants use solution-mined hermetic salt caverns as the air storage volume, allowing the pressure to increase as the system charges and decrease as the system discharges. The pressure changes in turn lead to temperature changes, so that the cavern temperature rises throughout the charging as air is added to the cavern and decreases as air is removed from the cavern during discharge. However, isochoric storage leads to several design challenges, which are particularly problematic in ACAES [2]. These are that the sliding pressure operation of the compressors and expanders increases the rate of exergy destruction (exergy is a measure of the extractable work from a given thermodynamic state), since the machinery is required to run in off-design conditions throughout the operation cycle. The sliding pressure also changes the temperature at the compressor outlets, leading to mixing of heat at different temperatures in the thermal energy stores and the air store, resulting in further exergy destruction. On the expansion side, the variable inlet pressure as the pressure in the air store decreases is normally dealt with by fixing the inlet pressure to the minimum cavern operation pressure via a throttling process. This throttling leads to a significant portion of the exergy destruction (up to 7% of the compressor work at normal storage pressures [3]), but accepting this loss is worth it to facilitate more straightforward operation of the expansion equipment. On top of all of these issues, control of the transient operation of isochoric systems is a major challenge [4].
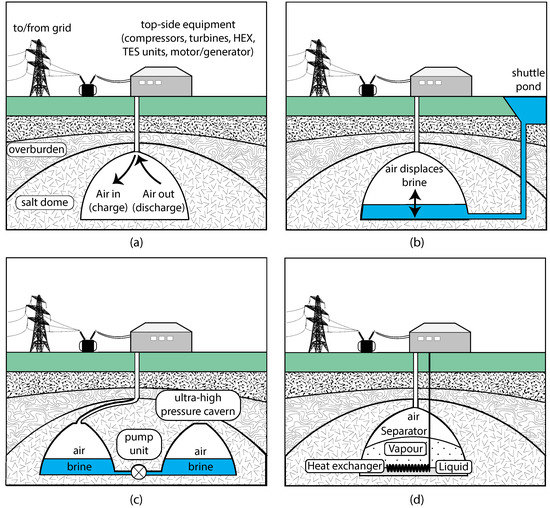
Figure 1.
Four primary mechanisms for air storage in ACAES. (a) Isochoric storage in a constant volume underground salt cavern. (b) Isobaric storage with a shuttle pond. (c) Isobaric storage with hydraulic compensation using a pump to regulate the fluid pressure. (d) Isobaric storage using the liquid-vapour phase change in a volatile fluid.
Isobaric operation is the alternative to isochoric operation, allowing machinery to operate at design point, removing the need for throttling and the requirement to deal with variable compressor outlet temperatures. However, an isobaric air store requires a variable volume, which is more complex to design, engineer, implement, and maintain than an isochoric air store. In engineering terms, the question of isochoric and isobaric air storage is then one of whether the additional complexity of isobaric storage, and its associated cost, is worth it.
Previous work on the topic of isobaric CAES has mainly been conceptual and has focused on the mechanism of providing the variable volume. Kim et al. [5] investigate hydraulically compensated isobaric CAES systems. The two methods proposed are maintaining a hydrostatic head of saturated brine with an underground cavern and a surface shuttle pond (see Figure 1b) or using a hydraulic pump to regulate the pressure (Figure 1c). A variation on this mechanism involves placing the store underwater, which offers potential advantages in terms of storage costs, as proposed by Pimm et al. [6]. Chen et al. [7] details the concept of isobaric air storage using a volatile cushion gas, exploiting the exceptionally high compressibility of two-phase CO2 at pressures below the critical pressure (Figure 1d). Changes from air in the gaseous state to the adsorbed state have also been proposed. Havel [8] proposes using zeolites for ‘Adsorption Enhanced CAES’, requiring heat to be added to the storage to de-adsorb the air during discharge.
While the aforementioned studies introduced several methods of achieving isobaric storage, there has been little work to compare isobaric and isochoric systems from a thermodynamic perspective. He et al. [9] builds isobaric and isochoric cavern models for ACAES, investigating the relationship between the stored exergy and the heat transfer across the cavern walls. Their main conclusions relate to the theoretical energy storage in the different operation modes, which is doubled from isochoric to isobaric, and the benefits in maintaining the cavern wall isothermal. While they do not investigate the operational differences between isobaric and isochoric systems outside of the cavern thermal parameters, their work is a useful basis for the modelling developed herein. Overall, there is a knowledge gap concerning how the isobaric and isochoric storage modes affect the performance of an ACAES system and how they impact design requirements of the constituent components. Moreover, compressor off-design performance has yet to be taken into account when comparing isobaric and isochoric systems.
Therefore, in this paper a high-level system oriented thermodynamic comparison between isobaric and isochoric CAES systems is undertaken. The key contributions and novelties are: (i) establishing a thermodynamic model capable of assessing the key operational and overall performance differences between isochoric and isobaric ACAES systems; (ii) investigating the system Round-Trip Efficiency (RTE) and TES discharge temperature sensitivity to the compressor off-design performance; and, (iii) illustrating that, even without any compressor off-design performance penalty, the isobaric system is likely to reach higher RTE levels and store significantly more energy than its isobaric counterpart.
We accomplish this through thermodynamic analysis which naturally leads to a wider discussion about the relative merits of each type of system. Our thermodynamic analysis reveals that the isobaric ACAES system may offer an improvement in performance of 7–15% compared with the isochoric system, depending on the level of the off-design efficiency penalty imposed by the turbomachinery operation. However, there are many other factors identified, as well as the increased efficiency, that favour isobaric storage, including ease of system control and reductions in the cyclic temperature and pressure stresses experienced by the storage cavern. Hence, we anticipate that the advantage of isobaric storage in a real system may be larger and suggest that further work on isobaric storage mechanisms is desirable.
2. ACAES Model
For both the isobaric and isochoric CAES systems, we consider a four-stage compression and two-stage expansion from atmospheric pressure to a high pressure of MPa. Although the asymmetrical nature of the system results in some of the input work being unavailable at discharge, this is a design choice imposed by the fact that close-to-adiabatic compressors with very high pressure ratios are difficult to design and expansion equipment typically works with higher pressure ratios (often pressure ratios of are used in gas turbines). We note that the McIntosh plant [10] and the TICC 500 demonstration plant [4] use 4 and 5 compression stages, respectively, while the Huntorf plant is split into two groups of compression stages, 20 axial stages and 6 centrifugal stages [11]. During charging the compressors add air to the High Pressure Air Store (HPST) and during discharge air is extracted from the HPST and used to drive turbines for power generation. The maximum HPST pressure is MPa and the minimum pressure is MPa. The choice of these conditions is somewhat arbitrary in the conceptual design—in reality the operational pressure available for an underground hermetic cavern depends strongly on the exact geology. However, the assumptions we use are based on the operational parameters of the McIntosh CAES plant, which cycles the cavern between and MPa in a regular cycle [11].
The CAES systems are shown in Figure 2a,b for the isochoric and isobaric systems, respectively. The maximum volume available for air storage in the HPST is equal in both systems. For the isochoric system (Figure 2a), the air is added to a constant volume HPST, increasing both the pressure and the temperature during charging (and decreasing during discharging). For the isobaric system (Figure 2b), it is assumed that the pressure is maintained at a constant value via a pressure compensation system. The exact nature of the pressure compensation is not specified and could be one of a number of mechanisms as described in Figure 1. Since the purpose of this paper is to compare the systems under isochoric and isobaric operation modes, our aim is discover the potential improvement in performance through the addition of isobaric storage. If the performance improvement is larger, this suggests that the additional complexity of isobaric storage is likely to be worthwhile, whereas if the improvement between the two modes is minimal then the additional costs associated with isobaric operation are unlikely to lead to an economically viable system.
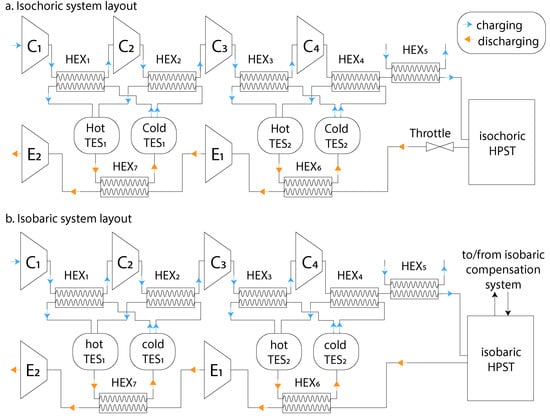
Figure 2.
Schematic diagram of the ACAES systems. (a) Isochoric—the air leaving the HPST is throttled to the minimum storage pressure. (b) Isobaric air storage is maintained so no throttle is included.
Other than the HPST, the key difference in the design layout of the two systems is the presence of the throttle valve in the isochoric system, which maintains constant pressure at the inlet to the expansion train. This strategy is employed in all existing CAES plants. Since off-design operation of the compressors has been identified as a key issue that must be accounted for isochoric systems [4], this is included in the compressor sub-models as detailed below. We model the air as a perfect gas with constant specific heats ( J kg K and J kg K). The inter-cooling heat exchangers in Figure 2 (HEX to HEX) feed insulated Thermal Energy Stores (TES units) with a liquid coolant. We do not specify an exact coolant, rather we assume that a coolant with a constant specific heat capacity J kg K is available and is stable at all the temperatures encountered. In practice, the cost of this fluid poses a challenge, however given our interest is in the comparative performance between the two systems we overlook this, taking parameters close to those of available thermal oils (our coolant is loosely based on the online information for Therminol 66 [12]). Each system also has a heat exchanger to control the temperature of the air entering the HPST (HEX). This is likely to be favourable from a design and control perspective.
The approach used for modelling the individual components is detailed below, including the relevant thermodynamic equations. We adopt a pseudo-equilibrium approach, whereby during charging an increment of air mass, , is passed through the compression train and is added to the HPST in time interval . All thermodynamic properties are considered constant during the interval . During discharge, the reverse process is true and is removed from the HPST and passes through the expansion train in time [3].
2.1. Compressors
The overall compression is divided into compressor stages, with each compression taking place in an adiabatic compressor and no dynamic effects are considered. The compressor power consumption, , for each compressor can be calculated using Equations (1) to (4),
The pressure ratio is equal for each compressor and is calculated based on the HPST pressure () and the pressure drop () introduced by each HEX. Hence:
is the pressure at the exit of the heat exchanger following the compression and is the atmospheric pressure.
In the isochoric ACAES case, the storage pressure changes constantly as the charging process takes place, thus is a function of the charge time, which causes the compressors to operate with variable pressure ratios. This impacts the outlet temperature, isentropic efficiency, and power consumption. In general, the magnitude of the off-design drop in isentropic efficiency depends on the machine technology (i.e., axial, centrifugal, positive-displacement), the exact compressor design and the operation strategy. We model the compressor performance as a second degree polynomial, whose maximum efficiency (design-point efficiency ) occurs at the end of the charging process. The off-design operation impact on efficiency tends to be more significant further away from the design point, while operation closer to the design point has a smaller impact on the compressor efficiency. This behaviour can be seen on the inset in Figure 3, where a compressor isentropic efficiency is plotted against the pressure ratio at four different speeds [13]. This approach allowed the off-design performance to be parameterised in terms of a single variable, however, it is a preliminary simplification that precludes any actual flow instability prediction, and cannot be considered a predictor of stable operating conditions. The compressor off-design performance is illustrated in Figure 3 for three arbitrary differences in isentropic efficiency between on-design and off-design operation. A smaller means that the compressor is less sensitive to off-design operation. The sensitivity to the value of the efficiency drop off is explored in our simulations.
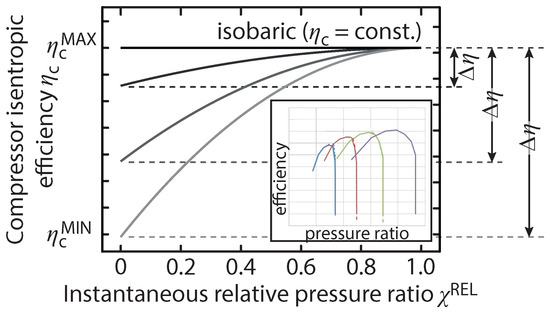
Figure 3.
Illustrating the compressor off-design performance with three arbitrary differences between on-design and off-design isentropic efficiency. The inset illustrates a path on a real compressor map (adapted from [13]), whose increasing efficiency portion we model as a second degree polynomial.
In this work, the compressor design condition has been chosen to correspond to the maximum (and isobaric) pressure ratio condition, such that only the increasing efficiency region of the presented compressor lines are considered. This way, the severe performance drop due to surge at higher pressure ratios is avoided [14]. The inset in Figure 3 depicts typical compressor performance lines over four rotational speeds, wherein the severe efficiency drop due to surge can be seen.
In Figure 3, is the instantaneous relative pressure ratio, defined as:
Therefore, ranges between zero and one when the storage pressure is equal to the minimum and maximum allowable pressures, respectively. The relative compressor efficiency, , is defined as the instantaneous efficiency over the design efficiency and is modelled as:
Here, is the instantaneous compressor isentropic efficiency, is the relative efficiency difference between operation at the minimum pressure ratio and the maximum pressure ratio over the efficiency at the maximum pressure ratio ().
2.2. Heat Exchangers
After each mass increment of air mass passes through a compressor, it is cooled in an intercooling Heat Exchanger (HEX) which supplies heat to a TES. During discharge the reverse is true, so an increment of air is heated by the fluid stored in the respective TES unit. We assume that all heat exchangers are adiabatic, so that all heat transferred from the hot fluid is absorbed in the cold fluid. The HEX effectiveness is given by:
We use this approach for HEX and HEX in Figure 2. However, for HEX, which is not an intercooling HEX and is used to control the air inlet temperature in the HPST, we use a fixed outlet temperature. For each system, the air inlet temperature to the HPST is fixed at 35 °C.
Each HEX also introduces a pressure drop. It is out-of-scope to generate a precise estimate of the HEX pressure drop, so we assume that each HEX introduces a pressure drop of MPa. This is equivalent to a pressure drop of 3.5% [11] and is consistent with pressure drops considered in previous work [15].
2.3. Isochoric HPST
For each HPST we consider a storage volume of 300,000 m, similar to the volume in the Huntorf CAES [11,16]. We assume a cylindrical storage geometry as shown in Figure 4, with a cavern radius of 38 m, giving a cavern height of 67 m. We assume that the cavern wall temperature is uniform with a constant value of 35 °C.
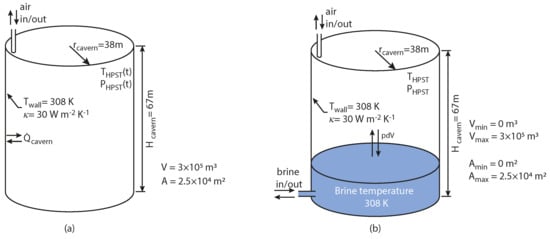
Figure 4.
The cavern is assumed to have cylindrical geometry, with constant wall temperature and convective heat transfer coefficient . The cavern internal temperature ( K) indicates a mid-point depth around 550 m [17]. (a) Cavern arrangement in the isochoric configuration, wherein volume and surface areas are constant, whilst pressure and temperature are variable. (b) Cavern arrangement in the isobaric configuration where pressure is maintained by changing the available air storage volume.
The isochoric HPST operates between minimum and maximum pressure levels, and . Using a pseudo-equilibrium approach, the conservation of mass and energy for the HPST are given by Equations (12) and (13) [3].
Here, and are the stored air mass at times t and , respectively, and is the mass flow rate. The positive value in Equation (12) corresponds to the charging process, with the negative during discharging. During the charging process, the enthalpy value used is outlet enthalpy of HEX (), whereas during the discharging, the stored air enthalpy in the HPST is used (). is the heat loss to the cavern, given by:
Here, is the heat transfer coefficient between the air and the cavern walls [18], is the air temperature in the HPST, is the cavern wall temperature (assumed isothermal with 35 °C) and A is the cavern wall area. If then heat will be transferred from the walls to the cavern air. We assume a uniform cavern temperature and consider heat transfer across the cavern area, hence A in Equation (14) is ) for the isochroic system.
2.4. Isobaric HPST
The isobaric HPST operates at a constant pressure of . During isobaric operation, there is additional work completed by (or completed during discharge) the air in the store. The ability to store and recover this work will depend on the exact mechanism of providing the isobaric storage. For example, with the shuttle pond (Figure 1b) there will be small losses associated with the friction in the brine borehole, or with the hydraulic compensation using a pump (Figure 1c) there will be losses associated with the efficiency of the pump. Since the purpose is of this study is to contrast the system operation in the different modes, we neglect this loss. It is therefore left to future work to determine the exact losses associated with each of the isobaric storage mechanisms and build on the analysis in this paper.
During charging, air is added at the same temperature as the cavern and the brine. Therefore, the air, brine, and cavern walls are in equilibrium and there is no net loss or gain of heat during either the charge, idle, or discharge processes. Hence we can write the conservation of mass and energy for the air in the store as:
Since the enthalpy of the air entering the store and the air in the store is the same, then the isobaric store remains in thermal equilibrium at the initial temperature.
2.5. Throttle Valve
On the isochoric system, a throttle valve is used to ensure that the pressure at the expansion train inlet remains constant regardless of the upstream HPST pressure. The throttle valve operation is considered isenthalpic, adiabatic, with no work or significant changes in kinetic energy. Since we treat air as a perfect gas, for which enthalpy is only a function of temperature, then there is no temperature change across the throttle.
2.6. Thermal Energy Stores
In both the isochoric and isobaric systems, there are two expansion stages. The air is reheated in HEX and HEX (as detailed in Section 2.2) using thermal energy stored from the compression. Since there are two expansion stages, only two TES units are required, despite the fact that there are four compression stages. Looking at Figure 2, TES is fed by HEX and HEX, while TES is fed by HEX and HEX. Since we assume constant specific heat capacity in the coolant, and all HEX have the same coolant flowrates, the inlet TES temperature is given by the mean of the respective HEX outlet temperatures.
In each TES unit we assume that the fluid is fully mixed so that the bulk coolant temperature in each TES unit is updated at each timestep as shown in Equation (17).
Here is the bulk coolant temperature in the TES at the time t and is the bulk coolant temperature in the TES at the time . is the specific heat capacity of the coolant which we assume constant and is the temperature at which the coolant enters the TES (equal to the outlet temperature of the respective intercooling HEX as given by Equation (10)).
2.7. Air Expansion
During discharge, the air leaves the HPST at the HPST temperature, as calculated by either Equation (13) for the isochoric system or Equation (16) for the isobaric system, given that for ideal gases . In the isochoric system, the air is throttled as discussed above so that the air enters the expansion train at the throttle pressure. Here, we assume a throttle pressure of MPa. In the isobaric system the air enters the expansion train at the HPST pressure and no throttling is used. For both systems there are expansion stages. Since for both systems the inlet pressure for the expansion is fixed, we consider that all expanders operate at their on-design isentropic efficiency of with constant mass flow rate. The pressure ratio in each expander is equal, returning the air to ambient pressure at outlet of the second expansion stage.
The expansion ratio is equal for each compressor and is a function of the inlet pressure to the expansion train, the pressure drops through the heating HEX and HEX and the ambient pressure. In the isochoric configuration, is determined by Equation (21) while for the isobaric configuration is determined by Equation (22).
In Equation (21) is the throttle outlet pressure.
2.8. Idle and Recovery
We also model the time periods between the charging and the discharging and between the discharging and the charging in the subsequent cycle. We denote the former as the idle period and the latter as the recovery period. During each of these periods we allow the HPST to come into thermal equilibrium with the cavern wall, with heat transfer driven by any temperature difference between the air in the cavern and the cavern walls, as implied by Equation (14). Thus the temperature of the store may be calculated using Equation (23).
In the above Equations (23) and (24), and are the HPST pressure and temperature respectively at time t, while and are the HPST pressure and temperature, respectively, at time . Therefore, in the isochoric configuration, after the heating observed during the charging period, the store cools down during the idle period. This cooling leads to an isochoric pressure drop between the charge and the discharge as implied by Equation (24).
Once the isochoric system is fully discharged, the temperature is colder than the cavern walls since the air in the store is decompressed by a significant degree. Thus, during the recovery period the store temperature will increase, driven again by the temperature difference between the cavern walls and the stored air mass (Equation (14). Then during the recovery period the air store pressure will rise according to Equation (24)).
In the isobaric configuration, the idle and recovery periods will not have any effect on the storage conditions. This is because we assume that the air added to the store, the cavern wall and the brine are at the same temperature and are, thus, always in thermal equilibrium.
Due to the pressure drop as the air in the isochoric store cools during discharge, in the first cycle, not all of the air added to the store will be extractable within the designated pressure limits. Therefore, we run the discharge operation of the isochoric store until the air mass added to the store equalises with the air mass removed from the store. As highlighted in the results, this happens after 3 cycles.
2.9. Model Parameters
A summary of the model parameters can be found in Table 1. The cavern volume, area, compressor mass flow rate and pressure limits (isochoric only) values have been chosen based on Huntorf [11,16]. The convective heat transfer coefficient has been taken from [19], whilst wall, brine and cavern temperature have been taken for a 550 m deep cavern, assuming a 25 °C km geothermal gradient [17]. Heat exchanger pressure drops are reported in [11], and the higher discharging effectiveness are justified by the greater coolant heat capacity, when compared to the charging HEX.

Table 1.
Key model parameters.
Finally, the model implementation algorithm is schematically depicted as flowcharts in Figure 5a,b, for charging and discharging processes, respectively. The internal algorithm routines for compressors, heat exchangers, expanders, air storage and TES follow the equations presented in Section 2.1, Section 2.2, Section 2.3, Section 2.4, Section 2.5, Section 2.6 and Section 2.7.
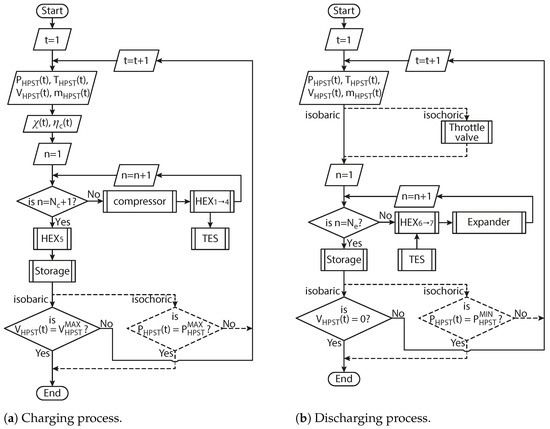
Figure 5.
Flowchart depicting the implemented model algorithm.
3. Results
The main results of our simulations are shown in Table 2. At steady state, the isochoric system starts at a pressure of MPa, charging for 31.2 h with a mass flow rate of 100 kg s. At the end of this time the HPST reaches the designated upper pressure limit of MPa and the system has consumed a total energy of GWh. During discharge, the pressure in the HPST decreases from MPa to 4 MPa and GWh of energy is generated yielding a Round-Trip Efficiency (RTE) of . The pressure recovers by MPa due to heating of the store by the cavern walls during the recovery period. For the isobaric system, the charging process takes more than double the time and requires more than double the energy input, at GWh. Of this, are returned during the discharging to yield a RTE of .

Table 2.
Simulation results for the isobaric and isochoric case in which .
The difference in the two simulated conditions charging and discharging time, and hence the quantities of energy stored and recovered, is at first sight surprising, given the same cavern volume. However, it is explained by the fact that the isobaric system requires no air cushion which must remain in the store at all times. All of the kg of stored air is extracted from the air store, as opposed to only kg for the isochoric store, with the remainder being kept in the store to maintain the low pressure limit.
The results of the variable pressure on the charging process of the isochoric store are shown in Figure 6. In Figure 6a, we see the evolution of the compressor outlet pressures in both systems. The effect of the variable pressure is clear as the pressure at the compressor outlets in the isochoric system rises, reaching the maximum value when the system is fully charged. This maximum value is maintained by the isobaric system throughout the operation. The absolute value of the compressor outlet pressure change is smaller in the lower stages. As shown in Figure 6b, the compressor efficiency drop is much more significant at earlier times, and increases rapidly as the charging process takes place. This is due to the shape of the efficiency function as given in Equation (9), which is typical of a compressor map, and shows an increasing performance drop as you move further from the design operation. It is interesting to note the combined effect of the increasing pressure ratio and the efficiency as shown in Figure 6c. Here we see that the compressor outlet temperatures in the isochoric system start at their maximum, when the inefficient compressor operation dominates, before falling rapidly and reaching a temperature level below the isobaric configuration when the compressor efficiency is high and the pressure ratio is just below the level in the isobaric system. Figure 6d shows the evolution of the charging power and the energy stored.
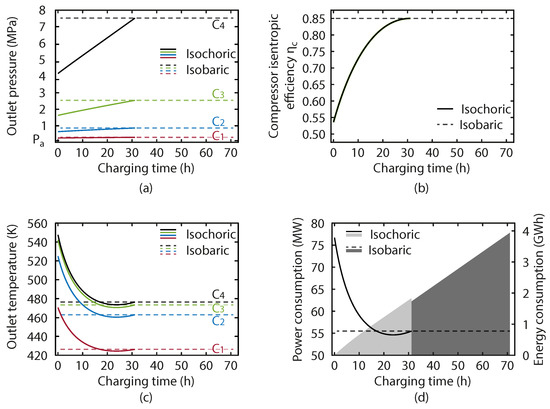
Figure 6.
Composite plot with main compressors operation figures during the charging process: (a) Compressors 1 through 4 outlet pressure; (b) isentropic efficiency (all machines operate with same efficiency in each case); (c) each compressor outlet temperature; and (d) total power (left axis, lines) and energy (right axis, shaded area) consumption, all for the isochoric and isobaric analysis. Note the isobaric scenario runs for longer than the isochoric. Data generated for .
Figure 7a shows the evolution of the HPST temperature during the charge and discharge periods for both the configurations. The dotted line gives the temperature in the isobaric system, which is constant since the air, brine, and cavern walls are always in thermal equilibrium. The red line in Figure 7a illustrates the HPST temperature during charging. The temperature rise is caused by the compression in the HPST as more air is added. This reaches a near-steady state value after around 10 h due to the increasing heat loss to the cavern walls. The temperature drop during discharging is much more severe, which is a result of the fact that during the charge air was being added to the store at constant temperature, whereas during the discharge it is removed from the HPST at . The temperature differences, and are also shown. Figure 7b shows the power output from the expansion and the cumulative energy released. The isobaric power generation is higher since there is no throttling required which reduces the expansion inlet pressure and the power generation is constant with both configurations since both have fixed expansion inlet pressures ( and for the isobaric and isochoric configurations, respectively).
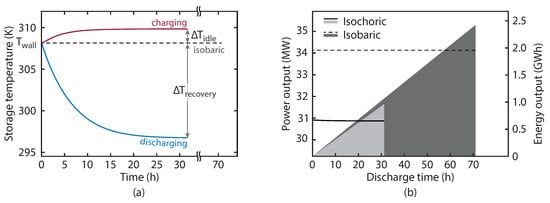
Figure 7.
Composite plot depicting: (a) storage temperature variation during the isochoric system charging and discharging periods (red and blue lines, respectively), as well the constant isobaric system temperature throughout charging and discharging. Additionally, the difference between final charging and initial discharging temperatures corresponds to the idle period temperature drop (), whilst the opposite corresponds to the recovery period temperature increase (). (b) power generation (left, lines) and cumulative energy generation (right, shaded areas) during the discharging period for both systems. Note the isobaric scenario runs for longer than the isochoric. Data generated for .
Finally, we examine the sensitivity of our results to the compressor off-design performance. Figure 8a shows the RTE as a function of the compressor efficiency loss. We see that the isochoric system is around 5% less efficient than the isobaric system even with no off-design penalty. This is predominantly a result of the throttling, as well as the mixing of heat at different temperatures at the compressor outlets during the charge. It is also apparent that as the off-design penalty exceeds beyond 40% the drop in RTE accelerates. The TES temperatures as a function of the off-design compressor efficiency loss is shown in Figure 8b. It is interesting to note the curve of the isochoric system, which results in a lower TES temperature than the isobaric configuration when there is a small off-design performance drop. This is due to the lower average compression ratio in the isochoric system. At higher off-design performance drops, the inefficiency in the compressor results in higher outlet temperatures, as more of the input work manifests as heat rather than increasing the air pressure. This work is not fully lost though, as the higher TES temperatures are beneficial in the expansion.
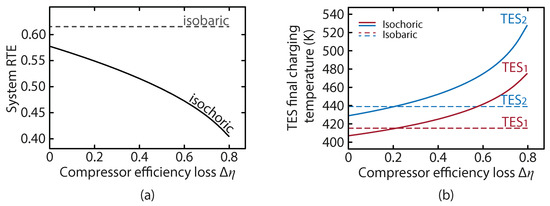
Figure 8.
Composite plot comparing key differences between the isobaric and isochoric system performance figures as a function of the compressor efficiency loss . In (a) Isochoric system Round-Trip Efficiency (RTE) compared to the isobaric system RTE (constant); and (b) TES 1 and 2 final charging temperatures in isobaric and several isochoric conditions.
4. Discussion
Our results highlight many of the thermodynamic differences between the operation of isochoric and isobaric CAES systems. While isochoric systems certainly offer simpler storage—the store is just a fixed volume pressure vessel—the variable pressure resulting from the fixed volume impacts the system performance, significantly reducing it in a number of aspects. In particular, the isochoric storage leads to a variable charging power with a fixed air mass flow rate and the variable pressure ratio the system experiences leads to variable compressor outlet temperatures and off-design compressor operation. In our base case simulation, where we stipulated a 35% drop in the compressor performance at the most severe off-design conditions encountered, the difference in RTE between the two systems was 9%. The main mechanisms driving this loss are the throttling required to fix the expansion train inlet pressure and the inefficient compressor operation. To precisely evaluate the losses, a system exergy analysis would be a useful future contribution. In contrast, there is no need for throttling in the isobaric system since the pressure at the expansion train inlet is constant and the compressors work at their design operation throughout the charging process.
When the compressor off-design penalty is not included, the isochoric system RTE figures are similar to values commonly reported in literature [3,20] for low-temperature ACAES systems. When the compressor off-design influence is included, there is a significant decrease on the round-trip efficiency and increase on TES discharge temperature. The power decrease tendency observed in Figure 6d has also been reported in [21]. The effect of the off-design compressor operation is not straightforward. This is because some of the work that ends up as heat as a result of the inefficient compressor operation leads to an increase in the temperature of the stored heat in the TES units. This, in turn, leads to a higher work output during the discharge. Indeed, increasing the turbine inlet temperatures may be desirable since it will also increase the outlet temperatures. In general, keeping the turbine outlet temperatures above freezing is likely to be important, particularly if the air has significant moisture content. We also note that the variable compressor operation poses control challenges, which we have not modelled here. For example, there needs to be real-time control of the pressure ratio to avoid significant extra work, which is a difficult challenge. Thus we may have underestimated the off-design performance drop.
The system we model is loosely based on the Huntorf and McIntosh systems, however it is interesting to note that with a similar cavern volume we end up with a much reduced discharging power and higher discharge duration. This is because the discharging mass flow rate at Huntorf is higher than the charging mass flowrate and there is a large gain in work output due to the supplementary natural gas use. The difference between energy stored and charging time between the system in isochoric and isobaric operation modes is also striking, with the isobaric system delivering more than times the energy generation of the isochoric system. While this does imply a significant gain in energy density for the isobaric system, this must be qualified by the fact that maintaining isobaric storage will require a larger footprint, either through a shuttle pond on the surface or another cavern for brine storage (as illustrated in Figure 1).
While the store could also be an above-ground manufactured pressure vessel, for example a steel cylinder or an innovative wire wound solution [22], for any large-scale HPST, underground caverns are likely to be the most cost-effective option considering the large volume of compressed air required. Additionally, the fact that underground storage caverns are not visible means that CAES plants can have fairly minimal overground footprints. However, the underground cavern also imposes strict limitations on the operation, since the geology will dictate maximum air mass flow rates, maximum temperature cyclability limits, maximum pressure cycling limits, and maximum rates of change for both temperature and pressure. The operation mode of the cavern will then be strongly influenced by the geology, with isobaric operation required where stress cycle induced/enhanced salt creep might threaten the cavern long term stability and integrity. Therefore, from a cavern engineering perspective the advantages of isobaric storage are a reduction in the thermal and pressure stresses on the cavern, and the ability to counteract cavern creep (since the cavern would be flushed with brine each cycle), which tends to reduce the volume of salt caverns and decrease long-term stability [23]. However, there could also be issues with this since the saturation of brine is temperature dependent and thus saturation levels would need to be carefully controlled if there were large temperature swings between the cavern and the shuttle pond. Overall, it seems likely that the question as to which system is a better choice for a particular location will depend on the various trade-offs presented. Of particular importance are the compressor off-design performance associated with the available compression machinery and the geological considerations associated with the cavern.
5. Conclusions
A number of mechanisms for isobaric storage in ACAES systems have been proposed in the literature, however, until now there has been little work comparing the effect isochoric and isobaric storage on ACAES systems. This paper develops reduced order thermodynamic models of isochoric and isobaric ACAES systems, illustrating the key operational differences. The key findings are related to the effects of isochoric and isobaric storage on the system components requirements and the consequences on a systematic level. For isochoric systems, it is important to maintain high efficiency levels for the components over the range of operating conditions encountered. For isobaric ACAES systems this operational flexibility is not required and the constant pressure ratio on the compressors will result in constant outlet temperature, which ultimately decreases the exergy destruction due to mixing heat at different temperatures. Furthermore there is a significant increase in storage capacity per unit of volume of the high-pressure air storage.
Our modelling suggests that isobaric systems are likely to have a RTE improvement of around 9% minus any losses associated with maintaining the isobaric storage. This may increase significantly if there are challenges with control of the isochoric system or if there is a large off-design penalty associated with the compressors. Isobaric systems also ease the cyclic temperature and pressure variations experienced by the high-pressure air store. However, an isobaric store is significantly more complex than its isochoric counterpart and will have a larger CAPEX. Thus, the question of whether isochoric or isobaric ACAES is better will depend on whether the additional expense and technical complexity of the isobaric store is justified by the performance increase. Further comparative studies between isochoric and isobaric systems, especially in terms of exergy flows and economic analysis, are required to assess these outstanding questions.
Author Contributions
Conceptualization, D.P. and E.B.; methodology, E.B.; software, D.P. and E.B.; validation, D.P. and E.B.; formal analysis, D.P., S.G., B.C., J.R., E.H., A.B. and E.B.; writing—original draft preparation, D.P., S.G., J.R., B.C., E.H., A.B. and E.B.; writing—review and editing, D.P., S.G., B.C., J.R., E.H., A.B. and E.B.; supervision, S.G., E.H., A.B. and E.B.; project administration, E.B.; funding acquisition, S.G., E.H., A.B. and E.B.; E.H. publishes with the permission of the Executive Director of the British Geological Survey (BGS, UKRI). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the UK EPSRC grant number EP/W027569/1, Sustainable, Affordable and Viable Compressed Air Energy Storage (SAVE-CAES).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
The following nomenclature is used in this manuscript:
| Symbols | |
| A | Area, , |
| Specific heat at constant pressure and volume, respectively, , | |
| Coolant specific heat, , | |
| C | Heat capacity, , |
| h | Specific enthalpy, , |
| H | Height, L, |
| m | Mass, M, |
| Mass flow rate, , | |
| Number of compressor and expander stages, | |
| P | Pressure, , |
| Pressure drop in the heat exchanger , | |
| Q | Heat transferred, , |
| Heat transfer rate, , | |
| r | Radius, L, |
| T | Temperature, , |
| t | time, T, |
| u | Specific internal energy, , |
| V | Volume, , |
| W | Work, , |
| Power, , | |
| Greek characters | |
| Heat exchanger effectiveness, | |
| Efficiency, | |
| Convective heat transfer coefficient, , | |
| Instantaneous pressure ratio, | |
| Expansion ratio, | |
| Subscripts | |
| 1 | Condition on the beginning of the timestep, |
| 2 | Condition on the end of the timestep, |
| a | Relative to ambient condition, |
| c | Compressor or cold fluid, |
| Relative to HPST cavern, | |
| e | Expander, |
| h | Hot fluid, |
| Relative to the High Pressure Storage, | |
| Inlet condition, | |
| N | Condition at the compressor or heat exchanger outlet, |
| Outlet condition, | |
| s | Isentropic condition, |
| HPST wall, | |
| Superscript | |
| Mixed conditions in TES, | |
| Condition at the heat exchanger outlet, | |
| Maximum condition, | |
| Minimum condition, | |
| Relative condition, | |
| Dimensions | |
| L | Length |
| T | Time |
| M | Mass |
| Temperature |
References
- Wang, J.; Lu, K.; Ma, L.; Wang, J.; Dooner, M.; Miao, S.; Li, J.; Wang, D. Overview of Compressed Air Energy Storage and Technology Development. Energies 2017, 10, 991. [Google Scholar] [CrossRef]
- Barbour, E.; Pottie, D.L. Adiabatic compressed air energy storage technology. Joule 2021, 5, 1914–1920. [Google Scholar] [CrossRef]
- Barbour, E.R.; Pottie, D.L.; Eames, P. Why is adiabatic compressed air energy storage yet to become a viable energy storage option? iScience 2021, 24, 102440. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhang, X.; Yang, L.; Zhou, Y.; Wang, J. Experimental study of compressed air energy storage system with thermal energy storage. Energy 2016, 103, 182–191. [Google Scholar] [CrossRef]
- Kim, Y.; Shin, D.; Favrat, D. Operating characteristics of constant-pressure compressed air energy storage (CAES) system combined with pumped hydro storage based on energy and exergy analysis. Energy 2011, 36, 6220–6233. [Google Scholar] [CrossRef]
- Pimm, A.J.; Garvey, S.D.; de Jong, M. Design and testing of energy bags for underwater compressed air energy storage. Energy 2014, 66, 496–508. [Google Scholar] [CrossRef]
- Chen, L.X.; Xie, M.N.; Zhao, P.P.; Wang, F.X.; Hu, P.; Wang, D.X. A novel isobaric adiabatic compressed air energy storage (IA-CAES) system on the base of volatile fluid. Appl. Energy 2018, 210, 198–210. [Google Scholar] [CrossRef]
- Havel, T.F. Adsorption-Enhanced Compressed Air Energy Storage. 2009. Available online: https://www.sandia.gov/files/ess/EESAT/2009_papers/Adsorption-Enhanced%20Compressed%20Air%20Energy%20Storage.pdf (accessed on 13 January 2023).
- He, W.; Luo, X.; Evans, D.; Busby, J.; Garvey, S.; Parkes, D.; Wang, J. Exergy storage of compressed air in cavern and cavern volume estimation of the large-scale compressed air energy storage system. Appl. Energy 2017, 208, 745–757. [Google Scholar] [CrossRef]
- Kaiser, F. Steady state analyse of existing compressed air energy storage plants. In Proceedings of the Power Energy Stud. Summit (PESS), Dortmund, Germany, 13–14 January 2015. [Google Scholar]
- Jafarizadeh, H.; Soltani, M.; Nathwani, J. Assessment of the Huntorf compressed air energy storage plant performance under enhanced modifications. Energy Convers. Manag. 2020, 209, 112662. [Google Scholar] [CrossRef]
- Therminol. Therminol 66 Heat Transfer Fluid. 2023. Available online: https://www.therminol.com/product/71093438?pn=Therminol-66-Heat-Transfer-Fluid (accessed on 13 January 2023).
- Prévost, F.; Le Moual, Y.; Maiboom, A.; Tauxia, X.; Payet-Burin, T.; Davodet, O. An analytical user-friendly methodology to transform compressor and turbine supplier characterization maps dedicated to 1D engine simulation: Modelling of turbocharger heat transfer and friction losses. Appl. Therm. Eng. 2023, 221, 119812. [Google Scholar] [CrossRef]
- Dixon, S.L.; Hall, C.A. Fluid Mechanics and Thermodynamics of Turbomachinery, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Barbour, E. Investigation into the Potential of Energy Storage to Tackle Intermittency in Renewable Energy Generation. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2013. [Google Scholar]
- Han, Y.; Cui, H.; Ma, H.; Chen, J.; Liu, N. Temperature and pressure variations in salt compressed air energy storage (CAES) caverns considering the air flow in the underground wellbore. J. Energy Storage 2022, 52, 104846. [Google Scholar] [CrossRef]
- Lowell, R.; Kolandaivelu, K.; Rona, P. Hydrothermal Activity. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Raju, M.; Kumar Khaitan, S. Modeling and simulation of compressed air storage in caverns: A case study of the Huntorf plant. Appl. Energy 2012, 89, 474–481. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, C.; Zhao, H.; Mei, S.; Zhou, S. An iterative method for evaluating air leakage from unlined compressed air energy storage (CAES) caverns. Renew. Energy 2018, 120, 434–445. [Google Scholar] [CrossRef]
- Mozayeni, H.; Wang, X.; Negnevitsky, M. Dynamic analysis of a low-temperature Adiabatic Compressed Air Energy Storage system. J. Clean. Prod. 2020, 276, 124323. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Li, Y.; Chen, H.; Wu, Y.; Wang, J.; Garvey, S.; Ding, Y. Dynamic simulation of Adiabatic Compressed Air Energy Storage (A-CAES) plant with integrated thermal storage—Link between components performance and plant performance. Appl. Energy 2017, 185, 16–28. [Google Scholar] [CrossRef]
- Cárdenas, B.; Hoskin, A.; Rouse, J.; Garvey, S.D. Wire-wound pressure vessels for small scale CAES. J. Energy Storage 2019, 26, 100909. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Zhang, Q.; Song, Z.; Liu, X.; Feng, S. Long-term stability analysis and evaluation of salt cavern compressed air energy storage power plant under creep-fatigue interaction. J. Energy Storage 2022, 55, 105843. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).