Abstract
This paper presents a resilience-oriented energy management approach (R-OEMA) designed to bolster the resilience of networked microgrids (NMGs) in the face of extreme events. The R-OEMA method strategically incorporates preventive scheduling techniques for hydrogen (H2) systems, renewable units, controllable distributed generators (DGs), and demand response programs (DRPs). It seeks to optimize the delicate balance between maximizing operating revenues and minimizing costs, catering to both normal and critical operational modes. The evaluation of the R-OEMA framework is conducted through numerical simulations on a test system comprising three microgrids (MGs). The simulations consider various disaster scenarios entailing the diverse durations of power outages. The results underscore the efficacy of the R-OEMA approach in augmenting NMG resilience and refining operational efficiency during extreme events. Specifically, the approach integrates hydrogen systems, demand response, and controllable DGs, orchestrating their collaborative operation with predictive insights. This ensures their preparedness for emergency operations in the event of disruptions, enabling the supply of critical loads to reach 82% in extreme disaster scenarios and 100% in milder scenarios. The proposed model is formulated as a mixed-integer linear programming (MILP) framework, seamlessly integrating predictive insights and pre-scheduling strategies. This novel approach contributes to advancing NMG resilience, as revealed by the outcomes of these simulations.
1. Introduction
Recently, the integration of distributed energy resources (DERs), smart grid technologies, and an upsurge in extreme events has brought to light the vulnerability and complexity that are inherent in modern power systems [1,2]. These events of an extreme nature, encompassing phenomena such as hurricanes, storms, earthquakes, and those induced by human intervention, present significant challenges to the operation of power systems, frequently instigating extensive blackouts, damage to infrastructure, and socio-economic repercussions [3]. In response to these challenges, research efforts have intensified, aiming to comprehensively understand the interplay between distributed energy resources and the resilience of power systems. Investigations into the dynamic interactions between DERs and the grid, coupled with the impacts of extreme events, are crucial for devising effective mitigation and adaptation strategies [4,5].
Consequently, an increasing sense of urgency has arisen to reexamine and improve the security and resilience measures that are fundamental to the functioning of energy systems [6]. Power systems are a crucial element of critical infrastructures that are susceptible to natural disasters and disruptions. They play a vital role in supporting essential services within modern societies, serving as a lifeline for the people. Ensuring a continuous and reliable provision of electricity, especially in the face of extreme occurrences, is of the utmost importance in facilitating a prompt emergency response and safeguarding public well-being. Therefore, there is a pressing need to develop approaches that can enhance the resilience of power systems, equipping them with the ability to endure and recover from such challenges [6]. These developments underscore the imperative of adopting forward-looking strategies that embrace technological advancements. Smart grid technologies, for instance, offer the potential to enhance the monitoring, control, and coordination of power systems in real-time, contributing to improved situational awareness and rapid response capabilities. Moreover, the integration of advanced data analytics and machine learning techniques can provide valuable insights for predicting and mitigating the impact of extreme events on power infrastructures [7].
The advent of microgrids (MGs), which are capable of operating independently or in concert with the central grid, has aroused significant attention in academic and industrial circles. The significance of these technologies lies in their ability to enhance energy efficiency, augment the integration of renewable energy sources, and strengthen the resilience of power systems [8]. Furthermore, the increased adoption of microgrids has the potential to revolutionize the current energy landscape by fostering decentralized energy generation. This shift towards decentralization aligns with global trends emphasizing sustainability and a reduction in carbon footprints.
Moreover, the connectivity of MGs has emerged as a pivotal factor, especially during an unanticipated event [9]. By implementing networked microgrids (NMGs), which refer to a network that interconnects multiple MGs, it becomes possible to avert the occurrence of complete load shedding, thereby guaranteeing a consistent supply to essential loads [10]. This internal linkage enables NMGs to effectively utilize their DERs to fulfill local demand, consequently decreasing their dependence on the central grid and enhancing the entire system’s resilience [11,12].
Moreover, the effectiveness of DER management plays a crucial role in guaranteeing efficient load supply and strengthening NMGs’ resilience. DERs comprising wind turbines (WTs), photovoltaics (PVs), diesel generators (DGs), and energy storage technologies possess considerable potential to augment the technical efficiency and resilience of MGs [13,14]. These diverse DERs contribute to a diversified and robust energy portfolio, ensuring a more adaptive response to dynamic energy demands. The integration of hydrogen (H2) systems is particularly noteworthy as it provides essential assistance in the event of severe faults, thereby enhancing this network’s ability to utilize renewable energy sources [15,16]. Furthermore, the adoption of H2 systems presents an avenue for exploring additional research and development opportunities in sustainable energy technologies. Investigating innovative approaches to enhance the efficiency of H2 production, storage, and utilization can lead to further advancements in NMGs’ overall sustainability and resilience. By implementing effective energy management techniques and incorporating H2 systems, NMGs could minimize their dependence on the main power grid and enhance their capacity to withstand unexpected interruptions [17,18]. This shift towards decentralized energy management not only ensures a more reliable power supply but also contributes to a more sustainable and environmentally friendly energy ecosystem. As NMGs explore these integrated solutions, it becomes imperative to analyze economic and environmental implications, paving the way for informed decision making in the pursuit of sustainable energy [19].
To augment these advantages, the incorporation of demand response programs (DRPs) presents itself as a crucial element in bolstering the resilience of NMGs. DRPs enable flexible load management, granting consumers the ability to modify their electricity consumption patterns in reaction to changes in supply and demand dynamics or critical events [20,21]. By incorporating a DRP into NMGs, it is possible to effectively manage load curtailment or shifting during high-demand periods or unexpected disruptions, thus significantly contributing to the grid’s stability and enhanced resilience [22]. In addition to these aforementioned benefits, the integration of DRPs introduces a dynamic dimension to the operational efficiency of NMGs. This dynamic responsiveness empowers consumers and grid operators to proactively address fluctuations in electricity demand, fostering a more adaptable and responsive energy ecosystem. Furthermore, the real-time adjustments facilitated by DRPs not only enhance the grid’s overall reliability but also play a pivotal role in optimizing the utilization of renewable energy sources, aligning with the broader goals of sustainability and environmental stewardship [23].
Expanding on the role of DRPs, their integration in NMGs not only contributes to immediate load management but also serves as a cornerstone for establishing a demand-centric energy landscape. This shift towards demand-centricity opens avenues for enhanced energy efficiency, reduced peak demand stress, and improved economic viability for both consumers and energy providers. As a result, the incorporation of DRPs not only fortifies the grid against unforeseen challenges but also propels NMGs towards a more resilient, sustainable, and economically viable energy future.
This paper highlights the potential of integrating H2 systems into NMGs for the purpose of enhancing their resilience. H2 systems represent a prime example of large-scale and long-duration energy storage, incorporating diverse technologies for H2 production, storage, and conversion [24,25]. The dominance of these solutions can be attributed to their capacity to provide a robust energy storage mechanism, which offers economic, environmental, and technical benefits that exceed those of conventional battery storage [26]. In contrast to conventional batteries that have limited storage capabilities, H2 storage exhibits extended energy retention and discharge abilities that extend over a period of days to months. H2 systems are effective in supporting critical loads and maintaining operations during extended disruptions or grid unavailability [27]. Moreover, the integration of DERs in NMGs enhances their synchronization, strengthening their resilience and reducing reliance on the central grid.
Although the proactive scheduling of H2 systems and DRPs has potential advantages, research on their incorporation in NMGs is still in its early stages. Previous studies have predominantly focused on the resilience of microgrids following extreme events and their interdependence with the central grid. These studies have largely adopted restoration strategies. Several of these methodologies involve exorbitant investment costs, which restrict their feasibility in real-life situations. Prior research has primarily addressed proactive scheduling in relation to DERs and enhancing MG’s resilience following extreme events. However, there is a significant research gap with regard to the integration of H2 energy systems, DRPs, and NMGs as a preventive strategy for augmenting resilience.
To overcome the difficulties inherent in strengthening NMG’s resilience and address this gap, the present study proposes a resilience-oriented energy management approach (R-OEMA) that enhances resilience using preventive measures. During the preventive scheduling phase, the distribution system operator (DSO) sends out signals to the proprietors of H2 systems, prompting them to replenish storage reservoirs prior to impending disruptions. This paper effectively addresses the challenge of coordinating with the proprietors of H2 systems by proposing appropriate signaling models for preventive operations, thereby ensuring their readiness for emergency operations. The utilization of stored H2 energy to provide power to stationary fuel cells (FCs) is an approach that maximizes the supply of critical loads, resulting in the enhancement of network resilience. Moreover, the DRP is implemented simultaneously to restrict non-essential loads, thus guaranteeing the supply of essential loads with the prioritization of demand and reinforcing network resilience. Furthermore, this paper presents a pre-scheduling management approach for controllable DGs. Due to the fuel limitation of DGs, managing their production power is crucial to reduce load shedding. The effectiveness of the proposed framework is investigated through the use of numerical simulations, which highlight its ability to enhance the resilience of NMG and improve operational efficiency during extreme events.
The main contributions of this paper can be summarized as follows:
- The development of a preventive framework for enhancing the resilience of NMGs through optimal energy management.
- The introduction of a coherent signaling model facilitating DSO and H2 system proprietor communication and cementing readiness for emergency operations.
- The integration of H2 energy systems to provide large-scale, long-duration energy storage during extreme events.
- The implementation of a preventive DRP, enabling efficient load prioritization and load curtailment during extreme events.
- The incorporation of DGs in the resilience-oriented energy management of NMGs supplying critical loads.
The subsequent sections of this paper are arranged as follows. In Section 2, a comprehensive approach to this research is presented. The discussion of the problem formulation is expounded upon in Section 3. In Section 4, the numerical results and performance evaluation of the proposed R-OEMA are presented and compared with the typical energy management approach (TEMA). Ultimately, the paper is concluded in Section 5.
2. The Proposed Approach
The proposed R-OEMA presents a comprehensive strategy with the objective of enhancing the resilience of NMGs. This is achieved through the utilization of preventive scheduling techniques for H2 systems, loads, and DGs. This particular framework addresses the challenges arising from natural disasters, utilizing established statistical knowledge and predictive abilities to enable informed scheduling. In this context, the integration of advanced weather forecasting technologies becomes crucial. By incorporating real-time meteorological data, the scheduling algorithm gains a dynamic edge, adapting to evolving weather conditions and further fortifying NMGs against unforeseen challenges. The incorporation of H2 systems, a DRP, and DGs, as depicted in Figure 1, coupled with preventive scheduling, the signaling model, and resilience-focused optimization, facilitate the augmentation of NMGs’ resilience. Moreover, the resilience-driven architecture of the R-OEMA emphasizes the importance of DERs in the broader energy landscape. This not only enhances the resilience of NMGs but also contributes to a more sustainable and adaptable energy infrastructure. The interconnectedness of these elements, as illustrated in the framework, underscores the holistic approach taken to bolster the resilience of NMGs in the face of diverse and unpredictable challenges.
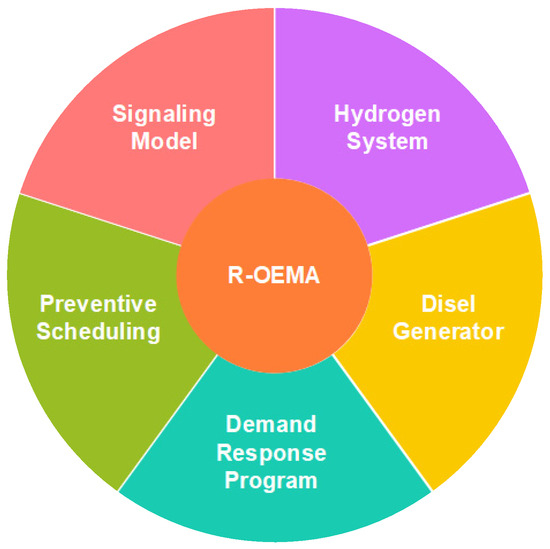
Figure 1.
The proposed R-OEMA to increase NMGs’ resilience.
In the resilience-focused framework, the NMG operations are encompassed by the purview of the DSO. The DSO holds responsibility for supervising the renewable energy units, DGs, H2 systems, and management demand. The primary aim of the framework is to enhance the profit of NMG operations under normal and emergency situations. The main objective function of this problem is to maximize supplied energy profits and minimize the total operating costs and unsupplied energy.
Integrating predictive insights into impending natural disasters is an essential component of this framework. Statistical databases related to such events facilitate the evaluation of system dynamics in different states and, thus, pave the way for the active planning of H2 systems, DGs, and loads. The energy scheduling framework for DGs also takes into account variables such as the geographic location of the NMG and environmental considerations, including fuel constraints.
The integration of capacity-based demand response signals into the optimization model is a crucial aspect of this framework. The injection of the said signals into H2 systems is seen as a means of enhancing system flexibility. This is achieved by endowing the DSO with the discretion to dispatch emergency signals to H2 systems in advance of entering emergency operational modes. These signals are directed towards the objective of completely filling up H2 storage tanks, thereby making them ready for use in post-event situations. This strategic move empowers the utilization of stored H2 for stationary FC consumption, resulting in enhanced adaptability among challenges.
Moreover, the framework incorporates DRP as a fundamental element of its strategy to enhance resilience. DRP presents a dynamic mechanism that allows NMGs to adeptly respond to situations with changing demands. This is achieved by curtailing non-critical loads in times of emergency to guarantee a continuous supply to the critical loads. The cooperation of DRP in the optimization process enhances NMG resilience by coordinating H2 systems and DGs. This framework guarantees a reliable supply of critical loads amidst disruptions while simultaneously accomplishing economical operations. Moreover, the proposed R-OEMA integrates predictive and preventive paradigms, offering valuable insights into system functionality and scheduling. This enables the optimal utilization of renewable energy resources and mitigates the potential impact of natural disasters.
3. Problem Formulation
In the present section, we present the formulation of the proposed optimization problem. To ensure global optimality, the proposed framework employs a mixed-integer linear programming (MILP) model in both normal and critical operations. The formulation of this problem has not been separated into normal and critical operational modes in order to maintain concision. However, prior to the occurrence of the extreme incident, all equations retain their validity with the exception of load-shedding terms, which require omission from the equations.
3.1. H2 System Operational Constraints
The equations governing the H2 systems, which include electrolyzers, FC units, and storage tanks, are formulated with the application of the subsequent constraints in Equations (1)–(8). These constraints encapsulate critical considerations such as the efficiency coefficients of the electrolyzers and FC units, the energy conversion rates, and the storage capacities of hydrogen storage tanks. Additionally, our model integrates dynamic factors, accounting for varying energy demands and renewable energy inputs, further enhancing the accuracy and applicability of the formulated equations. This comprehensive approach ensures a holistic representation of H2 systems, addressing not only the technical intricacies of individual components but also their dynamic interplay within the broader energy ecosystem.
Constraints (1) and (2) demonstrate the magnitude of H2 generation and consumption in electrolyzers and FC units, respectively, based on the conversion factors and efficiencies employed. Equations (3) and (4) establish the limits within which H2 production and consumption take place, taking into account the capacity constraints of electrolyzers and FC units. Furthermore, it must be noted that the utilization of electrolyzers and FC units cannot occur simultaneously due to the presence of the binary variable . The formulation in Equation (5) is concerned with the H2 mass balance, which takes into account the dissipation rate. The constraint (6) outlines the upper and lower limits of the storage tank capacity [28,29,30].
In the context of the TEMA, the management of the repeated H2 tank charge and discharge cycle is achieved by imposing a restriction on the volume of H2 stored at the beginning and end of each day, as presented in constraint (7). In the R-OEMA, it is of the utmost importance for the system operator to implement the resilient modification of the operational mode of H2 systems in order to provide MG loads during critical periods. Therefore, depending on the predicted time of disturbance (referred to as ) within the system, the dynamic H2 mass is restricted in Equation (8).
3.2. DER Operational Constraints
This sub-section presents the operational limitations associated with renewable units and controllable DGs in Equations (9)–(18). Understanding these limitations is crucial for ensuring the realistic representation of renewable energy sources and controllable distributed generators (DGs) in the proposed model. It provides insights into the dynamic constraints that shape the performance of these units, thereby contributing to the accuracy and reliability of our simulations.
The maximum capacity of renewable energy sources is restricted by constraint (9). Equation (10) provides both the maximum and minimum bounds of DGs in electricity production. Constraints (11) and (12) impose limitations on the boundaries for the ramp-up and ramp-down of DGs, respectively. The constraints for the start-up and shout-down of DGs are explained in Equations (13) and (14), respectively. The management of DGs’ activation and deactivation is conducted through the utilization of binary variables, namely , , and . This process is expressed through the application of constraints (15) and (16). Equation (17) represents the fuel constraint as a decisive factor in the operation of DGs due to the geographical location impeding access to this resource [31].
As has been previously stated, the binary parameter denoted as serves to indicate the operational status of DGs.
This particular value is determined through an analysis of the existing electricity tariff and the precise timing of the natural disaster. Despite this, the limitation on fuel prompts the system operator to modify the operational approach of DGs. As a consequence of anticipating the duration of a potential disaster in the grid, a limitation is imposed on the aforementioned variable in the following equation [32].
3.3. Demand Constraints
Equations (19)–(22) present the constraints imposed by MG loads, load shedding, and critical loads on the distribution feeders [33,34,35].
Constraint (19) limits the load shedding based on different levels of the MG load at time t. Constraint (20) exhibits the load control mechanism in the microgrids, whereas constraint (21) specifies the controllable load limits at different levels. The binary variable provides the possibility of load control in normal and resilience-oriented operating states. Furthermore, constraint (22) signifies the limitation imposed on the restoration of the critical load on distribution feeders.
3.4. Power Balance Constraints
The equations that govern the balance of power in relation to the variable , which can take on different values due to the exchange of energy between MGs, are presented in constraints (23)–(25).
The expression of the power equilibrium at every microgrid (MG) is conveyed by the left-hand side of constraint (23), while the right-hand side variable (i.e., ) describes the condition of MGs in the network. To further explicate, a positive value signifies the role of the MG as a provider. In contrast, a negative value denotes the requirement of acquiring energy from alternative MGs or the upstream grid. The effects of power losses within the system are explicated through the utilization of the line efficiency parameter , as expressed in Equation (24). The energy exchange between NMGs and the upstream network can be established through the utilization of Equation (25).
3.5. Objective Function
The main goal of the objective function is to maximize the overall operating revenues and minimize the operating costs in both normal and critical operations, as presented in Equation (26).
Based on Equation (27), the total income of NMGs is from the selling power to the MG loads and critical load restoration on the distribution feeders. Moreover, the overall costs associated with NMGs include the operational cost of DGs, the cost of purchasing electricity from the upstream grid, and the costs of load shedding and load control, as illustrated in Equation (28). The total operating income and costs are rewritten in Equations (29) and (30) with more details. It is noteworthy to mention that the costs related to H2 systems have not been considered.
4. Input Data and Numerical Results
The effectiveness of the proposed framework within a 72 h timeframe is assessed on a power grid consisting of three MGs. Each MG is equipped with a DG and H2 system, and PVs are installed in both MG1 and MG3, while MG2 is outfitted with a WT. The distribution feeders are interconnected to every MG via the distribution switches, and the MGs are further interlinked through tie switches. The test system’s schematic diagram is presented in Figure 2. The effectiveness of the power lines is considered to be 98%. Additionally, the average hourly values of wind speed and solar radiation are provided in reference [36].
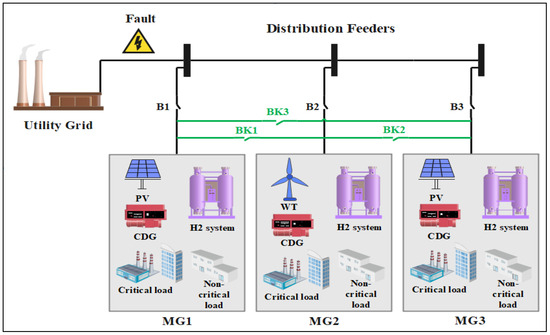
Figure 2.
Schematic of the test power grid, including NMGs and DFs.
The parameters utilized in the modeling of H2 systems are clearly delineated in Table 1 [29]. The DERs’ parameters and the hourly rates of the electricity market in both the upstream grid and MGs are sourced from [31]. Additionally, the maximum power output for each DG is purportedly limited to 10 MW for a period of three consecutive days [32].

Table 1.
Characteristics of H2 system parameters.
The hourly load demand of the distributed feeders and each MG is depicted in Figure 3. Through the process of the prioritization of load demands, three levels of demands are considered, where levels I and II are critical, and level III is considered non-critical. Table 2 presents the load-shedding cost of the different levels of demand.
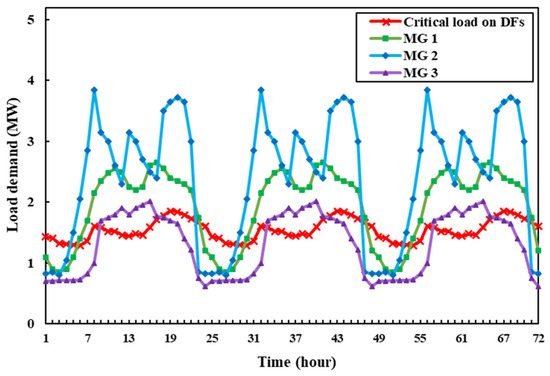
Figure 3.
Load profile of MGs and distribution feeders.

Table 2.
Load ratio and load shedding cost in each MG.
The simulations were executed by means of a personal computer equipped with an Intel Corei7 CPU of 1.8 GHz and 16 GB RAM. The proposed MILP framework was realized by employing the general algebraic modeling system (GAMS) and was resolved utilizing the CPLEX optimization solver.
The effectiveness of the proposed method has been assessed for two scenarios, including diverse magnitudes of disasters, and the advantages of R-OEMA over TEMA have been illustrated. In this article, the worst-case scenario of faults (disconnecting the system from the upstream network) is considered. The two examined scenarios are as follows:
- The first scenario: NMGs are disconnected from the utility grid for 16 h (39 to 54).
- The second scenario: NMGs are disconnected from the utility grid for 32 h (31 to 62).
In the subsequent sub-sections, the achievements realized for these aforementioned scenarios are itemized and compared in terms of their resilience and non-resilience models.
4.1. First Scenario
In the context of the TEMA, the DSO follows a conventional operational procedure. More specifically, the H2 systems, DGs, and shiftable loads are not pre-arranged in order to diminish the magnitude of power interruptions during the disaster. However, TEMA takes into consideration precautionary measures in order to augment the system’s resilience by implementing cost-effective strategies. In R-OEMA, all the introduced measures are used to increase the profit of the network. The depiction of the contribution provided by the utility grid, H2 systems, renewable units, and DGs in supplying the power demand of NMGs is presented in Figure 4 for TEMA and R-OEMA in Scenario 1. The commitment of DGs in TEMA is clearly demonstrated during periods of high energy demand, which are identified by a decrease in the purchase of energy from the utility grid during these time intervals. However, it must be noted that H2 systems fail to utilize the complete volume of their tanks, thereby resulting in inadequate electricity generation via the FC units. In the R-OEMA, the precise regulation of power consumption by electrolyzers and power generation by FC units and DGs using DRP is achieved through pre-scheduling techniques. Thus, it can be observed in Figure 4 that the supplied load attains its pinnacle during the period of power interruption.
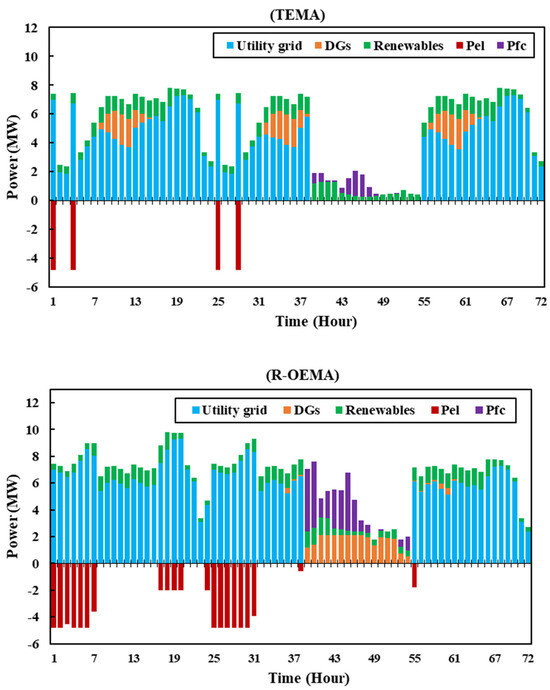
Figure 4.
Contribution provided by the utility grid, H2 systems, renewable units, and DGs in supplying NMG loads for TEMA and R-OEMA in Scenario 1.
Figure 5 illustrates the quantity of H2 gas present within the storage tanks both prior to and subsequent to the catastrophic event for both R-OEMA and TEMA systems. In the TEMA, it is observed that the generation of electric power by DGs and renewable units during peak hours effectively diminishes the prevalence of H2 systems in the grid. This is due to the reduction in the amount of electric power generated by FC units. It is possible that there is a lack of awareness regarding the potential for a power outage within the network in the hours following this. In the R-OEMA, it is of utmost importance that H2 systems carry out the filling of their tanks before the occurrence of any incident, as per the signal conveyed by the DSO. As a result, during the 38th hour, the storage tanks of all H2 systems attain their utmost capacity.
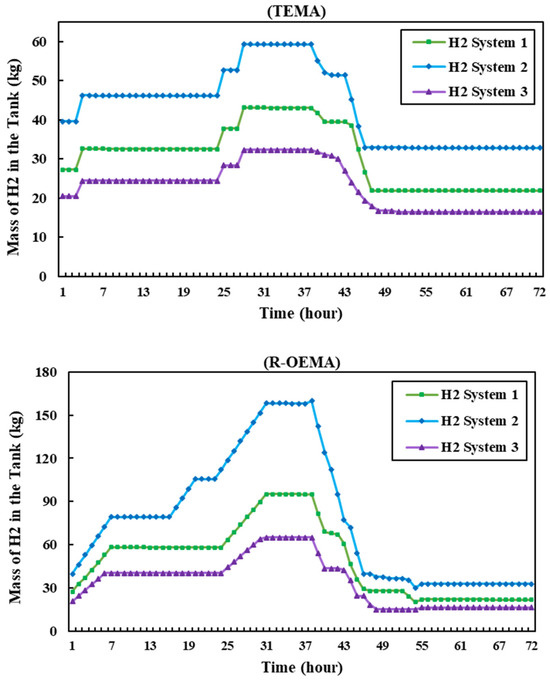
Figure 5.
Mass of H2 for TEMA and R-OEMA in Scenario 1.
In Table 3, a comparison is made between the load-controlled and load shedding of MGs and the restored load of distribution feeders for the TEMA and R-OEMA. This table illustrates that the TEMA is solely capable of supplying the internal loads of MGs without any support for the load restoration of the distribution feeders. On the other hand, the proposed R-OEMA restores 21.862 MW critical loads on the distribution feeders while the amount of load shedding is even lower than the TEMA. Hence, it is evident from this table that the proposed approach plays a crucial role in supporting the load of NMGs and emphasizes its significance in delivering energy services to distribution feeders during emergency circumstances.

Table 3.
Load restoration and shedding for TEMA and R-OEMA in Scenario 1.
4.2. Second Scenario
In the second scenario, the intensity of the natural disaster is significant, leading to a substantial period of grid disruption. The scheduling of energy from H2 systems, renewable units, DGs, and the proportion of energy provided by the utility power grid for both the TEMA and R-OEMA are shown in Figure 6. Given the 32 h power outage, the responsibility for powering the loads lies with the DGs, renewables, and H2 systems, making their energy management of the utmost importance. In the R-OEMA, it is evident that the full capacity of both DGs and FC units was utilized during hours 31 to 62 in order to provide power to the crucial loads of NMGs.
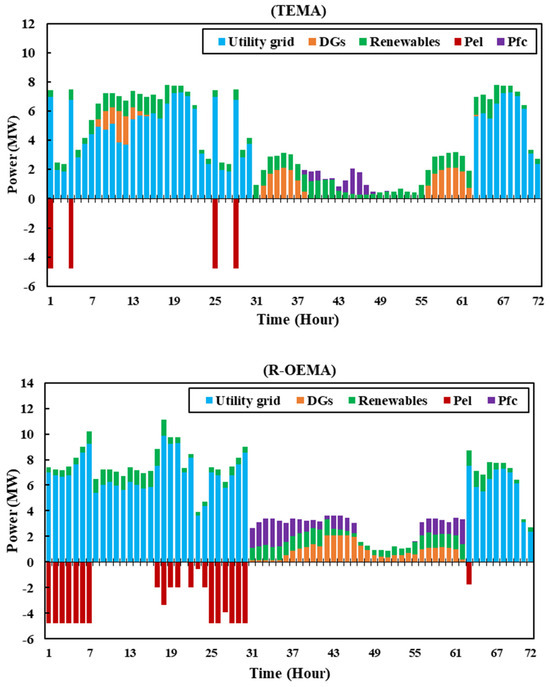
Figure 6.
Contribution provided by the utility grid, H2 systems, renewable units, and DGs in supplying NMG loads for TEMA and R-OEMA in Scenario 2.
The amount of H2 present in the tanks prior to and following the catastrophe for both energy management methodologies is graphically presented in Figure 7. In TEMA, due to the absence of the stored H2, the FC units are incapable of providing electrical loads during the disruption. The effect of the signal dispatched by DSO in R-OEMA is clearly apparent as, by the 30th hour, all the H2 system tanks were completely refilled.
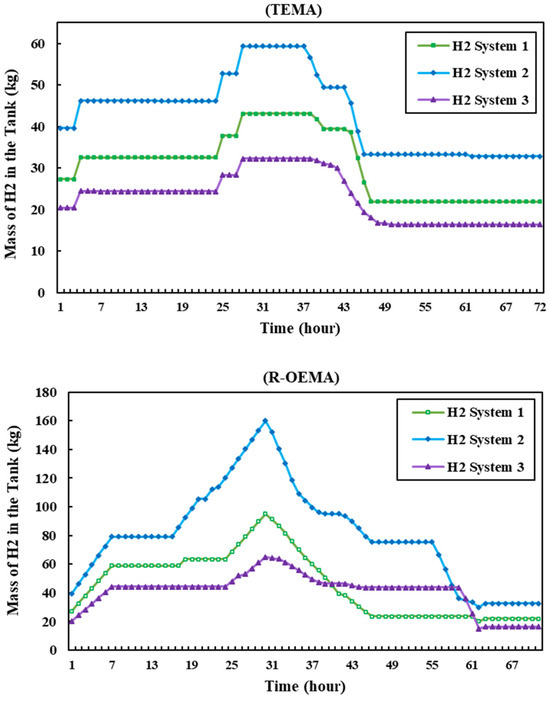
Figure 7.
Mass of H2 for TEMA and R-OEMA in Scenario 2.
In Table 4, a comparison is presented between the controlled load and load shedding in MGs, as well as the restoration of the load in distribution feeders for both TEMA and R-OEMA.

Table 4.
Load restoration and shedding for TEMA and R-OEMA in Scenario 2.
4.3. Discussion
The operational benefits and costs of the two energy management methods are fully detailed in Table 5. It is apparent that R-OEMA supplied a greater amount of loads in comparison to TEMA, resulting in an increased profit and decreased cost margin. In the R-OEMA, the costs involved in purchasing energy from the utility grid are also elevated as a consequence of H2 storage. The load restoration on distribution feeders is conducted solely in Scenario 1 for R-OEMA, as illustrated in Table 3 and Table 4. This approach yielded a considerable profit of USD 58,204.5, which outshone the other approaches. Furthermore, in TEMA, the DGs are activated during the peak load of the studied three-day timeframe, whereas, in R-OEMA, they are only activated during emergencies, resulting in a lower turning-on cost. Moreover, the suggested model managed to decrease the expenses related to load shedding by 78% and 63% in the first and second scenarios, respectively. It is important to note that the cost of load shedding holds a pivotal position in determining the value of the objective function. For example, given that this cost is the least possible amount in R-OEMA, the system in the first scenario remains profitable even in the occurrence of a natural disaster.

Table 5.
Economic components of the objective function in Scenario 1 and Scenario 2.
5. Conclusions
In this paper, a novel R-OEMA was introduced to address the pressing need for enhancing the resilience of NMGs in the face of extreme events. This paper presents the integration of H2 systems, DRPs, and controllable DGs in the R-OEMA, aiming to enhance the resilience and reliability of NMGs during disruptions. The numerical simulations of different scenarios compared to R-OEMA’s effectiveness with the TEMA reveal that the R-OEMA outperformed TEMA in supplying critical loads, minimizing load shedding, and maximizing economic benefits. The R-OEMA employed preventive scheduling techniques, signaling models, and coordinated energy strategies to optimize the power supply, H2 system operation, DG commitment, and load control. By proactively utilizing stored H2 energy, DGs, and DRPs, the R-OEMA ensured continuous energy supply to critical loads during grid disturbances.
The proposed approach addresses a critical need in modern power systems to enhance resilience through a comprehensive preventive strategy. Integrating multiple energy resources and management techniques, the R-OEMA went beyond reactive restoration measures, emphasizing proactive measures to ensure the sustained functionality of NMGs during disruptions. For example, the R-OEMA reduced 63% of load shedding and 56% of system operation costs in the more severe scenario of the disaster. Moreover, applying the proposed approach in the first scenario decreased the load outage to 78%, and the system even became profitable on the day of the disruption. This study serves as a significant step forward in addressing the challenges posed by extreme events, offering a valuable framework for bolstering the resilience of NMGs. Through its demonstrated effectiveness in both critical load restoration and economic performance, the R-OEMA holds promise as a practical tool for guiding the energy management decisions of NMGs.
In consideration of future work, this study acknowledges the necessity of evaluating the efficiency and economic practicality of existing resilience strategies for power systems. In the continuation of this research, a comparative analysis of different strategies will be undertaken, seeking to establish a compromise through cost–benefit analysis. This multi-objective approach, encompassing both operating and investment costs within existing financial budget constraints, contributes to the ongoing development of robust and economically viable resilience improvement strategies for NMGs.
Author Contributions
Conceptualization, M.S. and M.T.A.; methodology, M.S. and H.A.; software, M.S.; validation, M.S., M.T.A. and H.A.; formal analysis, M.S.; investigation, M.T.A.; resources, M.T.A. and G.S.; data curation, M.S.; writing—original draft preparation, M.S. and H.A.; writing—review and editing, H.A. and M.T.A.; visualization, M.S.; supervision, M.T.A. and G.S.; project administration, M.T.A.; funding acquisition, G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EPSRC-funded programs, grant number EP/W003597/1 and EP/T022949/1. The APC was funded by EPSRC.
Data Availability Statement
Data are contained within the article.
Acknowledgments
Hossein Ameli and Goran Strbac gratefully acknowledge the EPSRC-funded programs “High efficiency reversible solid oxide cells for the integration of offshore renewable energy using hydrogen” under grant number EP/W003597/1 as well as the “ZeroCarbon Emission Integrated Cooling, Heating and Power (ICHP) Networks” under award number EP/T022949/1.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Indices and Sets | |
| Index of MGs | |
| Index of load levels | |
| Index of time | |
| Set of MGs | |
| Set of load levels | |
| Set of time | |
| Parameters | |
| Load control cost of DG at level l | |
| start-up/shut-down/fuel cost of DG in MG i | |
| Load shedding cost at level l | |
| Profit of critical load restoration on distribution feeders at time t | |
| Market price to buy energy from the utility grid/sell energy to MGs at time t | |
| Maximum/minimum H2 generated by electrolyzer in MG i | |
| Maximum/minimum H2 consumed by FC in MG i | |
| Maximum/minimum mass of H2 in storage tank in MG i | |
| Initial/reservation mass of H2 in storage tank in MG i | |
| Maximum/minimum power generated of DG in MG i | |
| Total DG generation in MG i | |
| Maximum power generated for the renewable unit in MG i at time t | |
| Critical load demand on DFs at time t | |
| Load demand in MG i, at level l and time t | |
| Maximum load control in MG i, at level l and time t | |
| Ramp up/down rate of DG in MG i | |
| Minimum up/down time of DG in MG i | |
| FC/electrolyzer efficiency | |
| Transmission lines efficiency | |
| Converting factor for FC/electrolyzer units | |
| H2 storage dissipation rate | |
| Time intervals | |
| Variables | |
| Power generated of DG in MG i at time t | |
| Consumed power by electrolyzer in MG i at time t | |
| Load demand before DRP in MG i, at level l and time t | |
| Generated power by FC in MG i at time t | |
| H2 generated by electrolyzer in MG i at time t | |
| H2 consumed by FC in MG i at time t | |
| Surplus power in MG i at time t | |
| Surplus power considering line losses in MG i at time t | |
| Load control in MG i, at level l and time t | |
| Critical load restored on distribution feeders by MG i at time t | |
| Load shedding in MG i, at level l and time t | |
| Power imported from the utility grid | |
| Generated power of renewable unit in MG i at time t | |
| Mass of H2 in storage tank in MG i at time t | |
| Operating cost of MG i at time t | |
| Operating income of MG i at time t | |
| Operating income from selling power to loads of MG i at time t | |
| Operating income from critical load restoration on the distribution feeders | |
| Operating cost of load control in MG i, at level l and time t | |
| Operating cost of DG in MG i at time t | |
| Cost of load shedding in MG i at time t | |
| Purchasing electricity cost from the upstream grid in MG i at time t | |
| Objective function | |
| DG commitment status | |
| Electrolyzer and FC operation status | |
| Load control status | |
| Start-up/shut-down indicator of DG in MG i at time t | |
| Abbreviations | |
| DG | Controllable distributed generator |
| DER | Distributed energy resource |
| DRP | Demand response program |
| DSO | Distribution system operator |
| FC | Fuel cell |
| H2 | Hydrogen |
| MG | Microgrid |
| MILP | Mixed-integer linear programming |
| NMG | Networked microgrid |
| R-OEMA | Resilience-oriented energy management approach |
| TEMA | Typical energy management approach |
| PV | Photovoltaic |
| WT | Wind turbine |
References
- Zografopoulos, I.; Hatziargyriou, N.D.; Konstantinou, C. Distributed energy resources cybersecurity outlook: Vulnerabilities, attacks, impacts, and mitigations. arXiv 2022, arXiv:2205.11171. [Google Scholar] [CrossRef]
- Tabar, V.S.; Ghassemzadeh, S.; Tohidi, S. Increasing resiliency against information vulnerability of renewable resources in the operation of smart multi-area microgrid. Energy 2021, 220, 119776. [Google Scholar] [CrossRef]
- Younesi, A.; Shayeghi, H.; Wang, Z.; Siano, P.; Mehrizi-Sani, A.; Safari, A. Trends in modern power systems resilience: State-of-the-art review. Renew. Sustain. Energy Rev. 2022, 162, 112397. [Google Scholar] [CrossRef]
- Jalilpoor, K.; Oshnoei, A.; Mohammadi-Ivatloo, B.; Anvari-Moghaddam, A. Network hardening and optimal placement of microgrids to improve transmission system resilience: A two-stage linear program. Reliab. Eng. Syst. Saf. 2022, 224, 108536. [Google Scholar] [CrossRef]
- Dugan, J.; Mohagheghi, S.; Kroposki, B. Application of mobile energy storage for enhancing power grid resilience: A review. Energies 2021, 14, 6476. [Google Scholar] [CrossRef]
- Wang, C.; Ju, P.; Wu, F.; Pan, X.; Wang, Z. A systematic review on power system resilience from the perspective of generation, network, and load. Renew. Sustain. Energy Rev. 2022, 167, 112567. [Google Scholar] [CrossRef]
- Zhou, Z.-C.; Wu, Z.; Jin, T. Deep reinforcement learning framework for resilience enhancement of distribution systems under extreme weather events. Int. J. Electr. Power Energy Syst. 2021, 128, 106676. [Google Scholar] [CrossRef]
- Ameli, M.T.; Jalilpoor, K.; Amiri, M.M.; Azad, S. Reliability analysis and role of energy storage in resiliency of energy systems. In Energy Storage in Energy Markets; Elsevier: Amsterdam, The Netherlands, 2021; pp. 399–416. [Google Scholar]
- Hamidieh, M.; Ghassemi, M. Microgrids and resilience: A review. IEEE Access 2022, 10, 106059–106080. [Google Scholar] [CrossRef]
- Wang, Y.; Rousis, A.O.; Strbac, G. Resilience-driven optimal sizing and pre-positioning of mobile energy storage systems in decentralized networked microgrids. Appl. Energy 2022, 305, 117921. [Google Scholar] [CrossRef]
- Yan, L.; Sheikholeslami, M.; Gong, W.; Shahidehpour, M.; Li, Z. Architecture, control, and implementation of networked microgrids for future distribution systems. J. Mod. Power Syst. Clean Energy 2022, 10, 286–299. [Google Scholar] [CrossRef]
- Liu, G.; Ollis, T.B.; Ferrari, M.F.; Sundararajan, A.; Tomsovic, K. Robust Scheduling of Networked Microgrids for Economics and Resilience Improvement. Energies 2022, 15, 2249. [Google Scholar] [CrossRef]
- Huang, Y.; Rong, X.; Li, G.; Chen, C.; Bie, Z. Resilience assessment of active distribution systems considering microgrid formation based on grid-edge DERs. IET Gener. Transm. Distrib. 2023. [Google Scholar] [CrossRef]
- Jalilpoor, K.; Ameli, M.T.; Azad, S.; Sayadi, Z. Resilient energy management incorporating energy storage system and network reconfiguration: A framework of cyber-physical system. IET Gener. Transm. Distrib. 2023, 17, 1734–1749. [Google Scholar] [CrossRef]
- Cao, X.; Cao, T.; Xu, Z.; Zeng, B.; Gao, F.; Guan, X. Resilience constrained scheduling of mobile emergency resources in electricity-hydrogen distribution network. IEEE Trans. Sustain. Energy 2022, 14, 1269–1284. [Google Scholar] [CrossRef]
- Shahbazbegian, V.; Shafie-khah, M.; Laaksonen, H.; Strbac, G.; Ameli, H. Resilience-oriented operation of microgrids in the presence of power-to-hydrogen systems. Appl. Energy 2023, 348, 121429. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, J.; Song, Y.; Xu, Y. A Robust Microgrid Formation Strategy for Resilience Enhancement of Hydrogen Penetrated Active Distribution Networks. IEEE Trans. Power Syst. 2023. [Google Scholar] [CrossRef]
- Ameli, H.; Ameli, M.T.; Hosseinian, S.H. Multi-stage frequency control of a microgrid in the presence of renewable energy units. Electr. Power Compon. Syst. 2017, 45, 159–170. [Google Scholar] [CrossRef]
- Fetisov, V.; Davardoost, H.; Mogylevets, V. Technological Aspects of Methane–Hydrogen Mixture Transportation through Operating Gas Pipelines Considering Industrial and Fire Safety. Fire 2023, 6, 409. [Google Scholar] [CrossRef]
- Rahgozar, S.; Seyyedi, A.Z.G.; Siano, P. A resilience-oriented planning of energy hub by considering demand response program and energy storage systems. J. Energy Storage 2022, 52, 104841. [Google Scholar] [CrossRef]
- Gilani, M.A.; Dashti, R.; Ghasemi, M.; Amirioun, M.H.; Shafie-khah, M. A microgrid formation-based restoration model for resilient distribution systems using distributed energy resources and demand response programs. Sustain. Cities Soc. 2022, 83, 103975. [Google Scholar] [CrossRef]
- Azimian, M.; Amir, V.; Habibifar, R.; Golmohamadi, H. Probabilistic optimization of networked multi-carrier microgrids to enhance resilience leveraging demand response programs. Sustainability 2021, 13, 5792. [Google Scholar] [CrossRef]
- Liu, J.; Hu, H.; Yu, S.S.; Trinh, H. Virtual Power Plant with Renewable Energy Sources and Energy Storage Systems for Sustainable Power Grid-Formation, Control Techniques and Demand Response. Energies 2023, 16, 3705. [Google Scholar] [CrossRef]
- Le, T.S.; Nguyen, T.N.; Bui, D.-K.; Ngo, T.D. Optimal sizing of renewable energy storage: A techno-economic analysis of hydrogen, battery and hybrid systems considering degradation and seasonal storage. Appl. Energy 2023, 336, 120817. [Google Scholar] [CrossRef]
- Giovanniello, M.A.; Wu, X.-Y. Hybrid lithium-ion battery and hydrogen energy storage systems for a wind-supplied microgrid. Appl. Energy 2023, 345, 121311. [Google Scholar] [CrossRef]
- Groppi, D.; Garcia, D.A.; Basso, G.L.; Cumo, F.; De Santoli, L. Analysing economic and environmental sustainability related to the use of battery and hydrogen energy storages for increasing the energy independence of small islands. Energy Convers. Manag. 2018, 177, 64–76. [Google Scholar] [CrossRef]
- Hassan, Q.; Sameen, A.Z.; Salman, H.M.; Jaszczur, M.; Al-Jiboory, A.K. Hydrogen energy future: Advancements in storage technologies and implications for sustainability. J. Energy Storage 2023, 72, 108404. [Google Scholar] [CrossRef]
- Haggi, H.; Sun, W.; Fenton, J.M.; Brooker, P. Proactive rolling-horizon-based scheduling of hydrogen systems for resilient power grids. IEEE Trans. Ind. Appl. 2022, 58, 1737–1746. [Google Scholar] [CrossRef]
- Haggi, H.; Sun, W.; Fenton, J.M.; Brooker, P. Proactive scheduling of hydrogen systems for resilience enhancement of distribution networks. In Proceedings of the 2021 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 19–20 April 2021; pp. 1–5. [Google Scholar]
- Shin, H.K.; Ha, S.K. A Review on the Cost Analysis of Hydrogen Gas Storage Tanks for Fuel Cell Vehicles. Energies 2023, 16, 5233. [Google Scholar] [CrossRef]
- Xie, H.; Teng, X.; Xu, Y.; Wang, Y. Optimal energy storage sizing for networked microgrids considering reliability and resilience. IEEE Access 2019, 7, 86336–86348. [Google Scholar] [CrossRef]
- Jalilpoor, K.; Nikkhah, S.; Sepasian, M.S.; Aliabadi, M.G. Application of precautionary and corrective energy management strategies in improving networked microgrids resilience: A two-stage linear programming. Electr. Power Syst. Res. 2022, 204, 107704. [Google Scholar] [CrossRef]
- Williams, B.; Bishop, D.; Gallardo, P.; Chase, J.G. Demand Side Management in Industrial, Commercial, and Residential Sectors: A Review of Constraints and Considerations. Energies 2023, 16, 5155. [Google Scholar] [CrossRef]
- Giannelos, S.; Borozan, S.; Aunedi, M.; Zhang, X.; Ameli, H.; Pudjianto, D.; Konstantelos, I.; Strbac, G. Modelling Smart Grid Technologies in Optimisation Problems for Electricity Grids. Energies 2023, 16, 5088. [Google Scholar] [CrossRef]
- Davari, M.M.; Ameli, H.; Ameli, M.T.; Strbac, G. Impact of Local Emergency Demand Response Programs on the Operation of Electricity and Gas Systems. Energies 2022, 15, 2144. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Fazlhashemi, S.S.; Javadi, H.; Taghvaei, M. Multi-objective day-ahead energy management of a microgrid considering responsive loads and uncertainty of the electric vehicles. J. Clean. Prod. 2020, 267, 121562. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).